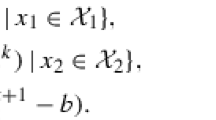First-Order Algorithms for Convex Optimization with Nonseparable Objective and Coupled Constraints

Abstract

In this paper, we consider a block-structured convex optimization model, where in the objective the block variables are nonseparable and they are further linearly coupled in the constraint. For the 2-block case, we propose a number of first-order algorithms to solve this model. First, the alternating direction method of multipliers (ADMM) is extended, assuming that it is easy to optimize the augmented Lagrangian function with one block of variables at each time while fixing the other block. We prove that iteration complexity bound holds under suitable conditions, where t is the number of iterations. If the subroutines of the ADMM cannot be implemented, then we propose new alternative algorithms to be called alternating proximal gradient method of multipliers, alternating gradient projection method of multipliers, and the hybrids thereof. Under suitable conditions, the iteration complexity bound is shown to hold for all the newly proposed algorithms. Finally, we extend the analysis for the ADMM to the general multi-block case.

1 Introduction

In this paper, we consider the following model:

$$\begin{aligned} \begin{array}{ll} \min &{} f(x,y)+h_1(x)+h_2(y) \\ \mathrm{s.t.}&{} Ax+By=b, \\ &{} x\in \mathcal {X}, y\in \mathcal {Y}, \end{array} \end{aligned}$$

(1.1)

where $x\in \mathbb R^{p}, y\in \mathbb R^{q}, A\in \mathbb R^{m\times p}, B\in \mathbb R^{m\times q}, b\in \mathbb R^{m}, \mathcal {X},\mathcal {Y}$ are closed convex sets, f is a smooth jointly convex function, and $h_1,h_2$ are (possibly nonsmooth) convex functions. The so-called augmented Lagrangian function for problem (1.1) is

$$\begin{aligned} \mathcal L_{\gamma }(x,y,\lambda )=f(x,y)+h_1(x)+h_2(y) -\lambda ^{\mathrm{T}}(Ax+By-b)+\frac{\gamma }{2}\Vert Ax+By-b\Vert ^2, \end{aligned}$$

where $\lambda$ is the multiplier.

Many emerging applications from various fields can be formulated as optimization problems in the form of (1.1). For instance, the constrained lasso (classo) problem is described as

$$\begin{aligned} \begin{array}{ll} \min \limits _{\beta } &{} \frac{1}{2}\Vert Y-X\beta \Vert _2^2+\tau \Vert \beta \Vert _1 \\ \mathrm{s.t.}&{} C\beta \leqslant b, \\ \end{array} \end{aligned}$$

(1.2)

where $X\in \mathbb R^{m\times p}, Y\in \mathbb R^m$ are the observed data, and $C\in \mathbb R^{n\times p}, b\in \mathbb R^n$ are predefined matrix and vector, respectively. The classo problem was first studied by James et al. [1] as a generalization of the lasso problem. By introducing additional linear constraints, [1] shows that many widely used statistical models can be expressed as special cases of (1.2), including the fused lasso, generalized lasso, monotone curve estimation, and so on. In fact, we can partition the variable $\beta$ into blocks as $\beta =(\beta _1^{\mathrm{T}},\cdots ,\beta _K^{\mathrm{T}})^{\mathrm{T}}$ where $\beta _i\in \mathbb R^{p_i}$ and partition other matrices and vectors in (1.2) correspondingly. Moreover, if we also introduce another slack variable z, then the classo problem can be cast in the form of (1.1) as follows:

$$\begin{aligned} \begin{array}{ll} \min \limits _{\beta } &{} \frac{1}{2}\left\| Y-\sum \limits _{i=1}^K X_i\beta _i\right\| _2^2+\tau \sum \limits _{i=1}^K\Vert \beta _i\Vert _1\\ \mathrm{s.t.}&{} \sum \limits _{i=1}^{K}C_i\beta _i+z=b, \,\, z\geqslant 0. \\ \end{array} \end{aligned}$$

(1.3)

The second example is the demand response (DR) control problem in the smart grid system [2–4]. Basically, it tries to minimize the cost incurred to a utility company which purchases electricity from the electricity market. To achieve this, the utility company controls the power consumption of some appliances of the users. Specifically, the problem can be formulated as

$$\begin{aligned} \begin{array}{ll} \min \limits _{x,p} &{} C_t\left( \left( \sum \limits _{i=1}^n\Psi _ix_i-p\right) ^+\right) +C_s\left( \left( p-\sum \limits _{i=1}^n\Psi _ix_i\right) ^+\right) +C_d(p)\\ \mathrm{s.t.}&{} x\geqslant 0, \,\,p\geqslant 0, \\ &{} x_i\in \mathcal {X}_i, \, i=1,2,...,n, \end{array} \end{aligned}$$

(1.4)

where $C_t(\cdot )$ and $C_s(\cdot )$ are the cost functions that measure the insufficient and the excessive power bids, respectively, and $C_d(\cdot )$ is the bidding cost function; see [3]. The variable $p\in \mathbb R^L$ represents the amount of electricity that the utility company bids from a day-ahead market, and $x_i$ is the control variable of the usage of the appliances of customer i, and $\Psi _i\in \mathbb R^{L\times n_i}$ is the matrix of the appliance load profile of customer i, thus $\Psi _i x_i$ is the total electricity consumption of customer i; see [5]. By introducing a new variable $z =\left( \sum \limits _{i=1}^n\Psi _ix_i-p\right) ^+$, the above problem can be rewritten in the form of (1.1) as

$$\begin{aligned} \begin{array}{ll} \min \limits _{x,p} &{} C_t(z)+C_s\left( z+p-\sum \limits _{i=1}^n\Psi _ix_i\right) +C_d(p)\\ \mathrm{s.t.}&{} z+p-\sum \limits _{i=1}^n\Psi _ix_i\geqslant 0,\\ &{} z\geqslant 0,\,\, x\geqslant 0, \,\,p\geqslant 0,x_i\in \mathcal {X}_i,\, i=1,2,...,n. \\ \end{array} \end{aligned}$$

(1.5)

In fact, optimization problems in the form of (1.1) have many other interesting applications in various areas including signal processing, image processing, machine learning, and statistical learning; see [6, 7] and the references therein.

In the case where no coupling term f(x, y) is in the objective, there is a well-known algorithm—Alternating Direction Method of Multipliers (ADMM)—established for solving (1.1). The iterative scheme of the ADMM runs as follows:

$$\begin{aligned} \left\{ \begin{array} {l}x^{k+1}=\arg \min _{x \in \mathcal {X}} \mathcal L_\gamma (x,y^k,\lambda ^k),\\ y^{k+1}=\arg \min _{y \in \mathcal {Y}} \mathcal L_\gamma (x^{k+1},y,\lambda ^k),\\ \lambda ^{k+1}=\lambda ^k-\gamma (Ax^{k+1}+By^{k+1}-b).\\ \end{array}\right. \end{aligned}$$

(1.6)

The ADMM is known to be a manifestation of the so-called operator splitting method which can be traced back to 1970s. Considerable amount of early studies on the ADMM can be found in, e.g., [8–11]. The method has gained new momentum in the recent years because of its first-order nature, and its potentials to compute distributively, which are important characteristics for solving very large scale problem instances. For an overview on its recent developments, one is referred to the surveys [12–15] and the references therein. The convergence properties of the ADMM are well known. In fact, its convergence follows from that of the so-called Douglas-Rachford operator splitting method; see [11, 16]. However, the rate of convergence was only established recently. In particular, [17, 18] show that the ADMM converges at the rate of O(1 / t), where t is the number of total iterations. Furthermore, with additional conditions on the objective function or the constraints, the ADMM can be shown to converge linearly; see [19–22]. One extension of the ADMM is to allow multi-block of variables. That extension of the ADMM turns out to perform very well for many instances encountered in practice, compared to other competing first-order alternatives. However, it may fail to converge in general. Specifically, in [23] by constructing a counterexample, the authors show that the ADMM may diverge with 3 blocks of variables. Therefore, it became clear that some additional conditions will be necessary in order to guarantee convergence, other than mere convexity. Indeed, under the strong convexity condition on some parts of the objective and certain assumptions on the constraint matrices, [24–27] show that an convergence rate can still be achieved for the multi-block ADMM. Another direction of study is to consider applications of ADMM to solve nonconvex problems. For instance, [28] shows that the ADMM can converge for some restricted class of nonconvex problems.

The current paper considers the ADMM in the presence of a coupling term f in the objective. Only a handful of papers in the literature considered this model so far, most noticeably [7] and [6]. In [7], the authors consider the general multi-block setting and they propose a upper-bound minimization method of multipliers (BSUMM) approach to cope with the nonseparability of the objective in (1.1); essentially, the nonseparable part of the augmented Lagrangian function is replaced by an upper bound. Under some error bound conditions and a diminishing dual stepsize assumption, the authors are able to show that the iterates produced by the BSUMM algorithm converge to the set of primal-dual optimal solutions. Very recently, Cui et al. [6] consider the problem (1.1) by introducing a quadratic upper bound function for the nonseparable part of augmented Lagrangian function; they show that their algorithm has an convergence rate.

Our contribution In this paper, we study the ADMM and its variants for (1.1). (Some adaptations of the ADMM are particularly relevant if there is a coupling term in the objective, as the minimization subroutines required by the ADMM may become difficult to implement; more discussions on this later.) Instead of using some upper bound approximation (a.k.a. majorization-minimization), we work with the original objective function. In this context, we may extend the ADMM approach directly to solve this more general formulation. It turns out that under the assumptions that the gradient of the coupling function $\nabla f$ is Lipschitz continuous and one of $h_1$ and $h_2$ is strongly convex, then an O(1 / t) convergence rate can still be assured. In some applications, it is difficult or impossible to implement the ADMM iteration, because the augmented Lagrangian function in (1.6) may be difficult to optimize even if the other block of variables and the Lagrangian multipliers are fixed. This motivates us to propose the Alternating Proximal Gradient Method of Multipliers (APGMM), which essentially iterates between proximal gradient methods of each block variables before the multiplier is updated. We show that the APGMM has a convergence rate of O(1 / t) if $\nabla f$ is Lipschitz continuous. If optimizing the augmented Lagrangian function for one block of variables is easy while optimizing the other block of variables is difficult, then a hybrid between ADMM and APGMM is a natural choice. We show in that case an O(1 / t) convergence rate remains valid. What if the gradient proximal subroutines are still too difficult to be implemented? One would then opt to compute the gradient projections. Hence, we propose the Alternating Gradient Projection Method of Multipliers (AGPMM), which replaces the proximal gradient steps in APGMM by the gradient projections. Fortunately, the same O(1 / t) iteration bound still holds for such simplifications as well as its ADMM hybrid version. At this stage, all the methods mentioned above are considered in the context of the 2-block model (1.1). In general however, they can be extended to the multi-block model with a coupling term. Similarly, under the Lipschitz continuity of $\nabla f$ and the assumptions in [27], an O(1 / t) iteration bound still holds for the multi-block model.

The rest of the paper is organized as follows. In Sect. 2, we present some preliminary results and notations. In Sects. 3 and 4, we introduce ADMM, APGMM, AGPMM, and their hybrids. The results on the rate of convergence of these algorithms are presented in the subsections of the same section, while the detailed proofs of the convergence results are presented in Appendix 1. In Sect. 5, we extend our analysis of the ADMM to a general setting with multiple (more than 2) blocks of variables. Finally, we conclude the paper in Sect. 6.

2 Preliminaries

Let us first introduce some notations that will be frequently used in the analysis later. The aggregated primal variables x, y and the primal-dual variables $x,y,\lambda$ are, respectively, denoted by u and w, and the primal-dual mapping F, namely

$$\begin{aligned} \begin{array}{lll} u :=\left( \begin{array}{c} x \\ y \\ \end{array} \right) ,&{} w :=\left( \begin{array}{c} x \\ y \\ \lambda \\ \end{array} \right) ,&{} F(w) :=\left( \begin{array}{c} -A^{\mathrm{T}}\lambda \\ -B^{\mathrm{T}}\lambda \\ Ax+By-b \\ \end{array} \right) , \end{array} \end{aligned}$$

(2.1)

and $h(u) :=f(x,y)+h_1(x)+h_2(y)$.

Throughout this paper, we assume f to be smooth and has a Lipschitz continuous gradient; i.e.,

Assumption 2.1

The coupling function f satisfies

$$\begin{aligned} \Vert \nabla f(u_2) - \nabla f(u_1) \Vert \leqslant L \Vert u_2 - u_1 \Vert , \;\forall \, u_1,u_2 \in \mathcal {X}\times \mathcal {Y}, \end{aligned}$$

(2.2)

where L is a Lipschitz constant for $\nabla f$.

For a function f satisfying Assumption 2.1, it is useful to note the following inequalities.

Lemma 2.2

Suppose that function f satisfies (2.2), then we have

$$\begin{aligned} f(u_2) \leqslant f(u_1) + \nabla f(u_1)^\mathrm{T}(u_2-u_1) + \frac{L}{2}\Vert u_2 - u_1\Vert ^2, \end{aligned}$$

(2.3)

for any $u_1,u_2$. In general, if f is also convex then

$$\begin{aligned} f(u_2) \leqslant f(u_1) + \nabla f(u_3)^\mathrm{T}(u_2-u_1) + \frac{L}{2}\Vert u_2 - u_3\Vert ^2, \end{aligned}$$

(2.4)

for any $u_1,u_2,u_3$.

Inequality (2.3) is well known; see [29]. Moreover, (2.4) can be found as Fact 2 in [30].

For convenience of the analysis, we introduce some matrix notations. Let

$$\begin{aligned} Q:= & {} \left( \begin{array}{lll} G &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \gamma B^{\mathrm{T}}B &{}\quad 0 \\ 0 &{}\quad -B &{}\quad \frac{1}{\gamma }I_m \\ \end{array} \right) , P:=\left( \begin{array}{lll} I_{p} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad I_{q} &{}\quad 0 \\ 0 &{}\quad -\gamma B &{}\quad I_m \\ \end{array} \right) ,\nonumber \\ M:= & {} \left( \begin{array}{lll} G &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \gamma B^{\mathrm{T}}B &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \frac{1}{\gamma }I_m \\ \end{array}\right) ; \end{aligned}$$

(2.5)

hence, $Q=MP$. Given a sequence $\{w^k\}$, we denote an associated auxiliary sequence to be

$$\begin{aligned} {\tilde{w}}^k :=\left( \begin{array}{c} {\tilde{x}}^k \\ {\tilde{y}}^k \\ {\tilde{\lambda }}^k \\ \end{array} \right) =\left( \begin{array}{c} x^{k+1} \\ y^{k+1} \\ \lambda ^k-\gamma (Ax^{k+1}+By^{k}-b) \\ \end{array} \right) . \end{aligned}$$

(2.6)

Based on (2.6) and (2.5), the relationship between the new sequence $\{{\tilde{w}}^k\}$ and the original $\{w^k\}$ is

$$\begin{aligned} w^{k+1}=w^k-P\left( w^k-{\tilde{w}}^k\right) . \end{aligned}$$

(2.7)

3 Alternating Direction Method of Multipliers

As we discussed earlier, the ADMM can be applied straightforwardly to solve (1.1), assuming that the augmented Lagrangian (with a proximal term) can be optimized for each block of variables, while the other variables are fixed. This gives rise to the following scheme:

In the above algorithm, G and H are two pre-specified positive semidefinite matrices. In fact, this algorithm is also known as the G-ADMM and proposed in [20] where no coupled objective function is involved. The main result concerning its convergence and iteration complexity is summarized in the following theorem, whose proof can be found in Appendix 1.

Theorem 3.1

Suppose that $\nabla f$ satisfies Lipschitz condition (2.2), and $h_2(y)$ is strongly convex with parameter $\sigma >0$, i.e.,

$$\begin{aligned} h_2(y)\geqslant h_2(z)+h'_2(z)^{\mathrm{{T}}}(y-z)+\frac{\sigma }{2}\Vert y-z\Vert ^2, \end{aligned}$$

(3.1)

where $h'_2(z)\in \partial h_2(z)$ is a subgradient of $h_2(z)$. Let $\{w^k\}$ be the sequence generated by the ADMM, and $G\succ 0, H \succ \left( L+\frac{L^2}{\sigma }\right) I_{q}$. Then the sequence $\{w^k\}$ generated by the ADMM converges to an optimal solution. Moreover, for any integer $n>0$ letting

$$\begin{aligned} {\bar{u}}_n:=\frac{1}{n}\sum \limits _{k=1}^{n} u^k, \end{aligned}$$

(3.2)

we have

(3.3)

where $\mathcal {X}^* \times \mathcal {Y}^*$ is the optimal solution set, $\mathrm{dist}(x,S)_M := \inf _{y\in S} \Vert x-y\Vert _M$, and $\hat{H}:=\gamma B^{\mathrm{{T}}}B+H$.

The following lemma shows the connection between different convergence measures.

Lemma 3.2

(Lemma 2.4 in [31]) Assume that $\rho >0$, and ${\bar{x}}\in X$ is an approximate solution of the problem $f^*:=\inf \{f(x): Ax-b=0, x\in X\}$ where f is convex, satisfying

$$\begin{aligned} f({\bar{x}})-f^*+\rho \Vert A{\bar{x}}-b\Vert \leqslant \varepsilon . \end{aligned}$$

(3.4)

Then, we have

$$\begin{aligned} \Vert A{\bar{x}}-b\Vert \leqslant \frac{\varepsilon }{\rho -\Vert \lambda ^*\Vert } \text{ and } f({\bar{x}})-f^* \leqslant \varepsilon , \end{aligned}$$

where $\lambda ^*$ is an optimal Lagrange multiplier associated with the constraint $Ax-b=0$ in the problem $\inf \{f(x): Ax-b=0, x\in X\}$, assuming $\Vert \lambda ^*\Vert < \rho$.

In other words, estimation (3.3) in Theorem 3.1 automatically establishes that

$$\begin{aligned} h({\bar{u}}_t)-h(u^*) \leqslant O(1/t) \text{ and } \Vert A{\bar{x}}_t+B{\bar{y}}_t-b\Vert \leqslant O(1/t). \end{aligned}$$

The same applies to all subsequent iteration complexity results presented in this paper.

4 Variants of the ADMM

In some applications, the augmented Lagrangian function may be difficult to minimize for some block of variables while fixing all others. For instance, consider the sparse logistic regression problem (see [32]) given by

$$\begin{aligned} \begin{array}{lll} \min \limits _{x,c}&l(x,c)+\beta \Vert x\Vert _1, \end{array} \end{aligned}$$

(4.1)

where $l(x,c)=\frac{1}{m}\sum \limits _{i=1}^m \text {log}(1+\exp (-b_i(a_i^{\mathrm{T}}x+c)))$ and $\{(a_i,b_i),\, i=1,\cdots ,m\}$ is a given training set with m samples $a_1,a_2,\cdots ,a_m$ and $b_i\in \{\pm 1\}, i=1,\cdots ,m$ as the binary class labels. To solve this problem within the ADMM framework, we can introduce a new variable z, and reformulate the problem as

$$\begin{aligned} \begin{array}{ll} \min \limits _{x,z,c} &{} l(x,c)+\beta \Vert z\Vert _1\\ \mathrm{s.t.}&{} x-z=0. \end{array} \end{aligned}$$

(4.2)

As in the ADMM, although the subroutine of solving z is easy, the subroutine of solving (x, c) can be difficult. In order to deal with those types of problems, we propose several variants of ADMM which incorporate different first-order methods into the ADMM framework.

4.1 Alternating Proximal Gradient Method of Multipliers

In this subsection, we consider an approach where we apply proximal gradient for each block of variables. The method bears some similarity to the Iterative Shrinkage-Thresholding Algorithm (ISTA) (cf. [33]), although we are dealing with multiple blocks of variables here. We shall call the new method APGMM, presented as follows:

The convergence property and iteration complexity are summarized in the following theorem, whose proof is in Appendix 1.

Theorem 4.1

Suppose that $\nabla f$ satisfies Lipschitz condition (2.2). Let $\{w^k\}$ be the sequence generated by the APGMM, and $G \succ LI_{p}$ and $H \succ LI_{q}$. Then, the sequence $\{w^k\}$ generated by the APGMM converges to an optimal solution. Moreover, with the same notations as before, it holds that $h({\bar{u}}_t)-h(u^*)+\rho \Vert A{\bar{x}}_t+B{\bar{y}}_t-b\Vert \leqslant O(1/t)$.

4.2 Alternating Gradient Projection Method of Multipliers

Implementing the proximal gradient step may be difficult for some applications. One may wonder if it is possible to further simplify the subroutines. It is therefore natural to consider the simple Gradient Projection method. Namely, for each block of variables, we simply sequentially compute the projection of the gradient of the augmented Lagrangian function before updating the multipliers. The method is depicted as follows:

where $[x]_{\mathcal {X}}$ denotes the projection of x onto $\mathcal {X}$, and $[y]_{\mathcal {Y}}$ denotes the projection of y onto $\mathcal {Y}$.

Note here that we used ‘PG’ as acronym for Proximal Gradient, and ‘GP’ as acronym for Gradient Projection. The acronyms are quite similar, and so some attention is needed not to confuse the two! Below we shall present the main convergence and the iteration complexity results for the above method; the proof of the theorem can be found in Appendix 1.

Theorem 4.2

Suppose that $\nabla f$ satisfies Lipschitz condition (2.2). Let ${w^k}$ be the sequence generated by the AGPMM, and $G:=\gamma A^{\mathrm{T}}A+\frac{1}{\alpha }I_{p}, H:=\frac{1}{\alpha }I_{q}-\gamma B^{\mathrm{T}}B$. Moreover, suppose that $\alpha$ is chosen to satisfy $H-2 L I_{q}\succ 0$ and $G-2 L I_{p}\succ 0$. Then, the sequence $\{w^k\}$ generated by the AGPMM converges to an optimal solution. Moreover, with the same notations as before, it holds that $h({\bar{u}}_t)-h(u^*)+\rho \Vert A{\bar{x}}_t+B{\bar{y}}_t-b\Vert \leqslant O(1/t)$.

4.3 Hybrids

Similar to the sparse logistic regression problem in (4.1), there are instances where one part of the block variables is easy to deal with, while the other part is difficult (e.g., the fused logistic regression in [34]). To take advantage of that situation, we propose the following two types of hybrid methods. The first one is to combine ADMM with Proximal Gradient (ADM-PG) in two blocks of variables:

The iteration complexity of the above method is as follows. The proof of the theorem can be found in Appendix 1.

Theorem 4.3

Suppose that $\nabla f$ satisfies Lipschitz condition (2.2). Let ${w^k}$ be the sequence generated by the ADM-PG, and $G\succ 0, H \succ LI_{q}$. Then, the sequence $\{w^k\}$ generated by the APGMM converges to an optimal solution. Moreover, with the same notations as before, it holds that $h({\bar{u}}_t)-h(u^*)+\rho \Vert A{\bar{x}}_t+B{\bar{y}}_t-b\Vert \leqslant O(1/t)$.

Another possible approach is to combine ADMM with Gradient Projection (ADM-GP), which works as follows:

The main convergence result is as follows, and the proof of the theorem can be found in Appendix 1.

Theorem 4.4

Let ${w^k}$ be the sequence generated by the ADM-GP, $G\succ 0$, and $H:=\frac{1}{\alpha }I_{q}-\gamma B^\mathrm{T}B$. Moreover, suppose that $\alpha$ is chosen to satisfy $H- L I_{q}\succ 0$. Then, the sequence $\{w^k\}$ generated by the ADM-GP converges to an optimal solution. Moreover, with the same notations as before, it holds that $h({\bar{u}}_t)-h(u^*)+\rho \Vert A{\bar{x}}_t+B{\bar{y}}_t-b\Vert \leqslant O(1/t)$.

Remark that for all the algorithms discussed above, besides showing the O(1 / t) rate of convergence in the ergodic sense, we have also shown the convergence of the iterates generated by the algorithms. Moreover, for all the variants of ADMM, we do not assume the strong convexity of the objective functions. Another point to note is that AGPMM and ADM-GP can be viewed as special cases of APGMM and ADM-PG, respectively. In fact, one can absorb the separable function $h_i$ into the nonseparable function f and choose matrices G and H appropriately in such a way that APGMM and ADM-PG actually become AGPMM and ADM-GP, respectively.

5 The General Multi-Block Model

Different variations of the ADMM have been a popular subject of study in the recent years. In particular, ADMM has been extended to solve general formulation with multiple blocks of variables; see [27] and the references therein for more information. In this section, we shall discuss the iteration complexity of the ADMM for multi-block optimization with a nonseparable objective function. In particular, the problem that we consider is as follows:

$$\begin{aligned} \begin{array}{ll} \min &{} f(x_1,x_2,\cdots ,x_n)+\sum \limits _{i=1}^{n}h_i(x_i) \\ \mathrm{s.t.}&{} A_1x_1+A_2x_2+\cdots +A_n x_n=b, \\ &{} x_i\in \mathcal {X}_i, i=1,2,\cdots ,n, \end{array}\end{aligned}$$

(5.1)

where $A_i\in \mathbb R^{m\times p_i}, b\in \mathbb R^{m}, \mathcal {X}_i\subset \mathbb R^{p_i}$ are closed convex sets, and $f,h_i$ $i=1,\cdots ,n$, are convex functions. Note that many important applications are in the form of (5.1), e.g., multi-stage stochastic programming. Accordingly, the ADMM algorithm for solving the problem (5.1) is

Here, $H_i, i=1,\cdots ,n$, are pre-specified positive semidefinite matrices, $\gamma$ is the augmented Lagrangian constant, and $\beta$ is the dual stepsize. In fact, this also generalizes the ADMM in the sense that a proximal term is included in the subproblem. Without the coupled objective function, this algorithm has also been analyzed in [35]. As we will show, an O(1 / t) convergence rate of the ADMM can still be achieved even for this general problem. In the following subsection, we sketch a convergence rate analysis highlighting the key components and steps. The details, however, will be omitted for succinctness.

Let us start with the assumptions.

Assumption 5.1

The functions $h_i, i=2,\cdots ,n$, are strongly convex with parameters $\sigma _i>0$:

$$\begin{aligned} h_i(y) \geqslant h_i(x)+(y-x)^\mathrm{T}h_i^{'}(x)+\frac{\sigma _i}{2}\Vert y-x\Vert ^2, \end{aligned}$$

where $h_i^{'}(x)\in \partial h_i(x)$ is in subdifferential of $h_i(x)$.

Assumption 5.2

The gradient of function $f(x_1,x_2,\cdots ,x_n)$ is Lipschitz continuous with parameter $L\geqslant 0$:

$$\begin{aligned} \Vert \nabla f(x_1^{\prime },x_2^{\prime },\cdots ,x_n^{\prime })-\nabla f(x_1,x_2,\cdots ,x_n)\Vert \leqslant L\Vert (x_1^{\prime }-x_1,x_2^{\prime }-x_2,\cdots ,x_n^{\prime }-x_n)\Vert \end{aligned}$$

for all $(x_1^{\prime },x_2^{\prime },\cdots ,x_n^{\prime }),(x_1,x_2,\cdots ,x_n)\in \mathcal {X}_1\times \cdots \times \mathcal {X}_{n}$.

In all the following propositions and theorems, we denote $w^k=(x_1^k,\cdots ,x_n^k,\lambda ^k)$ to be the iterates generated by ADMM, and $u=(x_1,\cdots ,x_n)$.

Proposition 5.3

Suppose that there are $\gamma , \beta$, and $\delta$ satisfying

$$\begin{aligned} \frac{n-1}{2}\max \limits _{2\leqslant i\leqslant n}\left\{ \lambda _{\max }(A_i^\mathrm{T}A_i)\right\} \gamma +\delta \leqslant \min \limits _{2\leqslant i\leqslant n}\sigma _i. \end{aligned}$$

Moreover, suppose that the matrices $H_i, i=2,\cdots ,n$, satisfy

$$\begin{aligned} H_i^s:=H_i-\left( L+\frac{(n-i+1)(n+i-2)L^2}{8\delta }\right) I_{p_i} \succeq 0\quad \forall \, 2\leqslant i\leqslant n. \end{aligned}$$

Let $(x_1^{k+1},\cdots ,x_n^{k+1},\lambda ^{k+1})\in \Omega$ be the sequence generated by ADMM. Then, for $u^*=(x_1^*,\cdots ,x_n^*)\in \Omega ^*$ and $\lambda \in \mathbb R^m$, the following inequality holds

The following proposition exhibits an important relationship between two consecutive iterates $w^k$ and $w^{k+1}$ from which the convergence readily follows.

Proposition 5.4

Let ${w^k}$ be the sequence generated by the ADMM, then

$$\begin{aligned}&\frac{\gamma }{2}\sum \limits _{i=2}^n\left( \Vert \mathcal {L}_i(w^*,w^k)\Vert ^2 -\Vert \mathcal {L}_i(w^*,w^{k+1})\Vert ^2\right) +\Vert w^*-w^{k}\Vert _{\hat{\mathcal {M}}}^2\\&\quad -\Vert w^*-w^{k+1}\Vert _{\hat{\mathcal {M}}}^2 -\Vert w^k-w^{k+1}\Vert _{\mathcal {H}}^2\geqslant 0, \end{aligned}$$

where $\mathcal {L}_i(w^*,w):=\sum \limits _{j=1}^{i-1}A_{j}x_{j}^* +\sum \limits _{j=i}^nA_jx_j-b, i=2,\cdots \,,n$, and

$$\begin{aligned} {\hat{\mathcal {M}}}=\mathrm{diag}\left( \frac{1}{2}H_1,\cdots ,\frac{1}{2}H_n, \frac{1}{\beta }I_m\right) , \mathcal {H}=\mathrm{diag}\left( \frac{1}{2}H_1,\frac{1}{2}H_2^s,\cdots , \frac{1}{2}H_n^s,\frac{\gamma -\beta }{2\beta ^2}I_m\right) . \end{aligned}$$

Propositions 5.3 and 5.4 lead to the following theorem:

Theorem 5.5

Under the assumptions of Propositions 5.3 and 5.4, and

$$\begin{aligned} \mathcal {H}=\mathrm{diag}\left( \frac{1}{2}H_1,\frac{1}{2}H_2^s, \cdots ,\frac{1}{2}H_n^s,\frac{\gamma -\beta }{2\beta ^2}I_m\right) \succ 0, \end{aligned}$$

we conclude that the sequence $\{w^k\}$ generated by the ADMM converges to an optimal solution. Moreover, for any integer $t>0$, let

$$\begin{aligned} {\bar{w}}_t:=\frac{1}{t}\sum \limits _{k=0}^{t-1}w^{k+1}, \end{aligned}$$

and for any $\rho >0$, we have

6 Concluding Remarks

In [36], the following model is considered

$$\begin{aligned} \min \,\,\, f(x) + g (y) + H(x,y), \end{aligned}$$

(6.1)

which can be regarded as (1.1) without constraints, and the so-called proximal alternating linearized minimization (PALM) algorithm is proposed. The main focus of [36] is to analyze the convergence of PALM for a class of nonconvex problems based on the Kurdyka–Łojasiewicz property. In that regard, it has an entirely different aim. We note, however, that PALM is similar to APGMM applied to (6.1) when there is no coupling linear constraint. On the linearized gradient part, one noticeable difference is that APGMM operates in a Jacobian fashion, while PALM is Gauss-Seidel. If the computation of gradient is costly, then the Jacobian style is cheaper to implement. As shown in [36], PALM can be extended to allow multiple blocks. Similarly, APGMM is also extendable to solve (5.1). The same is true for the other variations of the ADMM proposed in this paper. It remains a future research topic to establish the convergence rate of such types of first-order algorithms. Other future research topics include the study of first-order algorithms for (1.1) where the objective is nonconvex but satisfies the Kurdyka–Łojasiewicz property. It is also interesting to consider stochastic programming models studied in [31], but now allowing the objective function to be nonseparable.

Appendix: Proofs of the Convergence Theorems

1.1 Appendix 1: Proof of Theorem 3.1

We have $F(w)=\left( \begin{array}{lll} 0 &{}\quad 0 &{}\quad -A^\mathrm{T} \\ 0 &{}\quad 0 &{}\quad -B^\mathrm{T} \\ A &{}\quad B&{}\quad 0 \\ \end{array} \right) \left( \begin{array}{l} x \\ y \\ \lambda \\ \end{array} \right) - \left( \begin{array}{l} 0 \\ 0 \\ b \\ \end{array} \right) ,$ for any $w_1$ and $w_2$, and so

$$\begin{aligned} (w_1-w_2)^\mathrm{T}(F(w_1)-F(w_2))=0. \end{aligned}$$

Expanding on this identity, we have for any $w^0,w^1,\cdots ,w^{t-1}$ and ${\bar{w}} = \frac{1}{t} \sum \limits _{k=0}^{t-1} w^k$, that

$$\begin{aligned} ({\bar{w}}-w)^\mathrm{T}F({\bar{w}})=\frac{1}{t} \sum \limits _{k=0}^{t-1}({w}^k-w)^\mathrm{T}F({w}^k). \end{aligned}$$

(7.1)

We begin our analysis with the following property of the ADMM algorithm.

Proposition 7.1

Suppose $h_2$ is strongly convex with parameter $\sigma >0$. Let $\{{\tilde{w}}^k\}$ be defined by (2.6), and the matrices Q, M, P be given in (2.5). First of all, for any $w\in \Omega$, we have

(7.2)

Furthermore,

(7.3)

Proof

By the optimality condition of the two subproblems in ADMM, we have

$$\begin{aligned}&(x-x^{k+1})^\mathrm{T}\left[ \nabla _x f(x^{k+1},y^k)+h_1'(x^{k+1}) -A^\mathrm{T}(\lambda ^k-\gamma (Ax^{k+1}+By^{k}-b))\right. \\&\quad \left. +\,G(x^{k+1}-x^k)\right] \geqslant 0,\quad \forall x\in \mathcal {X}, \end{aligned}$$

where $h'_1(x^{k+1})\in \partial h_1(x^{k+1})$, and

$$\begin{aligned}&(y-y^{k+1})^{\mathrm{{T}}}\left[ \nabla _y f(x^{k+1},y^{k+1})+h'_2(y^{k+1})\right. \\&\quad \left. -B^{\mathrm{{T}}}(\lambda ^k-\gamma (Ax^{k+1}+By^{k+1}-b))+H(y^{k+1}-y^k)\right] \geqslant 0,\quad \forall y\in \mathcal {Y}\end{aligned}$$

where $h'_2(x^{k+1})\in \partial h_2(x^{k+1})$.

Note that ${\tilde{\lambda }}^k=\lambda ^k-\gamma (Ax^{k+1}+By^{k}-b)$. The above two inequalities can be rewritten as

$$\begin{aligned} (x-{\tilde{x}}^{k})^{\mathrm{T}}\left[ \nabla _x f({\tilde{x}}^k,y^k)+ h'_1({\tilde{x}}^k)-A^\mathrm{T}{\tilde{\lambda }}^k+G({\tilde{x}}^k -x^k)\right] \geqslant 0,\quad \forall x\in \mathcal {X}, \end{aligned}$$

(7.4)

and

$$\begin{aligned}&\quad (y-{\tilde{y}}^{k})^\mathrm{T}\left[ \nabla _y f({\tilde{x}}^k,{\tilde{y}}^k)+ h'_2({\tilde{y}}^k)-B^{\mathrm{T}}{\tilde{\lambda }}^k+\gamma B^\mathrm{T}B({\tilde{y}}^k-y^{k})+H({\tilde{y}}^k-y^k)\right] \nonumber \\&\geqslant 0,\quad \forall y\in \mathcal {Y}. \end{aligned}$$

(7.5)

Observe the following chain of inequalities

(7.6)

Since

$$\begin{aligned} (A{\tilde{x}}^k+B{\tilde{y}}^k-b)-B({\tilde{y}}^k-y^k) -\frac{1}{\gamma }(\lambda ^k-{\tilde{\lambda }}^k)=0, \end{aligned}$$

we have

(7.7)

By the strong convexity of the function $h_2(y)$, we have

$$\begin{aligned} (y-{\tilde{y}}^{k})^\mathrm{T}h'_2({\tilde{y}}^k)\leqslant h_2(y)-h_2({\tilde{y}}^k)-\frac{\sigma }{2}\Vert y-{\tilde{y}}^{k}\Vert ^2. \end{aligned}$$

(7.8)

Because of the convexity of $h_1(x)$ and combining (7.8), (7.7), (7.6), (7.5), and (7.4), we have

$$\begin{aligned}&{h(u)-h(\tilde{u}^k)+\left( \frac{L}{2} +\frac{L^2}{2\sigma }\right) \Vert y^k-{\tilde{y}}^k\Vert ^2+(y -{\tilde{y}}^k)^\mathrm{T}H({\tilde{y}}^k-y^k)}\nonumber \\&\quad + \left( \begin{array}{c} x-{\tilde{x}}^k\\ y-{\tilde{y}}^k\\ \lambda -{\tilde{\lambda }}^k\\ \end{array}\right) ^\mathrm{T}\left[ \left( \begin{array}{c} -A^\mathrm{T}{\tilde{\lambda }}^k\\ -B^\mathrm{T}{\tilde{\lambda }}^k\\ A{\tilde{x}}^k+B{\tilde{y}}^k-b\\ \end{array}\right) -\left( \begin{array}{c} G(x^k-{\tilde{x}}^k)\\ \gamma B^\mathrm{T}B(y^k-{\tilde{y}}^k)\\ -B(y^k-{\tilde{y}}^k)+\frac{1}{\gamma }(\lambda ^k-{\tilde{\lambda }}^k)\\ \end{array}\right) \right] \geqslant 0 \end{aligned}$$

for any $w\in \Omega$ and ${\tilde{w}}^k$.

By definition of Q, (7.2) of Proposition 7.1 follows. For (7.3), due to the similarity, we refer to Lemma 3.2 in [17] (noting the matrices Q, P, and M).

The following theorem exhibits an important relationship between two consecutive iterates $w^k$ and $w^{k+1}$ from which the convergence would follow.

Proposition 7.2

Let ${w^k}$ be the sequence generated by the ADMM, ${{\tilde{w}}^k}$ be defined as in (2.6) and H satisfies $H_s:=H-\left( L+\frac{L^2}{\sigma }\right) I_{q}\succeq 0$. Then the following holds:

$$\begin{aligned} \frac{1}{2}\left( \Vert w^*-w^{k}\Vert _{\hat{M}}^2-\Vert w^*-w^{k+1} \Vert _{\hat{M}}^2\right) -\frac{1}{2}\Vert w^k-{\tilde{w}}^k\Vert _{H_d}^2\geqslant 0, \end{aligned}$$

(7.9)

where

$$\begin{aligned} {\hat{H}}=\gamma B^\mathrm{T}B+H, \, \begin{array}{cc} {\hat{M}}=\left( \begin{array}{lll} G &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \hat{H} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \frac{1}{\gamma }I_m \\ \end{array} \right) \end{array} \text{ and } H_d=\left( \begin{array}{lll} G &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad H_s &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \frac{1}{\gamma }I_m \\ \end{array} \right) .\nonumber \\ \end{aligned}$$

(7.10)

Proof

It follows from Proposition 7.1 that

(7.11)

Note that $H_{s}:=H-(L+\frac{L^2}{\sigma })I_{q}\succeq 0$, we have the following

$$\begin{aligned}&\quad \left( \frac{L}{2}+\frac{L^2}{2\sigma }\right) \Vert y^k -{\tilde{y}}^k\Vert ^2+(y-{\tilde{y}}^k)^\mathrm{T}H({\tilde{y}}^k-y^k)\nonumber \\&=\left( \frac{L}{2}+\frac{L^2}{2\sigma }\right) \Vert y^k -{\tilde{y}}^k\Vert ^2+\frac{1}{2}\left( \Vert y-y^k\Vert _H^2-\Vert y -{\tilde{y}}^k\Vert _H^2-\Vert y^k-{\tilde{y}}^k\Vert _H^2\right) \nonumber \\&=\frac{1}{2}\left( \Vert y-y^k\Vert _H^2-\Vert y-{\tilde{y}}^k\Vert _H^2\right) -\frac{1}{2}\Vert y^k-{\tilde{y}}^k\Vert _{H_{s}}^2. \end{aligned}$$

(7.12)

Thus, combining (7.11) and (7.12), we have

(7.13)

By the definition of $\hat{M}$ and $H_d$ according to (7.10), it follows from (7.13) that

(7.14)

Letting $w=w^*$ in (7.14), we have

(7.15)

By the monotonicity of F and using the optimality of $w^*$, we have

$$\begin{aligned}&\quad \frac{1}{2}\left( \Vert w^*-w^{k}\Vert _{\hat{M}}^2-\Vert w^* -w^{k+1}\Vert _{\hat{M}}^2\right) -\frac{1}{2}\Vert w^k -{\tilde{w}}^k\Vert _{H_d}^2 \\&\geqslant h(\tilde{u}^k)-h(u^*)+({\tilde{w}}^k-w^*)^\mathrm{T}F({\tilde{w}}^k) \\&\geqslant h(\tilde{u}^k)-h(u^*)+({\tilde{w}}^k-w^*)^\mathrm{T}F(w^*) \\&\geqslant 0, \end{aligned}$$

which completes the proof.

1.2 Appendix 2: Proof of Theorem 3.1.

Proof

First, according to (7.9), it holds that $\{w^k\}$ is bounded and

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }\Vert w^k-{\tilde{w}}^k\Vert _{H_d}=0. \end{aligned}$$

(7.16)

Thus, those two sequences have the same cluster points: For any $w^{k_n}\rightarrow w^\infty$, by (7.16) we also have ${\tilde{w}}^{k_n}\rightarrow w^\infty$. Applying inequality (7.2) to $\{w^{k_n}\},\{{\tilde{w}}^{k_n}\}$ and taking the limit, it yields that

$$\begin{aligned} h(u)-h(u^\infty )+(w-w^\infty )^\mathrm{T} F(w^\infty )\geqslant 0. \end{aligned}$$

(7.17)

Consequently, the cluster point $w^\infty$ is an optimal solution. Since (7.9) is true for any optimal solution $w^*$, it also holds for $w^\infty$, and that implies ${w^k}$ will converge to $w^\infty$.

Recall (7.2) and (7.3) in Proposition 7.1, those would imply that

(7.18)

Furthermore, since $H-\left( L+\frac{L^2}{\sigma }\right) I_{q}\succeq 0$, we have

$$\begin{aligned}&\quad \left( \frac{L}{2}+\frac{L^2}{2\sigma }\right) \Vert y^k -{\tilde{y}}^k\Vert ^2+(y-{\tilde{y}}^k)^\mathrm{T}H({\tilde{y}}^k-y^k)\nonumber \\&= \left( \frac{L}{2}+\frac{L^2}{2\sigma }\right) \Vert y^k -{\tilde{y}}^k\Vert ^2+\frac{1}{2}\left( \Vert y-y^k\Vert _H^2-\Vert y -{\tilde{y}}^k\Vert _H^2-\Vert y^k-{\tilde{y}}^k\Vert _H^2\right) \nonumber \\&\leqslant \frac{1}{2}\left( \Vert y-y^k\Vert _H^2 -\Vert y-{\tilde{y}}^k\Vert _H^2\right) . \end{aligned}$$

(7.19)

Thus, combining (7.18) and (7.19) leads to

(7.20)

By the definition of M in (2.5) and denoting $\hat{H}=\gamma B^{\top }B+H$, (7.20) leads to

(7.21)

Before proceeding, let us introduce ${\bar{w}}_n:=\frac{1}{n}\sum \limits _{k=0}^{n-1} {\tilde{w}}^k$. Moreover, recall the definition of ${\bar{u}}_n$ in (3.2), we have

$$\begin{aligned} {\bar{u}}_n=\frac{1}{n}\sum \limits _{k=1}^{n} u^k =\frac{1}{n}\sum \limits _{k=0}^{n-1} \tilde{u}^k.\\ \end{aligned}$$

Now, summing the inequality (7.21) over $k=0,1,\cdots ,t-1$ yields

(7.22)

where the first inequality is due to the convexity of h and (7.1).

Note the above inequality is true for all $x\in \mathcal {X}, y\in \mathcal {Y}$, and $\lambda \in \mathbb R^m$, hence it is also true for any optimal solution $x^*, y^*$, and ${\mathcal {B}}_\rho =\{\lambda : \Vert \lambda \Vert \leqslant \rho \}$. As a result,

$$\begin{aligned}&\quad \,\, \sup \limits _{\lambda \in {\mathcal {B}}_\rho }\left\{ h({\bar{u}}_t)-h(u^*)+({\bar{w}}_t-w^*)^\mathrm{T}F({\bar{w}}_t)\right\} \nonumber \\&= \sup \limits _{\lambda \in {\mathcal {B}}_\rho }\left\{ h({\bar{u}}_t)-h(u^*)+({\bar{x}}_t-x^*)^\mathrm{T}(-A^{\mathrm{T}}\bar{\lambda }_t)\right. \nonumber \\&\quad \,\,\left. +\,({\bar{y}}_t-y^*)^{\mathrm{T}}(-B^{\mathrm{T}}\bar{\lambda }_t)+(\bar{\lambda }_t-\lambda )^\mathrm{T}(A{\bar{x}}_t+B{\bar{y}}_t-b)\right\} \nonumber \\&= \sup \limits _{\lambda \in {\mathcal {B}}_\rho }\left\{ h({\bar{u}}_t)-h(u^*)+\bar{\lambda }_t^\mathrm{T}(Ax^*+By^*-b)-\lambda ^{\mathrm{T}}(A{\bar{x}}_t+B{\bar{y}}_t-b)\right\} \nonumber \\&= \sup \limits _{\lambda \in {\mathcal {B}}_\rho }\left\{ h({\bar{u}}_t)-h(u^*)-\lambda ^\mathrm{T}(A{\bar{x}}_t+B{\bar{y}}_t-b)\right\} \nonumber \\&= h({\bar{u}}_t)-h(u^*)+\rho \Vert A{\bar{x}}_t+B{\bar{y}}_t-b\Vert , \end{aligned}$$

(7.23)

which, combined with (7.22), implies that

and so by optimizing over $(x^*,y^*)\in \mathcal {X}^* \times \mathcal {Y}^*$, we have

(7.24)

This completes the proof.

1.3 Appendix 3: Proof of Theorem 4.1

Similar to the analysis for ADMM, we need the following proposition in the analysis of APGMM.

Proposition 7.3

Let $\{{\tilde{w}}^k\}$ be defined by (2.6), and the matrices Q, M, P be given as in (2.5). For any $w\in \Omega$, we have

$$\begin{aligned}&\quad \,\,h(u)-h(\tilde{u}^k)+(w-{\tilde{w}}^k)^\mathrm{T} F({\tilde{w}}^k)\nonumber \\&\geqslant (w-{\tilde{w}}^k)^{\mathrm{T}} Q(w^k-{\tilde{w}}^k)-\left( \frac{L}{2}(\Vert x^k-{\tilde{x}}^k\Vert ^2+\Vert y^k-{\tilde{y}}^k\Vert ^2)+(y-{\tilde{y}}^k)^{\mathrm{T}}H({\tilde{y}}^k-y^k)\right) \qquad \qquad \quad \end{aligned}$$

(7.25)

$$\begin{aligned}&= \frac{1}{2}\left( \Vert w-w^{k+1}\Vert _{M}^2-\Vert w-w^k\Vert _{M}^2\right) +\frac{1}{2}\Vert x^k-{\tilde{x}}^k\Vert ^2_G+\frac{1}{2\gamma }\Vert \lambda ^k-{\tilde{\lambda }}^k\Vert ^2 \nonumber \\&\quad \,\, -\left( \frac{L}{2}\left( \Vert x^k-{\tilde{x}}^k\Vert ^2+\Vert y^k-{\tilde{y}}^k\Vert ^2\right) +(y-{\tilde{y}}^k)^{\mathrm{T}}H({\tilde{y}}^k-y^k)\right) . \end{aligned}$$

(7.26)

Proof

First, by the optimality condition of the two subproblems in APGMM, we have

$$\begin{aligned}&(x-x^{k+1})^{\mathrm{T}}\left[ \nabla _x f(x^{k},y^k)+h'_1(x^{k+1}) -A^{\mathrm{T}}(\lambda ^k-\gamma (Ax^{k+1}+By^{k}-b))\right. \\&\quad \left. +\,G(x^{k+1}-x^k)\right] \geqslant 0 , \quad \forall x\in \mathcal {X}\end{aligned}$$

and

$$\begin{aligned}&(y-y^{k+1})^{\mathrm{T}}\left[ \nabla _y f(x^{k},y^{k})+h'_2(y^{k+1}) -B^{\mathrm{T}}(\lambda ^k-\gamma (Ax^{k+1}+By^{k+1}-b))\right. \\&\quad \left. +\,H(y^{k+1}-y^k)\right] \geqslant 0,\, \quad \forall y\in \mathcal {Y}. \end{aligned}$$

Note that ${\tilde{\lambda }}^k=\lambda ^k-\gamma (Ax^{k+1}+By^{k}-b)$, and by the definition of ${\tilde{w}}^k$, the above two inequalities are equivalent to

$$\begin{aligned} (x-{\tilde{x}}^{k})^{\mathrm{T}}\left[ \nabla _x f(x^k,y^k)+ h'_1({\tilde{x}}^k)-A^{\mathrm{T}}{\tilde{\lambda }}^k +G({\tilde{x}}^k-x^k)\right] \geqslant 0,\quad \forall x\in \mathcal {X} \end{aligned}$$

(7.27)

and

$$\begin{aligned}&(y-{\tilde{y}}^{k})^{\mathrm{T}}\left[ \nabla _y f(x^k,y^k)+h'_2({\tilde{y}}^k)-B^{\mathrm{T}}{\tilde{\lambda }}^k+\gamma B^{\mathrm{T}}B({\tilde{y}}^k-y^{k})\right. \nonumber \\&\quad \left. +\,H({\tilde{y}}^k-y^k)\right] \geqslant 0,\quad \forall y\in \mathcal {Y}. \end{aligned}$$

(7.28)

Notice that

(7.29)

Besides, we also have

$$\begin{aligned} (A{\tilde{x}}^k+B{\tilde{y}}^k-b)-B({\tilde{y}}^k-y^k) -\frac{1}{\gamma }\left( \lambda ^k-{\tilde{\lambda }}^k\right) =0. \end{aligned}$$

Thus

$$\begin{aligned} (\lambda -{\tilde{\lambda }}^k)^{\mathrm{T}}(A{\tilde{x}}^k +B{\tilde{y}}^k-b)=(\lambda -{\tilde{\lambda }}^k)^{\mathrm{T}}\left( -B(y^k -{\tilde{y}}^k) +\frac{1}{\gamma }(\lambda ^k-{\tilde{\lambda }}^k)\right) .\nonumber \\ \end{aligned}$$

(7.30)

By the convexity of $h_1(x)$ and $h_2(y)$, combining (7.30), (7.29), (7.28), and (7.27), we have

$$\begin{aligned}&h(u)-h(\tilde{u}^k)+\frac{L}{2}\left( \Vert x^k-{\tilde{x}}^k\Vert ^2+\Vert y^k-{\tilde{y}}^k\Vert ^2\right) +(y-{\tilde{y}}^k)^{\mathrm{T}}H({\tilde{y}}^k-y^k) \\&\quad +\left( \begin{array}{c} x-{\tilde{x}}^k\\ y-{\tilde{y}}^k\\ \lambda -{\tilde{\lambda }}^k\\ \end{array}\right) ^{\mathrm{T}}\left[ \left( \begin{array}{c} -A^{\mathrm{T}}{\tilde{\lambda }}^k\\ -B^{\mathrm{T}}{\tilde{\lambda }}^k\\ A{\tilde{x}}^k+B{\tilde{y}}^k-b\\ \end{array}\right) -\left( \begin{array}{c} G(x^k-{\tilde{x}}^k)\\ \gamma B^{\mathrm{T}}B(y^k-{\tilde{y}}^k)\\ -B(y^k-{\tilde{y}}^k)+\frac{1}{\gamma }(\lambda ^k-{\tilde{\lambda }}^k)\\ \end{array}\right) \right] \geqslant 0 \end{aligned}$$

for any $w\in \Omega$ and ${\tilde{w}}^k$.

By definition of Q, we have shown (7.25) in Proposition 7.3. Equality (7.26) directly follows from (7.3) in Proposition 7.1.

With Proposition 7.3 in place, we can show Theorem 4.1 by exactly following the same steps as in the proof of Theorem 3.1, noting of course the altered assumptions on the matrices G and H. In the meanwhile, we also point out the following proposition which is similar to Proposition 7.2. Since most steps of the proofs are almost identical to that of the previous theorems, we omit the details for succinctness.

Proposition 7.4

Let ${w^k}$ be the sequence generated by the APGMM, ${{\tilde{w}}^k}$ be as defined in (2.6), and H and G are chosen so as to satisfy $H_s:=H-LI_{q}\succ 0$ and $G_s:=G-LI_{p}\succ 0$. Then the following holds : 

$$\begin{aligned} \frac{1}{2}\left( \Vert w^*-w^{k}\Vert _{\hat{M}}^2-\Vert w^*-w^{k +1}\Vert _{\hat{M}}^2\right) -\frac{1}{2}\Vert w^k-{\tilde{w}}^k\Vert _{H_d}^2\geqslant 0, \end{aligned}$$

where

$$\begin{aligned} \begin{array}{c@{\quad }c} \hat{M}=\left( \begin{array}{c@{\quad }c@{\quad }c} G &{} 0 &{} 0 \\ 0 &{} \hat{H} &{} 0 \\ 0 &{} 0 &{} \frac{1}{\gamma }I_m \\ \end{array} \right) , \end{array} H_d=\left( \begin{array}{c@{\quad }c@{\quad }c} G_s &{} 0 &{} 0 \\ 0 &{} H_s &{} 0 \\ 0 &{} 0 &{} \frac{1}{\gamma }I_m \\ \end{array} \right) \end{aligned}$$

and $\hat{H}=\gamma B^{\mathrm{T}}B+H$.

Theorem 4.1 follows from the above propositions.

1.4 Appendix 4: Proof of Theorem 4.2

Similar to the analysis for APGMM, we do not need any strong convexity here, but we do need to assume that the gradients $\nabla _x h_1(x)$ and $\nabla _y h_2(y)$ are Lipschitz continuous. Without loss of generality, we further assume that the Lipschitz constant is the same as $\nabla f(x,y)$ which is L, that is,

$$\begin{aligned}&\Vert \nabla _x h_1(x_2) - \nabla _x h_1(x_1)\Vert \leqslant L \Vert x_2-x_1\Vert , \;\forall \, x_1,x_2\in \mathcal {X},\nonumber \nonumber \\&\Vert \nabla _y h_2(y_2) - \nabla _y h_2(y_1)\Vert \leqslant L \Vert y_2-y_1\Vert , \;\forall \, y_1,y_2\in \mathcal {Y}. \end{aligned}$$

(7.31)

Proposition 7.5

Let $\{{\tilde{w}}^k\}$ be defined by (2.6), and the matrices Q, M, P be as given in (2.5), and $G:=\gamma A^{\mathrm{T}}A+\frac{1}{\alpha }I_{p}, H:=\frac{1}{\alpha }I_{q}-\gamma B^{\mathrm{T}}B\succeq 0$. First of all, for any $w\in \Omega$, we have

$$\begin{aligned}&\quad \,\, h(u)-h(\tilde{u}^k)+(w-{\tilde{w}}^k)^\mathrm{T} F({\tilde{w}}^k) \nonumber \\&\geqslant (w-{\tilde{w}}^k)^{\mathrm{T}} Q(w^k-{\tilde{w}}^k)-\left( L(\Vert x^k-{\tilde{x}}^k\Vert ^2+\Vert y^k-{\tilde{y}}^k\Vert ^2)\right. \nonumber \\&\quad \,\,\left. +\,(y-{\tilde{y}}^k)^{\mathrm{T}}H({\tilde{y}}^k-y^k)\right) \end{aligned}$$

(7.32)

$$\begin{aligned}&=\frac{1}{2}\left( \Vert w-w^{k+1}\Vert _{M}^2-\Vert w-w^k\Vert _{M}^2\right) +\frac{1}{2}\Vert x^k-{\tilde{x}}^k\Vert ^2_G+\frac{1}{2\gamma }\Vert \lambda ^k-{\tilde{\lambda }}^k\Vert ^2\nonumber \\&\quad \,\,-\left( L(\Vert x^k-{\tilde{x}}^k\Vert ^2+\Vert y^k-{\tilde{y}}^k\Vert ^2)+(y-{\tilde{y}}^k)^{\mathrm{T}}H({\tilde{y}}^k-y^k)\right) . \end{aligned}$$

(7.33)

Proof

First, by the optimality condition of the two subproblems in AGPMM, we have

$$\begin{aligned}&(x-x^{k+1})^{\mathrm{T}}\left[ x^{k+1}-x^k+\alpha \left( \nabla _x f(x^{k},y^{k})+\nabla _y h_1(x^{k})\right. \right. \\&\quad \left. \left. -A^{\mathrm{T}}(\lambda ^k-\gamma (Ax^{k}+By^{k}-b))\right) \right] \geqslant 0,\quad \forall x\in \mathcal {X}\end{aligned}$$

and

$$\begin{aligned}&(y-y^{k+1})^{\mathrm{T}}\left[ y^{k+1}-y^k+\alpha \left( \nabla _y f(x^{k},y^{k})+\nabla _y h_2(y^{k})\right. \right. \\&\quad \left. \left. -B^{\mathrm{T}}(\lambda ^k-\gamma (Ax^{k+1}+By^{k}-b))\right) \right] \geqslant 0,\quad \forall y\in \mathcal {Y}. \end{aligned}$$

Noting ${\tilde{\lambda }}^k=\lambda ^k-\gamma (Ax^{k+1}+By^{k}-b)$ and the definition of ${\tilde{w}}^k$, the above two inequalities are, respectively, equivalent to

$$\begin{aligned}&(x-{\tilde{x}}^{k})^{\mathrm{T}}\left[ \nabla _x f(x^k,y^k)+\nabla _x h_2(x^k)-A^{\mathrm{T}}{\tilde{\lambda }}^k+\gamma A^{\mathrm{T}}A({\tilde{x}}^k-x^k) \right. \nonumber \\&\quad \quad \left. +\frac{1}{\alpha }({\tilde{x}}^k-x^k)\right] \geqslant 0,\quad \forall x\in \mathcal {X}\end{aligned}$$

(7.34)

and

$$\begin{aligned}&\quad (y-{\tilde{y}}^{k})^{\mathrm{T}}\left[ \nabla _y f(x^k,y^k)+\nabla _y h_2(y^k)-B^{\mathrm{T}}{\tilde{\lambda }}^k+\frac{1}{\alpha }({\tilde{y}}^k -y^k)\right] \nonumber \\&\geqslant 0,\quad \forall y\in \mathcal {Y}. \end{aligned}$$

(7.35)

Similar to Proposition 7.3, we have

(7.36)

Moreover, by (2.4), we have

$$\begin{aligned}&(x-{\tilde{x}}^{k})^{\mathrm{T}}\nabla _x h_1(x^k)\leqslant h_1(x)-h_1({\tilde{x}}^k)+\frac{L}{2}\Vert x^k-{\tilde{x}}^k\Vert ^2, \nonumber \\&(y-{\tilde{y}}^{k})^{\mathrm{T}}\nabla _y h_2(y^k)\leqslant h_2(y)-h_2({\tilde{y}}^k)+\frac{L}{2}\Vert y^k-{\tilde{y}}^k\Vert ^2. \end{aligned}$$

(7.37)

Besides,

$$\begin{aligned} (A{\tilde{x}}^k+B{\tilde{y}}^k-b)-B({\tilde{y}}^k-y^k) -\frac{1}{\gamma }\left( \lambda ^k-{\tilde{\lambda }}^k\right) =0. \end{aligned}$$

Thus

$$\begin{aligned}&\quad (\lambda -{\tilde{\lambda }}^k)^{\mathrm{T}}(A{\tilde{x}}^k+B{\tilde{y}}^k-b)\nonumber \\&=(\lambda -{\tilde{\lambda }}^k)^{\mathrm{T}} \left( -B(y^k-{\tilde{y}}^k)+\frac{1}{\gamma }\left( \lambda ^k -{\tilde{\lambda }}^k\right) \right) . \end{aligned}$$

(7.38)

Combining (7.38), (7.37), (7.36), (7.35), and (7.34), and noticing that $G:=\gamma A^{\mathrm{T}}A+\frac{1}{\alpha }I_{p}, H:=\frac{1}{\alpha }I_{q}-\gamma B^{\mathrm{T}}B$, we have, for any $w\in \Omega$ and ${\tilde{w}}^k$, that

$$\begin{aligned}&h(u)-h(\tilde{u}^k)+L(\Vert x^k-{\tilde{x}}^k\Vert ^2+\Vert y^k -{\tilde{y}}^k\Vert ^2)+(y-{\tilde{y}}^k)^{\mathrm{T}}H({\tilde{y}}^k-y^k)\nonumber \\&+ \left( \begin{array}{c} x-{\tilde{x}}^k\\ y-{\tilde{y}}^k\\ \lambda -{\tilde{\lambda }}^k\\ \end{array}\right) ^{\mathrm{T}} \left\{ \left( \begin{array}{c} -A^{\mathrm{T}}{\tilde{\lambda }}^k\\ -B^{\mathrm{T}}{\tilde{\lambda }}^k\\ A{\tilde{x}}^k+B{\tilde{y}}^k-b\\ \end{array}\right) -\left( \begin{array}{c} G(x^k-{\tilde{x}}^k)\\ \gamma B^{\mathrm{T}}B(y^k-{\tilde{y}}^k)\\ -B(y^k-{\tilde{y}}^k)+\frac{1}{\gamma }(\lambda ^k -{\tilde{\lambda }}^k)\\ \end{array}\right) \right\} \geqslant 0. \end{aligned}$$

Using the definition of Q, (7.32) follows. In view of (7.3) in Proposition 7.1, equality (7.33) also readily follows.

With Proposition 7.5, similar as before, we can show Theorem 4.2 by following the same approach as in the proof of Theorem 3.1. We skip the details here for succinctness.

Proposition 7.6

Let ${w^k}$ be the sequence generated by the AGPMM, ${{\tilde{w}}^k}$ be defined in (2.6), and $G:=\gamma A^{\mathrm{T}}A+\frac{1}{\alpha }I_{p}, H:=\frac{1}{\alpha }I_{q}-\gamma B^{\mathrm{T}}B$. Suppose that $\alpha$ satisfies that $H_s:=H-2 L I_{q}\succ 0$ and $G_s:=G-2 L I_{p}\succ 0$. Then the following holds

$$\begin{aligned} \frac{1}{2}\left( \Vert w^*-w^{k}\Vert _{\hat{M}}^2-\Vert w^* -w^{k+1}\Vert _{\hat{M}}^2\right) -\frac{1}{2}\Vert w^k -{\tilde{w}}^k\Vert _{H_d}^2\geqslant 0, \end{aligned}$$

where

$$\begin{aligned} \begin{array}{l@{\quad }l} \hat{M}=\left( \begin{array}{l@{\quad }l@{\quad }l} G &{} 0 &{} 0 \\ 0 &{} \hat{H} &{} 0 \\ 0 &{} 0 &{} \frac{1}{\gamma }I_m \\ \end{array} \right) , \end{array} H_d=\left( \begin{array}{l@{\quad }l@{\quad }l} G_s &{} 0 &{} 0 \\ 0 &{} H_s &{} 0 \\ 0 &{} 0 &{} \frac{1}{\gamma }I_m \\ \end{array} \right) , \end{aligned}$$

and ${\hat{H}}=\gamma B^{\mathrm{T}}B+H$.

Theorem 4.2 now follows from the above propositions.

1.5 Appendix 5: Proofs of Theorems 4.3 and 4.4

Proposition 6.1

Let $\{{\tilde{w}}^k\}$ be defined by (2.6), and the matrices Q, M, P be given in (2.5). For any $w\in \Omega$, we have

(7.39)

Proof

First, by the optimality condition of the two subproblems in ADM-PG, we have

$$\begin{aligned}&(x-x^{k+1})^{\mathrm{T}}\left[ \nabla _x f(x^{k+1},y^k)+h'_1(x^{k+1}) -A^{\mathrm{T}}(\lambda ^k-\gamma (Ax^{k+1}+By^{k}-b))\right. \nonumber \\&\quad \left. +\,G(x^{k+1}-x^k)\right] \geqslant 0,\quad \forall x\in \mathcal {X}\end{aligned}$$

and

$$\begin{aligned}&(y-y^{k+1})^{\mathrm{T}}\left[ \nabla _y f(x^{k+1},y^{k}) +h'_2(y^{k+1})-B^{\mathrm{T}}(\lambda ^k-\gamma (Ax^{k+1}+By^{k+1}-b)) \right. \\&\quad \left. +\,H(y^{k+1}-y^k)\right] \geqslant 0,\quad \forall y\in \mathcal {Y}. \end{aligned}$$

Noting ${\tilde{\lambda }}^k=\lambda ^k-\gamma (Ax^{k+1}+By^{k}-b)$ and the definition of ${\tilde{w}}^k$, the above two inequalities are equivalent to

$$\begin{aligned}&\quad (x-{\tilde{x}}^{k})^{\mathrm{T}}\left[ \nabla _x f({\tilde{x}}^k,y^k)+\nabla _x h_1({\tilde{x}}^k)-A^{\mathrm{T}}{\tilde{\lambda }}^k+G({\tilde{x}}^k -x^k)\right] \nonumber \\&\geqslant 0,\quad \forall x\in \mathcal {X}\end{aligned}$$

(7.40)

and

$$\begin{aligned}&(y-{\tilde{y}}^{k})^{\mathrm{T}}\left[ \nabla _y f({\tilde{x}}^k,y^k) +g_2({\tilde{y}}^k)-B^{\mathrm{T}}{\tilde{\lambda }}^k+\gamma B^{\mathrm{T}}B({\tilde{y}}^k-y^{k})\right. \nonumber \\&\quad \left. +\,H({\tilde{y}}^k-y^k)\right] \geqslant 0,\quad \forall y\in \mathcal {Y}. \end{aligned}$$

(7.41)

Moreover,

$$\begin{aligned}&\quad \,(x-{\tilde{x}}^{k})^{\mathrm{T}}\nabla _x f({\tilde{x}}^k,y^k) +(y-{\tilde{y}}^{k})^{\mathrm{T}}\nabla _y f({\tilde{x}}^k,y^k)\nonumber \\&=(x-{\tilde{x}}^{k})^{\mathrm{T}}\nabla _x f({\tilde{x}}^k,y^k) +(y-y^{k})^{\mathrm{T}}\nabla _y f({\tilde{x}}^k,y^k)+(y^k -{\tilde{y}}^{k})^{\mathrm{T}}\nabla _y f({\tilde{x}}^k,y^k)\nonumber \\&\leqslant f(x,y)-f({\tilde{x}}^k,y^k)-({\tilde{y}}^{k} -y^k)^{\mathrm{T}}\nabla _y f({\tilde{x}}^k,y^k)\nonumber \\&\quad \,\,(\hbox {from}~(2.3))\nonumber \\&\leqslant f(x,y)-f({\tilde{x}}^k, {\tilde{y}}^k)+\frac{L}{2}\Vert y^k-{\tilde{y}}^k\Vert ^2. \end{aligned}$$

(7.42)

Besides,

$$\begin{aligned} (A{\tilde{x}}^k+B{\tilde{y}}^k-b)-B({\tilde{y}}^k-y^k) -\frac{1}{\gamma }\left( \lambda ^k-{\tilde{\lambda }}^k\right) =0, \end{aligned}$$

and so

$$\begin{aligned}&\quad (\lambda -{\tilde{\lambda }}^k)^{\mathrm{T}}(A{\tilde{x}}^k+B{\tilde{y}}^k-b)\nonumber \\&=(\lambda -{\tilde{\lambda }}^k)^{\mathrm{T}}\left( -B(y^k-{\tilde{y}}^k)+\frac{1}{\gamma } (\lambda ^k-{\tilde{\lambda }}^k)\right) . \end{aligned}$$

(7.43)

By the convexity of $h_1(x)$ and $h_2(y)$, combining (7.43), (7.42), (7.41), and (7.40), we have

$$\begin{aligned}&h(u)-h(\tilde{u}^k)+\frac{L}{2}\Vert y^k-{\tilde{y}}^k\Vert ^2 +(y-{\tilde{y}}^k)^{\mathrm{T}}H({\tilde{y}}^k-y^k) \\&+\left( \begin{array}{c} x-{\tilde{x}}^k\\ y-{\tilde{y}}^k\\ \lambda -{\tilde{\lambda }}^k\\ \end{array}\right) ^{\mathrm{T}}\left[ \left( \begin{array}{c} -A^{\mathrm{T}}{\tilde{\lambda }}^k\\ -B^{\mathrm{T}}{\tilde{\lambda }}^k\\ A{\tilde{x}}^k+B{\tilde{y}}^k-b\\ \end{array}\right) -\left( \begin{array}{c} G(x^k-{\tilde{x}}^k)\\ \gamma B^{\mathrm{T}}B(y^k-{\tilde{y}}^k)\\ -B(y^k-{\tilde{y}}^k)+\frac{1}{\gamma }(\lambda ^k-{\tilde{\lambda }}^k)\\ \end{array}\right) \right] \geqslant 0 \end{aligned}$$

for any $w\in \Omega$ and ${\tilde{w}}^k$.

By similar derivations as in the proofs for Proposition 7.5, (7.39) follows.

With Proposition 6.1 in place, we can prove Theorem 4.3 similarly as in the proof of Theorem 3.1. We skip the details here for succinctness.

For ADM-GP, we do not need strong convexity, but we do need to assume that the gradient $\nabla _y h_2(y)$ of $h_2(y)$ is Lipschitz continuous. Without loss of generality, we further assume that the Lipschitz constant of $\nabla _y h_2(y)$ is the same as $\nabla f(x,y)$ which is L:

$$\begin{aligned} \Vert \nabla _y h_2(y_2) - \nabla _y h_2(y_1)\Vert \leqslant L \Vert y_2-y_1\Vert , \;\forall \, y_1,y_2\in \mathcal {Y}. \end{aligned}$$

(7.44)

Proposition 6.2

Let $\{{\tilde{w}}^k\}$ be defined by (2.6), and the matrices Q, M, P be given in (2.5), and $H:=\frac{1}{\alpha }I_{q}-\gamma B^{\mathrm{T}}B\succeq 0$. For any $w\in \Omega$, we have

(7.45)

Proof

By the optimality condition of the two subproblems in ADMM, we have

$$\begin{aligned}&(x-x^{k+1})^{\mathrm{T}}\left[ \nabla _x f(x^{k+1},y^k)+h'_1(x^{k+1}) -A^{\mathrm{T}}(\lambda ^k-\gamma (Ax^{k+1}+By^{k}-b))\right. \\&\quad \left. +\,G(x^{k+1}-x^k)\right] \geqslant 0, \quad \quad \forall x\in \mathcal {X}\end{aligned}$$

and

$$\begin{aligned}&(y-y^{k+1})^{\mathrm{T}}\left[ y^{k+1}-y^k+\alpha \left( \nabla _y f(x^{k+1},y^{k})+\nabla _y h_2(y^{k})-B^{\mathrm{T}}(\lambda ^k-\gamma (Ax^{k+1} \right. \right. \\&\quad \left. \left. +\,By^{k}-b))\right) \right] \geqslant 0, \quad \quad \forall y\in \mathcal {Y}. \end{aligned}$$

Noting ${\tilde{\lambda }}^k=\lambda ^k-\gamma (Ax^{k+1}+By^{k}-b)$ and the definition of ${\tilde{w}}^k$, the above two inequalities are equivalent to

$$\begin{aligned} (x-{\tilde{x}}^{k})^{\mathrm{T}}\left[ \nabla _x f({\tilde{x}}^k,y^k)+h'_1({\tilde{x}}^k)-A^{\mathrm{T}}{\tilde{\lambda }}^k +G({\tilde{x}}^k-x^k)\right] \geqslant 0,\quad \forall x\in \mathcal {X} \end{aligned}$$

(7.46)

and

$$\begin{aligned}&\quad (y-{\tilde{y}}^{k})^{\mathrm{T}}\left[ \nabla _y f({\tilde{x}}^k,y^k)+\nabla _y h_2(y^k)-B^{\mathrm{T}}{\tilde{\lambda }}^k+\frac{1}{\alpha }({\tilde{y}}^k -y^k)\right] \nonumber \\&\geqslant 0,\quad \forall y\in \mathcal {Y}. \end{aligned}$$

(7.47)

Therefore,

$$\begin{aligned}&\quad \, (x-{\tilde{x}}^{k})^{\mathrm{T}}\nabla _x f({\tilde{x}}^k,y^k)+(y-{\tilde{y}}^{k})^{\mathrm{T}}\nabla _y f({\tilde{x}}^k,y^k)\nonumber \\&= (x-{\tilde{x}}^{k})^{\mathrm{T}}\nabla _x f({\tilde{x}}^k,y^k)+(y-y^{k})^{\mathrm{T}}\nabla _y f({\tilde{x}}^k,y^k)+(y^k-{\tilde{y}}^{k})^{\mathrm{T}}\nabla _y f({\tilde{x}}^k,y^k)\nonumber \\&\leqslant f(x,y)-f({\tilde{x}}^k,y^k)-({\tilde{y}}^{k}-y^k)^{\mathrm{T}} \nabla _y f({\tilde{x}}^k,y^k)\nonumber \\&\leqslant f(x,y)-f({\tilde{x}}^k,{\tilde{y}}^k)+\frac{L}{2}\Vert y^k -{\tilde{y}}^k\Vert ^2. \end{aligned}$$

(7.48)

Moreover, by (2.4), we have

$$\begin{aligned} (y-{\tilde{y}}^{k})^{\mathrm{T}}\nabla _y h_2(y^k)\leqslant h_2(y)-h_2({\tilde{y}}^k)+\frac{L}{2}\Vert y^k-{\tilde{y}}^k\Vert ^2. \end{aligned}$$

(7.49)

Since

$$\begin{aligned} A{\tilde{x}}^k+B{\tilde{y}}^k-b - B({\tilde{y}}^k-y^k)-\frac{1}{\gamma }\left( \lambda ^k-{\tilde{\lambda }}^k\right) =0, \end{aligned}$$

we have

$$\begin{aligned}&\quad \,(\lambda -{\tilde{\lambda }}^k)^{\mathrm{T}}(A{\tilde{x}}^k +B{\tilde{y}}^k-b)\nonumber \\&=(\lambda -{\tilde{\lambda }}^k)^{\mathrm{T}} \left( -B(y^k-{\tilde{y}}^k)+\frac{1}{\gamma } (\lambda ^k-{\tilde{\lambda }}^k)\right) . \end{aligned}$$

(7.50)

By the convexity of $h_1(x)$, combining (7.50), (7.49), (7.48), (7.47), (7.46), and noticing $H:=\frac{1}{\alpha }I_{q}-\gamma B^{\mathrm{T}}B$ for any $w\in \Omega$ and ${\tilde{w}}^k$, we have

$$\begin{aligned}&h(u)-h(\tilde{u}^k)+L\Vert y^k-{\tilde{y}}^k\Vert ^2+(y -{\tilde{y}}^k)^{\mathrm{T}}H({\tilde{y}}^k-y^k)\\&\quad +\left( \begin{array}{c} x-{\tilde{x}}^k\\ y-{\tilde{y}}^k\\ \lambda -{\tilde{\lambda }}^k\\ \end{array}\right) ^{\mathrm{T}}\left\{ \left( \begin{array}{c} -A^{\mathrm{T}}{\tilde{\lambda }}^k\\ -B^{\mathrm{T}}{\tilde{\lambda }}^k\\ A{\tilde{x}}^k+B{\tilde{y}}^k-b\\ \end{array}\right) -\left( \begin{array}{c} G(x^k-{\tilde{x}}^k)\\ \gamma B^{\mathrm{T}}B(y^k-{\tilde{y}}^k)\\ -B(y^k-{\tilde{y}}^k)+\frac{1}{\gamma }(\lambda ^k-{\tilde{\lambda }}^k)\\ \end{array}\right) \right\} \geqslant 0. \end{aligned}$$

As a result, (7.45) follows.

The proof of Theorem 4.4 follows a similar line of derivations as in the proof of Theorem 3.1, and so we omit the details here.