A Stabilized Crank–Nicolson Mixed Finite Volume Element Formulation for the Non-stationary Incompressible Boussinesq Equations

Abstract

At first, a semi-discrete Crank–Nicolson (CN) formulation with respect to time for the non-stationary incompressible Boussinesq equations is presented. Then, a fully discrete stabilized CN mixed finite volume element (SCNMFVE) formulation based on two local Gauss integrals and parameter-free is established directly from the semi-discrete CN formulation with respect to time. Next, the error estimates for the fully discrete SCNMFVE solutions are derived by means of the standard CN mixed finite element method. Finally, some numerical experiments are presented illustrating that the numerical errors are consistent with theoretical results, the computing load for the fully discrete SCNMFVE formulation are far fewer than that for the stabilized mixed finite volume element (SMFVE) formulation with the first time accuracy, and its accumulation of truncation errors in the computational process is far lesser than that of the SMFVE formulation with the first time accuracy. Thus, the advantage of the fully discrete SCNMFVE formulation for the non-stationary incompressible Boussinesq equations is shown sufficiently.

1 Introduction

The non-stationary incompressible Boussinesq equations are a nonlinear system of partial differential equations (PDEs) including the velocity vector field and the pressure field as well as the temperature field (see [17, 18, 23]), which are also known as the non-stationary conduction-convection problem and may be denoted by the following nonlinear system of PDEs.

Problem I Find ${{\varvec{u}}}=(u_1,u_2),\ p$, and $T$ such that, for $t_N>0$,

$$\begin{aligned} \left\{ \begin{array}{lll} {{\varvec{u}}}_t-\nu {\varDelta }{{\varvec{u}}}+({{\varvec{u}}}\cdot \nabla ){{\varvec{u}}}+\nabla p= T{{\varvec{j}}}, &{} (x,y,t){\in } {\varOmega }\times (0,t_N), \\ \displaystyle \nabla \cdot {{\varvec{u}}}=0, &{} (x,y,t){\in } {\varOmega }\times (0,t_N),\\ \displaystyle T_t- \gamma _0^{-1}{\varDelta }T+ ({{\varvec{u}}}\cdot \nabla ) T = 0, &{} (x,y,t){\in } {\varOmega }\times (0,t_N), \\ {{\varvec{u}}}(x,y,t)= {{\varvec{u}}}_0(x,y,t), \; T(x,y,t)=\varphi (x,y,t), &{} (x,y,t){\in }\partial {\varOmega }\times (0,t_N),\\ {{\varvec{u}}}(x,y,0)={{\varvec{u}}}^0(x,y), \; T(x,y,0)=\psi (x,y) &{} (x,y){\in } {\varOmega }, \end{array} \right. \end{aligned}$$

(1)

where ${\varOmega }\subset R^2$ is a bounded and connected domain, ${{\varvec{u}}}=(u_1,u_2)$ represents the fluid velocity vector, $p$ the pressure, $T$ the temperature, $t_N$ the total time, ${{\varvec{j}}}=(0,1)$ the unit vector, $\nu =\sqrt{{{Pr}/Re}}$, ${{Re}}$ the Reynolds number, ${Pr}$ the Prandtl number, $\gamma _0=\sqrt{{Re Pr}}$, and ${{\varvec{u}}}_0(x,y,t)$, ${{\varvec{u}}}^0(x,y)$, $\varphi (x,y,t)$ and $\psi (x,y)$ are given functions. For the sake of convenience and without loss of generality, we may as well suppose that ${{\varvec{u}}}_0(x,y,t)={{\varvec{u}}}^0(x,y)={\varvec{0}}$ and $\varphi (x,y,t)=0$ in the following theoretical analysis.

In general, there are no analytical solutions for Problem I due to it being a system of nonlinear PDEs including the velocity vector, the pressure, and the temperature. One has to rely on numerical solutions (see, e.g., [9, 17, 18]). However, most of the existing papers use either the finite element (FE) method or finite difference (FD) schemes as discretization tools.

Compared to FD and FE methods, the finite volume element (FVE) method (see [6, 13, 22]) is considered as most effective discretization approach for PDEs, since it is generally easier to implement and offer flexibility in handling complicated computing domains. More importantly, it can ensure local mass conservation and a highly desirable property in many applications. It is also referred to as a box method (see [3]) or a generalized difference method (see [14, 15]). It has been widely used to find numerical solutions of various types of PDEs, for example, second order elliptic equations, parabolic equations, Stokes equations, and the Navier–Stokes equations (see, e.g., [2–4, 6–8, 11, 13–15, 22, 24, 25]).

A fully discrete FVE formulation without any stabilization (see [16]) and a fully discrete stabilized mixed FVE (SMFVE) formulation (see [17]) for the non-stationary incompressible Boussinesq equations are proposed, but they do only have the first-order time accuracy. Thus, in order to obtain sufficiently time accuracy, they need to refine time steps so that moving forward steps and the accumulation of truncation errors in the computational process could greatly increase. Therefore, in this study, we improve the methods in [16, 17] and establish a fully discrete stabilized Crank–Nicolson (CN) mixed finite volume element (SCNMFVE) formulation based on two local Gauss integrals and parameter-free for the non-stationary incompressible Boussinesq equations. Thus, although the trial function spaces of velocity, temperature, and pressure of SCNMFVE formulation are the same as those in [16, 17], the SCNMFVE solutions improve one-order time accuracy more than those in [16, 17] such that it could alleviate the calculating load and the accumulation of truncation errors in the computational process. In addition, an optimizing reduced Petrov–Galerkin least squares mixed FE formulation based on residuals (see [19]) and a reduced mixed FE formulation without any stabilization (see [20]) have been established for the non-stationary incompressible Boussinesq equations, but they are completely different from the fully discrete SCNMFVE formulation since the FVE method is entirely different from and far more advantageous than the FE method as is mentioned above.

The remainder of this article is organized as follows. In Sect. 2, we first present the semi-discrete CN formulation with respect to time for the non-stationary incompressible Boussinesq equations. And then, we establish directly the fully discrete SCNMFVE formulation from the semi-discrete formulation with respect to time. Thus, we could avoid the discussion for semi–discrete SCNMFVE formulation with respect to spatial variables such that our theoretical analysis becomes simpler than the existing other methods (see, e.g., [11, 12, 17]). In Sect. 3, the error estimates for the fully discrete SCNMFVE solutions are derived by means of the standard CN mixed FE (CNMFE) method. In Sect. 4, some numerical experiments are presented illustrating that the numerical errors are consistent with theoretical results, the computing load of the fully discrete SCNMFVE formulation are far fewer than those of the SMFVE formulation with the first time accuracy, and the accumulation of its truncation errors in the computational process is far lesser than those of the SMFVE formulations with the first time accuracy. Thus, it is shown that the fully discrete SCNMFVE formulation for the non-stationary incompressible Boussinesq equations is far more advantageous than the SMFVE formulation in [17]. Section 5 provides main conclusions and some discussions.

2 Semi-Discrete Formulation About Time and Fully Discrete SCNMFVE Formulation

2.1 Semi-Discrete CN Formulation About Time

The Sobolev spaces along with their properties used in this context are standard (see [1]). Let $X=H^1_0({\varOmega })^2$, $M=L_0^2({\varOmega })=\left\{ q\in L^2({\varOmega });~\int _{{\varOmega }} q\hbox {d}x\hbox {d}y=0\right\}$, and $W=H^1_0({\varOmega })$. Thus, a mixed variational formulation for Problem I is written as follows.

Problem II Find $({\varvec{u}},p,T)\in H^1(0,t_N;X)^2\times L^2(0,t_N;M)\times H^1(0,t_N;W)$ such that, for almost all $t\in (0, t_N)$,

$$\begin{aligned} \left\{ \begin{array}{lll} ({\varvec{u}}_t,{\varvec{v}})+a({\varvec{u}},{\varvec{v}})+a_1({\varvec{u}},{\varvec{u}},{\varvec{v}})-b(p,{\varvec{v}})= (T{\varvec{j}},{\varvec{v}}), &{} \forall {\varvec{v}}\in X,\\ \displaystyle b(q,{\varvec{u}})=0,&{} \forall q\in M,\\ \displaystyle (T_t,\phi )+d(T,\phi )+ a_2({\varvec{u}},T,\phi ) = 0, &{} \forall \phi \in W,\\ {{\varvec{u}}}(x,y,0)={\varvec{0}}, T(x,y,0)=\psi (x,y), &{} (x,y){\in } {\varOmega }, \end{array}\right. \end{aligned}$$

(2)

where $(\cdot ,\cdot )$ denotes inner product in $L^2({\varOmega })^2$ or $L^2({\varOmega })$ and

$$\begin{aligned} \displaystyle a({\varvec{u}},{\varvec{v}})= & {} \nu \int _{\varOmega }\nabla {\varvec{u}}\cdot \nabla {\varvec{v}}\hbox {d}x\hbox {d}y, \forall {\varvec{u}},{\varvec{v}} \in X, \displaystyle b(q,{\varvec{v}})= \int _{{\varOmega }} q\ \hbox {div}{\varvec{v}}\hbox {d}x\hbox {d}y, \forall {\varvec{v}} \in X, q\in M, \\ \displaystyle a_1({\varvec{u}},{\varvec{v}},{\varvec{w}})= & {} \frac{1}{2}\int _{{\varOmega }}\left[ ({\varvec{u}}\nabla {\varvec{v}})\cdot {\varvec{w}}-({\varvec{u}}\nabla {\varvec{w}})\cdot {\varvec{v}}\right] \hbox {d}x\hbox {d}y, \ \ \forall {\varvec{u}},{\varvec{v}},{\varvec{w}}\in X, \\ \displaystyle a_2({\varvec{u}},T,\phi )= & {} \frac{1}{2}\int _{{\varOmega }}\left[ ({\varvec{u}}\cdot \nabla T)\phi -({\varvec{u}}\cdot \nabla \phi )T\right] \hbox {d}x\hbox {d}y, \ \ \forall {\varvec{u}}\in X, \forall T,\phi \in W, \\ \displaystyle d(T,\phi )= & {} \gamma _0^{-1}\int _{{\varOmega }}\nabla T\cdot \nabla \phi \hbox {d}x\hbox {d}y, \ \forall T,\phi \in W. \end{aligned}$$

The above trilinear forms $a_1(\cdot ,\cdot ,\cdot )$ and $a_2(\cdot ,\cdot ,\cdot )$ hold the following properties (see [16, 18]):

$$\begin{aligned} a_1({\varvec{u}},{\varvec{v}},{\varvec{w}})= & {} -a_1({\varvec{u}},{\varvec{w}},{\varvec{v}}),\ \ a_1({\varvec{u}},{\varvec{v}},{\varvec{v}})=0, \ \ \ \forall {\varvec{u}},{\varvec{v}}, {\varvec{w}}\in X, \end{aligned}$$

(3)

$$\begin{aligned} \displaystyle a_2({\varvec{u}},T,\phi )= & {} -a_2({\varvec{u}},\phi ,T),\ \ a_2({\varvec{u}},\phi ,\phi )=0, \ \ \ \forall {\varvec{u}}\in X, \ \forall T,\phi \in W. \end{aligned}$$

(4)

The above bilinear forms $a(\cdot ,\cdot )$, $d(\cdot ,\cdot )$, and $b(\cdot ,\cdot )$ have the following properties (also see [16, 18]):

$$\begin{aligned} a({\varvec{v}},{\varvec{v}})\ge & {} \nu |{\varvec{v}} |_1^2, \ \ \forall {\varvec{v}}\in X; \ |a({\varvec{u}},{\varvec{v}})|\le \nu |{\varvec{u}} |_1 |{\varvec{v}} |_1, \ \ \forall {\varvec{u}}, \ {\varvec{v}}\in X, \end{aligned}$$

(5)

$$\begin{aligned} d(\phi ,\phi )\ge & {} \gamma _0^{-1}|\phi |_1^2, \ \ \forall \phi \in W; \ |d(T,\phi )|\le \gamma _0^{-1}|T|_1 |\phi |_1, \ \ \forall T, \ \phi \in W, \end{aligned}$$

(6)

$$\begin{aligned} \sup \limits _{{\varvec{v}}\in X}\frac{b(q,{\varvec{v}})}{ |{\varvec{v}} |_1}\ge & {} \beta \Vert q\Vert _0,\ \ \ \forall q\in M, \end{aligned}$$

(7)

where $\beta$ is a constant. Define

$$\begin{aligned} N_0 = \sup \limits _{{\varvec{u}},{\varvec{v}},{\varvec{w}}\in X}\frac{a_1({\varvec{u}},{\varvec{v}},{\varvec{w}})}{|{\varvec{u}}|_1\cdot |{\varvec{v}}|_1\cdot |{\varvec{w}}|_1}, \quad \tilde{N}_0 = \sup \limits _{{\varvec{u}}\in X,(T,\phi )\in W\times W}\frac{a_2({\varvec{u}},T,\phi )}{|{\varvec{u}}|_1\cdot |T|_1\cdot |\phi |_1}. \end{aligned}$$

(8)

The following result is classical (see Theorem 1.4.1 in [23] or Theorem 5.2 in [18]).

Theorem 2.1

If $\psi \in L^2({\varOmega })$, then the problem II has at least a solution which, in addition, is unique provided that $\Vert \psi \Vert _0^2\le 2\nu ^2t_N/(2 N_0 t_N^{-1}\exp (t_N)+\nu \gamma _0\tilde{N}_0^2)$, and there are the following prior estimates

$$\begin{aligned} \displaystyle \Vert {\varvec{u}}\Vert _0^2+\nu \Vert \nabla {\varvec{u}}\Vert _{L^2(L^2)}^2\le t_N^2 \Vert \psi \Vert _0^2\exp (t_N), \quad \displaystyle \Vert T\Vert _0^2+\gamma _0^{-1}\Vert \nabla T\Vert _{L^2(L^2)}^2\le \Vert \psi \Vert _0^2. \end{aligned}$$

Let $N$ be the positive integer, $k=t_N/N$ denote the time step increment, $t_n=nk$ ($0\le n\le N$), and $({\varvec{u}}^n, p^n,T^n)$ be the semi–discrete approximation of $({\varvec{u}}(t), p, T)$ at $t_n=n k (n=0,1, \ldots , N)$ about time, $\bar{{\varvec{u}}}^n=({\varvec{u}}^n+{\varvec{u}}^{n-1})/2$, and ${\bar{T}}^n=(T^n+T^{n-1})/2$. If the differential quotients ${\varvec{u}}_{t}$ and $T_{t}$ in Problem II at time $t=t_n$ are, respectively, approximated by means of the backward difference quotients $\bar{\partial }_t{\varvec{u}}^n=({\varvec{u}}^n-{\varvec{u}}^{n-1})/k$ and $\bar{\partial }_tT^n=(T^n-T^{n-1})/k$. Thus, the semi–discrete CN scheme for Problem II with respect to time is written as follows.

Problem III Find $({\varvec{u}}^n,p^n,T^n)\in X\times M\times W$ $(1\le n\le N)$ such that

$$\begin{aligned} \left\{ \begin{array}{lll} ({\varvec{u}}^n,{\varvec{v}})+k a(\bar{{\varvec{u}}}^n,{\varvec{v}})+ka_1(\bar{{\varvec{u}}}^{n},\bar{{\varvec{u}}}^n,{\varvec{v}})-kb(p^n,{\varvec{v}})\\ \displaystyle \quad =k ({\bar{T}}^n{\varvec{j}},{\varvec{v}})+({\varvec{u}}^{n-1},{\varvec{v}}), &{}\forall {\varvec{v}}\in X, \\ b(q,{\varvec{u}}^n) =0, &{} \forall q\in M, \\ \displaystyle (T^n,\phi )+kd({\bar{T}}^n,\phi )+ ka_2(\bar{{\varvec{u}}}^{n},{\bar{T}}^n,\phi ) = (T^{n-1},\phi ), &{}\forall \phi \in W, \\ {\varvec{u}}^0=0, \quad T^0=\psi (x,y), &{}(x,y)\in {\varOmega }. \end{array}\right. \end{aligned}$$

(9)

There are the following results for Problem III.

Theorem 2.2

Under the assumptions of Theorem 2.1, Problem III has a unique series of solutions $({\varvec{u}}^n,p^n,$ $T^n)\in X\times M\times W (n=1,2, \ldots , N)$ such that

$$\begin{aligned}&\displaystyle \Vert {\varvec{u}}^n\Vert _0^2+k\sqrt{\nu }\Vert \nabla {\varvec{u}}^n\Vert _0\displaystyle \le \sqrt{{\nu ^{-1}\gamma _0}}\Vert \psi \Vert _0, \end{aligned}$$

(10)

$$\begin{aligned}&\displaystyle \displaystyle \Vert T^n\Vert _0+k{\gamma _0^{-1/2}}\Vert \nabla T^n\Vert _0\displaystyle \le \max \{2, \sqrt{2}k{\gamma _0^{-1/2}}\}\Vert \psi \Vert _1,\quad k\Vert p^n\Vert _0\le C\Vert \psi \Vert _1, \end{aligned}$$

(11)

where $C$ used next is a constant independent of $k$, but dependent on $\psi$ and known data. And if $({{\varvec{u}}},p, T)\in [H_0^1({\varOmega })\cap H^{2}({\varOmega })]^2\times [H^{1 }({\varOmega })\cap M]\times [H_0^1({\varOmega })\cap H^{2}({\varOmega })]$ is the exact solution for the problem I, we have the following error estimates

$$\begin{aligned}&\displaystyle \Vert {\varvec{u}}(t_n)-{\varvec{u}}^n\Vert _0+k[\Vert \nabla ({\varvec{u}}(t_n)-{\varvec{u}}^n)\Vert _0+\Vert p(t_n)-p^n\Vert _0]\le C k^2, \end{aligned}$$

(12)

$$\begin{aligned}&\displaystyle \Vert T(t_n)-T^n\Vert _0+ k\Vert \nabla (T(t_n)-T^n)\Vert _0 \le C k^2, \ 1\le n\le N. \end{aligned}$$

(13)

Proof

First, we prove that Problem III has a unique series of solutions. For $1\le n\le N$, we consider the following linearized auxiliary problem:

$$\begin{aligned} \left\{ \begin{array}{lll} \left( {\varvec{u}}_m^n,{\varvec{v}}\right) +k a\left( \bar{{\varvec{u}}}_m^n,{\varvec{v}}\right) +ka_1\left( \bar{{\varvec{u}}}_{m-1}^{n},\bar{{\varvec{u}}}_m^n,{\varvec{v}}\right) -kb\left( p_m^n,{\varvec{v}}\right) \\ \displaystyle \quad =k \left( {\bar{T}}_m^n{\varvec{j}},{\varvec{v}}\right) +\left( {\varvec{u}}_m^{n-1},{\varvec{v}}\right) , &{}\forall {\varvec{v}}\in X, m=1,2,\ldots , \\ b\left( q,{\varvec{u}}_m^n\right) =0, &{}\forall q\in M, m=1,2,\ldots ,\\ \displaystyle \left( T_m^n,\phi \right) +kd\left( {\bar{T}}_m^n,\phi \right) + ka_2\left( \bar{{\varvec{u}}}_{m-1}^{n},{\bar{T}}_m^n,\phi \right) = \left( T_m^{n-1},\phi \right) , &{}\forall \phi \in W, m=1,2,\ldots ,\\ {\varvec{u}}_m^0=0, m=0,1,\ldots ,\quad T_m^0=\psi (x,y), m=1,2,\ldots , &{} (x,y)\in {\varOmega }. \end{array}\right. \end{aligned}$$

(14)

By taking ${\varvec{v}}={\varvec{u}}_m^n+{\varvec{u}}_m^{n-1}$, $q=p_m^n$, and $\phi =T_m^n+T_m^{n-1}$ in the system of equations (14), and by using (3) and (4), Hölder inequality, and Cauchy inequality, we obtain

$$\begin{aligned} \displaystyle \displaystyle 2\left( \Vert {\varvec{u}}_m^n\Vert _0^2-\Vert {\varvec{u}}_m^{n-1}\Vert _0^2\right) +k\nu \Vert \nabla \left( {\varvec{u}}_m^n+{\varvec{u}}_m^{n-1}\right) \Vert _0^2\displaystyle= & {} 2k\left( {\bar{T}}_m^n{\varvec{j}},{\varvec{u}}_m^n+{\varvec{u}}_m^{n-1}\right) \nonumber \\ \displaystyle\le & {} k\Vert T^{n}_m+T^{n-1}_m\Vert _{-1}\Vert \nabla \left( {\varvec{u}}^n_m+{\varvec{u}}^{n-1}_m\right) \Vert _0 \\\le & {} \frac{k}{2\nu }\Vert T^{n}_m+T^{n-1}_m\Vert _{-1}^2+\frac{k\nu }{2}\Vert \nabla \left( {\varvec{u}}^n_m+{\varvec{u}}^{n-1}_m\right) \Vert _0^2 \nonumber \end{aligned}$$

(15)

and

$$\begin{aligned} \begin{array}{l}\displaystyle \displaystyle 2\left( \Vert T_m^n\Vert _0^2-\Vert T^{n-1}_m\Vert _0^2\right) +k\gamma _0^{-1}\Vert \nabla \left( T^n_m+T^{n-1}_m\right) \Vert _0^2\displaystyle =0. \end{array} \end{aligned}$$

(16)

Summing (15) and (16) from 1 to $n$ and simplifying yield

$$\begin{aligned} \begin{array}{l}\displaystyle \displaystyle \Vert {\varvec{u}}^n_m\Vert _0^2+k\nu \sum \limits _{i=1}^n\Vert \nabla \left( {\varvec{u}}_m^i+{\varvec{u}}_m^{i-1}\right) \Vert _0^2\displaystyle \le \frac{k}{2\nu }\sum \limits _{i=1}^n\Vert T_m^{i}+T_m^{i-1}\Vert _{-1}^2 \end{array} \end{aligned}$$

(17)

and

$$\begin{aligned} \begin{array}{l}\displaystyle \displaystyle \Vert T_m^n\Vert _0^2+k\gamma _0^{-1}\sum \limits _{i=1}^n\Vert \nabla \left( T_m^i+T_m^{i-1}\right) \Vert _0^2\displaystyle \le 2\Vert \psi \Vert _0^2. \end{array} \end{aligned}$$

(18)

By using (18), from (17), we obtain

$$\begin{aligned} \begin{array}{l}\displaystyle \displaystyle \Vert {\varvec{u}}_m^n\Vert _0^2+k\nu \sum \limits _{i=1}^n\Vert \nabla \left( {\varvec{u}}_m^i+{\varvec{u}}_m^{i-1}\right) \Vert _0^2\displaystyle \le {\nu ^{-1}\gamma _0}\Vert \psi \Vert _0^2. \end{array} \end{aligned}$$

(19)

By extracting square root for (18) and (19) and using $\left( \sum _{i=1}^nb_i^2\right) ^{1/2}\ge \sum _{i=1}^n|b_i|/\sqrt{n}$ and $\Vert a+b\Vert _0\ge \Vert a\Vert _0-\Vert b\Vert _0$, we obtain

$$\begin{aligned} \displaystyle \displaystyle \Vert T_m^n\Vert _0+k{\gamma _0^{-1/2}}\Vert \nabla T_m^n\Vert _0\displaystyle\le & {} \max \{2, \sqrt{2}k{\gamma _0^{-1/2}}\}\Vert \psi \Vert _1, \end{aligned}$$

(20)

$$\begin{aligned} \displaystyle \displaystyle \Vert {\varvec{u}}_m^n\Vert _0^2+k\sqrt{\nu }\Vert \nabla {\varvec{u}}_m^n\Vert _0\displaystyle\le & {} \sqrt{{\nu ^{-1}\gamma _0}}\Vert \psi \Vert _0. \end{aligned}$$

(21)

By using the first equation of (9), (7), (20), and (21), we easily obtain

$$\begin{aligned} \begin{array}{l}\displaystyle \displaystyle \Vert p_m^n\Vert _0\le C\Vert \psi \Vert _1. \end{array} \end{aligned}$$

(22)

Thus, for $1\le n\le N$, if $\psi =0$, the system of linear equations (14) has only zero solution. Therefore, the system of linear equations (14) has a unique series of solutions $({\varvec{u}}^n_m,p_m^n, T_m^n)\in X\times M\times W$ $(m=1,2, \ldots )$. Because the spaces $X\times M\times W$ are weakly and sequentially compact Hilbert spaces, by fixed point theorem (see [21]), we can conclude that the sequence of solutions $({\varvec{u}}_m^n,p_m^n, T_m^n)\in X\times M\times W$ has a subsequence [without loss of generality, we still might denote by $({\varvec{u}}_m^n,p_m^n, T_m^n)$] that is uniquely and weakly convergent to $({\varvec{u}}^n,p^n, T^n)\in X\times M\times W$ for Problem III, i.e., Problem III has at least a series of solutions $({\varvec{u}}^n,p^n,T^n)\in X\times M\times W (n=1,2, \ldots , N)$. Using the same technique as the proof of the uniqueness of solution for Problem II (see Theorem 1.4.1 in [23] or Theorem 5.2 in [18]), we can prove that the series of solutions for Problem III is unique.

Second, we prove that (10) and (11) hold. By taking ${\varvec{v}}={\varvec{u}}^n+{\varvec{u}}^{n-1}$, $q=p^n$, and $\phi =T^n+T^{n-1}$ in Problem III, and by using (3) and (4), Hölder inequality, and Cauchy inequality, we obtain

$$\begin{aligned} \displaystyle \displaystyle 2\left( \Vert {\varvec{u}}^n\Vert _0^2-\Vert {\varvec{u}}^{n-1}\Vert _0^2\right) +k\nu \Vert \nabla \left( {\varvec{u}}^n+{\varvec{u}}^{n-1}\right) \Vert _0^2\displaystyle= & {} 2k\left( {\bar{T}}^n{\varvec{j}},{\varvec{u}}^n+{\varvec{u}}^{n-1}\right) \nonumber \\ \displaystyle\le & {} k\Vert T^{n}+T^{n-1}\Vert _{-1}\Vert \nabla \left( {\varvec{u}}^n+{\varvec{u}}^{n-1}\right) \Vert _0\\\le & {} \frac{k}{2\nu }\Vert T^{n}+T^{n-1}\Vert _{-1}^2+\frac{k\nu }{2}\Vert \nabla \left( {\varvec{u}}^n+{\varvec{u}}^{n-1}\right) \Vert _0^2\nonumber \end{aligned}$$

(23)

and

$$\begin{aligned} \begin{array}{l}\displaystyle \displaystyle 2\left( \Vert T^n\Vert _0^2-\Vert T^{n-1}\Vert _0^2\right) +k\gamma _0^{-1}\Vert \nabla \left( T^n+T^{n-1}\right) \Vert _0^2\displaystyle =0. \end{array} \end{aligned}$$

(24)

Summing (23) and (24) from 1 to $n$ and simplifying yield

$$\begin{aligned} \begin{array}{l}\displaystyle \displaystyle \Vert {\varvec{u}}^n\Vert _0^2+k\nu \sum \limits _{i=1}^n\Vert \nabla \left( {\varvec{u}}^i+{\varvec{u}}^{i-1}\right) \Vert _0^2\displaystyle \le \frac{k}{2\nu }\sum \limits _{i=1}^n\Vert T^{i}+T^{i-1}\Vert _{-1}^2 \end{array} \end{aligned}$$

(25)

and

$$\begin{aligned} \begin{array}{l}\displaystyle \displaystyle \Vert T^n\Vert _0^2+k\gamma _0^{-1}\sum \limits _{i=1}^n\Vert \nabla \left( T^i+T^{i-1}\right) \Vert _0^2\displaystyle \le 2\Vert \psi \Vert _0^2. \end{array} \end{aligned}$$

(26)

By using (26), from (25), we obtain

$$\begin{aligned} \begin{array}{l}\displaystyle \displaystyle \Vert {\varvec{u}}^n\Vert _0^2+k\nu \sum \limits _{i=1}^n\Vert \nabla \left( {\varvec{u}}^i+{\varvec{u}}^{i-1}\right) \Vert _0^2\displaystyle \le {\nu ^{-1}\gamma _0}\Vert \psi \Vert _0^2. \end{array} \end{aligned}$$

(27)

By extracting square root for (26) and (27) and using $\left( \sum _{i=1}^nb_i^2\right) ^{1/2}\ge \sum _{i=1}^n|b_i|/\sqrt{n}$ and $\Vert a+b\Vert _0\ge \Vert a\Vert _0-\Vert b\Vert _0$, we obtain

$$\begin{aligned} \displaystyle \displaystyle \Vert T^n\Vert _0+k{\gamma _0^{-1/2}}\Vert \nabla T^n\Vert _0\displaystyle\le & {} \max \left\{ 2, \sqrt{2}k{\gamma _0^{-1/2}}\right\} \Vert \psi \Vert _1, \end{aligned}$$

(28)

$$\begin{aligned} \displaystyle \displaystyle \Vert {\varvec{u}}^n\Vert _0^2+k\sqrt{\nu }\Vert \nabla {\varvec{u}}^n\Vert _0\displaystyle\le & {} \sqrt{{\nu ^{-1}\gamma _0}}\Vert \psi \Vert _0. \end{aligned}$$

(29)

By using the first equation of (9), (7), (28), and (29), we easily obtain

$$\begin{aligned} \begin{array}{l}\displaystyle \displaystyle \Vert p^n\Vert _0\le C\Vert \psi \Vert _1. \end{array} \end{aligned}$$

(30)

Finally, we prove that the error estimates (12) and (13) hold. Put ${\varvec{e}}^n={\varvec{u}}(t_n)-{\varvec{u}}^{n}$, $\theta ^n=T(t_n)-T^{n}$, and $\eta ^n=p(t_n)-p^n$. Subtracting Problem III from Problem II taking $t=t_{n-\frac{1}{2}}$, ${\varvec{v}}={\varvec{e}}^{n}+{\varvec{e}}^{n-1}$, $\varphi =\theta ^n+\theta ^{n-1}$, and $q=\eta ^n$, using Taylor’s formula, we obtain that

$$\begin{aligned} \displaystyle \Vert {\varvec{e}}^n\Vert _0^2-\Vert {\varvec{e}}^{n-1}\Vert _0^2+\frac{k\nu }{2}\Vert \nabla \left( {\varvec{e}}^n+{\varvec{e}}^{n-1}\right) \Vert _0^2= & {} k\left( (\theta ^n+\theta ^{n-1}){\varvec{j}},{\varvec{e}}^{n}+{\varvec{e}}^{n-1}\right) \nonumber \\&+\frac{k^3}{24}\left( {\varvec{u}}_{ttt}(\xi _{1n}),{\varvec{e}}^n+{\varvec{e}}^{n-1}\right) \\&+\frac{k^3\nu }{4}\left( \nabla {\varvec{u}}_{tt}(\xi _{2n}),\nabla ({\varvec{e}}^n+{\varvec{e}}^{n-1})\right) \nonumber \\&-\frac{k^3}{4}\left( T_{tt}(\xi _{3n}){\varvec{j}},{\varvec{e}}^{n}+{\varvec{e}}^{n-1}\right) +\varvec{\varPhi },\nonumber \end{aligned}$$

(31)

$$\begin{aligned} \displaystyle&\Vert \theta ^n\Vert _0^2-\Vert \theta ^{n-1}\Vert _0^2+\frac{k}{2\gamma _0}\Vert \nabla (\theta ^n+\theta ^{n-1})\Vert _0^2\nonumber \\&\quad =\frac{k^3}{24}\left( T_{ttt}(\zeta _{1n}),\theta ^n+\theta ^{n-1}\right) +\frac{k^3}{4\gamma _0}\left( \nabla T_{tt}(\zeta _{2n}),\nabla (\theta ^n+\theta ^{n-1})\right) +\varPsi , \end{aligned}$$

(32)

where $\varvec{\varPhi }=ka_1({\varvec{u}}(t_{n-\frac{1}{2}}),{\varvec{u}}(t_{n-\frac{1}{2}}),{\varvec{e}}^n+{\varvec{e}}^{n-1})-ka_1(\bar{{\varvec{u}}}^{n}, \bar{{\varvec{u}}}^{n}, {\varvec{e}}^n+{\varvec{e}}^{n-1})$ and $\varPsi =$ $ka_2({\varvec{u}}(t_{n-\frac{1}{2}}),T(t_{n-\frac{1}{2}}),\theta ^n+\theta ^{n-1})-ka_2(\bar{{\varvec{u}}}^{n},\bar{ T}^{n}, \theta ^n+\theta ^{n-1})$ $(t_{n-1}\le \xi _{1n},$ $\xi _{2n}, \xi _{3n}, \zeta _{1n},$ $\zeta _{2n}\le t_n)$. By using Taylor’s formula, Hölder inequality, and Cauchy inequality, there are $\xi _{in}\in [t_{n-1},t_n]$ $(i=4,5)$ such that

$$\begin{aligned} \varvec{\varPhi }= & {} ka_1\left( {\varvec{u}}(t_{n-\frac{1}{2}}),{\varvec{u}}(t_{n-\frac{1}{2}}),{\varvec{e}}^n+{\varvec{e}}^{n-1}\right) -ka_1\left( \bar{{\varvec{u}}}^{n}, \bar{{\varvec{u}}}^{n}, {\varvec{e}}^n+{\varvec{e}}^{n-1}\right) \nonumber \\= & {} ka_1\left( {\varvec{u}}(t_{n-\frac{1}{2}})-\bar{{\varvec{u}}}^{n},{\varvec{u}}(t_{n-\frac{1}{2}}),{\varvec{e}}^n+{\varvec{e}}^{n-1}\right) +ka_1\left( \bar{{\varvec{u}}}^{n},{\varvec{u}}(t_{n-\frac{1}{2}})-\bar{{\varvec{u}}}^{n},{\varvec{e}}^n+{\varvec{e}}^{n-1}\right) \nonumber \\= & {} \frac{k^3}{16}a_1\left( {\varvec{u}}_{tt}(\xi _{4n}),{\varvec{u}}(t_{n-\frac{1}{2}}),{\varvec{e}}^n+{\varvec{e}}^{n-1}\right) +\frac{k^3}{16}a_1\left( \bar{{\varvec{u}}},{\varvec{u}}_{tt}(\xi _{5n}),{\varvec{e}}^n+{\varvec{e}}^{n-1}\right) \nonumber \\\le & {} \frac{k\nu }{12} \Vert \nabla \left( {\varvec{e}}^n+{\varvec{e}}^{n-1}\right) \Vert _0^2+\frac{k^5N_0^2}{128\nu }\Vert \nabla {\varvec{u}}(t)\Vert _{W^{2,\infty }(t_{n-1},t_n;L^2)}^2\nonumber \\&\times \left( \Vert \nabla {\varvec{u}}(t)\Vert _{L^{2,\infty }(t_{n-1},t_n;L^2)}^2+\Vert \nabla \bar{{\varvec{u}}}^n\Vert _0^2\right) .\nonumber \\ \end{aligned}$$

(33)

By using Hölder inequality and Cauchy inequality, we have that

$$\begin{aligned}&|\frac{k^3}{24}\left( {\varvec{u}}_{ttt}(\xi _{1n}),{\varvec{e}}^n+{\varvec{e}}^{n-1}\right) +\frac{k^3\nu }{4}\left( \nabla {\varvec{u}}_{tt}(\xi _{2n}),\nabla ({\varvec{e}}^n+{\varvec{e}}^{n-1})\right) -\frac{k^3}{4}\left( T_{tt}(\xi _{3n}){\varvec{j}},{\varvec{e}}^{n}+{\varvec{e}}^{n-1}\right) |\nonumber \\&\quad \le \frac{k\nu }{12} \Vert \nabla \left( {\varvec{e}}^n+{\varvec{e}}^{n-1}\right) \Vert _0^2 +\frac{k^5}{64\nu }\Vert {\varvec{u}}\Vert ^2_{W^{3,\infty }(t_{n-1},t_n;H^{-1})} +\frac{{9\nu k^5}}{16}\Vert \nabla {\varvec{u}}\Vert ^2_{W^{2,\infty }(t_{n-1},t_n;L^{2})}\nonumber \\&\qquad +\frac{9k^5}{16\nu }\Vert T\Vert ^2_{W^{3,\infty }(t_{n-1},t_n;H^{-1})}. \end{aligned}$$

(34)

Combining (33) and (34) with (31), using Hölder inequality and Cauchy inequality, and simplifying yield

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert {\varvec{e}}^n\Vert _0^2-\Vert {\varvec{e}}^{n-1}\Vert _0^2+\frac{k\nu }{4}\Vert \nabla \left( {\varvec{e}}^n+{\varvec{e}}^{n-1}\right) \Vert _0^2\le \frac{3k}{\nu } \Vert \theta ^n+\theta ^{n-1}\Vert _{-1}^2 +\tilde{C}^2k^5, \end{array} \end{aligned}$$

(35)

where $\tilde{C}^2=\frac{1}{64\nu }\Vert {\varvec{u}}\Vert ^2_{W^{3,\infty }(t_{n-1},t_n;H^{-1})} +\frac{{9\nu }}{16}\Vert \nabla {\varvec{u}}\Vert ^2_{W^{2,\infty }(t_{n-1},t_n;L^{2})}+$ $\frac{9}{16\nu }\Vert T\Vert ^2_{W^{3,\infty }(t_{n-1},t_n;H^{-1})}$ $+\frac{N_0^2}{128\nu }\Vert \nabla {\varvec{u}}(t)\Vert _{W^{2,\infty }(t_{n-1},t_n;L^2)}^2\left( \Vert \nabla {\varvec{u}}(t)\Vert _{L^{2,\infty }(t_{n-1},t_n;L^2)}^2+\Vert \nabla \bar{{\varvec{u}}}^n\Vert _0^2\right) .$

By using the same techniques as proving (33), there are $\zeta _{in}\in [t_{n-1},t_n]$ $(i=3,4)$ such that

$$\begin{aligned} \varPsi= & {} ka_2\left( {\varvec{u}}(t_{n-\frac{1}{2}}),T(t_{n-\frac{1}{2}}),\theta ^n+\theta ^{n-1}\right) -ka_2\left( \bar{{\varvec{u}}}^{n},\bar{ T}^{n}, \theta ^n+\theta ^{n-1}\right) \nonumber \\\le & {} \frac{k}{8\gamma _0} \Vert \nabla \left( \theta ^n+\theta ^{n-1}\right) \Vert _0^2+\frac{k^5\tilde{N}_0^2\gamma _0}{64}\Vert \nabla T(t)\Vert _{W^{2,\infty }(t_{n-1},t_n;L^2)}^2\Vert \nabla \bar{{\varvec{u}}}^n\Vert _0^2\nonumber \\&+\frac{k^5\tilde{N}_0^2\gamma _0}{64}\Vert \nabla {\varvec{u}}(t)\Vert _{W^{2,\infty }(t_{n-1},t_n;L^2)}^2\Vert \nabla T(t)\Vert _{L^{2,\infty }(t_{n-1},t_n;L^2)}^2. \end{aligned}$$

(36)

By using Hölder inequality and Cauchy inequality, we have that

$$\begin{aligned}&\left| \frac{k^3}{24}\left( T_{ttt}(\zeta _{1n}),\theta ^n+\theta ^{n-1}\right) +\frac{k^3}{4\gamma _0}\left( \nabla T_{tt}(\zeta _{2n}),\nabla (\theta ^n+\theta ^{n-1})\right) \right| \nonumber \\&\quad \le \frac{k}{8\gamma _0} \Vert \nabla \left( \theta ^n+\theta ^{n-1}\right) \Vert _0^2 +\frac{k^5\gamma _0}{144}\Vert T\Vert ^2_{W^{3,\infty }(t_{n-1},t_n;H^{-1})} +\frac{{k^5}}{4}\Vert \nabla T\Vert ^2_{W^{2,\infty }(t_{n-1},t_n;L^{2})}.\qquad \end{aligned}$$

(37)

Combining (36) and (37) with (32) and simplifying yield

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert \theta ^n\Vert _0^2-\Vert \theta ^{n-1}\Vert _0^2+\frac{k}{4\gamma _0}\Vert \nabla \left( \theta ^n+\theta ^{n-1}\right) \Vert _0^2\le \hat{C}^2k^5, \end{array} \end{aligned}$$

(38)

where $\hat{C}^2k^5=\frac{\tilde{N}_0^2\gamma _0}{64}\Vert \nabla {\varvec{u}}(t)\Vert _{W^{2,\infty }(t_{n-1},t_n;L^2)}^2\Vert \nabla T(t)\Vert _{L^{2,\infty }(t_{n-1},t_n;L^2)}^2$ $+\frac{1}{4}\Vert T\Vert ^2_{W^{2,\infty }(t_{n-1},t_n;H^{1})}$ $+\frac{\gamma _0}{144}\Vert T\Vert ^2_{W^{3,\infty }(t_{n-1},t_n;H^{-1})}$ $+\frac{\tilde{N}_0^2\gamma _0}{64}\Vert \nabla T(t)\Vert _{W^{2,\infty }(t_{n-1},t_n;L^2)}^2\Vert \nabla \bar{{\varvec{u}}}^n\Vert _0^2$.

Summing (38) from $1$ to $n$ yields that

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert \theta ^n\Vert _0^2+\frac{k}{4\gamma _0}\sum \limits _{i=1}^n\Vert \nabla \left( \theta ^i+\theta ^{i-1}\right) \Vert _0^2\le \hat{C}^2nk^5. \end{array} \end{aligned}$$

(39)

By extracting square root for (39) and using $\left( \sum _{i=0}^nb_i^2\right) ^{1/2}\ge \sum _{i=0}^n|b_i|/\sqrt{n}$ and $\Vert a+b\Vert _0\ge \Vert a\Vert _0-\Vert b\Vert _0$, we obtain

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert \theta ^n\Vert _0+\frac{k}{2\sqrt{\gamma _0}}\Vert \nabla \theta ^n\Vert _0\le \hat{C}\sqrt{t_N}k^2, \end{array} \end{aligned}$$

(40)

which yields (13). By (35) and (40), we have

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert {\varvec{e}}^n\Vert _0^2-\Vert {\varvec{e}}^{n-1}\Vert _0^2+\frac{k\nu }{4}\Vert \nabla \left( {\varvec{e}}^n+{\varvec{e}}^{n-1}\right) \Vert _0^2\le \hat{C}_0^2k^5, \end{array} \end{aligned}$$

(41)

where $\hat{C}_0^2={12\gamma _0\hat{C}^2T_\infty }{\nu ^{-1}}k^3+\tilde{C}^2$. Summing (41) from $1$ to $n$ yields that

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert {\varvec{e}}^n\Vert _0^2+\frac{k\nu }{4}\sum \limits _{i=1}^n\Vert \nabla \left( {\varvec{e}}^i+{\varvec{e}}^{i-1}\right) \Vert _0^2\le \hat{C}_0^2nk^5, \end{array} \end{aligned}$$

(42)

By extracting square root for (42) and using $\left( \sum _{i=0}^nb_i^2\right) ^{1/2}\ge \sum _{i=0}^n|b_i|/\sqrt{n}$ and $\Vert a+b\Vert _0\ge \Vert a\Vert _0-\Vert b\Vert _0$, we obtain

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert {\varvec{e}}^n\Vert _0+\frac{k\sqrt{\nu }}{2}\Vert \nabla {\varvec{e}}^n\Vert _0\le \hat{C}_0^2\sqrt{t_N}k^2. \end{array} \end{aligned}$$

(43)

By using Taylor’s formula, there are $\xi _{in}\in [t_{n-1},t_n] (i=5,6,7,8,9,10,11)$ such that

$$\begin{aligned} b(p(t_n)-p^n,{\varvec{v}})= & {} \frac{1}{k}( {{\varvec{e}}^n-{\varvec{e}}^{n-1}},{\varvec{v}})+\frac{\nu }{2}\left( \nabla ({\varvec{e}}^n+{\varvec{e}}^{n-1}),\nabla {\varvec{v}}\right) \nonumber \\&+\frac{1}{2}\left[ a_1\left( {\varvec{e}}^n+{\varvec{e}}^{n-1},{\varvec{u}}(t_{n-\frac{1}{2}}),{\varvec{v}}\right) +a_1\left( \bar{{\varvec{u}}}^n,{\varvec{e}}^n+{\varvec{e}}^{n-1},{\varvec{v}}\right) \right. \nonumber \\&\left. -\left( (\theta ^n+\theta ^{n-1}){\varvec{j}},{\varvec{v}}\right) \right] \nonumber \\&-\frac{k^2}{48}\left( {\varvec{u}}_{ttt}(\xi _{5n}),{\varvec{v}}\right) -\frac{k^2}{48}\left( {\varvec{u}}_{ttt}(\xi _{6n}),{\varvec{v}}\right) -\frac{\nu k^2}{16}\left( \nabla {\varvec{u}}_{tt}(\xi _{7n}),\nabla {\varvec{v}}\right) \nonumber \\&-\frac{\nu k^2}{16}\left( \nabla {\varvec{u}}_{tt}(\xi _{8n}),\nabla {\varvec{v}}\right) +\frac{k}{2}b({\varvec{v}},p_t(\xi _{9n}))-\frac{k^2}{16}a_1({\varvec{u}}_{tt}(\xi _{10n}),{\varvec{u}}(t_{n-\frac{1}{2}}),{\varvec{v}})\nonumber \\&-\frac{k^2}{16}a_1(\bar{{\varvec{u}}}^n,{\varvec{u}}_{tt}(\xi _{11n}),{\varvec{v}})-\frac{k^2}{16}(T_{tt}(\xi _{3n}){\varvec{j}},{\varvec{v}}),\quad \forall {\varvec{v}}\in X. \end{aligned}$$

(44)

Then, with (40), (43), (44), (7), Hölder inequality, and Cauchy inequality, we have that

$$\begin{aligned} \begin{array}{l} \displaystyle \Vert p(t_n)-p^n\Vert _0\le \beta ^{-1}\sup \limits _{{\varvec{v}}\in X}\frac{b\left( p(t_n)-p^n,{\varvec{v}}\right) }{\Vert \nabla v\Vert _0}\le {C}k. \end{array} \end{aligned}$$

(45)

Combining (45) and (43) yields (12), which completes the proof of Theorem 2.2. $\square$

2.2 Fully Discrete SCNMFVE Formulation for Problem I

In order to establish the fully discrete SCNMFVE formulations for Problem II, it is necessary to introduce an FVE approximation for the spatial variables of Problem III (more details see [2, 3, 14, 15]).

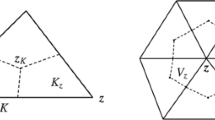
Firstly, let $\mathfrak {I}_h = \{K\}$ be a quasi-uniform triangulation of ${\varOmega }$ with $h = \max h_K$, where $h_K$ is the diameter of the triangle $K\in \mathfrak {I}_h$ (see [5, 10, 18]). In order to describe the SCNMFVE formulation, we introduce a dual partition $\mathfrak {I}_h^*$ based on $\mathfrak {I}_h$ whose elements are called the control volumes. We construct the control volume in the same way as in [2, 3, 14, 15]. Let ${\varvec{z}}_K=(x_K,y_k)$ be the barycenter of $K\in \mathfrak {I}_h$. We connect ${\varvec{z}}_K$ with line segments to the midpoints of the edges of $K$, thus partitioning $K$ into three quadrilaterals $K_z({\varvec{z}}=(x,y)\in Z_h(K)$, where $Z_h(K)$ are the vertices of $K$). Then with each vertex ${\varvec{z}}\in Z_h =\bigcup _{K\in \mathfrak {I}_h}Z_h(K)$ we associate a control volume $V_z$, which consists of the union of the sub-regions $K_z$, sharing the vertex ${\varvec{z}}$. Finally, we obtain a group of control volumes covering the domain ${\varOmega }$, which is called a barycenter-type dual partition $\mathfrak {I}_h^*$ of the triangulation $\mathfrak {I}_h$ (see Fig. 1). We denote the set of interior vertices of $Z_h$ by $Z^\circ _h$.

Fig. 1

Left chart is a triangle $K$ partitioned into three sub-regions $K_z$. Right chart is a sample region with dotted lines indicating the corresponding control volume $V_z$

Since the FE triangulation $\mathfrak {I}_h$ is quasi-uniform, the dual partition $\mathfrak {I}_h^*$ is also quasi-uniform (see [2, 3, 5, 10, 14, 15, 18]). Moreover, the barycenter-type dual partition can lead to relatively simple calculations. To this end, the trial function spaces $X_h$, $W_h$, and $M_h$ of the velocity, temperature, and pressure the velocity, the temperature and the pressure are, respectively, defined as follows:

$$\begin{aligned} \displaystyle X_h= & {} \left\{ {\varvec{v}}_h\in X\cap C(\overline{{\varOmega }})^2;~ {\varvec{v}}_h|_K\in [{\fancyscript{P}}_{1}(K)]^2, \forall K\in \mathfrak {I}_h\right\} ,\\ W_h= & {} \left\{ w_h\in W\cap C(\overline{{\varOmega }});~ w_h|_K\in {\fancyscript{P}}_1(K), \forall K\in \mathfrak {I}_h\right\} ,\\ M_h= & {} \left\{ q_h\in M; \ q_h|_K\in {\fancyscript{P}}_1(K), \ \forall K\in \mathfrak {I}_h\right\} , \end{aligned}$$

where ${\fancyscript{P}}_1(K)$ is the linear function space on $K$. Note that they are different from those in [16]. It is obvious that $X_h\subset X= H^1_0({\varOmega })^2$ and $W_h\subset W= H^1_0({\varOmega })$. For $({\varvec{u}}, T)\in X\times W$, let $({\varPi }_h{\varvec{u}},\rho _hT)$ be the interpolation projection of $({\varvec{u}}, T)$ onto the trial function spaces $X_h\times W_h$. Then, due to the interpolation theory of Sobolev spaces (see [5, 10, 14, 16, 18]), we have the following error estimates

$$\begin{aligned} |{\varvec{u}}-{\varPi }_h{\varvec{u}}|_m\le & {} Ch^{2-m}|{\varvec{u}}|_2, \quad \forall {\varvec{u}}\in H^2({\varOmega })^2, m=0,1, \end{aligned}$$

(46)

$$\begin{aligned} |T-\rho _hT|_m\le & {} Ch^{2-m}|T|_2, \quad \forall T\in H^2({\varOmega }), m=0,1, \end{aligned}$$

(47)

where $C$ in this context indicates a positive constant which is possibly different at different occurrences, being independent of the spatial mesh size $h$ and temporal mesh size $k$.

The test spaces $\tilde{X}_h$ and $\tilde{W}_h$ of the velocity and temperature are, respectively, chosen as follows:

$$\begin{aligned} \displaystyle \tilde{X}_h= & {} \displaystyle \left\{ {\varvec{v}}_h\in L^2({\varOmega })^2; \ {\varvec{v}}_h|_{V_z}\in [{\fancyscript{P}}_0(V_z)]^2 (V_z\cap \partial {\varOmega }=\emptyset ),\right. \nonumber \\&\left. \displaystyle {\varvec{v}}_h|_{V_z} = {\varvec{0}} (V_z\cap \partial {\varOmega }\not =\emptyset ), \forall V_z\in \mathfrak {I}_h^*\right\} ,\nonumber \\ \displaystyle \tilde{W}_h= & {} \displaystyle \left\{ w_h\in L^2({\varOmega }); \ w_h|_{V_z}\in {\fancyscript{P}}_0(V_z) (V_z\cap \partial {\varOmega }=\emptyset ),\right. \nonumber \\&\left. w_h|_{V_z} = 0 (V_z\cap \partial {\varOmega }\not =\emptyset ), \forall V_z\in \mathfrak {I}_h^*\right\} , \end{aligned}$$

(48)

where ${\fancyscript{P}}_0(V_z)$ is the constant function space on $V_z$. In fact, they can be spanned by the following basis functions

$$\begin{aligned} \phi _z(x,y)=\left\{ \begin{array}{ll} 1,&{} (x,y)\in V_z, \\ 0,&{} \hbox {elsewhere}, \end{array} \quad \forall {\varvec{z}}\in Z^\circ _h. \right. \end{aligned}$$

(49)

For $({\varvec{u}}, w)\in X\times W$, let $({\varPi }_h^*{\varvec{u}}, \rho _h^* w)$ be the interpolation projection of $({\varvec{u}}, w)$ onto the test spaces $\tilde{X}_h\times \tilde{W}_h$, i.e.,

$$\begin{aligned} \left( {\varPi }_h^*{\varvec{u}},\rho _h^* w\right) =\sum \limits _{{\varvec{z}}\in Z^\circ _h}({\varvec{u}}({\varvec{z}}),w({\varvec{z}}))\phi _{{\varvec{z}}}. \end{aligned}$$

(50)

By the interpolation theory of Sobolev spaces (see [5, 10, 14, 16, 18, 26]), we have

$$\begin{aligned} \Vert {\varvec{u}}-{\varPi }_h^*{\varvec{u}}\Vert _0\le Ch|{\varvec{u}}|_1; \quad \Vert w-\rho _h^*w\Vert _0\le Ch|w|_1. \end{aligned}$$

(51)

By using the same principle as mentioned in [16, 17], the fully discrete SCNMFVE formulation for Problem II is written as follows.

Problem IV Find $({\varvec{u}}_h^n,p_h^n,T_h^n)\in X_h\times M_h\times W_h$ $(1\le n\le N)$ such that

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \left( \bar{\partial }_t{\varvec{u}}_h^n,{\varPi }_h^*{\varvec{v}}_h\right) + a_h\left( \bar{{\varvec{u}}}_h^n, {\varPi }_h^*{\varvec{v}}_h\right) +a_{1h}\left( \bar{{\varvec{u}}}_h^{n},\bar{{\varvec{u}}}_h^n,{\varPi }_h^*{\varvec{v}}_h\right) +b_h\left( p_h^n,{\varPi }_h^*{\varvec{v}}_h\right) \\ \quad = \left( \bar{T}_h^{n}{\varvec{j}},{\varPi }_h^*{\varvec{v}}_h\right) ,&{} \forall {\varvec{v}}_h\in X_h, \\ b\left( q_h,{\varvec{u}}_h^n\right) +D_h\left( p_h^n,q_h\right) =0, &{} \forall q_h\in M_h, \\ \left( \bar{\partial }_tT_h^n,\rho _h^*\varphi _h\right) +d_h\left( \bar{T}_h^n,\rho _h^*\varphi _h\right) + a_{2h}\left( \bar{{\varvec{u}}}_h^{n},\bar{T}_h^n,\rho _h^*\varphi _h\right) =0, &{} \forall \varphi _h\in W_h, \\ \displaystyle {\varvec{u}}_h^0={\varvec{0}},\quad T_h^0=\rho _h\psi (x,y), &{} (x,y)\in {\varOmega }, \end{array} \right. \end{aligned}$$

(52)

where

$$\begin{aligned} \displaystyle a_h\left( {\varvec{u}}_h^n,{\varPi }_h^*{\varvec{v}}_h\right)= & {} -\nu \sum \limits _{V_z\in \mathfrak {I}_h^*}\int _{\partial V_{z}}\left( {\varvec{v}}_h(z)\nabla {\varvec{u}}_h^n\right) \cdot {\varvec{n}}\hbox {d}s; \end{aligned}$$

(53)

$$\begin{aligned} b_h\left( q_h,{\varPi }_h^*{\varvec{v}}_h\right)= & {} \sum \limits _{V_z\in \mathfrak {I}_h^*}{\varvec{v}}_h(z) \int _{\partial V_{z}}q_h{\varvec{n}}\hbox {d}s; \end{aligned}$$

(54)

$$\begin{aligned} \displaystyle \displaystyle \displaystyle a_{1h}\left( {\varvec{u}}_h^{n},{\varvec{w}}_h^n,{\varPi }_h^*{\varvec{v}}_h\right)= & {} \left( \left( {\varvec{u}}_h^{n}\cdot \nabla \right) {\varvec{w}}_h^n, {\varPi }_h^*{\varvec{v}}_h\right) +\left( \left( \hbox {div}{\varvec{u}}_h^{n}\right) {\varvec{w}}_h^n, {\varPi }_h^*{\varvec{v}}_h\right) /2;\nonumber \\ \displaystyle d_h\left( T_h^n,\rho _h^*w_h\right)= & {} -\gamma _0^{-1}\sum \limits _{V_z\in \mathfrak {I}_h^*}w_h(z)\int _{\partial V_{z}}\nabla T\cdot {\varvec{n}}\hbox {d}s; \end{aligned}$$

(55)

$$\begin{aligned} \displaystyle a_{2h}\left( {\varvec{u}}_h^{n},T_h^n,\rho _h^*\varphi _h\right)= & {} \left( \left( {\varvec{u}}_h^{n}\cdot \nabla \right) T_h^n,\rho _h^*\varphi _h\right) +\left( \left( \hbox {div}{\varvec{u}}_h^{n}\right) T_h,\rho _h^*\varphi _h^n\right) /2; \end{aligned}$$

(56)

$$\begin{aligned} \displaystyle D_h\left( p_h^n,q_h\right)= & {} \varepsilon \sum \limits _{K\in \mathfrak {I}_h}\left\{ \int _{K,2}p_h^nq_h\hbox {d}x\hbox {d}y-\int _{K,1}p_h^nq_h\hbox {d}x\hbox {d}y\right\} , \end{aligned}$$

(57)

here $\varepsilon$ is a positive real number and $\int _{K,i} g(x,y)\hbox {d}x\hbox {d}y$ indicate an appropriate Gauss integral on $K$ that is exact for polynomials of degree $i$ ($i = 1, 2)$ and $g(x,y) = p_hq_h$ is a polynomial of degree not more than $i$ ($i = 1, 2)$.

Thus, for all test functions $q_h\in M_h$, the trial function $p_h \in M_h$ must be piecewise constant when $i = 1$. Consequently, we define the $L^2$—projection operator $\varrho _h : L^2({\varOmega })\rightarrow \hat{W}_h$ such that $\forall p\in L^2({\varOmega })$ satisfies

$$\begin{aligned} (p, q_h) = (\varrho _hp, q_h), \quad \forall q_h\in \hat{W}_h, \end{aligned}$$

(58)

where $\hat{W}_h\subset L^2({\varOmega })$ denotes the piecewise constant space associated with $\mathfrak {I}_h$. The projection operator $\varrho _h$ has the following properties (see [5, 18]).

$$\begin{aligned}&\Vert \varrho _hp\Vert _0\le C\Vert p\Vert _0, \quad \forall p\in L^2({\varOmega }), \end{aligned}$$

(59)

$$\begin{aligned}&\Vert p-\varrho _hp\Vert _0\le Ch\Vert p\Vert _1 , \quad \forall p\in H^1({\varOmega }). \end{aligned}$$

(60)

Now, using the definition of $\varrho _h$, we can rewrite the bilinear form $D_h(\cdot ,\cdot )$ as follows:

$$\begin{aligned} \begin{array}{ll} \displaystyle D_h(p_h, q_h) = \varepsilon (p_h-\varrho _hp_h, q_h) = \varepsilon (p_h -\varrho _hp_h, q_h-\varrho _hq_h). \end{array} \end{aligned}$$

(61)

3 Existence, Uniqueness, Stability, and Error Estimates for the SCNMFVE Solutions

In order to discuss the existence, the uniqueness, the stability, and the error estimates of the solutions for fully discrete SCNMFVE formulation with the second-order time accuracy or Problem IV, it is necessary to introduce some preliminary lemmas.

From [3, 14, 15, 22] we have the following two lemmas.

Lemma 3.1

There hold the following results:

$$\begin{aligned} a_h\left( {\varvec{u}}_h,{\varPi }^*_h{\varvec{v}}_h\right)= & {} a({\varvec{u}}_h, {\varvec{v}}_h),\quad a_{1h}\left( {\varvec{v}}_h,{\varvec{u}}_h,{\varPi }^*_h{\varvec{u}}_h\right) =0, \quad \forall {\varvec{u}}_h,{\varvec{v}}_h,{\varvec{w}}_h\in U_h,\\ d_h\left( T_h,\rho _h^*\phi _h\right)= & {} d(T_h,\phi _h), \quad a_{2h}\left( {\varvec{u}}_h,T_h,\rho _h^*T_h\right) =0, \quad \forall T_h, \phi _h\in W_h, \forall {\varvec{u}}_h\in X_h,\\ b_h\left( p_h,{\varPi }^*_h{\varvec{v}}_h\right)= & {} -b(p_h,{\varvec{v}}_h), \quad \forall {\varvec{v}}_h\in X_h, \forall p_h\in M_h. \end{aligned}$$

Further, $a_h({\varvec{u}}_h,{\varPi }^*_hv_h)$ and $d_h(T_h,\rho _h^*w_h)$ are all symmetric, bounded, and positive definite, that is,

$$\begin{aligned} a_h\left( {\varvec{u}}_h,{\varPi }^*_h{\varvec{v}}_h\right)= & {} a_h\left( {\varvec{v}}_h,{\varPi }^*_h{\varvec{u}}_h\right) , \quad \forall {\varvec{u}}_h,{\varvec{v}}_h\in U_h;\\ d_h\left( T_h,\rho _h^*w_h\right)= & {} d_h\left( w_h,\rho _h^*T_h\right) ,\quad \forall T_h,w_h\in W_h, \end{aligned}$$

and there exist a positive constants $h_0\ge h>0$ such that

$$\begin{aligned} a_h\left( {\varvec{u}}_h,{\varPi }^*_h{{\varvec{u}}}_h\right)= & {} \nu |{\varvec{u}}_h|_1^2, \quad |a_h\left( {\varvec{u}}_h,{\varPi }^*_h {\varvec{v}}_h\right) |\le \nu \Vert {\varvec{u}}_h\Vert _1\Vert {\varvec{v}}_h\Vert _1, \quad \forall {\varvec{u}}_h,{\varvec{v}}_h\in X_h.\\ d_h\left( T_h,\rho _h^*T_h\right)\ge & {} \gamma _0^{-1}|T_h|_1^2,\quad |d_h\left( T_h,\rho ^*_hw_h\right) |\le \tilde{C}_0\Vert T_h\Vert _1\Vert w_h\Vert _1, \quad \forall T_h,w_h\in W_h. \end{aligned}$$

Lemma 3.2

There holds the following statement:

$$\begin{aligned} \left( {\varvec{u}}_h,{\varPi }_h^* {{\varvec{v}}}_h\right) =\left( {{\varvec{v}}}_h,{\varPi }_h^*{\varvec{u}}_h\right) , \quad \forall {\varvec{u}}_h, {{\varvec{v}}}_h\in X_h. \end{aligned}$$

For any ${\varvec{u}}\in H^m({\varOmega })^2$ $(m = 0, 1)$ and ${\varvec{v}}_h\in X_h,$

$$\begin{aligned} |({\varvec{u}}, {\varvec{v}}_h)-\left( {\varvec{u}}, {\varPi }_h^*v_h\right) |\le Ch^{m+n}\Vert {\varvec{u}}\Vert _m\Vert {\varvec{v}}_h\Vert _n, \quad \ n = 0, 1. \end{aligned}$$

Set $|\Vert {\varvec{u}}_h\Vert |_0=({\varvec{u}}_h,{\varPi }_h^*{{\varvec{u}}}_h)^{1/2}$, then $|\Vert \cdot \Vert |_0$ is equivalent to $\Vert \cdot \Vert _0$ on $X_h$, namely there exist two positive constants $C_1$ and $C_2$ such that

$$\begin{aligned} C_1\Vert {\varvec{u}}_h\Vert _0\le |\Vert {\varvec{u}}_h\Vert |_0\le C_2\Vert {\varvec{u}}_h\Vert _0, \quad \forall {\varvec{u}}_h\in X_h. \end{aligned}$$

(62)

Remark 1

For scalar functions, i.e., if ${\varvec{u}}_h$ and ${\varvec{v}}_h$ in $X_h$ are, respectively, substituted with $w_h$ and $T_h$ in $W_h$, the results of Lemma 3.2 hold (see Theorem 3.2.1 and Lemma 5.1.5 in [14]).

The following discrete Gronwall Lemma (see [5, 17, 18]) is useful for the proofs of the existence, the uniqueness, the stability, and the error estimates of the solutions for Problem IV.

Lemma 3.3

If $\{a_n\}$ and $\{b_n\}$ are two positive sequences, $\{c_n\}$ is a monotone positive sequence, and they satisfy $a_n+b_n\le c_n+\bar{\lambda }\sum \nolimits _{i=0}^{n-1}a_i (\bar{\lambda }>0)$ and $a_0+b_0\le c_0$, then $\displaystyle a_n+b_n\le c_n\exp (n\bar{\lambda }) (n=0,1,2,\ldots ).$

There are the following results of the existence, the uniqueness, and the stability of the solutions for Problem IV.

Theorem 3.4

Under the hypotheses of Theorems 2.1 and 2.2, there exists a unique series of solutions $({\varvec{u}}_h^n,p_h^n,T_h^n)(n=1,2,\ldots ,N)$ for the fully discrete SCNMFVE formulation with the second-order time accuracy, i.e., Problem IV satisfying

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert {\varvec{u}}_h^n\Vert _0+ \Vert T_h^n\Vert _0+k\Vert \nabla {{\varvec{u}}}_h^n\Vert _0+k\Vert \nabla T_h^n\Vert _0+\sqrt{k}\Vert p_h^n\Vert _0 \le C(\Vert \psi \Vert _0+k\Vert \nabla \psi |\Vert _0), \end{array} \end{aligned}$$

(63)

which shows that the series of solutions of Problem IV is stable.

Proof

First, we prove that Problem IV has a unique series of solutions. Because the finite dimensional subspaces $X_h\times M_h\times W_h$ are also weakly and sequentially compact Hilbert spaces, by using the same as the technique to prove that Problem III has a unique series of solutions and apply to fixed point theorem (see [21]) to Problem IV, we can prove that Problem VI has a unique sequence of solutions $({\varvec{u}}_h^n,p_h^n, T_h^n)\in X_h\times M_h\times W_h$.

And then, we prove that (63) holds. By taking ${\varvec{v}}_h= \bar{{\varvec{u}}}_h^n$ in the first equation of Problem IV and $q_h=p_h^n$ in the second equation of Problem IV and by using Lemmas 3.1 and 3.2, Hölder inequality, and Cauchy inequality, we obtain

$$\begin{aligned} \displaystyle \frac{1}{2}\left( \Vert |{\varvec{u}}_h^n|\Vert _0^2-\Vert |{\varvec{u}}_h^{n-1}|\Vert _0^2\right) + k\nu \Vert \nabla \bar{{\varvec{u}}}_h^n\Vert _0^2+k\varepsilon \Vert p_h^n-\rho _hp_h^n\Vert _0^2= & {} k\left( \bar{T}_h^n{\varvec{j}},{\varPi }_h^*\bar{{\varvec{u}}}_h^n\right) \\\le & {} \frac{k}{2\nu }\Vert \bar{T}_h^n\Vert _{-1}^2+\frac{k\nu }{2}\Vert \nabla \bar{{\varvec{u}}}_h^{n}\Vert _0^2.\nonumber \end{aligned}$$

(64)

It follows from (64) that

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert |{\varvec{u}}_h^n|\Vert _0^2-\Vert |{\varvec{u}}_h^{n-1}|\Vert _0^2+ 2k\nu \Vert \nabla \bar{{\varvec{u}}}_h^n\Vert _0^2+2k\varepsilon \Vert p_h^n-\rho _hp_h^n\Vert _0^2 \le k \nu ^{-1}\Vert \bar{T}_h^n\Vert _{-1}^2. \end{array} \end{aligned}$$

(65)

Summing (65) from 1 to $n$ yields that

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert |{\varvec{u}}_h^n|\Vert _0^2+ \frac{k\nu }{2}\sum \limits _{i=1}^n\Vert \nabla \left( {\varvec{u}}_h^i+{\varvec{u}}_h^{i-1}\right) \Vert _0^2+2k\varepsilon \Vert p_h^n-\rho _hp_h^n\Vert _0^2 \le k \nu ^{-1}\sum \limits _{i=1}^n\Vert \bar{T}_h^i\Vert _{-1}^2. \end{array} \end{aligned}$$

(66)

If $p_h^n\not =0$, then it is easily see that $\Vert p_h^n\Vert _0>\Vert \rho _hp_h^n\Vert _0$ from (2.51). Therefore, there exists a constant $\delta \in (0,1)$ such that $\delta \Vert p_h^n\Vert _0=\Vert \rho _hp_h^n\Vert _0$. By extracting square root for (66), using $\left( \sum _{i=1}^nb_i^2\right) ^{1/2}\ge \sum _{i=1}^n|b_i|/\sqrt{n}$, $\Vert a+b\Vert _0\ge \Vert a\Vert _0-\Vert b\Vert _0$, and Lemma 3.2, and then, simplifying, we obtain

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert {\varvec{u}}_h^n\Vert _0+ k\Vert \nabla {{\varvec{u}}}_h^n\Vert _0+\sqrt{k}\Vert p_h^n\Vert _0 \le C\left( k \sum \limits _{i=1}^n\Vert \bar{T}_h^i\Vert _{-1}^2\right) ^{1/2}. \end{array} \end{aligned}$$

(67)

By taking $\varphi _h=\bar{T}_h^n$ in the third equation of Problem IV and by using Lemmas 3.1 and 3.2, Hölder inequality, and Cauchy inequality, we obtain

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert |T_h^n|\Vert _0^2-\Vert |T_h^{n-1}|\Vert _0^2+ \frac{k}{2\gamma _0}\Vert \nabla \left( T_h^n+T_h^{n-1}\right) \Vert _0^2=0. \end{array} \end{aligned}$$

(68)

Summing (68) from 1 to $n$ yields that

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert |T_h^n|\Vert _0^2+ \frac{k}{2\gamma _0}\sum \limits _{i=1}^n\Vert \nabla \left( T_h^i+T_h^{i-1}\right) \Vert _0^2=\Vert |\psi |\Vert _0^2. \end{array} \end{aligned}$$

(69)

By extracting square root for (69) and using $\left( \sum _{i=0}^nb_i^2\right) ^{1/2}\ge \sum _{n=0}^n|b_i|/\sqrt{n}$, $\Vert a+b\Vert _0\ge \Vert a\Vert _0-\Vert b\Vert _0$, and Lemma 3.2, we obtain

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert T_h^n\Vert _0+ k \Vert \nabla T_h^n\Vert _0 \le C(\Vert \psi \Vert _0+k\Vert \nabla \psi |\Vert _0). \end{array} \end{aligned}$$

(70)

From (67) and (69) and by using Lemma 3.2, we obtain

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert {\varvec{u}}_h^n\Vert _0+ k\Vert \nabla {{\varvec{u}}}_h^n\Vert _0+\sqrt{k} \Vert p_h^n\Vert _0 \le C \Vert \psi \Vert _{0} \le C(\Vert \psi \Vert _0+k\Vert \nabla \psi |\Vert _0). \end{array} \end{aligned}$$

(71)

Combining (70) with (71) yields (63). If $p_h^n=0$, (63) is correct, which completes the proof of Theorem 3.4. $\square$

Put

$$\begin{aligned} \displaystyle \displaystyle \displaystyle {\fancyscript{A}}\left( (S_h\bar{{\varvec{u}}}^n,Q_hp^n);({\varvec{v}}_h,q_h)\right)= & {} a(S_h\bar{{\varvec{u}}}^n,{\varvec{v}}_h)+a_{1}(S_h\bar{{\varvec{u}}}^n,S_h\bar{{\varvec{u}}}^n, {\varvec{v}}_h)\nonumber \\&-b(Q_hp^n,{\varvec{v}}_h) +b(q_h,S_h{\varvec{u}}^n),\nonumber \\ \displaystyle {\fancyscript{A}}\left( (\bar{{\varvec{u}}}^n,p^n);({\varvec{v}}_h,q_h)\right)= & {} a(\bar{{\varvec{u}}}^n,{\varvec{v}}_h)+a_{1}(\bar{{\varvec{u}}}^n,\bar{{\varvec{u}}}^n, {\varvec{v}}_h){-}b(p^n,{\varvec{v}}_h)+b(q_h,{\varvec{u}}^n). \end{aligned}$$

(72)

By using the stabilized CN mixed FE (SCNMFE) methods (for example, see [12, 17, 18]) for the non-stationary Navier–Stokes equations, we obtain the following Lemma 3.5.

Lemma 3.5

Let $(S_h{\varvec{u}}^n, Q_h{p}^n)$ be the Navier–Stokes projection of the solutions $({\varvec{u}}^n,$ ${p}^n)$ for Problem III on $U_h\times M_h$, that is, for the solutions $({\varvec{u}}^n, p^n)\in U\times M$ for Problem III, there exist $(S_h{\varvec{u}}^n, Q_h{p}^n)$ ($n=1, 2, \ldots , N$) such that

$$\begin{aligned} \displaystyle \displaystyle&k{\fancyscript{A}}\left( (S_h\bar{{\varvec{u}}}^n,Q_h{p}^n);({\varvec{v}}_h,q_h)\right) +(S_h{\varvec{u}}^n-S_h{\varvec{u}}^{n-1},{\varvec{v}}_h)+kD_h(Q_hp^n,q_h)\\&\quad =k{\fancyscript{A}}\left( (\bar{{\varvec{u}}}^n,p^n);({\varvec{v}}_h,q_h)\right) +({\varvec{u}}^n-{\varvec{u}}^{n-1},{\varvec{v}}_h),\forall ({\varvec{v}}_h,q_h)\in U_h\times M_h, \quad n=1,2,\ldots ,N,\nonumber \end{aligned}$$

(73)

$$\begin{aligned}&S_h{\varvec{u}}^0={\varPi }_h{\varvec{u}}^0(x,y),\quad {\varvec{u}}^0={\varvec{u}}^0(x,y),\quad (x, y)\in {\varOmega }. \end{aligned}$$

(74)

Then, there hold

$$\begin{aligned} \Vert S_h{\varvec{u}}^n\Vert _1+\Vert Q_h{p}^n\Vert _0\le C\left( \Vert {\varvec{u}}^n\Vert _1+\Vert p^n\Vert _0\right) ,\quad 1\le n\le N. \end{aligned}$$

(75)

If $k=O(h)$ and the solution $({\varvec{u}}^n, p^n)\in H^2({\varOmega })^2\times H^1({\varOmega })$ ($n=1, 2, \ldots , N$) for Problem III, then there hold the following error estimates

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert {\varvec{u}}^n-S_h{\varvec{u}}^n\Vert _0+k \Vert \nabla \left( {\varvec{u}}^n-S_h{\varvec{u}}^n\right) \Vert _0+k\Vert p^n-Q_hp^n\Vert _0\le Ch^2, \quad n=1,2,\ldots ,N. \end{array} \end{aligned}$$

(76)

Remark 2

In fact, (73) and (74) are the system of error equations between standard SCNMFE formulation and the semi-discrete CN formulation about time of the non-stationary Navier–Stokes equations, thus (75) and (76) are directly obtained from SCNMFE method (for example, see [12, 17, 18]).

By the FE methods (see, e.g., [5, 10, 18]) for elliptic equations, we have the following Lemma 3.6.

Lemma 3.6

Let $R_h: W\rightarrow W_h$ be a generalized Ritz projection, i.e., for given ${\varvec{u}}_h^{n}\in X_h$, $T^{n-1}\in W$, and $T_h^{n-1}\in W_h$, and for any $T^n\in W$ ($n=1,2,\ldots ,N$), there exist $R_hT^n\in W_h$ ($n=1,2,\ldots ,N$) such that

$$\begin{aligned}&\left( R_hT^n,w_h\right) +kd\left( R_h\bar{T}^n,w_h\right) +ka_2\left( \bar{{\varvec{u}}}_h^{n},R_h\bar{T}^n,w_h\right) -\left( R_hT^{n-1},w_h\right) =\left( T^n,w_h\right) \nonumber \\ \displaystyle&\quad +\,kd\left( \bar{T}^n,w_h\right) +ka_2\left( \bar{{\varvec{u}}}^{n},\bar{T}^n,w_h\right) -\left( T^{n-1},w_h\right) , \quad \forall w_h\in W_h, \quad n=1,2, \ldots , N.\qquad \quad \end{aligned}$$

(77)

If $({\varvec{u}}^n,p^n,T^n)$ ($n=1,2,\ldots ,N$) are the solutions of Problem III and $T^n\in H^2({\varOmega })\cap W$, we have the following inequalities

$$\begin{aligned} \displaystyle \Vert R_hT^n\Vert _0+k\Vert \nabla R_hT^n\Vert _0\le & {} C\Vert \nabla T^n\Vert _0, \quad n=0,1,2, \ldots , N, \end{aligned}$$

(78)

$$\begin{aligned} \displaystyle \Vert R_hT^n-T^n\Vert _0+k\Vert \nabla \left( R_hT^n-T^n\right) |_0\le & {} Ch^2 \Vert \psi \Vert _2,\quad n=0,1,2, \ldots , N. \end{aligned}$$

(79)

Theorem 3.7

Let $({\varvec{u}}, p, T)$ be the solution for Problem II and $({\varvec{u}}_h^n,p_h^n, T_h^n)$ the series of solutions of fully discrete SCMNFVE formulation with the second-order time accuracy (that is, Problem IV). Then, under the hypotheses of Theorems 2.2 and 3.4, if $p_h^0=p^0=0$ (or $p_h^0=Q_hp^0$), $h=O(k)$, $N_0\nu ^{-1}\Vert \nabla \bar{{\varvec{u}}}_h^n\Vert _0\le 1/4$, and $\psi \in H^1({\varOmega })$, we have the following error estimates

$$\begin{aligned}&\displaystyle \Vert {\varvec{u}}(t_n)-{\varvec{u}}_h^{n}\Vert _0+\Vert T(t_n)-T_h^{n}\Vert _0+k[\Vert p(t_n)-p_h^{n}\Vert _0 + \Vert \nabla ({\varvec{u}}(t_n)-{\varvec{u}}_h^{n})\Vert _0 \nonumber \\&\quad \displaystyle + \Vert \nabla \left( T(t_n)-T_h^{n}\right) \Vert _0]\le Ch^2 \Vert \psi \Vert _1,\quad n=1, 2, \ldots , N. \end{aligned}$$

(80)

Proof

By subtracting Problem IV from Problem III taking ${\varvec{v}}={\varvec{v}}_h$, $q=q_h$, and $\varphi =\varphi _h$, and by using Lemmas 3.1 and 3.2, we obtain the system of error equations:

$$\begin{aligned} \left\{ \begin{array}{l}\displaystyle \left( {\varvec{u}}^n-{\varvec{u}}_h^n, {\varvec{v}}_h\right) +\left( {\varvec{u}}_h^n-{\varPi }_h^*{\varvec{u}}_h^n, {\varvec{v}}_h-{\varPi }_h^*{\varvec{v}}_h\right) + k a\left( \bar{{\varvec{u}}}^n-\bar{{\varvec{u}}}_h^n, {\varvec{v}}_h\right) \\ \quad +ka_1\left( \bar{{\varvec{u}}}^{n}, \bar{{\varvec{u}}}^n, {\varvec{v}}_h\right) -ka_{1h}\left( \bar{{\varvec{u}}}_h^{n}, \bar{{\varvec{u}}}_h^n, {\varPi }^*{\varvec{v}}_h\right) -kb\left( p^n-p_h^n,{\varvec{v}}_h\right) \\ \quad = k\left( (\bar{T}^n- \bar{T}_h^{n}){\varvec{j}},{\varvec{v}}_h\right) -k\left( \bar{T}_h^{n}{\varvec{j}},{\varPi }_h^*{\varvec{v}}_h-{\varvec{v}}_h\right) +\left( {\varvec{u}}^{n-1}-{\varvec{u}}_h^{n-1},{\varvec{v}}_h\right) \\ \qquad -\left( {\varvec{u}}_h^{n-1},{\varPi }_h^*{\varvec{v}}_h-{\varvec{v}}_h\right) ,\quad \forall {\varvec{v}}_h\in X_h,\quad n=1, 2, \ldots , N,\\ b\left( q_h,{\varvec{u}}^n-{\varvec{u}}_h^n\right) -\varepsilon \left( p_h^n-\varrho _hp_h^n, q_h-\varrho _hq_h\right) =0, \forall q_h\in M_h, \quad n=1, 2, \ldots , N,\\ \left( T^n-T_h^n,\varphi _h\right) - \left( T_h^n,\rho _h^*\varphi _h-\varphi _h\right) +kd\left( \bar{T}^n-\bar{T}_h^n,\varphi _h\right) +ka_{2}\left( \bar{{\varvec{u}}}^{n},\bar{T}^n,\varphi _h\right) \\ \quad -ka_{2h}\left( \bar{{\varvec{u}}}_h^{n},\bar{T}_h^n,\rho _h^*\varphi _h\right) =\left( T^{n-1}-T_h^{n-1},\varphi _h\right) \\ \quad -\left( T_h^{n-1},\rho _h^*\varphi _h-\varphi _h\right) , \forall \varphi _h\in W_h,\quad n=1,2,\ldots ,N,\\ \displaystyle {\varvec{u}}^0-{\varvec{u}}_h^0={\varvec{0}},\quad T^0-T_h^0=\psi (x,y)-\rho _h\psi (x,y), \quad (x,y)\in {\varOmega }. \end{array} \right. \end{aligned}$$

(81)

Let $\zeta ^n=Q_hp^n-p_h^n$, $\varvec{E}^n=S_h{\varvec{u}}^n-{\varvec{u}}_h^n$, and $\bar{\varvec{E}}^n=S_h\bar{{\varvec{u}}}^n-\bar{{\varvec{u}}}_h^n$. By using (73) and the system of error equations (81), we obtain

$$\begin{aligned} \frac{1}{2}\Vert \varvec{E}^n\Vert _0^2+ k\nu |\bar{\varvec{E}}^n|_1^2= & {} \left( S_h{\varvec{u}}^n-{\varvec{u}}^n, \bar{\varvec{E}}^n\right) +ka\left( S_h\bar{{\varvec{u}}}^n-\bar{{\varvec{u}}}^n, \bar{\varvec{E}}^n\right) \nonumber \\&+\left( {\varvec{u}}^n-{\varvec{u}}_h^n, \bar{\varvec{E}}^n\right) +ka\left( \bar{{\varvec{u}}}^n-\bar{{\varvec{u}}}_h^n, \bar{\varvec{E}}^n\right) -\frac{1}{2}\left( \varvec{E}^{n-1}, \varvec{E}^n\right) \nonumber \\= & {} \left( S_h{\varvec{u}}^{n-1}-{\varvec{u}}^{n-1}, \bar{\varvec{E}}^n\right) +kb\left( Q_hp^n-p^n,\bar{\varvec{E}}^n\right) +ka_1\left( \bar{{\varvec{u}}}^n,\bar{{\varvec{u}}}^n, \bar{\varvec{E}}^n\right) \nonumber \\&-ka_1\left( S_h\bar{{\varvec{u}}}^n,S_h\bar{{\varvec{u}}}^n,\bar{\varvec{E}}^n\right) -ka_1\left( \bar{{\varvec{u}}}^{n},\bar{ {\varvec{u}}}^n, \bar{\varvec{E}}^n\right) +ka_{1h}\left( \bar{{\varvec{u}}}_h^{n}, \bar{{\varvec{u}}}_h^n,{\varPi }_h^*\bar{\varvec{E}}^n\right) \nonumber \\&+kb\left( p^n-p_h^n,\bar{\varvec{E}}^n\right) -\left( {\varvec{u}}_h^{n}-{\varPi }_h^*{\varvec{u}}_h^{n}, \bar{\varvec{E}}^n-{\varPi }_h^*\bar{\varvec{E}}^n\right) \nonumber \\&+\left( {\varvec{u}}_h^{n-1}-{\varPi }_h^*{\varvec{u}}_h^{n-1}, \bar{\varvec{E}}^n-{\varPi }_h^*\bar{\varvec{E}}^n\right) -\frac{1}{2}(S_h{\varvec{u}}^{n-1}-{\varvec{u}}_h^{n-1}, \varvec{E}^n)\nonumber \\&+\left( {\varvec{u}}^{n-1}-{\varvec{u}}_h^{n-1}, \bar{\varvec{E}}^n\right) +k\left( (\bar{T}^n- \bar{T}_h^{n}){\varvec{j}},\bar{\varvec{E}}^n\right) \nonumber \\&-k\left( \bar{T}_h^{n}{\varvec{j}},{\varPi }_h^*\bar{\varvec{E}}^n-\bar{\varvec{E}}^n\right) \nonumber \\= & {} k\left( (\bar{T}^n- \bar{T}_h^{n}){\varvec{j}},\bar{\varvec{E}}^n\right) -k\left( \bar{T}_h^{n}{\varvec{j}},{\varPi }_h^*\bar{\varvec{E}}^n-\bar{\varvec{E}}^n\right) -ka_1\left( \bar{\varvec{E}}_h^{n}, \bar{{\varvec{u}}}_h^n, \bar{\varvec{E}}^n\right) \nonumber \\&+ka_{1h}\left( \bar{{\varvec{u}}}_h^{n}, \bar{{\varvec{u}}}_h^n, \bar{\varvec{E}}^n-{\varPi }_h^*\bar{\varvec{E}}^n\right) +\frac{1}{2}\left( \varvec{E}^{n-1}, \varvec{E}^{n-1}\right) +{k}b\left( \zeta ^n,\bar{\varvec{E}}^n\right) \nonumber \\&-\left( {\varvec{u}}_h^{n}-{\varvec{u}}_h^{n-1}-{\varPi }_h^*\left( {\varvec{u}}_h^{n}-{\varvec{u}}_h^{n-1}\right) ,\bar{\varvec{E}}^n-{\varPi }_h^*\bar{\varvec{E}}^n\right) . \end{aligned}$$

(82)

By using Lemma 3.2, Hölder inequality, and Cauchy inequality, we have

$$\begin{aligned}&|k\left( (\bar{T}^n-\bar{T}_h^n){\varvec{j}},\bar{\varvec{E}}^n\right) -k\left( T_h^{n}{\varvec{j}},{\varPi }_h^*\bar{\varvec{E}}^n-\bar{\varvec{E}}^n\right) |\nonumber \\&\quad \le Ck\Vert \bar{T}^n-\bar{T}_h^n\Vert _0\Vert \bar{\varvec{E}}^n\Vert _0+Ckh^2\Vert \nabla \bar{T}_h^{n}\Vert _0\Vert \nabla \bar{\varvec{E}}_n\Vert _0\nonumber \\&\quad \le Ck\Vert \bar{T}^n-\bar{T}_h^n\Vert _0^2+Ck\Vert \bar{\varvec{E}^n}\Vert _0^2+Ckh^4+\frac{\nu k}{8}\Vert \nabla \bar{\varvec{E}}^n\Vert _0^2, \end{aligned}$$

(83)

If $k=O(h)$, by using inverse error estimate and Taylor’s formula, we obtain

$$\begin{aligned} \displaystyle&|\left( {\varvec{u}}_h^{n}-{\varvec{u}}_h^{n-1}-{\varPi }_h^*\left( {\varvec{u}}_h^{n}-{\varvec{u}}_h^{n-1}\right) ,\bar{\varvec{E}}^n-{\varPi }_h^*\bar{\varvec{E}}^n\right) | \displaystyle \le Ch^2\Vert {\varvec{u}}_h^{n}-{\varvec{u}}_h^{n-1}\Vert _1|\bar{\varvec{E}}^n|_1 \nonumber \\&\quad \displaystyle \le Ch^3\left( \Vert \nabla \varvec{E}^{n}\Vert _0^2+ \Vert \nabla \left( S_h{\varvec{u}}^{n}-S_h{\varvec{u}}^{n-1}\right) \Vert _0^2+\Vert \nabla \varvec{E}^{n-1}\Vert _0^2\right) +\frac{k\nu }{8}\Vert \nabla \bar{\varvec{E}}^n\Vert _0^2 \nonumber \\ \displaystyle&\quad \le Ch\Vert \varvec{E}^{n}\Vert _0^2+ Ck^2h^3\displaystyle +Ch\Vert \varvec{E}^{n-1}\Vert _0^2 +\frac{k\nu }{8}\Vert \nabla \bar{\varvec{E}}^n\Vert _0^2. \end{aligned}$$

(84)

$\square$

Noting that $b(q_h,S_h{{\varvec{u}}}^n-{{\varvec{u}}}^n)=-k\varepsilon (Q_hp^n-\rho _h(Q_hp^n),q_h-\rho _hq_h)$, by the properties of operator $\varrho _h$ and the second equation of (81), we have

$$\begin{aligned} \displaystyle&b(\zeta ^n,\bar{\varvec{E}}^n)=b(\zeta ^n,S_h\bar{{\varvec{u}}}^n-\bar{{\varvec{u}}}^n)+b\left( \zeta ^n,\bar{{\varvec{u}}}^n-\bar{{\varvec{u}}}_h^n\right) \nonumber \\ \displaystyle&\quad =-\frac{\varepsilon }{2}(\zeta ^n-\varrho _h\zeta ^n,\zeta ^n-\varrho _h\zeta ^n) -\frac{\varepsilon }{2}(\zeta ^{n-1}-\varrho _h\zeta ^{n-1},\zeta ^n-\varrho _h(\zeta ^n) \nonumber \\ \displaystyle&\quad \le -\frac{\varepsilon }{4}\Vert \zeta ^n-\varrho _h\zeta ^n\Vert _0^2+\frac{\varepsilon }{4}\Vert \zeta ^{n-1}-\varrho _h\zeta ^{n-1}\Vert _0^2. \end{aligned}$$

(85)

If $N_0\nu ^{-1}\Vert \nabla \bar{{\varvec{u}}}_h^n\Vert _0\le 1/4$ ($n=1, 2, \ldots , N$), by Lemma 3.2, (3), and (8), we obtain

$$\begin{aligned} \begin{array}{l}\displaystyle k|a_{1h}\left( \bar{{\varvec{u}}}_h^{n}, \bar{{\varvec{u}}}_h^n, \bar{\varvec{E}}^n-{\varPi }_h^*\bar{\varvec{E}}^n\right) -a_1\left( \bar{\varvec{E}}^{n}, \bar{{\varvec{u}}}_h^n, \bar{E}^n\right) |\le Ckh^4+\frac{k\nu }{4}\Vert \nabla \bar{\varvec{E}}^n\Vert _0^2. \end{array} \end{aligned}$$

(86)

Combining (83–86) with (82) yields that

$$\begin{aligned} \displaystyle&\Vert {\varvec{E}}^n\Vert _0^2+k \nu \Vert \nabla \bar{\varvec{E}}^n\Vert _0^2 +\frac{k\varepsilon }{2}\Vert \zeta ^n-\varrho _h\zeta ^n\Vert _0^2 -\frac{k\varepsilon }{2}\Vert \zeta ^{n-1}-\varrho _h\zeta ^{n-1}\Vert _0^2 \nonumber \\ \displaystyle&\quad \le Ckh^4+ Ck^2h^3+\Vert E^{n-1}\Vert _0^2 +Ch\Vert \varvec{E}^{n-1}\Vert _0^2+ Ch\Vert \varvec{E}^{n}\Vert _0^2+Ck\Vert \bar{T}^n-\bar{T}_h^n\Vert _0^2. \end{aligned}$$

(87)

By summing (87) from $1$ to $n$, if $h$ is sufficiently small such that $Ch\le 1/2$ in (87) and $p_h^0=p^0=0$ (or $p_h^0=Q_hp^0$), we obtain that

$$\begin{aligned} \displaystyle&\Vert \varvec{E}_n\Vert _0^2+2k \nu \sum \limits _{i=1}^n\Vert \bar{\varvec{E}}_i\Vert _0^2+{k\varepsilon }\Vert \zeta ^n-\varrho _h\zeta ^n\Vert _0^2 \nonumber \\ \displaystyle&\quad \le Cnkh^4+Ck\sum \limits _{i=1}^n\Vert \bar{T}^i-\bar{T}_h^i\Vert _0^2+Ck\sum \limits _{i=0}^{n-1}\Vert \varvec{E}_i\Vert _0^2. \end{aligned}$$

(88)

Applying Gronwall Lemma 3.3 to (88) yields that

$$\begin{aligned} \displaystyle&\Vert \varvec{E}_n\Vert _0^2+k\sum \limits _{i=1}^n\Vert \nabla \bar{\varvec{E}}_i\Vert _0^2+k\Vert \zeta ^n-\varrho _h\zeta ^n\Vert _0^2 \nonumber \\ \displaystyle&\quad \le C \left( h^4+k\sum \limits _{i=1}^n\Vert \bar{T}^i-\bar{T}_h^i\Vert _0^2\right) \exp (Ckn). \end{aligned}$$

(89)

By extracting square root for (89) and using $\left( \sum _{i=0}^nb_i^2\right) ^{1/2}\ge \sum _{i=0}^n|b_i|/\sqrt{n}$, $\Vert a+b\Vert _0\ge \Vert a\Vert _0-\Vert b\Vert _0$, we obtain

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert \varvec{E}_n\Vert _0+k\Vert \nabla \bar{\varvec{E}}_n\Vert _0+k(\Vert \zeta ^n\Vert _0-\Vert \varrho _h\zeta ^n\Vert _0) \le C \left( h^4+k\sum \limits _{i=1}^n\Vert \bar{T}^i-\bar{T}_h^i\Vert _0^2\right) ^{1/2}. \end{array} \end{aligned}$$

(90)

If $\zeta ^n\not =0$, then $\Vert \zeta ^n\Vert _0>\Vert \varrho _h\zeta ^n\Vert _0$. Thus, there is a constant $\omega \in (0,1)$ such that $\omega \Vert \zeta ^n\Vert _0=\Vert \varrho _h\zeta ^n\Vert _0$. Then, by using triangle inequality, (90), and Lemma 3.4, we obtain

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert {\varvec{u}}^n-{\varvec{u}}_h^n\Vert _0+k[\Vert \nabla ({\varvec{u}}^n-{\varvec{u}}_h^n)|_0+\Vert p^n-p_h^n\Vert _0]\le C \left( h^4+k\sum \limits _{i=1}^n\Vert \bar{T}^i-\bar{T}_h^i\Vert _0^2\right) ^{1/2}. \end{array} \end{aligned}$$

(91)

Let $e_n=R_hT^n-T_h^n$. On the one hand, by using the system of error equations (71), and Lemma 3.6, we obtain that

$$\begin{aligned} \frac{1}{2}\Vert e_n\Vert _0^2+k \gamma _0^{-1} \Vert \nabla \bar{e}_n\Vert _0^2= & {} (e_n,\bar{e}_n)+kd(\bar{e}_n,\bar{e}_n)-\frac{1}{2}(e_n,e_{n-1})\nonumber \\= & {} \left[ \left( R_hT^n-T^n,\bar{e}_n\right) +kd\left( R_h\bar{T}^n-\bar{T}^n,\bar{e}_n\right) \right] \nonumber \\&+\left[ \left( T^n-T_h^n,\bar{e}_n\right) +kd\left( \bar{T}^n-\bar{T}_h^n,\bar{e}_n\right) \right] -\frac{1}{2}(e_n,e_{n-1})\nonumber \\= & {} \left[ \left( R_hT^{n-1}-T^{n-1},\bar{e}_n\right) +ka_2\left( \bar{{\varvec{u}}}^{n},\bar{T}^n,\bar{e}_n\right) -ka_2\left( \bar{{\varvec{u}}}_h^{n},R_h\bar{T}^n,\bar{e}_n\right) \right] \nonumber \\&+\left[ \left( T_h^n,\rho _h^*\bar{e}_n-\bar{e}_n\right) +ka_{2h}\left( \bar{{\varvec{u}}}_h^{n},\bar{T}_h^n,\rho _h^*\bar{e}_n\right) -ka_2\left( \bar{{\varvec{u}}}^{n},\bar{T}^n,\bar{e}_n\right) \right. \nonumber \\&\left. +\left( T^{n-1}-T_h^{n-1},\bar{e}_n\right) -\left( T_h^{n-1},\rho _h^*\bar{e}_n-\bar{e}_n\right) \right] -\frac{1}{2}(e_{n-1},e_n)\nonumber \\= & {} \frac{1}{2}(e_{n-1},e_n)+\left( T_h^{n}-T_h^{n-1},\rho _h^*\bar{e}_n-\bar{e}_n\right) \nonumber \\&+ka_{2h}\left( \bar{{\varvec{u}}}_h^{n},\bar{T}_h^n,\rho _h^*\bar{e}_n\right) -ka_2\left( \bar{{\varvec{u}}}_h^{n},R_h\bar{T}^n,\bar{e}_n\right) . \end{aligned}$$

(92)

By using Lemma 3.2, Hölder inequality, and Cauchy inequality, we obtain

$$\begin{aligned} \displaystyle (T_h^{n}-T_h^{n-1},\rho _h^*\bar{e}_n-\bar{e}_n)\le & {} Ch(\Vert e_n\Vert _0+\Vert R_hT^n-T^n\Vert _0+h\Vert T^n-T^{n-1}\Vert _1 \nonumber \\ \displaystyle&+\Vert T^{n-1}-R_hT^{n-1}\Vert _0+\Vert e_{n-1}\Vert _0)\Vert \nabla \bar{e}_n\Vert _0 \nonumber \\ \displaystyle\le & {} Ch\left( h^4+k^2h^2+\Vert e_n\Vert _0^2+\Vert e_{n-1}\Vert _0^2\right) +\frac{k}{4\gamma _0}\Vert \nabla \bar{e}_n\Vert _0^2, \end{aligned}$$

(93)

$$\begin{aligned} \displaystyle \frac{1}{2}(e_{n-1},e_n)\le & {} \frac{1}{2}\Vert e_{n-1}\Vert _0\Vert e_n\Vert _0\le \frac{1}{4}\Vert e_{n-1}\Vert _0^2+\frac{1}{4}\Vert e_n\Vert _0^2. \end{aligned}$$

(94)

If $N_0\nu ^{-1}\Vert \nabla \bar{{\varvec{u}}}_h^n\Vert _0\le 1/4$ ($n=1, 2, \ldots , N$), by using Lemmas 3.1 and 3.2, (4), Hölder inequality, and Cauchy inequality, we obtain

$$\begin{aligned} \begin{array}{l}\displaystyle ka_{2h}(\bar{{\varvec{u}}}_h^{n},\bar{T}_h^n,\rho _h^*\bar{e}_n)-ka_2(\bar{{\varvec{u}}}_h^{n},R_h\bar{T}^n,\bar{e}_n)\le \frac{k}{4\gamma _0}\Vert \nabla \bar{e}_n\Vert _0^2+Ckh^4. \end{array} \end{aligned}$$

(95)

If $k=O(h)$, by combining (93–95) with (92), we obtain

$$\begin{aligned} \displaystyle \Vert e_n\Vert _0^2+k\Vert \nabla \bar{e}_n\Vert _0^2 \le Ck\left( h^4+\Vert e_n\Vert _0^2+\Vert e_{n-1}\Vert _0^2\right) +\Vert e_{n-1}\Vert _0^2. \end{aligned}$$

(96)

Summing (96) from 1 to $n$ and using Lemma 3.6 and (27) yield that

$$\begin{aligned}&\Vert e_n\Vert _0^2+k \gamma _0^{-1}\sum \limits _{i=1}^n \Vert \nabla \bar{e}_i\Vert _0^2 \le Cnkh^4+ \Vert e_{0}\Vert _0^2+Ck\sum \limits _{i=1}^n \Vert e_i\Vert _0^2\nonumber \\&\quad \le Ch^4+Ck\sum \limits _{i=1}^n \Vert e_i\Vert _0^2+C\Vert R_h\psi -\psi \Vert _0^2+C\Vert \psi -\rho _h\psi \Vert _0^2 \le Ch^4+Ck\sum \limits _{i=1}^n \Vert e_i\Vert _0^2.\quad \end{aligned}$$

(97)

If $k$ is sufficiently small such that $Ck\le 1/2$ in (97), we obtain

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert e_n\Vert _0^2+k \gamma _0^{-1}\sum \limits _{i=1}^n \Vert \nabla \bar{e}_i\Vert _0^2 \le Ch^4+Ck\sum \limits _{i=0}^{n-1} \Vert e_i\Vert _0^2. \end{array} \end{aligned}$$

(98)

Applying Gronwall Lemma 3.3 to (98) yields that

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert e_n\Vert _0^2+k \gamma _0^{-1}\sum \limits _{i=1}^n \Vert \nabla \bar{e}_i\Vert _0^2 \le Ch^4\exp (Cnk)\le Ch^4. \end{array} \end{aligned}$$

(99)

By extracting square root for (99) and using $\left( \sum _{i=1}^nb_i^2\right) ^{1/2}\ge \sum _{i=1}^n|b_i|/\sqrt{n}$ and $\Vert a+b\Vert _0\ge \Vert a\Vert _0-\Vert b\Vert _0$, we obtain

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert e_n\Vert _0+k\Vert \nabla {e}_n\Vert _0 \le Ch^2. \end{array} \end{aligned}$$

(100)

By using triangle inequality, (100), and Lemma 3.6, we obtain

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert T^n-T_h^n\Vert _0+k \Vert \nabla \left( T^n-T_h^n\right) \Vert _0\le Ch^2. \end{array} \end{aligned}$$

(101)

Combining (91) with (101) yields that

$$\begin{aligned} \begin{array}{l}\displaystyle \Vert {\varvec{u}}^n-{\varvec{u}}_h^n\Vert _0+k[\Vert \nabla \left( {\varvec{u}}^n-{\varvec{u}}_h^n\right) |_0+\Vert p^n-p_h^n\Vert _0]\le Ch^2. \end{array} \end{aligned}$$

(102)

Combining (101) and (102) with Theorem 2.2 yields (80). If $\zeta ^n=0$, (80) is also correct, which completes the proof of Theorem 3.7.

Remark 3

It is known from Theorem 3.4 and its proof that, if $\Vert \psi \Vert _1$ is sufficiently small, then the conditions $N_0\nu ^{-1}\Vert \nabla \bar{{\varvec{u}}}_h^n\Vert _0\le 1/4$ ($n=1, 2, \ldots , N$) in Theorem 3.7 hold.

4 Some Numerical Experiments

In this section, some numerical experiments are used to show that the advantage of the fully discrete SCNMFVE formulation for the non-stationary incompressible Boussinesq equations.

Computational field $\bar{{\varOmega }}$ consists of the channel of width to 6 and length to 20 and two same rectangular cavities at the bottom and top of the channel. Its two rectangular cavities all are width to 2 and length to 4 (see Fig. 2). It is first divided into some small squares with side length $\triangle x =\triangle y= 0.01$, and then each square is linked with diagonal in the same direction divided into two triangles, which constitutes triangularizations $\mathfrak {I}_h$ with $h=\sqrt{2}\times 10^{-2}$. The dual decomposition $\mathfrak {I}^*_h$ is taken as barycenter form, namely the barycenter of the right triangle $K\in \mathfrak {I}_h$ is taken as the node of the dual decomposition. Take $Re=1000$, $Pr=7$, and $\varepsilon =1$. Except inflow of left boundary with a velocity of ${\varvec{u}}=(0.1(y-4.5)(5.5-y),0)^T ~~(4.5\le y\le 5.5)$ and outflow of right boundary with velocity of ${\varvec{u}}=(u_1,u_2)^T$ satisfying $u_2=0$ and $\displaystyle u_1(x,y,t)=u_1(19,y,t)~~(19\le x\le 20, 2\le y\le 8, 0\le t\le t_N)$, all initial and boundary value conditions are taken as $\varvec{0}$. Time step increment is taken as ${\varDelta }t=0.01$.

Fig. 2

The computational field and boundary conditions of flow

Firstly, the numerical solutions of the velocity, temperature, and pressure obtained by the SCNMFVE formulation Problem IV with the second-order time accuracy at $t =5000$ are depicted graphically at the bottom charts in Figs. 3, 4, and 5, respectively. If we find the solution at $t =5000$ by means of the SMFVE formulation with the first-order time accuracy in [17], in order to obtain the same accuracy solution as that of the SCNMFVE formulation, the time step for the SMFVE formulation must be taken as $k=0.0001$. Thus, the numerical solutions of the velocity, temperature, and pressure obtained by the SMFVE formulation at $t =5000$ need implement $5\times 10^7$ steps, which are 100 times for implementing steps $5\times 10^5$ of SCNMFVE formulation such that it increases greatly the truncation error accumulation in computational process. The numerical solutions of the velocity, temperature, and pressure obtained by the SMFVE formulation at $t =5000$ are depicted graphically at the top charts in Figs. 3, 4, and 5, respectively. Comparing every two charts in Figs. 3, 4, and 5 shows that the solutions obtained by the SCNMFVE formulation are better than the SMFVE solutions. Especially, the the SCNMFVE solutions of the temperature and pressure are far better than the SMFVE solutions.

Fig. 3

Top chart is the SMFVE solution of velocity ${{\varvec{u}}}$ and bottom chart is the SCNMFVE solution of velocity ${{\varvec{u}}}$ when $Re=1000$ and $Pr=7$ at time $t =5000$

Fig. 4

Top chart is the SMFVE solution of temperature $T$ and bottom chart is the SCNMFVE solution of temperature $T$ when $Re=1000$ and $Pr=7$ at time $t =5000$

Fig. 5

Top chart is the SMFVE solution of pressure $p$ and bottom chart is the SCNMFVE solution of pressure $p$ when $Re=1000$ and $Pr=7$ at time $t =5000$

The curves of the top and bottom charts in Fig. 6 are the relative errors ($\log 10$) of the SMFVE solutions and the SCNMFVE solutions at time $t\in (0, 5000]$ with respect to $L^2$-norm, respectively. Due to the truncation error accumulation in computational process, the errors of numerical solutions appear increase (see Fig. 6), but the truncation error accumulation for the SCNMFVE formulation Problem IV is far smaller than that for the SMFVE formulation and the relative errors (which illustrate that the numerical errors are consistent with theoretical results, since they does not exceed $2\times 10^{-4}$) of SCNMFVE numerical solutions are far smaller than those of the SMFVE solutions (also see Fig. 6). Moreover, it is shown that the fully discrete SCNMFVE formulation for the non-stationary incompressible Boussinesq equations is far more advantageous than the SMFVE formulation in [17].

Fig. 6

When $Re=10^3$ and $Pr=0.71$, the top chart and the bottom chart are the relative errors ($\log 10$) of the SMFVE solutions and the SCNFVE solution of the velocity ${{\varvec{u}}}$, the temperature $T$, and the pressure $p$ at the time $t\in (0, 5000]$, respectively

5 Conclusions and Discussions

In this study, we have established the semi-discrete CN formulation with respect to time for the non-stationary incompressible Boussinesq equations and have built the fully discrete SCNMFVE formulation based on two local Gauss integrals and parameter-free directly from the semi-discrete CN formulation with respect to time. Thus, we have avoided the discussion for semi-discrete SCNMFVE formulation with respect to spatial variables such that our theoretical analysis becomes simpler than the existing other methods (for example, see [11, 16, 17]). We have also provided the error estimates for the fully discrete SCNMFVE solutions and have used some numerical experiments to illustrate that the numerical errors were consistent with theoretical results, the computing load for the fully discrete SCNMFVE formulation was far fewer than that for the SMFVE formulation with the first time accuracy, and its accumulation of truncation errors in the computational process was far lesser than that of the SMFVE formulation with the first time accuracy. Thus, we have shown the advantage of the fully discrete SCNMFVE formulation for the non-stationary incompressible Boussinesq equations, i.e., the fully discrete SCNMFVE formulation not only has the second-order time accuracy, but it also satisfies the discrete B-B inequality. Thereby, it is different from existing other methods (for example, see [11, 16, 17]).