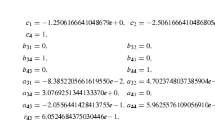Functionally Fitted Explicit Two Step Peer Methods

Abstract

In this paper we study functionally fitted methods based on explicit two step peer formulas. We show that with $s$ stages it is possible to get explicit fitted methods for fitting spaces of high dimension $2s$, by proving the existence and uniqueness of such formulas. Then, we obtain particular methods with 2 and 3 stages fitted to trigonometric and exponential spaces of dimension 4 and 6 respectively. By means of several numerical examples we show the performance of the obtained methods, comparing them to fitted Adams–Bashforth–Moulton methods with the same order.

1 Introduction

We consider the numerical solution of IVPs for first order differential systems

$$\begin{aligned} \frac{\text{ d }}{\text{ d }t} y(t) = f( t, y(t) ), \quad t \in [t_0, t_0+T], \quad y(t_0)= y_0 \in \, \mathbb {R}^m, \end{aligned}$$

(1)

with a sufficiently smooth vector field $f(t,y)$ where some properties of the behaviour of their unique global solution $y = y(t;t_0,y_0)$ are known in advance. In the case that the solution of (1) has an oscillatory behaviour and further we know an estimate of the frequency, some modified Runge–Kutta (RK) methods using this information, usually called trigonometrically fitted or more generally exponentially fitted methods [1, 3, 4, 9, 13, 14], have been proposed to improve their accuracy and efficiency over standard RK methods that are based on a polynomial approximation of the local solution at each point. More generally, for IVPs (1) with solutions belonging to (or that can be well approximated by) a functional space $\mathcal {F}$, functionally fitted RK methods specially adapted to this space have been analyzed in [5–8].

Concerning the highest dimension of the fitting space that can be attained for a RK method, it is known that it is closely related to the stage order of the method. Thus, assuming $(q+1)$-dimensional fitting spaces $\mathcal {F} = \mathcal {F}_q = \langle \varphi _0(t), \varphi _1(t), \ldots , \varphi _q(t) \rangle$ of smooth linearly independent real functions in $[t_0, t_0+T]$ in the sense that the Wronskian matrix is non singular for all $t \in [t_0, t_0+T]$, it has been proved by Ozawa [8] that for any fitting space $\mathcal {F}_q$ there exists a RK method with $s=q$ stages fitted to $\mathcal {F}_q$ for all $h \in (0, h_0]$ with $h_0$ sufficiently small. However, for explicit RK methods the stage order is limited to one and this implies serious restrictions in the dimensionality of the fitting space. In particular, Berghe et al. [13] have derived explicit four stage RK methods trigonometrically fitted to the space $\mathcal {F}_2 = \langle 1, \cos (\omega \, t), \sin (\omega \, t) \rangle$, where $\omega$ is a fixed frequency, with coefficients that depend on $\nu = \omega \, h$, and such that when $\nu \rightarrow 0$ they tend to the coefficients of the classical fourth order RK method. Higher dimensions of the fitting space are not possible for explicit methods.

Linear multistep methods do not have such a limitation, as shown for example in the early paper of Gautschi [4]. In this case, with $k$ steps, an explicit method can be fitted to $k+1$ dimensional spaces.

In this paper we will consider the so called explicit two step peer methods introduced by Weiner, Schmitt et al. [10–12, 15–18] in a series of papers as an alternative to classical Runge–Kutta (RK) and multistep methods attempting to combine the advantages of these two classes of methods. For a given set of admissible fixed nodes $c_j, j=1, \ldots ,s$ in the sense that $|c_i -c_j | \ne 0,1$ for all $i \ne j$, that is

$$\begin{aligned} c_1, c_2, \ldots , c_s, 1+c_1, 1+c_2, \ldots , 1+c_s, \end{aligned}$$

is a non confluent set of nodes, and starting from known approximations $Y_{0,j}$ to $y(t_0+ c_j h),\, j=1, \ldots ,s$ we obtain a new set of approximations

$$\begin{aligned} Y_{1,j} \; \simeq \quad y(t_1 + c_j h) \quad \hbox {where} \quad t_1 = t_0 + h, \end{aligned}$$

by means of the equations

$$\begin{aligned} Y_{1,j}&= \sum _{k=1}^s a_{jk} Y_{0,k} + h \; \sum _{k=1}^s b_{jk} f(t_0+c_k h, Y_{0,k}) \nonumber \\&\quad +\, h \; \sum _{k=1}^{j-1} r_{jk} f(t_1+c_k h, Y_{1,k}), \qquad j=1, \ldots ,s, \end{aligned}$$

(2)

where the elements of

$$\begin{aligned} A = ( a_{jk}) \in \, \mathbb {R}^{s \times s}, \quad B = ( b_{jk}) \in \, \mathbb {R}^{s \times s}, \quad R = ( r_{jk}) \in \, \mathbb {R}^{s \times s}, \end{aligned}$$

with $A$ and $B$ full matrices and $R$ strictly lower triangular are the free parameters that define the method with $A \mathbf {e} = \mathbf {e}= \left( 1, \ldots , 1 \right) ^T \in \, \mathbb {R}^s$ to ensure the preconsistency condition.

Extending in a natural way the definition of fitted RK and multistep methods we will say that the explicit two step peer method (2) is fitted to $\mathcal {F}_q$ if

$$\begin{aligned} \varphi (t_1 + c_j h)&= \sum _{k=1}^s a_{jk} \; \varphi (t_0+c_k h) + h \sum _{k=1}^s b_{jk}\; \dot{\varphi } (t_0 + c_k h) \nonumber \\&\quad +\, h \sum _{k=1}^{j-1} r_{jk}\; \dot{\varphi } (t_1 + c_k h), \quad j=1, \ldots ,s \end{aligned}$$

(3)

holds for all $\varphi \in \mathcal {F}_q$.

From this definition it is clear that for a given set of admissible nodes at each stage we have at least $2 s$ free parameters and this flexibility allow us to obtain explicit methods that attain high stage order. The authors of the present paper have proved in [2] that $s$ stage peer methods can attain order $q= 2 s -1$, also with the same stage order. In this paper we will show that it is possible to obtain explicit peer methods fitted to spaces $\mathcal {F}_q$ with $q$ large, taking enough number of stages. Recall also that in the case of fitting to polynomial spaces i.e. $\mathcal {F}_q = {\varPi }_q = \langle 1,\,t,\,\ldots ,\,t^q \rangle$, several methods have been proposed in [16–18] that are competitive with the standard integrators in use, and in particular, in [2] methods with 2 and 3 stages and order 3 and 5 respectively were obtained with optimal stability and accuracy properties. This is important since usually fitted methods tend to standard ones when the fitting parameter $\nu = \omega \,h$ tend to zero.

The paper is organized as follows: In Sect. 2, after introducing a class of explicit two step peer methods with $s$-stages that are strongly zero-stable, we show that under some minor restrictions on the nodes for any fitting space $\mathcal {F}_q$ with $q= 2 s -1$ there exists a unique fitted method for $|h|$ sufficiently small. A remarkable property is that, as in the polynomial case [2], in the fitting conditions the $2s^2 -s$ free parameters that define the coefficients of (2) can be separated into $s$ sets of linear equations with $(2 s-1)$ parameters in each set, and this fact simplifies greatly the calculation of the coefficients. In particular if $\mathcal {F}_q$ is the space of solutions of a linear homogeneous differential equation with constant coefficients of order $(q+1)$ then the coefficients of (2) are independent of the starting time $t_0$.

In Sect. 3, fitted two stage peer methods to some four dimensional fitting spaces $\mathcal {F}_3$ are constructed. For $\mathcal {F}_3(\omega ) = \langle 1, t, \cos (\omega \, t), \sin (\omega \, t) \rangle$ the coefficients are explicitly given in terms of $d=c_2-c_1$ and $\nu = \omega \, h$ showing that they tend to those of the polynomial case when $\omega \rightarrow 0$ i.e. $\nu \rightarrow 0$. Also a study of the stability on the real and imaginary axes is given.

In Sect. 4, the three-stage peer methods fitted to some 6-dim, fitting spaces $\mathcal {F}_5$ are studied. Here the nodes are taken from [2] and only fitting spaces that are solution of linear homogeneous equations with constant coefficients are considered. Finally, in Sect. 5 some numerical experiments are presented to show the performance of the above fitted methods for problems with oscillatory solutions. The proposed methods are compared to exponentially fitted Adams–Bashforth–Moulton method with the same order in PECE mode.

2 Fitted Two Step Peer Methods

In our study of fitted peer methods of type (2) it will be sufficient to consider a scalar equation ($m=1$) and the methods can be written in the vector form

$$\begin{aligned} \mathbf {Y}_1 = A \; \mathbf {Y}_0 + h \; B \; \mathbf {f}_0 + h \; R \; \mathbf {f}_1, \end{aligned}$$

(4)

where, to simplify, we have used the following notations

$$\begin{aligned} \mathbf {Y}_k&= \left( Y_{k,1}, \ldots , Y_{k,s} \right) ^T \in \, \mathbb {R}^s,\end{aligned}$$

(5)

$$\begin{aligned} \mathbf {c}&= \left( c_1, \ldots , c_s \right) ^T \in \, \mathbb {R}^s, \end{aligned}$$

(6)

$$\begin{aligned} \mathbf {f}_k&= f( t_k \mathbf {e} + h \mathbf {c} , \mathbf {Y}_k ) = \left( f(t_k + h c_j, Y_{k,j} )\right) _{j=1}^s \in \, \mathbb {R}^s. \end{aligned}$$

Before imposing the fitting conditions observe that (4) is a multivalued method and the zero stability requires that $A$ has a unit eigenvalue $\lambda _1(A)=1$ and the remaining eigenvalues $| \lambda _j(A)| \, \le 1$, $j=2, \ldots ,s$ and those of modulus one correspond to simple elementary divisors. Here as in [2, 16–18] we will consider methods with the stronger requirement

$$\begin{aligned} \lambda _1 (A)=1, \qquad \lambda _j (A)=0, \quad j=2, \ldots ,s. \end{aligned}$$

(7)

Furthermore, following the ideas of [2], to simplify the derivation of the fitting methods and to get methods with high stage order, we will take $A$ with the form

$$\begin{aligned} A = P^{-1} \; \widehat{A} \; P, \end{aligned}$$

(8)

with $P=(p_{ij}) \in \, \mathbb {R}^{s \times s}$ a lower triangular matrix with ones at the diagonal, and $\widehat{A}=(\hat{a}_{ij}) \in \, \mathbb {R}^{s \times s}$ upper triangular whose diagonal is $\hbox {diag}(\widehat{A})=(1, 0, \ldots , 0)$, that clearly satisfy (7). Note that the preconsistency condition of (4) $A \mathbf {e} = \mathbf {e}$ implies that $P \mathbf {e} = \mathbf {e}_1 = \left( 1, \,0,\, \ldots , 0 \right) ^T \in \, \mathbb {R}^s$ and then we have $s(s-1)/2$ free parameters in $\widehat{A}$ and $s(s-1)/2$ free parameters in $P$ together with the $s-1$ consistency conditions of $P \mathbf {e} = \mathbf {e}_1$.

By using (8), Eq. (4) can be rewritten as

$$\begin{aligned} P \; \mathbf {Y}_1 = \widehat{A} \; P \; \mathbf {Y}_0 + h \; \widehat{B} \; P \; \mathbf {f}_0 + h \; \widehat{R} \; P \; \mathbf {f}_1 \end{aligned}$$

(9)

with

$$\begin{aligned} B = P^{-1} \; \widehat{B} \; P, \qquad R = P^{-1} \; \widehat{R} \; P \,. \end{aligned}$$

(10)

We associate to (4) the linear $s$-dim vector valued operator $\mathcal {L} [\varphi ; h]$ defined for a smooth scalar function $\varphi$ and a step size $h$ at time $t$ by

$$\begin{aligned} \mathcal {L} [\varphi ; h](t)&\equiv \varphi ( (t+h) \mathbf {e} + h \mathbf {c} ) - A \; \varphi ( t \mathbf {e} + h \mathbf {c}) \nonumber \\&\quad - h \; B \; \dot{\varphi } ( t \mathbf {e} + h \mathbf {c}) - h \; R \; \dot{\varphi } ( (t+h) \mathbf {e} + h \mathbf {c} ). \end{aligned}$$

(11)

Now we introduce the following definition:

Definition 1

For a given set of admissible nodes and a fitting space $\mathcal {F}_q = \langle \varphi _0(t), \varphi _1(t), \ldots ,\varphi _q(t) \rangle$ the method (4) is fitted to the linear space $\mathcal {F}_q$ with step size $h$ at $t_0$ if

$$\begin{aligned} \mathcal {L} [\varphi ; h] (t_0) = 0, \qquad \forall \varphi \in \mathcal {F}_q. \end{aligned}$$

(12)

As a first remark observe that if the starting values $\left( Y_{0,j} \right) _{j=1}^s$ of the peer method (9) belong to a solution of the differential equation contained in the fitting space $\mathcal {F}_q$ in the sense that there exist $\varphi \in \mathcal {F}_q$ such that

$$\begin{aligned} \dot{\varphi }(t) = f( t, \varphi (t) ), \quad \varphi (t_0+c_j h) = Y_{0,j}, \quad j=1, \ldots ,s, \end{aligned}$$

then the unique solution of (4) gives the exact values of the solution i.e. $Y_{1,j}= \varphi (t_1+ c_j h)$.

For $\mathcal {F}_q = {\varPi }_q$ i.e. in the polynomial case, $q$ is called the stage order of (4) and then (12) is equivalent to

$$\begin{aligned} \mathcal {L} [y; h] (t) = \mathcal {O} ( h^{q+1} ) \quad \hbox {for all} \quad y \in \mathcal {C}^{\infty } \end{aligned}$$

and this condition turns out to be independent of $t$.

For our class of strongly zero stable peer methods where $A$ is given by (8) we have

$$\begin{aligned} \mathcal {L} [\varphi ; h] (t_0) = P^{-1} \; \widehat{\mathcal {L}} [\varphi ; h] (t_0), \end{aligned}$$

(13)

with

$$\begin{aligned} \widehat{\mathcal {L}} [\varphi ; h] (t_0) = \mathbf {Z}(t+h) - \widehat{A} \; \mathbf {Z}(t) - h \widehat{B} \; \dot{\mathbf {Z}}(t) - h \widehat{R} \; \dot{\mathbf {Z}}(t+h) \end{aligned}$$

(14)

and $\mathbf {Z}(t) = P \; \varphi ( t \mathbf {e} + h \mathbf {c})$. In view of (13) the method (4) is fitted to $\mathcal {F}_q$ at $t_0$ with step size $h$ iff

$$\begin{aligned} \widehat{\mathcal {L}} [\varphi ; h] (t_0) = 0, \qquad \forall \varphi \in \mathcal {F}_q. \end{aligned}$$

(15)

Next we give sufficient conditions on the functions of $\mathcal {F}_q$ that ensure that $\mathcal {L} [\varphi ; h](t_0)$ is independent of $t_0$ and therefore the coefficients of the fitted method can be chosen independent of $t_0$.

Theorem 1

Let $\mathcal {F}_q$ be the $(q+1)$-dim space of solutions of a homogeneous linear differential equation with constant coefficients with order $(q+1)$. If the linear operator $\mathcal {L}$ given by (11) with $A,\, B$ and $R$ independent of $t$ satisfies

$$\begin{aligned} \mathcal {L} [\varphi ; h](t_0) = 0 , \quad \forall \varphi \in \mathcal {F}_q \end{aligned}$$

then

$$\begin{aligned} \mathcal {L} [\varphi ; h](t) = 0 , \quad \forall \varphi \in \mathcal {F}_q, \quad \forall \; t \in [t_0, t_0+T]. \end{aligned}$$

Proof

For simplicity we will take $t_0=0$. Suppose that $\mathcal {F}_q$ is the basis of solutions of the linear equation

$$\begin{aligned} Q(D) u (t) \equiv \left( D^{q+1} + a_q \; D^q + \ldots + a_0 \right) u(t) = 0, \end{aligned}$$

(16)

with real constants $a_j,\, j=0, \ldots ,q$ where $D$ denotes the time derivative. By the theory of ODEs we know that for every root $\alpha \in \mathbb {C}$ of the characteristic polynomial of (16) $Q(z)=0$ with multiplicity $k$ then there exists an invariant subspace of linearly independent solutions of the form

$$\begin{aligned} \varphi _0(t)= \exp ( \alpha t), \quad \varphi _1(t)= t \; \exp ( \alpha t), \; \ldots , \varphi _{k-1}(t)= t^{k-1} \; \exp ( \alpha t). \end{aligned}$$

(17)

Next we will show that the time invariance of $\mathcal {L}$ holds for the invariant subspace associated to $\alpha$, i.e. $\mathcal {L}[\varphi _j; h](0)=0,\, j=0, \ldots ,k-1$ implies $\mathcal {L}[\varphi _j; h](t)=0,\, j=0, \ldots ,k-1$.

For $\varphi _0 ( \cdot ) = \exp ( \alpha \cdot )$ the terms of the vector valued functions of $\varphi _0$ in (9), e.g. $\varphi _0 ( t \mathbf {e} + h \mathbf {c} )$ satisfy

$$\begin{aligned} \varphi _0 ( t \mathbf {e} + h \mathbf {c})&= \exp \left[ \alpha ( t \mathbf {e} + h \mathbf {c} ) \right] \\&= \exp ( \alpha t) \; \exp ( \alpha h \mathbf {c} ) \\&= \exp ( \alpha t) \; \varphi _0 ( h \mathbf {c} ). \end{aligned}$$

Then substituting into the right hand side of (11) we have

$$\begin{aligned} \mathcal {L} [\varphi _0; h] (t) = \exp ( \alpha t ) \, \mathcal {L} [\varphi _0; h] (0). \end{aligned}$$

(18)

For the function $\varphi _1(t) = t \, \exp ( \alpha t )$ that satisfies $\varphi _1 (t) \equiv \partial _{\alpha } \varphi _0 (t)$, by the linearity of $\mathcal {L}$ and (18) we have

$$\begin{aligned} \mathcal {L} [\varphi _1; h] (t)&= \mathcal {L} [\partial _{\alpha } \varphi _0; h] (t) \\&= \partial _{\alpha } \mathcal {L} [\varphi _0; h] (t) \\&= \partial _{\alpha }\left[ \exp ( \alpha t) \, \mathcal {L} [\varphi _0 ; h ](0) \right] \\&= t \exp ( \alpha t) \;\mathcal {L}[ \varphi _0 ; h](0) + \exp ( \alpha t) \; \partial _{\alpha } \mathcal {L}[\varphi _0 ; h](0) \\&= t \exp ( \alpha t) \; \mathcal {L}[ \varphi _0 ; h](0) + \exp ( \alpha t) \; \mathcal {L}[\varphi _1 ,h](0). \end{aligned}$$

Hence if $\mathcal {L} [\varphi _1; h] (0) = \mathcal {L} [\varphi _0; h] (0) = 0$ then $\mathcal {L} [\varphi _1; h] (t)= 0$ for all $t$.

The above approach extends successively to

$$\begin{aligned} \varphi _j (t) = t^j \; \exp ( \alpha t) = \dfrac{1}{j!} \partial _{\alpha }^{j} \varphi _0 (t), \quad j=2, \ldots , k-1. \end{aligned}$$

Finally since the sets of functions (17) for all roots $\alpha$ of the characteristic polynomial of (16) are a basis of $\mathcal {F}_q$, the theorem holds for this particular basis and due to the linearity of $\mathcal {L}$ it also holds for any basis. $\square$

Remarks

• From this Theorem it follows that for fitting spaces of solutions of linear homogeneous differential equations with constant coefficients if the available coefficients $A, B, R$ (that may depend on the nodes and the step size $h$) of (9) are fitted for some particular $t_0$ then they are fitted for all $t$ in the sense of above Definition 1. Further due to (12) this Theorem also holds for the operator $\widehat{\mathcal {L}}$.

• For fitting spaces that satisfy the assumptions of Theorem 1 if we take as basis point $t_0= -h c_1$ then $\widehat{\mathcal {L}} [\varphi ; h] (- h c_1)$ depends on the nodes in the form of differences $(c_2-c_1), \ldots (c_s-c_1)$, therefore for the fitting conditions we may consider the differences to a fixed node.

• For a $(q+1)$-dim basis of solutions $F_q = \langle \varphi _0(t)=1, \varphi _1(t), \ldots , \varphi _q(t) \rangle$ of the linear homogeneous equation with constant coefficients

  $$\begin{aligned} Q(D) u(t) \equiv u^{(q+1)}(t) + a_q u^{(q)}(t)+ \ldots + a_1 u^{(1)}(t) = 0 \end{aligned}$$

  the functions $\varphi _j$ depend on the roots $0, \omega _1, \ldots ,\omega _r$ of the characteristic polynomial

  $$\begin{aligned} Q(z)= z^{q+1}+ a_q z^q + \ldots +a_1 z = z^{\beta _0} \; (z- \omega _1)^{\beta _1} \ldots (z- \omega _r)^{\beta _r} \end{aligned}$$

  with $\beta _0 + \beta _1 + \ldots + \beta _r = q+1$. Clearly when all $\omega _j \rightarrow 0$ then $Q(z) \rightarrow z^{q+1}$ and the solutions of $D^{q+1} u(t)=0$ is the polynomial basis $\varphi _j (t) = t^j, j=0, \ldots ,q$. Because of this the coefficients of a two step peer fitted method will be functions of $h \omega _j = \nu _j$ such that when all $\nu _j \rightarrow 0$, tend to those of a polynomially fitted two step peer method.

The fitting conditions (14, 15) define the available parameters $\widehat{A} , \widehat{B}$ and $\widehat{R}$ as solutions of $s$ independent, decoupled sets of $q+1$ linear equations each of them containing $2s$ unknowns, corresponding to one row of the three matrices. In the polynomial case it has been studied in [2] the conditions under which the order conditions (15) have a unique solution with maximal order $q=2s-1$.

Next we will study the existence of two step peer methods with $s$ stages fitted to general $2s$ dimensional spaces $\mathcal {F}_{2s-1} = \langle \varphi _0=1, \varphi _1, \ldots ,\varphi _{2s-1} \rangle$ at a given time $t_0$, that is, the existence of a unique solution of the order conditions (15) with $\widehat{\mathcal {L}}$ defined by (14) in the free parameters of $\widehat{A} , \widehat{B}$ and $\widehat{R}$.

We start considering the first component of $\widehat{\mathcal {L}}$ that is given by

$$\begin{aligned} \widehat{\mathcal {L}}_1[\varphi ; h ] (t_0)&= z_1(t_0 + h) - z_1(t_0) \nonumber \\&\quad - \sum _{k=1}^s \widehat{a}_{1k} z_k (t_0) - h \sum _{k=1}^s \widehat{b}_{1k} \dot{z}_k (t_0), \end{aligned}$$

(19)

where $z_j(t)$, the components of $\mathbf {Z} (t)$, are defined in terms of $\varphi (t)$ by

$$\begin{aligned} (z_1(t), z_2(t), \ldots , z_s(t) )^T = P \; \varphi ( t \mathbf {e} + h \mathbf {c}) \end{aligned}$$

Putting

$$\begin{aligned} \widehat{\mathbf {a}} =(1, \widehat{a}_{12}, \ldots , \widehat{a}_{1s}), \qquad \widehat{\mathbf {b}} = ( \widehat{b}_{11}, \widehat{b}_{12}, \ldots , \widehat{b}_{1s}) \end{aligned}$$

the operator (19) becomes

$$\begin{aligned} \widehat{\mathcal {L}}_1[\varphi ; h](t_0)&= \varphi (t_0+ (1+c_1)h) - \varphi (t_0+ c_1 h) \nonumber \\&\quad - \widehat{\mathbf {a}} \; P \; \varphi (t_0 \mathbf {e} + h \mathbf {c}) - h \widehat{\mathbf {b}} \; P \; \dot{\varphi } (t_0 \mathbf {e} + h \mathbf {c}) \end{aligned}$$

(20)

and substituting the Taylor expansion of $\varphi$ at $t_0$ in the right hand sides of (20) we have

$$\begin{aligned} \widehat{\mathcal {L}}_1[\varphi ; h](t_0) = \sum _{j \ge 1} \dfrac{ h^j}{ j!} \; \mu _j \; \varphi ^{(j)} (t_0), \end{aligned}$$

(21)

where

$$\begin{aligned} \mu _j = (1+c_1)^j - c_1^j - \widehat{\mathbf {a}} \; P \; \mathbf {c}^j - j \; \widehat{\mathbf {b}} \; P \; \mathbf {c}^{j-1}. \end{aligned}$$

(22)

As remarked above for the polynomial basis $\varphi = t^k, k=1, \ldots , 2s-1$ the fitting conditions

$$\begin{aligned} \widehat{\mathcal {L}}_1[t^k; h](t_0) = 0, \quad k=1, \ldots , 2s-1, \end{aligned}$$

are equivalent to

$$\begin{aligned} \mu _k = 0, \qquad k=1, \ldots , 2s-1 \end{aligned}$$

that are linear equations in the unknowns $\widehat{\mathbf {a}}$ and $\widehat{\mathbf {b}}$ that possess a unique solution.

For a general fitting space $\mathcal {F}_{2s-1}$ the fitting conditions

$$\begin{aligned} \widehat{\mathcal {L}}_1[\varphi _k ; h](t_0) = 0, \quad k=1, \ldots , 2s-1, \end{aligned}$$

taking into account (21) can be written as

$$\begin{aligned} \sum _{j=1}^{2s-1} \dfrac{ h^j}{ j!} \; \mu _j \; \varphi _k^{(j)} (t_0) = \mathcal {O} ( h^{2s}), \quad k=1, \ldots , 2s-1, \end{aligned}$$

or else

$$\begin{aligned} \Big ( \mu _1 h , \mu _2 \dfrac{h^2}{2!}, \ldots , \mu _{2s-1} \dfrac{h^{2s-1}}{(2s-1)!} \Big ) \; W ( \varphi _1, \ldots , \varphi _{2s-1} )(t_0) = \mathcal {O} ( h^{2s} ). \end{aligned}$$

Since the Wronskian matrix $W ( \varphi _1, \ldots , \varphi _{2s-1})(t_0)$ is non-singular these equations define for sufficiently small $h>0$

$$\begin{aligned} \mu _j = \mu _j (h, t_0), \qquad j=1, \ldots , 2s-1, \end{aligned}$$

further $\mu _j(h, t_0) \rightarrow 0$ as $h \rightarrow 0$.

Now taking into account (22) we have

$$\begin{aligned} \widehat{\mathbf {a}} \; P \; \mathbf {c}^j + j \; \widehat{\mathbf {b}} \; P \; \mathbf {c}^{j-1} = (1+c_1)^j - c_1^j - \mu _j(h, t_0), \end{aligned}$$

that define uniquely the unknowns $\widehat{\mathbf {a}}$ and $\widehat{\mathbf {b}}$ with the same restrictions as in polynomial case for $h$ sufficiently small. Also these coefficients tend to those of the polynomial case when $h \rightarrow 0$.

Since a similar study can be carried out for the remaining components of $\widehat{\mathcal {L}}$ we may conclude with the following Theorem.

Theorem 2

Suppose that for a given set of admissible fixed nodes and constant matrix $P$ the polynomially fitted two step peer method (4), (8) with $s$ stages has a unique solution with stage order $2s-1$, then

• 1. For any linear space $\mathcal {F}_{2s-1} = \langle 1, \varphi _1(t), \ldots , \varphi _{2s-1}(t) \rangle$ there exist a unique $s$-stage two step peer method fitted to this space for $h$ sufficiently small. This peer method has the same nodes and $P$-matrix as the polynomially fitted method to ${\varPi }_{2s-1}$ and the coefficients

  $$\begin{aligned} \widehat{A}_{\mathcal {F}} = \widehat{A}(t_0, h), \quad \widehat{B}_{\mathcal {F}} = \widehat{B}(t_0, h), \quad \widehat{R}_{\mathcal {F}} = \widehat{R}(t_0, h), \end{aligned}$$

  may depend (apart from the fitting space) on $t_0$ and $h$.

• 2. If $\mathcal {F}_{2s-1}$ is a separable basis the coefficients are independent of $t_0$.

• 3. Further when all the roots of the polynomial $Q(D)$ tend to zero the coefficients $\widehat{A}_{\mathcal {F}},\,\widehat{B}_{\mathcal {F}},\,\widehat{R}_{\mathcal {F}}$ tend to those of the polynomial case.

3 Two Stage Functionally Fitted Peer Methods

With $s=2$ the preconsistency condition $P \mathbf {e} = \mathbf {e}_1$ implies that the lower triangular matrix $P$ is the constant matrix

$$\begin{aligned} P = \begin{pmatrix} 1 &{}\quad 0 \\ -1 &{}\quad 1 \end{pmatrix}. \end{aligned}$$

(23)

On the other hand the matrices $\widehat{A} , \widehat{B} , \widehat{R}$ will have the form

$$\begin{aligned} \widehat{A} = \begin{pmatrix} 1 &{}\quad \widehat{a}_{12} \\ 0 &{}\quad 0 \end{pmatrix}, \quad \widehat{B} = \begin{pmatrix} \widehat{b}_{11} &{}\quad \widehat{b}_{12} \\ \widehat{b}_{21} &{}\quad \widehat{b}_{22} \end{pmatrix}, \quad \widehat{R} = \begin{pmatrix} 0 &{}\quad 0 \\ \widehat{r}_{21} &{}\quad 0 \end{pmatrix}, \quad \end{aligned}$$

(24)

and

$$\begin{aligned} \mathbf {Z}(t) = P \; \varphi ( t \mathbf {e} + h \mathbf {c}) = \begin{pmatrix} \varphi (t+ c_1 h) \\ - \varphi (t+ c_1 h) + \varphi (t+c_2 h) \end{pmatrix}. \end{aligned}$$

(25)

Since the linear operator $\widehat{\mathcal {L}}$ of (14) is

$$\begin{aligned} \widehat{\mathcal {L}} [\varphi ; h](t)= \mathbf {Z}(t+h) - \widehat{A} \; \mathbf {Z}(t) - h \widehat{B} \; \dot{\mathbf {Z}}(t) - h \widehat{R}\; \dot{\mathbf {Z}}(t+h) \end{aligned}$$

(26)

we have two order conditions and in each condition there are three free parameters. The first equation with the parameters $\widehat{a}_{12}, \widehat{b}_{11}, \widehat{b}_{12}$ can be written in the form

$$\begin{aligned}&[\varphi (t+c_2 h) - \varphi (t+c_1 h)] \widehat{a}_{12} + h \dot{\varphi } (t+c_1 h) \widehat{b}_{11} \nonumber \\&+\, h [ \dot{\varphi } (t+c_2 h) - \dot{\varphi } (t+c_1 h)] \widehat{b}_{12} = \varphi (t+h + c_1 h) - \varphi (t+c_1 h). \end{aligned}$$

(27)

The second one with the parameters $\widehat{b}_{21}, \widehat{b}_{22}, \widehat{r}_{21}$ is

$$\begin{aligned} h \dot{\varphi } (t+c_1 h) \widehat{b}_{21}&+ h [ \dot{\varphi } (t+c_2 h) - \dot{\varphi } (t+c_1 h)] \widehat{b}_{22} \nonumber \\&+ h \dot{\varphi } (t+h + c_1 h) \widehat{r}_{21} = \varphi (t+ h + c_2 h) - \varphi (t+ h +c_1 h). \end{aligned}$$

(28)

These parameters will be determined by imposing that (27), (28) hold for the functions $\varphi _j(t), j=1,2,3$ of a fitting space

$$\begin{aligned} \mathcal {F}_3 = \langle 1 , \varphi _1(t), \varphi _2(t), \varphi _3(t) \rangle , \end{aligned}$$

therefore we have two sets of three linear equations that are independent between them.

If $\mathcal {F}_3$ is the space of solutions of a homogeneous linear differential equation with constant coefficients of order four, as shown in Theorem 1 the unknowns in (27), (28) are independent of $t$, hence by taking $t= - h c_1$ and putting $d=c_2-c_1$, the above equations can be written as

$$\begin{aligned}{}[\varphi (h d) - \varphi (0)] \widehat{a}_{12} + h \dot{\varphi } (0) \widehat{b}_{11} + h [ \dot{\varphi } (h d) - \dot{\varphi } (0)] \widehat{b}_{12} = \varphi (h) - \varphi (0). \end{aligned}$$

(29)

and

$$\begin{aligned} h \dot{\varphi } (0) \widehat{b}_{21} + h [ \dot{\varphi } (h d) - \dot{\varphi } (0)]+ \widehat{b}_{22} h \dot{\varphi } (h) \widehat{r}_{21} = \varphi ((d+1) h) - \varphi (h). \end{aligned}$$

(30)

Next we assume that $\mathcal {F}_3$ is the space of solutions of a linear homogeneous equation with constant coefficients that includes the pair of trigonometric functions $\sin ( \omega \, t), \cos (\omega \, t)$ with a constant positive frequency $\omega$, then we can take an additional function that will have the form $\varphi (t)= \exp ( \alpha t)$ with real $\alpha \ne 0$ or else $\varphi (t) = t$. With this last choice

$$\begin{aligned} \mathcal {F}_3(\omega ) = \langle 1 , t, \sin (\omega \,t), \cos (\omega \,t) \rangle \equiv \langle 1 , t, \hbox {Re}(e^{i\omega \,t}), \hbox {Im}(e^{i\omega \,t}) \rangle \end{aligned}$$

(31)

Now substituting into (27) the basis functions, the coefficients $\widehat{a}_{12}, \widehat{b}_{11}, \widehat{b}_{12}$ are defined by

$$\begin{aligned} \widehat{a}_{12}&= \dfrac{ -1 + \cos \nu + \cos (d\nu ) - \cos \nu \cos (d\nu ) + \nu \sin (d\nu ) - \sin \nu \sin (d\nu )}{{\Delta }_1}, \nonumber \\ \widehat{b}_{11}&= \dfrac{ (-2 +d - d \cos \nu )(1- \cos (d\nu ) + d \sin \nu \sin (d\nu )}{ {\Delta }_1}, \nonumber \\ \widehat{b}_{12}&= - \dfrac{ \nu - d\nu + d\nu \cos \nu - \nu \cos (d\nu ) - \sin \nu + \sin (d\nu ) \sin (\nu -d\nu )}{\nu {\Delta }_1}, \end{aligned}$$

(32)

with $d=c_2-c_1,\, \nu = h \omega$ and ${\Delta }_1 = -2 + 2 \cos (d\nu ) + d\nu \sin (d\nu )$.

Similarly from the Eq. (28) we get

$$\begin{aligned} \widehat{r}_{21}&= \dfrac{ \sin (d\nu /2) \left( d\nu \cos (d\nu /2) - 2 \cos \nu \sin (d\nu /2) \right) }{{\Delta }_2}, \nonumber \\ \widehat{b}_{21}&= - \dfrac{ \sin (d\nu /2) \left( d\nu \cos (\nu -d\nu /2) - 2 \cos \nu \sin (d\nu /2) \right) }{ {\Delta }_2}, \nonumber \\ \widehat{b}_{22}&= - \dfrac{ \sin (\nu /2) \left( d\nu \cos (\nu /2) + \sin (\nu /2) - \sin (d\nu + \nu /2) \right) }{ {\varDelta }_2}, \end{aligned}$$

(33)

with ${\Delta }_2 = 2 \nu \sin (d\nu /2) \sin (\nu /2) \sin ((\nu -d\nu )/2)$.

Note that when $\nu \rightarrow 0$ the above expressions tend to those of the polynomial case

$$\begin{aligned} \widehat{a}_{12}&= \frac{-2 +3 d}{d^3}, \qquad \widehat{r}_{21} = \frac{d\,(d^2-6)}{6\,(d-1)},\nonumber \\ \widehat{b}_{11}&= \frac{2 -3\, d + d^2}{d^2}, \qquad \widehat{b}_{12} = \frac{1 -d}{d^2}, \nonumber \\ \widehat{b}_{21}&= \frac{(6-d)\, d^2}{6\,(d-1)}, \qquad \widehat{b}_{22} = \frac{d\,(3+2 \,d)}{6\,(d-1)}. \end{aligned}$$

(34)

In [2] a detailed study was made of the stability region of the classical peer method, in particular of the stability intervals along the real axis and along the imaginary axis, as a function of $d$. Choosing $d=d_1$ where $d_1=(-15 + \sqrt{609})/8 \approx 1.2097$, the stability interval along the real axis is maximised, while the size of the stability interval along the imaginary axis is quite acceptable and at the same time the error constants of both stages (see [2], p. 397 and 402) are kept sufficiently small. The corresponding region of stability is displayed in the left part of Fig. 1. As we will mainly focus in this paper on oscillatory problems, i.e. problems for which all eigenvalues of the Jacobian lie along the imaginary axis, we have searched for alternative choices of $d$ for which the size of the stability interval along the imaginary axis is approximately equally large. Therefore, in the right part of Fig. 1, we have made the choice $d=d_2$, where $d_2=0.85$. This choice leads to a peer method with a smaller interval of stability along the real axis, but along the imaginary axis the stability interval is almost the same as for the choice $d=d_1$. In the case $d=d_2$ however, the error constants are half as large as in the case $d=d_1$ and moreover, since $d_2 \in [0,1]$, this method allows to integrate a problem without function evaluations beyond the endpoint of the integration interval.

Fig. 1

Left: plot of the stability region of the non-fitted peer $s=2$ method for $d=d_{1}$ (left) and $d=d_2$ (right)

From Fig. 1 we see that the border of the stability region is very close to the imaginary axis for sufficiently small values of $z=\lambda \,h$, where $y'=\lambda \, y$ is the test equation. This behaviour, which makes the methods very suited for solving problems with oscillatory solutions, is also present (even more in the $d=d_2$ case than in the $d=d_1$ case) for the EF versions as long as $\omega \,h$ is sufficiently small (recall that for $\omega \rightarrow 0$ an EF method reduces to the underlying polynomial method). As an example, in Fig. 2 the stability regions are shown for methods fitted to $\omega \,h=1$. We notice in both cases that the border of the stability region crosses the imaginary axis at $z=i$. Recall that when an $s$-stage peer method fitted to $\mathcal {F}_3(\omega )$ is applied with step size $h$ to the complex test equation $y'=i\,\omega \,y$, the numerical solution is supposed to coincide with the exact one. Since the numerical solution can be expressed in terms of powers of the eigenvalues of the stability matrix $M(i\,\omega \,h)$ of the method, this means that one of these eigenvalues, $\lambda _1$ say, must take the form $\lambda _1=\exp (i\,\omega \,h)$, such that $|\lambda _1|=1$, i.e. $z=i\,\omega \,h$ cannot lie in the interior part of the region of stability, it can at the best lie on the border of the stability region, which is the case if all $s-1$ other eigenvalues of the stability matrix $M(z)$ have modulus one at most. Choosing $d=d_1$ this is the case as long as $\omega \,h < 2.72\ldots$, for the choice $d=d_2$ as long as $\omega \,h \approx 1.41\ldots$. This imposes however no extra restriction in practice, since we already assume $\omega \,h$ to be small enough (smaller than $\pi /2$ say) in order to avoid singularities in the coefficients of the method.

Fig. 2

Left: plot of the stability region of the peer $s=2$ method fitted to $\mathcal {F}_3$ with $\omega \,h=1$ for $d=d_{1}$ (left) and $d=d_2$ (right)

Taking into account all above arguments, we can conclude that for oscillatory problems the method with $d=d_2$ should be preferred above $d=d_1$. Numerical experiments (see Sect. 5) confirm this.

4 Three Stage Functionally Fitted Peer Methods

In [2] the class of 3-stage 2-step peer methods fitted to

$$\begin{aligned} \mathcal {F} = \langle 1, t, t^2, t^3, t^4, t^5 \rangle ={\varPi }_5 \end{aligned}$$

(35)

was studied. The coefficients of the peer method can be expressed in terms of the free parameters $p_{32}, d_2=c_2-c_1$ and $d_3=c_3-c_1$, which were chosen to maximize the stability interval along the real axis and along the imaginary axis and to minimize the coefficients of the leading term of the local error. After extensive numerical search it was found that for $p_{32}= -0.522, d_2= 0.904$ and $d_3= 1.141$ the corresponding fifth order method has a real stability interval $[-2.02, 0]$ and a stability interval along the imaginary axis of $[-0.24,\, 0.24]$. Figure 3, which plots this stability region, shows however that along the imaginary axis the spectral radius of the stability matrix remains very close to unity for a much larger interval: in practice, for $y'=i\,\lambda \,y$, stability is obtained for $\lambda \,h \in [-0.6,\,0.6]$.

Fig. 3

Stability region for the three-stage peer method with $p_{32}=-0.522,\, d_2= 0.904$ and $d_3=1.141$

Now, we consider EF variants of this particular 3-stage peer method, which are fitted to

$$\begin{aligned} \mathcal {F}_5(\omega _1,\omega _2) = \langle 1 , t, \sin (\omega _1\,t), \cos (\omega _1\,t), \sin (\omega _2\,t), \cos (\omega _2\,t) \rangle \end{aligned}$$

(36)

and will especially focus on three particular cases:

• $\mathcal {F}_5(\omega ,0)= \langle 1 , t, t^2, t^3, \sin (\omega \,t), \cos (\omega \,t) \rangle$

• $\mathcal {F}_5(\omega ,\omega )= \langle 1 , t, \sin (\omega \,t), \cos (\omega \,t), t\,\sin (\omega \,t), t\,\cos (\omega \,t) \rangle$

• $\mathcal {F}_5(\omega ,2\,\omega )=\langle 1 , t, \sin (\omega \,t), \cos (\omega \,t), \sin (2\omega \,t), \cos (2\omega \,t) \rangle$

In Fig. 4 the value $\eta$ of the (apparent) stability interval $[-i \eta ,\,i\,\eta ]$ along the imaginary axis for these three choices are shown as a function of $\nu =\omega \,h$. In Fig. 5 we focus on the particular choice $\nu =\omega \,h=1$ and the stability regions of these three EF variants of the peer $s=3$ stage method are shown. Since in all three cases there is a non-empty stability interval along the imaginary axis and since the boundary of the stability region is also quite close to the imaginary axis (indicating there is almost no dissipation), each of the three methods are suited to solve problems with periodic solutions.

Fig. 4

Plots of the value $\eta$ of the (apparent) stability interval $[-i\,\eta ,\,i\,\eta ]$ along the imaginary axis of the peer method fitted to $\mathcal {F}_5(\omega ,\omega _2)$ as a function of $\nu =\omega \,h$ for the peer $s=3$ method with $\omega _2=0$ (lower curve) and $\omega _2=\omega$ (middle curve) and $\omega _2=2\,\omega$ (upper curve)

Fig. 5

Plot of the stability region of the peer method fitted to $\mathcal {F}_5(\omega ,\omega _2)$ with $\omega \,h=1$ for the peer $s=3$ method with $\omega _2=0$ (left) and $\omega _2=\omega$ (middle) and $\omega _2=2\,\omega$ (right)

5 Numerical Experiments

In this section we present the results of some numerical experiments comparing the behaviour of several fitted and non fitted methods for some test problems. Due to the linear, explicit, multistep nature of the stages of the peer schemes, we use predictor-corrector pairs of linear multistep methods for comparison. First, we compare the third order peer method given in [2] with $d=0.85$ against the classical two step third-order Adams–Bashforth–Moulton pair in PECE mode (denoted by AM3). Also, we include the corresponding fitted version of the peer method and of the Adams–Bashforth–Moulton method to $\mathcal {F}_3(\omega )=\langle 1,t, \cos (\omega t), \sin (\omega t)\rangle$ (denoted by PEER2($\omega$) and AM3($\omega$) respectively).

For fifth-order schemes, we choose the classical four-step Adams–Bashforth–Moulton pair of order 5 (denoted by AM5), the fitted versions of the previous scheme to $\mathcal {F}_5(\omega ,0)$ (denoted by AM5($\omega$)), to $\mathcal {F}_5(\omega ,2\omega )$ (denoted by AM5($\omega ,\, 2\omega$)) and to $\mathcal {F}_5(\omega ,\omega )$ (denoted by AM5($\omega$, $\omega$)). The fitted multistep methods have been obtained following the ideas in [4]. For peer schemes, we present the standard PEER3 method given by the authors in [2], and similar fitted methods as the multistep ones denoted by PEER3($\omega$), PEER3($\omega ,\, 2\omega$) and PEER3($\omega ,\, \omega$) respectively.

It is worth to note that the PECE implementation of the AM3 pair as well as of the AM5 requires 2 function evaluations per step. For the PEER2 methods, we need 2 function evaluations per step as well, but for the PEER3 methods, 3 function evaluations are needed. In order to be able to compare the computational cost (total number of function evaluations, denoted as nfcn), we have applied AM3 and PEER2 with the same step sizes, but the PEER3 methods were applied with step sizes that are 50 % larger than those of the AM5 methods. The step sizes that are reported, are the ones used for the PEER3 methods.

The criterion used in the numerical comparisons is the usual test based on computing the maximum global error in the solution over the whole integration interval. All computations were carried out with 30 digits on a PC computer running python using the mpmath library. The starting approximations $Y_{0,j}$ of the peer methods as well as the ones needed for the Adams methods are the exact ones.

Problem 1

Our first test problem is the Duffing’s equation

$$\begin{aligned} q'' + (\beta ^2+k^2)q = 2k^2q^3, \end{aligned}$$

where $\beta$ and $k$ are positive constants. In our tests we have taken $\beta = 5, k=0.035$ and the initial conditions $q(0)=0, q'(0)= \beta$ which correspond to the periodic solution $q(t)=\mathrm{sn}(\beta t, k/\beta )$. In Figs. 6 and 7 we display the global errors obtained for third and fifth order schemes respectively for step sizes $h = 2^{-i}/10$, $i=1,\ldots ,5$ in the integration interval $[0,20]$ and $\omega =5$ as an estimation of the frequency.

Fig. 6

Efficiency plot of third order schemes for the Duffing problem

Fig. 7

Efficiency plot of fifth order schemes for the Duffing problem

As can be seen in Fig. 6, the efficiency curves for the two stage peer schemes with $d=1.20\ldots$ are practically the same as those for the AM3 ones. Moreover, the new peer scheme with $d=0.85$ is slighty superior to the others, as was expected due to the smaller coefficients of the leading term of the local error.

From Fig. 7 we can observe that in all cases, the fitting methods improve greatly the performance with respect to the standard non fitted methods. Also, it is worth to note that peer schemes are slighty more efficient that AM ones.

We can also see that the three fitted PEER5 methods produce results that are quite close to each other, and there is not really an advantage in choosing $\omega _2=2\,\omega =10$. This can however be explained by applying an FFT to the numerical solution over one (approximate) period of length $2\,\pi /5$. The analysis of the energy of the transformed signal reveals that the contributions of the frequencies $2\,\omega$ in $q$ and $3\,\omega \,q'$ are about equally large.

For the next problems we will consider only fifth order methods because we are interested in testing the performance when the dimension of the fitting space is large.

Problem 2

Kepler’s problem defined by the Hamiltonian function

$$\begin{aligned} H = \frac{1}{2}(p_1^2+p_2^2) -\left( q_1^2+q_2^2\right) ^{-1/2}, \end{aligned}$$

with initial conditions $q_1(0)=1-e,\; q_2(0)= 0,\; p_1(0)=0,\; p_2(0)=\left( (1+e)/(1-e) \right) ^{1/2}$, where $e \in [0,1)$ is the eccentricity of the elliptic orbit.

In the numerical experiments presented here we have chosen the values $e=0.05,\, \omega = 1$, and the integration is carried out on the interval $[0,20\pi ]$ with the steps $h= \pi / ( 10 \times 2^{i-1}) ,\, i=1,\ldots ,6$. The behaviour of the global error for the selected schemes are presented in Fig. 8.

Fig. 8

Efficiency plot of fifth-order schemes for the two body problem with eccentricity 0.05

Here again, peer schemes are more efficient than AM ones. We also observe that for both peer and AM methods, the $(\omega ,\,2\,\omega )$ combination gives the best results. Again this can be explained with an FFT applied to the numerical solution. This time, the energy spectrum reveals that the three most important contributions (in that order) correspond to the frequency $\omega$, to the constant function and to the frequency $2\,\omega$.

Problem 3

A perturbed Kepler’s problem given by the Hamiltonian function

$$\begin{aligned} H = \frac{1}{2}\left( {p}_1^2 + {p}_2^2 \right) - {\frac{1}{\left( q_1^2+q_2^2\right) ^{1/2}}} - {\frac{2\delta + \delta ^2}{3\left( q_1^2+q_2^2\right) ^{3/2}}}, \end{aligned}$$

where $\delta$ is a small positive parameter and with the initial conditions

$$\begin{aligned} q_1(0)=1, \quad q_2(0)=0, \quad p_1(0)=0, \quad p_2(0)= 1+\delta , \end{aligned}$$

whose exact solution is $q_1(t) = \cos (t + \delta t), \; q_2(t) = \sin (t + \delta t), p_i(t)= q_i'(t),i=1,2$.

The numerical results presented in Fig. 9 have been computed with the integration steps $h=\pi /(10\times 2^i), \, i=1,\dots , 5$. We take the parameter values $\delta = 10^{-2}$, $\omega = 1$ and the problem is integrated up to $t_\mathrm{end} = 10\pi$.

Fig. 9

Efficiency plot of fifth-order schemes for the perturbed Kepler’s problem with $\delta =0.01$

In this case, we again notice that the PEER3 methods perform better than the AM5 methods. Taking into account that the exact frequency is $1+\delta$ with $\delta$ small, we can understand why the $(\omega ,\omega )=(1,1)$ combination (which may be considered as the limit case of $(\omega ,\omega +\delta )$ for $\delta \rightarrow 0$) gives the best results.

Problem 4

Our last example is the Euler equation given by

$$\begin{aligned} q' = f(q)=\big ( (\alpha -\beta ) q_2 q_3,\; (1-\alpha )q_3 q_1,\; (\beta -1)q_1 q_2\big )^T, \end{aligned}$$

with the initial values $q(0)=(0,1,1)^T$. We choose the parameter values $\alpha =1+\frac{1}{\sqrt{1.51}}$ and $\beta =1-\frac{0.51}{\sqrt{1.51}}$. $\omega = 2\pi /T$, with $T=7.45056320933095$. The exact solution of this IVP is given by

$$\begin{aligned} q(t)=\bigg (\sqrt{1.51}\,\text{ sn }(t,0.51),\, \text{ cn }(t,0.51),\, \text{ dn }(t,0.51)\bigg )^T, \end{aligned}$$

where sn, cn, dn are the elliptic Jacobi functions. The integration is carried out on the interval $[0,40]$ with step sizes $h=1/(5\times 2^{j}),\, j=0,\ldots ,4$ and $w=2\pi \,i/T$ and we plot the efficiency results in Fig. 10.

Fig. 10

Efficiency plot of fifth-order schemes for the Euler equation

Once more, the PEER3 methods perform better than the AM5 methods. A Fourier analyis reveals that in the first and second component of the solution the frequencies $\omega ,\, 3\,\omega ,\, 5\,\omega ,\, \dots$ are present, while the third component can be expressed in terms of $2\,\omega ,\, 4\,\omega$, .... Taking into account the energy spectrum of the solution, it is clear why the $(\omega ,2\,\omega )$ variant produces the best results.

For the perturbed Kepler’s problem and for the Euler equation, we have examined how well invariants are preserved by peer methods, compared with the corresponding polynomial fitting peer method. In Fig. 11 the errors produced by fifth order PEER3 methods are displayed. The results agree with those displayed in Figs. 9 and 10.

Fig. 11

At the top the error in the Hamiltonian for the Perturbed Kepler’s problem and at the bottom the error in the quadratic invariant $I=y_1^2 + y_2^2 + y_3^2$ for the Euler equation

Finally, we also make a comparison of the fifth order peer methods with a standard solver like DOPRI54. We have applied the well known code with variable step size to the perturbed Kepler’s problem with $\delta =0.1$. The efficiency plot shown in Fig. 12 (which for the DOPRI54 method is practically the same in constant step size mode) illustrates the power of the peer methods for oscillatory problems.

Fig. 12

Efficiency plot of peer methods and DOPRI54 for the Perturbed Kepler’s problem with $\delta =0.1$

From the results of the above numerical experiments we can conclude that for the problems under consideration it is essential to have an accurate estimation of the dominant frequency (or frequencies). This estimate can be given, or given a numerical solution of low accuracy and an estimate of the period, an estimation for this frequency can be computed by means of a FFT. The numerical results obtained in the four examples with various choices for the frequency (or frequencies) can be well understood by such an analysis. Furthermore, for all problems the peer schemes appear to be superior in efficiency (using the number of function evaluations as a comparison tool) to the corresponding Adams–Bashforth–Moulton pairs of the same order, which were applied in PECE mode.