Negative-Order Norm Estimates for Nonlinear Hyperbolic Conservation Laws

Abstract

In this paper, we establish negative-order norm estimates for the accuracy of discontinuous Galerkin (DG) approximations to scalar nonlinear hyperbolic equations with smooth solutions. For these special solutions, we are able to extract this “hidden accuracy” through the use of a convolution kernel that is composed of a linear combination of B-splines. Previous investigations into extracting the superconvergence of DG methods using a convolution kernel have focused on linear hyperbolic equations. However, we now demonstrate that it is possible to extend the Smoothness-Increasing Accuracy-Conserving filter for scalar nonlinear hyperbolic equations. Furthermore, we provide theoretical error estimates for the DG solutions that show improvement to $(2k+m)$-th order in the negative-order norm, where $m$ depends upon the chosen flux.

1 Introduction

In this paper, we present negative-order norm estimates of the error for the Discontinuous Galerkin (DG) methods for smooth solutions to nonlinear hyperbolic conservation laws of the form

$$\begin{aligned}&u_t+ \sum \limits _{i=1}^{d}\, (f_i(u))_{x_i} =0,\quad ({\varvec{x}},t)\in \Omega \times (0,T],\end{aligned}$$

(1.1)

$$\begin{aligned}&u({\varvec{x}},0)=u_0({\varvec{x}}), \end{aligned}$$

(1.2)

where ${\varvec{x}}=(x_1,\ldots , x_d)$ and $d$ represents the highest spatial dimension. In giving these estimates, we concentrate on the method in the interior of the domain and not on the effect of the boundary terms. Therefore we always consider periodic boundary conditions (or compactly supported) and a hyperrectangular domain $\Omega =[0,1]^d.$ We assume that the flux $f_i(u), \, i=1,\cdots ,d$ is smooth enough in the variable $u$ for the requirements on our approximation. That is, when a classical solution to (1.1) exists. We note that discontinuous solutions with shocks are not covered by the analysis contained in this paper.

Recently, a priori error estimates in the $L^2$-norm for the Runge-Kutta Discontinuous Galerkin (RKDG) method for smooth solutions of nonlinear conservation laws were obtained by Zhang and Shu in a series of papers [22–24]. Optimal order estimates were given for upwind fluxes. However, there has been relatively little work on error estimates in the negative-order norm, which is related to capturing the superconvergence from specific points. The first version of these negative-order norm estimates for approximations obtained by discontinuous Galerkin methods for linear conservation laws was analyzed by Cockburn et al. [8]. Later Mirzaee et al. [14] extended these estimates to variable coefficient equations for structured triangular meshes.

The local post-processing technique that makes use of the information contained in the negative-order norm was originally developed by Bramble and Schatz [4] in the context of continuous finite element methods for elliptic problems and extended for parabolic equations by Bramble et al. [5]. They demonstrated that it is possible to construct a better approximation by convolving the finite element solution with a local averaging operator in the neighborhood of a point ${\varvec{x}}$, where the convergence in the negative-order norm was higher than $L^2$-norm. This technique was further studied by Thomée in [18] to obtain a similar superconvergent order approximation for derivatives, which was not restricted to any particular type of equation and could be applied in any situation where negative-order norms for difference quotients of the error were available with higher order. Cockburn et al. [8] established a framework to apply this technique to linear hyperbolic equations in the context of the Discontinuous Galerkin methods. Numerical experiments showed that the post-processing had a positive impact on nonlinear hyperbolic equations. Furthermore, this technique is labeled as a Smoothness-Increasing Accuracy-Conserving (SIAC) filter by Ryan et al. and was extended to nonuniform meshes, higher-order derivatives, and as a filtering technique to improve the visualization of streamlines [17]. The extension of this technique to nonlinear equations is a significant advancement towards proving the eventual applicability to Navier-Stokes type equations. In order to accomplish this extension, we address one important ingredient of this post-processing technique — the negative-order norm estimate for the errors of the DG solution. This estimate should be of higher order than the $L^2$-error estimate.

In this paper, we present an analysis of the negative-order norm for solutions obtained via the discontinuous Galerkin method for solving nonlinear scalar conservation laws. We use a technical dual argument to obtain an a priori error estimate in the negative-order norm for smooth solutions of scalar nonlinear conservation laws, which is $2k+m$ higher than the $k+m$ order in the $L^2$-norm, where $m$ depends upon the flux and $k$ is the highest degree polynomial used in the approximation. This generalizes the negative-order norm estimates for linear hyperbolic equations in [8].

We would like to mention briefly recent superconvergent results for DG solutions of hyperbolic equations relevant to these results. Adjerid et al. [1–3] established a strong $2k+1$ order superconvergence at the downwind of every element and $k+2$ superconvergence at the Radau points. These a posteriori error estimates are for hyperbolic equations. Recently, Ryan et al. developed a new post-processing technique, the so-called position-dependent SIAC post processing for nonperiodic boundary problems in [16], whose kernel is the same for the interior of the domain, and for points near the boundary the kernel is modified and depends on the position of the evaluation point to get the exact $2k+1$ order under $L^2$-norm by convolving the DG solution with the new kernel. Numerical results have been tested for the linear hyperbolic equations.

The paper is organized as follows. In Sect. 2, we introduce the DG method and SIAC filtering as well as the relevant notation that will be required for the proof of our method. In Sect. 3 we prove the negative-order norm estimates of the DG solutions for multi-dimensional nonlinear hyperbolic conservation laws. The superconvergence results are confirmed numerically in Sect. 4.

2 Notation, Definitions and Projections

We begin by defining the necessary notation used in the proof of accuracy enhancement of discontinuous Galerkin solutions for general nonlinear hyperbolic equations. This is done for projections and interpolations for the finite element spaces used in the error analysis.

2.1 Tessellation and Function Spaces

Suppose that for each $h>0,$ $\mathcal T _h$ denotes a tessellation of the domain $\Omega$ with shape-regular elements $K$, invariant under translations, and $\Gamma$ denotes the union of the boundary faces of elements $K \in \mathcal T _h$, i.e. $\Gamma =\cup _{K \in \mathcal T _h} \partial K$. In this paper we only consider a uniform mesh of size $h$.

The discontinuous Galerkin method uses a piecewise polynomial basis for the test function space as well as the basis functions. Therefore, we define $\mathcal Q ^k(K)$ to be the space of tensor product polynomials of degree at most $k \geqslant 0$ on $K \in \mathcal T _h$ in each variable. That is,

$$\begin{aligned} V_{h}=\left\{ v\in L^2(\Omega ): \;\;\;v\vert _K\in \mathcal Q ^k(K),\quad \forall K\in \mathcal T _{h}\right\} . \end{aligned}$$

We can also consider the space

$$\begin{aligned} V_{h}=\Bigl \{v\in L^2(\Omega ): \;\;\;v\vert _K\in \mathcal P ^k(K),\;\;\;\; \; \forall K\in \mathcal T _{h}\Bigr \}, \end{aligned}$$

where $\mathcal P ^k(K)$ is the polynomial space of functions of total degree at most $k$. These two spaces are the same for the one-dimensional case. We remark that the proofs of the effectivity of the post-processor do not rely on any special projections and so either space can be used.

Because the discontinuous Galerkin method consists of piecewise polynomials, we must have a way of denoting the values of the approximation on the “left” and “right” side of an element boundary, $e.$ We give the designation $K_L$ for values to the left of $e$ and $K_R$ for values to the right, following the notation of [21] and [20].

2.2 Norms

We now define the $L^2$- and the Sobolev norms that we use throughout the paper. Additionally we define the negative-order Sobolev norm.

The definition for the $L^2$-norm in $\Omega$ and on the boundary are given by the standard definitions:

$$\begin{aligned} \Vert \eta \Vert _\Omega =\left(\ \int _{\Omega }\eta ^2d{\varvec{x}}\right)^{\frac{1}{2}},\quad \Vert \eta \Vert _{\partial \Omega }=\left(\,\ \int _{\partial \Omega }\eta ^2ds\right) ^{\frac{1}{2}}. \end{aligned}$$

(2.1)

The $\ell$-th order Sobolev norm over $\Omega$ is given by

$$\begin{aligned} \Vert \eta \Vert _{\ell ,\Omega }=\left( \sum \limits _{|\alpha |\leqslant \ell }\Vert D^\alpha \eta \Vert _\Omega ^2\right)^{\frac{1}{2}}, \quad \ell > 0. \end{aligned}$$

(2.2)

We note that the notation is simplified for these norms and only designate the norm type and not the domain. Furthermore, the inner product is defined as

$$\begin{aligned} (w,v )_\Omega =\sum _K\int _{ K}wv \, dK. \end{aligned}$$

(2.3)

This will be helpful in the error analysis of the negative-order norm. The negative-order norm is defined as: Given $\ell > 0$ and domain $\Omega ,$

$$\begin{aligned} \Vert \eta \Vert _{-\ell ,\Omega }=\sup _{\Phi \in C_0^\infty (\Omega ) }\frac{(\eta ,\Phi )_{\Omega }}{\Vert \Phi \Vert _{\ell ,\Omega }}. \end{aligned}$$

(2.4)

2.3 Projection and Interpolation Properties

We note that the proof of accuracy enhancement of the DG solution relies on an $L^2$-projection of the initial function. Therefore, $P$ is defined to be the $L^2$-projection for a scalar function and $\Pi$ to be the $L^2$-projection for vector-valued functions. We recall the following error estimate for $L^2$-projections (c.f.[7] Chapter 3):

$$\begin{aligned} \Vert \eta ^e \Vert _\Omega + h^{\frac{d}{2}} \Vert \eta ^e \Vert _{L^{\infty }(\Omega )} + h^{\frac{1}{2}} \Vert \eta ^e \Vert _{\Gamma } \leqslant C h^{k+1}\Vert \eta \Vert _{k+1,\Omega }, \end{aligned}$$

(2.5)

where $\eta ^e ={P}\eta -\eta$ and $C$ is a positive constant independent of $h$.

2.4 Regularity for the Variable-Coefficient Hyperbolic Equations

We now need to establish a regularity result that is used to complete the error analysis of the nonlinear hyperbolic equation. That is:

Lemma 2.1

Consider the variable coefficient hyperbolic equation with a periodic boundary condition for all $t\in [0,T]$:

$$\begin{aligned}&\varphi _t({\varvec{x}},t) + \sum \limits _{i=1}^{d}\, (a_i({\varvec{x}},t))\varphi _{x_i}({\varvec{x}},t) =0, \end{aligned}$$

(2.6)

$$\begin{aligned}&\varphi ({\varvec{x}},0)=\varphi _0({\varvec{x}}), \end{aligned}$$

(2.7)

where $a({\varvec{x}},t)$ is a given smooth periodic function. For any $\ell \geqslant 0,$ fix time $t$ and $a({\varvec{x}},t)\in L^\infty ((0,T);W^{2\ell +1,\,\infty }(\Omega ))$, then solution of Eq. (2.6) satisfies the following regularity property

$$\begin{aligned} \Vert \varphi ({\varvec{x}},t)\Vert _{\ell ,\Omega }\leqslant C\Vert \varphi ({\varvec{x}},0)\Vert _{\ell ,\Omega }, \end{aligned}$$

(2.8)

where $C$ is a constant which depends on $\Vert a(x,t)\Vert _{L^\infty ((0,T);W^{2\ell +1,\,\infty }(\Omega ))}$.

We neglect to provide a proof of this lemma as it can easily be obtained by using an energy estimate (see [10], Chapter II).

2.5 The DG Method for General Nonlinear Scalar Hyperbolic Equations

We now define the discontinuous Galerkin method for a general nonlinear scalar hyperbolic equation

$$\begin{aligned} u_t + \sum \limits _{i=1}^{d}\, (f_i(u))_{x_i}=0,\quad ({\varvec{x}},t)\in \Omega \times (0,T], \end{aligned}$$

(2.9)

with a smooth initial condition,

$$\begin{aligned} u({\varvec{x}},0)=u_0({\varvec{x}}). \end{aligned}$$

(2.10)

We assume that a periodic boundary condition is given. We are interested in establishing error estimates as long as this equation has a unique solution (the solution behaves linearly), before a shock develops.

We seek an approximate solution $u_h({\varvec{x}},t) \in V_h$ given by the DG method. That is, given $\psi \in V_h, \,u_h$ must satisfy

$$\begin{aligned} \int _{K}(u_h)_t\psi \, dK- \sum \limits _{i=1}^{d}\int _{K}f_i(u_h) \, \psi _{x_i} \, dK + \sum \limits _{i=1}^{d}\int _{\partial K} \widehat{f_i}(u_h^L, \, u_h^R) \nu _i \psi \, ds =0, \end{aligned}$$

(2.11)

where ${\varvec{\nu }}=(\nu _1,\ldots ,\nu _d)$ is the unit outward normal vector to the integration domain. We enforce weak continuity at the element boundaries through the fluxes, which are given by the “hat” terms (2.11). We define these numerical fluxes to be single-valued functions such that $\widehat{f}_i(a,b)$ is a monotone flux, i.e. Lipschitz continuous in both arguments, consistent (i.e. $\widehat{f_i}(a,a)=f_i(a)$), and non-decreasing in the first argument and non-increasing in the second (c.f. [9]). An example is the Lax–Friedrichs flux

$$\begin{aligned} \widehat{f_i}(a,b) =\frac{1}{2}(f_i(a)+f_i(b)-\alpha (b-a)), \end{aligned}$$

(2.12)

here the viscosity coefficient function $\alpha =\alpha (a,b)$ satisfies $\max _{\xi \in [a,b]} |f_i^{\prime }(\xi )|\ge \alpha (a,b)>\alpha _0>0$. The Lax–Friedrichs flux is used in the numerical experiment of Sect. 4.

We sum the scheme (2.11) over $K$ to obtain

$$\begin{aligned} ((u_h)_t,\psi )_\Omega +B(u_h;\psi )=0, \end{aligned}$$

(2.13)

where $B$ is defined as

$$\begin{aligned} B(u_h;\psi ) =\sum \limits _{i=1}^{d}\sum \limits _K\left( -(f_i(u_h),\psi _{x_i})_K + \int _{\partial K} \widehat{f_i}(u_h^L, \, u_h^R) \nu _i \psi \, ds \right). \end{aligned}$$

In this formulation, $\psi _{x_i}$ refers to the broken derivative of $\psi$ with respect to the $i^{th}$ space variable when sums of integrals over elements $K \in \mathcal T _h$ are replaced by integrals over $\Omega .$ Notice that if we change our choice of flux, we would obtain a different method that would influence the accuracy results [22]. We limit the scope of this paper to considering the flux in (2.12).

Another lemma will be needed to describe the influence of the choice of the fluxes on the result, which is proven in [22]. When the solution is smooth, i.e for small times, the result is given by the following:

Lemma 2.2

([19]) For $0<T<T^*$, where $T^*$ is the maximal time of existence of the classical solution, let $u$ be the exact solution of the problem (2.9) and assume $f_i,\,(i=1,\cdots , d)$ is in $W^{3,\infty }(\Omega )$, and subject to smooth initial conditions and periodic boundary conditions. If $u_h$ is a solution to (2.11), then

$$\begin{aligned} \max _t\Vert u-u_h\Vert _\Omega \,\leqslant Ch^{k+m}, \end{aligned}$$

(2.14)

where the constant $C$ depends on $T, \,\Vert f_i\Vert _{W^{3,\infty }(\Omega )}, \,\Vert u_0\Vert _{k+1,\Omega }$ and is independent of $h.$ $m$ is some constant that depends on the choice of numerical flux in (2.11).

Remark 2.1

In Lemma 2.2, $m \geqslant 0$ corresponds to different theoretical results. For one-dimensional problems or Cartesian meshes in high dimensions, $m=\frac{1}{2}$ can be proven to correspond to a general monotone flux and $m=1$ corresponds to an upwind flux. For general triangulations in high dimensions, $m=0$ for monotone fluxes. We refer the reader to [19, 22] for details of how the choice of the flux influences the theoretical accuracy results. For the numerical implementation, the optimal order $k+1$ can be observed for the different choices of the numerical fluxes.

2.6 Smoothness-Increasing Accuracy-Conserving Filters

We extract higher-order accuracy of the DG method solved over a uniform mesh contained in the negative-order norm through the use of a SIAC filter. This filter improves the order of accuracy by increasing the smoothness of the solution and reducing the number of oscillations in the error. This is done by convolving the numerical approximation with a specially chosen kernel,

$$\begin{aligned} u_h^{\star }=K_h^{2(k+1),k+1}\star u_h, \end{aligned}$$

(2.15)

where $u_h^\star$ is the filtered solution, $u_h$ is the DG solution calculated at the final time, and $K_h^{2(k+1),k+1}$ is the convolution kernel. The kernel is translation-invariant and composed of a linear combination of B-splines of order $k$+1, scaled by the uniform mesh size:

$$\begin{aligned} K_h^{2(k+1),k+1}(x)=\frac{1}{h}\sum _{\gamma =-k}^k c_\gamma ^{2(k+1),k+1} \psi ^{(k+1)}\left(\frac{x}{h}-\gamma \right). \end{aligned}$$

(2.16)

The weights of the B-splines, $c_\gamma ^{2(k+1),k+1},$ are chosen so that accuracy is not destroyed (the kernel can reproduce polynomials of degree up to 2$k$), i.e. $K_h^{2(k+1),k+1}*p=p$ for $p=1,x,\cdots ,x^{2k}.$ See [17] for more details.

The following notation for the difference quotients over elements of size $h$ is used:

$$\begin{aligned} \partial _{h,j} v({\varvec{x}})=\frac{1}{h}\left(v\left({\varvec{x}}+\frac{1}{2}h {\varvec{e}}_j\right)-v\left({\varvec{x}}-\frac{1}{2}h {\varvec{e}}_j\right)\right), \end{aligned}$$

(2.17)

here ${\varvec{e}}_j$ is the unit multi-index whose $j$-th component is $1$ and all others $0.$ For any multi-index $\alpha =(\alpha _1,\cdots , \alpha _d)$ we set $\alpha$-th order difference quotient to be

$$\begin{aligned} \partial _h^{\alpha }v({\varvec{x}})=(\partial _{h,1}^{\alpha _1} \cdots \partial _{h,d}^{\alpha _d})v({\varvec{x}}). \end{aligned}$$

(2.18)

Theorem 2.3

(Bramble and Schatz [4]) For $0<T<T^*$, where $T^*$ is the maximal time of existence of the classical solution, let $u\in L^\infty ((0,T);H^{2k+2}(\Omega ))\bigcap L^2((0,T);H^{2k+2}(\Omega ))$ be the exact solution of the problem (2.9). Let $\Omega _0+2supp(K_h^{2(k+1),k+1}(x))\subset \subset \Omega$ and $U$ is any approximation to $u$, then

$$\begin{aligned}&\Vert u(T)-K_h^{2(k+1),k+1}\star U\Vert _{0,\Omega _0}\le \frac{h^{2k+2}}{(2k+2)!}C_1|u|_{2k+2,\Omega }\\&\qquad \qquad \quad +C_1C_2\sum _{|\alpha |\le k+1}\Vert \partial _h^\alpha (u-U)\Vert _{-(k+1),\Omega }. \end{aligned}$$

where $C_1$ and $C_2$ depends solely on $\Omega _0, \Omega _1, d, k, c_\gamma ^{2(k+1),k+1},$ and is independent of $h.$

Remark 2.2

For our problem we only consider periodic boundary conditions and $U=u_h$ represents the DG approximation. We can obtain the estimate for the entire domain, i.e., $\Omega _0=\Omega$ by considering $\Omega \backslash \Omega _0$ as the interior part of a new period of the domain.

Remark 2.3

Error estimates using the divided differences of the error in the negative-order norm will be important for the SIAC filter which requires a local transition invariance of the mesh and the kernel size of $\mathcal O (h)$. In the following, we will only give the negative-order norm error estimates for $\Vert u-U\Vert _{-(k+1),\Omega }$. The proof for the error estimates of the divided differences is not straight forward from the estimates of the solution itself and not trivial for the nonlinear equation. We will leave the estimates for the divided differences for further work.

Remark 2.4

Even though the theory indicates that it is not possible to extract a higher rate of convergence through the use of the SIAC filter using the estimate $\Vert u-U\Vert _{-(k+1),\Omega }$, it can still be used for some global post-processing techniques, such as in [12, 15]. However, numerical experiments still indicate that the $(2k+1)$-th order accuracy can be achieved using the SIAC filter.

3 Superconvergent Error Estimates

The goal of this paper is to demonstrate that the higher-order convergence in the negative-order norm is not just reserved for linear hyperbolic equations, but that we can also obtain higher-order convergence for nonlinear scalar hyperbolic equations before a shock develops.

We give our main theorem for the negative-order norm of the error for the DG solutions as follows:

Theorem 3.1

For $0<T<T^*$, where $T^*$ is the maximal time of existence of the classical solution, let $u\in L^\infty ((0,T);W^{2k+2,\,\infty }(\Omega ))\bigcap L^\infty ((0,T);H^{k+2}(\Omega ))\bigcap L^2((0,T); H^{k+2}(\Omega ))$ be the exact solution of the problem (2.9) and assume $f_i,\,i=1,\cdots , d$ is also in $W^{2k+2,\,\infty }(\Omega )$, and subject to smooth initial conditions and periodic boundary conditions. If $u_h$ is a solution to (2.11), then for any polynomial of degree $k>\frac{d}{2},$

$$\begin{aligned} \Vert u(T)-u_h(T)\Vert _{-(k+1),\Omega } \le C h^{2k+m}, \end{aligned}$$

where $C$ is a constant independent of $h$ and depends on $\Vert u_0\Vert _{k+1,\Omega }$,$\Vert f_i\Vert _{W^{2k+2,\,\infty }(\Omega )}$ and $T$. $m$ is some constant that depends on the choice of numerical flux in (2.11).

Remark 3.1

For polynomials of highest degree $k$, the theorem states that accuracy enhancement in $d$-dimensions is only possible provided $k$ is chosen to be greater than $d/2$ this means that:

• If $d=1$, then $k\geqslant 1$.

• If $d=2$, then $k\geqslant 2$.

• If $d=3$, then $k\geqslant 2$.

Remark 3.2

In the following proof, it becomes evident that both an approximation space consisting of $\mathcal P ^k$- or $\mathcal Q ^k$-polynomials can be used for the DG solutions. The proof of the post-processor does not rely on any special projections.

3.1 A Proof of Theorem 3.1

In order to show higher-order accuracy is obtained in the negative-order norm (cf. definition (2.4)), we need to follow the analysis given in [8] to estimate the inner product

$$\begin{aligned} \left(u(T)-u_h(T),\Phi \right)_{ \Omega }. \end{aligned}$$

(3.1)

Estimating the inner product requires considering the dual equation to a nonlinear problem. This dual equation is not uniquely defined (see [13]), so we have the freedom to choose the form of the dual equation. Therefore, we choose the dual equation of the form: Find a function $\varphi$ such that $\varphi (\cdot ,t)$ is one-periodic in all dimensions for all $t\in [0,T]$ and

$$\begin{aligned}&\varphi _t+\sum \limits _{i=1}^{d}f_i^{\prime }(u)\varphi _{x_i} =0, \quad \Omega \times [0,T),\end{aligned}$$

(3.2)

$$\begin{aligned}&\varphi ({\varvec{x}},T)=\Phi ({\varvec{x}}). \end{aligned}$$

(3.3)

Notice that this form of the dual equation introduces an added difficulty as it no longer gives $\frac{d}{dt}(u,\varphi )=0$ as it did for the linear case. In fact, we can see that when we multiply Eq. (2.9) by $\varphi$ and equation (3.2) by $u$ and integrate over $\Omega$, we have

$$\begin{aligned} 0=(u_t,\varphi )_\Omega +(u,\varphi _t)_\Omega +\sum \limits _{i=1}^{d}\left(\left(\left(f_i(u)\right)_{x_i},\varphi \right)_ \Omega +(f_i^{\prime }(u)u,\varphi _{x_i})_\Omega \right). \end{aligned}$$

Integrating by parts and using the one-periodic nature of the boundary conditions,

$$\begin{aligned} ((f_i(u))_{x_i},\varphi )_\Omega =-(f_i(u),\varphi _{x_i})_\Omega . \end{aligned}$$

We therefore have

$$\begin{aligned} \frac{d}{dt}(u,\varphi )_\Omega + \mathcal F (u;\varphi ) =0, \end{aligned}$$

(3.4)

where

$$\begin{aligned} \mathcal F (u;\varphi )= \sum \limits _{i=1}^{d} \left(\left(f_i^{\prime }(u)u-f_i(u)\right),\varphi _{x_i}\right)_\Omega . \end{aligned}$$

(3.5)

Integrate equation (3.4) in time to obtain

$$\begin{aligned} (u(T),\varphi (T))_\Omega =(u(0),\varphi (0))_\Omega -\int _0^T \mathcal F (u;\varphi ) \,dt. \end{aligned}$$

(3.6)

This relation allows us to estimate the term $(u(T)-u_h(T),\Phi )_\Omega$ appearing in the definition of the negative-order norm (2.4). Now we can make use of similar ideas to those used in [8]. That is,

$$\begin{aligned}&(u(T)-u_h(T),\Phi )_\Omega \\&=(u(T),\Phi )_\Omega -(u_h(T),\Phi )_\Omega \\&=(u(T),\varphi (T))_\Omega -(u_h(T),\varphi (T))_\Omega \\&\stackrel{(3.6)}{=}(u(0),\varphi (0))_\Omega -\int _0^T \mathcal F (u;\varphi ) \,dt -(u_h(T),\varphi (T))_\Omega \\&=(u(0),\varphi (0))_\Omega -(u_h(0),\varphi (0))_\Omega -\int _0^T\frac{d}{dt}(u_h,\varphi )_\Omega dt -\int _0^T \mathcal F (u;\varphi ) \,dt\\&=(u(0)-u_h(0),\varphi (0))_\Omega -\int _0^T(((u_h)_t,\varphi )_\Omega +(u_h,\varphi _t)_\Omega ) dt -\int _0^T \mathcal F (u;\varphi ) \,dt. \end{aligned}$$

Let us consider the second term more closely. Because our approximation, given by (2.13), relies on a piecewise polynomial subspace, we add and subtract the function $\chi \in V_h$ to obtain a formulation that relies on the DG method

$$\begin{aligned} ((u_h)_t,\varphi )_\Omega = ((u_h)_t,\varphi -\chi )_\Omega +B(u_h;\varphi -\chi )-B(u_h;\varphi ) \end{aligned}$$

as in [8]. Combining the above with $(u_h,\varphi _t)_\Omega$, we have

$$\begin{aligned}&((u_h)_t,\varphi )_\Omega +(u_h,\varphi _t)_\Omega \\&\quad =((u_h)_t,\varphi -\chi )_\Omega +B(u_h;\varphi -\chi )+(u_h,\varphi _t)_\Omega -B(u_h;\varphi ). \nonumber \end{aligned}$$

(3.7)

This gives the estimate

$$\begin{aligned}&(u(T)-u_h(T),\Phi )_\Omega \\&\quad =(u(0)-u_h(0),\varphi (0))_\Omega -\int _0^T\bigl (((u_h)_t,\varphi -\chi )_\Omega +B(u_h;\varphi -\chi )\bigr )dt\\&\quad \quad -\int _0^T\bigl ((u_h,\varphi _t)_\Omega -B(u_h;\varphi )+ \mathcal F (u;\varphi )\bigr )dt\\&\quad =\Theta _1+\Theta _2+\Theta _3, \end{aligned}$$

where

$$\begin{aligned}&\Theta _1=(u(0)-u_h(0),\varphi (0))_\Omega ,\\&\Theta _2=-\int _0^T\bigl (((u_h)_t,\varphi -\chi )_\Omega +B(u_h;\varphi -\chi )\bigr )dt,\\&\Theta _3=-\int _0^T\bigl ((u_h,\varphi _t)_\Omega -B(u_h;\varphi )+ \mathcal F (u;\varphi )\bigr )dt. \end{aligned}$$

We prove the estimates for $\Theta _2,$ and $\Theta _3$ below. We remind the reader that the estimate for $\Theta _1,$ is given by:

Lemma 3.2

(Projection Estimate) There exists a positive constant $C,$ independent of $h,$ such that

$$\begin{aligned} |\Theta _1|\leqslant C\, h^{2k+2}\Vert u_0\Vert _{k+1}\Vert \varphi (0)\Vert _{k+1}. \end{aligned}$$

(3.8)

Proof

We neglect the proof of this estimate and point the interested reader to [11]. $\square$

For the second term, we have the following result:

Lemma 3.3

(Estimating the second term: residual) There exists a positive constant $C,$ independent of $h,$ such that

$$\begin{aligned} |\Theta _2|&\leqslant C h^k \left(\int _0^T\Vert u_h-u\Vert _\Omega ^2dt\right)^{1/2} \left(\int _0^T\Vert \varphi \Vert _{k+1}^2dt\right)^{1/2} + C h^{2k+2} \left(\int _0^T\Vert \varphi \Vert _{k+1}^2dt\right)^{1/2}\nonumber \\&\quad +C h^{2k+1}\left(\int _0^T\Vert u\Vert _{k+1}^2dt\right) ^{1/2}\left(\int _0^T\Vert \varphi \Vert _{k+1}^2dt\right)^{1/2}.\nonumber \\ \end{aligned}$$

(3.9)

Proof

Using the definition of $\Theta _2,$

$$\begin{aligned} \Theta _2=-\int _0^T\bigl (((u_h)_t,\varphi -\chi )_\Omega +B(u_h;\varphi -\chi )\bigr )dt, \end{aligned}$$

we consider the terms inside the integral and let $\chi =P\varphi .$ This gives

$$\begin{aligned} ((u_h)_t,\varphi -P\varphi )_\Omega =0, \end{aligned}$$

and reduces the terms inside the integral to the following:

$$\begin{aligned} B(u_h;\varphi -P\varphi )=\sum \limits _{i=1}^{d} \sum \limits _K \left(-(f_i(u_h), (\varphi -P\varphi )_{x_i})_K + \int _{\partial K}\widehat{f_i}(u_h^L,u_h^R) \nu _i (\varphi -P\varphi ) ds\right). \end{aligned}$$

Let us look at the term for the $i$ th-dimension:

$$\begin{aligned}&\sum \limits _K\left( -(f_i(u_h), (\varphi -P\varphi )_{x_i})_K + \int _{\partial K}\widehat{f_i}(u_h^L,u_h^R) \nu _i (\varphi -P\varphi ) ds\right)\\&\quad =\sum \limits _K\left(- (f_i(u_h)-f_i(u), (\varphi -P\varphi )_{x_i})_K -(f_i(u), (\varphi -P\varphi )_{x_i})_K\right) \\&\qquad + \sum \limits _K \int _{\partial K}\widehat{f_i}(u_h^L,u_h^R) \nu _i (\varphi -P\varphi ) ds\\&\quad =\sum \limits _K\left(- (f_i(u_h)-f_i(u), (\varphi -P\varphi )_{x_i})_K +((f_i(u))_{x_i}, (\varphi -P\varphi ))_K\right)\\&\qquad + \sum \limits _K \int _{\partial K}( \widehat{f_i}(u_h^L,u_h^R)-f_i(u)) \nu _i (\varphi -P\varphi ) ds\\&\quad = (I)+(II)+(III), \end{aligned}$$

where we have added and subtracted the term $\sum \limits _K((f_i(u))_{x_i}, (\varphi -P\varphi ))_K$ and integrated by parts. We can now define

$$\begin{aligned} (I)&= - \sum \limits _K(f_i(u_h)-f_i(u), (\varphi -P\varphi )_{x_i})_K,\\ (II)&= \sum \limits _K((f_i(u))_{x_i}, (\varphi -P\varphi ))_K,\\ (III)&= \sum \limits _K \int _{\partial K}( \widehat{f_i}(u_h^L,u_h^R)-f_i(u)) \nu _i (\varphi -P\varphi ) ds. \end{aligned}$$

To obtain an estimate for $\Theta _2$, it is necessary to estimate $(I),\, (II),\, (III)$ respectively. These are given below.

• Estimate of $(I)$: We use the Lipschitz continuity of $f$ and Cauchy–Schwarz inequality and get

  $$\begin{aligned} |(I)|\leqslant C\Vert u-u_h\Vert _\Omega \Vert (\varphi -P\varphi )_{x_i}\Vert _\Omega . \end{aligned}$$

  (3.10)

• Estimate of $(II)$: For the estimate of $(II),$ it is necessary to add and subtract $P((f_i(u))_{x_i})$ which is the $L^2$ projection of $(f_i(u))_{x_i}$ onto $V_h.$ We then have

  $$\begin{aligned} (II)&= \sum \limits _K\left(((f_i(u))_{x_i}- P((f_i(u))_{x_i}), (\varphi -P\varphi )\right)_K+ \left(P((f_i(u))_{x_i}), (\varphi -P\varphi ))_K\right)\\&= \sum \limits _K ((f_i(u))_{x_i}- P((f_i(u))_{x_i}), (\varphi -P\varphi ))_K, \end{aligned}$$

  where the last equality uses the property of the $L^2$ projection. This gives the estimate of $(II)$ as

  $$\begin{aligned} |(II)|\leqslant C\Vert (f_i(u))_{x_i}- P((f_i(u))_{x_i})\Vert _\Omega \Vert \varphi -P\varphi \Vert _\Omega . \end{aligned}$$

  (3.11)

• Estimate of $(III)$: For this estimate, we use the Lipschitz continuity of the numerical fluxes $\widehat{f_i}$ and the inverse inequality and obtain

  $$\begin{aligned} |(III)|&\leqslant C \sum \limits _K \int _{\partial K} |u_h-u| |\varphi -P\varphi | ds\nonumber \\&\leqslant C \Vert u_h-u\Vert _{L^2( \Gamma )} \Vert \varphi -P\varphi \Vert _{L^2( \Gamma )}\nonumber \\&\leqslant Ch^{k+\frac{1}{2}} \Vert u_h-u\Vert _{L^2( \Gamma )} \Vert \varphi \Vert _{k+1}\nonumber \\&\leqslant C h^{k+\frac{1}{2}} ( \Vert u_h-Pu\Vert _{L^2( \Gamma )}+ \Vert Pu-u\Vert _{L^2(\Gamma )})\Vert \varphi \Vert _{k+1} \nonumber \\&\leqslant C h^{k+\frac{1}{2}} ( h^{-\frac{1}{2}}\Vert u_h-Pu\Vert _{L^2( \Omega )}+ h^{k+\frac{1}{2}}\Vert u\Vert _{k+1})\Vert \varphi \Vert _{k+1}\nonumber \\&\leqslant C h^k \Vert u_h-Pu\Vert _\Omega \Vert \varphi \Vert _{k+1}+ C h^{2k+1}\Vert u\Vert _{k+1}\Vert \varphi \Vert _{k+1}\nonumber \\&\leqslant C h^k \Vert u_h-u\Vert _\Omega \Vert \varphi \Vert _{k+1}+C h^k \Vert u-Pu\Vert _\Omega \Vert \varphi \Vert _{k+1}+C h^{2k+1}\Vert u\Vert _{k+1}\Vert \varphi \Vert _{k+1}\nonumber \\&\leqslant C h^k \Vert u-u_h\Vert _\Omega \Vert \varphi \Vert _{k+1}+ C h^{2k+1}\Vert u\Vert _{k+1}\Vert \varphi \Vert _{k+1}. \end{aligned}$$

  (3.12)

We can now combine estimates (3.10), (3.11), (3.12) in order to estimate the second term, $\Theta _2:$

$$\begin{aligned} |\Theta _2|&\leqslant C \int _0^T\sum \limits _{i=1}^{d} \left(I+II+III\right)dt\\&\leqslant C h^k \left(\int _0^T\Vert u_h-u\Vert _\Omega ^2dt\right)^{1/2} \left(\int _0^T\Vert \varphi \Vert _{k+1}^2dt\right)^{1/2} + C h^{2k+2} \left(\int _0^T\Vert \varphi \Vert _{k+1}^2dt\right)^{1/2} \\&\quad +C h^{2k+1}\left(\int _0^T\Vert u\Vert _{k+1}^2dt\right)^{1/2} \left(\int _0^T\Vert \varphi \Vert _{k+1}^2dt\right)^{1/2}. \end{aligned}$$

$\square$

Lastly, we need to estimate the third term, $\Theta _3.$

Lemma 3.4

(Estimating the third term: consistency) There exists a positive constant $C,$ independent of $h,$ such that

$$\begin{aligned} |\Theta _3|\leqslant C\, \int _0^T\Vert u_h-u\Vert _\Omega ^2\Vert \varphi \Vert _{k+1}\,dt. \end{aligned}$$

(3.13)

Proof

We first denote the terms inside the integral of $\Theta _3$ by

$$\begin{aligned} (IV)=(u_h,\varphi _t)_\Omega -B(u_h;\varphi )+ \mathcal F (u;\varphi ). \end{aligned}$$

The estimate of $(IV)$ uses the dual equation (3.2) and the definition of $B,\, \mathcal F :$

$$\begin{aligned} (IV)&= -(u_h, \sum \limits _{i=1}^{d}f_i^{\prime }(u)\varphi _{x_i})_\Omega -B(u_h;\varphi )+ \mathcal F (u;\varphi )\\&= \sum \limits _{i=1}^{d} \Bigl (-(u_hf_i^{\prime }(u),\varphi _{x_i})_\Omega +(f_i(u_h),\varphi _{x_i})_\Omega +((f_i^{\prime }(u)u-f_i(u)),\varphi _{x_i})_\Omega \\&- \sum \limits _K \int _{\partial K}\widehat{f_i}(u_h^L, \, u_h^R) \nu _i \varphi \, ds \Bigr )\\&= \sum \limits _{i=1}^{d} \Bigl ( \bigl (f_i(u_h)-f_i(u)-f_i^{\prime }(u)(u_h-u),\varphi _{x_i}\bigr )_\Omega \Bigr ), \end{aligned}$$

where for the last equality we use the continuity of $\varphi$ and periodic boundary conditions. To complete the estimate, it is necessary to use a Taylor expansion of $f_i(u_h)$ about $u$:

$$\begin{aligned} f_i(u_h)=f_i(u)+f_i^{\prime }(u)(u_h-u)+\frac{f_i^{\prime \prime }(\xi _i)}{2}(u_h-u)^2, \end{aligned}$$

where $\xi _i$ is some value between $u_h,\,u$. This gives

$$\begin{aligned} |(IV)|&= \left|\frac{1}{2}\sum \limits _{i=1}^{d} (f_i^{\prime \prime }(\xi _i)(u_h-u)^2,\varphi _{x_i})\right|\\&\leqslant \frac{1}{2}\sum \limits _{i=1}^{d} \sup \{|f_i^{\prime \prime }|\}\Vert \varphi _x\Vert _{L^\infty }\Vert u-u_h\Vert _\Omega ^2\\&\leqslant C \Vert u-u_h\Vert _\Omega ^2\Vert \varphi \Vert _{k+1}, \end{aligned}$$

where we use the Sobolev inequality by Brenner [6], i. e.

$$\begin{aligned} \Vert \varphi _x\Vert _{L^\infty }\leqslant C\Vert \varphi \Vert _{k+1}, \end{aligned}$$

which requires that $k>d/2$. $\square$

Remark 3.3

If $f_i(u)=c_i u, i=1, \cdots , d$ the third term equals zero and the dual equation we defined above is consistent with the linear case in [8].

We can now combine Lemmas 3.2, 3.3, and 3.4, to estimate the numerator of the negative-order norm:

$$\begin{aligned}&|(u(T)-u_h(T),\Phi )_\Omega | = |\Theta _1+\Theta _2+\Theta _3|\\&\le C\, h^{2k+2}\Vert u_0\Vert _{k+1}\Vert \varphi (0)\Vert _{k+1} + \int _0^T\Vert u_h-u\Vert _\Omega ^2\Vert \varphi \Vert _{k+1}\,dt\\&+ Ch^k \left(\int _0^T\Vert u_h-u\Vert _\Omega ^2dt\right)^{1/2} \left(\int _0^T\Vert \varphi \Vert _{k+1}^2dt\right)^{1/2} + C h^{2k+2} \left(\int _0^T\Vert \varphi \Vert _{k+1}^2dt\right)^{1/2}\\&+C h^{2k+1}\left(\int _0^T\Vert u\Vert _{k+1}^2dt\right)^{1/2} \left(\int _0^T\Vert \varphi \Vert _{k+1}^2dt\right)^{1/2}. \end{aligned}$$

It is easy to convert the final time dual problem (3.2) to an initial problem by changing time $t^{\prime }=T-t$. Then using Lemma 2.1, where $a_i(x,t)$ is replaced by $f_i$ and $\ell =k+1$,

$$\begin{aligned} \Vert \varphi \Vert _{k+1}\le C\Vert \varphi (T)\Vert _{k+1}=C \Vert \Phi \Vert _{k+1,\Omega } \end{aligned}$$

(3.14)

and

$$\begin{aligned} |(u(T)-u_h(T),\Phi )_\Omega | \le C h^s \Vert \Phi \Vert _{k+1,\Omega }. \end{aligned}$$

(3.15)

In these relations $s=\min (2k+2,2k+1,2k+m,2k+2m)=2k+m$ and $C$ depends upon the smoothness of the solution and the final time. Notice that for the second and third terms, the convergence depends on the fluxes (c.f. Lemma 2.2). Therefore the estimate for the negative-order norm is given by

$$\begin{aligned} \Vert u(T)-u_h(T)\Vert _{-(k+1),\Omega } =\sup _{\Phi \in C_0^\infty (\Omega ) }\frac{(u(T)-u_h(T),\Phi )_\Omega }{\Vert \Phi \Vert _{k+1,\Omega }} \le C h^{s}, \end{aligned}$$

where $s=2k+m$. This indicates that it may be possible to use the SIAC filter to extract accuracy of order $s$.

4 Numerical Studies

In this section, we present the performance of the post-processing technique for different nonlinear hyperbolic equations. The numerical results confirm that for Discontinuous Galerkin solutions to nonlinear hyperbolic equations superconvergence can be obtained through the use of this SIAC filter. In [8] a scalar nonlinear Burgers’ equation with periodic boundary conditions has already been demonstrated to exhibit superconvergence. Here, we consider more general hyperbolic equations. First we investigate a completely nonlinear scalar equation where the nonlinear flux is given by $f(u)=e^u.$ For the second example we consider the two dimensional Burgers’ equation using $\mathcal P ^k$-polynomials. In the third example we show a Burgers’ equation with a forcing term using a tensor-product polynomial space, $\mathcal Q ^k.$ In all cases, the flux has been taken to be an upwind monotone flux. Additionally, the errors are calculated for relative short times, before the shock has developed. We note that because the errors are calculated for short times the $\mathcal O (h^{2k+2})$ error term from the initial projection still dominates the error calculation in many examples. However, if a forcing function is added so that a shock does not develop, the error will settle down to the theoretically predicted $\mathcal O (h^{2k+1})$ accuracy. The $L^2$-error is computed using a six-point Gauss quadrature rule and the $L^\infty$-error is calculated using the same six Gauss points in each element for all elements.

Example 4.1

We begin by presenting the nonlinear scalar hyperbolic equation on the domain $I=[0,2\pi ]$:

$$\begin{aligned} u_t+(e^u)_x=0, \quad I\times (0,T],\quad u(x,0)=\sin (x),\quad x\in I \end{aligned}$$

(4.1)

with periodic boundary conditions. The errors are presented in Table 1 and are computed at time $T=0.1$, when the solution is still smooth.

Table 1 $L^2$- and $L^{\infty }$-errors for the scalar conservation law with exponential flux given in Example 4.1 before and after post-processing at time $T=0.1$ using the discontinuous Galerkin method. We clearly see $\mathcal O (h^{2k+1})$ in both the $L^2$- and $L^\infty$-norms

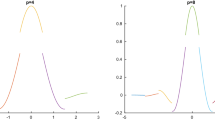
In Table 1, we clearly see that we can improve the order of the error from $\mathcal O (h^{k+1})$ to at least $\mathcal O (h^{2k+1}).$ Furthermore, we can also see that the magnitude of the errors are reduced as we refine the mesh. Plots of the pointwise errors are given in Fig. 1. The SIAC filter clearly works to rid the DG errors of oscillations and improve the order of accuracy. However, we notice that not all oscillations in the errors have been removed by post-processing, which is similar to the results for Burgers’ equation in [8]. From the theory we know that the error depends on the smoothness of the exact solution. For hyperbolic conservation laws, we also know that a shock will develop as the time advances. We speculate that this effect may be due to the nonlinear property and equations themselves.

Fig. 1

Plot of pointwise errors in log scale before (left) and after post-processing (right) for the one-dimensional conservation law given in Eq. (4.1) solved at time $T=0.1$ using the discontinuous Galerkin method. The SIAC filter reduces the oscillations in the DG solution and improves the smoothness and accuracy

Example 4.2

In this example, we consider the two dimensional Burgers’ equation with a smooth solution on the domain $I=[0,2\pi ]\times [0,2\pi ]$:

$$\begin{aligned}&u_t+\left(\frac{u^2}{2}\right)_x+\left(\frac{u^2}{2}\right)_y=0, \quad I\times (0,T],\quad \end{aligned}$$

(4.2)

$$\begin{aligned}&u(x,y,0)=\sin (x+y),\quad (x,y)\in I, \end{aligned}$$

(4.3)

with periodic boundary conditions. The errors are presented in Table 2 and are computed at time $T=0.1.$ This example makes use of $\mathcal P ^k$ polynomials for the approximation space.

Table 2 $L^2$- and $L^{\infty }$-errors for the two-dimensional Burgers’ equation given in Example 4.2 before and after post-processing using the discontinuous Galerkin method using a $\mathcal P ^k$ polynomial approximation space. We clearly see improvement to $\mathcal O (h^{2k+1})$ after post-processing

When we compare this result with the one dimensional result in [8] we see that we obtain similar error and order improvement when the solution is smooth. That is, the order of the error improves from $k+1$ to $2k+1$.

In the following example we consider Burgers’ equation with a forcing term, which is not covered by the theory. We test this example using $\mathcal Q ^k$ polynomials, which should not affect the results from the theory.

Example 4.3

The two dimensional Burgers’ equation with a forcing term on domain $I=[0,2\pi ]\times [0,2\pi ]$ is given by

$$\begin{aligned}&u_t+\left(\frac{u^2}{2}\right)_x+\left(\frac{u^2}{2}\right) _y=g(x,y,t), \quad I\times (0,T],\quad \end{aligned}$$

(4.4)

$$\begin{aligned}&u(x,y,0)=\sin (x)\sin (y),\quad (x,y)\in I, \end{aligned}$$

(4.5)

where periodic boundary conditions are prescribed. We take the exact solution to be $u(x,y,t)=e^t\sin (x)\sin (y).$ The errors are presented in Table 3 and are computed at time $T=0.1.$

Table 3 $L^2$- and $L^{\infty }$-errors for the Burgers equation with a forcing term as given in Example 4.3 before and after post-processing using the discontinuous Galerkin method with a $\mathcal Q ^k$ polynomial approximation space. We clearly see improvement to $\mathcal O (h^{2k+1})$ after post-processing

In Table 3, we show that we can improve the orders from $\mathcal O (h^{k+1})$ to $\mathcal O (h^{2k+1})$ and the errors are greatly improved when we use $\mathcal Q ^k$ polynomials.

Remark 4.4

For the two-dimensional examples, we implement $\mathcal P ^k$-polynomials and $\mathcal Q ^k$-polynomials separately. We found that for both cases we obtained accuracy of order $2k+1$ for the post-processed solution. However, the errors are greatly improved when using $\mathcal Q ^k$-polynomials versus $\mathcal P ^k$-polynomials.

5 Concluding Remarks

In this paper, we have established the existence of higher-order accuracy of the discontinuous Galerkin solution to nonlinear scalar hyperbolic equations in the negative-order norm. This opens the door for extracting superconvergence of the numerical solution through the use of SIAC filters for more complex equations. These filters improve the accuracy of the discontinuous Galerkin approximation from $\mathcal O (h^{k+1})$ to $\mathcal O (h^{2k+m}),$ where $m$ depends upon the numerical flux. Furthermore, in addition to this theoretical result, we demonstrated numerically that for smooth solutions we can extract this higher order accuracy using a SIAC filter provided the solution is smooth enough. These results can be easily extended to high dimensional space following the same ideas. Error estimates using the divided differences of the error in negative-order norm will be important for the SIAC filter. The proof for the error estimates of the divided differences is not straight forward from the estimates of the solution itself and not trivial for nonlinear equations. We leave the estimates for the divided differences as further work.