Discontinuous Galerkin Difference Methods for Symmetric Hyperbolic Systems

Abstract

We develop dissipative, energy-stable difference methods for linear first-order hyperbolic systems by applying an upwind, discontinuous Galerkin construction of derivative matrices to a space of discontinuous piecewise polynomials on a structured mesh. The space is spanned by translates of a function spanning multiple cells, yielding a class of implicit difference formulas of arbitrary order. We examine the properties of the method, including the scaling of the derivative operator with method order, and demonstrate its accuracy for problems in one and two space dimensions.

1 Introduction

Prominent among Saul Abarbanel’s many contributions to computational and applied mathematics is his important work on the strict stability of difference approximations to hyperbolic initial-boundary value problems, including the often-neglected development of high-order implicit (or compact) methods [1, 2, 10], as well as their accuracy when used in a method-of-lines context [4, 11]. In this work we continue our development of a class of arbitrary-order implicit difference methods which are automatically energy-stable for symmetric hyperbolic systems. The methods, which we call Galerkin difference (GD) methods, are based on the use of the standard discontinuous Galerkin technology with nonstandard, tensor-product basis functions which span multiple elements. As the interior basis functions are translates of a single, compactly-supported Lagrange function, the mass and derivative or stiffness matrices are also banded and translation-invariant; that is they have the structure of a compact difference method. Using the Galerkin analysis, one can directly prove energy stability and convergence for any sufficiently accurate boundary closure, so the only potential problem is artificial stiffness associated with one-sided approximations at boundaries. In [8] we introduced continuous GD methods for both first and second order hyerbolic equations. Among our findings were that there was no appreciable artificial stiffness for a range of methods including free and extrapolated values at ghost nodes. (The meaning of these terms will be made clear in Sect. 2.) Precisely, for first order problems in one space dimension the spectral radii of the derivative matrices were almost independent of order, while for second order derivatives they showed linear growth. As we argue below, linear growth poses no practical problem if one matches the temporal order with the spatial order, which is natural in the hyperbolic case. In addition, we identified a superconvergence phenomenon; the truncation error of the interior methods is roughly twice the design order, and for problems with long range propagation this results in superconvergence of the solution at practically important accuracy levels. In [9] we apply the continuous GD method to second order problems in two space dimensions, including applications to elastic waves with free surface boundary conditions, and show one way to maintain their efficiency on mapped coordinate boxes. In [21] we consider the practically important case of multiple mapped grid components. Due to the Galerkin construction, there is no difficulty in handling the interface conditions via appropriate flux definitions. Moreover, we show that we can directly treat hybrid structured-unstructured grids in a provably stable and accurate manner. However, for first order problems some artificial stiffness associated with corner modes was observed, leading to a linear growth in the norm of the derivative matrices with order.

Although boundary and interface treatments in the works above introduce some dissipation, the bulk schemes are energy-conserving. For nonlinear problems or nonsmooth media, it is likely that methods which are dissipative rather than dispersive will perform better. The goal of this paper is to introduce a dissipative GD method for first order hyperbolic systems. Precisely, by using a basis of translated discontinuous Lagrange functions, we develop dissipative discontinuous Galerkin difference (DGD) methods for symmetric hyperbolic systems:

$$\begin{aligned} T \frac{\partial {\mathbf {w}}}{\partial t} + \sum _{j=1}^d A_j \frac{\partial {\mathbf {w}}}{\partial x_j} = {\mathbf {0}} , \end{aligned}$$

(1)

with $A_j=A_j^T$, $T=T^T >0$.

The obvious comparison for GD (continuous or discontinuous) methods is to difference methods with the summation-by-parts property (SBP) [22, 25, 26]. SBP methods provide stability in a discrete rather than continuous energy norm. Advantages of the GD approach are:

• (i) The derivation of SBP methods is algebraically complex and as a result that have not been constructed at very high order, while GD methods can easily be constructed at any order.

• (ii) Stable coupling between nonconforming grids, some of which can be unstructured to treat very complex geometry, is automatic.

• (iii) Dissipation for SBP methods is typically achieved via the the addition of ad hoc parametrized dissipation operators (e.g., [23]), while we show here how we can add it via upwinding.

The relative disadvantage is that, when an SBP method of the same order is available, the absence of a mass matrix inversion means that the difference operators can be applied at roughly half the cost.

The remainder of the paper is as follows. In Sect. 2 we describe the basis functions and boundary closures, show how the upwind derivative operator is constructed, and examine its spectral properties. In Sect. 3 we carry out numerical experiments in one and two space dimensions, observing high-order convergence in general and superconvergence at up to double the design order in some circumstances. This includes a first-order reformulation of the sine-Gordon equation with smooth soliton solutions. Lastly we apply the method in a slightly more complicated setting: the elastic wave equation with variable material properties and a free surface boundary conditions combined with perfectly matched layers to approximate radiation boundary conditions.

2 Discontinuous Galerkin Difference Approximations to d / dx

The construction of the discontinuous Galerkin difference approximations to d / dx follows directly from:

• (i) Specification of the approximation space;

• (ii) Application of the standard discontinuous Galerkin methodology (e.g., [20]).

Here we will focus on dissipative methods which result from the imposition of upwind fluxes. We note that nondissipative approximations could also be constructed using central fluxes. However, as the Galerkin difference methods used in earlier works are also nondissipative (except for boundary/interface treatments), we wish to explore this distinct feature enabled by the discontinuous approximation space.

2.1 The DGD Approximation Space

Consider the interval $x \in [a,b]$ with uniform cell-centered nodes

$$\begin{aligned} x_{j-1/2}=a+(j-1/2)h, \quad j=1, \ldots n, \ h= \frac{b-a}{n}, \end{aligned}$$

and a partition into subintervals

$$\begin{aligned} I_{j-1/2}=(x_{j-1},x_j), \quad x_j=jh, \ j=1, \ldots , n. \end{aligned}$$

Choosing an even degree, $p=2q$, the DGD space consists of functions, P(x), whose restriction $P_{j-1/2}(x)$ to $I_{j-1/2}$ is a degree-p polynomial satisfying

$$\begin{aligned} P_{j-1/2} (x_{k-1/2})=P(x_{k-1/2}), \quad \arrowvert k-j \arrowvert \le q. \end{aligned}$$

(2)

Note that (2) completely specifies $P_{j-1/2}(x)$ in terms of the nodal data in the interior, $q< j < n+1-q$. To complete the specification it is convenient to introduce nodal values at ghost nodes, $x_{j-1/2}$, $j=1-q, \ldots ,0$ and $j=n+1, \ldots , n+q$. One can simply view these as convenient degrees-of-freedom or, viewing them as extensions of the function beyond the domain, reduce the dimensionality of the space by replacing them by extrapolated values. In general we choose to extrapolate r values for r ranging from 0 (no extrapolation) to $q-1$ with, for $r > 0$ and $k=1, \ldots ,r$

$$\begin{aligned} P(x_{k-q-1/2})= & {} \sum _{\ell =1}^{p+1} \alpha _{\ell ,(k,r,p)} P(x_{r+\ell -q-1/2}) , \\ P(x_{n+q-k+1/2})= & {} \sum _{\ell =1}^{p+1} \alpha _{\ell ,(k,r,p)} P(x_{n+q-r-\ell +1/2}) , \end{aligned}$$

with $\alpha _{\ell ,(k,r,p)}$ uniquely determined by the condition that polynomials of degree p are contained in the space. The linear space ${\mathcal {V}}_{n,p,r}$ thus defined has the following properties:

• (i) ${\mathcal {V}}_{n,p,r}$ contains the polynomials of degree p;

• (ii) ${\mathcal {V}}_{n,p,r}$ has dimension $n+2q-2r$;

• (iii) ${\mathcal {V}}_{n,p,r}$ contains functions which have discontinuities at the interior cell boundaries, $x_j$, $j=1, \ldots , n-1$.

Interior nodal basis functions for ${\mathcal {V}}_{n,p,r}$ associated with a node $x_{k-1/2}$, which we denote by $\phi _{k-1/2,p}$, are simply the amalgamation of the Lagrange functions for the given node restricted to the cells. Since the polynomial in cell $j-1/2$ is the interpolant of the data at nodes $\ell$ satisfying $\arrowvert j-\ell \arrowvert \le q$, the support of $\phi _{k-1/2,p}$ will be restricted to $(x_{k-1-q},x_{k+q})$. Obviously these are translates of a single function $\psi _p$ which can be written in the standard form assuming cell widths h. In particular, for $z \in ( (k-1/2)h, (k+1/2)h )$, $k=-q, \ldots , q$,

$$\begin{aligned} \psi _{p}(z) = \prod _{\ell =-q , \ \ell \ne -k}^{\ell =q} \left( 1 - \frac{z}{(k+\ell )h} \right) , \end{aligned}$$

(3)

Fig. 1

DGD basis functions $\psi _p$ for $p=4,8$

with $\psi _{p}(z)=0$ for $\arrowvert z \arrowvert > (q+1/2)h$. We plot $\psi _p$ for $p=4,8$ in Fig. 1. For ghost nodes which are not determined by extrapolation (which we will call free ghost nodes), the basis functions are simply the restriction of $\psi _p$ to the cells within the domain. On the other hand, if k is a node whose value is used in an extrapolation formula, its associated basis function is a linear combination of $\phi _{k-1/2,p}$ with all the $\phi _{\ell -1/2,p}$ of extrapolated ghost values. For example, for $r>0$ and at the left boundary, $k=r-q+1, \ldots , q+r+1$:

$$\begin{aligned} \phi _{k-1/2,p}(x) = \psi _p(x-x_{k-1/2}) + \sum _{\ell =1-q}^{r-q} \alpha _{k+q-r,(\ell +q,r,p)} \psi _p ( x-x_{\ell -1/2}) . \end{aligned}$$

(4)

In summary, a function $P(x) \in {\mathcal {V}}_{n,p,r}$ is given by

$$\begin{aligned} P(x)= \sum _{k=1-q+r}^{n+q-r} y_{k-1/2} \phi _{k-1/2,p}(x) , \end{aligned}$$

(5)

where $\phi _{k-1/2,p}(x)=\psi _p(x-x_{k-1/2})$ if $r=0$ or, for $r > 0$, $q+r+1< k < n-q-r$, and $\phi _{k-1/2,p}$ given by (4) and its analogue on the right for $k \le q+r+1$ or $k \ge n-q-r$. Note that

$$\begin{aligned} P(x_{k-1/2})=y_{k-1/2} , \end{aligned}$$

but P is discontinuous at the cell boundaries $x_j$.

2.2 Upwind Derivative Operator

To construct an upwind derivative operator we consider the transport equation

$$\begin{aligned} \frac{\partial u}{\partial t}+ \frac{\partial u}{\partial x}=0, \quad u(a,t)=0 . \end{aligned}$$

Denoting by $u^h (x,t)$ the approximate solution

$$\begin{aligned} u^h(x,t) = \sum _{k=r-q+1}^{n+q-r} u^h(x_{k-1/2},t) \phi _{k-1/2}(x) , \end{aligned}$$

(6)

we impose, for all $r-q+1 \le \ell \le n+q-r$, the standard upwind formula on each interval $I_{j-1/2}$, rewritten to expose skew-symmetric and symmetric forms:

$$\begin{aligned}&\int _{x_{j-1}}^{x_j} \left( \phi _{\ell -1/2} (x) \frac{\partial u^h}{\partial t} (x,t) + \frac{1}{2} \phi _{\ell -1/2} (x) \frac{\partial u^h}{\partial x} (x,t) - \frac{1}{2} \frac{\partial \phi _{\ell -1/2}}{\partial x} (x) u^h (x,t) \right) dx \nonumber \\&\quad +\, \frac{1}{2} \phi _{\ell -1/2} (x_{j}^{-}) u^h(x_{j}^{-},t) + \frac{1}{2} \phi _{\ell -1/2} (x_{j-1}^{+}) \left( u^h(x_{j-1}^{+},t) - 2 u^{*}(x_{j-1},t) \right) = 0, \end{aligned}$$

(7)

where

$$\begin{aligned} u^{*}(x_j,t) = \left\{ \begin{array}{ll} u^h(x_j^{-},t)), &{} j > 0, \\ 0, &{} j=0. \end{array} \right. \end{aligned}$$

with

$$\begin{aligned} u^h (x_j^{\pm },t) = \lim _{x \rightarrow x_j^{\pm }} u^h(x,t) . \end{aligned}$$

Using (6) and summing (7) over the partition we obtain

$$\begin{aligned} \frac{dU^h}{dt} + D_p U^h =0 , \end{aligned}$$

where $U^h=\left( u^h(x_{r-q+1/2}), \ldots , u^h(x_{n+q-r-1/2}) \right) ^T$. To express $D_p$ we introduce the usual mass, derivative and lift matrices, $M_p$, $S_p$, and $L_p$, and note that the finite support of the basis functions leads to a band structure for all of them. To succinctly express the lift matrix we introduce the usual notation for the average and jump of the basis functions:

$$\begin{aligned} \left\{ \phi _{k-1/2} (x_j) \right\}= & {} \frac{1}{2} \left( \phi _{k-1/2} (x_j^{+}) + \phi _{k-1/2} (x_j^{-}) \right) , \\ \left[ \phi _{k-1/2} (x_j) \right]= & {} \left( \phi _{k-1/2} (x_j^{+}) - \phi _{k-1/2} (x_j^{-}) \right) . \end{aligned}$$

We then have

$$\begin{aligned} M_{\ell k,p}= & {} \sum _{j=1}^n \int _{x_{j-1}}^{x_j} \phi _{\ell -1/2}(x) \phi _{k-1/2}(x) dx , \end{aligned}$$

(8)

$$\begin{aligned} S_{\ell k,p}= & {} \sum _{j=1}^n \frac{1}{2} \int _{x_{j-1}}^{x_j} \phi _{\ell -1/2}(x) \phi '_{k-1/2}(x) - \phi '_{\ell -1/2}(x) \phi _{k-1/2}(x) dx , \end{aligned}$$

(9)

$$\begin{aligned} L_{\ell k,p}= & {} \Bigg ( \frac{1}{2} \phi _{\ell -1/2} (x_0^{+}) \phi _{k-1/2}(x_0^{+}) + \sum _{j=1}^{n-1} \left[ \phi _{\ell -1/2} (x_j) \right] \cdot \left[ \phi _{k-1/2} (x_j) \right] \nonumber \\&+\, \frac{1}{2} \phi _{\ell -1/2} (x_n^{+}) \phi _{k-1/2}(x_n^{+}) \Bigg ) \nonumber \\&+ \,\frac{1}{2} \sum _{j=1}^{n-1} \left( \left\{ \phi _{\ell -1/2} (x_j) \right\} \left[ \phi _{k-1/2}(x_j) \right] - \left[ \phi _{\ell -1/2} (x_j) \right] \left\{ \phi _{k-1/2}(x_j) \right\} \right) . \end{aligned}$$

(10)

Then

$$\begin{aligned} D_p= M_p^{-1} \left( S_p+L_p \right) . \end{aligned}$$

(11)

Away from boundaries (or with periodic boundary conditions) this clearly produces a compact difference method. As for an internal interval the nonzero basis functions are associated with $p+1$ nodes, the support of a given basis function will intersect with the support of 2p others. Thus M and S will have upper and lower bandwidths of p, with M symmetric and S skew-symmetric. At a cell boundary $x_j$ there is an additional interaction so that L will have upper and lower bandwidths of $p+1$. The first group of terms in (10) form its symmetric part which accounts for the dissipation.

We note that the generalization of the method to a constant coefficient symmetric system (1) in one space dimension follows directly from considering its diagonal form:

$$\begin{aligned} \frac{\partial {\mathbf {u}}}{\partial t} + \varLambda _R \frac{\partial {\mathbf {u}}}{\partial x} = {\mathbf {0}} ,&&\frac{\partial {\mathbf {v}}}{\partial t} - \varLambda _L \frac{\partial {\mathbf {v}}}{\partial x} = {\mathbf {0}} , \\ {\mathbf {u}}(a,t)+R_a {\mathbf {v}}(a,t) = {\mathbf {0}} ,&&{\mathbf {v}}(b,t)+R_b {\mathbf {u}}(b,t) = {\mathbf {0}} , \nonumber \end{aligned}$$

(12)

where $\varLambda _{R,L}$ are positive matrices. Only the flux terms change in the construction of the derivative operators. In particular

$$\begin{aligned} {\mathbf {v}}^{*}(x_j,t)={\mathbf {v}}^h (x_j^{+},t) \end{aligned}$$

and to be consistent with the boundary conditions

$$\begin{aligned} {\mathbf {u}}^{*} (x_0,t)= -R_a {\mathbf {v}}^h (x_0^{+},t) , \ \ \ \ {\mathbf {v}}^{*} (x_n,t) = -R_b {\mathbf {u}}^h (x_n^{-},t) . \end{aligned}$$

Thus if the problem is written in noncharacteristic variables we see that while the operator $M_p^{-1} S_p$ is applied directly to each variable, the lift terms, which provide the artificial dissipation, couple variables in a way which accounts for the characteristic structure and the boundary conditions.

In more complex situations an upwind flux can be constructed without looking at the characteristic variables. For example we can choose for $\tau > 0$

$$\begin{aligned} {\mathbf {w}}^{*}= & {} \frac{1}{2} \left( {\mathbf {w}}^h ({\mathbf {x}}^{+} ,t) + {\mathbf {w}}^h ({\mathbf {x}}^{-} ,t) \right) \\&-\, \tau \left( \sum _j n_j A_j \right) \left( {\mathbf {w}}^h ({\mathbf {x}}^{+} ,t) - {\mathbf {w}}^h ({\mathbf {x}}^{-} ,t) \right) , \ \ \end{aligned}$$

where $n_j$ are the components of the normal vector in the $+$ direction.

2.3 Dispersion and Dissipation

As ${\mathcal {V}}_{n,p,r}$ contains the polynomials of degree p, the standard error analysis for upwind DG methods [20] implies that D is dissipative and has accuracy at least $p+1$ including the boundary treatment. Focusing only on the interior operator (or periodic boundary conditions), we can use Fourier analysis (e.g., [17]) to directly study the properties of D. A symbolic computation yields the following results, which we list for $p=2,4, \ldots ,10$. Note that we define $\lambda _p$ by

$$\begin{aligned} D_p e^{ikx} = \lambda _p e^{ikx} , \end{aligned}$$

setting $h=1$. We then find

$$\begin{aligned} \lambda _2= & {} ik+ \frac{1}{128} k^6 -i \frac{169}{40320} k^7 + O(k^8) , \nonumber \\ \lambda _4= & {} ik + \frac{9}{32768} k^{10}- i \frac{102197}{613122048} k^{11} +O(k^{12}) , \nonumber \\ \lambda _6= & {} ik + \frac{25}{2097152} k^{14} -i \frac{41854909}{5465545113600} k^{15} + O(k^{16}) , \\ \lambda _8= & {} ik + \frac{1225}{2147483648} k^{18} -i \frac{17609039251200347}{46504110918960414720000} k^{19} + O(k^{20}) , \nonumber \\ \lambda _{10}= & {} ik + \frac{3969}{137438953472} k^{22} -i \frac{49354947289377308699}{2520353705949767349043200000} k^{23} + O(k^{24}) . \nonumber \end{aligned}$$

(13)

We see, then, that the interior scheme is dissipative to leading order and accurate of order $2p+1$. In our numerical experiments this superconvergence is sometimes realized.

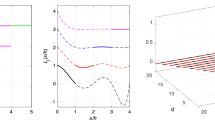
We can also study the spectrum of $\lambda _p$ numerically when boundaries are present. Here we consider the interval (0, 1), fix $n=100$, and calculate the eigenvalues of $D_p$ as p and r vary. To limit the number of results shown we focus on the extreme cases of the maximum and minimum number of ghost nodes: $r=q-1$ and $r=0$. In Table 1 we list the spectral radius of $hD_p$, $p=2, \ldots ,16$ with $r=q-1$ and $r=0$. We see that for $r=q-1$ the spectral radius grows slowly with p and for p tested remains well below $\pi /h$. With $r=0$, on the other hand, although the growth is slow the spectral radius is much larger. We note that for other values of $r > 0$ the radius is not much greater than for $r=q-1$, and there are some gains in accuracy if r is chosen slightly smaller. We have no theoretical explanation for this observation, but note that it matches what was observed for continuous basis functions in [8]. We do note that at high order the expected ill-conditioning in the boundary treatment does have an effect on accuracy for large p and fine grids.

Table 1 Spectral radius of $hD_p$ with $r=q-1$ and $r=0$ for (0, 1) and $n=100$

Now fixing $r=q-1$, in Fig. 2 we plot the spectra of $-D_p$ for $p=4$, $p=8$, $p=12$ and $p=16$ as well as the matrix arising in the approximation to the system (14)–(15) solved in Sect. 3. We note that $-D_p$ itself approximates a differential operator with no spectrum, while in the second case the system has purely imaginary eigenvalues $\pm i (k+1/2) \pi$, $k=0, 1, \ldots$. We again note the dissipative nature of the approximations and the slow growth of the spectrum with order. The spectral radii for the system are comparable to those for the transport equation.

Fig. 2

Spectra scaled by h of DGD derivative operators for $p=4,8,12,16$

3 Numerical Experiments

We finish with a series of numerical experiments to illustrate the performance of the method for problems in one and two space dimensions.¹ For linear problems we use a Taylor time stepping scheme. Precisely, if the semidiscretized system is of the form:

$$\begin{aligned} \frac{dU^h}{dt} = L_h U^h , \end{aligned}$$

then the method simply is

$$\begin{aligned} U^h(t+\varDelta t) = \sum _{j=0}^s \frac{(\varDelta t)^j}{j!} L_h^j U^h (t) . \end{aligned}$$

In order to observe any possible superconvergence we take $s=2p$. For the nonlinear example in Sect. 3.2 we use the standard fourth order Runge–Kutta method, again with time steps taken small to focus on the behavior of the spatial difference approximations.

3.1 Linear System in $1+1$ Dimensions

We consider

$$\begin{aligned} \frac{\partial u}{\partial t} + \frac{\partial u}{\partial x}=0, \ \ \ \ \ \frac{\partial v}{\partial t} - \frac{\partial v}{\partial x}=0 , \end{aligned}$$

(14)

$$\begin{aligned} u(0,t)+v(0,t)=0 , \ \ \ \ \ u(1,t)-v(1,t)=0 . \end{aligned}$$

(15)

As we have written the system in terms of characteristic variable, the DGD method is obtained as in the discussion around (12). In particular $u^{*}(x_j,t)=u^h(x_j^{-},t)$, $v^{*}(x_j,t)=v^h(x_j^{+},t)$ and the boundary fluxes are made consistent with the boundary conditions:

$$\begin{aligned} u^{*}(0,t)=-v^h(0^{+},t),&&v^{*}(0,t)= v^h(0^{+},t) , \\ u^{*}(1,t)=u^h(1^{-},t) ,&&v^{*}(1,t)=u^h(1^{-},t) . \end{aligned}$$

We approximate the solution

$$\begin{aligned} u(x,t)= & {} \sin {(20.5 \pi x)} \cdot \cos {(20.5 \pi t)} - \cos {(20.5 \pi x)} \cdot \sin {(20.5 \pi t)} , \\ v(x,t)= & {} \sin {(20.5 \pi x)} \cdot \cos {(20.5 \pi t)} + \cos {(20.5 \pi x)} \cdot \sin {(20.5 \pi t)} , \nonumber \end{aligned}$$

(16)

up to $t=100$, more than 1000 periods. We consider various meshes (depending on p) and observe the convergence rate as determined by the relative $l_2$ error in the interior at the final time. In Table 2 we only display results for $p=4$, $p=8$, $p=10$ and $p=12$. We choose the number of free ghost nodes to be $\frac{p}{4}$, which we found to be a good balance of small spectral radius and high accuracy. For larger values of p we obtain good results at low resolution, but convergence stagnates due to the ill-conditioning of the boundary treatments; for example with $p=16$ we obtain an error less than $0.5\%$ at 4.4PPW, but cannot reduce the relative error below $10^{-7}$ The table displays the errors and rates as a function of points-per-wavelength. This can be translated to n by noting that the domain contains 10.25 wavelengths. In all cases we chose $\varDelta t = \frac{2}{3} h$.

Table 2 Accuracy of approximations to the solution (16) to (14)–(15) at $t=100$ (1025 periods)

We see that for $p=4$ we observe superconvergence at an order near that of the interior scheme, $2p+1$, for all resolutions tested. For larger values of p it is only observed at the coarsest resolutions, though it is worth noting that at these coarse resolutions the accuracy is excellent; convergence at a rate greater than the design accuracy seems to hold until 4 or 5 digits of accuracy are attained.

3.2 A Nonlinear Problem in $1+1$ Dimensions

We have not as yet considered the use of DGD methods for problems with shocks. However, it can be used for nonlinear problems with smooth solutions. As an example we consider the system

$$\begin{aligned} \frac{\partial u}{\partial t} + \frac{\partial u}{\partial x} = -\frac{\sin {w}}{\sqrt{2}}, \ \ \ \ \frac{\partial v}{\partial t} - \frac{\partial v}{\partial x} = -\frac{\sin {w}}{\sqrt{2}} , \ \ \ \ \frac{\partial w}{\partial t} = \frac{u+v}{\sqrt{2}} . \end{aligned}$$

(17)

The system is satisfied if w satisfies the sine-Gordon equation, $\frac{\partial ^2 w}{\partial t^2} = \frac{\partial ^2 w}{\partial x^2} - \sin {w}$, $\sqrt{2} u = \frac{\partial w}{\partial t} - \frac{\partial w}{\partial x}$, $\sqrt{2} v = \frac{\partial w}{\partial t} + \frac{\partial w}{\partial x}$. Here we approximate the Perring-Skyrme solution involving the interaction of two solitary waves [28, Ch. 17]:

$$\begin{aligned} w= 4 \arctan { \left( c \frac{\sinh {rx}}{\cosh {crt}} \right) } , \quad c=\frac{1}{2} , \ r= (1-c^2 )^{-1/2} . \end{aligned}$$

We solve in the domain $x \in (-20,20)$, $t \in (-30,30)$; the solitary waves meet at the origin at $t=0$. The spatial derivatives in this case are approximated in exactly the same way as in the previous example. The Galerkin approximation to the nonlinear right-hand side, on the other hand, is approximated by a quadrature rule with $n_Q$ nodes $x_{j+1/2,k}$ and positive weights $\gamma _k$ on each interval. Precisely, on the interval $(x_{j-1},x_j)$ this leads to terms on the right-hand side of the approximations to (17) of the form:

$$\begin{aligned} \sum _{k=1}^{n_Q} \gamma _k \phi _{\ell -1/2} (x_{j+1/2,k}) \sin {\left( w_{j+1/2,k} (t) \right) } , \end{aligned}$$

with a pointwise approximation to the third equation:

$$\begin{aligned} \frac{d w_{j+1/2,k}}{dt} = \frac{u^h(x_{j+1/2,k},t) +v^h (x_{j+1/2,k},t)}{\sqrt{2}} . \end{aligned}$$

With upwind fluxes one can prove this scheme dissipates the energy

$$\begin{aligned} \frac{1}{2} \int \left( u^h \right) ^2 + \left( v^h \right) ^2 + \sum _j \sum _k \gamma _k \left( 1- \cos {\left( w_{j+1/2,k} (t) \right) } \right) . \end{aligned}$$

In our experiments we consider $p=4$, $p=6$, $p=8$ and $p=10$ with time steps scaled with $\varDelta t \propto h^{p/2}$ to observe any superconvergence, measuring relative $L^2$ errors at all integral times. Here we use Gaussian quadrature rules with 4p points in each interval. The results, shown in Table 3, demonstrate superconvergence for some range of resolutions tested for all cases.

Table 3 Maximum (in time) relative $L^2$ errors in u and v for approximations to the interacting solitary wave solutions to (17)

3.3 Extensions to Higher Dimensions

Extensions to higher space dimensions, as discussed for the continuous Galerkin difference basis in [9, 21], is straightforward. We assume a Cartesian domain, $\bigotimes _{k=1}^d (a_k,b_k)$, and regular grids with nodes $x_{k,j_k}=a_k+(j_k-1/2)h_k$ and cells $\bigotimes _{k=1}^d (x_{k,j_k-1},x_{k,j_k})$. Our basis will simply consist of tensor products of the one-dimensional basis functions:

$$\begin{aligned} \varPhi _{j_1-1/2, \ldots , j_d-1/2}(x_1, \ldots ,x_d) = \prod _{k=1}^d \phi _{k,j_k-1/2} (x_k) . \end{aligned}$$

(18)

Then, with approximations to $\frac{\partial {\mathbf {w}}}{\partial x_k}$ denoted by $D_{h_k} W^h$ constructed as above, and including one-dimensional upwind flux definitions, the semidiscrete problem can be succinctly written in tensor product form (for example if $d=2$):

$$\begin{aligned} (I_1 \otimes I_2 \otimes T) \frac{dW^h}{dt} + (D_{h_1} \otimes I_2 \otimes A_1) W^h + (I_1 \otimes D_{h_2} \otimes A_2 ) W^h = 0 . \end{aligned}$$

(19)

As each of the operators $D_{h_k}$ can be applied with linear cost (multiplication and back substitution by tightly banded matrices), the entire computation of $\frac{dW^h}{dt}$ is still linear. Moreover, proofs of convergence at design order are immediate.

To provide geometric flexibility one can couple the method with standard DG approximations on hybrid structured-unstructured grids as in [21]. Here we note that the analysis of stability and convergence in such cases follows automatically as we can view the DGD component grids as nothing more than large elements. It is also possible to apply the DGD method in mapped Cartesian grids. However, in this case the method must be altered to retain linear complexity. In particular, using the tensor-product basis functions, integration in the mapped domain will destroy the tensor-product structure of (19). For the derivative and lift matrices this is not so important. They will still be sparse and so we can multiply by them in linear time. However, losing the tensor product structure of the mass matrix is a serious issue, as there will be fill-in of its Cholesky factors and linear complexity will be lost. We propose two different solutions to this problem.

Curvilinear DGD:

Here, following [27], we scale the basis functions by the reciprocal of the square root of the Jacobian of the coordinate transform, $J({\mathbf {x}})$:

$$\begin{aligned}&\varPhi _{j_1-1/2, \ldots , j_d-1/2}(x_1, \ldots ,x_d) \\&\quad = J^{-1/2} (x_1, \ldots ,x_d) \prod _{k=1}^d \phi _{k,j_k-1/2} (x_k) . \end{aligned}$$

Now the mass matrix retains its tensor-product form $\bigotimes _{k=1}^d M_{k,p}$ which can be inverted in linear time. We demonstrate this approach for continuous GD methods in [9]. The results in [27] establish that optimal convergence is retained, and the experiments in [9] show superconvergence.

Weight-adjusted DGD:

Here, following [13], we keep the tensor-product basis functions but approximate the mass matrix by the inverse of the mass matrix computed with $J^{-1}$:

$$\begin{aligned} M \approx \left( \bigotimes _{k=1}^d M_{k,p}\right) M_{J^{-1}}^{-1} \left( \bigotimes _{k=1}^d M_{k,p}\right) . \end{aligned}$$

Then the application of $M^{-1}$ has linear complexity as it only involves the inversion of the tensor-product of the one-dimensional mass matrices and multiplication by $M_{J^{-1}}$, a sparse matrix. We demonstrate this approach for the continuous GD basis functions in [21], and use a matrix version in the variable coefficient example below. Again, optimal convergence follows from the results in [13]; we did not test for superconvergence there.

3.4 Stability Constraints and Convergence

To study the time step stability constraints of the method in two space dimensions as well as its accuracy we approximate the acoustic wave system:

$$\begin{aligned} \frac{\partial p}{\partial t} + \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0, \ \ \frac{\partial u}{\partial t} + \frac{\partial p}{\partial x} = 0, \ \ \frac{\partial v}{\partial t} + \frac{\partial p}{\partial y} = 0, \end{aligned}$$

(20)

$$\begin{aligned} u(0,y,t)=u(1,y,t) = 0, \ \ \ \ \ v(x,0,t)=v(x,1,t) = 0, \end{aligned}$$

(21)

and in particular the solution up to $t=100$

$$\begin{aligned} p=\cos {(k t)} \cdot \cos {(11 \pi x)} \cdot \cos {(11 \pi y)} ,&u=\sin {(k t)} \cdot \sin {(11 \pi x)} \cdot \cos {(11 \pi y)} , \nonumber \\ v=\sin {(k t)} \cdot \cos {(11 \pi x)} \cdot \sin {(11 \pi y)} ,&k= 11 \sqrt{2} \pi . \end{aligned}$$

(22)

Here flux terms are determined by the normal characteristic variables at interior interfaces:

$$\begin{aligned} p^{*}(x_j,y,t) \pm u^{*}(x_j,y,t)= & {} p(x_j^{\mp },y,t) \pm u(x_j^{\mp },y,t) , \\ p^{*}(x,y_k,t) \pm v^{*}(x,y_k,t)= & {} p(x,y_k^{\mp },t) \pm u(x,y_k^{\mp },t) , \end{aligned}$$

with the starred states at the boundaries constrained to satisfy the boundary conditions and the equations above involving the volume variables.

First, fixing the mesh width to be $h_1=h_2 \equiv h =10^{-2}$, we determine the time step stability constraints for a fixed temporal order of $s=8$ and for temporal orders growing in proportion to spatial order, $s=p$ and $s=2p$. Here again we display the results for the number of ghost nodes equal to p / 4, As seen in Table 4, when we fix $s=8$ the stability constraint, represented as $\varDelta t/h$, decreases in rough proportion to $p^{-1}$. However, increasing s linearly, which we argue would be necessary to balance temporal and spatial accuracy, it is roughly fixed. Although doubling the time step order does not quite allow us to double the time step on the basis of stability, choosing $s=2p$ was often better in terms of accuracy.

Table 4 Experimentally determined maximum value of $\varDelta t/h$ when solving (20) with $h=10^{-2}$

Second, we test convergence. Again we see that the boundary stiffness has a serious effect on the attainable accuracy when the degree is large. In particular, although at low resolutions we do get excellent accuracy, for example a relative error at $t=100$ of less than $1\%$ at 4.5PPW when $p=14$, convergence stalls at certain accuracies—$10^{-8}$ for $p=14$ and $10^{-7}$ for $p=16$. We tabulate errors and convergence rates for $p=4,8,10,12$ in Table 5. We generally observe convergence at design order, with superconvergence evident at the lower resolutions for $p=4$. Note that in these experiments we take $\varDelta t = h/3$.

Table 5 Accuracy of approximations to the solution (22) to (20) at $t=100$ (approximately 778 periods)

3.5 Application to the Elastic Wave Equation

In our final example we solve the elastic wave equation in an isotropic two-dimensional domain with smooth but variable material parameters. We use the Friedrichs-symmetrized form of the stress-velocity system and use a perfectly matched layer or PML at three boundaries. (The theory of PMLs is another field where Saul Abarbanel made important contributions [3, 5, 6].) Outside the layers we solve:

$$\begin{aligned} T(x,y) \frac{\partial {\mathbf {w}}}{\partial t} = A_1 \frac{\partial {\mathbf {w}}}{\partial x} + A_2 \frac{\partial {\mathbf {w}}}{\partial y} , \end{aligned}$$

where

$$\begin{aligned} {\mathbf {w}} = \left( \sigma _{xx} \ \ \sigma _{yy} \ \ \sigma _{xy} \ \ v_x \ \ v_y \right) ^T \end{aligned}$$

and in block form

$$\begin{aligned}&T= \left( \begin{array}{cc} C^{-1} &{}\quad 0 \\ 0 &{}\quad \rho I \end{array} \right) , \quad C= \left( \begin{array}{ccc} \lambda + 2 \mu &{}\quad \lambda &{}\quad 0 \\ \lambda &{}\quad \lambda + 2 \mu &{}\quad 0 \\ 0 &{} \quad 0 &{}\quad \mu \end{array} \right) , \\&A_1 = \left( \begin{array}{cc} 0 &{}\quad E_1 \\ E_1^T &{} \quad 0 \end{array} \right) , \quad E_1 = \left( \begin{array}{cc} 1 &{}\quad 0 \\ 0 &{}\quad 0 \\ 0 &{}\quad 1 \end{array} \right) , \quad A_2 = \left( \begin{array}{cc} 0 &{}\quad E_2 \\ E_2^T &{}\quad 0 \end{array} \right) , \quad E_2 = \left( \begin{array}{cc} 0 &{}\quad 0 \\ 0 &{}\quad 1 \\ 1 &{}\quad 0 \end{array} \right) . \end{aligned}$$

Here $\lambda$ and $\mu$ are the Lamé parameters, $\rho$ is the density, and the characteristic velocities are $c_S=\sqrt{\frac{\mu }{\rho }}$ and $c_L=\sqrt{\frac{\lambda +2 \mu }{\rho }}$.

Our experiment will treat the case of smooth but variable coefficients. Here we chose a case with an inclusion with wave speeds higher than those in the surrounding domain:

$$\begin{aligned} \lambda =1+9g, \ \ \ \mu =1+19g, \ \ \ \rho =1+g, \ \ \ g=e^{-\left( x^{10} + (y+7)^{10} \right) } . \end{aligned}$$

We solve on the domain $(-10,10) \times (-10,0)$ and impose free surface boundary conditions at $y=0$:

$$\begin{aligned} \sigma _{xx}=\sigma _{xy} = 0. \end{aligned}$$

(23)

At the other three edges we introduce a PML to avoid reflections. Precisely we follow the general form given in [7], enhancing the elastic system by:

$$\begin{aligned} T \frac{\partial {\mathbf {w}}}{\partial t}= & {} A_1 \left( \frac{\partial {\mathbf {w}}}{\partial x} + \nu _x(x) {\phi }_x \right) + A_2 \left( \frac{\partial {\mathbf {w}}}{\partial y} + \nu _y(y) {\phi }_y \right) , \nonumber \\ \frac{\partial {\phi }_x}{\partial t}= & {} - \left( \alpha + \nu _x(x) \right) {\phi }_x - \frac{\partial {\mathbf {w}}}{\partial x} , \\ \frac{\partial {\phi }_y}{\partial t}= & {} - \left( \alpha + \nu _y(y) \right) {\phi }_y - \frac{\partial {\mathbf {w}}}{\partial y} , \nonumber \end{aligned}$$

(24)

where the absorption parameters, $\nu _{x,y}$, are 0 in the domain $(-10,10) \times (-10,0)$. For this experiment we were not concerned with maximizing the efficiency of the layers and took them to be rather thick, of width 4. Precisely, with p the method order,

$$\begin{aligned} \nu _x&= 20 \left( 1- e^{\left( \frac{x-10}{4} \right) ^{p+1}} \right)& x > 10 , \\ \nu _x&= 20 \left( 1- e^{\left( \frac{-(x+10)}{4} \right) ^{p+1}} \right)& x< -10 , \\ \nu _y&= 20 \left( 1- e^{\left( \frac{-(y+10)}{4} \right) ^{p+1}} \right)& y < -10 . \end{aligned}$$

Lastly, we chose the complex frequency shift $\alpha =.01$ and terminated the layers with normal characteristic boundary conditions. We note that there has been extensive work on elastic PMLs, and long time stability can be lost without careful treatment [15, 16]. In fact, for sufficiently long time computations, we also observed instability originating at the layer terminations; as our flux formulations are different the analyses in [15, 16] do not apply. However, up to the times used to compare the solutions on different grids, the solution within the PML was well-behaved.

A direct DG approximation to (24) would lead to a mass matrix which would not have tensor product form. To avoid this we adopt the ideas presented in [12], a weight-adjusted DG method with matrix-valued weights. Precisely we solve:

$$\begin{aligned} \frac{d W^h}{dt}= & {} (M_1 \otimes M_2 \otimes I)^{-1} M_{T^{-1}} \left[ \left( D_{h_1} \otimes I_2 \otimes A_1 + I_1 \otimes D_{h_2} \otimes A_2 \right) W^h \right. \\&\left. +\, \nu _x (I_1 \otimes I_2 \otimes A_1) \varPhi _x + \nu _y (I_1 \otimes I_2 \otimes A_2 ) \varPhi _y \right] , \\ \frac{d \varPhi _x}{dt}= & {} -(\alpha + \nu _x ) \varPhi _x - (D_x \otimes I_2 \otimes I) W^h , \\ \frac{d \varPhi _y}{dt}= & {} -(\alpha + \nu _y ) \varPhi _y - (I_1 \otimes D_y \otimes I) W^h . \end{aligned}$$

Here $M_{T^{-1}}$ is the sparse matrix given in block form by

$$\begin{aligned} M_{T^{-1}} = \left( \begin{array}{ccccc} \lambda ^h + 2 \mu ^h &{}\quad \lambda ^h &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \lambda ^h &{}\quad \lambda ^h + 2 \mu ^h &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \mu ^h &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{} \quad 0 &{}\quad \upsilon ^h &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \upsilon ^h \end{array} \right) , \end{aligned}$$

where, for example,

$$\begin{aligned} \lambda ^h_{j_1,j_2,k_1,k_2}= & {} \sum _{\ell _1,\ell _2} \lambda (x_{\ell _1-1/2},y_{\ell _2-1/2} ) {\tilde{m}}_{1,j_1,k_1,\ell _1} {\tilde{m}}_{2,j_2,k_2,\ell _2} , \\ {\tilde{m}}_{1,j_1,k_1,\ell _1}= & {} \int \phi _{j_1-1/2} (x) \phi _{k_1-1/2} (x) \phi _{\ell _1-1/2} (x) dx , \\ {\tilde{m}}_{2,j_2,k_2,\ell _2}= & {} \int \phi _{j_2-1/2} (y) \phi _{k_2-1/2} (y) \phi _{\ell _2-1/2} (y) dy , \end{aligned}$$

with the analogous definitions of the matrix entries of $\mu ^h$ based on the values of $\mu$ and $\upsilon ^h$ on the values of $\rho ^{-1}$ on the nodes. Note that as these matrices explicitly depend on the nodal values of the material parameters there is negligible cost in updating them should the values change as part of an iterative inversion process. The operators $D_{h_j}$ again involve the upwind derivative operators computed using the constant coefficient mass matrices $M_j$. Thus the evaluation of the time derivatives now involves two multiplications by sparse matrices and two applications of $M_1^{-1} \otimes M_2^{-1}$, retaining linear complexity.

In the upwind derivative operators we determine flux terms by:

$$\begin{aligned} {\mathbf {w}}^{*}(x_j,y,t)= & {} \frac{1}{2} \left( {\mathbf {w}}(x_j^{+},y,t) + {\mathbf {w}}(x_j^{-},y,t) \right) + A_1 \left( {\mathbf {w}}(x_j^{+},y,t) - {\mathbf {w}}(x_j^{-},y,t) \right) , \\ {\mathbf {w}}^{*}(x,y_k,t)= & {} \frac{1}{2} \left( {\mathbf {w}}(x,y_k^{+},t) + {\mathbf {w}}(x,y_k^{-},t) \right) + A_2 \left( {\mathbf {w}}(x,y_k^{+},t) - {\mathbf {w}}(x,y_k^{-},t) \right) . \end{aligned}$$

This choice can be shown to be dissipative, but may affect the time step stability constraints. Note that the auxiliary variables in the PMLs are not differentiated and thus do not appear in the fluxes, and that the full DGD derivative operators, including the flux corrections, were used in the equations for evolving the auxiliary variables. Fluxes are modified at the free surface to be consistent with (23) and at the PML terminations by insisting that the outer states satisfy the boundary conditions.

Here we take as an initial condition a Gaussian disturbance in $v_x$ centered at $y=-3$:

$$\begin{aligned} w_4(x,y,0)=10e^{-5(x^2+(y+3)^2)} , \ \ \ w_j(x,y,0)=0, \ \ j \ne 4. \end{aligned}$$

We solve up to $t=14$ on three grids, $h_1 = h_2 \equiv h=\frac{1}{10}$, $h =\frac{1}{15}$ and $h = \frac{1}{20}$, with $p=10$ and two free ghost nodes. As above we march in time with a Taylor method of order 2p and, to safely accommodate the faster waves in the inclusion, a time step of $\varDelta t = \frac{h}{30}$.

Here we estimate the error and the convergence rate by extrapolation; that is we fit the data obtained with the three values of h to the model at points $(x_i,y_j,t_k)$

$$\begin{aligned} {\mathbf {w}}(x_i,y_j,t_k) = W^h(x_i,y_j,t_k) + A (x_i,y_j,t_k) h^r . \end{aligned}$$

As the meshes do not overlap we used degree 12 interpolation of the finer grid solutions onto the coarse mesh. Simply using the DGD basis to evaluate (which would be equivalent to degree 10 interpolation) yielded essentially the same errors. The estimated errors are plotted in Fig. 3. For most of the times $t_k > 5$ where data was recorded the estimated convergence rate was between 9.5 and 10.3, consistent with the design order. we plot snapshots of $\sigma _{xx}$ computed with $h =\frac{1}{20}$ as the waves progress and interact with the inclusion and the free surface.

Fig. 3

Upper left: error estimates for the variable coefficient elastic wave problem. Counterclockwise from the upper right: evolution of $\sigma _{xx}$

4 Conclusion

In conclusion, we have developed and applied dissipative discontinuous Galerkin difference operators for first order linear hyperbolic systems. We demonstrate that high accuracy can be obtained and that the time step stability constraints depend mildly on the method order. Besides testing the method in more complex geometries as in [21], there are two avenues for improvement which we plan to consider in future work. First, it may be possible to reduce the accuracy limitations and growth of the spectrum of the derivative matrices at high order by incorporating the grid stabilization techniques introduced for standard difference operators in [18, 19]. Second, it should be possible to increase the accuracy using the post-processing techniques proposed in [14, 24].