1 Introduction

The chemical reaction for the classical Lindemann Mechanism with three reaction rate constants \(k_1\), \(k_{-1}\) and \(k_2\) usually reads [1,2,3]

(1)

which describes that a reactant A decays into a product P by colliding with itself. Nowadays some modifications related to the Lindemann Mechanism have been widely investigated, such as the oxidation of dimethyl ether, see e.g. [4,5,6] for reference.

In the present work, by using \(2B \rightarrow P\) instead of \(B \rightarrow P\) in Eq. (1), we would like to investigate a modified version of the Lindemann mechanism introduced in Ref. [7], as follows:

(2)

The Law of Mass Action (see [2,3,4] for details) applied to this modified mechanism corresponds to a Cauchy initial value problem (IVP) governed by the following three nonlinear ordinary differential equations (ODEs), i.e. [7]

figure a

with the initial conditions (ICs)

$$\begin{aligned} a(0)=a_0, \quad b(0)=0, \quad p(0)=0, \end{aligned}$$
(4)

where a, b and c are the concentrations of the reactant A, the activated complex B and the product of the decay P respectively, t is the time and the initial value \(a_0\) is one positive constant. In Eq. (3), the units of the concentrations for a, b and c can be taken as \(\text {mol} \cdot \text {L}^{-1}\), and the unit of the time t is commonly taken as \(\text {s}\), \(\text {min}\) or \(\text {h}\).

Analytical studies play significant roles in analyzing dynamics of various nonlinear phenomena [8,9,10,11,12]. In Ref. [7] authors have studied the dynamical properties of system (3a) and (3b) by means of the blow–up technique, particularly they have also shown the existence of the invariant lines, and given the power series expansion of the solutions of a vector field defined by (3a) and (3b) via Newton–Puiseux polygon technique. More details for blow–up technique and Newton–Puiseux polygon technique, see e.g. Refs. [13, 14]. Nevertheless, both the exact analytical expressions for a and b and the detailed analytical form of the invariant lines have not been given.

The main aim of this work is to present a further analytical analysis for the modified Lindemann mechanism governed by Eqs. (3) and (4). We will focus on the following points: (i) the exact analytical expressions among a, b and p; (ii) the invariant lines and the feasible regions in planes (a, b), (a, p) and (b, p); (iii) the semi-numerical and semi-analytical solution by means of Piecewise differential transform method (PDTM) [15], for Eqs. (3) and (4). We note that the above points, to some extent, refine and improve the previous results in Ref. [7].

The rest of this work is arranged as follows. In Sect. 2, the exact analytical expressions among a, b and p are derived and briefly discussed. Section 3 provides the detailed analytical forms of the invariant lines and feasible regions. A semi-numerical and semi-analytical solution is established in Sect. 4. Finally in Sect. 5 we give the conclusion of this work.

2 Exact analytical expressions among a, b and p

    This part is devoted to provide an exact analytical analysis for the relations among the three relevant concentrations a, b and p in the reaction process, i.e. exact analytical expressions for (i) a and b, (ii) a and p, (iii) b and p respectively.

In view of system (3), we can easily see that \(d(a+b+2p)/dt=0\) whose time integral is a constant of the motion. So combining this with the ICs (4), we arrive at the first integral

$$\begin{aligned} a(t)+b(t)+2p(t)=a_0. \end{aligned}$$
(5)

Actually, in Ref. [7], Bayón et al. also presented the above first integral (5) as the conservation law. More about conservation law, see e.g. Refs [1, 4] for reference.

In view of system (3), it is easy to see that Eqs. (3a) and (3b) only include the variables a and b, and the item p only exists in Eq. (3c). Hence, dividing Eq. (3b) by Eq. (3a) to eliminate the time variable t, we immediately get the following scalar reduction

$$\begin{aligned} \frac{db}{da}=\frac{k_1 a^2 - k_{-1} a b -2 k_2 b^2}{k_{-1} a b - k_1 a^2}. \end{aligned}$$
(6)

It is obvious that Eq. (6) only contains two variables a and b, hence, in which form b could be considered as a function of a.

Now let us solve Eq. (6) with ICs (4). After simplifying Eq. (6), we can obtain

$$\begin{aligned} \frac{db}{da}=-1-\frac{2 \sigma \left( \frac{b}{a}\right) ^2}{\varepsilon \left( \frac{b}{a}\right) - 1}, \end{aligned}$$
(7)

where the new parameters \(\varepsilon \) and \(\sigma \) are [7]

$$\begin{aligned} \varepsilon =\frac{k_{-1}}{k_1}, \quad \sigma =\frac{k_{2}}{k_1}. \end{aligned}$$
(8)

Clearly, the physical quantities \(\varepsilon \) and \(\sigma \) are dimensionless. By introducing the transformation \(b(a)=u(a) a\) into Eq. (7) implies

$$\begin{aligned} u+a \frac{du}{da}=-1-\frac{2 \sigma u^2}{\varepsilon u - 1}. \end{aligned}$$
(9)

Therefore, with the aid of separation of variables, i.e. separating variables u and a from Eq. (9) we gain

$$\begin{aligned} \frac{du}{u+1+\frac{2 \sigma u^2}{\varepsilon u - 1}}=- \frac{da}{a}. \end{aligned}$$
(10)

As a consequence, integrating u and a on both sides of Eq. (10) respectively and substituting \(u=b/a\) and ICs (4) into the result, we then achieve the following exact analytical expression between a and b, and it takes the form

$$\begin{aligned}&2 \varepsilon b+4 b \sigma - a + \varepsilon a =\nonumber \\&\quad a \Psi \tanh \left[ \frac{\Psi \left( -\varepsilon \ln |-\varepsilon b^2 + a b - \varepsilon a b + a^2 - 2 \sigma b^2|-4 \sigma \ln |a| +C_1 \right) }{2(\varepsilon +4\sigma +\varepsilon ^2)}\right] , \end{aligned}$$
(11)

where

$$\begin{aligned}&\Psi =\sqrt{2\varepsilon +8\sigma +1+\varepsilon ^2}, \nonumber \\&C_1=(2 \varepsilon +4\sigma ) \ln |a_0|+\frac{2\left( \varepsilon +4\sigma +\varepsilon ^2\right) }{\Psi } \text{ arctanh }\left( \frac{\varepsilon -1}{\Psi }\right) . \end{aligned}$$
(12)

Finally, using the first integral or the conservation law (5) and substituting \(b=a_0-a-2p\) and \(a=a_0-b-2p\) into Eq. (11) respectively, we could also obtain the exact analytical expression between a and p, that is,

$$\begin{aligned} 2 \varepsilon a_0 + 4 \sigma a_0 - (4 \varepsilon + 8 \sigma ) p - (\varepsilon +4 \sigma +1) a= a \Psi \tanh \Phi , \end{aligned}$$
(13)

where

$$\begin{aligned} \Phi =\frac{\Psi \left[ -\varepsilon \ln |-(\varepsilon +2 \sigma ) (a_0-a-2p)^2 +(1 - \varepsilon ) (a_0-a-2p)a + a^2|-4 \sigma \ln |a| +C_1 \right] }{2(\varepsilon +4\sigma +\varepsilon ^2)}, \end{aligned}$$
(14)

and the exact analytical expression between b and p can be written as

$$\begin{aligned} \varepsilon a_0 - a_0 + (2-2\varepsilon ) p + (\varepsilon +1+4\sigma ) b = (a_0-b-2p) \Psi \tanh \Lambda , \end{aligned}$$
(15)

where

$$\begin{aligned} \Lambda =\frac{\Psi \left[ -\varepsilon \ln |4 p^2 + (2 b - 4 a_0 +2 \varepsilon b) p - b a_0 - \varepsilon b a_0 - 2 \sigma b^2 + a_0^2|-4 \sigma \ln |a_0-b-2p| +C_1 \right] }{2(\varepsilon +4\sigma +\varepsilon ^2)}. \end{aligned}$$
(16)

Let us discuss the dynamical behavior through the exact analytical expressions (11), (13) and (15), by considering the initial conditions

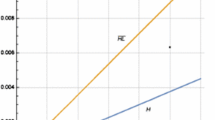
$$\begin{aligned} a(0)=0.4, \quad b(0)=0, \quad p(0)=0, \end{aligned}$$
(17)

as plotted in Fig. 1. It is found that, in the reaction process, as a varies from the initial value \(a(0)=0.4\) to its limiting value zero, b first increases from the initial value \(b(0)=0\) to the maximal value \(b_{max}\) then approaches to its limiting value zero, and p first rapidly increases from the initial value \(p(0)=0\) then tends to the maximal/limiting value \(p_{max}=a(0)/2=0.2\). It is also interesting that one can directly determine the maximal value \(b_{max}\) by solving the system governed by (11) and its derivative \(\frac{d}{da} b(a)=0\). Particularly, under the initial conditions (17) the maximal value \(b_{max}\approx 0.17134\), and at the same time the corresponding value of a can be also determined, namely 0.17134.

Fig. 1
figure 1

Plots of the relations of a, b and p through the exact analytical expressions in Eqs. (11), (13) and (15) (solid lines) and the rkf45 numerical result (solid circles) by solving Eq. (6), with the ICs \(a(0)=0.4\), \(b(0)=0\) and \(p(0)=0\)

Full size image

3 Invariant lines and feasible regions

Define the vector field X by the planar system (3a) and (3b). We should remark that the authors in Ref. [7] has proved the following two conclusions (as summarized in page 126), i.e.,

(Case I):

There is a single invariant line \(b=\zeta _1^{+} a\), with \(\zeta _1^{+}>0\) , on which X flows towards (0, 0);

(Case II):

There is an invariant line \(b=\zeta _1^{-} a\) with \(\zeta _1^{-}<0\), on which X flows towards (0, 0).

Hence, the next aim is to present the specific forms of these two invariant lines by determining \(\zeta _1^{+}\) and \(\zeta _1^{-}\). Now let us pay more attention to the logarithmic function \(\ln |-\varepsilon b^2 + a b - \varepsilon a b + a^2 - 2 \sigma b^2|\) in Eq. (11). Actually, one can obtain the invariant lines of X by solving \(-\varepsilon b^2 + a b - \varepsilon a b + a^2 - 2 \sigma b^2=0\), since such case corresponding to the separatrix of this logarithmic function. As a consequence, the two invariant lines can be directly solved and have the form

$$\begin{aligned} b=\frac{1-\varepsilon +\sqrt{(1+\varepsilon )^2+8\sigma }}{2(\varepsilon +2 \sigma )} a~\text {(Case~I)}, \quad b=\frac{1-\varepsilon -\sqrt{(1+\varepsilon )^2+8\sigma }}{2(\varepsilon +2 \sigma )} a~\text {(Case~II)}. \end{aligned}$$
(18)

With the aid of the fact that the parameters \(\varepsilon >0\) and \(\sigma >0\), it should be note that the relations in Eq. (18) respectively correspond to (Case I) and (Case II) since

$$\begin{aligned} \zeta _1^{+}\equiv \frac{1-\varepsilon +\sqrt{(1+\varepsilon )^2+8\sigma }}{2(\varepsilon +2 \sigma )}>0, \quad \zeta _1^{-}\equiv \frac{1-\varepsilon -\sqrt{(1+\varepsilon )^2+8\sigma }}{2(\varepsilon +2 \sigma )}<0. \end{aligned}$$
(19)

Specially, when \(k_1=1\), \(k_2=0.4\) and \(k_{-1}=0.2\), i.e., \(\varepsilon =0.2\) and \(\sigma =0.4\) from the relation (8), then the invariant lines (18) becomes \(b=(2+\sqrt{29})a/5 \approx 1.477 a\) [7] and \(b=(2-\sqrt{29})a/5\approx -0.677 a\), as shown in Fig. 2. Figure 2 is also coincide with Figs. 4 and 6 in Ref. [7].

Below let us consider the feasible region of plane (a, b) for X. In practice, considering that the concentrations a and b are always non-negative in the reaction process, and with the help of the fact that \((a,b)=(0,0)\) is the equilibrium point of the vector field X [7], one only need to consider the filled area in Fig. 2 (left one) as the feasible region where the initial data in Eq. (4) should be included in. In other words, the feasible region for the concentrations a and b restricted to the field X is

$$\begin{aligned} \Omega _{ab}=\{(a,b)|0<a<\infty ,0\le b<\zeta _1^{+} a\}, \end{aligned}$$
(20)

where \(\zeta _1^{+}\) is defined in Eq. (19). We remark that this feasible region admits the inequality \(-\varepsilon b^2 + a b - \varepsilon a b + a^2 - 2 \sigma b^2>0\), thus in such case the symbols of absolute value in Eq. (11) can be eliminated straightforwardly.

Fig. 2
figure 2

Plots of the invariant lines (red-straight lines) and feasible regions (cyan-filled areas), based on Eqs. (18), (20), (21), (22), (24), (25) with \(k_1=1\), \(k_2=0.4\) and \(k_{-1}=0.2\)

Full size image

Similarly, based on (13) and (15) we can also discuss the invariant lines and feasible region for planes (a, p) and (b, p). Actually, from the part of logarithmic functions in Eqs. (13) and (15) one can easily obtain the two invariant lines in plane (a, p)

$$\begin{aligned} a=\zeta _2^{\pm } (a_0-2p), \end{aligned}$$
(21)

and the two invariant lines in plane (b, p)

$$\begin{aligned} b=\zeta _3^{\pm } (a_0-2p), \end{aligned}$$
(22)

where

$$\begin{aligned} \zeta _2^{\pm }\equiv \frac{4 \sigma + 1 + \varepsilon \pm \sqrt{(1+\varepsilon )^2+8\sigma }}{4 \sigma },\quad \zeta _3^{\pm }\equiv \frac{-1-\varepsilon \pm \sqrt{(1+\varepsilon )^2+8\sigma }}{4 \sigma }. \end{aligned}$$
(23)

It is easy to prove that \(\zeta _2^{\pm }>0\), \(\zeta _3^{+}>0\) and \(\zeta _3^{-}<0\). Also according to the invariant lines (21) and (22), one can immediately determine the feasible region \(\Omega _{ap}\) for a and p, and the feasible region \(\Omega _{bp}\) for b and p, i.e.,

$$\begin{aligned} \Omega _{ap}=\left\{ (a,p)\left| 0\le p< \frac{a_0}{2}, \zeta _2^{-} (a_0-2p)< a < \zeta _2^{+} (a_0-2p) \right. \right\} , \end{aligned}$$
(24)

and

$$\begin{aligned} \Omega _{bp}=\left\{ (b,p)\left| 0\le p< \frac{a_0}{2}, 0 \le b < \zeta _3^{+} (a_0-2p) \right. \right\} . \end{aligned}$$
(25)

Specific plots of the invariant lines (21) and (22), and the feasible regions (24) and (25) are also given in Fig. 2 (middle and right ones).

4 Semi-numerical and semi-analytical solution

It seems that the exact analytical solution to IVP (3) and (4) is not easy to found, and in what follows we will focus on the construction of its semi-numerical and semi-analytical solution, based on the piecewise differential transform method (PDTM) suggested in Ref. [15]. More about DTM and DTM-based approaches, see Refs. [16,17,18] for reference and the references therein.

Table 1 Basic differential transforms at the node \(t=t_m\)
Full size table

We first start by segmenting the time interval \([0,+\infty ]\) into the following piecewise intervals \([0,t_1]\), \([t_1,t_2]\), ..., \([t_{m-1},t_m]\), ..., with a given equal step-size \(h\equiv \triangle t_m = t_m - t_{m-1}\) (here \(t_0 = 0\)), namely

$$\begin{aligned} t_m=mh. \end{aligned}$$
(26)

Now let us expand a(t), b(t) and p(t) at the node \(t=t_m\) in Taylor series

$$\begin{aligned}&a(t)=\sum _{j=0}^{\infty } A_m(j) (t-t_m)^j, \quad b(t)=\sum _{j=0}^{\infty } B_m(j) (t-t_m)^j, \nonumber \\&\quad p(t)=\sum _{j=0}^{\infty } P_m(j) (t-t_m)^j, \end{aligned}$$
(27)

where \(A_m(0)\), \(B_m(0)\) and \(P_m(0)\) clearly denote the function values of a(t), b(t) and p(t) at \(t=t_m\) respectively. In such case, according to the operations in Table 1 the differential transforms to system (3) yield

$$\begin{aligned} \left\{ \begin{aligned}&(j+1) A_m(j+1)=k_{-1} \sum _{i=0}^{j} A_m(j) B_m(j-i)-k_1 \sum _{i=0}^{j} A_m(j) A_m(j-i),\\&(j+1) B_m(j+1)=k_1 \sum _{i=0}^{j} A_m(j) A_m(j-i)\\ {}&-k_{-1} \sum _{i=0}^{j} A_m(j) B_m(j-i)-2k_2\sum _{i=0}^{j} B_m(j) B_m(j-i),\\&(j+1) P_m(j+1)=k_2\sum _{i=0}^{j} B_m(j) B_m(j-i). \end{aligned} \right. \end{aligned}$$
(28)

By substituting \(j=0,1,2,...\) into Eq. (28) one after another, we can get the explicit analytical expressions of \(A_m(j)\), \(B_m(j)\) and \(P_m(j)\) with respect to \(A_m(0)\), \(B_m(0)\) and \(P_m(0)\), see Table 2. As a result one immediately achieves the \(M^{\text {th}}\)-order analytical approximations for a(t), b(t) and p(t) respectively whose centers are located at the point \(t=t_m\), i.e.,

$$\begin{aligned} \left\{ \begin{aligned}&a^{[M]}\left( t;A_m(0),B_m(0),P_m(0)\right) \equiv \sum _{j=0}^{M} A_m(j) (t-t_m)^j,\\&b^{[M]}\left( t;A_m(0),B_m(0),P_m(0)\right) \equiv \sum _{j=0}^{M} B_m(j) (t-t_m)^j,\\&p^{[M]}\left( t;A_m(0),B_m(0),P_m(0)\right) \equiv \sum _{j=0}^{M} P_m(j) (t-t_m)^j, \end{aligned} \right. \end{aligned}$$
(29)

with a local truncation error \(o((t-t_m)^M)\). We should note that, in Eq. (29), the item \(P_m(0)\) only exists in \(p^{[M]}\left( t;A_m(0),B_m(0),P_m(0)\right) \), that is to say, \(p^{[M]}\left( t;A_m(0),B_m(0),P_m(0)\right) \) and \(p^{[M]}\left( t;A_m(0),B_m(0),P_m(0)\right) \) just include \(A_m(0)\) and \(B_m(0)\), as shown in Table 2. However, for the sake of talking convenience in this work we still use the above forms in Eq. (29).

Suppose that \(\tilde{a}_{m}\), \(\tilde{b}_{m}\) and \(\tilde{p}_{m}\) are the approximate values for a(t), b(t) and p(t) at \(t=t_m\) respectively. Thus substituting \(\tilde{a}_{m}=A_m(0)\), \(\tilde{b}_{m}=B_m(0)\) and \(\tilde{p}_{m}=P_m(0)\) into Eq. (29) directly indicates the analytical approximations for a(t), b(t) and p(t) on the interval \([t_m,t_{m+1}]\).

Below we would like to determine the values of \(\tilde{a}_{m}\), \(\tilde{b}_{m}\) and \(\tilde{p}_{m}\). For Cauchy IVP (3) and (4), it is natural that

$$\begin{aligned} \tilde{a}_{0}=A_0(0)=a_0, \quad \tilde{b}_{0}=B_0(0)=0, \quad \tilde{p}_{0}=P_0(0)=0. \end{aligned}$$
(30)

Meanwhile \(a^{[M]}\left( t;a_0,0,0\right) \), \(b^{[M]}\left( t;a_0,0,0\right) \) and \(p^{[M]}\left( t;a_0,0,0\right) \) are also determined as the analytical approximations to approximate a(t), b(t) and p(t) on the interval \([0,t_1]\), i.e. [0, h], by substituting \(t=t_1=h\) into which one could then determine \(\tilde{a}_{1}=a^{[M]}\left( h;a_0,0,0\right) \), \(\tilde{b}_{1}=b^{[M]}\left( h;a_0,0,0\right) \) and \(\tilde{p}_{1}=p^{[M]}\left( h;a_0,0,0\right) \). Generally, we can progressively obtain

$$\begin{aligned} \left\{ \begin{aligned}&\tilde{a}_{m}=a^{[M]}\left( mh;\tilde{a}_{m-1},\tilde{b}_{m-1},\tilde{p}_{m-1}\right) ,\\&\tilde{b}_{m}=b^{[M]}\left( mh;\tilde{a}_{m-1},\tilde{b}_{m-1},\tilde{p}_{m-1}\right) ,\\&\tilde{p}_{m}=p^{[M]}\left( mh;\tilde{a}_{m-1},\tilde{b}_{m-1},\tilde{p}_{m-1}\right) .\\ \end{aligned} \right. \end{aligned}$$
(31)

Finally, the semi-numerical and semi-analytical solution for Cauchy IVP (3) and (4) can be constructed and written as follows:

$$\begin{aligned}&a_{\text { PDTM}}(t)=\left\{ \begin{aligned}&a^{[M]}\left( t;a_0,0,0\right) , \quad 0 \le t \le h,\\&a^{[M]}\left( t;\tilde{a}_{1},\tilde{b}_{1},\tilde{p}_{1}\right) , \quad h \le t \le 2h,\\&\cdots \cdots ,\\&a^{[M]}\left( t;\tilde{a}_{m},\tilde{b}_{m},\tilde{p}_{m}\right) , \quad mh \le t \le (m+1)h,\\&\cdots \cdots ,\\ \end{aligned} \right. \end{aligned}$$
(32)
$$\begin{aligned}&b_{\text { PDTM}}(t)=\left\{ \begin{aligned}&b^{[M]}\left( t;a_0,0,0\right) , \quad 0 \le t \le h,\\&b^{[M]}\left( t;\tilde{a}_{1},\tilde{b}_{1},\tilde{p}_{1}\right) , \quad h \le t \le 2h,\\&\cdots \cdots ,\\&b^{[M]}\left( t;\tilde{a}_{m},\tilde{b}_{m},\tilde{p}_{m}\right) , \quad mh \le t \le (m+1)h,\\&\cdots \cdots ,\\ \end{aligned} \right. \end{aligned}$$
(33)
$$\begin{aligned}&p_{\text { PDTM}}(t)=\left\{ \begin{aligned}&p^{[M]}\left( t;a_0,0,0\right) , \quad 0 \le t \le h,\\&p^{[M]}\left( t;\tilde{a}_{1},\tilde{b}_{1},\tilde{p}_{1}\right) , \quad h \le t \le 2h,\\&\cdots \cdots ,\\&p^{[M]}\left( t;\tilde{a}_{m},\tilde{b}_{m},\tilde{p}_{m}\right) , \quad mh \le t \le (m+1)h,\\&\cdots \cdots .\\ \end{aligned} \right. \end{aligned}$$
(34)
Table 2 Specific analytical expressions of \(A_m(j)\), \(B_m(j)\) and \(P_m(j)\) for \(j=1,2,...\) with respect to \(A_m(0)\), \(B_m(0)\) and \(P_m(0)\)
Full size table

Figure 3 presents the comparisons between the PDTM solutions (32), (33) and (34) and the corresponding rkf45 numerical solutions under suitable parameter values. It is seen that they have a good agreement with each other. It is also interesting to note that one can achieve higher accuracy of the PDTM solutions expressed by Eqs. (32), (33) and (34) to meet the requirement through choosing a larger approximation order M and a smaller step-size h [15]. Moreover, from Fig. 3 it is easy to find that the reaction dynamics are coincide with those arising from Fig. 1 in Sect. 2. We can also straightforwardly see the limiting behaviors of the reaction dynamics, i.e., as the time t goes to infinity, the values of a and b tend to zero, and the value of p approaches to a(0)/2 (=0.2 in Fig. 3).

Fig. 3
figure 3

Evolutions of a(t), b(t) and p(t) using the \(4^{\text {th}}\)-order PDTM solutions (32), (33) and (34) with a step-size \(h=0.5\) (lines) and the relevant rkf45 numerical solutions (solid circles), for Cauchy IVP (3) and (17) with \(k_1=1\), \(k_2=0.4\) and \(k_{-1}=0.2\)

Full size image

5 Conclusion

A modified Lindemann mechanism has been studied analytically. We have obtained the exact analytical expressions among the three concentrations in Eqs. (11), (13) and (15), the detailed forms of the invariant lines and feasible regions in Eqs. (18), (21), (22) and (20), (24), (25) respectively, and also the semi-numerical and semi-analytical solution by utilizing PDTM in Eqs. (32), (33) and (34). The semi-numerical and semi-analytical solutions are valid by comparison with the numerical ones. Additionally, the reaction dynamics, even the limiting behaviors, have also been discussed due to the obtained analytical results.