Bogdanov–Takens singularity for a system of reaction–diffusion equations

Abstract

In this manuscript, we provide a framework of the Bogdanov–Takens singularity for general reaction–diffusion equations. The explicit conditions for this singularity are established and the corresponding normal form up to the second order terms is derived. As an application of our framework, the Schnackenberg model is presented to illustrate the theoretical results.

1 Introduction

In this manuscript, we study the Bogdanov–Takens singularity of general diffusion-reaction equations

$$\begin{aligned} \frac{\partial u}{\partial t}=\tilde{D}\frac{\partial ^2 u}{\partial x^2}+Au+R(u,\mu ), \end{aligned}$$

(1)

where $u=(u_1,\ldots ,u_n)^T$ is a function of $(x,t)\in (0,1)\times \mathbb {R}^+$ together with the boundary conditions

$$\begin{aligned} u_k(0,t)=u_k(1,t)=0, k=1,2,\ldots ,n, \end{aligned}$$

(2)

and $\mu =(\mu _1,\ldots ,\mu _m)^T\in \mathbb {R}^m$ is a bifurcation parameter. In (1), we assume that

$$\begin{aligned} \tilde{D}=\left( \begin{matrix} D_1&{}0&{}\cdots &{}0\\ 0&{}D_2&{}\cdots &{}0\\ \vdots &{}\vdots &{}\vdots &{}\vdots \\ 0&{}0&{}\cdots &{}D_n \end{matrix}\right) , A=\left( \begin{matrix} a_{11}&{}\cdots &{}a_{1n}\\ \vdots &{}\vdots &{}\vdots \\ a_{n1}&{}\cdots &{}a_{nn} \end{matrix}\right) , \end{aligned}$$

are two $n\times n$ constant matrices with $D_i>0$ and $a_{ij}\in \mathbb {R},\, i,j=1,2,\ldots ,n$ and $R(u,\mu )$ a $C^3(\mathbb {R}^{m+n},\mathbb {R}^n)$ function satisfying $R(0,\mu )=0$ and $D_u(0,\mu )=0$. Clearly $(0,\ldots ,0)^T$ is a trivial equilibrium of (1). Sys. (1) defines an infinite dimensional dynamical system $\{\mathbb {R}^+,\varphi _\mu ^t\}$ on a functional space

$$\begin{aligned} \mathscr {H}=(H^2(0,1)\cap H^1_0(0,1))^n \end{aligned}$$

with normal $\Vert u\Vert =\left<u,u\right>^{1/2}$. See [2, 4] for detail. Here

$$\begin{aligned} \left<u,v\right>=\frac{1}{1+\pi ^2+\pi ^4}\sum _{k=1}^n\int _0^1\left( u_kv_k+\frac{\partial u_k}{\partial x}\frac{\partial v_k}{\partial x}+\frac{\partial ^2 u_k}{\partial x^2}\frac{\partial ^2 v_k}{\partial x^2}\right) dx. \end{aligned}$$

Let $\mathscr {L}=(L^2(0,1))^n$. Then $\mathscr {H}\hookrightarrow \mathscr {L}$. Define $L: \mathscr {H}\rightarrow \mathscr {L}$ by

$$\begin{aligned} Lu=\tilde{D}\frac{\partial ^2u}{\partial x^2}+Au. \end{aligned}$$

(3)

Then L is a linear operator and Eq. (1) becomes

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial u}{\partial t}=Lu+R(u,\mu ),\\ u(0,t)=u(1,t)=0,u(x,0)=u_0(x). \end{array}\right. \end{aligned}$$

(4)

In order to study the dynamical behavior of Sys. (4), we have to investigate the distribution of eigenvalues of L. There are some critical cases we have to address:

• 1. L has a pair of purely imaginary eigenvalues and the others have negative real parts. Then Sys. (4) undergoes a Hopf bifurcation. If $n=2$, Haragus and Iooss [2] and Kuznetsov [4] gave algorithms to calculate the normal form for the Brusselator model. In the literature, there are lots of publications which discuss Hopf bifurcation for different types of reaction–diffusion equations ([5, 6]).

• 2. L has a double zero eigenvalue (a zero eigenvalue with multiplicity 2) and the others have negative real parts. For general reaction–diffusion equations, to the authors’ knowledge, this has not been studied in the literature.

Note that, for a double zero eigenvalue, the corresponding Jordan block is either $\left( {\begin{matrix} 0&{}0\\ 0&{}0 \end{matrix}}\right)$ or $\left( {\begin{matrix} 0&{}1\\ 0&{}0 \end{matrix}}\right)$. In this research, we only focus on the latter case, which means that the algebraic and geometric multiplicities of the eigenvalue zero are 2 and 1, respectively. This is so-called Bogdanov–Takens (BT) singularity. We will use the normal form theory to transform Eq. (4) to a system of planar ordinary differential equations whose dynamical behavior is well-known. In this manuscript, for simplicity, we try to derive the terms of normal form up to order 2 for BT singularity in case of $m=n=2$.

In 1979, J. Schnakenberg [7] introduced a system of partial differential equations describing the trimolecular reactions between two chemical products X and Y and two chemical sources A and B which are in the following form:

$$\begin{aligned} A\rightleftarrows X, B\rightarrow Y, 2X+Y\rightarrow 3X. \end{aligned}$$

(5)

Let $u_1$ and $u_2$ be the concentrations of two chemical products X and Y, respectively. Then the dimensionless form of the equations of (5) can be written as

$$\begin{aligned} \left\{ \begin{array}{rcl} \frac{\partial u_1}{\partial t}&{}=&{}D_1\frac{\partial ^2 u_1}{\partial x^2}+a-u_1+u_1^2u_2, x\in (0,1),t>0,\\ \frac{\partial u_2}{\partial t}&{}=&{}D_2\frac{\partial ^2 u_2}{\partial x^2}+b-u_1^2u_2, x\in (0,1),t>0. \end{array}\right. \end{aligned}$$

(6)

Here $D_1$ and $D_2$ are the diffusion coefficients of the chemicals X and Y, respectively, and a and b the concentrations of A and B, respectively. For simplicity, we assume that $u=(u_1,u_2)^T$ is a function of $(x,t)\in (0,1)\times \mathbb {R}^+$. The reason to study the reaction–diffusion version of the Schnakenberg model is the assumption that the products are not homogeneously mixed during the reaction. As in [2] and [4], in this research, we use the following Dirichlet boundary conditions

$$\begin{aligned} u_1(0,t)=u_1(1,t)=a+b,u_2(0,t)=u_2(1,t)=\frac{b}{(a+b)^2}. \end{aligned}$$

(7)

Note that with these boundary conditions, the equilibrium $E(a+b,\frac{b}{(a+b)^2})$ is a trivial solution of (6) and that, after shifting it to 0, (6) with (7) becomes the form of (4). We can find the conditions such that the equilibrium point is asymptotically stable. But we are more interested in periodic solutions, namely the reaction repeats cyclically. This leads to study Hopf singularity. But the condition for Hopf singularity is not always satisfied. For BT singularity, we still can obtain limit cycles under small perturbations of the critical values $a^*$ and $b^*$ of a and b (see Sect. 3) despite the fact that the condition for Hopf singularity is violated.

Recently, the reaction–diffusion Schnakenberg model has been studied extensively. In [1], Grampin et al. obtained the frequency-doubling sequence of Sys. (6) in the exponentially growing domain and pattern transitions by activator peak splitting. In [3], Iron et al. studied the stability of symmetric N-peaked steady-states which can be reduced to computing two matrices in terms of the diffusion coefficients $D_1$ and $D_2$ and the number N of peaks. In [5], Liu et al. showed that Sys. (6) has spatially nonhomogeneous periodic orbits bifurcating from the equilibrium point. In this manuscript, we will apply our result for Eq. (4) to the Schnakenberg model (6) to obtain BT bifurcation and the corresponding bifurcation diagram.

The rest of this manuscript is organized as follows. In Sect. 2, the explicit conditions are obtained such that the linearized system has a zero eigenvalue with algebraic multiplicity 2 and geometric multiplicity 1 (BT singularity); moreover, the normal form theory in [2] is applied to compute the terms of the normal form of BT singularity for Sys. (4) up to the second order. In Sect. 3, we apply the result in Sect. 2 to the Schnackenberg model (6) to study BT bifurcation.

2 Bogdanov–Takens bifurcation and computation of the normal form

For simplicity, we set $m=n=2$. Note that the set $\{\sin (k\pi x): k\in \mathbb {N}\}$ forms a basis of $H_0^1(0,1)$. Let

$$\begin{aligned} u(x)=\sum _{k=1}^\infty \left( {\begin{array}{c}u^1_k\\ u^2_k\end{array}}\right) \sin (k\pi x)\in \mathscr {H} \end{aligned}$$

be the solution of the eigenvalue problem

$$\begin{aligned} Lu=\lambda u, \lambda \in \mathbb {C}. \end{aligned}$$

Here $\left( {\begin{array}{c}u^1_k\\ u^2_k\end{array}}\right) \in \mathbb {R}^2$ is constant, $k=1,2,\ldots$. Then we have

$$\begin{aligned} \sum _{k=1}^\infty \left( \begin{matrix} \lambda +D_1n^2\pi ^2-a_{11}&{}-a_{12}\\ -a_{21}&{}\lambda +D_2k^2\pi ^2-a_{22} \end{matrix}\right) \left( {\begin{array}{c}u^1_k\\ u^2_k\end{array}}\right) \sin (k\pi x)=0 \end{aligned}$$

from which we know that $\lambda$ satisfies

$$\begin{aligned} P_k(\lambda )\equiv \lambda ^2+r_k\lambda +s_k=0 \end{aligned}$$

where

$$\begin{aligned} r_k= & {} \pi ^2(D_1+D_2)k^2-\text {tr}(A), \\ s_k= & {} D_1D_2\pi ^4k^4-\pi ^2(D_1a_{22}+D_2a_{11})k^2+\det (A). \end{aligned}$$

Clearly two roots of $P_k$ have negative real parts if and only if

$$\begin{aligned} r_k>0, s_k>0 \end{aligned}$$

which are equivalent to

$$\begin{aligned} \pi ^2(D_1+D_2)k^2>\text {tr}(A), D_1D_2\pi ^4k^4+\det (A)>\pi ^2(D_1a_{22}+D_2a_{11})k^2, \end{aligned}$$

respectively.

Noting that $\{r_k\}$ is strictly increasing. We assume that $\det (A)>0$. By $a^2+b^2\ge 2ab$, we have

$$\begin{aligned} D_1D_2\pi ^4k^4+\det (A)\ge 2\pi ^2k^2\sqrt{D_1D_2\det (A)} \end{aligned}$$

and hence if $2\sqrt{D_1D_2\det (A)}\ge D_1a_{22}+D_2a_{11}$, we have $s_k\ge 0$.

Now we study the distribution of roots of $P_1(\lambda )$. Note that $r_1>0$ is equivalent to

$$\begin{aligned} \pi ^2(D_1+D_2)>\text {tr}(A). \end{aligned}$$

If $r_1=0$ and $s_1>0$, then $P_1(\lambda )$ has a pair of purely imaginary roots $\pm i\sqrt{s_1}$. If $r_1=s_1=0$, then $P_1(\lambda )$ has a double zero root. Note that $r_1=s_1=0$ is equivalent to

$$\begin{aligned} \left\{ \begin{array}{ll} a_{11}+a_{22}=\pi ^2(D_1+D_2),\\ D_1D_2\pi ^4+a_{11}a_{22}-a_{21}a_{12}=\pi ^2(D_1a_{22}+D_2a_{11}). \end{array}\right. \end{aligned}$$

If, in addition to the assumptions up to now, we also assume that $a_{12}a_{21}<0$, then the values of the diagonal elements will be real and can be expressed as follows

$$\begin{aligned} a_{11}=\pi ^2D_1\pm \sqrt{-a_{12}a_{21}},a_{22}=\pi ^2D_2\mp \sqrt{-a_{12}a_{21}} \end{aligned}$$

From this, we have

$$\begin{aligned} s_n=(n^2-1)\pi ^2[(n^2-1)\pi ^2D_1D_2+\sqrt{-a_{12}a_{21}}(D_1-D_2)] \end{aligned}$$

and hence $\{s_n\}$ is strictly increasing.

Let us make the following assumption

• (H1). $\det (A)>0$, $\pi ^2(D_1+D_2)>\text {tr}(A)$, and $2\pi ^2\sqrt{D_1D_2\det (A)}-(D_1a_{22}+D_2a_{11})>0$;

• (H2). $\det (A)>0$, $\pi ^2(D_1+D_2)=\text {tr}(A)$, and $2\pi ^2\sqrt{D_1D_2\det (A)}-(D_1a_{22}+D_2a_{11})>0$;

• (H3). $a_{12}a_{21}<0$, $3\pi ^2D_1D_2+\sqrt{-a_{12}a_{21}}(D_1-D_2)>0$.

Thus we have the following result.

Theorem 2.1

If (H1) holds, then all eigenvalues of L have negative real parts and hence (0, 0) is stable. If (H2) holds, then L has a pair of purely imaginary roots $\pm \omega _0 i$ and all other eigenvalues have negative real parts and hence Sys.(4) undergoes Hopf bifurcation. Under (H3), if

$$\begin{aligned} a_{11}=\pi ^2D_1+\sqrt{-a_{12}a_{21}},a_{22}=\pi ^2D_2-\sqrt{-a_{12}a_{21}}, \end{aligned}$$

or

$$\begin{aligned} a_{11}=\pi ^2D_1-\sqrt{-a_{12}a_{21}},a_{22}=\pi ^2D_2+\sqrt{-a_{12}a_{21}}, \end{aligned}$$

then L has a double zero eigenvalue and all other eigenvalues have negative real parts and hence Sys.(4) undergoes BT bifurcation.

Now we compute the normal form of BT bifurcation under the assumption (H3). Note that the first part of (H3) is

$$\begin{aligned} a_{12}a_{21}<0. \end{aligned}$$

Without loss of generality, we assume that

$$\begin{aligned} a_{12}=\delta ^2, a_{21}=-\gamma ^2 \end{aligned}$$

where $\delta >0,\gamma >0$ and then

$$\begin{aligned} a_{11}=\pi ^2D_1+\sqrt{-a_{12}a_{21}}=\pi ^2D_1+\gamma \delta ,a_{22}=\pi ^2D_2-\sqrt{-a_{12}a_{21}}=\pi ^2D_2-\gamma \delta . \end{aligned}$$

Hence

$$\begin{aligned} A=\left( \begin{matrix} \pi ^2D_1+\gamma \delta &{}\delta ^2\\ -\gamma ^2&{}\pi ^2D_2-\gamma \delta \end{matrix}\right) . \end{aligned}$$

Let

$$\begin{aligned} q_1= & {} (\delta ^2,-\gamma \delta )^T\sin (\pi x),\\ q_2= & {} (\delta ^2,1-\gamma \delta )^T\sin (\pi x),\\ p_1= & {} \frac{2}{\delta ^2}(1-\gamma \delta ,-\delta ^2)^T\sin (\pi x),\\ p_2= & {} \frac{2}{\delta }(\gamma ,\delta )^T\sin (\pi x). \end{aligned}$$

It is easy to check that

$$\begin{aligned} Lq_1=0,Lq_2=q_1,L^Tp_1=p_2,L^Tp_2=0 \end{aligned}$$

and

$$\begin{aligned} \left<p_1,q_1\right>=\left<p_2,q_2\right>=1, \left<p_1,q_2\right>=\left<p_2,q_1\right>=0. \end{aligned}$$

Note that, according to [2], for BT singularity, through the change of variable from $u=(u_1,u_2)$ to $z=(z_1,z_2)$ by

$$\begin{aligned} u=z_1q_1+z_2q_2+\Phi _\mu (z_1,z_2), \end{aligned}$$

Equation (4) can be transformed into the following normal form up to order 2

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{z}_1&{}=&{}z_2\\ \dot{z}_2&{}=&{}\nu _1z_1+\nu _2z_2+a_1z_1^2+b_1z_1z_2\\ &{}&{}+\,\mathcal {O}(|\mu |^2+|\mu |(|z_1|+|z_2|)^2+(|z_1|+|z_2|)^3), \end{array}\right. \end{aligned}$$

(8)

In this case, let

$$\begin{aligned} \Phi _\mu (z_1,z_2)=\Phi _{101}(\mu )z_1+\Phi _{011}(\mu )z_2+\Phi _{200}z_1^2+\Phi _{110}z_1A_2+\Phi _{020}z_2^2. \end{aligned}$$

For simplicity, write $R(u,\mu )$ as

$$\begin{aligned} R(u,\mu )=R_{11}(u,\mu )+R_{2}(u,u)+o((|u|+|\mu |)^3) \end{aligned}$$

where $R_{11}(u,\mu ): \mathbb {R}^2\times \mathbb {R}^2\rightarrow \mathbb {R}^2$ and $R_2(u,v): \mathbb {R}^2\times \mathbb {R}^2\rightarrow \mathbb {R}^2$ are linear symmetric maps of u, v and $\mu$ respectively. Replacing u by $z_1q_1+z_2q_2+\Phi _\mu (z_1,z_2)$ in Eq. (4) and comparing the terms with order $\mathcal {O}(z_1)$ and $\mathcal {O}(z_2)$, we obtain

$$\begin{aligned} \nu _1q_2= & {} L\Phi _{101}+R_{11}(q_1,\mu ), \end{aligned}$$

(9)

$$\begin{aligned} \nu _2q_2+\Phi _{101}= & {} L\Phi _{011}+R_{11}(q_2,\mu ), \end{aligned}$$

(10)

Similarly comparing the terms with order $\mathcal {O}(z_1^2), \mathcal {O}(z_1z_2)$, and $\mathcal {O}(z_2^2)$, and terms with order $\mathcal {O}(A_1^3), \mathcal {O}(z_1^2z_2)$, $\mathcal {O}(z_1z_2^2)$, and $\mathcal {O}(z_2^3)$, respectively, we obtain

$$\begin{aligned} a_1q_2= & {} L\Phi _{200}+R_{20}(q_1,q_1), \end{aligned}$$

(11)

$$\begin{aligned} b_1q_2+2\Phi _{200}= & {} L\Phi _{110}+2R_{20}(q_1,q_2). \end{aligned}$$

(12)

From (9) and (10), we have

$$\begin{aligned} \nu _1= & {} \left<p_2,R_{11}(q_1,\mu )\right>,\\ \nu _2= & {} \left<p_2,-\Phi _{101}+R_{11}(q_1,\mu )\right>, \end{aligned}$$

and from (11) and (12), we have

$$\begin{aligned} a_1= & {} \left<p_2,R_{20}(q_1,q_1)\right>,\\ b_1= & {} \left<p_2,-2\Phi _{200}+2R_{20}(q_1,q_2)\right>. \end{aligned}$$

Remark 2.1

In this manuscript, for simplicity, we only calculate the coefficients of the normal form up to order 2. For the coefficients of the normal form order 3, the computation is complicated and we omit the detail.

In order to determine $\nu _1,\nu _2, a_1$ and $b_1$, we need the following lemma which solves a system of differential equations with boundary value problems.

Lemma 2.1

Let a, b, c, d be constants. Then the system of DEs

$$\begin{aligned} \left\{ \begin{array}{lll} Lu=\left( {\begin{array}{c}a\\ b\end{array}}\right) \sin (\pi x)+\left( {\begin{array}{c}c\\ d\end{array}}\right) \sin ^2(\pi x),\\ u_1(0)=u_1(1)=u_2(0)=u_2(1)=0, \end{array}\right. \end{aligned}$$

(13)

has a solution if and only if the following solvability condition holds

$$\begin{aligned} 3 \pi a \gamma +3 \pi b \delta +8 c \gamma +8 \delta d=0. \end{aligned}$$

(14)

Moreover for $D=D_1=D_2$, if the condition (14) holds, Eq. (13) has at least one solution

$$\begin{aligned} u_1(x)= & {} \frac{1}{72 \pi ^5 D^2}[9 \pi ^3 a \gamma \delta x^2 \sin (\pi x)+9 \pi ^3 b \delta ^2 x^2 \sin (\pi x)-36 \pi c \gamma \delta \\&+16 \pi (2 x-1) \cos (\pi x) \\&\times \left( -2 c \gamma \delta +3 \pi ^2 c D-2\delta ^2 d\right) +4 \pi \cos (2 \pi x) \left( c \gamma \delta +3 \pi ^2 c D+\delta ^2 d\right) \\&-96 \pi ^2 c D \sin (\pi x)+36 \pi ^3 c D+64 c \gamma \delta \sin (\pi x)+24 \pi ^2 c \gamma \delta x \sin (\pi x)\\&+72 \pi ^4 D^2 C \sin (\pi x)-36 \pi \delta ^2 d+64 \delta ^2 d \sin (\pi x)+24 \pi ^2 \delta ^2 d x \sin (\pi x)],\\ u_2(x)= & {} -\frac{1}{72 \pi ^5 D^2 \delta ^2}[4\pi \delta \cos (\pi x) (9 \pi ^3 a \gamma D x\\&+\,\delta \left( 3 \pi ^2 D (3 \pi b x+4 d)+8 \gamma \delta d (1-2 x)\right) +8 c \gamma \left( 3 \pi ^2 D x+\gamma \delta (1-2 x)\right) )\\&-\,72 \pi ^5 a D^2 \sin (\pi x)+18 \pi ^3 a \gamma D \delta \sin (\pi x)\\&+\,9 \pi ^3 a \gamma ^2 \delta ^2 x^2 \sin (\pi x)+18 \pi ^3 b D \delta ^2 \sin (\pi x)+9 \pi ^3 b \gamma \delta ^3 x^2 \sin (\pi x) \\&-\,36 \pi c \gamma ^2 \delta ^2-192 \pi ^4 c D^2 \sin (\pi x)\\&-\,4 \pi \delta ^2 \cos (2 \pi x) \left( 3 \pi ^2 D d-\,\gamma (c \gamma +\delta d)\right) \\&+\,32 \pi ^2 c \gamma D \delta \sin (\pi x)\\&+\,64 c \gamma ^2 \delta ^2 \sin (\pi x)+24 \pi ^2 c \gamma ^2 \delta ^2 x \sin (\pi x)+72 \pi ^4 \gamma D^2 \delta C \sin (\pi x) \\&-\,36 \pi ^3 D\delta ^2 d+128\pi ^2 D \delta ^2 d \sin (\pi x) -36 \pi \gamma \delta ^3 d+64 \gamma \delta ^3 d \sin (\pi x)\\&+\,24 \pi ^2 \gamma \delta ^3 d x \sin (\pi x)] \end{aligned}$$

where C is an arbitrary constant.

Proof

Since $L^Tp_2=0$, we have $\langle p_2,Lu\rangle =\langle L^Tp_2,u\rangle =0$ and hence obtain

$$\begin{aligned} \langle p_2,\left( {\begin{array}{c}a\\ b\end{array}}\right) \sin (\pi x)+\left( {\begin{array}{c}c\\ d\end{array}}\right) \sin ^2(\pi x)\rangle =0 \end{aligned}$$

or

$$\begin{aligned} 3 \pi a \gamma +3 \pi b \delta +8 c \gamma +8 \delta d=0 \end{aligned}$$

and hence the condition (14) holds. For $D_1=D_2$, suppose the condition (14) holds, we can solve Sys. (13). In fact, Sys. (13) is equivalent to the following system

$$\begin{aligned} \left\{ \begin{array}{l} Du_1''+(\pi ^2D+\gamma \delta )u_1+\delta ^2u_2=a\sin (\pi x)+c\sin ^2(\pi x),\\ Du_2''+(\pi ^2D-\gamma \delta )u_2-\gamma ^2u_1=b\sin (\pi x)+d\sin ^2(\pi x),\\ u_1(0)=u_1(1)=u_2(0)=u_2(1)=0. \end{array}\right. \end{aligned}$$

(15)

Let the Laplace transforms of $u_1(x)$ and $u_2(x)$ be $U_1(s)$ and $U_2(s)$, respectively. Then, after taking the Laplace transform from both sides the first and second equations of (15), we have

$$\begin{aligned} (D(\pi ^2+s^2)+\gamma \delta )U_1+\delta ^2U_2-Du_1'(0)= & {} \frac{a\pi }{\pi ^2+s^2}+\frac{2c\pi ^2}{4\pi ^2s+s^3},\\ -\gamma ^2 U_1+(D(\pi ^2+s^2)-\gamma \delta )U_2-Du_2'(0)= & {} \frac{b\pi }{\pi ^2+s^2}+\frac{2d\pi ^2}{4\pi ^2s+s^3}. \end{aligned}$$

Solving for $U_1(s)$ and $U_2(s)$ from the above system of DEs and taking the inverse Laplace transform for each and using the condition $u_1(0)=u_2(0)=0$, we obtain the expressions of $u_1$ and $u_2$ in the lemma. $\square$

Now we use the result of this lemma to calculate the coefficients of $\nu _1,\nu _2,a_1,b_1,a_2,b_2$. Let

$$\begin{aligned} R_{11}(u,\mu )= & {} \left( \begin{matrix} r_{11}&{}r_{12}\\ r_{21}&{}r_{22}\\ \end{matrix}\right) \left( {\begin{array}{c}u_1\\ u_2\end{array}}\right) ,\\ R_{20}(u,v)= & {} \left( \begin{matrix} \rho _{20}u_1v_1+\frac{1}{2}\rho _{11}(u_1v_2+u_2v_1)+\rho _{02}u_2v_2\\ \eta _{20}u_1v_1+\frac{1}{2}\eta _{11}(u_1v_2+u_2v_1)+\eta _{02}u_2v_2 \end{matrix}\right) , \end{aligned}$$

where $r_{ij}$ ($i,j=1,2$) are linear functions of $\mu _1,\mu _2$. Let us compute $\nu _1,\Phi _{101}$ in (9) first.

Lemma 2.2

In fact, we have

$$\begin{aligned} \nu _1= & {} \gamma \delta (r_{11}-r_{22})-\gamma ^2r_{12}+\delta ^2r_{21},\\ \nu _2= & {} r_{11}-\frac{\gamma r_{12}}{\delta }. \end{aligned}$$

Proof

Rewrite Eq. (9) as

$$\begin{aligned} L\Phi _{101}=\nu _1 q_2-R_{11}(q_1,\mu ). \end{aligned}$$

It is easy to easy to see

$$\begin{aligned} \nu _1 q_2-R_{11}(q_1,\mu )=\left( {\begin{array}{c}\delta (\delta \nu _1-\delta r_{11}+\gamma r_{12})\\ (1-\gamma \delta )\nu _1-\delta ^2 r_{21}+\gamma \delta r_{22}\end{array}}\right) \sin (\pi x). \end{aligned}$$

Thus set

$$\begin{aligned} a=\delta \nu _1-\delta r_{11}+\gamma r_{12},b=(1-\gamma \delta )\nu _1-\delta ^2 r_{21}+\gamma \delta r_{22}, c=d=0 \end{aligned}$$

in Lemma 2.1 and hence the solvability condition (14) becomes

$$\begin{aligned} \delta (\delta \nu _1-\delta r_{11}+\gamma r_{12})\gamma +((1-\gamma \delta )\nu _1-\delta ^2 r_{21}+\gamma \delta r_{22})\delta =0. \end{aligned}$$

From this we solve for $\nu _1$ to get

$$\begin{aligned} \nu _1=\gamma \delta (r_{11}-r_{22})-\gamma ^2r_{12}+\delta ^2r_{12} \end{aligned}$$

and hence

$$\begin{aligned} a=\delta [-\delta r_{11}+\gamma r_{12}+\delta (\gamma \delta r_{11}-\gamma ^2 r_{12}+\delta (\delta r_{21}-\gamma r_{12}))]. \end{aligned}$$

By setting $c=d=0$ in Lemma 2.1, it is easy to compute the expressions of $\Phi _{101}=\left( {\begin{array}{c}u_1\\ u_2\end{array}}\right)$ in Eq. (9), which is the following

$$\begin{aligned} u_1=\frac{C}{\pi }\sin (\pi x),u_2=\frac{a\pi -\gamma \delta C}{\pi \delta ^2}\sin (\pi x) \end{aligned}$$

where $C=u_1'(0)$ is an arbitrary constant. The solvability of (10) gives

$$\begin{aligned} \nu _2=\left<p_2,-\Phi _{101}+R_{11}(q_1,\mu )\right>=\gamma _{11}-\frac{\gamma r_{12}}{\delta }. \end{aligned}$$

This completes the lemma. $\square$

Next we compute $a_1$ and $b_1$.

Lemma 2.3

In fact, we have

$$\begin{aligned} a_1= & {} \frac{8\delta }{3\pi }[\gamma ^2\delta (\eta _{02}-\rho _{11})+\gamma \delta ^2(\rho _{20}-\eta _{11})+\delta ^3\eta _{20}+\gamma ^2\rho _{02}],\\ b_1= & {} \frac{8\delta }{3\pi }(2\delta \rho _{20}-2\gamma \eta _{02}+\delta \eta _{11}-\gamma \rho _{11}). \end{aligned}$$

Proof

Rewrite Eq. (11) as

$$\begin{aligned} L\Phi _{200}=a_1 q_2-R_{20}(q_1,q_1). \end{aligned}$$

It is easy to see that

$$\begin{aligned} a_1q_2= & {} \left( {\begin{array}{c}a_1\delta ^2\\ a_1(1-\gamma \delta )\end{array}}\right) \sin (\pi x), R_{20}=\left( {\begin{array}{c}\delta ^2(\gamma ^2\rho _{02}-\gamma \delta \rho _{11}+\delta ^2\rho _{20})\\ \delta ^2(\eta ^2\rho _{02}-\gamma \delta \eta _{11}+\delta ^2\eta _{20})\end{array}}\right) \sin ^2(\pi x). \end{aligned}$$

Thus in Lemma 2.1,

$$\begin{aligned} a= & {} a_1\delta ^2,\\ b= & {} a_1(1-\gamma \delta ),\\ c= & {} \delta ^2(\gamma ^2\rho _{02}-\gamma \delta \rho _{11}+\delta ^2\rho _{20}),\\ d= & {} \delta ^2(\gamma ^2\eta _{02}-\gamma \delta \eta _{11}+\delta ^2\eta _{20}). \end{aligned}$$

From the solvability condition (14), it is not hard to solve $a_1$ and the expression of $\Phi _{200}=(u_1,u_2)^T$ in Eq. (11). In fact, we have

$$\begin{aligned} u_1= & {} \frac{1}{72D^2\pi ^4}[-9\delta ^2(\pi (-3+4D\pi ^2)x\cos (\pi x)-(-3+4D\pi ^2+\pi ^2x^2)\sin (\pi x))a_1\\&+\,4((-9D\pi ^2+9\gamma \delta +4(3D\pi ^2-2\gamma \delta )\cos (\pi x)-(3D\pi ^2+\gamma \delta )\cos (2\pi x)\\&-6\pi x\gamma \delta \sin (\pi x))c_1-\delta ^2(-9+8\cos (\pi x)+\cos (2\pi x)+6\pi x\sin (\pi x))c_2\\&+\,9D\pi (\pi x\delta \cos (\pi x)(\gamma u_1'(0)+\delta u_2'(0)) \\&+\sin (\pi x)(2D\pi ^2u_1'(0)-\delta (\gamma u_1'(0)+\delta u_2'(0)))))],\\ u_2= & {} \frac{1}{72D^2\pi ^4}[9(\pi x(-3\delta \delta +4D\pi ^2(-1+\gamma \delta ))\cos (\pi x) \\&+((3-\pi ^2x^2)\gamma \delta -4D\pi ^2(-1 +\gamma \delta )\sin (\pi x))a_1+4(\gamma ^2(-9+8\cos (\pi x)\\&+\,\cos (2\pi x)+6\pi x\sin (\pi x))c_1 +(-9D\pi ^2 -9\gamma \delta +4(3d\pi ^2+2\gamma \delta )\cos (\pi x)\\&+\,(-3D\pi ^2+\gamma \delta )\cos (2\pi x) +6\pi x\gamma \delta \sin (\pi x))c_2\\&+\,9D\pi (-\pi x\delta \cos (\pi x)(\gamma u_1'(0)+\delta u_2'(0)) \\&+\sin (\pi x)(2D\pi ^2u_2'(0)+\gamma ^2 u_1'(0)+\gamma \delta u_2'(0)))))]. \end{aligned}$$

where

$$\begin{aligned} u_2'(0)= & {} \frac{1}{36D\pi ^2\gamma \delta }(9(-3\pi \gamma \delta +4D\pi ^2(-1+\gamma \delta ))a_1 \\&+\,64\gamma ^2c_1+96D\pi ^2c_2+64\gamma \delta c_2-36D\pi ^2\gamma ^2u_1'(0)), \end{aligned}$$

with $u_1'(0)$ a arbitrary constant. Using this, we obtain

$$\begin{aligned} b_1=\left<p_2,-2\Phi _{200}+2R_{20}(q_1,q_2)\right>=\frac{8\delta }{3\pi }(2\delta \rho _{20}-2\gamma \eta _{02}+\delta \eta _{11}-\gamma \rho _{11}). \end{aligned}$$

$\square$

Remark 2.2

If $D_1\ne D_2$, the expressions of $\nu _1,\nu _2,a_1,b_1$ are the same. However the computation is more complicated, here we omit the details.

3 Example: the Schnakenberg model

In this section, we use the result in Sect. 2 in the Schnakenberg Model (6). First we shift the equilibrium point $E(a+b,\frac{b}{(a+b)^2})$ to (0,0) by letting $u_1=a+b+v_1,u_2=\frac{b}{(a+b)^2}+v_2$. Then Sys. (6) becomes

$$\begin{aligned} \left\{ \begin{array}{rcl} \frac{\partial v_1}{\partial t}&{}=&{}D_1\frac{\partial ^2 v_1}{\partial x^2}+\frac{b-a}{a+b}v_1+(a+b)v_2+\frac{b}{(a+b)^2}v_1^2+2(a+b)v_1v_2+v_1^2v_2, x\in (0,1),t>0,\\ \frac{\partial v_2}{\partial t}&{}=&{}D_2\frac{\partial ^2 v_2}{\partial x^2}-\frac{2b}{a+b}v_1-(a+b)^2v_2-\frac{b}{(a+b)^2}v_1^2-2(a+b)v_1v_2-v_1^2v_2, x\in (0,1),t>0. \end{array}\right. \nonumber \\ \end{aligned}$$

(16)

with the boundary conditions

$$\begin{aligned} v_1(0,t)=v_1(1,t)=v_2(0,t)=v_2(1,t)=0. \end{aligned}$$

Let

$$\begin{aligned} A=\left( \begin{array}{ll} \frac{b-a}{a+b}&{}(a+b)^2 \\ -\frac{2b}{a+b}&{}-(a+b)^2 \end{array}\right) . \end{aligned}$$

Hence

$$\begin{aligned} a_{11}=\frac{b-a}{a+b}, a_{12}=(a+b)^2, a_{21}=-\frac{2b}{a+b}, a_{22}=-(a+b)^2. \end{aligned}$$

It is easy to check that $\det (A)=(a+b)^2>0$. In order to seek BT bifurcation, we have to assume that the second part of the assumption (H3) is satisfied. Let

$$\begin{aligned} a_{12}=(a+b)^2=\delta ^2,a_{21}=-\frac{2b}{a+b}=-\gamma ^2 \end{aligned}$$

and then $\delta =a+b$ and $\gamma =\sqrt{\frac{2b}{a+b}}$. Letting

$$\begin{aligned} a_{11}=\pi ^2D_1+\gamma \delta , a_{22}=\pi ^2D_2-\gamma \delta \end{aligned}$$

we obtain

$$\begin{aligned} a=a^*\equiv \frac{\pi ^2 D_2(1-\pi ^4D_1^2+2\pi ^2D_2)}{2(1+\pi ^2 D_1-\pi ^2D_2)^{3/2}},b=b^*\equiv \frac{(\pi +\pi ^3 D_1)^2D_2}{2\sqrt{(1+\pi ^2 D_1-\pi ^2 D_2)^{3/2}}}. \end{aligned}$$

and hence

$$\begin{aligned} \delta =\frac{\pi ^2 D_2}{\sqrt{\pi ^2 D_1-\pi ^2 D_2+1}},\gamma =\frac{\pi ^2 D_1+1}{\sqrt{\pi ^2 D_1-\pi ^2 D_2+1}}. \end{aligned}$$

Now we apply the result in Sect. 2 by using (a, b) near $(a^*,b^*)$ as bifurcation parameter to perform center manifold reduction and hence obtain the normal form. Let

$$\begin{aligned} a=a^*+\mu _1,b=b^*+\mu _2. \end{aligned}$$

Then Sys. (6) becomes

$$\begin{aligned} \frac{\partial v}{\partial t}=D\frac{\partial ^2v}{\partial x^2}+Av+R(v,\mu )+\mathcal {O}(|\mu |^2+|\mu |^2v+|\mu ||v|^2) \end{aligned}$$

(17)

where

$$\begin{aligned} D= & {} \left( \begin{matrix} D_1&{}0\\ 0&{}D_2 \end{matrix}\right) , \\ A= & {} \left( \begin{matrix} \gamma \delta &{}\delta ^2\\ -\gamma ^2&{}-\gamma \delta \end{matrix}\right) ,\\ R(v,\mu )= & {} R_{11}(v,\mu )+R_{20}(v,v)+R_{30}(v,v,v). \end{aligned}$$

Here

$$\begin{aligned} R_{11}(v,\mu )= & {} \left( \begin{matrix} r_{11}&{}r_{12}\\ r_{21}&{}r_{22} \end{matrix}\right) \left( {\begin{array}{c}v_1\\ v_2\end{array}}\right) ,\\ R_{20}(u,v)= & {} \left( \begin{matrix} \rho _{20}u_1v_1+\frac{1}{2}\rho _{11}(u_1v_2+u_2v_1)+\rho _{02}u_2v_2\\ \eta _{20}u_1v_1+\frac{1}{2}\eta _{11}(u_1v_2+u_2v_1)+\eta _{02}u_2v_2 \end{matrix}\right) . \end{aligned}$$

Thus

$$\begin{aligned} r_{11}= & {} \frac{\left( \pi ^2 D_1-\pi ^2 D_2+1\right) \mu _1-\pi ^2 \left( \pi ^2D_1^2+D_1+D_2\right) \mu _2}{\pi ^2D_2 \sqrt{\pi ^2D_1-\pi ^2D_2+1}},\\ r_{21}= & {} -\frac{\left( \pi ^2 D_1-\pi ^2 D_2+1\right) \mu _1-\pi ^2 \left( \pi ^2D_1^2+D_1+D_2\right) \mu _2}{\pi ^2D_2 \sqrt{\pi ^2D_1-\pi ^2D_2+1}},\\ r_{12}= & {} \frac{2 \pi ^2 D_2 \mu _2}{\sqrt{\pi ^2 D_1-\pi ^2 D_2+1}},r_{22}=-\frac{2 \pi ^2 D_2 \mu _2}{\sqrt{\pi ^2 D_1-\pi ^2 D_2+1}},\\ \rho _{20}= & {} -\eta _{20}=\frac{(1+\pi ^2D)^2}{\pi ^2D},\rho _{11}=-\eta _{11}=4\pi ^2D,\rho _{02}=\eta _{02}=0. \end{aligned}$$

From Lemmas 2.2 and 2.3, we obtain the coefficients in the normal form (8)

$$\begin{aligned} \nu _1= & {} \gamma \delta (r_{11}-r_{22})-\gamma ^2r_{12}+\delta ^2r_{12}\\= & {} -\frac{(1+\pi ^2D_1)(1+\pi ^2D_1-\pi ^2D_2)\mu _1+(-1+\pi ^4D_1^2++4\pi ^2D_2+2\pi ^4D_1D_2) \mu _2}{\sqrt{1+\pi ^2D_1-\pi ^2D_2}},\\ \nu _2= & {} r_{11}-\frac{\gamma r_{12}}{\delta }\\= & {} -\frac{(1+2\pi ^2D_1+\pi ^4D_1^2+2\pi ^4D_2^2)\mu _1+(-1+\pi ^4D_1^2+2\pi ^2D_2+2\pi ^4D_2^2) \mu _2}{\pi ^2D_2\sqrt{1+\pi ^2D_1-\pi ^2D_2}},\\ a_1= & {} \frac{8 \delta \left( \gamma ^3 \rho _2+\gamma ^2 \delta \eta _2-\gamma ^2 \delta \rho _{11}-\gamma \delta ^2 \eta _{11}+\gamma \delta ^2 \rho _{20}+\delta ^3 \eta _{20}\right) }{3 \pi }\\= & {} \frac{8\pi ^3(1+\pi ^2D_1)D_2^2(1+\pi ^2D_1-4\pi ^2D_2)}{3\sqrt{1+\pi ^2D_1-\pi ^2D_2}^3},\\ b_1= & {} \frac{8\delta }{3\pi }(2\delta \rho _{20}-2\gamma \eta _{02}+\delta \eta _{11}-\gamma \rho _{11})\\= & {} \frac{16\pi D_2(1+\pi ^4D_1^2-2\pi ^2D_2-2\pi ^4D_2^2+2\pi ^2D_1-2\pi ^4D_1D_2)}{3\sqrt{1+\pi ^2D_1-\pi ^2D_2}^3}. \end{aligned}$$

It is easy to check that

$$\begin{aligned} \det \frac{\partial (\nu _1,\nu _2)}{\partial (\mu _1,\mu _2)}=-4(1+\pi ^2D_1-\pi ^2D_2)\ne 0. \end{aligned}$$

Therefore the map $(\mu _1,\mu _2)\rightarrow (\nu _1,\nu _2)$ is regular and hence the transversality holds. Thus we have the following result.

Theorem 3.1

If $a=a^*,b=b^*$, then the Schnakenberg model (16) undergoes BT bifurcation.

Equation (17) is equivalent to the following truncated system

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{z}_1&{}=&{}z_2,\\ \dot{z}_2&{}=&{}\nu _1z_1+\nu _2z_2+a_1z_1^2+b_1z_1z_2. \end{array}\right. \end{aligned}$$

(18)

The complete bifurcation diagram of (18) can be found in [4]. Here we are more interested in periodic orbits which are described in the following lemma (see [8]).

Lemma 3.1

Assume that $a_1b_1\ne 0$. Define

$$\begin{aligned} H= & {} \left\{ (\nu _1,\nu _2): \ \nu _2=\frac{b_1}{a_1}\nu _1+\mathcal {O}(\nu ^2), \, \nu _1>0 \right\} , \\ HL= & {} \left\{ (\nu _1,\nu _2): \ \nu _2=\frac{6b_1}{7a_1}\nu _1+\mathcal {O}(\nu _1^2), \ \nu _1>0 \right\} . \end{aligned}$$

For $(\nu _1,\nu _2)$ small enough, when $(\nu _1,\nu _2)$ is in the region between the curves H and HL, Sys.(18) has a unique stable periodic orbit.

Upon using the expressions of $(\nu _1,\nu _2)$, we have the following result.

Theorem 3.2

Assume that $a_1b_1\ne 0$. Define

$$\begin{aligned} \overline{H}= & {} \left\{ (\mu _1,\mu _2): \ \mu _2=-\frac{1}{\tau _1}[(\pi ^2 D_1+1){}^2(\pi ^4 D_1^2+2(2 \pi ^4 D_2+\pi ^2) D_1\right. \\&\left. -14 \pi ^4 D_2^2 +4 \pi ^2 D_2+1)] \mu _1+\mathcal {O}(|\mu |^2), \mu _1>0 \right\} , \\ \overline{HL}= & {} \left\{ (\mu _1,\mu _2): \ \mu _2=-\frac{1}{\tau _2}(\pi ^2 D_1+1)(5 \pi ^6D_1^3+\pi ^4(28 \pi ^2 D_2+15)D_1^2 \right. \\&+\,(-86 \pi ^6D_2^2 +56 \pi ^4D_2+15 \pi ^2) D_1+8 \pi ^6 d_2^3-86 \pi ^4D_2^2+28 \pi ^2 D_2+5) \mu _1\\&\left. +\,\mathcal {O}(|\mu |^2), \mu _1>0 \right\} . \end{aligned}$$

Here

$$\begin{aligned} \tau _1= & {} \pi ^8 D_1^4+2 \left( 2 \pi ^8 D_2+\pi ^6\right) D_1^3-14 \pi ^6 D_2 \left( \pi ^2 D_2-1\right) D_1^2 \\&-2\left( 10 \pi ^6D_2^2-8 \pi ^4 D_2+\pi ^2\right) D_1 -8 \pi ^6 D_2^3-6 \pi ^4 D_2^2+6 \pi ^2 D_2-1,\\ \tau _2= & {} 5 \pi ^8 D_1^4+2 \pi ^6\left( 14 \pi ^2 D_2+5\right) D_1^3-86 \pi ^6D_2 \left( \pi ^2 d_2-1\right) D_1^2 \\&+2 \pi ^2\left( 4 \pi ^6D_2^3-58 \pi ^4 D_2^2 +44 \pi ^2D_2-5\right) \\&\times D_1-5\left( 8 \pi ^6D_2^3+6 \pi ^4D_2^2-6 \pi ^2D_2+1\right) . \end{aligned}$$

For $(\mu _1,\mu _2)$ small enough, when $(\mu _1,\mu _2)$ is in the region between the curves $\overline{H}$ and $\overline{HL}$, Sys.(17) has a unique stable periodic orbit.

Example 3.1

Theorem 3.2 gives us the condition of $(\mu _1,\mu _2)$ so that the Schnakenberg model (6) has a stable periodic solution; namely the reaction repeats cyclically. Now we give a numerical example to illustrate this. Choose $D_1=0.01,D_2=0.02$ and then

$$\begin{aligned} a^*=0.06868411401512152,b^*=0.1392348499288601. \end{aligned}$$

Easy calculation shows that

$$\begin{aligned} \overline{H}= & {} \left\{ (\mu _1,\mu _2), \mu _2=37.540424086156456\mu _1+\mathcal {O}(|\mu |^2)\right\} \\ \overline{HL}= & {} \left\{ (\mu _1,\mu _2), \mu _2=89.21928378011161\mu _1+\mathcal {O}(|\mu |^2)\right\} . \end{aligned}$$

Let $\mu _1= 0.000001, \mu _2=0.00633799$ and hence

$$\begin{aligned} a=a^*+\mu _1=0.06878411401512152,b=b^*+\mu _2=0.1455728353221735. \end{aligned}$$

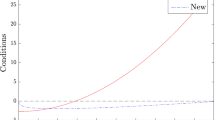
It is not hard to check that $(\mu _1,\mu _2)$ is between $\overline{H}$ and $\overline{HL}$ (Fig. 1). Now we use the following initial condition

$$\begin{aligned} u_1(x,0)=a+b+0.001\sin (6\pi x), u_2(x,0)=\frac{b}{2(a+b)^2}-0.001\sin (3\pi x). \end{aligned}$$

to numerically solve Sys. (6). The graph of the solution of Sys. (6) is shown in Fig. 2. From this, we can see the repeated pattern in the direction of the time t, which verifies the result of Theorem 3.2 and hence concludes that Sys. (6) has a unique stable periodic orbit. Note that in this model, the critical concentrations $a^*$ and $b^*$ of A and B are very important since they determine the BT bifurcation and hence the dynamical behavior of Sys. (6). Small purterbations of $a^*$ and $b^*$ result in the change of the dynamical behavior. If $(\mu _1,\mu _2)$ is in the region between $\overline{H}$ and $\overline{HL}$, a stable periodic orbit bifurcates from the equilibrium point E; otherwise the bifurcation diagram is different and here we omit the detail.

Fig. 1

$(\mu _1,\mu _2)=(0.000001,0.00633799)$ lies between the curves $\overline{H}$ and $\overline{HL}$

Fig. 2

$u_1(0,x)=2\sin (5\pi x),u_2(t,x)=10\sin (10\pi x)$. The unique stable orbit for $(\mu _1,\mu _2)=(0.000001,1.08982\times 10^{-8})$

4 Conclusion

BT bifurcation is one of so-called codimension 2 bifurcations. Hopf bifurcation is codimension 1 bifurcation and has been studied extensively for many special models of reaction–diffusion equations (see [2, 4–6]). However, the study of BT bifurcation for reaction–diffusion equations in the literature has not often been seen. In this manuscript, we found the explicit conditions such that BT bifurcation occurs for general reaction–diffusion equations and then performed the center manifold reduction to calculate the coefficients of the corresponding normal form up to order 2 ($a_1b_1\ne 0$). Note that, if $a_1=b_1=0$, we have to calculate the coefficients of order 3 in the normal form. Since the calculation of those coefficients is very complicated, we omit the detail.

As one application, our result was used to study BT bifurcation for the Schnackenberg model. It is worth noting that most of the research of this model done so far is based on one of two parameters a and b (for example, see [5]). In this manuscript, we used both to study BT bifurcation. We believe that our results will shed light on the study of the mechanisms of dynamical behaviors of reaction–diffusion equations.