Abstract
In this paper, a numerical method based on Bernstein polynomial for nonlinear singularly perturbed reaction-diffusion problems is proposed. The solution of this type of problem is polluted by a small positive parameter \(\varepsilon \) along with non-linearity due to which the solution often shows boundary layers, interior layers, and shock waves that arise due to non-linearity. The existence and uniqueness of the solution of the said problems are proved using Nagumo’s condition. Moreover, the convergence analysis is carried out of the proposed problem in maximum norm. To illustrate the proposed method’s efficiency, three nonlinear test problems have been taken into account, and a comparative analysis has been done with other existing methods. The proposed method’s approximated solution seems to be superior or in good agreement with the existing method.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Whenever a real-life phenomenon is converted into a mathematical model, differential equation, partial differential equation and system of differential equation plays a vital role in modelling natural evolution, we researcher primarily try to obtain what is important, retaining the essential physical quantities and neglecting the negligible ones which involve small positive parameters. Due to their occurrence in a wide range of applications, the study of nonlinear singularly perturbed reaction-diffusion (SPNRD) problems has always been the topic of considerable interest for many mathematicians and engineers. These problems seem to be of significance to the environmental sciences in analyzing pollution from manufacturing sources that is entering the atmosphere. These type of problem occurs in chemical kinetics in catalytic reaction theory. The SPNRD problem models an isothermal reaction which is catalyzed in a pellet and modelled by Eq. (3.1) [29]. Where the concentration of reactant is denoted by v and \(\frac{1}{\sqrt{\varepsilon }}\) is called the Thiele module defined by \(\frac{K}{D}\), K is the reaction rate and D is the diffusion coefficient. In considering these types of problems, it is essential to acknowledge that the diffusion coefficient of the admixture in the material may be sufficiently small, resulting in substantial variations of concentration along with the material depth. Then, the diffusion boundary layers rise. Hence these type of problems exhibit a singularly perturbed character. The mathematical model of such problems has a perturbation parameter, which is a small coefficient multiplying the differential equation’s highest derivatives. Such specific problems rely on a small positive factor so that the solution changes swiftly in some areas of the domain and changes gradually in other sections of the domain. The mathematical model for an adiabatic tubular chemical reactor which processes an irreversible exothermic chemical reaction is also represented by SPNRD problems. The concentrations of the various chemical species involved in the reaction can be determined in a simple manner from a knowledge of v.
We rely on the numerical schemes to get the approximate solution of nonlinear systems by linearizing the nonlinear problems as only few nonlinear systems can be solved explicitly. On a uniform mesh, the existing numerical technique, such as finite difference, finite element, spline collocation, etc., gives unsatisfactory results or one has to modify the local mesh that works fine near the layer region and standard away from the layer region by designing a suitable layer adaptive mesh [2, 6, 16, 20, 28]. These type of problems have been studied by many author’s and proposed a numerical and iterative techniques such as, Natalia Kopteva et al proposed a finite element method and given the error analysis in maximum norm using green function approach [3, 4, 8, 14, 15]. Pankaj Mishra et al developed a cubic spline orthogonal collocation for SPNRD [20]. Relja Vulanovic proposed a six-order finite difference for the said problem [28]. M.K Kadalbajoo et al developed a spline technique on non-unifrom grids for the said problem [11]. SCS Rao et al presented a B-spline collocation method on piece-wise uniform girds for SPNRD [26]. S A Khuri et al developed a patching approach which is a based on the combination of variation of iteration method and adaptive cubic spline collocation scheme [13]. Muhammad Asif Zahoor Raja et al developed a neuro-evolutionary technique which is an artificial intelligent technique for solving SPNRD [25] and other [12, 16, 17].
The novelty of this article is to drive an analytic iterative approximation to nonlinear singularly perturbed reaction diffusion problems using a Bernstein collocation method based on Bernstein polynomial and operational matrix. Bernstein polynomials perform a vital role in numerous mathematics areas, e.g., in approximation theory and computer-aided geometry design [10]. The Bernstein polynomial method’s main advantage over the other existing approach is its simplicity of implementation for nonlinear problems. The key feature of this approach is that it reduces such problem to one of solving the system of algebraic equation via operational matrices [31].
Due to the flexibility and ability, the Bernstein collocation method (BCM) has emerged as a powerful tool to solve linear and nonlinear systems. Consequently, it was successfully applied to find solution of high even-order differential equations using integrals of Bernstein polynomials approach [9], to first order nonlinear differential equations with the mixed non-linear conditions [30], to high order system of linear volterra-fredholm integro-differential equation [19], to riccati differential equation and volterra population model [22], to nonlinear fredholm-volterra integro differential equations [32], to fractional differenital equation [1] and others [7, 27, 31].
The main advantages of this method are (i) it provides the approximate solution over the entire domain while other existing numerical method provide the approximate solution on the discrete point of the domain, (ii) to solve the nonlinear problem, one often use a quasi-linearization technique to linearize the problem and then solve the linearize problem by numerical or other existing techniques. Due to linearization of nonlinear problem the accuracy of nonlinear problem somehow degenerate, which may lead to deceptive solution some time. In this method, we solve the nonlinear problem without linearization. (iii) It is easy to implement.
The paper is organised as, in Section 2 brief sketch of Bernstein collocation method and auxiliary results are presented. Then in Section 3 the existence and uniqueness of the said problem is carried out. In Section 4 the error analysis is done. In Section 5, two nonlinear test problems are taken into account to validate the theoretical finding of the proposed method and a comparative analysis is carried out with the other existing methods. Section 6, contains the conclusion.
2 Brief sketch of the method
In this section we give some brief sketch and auxiliary results corresponding to our proposed method.
2.1 Properties of bernstein polynomial
Generalized form of Bernstein polynomial of \(m^{th}\) order on interval [0, 1] is defined as
Using Binomial expansion of \((x-1)^{m-i}\), Bernstein polynomial of \(m^{th}\) order reads as:
\(\mathbf{B} _{i,m}(x)\) has the following properties:
-
1.
\(\mathbf{B} _{i,m}(x)\) is continuous over interval [0, 1],
-
2.
\(\mathbf{B} _{i,m}(x)\ge 0\) \(\forall \) \(x\in [0,1]\),
-
3.
Sum of Bernstein polynomial is 1 (unity) i.e
$$\begin{aligned} \sum _{i=0}^{m}{} \mathbf{B} _{i,m}(x)=1 \quad x\in [0,1]. \end{aligned}$$(2.4) -
4.
Bernstein polynomial \(\mathbf{B} _{i,m}(x)\) can be written in form of recursive relation as
$$\begin{aligned} \mathbf{B} _{i,m}(x)=(1-x)\mathbf{B} _{i,m-1}(x)+x \mathbf{B} _{i-1,m-1}(x). \end{aligned}$$(2.5)Let \(\varphi (x)=[\mathbf{B} _{0,m}(x),\mathbf{B} _{1,m}(x),\cdots ,\mathbf{B} _{m,m}(x)]^{T}\), then we can write \(\varphi (x)\) as:
$$\begin{aligned} \varphi (x)=Q\times T_m(x). \end{aligned}$$(2.6)Where vector \(Q_{i+1}\) is defined as follows:
$$\begin{aligned} Q_{i+1}=\left\{ \overbrace{ 0,0,\cdots ,0}^{i times}, (-1)^{0}\left( {\begin{array}{c}m\\ i\end{array}}\right) ,(-1)^{1}\left( {\begin{array}{c}m\\ i\end{array}}\right) \left( {\begin{array}{c}m-i\\ 1\end{array}}\right) ,\cdots (-1)^{m-i}\left( {\begin{array}{c}m\\ i\end{array}}\right) \left( {\begin{array}{c}m-i\\ m-i\end{array}}\right) \right\} ,\nonumber \\ \end{aligned}$$(2.7)\(T_{m}(x)\) as
$$\begin{aligned} T_{m}(x)= \begin{bmatrix} 1\\ x\\ \vdots \\ x^{m} \end{bmatrix}, \end{aligned}$$(2.8)and Q is an \((m+1)\times (m+1)\) matrix and written as follows:
$$\begin{aligned} Q_{m}(x)= \begin{bmatrix} Q_1\\ Q_2\\ \vdots \\ Q_{m+1} \end{bmatrix}, \end{aligned}$$(2.9)and
$$\begin{aligned} \varphi (x)= \begin{bmatrix} \mathbf{B} _{0,m}(x)\\ \mathbf{B} _{1,m}(x)\\ \vdots \\ \mathbf{B} _{m,m}(x) \end{bmatrix}. \end{aligned}$$(2.10)
From Eq. (2.7), it is concluded that matrix Q is an invertible matrix as it is an upper triangular matrix with non zero diagonal entries and determinant \(\vert Q \vert =\prod _{i=0}^{i=m}\left( {\begin{array}{c}m\\ i\end{array}}\right) .\)
2.2 Operational matrix for differentiation
In this subsection a Bernstein operational matrix associated with differentiation is derived. From Eq. (2.6) we have
and differentiation of \(\varphi (x)\) is calculated as:
the above expression can be written as:
Where \(\Lambda ^{'}\) and \(X^{'}\) are written as:
and
Now vector \(X^{'}(x)\) can be expressed in form of Bernstein polynomial basis as \(\mathbf{B} _{i,m}\) as \(X^{'}(x)= \Delta ^{*}\varphi (x)\), where
hence,
Where \(\mathcal {O}=Q_{m}\Lambda ^{'}\Delta ^{*}\) is called the operational matrix of the derivatives. Let us assume that v(x) is approximated as:
Then the differentiation of v(x) in term of operational matrix is defined as:
2.3 Operational matrix of product
The main concern of this subsection is to explicitly evaluate the product of operational matrix corresponding to Bernstein polynomial of \(m^{th}\) degree operational matrix. Let c be a column vector of \((m+1)\times 1\) and Let \(\breve{C}\) be a \((m+1)\times (m+1)\) product of operational matrices.
where \(\varphi (x)\) is defined in (2.6) and we have \(c^{T}\varphi (x)=\sum _{i=0}^{i=m}c_{i} \mathbf{B} _{i,m}\) , we rewrite Eq. (2.20) in form of Bernstein basis as
Now we evaluate all \(x^{k} \mathbf{B} _{i,m}\) in term of \( \lbrace \mathbf{B} _{i,m}\rbrace \) for all \(k, i=0, 1, \cdots , m\). Let
Let D be a \((m+1)\times (m+1)\) dual matrix of \(\varphi (x)\) such that
Now for \(i, k=0, 1, \cdots , m\) we have
Now we define
Let \(\check{C}_{m+1}\) be a \((m+1)\times (m+1)\) matrix of columns vectors \([\check{C}_1, \check{C}_2 ,\cdots , \check{C}_{m+1}]\) and \(\check{C}_{k+1}\) is defined as
Then from Eq. (2.23)
Hence, the operational matrix of product is defined as:
3 Existence and uniqueness
Consider the following class of singularly perturbed non-linear reaction diffusion problem.
where \(\varepsilon \) is singular perturbation parameter with \(0< \varepsilon<<1\) and \(g \in C^{\infty }[0,1]\times R\). Let assume that
Let \(\alpha (x)\) and \(\beta (x)\) are two smooth function such that \(\alpha (x)\le \beta (x)\) and satisfies
Nagumo condition holds:
Theorem 1
Condition (3.3) and Nagumo condition (3.4) provides the existence of solution \(v(x)\in C^{2}[0,1]\) of problem (3.1), satisfying the condition \(\alpha (x)\le v(x) \le \beta (x)\) for all \(x\in [0,1]\).
Proof
Let us write the problem in operator form as:
where \(\pounds =\varepsilon \dfrac{d^2}{d x^2}\)
As g is continuous for (x, v) \(\in \) \([a,b]\times R\), which ensure the existence of v(x) s.t. \(\alpha (x) \le v(x) \le \beta (x)\) and satisfing the boundary value problem (3.1).
The proof of the above theorem can be done by using maximum principal [21, 24]. \(\square \)
Theorem 2
Let the function g be continuous with respect to (x, v) and also g belongs to the class of \(C^1\) with respect to v for (x, v) in \((\alpha ,\beta )\times [0,1]\) and there exist a positive constant m such that \(g_{v}(x,v)\ge m >0\) for \([0,1]\times \mathcal {R}\). Then for each \(\varepsilon >0\), the problem (3.1) has a unique solution \(v(x,\varepsilon )\in [0,1]\) such that \(\vert v(x,\varepsilon ) \vert \le \frac{\mathcal {M}}{m}\). Where \(\mathcal {M}=\max \lbrace \max \vert g(x,0) \vert , m \vert B \vert , m \vert A \vert \rbrace \)
Proof
Suppose for \(x\in [0,1]\),
Applying Taylor’s theorem for some point \(\zeta \in (\alpha ,0)\), it is obtained as:
Similarly for intermediate point \(\eta \in (0,\beta )\),
Hence, it follows from Theorem 1 that for each \(\varepsilon >0\) the problem (3.1) has a solution \(v(x,\varepsilon )\) on [0, 1] satisfying :
The uniqueness of the solution of problem (3.1) follows from maximum principle. \(\square \)
3.1 Stability of degenerate solution
In this subsection we are concern with the existence and stability of solution for problem (3.1). However we only stick with stable solution of the proposed problem. Let \(z(x) \in C^{1}[a,b]\) be the solution of equation \(g(x,v(x))=g(x,z(x))\) in \(\Omega =[a,b]\). Then we define
where \(\psi (x)\) is defined as
Where \(\varrho \) be a small positive constant and suppose if \(A\ge z(a)\) and \(B\ge z(b)\), then we define
IIrly if \(A\le z(a)\) and \(B\le z(b)\) then
Now we discuss and define the stability for the solution of problem (3.1). Let us presume that g(x, v(x)) has the stated number of continuous partial derivatives w.r.t v(x) in \(\phi _{i}\), \(i=0,1\) or 2 and \(n\ge 2\), \(q \ge 0\) be the integers.
Definition 3.1
The function \(z=z(x)\) be \(I_{q}\)-stable on \(\Omega \) if \(\exists \) a constant m such that
and
Definition 3.2
The function \(z=z(x)\) be \(II_{n}\)-stable on \(\Omega \) and \(A\le z(a)\), \(B\le z(b)\) if \(\exists \) a constant \(m\ge 0\) such that
and
Theorem 3.3
Let \(g(x,v(x))=0\) satisfies definition 3.1 i.e have \(I_q\) stable solution \(z=z(x)\in C^2(\Omega )\). Then \(\exists \) \(\varepsilon _{0}>0\) such that \(0<\varepsilon <\varepsilon _{0}\). Then problem (3.1) has a solution \(v(x)=v(x,\varepsilon )\) which satisfies the following
where \(s_l\) and \(s_r\) is defined as
And
where \(\rho =\sqrt{mq}[(q+1)(2q+1)!]^{-1/2}.\)
Proof
For detail proof [5] \(\square \)
Theorem 3.4
Let \(g(x,v(x))=0\) satisfies definition 3.2 i.e have \(II_{n}\) stable solution \(z=z(x)\in C^2(\Omega )\) such that \(z(a)\le A\), \(z(b) \le B\) and \(z^{''} \ge 0\) in (a, b). Then \( \exists \) \(\varepsilon _{0}>0\) such that \(0<\varepsilon <\varepsilon _{0}\). Then problem (3.1) has a solution \(v(x)=v(x,\varepsilon )\) which satisfies the following
where \(w_l\) and \(w_r\) is defined as
and
and \(\rho _1\) \( =(n-1)(\frac{m}{2}(m+1)!)^{1/2}\).
Proof
For detail proof [5]. \(\square \)
4 Error Analysis
In this section error analysis is carried out in maximum norm of proposed problem (3.1). Let us assume that \(\varepsilon \le Ch\) where C is a positive constant independent. Let us define the collocation points as \(x_j=x_0+\frac{j}{m}\) and \(h_j=x_j-x_{j-1}\) \(\forall \) \(j=0,1,\cdots ,m\).
First, let us consider the possible cases with g(x, v(x)) as
There only three possible cases associated with g(x, v(x)). In first case g(x, v(x)) is nonlinear function and other two cases are when, linear part is extracted out from g(x, v(x)) with positive and negative signs. Let \(p(x)\le \vert \wp \vert \).
Suppose \(\chi =C[0,1]\) be the Banach space equipped with norm defined as
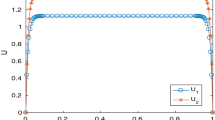
“Comparison between exact solution and the numerical solution computed by BCM of Example 5.1 for \(\varepsilon =0.1.\)”
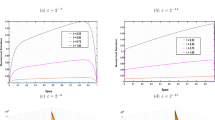
“Comparison between exact solution and the numerical solution computed by BCM of Example 5.1 for \(\varepsilon =0.01.\)”
“Comparison between exact solution and the numerical solution computed by BCM of Example 5.2 for \(\varepsilon =0.1.\)”
“Comparison between exact solution and the numerical solution computed by BCM of Example 5.2 for \(\varepsilon =0.01.\)”
Theorem 4.1
Let v(x) is the solution of (3.1) and \(g \in C^{\infty }[0,1]\times R\) then we have the following bound on the derivative of v(x)
for \(i=1,2,3\).
Proof
For proof of the above theorem see [14]. \(\square \)
Theorem 4.2
Suppose \(\mathcal {F}\in \chi \) and \(\mathbf{B} _{m}(\mathcal {F})\) be a sequence converges to \(\mathcal {F}\) uniformly, where \(\mathbf{B} _{m}(\mathcal {F})\) is defined in (2.1). Then for any \(\delta \ge 0\) \(\exists \) m such that
Proof
For detailed proof see [23]. \(\square \)
Theorem 4.3
Let \(\mathcal {F}\) be a bounded and continuous function and \(\mathcal {F}^{''}\) exist in [0,1], then we have the following error bound
Proof
For detail proof see [18]. \(\square \)
Theorem 4.4
Let v be the exact solution and \(v_m\) denotes the approximate solution by BCM. Suppose nonlinear function g(x, v) satisfies the Lipschitz condition
then the error bound for the BCM is given as:
where \(\mathcal {L}\) is known as Lipschitz constant.
Proof
Let
Case 1 When \(g(x,v(x))=f(x,v(x))\), then
now using Lipschitz condition (4.6)
now we have approximated v(x) by BCM then we have
Now from theorem 4.3, we have
Case 2 When \(g(x,v(x))=f(x,v(x))+p(x)v(x)\), then
using Lipschitz condition (4.6)
Now the proof is straight forward. Using conditions (4.11), (4.124.13). We obtain the following bound
Case 3 When \(g(x,v(x))=f(x,v(x))-p(x)v(x)\), The proof is similar and we have
\(\square \)
Theorem 4.5
Let v be the exact solution of Problem (3.1) and \(v_m\) be the approximate solution evaluated by BCM method. Then we have the following error bound
Where C is a constant independent of \(\varepsilon \) and h.
Proof
From Theorem 4.4 we have the following bound,
From Theorem 4.1 we have the following bound,
Now \(e^{-\Im x/\sqrt{\varepsilon }}\ge e^{\Im (-1+x)/\sqrt{\varepsilon }}\) for \(x\in [0,1/2]\), and \(e^{-\Im x/\sqrt{\varepsilon }}\le e^{\Im (-1+x)/\sqrt{\varepsilon }}\) for \(x\in [1/2,0]\). So we omit the function \(e^{\Im (-1+x)/\sqrt{\varepsilon }}\) and we do analysis for \(x\in [0,1/2]\). Now using assumption that \(\varepsilon \le Ch^2\) and inequality \(1-e^{-x} \le x \) \(\forall x>0\). The proof is straight forward and we have following bound
\(\square \)
5 Numerical results and discussion
This section analyzes the proposed method’s efficiency and implements the BCM to solve two nonlinear singularly perturbed reaction-diffusion problems. The proposed method approximated solution is compared with spline technique [11], B-spline collocation method [26], a patching approach based on novel combination of variation of iteration and cubic spline collocation method [13] and a neuro-evolutionary artificial technique [25].
Example 5.1
Consider the non-linear problem singularly pertubed problem used as a model of Michaelis-Menten process, the model takes the form of an equation describing the rate of enzymatic reaction in biology [20].
The f(x) of the above problem is calculate so that the exact solution of the above problem is \(v(x)=1-\frac{e^{\frac{-x}{\sqrt{\varepsilon }}}+e^{\frac{-(1-x)}{\sqrt{\varepsilon }}}}{1+e^{\frac{-1}{\sqrt{\varepsilon }}}}\). The approximate solution obtained by BCM and exact solution of Example 5.1 for different values of \(\varepsilon \) are given in Tables 1 and 3. The absolute error calculated for Example 5.1 is given in Tables 2 and 6.
Example 5.2
Consider the following non-linear singularly perturbed problem from [11, 13, 25, 26]. This problem can be used to describe a mathematical model of an adiabatic tubular chemical reactor that processes an irreversible exothermic chemical reaction. Where \(\varepsilon \) represents the dimensionless adiabatic temperature. In fact, the steady state temperature of the reaction is equivalent to a positive solution v.
The exact solution of the above problem is given as: \(v(x)=e^{\frac{-x}{\sqrt{\varepsilon }}}\). The approximate solution obtained by the BCM and the exact solution of Example 5.2 for different values of \(\varepsilon \) are given in Tables 7 and 9. The absolute error calculated for Example 5.2 is given in Tables 8 and 10. We have compared the error obtained by the BCM for Example 5.2 with spline technique [11], B-spline collocation method [26], a patching approach based on novel combination of variation of iteration and cubic spline collocation method [13] and a neuro-evolutionary artificial technique [25] in Tables 11, 12, 14, and 13 respectively.
Figures 1 and 2 depict the comparison between the exact solution and the approximate solution obtained from the proposed method for Example 5.1 with \(\varepsilon =0.1 \) and 0.01 respectively and Figs. 3 and 4 depict the comparison between the exact solution and the approximate solution obtained from the proposed method for Example 5.2 with \(\varepsilon =0.1\) and 0.01 respectively. It is observed in all figures as m increases the approximate solution converges to the exact solutions, which demonstrate the convergence of our proposed method.
Example 5.3
Consider the following non-linear singularly perturbed problem.
The exact solution of the above problem is not known. The approximate solution obtained by the BCM and the absolute error calculated for Example 5.3 is given in Tables 15 and 16. As the true solution of problem 5.3 is not known to us. So to calculate the error we take a reference solution computed using \(m=20\).
6 Conclusion
In this article, we have successfully implemented the Bernstein collocation method for solving SPNRD problems. To solve the nonlinear problems, one often uses a quasi-linearization technique to linearize the problem and then solve the linearized problem by numerical or other existing techniques. Due to the linearization of the nonlinear problem, the approximated solution’s accuracy somehow degenerates, which may leads to deceptive solutions sometimes. Here we address this issue and solve the nonlinear problem without linearization. The proposed method is easy to implement as it changes complex nonlinear problems to a system of algebraic equation system and can be extended to even a general class of problems. This method yield a higher level of precision just using lower degree polynomials without any limiting assumption.
Data availability
“This manuscript has no associated data.”
References
M.H.T. Alshbool, A.S. Bataineh, I. Hashim, Solution of fractional-order differential equations based on the operational matrices of new fractional bernstein functions. J. King Saud Univ. Sci. 29(1), 1–18 (2017)
Tesfaye Aga Bullo, Guy Aymard Degla, Gemechis File Duressa, Fitted mesh method for singularly perturbed parabolic problems with an interior layer. Math. Comput. Simul. 193, 371–384 (2022)
N. Chadha, N. Kopteva, A robust grid equidistribution method for a one dimensional singularly perturbed semilinear reaction diffusion problem. IMA J. Numer. Anal. 31, 188–211 (2011)
N.M. Chadha, N. Kopteva, Maximum norm a posteriori error estimate for a 3d singularly perturbed semilinear reaction diffusion problem. Adv. Comput. Math. 35, 33–55 (2011)
K.W. Chang, F.A. Howes, Nonlinear Singular Perturbation Phenomena: Theory and Application (Springer-Verlag, New York, 1984)
Imiru Takele Daba, Gemechis File Duressa, Collocation method using artificial viscosity for time dependent singularly perturbed differential-difference equations. Math. Comput. Simul. 192, 201–220 (2022)
Aysegul Akyuz Dascioglu, Nese Isler, Bernstein collocation method for solving nonlinear differential equations. Math. Comput. Appl. 18(3), 293–300 (2013)
A. Demlow, N. Kopteva, Maximum norm a posteriori error estimates for singularly perturbed elliptic reaction diffusion problems. Numer. Math. 133, 707–742 (2016)
Eid H. Doha, Ali H. Bhrawy, M.A. Saker, Integrals of bernstein polynomials: an application for the solution of high even-order differential equations. Appl. Math. Lett. 24(4), 559–565 (2011)
Josef Hoschek, Dieter Lasser, Fundamentals of computer aided geometric design (AK Peters, Ltd., USA, 1993)
M.K. Kadalbajoo, K.C. Patidar, Spline techniques for solving singularly-perturbed nonlinear problems on nonuniform grids. J. Optim. Theory Appl. 114(3), 573–591 (2002)
Aditya Kaushik, Vijayant Kumar, Manju Sharma, Nitika Sharma, A modified graded mesh and higher order finite element method for singularly perturbed reaction-diffusion problems. Math. Comput. Simul. 185, 486–496 (2021)
S.A. Khuri, A. Sayfy, Self-adjoint singularly perturbed second-order two-point boundary value problems: A patching approach. Appl. Math. Model. 38(11–12), 2901–2914 (2014)
N. Kopteva, Maximum norm a posteriori error estimates for a one dimensional singularly perturbed semilinear reaction diffusion problem. IMA J. Numer. Anal. 27, 576–592 (2007)
N. Kopteva, Maximum-norm a posteriori error estimates for singularly perturbed reaction diffusion problems on anisotropic meshes. SIAM J. Numer. Anal. 53, 2519–2544 (2015)
Chein-Shan. Liu, Chih-Wen. Chang, Modified asymptotic solutions for second-order nonlinear singularly perturbed boundary value problems. Math. Comput. Simul. 193, 139–152 (2022)
Chein-Shan. Liu, Essam R. El-Zahar, Chih-Wen. Chang, A boundary shape function iterative method for solving nonlinear singular boundary value problems. Math. Comput. Simul. 187, 614–629 (2021)
GG Lorentz, RA DeVore, Constructive approximation, polynomials and splines approximation, (1993)
Khosrow Maleknejad, Behrooz Basirat, Elham Hashemizadeh, A bernstein operational matrix approach for solving a system of high order linear volterra-fredholm integro-differential equations. Math. Comput. Model. 55(3–4), 1363–1372 (2012)
Pankaj Mishra, Graeme Fairweather, Kapil K Sharma, A parameter uniform orthogonal spline collocation method for singularly perturbed semilinear reaction-diffusion problems in one dimension. Int. J. Comput. Methods Eng. Sci. Mech. 20(5), 336–346 (2019)
R.E. O’Malley, Introduction to Singular Perturbations (Academic Press, New York, 1974)
K. Parand, Sayyed A Hossayni, and JA Rad, Operation matrix method based on bernstein polynomials for the riccati differential equation and volterra population model. Appl. Math. Model 40(2), 993–1011 (2016)
Michael James David Powell et al., Approximation theory and methods (Cambridge university press, UK, 1981)
M.H. Protter, H.F. Weinberger, Maximum Principles in Differential Equations (Springer-Verlag, New York, 1984)
Muhammad Asif Zahoor. Raja, Saleem Abbas, Muhammed Ibrahem Syam, and Abdul Majid Wazwaz, Design of neuro-evolutionary model for solving nonlinear singularly perturbed boundary value problems. Appl. Soft Comput. 62, 373–394 (2018)
S.C.S. Rao, M. Kumar, B-spline collocation method for nonlinear singularly-perturbed two-point boundary-value problems. J. Optim. Theory Appl. 134(1), 91–105 (2007)
Hamid Reza Tabrizidooz and Khadigeh Shabanpanah, Bernstein polynomial basis for numerical solution of boundary value problems. Numer. Algorithms 77(1), 211–228 (2018)
Relja VUlanović, An Almost Sixth-Order Finite-Difference Method for Semilinear Singular Perturbation Problems, Comput. Methods Appl. Math. 4, 368–383 (2004)
Relja Vulanovic, Paul A Farrell, and Ping Lin (Applications of Advanced Computational Methods for Boundary and Interior Layers, Press, Numerical solution of nonlinear singular perturbation problems modeling chemical reactions, 1993), pp. 192–213
Salih Yalçınbaş, Huriye Gürler, Bernstein collocation method for solving the first order nonlinear differential equations with the mixed non-linear conditions. Math. Comput. Appl. 20(3), 160–173 (2015)
S.A. Yousefi, Mahmoud Behroozifar, Operational matrices of bernstein polynomials and their applications. Int. J. Syst. Sci. 41(6), 709–716 (2010)
Şuayip Yüzbaşı, A collocation method based on bernstein polynomials to solve nonlinear fredholm-volterra integro-differential equations. Appl. Math. Comput. 273, 142–154 (2016)
Acknowledgements
“We thank the anonymous referees for their constructive comments that lead to a significant improvement of this article”.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Author contribution
“Kartikay Khari: Conceptualization, Methodology, Writing-Original draft, Supervision; Vivek Kumar: Supervision, Methodology”.
Conflict of interest
“The authors declare no conflict of interest”.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Khari, K., Kumar, V. An efficient numerical technique for solving nonlinear singularly perturbed reaction diffusion problem. J Math Chem 60, 1356–1382 (2022). https://doi.org/10.1007/s10910-022-01365-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10910-022-01365-4