Abstract
Residual-type a posteriori error estimates in the maximum norm are given for singularly perturbed semilinear reaction-diffusion equations posed in polyhedral domains. Standard finite element approximations are considered. The error constants are independent of the diameters of mesh elements and the small perturbation parameter. In our analysis, we employ sharp bounds on the Green’s function of the linearized differential operator. Numerical results are presented that support our theoretical findings.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Our goal is to prove residual-type a posteriori error estimates in the maximum norm for singularly perturbed semilinear reaction-diffusion equations of the form
Here we assume that \(0<\varepsilon \le 1\), that f is continuous on \(\Omega \times \mathbb {R}\) and satisfies \(f(\cdot , s) \in L_\infty (\Omega )\) for all \(s \in \mathbb {R}\), and the one-sided Lipschitz condition \(f(x, u)-f(x,v) \ge C_f [u-v]\) whenever \(u\ge v\). Here \(C_f \ge 0\). Nonhomogeneous Dirichlet boundary conditions can also be considered with modest modification to our development. We additionally assume that \(\Omega \) is a, possibly non-Lipschitz, polyhedral domain in \(\mathbb {R}^n\), \(n=2, 3\). Then there is a solution \(u\in H_0^1(\Omega )\cap C(\bar{\Omega })\) (see Lemma 1 below). We consider a standard finite element approximation to (1.1). Let \(S_h \subset H_0^1(\Omega )\) be a Lagrange finite element space of fixed degree r relative to a shape regular mesh \(\mathcal {T}\), and let \(u_h \in S_h\) satisfy
Here \(( \cdot , \cdot )\) is an exact \(L_2\) inner product over \(\Omega \) (which is reasonable to assume when computing the stiffness matrix above), while \((\cdot , \cdot )_h\) is an approximate inner product resulting from application of a quadrature rule; we make more precise assumptions below.
Equations of type (1.1) and its parabolic version \(\partial _t u+Lu=0\) arise in modeling of thin plates as well as biological, chemical and engineering applications. Note that the usefulness of our results is not restricted to the steady-state case; in fact, plugging them (as error estimators for elliptic reconstructions) into the parabolic estimators [26] yields fully computable a posteriori error estimates in the maximum norm for the more challenging parabolic case.
Residual-type a posteriori error estimates in the maximum norm for finite element methods have previously been considered in a number of works. The papers [15, 32] were the earliest such works; both contain \(L_\infty \) residual estimators for linear elliptic problems on two-dimensional domains. The approach of [32] was extended to three space dimensions in [10], while [33–35] consider elliptic obstacle problems and monotone semilinear problems. Finally, [11] contains a posteriori maximum-norm estimates for an interior penalty discontinuous Galerkin method for the Laplacian as well as improved estimates for standard continuous Galerkin methods. Our approach draws most heavily from [11] and [33]. We use the techniques of [11] in order to admit arbitrary polyhedral domains in our analysis, whereas the results of [33] are restricted to Lipschitz polyhedral domains. In [33], the authors develop a multilevel estimator for controlling consistency errors resulting from numerical quadrature, and we employ much of their framework for the same purpose.
A number of works have also previously considered a posteriori error estimation and adaptivity for singularly perturbed reaction-diffusion equations, with the error generally measured in the energy (reaction-diffusion) norm. The article [42] appears to be the first to provide residual-based a posteriori estimates for FEM for scalar stationary reaction-diffusion problems that are robust with respect to the perturbation parameter. In [22], results of a similar spirit are announced, and then extended to the Brinkman problem in [23]. Residual-based estimates for singularly perturbed reaction-diffusion problems on anisotropic methods have also been studied, for example in [28, 29]. Two essential features of all of these works are that the weighting of the residual terms is of a different form depending on whether the local mesh parameter \(h_T <\varepsilon \) or \(h_T \ge \varepsilon \), and that no unknown constants in the estimates depend on \(\varepsilon \). Convergence of adaptive algorithms based on such a posteriori estimates is also considered in [27, 40]. Finally, a number of authors have considered other types of a posteriori error estimates which are robust with respect to \(\varepsilon \), as for example [2], [3] in which constant-free upper bounds are established by solving local subproblems.
The energy norm for singularly perturbed reaction-diffusion equations of type (1.1) is too weak, as it involves an excessive power of the small parameter \(\varepsilon \) and so is essentially no stronger than the \(L_2(\Omega )\) norm [31]. The maximum norm, by contrast, is sufficiently strong to capture sharp layers in the exact solution, so it appears more suitable for such problems. A posteriori estimates in the maximum norm for equations of type (1.1) are given in [7, 24]; the results are independent of the mesh aspect ratios, but apply only to tensor-product meshes. The situation with a priori error estimates in the maximum norm for such equations is much more satisfactory. In [30, 37], such bounds are given for finite element methods on globally quasiuniform meshes, while for a priori bounds in the maximum norm on locally-anisotropic layer-adapted meshes (for both finite element and finite difference methods) we refer the reader to [4, 5, 9, 24, 39] and references therein.
Our main contribution is the development of a posteriori error estimates in the maximum norm that are robust with respect to \(\varepsilon \), as in similar a posteriori estimates for the energy norm described above. In addition, we make an improvement to underlying techniques for estimating pointwise errors which even for the Laplacian leads to a sharper exponent in the logarithmic factors commonly present in maximum-norm estimates. We now outline our results in order to illustrate these improvements. For simplicity of presentation we for the time being assume exact quadrature, i.e., that \((\cdot , \cdot )_h = (\cdot , \cdot )\). Our full results below include error indicators that as in [33] account for consistency errors arising from inexact quadrature as well as a posteriori lower bounds. Let \(\widetilde{C}_f = C_f+ \varepsilon ^2\). We prove below that
Here \(h_T=\mathrm{diam}(T)\), \(\llbracket \nabla u_h \rrbracket \) is the standard jump in the normal derivative of \(u_h\) across an element interface, and \(\ell _h=\ln (2+\varepsilon \underline{h}^{-1}\widetilde{C}_f^{-1/2})\) with \(\underline{h}= \min _{T \in \mathcal {T}} h_T\). We also prove \(\varepsilon \)-robust a posteriori lower bounds (efficiency estimates) below. For the sake of comparison, note that the a posteriori analysis of [33] applies to (1.1), although robust analysis of singularly perturbed problems is not a focus of that work. The estimates in [33] are obtained by employing arguments similar to ours below, but essentially with \(C_f\) taken to be 0 and thus \(\widetilde{C}_f =\varepsilon ^2\). Thus applying these results yields
Here \(\tilde{\ell }_h= \ln 1/\underline{h} \) with \(\alpha _2=2\) and \(\alpha _3=4/3\). In both cases above C is independent of \(\varepsilon \). The essential improvement in (1.3) versus (1.4) comes in the weighting of the residual terms when \(\varepsilon ^2 \ll C_f\), i.e., when the problem is uniformly singularly perturbed. In this case (1.3) is significantly sharper in regions where \(h_T \gg \varepsilon \). For fixed \(\varepsilon \), the two estimators are equivalent with the exception of logarithmic factors if \(\max h_T \le \varepsilon \). Numerical results in Sect. 4 below show that the estimator (1.4) is not \(\varepsilon \)-uniformly robust in the sense that its effectivity index (estimator divided by error) blows up for a fixed \(\max h_T\) as \(\varepsilon \rightarrow 0\). These tests also confirm that the elementwise error indicators naturally derived from (1.4) may not perform well when used to drive marking in an adaptive FEM.
Our estimator (1.3) essentially reduces to (1.4) when \(C_f \lesssim \varepsilon \), i.e., when the problem is not singularly perturbed, and we can in fact recover (1.4) (with the exponents of the log factors improved to 1) by taking \(C_f=0\) since then our one-sided Lipschitz condition reduces to a monotonicity condition. We thus allow for unified consideration of problems in both singularly perturbed and elliptic regimes and continuously track the transition between these two regimes. However, obtaining \(\varepsilon \)-robust estimates in the singularly perturbed regime requires us to assume more regularity of f than monotonicity.
Note also the improvement in the logarithmic terms in (1.3) versus (1.4). First, \(\ell _h\) in (1.3) is smaller than \(\tilde{\ell }_h\) in (1.4) when \(\varepsilon \ll 1\). (Note that the a priori error bounds in [37] also involve \(\ell _h\).) In addition, the exponent of \(\ell _h\) in (1.3) is 1 for both \(n=2\) and \(n=3\), whereas the exponent of \(\tilde{\ell }_h\) in (1.4) is greater than 1. The exponent of the logarithmic factor when \(n=3\) was already improved to 1 in [11], and we carry out a similar improvement for the case \(n=2\) here. We additionally show below that the logarithmic factor is necessary at least when piecewise linear elements are used by proving that standard maximum-norm estimators in actuality reliably and efficiently control the error in a suitable bounded mean oscillation (BMO) norm with no logarithmic factors present on convex polyhedral domains. This result also may have implications for understanding convergence of adaptive algorithms for controlling maximum errors, since it indicates that the standard \(L_\infty \) AFEM is in fact better designed to control a different measure of the error.
As in previous works concerning a posteriori error analysis of elliptic problems in the maximum norm, we employ Green’s functions in order to represent the error pointwise, and estimates for Green’s functions play a critical role in our proofs. Such estimates are most readily available for the Laplacian. In [33], the authors obtain (1.4) by employing a Riesz representation of the residual along with a barrier argument in order to use estimates for a regularized Green’s function for the Laplacian. We similarly employ an argument involving the maximum principle in order to reduce proving (1.3) to obtaining appropriate bounds for a Green’s function for a simplified differential operator, though as in [11] we employ the actual instead of a regularized Green’s function. It is however critical that our simplified operator \(-\varepsilon ^2 \Delta + C_f\) retains the essential singularly perturbed character of (1.1).
Note that the present paper is complemented by a subsequent paper [25], in which the consideration is restricted to \(\Omega \subset \mathbb {R}^2\) and linear finite elements, but a posteriori error bounds of type (1.3) are extended to more challenging anisotropic meshes. The analysis in [25] partially relies on our results and findings, the Green’s function bounds being particularly essential.
The paper is organized as follows. Section 2 contains analytical preliminaries, most notably bounds for Green’s functions for singularly perturbed problems which allow us to translate maximum-norm error estimation techniques used for the Laplacian in [11] to the current situation. Section 3 contains proofs of a posteriori upper and lower bounds in the maximum norm that are \(\varepsilon \)-robust and account for consistency errors arising from numerical quadrature. Several numerical examples are presented in Sect. 4. Finally, in Appendix A we show that logarithmic factors must be present in a posteriori upper bounds and further discuss their role in a posteriori error estimates and adaptivity for controlling maximum errors.
2 Analytical preliminaries
In this section we first sketch a proof of existence and uniqueness for (1.1) and then prove a number of essential bounds for Green’s functions for singularly perturbed problems.
2.1 The continuous problem: existence and uniqueness
We are not aware of an existence and uniqueness result for (1.1) under the precise assumptions that we make, so we sketch a proof.
Lemma 1
Assume that \(f \in C(\Omega \times \mathbb {R})\), \(f(\cdot , s) \in L_\infty (\Omega )\) for all \(s \in \mathbb {R}\), that for all \(x \in \Omega \) we have \(f(x,u)-f(x,v) \ge 0\) whenever \(u \ge v\), and that \(\Omega \) is a polyhedral domain in \(\mathbb {R}^n\), \(n=2\) or \(n=3\). Then (1.1) has a unique solution \( u \in H_0^1(\Omega )\) which additionally satisfies \(u\in W_l^2(\Omega )\subseteq W_q^1\subset C(\bar{\Omega })\) for some \(l>\frac{n}{2}\) and \(q>n\).
Proof
Let \(\Omega '\) be a subdomain of \(\Omega \), and let \(\tilde{L}:=-\varepsilon ^2\triangle +\tilde{p}\) for some \(\tilde{p}\ge 0\) in \(L_\infty (\Omega ')\). Then, an application of the weak maximum principle for functions in \(H^1(\Omega )\) [17, Theorem 8.1] implies that there exists a constant \(\mu _0=\mu _0(\varepsilon ,\mathrm{diam}\,\Omega )\), independent of \(\tilde{p}\), such that \(\Vert v\Vert _{\infty \,;\Omega '}\le \max \bigl \{\mu _0\Vert \tilde{L} v\Vert _{\infty \,;\Omega '},\Vert v\Vert _{\infty \,;\partial \Omega '}\bigr \}\) for any \(v\in H^1(\Omega )\cap L_\infty (\Omega )\). Next, set \(\mu _1:=\mu _0\Vert f(\cdot ,0)\Vert _{\infty \,;\Omega }\) and define the function \(\tilde{f}(\cdot , s)\) to be equal to \(f(\cdot , s)\) for \(|s|\le \mu _1\) and equal to \(f(\cdot ,\pm \mu _1)\) for \(\pm s>\mu _1\). Note that \(|\tilde{f}|\le \mu _2 =\max \{ \Vert f(\cdot , -\mu _1)\Vert _{\infty \,;\Omega }, \Vert f(\cdot , \mu _1)\Vert _{\infty \,;\Omega } \} \) and \(\tilde{f}\) is monotone in the second argument. By an application of [6, Lemma 16], there exists a solution \(\tilde{u}\in H_0^1(\Omega )\) of \(-\varepsilon ^2\triangle \tilde{u}+\tilde{f}(x,\tilde{u})=0\). Furthermore, \(\tilde{u}\in H_0^1(\Omega )\) and \(|\tilde{f}|\le \mu _2\) imply \(\triangle \tilde{u}=\varepsilon ^{-2}\tilde{f}(\cdot , \tilde{u})\in {L_2}(\Omega )\), so an application of [11, Lemma 2.1] yields, with some \(l>\frac{n}{2}\) and \(q>n\), that \(\tilde{u}\in W_l^2(\Omega )\subseteq W_q^1(\Omega )\subset C(\bar{\Omega })\). Finally, let \(\Omega ':=\{|\tilde{u}|>\mu _1\}\subset \Omega \). As \(\tilde{u}\) is continuous, \(\Omega '\) is a well-defined subdomain of \(\Omega \). Also, \(\tilde{p}(x):= \frac{\tilde{f}(x, \tilde{u})-\tilde{f}(x, 0)}{\tilde{u}}\ge 0\) is in \(L_\infty (\Omega ')\), and by a simple computation \(-\varepsilon ^2\triangle \tilde{u}+\tilde{p} \tilde{u}=-\tilde{f}(x,0)=- f(x,0)\) in \(\Omega '\). Thus the above maximum-principle bound yields \(\Vert \tilde{u}\Vert _{\infty \,;\Omega ' }\le \mu _1\), so \(\Omega ' = \emptyset \) and \(\Vert \tilde{u}\Vert _{\infty \,; \Omega } \le \mu _1\). Hence \(\tilde{f}(\cdot , \tilde{u})=f(\cdot ,\tilde{u})\), that is, \(\tilde{u}\) is a solution to (1.1). \(\square \)
Assuming a nonhomogeneous boundary condition \(u=g\) on \(\partial \Omega \) with some \(g\in W_l^2(\Omega )\subseteq W_q^1\subset C(\bar{\Omega })\), the above lemma can be generalized as follows. Let \(-\triangle \hat{g}=0\) in \(\Omega \) and \(\hat{g}=g\) on \(\partial \Omega \). Then [11] gives \(\hat{g}\in W_l^2(\Omega )\subseteq W_q^1\subset C(\bar{\Omega })\). Now, \(\hat{u}:=u-\hat{g}\) satisfies \(-\varepsilon ^2\triangle \hat{u}+\hat{f}(x,\hat{u})=0\) subject to \(\hat{u}=0\) on \(\partial \Omega \), where \(\hat{f}(x,s):=f(x,s+\hat{g})\). Note that this problem satisfies the hypotheses of the above lemma. In particular, for each \(s\in \mathbb {R}\), one has \(|\hat{f}(\cdot ,s)|\le \max \bigl \{ \Vert \hat{f}(\cdot ,s-\Vert \hat{g}\Vert _{\infty })\Vert _{\infty \,;\Omega },\Vert \hat{f}(\cdot ,s+\Vert \hat{g}\Vert _{\infty })\Vert _{\infty \,;\Omega }\bigr \}\) so \(\hat{f}(\cdot ,s)\in L_\infty (\Omega )\) for each s. An application of the above lemma gives existence and uniqueness of \(\hat{u}\) and thus also of u.
2.2 Bounds for the Green’s function
As is standard in the literature on maximum-norm error bounds in FEM, we employ a Green’s function in order to represent the error pointwise. It is possible to obtain such a representation employing the Green’s function for a standard linearization about u and \(u_h\), but proving the necessary bounds on this Green’s function is at least significantly more difficult unless we assume that the Lipschitz constant of f in u is uniformly bounded above by some constant \(\bar{C}_f\). (Note that we have only assumed a corresponding lower bound on the Lipschitz constant.) In Sect. 3.1 below we show that we can instead employ the Green’s function for the simplified linear operator \(\bar{L} := -\varepsilon ^2 \Delta + C_f\), so we only analyze the Green’s function for this operator. The bounds below do however hold for the corresponding Green’s function for a linearized operator under the assumption \(C_f \le f_u \lesssim C_f\).
There exists a Green’s function \(G(x,\xi ): \Omega \times \Omega \rightarrow \mathbb {R}\) such that for any \(v \in H_0^1(\Omega )\cap {W}_1^q(\Omega )\) with \(q>n\),
For each \(x\in \Omega \), this function G, satisfies
Here \(\delta (\cdot )\) is the n-dimensional Dirac \(\delta \)-distribution.
Before stating regularity results for G we define notation. We write \(a\sim b\) when \(a \lesssim b\) and \(a \gtrsim b\), and \(a \lesssim b\) when \(a \le Cb\) with a constant C depending on \(\Omega \), r, and shape regularity properties of \(\mathcal {T}\), but not on other essential quantities. In particular, C does not depend on the diameters of elements in \(\mathcal {T}\), \(\varepsilon \), or \(C_f\). Also, for \(\mathcal {D} \subseteq \overline{\Omega }\), \(1 \le p \le \infty \), and \(k \ge 0\), \(\Vert v\Vert _{p\,;\mathcal {D}}=\Vert v\Vert _{L_p(\mathcal {D})}\) and \(|v|_{k,p\,;\mathcal {D}}=|v|_{W_p^k(\mathcal {D})}\), where \(|\cdot |_{W_p^k(\mathcal {D})}\) is the standard Sobolev seminorm with integrability index p and smoothness index k.
We shall employ the following bounds.
Theorem 1
Let G be from (2.2), and let \(\widetilde{C}_f = C_f + \varepsilon ^2 \). Then for any \(x \in \Omega \),
In addition, for the ball \(B(x, \rho )\) of radius \(\rho \) centered at \(x \in \Omega \), let \(\ell _\rho :=\ln (2+ \widetilde{\varepsilon }\rho ^{-1} )\), where \(\widetilde{\varepsilon }=\frac{\varepsilon }{\sqrt{C_f + \varepsilon ^2}}\). Then
Remark 1
The work [11] contains similar Green’s function estimates in the case \(\varepsilon =1\), \(C_f = 0\). When \(n=2\), (2.4e) gives a sharper version of the bound [11, (5.21)] in that \(\ln ^2(1/\mathrm{h})\) in the latter can be improved to \(\ln (1/\mathrm{h})\). Hence a similar amendment applies to all error estimators obtained in [11].
Remark 2
Similar Green’s function bounds for the case \(\varepsilon \ll 1\) and \(C_f\sim 1\), but on significantly simpler tensor-product domains are given in [7, 24]. An inspection of the proofs in these papers reveals that in this case, all bounds of Theorem 1 are sharp with respect to \(\varepsilon \), \(\rho \) and \(\ell _\rho \).
2.3 Proof of Theorem 1
First, we give a version of the bounds from [11] for the Green’s function of the Laplace operator.
Lemma 2
If \(\varepsilon =1\) and \(C_f=0\), then G of (2.2) satisfies (2.3), (2.4d), and (2.4e).
Proof
If \(\varepsilon =1\) and \(C_f=0\), the bound for \(|G(x, \cdot )|_{1,1;\Omega }\) in (2.3) follows immediately from (2.4d) with \(\varepsilon =1\), \(\rho =\mathrm{diam}(\Omega )\), while the remaining results in (2.3) are easily obtained using the pointwise upper bounds on G from [11, (2.6)].
For \(n=3\), the bounds (2.4d) and (2.4e) with \(\varepsilon =1\) immediately follow from [11, (5.23 and 5.26)].
For \(n=2\), the bounds [11, (5.23 and 5.27)] involve an additional logarithmic factor, but can be improved to (2.4d) and (2.4e) as follows. Note that the first line in [11, (5.23)] and [11, (5.25)] remains valid if G is replaced in each considered subdomain \(\Omega _j\) by \(G-\min _{\Omega _j}G\). With this observation, the proofs of the bounds [11, (5.23) and (5.27)] yield their sharper versions (2.4d) and (2.4e) after we prove the following lemma. \(\square \)
Lemma 3
Let \(n=2\), \(\varepsilon =1\), \(C_f=0\), and \(\Omega _\rho =[B(x,\rho )\backslash B(x,\frac{1}{2}\rho )]\cap \Omega \) for any \(\rho >0\) and \(x\in \Omega \). Then the Green’s function G of (2.2) satisfies
where C is independent of \(\rho \) and x.
Proof
Fix \(x\in \Omega \) and let \(r_0=\mathrm{dist}(x,\partial \Omega )\). Note that it suffices to show that
Here the lower bound is easily obtained using the maximum principle and the standard formula \(\Gamma (x,\xi ) = \frac{1}{2\pi } \ln |x-\xi |^{-1}\) for the fundamental solution \(\Gamma \) on \(\mathbb {R}^2\). For the upper bound, we assume, without loss of generality, that the nearest point to x on \(\partial \Omega \) is O, and that \(\Omega \subset S\), where the domain S is either (i) \(S=R^2\backslash \{(\xi _1,0),\;\xi _1\ge 0\}\), or, for a more complicated polygonal \(\Omega \), (ii) \(S=\{|\xi -x|<\mathrm{diam}(\Omega )\}\backslash \{(\xi _1,0),\;0\le \xi _1\le C_S\}\) with \(C_S\gtrsim 1\). As \(\Omega \subset S\) implies \(G(x,\xi )\le G_S(x,\xi )\), where \(G_S\) is the Green’s function for the domain S, the upper bound in (2.5) immediately follows from
To complete the proof, we establish (2.6) for cases (i) and then (ii).
-
(i)
The Green’s function for the domain \(S=R^2\backslash \{(\xi _1,0),\;\xi _1\ge 0\}\) is explicitly given by [18, p. 143, (16.55)]
$$\begin{aligned} G_S(x,\xi ):={\textstyle \frac{1}{4\pi }}\, \ln \left( \frac{t^2-2t\,\cos \bigl (\frac{1}{2}[\theta +\theta _0]\bigr )+1}{t^2-2t\,\cos \bigl (\frac{1}{2}[\theta -\theta _0]\bigr )+1} \right) ,\qquad t=\sqrt{\frac{r}{r_0}}, \end{aligned}$$where \((r_0,\theta _0)\) and \((r,\theta )\) are respectively the polar coordinates of x and \(\xi \). If \(r\ge 4 r_0\), then \(t\ge 2\) and one easily gets \(G_S\le \frac{1}{2\pi }\ln |\frac{t+1}{t-1}|\le \frac{1}{2\pi }\ln 3\). This bound remains valid in \(\{|\xi -x|\ge 5r_0\}\subset \{r\ge 4 r_0\}\). Now, for the domain \(\{|\xi -x|\le 5r_0\}\), the maximum principle yields \(G_S\le {\frac{1}{2\pi }} \ln \frac{5r_0}{|\xi -x|}+\frac{1}{2\pi }\ln 3\). This completes the proof of (2.6) with \(C=\frac{1}{2\pi }\ln 3\) for case (i).
-
(ii)
Let \(S=\{|\xi -x|\le \mathrm{diam}(\Omega )\}\backslash \{(\xi _1,0),\;0\le \xi _1\le C_S\}\). First, note that \(G_S(x,\xi )\le \frac{1}{2\pi }\ln \frac{\mathrm{diam}(\Omega )}{C_S}\) for \(|\xi -x|\ge C_S\). Next, let \(G'_{S}\) denote the Green’s function in case (i). Now an application of the maximum principle to \(G_{S}-G'_{S}\) in the domain \( |\xi -x|\le C_S\) yields \( |G_{S}-G'_{S}|\le C\). So the bound (2.6) in this domain follows from the corresponding result in case (i).\(\square \)
Lemma 4
Let \(D\subset D'\subseteq \hat{\Omega }:=\varepsilon ^{-1}\Omega \) with \(\mathrm{dist}\{\partial D\backslash \partial \hat{\Omega },\partial D'\backslash \partial \hat{\Omega }\}\gtrsim 1\) and \(\mathrm{diam}( D')\simeq d\). Then for any \(v\in L_2(\Omega )\) such that \(\triangle v\in L_2(\Omega )\)
Proof
Set \(\alpha \in (1,\frac{4}{3})\). Note that \(|v|_{2,\alpha \,;\Omega } \le C_\alpha \Vert \triangle v\Vert _{\alpha \,;\Omega }\) in the original domain \(\Omega \) [11, Lemma 2.1], where \(C_\alpha =C_\alpha (\Omega )\) remains fixed throughout this proof. This implies that \(| v|_{2,\alpha \,;\hat{\Omega }} \le C_\alpha \Vert \triangle v\Vert _{\alpha \,;\hat{\Omega }}\) in the stretched domain \(\hat{\Omega }\). Furthermore, we have that \(|\omega v|_{2,\alpha \,;\hat{\Omega }}\le C_\alpha \Vert \triangle (\omega v)\Vert _{\alpha \,;\hat{\Omega }}\), with a cutoff function \(\omega \) that equals 1 in D and vanishes in \(\hat{\Omega }\backslash D'\), so
where we used \(\mathrm{dist}\{\partial D\backslash \partial \hat{\Omega },\partial D'\backslash \partial \hat{\Omega }\}\gtrsim 1\). Next, as \(|D|\le |D'|\lesssim d^n\), so \(|\cdot |_{2,1\,;D}\le |\cdot |_{2,\alpha \,;D}\cdot |D'|^{1-1/\alpha }\), and \(\Vert \cdot \Vert _{\alpha \,;D'}\le \Vert \cdot \Vert _{2\,;D'}\cdot |D'|^{1/\alpha -1/2}\), so
Combine this with \(\Vert \nabla v\Vert _{2\,;D'}\le C ( \Vert \triangle v\Vert _{2\,;D''}+\Vert v\Vert _{2\,;D''})\), where the domain \(D''\) is related to \(D'\) in the same way as \(D'\) to D (while the constant C is independent of the domain size). Now the notation change \(D''=:D'\) yields the desired assertion. \(\square \)
Proof of Theorem 1
We divide the proof into two essentially different cases and their three generalizations.
Case 1 \(0< \varepsilon ^2 \le C_f=1\). We start with (2.4a). Using the maximum principle, one can show that \(0\le G(x;\xi )\le g_n(x;\xi )\), where \(g_n\) is the Green’s function for the operator \(-\varepsilon ^2\triangle +C_f\) in \(\mathbb {R}^n\). In particular, from [41] we have
Here \(K_0\) is the modified Bessel function of the second kind of order zero and satisfies [1]
(2.4a) follows from the corresponding bounds on \(\Vert g_n(x,\cdot )\Vert _{1, B(x,\rho ) }\).
Next, (2.4b) and the bounds for \(\Vert G(x,\cdot )\Vert _{1, \Omega }\) and \(\Vert G(x,\cdot )\Vert _{\frac{n}{n-1}\,;\Omega }\) in (2.3) are obtained similarly using (2.8) and (2.9).
Note that the bound (2.4c) follows from (2.4a), (2.4d) and (2.4e). To show this, let a smooth cut-off function \(\omega \) equal 1 on \(\Omega {\setminus } B(x,\rho )\) and vanish on \(B(x,\frac{1}{2}\rho )\cap \Omega \). Then the Sobolev embedding \(W_1^2(\Omega ) \hookrightarrow W_{\frac{n}{n-1}}^1(\Omega )\) implies that
Now (2.4c) indeed follows by (2.4a), (2.4d) and (2.4e).
To prove the remaining bounds, introduce an auxiliary Green’s function \(\bar{G}\) for the operator \(-\varepsilon ^2 \triangle \) in the domain \(B(x\,;2\varepsilon ) \cap \Omega \). Note that \(\bar{G}\) is a scaled normalized Green’s function of the operator \(- \triangle \), for which we have Lemma 2. More precisely, \(\bar{G}(x,\xi )=\varepsilon ^{-n}G_0(x/\varepsilon , \xi /\varepsilon )\), where \(G_0\) is the Green’s function of \(- \triangle \) in the domain \(\varepsilon ^{-1}[B(x\,;2\varepsilon ) \cap \Omega ]\), so Lemma 2 for \(G_0\) implies bounds (2.4d) and (2.4e) for \(\bar{G}\) with \(\Omega \) replaced by \(B(x\,;2\varepsilon ) \cap \Omega \).
In view of this observation, to complete the proof, it suffices to show that
Indeed, the bound for \(|G(x,\cdot )|_{1,1; \Omega }\) in (2.3) follows from (2.11a), (2.11c) and a version of (2.3) for \(\bar{G}\). Note that (2.3) implies (2.4d) for \(\rho \ge \varepsilon \). For \(\rho \le \varepsilon \), the bound (2.4d) follows from (2.11b), (2.11c) and a version of (2.4d) for \(\bar{G}\). Finally, the bound (2.4e) follows from (2.11a), (2.11c) and a version of (2.4e) for \(\bar{G}\).
Now we establish each of the estimates in (2.11).
For (2.11a), let \(w(\xi ):=\bar{G}-G\) for \(\xi \in B(x\,;2\varepsilon ) \cap \Omega \). Note that (2.2) implies that \(-\varepsilon ^2\triangle _{\xi }\,w ={C_f}\,{G}\). Next, using the variable \(\hat{\xi }=\xi /\varepsilon \) and the notation \(\hat{v}(\hat{\xi }):=v(\xi )\) for any function v, and \(\hat{D}:=\varepsilon ^{-1}D\) for any domain D, one gets \(-\triangle \hat{w} = {C_f}\,\hat{{G}}\) in \(\hat{B}(x\,;2\varepsilon )\cap \hat{\Omega }\), so \(|\triangle \hat{w}|+|\hat{w}|\lesssim \hat{G}+\hat{\bar{G}}\). Now, an application of (2.7) with \(d=1\) yields
Rewriting this in terms of the original variable \(\xi \), one gets
where we used \(G+\bar{G}\le g_n\) and (2.8). The above result immediately implies (2.11a).
To show (2.11b), we partly imitate the argument used to prove (2.11a) with \(B(x\,;\varepsilon )\) and \(B(x\,;2\varepsilon )\) replaced by \(B( x\,;\rho )\) and \(B( x\,;\rho +\varepsilon )\). In particular,
while \(-\triangle \hat{w} = \hat{p}\,\hat{{G}}\) implies
The desired assertion (2.11b) follows as \((\rho /\varepsilon )^{n/2}\le \rho /\varepsilon \) for \(\rho \le \varepsilon \) and \(n=2,3\).
For (2.11c), let \(\rho _{j}:= 2^{j}\) and divide the domain \(\Omega \backslash B(x\,;\varepsilon )\) into the non-overlapping subdomains \(\mathcal {D}_{j}:= [B(x,\varepsilon \rho _{j+1})\backslash B(x,\varepsilon \rho _j)]\cap \Omega \) where \(j = 0,1,\ldots \). Furthermore, \(\mathcal {D}_{j} \subset \mathcal {D}'_{j} := \mathcal {D}_{j-1}\cup \bar{\mathcal {D}}_{j} \cup \mathcal {D}_{j+1},\) so that \(\text{ dist }(\partial \mathcal {D}'_{j}\backslash \partial \Omega ,\partial \mathcal {D}_{j}\backslash \partial \Omega ) \ge \varepsilon /2\). The equation from (2.2) implies \(-\Delta \hat{G} +\hat{p}\,\hat{G} = 0\) in each \(\mathcal {D}'_{j}\), so an application of (2.7) with \(d=\rho _{j-1}\ge \frac{1}{2}\) yields
Using \(G\le g_n\) and (2.8), one gets \(\rho _j^{n}\,\Vert {G}\Vert _{\infty \,;{\mathcal {D}}'_{j}} \lesssim \rho _j^{\mu _n} \varepsilon ^{-n} e^{-c\rho _j}\), where by (2.8) and (2.9) \(\mu _2 = 3/2\) and \(\mu _3 = 2\). So, in terms of the original variable \(\xi \),
This immediately implies the final bound (2.11c) in (2.11) when \(0 \le \varepsilon ^2 \le C_f=1\).
Case 2 \(\varepsilon ^2=1\), \(C_f=0\). We complete the proof of (2.4a), (2.4b), and (2.4c) for the case \(C_f=0\), \(\varepsilon =1\); the remaining estimates are contained in Lemma 2. (2.4a) and (2.4b) follow immediately from standard pointwise estimates for Green’s function for the Laplacian; cf. [11, (2.6)]. (2.4c) follows exactly as in (2.10).
Case 1 \({'}\) \(0 < \varepsilon ^2 \le C_f\). In this case \(G=\frac{1}{C_f} \tilde{G}\), where \(\tilde{G}\) is the Green’s function for \(-\frac{\varepsilon ^2}{C_f} \Delta + 1\). Bounds for \(\tilde{G}\) were obtained in Case 1, so we may obtain all of the asserted bounds for G by rescaling by \(\frac{1}{C_f}\), making the identifications \(C_f =1\) and \(\varepsilon = \frac{\varepsilon }{\sqrt{C_f}}\), and noting that \({\widetilde{C}_f}\sim C_f\). For example, \({\widetilde{C}_f} \Vert G\Vert _{1; \, \Omega } = {\widetilde{C}_f} C_f^{-1} \Vert \tilde{G}\Vert _{1 ; \, \Omega } \sim \Vert \tilde{G}\Vert _{1; \, \Omega } \lesssim 1\).
Case 2 \({'}\) \(\varepsilon ^2=1\), \(0< C_f \le 1\). Let \(G_0\) be the Green’s function for \(-\Delta \) considered in Case 2. A maximum principle and positivity of the Green’s function yields \(0 \le G \le G_0\). The bounds for \(\Vert G\Vert _{1; \, \Omega }\) and \(\Vert G\Vert _{\frac{n}{n-1}; \, \Omega }\) in (2.3) along with (2.4a) and (2.4b) follow immediately. The other bounds are established as in Case 1 with the modification that whenever \(\bar{G}\) is defined and employed, the domains \(B(x\,;2\varepsilon ) \cap \Omega \) and \(B(x\,;\varepsilon ) \cap \Omega \) are replaced by \(\Omega \) (so \(\bar{G}=G_0\)), while \( \Omega {\setminus }B(x\,;\varepsilon )\) is replaced by \(\emptyset \).
Case 2 \({''}\) \(0 \le C_f \le \varepsilon ^2.\) Here \(G = \frac{1}{\varepsilon ^2} \tilde{G}\), where \(\tilde{G}\) is the Green’s function for \(-\Delta u + \frac{C_f}{\varepsilon ^2}\). Bounds for \(\tilde{G}\) were obtained in Case 2 and Case 2\({'}\) above, so we may obtain the asserted bounds for G by rescaling those for \(\tilde{G}\) by \(\frac{1}{\varepsilon ^2}\) and making the identifications \(\varepsilon =1\), \(C_f= \frac{C_f}{\varepsilon ^2}\). \(\square \)
3 A posteriori error analysis
In this section we carry out our a posteriori error analysis in several steps. In the final subsection we summarize and discuss our results.
3.1 Error representation
In [33, Sect. 4.1], the authors employ a barrier argument to show that the Green’s function for the Laplacian may be used in order to obtain pointwise a posteriori error bounds for a monotone semilinear problem. We employ a version of their argument which is in most respects simpler, but which in contrast to [33] retains the singularly perturbed character of the problem.
For arbitrary \(u, v\in C(\bar{\Omega })\), we first define an auxiliary function w by
The following lemma gives a representation for the difference \(v-u\) (where we may think of \(v=u_h\)) via the Green’s function of the operator \(-\varepsilon ^2\triangle +C_f\).
Lemma 5
Let \(e=[v-u]+w\), with w defined by (3.1) and \(C_f \ge 0\). Then
where G satisfies (2.2).
Proof
For any \(\theta >0\), let \(\Omega '=\{|u-v|>\theta \}\). \(\Omega '\) is a well-defined subdomain of \(\Omega \) as \(u,v\in C(\bar{\Omega })\). Then \(|w|\le \Vert e\Vert _{\infty \,;\Omega }+\theta \) in \(\Omega {\setminus } \Omega '\), including on \(\partial \Omega '\). Next, in \(\Omega '\), let \(p(x) := \frac{f(\cdot , v) - f( \cdot , u)}{v-u} \ge C_f\) and note that \(p\in L_\infty (\Omega ')\). The Eq. (3.1) for w is equivalent in \(\Omega '\) to \(-\varepsilon ^2 \Delta w + p w =(p-C_f)e\). Let \(w^\pm :=\Vert e\Vert _{\infty \,;\Omega }+\theta \pm w\). Then a calculation shows that \([-\varepsilon ^2 \Delta + p]\, w^\pm \ge p\,\Vert e\Vert _{\infty \,;\Omega }\pm (p-C_f)e\ge 0\) in \(\Omega '\), and \(w^\pm \ge 0\) on \(\partial \Omega '\). Now an application of the weak maximum principle (cf. [17, Theorem 8.1]) yields \(w^\pm \ge 0\) or \(|w|\le \Vert e\Vert _{\infty \,;\Omega }+\theta \) in \(\Omega '\), and so in \(\Omega \). As this conclusion is valid for any \(\theta >0\), so \(|w|\le \Vert e\Vert _{\infty \,;\Omega }\) in \(\Omega \). This immediately implies (3.2a). For (3.2b), note that the definition of G implies
Now a calculation using (3.1) and (1.1) yields (3.2b). \(\square \)
Assuming the nonhomogeneous boundary condition \(u=g\) on \(\partial \Omega \), the above is easy to generalize as follows. For (3.2b), we need to impose \(e=0\) on \(\partial \Omega \), but now \(w=-[v-u]=-[v-{g}]\) on \(\partial \Omega \) so the bound (3.2a) will be modified to \(\Vert v-u\Vert _{\infty \,;\Omega }\le 2 \Vert e\Vert _{\infty \,;\Omega }+\Vert v-{g}\Vert _{\infty \,;\partial \Omega }\). In the proof of the above lemma, we use positive \(\theta \ge \Vert v-g\Vert _{\infty \,;\partial \Omega }\) (or \(\theta := \Vert v-{g}\Vert _{\infty \,;\partial \Omega }\) if \(\Vert v-u\Vert _{\infty \,;\partial \Omega }>0\), and \(\theta \rightarrow 0^+\) if \(\Vert v-g\Vert _{\infty \,;\partial \Omega }=0\)).
We finally give a formula for e(x) that we shall use to derive our bounds. Fix \(x \in \Omega \), for example by choosing x so that |e(x)| is maximized over \(\Omega \), and write \(G=G(x, \cdot )\) for the Green’s function of (2.2). Equations (3.2b) and (1.2) then yield that for any \(G_h \in S_h\),
3.2 Derivation of bounds for residual portion of the error
Let \(G_h\) denote the Scott-Zhang interpolant of \(G=G(x,\cdot )\) lying in the space of continuous piecewise linear functions with respect to \(\mathcal {T}\). Here \(x\in \Omega \) remains fixed and the interpolant is calculated with respect to the second argument of G. We then have that \(G_h\) is the Scott-Zhang interpolant into \(S_h\) when \(r=1\), and \(G_h \in S_h\) in any case. We briefly recall the definition of \(G_h\). Let \(\mathcal {N}\) be the set of linear Lagrange nodes (vertices) in \(\mathcal {T}\), and let \(\phi _z\) be the standard linear hat function corresponding to \(z \in \mathcal {N}\). If \(z \in \Omega \), then \(F_z\) is taken to be an element \(T \in \mathcal {T}\) for which \(z \in T\). Alternatively, if \(z \in \partial \Omega \), then \(F_z\) is taken to be a face (\(n-1\)-simplex) of some \(T \in \mathcal {T}\) such that \(z \in \bar{F}_z \subset \partial \Omega \). \(\psi _z \in \mathbb {P}_1(F_z)\) is taken to be dual to \(\phi _z\) on \(F_z\) in the sense that \(\int _{F_z} \psi _{z'} \phi _z=1\) if \(z=z'\) and 0 otherwise. Here \(\mathbb {P}_m\) denotes the polynomials of degree at most m. Letting \(\mathcal {N}_I\) be the set of interior nodes, we have \(G_h = \sum _{z \in \mathcal {N}} \phi _z \int _{F_z} G \psi _z = \sum _{z \in \mathcal {N}_I} \phi _z \int _{F_z} G \psi _z \). All elements \(F_z\) in the final sum are d-simplices. Thus defined, \(G_h\) satisfies the local stability and approximation property
for any \(0 \le k \le j \le 2\), \( 1 \le p \le \infty \) for which the right hand side of (3.4) is defined. Here \(\omega _T\) is the patch of elements in \(\mathcal {T}\) touching T.
We will prove the following lemma.
Lemma 6
Let x be an arbitrary point in \(\Omega \). With \(G=G(x,\cdot )\) and \(G_h\) the piecewise linear Scott-Zhang interpolant of G as above,
Here we use the standard notation \(\llbracket \nabla u_h \rrbracket \) for the jump of the normal derivatives across an inter-element side. Also, \(\widetilde{C}_f = C_f + \varepsilon ^2\) and \(\widetilde{\varepsilon }={\frac{\varepsilon }{\sqrt{C_f + \varepsilon ^2}}}=\varepsilon \widetilde{C}_f^{-1/2}\) as above, and
Proof
Note first that (3.5) for the general case \(\widetilde{C}_f>0\) follows easily if we prove (3.5) for \(\widetilde{C}_f=1\) (and thus also \(\widetilde{\varepsilon }=\varepsilon \)). Assuming that we have done so, let \(\widetilde{f} = f \widetilde{C}_f^{-1}\) and similarly for \(f_h\). Then \(-\widetilde{\varepsilon }^2 \Delta u + \widetilde{f}(x,u)=0\), and similarly for \(u_h\). The Green’s function for this problem is \(\widetilde{G}=\widetilde{C}_f G\). In addition, we have \(\widetilde{C}_{\widetilde{f}} =\widetilde{\varepsilon }^2 + C_f \widetilde{C}_f^{-1}= 1\), and so (3.5) holds with the substitutions \(\varepsilon , \widetilde{\varepsilon } \rightarrow \widetilde{\varepsilon }\), \(f \rightarrow \widetilde{f}\), \(G \rightarrow \widetilde{G}\), and \(\widetilde{C}_f \rightarrow 1\). Rearranging constants immediately yields (3.5) in the general case.
We now prove (3.5) for \(\widetilde{C}_f =1\). In this case we may interchangably write \(\widetilde{\varepsilon }=\varepsilon \) and so use only the notation \(\varepsilon \) below. A standard calculation shows that
Now
By (3.4),
Since \(\alpha _T^{-1}\le {\varepsilon }^{\,-2}+\ell ^{-1}_{h,x} h_T^{-2}\),
Given \(T \in \mathcal {T}\) we let \(\omega _T'\) denote the patch of elements touching \(\omega _T\). Also let \(x\in T_0\). Then
where by employing (2.3), (2.4a), (2.4e), and \(\widetilde{C}_f=1\), we find
Thus
Next consider I:
A standard trace inequality and (3.4) yield
Note that \(\beta _T^{-1}\le { \varepsilon ^{\,-1}} +(\ell _{h,{x}} h_T)^{-1}\) and \(\ell _{h,{x}}^{-1}\lesssim 1\) so that
Then
where by employing (2.3), (2.4d), and (2.4e), we find
Finally
Collecting the previous estimates completes the proof of Lemma 6. \(\square \)
3.3 Derivation of bounds for the consistency error
We next bound the quadrature error terms in (3.3). This portion of our argument closely follows the proof of Lemma 3.2 of [33] in many details, but we make some essential changes to account for the singularly perturbed nature of our model problem. Let \(E_T(g) = \int _T g \,\mathrm{d}x- (g, 1)_{h,T}\) be the quadrature error on T. We assume following [33] that the employed quadrature rule is exact for polynomials of degree q:
and stable in \(L_\infty \) in the following sense:
In addition, we assume that our quadrature rule is a linear functional of its argument. These assumptions are easily seen to be satisfied by for example the Gaussian quadrature rules widely employed in finite element codes.
Lemma 7
Let \(I_h^j\) be the Lagrange interpolant of degree j, and let \(\mu ^j\) and \(\lambda \) be piecewise constant functions defined by \(\mu ^j=\mu _T^j:=\Vert f_h-I_h^j f_h \Vert _{\infty \,; T}\) and \(\lambda =\lambda _T:= \widetilde{C}_f^{-1} \min \{1 ,\widetilde{\varepsilon }^{-1}h_T\} \) on each T. Let also \(\mathcal {T}_1 \cup \mathcal {T}_1'=\mathcal {T}\) and \(\mathcal {T}_2 \cup \mathcal {T}_2'=\mathcal {T}\) be arbitrary disjoint partitions of \(\mathcal {T}\). Then, under conditions [SubEquationDirect](3.8a),
Additionally, \(\mathcal {T}_i, \mathcal {T}_i'\), \( i=1,2\), may be chosen so that
Proof
As in the proof of Lemma 6 we may consider first the case \(\widetilde{C}_f=1\) and then obtain the general case by using the identifications \(\varepsilon , \widetilde{\varepsilon } \rightarrow \widetilde{\varepsilon }\), \(f, f_h \rightarrow f \widetilde{C}_f^{-1}, f_h \widetilde{C}_f^{-1}\), \(G \rightarrow \widetilde{G}\), and \(\widetilde{C}_f \rightarrow 1\) (so, in particular, \(\mu ^j\rightarrow \mu ^j \widetilde{C}_f^{-1}\) and \(\lambda \mu ^{q-1}\rightarrow \lambda \mu ^{q-1}\)). Thus let \(\widetilde{C}_f = 1\) and for notational simplicity \(\widetilde{\varepsilon }=\varepsilon \).
Note that \((f_h, G_h )-(f_h, G_h)_h=E_T(f_h\, G_h)\). Let \(G_{h,T}= \frac{1}{|T|} \int _T G_h \,\mathrm{d}x\). Then for \(T \in \mathcal {T}\),
where we used (3.8a) combined with \([I_h^q f_h]\, G_{h,T}\in \mathbb {P}_q\) and \(I_h^{q-1}f_h\,[ G_h -G_{h,T}]\in \mathbb {P}_q\) (the latter is due to \(G_{h,T}\) being elementwise constant and \(G_h\) elementwise linear).
For the first term in (3.11), we apply (3.8b) and the definition of \(G_{h,T}\) to find
Let \(T_0\) be any element containing the point x in (3.3), let \(\omega _{T_0}'\) be the patch of elements touching \(\omega _{T_0}\), and let \(\omega _{T_0}''\) be the patch of elements surrounding \(\omega _{T_0}'\). For any disjoint partition \(\mathcal {T}= \mathcal {T}_1 \cup \mathcal {T}_1'\) of the mesh, we thus have
Next, using (3.4) and then (2.3), (2.4a) and (2.4b), we get
Here we also used that \(\omega ''_{T_0}\subset B(x,c h_{T_0})\) and \(\omega _{T_0}\supset B(x,c' h_{T_0})\) for some c and \(c'\). Now we arrive at
Note that \( h_T^{2}\,\Vert \mu ^q\Vert _{\infty \,;T}\lesssim \Vert \mu ^q\Vert _{\frac{n}{2}\,;T}\). This observation is useful for \(T\in \omega _{T_0}'\cap \mathcal {T}_1'\). As there is a finite number of such T, and for each of them \(h_T\sim h_{T_0}\), one immediately gets \(h_{T_0}^2\Vert \mu ^q\Vert _{\infty \,;\omega _{T_0}'\cap \mathcal {T}_1'}\lesssim \Vert \mu ^q\Vert _{\frac{n}{2}\,;\omega _{T_0}'\cap \mathcal {T}_1'}\). So for the first term in (3.11) we finally have
The second term in (3.11) is treated similarly. We again apply (3.8b) and then an inverse inequality to get
Here the auxiliary function \(z_h:=\lambda _T^{-1}|G_h -G_{h,T}|\) on each T. For any disjoint partition \(\mathcal {T}= \mathcal {T}_2 \cup \mathcal {T}_2'\) of the mesh, we now have
Note that \(\lambda _T= \min \{1,\varepsilon ^{-1 } h_T\}\) implies \(\lambda _T^{-1}\le 1+ {\varepsilon } h_T^{-1} \). Using this observation as well as the definition and approximation properties of \(G_{h,T}\) and then (3.4) with \(k=j=0,1\) and \(p=1,\,\frac{n}{n-1}\), one gets
Combining this with (2.3), (2.4a), (2.4c) and (2.4d) yields
Here we also again used \(\omega ''_{T_0}\subset B(x,c h_{T_0})\) and \(\omega _{T_0}\supset B(x,c' h_{T_0})\). Thus
Note that \(h_T\Vert \lambda \mu ^{q-1}\Vert _{\infty \,;T}\lesssim \Vert \lambda \mu ^{q-1}\Vert _{n\,;T}\). As there is a finite number of such T that \(T\in \omega _{T_0}'\cap \mathcal {T}_2'\), and for each of them \(h_T\sim h_{T_0}\), so \(h_{T_0}\Vert \lambda \mu ^{q-1}\Vert _{\infty \,;\omega _{T_0}'\cap \mathcal {T}_2'}\lesssim \Vert \lambda \mu ^{q-1}\Vert _{n\,;\omega _{T_0}'\cap \mathcal {T}_2'}\). So for the second term in (3.11) we finally get
Combining this with (3.11) and (3.12), one gets the desired assertion (3.9). The bound (3.10) may be proved by noting that \(\Vert \mu ^q\Vert _{\infty \,;T} \lesssim h_T^{-2} \Vert \mu ^q\Vert _{\frac{n}{2} \, ;T}\), so
Choosing \(\mathcal {T}_1\) to be those elements for which \(h_T^{-2} \lesssim \varepsilon ^{-2} \ell _{h,x}\) and then performing a similar calculation for the term \(\Vert \lambda \mu ^{q-1}\Vert _{\infty \,;\mathcal {T}_2}\) completes the proof of (3.10). \(\square \)
3.4 Efficiency of the estimators
We first give some definitions. First, let \(\ell _h = \max _{x \in \Omega } \ell _{h,x}\), and
Recalling that \(f_h(x)=f(x, u_h)\), we let \(f_{h,T}\) be the \(L_2\) projection of \(f_h\) onto \(\mathbb {P}_{r-1}(T)\) for \(T \in \mathcal {T}\). In addition, we define the oscillation
In addition, we define an \({\varepsilon }\)-scaled Sobolev norm and corresponding negative norm. Let
When \(\widetilde{C}_f =1\) we write \(\Vert w\Vert _{2,1, \varepsilon \,;\omega }\) instead of \(\Vert w\Vert _{2,1,{\widetilde{\varepsilon }, 1 } \,;\omega }\), and similarly for \(\Vert w\Vert _{-2, \infty , { \varepsilon } \,;\omega } \).
Lemma 8
There holds for \(T \in \mathcal {T}\)
Here \(f=f(\cdot , u)\). In addition, if \(q \ge r-1\) we have
Proof
As in the proofs of the previous two lemmas we first consider the case \(\widetilde{C}_f=1\) and then rescale. When doing so it is helpful to note that \(\Vert f-f_h\Vert _{-\infty , 2, \widetilde{\varepsilon }, \widetilde{C}_f; \, T} = \Vert \widetilde{f}-\widetilde{f}_h\Vert _{-\infty , 2, \widetilde{\varepsilon }; \, T}\), where as before \(\widetilde{f}=f \widetilde{C}_f^{-1}\).
Assuming then that \(\widetilde{C}_f=1\), note first the residual identity
Here with slight abuse of notation we denote by \(\Delta u_h\) be the elementwise Laplacian of \(u_h\).
We first consider the volume residual \(\min \{1, \ell _h h_T^2 \varepsilon ^{-2}\} \Vert \varepsilon ^2 \Delta u_h -f_h\Vert _{\infty \,;T}\). By standard arguments, there exists \(b_T \in \mathbb {P}_{2n+r+1}\) such that \(b_T=0\) and \(\nabla b_T=0\) on \(\partial T\), \(\Vert b_T\Vert _{1 \,; T} \lesssim 1\), and
Subtracting \(\varepsilon ^2 \Delta u -f=0\) from \(\varepsilon ^2 \Delta u_h -f_{h}\), applying (3.19), subsequently integrating by parts while recalling \(\nabla b_T = 0\) on \(\partial T\), and finally employing inverse inequalities along with \(\Vert b_T\Vert _1 \lesssim 1\) yields
Applying the triangle inequality to find \(\Vert \varepsilon ^2 \Delta u_h -f_h\Vert _{\infty \,;T} \le \Vert \varepsilon ^2 \Delta u_h -f_{h,T}\Vert _{\infty \,;T}+ \Vert f_h-f_{h,T}\Vert _{\infty \,;T}\), using the above bounds (3.20) and (3.21), and calculating that \(\min \{1, \ell _h h_T^2 \varepsilon ^{-2}\} \Vert b_T\Vert _{2,1,\varepsilon \,;T} \lesssim \ell _h\) finally yields
which is bounded by the right-hand-side of (3.17), as desired.
We now bound the local edge residual \(\min \{ \varepsilon , \ell _h h_{\tilde{e}} \} \Vert \llbracket \nabla u_h \rrbracket \Vert _{\infty \,;\tilde{e} }\), where \(\tilde{e}=\tilde{T}_1 \cap \tilde{T}_2\), \(T_1, T_2 \in \mathcal {T}\), is an interior edge in the mesh (the edge residual disappears on boundary edges). The standard argument must be modified somewhat in order to maintain proper scaling with respect to \(\varepsilon \). If \(h_e \le \varepsilon \), we set \(e = \tilde{e}\) and \(T_i = \tilde{T}_i\), \(i=1,2\). Otherwise choose \(x \in e\) with \(\Vert \llbracket \nabla u_h \rrbracket \Vert _{\infty \,;\tilde{e}} = \llbracket \nabla u_h \rrbracket (x)\), and let \(e \subset \tilde{e}\) be a shape-regular \((n-1)\)-simplex of diameter \(\varepsilon \). In addition, let \(T_i \subset \tilde{T}_i\), \(i=1,2\), be shape-regular d-simplices such that \(e = T_1 \cap T_2\). Let \(\alpha = \mathrm{diam} (e) = \min \{ h_{\tilde{e}}, \varepsilon \} \).
By standard arguments, there is an edge bubble function \(b_e \in \mathbb {P}_{4n+r-4}(T_1 \cup T_2)\) with \(\Vert b_e\Vert _{1 \,;e} \lesssim 1\) and \(\Vert b_e\Vert _{1 \,; T_1 \cap T_2} \lesssim \alpha \) such that
Employing (3.19), integrating by parts, and again employing \(\varepsilon ^2 \Delta u -f=0\) yields
A short calculation yields \(\min \{ \varepsilon , h_e \ell _h \} \Vert b_e\Vert _{2,1,\varepsilon \,;T_i} \lesssim \varepsilon ^2 \ell _h\), so
Combining (3.25) with (3.22) yields (3.17).
We finally investigate efficiency of the quadrature (consistency) estimators. Note that for \(q \ge r-1\), on any element T we have \(I_h^{q} \Delta u_h = I_h^{q-1} \Delta u_h = \Delta u_h\) and so \(f_h -I_h^q f_h = (Id-I_h^q) (f_h -\varepsilon ^2 \Delta u_h)\), where Id is the identity operator. Because the Lagrange interpolant \(I_h^j\) is \(L_\infty \)-stable, we thus have for \(q \ge r-1\)
Employing Hölder’s inequality yields
Similarly,
Combining (3.20) and (3.21) with (3.26) and then with (3.27) and (3.28) yields () and (3.18a 3.18b), respectively, after noting that \(\Vert b_T\Vert _{2, 1, \varepsilon \,; T} \lesssim 1+ \varepsilon ^2 h_T^{-2}\) (3.18c) follows after a similar argument. \(\square \)
3.5 Choosing mesh partitions for the consistency estimators
In this subsection we address how to make a practical choice of the mesh partitions \(\mathcal {T}_1 \cup \mathcal {T}_2\) and \(\mathcal {T}_1' \cup \mathcal {T}_2'\) appearing in the consistency estimators in Lemma 7. The weighting of the quadrature estimators in (3.10) is essentially the same as that in \(\eta _\infty \), thus the efficiency estimate (3.18c). As noted in [33], however, the efficiency bound for the quadrature estimator cannot be used to obtain a meaningful global lower bound for the error since the quadrature estimators accumulate over the mesh in a different fashion than do the residual estimators. On the other hand, we demonstrate the existence of a computationally convenient partition that is quasi-optimal in the sense that choosing \(\mathcal {T}_i\) and \(\mathcal {T}_i'\) differently cannot lower the achieved estimate by more than a factor of 2. Our numerical experiments below confirm that the overall bound for the quadrature error sometimes is substantially reduced if this choice of \(\mathcal {T}_i\), \(\mathcal {T}_i'\) is made instead of that leading to (3.10). Thus there is never a strong practical advantage to employing (3.10) and sometimes a strong practical disadvantage. We include (3.10) mainly because it yields a local efficiency estimate that mirrors that for the residual terms.
We next give our partitioning algorithm. For simplicity of presentation we assume \(\widetilde{C}_f=1\) in this discussion; obvious modifications can be made to obtain the general case. We choose \(\mathcal {T}_1, \mathcal {T}_1'\) by the following simple algorithm. First index \(\mathcal {T}\) so that \(\mu _{T_1}^q \ge \mu _{T_2}^q \ge \cdots \ge \mu _{T_N}^q\), where \(N =\# \mathcal {T}\). Then take \(\mathcal {T}_1=\{T_i\}_{j \le i \le N}\) and \(\mathcal {T}_1'=\mathcal {T}{\setminus } \mathcal {T}_1\), where j is the maximal index so that \(\mathcal {T}_1\), \(\mathcal {T}_1'\) thus defined satisfy \(\varepsilon ^{-2} \ell _h \Vert \mu ^q\Vert _{\frac{n}{2} \, ; \mathcal {T}_1'} =\varepsilon ^{-2} \ell _h ( \sum _{i=1}^{j-1} |T| {\mu ^q_{T_i}}^{n/2})^{2/n} < \mu ^q_{T_{j-1}}\). A simple modification leads to a similar algorithm for finding \(\mathcal {T}_2, \mathcal {T}_2'\). We let
and similarly for \(\mu ^{q-1}_\mathcal {T}\). This algorithm for partitioning \(\mathcal {T}\) can be efficiently implemented and did not add significant computational overhead to our computations.
The above choice of \(\mathcal {T}_1\) and \(\mathcal {T}_1'\) is quasioptimal in the sense that \(\Vert \mu ^q\Vert _{\infty \,; \mathcal {T}_1} + \varepsilon ^{-2} \ell _h \Vert \mu ^q\Vert _{\frac{n}{2} \,; \mathcal {T}_1'} \le 2 ( \Vert \mu ^q\Vert _{\infty \,; \tilde{\mathcal {T}}_1} + \varepsilon ^{-2} \ell _h \Vert \mu ^q\Vert _{\frac{n}{2} \,; \tilde{\mathcal {T}}_1'})\) for any other partition \(\mathcal {T}= \tilde{\mathcal {T}}_1 \cup \tilde{\mathcal {T}}_1'\). To see this, first note that since \(\mu ^q\) accumulates over \(\mathcal {T}_1\) in the maximum norm, \(\mu ^q_{T_i} \in \mathcal {T}_1 \Rightarrow \mu ^q_{T_k} \in \mathcal {T}_1\) whenever \(k \le i\) for the optimal choice of \(\mathcal {T}_1\). Defining j as above, we have for \(k<j\)
For \(k>j\), we have
This proves the desired assertion.
3.6 Summary of results and discussion
We first define the global residual estimator
We also summarize our major notation in Table 1 below in order to simplify the task of reading our results and numerical experiments.
Combining the results of the previous subsections yields the following theorem.
Theorem 2
For arbitrary disjoint decompositions \(\mathcal {T}= \mathcal {T}_1 \cup \mathcal {T}_2\) and \(\mathcal {T}= \mathcal {T}_1' \cup \mathcal {T}_2'\),
Additionally, \(\mathcal {T}_i, \mathcal {T}_i'\), \( i=1,2\), may be chosen so that
Alternatively, making a quasi-optimal choice of \(\mathcal {T}_i\), \(\mathcal {T}_i'\) as in Sect. 3.5 yields
with no other choice of \(\mathcal {T}_i\), \(\mathcal {T}_i'\) lowering the magnitude of the quadrature estimator by a factor of more than two.
For \(T \in \mathcal {T}\) there also holds the efficiency estimate
In addition, if \(q \ge r-1\) we have
In order to provide context for Theorem 2, we first comment on the relationship between the residual and the error. The residual \(\mathcal {R}_h\) is given by
Lemma 5 may be rephrased as \(\Vert u-u_h\Vert _{\infty \,; \Omega } \lesssim |\langle \mathcal {R}_h, G \rangle |\), whereas Lemma 6 and Lemma 7 together provide a computable bound for \(\langle \mathcal {R}_h, G \rangle \) in terms of residual and quadrature estimators. Typically in residual-type a posteriori error estimation the error is bounded by a dual Sobolev norm of the residual, such as for example \(\Vert \mathcal {R}_h\Vert _{H^{-1}(\Omega )}\) in the case of energy norm bounds. However, such a simple relationship is not possible in the case of maximum norm error estimates. In [33], the maximum error in a finite element approximation to \(-\Delta u + f(x,u)=0\) is related to \(\Vert \mathcal {R}_h\Vert _{-2, \infty , 1,1 \,;\Omega }\) by using a regularized Green’s function that lies in \(W_1^2(\Omega )\). However, an additional “regularization penalty” term arises, and the method used to bound it requires that \(\partial \Omega \) be Lipschitz. We circumvent this issue by directly employing the Green’s function as in [11], but we thereby complicate the relationship between the error and \(\mathcal {R}_h\).
Note next that following the discussion in [33], the term \(\Vert f-f_h\Vert _{-2, \infty , \widetilde{\varepsilon }, \widetilde{C}_f \,;\Omega }\) may properly be regarded as part of the error notion bounded by our estimates. Integrating by parts in (3.38) easily yields
Both terms in (3.39) are bounded by the right hand side of (3.33); the arguments needed to prove it are modest simplifications of those used to prove (3.33). Heuristically, one can regard (2.3) and (2.4e) as stating that the Green’s function G almost satisfies \(\Vert G\Vert _{2, 1, \widetilde{\varepsilon }, \widetilde{C}_f \, ;\Omega } \lesssim 1\). Thus the terms of \( \Vert f-f_h\Vert _{-2, \infty , \widetilde{\varepsilon }, \widetilde{C}_f \,;\Omega }\) which appear in the above efficiency estimates are in fact bounded by the estimators at hand, and their appearance is quite natural.
In contrast to [33], we observe that we may include factors of \(\Vert f-f_h\Vert _{\infty }\) (with proper weights) in our efficiency estimates instead of factors of \(\Vert f-f_h\Vert _{-2, \infty , \widetilde{\varepsilon }, \widetilde{C}_f }\), as in (3.36). These terms may be simply folded into the term \(\Vert u-u_h\Vert _{\infty }\) if \(f_u\) exists and is uniformly bounded, as when we for example consider the linear model problem \(f(x,u)= u -f(x)\). Note as well that \(\Vert f-f_h\Vert _{\infty }\) is multiplied by \(\min \{\widetilde{C}_f^{-1} , \varepsilon ^{-2} h_T^2 \ell _h \}\) in (3.36) and is thus asymptotically negligible. Thus bounding \(f-f_h\) in \(L_\infty \) is not always feasible, but when possible doing so gives the term a more concrete form.
4 Numerical experiments
4.1 Experimental setup
Our numerical experiments were run using a MATLAB-based code built on top of the iFEM library [8]. All tests were run using linear Lagrange elements on two-dimensional domains and a standard adaptive FEM iteration. Nonlinear problems were solved using a damped Newton iteration. Recalling the definitions in Table 1, our overall error estimator is \(\eta =\eta _\mathcal {T}^\infty + \mu ^q_{\mathcal {T}_1} + \mu ^q_{\mathcal {T}_1'} + \mu ^{q-1}_{\mathcal {T}_2} + \mu ^{q-1}_{\mathcal {T}_2'}\). Here \(\eta \) is a sum of five different estimators some of which accumulate differently over the mesh and so an integrated marking strategy based on a single elementwise indicator is not possible. For each of the five estimators, we marked for refinement in each AFEM iteration with a maximum strategy using the corresponding indicators if the given estimator counted for at least 10 % of the overall estimator \(\eta \). We used a similar strategy, but with three components instead of five, when employing the estimators and indicators from [33] for comparison purposes. Also, we used a standard Gaussian quadrature rule of degree \(q=3\) in all of our experiments below. The rule has barycentric quadrature points (1 / 3, 1 / 3, 1 / 3), (0.6, 0.2, 0.2), (0.2, 0.6, 0.2), and (0.2, 0.2, 0.6) with weights \(-27/48\), 25 / 48, 25 / 48, and 25 / 48 and clearly satisfies the assumptions of Sect. 3.3.
4.2 Experiment 1: advantages of \(\varepsilon \)-robust estimators
To demonstrate the advantages of using an \(\varepsilon \)-robust error estimator we first take \(\Omega \) to be the unit square and define
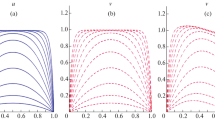
\(u_1\) has prototypical boundary layers along the portions of \(\Omega \) abutting the \(x-\) and \(y-\) axes. Let also \(u_2(x,y)=0.01 \sin (100 \pi x) \sin (100 \pi y)\) and \(u=u_1+u_2\), and solve \(-\varepsilon ^2 \Delta u + u - g=0\) with g defined in the obvious fashion. Also, we take \(\varepsilon ^2=10^{-6}\). In Fig. 1 we display the decrease in errors and estimators obtained by marking with the non-robust estimators (1.4) derived from [33] and then with the \(\varepsilon \)-robust estimator derived from (3.33). The corresponding quadrature estimators are included in both cases but do not play a prominent role in driving marking and refinement.
In Fig. 1 we observe that the non-robust estimator overestimates the actual error by a factor of about \(10^4\) at the beginning of the computation; this overestimation is \(\varepsilon \)-dependent and becomes more pronounced as \(\varepsilon \rightarrow 0\). In addition, the error decrease in the adaptive computation employing the non-robust estimators also is significantly slower than that observed when using robust estimators. This is because the estimators in (1.4) initially direct too much refinement towards regions of \(\Omega \) removed from the boundary layers; little refinement is needed in these regions until the error reaches the scale of the oscillations, which is about \(10^{-2}\). In other computations we generally observed that the ability of the robust and non-robust estimators to efficiently direct adaptive refinement was not nearly as dissimilar as here. The widespread fine-scale oscillations in this example helped to highlight the tendency of the non-robust estimators to overestimate local residual contributions of elements T for which \(h_T \gg \varepsilon \). Poor efficiency indices for the non-robust indicators were however consistently observed across a range of examples in the pre-asymptotic range.
Comparison of decrease in maximum errors and estimators when marking using our estimators (with subscript “DK”) and with those derived from [33] (with subscript “NSSV”)
4.3 Experiment 2: the effects of \(C_f\)
In order to illustrate the robustness of our estimates with respect to \(C_f\) we solve the simple linear problem \(-\varepsilon ^2 \Delta u + C_f u=g\) while varying \(\varepsilon \) and \(C_f\). First we take \(\varepsilon ^2=10^{-6}\) and let \(C_f=1, 10^{-2}, 10^{-4}, 10^{-6}\). We let \(u=u_1+u_3\), where \(u_1\) is given in (4.1) but with \(\varepsilon = 10^{-6}/C_f\), and \(u_3(x,y)=2 \sin (4 \pi x) \sin (4 \pi y)\). In Figure 2 we plot the observed error \(\Vert u-u_h\Vert _{\infty \,; \Omega }\) versus degrees of freedom for the given values of \(C_f\). We also plot the efficiency indices given by \(\eta /\Vert u-u_h\Vert _{\infty ; \, \Omega }\). Both the efficiency indices and the ability of the generated algorithm to direct adaptive refinement are essentially stable as \(C_f\) is varied.
4.4 Experiment 3: effects of the quadrature indicators
In order to illustrate the effects of the quadrature estimators we consider the test problem \(-\varepsilon ^2\triangle u + u = f\) on the unit square \(\Omega =(0,1) \times (0,1)\), where \(f(x,y)=2x\) if \(x^2+y^2<1/4\) and \(f(x,y)=1\) otherwise. f is thus discontinuous across \(x^2+y^2=1/4\), except at \((x,y)=(1/2, 0)\). The solution u is unknown but exhibits sharp interior layers across \(x^2+y^2=1/4\) and at the boundary for \(\varepsilon \ll 1\), as is confirmed in the computed solutions for \(\varepsilon ^2=1\) and \(\varepsilon ^2=10^{-4}\) displayed in Fig. 3.
Some elements in any triangular mesh are cut by the curve \(x^2+y^2=1/4\) across which f is discontinuous. Thus \(\Vert \mu ^q\Vert _{\infty \,;\mathcal {T}}\) is bounded away from 0 uniformly, since f cannot be approximated to arbitrary accuracy in \(L_\infty \) by continuous functions. On the other hand, f is affine and thus the quadrature error and indicators 0 on any element not touching this curve. In Fig. 4 we depict the decrease in various estimators when \(\varepsilon ^2=10^{-4}\). In the left graph we depict the decrease in the residual estimator \(\eta _\mathcal {T}^\infty \) and both quadrature estimators \(\mu _\mathcal {T}^{q}\) and \(\mu _\mathcal {T}^{q-1}\). Here the quadrature estimator \(\mu _\mathcal {T}^q\) dominates the overall error estimate and drives refinement. While initially overlapping with \(\mu _\mathcal {T}^q\), \(\mu _\mathcal {T}^{q-1}\) begins asymptotic decrease much sooner than does \(\mu _\mathcal {T}^q\) due to the presence of the factor \(\lambda \) in its definition in Lemma 7. In the right graph we illustrate the composition of \(\mu _\mathcal {T}^q\). Here \(\mu ^q_\Sigma =\Vert \min \{h_T^{-2}, \varepsilon ^{-2} \ell _h \} \mu ^q\Vert _{\frac{n}{2} \, ; \mathcal {T}}\) as in (3.10). We observe that initially \(\mu _\mathcal {T}^q=\Vert \mu ^q\Vert _{\infty \,; \Omega }\), that is, \(\mathcal {T}_1=\mathcal {T}\) in the definition of \(\mu _\mathcal {T}^q\). Our partitioning algorithm eventually begins adding elements to \(\mathcal {T}_1'\), and initially we observe that \(\Vert \mu ^q\Vert _{\infty \,; \Omega } < \mu _\mathcal {T}^q \le 2 \Vert \mu ^q\Vert _{\infty \,;\Omega }\). Between roughly \(10^5\) and \(10^6\) DOF the partitioned quadrature estimator \(\mu _\mathcal {T}^q\) is smaller than either \(\mu ^q_\Sigma \) or \(\Vert \mu ^q\Vert _{\infty \,; \Omega }\), and then asymptotically \(\mu _\mathcal {T}^q = \mu ^q_\Sigma \), that is, \(\mathcal {T}_1'=\mathcal {T}\). The corresponding graphs for the case \(\varepsilon ^2=1\) are displayed in Fig. 5. There we observe that \(\mu _\mathcal {T}^q\) and \(\mu ^q_\Sigma \) are essentially the same size, and much smaller than \(\Vert \mu ^q\Vert _{\infty \,; \Omega }\), over the whole range of DOF in the calculation. Combining data from these two cases, we conclude that our partitioned quadrature estimator conveniently and robustly estimates the consistency error.
4.5 Experiment 4: nonlinearity of Poisson-Boltzmann type
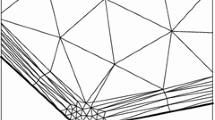
Singularly perturbed problems of Poisson-Boltzmann type have been studied in the literature; cf. [16]. As a simple prototype, we considered the problem \(-\varepsilon ^2\triangle u + \sinh u = f(x,y)\) with \(\varepsilon ^2=10^{-6}\). We first took \(\Omega \) to be the unit square and \(u=u_1+u_3\) as in Experiment 2 above. Our AFEM performs well on this example, as shown in the left graph in Fig. 6. We then took \(\Omega \) to be a protypical L-shaped domain so that one can expect a singularity to develop at the reentrant corner, and \(f(x,y)=1+x^3\). Estimator decrease is shown in the right graph in Fig. 6, and the computed solution and adaptively generated mesh are shown in Fig. 7.
References
Abramowitz, M., Stegun, I.A. (eds.): Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover Publications Inc, New York (1992). (Reprint of the 1972 edition)
Ainsworth, M., Babuška, I.: Reliable and robust a posteriori error estimating for singularly perturbed reaction-diffusion problems. SIAM J. Numer. Anal. 36, 331–353 (1999)
Ainsworth, M., Vejchodský, T.: Fully computable robust a posteriori error bounds for singularly perturbed reaction-diffusion problems. Numer. Math. 119, 219–243 (2011)
Andreev, V.B., Kopteva, N.: Pointwise approximation of corner singularities for a singularly perturbed reaction-diffusion equation in an \(L\)- shaped domain. Math. Comput. 77, 2125–2139 (2008)
Blatov, I.A.: Galerkin finite element method for elliptic quasilinear singularly perturbed boundary problems. I. Differ. Uravn. 28, 1168–1177 (1992) (translation Differ. Equ. 28, 931–940 (1992))
Brézis, H., Strauss, W.A.: Semi-linear second-order elliptic equations in \(L^{1}\). J. Math. Soc. Jpn. 25, 565–590 (1973)
Chadha, N.M., Kopteva, N.: Maximum norm a posteriori error estimate for a 3d singularly perturbed semilinear reaction-diffusion problem. Adv. Comput. Math. 35, 33–55 (2011)
Chen, L.: iFEM: An Innovative Finite Element Method Package in Matlab, tech. rep., University of California-Irvine, California (2009)
Clavero, C., Gracia, J.L., O’Riordan, E.: A parameter robust numerical method for a two dimensional reaction-diffusion problem. Math. Comput. 74, 1743–1758 (2005)
Dari, E., Durán, R.G., Padra, C.: Maximum norm error estimators for three-dimensional elliptic problems. SIAM J. Numer. Anal. 37, 683–700 (2000). (electronic)
Demlow, A., Georgoulis, E.: Pointwise a posteriori error control for discontinuous Galerkin methods for elliptic problems. SIAM J. Numer. Anal. 50, 2159–2181 (2012)
Demlow, A., Leykekhman, D., Schatz, A.H., Wahlbin, L.B.: Best approximation property in the \({W}_\infty ^1\) norm for finite element methods on graded meshes. Math. Comput. 81, 743–764 (2012)
Duong, X.T., Hofmann, S., Mitrea, D., Mitrea, M., Yan, L.: Hardy spaces and regularity for the inhomogeneous Dirichlet and Neumann problems. Rev. Mat. Iberoam. 29, 183–236 (2013)
Durán, R.G.: A note on the convergence of linear finite elements. SIAM J. Numer. Anal. 25, 1032–1036 (1988)
Eriksson, K.: An adaptive finite element method with efficient maximum norm error control for elliptic problems. Math. Models Methods Appl. Sci. 4, 313–329 (1994)
Fellner, K., Kovtunenko, V.: A singularly Perturbed Nonlinear Poisson-Boltzmann Equation: Uniform and Super-Asymptotic Expansions. Tech. rep., SFB F 32/Universität Graz (2014)
Gilbarg, D., Trudinger, N.S.: Elliptic Partial Differential Equations of Second Order, 2nd edn. Springer-Verlag, Berlin (1998)
Grinberg, G.A.: Some topics in the mathematical theory of electrical and magnetic phenomena (Nekotorye voprosy matematicheskoi teorii elektricheskih i magnitnyh yavlenii). USSR Academy of Sciences, Leningrad (1943). (Russian)
Guzmán, J., Leykekhman, D., Rossmann, J., Schatz, A.H.: Hölder estimates for Green’s functions on convex polyhedral domains and their applications to finite element methods. Numer. Math. 112, 221–243 (2009)
Haverkamp, R.: Eine Aussage zur \(L_{\infty }\)- Stabilität und zur genauen Konvergenzordnung der \(H^{1}_{0}\)- Projektionen. Numer. Math. 44, 393–405 (1984)
Jerison, D., Kenig, C.E.: The inhomogeneous Dirichlet problem in Lipschitz domains. J. Funct. Anal. 130, 161–219 (1995)
Juntunen, M., Stenberg, R.: A residual based a posteriori estimator for the reaction-diffusion problem. C. R. Math. Acad. Sci. Paris 347, 555–558 (2009)
Juntunen, M., Stenberg, R.: Analysis of finite element methods for the Brinkman problem. Calcolo 47, 129–147 (2010)
Kopteva, N.: Maximum norm a posteriori error estimate for a 2d singularly perturbed reaction-diffusion problem. SIAM J. Numer. Anal. 46, 1602–1618 (2008)
Kopteva, N.: Maximum-norm a posteriori error estimates for singularly perturbed reaction-diffusion problems on anisotropic meshes. SIAM J. Numer. Anal. (2015, to appear). http://www.staff.ul.ie/natalia/pdf/rd_ani_R1_mar15.pdf
Kopteva, N., Linß, T.: Maximum norm a posteriori error estimation for parabolic problems using elliptic reconstructions. SIAM J. Numer. Anal. 51, 1494–1524 (2013)
Kreuzer, C., Siebert, K.G.: Decay rates of adaptive finite elements with Dörfler marking. Numer. Math. 117, 679–716 (2011)
Kunert, G.: Robust a posteriori error estimation for a singularly perturbed reaction-diffusion equation on anisotropic tetrahedral meshes. Adv. Comput. Math. 15, 237–259 (2001)
Kunert, G.: A posterior \(H^1\) error estimation for a singularly perturbed reaction diffusion problem on anisotropic meshes. IMA J. Numer. Anal. 25, 408–428 (2005)
Leykekhman, D.: Uniform error estimates in the finite element method for a singularly perturbed reaction-diffusion problem. Math. Comput. 77(261), 21–39 (2008)
Lin, R., Stynes, M.: A balanced finite element method for singularly perturbed reaction-diffusion problems. SIAM J. Numer. Anal. 50, 2729–2743 (2012)
Nochetto, R.H.: Pointwise a posteriori error estimates for elliptic problems on highly graded meshes. Math. Comput. 64, 1–22 (1995)
Nochetto, R.H., Schmidt, A., Siebert, K.G., Veeser, A.: Pointwise a posteriori error estimates for monotone semilinear problems. Numer. Math. 104, 515–538 (2006)
Nochetto, R.H., Siebert, K.G., Veeser, A.: Pointwise a posteriori error control for elliptic obstacle problems. Numer. Math. 95, 163–195 (2003)
Nochetto, R.H., Siebert, K.G., Veeser, A.: Fully localized a posteriori error estimators and barrier sets for contact problems. SIAM J. Numer. Anal. 42, 2118–2135 (2005). (electronic)
Rannacher, R., Scott, R.: Some optimal error estimates for piecewise linear finite element approximations. Math. Comput. 38, 437–445 (1982)
Schatz, A.H., Wahlbin, L.B.: On the finite element method for singularly perturbed reaction-diffusion problems in two and one dimensions. Math. Comput. 40, 47–89 (1983)
Schatz, A.H., Wahlbin, L.B.: Interior maximum-norm estimates for finite element methods, Part II. Math. Comput. 64, 907–928 (1995)
Shishkin, G.I.: Grid approximation of singularly perturbed elliptic and parabolic equations. Ur. O Ran, Ekaterinburg (1992). (Russian)
Stevenson, R.P.: The uniform saturation property for a singularly perturbed reaction-diffusion equation. Numer. Math. 101, 355–379 (2005)
Tikhonov, A.N., Samarskiĭ, A.A.: Equations of Mathematical Physics. Dover Publications Inc, New York (1990). Translated from the Russian by A.R.M. Robson and P. Basu, Reprint of the 1963 translation
Verfürth, R.: Robust a posteriori error estimators for a singularly perturbed reaction-diffusion equation. Numer. Math. 78, 479–493 (1998)
Author information
Authors and Affiliations
Corresponding author
Additional information
The first author was partially supported by National Science Foundation Grants DMS-1016094 and DMS-1318652. The second author was partially supported by DAAD Grant A/13/05482 and Science Foundation Ireland Grant SFI/12/IA/1683.
Appendix A: Sharpness of log factors
Appendix A: Sharpness of log factors
In this section we prove that there are cases in which the logarithmic factor in the a posteriori upper bound (1.3) is necessary. Using an idea of Durán [14], we first prove a priori upper bounds and a posteriori upper and lower bounds for \(u-u_h\) in a modified BMO norm in the case that \(\Omega \) is a convex polygonal domain. These estimates are essentially the same as our \(L_\infty \) bounds, but with no logarithmic factors present. The proof is completed by employing the counterexample of Haverkamp [20] showing that a similar logarithmic factor is necessary in \(L_\infty \) a priori upper bounds for piecewise linear finite element methods. Note that our counterexample is only valid for piecewise linear elements. Logarithmic factors are not present in standard a priori \(L_\infty \) bounds for elements of degree two or higher on quasi-uniform grids, and it remains unclear whether there are cases for which they are necessary in the corresponding \(L_\infty \) a posteriori bounds. In addition, both the result of Durán [14] and ours below only consider Poisson’s problem and not the broader class of problems described in (1.1).
1.1 A.1: Adapted Hardy and BMO spaces
We begin by describing operator-adapted BMO and Hardy spaces, following [13]. Let \(-\Delta \) denote the Dirichlet Laplacian on \(\Omega \), i.e., the Laplacian with domain restricted to functions which vanish on \(\partial \Omega \). Let
The space \(\mathrm{bmo}_\Delta (\Omega )\) then consists of functions \(v \in L_2(\Omega )\) for which \(\Vert v\Vert _{\mathrm{bmo}_\Delta (\Omega )} <\infty \). Note that the resolvent \((I-r^2 \Delta )^{-1}\) replaces the usual average over B in the definition of BMO. We also define an operator-adapted atomic Hardy space \(h_\Delta ^1\) which is dual to \(\mathrm{bmo}_\Delta \). A bounded, measurable function a supported in \(\Omega \) is a local atom if there is a ball B centered in \(\Omega \) with radius \(r<2 \mathrm{diam}(\Omega )\) such that \(\Vert a\Vert _{2; \, \mathbb {R}^n} \le |B \cap \Omega |^{-1/2}\) and either \(r>1\), or \(r \le 1\) and there exists b in the domain of the Dirichlet Laplacian such that \(a = -\Delta b\), \(\mathrm{supp}(b) \cup \mathrm{supp} (-\Delta b) \subset B \cap \overline{\Omega }\), and
An atomic representation of w is a series \(w = \sum _{j} \lambda _j a_j\), where \(\{\lambda _j\}_{j=0}^\infty \in \ell ^1\), each \(a_j\) is a local atom, and the series converges in \(L_2(\Omega )\). We then define the norm
The Hardy space \(h_\Delta ^1(\Omega )\) is the completion in \((\mathrm{bmo}_\Delta (\Omega ))^*\) of the set of functions having an atomic representation with respect to the metric induced by the above norm. In addition, \(\mathrm{bmo}_\Delta \) is the dual space of \(h_\Delta ^1\) in the sense that if \(w= \sum _{j=0}^\infty \lambda _j a_j \in h_\Delta ^1(\Omega )\), then
is a well-defined and continuous linear functional for each \(v \in \mathrm{bmo}_\Delta (\Omega )\) whose norm is equivalent to \(\Vert v\Vert _{\mathrm{bmo}_\Delta (\Omega )}\). In addition, each continuous linear functional on \(h_\Delta ^1(\Omega )\) has this form (cf. Theorem 3.11 of [13]).
We finally list an essential regularity result; cf. Theorem 4.1 of [13].
Lemma 9
Let \(\Omega \) be a bounded, simply connected, semiconvex domain in \(\mathbb {R}^n\), and let G be the Dirichlet Green’s function for \(-\Delta \). Let \(\mathbb {G}_\Delta \) be the corresponding Green operator given by \(\mathbb {G}(v)(x) = \int _\Omega G(x,y) v(y) \, \mathrm{d}y\). Then the operators \(\frac{\partial \mathbb {G}}{\partial x_i \partial x_j}\) are bounded from \(h_\Delta ^1(\Omega )\) to \(L_1(\Omega )\). In other terms, given \(u \in H_0^1(\Omega )\) with \(-\Delta u \in h_\Delta ^1(\Omega )\), we have \(u \in W_1^2(\Omega )\) with
We remark that the above regularity result does not in general hold on nonconvex Lipschitz (or even \(C^1\)) domains; cf. Theorem 1.2.b of [21]. It is not clear whether (5.5) holds on nonconvex polyhedral domains, but a different approach to the analysis than that taken in [13] would be in any case needed to establish this. Such a result would allow us to extend a posteriori estimates in \(bmo_{\Delta }\) that we obtain below for convex polyhedral domains to general polyhedral domains, which would be desirable since the corresponding \(L_\infty \) estimates also hold on general polyhedral domains. However, for our immediate purpose of providing a counterexample it suffices to consider convex domains.
1.2 A.2: A priori and a posteriori estimates in \(bmo_{\Delta }\)
In [14], Durán proved that given a smooth convex domain \(\Omega \subset \mathbb {R}^2\) and piecewise linear finite element solution \(u_h\) on a quasi-uniform mesh of diameter h, \(\Vert u-u_h\Vert _{\mathrm{BMO}(\Omega )} \lesssim h^2 |u|_{W_\infty ^2(\Omega )}\). Here BMO\((\Omega )\) is the classical BMO space; cf. [14] for a definition. We prove the same on convex polyhedral domains in arbitrary space dimension, but with BMO replaced by its operator-adapted counterpart. For notational simplicity we also consider only piecewise linear finite element spaces below, but our a priori and a posteriori bounds easily generalize to arbitrary polynomial degree.
Lemma 10
Assume that \(\Omega \subset \mathbb {R}^n\) is convex and polyhedral, and \(u \in W_\infty ^2(\Omega )\). Let also \(u_h\) be the piecewise linear finite element approximation to u with respect to a quasi-uniform simplicial mesh of diameter h. Then
Proof
Let \(\sum _{j=0}^k \lambda _j a_j = z \in h_\Delta ^1(\Omega )\) with k arbitrary but finite. Such functions are dense in \(h_\Delta ^1\), so to prove our claim it suffices by the duality of \(\mathrm{bmo}_\Delta \) and \(h_\Delta ^1\) to show that \(\int _\Omega (u-u_h) z \, \mathrm{d}x \lesssim h^2 |u|_{2, \infty ; \, \Omega } \Vert z\Vert _{h_\Delta ^1(\Omega )}\). Let \(-\Delta v=z\) with \(v=0\) on \(\partial \Omega \). Letting \(I_h v\) be a Scott-Zhang interpolant of v, we have
The proof is completed by recalling the \(W_\infty ^1\) error estimate \(\Vert u-u_h\Vert _{1, \infty ; \, \Omega } \lesssim h |u|_{2, \infty ; \, \Omega }\); cf. [12, 19, 36]. \(\square \)
We next prove a posteriori upper and lower bounds for \(\Vert u-u_h\Vert _{\mathrm{bmo}_\Delta (\Omega )}\). Note that the a posteriori lower bound for the error is critical in establishing that the logarithmic factor in (1.3) is necessary.
Lemma 11
Assume that \(\Omega \subset \mathbb {R}^n\) is convex and polyhedral. Let also \(u_h\) be the piecewise linear finite element approximation to u with respect to a shape-regular simplicial mesh, where \(u \in H_0^1(\Omega )\) with \(-\Delta u = f \in L_\infty (\Omega )\). Then
Here \(f_T = \frac{1}{|T|} \int _T f \,\mathrm{d}x\).
Proof
The upper bound for \(\Vert u-u_h\Vert _{\mathrm{bmo}_\Delta (\Omega )}\) follows by first noting that \(h_T^2 \Vert f-f_T \Vert _{\infty ; \, T} \le h_T^2 \Vert f+ \Delta u_h\Vert _{\infty ; \, T}\) and then employing a duality argument precisely as in the preceding lemma; one must only substitute standard residual error estimation techniques for the a priori error analysis techniques above. In order to prove the lower bound we employ a discrete \(\delta \)-function; cf. (A.5) of [38]. Given \(x_0 \in T \in \mathcal {T}_h\), let \(\delta _{x_0}\) be a smooth, fixed function compactly supported in T such that \((v_h, \delta _{x_0})=v_h(x_0)\) for all \(v_h \in S_h\). \(\delta _{x_0}\) may be constructed to satisfy \(\Vert \delta _{x_0}\Vert _{m, p ; \, T} \lesssim h_T^{-m-n(1-\frac{1}{p})}\) with constant independent of \(x_0\). A short computation shows that \(-c h_T^2 \Delta \delta _{x_0}\) is an atom satisfying (5.2) with the required value of c and the constant in \(r \simeq h_T\) independent of essential quantities. Thus
To bound \(h_T \Vert \llbracket \nabla u_h \rrbracket \Vert _{\infty ; \, e}\) on a face e of the triangulation, let \(e = T_1 \cap T_2\) with \(T_1,T_2 \in \mathcal {T}_h\). Modest modification of the arguments in (A.5) of [38] yields that for \(x_0 \in e\) and fixed polynomial degree \(r-1\), there is a function \(\widetilde{\delta }_{x_0}\) compactly supported in \(\mathcal {T}_1 \cup T_2\) such that \(v_h (x_0) = \int _e \widetilde{\delta }_{x_0} v_h \, \mathrm{d}s\) for \(v_h \in \mathbb {P}_{r-1}\), and in addition, \(\Vert \widetilde{\delta }_{x_0} \Vert _{m,p; \,T_1 \cup T_2} \lesssim h_T^{-m+1+n (1-\frac{1}{p})}\). Similar to above, \(-c h_T \Delta \widetilde{\delta }_{x_0}\) is an atom with \(r \simeq h_T\). Thus
Combining (5.9) and (5.10) completes the proof. \(\square \)
1.3 A.3: Necessity of logarithmic factors
In this section we show that logarithmic factors are necessary in maximum-norm a posteriori upper bounds at least in the case of piecewise linear function spaces in two space dimensions. In [20], Haverkamp showed that given a convex polygonal domain \(\Omega \) and quasi-uniform mesh of size h, there exists u (which depends on h) such that \(\Vert u-u_h\Vert _{ \infty ; \, \Omega } \gtrsim h^2 \log h^{-1} |u|_{2, \infty ; \, \Omega }\). Given such a u, employing this result, (1.3), and the preceding two lemmas yields
We have thus proved the following lemma.
Lemma 12
The bound
does not in general hold if the term \(\log \underline{h}^{-1}\) is omitted.
We now also remark on two further important consequences of Lemma 11. First, the standard a priori and a posteriori upper bounds for \(L_\infty \) are
Lemma 12 establishes that the logarithmic factor in the first inequality above is necessary. Our estimates also show that the logarithmic factor in the second inequality (efficiency estimate) sometimes is not sharp, since \(\Vert u-u_h\Vert _{\infty ; \, \Omega }\) in the third line above may be replaced by \(\Vert u-u_h\Vert _{\mathrm{bmo}_\Delta (\Omega )}\) and the latter may grow strictly (logarithmically) slower than the former.
Secondly, an interesting question that has yet to be successfully approached in the literature is proof of convergence of adaptive FEM for controlling maximum errors. Among other difficulties, the presence of the logarithmic factor in the a posteriori bounds for the maximum error makes adaptation of standard AFEM convergence and optimality proofs much more challenging. Because logarithmic factors are global, they play no role in AFEM marking schemes, so the natural AFEM for controlling \(\Vert u-u_h\Vert _{\infty ; \, \Omega }\) is precisely the same as that for controlling \(\Vert u-u_h\Vert _{\mathrm{bmo}_\Delta (\Omega )}\). Lemma 11 indicates that at least for convex domains the BMO norm of the error is more directly controlled by the standard \(L_\infty \) AFEM since the bounds involve no logarithmic factors.
Rights and permissions
About this article
Cite this article
Demlow, A., Kopteva, N. Maximum-norm a posteriori error estimates for singularly perturbed elliptic reaction-diffusion problems. Numer. Math. 133, 707–742 (2016). https://doi.org/10.1007/s00211-015-0763-0
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-015-0763-0