Spatiotemporal complexity in a diffusive Brusselator model

Abstract

Turing–Hopf bifurcation of the diffusive Brusselator model with homogeneous Neumann boundary conditions is considered in this paper. By stability analysis, the conditions of the Turing instability are obtained and the critical values of the Turing–Hopf bifurcation are also given. In order to better understand the dynamics near the Turing–Hopf bifurcation, the amplitude equations are derived by the method of the multiple time scale. Through the analysis of amplitude equations, complex dynamics are found, such as nonconstant steady state solutions, spatially homogeneous periodic solutions and spatially inhomogeneous periodic solutions, near the Turing–Hopf bifurcation point. The results show that, compared with the codimension-one Turing instability or Hopf bifurcation, the codimension-two Turing–Hopf bifurcation can induce more complex patterns: spatially inhomogeneous periodic solutions, which could be used to explain the phenomenon of spatiotemporal resonance between activators and inhibitors of chemical reactions. For bifurcation illustration of Brusselator model, the neighbourhood of bifurcation point is divided into six regions and various bifurcation solutions corresponding to different regions are presented via numerical simulations, respectively, which verify the theoretical analysis.

1 Introduction

In 1952, the mechanism to explain the formation of patterns was proposed by Turing. He found that stable equilibria could become unstable through introducing diffusion and developed into a pattern [1]. This phenomenon is called the Turing instability or diffusion-driven instability [2]. As a result, patterns will follow from the bifurcation of system. Since then, more and more scholars studied pattern formation of different reaction diffusion models (see [3,4,5,6,7,8]). Turing patterns can be produced in chemical systems through some reaction–diffusion models, such as the Belousov–Zhabotinsky (BZ) reaction (see [9]), which is a typical example of the formation of chemical reaction patterns. The Brusselator model is a simple model for the Belousov–Zhabotinsky reaction.

In this paper, consider a classical diffusive Brusselator model (see [10]). The reaction steps are as follows

$$\begin{aligned} {\mathcal {A}}&\rightarrow {\mathcal {X}},\\ {\mathcal {B}}+{\mathcal {X}}&\rightarrow {\mathcal {Y}}+{\mathcal {D}},\\ 2{\mathcal {X}}+{\mathcal {Y}}&\rightarrow 3{\mathcal {X}},\\ {\mathcal {X}}&\rightarrow {\mathcal {E}}. \end{aligned}$$

The global reaction is ${\mathcal {A}}+{\mathcal {B}} \rightarrow {\mathcal {D}}+{\mathcal {E}}$, where ${\mathcal {A}}$ and ${\mathcal {B}}$ are input chemicals, ${\mathcal {D}}$ and  ${\mathcal {E}}$ are output chemicals, ${\mathcal {X}}$ and  ${\mathcal {Y}}$ are intermediates. According to the law of mass action, the following kinetic equations are obtained

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} \frac{\partial X}{\partial t'}=D_X\Delta X+k_1A-k_2BX+k_3X^2Y-k_4X,\\ \frac{\partial Y}{\partial t'}=D_Y\Delta Y+k_2BX-k_3X^2Y. \end{array}} \right. \end{aligned}$$

(1)

Here A, B, X and Y stand for the corresponding concentrations of ${\mathcal {A}}$, ${\mathcal {B}}$, ${\mathcal {X}}$, ${\mathcal {Y}}$, respectively; $D_x$ and $D_y$ are the diffusion coefficients of X and Y, respectively; $k_i(i=1,2,3,4)$ represents the reaction constant. To simplify system (1), one uses scaling transformation (see Ref. [11])

$$\begin{aligned} t=k_4t', \quad u=\sqrt{\frac{k_3}{k_4}}X, \quad v=\sqrt{\frac{k_3}{k_4}}Y, \quad a= \frac{k_1\sqrt{k_3}}{k_4\sqrt{k_4}}A, \quad b=\frac{k_2}{k_4}B, \end{aligned}$$

then one obtains the Brusselator model with homogeneous Neumann boundary conditions and the initial conditions as follows

$$\begin{aligned} \left\{ {\begin{array}{ll} \frac{\partial u(x,t)}{\partial t}=d_{1}\frac{\partial ^{2}u(x,t)}{\partial x^{2}}+a-(b+1)u(x,t)+u(x,t)^{2}v(x,t), \quad &{}x\in \Omega , \quad t>0,\\ \frac{\partial v(x,t)}{\partial t}=d_{2}\frac{\partial ^{2}v(x,t)}{\partial x^{2}}+bu(x,t)-u(x,t)^{2}v(x,t), \quad &{}x\in \Omega , \quad t>0,\\ \frac{\partial u(0,t)}{\partial x}=\frac{\partial v(0,t)}{\partial x}=\frac{\partial u(l\pi ,t)}{\partial x}=\frac{\partial v(l\pi ,t)}{\partial x}, \quad &{}t\ge 0,\\ u(x,0)=u_{0}(x)\ge 0, \quad v(x,0)=v_{0}(x)\ge 0, \quad &{}x\in \Omega , \end{array}} \right. \end{aligned}$$

(2)

u(x, t) and v(x, t) represent the concentrations of activator and inhibitor at spatial position x and time t, respectively; $d_1$ and $d_2$ are the diffusion coefficients of u and v, respectively; a and b are the fixed concentrations; $\Omega =(0,l\pi )$; $d_1$, $d_2$, a, b and l are all positive constants.

The Brusselator model has been extensively employed to explain the formation of Turing patterns. In [12], Peng et al. discussed the non-existence and existence of positive non-constant steady states. Turing instability and pattern formation in a semi-discrete Brusselator model were studied in [13]. Xu et al. also performed a series of numerical simulations of the system in the Turing instability regions, and exhibited various patterns such as spotted patterns, square patterns, labyrinthine patterns. By applying global bifurcation theory, Ma and Hu proved the existence and boundedness of continua of the steady state solutions in [14]. The coexistence of non-constant positive solutions was considered in [15]. Many authors have also studied the phenomenon of Hopf bifurcation for the Brusselator model, which can lead to the formation of temporal patterns (see [9]). By applying the center manifold theory and normal form theorem, the periodic solution from the Hopf bifurcation was discussed in [16,17,18,19,20]. We can refer to references [21, 22] for more details about Brusselator model. As for the Brusselator model, there are very few literatures on the study of high codimension bifurcation, especially the Turing–Hopf bifurcation. It can produce much more complex dynamics behaviors, such as constant steady state solutions, spatially homogeneous periodic solutions, nonconstant steady state solutions and spatially inhomogeneous periodic solutions.

In the chemical reaction between the concentrations of activators and inhibitors, spatially inhomogeneous periodic solutions could not appear when only Turing or Hopf bifurcation is present. Spatially inhomogeneous periodic solutions could be better to explain the chemical oscillation between the concentrations of activators and inhibitors. However, the dynamical phenomena within the Turing–Hopf bifurcation are always formidable and difficult to explore. Since the Turing–Hopf bifurcation means the coexistence of the Turing instability and Hopf bifurcation, two bifurcation parameters are needed and the bifurcation point is just the intersection of Hopf and Turing bifurcation curves in the two-dimensional parametric plane. Note that center manifold theorem and the normal form theory are important methods to study the bifurcation of system (see [23]). Several scholars calculated the normal forms near the Turing–Hopf bifurcation point through the method of the center manifold theorem and the normal form (see [24,25,26]). Now we will employ the multiple time scale analysis (see [27]) to get the spatiotemporal patterns from the bifurcation. To this end, two bifurcation parameters are expanded as perturbation of bifurcation values and time is expanded into multiple scales. A series of substitution calculations are performed to obtain the amplitude equations. Then through the analysis of amplitude equations of the Brusselator model, one gets the spatial and spatiotemporal patterns.

The framework of this paper is organized as follows. Hopf bifurcation, the existence of the Turing–Hopf bifurcation and the Turing instability are demonstrated in Sect. 2. In Sect. 3, by using the multiple time scale method, amplitude equations near the Turing–Hopf bifurcation point are obtained. In Sect. 4, the neighborhood of bifurcation are divided into six regions and numerical simulations are carried out to verify theoretical analysis respectively in each region. Spatially inhomogeneous periodic solutions are produced near the Turing–Hopf bifurcation point. Some conclusions are presented in Sect. 5.

2 Existence of the Turing–Hopf bifurcation

2.1 Stability and bifurcation analysis of ODE system

In this subsection, we would like to study stability and Hopf bifurcation of system (2). Consider the following ODE system

$$\begin{aligned} \left\{ {\begin{array}{ll} \frac{du}{dt}=a-(b+1)u+u^{2}v,\\ \frac{dv}{dt}=bu-u^{2}v.\\ \end{array}} \right. \end{aligned}$$

(3)

Let

$$\begin{aligned} a-(b+1)u+u^{2}v=0,\, bu-u^{2}v=0. \end{aligned}$$

It is not difficult to show that system (3) has a unique positive equilibrium $E^*:=(u^*,v^*)=(a,b/a)$. $a^2$ will be denoted as s in the following sections. By calculation, one gets a Jacobian matrix (3) at positive equilibrium $E^*$

$$\begin{aligned} J_{0}= \left( \begin{array}{cc} b-1 &{}\quad a^2 \\ -b &{}\quad -a^2 \\ \end{array} \right) , \end{aligned}$$

hence the characteristic equation is

$$\begin{aligned} \lambda ^2-T_0\lambda +D_0=0, \end{aligned}$$

(4)

where $T_0\triangleq b-1-s$, $D_0\triangleq s$.

Setting $T_0=0$, it shows $s=b-1$. Then system (2) can occur Hopf bifurcation when

$$\begin{aligned} s=b-1 \triangleq s_ {H_0}(b),\, b>1, \end{aligned}$$

(5)

so Eq. (4) has a pair of pure imaginary roots $\lambda _{1,2}=\pm iw_0$ with $w_0^2\triangleq s$.

Selecting s as a bifurcation parameter, it takes

$$\begin{aligned} \frac{d\text{ Re }\left( \lambda (s)\right) }{d s}|_{s= s_ {H_0(b)}}=-\frac{1}{2}<0. \end{aligned}$$

The above calculation presents that the transversality condition is satisfied. Referring to Theorem 2.1 in [18], system (2) has the following results without diffusion.

Lemma 1

For system (3), we have

(i) the positive equilibrium $E^{*}$ is locally asymptotically stable for $(b,s)\in G_1$ or $b\le 1$, and unstable for $(b,s)\in G_2,$ where $G_1$ and $G_2$ are defined by

$$\begin{aligned} G_1&=\left\{ (b,s)\mid s>max\{0,\, s_ {H_0(b)}\}\right\} ,\\ G_2&=\left\{ (b,s)\mid 0<s<s_ {H_0(b)},\, b>1\right\} . \end{aligned}$$

(ii) Hopf bifurcation occurs when $s=s_ {H_0(b)},\, b>1$, so one obtains the Hopf bifurcation straight line in $b-s$ plane, marked as ${\mathcal {H}}_0(b)$.

2.2 Existence of the Turing–Hopf bifurcation

In this part, we will discuss the Turing instability and the existence conditions of the Turing–Hopf bifurcation. Put $u=u-u_*, v=v-v_*$, then the linearization of system (2) at the positive equilibrium $E*$ can be written as follows

$$\begin{aligned} \left( \begin{array}{cc} \frac{\partial u}{dt} \\ \frac{\partial v}{dt} \\ \end{array} \right) \triangleq&L\left( \begin{array}{cc} u \\ v \\ \end{array} \right) =\left( \begin{array}{cc} d_{1}\frac{\partial ^{2}}{\partial x^{2}} &{}\quad 0 \\ 0 &{}\quad d_{2}\frac{\partial ^{2}}{\partial x^{2}} \\ \end{array} \right) \left( \begin{array}{cc} u \\ v \\ \end{array} \right) +J_0 \left( \begin{array}{cc} u\\ v\\ \end{array} \right) . \end{aligned}$$

(6)

System (6) has solution (u, v), which is

$$\begin{aligned} \left( \begin{array}{cc} u(x,t)\\ v(x,t)\\ \end{array} \right) =\sum _{k=0}^{\infty }\left( \begin{array}{cc} a_{k}\\ b_{k}\\ \end{array} \right) e^{\lambda t}cos(kx/l), \end{aligned}$$

(7)

here $\lambda$ is the wavelength and k is the wave number, $a_k$ and $b_k$ are constants. Next substituting (7) into (6), we get the following equation

$$\begin{aligned} \lambda \left( \begin{array}{cc} a_k \\ b_k\\ \end{array} \right) =\left( \begin{array}{cc} b-1- d_{1}(k/l)^{2} &{}\quad a^2\\ -b &{}\quad -a^2-d_{2}(k/l)^{2}\\ \end{array} \right) \left( \begin{array}{cc} a_k \\ b_k\\ \end{array} \right) , \quad k\in {\mathbb {N}} _0\triangleq \{0,1,2,...\}. \end{aligned}$$

(8)

Solving Eq. (8), one gets the following characteristic equation

$$\begin{aligned} \Gamma _k\triangleq \lambda ^2-T_k\lambda +D_k=0, \quad k\in {\mathbb {N}} _0\triangleq \{0,1,2,...\}. \end{aligned}$$

(9)

where

$$\begin{aligned} T_k&\triangleq -(k/l)^2(d_1+d_2)+T_0,\\ D_k&\triangleq d_1d_2(k/l)^4+[sd_1+(1-b)d_2](k/l)^2+D_0. \end{aligned}$$

The eigenvalues of Eq. (9) can be shown as

$$\begin{aligned} \lambda _{1,2}=\frac{T_k \pm \sqrt{T_k^2-4D_k}}{2}, \quad k\in {\mathbb {N}} _0=\{0,1,2,...\}. \end{aligned}$$

Letting $D_k=0$, the above equation becomes

$$\begin{aligned} s=\frac{d_2(k/l)^2}{d_1(k/l)^2+1}(b-1)-\frac{d_1d_2(k/l)^4}{1+d_1(k/l)^2}\triangleq s_ {T_k}(b), \quad k\in {\mathbb {N}}_0\backslash \{0\}, \end{aligned}$$

(10)

one obtains the Turing bifurcation straight line in $b-s$ plane, marked as ${\mathcal {T}}_k(b)$. Then, assuming the slope of $s_ {T_k}(b)$ is equal to 1, we derive $k=\frac{l}{\sqrt{d_2-d_1}}$, $(d_2>d_1)$. In light of equation (10), it is noticed that the slope of straight line ${T}_k(b)$ is increasing with k. Let $[\frac{l}{\sqrt{d_2-d_1}}]\triangleq k_{1*} \quad (d_2>d_1)$, where [.] expresses the part of integer. Furthermore, comparing Eq. (10) with Eq. (9), only when $k>k_{1*}$, the straight line ${\mathcal {H}}_0(b)$ has intersection points with the straight line ${\mathcal {T}}_k(b).$

Combining equations (5) and (10), ${\mathcal {H}}_0(b)$ and ${\mathcal {T}}_k(b)$ intersect at

$$\begin{aligned} b_k=\frac{d_1d_2(k/l)^4}{(d_2-d_1)(k/l)^2-1}+1>1, \quad k>k_{1*}, \quad k\in {\mathbb {N}}, \quad d_2>d_1. \end{aligned}$$

(11)

Assuming $z=(k/l)^2$, we have

$$\begin{aligned} f(z)=\frac{d_1d_2z^2}{(d_2-d_1)z-1}+1>1, \quad (x>0), \end{aligned}$$

then taking the derivative of f(z) with respect to z, one has

$$\begin{aligned} f^\prime (z)=\frac{d_1d_2z^2(d_2-d_1)-2d_1d_2z}{[(d_2-d_1)z-1]^2}. \end{aligned}$$

Note that the sign of $f^\prime (z)$ is the same as $\alpha (z)=d_1d_2z^2(d_2-d_1)-2d_1d_2z$. Clearly, f(z) is monotone decreasing in $(0,\frac{2}{d_2-d_1})$ and monotone increasing in $(\frac{2}{d_2-d_1},+\infty )$, we can assume $k_{2*}\triangleq \left[ \frac{\sqrt{2}l}{\sqrt{d_2-d_1}}\right]$, $d_2>d_1.$ Let

$$\begin{aligned} k_*\triangleq \left\{ {\begin{array}{*{20}{l}} k_{2*}, \quad &{}\text{ if } \quad b_{k_{2*}}\le b_{k_{{2*}}+1},\\ k_{2*}+1, \quad &{}\text{ if } \quad b_{k_{2*}}> b_{k_{{2*}}+1}. \end{array}} \right. \end{aligned}$$

(12)

From the above analysis, there exists a positive integer $k_*>k_{1*}$, $b_* \triangleq b_{ k_{*}}=min_{k>k_{1*}}b_{k}$. When $k\ne 0$ and $k\ne k_*$, then $D_k>0$ for $k>k_{1*}$. Consequently, we have the following theorem.

Theorem 1

Assuming that $d_1,d_2>0$, $s_ {H_0}(b)$ and $s_ {T_k}(b)$ are defined by Eq. (10). For $k=k_*$, from Eq. (10), one obtains $s_ {T_{k_*}}(b)$. Therefore, we have

(I) If $d_1 \ge d_2$, then the equilibrium $E^*$ is locally asymptotically stable for $(b,s)\in M_1$, and unstable for $(b,s)\in M_2$, and system (2) has no diffusion driven Turing instability, where

$$\begin{aligned} M_1&=\left\{ (b,s)\mid s>0,\, 0<b\le 1\right\} \cup \left\{ (b,s)\mid s>s_ {H_0}(b),\, b>1\right\} ,\\ M_2&=\left\{ (b,s)\mid s<s_ {H_0}(b),\, b>1\right\} . \end{aligned}$$

(II) If $d_2>d_1$, then we have the following conclusions

(i) the equilibrium $E^*$ is locally asymptotically stable for $(b,s)\in M_{11}$, and unstable when $(b,s)\in M_{21}\cup M_2$, here

$$\begin{aligned} M_{11}&=\left\{ (b,s)\mid s>0,\, 0<b\le 1\right\} \cup \left\{ (b,s)\mid s>{\mathcal {N}}(b),\, b>1\right\} ,\\ M_{21}&=\left\{ (b,s)\mid s_ {H_0}(b)\le s<{\mathcal {N}}(b),\, b>b_{ k_{*}}\right\} , \end{aligned}$$

with

$$\begin{aligned} {\mathcal {N}}(b)= \left\{ \begin{array}{*{20}{l}} s_ {H_0}(b),\, when\, 1<b<b_{k_*},\\ s_ {T_{k_*}}(b),\, when \quad b_{k_*}<b<{\widetilde{b}}_{k_*},\\ s_ {T_k}(b), \quad when \quad k>{k_*},\, {\widetilde{b}}_{k-1}<b<{\widetilde{b}}_{k}.\\ \end{array}\right. \end{aligned}$$

Therefore, the Turing instability critical line is defined by $s={\mathcal {N}}(b)$ with $b>b_{k_*}$. The Turing instability occurs on the curves $s={\mathcal {N}}(b)$ with $b>b_{k_*}$.

(ii) system (2) undergoes the codimension-two Turing–Hopf bifurcation at the point $(b,s)=(b_*,s_*).$

Proof

If $0<b\le 1$, we obtain $T_k<0,\, D_k>0,\, k\in {\mathbb {N}}_0\backslash \{0\}$. If $b>1$, for any $k\in {\mathbb {N}}_0$, when $s>s_ {H_0}(b)$, we get $T_k<0$, and $D_k>0$ is equivalent to $s>s_ {T_k}(b)$.

(I) When $d_1\ge d_2$, $b>1$, we have

$$\begin{aligned} b-1>\frac{d_2(k/l)^2}{d_1(k/l)^2+1}(b-1)-\frac{d_1d_2(k/l)^4}{1+d_1(k/l)^2},\, k\in {\mathbb {N}}_0. \end{aligned}$$

Combined with the above analysis of $T_k$ and $D_k$, this shows $s>s_ {H_0}(b)>s_ {T_k}(b)$ when $s>s_ {H_0}(b)$, Thus we obtain $T_k<0,\, D_k>0,\, k\in {\mathbb {N}}_0\backslash \{0\}$. So all roots of Eq. (9) have negative real parts, the equilibrium $E^*$ is asymptotically stable for $(b,s)\in M_1$. The proof of (I) is completed.

(II) (i) When $d_2>d_1$. From Eq. (10), it is found that the slope of straight line ${T}_k(b)$ is increasing with k. On the basis of the above analysis, ${H_0}(b)$ has no intersection point with the straight line $T_k(b)$ for $k>k_{1*}$. For $k\ge k_*$, the straight lines ${\mathcal {T}}_k(b)$ and ${\mathcal {T}}_{k+1}(b)$ have an intersection point at $b={\widetilde{b}}_{k}$ in the first quadrant, where

$$\begin{aligned} {\widetilde{b}}_{k}=1+d_1\left( d_1(k/l)^2(k/l+1)^2+((k/l)^2)+(k/l+1)^2)\right) ,\, k\ge k_*. \end{aligned}$$

If $1<b<b_{k_*}$, then $s_ {H_0}(b)>s_ {T_{k_*}}(b)$. It is not difficult to get $T_k<0,\, D_k>0$ only when $s>s_ {H_0}(b)$.

If $b_{k_*}<b<{\widetilde{b}}_{k_*}$, then $s_ {T_{k_*}}(b)>s_ {H_0}(b)$. Therefore, one has $T_k<0,\, D_k>0$ when $s>s_ {T_{k_*}}(b)$.

If $k>{k_*},\, {\widetilde{b}}_{k-1}<b<{\widetilde{b}}_{k}$, then $s_ {T_{k}}(b)>s_ {H_0}(b)$. One has $T_k<0,\, D_k>0$ when $s>s_ {T_{k}}(b)$.

Therefore, the equilibrium $E^*$ is locally asymptotically stable when $(b,s)\in M_{11}$. What is more, in the first quadrant of the $b-s$ plane, $s_ {H_0}(b)$ with $0<b<b_{k_*}$, $s_ {T_{k_*}}(b)$ with $b_{k_*}<b<{\widetilde{b}}_{k_*}$ and $s_ {T_k}(b)$ with $k>{k_*},\, {\widetilde{b}}_{k-1}<b<{\widetilde{b}}_{k}$ form the boundaries of stable region of the equilibrium $E^*$.

(ii) According to the above calculation, one shows

$$\begin{aligned} b_*=\frac{d_1d_2(k_*/l)^4+(d_2-d_1)(k_*/l)^2-1}{(d_2-d_1)(k_*/l)^2-1}, \quad s_*=b_*-1, \quad b_*>1, \end{aligned}$$

(13)

and

$$\begin{aligned} \frac{d\text{ Re }\left( \lambda (s)\right) }{d s}|_{s=s_ {T_k}(b)}=\frac{d_1(k/l)^2+1}{T_{k}}\ne 0, \end{aligned}$$

(14)

Substituting $k=k_*$ into Eq. (9), one has $T_{k_*}=-(k_*/l)^2(d_1+d_2)+T_0$. When $\Gamma _0=0$, system (2) has a pair of purely imaginary roots $\pm i\sqrt{s_*}$; When $k=k_*$ and $\Gamma _k=0$, it has two roots, one is 0 and the other is $-T_{k^*}$; If $k\ne 0$ and $k\ne k_*$, all roots of characteristic equation (9) have negative real parts. Together with the transversality condition of the Hopf bifurcation, so there exists the codimension-two Turing–Hopf bifurcation at $(b,s)=(b_*,s_*)$ of system (2). The conclusion of (ii) of (II) is verified.□

Remark 1

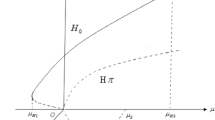
To verify the existence of the Turing–Hopf points, we plot the Turing and Hopf bifurcation curve diagram, see Fig. 1. Here, choosing $d_1=0.2 \, \text{ and }\, d_2=1.6$, we have $k_*=7$ from (5), (10) and (12). Furthermore, from (5) and (10), we get

$$\begin{aligned} {\mathcal {H}}_0(b): s&=b-1, \quad b>1,\\ {\mathcal {T}}_7(b): s&=1.7118b-2.1778, \quad b>1.2722,\\ {\mathcal {T}}_8(b): s&=3.8739b-7.5111, \quad b>1.9389,\\ \end{aligned}$$

As exhibited in Fig. 1, there exist two intersection points, the Turing–Hopf bifurcation point $A=(1.6547,0.6547)$ and the Turing–Turing bifurcation point $B=(2.4668, 2.0447)$. The region above the curve ${\mathcal {H}}_0(b)$, ${\mathcal {T}}_7(b)$ and ${\mathcal {T}}_8(b)$ are the stable region of the unique positive equilibrium $E^*$.

Fig. 1

Turing and Hopf bifurcation diagram in the b–s plane

3 Amplitude equations

In this section, choose $b=b_*$ and $s=s_*$ as critical bifurcation values. In what follows, we will use the method of the multiple time scale to derive the amplitude equations near the Turing–Hopf bifurcation point $S_*\triangleq (b_*,s_*)$ in system (2). Then, letting $u=u-u_*$, $v=v-v_*$ and ${\mathbf {U}}=(u,v)^\mathrm {T}$, system (2) becomes

$$\begin{aligned} \frac{\partial {\mathbf {U}}}{\partial t}={\mathbf {L}}{\mathbf {U}}+{\mathbf {F}}({\mathbf {U}},{\mathbf {U}}). \end{aligned}$$

(15)

Where L is the linear operator, F is the nonlinear term

$$\begin{aligned} {\mathbf {L}}=\left( \begin{array}{ll} b-1+d_1\frac{\partial ^{2}}{\partial x^{2}} &{}\quad s \\ -b &{}\quad -s+d_2\frac{\partial ^{2}}{\partial x^{2}} \\ \end{array} \right) ,\, {\mathbf {F}}=\left( \begin{array}{c} f_{1}u^2+f_{2}uv+u^2v\\ -f_{1}u^2-f_{2}uv-u^2v\\ \end{array} \right) +{o(3)}, \end{aligned}$$

(16)

with $f_{1}\triangleq \frac{b}{\sqrt{s}}$, $f_{2}\triangleq 2\sqrt{s}$. o(3) represents terms of order higher than third. Next expanding the solution ${\mathbf {U}}$ of system (2) in the light of the small parameter $\varepsilon$, we have

$$\begin{aligned} {\mathbf {U}}=\varepsilon \left( \begin{array}{cc} u_1\\ v_1\\ \end{array} \right) +\varepsilon ^2 \left( \begin{array}{cc} u_2\\ v_2\\ \end{array} \right) +\varepsilon ^3 \left( \begin{array}{cc} u_3\\ v_3\\ \end{array} \right) +{o(\varepsilon ^{3})}, \end{aligned}$$

(17)

where $\varepsilon$ is the small parameter. To calculate the amplitude equations near the Turing–Hopf bifurcation point, we expand bifurcation parameters b and s in the small neighborhood. For the Hopf bifurcation parameter s, one gets

$$\begin{aligned} s-s_*=\varepsilon ^2 s_2. \end{aligned}$$

(18)

and the Turing bifurcation parameter, one derives

$$\begin{aligned} b-b_*=\varepsilon ^2 b_2. \end{aligned}$$

(19)

Let $T_0=t,\, T_2=\varepsilon ^2 t$. Taking the derivative of U with respect to time scale, we represent the following form

$$\begin{aligned} \frac{\partial {\mathbf {U}}}{\partial t}= \frac{\partial {\mathbf {U}}}{\partial T_0}+\varepsilon ^2\frac{\partial {\mathbf {U}}}{\partial T_2}. \end{aligned}$$

(20)

The linear operator ${\mathbf {L}}$ can be decomposed into the following form

$$\begin{aligned} {\mathbf {L}}=\,&\left( \begin{array}{cc} b_*-1+d_1\frac{\partial ^2}{\partial x^2} &{}\quad s_*\\ -b_* &{}\quad -s_*+d_2\frac{\partial ^2}{\partial x^2} \\ \end{array} \right) +(b-b_*)\left( \begin{array}{cc} 1 &{}\quad 0 \\ -1&{}\quad 0 \\ \end{array} \right) +(s-s_*)\left( \begin{array}{cc} 0 &{}\quad 1 \\ 0 &{}\quad -1 \\ \end{array} \right) \\\triangleq&\begin{array}{c} \mathbf {L_{c}}+(b-b_*)\mathbf {M_{b_*}}+(s-s_*)\mathbf {M_{s_*}}. \end{array}\nonumber \end{aligned}$$

(21)

the nonlinear term ${\mathbf {F}}$ is

$$\begin{aligned} {\mathbf {F}}=\,&\varepsilon ^2\left( \begin{array}{cc} f_{1}u_{1}^2+f_2u_1v_1 \\ - f_1{u_1}^2-f_2u_1v_1 \\ \end{array} \right) +\varepsilon ^3\left( \begin{array}{c} 2f_1u_1u_2+f_2(u_1v_2+u_2v_1)+u_{1}^2v_1 \\ -2f_1u_1u_2-f_2(u_1v_2+u_2v_1)-u_{1}^2v_1 \\ \end{array} \right) +{o(\varepsilon ^{3})} \\ \triangleq&\varepsilon ^2 \mathbf {F_2}+\varepsilon ^3 \mathbf {F_3} +{o(\varepsilon ^{3})}. \nonumber \end{aligned}$$

(22)

Next, substitute (16)–(22) into (15). The coefficients of the corresponding terms are equal, and then the perturbations are separated by the power series of $\varepsilon ^{i}(1=1,2,3)$

$\varepsilon :$

$$\begin{aligned} \left( \frac{\partial }{\partial T_0} -\mathbf {L_c} \right) \left( \begin{array}{c} u_1 \\ v_1\\ \end{array} \right) ={\mathbf {0}}, \end{aligned}$$

(23)

$\varepsilon ^{2}:$

$$\begin{aligned} \left( \frac{\partial }{\partial T_0} -\mathbf {L_c} \right) \left( \begin{array}{c} u_2 \\ v_2 \\ \end{array} \right) =\mathbf {F_2}, \end{aligned}$$

(24)

$\varepsilon ^{3}:$

$$\begin{aligned} \left( \frac{\partial }{\partial T_0} -\mathbf {L_c} \right) \left( \begin{array}{c} u_3 \\ v_3 \\ \end{array} \right) = -\frac{\partial }{\partial T_2}\left( \begin{array}{c} u_1 \\ v_1 \\ \end{array} \right) +b_2\mathbf {M_{b_*}}\left( \begin{array}{c} u_1 \\ v_1\\ \end{array} \right) +s_2\mathbf { M_{s_*}}\left( \begin{array}{c} u_1 \\ v_1 \\ \end{array} \right) +\mathbf {F_3}. \end{aligned}$$

(25)

With regard to the linear equation (23), we obtain the general solution as follows

$$\begin{aligned} \left( \begin{array}{c} u_1\\ v_1\\ \end{array} \right) =\left( \begin{array}{cc} 1\\ A_1\\ \end{array}\right) W_{1}e^{iw_*T_0} +\left( \begin{array}{cc} 1\\ B_1\\ \end{array}\right) W_2e^{ik_{*}x}+c.c., \end{aligned}$$

(26)

where $A_1\triangleq \frac{iw_*-b_*+1}{s_*}$, $B_1\triangleq \frac{d_1(k_*/l)^{2}-b_*+1}{s_*}$, $w_*=\sqrt{s_*}$, $W_1$ and $W_2$ are the amplitudes of the first order perturbed modes $e^{iw_*T_0}$ and $e^{ik_{*}x}$, c.c. denotes the conjugate of the former terms.

From (26), one gets

$$\begin{aligned} u_1^{2}=\,&|W_1|^{2}+|W_2|^{2}+W_1^{2}e^{2iw_*T_0}+2W_1W_2e^{iw_*T_0+ik_*x}\\ {}&+2W_1\bar{W_2}e^{iw_*T_0-ik_*x}+W_2^2e^{2ik_*x}+c.c.,\\ u_1v_1=\,&A_1|W_1|^{2}+B_1|W_2|^{2}+A_1W_1^{2}e^{2iw_*T_0}+(A_1+B_1)W_1W_2e^{iW_*T_0 +ik_*x}\\ {}&+(A_1+\bar{B_1})W_1\bar{W_2}e^{iw_*T_0-ik_*x}+B_1W_2^{2}e^{2ik_*x}+c.c.. \end{aligned}$$

In what follows, assume that

$$\begin{aligned} \left( \begin{array}{c} u_2\\ v_2\\ \end{array} \right) =\,&\mathbf {q_1}|W_1|^{2}+\mathbf {q_2}|W_2|^{2}+\mathbf {q_3}W_1^{2}e^{2iw_*T_0}+\mathbf {q_4}W_1W_2e^{iw_*T_0+ik_*x}\\ {}&+\mathbf {q_5}W_1\bar{W_2}e^{iw_*T_0-ik_*x}+\mathbf {q_6}W_2^{2}e^{2ik_*x}.\nonumber \end{aligned}$$

(27)

Substituting $u_1^{2}$, $u_1v_1$, $u_1$ and $v_1$ into Eq. (24), one shows

$$\begin{aligned}&\mathbf {q_{1}}\triangleq \left( \begin{array}{c} q_{11} \\ q_{12} \\ \end{array} \right) =\left( \begin{array}{c} 0\\ -\frac{f_1+|A_1|f_2}{s_*}\\ \end{array} \right) ,\\&\mathbf {q_{2}}\triangleq \left( \begin{array}{c} q_{21} \\ q_{22} \\ \end{array} \right) =\left( \begin{array}{c} 0 \\ -\frac{f_1+|B_1|f_2}{s_*} \end{array} \right) ,\\&\mathbf {q_{3}}\triangleq \left( \begin{array}{c} q_{31} \\ q_{32} \\ \end{array} \right) =\left( \begin{array}{c} \frac{(2iw_*)(f_1+A_1f_2)}{(2iw_*-b_*+1)(2iw_*+s_*)+b_*s_*}\\ \frac{(-2iw_*-1)(f_1+A_1f_2)}{(2iw_*-b_*+1)(2iw_*+s_*)+b_*s_*} \\ \end{array} \right) ,\\&\mathbf {q_{4}}\triangleq \left( \begin{array}{c} q_{41} \\ q_{42} \\ \end{array} \right) =\left( \begin{array}{c} \frac{(2f_1+A_1f_2+B_1f_2)(iw_*+d_2k_{*}^2)}{H}\\ \frac{(2f_1+A_1f_2+B_1f_2)(-iw_*-1-d_1k_{*}^2)}{H} \\ \end{array} \right) ,\\&\mathbf {q_{5}}\triangleq \left( \begin{array}{c} q_{51} \\ q_{52} \\ \end{array} \right) =\left( \begin{array}{c} \frac{(2f_1+A_1f_2+\bar{B_1}f_2)(iw_*+d_2k_{*}^2))}{H}\\ \frac{2f_1+A_1f_2+\bar{B_1}f_2)(-iw_*-1-d_1k_{*}^2)}{H} \end{array} \right) ,\\&\mathbf {q_{6}}\triangleq \left( \begin{array}{c} q_{61} \\ q_{62} \\ \end{array} \right) =\left( \begin{array}{c} \frac{(f_1+B_1f_2)(4d_2k_{*}^2)}{J}\\ \frac{(f_1+B_1f_2)(-1-4d_1k_{*}^2)}{J}\\ \end{array} \right) ,\\ \end{aligned}$$

where

$$\begin{aligned}&H\triangleq (iw_*-b_*+1+d_1k_{*}^2)(iw_*+s_*+d_2k_{*}^2)+b_*s_*,&\\&J\triangleq (s_*+4d_2k_{*}^{2})(1-b_*+4d_1k_{*}^{2})+b_*s_*.&\\ \end{aligned}$$

In order to derive the amplitude equations near the Turing–Hopf bifurcation point, we need to calculate $u_1u_2,u_1v_2,u_2v_1$,$u_{1}^2v_1.$

$$\begin{aligned} u_1u_2=\,&q_{31}W_1^3e^{3iw_*T_0}+(q_{41}+q_{31})W_{1}^2W_2e^{2iw_*T_0+ik_*x}+(q_{51}+q_{31})W_1^2{\bar{W}}_2e^{2iw_*T_0-ik_*x}\\ {}&+(q_{61}+q_{41})W_{1}W_{2}^2e^{iw_*T_0+2ik_*x}+({\bar{q}}_{61}+q_{51})W_1{\bar{W}}_{2}^2e^{iw_*T_0-2ik_*x}+q_{31}W_1|W_1|^2e^{iw_*T_0}\\ {}&+(q_{51}+q_{41})W_1|W_2|^2e^{iw_*T_0}+({\bar{q}}_{51}+q_{41})|W_1|^2W_2e^{ik_{*}x}\\ {}&+q_{61}|W_2|^2W_2e^{ik_{*}x}+q_{61}W_{2}^3e^{3ik_*x}+c.c.,\\ u_1v_2=\,&q_{32}W_1^3e^{3iw_*T_0}+(q_{42}+q_{32})W_{1}^2W_2e^{2iw_*T_0+ik_*x}+(q_{52}+q_{32})W_1^2{\bar{W}}_2e^{2iw_*T_0-ik_*x}\\ {}&+(q_{62}+q_{42})W_{1}W_{2}^2e^{iw_*T_0+2ik_*x}+({\bar{q}}_{62}+q_{52})W_1{\bar{W}}_{2}^2e^{iw_*T_0-2ik_*x}\\ {}&+(q_{32}+2{{\mathbf {R}}}{{\mathbf {e}}}\{q_{12}\})W_1|W_1|^2e^{iw_*T_0}+(q_{52}+q_{42}+2{{\mathbf {R}}}{{\mathbf {e}}}\{q_{22}\})W_1|W_2|^2e^{iw_*T_0}\\ {}&+({\bar{q}}_{52}+q_{42}+2{{\mathbf {R}}}{{\mathbf {e}}}\{q_{12}\})|W_1|^2W_2e^{ik_{*}x}+(q_{62}+2{{\mathbf {R}}}{{\mathbf {e}}}\{q_{22}\})|W_2|^2W_2e^{ik_{*}x}\\ {}&+q_{62}W_{2}^3e^{3ik_*x}+c.c.,\\ u_2v_1=\,&A_1q_{31}W_1^3e^{3iw_*T_0}+(A_1q_{41}+B_1q_{31})W_{1}^2W_2e^{2iw_*T_0+ik_*x} +(A_1q_{51}+{\bar{B}}_1q_{31})W_1^2{\bar{W}}_2e^{2iw_*T_0-ik_*x}\\ {}&+(A_1q_{61}+B_1q_{41})W_{1}W_{2}^2e^{iw_*T_0+2ik_*x}+(A_1{\bar{q}}_{61}+{\bar{B}}_1q_{51})W_1{\bar{W}}_{2}^2e^{iw_*T_0-2ik_*x}\\ {}&+{\bar{A}}_1q_{31}W_1|W_1|^2e^{iw_*T_0}+(B_1q_{51}+{\bar{B}}_1q_{41})W_1|W_2|^2e^{iw_*T_0}+(A_1{\bar{q}}_{51}\\ {}&+{\bar{A}}_1q_{41})|W_1|^2W_2e^{ik_{*}x} +{\bar{B}}_1q_{61}|W_2|^2W_2e^{ik_{*}x}+B_1q_{61}W_{2}^2e^{3ik_*x}+c.c.,\\ u_{1}^2v_1=\,&A_1W_1^3e^{3iw_*T_0}+(B_1+2A_1)W_{1}^2W_2e^{2iw_*T_0+ik_*x}+(\bar{B_1}+2A_1)W_1^2{\bar{W}}_2e^{2iw_*T_0-ik_*x}\\ {}&+(2B_1+A_1)W_{1}W_{2}^2e^{iw_*T_0+2ik_*x}+(A_1+2{\bar{B}}_1)W_1{\bar{W}}_{2}^2e^{iw_*T_0-2ik_*x}\\ {}&+(2A_1+{\bar{A}}_1)W_1|W_1|^2e^{iw_*T_0}+(2A_1+2\bar{B_1}+2B_1)W_1|W_2|^2e^{iw_*T_0}\\ {}&+(2B_1+2{\bar{A}}_1+2A_1)|W_1|^2W_2e^{ik_{*}x}+(2B_1+{\bar{B}}_1)|W_2|^2W_2e^{ik_{*}x}+B_{1}W_{2}^3e^{3ik_*x}+c.c..\\ \end{aligned}$$

Substituting $u_1u_2,u_1v_2,u_2v_1,u_{1}^2v_1$ into Eq. (25), one derives

$$\begin{aligned} \left( \frac{\partial }{\partial T_0}-L_c\right) \left( \begin{array}{c} u_3 \\ v_3 \end{array}\right) =\,&\mathbf {P_{1}}e^{iw_*T_0}+\mathbf {P_{2}}e^{ik_{*}x}+\mathbf {P_{3}}e^{3iw_*T_0}+\mathbf {P_{4}}e^{2iw_*T_0+ik_{*}x}\\ {}&+\mathbf {P_{5}}e^{2iw_*T_0-ik_{*}x}+\mathbf {P_{6}}e^{iw_*T_0+2ik_{*}x}\\ {}&+\mathbf {P_{7}}e^{iw_*T_0-2ik_{*}x}+\mathbf {P_{8}}e^{3ik_{*}x}++c.c., \end{aligned}$$

where

$$\begin{aligned}&\mathbf { P_1}=\left( \begin{array}{c} P_{11} \\ P_{12} \end{array}\right) , \mathbf {P_2}=\left( \begin{array}{c} P_{21} \\ P_{22} \end{array}\right) , \mathbf {P_3}=\left( \begin{array}{c} P_{31} \\ - P_{31} \end{array}\right) , \mathbf { P_4}=\left( \begin{array}{c} P_{41} \\ - P_{41} \end{array}\right) ,\\ {}&\mathbf {P_5}=\left( \begin{array}{c} P_{51} \\ - P_{51} \end{array}\right) , \mathbf {P_6}=\left( \begin{array}{c} P_{61} \\ - P_{61} \end{array}\right) , \mathbf { P_7}=\left( \begin{array}{c} P_{71} \\ - P_{71} \end{array}\right) , \mathbf { P_8}=\left( \begin{array}{c} P_{81} \\ - P_{81} \end{array}\right) , \end{aligned}$$

with

$$\begin{aligned} P_{11}=\,&\frac{-\partial W_1}{\partial T_2}+b_2M_{b_*}W_1+s_2M_{s_*}W_1\\ {}&+[2f_1q_{31}+f_2(2{{\mathbf {R}}}{{\mathbf {e}}}\{q_{12}\}+q_{32}+{\bar{A}}_{1}q_{31})+2A_1+{\bar{A}}_{1}]W_1|W_{1}|^2+[2f_1(q_{51}+q_{41})\\ {}&+f_2(2{{\mathbf {R}}}{{\mathbf {e}}}\{q_{22}\}+q_{52}+q_{42}+B_1q_{51}+{\bar{B}}_1q_{41})+2A_1+2{\bar{B}}_1+2B_1]W_1|W_2|^2\\ {}&\triangleq \frac{-\partial W_1}{\partial T_2}+b_2M_{b_*}W_1+s_2M_{s_*}W_1+CW_1|W_{1}|^2+DW_1|W_2|^2,\\ P_{12}=\,&\frac{-A_1\partial W_1}{\partial T_2}+b_2M_{b_*}A_1W_1+s_2M_{s_*}A_1W_1-CW_1|W_1|^2-DW_1|W_2|^2,\\ P_{21}=\,&\frac{-\partial W_1}{\partial T_2}+b_2M_{b_*}W_1+s_2M_{s_*}W_1+[2f_1({\bar{q}}_{51}+q_{41})\\ {}&+f_2(2{{\mathbf {R}}}{{\mathbf {e}}}\{q_{12}\}+{\bar{q}}_{52}+q_{42}+A_1{\bar{q}}_{51}+{\bar{A}}_1q_{41})+2B_1+2{\bar{A}}_1+2A_1]|W_1|^2W_2\\ {}&+[2f_1q_{61}+f_2(2{{\mathbf {R}}}{{\mathbf {e}}}\{q_{22}\}+q_{62}+{\bar{B}}_1q_{61})+2B_1+{\bar{B}}_1]|W_2|^2W_2\\ {}&\triangleq \frac{-\partial W_1}{\partial T_2}+b_2M_{b_*}W_1+s_2M_{s_*}W_1+E|W_1|^2W_2+F|W_2|^2W_2,\\ P_{22}=\,&\frac{-B_1\partial W_1}{\partial T_2}+b_2M_{b_*}B_1W_2+s_2M_{s_*}B_1W_2-EW_2|W_1|^2-FW_2|W_2|^2,\\ P_{31}=\,&[2f_1q_{31}+f_2(q_{32}+A_1q_{31})+A_{1})]W_{1}^3,\\ P_{41}=\,&[2f_1(q_{41}+q_{31})+f_{2}(q_{42}+q_{32}+A_1q_{41}+B_1q_{31})]+(B_{1}+2A_1)]W_{1}^2W_{2},\\ P_{51}=\,&[2f_1(q_{51}+q_{31})+f_{2}(q_{52}+q_{32}+A_1q_{51}+{\bar{B}}_1q_{31})+{\bar{B}}_1+2A_1]W_{1}^2{\bar{W}}_{2},\\ P_{61}=\,&[2f_1(q_{61}+q_{41})+f_{2}(q_{61}+q_{42}+A_1q_{61}+B_1q_{41})+2B_{1}+2A_1]W_{1}W_{2}^2,\\ P_{71}=\,&[2f_1({\bar{q}}_{61}+q_{51})+f_{2}({\bar{q}}_{62}+q_{52}+A_1{\bar{q}}_{61}+{\bar{B}}_1q_{51})+A_1+2{\bar{B}}_1]W_{1}{\bar{W}}_{2}^2,\\ P_{81}=\,&[2f_1q_{61}+f_2(q_{62}+B_1q_{61})+B_{1}]W_{2}^3.\\ \end{aligned}$$

In light of the above discussion, the solutions of equation (25) can be rewritten into the following form

$$\begin{aligned} \left( \frac{\partial }{\partial T_0}-L_c\right) \left( \begin{array}{c} u_3 \\ v_3 \end{array}\right) = \mathbf {P_{1}}e^{iw_*T_0}+\mathbf {P_{2}}e^{ik_{*}x}+\mathbf {NST}+c.c., \end{aligned}$$

(28)

where $\mathbf {NST}$ represents the non-secular terms. According to the Fredholm solvability conditions in [11], one gets the vector function on the right hand side of Eq. (23) should be orthogonal to the zero eigenvectors of the adjoint operator of the operator $L_{c}$. Then, we apply the orthogonal condition to the equation on the right side of Eq. (25)

$$\begin{aligned}<\mathbf {G^{*}},{\mathbf {P}}_1>=0\, \text{ and }\, <\mathbf {H^{*}},{\mathbf {P}}_2>=0, \end{aligned}$$

(29)

where

$$\begin{aligned} \mathbf {G^{*}}=\,&\left( \begin{array}{c} \frac{-iw_*+s_*}{-2iw_*-b_*+1+s_*}\\ \frac{s_*}{-2iw_*-b_*+1+s_*}\\ \end{array} \right) \triangleq \left( \begin{array}{c} G_1\\ G_2\\ \end{array}\right) ,\\ \mathbf {H^{*}}=\,&\left( \begin{array}{c} \frac{d_2(k_{*}/l)^{2}+s_*}{(d_1+d_2)(k_{*}/l)^{2}-b_*+1+s_*}\\ \frac{s_*}{(d_1+d_2)(k_{*}/l)^{2}-b_*+1+s_*} \\ \end{array} \right) \triangleq \left( \begin{array}{c} H_1 \\ H_2 \\ \end{array}\right) , \end{aligned}$$

and the inner product satisfies $<\mathbf {G^{*}},{\mathbf {P}}_1>=(\bar{\mathbf {G^{*}}})^{T}{\mathbf {P}}_1$, $<\mathbf {H^{*}},{\mathbf {P}}_2>=(\bar{{\mathbf {H}}^{*}})^{T}{\mathbf {P}}_2.$ Finally, the amplitude equations are

$$\begin{aligned} \left\{ \begin{array}{*{20}{l}} \frac{\partial W_1}{\partial T_2}=r_1W_1+r_2W_1|W_1|^2+r_3 W_1|W_2|^2,\\ \frac{\partial W_2}{\partial T_2}=m_1W_2+m_2W_2|W_2|^2+m_3 W_2|W_1|^2, \end{array}\right. \end{aligned}$$

(30)

where

$$\begin{aligned} r_1=\,&\frac{(\bar{G_1}-\bar{G_2})(b_2+s_2A_1)}{\bar{G_1}+A_1\bar{G_2}}, \quad r_2=\frac{(\bar{G_1}-\bar{G_2})C}{\bar{G_1}+A_1\bar{G_2}}, \quad r_3=\frac{(\bar{G_1}-\bar{G_2})D}{\bar{G_1}+A_1\bar{G_2}}, \\ m_1=\,&\frac{(H_1-H_2)(b_2+s_2B_1)}{H_1+B_1H_2}, \quad m_2=\frac{(H_1-H_2)F}{H_1+B_1H_2}, \quad m_3=\frac{(H_1-H_2)E}{H_1+B_1H_2}.\\ \end{aligned}$$

Therefore, let $W_1=\rho _{1}e^{i\theta },W_2=\rho _{2}$, we obtain the Turing–Hopf bifurcation in the real coordinates

$$\begin{aligned} \left\{ \begin{array}{*{20}{l}} {\dot{\rho }}_1&{}=\kappa _1\rho _1+\kappa _2\rho _{1}^3+\kappa _{3}\rho _1\rho _{2}^2,\\ {\dot{\rho }}_2&{}=\zeta _1\rho _2+\zeta _2\rho _{2}^3+\zeta _{3}\rho _2\rho _{1}^2,\\ {\dot{\theta }}&{}=\xi _1+\xi _2\rho _{1}^2+\xi _3\rho _{1}^2. \end{array} \right. \end{aligned}$$

Here, $\kappa _1={{\mathbf {R}}}{{\mathbf {e}}}\{r_1\},\, \kappa _2={{\mathbf {R}}}{{\mathbf {e}}}\{r_2\},\, \kappa _3={{\mathbf {R}}}{{\mathbf {e}}}\{r_3\},\, \zeta _1={{\mathbf {R}}}{{\mathbf {e}}}\{m_1\},\, \zeta _2={{\mathbf {R}}}{{\mathbf {e}}}\{m_2\},\, \zeta _3={{\mathbf {R}}}{{\mathbf {e}}}\{m_3\},\, \xi _1={{\mathbf {I}}}{{\mathbf {m}}}\{r_1\},\, \xi _2={{\mathbf {I}}}{{\mathbf {m}}}\{r_2\},\, \xi _3={{\mathbf {I}}}{{\mathbf {m}}}\{r_3\}$ and remove the azimuthal term, we gain the amplitude equations near the Turing–Hopf bifurcation point

$$\begin{aligned} \left\{ \begin{array}{c} {\dot{\rho }}_1=\kappa _1\rho _1+\kappa _2\rho _{1}^3+\kappa _{3}\rho _1\rho _{2}^2,\\ {\dot{\rho }}_2=\zeta _1\rho _2+\zeta _2\rho _{2}^3+\zeta _{3}\rho _1\rho _{2}^2.\\ \end{array} \right. \end{aligned}$$

(31)

4 Numerical simulations

In this section, some numerical simulations are applied to confirm the theoretical analysis. In Sect. 3, we get the amplitude equations through the multiple time scale method. By direct calculation of Eq. (31), we obtain four kinds of equilibria: constant steady state solutions, nonconstant steady state solutions, spatially homogeneous periodic solutions and spatially inhomogeneous periodic solutions, respectively. Next, we need to find the equilibria of Eq. (31), thereby let ${\dot{\rho }}_1=0$ and ${\dot{\rho }}_2=0$. Notice that $\rho _{1}>0$ and $\rho _{2}$ is an arbitrary real number. By computation, one obtains a zero equilibrium

$$\begin{aligned} E_{0}=(0,0), \end{aligned}$$

three boundary equilibria

$$\begin{aligned} E_{1}=\left( \sqrt{-\frac{\kappa _1}{\kappa _2}},0\right) ,\, \frac{\kappa _1}{\kappa _2}<0, \end{aligned}$$

and

$$\begin{aligned} E_{2}^{\pm }=\left( 0,\pm \sqrt{-\frac{\zeta _1}{\zeta _2}}\right) ,\, \frac{\zeta _1}{\zeta _2}<0, \end{aligned}$$

and two internal equilibria

$$\begin{aligned} E_{3}^\pm =\left( \sqrt{\frac{\kappa _1\zeta _2-\kappa _3\zeta _1}{\kappa _3\zeta _3-\kappa _2\zeta _2}}, \, \pm \sqrt{\frac{\kappa _2\zeta _1-\kappa _1\zeta _3}{\kappa _3\zeta _3-\kappa _2\zeta _2}}\right) ,\, \end{aligned}$$

with $\frac{\kappa _1\zeta _2-\kappa _3\zeta _1}{\kappa _3\zeta _3-\kappa _2\zeta _2}>0,\,$ $\frac{\kappa _2\zeta _1-\kappa _1\zeta _3}{\kappa _3\zeta _3-\kappa _2\zeta _2}>0$. The first equation of (31) represents the amplitude equation corresponding to Hopf bifurcation, and the second equation of (31) represents the amplitude equation to the Turing bifurcation. Hence, $E_{0}$, $E_{1}$, $E_{2}$, $E_{3}$ correspond to the constant steady state solution, the spatially homogeneous periodic solution, the nonconstant steady state solution and the spatially inhomogeneous periodic solution, respectively.

Choosing $d_1=0.2$, $d_2=1.6$ and $l=6$, according to (5), (10)–(12), we calculate $k_*=7$, $b_*=1.6547$, $s_*=0.6547$ and $w_*=0.8091$. From Eq. (31), it follows that

$$\begin{aligned} \kappa _1&=0.5b_2-0.5s_2,\, \kappa _2=-2.0274,\, \kappa _3=-4.3490, \\ \zeta _1&=0.8889b_2-0.5193s_2,\, \zeta _2=-6.3156,\, \zeta _3=-5.0203. \end{aligned}$$

Therefore, with these given parameters, Eq. (31) becomes

$$\begin{aligned} \left\{ \begin{array}{*{20}{l}} {\dot{\rho }}_1=(0.5b_2-0.5s_2)\rho _1-2.0274\rho _{1}^3-4.3490\rho _1\rho _{2}^2,\\ {\dot{\rho }}_2=(0.8889b_2-0.5193s_2)\rho _2-6.3156\rho _{2}^3-5.0203\rho _2\rho _{1}^2.\\ \end{array} \right. \end{aligned}$$

(32)

Furthermore, a zero equilibrium

$$\begin{aligned} E_{0}=(0,0), \end{aligned}$$

three boundary equilibria

$$\begin{aligned} E_{1}=(\sqrt{0.2466b_2-0.2466s_2},0),\, s_2<b_2, \end{aligned}$$

and

$$\begin{aligned} E_{2}^\pm =(0,\pm \sqrt{0.1407b_2-0.0822s_2}),\, s_2<1.7117b_2, \end{aligned}$$

and two internal equilibria

$$\begin{aligned} E_{3}^\pm =(\sqrt{0.6994b_2+0.0962s_2},\pm \sqrt{0.0784b_2+0.1614s_2}), \end{aligned}$$

where $-0.7872b_2<s_2<0.4858b_2$, respectively. Next the critical bifurcation lines

$$\begin{aligned}&{\mathcal {L}}_1:s_2=b_2,\\&{\mathcal {L}}_2:s_2=1.7117b_2,\\&{\mathcal {L}}_3:s_2=-0.7872b_2, \quad b_2>0,\\&{\mathcal {L}}_4:s_2=0.4858b_2, \quad b_2>0.\\ \end{aligned}$$

The parameter $(b_2,s_2)$ plane is divided into six regions by the four straight line ${\mathcal {L}}_1$, ${\mathcal {L}}_2$, ${\mathcal {L}}_3$ and  ${\mathcal {L}}_4$, which are represented as ${\mathcal {D}}_1$, ${\mathcal {D}}_2$, ${\mathcal {D}}_3$, ${\mathcal {D}}_4$, ${\mathcal {D}}_5$ and ${\mathcal {D}}_6$, respectively, see Fig. 2 a and b. In what follows, we shall analyze the existence and stability of equilibria in six regions, and adopt numerical simulations respectively.

Fig. 2

a Bifurcation curves in $b_2-s_2$ plane. b Phase portraits of Regions ${\mathcal {D}}_1$, ${\mathcal {D}}_2$, ${\mathcal {D}}_3$, ${\mathcal {D}}_4$, ${\mathcal {D}}_5$ and ${\mathcal {D}}_6$

In region ${\mathcal {D}}_1$, system (32) has six equilibria: $E_{0}$, $E_{1}$, $E_{2}^{\pm }$ and $E_{3}^{\pm }$. The equilibria $E_{1}$ and $E_{2}^{\pm }$ are stable, and $E_{0}$ and $E_{3}^{\pm }$ are unstable equilibria. This implies that system (2) has an unstable positive constant equilibrium, a stable spatially homogeneous periodic solution, two stable nonconstant steady states and two unstable spatially inhomogeneous periodic solutions. Therefore, system (2) is transformed from two unstable spatially inhomogeneous periodic solutions to the stable spatially homogeneous periodic solution, as shown in Fig. 3, with $(b_2,s_2)=(0.003,0.0013)$ and initial conditions $u(x,0)=0.8104+0.05cos(7x)$, $v(x,0)=2.0455+0.05cos(7x)$.

Fig. 3

When $(b_2,s_2)=(0.003,0.0013)$, the positive equilibrium $E^*$ is unstable and there are a pair of unstable spatially inhomogeneous periodic solutions to a stable spatially homogeneous periodic solution. The initial values as $u(x,0)=0.8104+0.05cos(7x),\, v(x,0)=2.0418+0.05cos(7x)$. Here a, c for u(x,t), b, d for v(x,t)

In region ${\mathcal {D}}_2$, system (32) has four equilibria: $E_{0}$, $E_{1}$ and $E_{2}^{\pm }$. The equilibria $E_{0}$ and $E_{1}$ are unstable, and $E_{2}^{\pm }$ are stable equilibria. This indicates that system (2) has an unstable positive constant equilibrium, an unstable spatially homogeneous periodic solution and two stable nonconstant steady states. Hence, system (2) evolves from an unstable spatially homogeneous periodic solution to two stable nonconstant steady states, as shown in Fig. 4, with $(b_2,s_2)=(0.04,0.021)$ and initial conditions $u(x,0)=0.8301+0.4cos(7x)$, $v(x,0)=1.9934+0.5cos(7x)$.

Fig. 4

When $(b_2,s_2)=(0.04,0.021)$, the positive equilibrium $E^*$ is unstable and there is an unstable spatially homogeneous periodic solution to two stable nonconstant steady states. The initial values as$u(x,0)=0.8301+0.4cos(7x),\, v(x,0)= 1.9934+0.4cos(7x)$. Here a, c for u(x, t), b, d for v(x, t)

In region ${\mathcal {D}}_3$, system (32) has two equilibria: $E_{0}$ and $E_{2}^{\pm }$. The equilibrium $E_{0}$ is unstable, and $E_{2}^{\pm }$ are stable equilibria. This shows that system (2) has an unstable positive constant equilibrium, and two stable nonconstant steady states, as shown in Fig. 5, with $(b_2,s_2)=(0.032,0.033)$ and initial conditions $u(x,0)=0.8421+0.05cos(7x)$, $v(x,0)=2.0030+0.05cos(7x)$.

Fig. 5

When $(b_2,s_2)=(0.032,0.033)$, the positive equilibrium $E^*$ is unstable and two nonconstant steady state solutions are stable. The initial values as $u(x,0)=0.8421+0.065cos(7x),\, v(x,0)=2.0030+0.065cos(7x)$. Here a, c for u(x, t), b, d for v(x, t)

In region ${\mathcal {D}}_4$, system (32) only has one equilibrium: $E_{0}$. Moreover, $E_{0}$ is locally asymptotically stable. Hence, the original system (2) has a stable positive constant equilibrium. This reveals that system (2) evolves from a stable positive constant equilibrium, as shown in Fig. 6, with $(b_2,s_2)=(-0.01,0.02)$ and initial conditions $u(x,0)=0.8191+0.65cos(7x)$, $v(x,0)=2.0079+0.65cos(7x)$.

Fig. 6

When $(b_2,s_2)=(-0.01,0.02)$, the positive equilibrium $E^*$ is locally asymptotically stable. The initial values as $u(x,0)=0.8191+0.065cos(7x),\, v(x,0)=2.0079+0.065cos(7x)$. Here a for u(x, t), b for v(x, t)

In region ${\mathcal {D}}_5$, system (32) has two equilibria: $E_{0}$ and $E_{1}$. $E_{0}$ is unstable and $E_{1}$ is stable. This manifests that system (2) has an unstable positive constant equilibrium and a stable spatially homogeneous periodic solution. Therefore, system (2) evolves from an unstable positive constant equilibrium to a stable spatially homogeneous periodic solution, as shown in Fig. 7, with $(b_2,s_2)=(-0.04,-0.05)$ and initial conditions $u(x,0)=0.7591+0.065cos(7x)$, $v(x,0)=2.1271+0.065cos(7x)$.

Fig. 7

When $(b_2,s_2)=(-0.04,-0.05)$, the positive equilibrium $E_*=(1.6547,0.6547)$ is unstable and a stable spatially homogeneous periodic solution. The initial values as $u(x,0)=0.7591+0.065cos(6x),\, v(x,0)=2.1271+0.065cos(6x)$. Here a for u(x,t), b for v(x,t)

In region ${\mathcal {D}}_6$, system (32) has four equilibria: $E_{0}$, $E_{1}$ and $E_{2}^{\pm }$. The equilibria $E_{0}$ and $E_{2}^{\pm }$ are unstable, and $E_{1}$ is  stable. This demonstrates that system (2) has an unstable positive constant equilibrium, two unstable nonconstant steady states and a stable spatially homogeneous periodic solution. Therefore, system (2) evolves from two unstable nonconstant steady states to a stable spatially homogeneous periodic solution, as shown in Fig. 8, with $(b_2,s_2)=(-0.002,-0.008)$ and initial conditions $u(x,0)=0.8011+0.065cos(7x)$, $v(x,0)=2.0630+0.065cos(7x)$.

Fig. 8

When $(b_2,s_2)=(-0.002,-0.008)$, the positive equilibrium $E^*$ is unstable and there are two unstable nonconstant steady states to a stable spatially homogeneous periodic solution. The initial values as $u(x,0)=0.8011+0.065cos(7x),\, v(x,0)=2.0630+0.065cos(7x)$. Here a, c for u(x, t), b, d for v(x, t)

5 Discussion

Spatiotemporal dynamics of system (2) near Turing–Hopf bifurcation point  are studied. First, under some conditions, the conditions of Turing instability and Hopf bifurcation are obtained. Then, choosing b and s as the bifurcation parameter, through qualitative calculation, one gets the existence of Turing–hopf bifurcation. Hence, the complex dynamical behaviours will appear.

In order to understand what kind of patterns will appears, the technique of the multiple time scale analysis is adopted to derive amplitude equations. System (2) exhibits rich spatiotemporal patterns, such as constant steady state solutions, nonconstant steady state solutions, spatially homogeneous periodic solutions and spatially inhomogeneous periodic solutions. The parameter plane is divided into six regions by the four straight lines. Within these regions different patterns are simulated, in particular, spatially inhomogeneous periodic solutions, which are generated by Turing–Hopf bifurcation. Note that spatially inhomogeneous periodic solutions only appear in ${\mathcal {D}}_1$ (see Fig. 3). Such spatiotemporal patterns can better explain the chemical oscillation between the concentrations of activators and inhibitors, and can be used for medical testing. In the end, numerical simulations are used to support the theoretical analysis. Actually, the Turing–Hopf bifurcation with two-dimensional spatial domain can produce more complicated spatiotemporal phenomena (see [28]), which will be further studied in the future.