Turing instability and Hopf bifurcation of a spatially discretized diffusive Brusselator model with zero-flux boundary conditions

Abstract

In the present paper, a spatially discretized diffusive Brusselator model with zero-flux boundary conditions is considered. Firstly, the global existence and uniqueness of the positive solution are proved. Then the local stability of the unique spatially homogeneous steady state is considered by analyzing the relevant eigenvalue problem with the aid of decoupling method. Hence, the occurrence conditions of Turing bifurcation and Hopf bifurcation for the model at this steady state are obtained. Meanwhile, the comparative simulations on the stability regions of the steady state between the spatially discretized diffusive Brusselator model and its counterpart in continuous space are given. Furthermore, the approximate expressions of the bifurcating periodic solutions are derived according to Hopf bifurcation theorem. The bifurcating spatially nonhomogeneous periodic solutions show the formation of a special kind of periodic structures for this model. Finally, numerical simulations are given to demonstrate the theoretical results.

1 Introduction

The Brusselator reaction-diffusion model, which was introduced by Prigogine and Lefever in 1968 as the first reaction-diffusion model to study chemical instabilities, became the classical paradigm used in many researches devoted to dissipative structures [1,2,3]. Actually, the theory of oscillating reactions was accepted in chemically mechanism until the named “Brusselator” was proposed [4]. And further, the Brusselator model can describe the chemical morphogenesis and pattern formation, the studies of which receive more and more attentions nowadays. The modeling of the Brusselator was based on the assumption of a simple reaction scheme, which consists of the following steps:

$$\begin{aligned}&A\rightarrow X,\\&2X+Y\rightarrow 3X, \\&B+X\rightarrow Y+F,\\&X\rightarrow E, \end{aligned}$$

wherein the overall reaction is $A+B\rightarrow E+F.$

In this process, X and Y represent the two intermediate components, A and B denote the two reactants, and E and F denote the two final products, respectively. In addition, the concentrations of the initial and final products A, B, E, F are maintained constant. In the following kinetic equations, A, B also denote the concentrations of the two reactants, respectively. Hence A, B are positive constants as follows.

For simplification, Prigogine and Lefever [5] assumed a one-dimensional medium and derived the following kinetic equations

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle X_t= D_X\frac{\partial ^2 X}{\partial r^2} +k_1A+k_2X^2Y-k_3BX-k_4X,\\ \displaystyle Y_t= D_Y\frac{\partial ^2 Y}{\partial r^2} +k_3BX-k_2X^2Y. \end{array} \right. \end{aligned}$$

(1.1)

(see, e.g., [5,6,7] for more details). Here X(r, t) and Y(r, t) denote the concentrations of the two intermediate components X and Y at space location r and time t, respectively. The parameters $D_X$ and $D_Y$ denote the Fickian molecular diffusion coefficients of X and Y, respectively. Moreover, $k_1,k_2,k_3,k_4$ denote the reaction coefficients of every step, respectively.

Due to the abundant dynamics, the Brusselator model has been widely studied in the literature. For examples, the existence and global behavior of spatially nonhomogeneous steady state were investigated in [8,9,10,11,12,13,14,15]. The existence of a global attractor was discussed in [6, 16, 17]. The existence of Turing instability and Turing patterns was established in [7, 12, 18, 19]. The existence of Hopf bifurcation was studied in [12, 19,20,21,22,23,24,25]. The spatiotemporal Turing–Hopf pinning solutions was found in [26]. Very recently, Turing instability and spatially homogeneous Hopf bifurcation subject to Neumann boundary condition was studied in [27].

By scaling of the variables as that in [7], we can assume all of $k_1,k_2,k_3,k_4$ equal to 1. Without loss of generality, we further assume r belongs to [0, 1] as that in [25], then model (1.1) becomes

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle X_t= d\frac{\partial ^2 X}{\partial r^2} -(B+1)X+X^2Y+A, \\ \displaystyle Y_t= \theta d\frac{\partial ^2 Y}{\partial r^2} +BX-X^2Y, \end{array} \right. \end{aligned}$$

(1.2)

where $d=D_X, \theta =D_Y/D_X,r \in [0,1].$ Model (1.2) has a unique stationary solution given by (A, B/A). To shift this stationary solution to the origin, let

$$\begin{aligned} x(r,t)=X(r,t)-A,\ y(r,t)=Y(r,t)-B/A, \end{aligned}$$

then model (1.2) becomes

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle x_t= d\frac{\partial ^2 x}{\partial r^2} +(B-1)x+A^2y+h(x,y),\\ \displaystyle y_t= \theta d\frac{\partial ^2 y}{\partial r^2} -Bx-A^2y-h(x,y), \end{array} \right. \end{aligned}$$

(1.3)

where $\displaystyle h(x,y)=(B/A)x^2+2Axy+x^2y,$ and r belongs to [0, 1].

As mentioned above, the existence of Hopf bifurcations of model (1.3) was considered, respectively, in [25], where both zero-flux boundary conditions and fixed boundary conditions were considered. In order to perform the numerical calculations of Hopf bifurcation formulae, the spatially discretized counterpart of model (1.3) was also derived by using a simple finite difference scheme therein. Actually, for some integer $n\ge 1$ and $k \in S_n\triangleq \{1,2,\cdots ,n\}$, let $\varDelta r=1/(n-1)$ and $r_k=k\varDelta r$, then $x(r_k,t)$ and $y(r_k,t)$ can be approximated by $x_k(t)$ and $y_k(t)$, respectively. Further, by using 3-point centered difference approximations for $\frac{\partial ^2 x}{\partial r^2}$ and $\frac{\partial ^2 y}{\partial r^2}$, they derived the spatially discretized diffusive Brusselator model:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{dx_k}{dt}= D\nabla ^{2} x_k+(B-1)x_k+A^2y_k+h(x_k,y_k),\\ \displaystyle \frac{dy_k}{dt}= \theta D\nabla ^{2} y_k-Bx_k-A^2y_k-h(x_k,y_k), \end{array} \right. \end{aligned}$$

(1.4)

where $k\in S_n,D=d/(\varDelta r)^2=(n-1)^2d$ and $\nabla ^{2}$ denotes the discrete diffusion $\nabla ^{2}u_k=u_{k-1}-2u_k+u_{k+1}$.

The spatially discretized equations had been studied a lot. To name a few, the spatially discretized FitzHugh–Nagumo equations was studied in [28] and the spatially discretized Ginzburg–Landau–BBM equations was studied in [29]. The spatially discretized equations are essentially coupled ordinary differential ones, which also arises from mathematical models in many scientific disciplines, such as CY-CNN models [30,31,32,33], epidemic models on patches [34,35,36]. In Turing’s famous paper [37], he exactly used this kind of differential equations to show his striking idea of “diffusion-driven instability”.

To ensure the positivities of $X(r_k,t)$ and $Y(r_k,t)$, we consider system (1.4) subject to the following initial conditions

$$\begin{aligned} x_k(0)\ge -A,y_k(0)\ge -B/A,\ \forall k \in S_n. \end{aligned}$$

(1.5)

Furthermore, we consider the zero-flux boundary conditions

$$\begin{aligned}&x_{0}(t)=x_1(t), x_{n+1}(t)=x_n(t), \nonumber \\&y_{0}(t)=y_1(t), y_{n+1}(t)=y_n(t),\ t\ge 0. \end{aligned}$$

(1.6)

The boundary conditions (1.6) correspond to the spatially discretized Neumann boundary conditions for reaction-diffusion equations.

In [25], model (1.4) was studied numerically to show that the Hopf bifurcating parameters agree quite well with its counterpart in continuous space, i.e., model (1.3), without theoretical analyses. In the present paper, we provide the rigorous theoretical analyses on Turing instability and Hopf bifurcation for model (1.4). The theoretical analyses suggest that the dynamical behaviors of model (1.4) may be different from that of the diffusive Brusselator model (1.3), when n is small. On the contrary, some of the dynamical behaviors of model (1.4) approximate that of (1.3) when n is large enough.

The remaining parts of this paper are organized as follows. In Sect. 2, the global existence and uniqueness of the positive solution to the initial-boundary value problem (1.4)–(1.6) are considered. In Sect. 3, the local stability of the unique spatially homogeneous steady state of (1.4)–(1.6) is studied. Then the conditions, which induce Turing bifurcation and Hopf bifurcation at the steady state, are derived. In Sect. 4, by choosing B as the bifurcation parameter, the existence of Hopf bifurcation for (1.4) -(1.6) at the steady state is considered. Furthermore, we derive the approximate expressions of the bifurcating periodic solutions, which show the formation of temporal periodic structures with spatially nonhomogeneous features. In Sect. 5, numerical simulations are carried out to illustrate the derived theoretical results.

2 Global existence and uniqueness of the positive solution

In this section, we prove the solution of the initial-boundary value problem (1.4)–(1.6) satisfies

$$\begin{aligned} x_k(t)+A\ge 0,\ y_k(t)+B/A\ge 0,\ \forall k \in S_n. \end{aligned}$$

Furthermore, we derive the global existence and uniqueness of the solution.

Obviously, the initial-boundary value problem (1.4)–(1.6) has a unique spatially homogeneous steady state

$$\begin{aligned} E^*=(0,0,0,0,\cdots ,0,0)\in \mathbb {R}^{2n}. \end{aligned}$$

Firstly, we have

Theorem 1

The initial-boundary value problem (1.4)–(1.6) has a locally unique solution $x_k(t), y_k(t)$ for all $k\in S_n$. Furthermore, the solution admits

$$\begin{aligned} x_k(t)+A\ge 0,\ y_k(t)+B/A\ge 0,\ \forall k \in S_n. \end{aligned}$$

Proof

The local existence and uniqueness of the solution of (1.4)–(1.6) can be derived from the theories of ODEs. Hence, we only need to prove $x_k(t)>-A$ and $y_k(t)>-B/A,\ \forall k\in S_n$. There are four steps.

Step I: We prove that the solution $x_k(t)>-A$ in the right neighborhood of $t=0,\ \forall k\in S_n$. That is, there exists a $t^i_0$ such that $x_k(t)>-A$ for any $0<t<t^i_0$. Actually, if $x_k(0)>-A$, then the result can be derived from the continuity of solutions. If $x_k(0)=-A$, then the result can be derived by the following observation that

$$\begin{aligned} \frac{dx^+_k(0)}{dt}=D(x_{k-1}(0)+x_{k+1}(0)+2A)+A\ge A>0. \end{aligned}$$

Step II: We then show $x_k(t)>-A, t>0$ for all $k\in S_n$ by contradiction. For this, we assume there exist some $i_1,i_2,\cdots ,i_n\in S_n$ and $t^{i_1},t^{i_2},\cdots ,t^{i_n}>0$ such that $x_{i_k}(t^{i_k})=0$. Here $t^{i_k}$ denote the first $t>0$ such that $x_{i_k}(t)=-A$. Hence, $\frac{dx_{i_k}(t^{i_k})}{dt}\le 0,\forall k=1,2 \cdots ,n.$ Denoting $t^{i_*}=\min \{t^{i_k} |~ k=1,2 \cdots ,n\}>0$, by the first equation of (1.4) , we have

$$\begin{aligned} \frac{dx_{i_*}(t^{i_*})}{dt}= & {} D(x_{i_*-1}(t^{i_*})+x_{i_*+1}(t^{i_*})+2A)\\&\quad +A\ge A>0. \end{aligned}$$

It is a contradiction. From the continuity of $x_k(t)$, we have $x_k(t)>-A.$

Step III: We prove that the solution $y_k(t)>-B/A$ in the right neighborhood of $t=0,\ \forall k\in S_n$. That is, there exists a $t^i_0$ such that $y_k(t)>-B/A$ for any $0<t<t^i_0$. Actually, if $y_k(0)>-B/A$, then the result can be derived from the continuity of solutions. If $y_k(0)=-B/A$, then the result can be derived by the following observation that

$$\begin{aligned} \frac{dy^+_k(0)}{dt}= & {} \theta D(y_{k-1}(0) +y_{k+1}(0)\\&+2B/A)+B(x_k(0)+A)>0. \end{aligned}$$

Step IV: We then show $y_k(t)>-B/A, t>0$ for all $k\in S_n$ by contradiction. For this, we assume there exist some $i_1,i_2,\cdots ,i_n\in S_n$ and $t^{i_1},t^{i_2},\cdots ,t^{i_n}>0$ such that $y_{i_k}(t^{i_k})=-B/A$. Here, $t^{i_k}$ denote the first $t>0$ such that $y_{i_k}(t)=-B/A$. Hence, $\frac{dy_{i_k}(t^{i_k})}{dt}\le 0,\forall k=1,2 \cdots ,n.$ Denoting $t^{i_*}=\min \{t^{i_k}|~ k=1,2 \cdots ,n\}>0$, by the second equation of system (1.4) and step II, we have

$$\begin{aligned}&\frac{dy_{i_*}(t^{i_*})}{dt}=\theta D(y_{i_*-1}(t^{i_*})+y_{i_*+1}(t^{i_*})+2B/A)\\&\quad +B(x_k(t^{i_*})+A)>0. \end{aligned}$$

It is a contradiction. From the continuity of $y_k(t)$, we have $y_k(t)>-B/A.$ $\square$

Secondly, we prove the global existence of the solution. For this, we denote

$$\begin{aligned} X(t)=\sum \limits _{k=1}^{n}x_k(t),Y(t)=\sum \limits _{k=1}^{n}y_k(t). \end{aligned}$$

According to system (1.4) and the boundary value (1.6), we have

$$\begin{aligned} \frac{d(X(t)+Y(t))}{dt}=-X(t), \end{aligned}$$

which further satisfy the initial value

$$\begin{aligned} X(0)\ge -nA, Y(0)\ge -nB/A, \end{aligned}$$

due to the initial value (1.5).

Hence, we have

$$\begin{aligned} X(t)+Y(t)=X(0)+Y(0)-\int _0^tX(s)\mathrm{d}s. \end{aligned}$$

On the other hand, we have

$$\begin{aligned} -\int _0^tX(s)\mathrm{d}s\le nAt, \end{aligned}$$

based on the result of Theorem 1. Hence, $x_k(t), y_k(t)$ are bounded for any given time t. This fact suggests the global existence of the solution. Combining with Theorem 1, we derive the global existence and uniqueness of the positive solution to the initial-boundary value problem (1.4)–(1.6).

3 Local stability of the spatially homogeneous steady state

In this section, we discuss the local stability of the steady state $E^*$ of the initial-boundary value problem (1.4)–(1.6). For this, we need to consider the following linearized system of (1.4)–(1.6) at $E^*$ :

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{dx_k}{dt}= D\nabla ^{2} x_k+(B-1)x_k+A^2y_k,\\ \displaystyle \frac{dy_k}{dt}= \theta D\nabla ^{2} y_k-Bx_k-A^2y_k. \end{array} \right. \end{aligned}$$

(3.1)

We firstly use the decoupling method to derive the characteristic equation of (3.1). Then we derive the results on the local stability of $E^*$ by analyzing the distribution of the roots of the characteristic equation. These results show the occurrence conditions of Hopf bifurcation and Turing bifurcation for model (1.4). Furthermore, we make some comparisons on the differences between the spatially discretized diffusive Brusselator model (1.4) and its counterpart in continuous space, i.e., model (1.3).

3.1 Decoupling method

In order to analyze (3.1), we use the decoupling method, which goes back at least as far as 1971 with the work of Othmer and Scrivens [38]. Nevertheless, we only need a simplified form of this method as that in [32, 39] here. For more details of this method, we also refer to [40]. The main idea of this technique is to look for the general solution of system (3.1) in the form

$$\begin{aligned} \left\{ \begin{array}{ll} x_k(t)= \sum \limits _{m=1}^{n}\phi (m,k)\hat{x}_m(t),\ k \in S_n, \ t\ge 0,\\ y_k(t)= \sum \limits _{m=1}^{n}\phi (m,k)\hat{y}_m(t),\ k \in S_n, \ t\ge 0. \end{array} \right. \end{aligned}$$

(3.2)

Here $\hat{x}_m(t),\hat{y}_m(t), m\in S_n$ denote the weighting coefficients, while $\phi (m,k),m\in S_n$ denote the spatial eigenfunctions of the operator $\nabla ^{2}$ corresponding to eigenvalues $-\mu ^2_m$. For the zero-flux boundary conditions (1.6), we choose the eigenvalues and their corresponding eigenfunctions to be

$$\begin{aligned} -\mu ^2_m=-4\sin ^2\frac{(m-1)\pi }{2n},\ m \in S_n, \end{aligned}$$

(3.3)

and

$$\begin{aligned} \phi (m,k)=\left\{ \begin{array}{ll} \displaystyle \sqrt{\frac{1}{n}}\cos {\frac{(2k-1)(m-1)\pi }{2n}},\ m=1,\ k \in S_n,\\ \displaystyle \sqrt{\frac{2}{n}}\cos {\frac{(2k-1)(m-1)\pi }{2n}},\ m\ne 1,\ k \in S_n, \end{array} \right. \end{aligned}$$

(3.4)

respectively. That is

$$\begin{aligned}&\nabla ^{2}\phi (m,k)=\phi (m,k-1)-2\phi (m,k)+\phi (m,k+1)\nonumber \\&\quad =-\mu ^2_m\phi (m,k), \end{aligned}$$

(3.5)

for any $m,k\in S_n,$ and

$$\begin{aligned} \left<\phi (m_1,\cdot ),\phi (m_2,\cdot )\right> =\left\{ \begin{array}{ll} 1,\ m_1=m_2,\\ 0,\ m_1\ne m_2, \end{array} \right. \end{aligned}$$

(3.6)

for any $m_1,m_2\in S_n$. Here $\left<\cdot ,\cdot \right>$ denotes the scalar product in $\mathbb {R}^n,$ i.e.,

$$\begin{aligned} \left<\phi (m_1,\cdot ),\phi (m_2,\cdot )\right>=\sum \limits _{k\in S_n}\phi (m_1,k)\phi (m_2,k). \end{aligned}$$

We note that the eigenfunctions chosen here are orthonormal as those in [39], which are slightly different from those in [32]. The choice of the normal eigenfunctions do not affect the analyses of the local stability, whereas it is important for the analyses of the Hopf bifurcation in the next section.

By the decoupling method similar to that in [32, 39], we can derive the following characteristic equation of (3.1):

$$\begin{aligned} \lambda ^2_m-T_m\lambda _m+D_m=0,\ m\in S_n, \end{aligned}$$

(3.7)

where

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle T_m= T_m(A,B,D,\theta )=-(\theta +1)D\mu ^2_m \\ \qquad \quad +B-1-A^2,\\ \displaystyle D_m=D_m(A,B,D,\theta )=\theta D^2\mu ^4_m \\ \qquad \quad +(A^2-\theta (B-1))D\mu ^2_m+A^2, \end{array} \right. \end{aligned}$$

(3.8)

and $\lambda _m$ denote the characteristic roots of the linearized system (3.1).

3.2 Local stability analysis

To analyze the local stability of the steady state $E^*$, we need to consider the signs of the real parts of the characteristic roots $\lambda _m$. For this purpose, we solve $T_m=0$ and $D_m=0$ for the parameter B, respectively. Then we have

$$\begin{aligned} B=1+A^2 +(\theta +1)D\mu ^2_m, \end{aligned}$$

and

$$\begin{aligned} B=\frac{1}{\theta }\left( 1+\frac{1}{D\mu _m^2}\right) A^2 +1+D\mu _m^2, ~m\ge 2. \end{aligned}$$

For fixed $\theta$ and $m\in S_n$, define the set of curves $H_m$ and $L_m$ in the $A-B$ plane by

$$\begin{aligned} H_m: ~~B=B_m^H(A) \triangleq 1+A^2 +(\theta +1)D\mu ^2_m,\ m\ge 1, \end{aligned}$$

(3.9)

and

$$\begin{aligned}&L_m:~~B=B_m^T(A) \triangleq \frac{1}{\theta }\left( 1+\frac{1}{D\mu _m^2}\right) A^2 +1+D\mu _m^2, \nonumber \\&\ m\ge 2, \end{aligned}$$

(3.10)

respectively.

Then it is easy to verify that

$$\begin{aligned} T_m\left\{ \begin{array}{ll}<0, &{} B<B_m^H(A), \\ \ge 0, &{} B\ge B_m^H(A), \end{array} \right. ~~ D_m\left\{ \begin{array}{ll} >0, &{} B<B_m^T(A), \\ \le 0, &{} B\ge B_m^T(A). \end{array} \right. \end{aligned}$$

(3.11)

For fixed D, define

$$\begin{aligned} \theta _c=1+\frac{1}{D\mu _n^2}. \end{aligned}$$

(3.12)

Then we have

Theorem 2

Assume that $\theta _c$ is defined by (3.12). When $0<\theta \le \theta _c$, we have the following results for the steady state $E^*$ of (1.4)–(1.6) .

• (i) $E^*$ is unstable when $B>B_1^H(A)$;

• (ii) $E^*$ is locally asymptotically stable when $0<B<B_1^H(A)$;

• (iii) Hopf bifurcation occurs at $E^*$ when $B=B_1^H(A)$.

Proof

By (3.3), it is easy to see that $\mu _m^2$ is strictly monotone increasing with respect to m. This, together with (3.9), implies that

$$\begin{aligned} B_m^H(A) < B_{m+1}^H(A), \text{ for }~ m\in \{1, 2, \cdots , n-1\}. \end{aligned}$$

Hence, by (3.11), $T_m<0$ for all $m\in S_n$ and $0<B<B_1^H(A)$, whereas $T_1>0$ for $B>B_1^H(A)$. Thus, when $m=1$, (3.7) has at least one root with positive real parts. Conclusion (i) follows immediately.

Meanwhile, it follows from (3.9) and (3.10) that the curves $L_m$ interacts with $H_1$ at

$$\begin{aligned} A_m=\sqrt{\frac{\theta D^2\mu _m^4}{(\theta -1) D\mu _m^2-1}}, \end{aligned}$$

(3.13)

if and only if

$$\begin{aligned} \theta >1+\frac{1}{D\mu _m^2} \end{aligned}$$

for $m=2, \cdots , n.$

Noticing again that $\mu _m^2$ is monotone increasing with respect to m, we have $\theta \le 1+\frac{1}{D\mu _m^2}$ when $\theta \le \theta _c$ for $m=2, \cdots , n$. Therefore, the curve $L_m$ cannot interact with $H_1$ for $m=2, \cdots , n$. Hence, all of the curves $L_m, m=2, \cdots , n$ are above the curve $H_1$. This implies that when $0<B<B_1^H(A)$, $T_m<0$ and $D_m>0$. Hence, all roots of (3.7) have negative real parts. Conclusion (ii) is confirmed.

In addition, noticing that $\mu _1=0$, we can conclude that if $B=B_1^H(A)$, then Eq.(3.7) admits a unique pair of purely imaginary roots $\pm iA.$ Furthermore, if we denote $\xi (B)\pm i\eta (B)$ to be the pair of conjugate complex eigenvalues admitting $\xi (B_1^H(A) )=0$, then we have $\xi '(B_1^H(A) )=\frac{1}{2}>0$. This completes the proof of (iii). $\square$

For fixed D and $\theta >\theta _c$, define the index

$$\begin{aligned} \widetilde{m}=\min \left\{ m\in \{2, \cdots , n\} \left| ~ 1+\frac{1}{D\mu _m^2}<\theta \right. \right\} . \end{aligned}$$

(3.14)

Then by the proof of Theorem 2, the curve $L_m$ interacts with $H_1$ at $A=A_m$ for $m\in \{\widetilde{m}, \cdots , n\}$. Let

$$\begin{aligned} A_{m^*}=\min \limits _{m\in \{\widetilde{m}, \cdots , n\} }\left\{ A_m \right\} . \end{aligned}$$

(3.15)

Then $L_{m^*}$ is the first Turing bifurcation curve that interacts with the Hopf bifurcation curve $H_1$ when the parameter A changes from zero to infinity.

By (3.10), it is easy to verify that $L_m$ and $L_{m+1}$ interact at

$$\begin{aligned} A_{m}^L=D\mu _m\mu _{m+1}\sqrt{\theta }. \end{aligned}$$

(3.16)

which is monotonously increasing with respect to m. Define the piecewise function $B=B_c(A)$ by the following

$$\begin{aligned} B_c(A)=\left\{ \begin{array}{ll} B_1^H(A), &{} 0<A\le A_{m^*}, \\ B_{m^*}^T(A), &{} A_{m^*}<A\le A_{m^*}^L, \\ B_m^T(A), &{} A_{m}^L<A\le A_{m+1}^L, m=m^*, \cdots , n-2, \\ B_n^T(A), &{} A> A_{n-1}^L. \end{array} \right. \end{aligned}$$

(3.17)

Then we have the following results on the stability of the steady state $E^*$ and bifurcation when $\theta >\theta _c$.

Theorem 3

Assume that $\theta _c$ is defined by (3.12). When $\theta > \theta _c$, we have the following results for the steady state $E^*$ of (1.4)–(1.6).

• (i) $E^*$ is unstable when $B>B_c(A)$;

• (ii) $E^*$ is locally asymptotically stable when $0<B<B_c(A)$;

• (iii) System (1.4) undergoes Hopf bifurcation at $B=B_c(A)$ for $0<A<A_{m^*}$, while it undergoes Turing bifurcation at $B=B_c(A)$ for $A_{m^*}<A\le A_{m^*}^L$, or $A_{m}^L<A< A_{m+1}^L, m=m^*, \cdots , n-2,$ or $A> A_{n-1}^L$;

• (iv) System (1.4) undergoes Turing–Hopf bifurcation at $(A, B)=\left( A_{m^*}, B_c\left( A_{m^*}\right) \right)$, and Turing–Turing bifurcation at $(A, B)=\left( A_m^L, B_c\left( A_m^L\right) \right)$ for $m=m^*, m^*+1, \cdots , n-1$.

Fig. 1

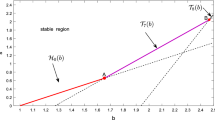
Stability region and bifurcation curves for the spatially homogeneous steady state $E^*$ of model (1.4) in the $A-B$ plane for the parameters $n=10$ and $d=0.1$. a For $\theta =0.5<\theta _c$, the upper boundary of the stability region consists of Hopf bifurcation curve $H_1$ only; b For $\theta =4>\theta _c$, the upper boundary of the stability region consists of both Hopf bifurcation and Turing bifurcation curves. These results show the importance of the choice of the parameter $\theta$ in determining the stability region for $E^*$

From Theorems 2 and 3, we see that the dynamical behaviors of (1.4)–(1.6) become more abundant when the parameter $\theta$ exceeds the Turing bifurcation critical value $\theta _c$. In what follows, we numerically illustrate the results described in Theorems 2 and 3. Choosing $n=10$, $d=0.1$, it then follows from (3.3) and (3.12) that $\theta _c=1.0316$. Then we have the following two simulations, which figuratively illustrate the “shrinkage” of the stability region when $\theta$ becomes larger than $\theta _c$. This result coincides with Turing’s arguments that different diffusion rates could lead to nonhomogeneous distributions of reactants in a system of equations modeling two interactive substances. For more details, we refer to [37, 41, 42].

• (1) Taking $\theta =0.5<\theta _c$, the condition of Theorems 2 is satisfied. The stability region of $E^*$ and bifurcation curves in the $A-B$ plane are shown in Fig. 1a. The steady state $E^*$ loses its stability when the parameter B changes from small to large and crosses the Hopf bifurcation curve $H_1$.

• (2) Taking $\theta =4>\theta _c$, the condition of Theorems 3 is satisfied. Furthermore, we have $\tilde{m}=2, A_{m^*}=A_2\doteq 1.3506$ by (3.14), (3.13) and (3.15), respectively. For this case, the stability region of $E^*$ and bifurcation curves in the $A-B$ plane are shown in Fig. 1b. The steady state $E^*$ loses its stability when the parameter B changes from small to large and crosses the Hopf bifurcation curve $H_1$ for small parameter A, while $E^*$ loses its stability when the parameter B changes from small to large and crosses Turing bifurcation curves $L_2$ or $L_3$ for larger parameter A. The Hopf bifurcation curve $H_1$ interacts with the Turing bifurcation $L_2$ at the point $P_1(1.3506, 2.8240)$, which is called Turing–Hopf bifurcation point. Furthermore, the Turing bifurcation curve $L_2$ interacts with $L_3$ at the point $P_2(3.1325,7.3399)$, which is called Turing–Turing bifurcation point.

3.3 Comparisons on the differences between model (1.4) and model (1.3)

It can be shown that there are similarities and differences of the dynamical behaviors between model (1.4) and that of model (1.3). We take the Turing bifurcation critical value $\theta _c$ for example.

For the Laplace operator $\varDelta$, the corresponding eigenvalues are $-((m-1)\pi )^2$ for $m\in \mathbb {N}$. Thus, for model (1.3), the critical value for the occurrence of Turing bifurcation is $\theta _c=D_Y/D_X=1$. For model (1.4), the critical value $\theta _c$ is always greater than 1 since the maximum $\mu ^2_k$ is $\mu ^2_n$. Hence, the critical value $\theta _c$ for model (1.4) is different from that for model (1.3). On the other hand, for model (1.4), it is seen that $\theta _c$ goes to 1, the critical value for model (1.3), as n approaches to $\infty$. It is seen that there are similarities and differences of the critical value $\theta _c$ between model (1.4) and that of model (1.3).

Fig. 2

Eigenfunctions for the Laplace operator $\varDelta$ and the difference operator $D^2_{\varDelta r}$. a and b are the cases when $m=2$, while c and d are the cases when $m=3$

Hence, it is interesting to compare the theoretical results for model (1.4)with that for model (1.3). In this subsection, we firstly show the relations of the characteristic equations between the linearized equation of model (1.4) and model (1.3).

Remark 1

For the linearized equation of diffusive Brusselator model (1.3), the corresponding characteristic equation has the same form as the equations (3.7), but different expressions

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle T_m=-(\theta +1)d\tilde{\mu }^2_m+B-1-A^2,\\ \displaystyle D_m=\theta d^2\tilde{\mu }^4_m+(A^2-\theta (B-1))d\tilde{\mu }^2_m+A^2, \end{array} \right. \end{aligned}$$

(3.18)

where $\tilde{\mu }^2_m= ((m-1)\pi )^2$ are the eigenvalues of the Laplace operator $\varDelta$ for $x\in (0,1)$ and $m\in \mathbb {N}=\{1, 2, \cdots \}$. Comparing (3.18) with (3.8), it can be verified that (3.8) approximates (3.18) when n is large enough. Actually, we have

$$\begin{aligned} D\mu ^2_m=4d(n+1)^2\sin ^2\frac{(m-1)\pi }{2n}\rightarrow d\tilde{\mu }^2_m,\ n\rightarrow \infty , \end{aligned}$$

since $\sin \frac{(m-1)\pi }{2n}\thicksim \frac{(m-1)\pi }{2n},\ n\rightarrow \infty$.

Secondly, we compare the eigenfunctions between the Laplace operator $\varDelta$ and the difference operator $D^2_{\varDelta r}$, where

$$\begin{aligned} D^2_{\varDelta r}u_k=\frac{u_{k-1}-2u_k+u_{k+1}}{{\varDelta r}^2}=(n-1)^2\nabla ^{2}u_k \end{aligned}$$

denote 3-point centered difference operator. Furthermore, we compare the stability regions for the steady state $E^*$ of model (1.4)with that of model (1.3) in the A-B plane numerically. Actually, if we denote the eigenfunctions of the Laplace operator $\varDelta$ corresponding to $\tilde{\mu }^2_m$ as $\tilde{\phi }(m,x)$, then it is seen $\tilde{\phi }(m,x)$ are actually the continuous corresponding forms of the multiples for $\phi (m,k)$ in (3.4), since $\tilde{\phi }(m,x)=\cos ((m-1)\pi x)$. To illustrate this result, we choose $n=10$ and simulate the eigenfunctions for $m=2$ and 3, respectively. See the following Fig. 2 for details.

Thirdly, we compare the eigenvalues between the Laplace operator $\varDelta$ and the difference operator $D^2_{\varDelta r}$. To illustrate their differences, we choose $n=10$ and derive the following Fig. 3. From this figure, it is seen that the eigenvalues of the Laplace operator differ from that of the difference operator when n is small.

Fig. 3

Eigenvalues for the Laplace operator $\varDelta$ and the difference operator $D^2_{\varDelta r}$

The last point of interest for this subsection is to compare the stability regions of $E^*$ of the spatially discretized diffusive Brusselator model (1.4) with that of its counterpart in continuous space, i.e., model (1.3). With the parameters $n=10,d=0.1,\theta =4$, we simulate the stability regions of the steady state $E^*$ both for model (1.4) and (1.3), then derive Fig. 4.

4 Hopf bifurcation

According to Theorem 2 and 3, there may exist bifurcating periodic solutions of the initial-boundary value problem (1.4)–(1.6) when B cross through $B_1^H(A)$. Hence in this section, by choosing B as the bifurcating parameter, we consider the occurrence of Hopf bifurcation of (1.4)–(1.6) at the spatially homogeneous steady state $E^*$. By using the summarized recipe in [25], we further calculate several quantities to determine the properties of the bifurcating periodic solutions, such as the period, stability, bifurcation direction and approximate expressions of the bifurcating periodic solutions.

Locating the steady state $E^*$, we rewrite system (1.4) subject to the boundary value (1.6) as the abstract form

$$\begin{aligned} \begin{array}{ll} \frac{dU}{dt}= L(B)U+F(U,B), \end{array} \end{aligned}$$

(4.1)

where the Jacobian matrix L(B) is

$$\begin{aligned} {\begin{pmatrix} -D+B-1 &{}A^2 &{} D &{} 0 &{} 0 &{} 0 &{} 0 &{} \dots \ 0 &{} 0 &{} 0 \\ -B &{} -\theta D-A^2 &{} 0 &{} \theta D &{} 0 &{} 0 &{} 0 &{} \dots \ 0 &{} 0 &{} 0\\ D &{} 0 &{} -2D+B-1 &{} A^2 &{} D &{} 0 &{} 0 &{} \dots \ 0 &{} 0 &{} 0\\ 0 &{} \theta D &{} -B &{} -2\theta D-A^2 &{} 0 &{} \theta D &{} 0 &{} \dots \ 0 &{} 0 &{} 0\\ \vdots &{}&{}\ddots &{}&{}&{}&{}&{}&{}&{}\vdots \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \dots \ 0 &{} -D+B-1 &{} A^2\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \dots \ \theta D &{} -B &{} -\theta D-A^2 \end{pmatrix}}, \end{aligned}$$

$U=(x_1,y_1,x_2,y_2,\cdots ,x_n,y_n)^T$ is the solution vector of system (1.4) , and

$$\begin{aligned}&F(U,B)=(h(x_1,y_1),-h(x_1,y_1),h(x_2,y_2),\\&\quad -h(x_2,y_2),\cdots ,h(x_n,y_n),-h(x_n,y_n)) \end{aligned}$$

contains the higher order terms. Hence, the abstract form of the linearization equation of system (1.4) at $E^*$ is

$$\begin{aligned} \begin{array}{ll} \frac{dU}{dt}= L(B)U. \end{array} \end{aligned}$$

(4.2)

In order to verify the conditions for the existence of Hopf bifurcation, we need to compute the eigenvalues and eigenvectors of matrix L(B). By a proof similar to that of Lemma 8 in [39], we can show that the eigenvalues of the Jacobian matrix L(B) are exactly the roots of (3.7). That is,

Fig. 4

Comparison of the stability regions for the steady state $E^*$ of model (1.4) with that of model (1.3) in the $A-B$ plane. For the light green region $D_1$, $E^*$ is stable both for model (1.4) and (1.3). For the pink region $D_2$, $E^*$ is stable for model (1.4) but unstable for (1.3), while the result is just the opposite for the green region $D_3$

Proposition 1

The eigenvalues of matrix L(B) are exactly $\lambda _m,m\in S_n$, i.e., the roots of Eq.(3.7) for all $m\in S_n$. Furthermore, suppose $\hat{X}$ is the eigenvector corresponding to the eigenvalue $\lambda$ of M(B), then $X=\varPhi ^{T}\hat{X}$ is the eigenvector corresponding to the eigenvalue $\lambda$ of Jacobian matrix L(B), where

$$\begin{aligned} \varPhi =\small {\begin{pmatrix} \displaystyle \phi (1,1) &{}0 &{} \phi (1,2) &{} 0 &{} \dots &{} \phi (1,n) &{} 0\\ 0 &{} \phi (1,1) &{}0 &{} \phi (1,2) &{}\dots &{} 0 &{} \phi (1,n)\\ \phi (2,1) &{}0 &{} \phi (2,2) &{} 0 &{}\dots &{} \phi (2,n) &{} 0\\ 0 &{} \phi (2,1) &{}0 &{} \phi (2,2) &{}\dots &{} 0 &{} \phi (2,n)\\ \vdots &{}&{}\ddots &{}&{}&{}&{}\vdots \\ \phi (n,1) &{}0 &{} \phi (n,2)&{}0 &{}\dots &{} \phi (n,n) &{} 0 \\ 0 &{} \phi (n,1) &{}0 &{} \phi (n,2) &{}\dots &{} 0 &{} \phi (n,n)\\ \end{pmatrix}} \end{aligned}$$

and

$$\begin{aligned} M(B)= & {} \begin{pmatrix} L_1 &{} &{} \\ &{} L_2\\ &{}&{}\ddots \\ &{}&{}&{}L_{n} \end{pmatrix} \textit{with}\\ L_m= & {} \begin{pmatrix} -D\mu ^2_m+B-1 &{}A^2 \\ -B&{} -\theta D \mu ^2_m-A^2 \end{pmatrix}. \end{aligned}$$

Proof

Under the transformation $X=\varPhi ^{T} X$, i.e., $\hat{X}=\varPhi X$, system (4.2) becomes

$$\begin{aligned} \begin{array}{ll} \frac{d\hat{X}}{dt}=\varPhi L(B)\varPhi ^{-1} \hat{X}\triangleq M(B)\hat{X}, \end{array} \end{aligned}$$

(4.3)

based on the decoupling transformation (3.2) in Sect. 3. Since $\varPhi$ is an invertible matrix, L(B) is real similar to M(B). Hence, L(B) has the same eigenvalues as that of M(B). Furthermore, it is easy to see that the eigenvalues of M(B) are the roots of Eq.(3.7). Furthermore, supposing $\hat{X}$ is the eigenvector corresponding to the eigenvalue $\lambda$ of M(B), then $X=\varPhi ^{T}\hat{X}$ is the eigenvector corresponding to the eigenvalue $\lambda$ of L(B). Hence, the proof is completed. $\square$

By Proposition 1 and Hopf bifurcation theorem, we next need to derive the conditions which ensure the positivity of $D_m$ for all $m\in S_n$ when B locates in the neighborhood of $B_1^H(A)$. For this, we define the following quadratic function of the variable $\mu$ as

$$\begin{aligned} F(\mu )\triangleq \theta D^2\mu ^2+(A^2-\theta (B-1))D\mu +A^2. \end{aligned}$$

It is easy to see that $F(\mu _m^2)=D_m$. Furthermore, when $B=B_1^H(A)$, $F(\mu )$ becomes

$$\begin{aligned} F(\mu ,B_1^H(A))=\theta D^2\mu ^2+A^2(1-\theta )D\mu +A^2. \end{aligned}$$

The discriminant function of $F(\mu ,B_1^H(A))=0$ is

$$\begin{aligned} \varGamma =A^4(1-\theta )^2D^2-4\theta D^2A^2=A^2D^2(A^2(1-\theta )^2-4\theta ). \end{aligned}$$

If $0<\theta \le 1$, then it is easy to see that $F(\mu ,B_1^H(A))>0$. Hence, $D_m>0$ for all $m\in S_n$. If $\theta >1$, we define

$$\begin{aligned} A_0=\displaystyle \frac{2\sqrt{\theta }}{\theta -1}, \end{aligned}$$

then we have

$$\begin{aligned} \displaystyle \varGamma \left\{ \begin{array}{ll} \displaystyle< 0,\ \text{ for } \ 0<A<A_0,\\ \displaystyle = 0,\ \text{ for } \ A=A_0,\\ \displaystyle>0,\ \text{ for } \ A>A_0. \end{array} \right. \end{aligned}$$

(4.4)

In the following, we denote the two real roots of $F(\mu ,B_1^H(A))=0$ as

$$\begin{aligned} \mu _\pm =\frac{(\theta -1)A^2\pm \sqrt{(\theta -1)^2A^4-4\theta A^2}}{2\theta D}, \end{aligned}$$

when $\varGamma >0$, while we denote the multiple root of $F(\mu )=0$ as

$$\begin{aligned} \mu _*=\frac{(\theta -1)A^2}{2\theta D} \end{aligned}$$

when $\varGamma =0$.

According to the above discussions, we have

Theorem 4

Assume the following conditions (C):

• 1. $0<\theta \le 1;$ or

• 2. $\theta >1,$ and $0<A< A_0;$ or

• 3. $\theta >1,$ $A=A_0$ and $\mu ^2_m\ne \mu _*,\forall m\in S_n;$ or

• 4. $\theta >1,$ $A>A_0$ and $\mu ^2_m\notin (\mu _-,\mu _+),\forall m\in S_n.$

Then Eq.(3.7) has periodic solutions bifurcating from $E^*$ when B locates in the neighbor of $B_1^H(A)$.

Proof

It is easy to see that the conditions (C) equals to $D_{m}>0$ for any $m\in S_n$. Furthermore, $T_1=0$ and $T_{m}<0$ for any $m\ge 2$ under the condition $B=B_1^H(A)$. Hence, Eq.(3.7) admits a pair of purely imaginary roots

$$\begin{aligned} \pm i\omega _0=\pm iA \end{aligned}$$

when $m=1$, while all the other eigenvalues $\lambda _{m_1}, \lambda _{m_2},\forall m\ge 2$ have negative real part. Hence, there exist periodic solutions bifurcating from $E^*$ according to Hopf bifurcation theorem [25]. $\square$

In the rest of this section, we mainly focus on the computations of the bifurcating parameters. In fact, we have the following result.

Theorem 5

Assuming (C), the Hopf bifurcation of the initial-boundary value problem (1.4)–(1.6) occurs at $E^*$ when the parameter B increasingly cross through $B_1^H(A)$, i.e., the Hopf bifurcation is supercritical. Furthermore, the bifurcating periodic solution is orbitally asymptotically stable with period

$$\begin{aligned} T=\frac{2\pi }{A}(1+\tau _2\epsilon ^2+o(\epsilon ^4)), \end{aligned}$$

where $\epsilon ^2=\frac{B-B_1^H(A)}{\mu _2}+o(B-B_1^H(A)).$

Proof

According to the summarized recipe in [25], the first quantity to be computed is the eigenvector $\nu _0$ corresponding to the eigenvalue iA of $L(B_1^H(A))$. Further, by Proposition 1, the eigenvector $\hat{\nu }_0$ of $M(B_1^H(A))$ corresponding to the eigenvalue iA should be computed in advance. It is easy to show that we can choose

$$\begin{aligned} \displaystyle \hat{\nu }_0=(1,-1+i \frac{1}{A},0,\cdots ,0)^T. \end{aligned}$$

Then we have

$$\begin{aligned} \begin{array}{ll} \displaystyle \tilde{\nu }_0=\varPhi ^{T}\hat{\nu }_0=(\phi (1,1),-\phi (1,1),\phi (1,2),-\phi (1,2),\\ \quad \quad \quad \quad \quad \quad \quad \times \cdots ,\phi (1,n),-\phi (1,n))^T\\ \quad \quad \quad \quad \quad \quad \displaystyle -i\frac{1}{A}(0,\phi (1,1),0,\phi (1,2),\cdots ,0,\phi (1,n))^T \end{array} \end{aligned}$$

to be an eigenvector corresponding to the eigenvalues iA of $L(B_1^H(A))$. Hence,

$$\begin{aligned} \nu _0= & {} \sqrt{n}\tilde{\nu }_0=(1,-1,1,-1,\cdots ,1,-1)^T\\&\quad +i\frac{1}{A}(0,1,0,1,\cdots ,0,1)^T \end{aligned}$$

is the eigenvector corresponding to the eigenvalues iA of $L(B_1^H(A))$, such that the first nonvanishing component is normalized to be 1.

Let P be the block matrix

$$\begin{aligned} (Re \nu _0, -Im \nu _0, \varepsilon _3, \varepsilon _4, \cdots , \varepsilon _{2n-1}, \varepsilon _{2n}), \end{aligned}$$

where $\varepsilon _k\in \mathbb {R}^{2n}$ denote the standard unit vectors, whose k-th component is 1 and the other components are 0.

By the change of variables

$$\begin{aligned} U=P V, \end{aligned}$$

where $V=(\hat{x}_1,\hat{y}_1,\hat{x}_2,\hat{y}_2,\cdots ,\hat{x}_n,\hat{y}_n)^T\in \mathbb {R}^{2n}$ is a vector function of t, system (4.1) becomes

$$\begin{aligned} \frac{dV}{dt}= & {} P^{-1}\frac{dU}{dt}=P^{-1}[L(B)U+F(U,B)]\nonumber \\= & {} P^{-1}L(B)P V+P^{-1}F(P V,B). \end{aligned}$$

(4.5)

where $P^{-1}L(B)PV$ is the linear part and $P^{-1}F(PV,B)$ is the higher-order terms.

To proceed with the summarized recipe in [25], we further need the concrete expressions of system (4.5). For the matrix $P^{-1}L(B_1^H(A))P$, we know it has the real canonical form

$$\begin{aligned} \begin{pmatrix} 0 &{} -A &{} \\ A&{} 0 &{}\\ &{}&{}\tilde{L} \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} \tilde{L}=\begin{pmatrix} L_2 &{} &{} \\ &{} L_3\\ &{}&{}\ddots \\ &{}&{}&{}L_n \end{pmatrix}. \end{aligned}$$

For the higher-order terms, denoting

$$\begin{aligned} P^{-1}F(P V,B)=(F^1,F^2,\cdots ,F^{2n})^T, \end{aligned}$$

we have

$$\begin{aligned} F^1= & {} h(x_1,y_1),\\ F^2= & {} 0, \end{aligned}$$

and

$$\begin{aligned} F^k=\left\{ \begin{array}{ll} \displaystyle -h(x_1,y_1)+h(x_{\frac{k+1}{2}},y_{\frac{k+1}{2}}), \text{ for } \text{ k } \text{ odd },\\ \displaystyle h(x_1,y_1)+h(x_{\frac{k}{2}},y_{\frac{k}{2}}),\text{ for } \text{ k } \text{ even }, \end{array} \ 3\le k\le 2n, \right. \end{aligned}$$

where $x_1=\hat{x}_1,y_1=-\hat{x}_1-\frac{1}{A}\hat{y}_1,$ $x_k=\hat{x}_1+\hat{x}_k,y_k=-\hat{x}_1-\frac{1}{A}\hat{y}_1+\hat{y}_k\ \text{ for }\ k\ge 2,$ according to the transformation $U=P V$.

With the above expressions and through tedious computations, we have

$$\begin{aligned}&\frac{\partial ^2 F^1}{\partial \hat{x}^2_1}=\frac{2}{A}-2A,\ \frac{\partial ^2 F^1}{\partial \hat{x}_1\hat{y}_1}=-2,\\&\frac{\partial ^3 F^1}{\partial \hat{x}^3_1}=-6,\ \frac{\partial ^3 F^1}{\partial \hat{x}^2_1\hat{y}_1}=-\frac{2}{A},\\&\frac{\partial ^2 F^1}{\partial \hat{y}^2_1}= \frac{\partial ^2 F^2}{\partial \hat{x}^2_1}=\frac{\partial ^2 F^2}{\partial \hat{y}^2_1}=\frac{\partial ^2 F^2}{\partial \hat{x}_1\hat{y}_1}=0,\\&\frac{\partial ^3 F^1}{\partial \hat{x}_1\hat{y}^2_1}=\frac{\partial ^3 F^1}{\partial \hat{y}^3_1}= \frac{\partial ^3 F^2}{\partial \hat{x}_1\hat{y}^2_1}=\frac{\partial ^3 F^2}{\partial \hat{x}^2_1\hat{y}_1}= \frac{\partial ^3 F^2}{\partial \hat{x}^3_1}=\frac{\partial ^3 F^2}{\partial \hat{y}^3_1}=0 \end{aligned}$$

at $B=B_1^H(A),V=0.$

Then we derive the following quantities by using the formulae in [25]:

$$\begin{aligned} 2g_{11}= & {} \frac{1}{A}-A,2g_{02}=\frac{1}{A}-A-2i=2\bar{g}_{20},\\ 4G_{21}= & {} -3+i\frac{1}{A}. \end{aligned}$$

Meanwhile, we have

$$\begin{aligned} \frac{\partial ^2 F^1}{\partial \hat{x}_1\hat{x}_k}=\frac{\partial ^2 F^1}{\partial \hat{x}_1\hat{y}_k}=\frac{\partial ^2 F^1}{\partial \hat{y}_1\hat{x}_k}=\frac{\partial ^2 F^1}{\partial \hat{y}_1\hat{y}_k}=0 \end{aligned}$$

for $k=3,4, \cdots , 2n$. Hence, $G^{k-2}_{110}=G^{k-2}_{101}=0$, which suggest that

$$\begin{aligned} g_{21}=G_{21}=-\frac{3}{4}+i\frac{1}{4A}. \end{aligned}$$

Let

$$\begin{aligned} c_1(0)= & {} \frac{i}{2A}\left[ g_{20}g_{11}-2\mid g_{11}\mid ^2-\frac{1}{3}\mid g_{02}\mid ^2\right] +\frac{g_{21}}{2}\\= & {} -\left\{ \frac{1}{4A^2}+\frac{1}{8}+i\left[ \frac{1}{6A} \left( \frac{1}{A}-A\right) ^2+\frac{1}{24A}\right] \right\} , \end{aligned}$$

then we have

$$\begin{aligned} Re(c_1(0))= & {} -\frac{1}{4A^2}-\frac{1}{8}<0,\\ \mu _2= & {} -Re(c_1(0))/\xi '(B_1^H(A))\\= & {} \frac{1}{2A^2}+\frac{1}{4}>0,\\ \tau _2= & {} -[Im(c_1(0))+\mu _2\eta '(B_1^H(A))]/\eta (B_1^H(A))\\= & {} \frac{1}{6A^2}\left[ \left( \frac{1}{A}-A\right) ^2+\frac{1}{4}\right] >0, \end{aligned}$$

and

$$\begin{aligned} \beta _2=-2\xi '(B_1^H(A))\mu _2<0. \end{aligned}$$

$\square$

We note that these bifurcating parameters Re$(c_1(0)),\mu _2,\tau _2,\beta _2$ for the initial-boundary value problem (1.4)–(1.6) are the same as that for the system (1.3) in the absence of diffusion in [25]. But the expressions of the bifurcating periodic solutions for the initial-boundary value problem (1.4)–(1.6) are different from that for the system (1.3) in the absence of diffusion. Actually, we have the following result.

Theorem 6

The bifurcating periodic solutions in Theorem 5 are spatially nonhomogeneous, which have the following approximate expressions:

$$\begin{aligned} \begin{array}{ll} \displaystyle x_1(t)=\hat{x}_1,\ y_1(t)=-\hat{x}_1-\frac{1}{A}\hat{y}_1,\\ \displaystyle x_k(t)=\hat{x}_1+\hat{x}_k,\ y_k(t)=-\hat{x}_1-\frac{1}{A}\hat{y}_1+\hat{y}_k,\\ \end{array} \end{aligned}$$

(4.6)

where $\ k=2,\cdots ,n.$

Proof

In order to show the difference, we compute the approximate expressions of the bifurcating periodic solution in the variables of U. For this, we compute the approximate expressions in the variables of V in advance.

According to the results in [25], it is easy to see that

$$\begin{aligned} \hat{x}_1= & {} \epsilon \cos \frac{2\pi t}{T}\\&+\frac{\epsilon ^2}{6A}\left[ 4\cos {\frac{4\pi t}{T}}+\left( \frac{2}{A}-2A\right) \sin {\frac{4\pi t}{T}}\right] +o(\epsilon ^2),\\ \hat{y}_1= & {} \epsilon \sin \frac{2\pi t}{T}\\&+\frac{\epsilon ^2}{6A} \left[ \left( A-\frac{1}{A}\right) \cos {\frac{4\pi t}{T}}\right. \\&\left. +2\sin {\frac{4\pi t}{T}}+\left( \frac{3}{A}-3A\right) \right] +o(\epsilon ^2). \end{aligned}$$

To compute $\hat{x}_2,\hat{y}_2,\cdots ,\hat{x}_{n},\hat{y}_{n},$ we need to compute $w_{11}$ and $w_{20}$ in advance. They are the solutions of the following linear systems

$$\begin{aligned} \tilde{L}w_{11}=-h_{11},\ (\tilde{L}-2iAI)w_{20}=-h_{20}, \end{aligned}$$

where $h_{11}$ and $h_{20}$ are $n-2$-dimensional vectors, whose components are

$$\begin{aligned} h^{k-2}_{11}= & {} \frac{1}{4}\left[ \frac{\partial ^2 F^k}{\partial \hat{x}^2_1}+\frac{\partial ^2 F^k}{\partial \hat{y}^2_1}\right] ,\\ h^{k-2}_{20}= & {} \frac{1}{4}\left[ \frac{\partial ^2 F^k}{\partial \hat{x}^2_1}-\frac{\partial ^2 F^k}{\partial \hat{y}^2_1}-2i\frac{\partial ^2 F^k}{\partial \hat{x}_1\hat{y}_1}\right] ,k=3,\cdots ,n. \end{aligned}$$

respectively.

After performing some computations, we have

$$\begin{aligned} h^{k-2}_{11}=\left\{ \begin{array}{ll} \displaystyle 0,\ \text{ for } \ k \ \text{ odd },\\ \displaystyle \frac{1}{A}-A,\ \text{ for } \ k \ \text{ even }, \end{array} \right. \end{aligned}$$

(4.7)

and

$$\begin{aligned} h^{k-2}_{20}=\left\{ \begin{array}{ll} \displaystyle 0,\ \text{ for } \ k \ \text{ odd },\\ \displaystyle \frac{1}{A}-A+2i,\ \text{ for } \ k \ \text{ even }, \end{array} \right. \end{aligned}$$

(4.8)

respectively.

We denote $w_{11}^{k}=(w_{11}^{k_1}, w_{11}^{k_2})^T$ as the solution of the linear system

$$\begin{aligned} L_kw_{11}^{k}=(0,A-\frac{1}{A})^T, \end{aligned}$$

(4.9)

and denote $w_{20}^{k}=(w_{20}^{k_1}, w_{20}^{k_2})^T$ as the solution of the linear system

$$\begin{aligned} (L_k-2iAI)w_{20}^{k}=(0,A-\frac{1}{A}-2i)^T. \end{aligned}$$

(4.10)

Hence, we have

$$\begin{aligned} \begin{array}{ll} \displaystyle \hat{x}_k=w_{11}^{k_1}\epsilon ^2+Re(w_{20}^{k_1}e^{4\pi it/T})\epsilon ^2+o(\epsilon ^2),\\ \displaystyle \hat{y}_k=w_{11}^{k_2}\epsilon ^2+Re(w_{20}^{k_2}e^{4\pi it/T})\epsilon ^2+o(\epsilon ^2),\\ \end{array} \end{aligned}$$

(4.11)

for $k=2,\cdots ,n.$

Due to the above results, Hopf bifurcation theorem in [25] and the transformation $U=P V$, we derive the result.$\square$

We note that the bifurcating periodic solutions in Theorem 6 are in essence different from the bifurcating periodic solutions derived for the cellular neural networks in [39], where the derived bifurcating periodic solutions are spatially homogeneous. The differences come from the different ”reactions” between the cellular neural networks and the Brusselator model. For the cellular neural networks, its ”reaction” is actually linear in the neighborhood of its steady state, while the ”reaction” is mild nonlinear for the Brusselator model. In the next section, we give some numerical simulations to illustrate the bifurcating periodic solutions.

5 Numerical simulations

In this section, some numerical simulations are carried out to demonstrate the theoretical analyses in Sect. 3 and 4. In all the following figures, interpolation has been used for the display as that in [32, 33] for better visual effects.

5.1 Numerical simulations on the results of Theorem 2 and Theorem 6

As the system parameters used in Fig. 1a, we choose

$$\begin{aligned} d=0.1, n=10,\theta =0.5<\theta _c=1.0316. \end{aligned}$$

Then for $A=1$, we derive the Hopf bifurcation value $B^H_1(A)=2$ by (3.9). According to Theorem 2, the steady state $E^*$ of the initial-boundary value problem (1.4)–(1.6) is locally asymptotically stable when $0<B<B^H_1(A)=2$, while it undergoes Hopf bifurcation at $B=B^H_1(A)=2$.

To show that the steady state $E^*$ is locally asymptotically stable, we choose $B=0.6$. For the spatially homogeneous initial values $x_k(0)=0.02, y_k(0)=0.01, k=1,2,\cdots , 10$, we derive Fig. 5, while for the spatially nonhomogeneous initial values $x_k(0)=0.02k/10,$ $y_k(0)=0.01k/10, k=1,2,\cdots , 10$, we derive Fig. 6. The simulation results show that the steady state $E^*$ is locally asymptotically stable, no matter the initial values are spatially homogeneous or not.

Fig. 5

$E^*$ is locally asymptotically stable for $B=0.6<B_1^H(A)$ with the spatially homogeneous initial values $x_k(0)=0.02, y_k(0)=0.01, k=1,2,\cdots , 10$

Fig. 6

$E^*$ is locally asymptotically stable for $B=0.6<B_1^H(A)$ with the spatially nonhomogeneous initial values $x_k(0)=0.02k/10,$ $y_k(0)=0.01k/10, k=1,2,\cdots , 10$

Next, we show model (1.4) undergoes Hopf bifurcation at $B=B^H_1(A)=2$. For this, we choose $B=2.05>B^H_1(A)=2$. According to Theorem 5, we know the Hopf bifurcation is supercritical and orbitally asymptotically stable. Furthermore, according to Theorem 6, we know the bifurcating periodic solutions are spatially nonhomogeneous.

For the spatially homogeneous initial values $x_k(0)=0.02, y_k(0)=0.01, k=1,2,\cdots , 10$, we derive Fig. 7, which show the existence of the supercritical orbitally asymptotically stable bifurcating periodic solutions. However, it is seen that the bifurcating periodic solutions are spatially homogeneous, which violate Theorem 6. The reason of this misunderstanding is due to the choice of the spatially homogeneous initial values, which actually eliminate the diffusion effect. Hence, we next choose the spatially nonhomogeneous initial values $x_k(0)=0.02k/10,$ $y_k(0)=0.01k/10, k=1,2,\cdots , 10$, then we derive Fig. 8. It is seen obviously that the bifurcating periodic solutions are spatially nonhomogeneous. The results coincide with the results of Theorem 6.

Fig. 7

Orbitally asymptotically stable spatially homogeneous bifurcating periodic solutions for $B=2.05>B_1^H(A)$ with the spatially homogeneous initial values $x_k(0)=0.02, y_k(0)=0.01, k=1,2,\cdots , 10$

Fig. 8

Orbitally asymptotically stable spatially nonhomogeneous bifurcating periodic solutions with large amplitude for $B=2.05>B_1^H(A)$ with the same system parameters as that in Fig.7 but different initial values, i.e., the spatially nonhomogeneous $x_k(0)=0.02k/10,y_k(0)=0.01k/10, k=1,2,\cdots , 10$

5.2 Numerical simulations on the results of Theorem 3

As the system parameters used in Fig. 1b, we choose

$$\begin{aligned} d=0.1, n=10,\theta =4>\theta _c=1.0316. \end{aligned}$$

Then for $A=2>A_{m^*}=1.3506$, we derive the Hopf bifurcation value $B^H_1(A)=5$ by (3.9) and Turing bifurcation value $B^T_2(A)=4.0541$ by (3.10). According to Theorem 3, the steady state $E^*$ of the initial-boundary value problem (1.4)–(1.6) is locally asymptotically stable when $0<B<B^T_2(A)=4.0541$, while it becomes unstable when $B>B^T_2(A)=4.0541$.

As it is explained in the previous subsection, we always choose the spatially nonhomogeneous initial values for the following simulations.

To show that the steady state $E^*$ is locally asymptotically stable when $0<B<B^T_2(A)$, we choose $B=0.6$ and the initial values $x_k(0)=0.02k/10,y_k(0)=0.01k/10, k=1,2,\cdots , 10$. Then we derive the following Fig. 9.

Fig. 9

$E^*$ is locally asymptotically stable for $B=0.6<B^T_2(A)$ with the spatially nonhomogeneous initial values $x_k(0)=0.02k/10,y_k(0)=0.01k/10, k=1,2,\cdots , 10$

To show that the steady state $E^*$ is unstable when $B>B^T_2(A)$, we choose $B=4.1$ and the initial values $x_k(0)=0.02k/10,y_k(0)=0.01k/10, k=1,2,\cdots , 10$. Then we derive the following Fig. 10.

Fig. 10

$E^*$ is unstable for $B=4.1>B^T_2(A)$ with the spatially nonhomogeneous initial values $x_k(0)=0.02k/10,y_k(0)=0.01k/10, k=1,2,\cdots , 10$

By Fig. 10, it is seen that the instability of $E^*$ is unlike that in Figs. 7 and 8, where the instability is caused by the occurrence of Hopf bifurcation. Here we note that it is impossible to simulate Hopf bifurcation with this group of parameters, since the conditions (C) are not satisfied. Actually, we can derive that $A>A_0=\frac{4}{3},\mu _-=0.0472,\mu _+=0.3232$ and $\mu _1^2=0.0979$ with this group of parameters. Hence, $\mu _1^2\in (\mu _-,\mu _+)$, which violates the conditions (C).

6 Discussion and conclusion

In this paper, we consider a spatially discretized diffusive Brusselator model, which is derived from the reaction-diffusion Brusselator model by using 3-point centered difference approximations. The dynamical behaviors, such as the global existence and uniqueness of the positive solution, the local stability of the unique spatially homogeneous steady state, Turing bifurcation and Hopf bifurcation, are discussed. The following are some of our considerations based on this paper.

Turing patterns and Hopf bifurcation for reaction-diffusion equations have been studied a lot. See [41,42,43,44,45,46,47,48,49,50,51] for examples. Of foremost interest regarding the diffusive Brusselator model is the formation of spatially periodic structures, such as hexagons or stripes and transitions between them. Based on the decoupling method and Hopf bifurcation theorem, we show the occurrence conditions of Turing bifurcation and Hopf bifurcation at the spatially homogeneous steady state for the spatially discretized diffusive Brusselator model. Although the Turing instability alone is not sufficient to explain the formation of Turing pattern, the bifurcating periodic solutions can be seen as a kind of patterns [51]. Generally, the existing studies on the pattern formations of the diffusive Brusselator model are investigated by numerical analysis. Here we supply the theoretical analyses on the occurrence of bifurcating periodic solutions for the spatially discretized diffusive Brusselator model (1.4). We further show the bifurcating periodic solutions are nonhomogeneous, which is a interesting result corresponding to the derived spatially homogeneous bifurcating periodic solutions for the diffusive Brusselator model in [27]. At the meantime, the bifurcating spatially nonhomogeneous periodic solutions provide a special kind of spatial patterns for model (1.4). We also believe that this method can be extended to study the spatially discretized diffusive Brusselator model on a disk in [25] and the Brusselator model with delayed feedback in [2, 3].

Furthermore, the spatially discretized reaction-diffusion equations can also be seen as a kind of systems on complex networks. Recently, the study of Turing patterns and Hopf bifurcation for systems on complex networks attracts many attentions. See [52,53,54,55,56,57,58,59] for examples. Among these literatures, Hopf bifurcation in an activator-inhibitor system with network was considered in [57], wherein the stable Hopf bifurcation with backward direction was derived. Turing instability of Brusselator in the reaction-diffusion network was studied in [58], wherein the approximate instability region about the diffusion coefficient and the connection probability was obtained. A ring of nonlocally coupled Brusselators was studied in [59], wherein a two-frequency chimera state with mixed phase regularities was found.

The present paper offers some references on the dynamical behaviors among the three kinds of equations, namely, the reaction-diffusion equations, the spatially discretized reaction-diffusion equations and systems on complex networks.