Spatiotemporal Patterns of a Reaction–Diffusion Substrate–Inhibition Seelig Model

Abstract

In this paper, the spatiotemporal patterns of a reaction–diffusion substrate–inhibition chemical Seelig model are considered. We first prove that this parabolic Seelig model has an invariant rectangle in the phase plane which attracts all the solutions of the model regardless of the initial values. Then, we consider the long time behaviors of the solutions in the invariant rectangle. In particular, we prove that, under suitable “lumped parameter assumption” conditions, these solutions either converge exponentially to the unique positive constant steady states or to the spatially homogeneous periodic solutions. Finally, we study the existence and non-existence of Turing patterns. To find parameter ranges where system does not exhibit Turing patterns, we use the properties of non-constant steady states, including obtaining several useful estimates. To seek the parameter ranges where system possesses Turing patterns, we use the techniques of global bifurcation theory. These two different parameter ranges are distinguished in a delicate bifurcation diagram. Moreover, numerical experiments are also presented to support and strengthen our analytical analysis.

1 Introduction

A fundamental problem in theoretical biology is to understand how patterns and shapes are formed. In his seminal paper, Turing [20] proposed a striking idea of “diffusion-driven instability,” which states that diffusion could destabilize an otherwise stable steady state of a reaction–diffusion system and generate new stable time-independent nonuniform spatial patterns. Over the years, Turing’s idea has attracted the attention of many researchers and has been successfully developed on the theoretical backgrounds. Not only has it been studied in biological and chemical fields, but also some investigations range as far as economics, semiconductor physics, and star formation [5].

The existence of Turing patterns in biology is still controversial, but it had been observed in chemistry. The first experimental evidence of Turing patterns was reported in 1990 by D. Kepper and her associates on the chlorite-iodide-malonic acid and starch reaction (CIMA reaction) in an open unstirred gel reactor [2, 4], nearly forty years after the publication of [20]. This CIMA reaction can be modeled by the famous Lengyel–Epstein system [12, 13] which has been extensively studied experimentally, numerically and theoretically (see [1, 7–11, 15, 22–24] and the references therein).

In this paper, we consider a reaction–diffusion model which has a very similar mathematical form to the Lengyel–Epstein CIMA reaction system, even though they describe different chemical reactions. Our model was first proposed by Seelig in [18] to explain the observed oscillatory behavior in substrate–inhibition chemical reaction: $X+Y\rightarrow P+Q$ effected by a catalyst $M$ such as an enzyme. The chemical reaction scheme is (see also Fig. 1): The substrates $X$ and $Y$ are supplied at constant rates $j_1$ and $j_2$ respectively. The substrate $X$ flows out at rate $k_0$. The substrate $X$ reacts with catalyst $M$ to form the inert complex $MX$ at rate $k_1$. This reaction is reversible in the sense that $MX$ can form $X$ and $M$ at rate $k_{-1}$. Whenever there is $MX$, then $X$ will react with $MX$, and form $MX_2$ at a rate $k_2$. This reaction is also reversible, $MX_2$ can form $X$ and $MX$ at rate $k_{-2}$. The substrate $Y$ reacts with $MX$, forming $P$, $Q$ and $M$ at rate $k_3$. This reaction is irreversiable. In the whole substrate–inhibition chemical reactions, all the reversible reactions are taken to be fast and all the irreversible ones are slow.

Fig. 1

Schematic chemical reaction of Seelig model (1.1)

Let $[\cdot ]$ denote the concentrations of the chemical substances at time $\tau$, then by the law of mass action, we obtain the following kinetic equations for the reaction mechanism:

$$\begin{aligned} \begin{aligned} \displaystyle \frac{d[X]}{d\tau }&=j_1-k_0[X]-k_1[X][M]+k_{-1}[MX]-k_2[X][MX]+k_{-2}[MX_2],\\ \displaystyle \frac{d[Y]}{d\tau }&=j_2-k_3[Y][MX],\\ \displaystyle \frac{d[M]}{d\tau }&=-k_1[X][M]+k_{-1}[MX]+k_3[Y][MX],\\ \displaystyle \frac{d[MX_2]}{d\tau }&=k_2[X][MX]-k_{-2}[MX_2],\\ \displaystyle \frac{d[MX]}{d\tau }&=k_1[X][M]-k_{-1}[MX]-k_2[X][MX]-k_3[Y][MX]+k_{-2}[MX_2]. \end{aligned} \end{aligned}$$

(1.1)

It is assumed that the sum of the various forms of the catalyst $M, MX, MX_2$ is constant and is represented by the adjustable parameter $[M]_{\text {total}}:=[M]+[MX]+[MX_2]$. We also assume a quasi steady state for the concentrations of $M$, $MX$, and $MX_2$, since their concentrations are normally small compared to $[X]$ and $[Y]$ so that they can follow virtually inertness the movements of $[X]$ and $[Y]$. Namely., letting $d[M]/d\tau$, $d[MX]/d\tau$ and $d[MX_2]/d\tau$ equal to zero. Thus,

$$\begin{aligned} \begin{aligned} \displaystyle \frac{d[X]}{d\tau }&=j_1-k_0[X]-k_3[Y][MX],\\ \displaystyle \frac{d[Y]}{d\tau }&=j_2-k_3[Y][MX],\\ 0&=-k_1[X][M]+k_{-1}[MX]+k_3[Y][MX],\\ 0&=k_2[X][MX]-k_{-2}[MX_2],\\ 0&=k_1[X][M]-k_{-1}[MX]-k_2[X][MX]-k_3[Y][MX]+k_{-2}[MX_2]. \end{aligned} \end{aligned}$$

(1.2)

From the last three equations of (1.2), we obtain

$$\begin{aligned} k_3[Y][MX]=k_{-1}[M]_{\text {total}}\cdot \displaystyle \frac{\displaystyle \frac{k_1[X]}{k_{-1}}\cdot \displaystyle \frac{k_3[Y]}{k_{-1}}}{1+\displaystyle \frac{k_1[X]}{k_{-1}}+\displaystyle \frac{k_1k_2[X]^2}{k_{-1}k_{-2}}+\displaystyle \frac{k_3[Y]}{k_{-1}}}. \end{aligned}$$

(1.3)

Introducing the following dimensionless quantities,

$$\begin{aligned} \begin{aligned} u=\displaystyle \frac{k_1[X]}{k_{-1}},\;v=\displaystyle \frac{k_3[Y]}{k_{-1}},\;t&=k_0\tau ,\;K=\displaystyle \frac{k_2k_{-1}}{k_{-2}k_1},\;\beta _1=\displaystyle \frac{k_1j_1}{k_0k_{-1}}, \beta _2=\displaystyle \frac{k_3j_2}{k_0k_{-1}},\\ \gamma _1&=\displaystyle \frac{[M]_{\text {total}}k_1}{k_0},\;\gamma _2=\displaystyle \frac{[M]_{\text {total}}k_3}{k_0}, \end{aligned} \end{aligned}$$

(1.4)

one can reduce the first two equations of (1.2) to the following system of ordinary differential equations (ODEs):

$$\begin{aligned} \begin{aligned} \displaystyle \frac{du}{dt}=\beta _1-u-\displaystyle \frac{\gamma _1uv}{1+u+v+Ku^2},\; \displaystyle \frac{dv}{dt}=\beta _2-\displaystyle \frac{\gamma _2uv}{1+u+v+Ku^2}. \end{aligned} \end{aligned}$$

(1.5)

Since the chemical reaction obeys the diffusion process, it is natural to add diffusion to the model (1.5), which leads to the following reaction–diffusion system

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial u}{\partial t}-d_1\Delta u=\beta _1-u-\displaystyle \frac{\gamma _1uv}{1+u+v+Ku^2},&{}x\in \Omega , t>0,\\ \displaystyle \frac{\partial v}{\partial t}-d_2\Delta v=\beta _2-\displaystyle \frac{\gamma _2uv}{1+u+v+Ku^2},&{}x\in \Omega , t>0,\\ \partial _{\nu } u=\partial _{\nu } v=0, \;\; &{} x\in \partial \Omega , \; t\ge 0, \\ \displaystyle u(x,0)=u_0(x)>0, v(x,0)=v_0(x)>0,&{}x\in \Omega , \end{array}\right. } \end{aligned}$$

(1.6)

where $u=u(x,t)$ and $v=v(x,t)$ stand for the rescaled concentrations of the chemical substances at time $t$ and position $x\in \Omega$. Here $\Omega$ is an open bounded domain in ${\mathbf R}^N$, $N\ge 1$, with smooth boundary $\partial \Omega$; $d_1$ and $d_2$ are diffusion coefficients of $u$ and $v$ respectively. $u_0,v_0\in C^2(\Omega )\cap C^0(\overline{\Omega })$ and the Neumann boundary conditions indicate that there are no flux of the chemical substances of $u$ and $v$ on the boundary.

The Seelig model (1.6) has been studied extensively by several authors, but most of the research focuses either on the corresponding ODE system (1.5) or on the R–D system (1.6) in the one-dimensional spatial domain. Seelig [18] considered the boundedness of the solutions of ODE system (1.5) by proving the existence of invariant rectangles. He also proved the existence of stable time-periodic limit cycle by applying Poincare–Bendixson theorem. However, the authors did not prove whether the PDE system (1.6) has the invariant rectangles or not. Mimura and Murray [14] studied the steady state patterns of system (1.6) subject to homogeneous Neumann boundary conditions. However, the spatial dimension is only restricted to one dimension. Nishiura [16] considered the global structure of the bifurcating steady state solutions of some reaction–diffusion equations whose reaction terms share with common properties. Seelig model is one of these reaction–diffusion models. In his work, to gain detailed information of global bifurcation branches, it is crucial to assume the uniform boundedness of the solutions (especially bounded regardless of the diffusion coefficients). To the best of our knowledge, for the Seelig model, the uniform boundedness of the solutions are still completely open so far.

In this paper, we first answer the open questions in [16] and [18]. We show that the R–D system (1.6) have an invariant rectangle which attracts all its solutions regardless of the initial values $u_0$ and $v_0$.

The second question arises naturally. Once the solutions of system (1.6) are attracted by the attraction region (rectangle), where do they go eventually? And what are the global attractors? We prove that, under suitable conditions, these solutions either converge exponentially to the unique positive constant equilibrium or to the spatially homogeneous periodic solutions. Our results thus verify the striking idea of “lumped parameter assumption”, stating that, under suitable conditions, the dynamics of the PDEs (1.6) can be completely determined by the dynamics of the ODEs (1.5) (see [3] for lumped parameter assumption).

Finally, we prove the existence and nonexistence of Turing patterns of system (1.6). Mathematically, Ni and Tang [15], and Peng et al. [17] have already reported the critical role of the system parameters in leading to Turing patterns of the Lengyel–Epstein system and Degn–Harrison system respectively. We show that, although these three chemical reaction models have similar mathematical forms, system parameters leading to Turing patterns are quite different.

This paper is organized as follows. In Sect. 2, we study the boundedness and uniqueness of global-in-time solutions of the system (1.6). In particular, we show that an invariant rectangle exists which attracts all the solutions of system (1.6) regardless of the initial values. Then, we consider the long time behaviors of the solutions of system (1.6), and derive precise conditions so that the solutions of R–D (1.6) converge exponentially either to its unique constant steady state solution, or to its spatially homogeneous orbitally periodic solutions. In Sect. 3, we derive conditions so that system (1.6) does not have non-constant positive steady states, including Turing patterns. In Sect. 4, we use global bifurcation theory to prove the existence of Turing patterns. In Sect. 5, we included the numerical simulations to support our analytical analysis. In appendix, we include the results on dynamics of ODEs system. Throughout this paper, we use $\mathbb {N}_0$ to stand for the set of nonnegative integers, and use $|\Omega |$ to represent the Lebesgue measure of $\Omega$.

2 Attraction Region and Large Time Behaviors of the Solutions

For convenience of our discussions, we copy (1.6) here:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial u}{\partial t}-d_1\Delta u=\beta _1-u-\displaystyle \frac{\gamma _1uv}{1+u+v+Ku^2},&{}\quad x\in \Omega , t>0,\\ \displaystyle \frac{\partial v}{\partial t}-d_2\Delta v=\beta _2-\displaystyle \frac{\gamma _2uv}{1+u+v+Ku^2},&{}\quad x\in \Omega , t>0,\\ \partial _{\nu } u=\partial _{\nu } v=0, \;\; &{} \quad x\in \partial \Omega , \; t\ge 0, \\ \displaystyle u(x,0)=u_0(x)>0, v(x,0)=v_0(x)>0,&{}\quad x\in \Omega . \end{array}\right. } \end{aligned}$$

(2.1)

System (2.1) has $(u_*,v_*)$ as the unique constant equilibrium solution, with

$$\begin{aligned} u_*:=\beta _1-\displaystyle \frac{\gamma _1}{\gamma _2}\beta _2, \;v_*:=\displaystyle \frac{\beta _2(1+u_*+Ku_*^2)}{\gamma _2u_*-\beta _2}, \end{aligned}$$

(2.2)

which are positive if and only if $\displaystyle \frac{\beta _1}{1+\gamma _1}>\frac{\beta _2}{\gamma _2}$ holds.

We first show that (2.1) has a unique solution $(u(x, t), v(x, t))$ defined for all $t>0$ and is bounded by some positive constants depending on $\beta _1$, $\beta _2$, $\gamma _1$, $\gamma _2$, $K$, and the maximum and minimum of the initial conditions, $u_0(x)$ and $v_0(x)$.

Proposition 1

Suppose that $\beta _1,\beta _2,\gamma _1,\gamma _2, K>0$, with $\displaystyle \frac{\beta _1}{1+\gamma _1}>\frac{\beta _2}{\gamma _2}$. Then, for any $d_1,d_2>0$, the initial boundary value problem (2.1) admits a unique solution $(u(x,t),v(x,t))$, defined for all $x\in \Omega$ and $t>0$. Moreover, there exist two positive constants $\mathcal {M}_1$ and $\mathcal {M}_2$, depending on $\beta _1$, $\beta _2$, $\gamma _1$, $\gamma _2$, $K$, $u_0(x)$ and $v_0(x)$, such that

$$\begin{aligned} \mathcal {M}_1<u(x,t), v(x,t)<\mathcal {M}_2,\;x\in \overline{\Omega },\;t>0. \end{aligned}$$

(2.3)

Proof

The existence and uniqueness of local-in-time solutions to the initial-boundary value problem (2.1) is classical [6].

For the global existence and the boundedness of the solutions, we partially use the techniques of invariant region [15, 21]. Recall from [15, 21] that a region (rectangle) $\mathcal {R}:=[U_1,U_2]\times [V_1,V_2]$ in the $(u, v)$ phase plane is called a positively invariant region of system (2.1) if the vector field

$$\begin{aligned} \left( \beta _1-u-\displaystyle \frac{\gamma _1uv}{1+u+v+Ku^2},\;\beta _2-\displaystyle \frac{\gamma _2uv}{1+u+v+Ku^2}\right) \end{aligned}$$

(2.4)

points inward on the boundary of $\mathcal {R}$ for all $t\ge 0$. Thus, if one can find such a positively invariant rectangle $\mathcal {R}$, then the solution $(u(x,t),v(x,t))$ of (2.1) exists for all $x\in \Omega$ and $t\ge 0$, and stays in $\mathcal {R}$.

We consider two cases:

Case 1 Suppose that $\min _{x\in \overline{\Omega }}\{u_0(x)\}>\beta _2/\gamma _2$ holds. We construct the invariant rectangle $\mathcal {R}:=[U_1,U_2]\times [V_1,V_2]$ in the following way:

$$\begin{aligned} \begin{aligned} U_1:&=\min \bigg \{\displaystyle \frac{\beta _1}{1+\gamma _1}, \min \limits _{x\in \overline{\Omega }}\{u_0(x)\}\bigg \},\;U_2:=\max \bigg \{\beta _1, \max \limits _{x\in \overline{\Omega }}\{u_0(x)\}\bigg \},\\ V_1:&=\min \bigg \{\displaystyle \frac{\beta _2}{\gamma _2}, \min \limits _{x\in \overline{\Omega }}\{v_0(x)\}\bigg \},\;V_2:=\max \bigg \{\displaystyle \frac{\beta _2(1+U_2+KU_2^2)}{\gamma _2U_1-\beta _2}, \max \limits _{x\in \overline{\Omega }}\{v_0(x)\}\bigg \}. \end{aligned} \end{aligned}$$

(2.5)

Clearly, $u_0(x)$ and $v_0(x)$ are closed by the rectangle $\mathcal {R}$. We now prove that the vector field (2.4) points inward on the boundary of $\mathcal {R}$. In fact,

On the left side $u=U_1$, $V_1\le v\le V_2$, by the definition of $U_1$, we have,

$$\begin{aligned} \beta _1-u-\displaystyle \frac{\gamma _1uv}{1+u+v+Ku^2}=\beta _1-U_1-\displaystyle \frac{\gamma _1U_1v}{1+U_1+v+KU_1^2}>\beta _1-U_1-\gamma _1U_1\ge 0. \end{aligned}$$

(2.6)

On the right side $u=U_2$, $V_1\le v\le V_2$, by the definition of $U_2$, we have

$$\begin{aligned} \beta _1-u-\displaystyle \frac{\gamma _1uv}{1+u+v+Ku^2}=\beta _1-U_2-\displaystyle \frac{\gamma _1U_2v}{1+U_2+v+KU_2^2}<\beta _1-U_2\le 0. \end{aligned}$$

(2.7)

On the bottom side $v=V_1$, $U_1\le u\le U_2$, by the definition of $V_1$, we have

$$\begin{aligned} \beta _2-\displaystyle \frac{\gamma _2uv}{1+u+v+Ku^2}=\beta _2-\displaystyle \frac{\gamma _2uV_1}{1+u+V_1+Ku^2}>\beta _2-\gamma _2V_1\ge 0. \end{aligned}$$

(2.8)

On the top side $v=V_2$, $U_1\le u\le U_2$, by the definition of $V_2$, we have

$$\begin{aligned} \beta _2-\displaystyle \frac{\gamma _2uv}{1+u+v+Ku^2}=\beta _2-\displaystyle \frac{\gamma _2uV_2}{1+u+V_2+Ku^2}<\beta _2-\displaystyle \frac{\gamma _2U_1V_2}{1+U_2+V_2+KU_2^2}\le 0. \end{aligned}$$

(2.9)

So far, we have proved that $\mathcal {R}:=[U_1,U_2]\times [V_1,V_2]$ is the invariant rectangle for the vector field (2.4). Thus, we can choose $\mathcal {M}_1=\min \{U_1,V_1\}$ and $\mathcal {M}_2=\max \{U_2,V_2\}$.

Case 2 Suppose that $0<\min _{x\in \overline{\Omega }}\{u_0(x)\}\le \beta _2/\gamma _2$ holds. In this case, the aforementioned $\mathcal {R}$ is not the invariant rectangle anymore, since the last inequality in (2.9) fails. (In fact, we have $U_1\le \beta _2/\gamma _2$. Thus, the term $\gamma _2U_1-\beta _2$ in the definition of $V_2$ is negative or zero.) But, the inequalities in (2.6), (2.7) and (2.8) still hold.

We divide $[U_1,U_2]$ into two parts: $[U_1,\beta _2/\gamma _2]$ and $[\beta _2/\gamma _2,U_2]$.

We now show that if $(u_0(x),v_0(x))\in [U_1,\beta _2/\gamma _2]\times [V_1,\infty )$ holds, then solutions initiating from $(u_0(x),v_0(x))$ will be bounded in $[U_1,\beta _2/\gamma _2]\times [V_1,\infty )$. Moreover, these solutions will go through the “line” $u\equiv \beta _2/\gamma _2$ and enter into $[\beta _2/\gamma _2,U_2]\times [V_1,\infty )$. Suppose not. Then, by (2.6) and (2.8), for any fixed $x^*\in \Omega$, there exist positive constants $\widehat{U}(\le \beta _2/\gamma _2)$, $T_\infty (0<T_\infty \le +\infty )$, and a subsequence of solutions $(u(x^*,t_k),v(x^*,t_k))$ of system (2.1), such that as $t_k\rightarrow T_\infty$, we have

$$\begin{aligned} u(x^*,t_k)\rightarrow \widehat{U},\;v(x^*,t_k)\rightarrow +\infty . \end{aligned}$$

(2.10)

Substituting $u(x^*,t_k)$ and $v(x^*,t_k)$ into (2.1), we have

$$\begin{aligned} \displaystyle \frac{\partial u(x^*,t_k)}{\partial t}-d_1\Delta u(x^*,t_k)=\beta _1-u(x^*,t_k)-\displaystyle \frac{\gamma _1u(x^*,t_k)v(x^*,t_k)}{1+u(x^*,t_k)+v(x^*,t_k)+Ku(x^*,t_k)^2}. \end{aligned}$$

(2.11)

Setting $k\rightarrow \infty$ (or equiv. $t_k\rightarrow T_\infty$) in (2.11), one has $0=\beta _1-\widehat{U}-\gamma _1\widehat{U}$. Thus, $\widehat{U}=\beta _1/(1+\gamma _1)$. However, this is impossible, since $\widehat{U}\le \beta _2/\gamma _2<\beta _1/(1+\gamma _1)$. We then reach a contradiction.

Since the solutions will eventually enter into $[\beta _2/\gamma _2,U_2]\times (V_1,\infty )$, one can construct a new invariant rectangle as we did in Case 1. This leads to another suitable positive constants $\mathcal {M}_1$ and $\mathcal {M}_2$. Thus, we have prove the global existence and boundedness of the solutions. $\square$

Our next result shows that system (2.1) has an attraction region defined by

$$\begin{aligned} {{\mathcal {A}}}:=\bigg (\displaystyle \frac{\beta _1}{1+\gamma _1},\beta _1\bigg )\times \bigg (\displaystyle \frac{\beta _2}{\gamma _2}, \displaystyle \frac{\beta _2(1+\beta _1+K\beta _1^2)(\gamma _1+1)}{\beta _1\gamma _2-\beta _2(1+\gamma _1)}\bigg ) \end{aligned}$$

(2.12)

in the phase plane which actually attracts all solutions of this system, regardless of the initial values $u_0$ and $v_0$.

Theorem 2

Suppose that $\displaystyle \frac{\beta _1}{1+\gamma _1}>\frac{\beta _2}{\gamma _2}$ holds and let $(u(x,t),v(x,t))$ be the unique solution of system (2.1). Then, for any $x\in \overline{\Omega }$, we have,

• 1. $\displaystyle \frac{\beta _1}{1+\gamma _1}<\lim {\inf \limits _{t\rightarrow \infty }}u\le \lim \sup \limits _{t\rightarrow \infty } u<\beta _1$;

• 2. $\displaystyle \frac{\beta _2}{\gamma _2}<\lim {\inf \limits _{t\rightarrow \infty }}v\le \lim \sup \limits _{t\rightarrow \infty }v<\displaystyle \frac{\beta _2(1+\beta _1+K\beta _1^2)(\gamma _1+1)}{\beta _1\gamma _2-\beta _2(\gamma _1+1)}$.

Proof

1) We first prove that $\lim {\inf \limits _{t\rightarrow \infty }} u>\displaystyle \frac{\beta _1}{1+\gamma _1}$. By Proposition 1, there exists a sufficiently small $\rho >0$ such that for all $x\in \overline{\Omega }$ and $t>0$, $\displaystyle \frac{\gamma _1uv}{1+u+v+Ku^2}+\rho <\displaystyle \frac{\gamma _1uv}{v}=\gamma _1u$ holds. Let $u_\rho$ be the unique solution of the following ODE:

$$\begin{aligned} \displaystyle \frac{du_\rho (t)}{dt}=\beta _{1}+\rho -(1+\gamma _1)u_\rho (t),\;u_\rho (0)=(1-\rho )\min _{x\in \overline{\Omega }} u_0(x). \end{aligned}$$

(2.13)

Setting $w_1(x,t)=u(x,t)-u_\rho (t)$, and by (2.1) and (2.13), we have

$$\begin{aligned} \begin{aligned} -\displaystyle \frac{\partial w_1(x,t)}{\partial t}+d_1\Delta w_1(x,t)&=w_1(x,t)-\gamma _1u_\rho (t)+\displaystyle \frac{\gamma _1uv}{1+u+v+Ku^2}+\rho \\&<w_1(x,t)-\gamma _1u_\rho (t)+\gamma _1u=(1+\gamma _1)w_1(x,t),\\ w_1(x,0)&>0. \end{aligned} \end{aligned}$$

(2.14)

Thus,

$$\begin{aligned} \begin{aligned} -\displaystyle \frac{\partial w_1(x,t)}{\partial t}+d_1\Delta w_1(x,t)-(1+\gamma _1)w_1(x,t)<0,\;w_1(x,0)>0. \end{aligned} \end{aligned}$$

(2.15)

Then by the maximum principle for parabolic equations, we have $w_1(x,t)>0$, which implies that $u(x,t)>u_\rho (t)$ for all $x\in \overline{\Omega }$ and $t\ge 0$. From (2.13), it follows that ${\mathop {\lim \limits _{t\rightarrow \infty }}} u_\rho (t)=(\beta _1+\rho )/(1+\gamma _1)$. Thus, we have $\hbox {lim}{\mathop {\inf \limits _{t\rightarrow \infty }}} u>\beta _1/(1+\gamma _1)$.

2) We then prove that $\lim \sup \limits _{t\rightarrow \infty } u<\beta _1$. By Proposition 1, there exists a sufficiently small $0<\delta <\beta _1$ such that for all $x\in \overline{\Omega }$ and $t>0$, $\delta <\gamma _1uv/(1+u+v+Ku^2)$ holds. Let $u_\delta =u_\delta (t)$ be the unique solution of the following ODE:

$$\begin{aligned} \displaystyle \frac{du_\delta (t)}{dt}=\beta _{1}-\delta -u_\delta (t),\;u_\delta (0)=(1+\delta )\max _{x\in {\overline{\Omega }}} u_0(x). \end{aligned}$$

(2.16)

Setting $w_2(x,t)=u(x,t)-u_\delta (t)$, and by (2.1) and (2.16), we have

$$\begin{aligned} -\displaystyle \frac{\partial w_2(x,t)}{\partial t}+d_1\Delta w_2(x,t)-w_2(x,t)=\displaystyle \frac{\gamma _1uv}{1+u+v+Ku^2}-\delta >0,\;w_2(x,0)<0. \end{aligned}$$

(2.17)

Then by the maximum principle for parabolic equations, we have $w_2(x,t)<0$, which implies that $u(x,t)<u_\delta (t)$ for all $x\in {\overline{\Omega }}$ and $t\ge 0$. From (2.16), it follows that ${\mathop {\lim \limits _{t\rightarrow \infty }}} u_\delta (t)=\beta _{1}-\delta$. Thus, we have $\lim \sup \limits _{t\rightarrow \infty } u<\beta _1$.

3) We now prove that $\lim {\inf \limits _{t\rightarrow \infty }}v>\displaystyle \frac{\beta _2}{\gamma _2}$. By Proposition 1, there exists a sufficiently small $\tau >0$ such that for all $x\in \overline{\Omega }$ and $t>0$, $\displaystyle \frac{\gamma _2uv}{1+u+v+Ku^2}+\tau <\displaystyle \frac{\gamma _2uv}{u}=\gamma _2v$ holds. Let $v_\tau$ be the unique solution of the following ODE:

$$\begin{aligned} \displaystyle \frac{dv_\tau (t)}{dt}=\beta _{2}+\tau -\gamma _2v_\tau (t),\;v_\tau (0)=(1-\tau )\min _{x\in \overline{\Omega }} v_0(x). \end{aligned}$$

(2.18)

Setting $p_1(x,t)=v(x,t)-v_\tau (t)$, and by (2.1) and (2.18), we have

$$\begin{aligned} \begin{aligned} -\displaystyle \frac{\partial p_1(x,t)}{\partial t}+d_2\Delta p_1(x,t)-\gamma _2p_1(x,t)&=\displaystyle \frac{\gamma _2uv}{1+u+v+Ku^2}+\tau -\gamma _2v<0,\\ p_1(x,0)&>0. \end{aligned} \end{aligned}$$

(2.19)

Then by the maximum principle for parabolic equations, we have $p_1(x,t)>0$, which implies that $v(x,t)>v_\tau (t)$ for all $x\in \overline{\Omega }$. From (2.18), it follows that ${\mathop {\lim \limits _{t\rightarrow \infty }}} v_\tau (t)=(\beta _2+\tau )/\gamma _2$. Thus, we have $\lim {\inf \limits _{t\rightarrow \infty }} v>\beta _2/\gamma _2$.

4) Finally, we prove that $\lim \sup \limits _{t\rightarrow \infty }v<\displaystyle \frac{\beta _2(1+\beta _1+K\beta _1^2)(\gamma _1+1)}{\beta _1\gamma _2-\beta _2(\gamma _1+1)}$. By

$$\begin{aligned} \lim \inf \limits _{t\rightarrow \infty } u>\displaystyle \frac{\beta _1}{1+\gamma _1},\;\lim \sup \limits _{t\rightarrow \infty } u<\beta _1, \end{aligned}$$

(2.20)

there exists a finite number $t_0$, depending on $u_0$ and $v_0$, such that for any $t\ge t_0$ and all $x\in \overline{\Omega }$,

$$\begin{aligned} \displaystyle \frac{\beta _1}{1+\gamma _1}<u(x,t)<\beta _1,\;t\ge t_0. \end{aligned}$$

(2.21)

By Proposition 1 and (2.21), there exists a sufficiently small $\chi >0$, such that for all $x\in \overline{\Omega }$ and $t\ge t_0$, one has

$$\begin{aligned} 0<\displaystyle \frac{\gamma _2\beta _1}{(1+\beta _1+v+K\beta _1^2-\chi )(\gamma _1+1)}<\displaystyle \frac{\gamma _2u}{1+u+v+Ku^2}. \end{aligned}$$

(2.22)

This can be done by choosing $\chi >0$ sufficiently small, since when $\chi =0$, (2.22) holds automatically.

Let $v_\chi$ be the unique solution of the following ODE:

$$\begin{aligned} \begin{aligned} \displaystyle \frac{dv_\chi (t)}{dt}&=\beta _2-\displaystyle \frac{\gamma _2\beta _1v_\chi }{(1+\beta _1+v_\chi +K\beta _1^2-\chi )(\gamma _1+1)},\;t>t_0,\\ v_\chi (t_0)&=(1+\chi )\max _{x\in \overline{\Omega }} v(x,t_0). \end{aligned} \end{aligned}$$

(2.23)

Setting $p_2(x,t)=v(x,t)-v_\chi (t)$, and by (2.1) and (2.23), we have

$$\begin{aligned} \begin{aligned} -\displaystyle \frac{\partial p_2(x,t)}{\partial t}+d_2\Delta p_2(x,t)&=\displaystyle \frac{\gamma _2uv}{1+u+v+Ku^2}-\displaystyle \frac{\gamma _2\beta _1v_\chi }{(1+\beta _1+v_\chi +K\beta _1^2-\chi )(\gamma _1+1)},\\ {}&\qquad t>t_0,p_2(x,t_0)<0. \end{aligned} \end{aligned}$$

(2.24)

The maximum principle for parabolic equations cannot be directly applicable to this case. Motivated by [15], we now use an elementary argument of Hopf’s boundary lemma for elliptic equations to prove that for all $x\in \overline{\Omega }$ and $t>t_0$, $p_2(x,t)<0$, and thus $v(x,t)<v_\chi (t)$.

Suppose not. Then, there exists a $T^*>t_0$, such that $p_2(x,t)<0$ for all $(x,t)\in \overline{\Omega }\times (t_0,T^*)$, and $p_2(x,T^*)=0$ for some $x\in \overline{\Omega }$. Thus, $\max \limits _{x\in \overline{\Omega }}p_2(x,T^*)=0$.

If for some $x_*\in \Omega$, such that $p_2(x_*, T^*)=0$. Then, we have $\partial p_2(x_*,T^*)/\partial t\ge 0$ and $\Delta p_2(x_*,T^*)\le 0$. Thus,

$$\begin{aligned} -\displaystyle \frac{\partial p_2(x_*,T^*)}{\partial t}+\Delta p_2(x_*,T^*)\le 0. \end{aligned}$$

(2.25)

At $(x,t)=(x_*,T^*)$, we have $v=v_\chi$. And $u<\beta _1$. Then, we have,

$$\begin{aligned} \begin{aligned} \displaystyle \frac{\gamma _2\beta _1v_\chi }{(1+\beta _1+v_\chi +K\beta _1^2-\chi )(\gamma _1+1)}&=\displaystyle \frac{\gamma _2\beta _1v}{(1+\beta _1+v+K\beta _1^2-\chi )(\gamma _1+1)}\\&<\displaystyle \frac{\gamma _2uv}{1+u+v+Ku^2}. \end{aligned} \end{aligned}$$

(2.26)

Then, (2.26) and (2.24) reveals that $-\partial p_2(x_*,T^*)/\partial t+d_2\Delta p_2(x_*,T^*)>0$, which contradicts with (2.25). Thus, one can not find such point $x_*\in \Omega$, such that $p_2(x_*, T^*)=0$.

If for some $x^*\in \partial \Omega$, such that $p_2(x^*, T^*)=0$. The right-hand side of (2.24) is positive at $(x^*,T^*)$, and by continuity it remains positive in $\Omega _0\times \{T^*\}$, where $\Omega _0$ is a sub-domain of $\Omega$ and $x^*\in \partial \Omega _0$. Then, on $\Omega _0\times \{T^*\}$, we have $-\partial p_2(x,t)/\partial t+d_2\Delta p_2(x,t)\ge 0$. Treating (2.24) as an elliptic equation in $\Omega _0\times \{T^*\}$ and by Hopf’s boundary lemma, we have $\partial _\nu p_2(x^*,T^*)=\partial _\nu v(x^*,T^*)>0$, which contradicts the Neumann boundary condition. Thus, for any $x\in \overline{\Omega }$ and $t>t_0$, we have $v(x,t)<v_\chi (t)$.

From (2.23), it follows that

$$\begin{aligned} \lim _{t\rightarrow \infty }v_\chi (t)=\displaystyle \frac{\beta _2(1+\beta _1+K\beta _1^2-\chi )(\gamma _1+1)}{\beta _1\gamma _2-\beta _2(\gamma _1+1)}<\displaystyle \frac{\beta _2(1+\beta _1+K\beta _1^2)(\gamma _1+1)}{\beta _1\gamma _2-\beta _2(\gamma _1+1)}. \end{aligned}$$

(2.27)

Thus, we have proved that $\lim \sup \limits _{t\rightarrow \infty }v<\displaystyle \frac{\beta _2(1+\beta _1+K\beta _1^2)(\gamma _1+1)}{\beta _1\gamma _2-\beta _2(\gamma _1+1)}$. $\square$

Our final result in this section is that under certain conditions (“lumped parameter assumption” [3]), the dynamics of system (2.1) can be determined by the dynamics of the corresponding ODEs (1.5).

Following [3], we define $\sigma :=d\lambda _1-{{\mathcal {Q}}}$, where $\lambda _1$ is the principal eigenvalue of $-\Delta$ on $\Omega$ subject to homogeneous Neumann boundary conditions, $d:=\min \{d_1,d_2\}$, and

$$\begin{aligned} {{\mathcal {Q}}}:=\sup \limits _{(u,v)\in {{\mathcal {A}}}}\{||J(u,v)||\}, \end{aligned}$$

(2.28)

where the Jacobin matrix $J(u,v)$ is given by

$$\begin{aligned} J(u,v)=\left( \begin{array}{cc} -1-\gamma _1\rho _1(u,v), &{}-\gamma _1\rho _2(u,v)\\ -\gamma _2\rho _1(u,v), &{}-\gamma _2\rho _2(u,v) \end{array}\right) , \end{aligned}$$

(2.29)

where

$$\begin{aligned} \rho _1(u,v):=\frac{v(1+v-Ku^2)}{(1+u+v+Ku^2)^2},\;\rho _2(u,v):=\frac{u(1+u+Ku^2)}{(1+u+v+Ku^2)^2}. \end{aligned}$$

(2.30)

Obviously, for $u,v>0$, the following inequalities hold

$$\begin{aligned} |\rho _1(u,v)|<\displaystyle \frac{1+u+Ku^2}{1+u+v+Ku^2},\quad |\rho _2(u,v)|<\displaystyle \frac{1+u+Ku^2}{1+u+v+Ku^2}. \end{aligned}$$

(2.31)

For any $(u,v)\in {{\mathcal {A}}}$, defined precisely in (2.12), we have

$$\begin{aligned} \displaystyle \frac{1+u+Ku^2}{1+u+v+Ku^2}<\xi :=\displaystyle \frac{\gamma _2(1+\gamma _1)^2(1+\beta _1+K\beta _1^2)}{\gamma _2(1+\gamma _1)^2+\beta _1\gamma _2(1+\gamma _1)+\beta _2(1+\gamma _1)^2+K\gamma _2\beta _1^2}. \end{aligned}$$

(2.32)

Thus,

$$\begin{aligned} \begin{aligned} {{\mathcal {Q}}}&=\max \left\{ \sup _{(u,v)\in {{\mathcal {A}}}}(\big |1+\gamma _1\rho _1(u,v)\big |+\gamma _1\rho _2(u,v)),\sup _{(u,v)\in {{\mathcal {A}}}}(\big |\gamma _2\rho _1(u,v)\big |+\gamma _2\rho _2(u,v))\right\} \\&<\mathcal {D}:=\max \{1+2\gamma _1\xi ,2\gamma _2\xi \}. \end{aligned} \end{aligned}$$

(2.33)

We conclude that, when $d_1$ and $d_2$ fall into certain ranges, the solutions of system (1.6) either converge exponentially to the unique positive constant steady states or to the spatially homogeneous periodic solutions.

Theorem 3

Suppose that $\beta _1/(1+\gamma _1)>\beta _2/\gamma _2$, and that $(d_1,d_2)\in [\mathcal {D}/\lambda _1,\infty )\times [\mathcal {D}/\lambda _1,\infty )$, where $\mathcal {D}$ is defined in (2.33). If (6.8) holds, then every solution $(u(x,t),v(x,t))$ of system (2.1) converges exponentially to $(u_*,v_*)$; while if (6.7) holds, then every solution $(u(x,t),v(x,t))$ of system (2.1) converges exponentially to the spatially homogeneous periodic solutions.

Proof

By Theorem 2, there exists $T>0$, such that for any $t>T$, the solution $(u(x,t),v(x,t))\in {{\mathcal {A}}}$ for all $x\in \overline{\Omega }$. Without loss of generality, we can assume that $T=0$.

Clearly, from (2.33), if $(d_1,d_2)\in [\mathcal {D}/\lambda _1,\infty )\times [\mathcal {D}/\lambda _1,\infty )$, then $\sigma >0$. Define

$$\begin{aligned} f(u,v):=\beta _1-u-\displaystyle \frac{\gamma _1uv}{1+u+v+Ku^2},\;g(u,v):=\beta _2-\displaystyle \frac{\gamma _2uv}{1+u+v+Ku^2}. \end{aligned}$$

(2.34)

Then by [3, 24], there exist constants ${{\mathcal {N}}}_i>0, i=1,2,3$, such that, for any solution $(u(t,x),v(t,x))$ of system (2.1)

$$\begin{aligned} ||\nabla _x (u(\cdot ,t),v(\cdot ,t))||_{L^2(\Omega )}\le {{\mathcal {N}}}_1e^{-\sigma t},\;||(u(\cdot ,t),v(\cdot ,t))-(\overline{u}(t),\overline{v}(t))||_{L^2(\Omega )}\le {{\mathcal {N}}}_2e^{-\sigma t}, \end{aligned}$$

(2.35)

where $\overline{u}, \overline{v}$ are the average of $u$ and $v$ over $\Omega$ respectively satisfying

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \displaystyle \frac{d\overline{u}}{dt}&{}=f(\overline{u},\overline{v})+o_1(t),\quad \overline{u}(0)=\displaystyle \frac{1}{|\Omega |}\int _\Omega u_0(x)dx, |o_1(t)|\le {{\mathcal {N}}}_3e^{-\rho t},\\ \displaystyle \frac{d\overline{v}}{dt}&{}=g(\overline{u},\overline{v})+o_2(t),\quad \overline{v}(0)=\displaystyle \frac{1}{|\Omega |}\int _\Omega v_0(x)dx, |o_2(t)|\le {{\mathcal {N}}}_3e^{-\rho t}. \end{aligned} \end{array}\right. } \end{aligned}$$

(2.36)

Moreover, the $\omega -$limit set of (2.36) is the subset of the $\omega -$limit set of the following ODEs

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \displaystyle \frac{du}{dt}&{}=f(u,v),\quad u(0)=\displaystyle \frac{1}{|\Omega |}\int _\Omega u_0(x)dx,\\ \displaystyle \frac{dv}{dt}&{}=g(u,v), \quad v(0)=\displaystyle \frac{1}{|\Omega |}\int _\Omega v_0(x)dx. \end{aligned} \end{array}\right. } \end{aligned}$$

(2.37)

Finally, combining the results of Lemmas 9 and 10 in Appendix, we complete the proof of the Theorem 3. $\square$

3 Non-existence of Turing Patterns: Some Estimates

In this section, we show the non-existence of the non-constant positive steady state solutions of the system:

$$\begin{aligned} {\left\{ \begin{array}{ll} -d_1\Delta u=\beta _1-u-\displaystyle \frac{\gamma _1uv}{1+u+v+Ku^2},&{}\quad x\in \Omega ,\\ -d_2\Delta v=\beta _2-\displaystyle \frac{\gamma _2uv}{1+u+v+Ku^2},&{}\quad x\in \Omega ,\\ \partial _{\nu } u=\partial _{\nu } v=0, \;\; &{} \quad x\in \partial \Omega .\\ \end{array}\right. } \end{aligned}$$

(3.1)

Lemma 4

(A priori estimates) Suppose that $\displaystyle \frac{\beta _1}{1+\gamma _1}>\frac{\beta _2}{\gamma _2}$ holds, and let $(u(x),v(x))$ be any given positive steady state solution of system (1.6). Then, for any $x\in \overline{\Omega }$, the following conclusions hold:

$$\begin{aligned} \displaystyle \frac{\beta _1}{1+\gamma _1}<u(x)<\beta _1,\;\displaystyle \frac{\beta _2}{\gamma _2}<v(x)<\displaystyle \frac{\beta _2(1+\beta _1+K\beta _1^2)(\gamma _1+1)}{\beta _1\gamma _2-\beta _2(\gamma _1+1)}. \end{aligned}$$

(3.2)

Remark 5

Lemma 4 is the direct consequence of Theorem 2.

For a steady state solution pair $(u(x),v(x))$ of system (3.1), we define

$$\begin{aligned} \overline{u}=\displaystyle \frac{1}{|\Omega |}\int _\Omega u(x)dx,\;\overline{v}=\displaystyle \frac{1}{|\Omega |}\int _\Omega v(x)dx. \end{aligned}$$

(3.3)

Multiplying the first equation of (3.1) by $\gamma _2$, the second equation of (3.1) by $-\gamma _1$, and adding them, we can obtain that

$$\begin{aligned} \Delta (\gamma _2d_1u-\gamma _1d_2v)+\gamma _2\beta _1-\gamma _1\beta _2-\gamma _2u=0. \end{aligned}$$

(3.4)

Integrating (3.4) over $\Omega$, we obtain

$$\begin{aligned} \overline{u}=\displaystyle \frac{1}{|\Omega |}\int _{\Omega }udx=\beta _1-\displaystyle \frac{\gamma _1}{\gamma _2}\beta _2=u_*>0. \end{aligned}$$

(3.5)

Define

$$\begin{aligned} \phi (x):=u(x)-\overline{u}, \;\psi (x):=v(x)-\overline{v}. \end{aligned}$$

(3.6)

We are now stating the following useful estimates on the steady state solutions:

Lemma 6

Suppose that $(u(x),v(x))$ is the solution pair of (3.1), and let $\phi (x),\psi (x)$ be defined in (3.6). Then,

$$\begin{aligned} \displaystyle \frac{\gamma _1^2d_2^2\lambda _1^2}{\gamma _2^2(2d_1^2\lambda _1^2+2d_1\lambda _1+1)} \int _\Omega |\nabla \psi |^2dx\le \int _\Omega |\nabla \phi |^2dx\le \displaystyle \frac{\gamma _1^2d_2^2}{\gamma _2^2d_1^2}\int _\Omega |\nabla \psi |^2dx, \end{aligned}$$

(3.7)

where $\lambda _1$ is the principle eigenvalue of $-\Delta$ on $\Omega$ subject to the homogeneous Neumann boundary conditions.

Proof

Rewrite (3.4) as

$$\begin{aligned} \Delta (\gamma _2d_1u-\gamma _1d_2v)=\gamma _2(u-\overline{u})=\gamma _2\phi . \end{aligned}$$

(3.8)

Multiplying (3.8) by $\gamma _2d_1u-\gamma _1d_2v$, integrating over $\Omega$ by parts, and noticing that $\displaystyle \int _\Omega \phi dx=\displaystyle \int _\Omega \psi dx=0$, we can yield

$$\begin{aligned} -\displaystyle \int _\Omega \big |\nabla (d_1\gamma _2u-d_2\gamma _1v)\big |^2dx=\gamma _2^2d_1\int _\Omega \phi ^2dx-\gamma _1\gamma _2d_2\int _\Omega \phi \psi dx. \end{aligned}$$

(3.9)

Thus, we have

$$\begin{aligned} \gamma _1\gamma _2d_2\int _\Omega \phi \psi dx=\gamma _2^2d_1\int _\Omega \phi ^2dx+\displaystyle \int _\Omega \big |\nabla (d_1\gamma _2u-d_2\gamma _1v)\big |^2dx\ge 0. \end{aligned}$$

(3.10)

If we multiplify (3.8) by $\phi$ and integrate over $\Omega$ by parts, we have

$$\begin{aligned} \gamma _2\displaystyle \int _\Omega \phi ^2dx=-d_1\gamma _2\int _\Omega |\nabla \phi |^2dx+d_2\gamma _1\int _\Omega \nabla \phi \nabla \psi dx, \end{aligned}$$

(3.11)

which implies that

$$\begin{aligned} d_2\gamma _1\int _\Omega \nabla \phi \nabla \psi dx=\gamma _2\displaystyle \int _\Omega \phi ^2dx+d_1\gamma _2\int _\Omega |\nabla \phi |^2dx. \end{aligned}$$

(3.12)

On the other hand, the left side of (3.9) also equals

$$\begin{aligned} \begin{aligned} -\displaystyle \int _\Omega \big |\nabla (d_1\gamma _2u-d_2\gamma _1v)\big |^2dx&=-\displaystyle \int _\Omega \bigg (d_1^2\gamma _2^2|\nabla u|^2-2d_1d_2\gamma _1\gamma _2\nabla u\nabla v+d_2^2\gamma _1^2|\nabla v|^2\bigg )dx\\&=-\displaystyle \int _\Omega \bigg (d_1^2\gamma _2^2|\nabla \phi |^2-2d_1d_2\gamma _1\gamma _2\nabla \phi \nabla \psi +d_2^2\gamma _1^2|\nabla \psi |^2\bigg )dx. \end{aligned} \end{aligned}$$

(3.13)

Then, from (3.9), (3.12) and (3.13), we have

$$\begin{aligned} d_2^2\gamma _1^2\int _\Omega |\nabla \psi |^2dx=d_1^2\gamma _2^2\int _\Omega |\nabla \phi |^2dx+d_1\gamma _2^2\int _\Omega \phi ^2dx+\gamma _1\gamma _2d_2\int _\Omega \phi \psi dx, \end{aligned}$$

(3.14)

which together with (3.10) implies that

$$\begin{aligned} d_1^2\gamma _2^2\int _\Omega |\nabla \phi |^2dx\le d_2^2\gamma _1^2\int _\Omega |\nabla \psi |^2dx. \end{aligned}$$

(3.15)

Thus,

$$\begin{aligned} \displaystyle \int _\Omega |\nabla \phi |^2dx\le \displaystyle \frac{d_2^2\gamma _1^2}{d_1^2\gamma _2^2}\displaystyle \int _\Omega |\nabla \psi |^2dx. \end{aligned}$$

(3.16)

On the other hand, by the Poincare inequality, it follows that

$$\begin{aligned} \displaystyle \int _\Omega \phi ^2dx\le \displaystyle \frac{1}{\lambda _1}\int _\Omega |\nabla \phi |^2dx. \end{aligned}$$

(3.17)

The Cauchy inequality says that, for any given real number $x$ and $y$, and $\epsilon >0$, the inequality $xy\le \displaystyle \frac{1}{4\epsilon }x^2+\epsilon y^2$ always holds. It then follows that

$$\begin{aligned} \displaystyle \int _\Omega \phi \psi dx\le \displaystyle \frac{\gamma _2}{2\lambda _1\gamma _1d_2}\int _\Omega \phi ^2dx+\displaystyle \frac{\lambda _1\gamma _1d_2}{2\gamma _2}\int _\Omega \psi ^2dx. \end{aligned}$$

(3.18)

Then,

$$\begin{aligned} \begin{aligned} \gamma _1\gamma _2d_2\displaystyle \int _\Omega \phi \psi dx&\le \displaystyle \frac{\gamma _2^2}{2\lambda _1}\int _\Omega \phi ^2dx+\displaystyle \frac{1}{2}\lambda _1\gamma _1^2d_2^2\int _\Omega \psi ^2dx\\&\le \displaystyle \frac{\gamma _2^2}{2\lambda _1^2}\int _\Omega |\nabla \phi |^2dx+\displaystyle \frac{1}{2}\gamma _1^2d_2^2\int _\Omega |\nabla \psi |^2dx. \end{aligned} \end{aligned}$$

(3.19)

Thus, from (3.14), (3.17) and (3.19), we have

$$\begin{aligned} \displaystyle \frac{1}{2}\gamma _1^2d_2^2\int _\Omega |\nabla \psi |^2dx\le \gamma _2^2\bigg (d_1^2+\displaystyle \frac{d_1}{\lambda _1}+\displaystyle \frac{1}{2\lambda _1^2}\bigg )\int _\Omega |\nabla \phi |^2dx, \end{aligned}$$

(3.20)

which implies

$$\begin{aligned} \displaystyle \frac{\gamma _1^2d_2^2\lambda _1^2}{\gamma _2^2(2d_1^2\lambda _1^2+2d_1\lambda _1+1)}\int _\Omega |\nabla \psi |^2dx\le \int _\Omega |\nabla \phi |^2dx. \end{aligned}$$

(3.21)

This completes the proof. $\square$

For the convenience of our later discussions, we define

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} h_1(u,v)&{}:=(1+u+v+Ku^2)^{-1}(K\overline{u}u-(1+\overline{v}))\displaystyle \frac{\overline{v}}{1+\overline{u}+\overline{v}+K\overline{u}^2},\\ h_2(u,v)&{}:=(1+u+v+Ku^2)^{-1}\bigg (\displaystyle \frac{\overline{u}\;\overline{v}}{1+\overline{u}+\overline{v}+K\overline{u}^2}-u\bigg ),\\ h_3(u,v)&{}:= (1+u+v+Ku^2)^{-1}\displaystyle \frac{1+\overline{u}+\overline{u}\;\overline{v}}{1+\overline{u}+\overline{v}+K\overline{u}^2},\\ h_4(u,v)&{}:=\displaystyle \frac{\overline{u}\;\overline{v}}{1+\overline{u}+\overline{v}+K\overline{u}^2}-\overline{u}, \end{aligned} \end{array}\right. } \end{aligned}$$

(3.22)

where $\overline{u}$ and $\overline{v}$ are defined precisely in (3.3).

From Lemma 4, it follows that, any positive solutions $(u,v)$ of system (3.1) satisfies $(u,v)\in {{\mathcal {A}}}$, where ${{\mathcal {A}}}$ is defined in (2.12). Define

$$\begin{aligned} {{\mathcal {H}}}_i:=\sup \limits _{(u,v)\in {{\mathcal {A}}}}|h_i(u,v)|,\;i=1,2,3,4, \end{aligned}$$

(3.23)

and

$$\begin{aligned} \chi _1(x):=\displaystyle \frac{{{\mathcal {H}}}_2\gamma _2x}{\lambda _1x-{{\mathcal {H}}}_1\gamma _1},\;\chi _2(x):=\displaystyle \frac{{{\mathcal {H}}}_4\gamma _2\sqrt{2\lambda _1^2x^2+2\lambda _1x+1}}{\lambda _1(\lambda _1x-{{\mathcal {H}}}_3\gamma _1)}. \end{aligned}$$

(3.24)

Clearly, the functions $\chi _1(x)$ and $\chi _2(x)$ are decreasing functions defined on $({{\mathcal {H}}}_2\gamma _1/\lambda _1,\infty )$ and $({{\mathcal {H}}}_3\gamma _1/\lambda _1,\infty )$ respectively, satisfying

$$\begin{aligned} \begin{aligned} \lim \limits _{x\rightarrow \displaystyle ({{\mathcal {H}}}_1\gamma _1/\lambda _1)^+}\chi _1(x)&=+\infty ,\; \quad \quad \lim \limits _{x\rightarrow +\infty }\chi _1(x)=\displaystyle \frac{{{\mathcal {H}}}_2\gamma _2}{\lambda _1},\\ \lim \limits _{x\rightarrow \displaystyle ({{\mathcal {H}}}_3\gamma _1/\lambda _1)^+}\chi _2(x)&=+\infty ,\;\quad \quad \lim \limits _{x\rightarrow +\infty }\chi _2(x)=\displaystyle \frac{\sqrt{2}{{\mathcal {H}}}_4\gamma _2}{\lambda _1}. \end{aligned} \end{aligned}$$

(3.25)

We are now in the position to state the following theorem regarding the non-existence of non-constant positive solutions of the system (3.1):

Theorem 7

Let $h_i(u,v)$, ${{\mathcal {H}}}_i$, $i=1,2,3,4$, and $\chi _j(x)$, $j=1,2$, be defined in (3.22), (3.23) and (3.25) respectively. Then, for any $(d_1,d_2)\in \Sigma$, system (3.1) does not have non-constant positive solutions, where

$$\begin{aligned} \Sigma&:=\left\{ (d_1,d_2)\in {\mathbf R}^2:d_1>\displaystyle \frac{{{\mathcal {H}}}_1\gamma _1}{\lambda _1},\;d_2>\chi _1(d_1)\right\} \cup \Big \{(d_1,d_2)\in {\mathbf R}^2:d_1\nonumber \\&>\displaystyle \frac{{{\mathcal {H}}}_3\gamma _1}{\lambda _1}, d_2>\chi _2(d_1)\Big \}. \end{aligned}$$

(3.26)

Proof

We first prove that if $(d_1,d_2)\in \{(d_1,d_2)\in {\mathbf R}^2:d_1>\displaystyle \frac{{{\mathcal {H}}}_1\gamma _1}{\lambda _1},\;d_2>\chi _1(d_1)\}$, then system (3.1) does not have non-constant positive solutions.

Multiplying the second equation of (3.1) by $\psi$ and integrating over $\Omega$, we have

$$\begin{aligned} -\int _\Omega d_{2}\psi \Delta \psi dx&=\beta _2\int _\Omega \psi dx-\gamma _2\int _\Omega \frac{uv\psi }{1+u+v+Ku^{2}}dx\nonumber \\&=-\gamma _2\int _\Omega \frac{uv\psi }{1+u+v+Ku^{2}}dx. \end{aligned}$$

(3.27)

Thus,

$$\begin{aligned} d_{2}\int _\Omega |\nabla \psi |^{2}dx=-\gamma _{2}\int _\Omega \frac{uv\psi }{1+u+v+Ku^{2}}dx. \end{aligned}$$

(3.28)

Direct calculations show that the right hand side of (3.28) is

$$\begin{aligned} \begin{aligned} -\gamma _2&\int _\Omega \bigg (\frac{u(v-\overline{v})}{1+u+v+Ku^{2}}+\frac{u\overline{v}}{1+u+v+Ku^{2}}-\frac{\overline{u}\;\overline{v}}{1+\overline{u}+\overline{v}+K\overline{u}^{2}}\bigg )\psi dx\\ =&-\gamma _2\int _\Omega \frac{u\psi ^2}{1+u+v+Ku^{2}}dx -\gamma _2\int _\Omega \frac{\overline{v}\psi (\phi +\overline{v}u-\overline{u}v-K\overline{u}u\phi )}{(1+u+v+Ku^{2})(1+\overline{u}+\overline{v}+K\overline{u}^{2})}dx\\ =&-\gamma _{2}\int _\Omega \frac{u\psi ^{2}}{1+u+v+Ku^{2}}dx-\displaystyle \frac{\gamma _2\overline{v}}{1+\overline{u}+\overline{v}+K\overline{u}^2}\int _\Omega \frac{(\phi +\overline{v}u-\overline{u}v-K\overline{u}u\phi )\psi }{1+u+v+Ku^{2}} dx\\ =&-\gamma _2\int _\Omega \displaystyle \frac{u}{1+u+v+Ku^2}\psi ^2dx-\displaystyle \frac{\gamma _2\overline{v}(1+\overline{v})}{1+\overline{u}+\overline{v}+K\overline{u}^2}\int _\Omega \displaystyle \frac{1}{1+u+v+Ku^2}\phi \psi dx\\&+\displaystyle \frac{\gamma _2\overline{u}\;\overline{v}}{1+\overline{u}+\overline{v}+K\overline{u}^2}\bigg (\int _\Omega \displaystyle \frac{Ku}{1+u+v+Ku^2}\phi \psi dx+\int _\Omega \displaystyle \frac{1}{1+u+v+Ku^2}\psi ^2 dx\bigg )\\ =&\gamma _2\int _\Omega h_1(u,v)\phi \psi dx+\gamma _2\int _\Omega h_2(u,v)\psi ^2dx,\\ \le&\gamma _2\int _\Omega {{\mathcal {H}}}_1|\phi \psi | dx+\gamma _2\int _\Omega {{\mathcal {H}}}_2\psi ^2dx. \end{aligned} \end{aligned}$$

(3.29)

Then,

$$\begin{aligned} \displaystyle \frac{d_2}{\gamma _2}\int _\Omega |\nabla \psi |^{2}dx\le {{\mathcal {H}}}_{1}\int _\Omega |\phi \psi |dx+{{\mathcal {H}}}_{2}\int \psi ^{2}dx\le {{\mathcal {H}}}_{1}\int _\Omega |\phi \psi |dx+\displaystyle \frac{{{\mathcal {H}}}_{2}}{\lambda _1}\int |\nabla \psi |^{2}dx. \end{aligned}$$

(3.30)

On the other hand, we have

$$\begin{aligned} \begin{aligned} \int _\Omega |\phi \psi |dx\le \left( \int _\Omega |\phi |^{2}dx\right) ^{\frac{1}{2}}\left( \int _\Omega |\psi |^{2}dx\right) ^{\frac{1}{2}}&\le \left( \frac{1}{\lambda _1}\int _\Omega |\nabla \phi |^{2}dx\right) ^{\frac{1}{2}}\left( \frac{1}{\lambda _1}\int _\Omega |\nabla \psi |^{2}dx\right) ^{\frac{1}{2}}\\&=\frac{1}{\lambda _1}\left( \int _\Omega |\nabla \phi |^{2}dx\right) ^{\frac{1}{2}}\left( \int _\Omega |\nabla \psi |^{2}dx\right) ^{\frac{1}{2}}. \end{aligned} \end{aligned}$$

(3.31)

Then, combining (3.7) and (3.31), we have

$$\begin{aligned} \int _\Omega |\phi \psi |dx\le \frac{d_{2}\gamma _{1}}{\lambda _{1}d_{1}\gamma _{2}}\displaystyle \int _\Omega |\nabla \psi |^2dx. \end{aligned}$$

(3.32)

So far, (3.30) is reduced to

$$\begin{aligned} \displaystyle \frac{d_2}{\gamma _2}\int _\Omega |\nabla \psi |^{2}dx\le \bigg (\frac{{{\mathcal {H}}}_{2}}{\lambda _{1}}+\frac{{{\mathcal {H}}}_{1}d_{2}\gamma _{1}}{\lambda _{1}d_{1}\gamma _{2}}\bigg )\int _\Omega |\nabla \psi |^{2}dx. \end{aligned}$$

(3.33)

For any $(d_1,d_2)\in \{(d_1,d_2)\in {\mathbf R}^2:d_1>\displaystyle \frac{{{\mathcal {H}}}_1\gamma _1}{\lambda _1},\;d_2>\chi _1(d_1)\}$, we have

$$\begin{aligned} \displaystyle \frac{d_2}{\gamma _2}>\frac{{{\mathcal {H}}}_{2}}{\lambda _{1}}+\frac{{{\mathcal {H}}}_{1}d_{2}\gamma _{1}}{\lambda _{1}d_{1}\gamma _{2}}. \end{aligned}$$

(3.34)

Thus, we have $\nabla \psi \equiv 0$. This together with (3.7), reveals that $\nabla \phi \equiv 0$. Then system (3.1) does not have non-constant positive solutions.

We then prove that if $(d_1,d_2)\in \{(d_1,d_2)\in {\mathbf R}^2:d_1>\displaystyle \frac{{{\mathcal {H}}}_3\gamma _1}{\lambda _1}, d_2>\chi _2(d_1)\}$, then system (3.1) does not have non-constant positive solutions.

Multiplying the first equation of system by $\phi$ and integrating over $\Omega$, we have

$$\begin{aligned} d_{1}\int _\Omega |\nabla \phi |^{2}dx=\int _\Omega \phi (\beta _{1}-u)dx-\int _\Omega \frac{\gamma _{1}uv}{1+u+v+Ku^{2}}\phi dx. \end{aligned}$$

(3.35)

A direct calculation shows that

$$\begin{aligned} \begin{aligned} d_{1}\int _\Omega |\nabla \phi |^{2}dx=&\gamma _1\int _\Omega \bigg (\displaystyle \frac{\overline{u}\;\overline{v}}{1+\overline{u}+\overline{v}+K\overline{u}^2}-\overline{u}\bigg )\phi \psi dx\\&-\int _\Omega \bigg (1+\displaystyle \frac{\gamma _1v}{1+u+v+Ku^2}\bigg )\psi ^2dx\\&+\gamma _1\int _\Omega (1+u+v+Ku^2)^{-1}\displaystyle \frac{1+\overline{u}+\overline{u}\;\overline{v}}{1+\overline{u}+\overline{v}+K\overline{u}^2}\phi ^2dx\\ \le&\gamma _1\int _\Omega \bigg (\displaystyle \frac{\overline{u}\;\overline{v}}{1+\overline{u}+\overline{v}+K\overline{u}^2}-\overline{u}\bigg )\phi \psi dx\\&+\gamma _1\int _\Omega (1+u+v+Ku^2)^{-1}\displaystyle \frac{1+\overline{u}+\overline{u}\;\overline{v}}{1+\overline{u}+\overline{v}+K\overline{u}^2}\phi ^2dx\\ =&\gamma _1\int _\Omega h_3(u,v)\phi ^2dx+\gamma _1\int _\Omega h_4(u,v)\phi \psi dx,\\ \le&\gamma _1\int _\Omega {{\mathcal {H}}}_3\phi ^2dx+\gamma _1\int _\Omega {{\mathcal {H}}}_4|\phi \psi | dx. \end{aligned} \end{aligned}$$

(3.36)

By (3.21) and (3.31), we have

$$\begin{aligned} \int _\Omega |\phi \psi |dx\le \frac{\gamma _{2}(2d_{1}^{2}\lambda _{1}^{2}+2d_{1}\lambda _{1}+1)^{\frac{1}{2}}}{\gamma _{1}d_{2}\lambda _{1}^{2}}\displaystyle \int _\Omega |\nabla \phi |^2dx. \end{aligned}$$

(3.37)

Thus,

$$\begin{aligned} d_{1}\int _\Omega |\nabla \phi |^{2}dx\le \bigg (\frac{{{\mathcal {H}}}_{3}\gamma _1}{\lambda _{1}}+\frac{{{\mathcal {H}}}_{4}\gamma _2(2d_{1}^{2}\lambda _{1}^{2}+2d_{1}\lambda _{1}+1)^{\frac{1}{2}}}{d_{2}\lambda _{1}^{2}}\bigg ) \int _\Omega |\nabla \phi |^{2}dx. \end{aligned}$$

(3.38)

For any $(d_1,d_2)\in \{(d_1,d_2)\in {\mathbf R}^2:d_1>\displaystyle \frac{{{\mathcal {H}}}_3\gamma _1}{\lambda _1}, d_2>\chi _2(d_1)\}$, we have

$$\begin{aligned} d_1>\frac{{{\mathcal {H}}}_{3}\gamma _1}{\lambda _{1}}+\frac{{{\mathcal {H}}}_{4}\gamma _2(2d_{1}^{2}\lambda _{1}^{2}+2d_{1}\lambda _{1}+1)^{\frac{1}{2}}}{d_{2}\lambda _{1}^{2}}. \end{aligned}$$

(3.39)

This together with (3.16), reveals that $\nabla \phi \equiv 0$. Then system (3.1) does not have non-constant positive solutions. $\square$

4 Existence of Turing Patterns: Global Steady State Bifurcations

In this section, we use the global bifurcation theory to prove the existence of positive non-constant of steady state system (3.1). In particular, we are concerned with the existence of Turing patterns.

Let $j_0$ and $k_0$ be defined precisely in (6.4) in Appendix. Then, if $j_0<-\displaystyle \frac{1}{\gamma _1}$ holds, system (2.1) is a substrate–inhibition system, that is the Jacobian matrix of the corresponding ODEs evaluated at $(u_*,v_*)$ takes in the form of

$$\begin{aligned} \left( \begin{array}{cc} +,&{} -\\ +,&{} - \end{array} \right) . \end{aligned}$$

(4.1)

And if

$$\begin{aligned} \displaystyle \frac{\beta _1}{1+\gamma _1}>\frac{\beta _2}{\gamma _2},\;-\displaystyle \frac{1}{\gamma _1}-\displaystyle \frac{\gamma _2k_0}{\gamma _1}<j_0, \end{aligned}$$

(4.2)

holds, then $(u_*,v_*)$ is positive and stable in the ODEs (1.5).

Thus, in the rest of the paper, we always assume that the conditions

$$\begin{aligned} \displaystyle \frac{\beta _1}{1+\gamma _1}>\frac{\beta _2}{\gamma _2},\;-\displaystyle \frac{1}{\gamma _1}-\displaystyle \frac{\gamma _2k_0}{\gamma _1}<j_0<-\displaystyle \frac{1}{\gamma _1} \end{aligned}$$

(4.3)

are satisfied.

The linearized operator of system (3.1) evaluated at $(u_*,v_*)$ is given by (choosing $d_1$ as the bifurcation parameter)

$$\begin{aligned} L(d_1)=\left( \begin{array}{cc} d_1\Delta -1-\gamma _1j_0,\ \ \ &{} -\gamma _1k_0\\ -\gamma _2j_0\ \ \ &{} d_2\Delta -\gamma _2k_0 \end{array} \right) . \end{aligned}$$

(4.4)

Let $\lambda _i$ and $\xi _i(x)$, $i\in \mathbb {N}_0$, be the eigenvalues and the corresponding eigenfunctions of $-\Delta$ in $\Omega$ subject to Neumann boundary conditions. Then, by [15, 25], the eigenvalues of $L(d_1)$ are given by those of the following operator $L_i(d_1)$:

$$\begin{aligned} L_i(d_1)=\left( \begin{array}{cc} - d_1\lambda _i-1-\gamma _1j_0,\ \ \ &{} -\gamma _1k_0\\ -\gamma _2j_0\ \ \ &{} - d_2\lambda _i-\gamma _2k_0 \end{array} \right) , \end{aligned}$$

(4.5)

whose characteristic equation is

$$\begin{aligned} \mu ^2-\mu T_i(d_1)+D_i(d_1)=0,\;\; \ i\in \mathbb {N}_0, \end{aligned}$$

where

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} T_i(d_1):&{}=-(d_1+d_2)\lambda _i-(1+\gamma _1j_0+\gamma _2k_0),\\ D_i(d_1):&{}=d_1d_2\lambda _i^2+(\gamma _2k_0d_1+(1+\gamma _1j_0)d_2)\lambda _i+\gamma _2k_0. \end{aligned} \end{array}\right. } \end{aligned}$$

(4.6)

According to [19, 25], if there exist $i\in \mathbb {N}_0$ and $d_1^*>0$, such that

$$\begin{aligned} D_i(d_1^*)=0,\;\;\;T_i(d_1^*)\ne 0,\;\;\;T_j(d_1^*)\ne 0,\;\;\;D_j(d_1^*)\ne 0\;\;\text {for all}\;j\ne i, \end{aligned}$$

(4.7)

and the derivative $\displaystyle \frac{d}{dd_1}D_i(d_1^*)\ne 0$, then a global steady state bifurcation occurs at the critical point $d_1^*$.

By (4.3), we have $T_0(d_1)<0$. Thus, for all $i\in \mathbb {N}_0$, we have $T_i(d_1)<0$. Solving $D_i(d_1)=0$, we have the set of critical values of $(d_1,d_2)$, given by the hyperbolic curves $C_i$, with $i\in \mathbb {N}:=\mathbb {N}_0\backslash \{0\}$ (see also page 561 of [16]):

$$\begin{aligned} (C_i): d_2^i=\displaystyle \frac{\gamma _1\gamma _2k_0j_0/{\lambda _i^2}}{d_1+(1+\gamma _1j_0)/\lambda _i}-\displaystyle \frac{\gamma _2k_0}{\lambda _i},\;i\in \mathbb {N}. \end{aligned}$$

(4.8)

Suppose that $\lambda _i$, $i\in \mathbb {N}$, is the simple eigenvalue of $-\Delta$. Following [16], we call $\mathcal {B}:=\bigcup _{i=1}^\infty C_i$ the bifurcation set with respect to $(u_*,v_*)$, and denote by $\mathcal {B}_0$ be the countable set of intersection points of two curves of $\{C_i\}_{i=1}^\infty$, and $\widehat{\mathcal {B}}=\mathcal {B}\backslash {\mathcal {B}_0}$.

Clearly, for any fixed $d_2>0$, there exists a unique $d_1^i$ such that $(d_1^i,d_2)\in \widehat{\mathcal {B}}\cap C_i$, and at $d=d_1^i$, both (4.7) and $\displaystyle \frac{d}{dd_1}D_i(d_1^i)\ne 0$ are satisfied.

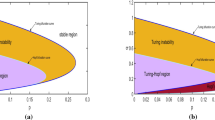
Then, from [16, 25], we have the following results regarding the existence of Turing patterns:

Theorem 8

Suppose that (4.3) holds and that $C_i$ is defined in (4.8), where $\lambda _i$, $i\in \mathbb {N}$, is the simple eigenvalue of $-\Delta$. Then for any $(d_1^i,d_2)\in \widehat{\mathcal {B}}\cap C_i$ with $d_2$ fixed, there is a smooth curve $\Gamma _{i}$ of positive solutions of (3.1) bifurcating from $(d_1,u,v)=(d_1^{i},u_*,v_*)$, with $\Gamma _{i}$ contained in a global branch ${\mathcal C}_{i}$ of the positive solutions of (3.1). Moreover

• 1. Near $(d_1,u,v)=(d_1^i,u_*,v_*)$, $\Gamma _{i}=\left\{ (d_1(s),u(s),v(s)):s \in (-\epsilon , \epsilon )\right\}$, where $u(s)=u_*+s\mathbf a _i\xi _i(x)+so_1(s)$, $v(s)=v_*+s\mathbf b _i\xi _i(x)+so_2(s)$ for $s \in (-\epsilon , \epsilon )$ for some $C^{\infty }$ smooth functions $d_1(s),o_1(s),o_2(s)$ such that $d_1(0)=d_1^i$ and $o_1(0)=o_2(0)=0$. Here $\mathbf a _i$ and $\mathbf b _i$ satisfy $L_i(d_1) (\mathbf a _i, \mathbf b _i)^T=(0,0)^T$, and $\xi _i(\cdot )$ is the corresponding eigenfunction of the eigenvalue $\lambda _i$ of $-\Delta$.

• 2. Moreover, the projection of ${\mathcal C}_{i}$ onto $d_1^i$-axis contains the interval $(0,d_1^i)$.

Proof

From discussions above, at $d_1=d_1^i$, we can apply Theorem 3.2 in [25] to assert the existence of local and global steady state bifurcations. By Theorem 2.3 of [16], we can rule out the possibility that ${\mathcal C}_{i}$ contains another $(d_1^j,u_*,v_*)$ with $i\ne j$. We thus complete the proof of this theorem (Fig. 2). $\square$

Fig. 2

Bifurcation diagram: For any $i\in \mathbb {N}$, $C_i$, defined precisely in (4.8), is the hyperbolic curve where the steady state bifurcation point $(d_1^i,d_2)$ locates (for fixed $d_2>0$). The area on the left side of the vertical line $d_1\equiv -(1+\gamma _1j_0)/\lambda _1$, Turing patterns are possible; While in the shaded area on the right side of vertical line $d_1\equiv {{\mathcal {H}}}_3\gamma _1/\lambda _1$, system (2.1) does not possess any non-constant positive steady states, including Turing patterns. Here ${{\mathcal {H}}}_i$, $i=1,2,3,4$, are defined in (3.23)

5 Numerical Experiments

In this section we perform two numerical experiments to show that for some sets of parameters chosen accordingly the system (2.1) produces Turing patterns, that is., the solutions converge to spatially non-homogenous steady state. On the other hand, for some parameters the solutions of the system (2.1) either converge exponentially to uniform steady state or spatially homogenous periodic solution.

Experiment 1: Turing patterns

In this experiment, we show that the model (2.1) produces Turing patterns in a two-dimensional domain. The model (2.1) is defined in the square domain $\Omega = [0,\pi ] \times [0,\pi ]$ in $\mathbb {R}^2\,$ and the final time of interest is $T=100$. Parameters are chosen according to the bifurcation analysis presented in Sect. 4 and by the eigenvalues of the Laplacian operator, $-\Delta$ in domain $\Omega$ which are $\lambda _{i,j} = i^2 + j^2$. The parameters for this experiment are $\beta _1 = 2.47, \beta _2 = 1, \gamma _1 = 150.8, \gamma _2 = 72.07, K = 25.5, d_1 = 0.09, d_2 = 2.$ The parameters $\beta _1,\,\beta _2,\, \gamma _1,\, \gamma _2,$ and $K$ are fixed so that the inequality (4.3) holds. Thus in the absence of diffusion the uniform steady state $u_* = 0.38$ and $v_* = 0.19$ is locally asymptotically stable. For $d_2 =2$, we find the diffusion constant $d_1$ such that the conditions in (4.7) satisfied. We take $\lambda = \lambda _{i,j} = 2^2 + 3^2 =13$, in which the corresponding eigenfunctions are $\cos (2\pi x) \cos (3\pi y)$. Hence,

$$\begin{aligned} d_1 = \displaystyle \frac{-\gamma _2 k_0 - (1 + \gamma _1 j_0)d_2 \lambda }{d_2 \lambda ^2 + \gamma _2 k_0 \lambda } = 0.09 \text{ for } d_2 = 2 \text{ and } \lambda = 13. \end{aligned}$$

We use finite element method for spatial discretization and implicit finite difference for the time derivative to approximate the solutions of the model (2.1). The mesh size $h = 0.0982$ which is achieved by $7938$ elements (triangles), and the time step size is $\Delta t =0.1$. Initial conditions are small random perturbations around the uniform steady state in the absence of diffusion. The chemical concentrations $u$ and $v$ at times $t=0,10, 50, 100$ are shown in the Fig. 5.

Fig. 3

Experiment 1: Turing patterns arising from the system (2.1) in a square domain $\Omega$. The figures in the first column correspond to the chemical concentration $u$ and the figures in the second column correspond to the chemical concentration $v$ at specific time levels

Experiment 2: Asymptotic behavior of the solutions

In this example we simulate the results of the Theorem 3. We show that for diffusion constants sufficiently large, namely for $(d_1,d_2)\in [\mathcal {D}/\lambda _1,\infty )\times [\mathcal {D}/\lambda _1,\infty )$, the solutions of the system (2.1) either converges to the constant steady state if (6.6) holds, or to the spatially homogenous periodic solutions if (6.7) holds. For the first case, we choose parameters as $\beta _1 =5, \beta _2 = 1,\gamma _1 = 150, \gamma _2 = 73,$ and take the diffusion constants to be $d_1 = 2 \times 10^{5}, d_2 = 3\times 10^{5}.$ As shown in Fig. 5, the solutions converge to the constant steady states $u_* = 2.95$ and $v_* =1.03$ (Figs. 3, 4).

Fig. 4

Experiment 2: The solutions of the system (2.1) converging to constant steady state solutions $u_* = 2.95$ (a) and $v_* =1.03$ (b)

For the latter case, we choose the parameters as $\beta _1 =5, \beta _2 = 2,\gamma _1 = 146, \gamma _2 = 71,$ and take the diffusion constants to be $d_1 = 2 \times 10^{5}, d_2 = 3\times 10^{5}.$ As shown in Fig. 5, the solutions converge to the spatially homogenous periodic solutions in time.

Fig. 5

Experiment 2: The solutions of the system (2.1) converging to the spatially homogenous temporally periodic steady state

Appendix: The Dynamics of ODEs

In this section, we consider the local/global asymptotic stability of $(u_*,v_*)$, as well as the occurrence of stable periodic solutions of the following Ordinary Differential Equations (ODEs):

$$\begin{aligned} \displaystyle \frac{du}{dt}=\beta _1-u-\displaystyle \frac{\gamma _1uv}{1+u+v+Ku^2}=:f(u,v),\;\displaystyle \frac{dv}{dt}=\beta _2-\displaystyle \frac{\gamma _2uv}{1+u+v+Ku^2}=:g(u,v). \end{aligned}$$

(6.1)

System (6.1) has a positive equilibrium $(u_*,v_*)$, with

$$\begin{aligned} u_*:=\beta _1-\displaystyle \frac{\gamma _1}{\gamma _2}\beta _2,\;v_*:=\displaystyle \frac{\beta _2(1+u_*+Ku_*^2)}{\gamma _2u_*-\beta _2}, \end{aligned}$$

(6.2)

if and only if $\displaystyle \frac{\beta _1}{1+\gamma _1}>\frac{\beta _2}{\gamma _2}$ holds.

The linearized operator of system (6.1) evaluated at $(u_*,v_*)$ is given by

$$\begin{aligned} J(u_*,v_*):= \left( \begin{array}{cc} -1-\gamma _1j_0 &{}-\gamma _1k_0\\ -\gamma _2j_0, &{}-\gamma _2k_0 \end{array}\right) , \end{aligned}$$

(6.3)

where

$$\begin{aligned} j_0:=\displaystyle \frac{v_*(1+v_*-Ku_*^2)}{(1+u_*+v_*+Ku_*^2)^2},\;k_0:=\displaystyle \frac{u_*(1+u_*+Ku_*^2)}{(1+u_*+v_*+Ku_*^2)^2}. \end{aligned}$$

(6.4)

Then, the characteristic equation of (6.3) is given by

$$\begin{aligned} \mu ^2+(1+\gamma _1j_0+\gamma _2k_0)\mu +\gamma _2k_0=0. \end{aligned}$$

(6.5)

Lemma 9

Suppose that $\displaystyle \frac{\beta _1}{1+\gamma _1}>\frac{\beta _2}{\gamma _2}$ is satisfied so that $(u_*,v_*)$ is the unique positive equilibrium of (6.1). If

$$\begin{aligned} j_0>-\displaystyle \frac{1+\gamma _2k_0}{\gamma _1} \end{aligned}$$

(6.6)

holds, then $(u_*,v_*)$ is locally asymptotically stable in system (6.1). However, if

$$\begin{aligned} j_0<-\displaystyle \frac{1+\gamma _2k_0}{\gamma _1} \end{aligned}$$

(6.7)

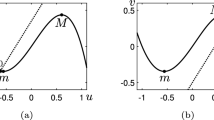
holds, then $(u_*,v_*)$ is unstable in system (6.1), and the system (6.1) has a locally orbitally stable periodic orbit, denoted by $(p(t),q(t))$.

Proof

Suppose that (6.6) holds. Then, all the eigenvalues of (6.5) has strictly negative real parts, thus $(u_*,v_*)$ is locally asymptotically stable; While if (6.7) holds, then (6.5) has one eigenvalue with positive real parts, thus $(u_*,v_*)$ is unstable. According to Theorem 2, the solutions is bounded, then from Poincare–Bendixson theorem, we conclude the existence of a locally orbitally stable periodic orbit, denoted by $(p(t),q(t))$. $\square$

The next result is on the global asymptotic stability of the positive equilibrium $(u_*,v_*)$ in (6.1):

Lemma 10

Suppose that $\displaystyle \frac{\beta _1}{1+\gamma _1}>\frac{\beta _2}{\gamma _2}$ is satisfied so that $(u_*,v_*)$ is the unique positive equilibrium of (6.1). Assume also that $0<\beta _1+\beta _2\le 1$ holds. Then, $(u_*,v_*)$ is globally asymptotically stable in system (6.1), if

$$\begin{aligned} K\in \bigg (0,\displaystyle \frac{\gamma _2+2}{2\beta _1}\bigg ]\cup \bigg [\displaystyle \frac{\gamma _2+2}{2\beta _1}+\displaystyle \frac{\epsilon _-}{2\beta _1^2},\displaystyle \frac{\gamma _2+2}{2\beta _1}+\displaystyle \frac{\epsilon _+}{2\beta _1^2}\bigg ], \end{aligned}$$

(6.8)

where

$$\begin{aligned} \epsilon _{\pm }:=\sqrt{9(1-\beta _1-\beta _2)^2+6\beta _1(\gamma _2+2)(1-\beta _1-\beta _2)}\pm 3(1-\beta _1-\beta _2)>0. \end{aligned}$$

(6.9)

Proof

We first use the Dulac criteria to exclude the existence of periodic orbits in the first quadrant. Define $b(u,v)=1+u+v+Ku^2$, then, we have

$$\begin{aligned} \displaystyle \frac{\partial (fb)}{\partial u}+\displaystyle \frac{\partial (gb)}{\partial v}=\mathcal {W}(u)-(\gamma _1+1)v, \end{aligned}$$

(6.10)

where $\mathcal {W}(u):=-3Ku^2-(\gamma _2+2-2\beta _1K)u+\beta _1+\beta _2-1$.

Let $u_\mathcal {W}$ be the symmetry axis of the function $\mathcal {W}(u)$. Then, $u_\mathcal {W}=\frac{1}{3}\beta _1K-\frac{1}{6}(2+\gamma _2)$. If $K\in \big (0,\displaystyle \frac{\gamma _2+2}{2\beta _1}\big ]$ holds, we have $u_\mathcal {W}\le 0$. Thus, $\mathcal {W}(u)\le 0$, which indicates that under $\partial (fb)/\partial u+\partial (gb)/\partial v<0$ in the first quadrant.

On the other hand, let $\Delta _{\mathcal {W}}$ be the discriminant of the function $\mathcal {W}(u)$. Then,

$$\begin{aligned} \Delta _{\mathcal {W}}=(2\beta _1K-2-\gamma _2)^2+12K(\beta _1+\beta _2-1). \end{aligned}$$

(6.11)

Suppose that $K\in \big [\displaystyle \frac{\gamma _2+2}{2\beta _1}+\displaystyle \frac{\epsilon _-}{2\beta _1^2},\displaystyle \frac{\gamma _2+2}{2\beta _1}+\displaystyle \frac{\epsilon _+}{2\beta _1^2}\big ]$ holds. Then $\Delta _{\mathcal {W}}\le 0$. Again, we can conclude that $\mathcal {W}(u)\le 0$, which indicates that under $\partial (fb)/\partial u+\partial (gb)/\partial v<0$ in the first quadrant.

So far, under (6.8) and $0<\beta _1+\beta _2\le 1$, by Dulac criteria, system (6.1) does not have closed orbits in the first quadrant. By Theorem 2, it follows that the solution is bounded. Thus, by Poincare–Bendixson theorem, we know that $(u_*,v_*)$ is globally asymptotically stable in ODEs. $\square$