An efficient method for solving coupled Lane–Emden boundary value problems in catalytic diffusion reactions and error estimate

Abstract

In this paper, we propose an efficient method for solving coupled Lane–Emden boundary value problems in catalytic diffusion reactions. The target is to obtain approximations of coupled Lane–Emden boundary value problems via series representation. Convergence and an error estimate are presented. Finally, two BVPs are solved to illustrative high accuracy of our method. Furthermore, our algorithm is easy to implement.

1 Introduction

Lane [1] and Emden [2] first studied the Lane–Emden equation. The applications of the Lane–Emden equation are found in many research fields like the theory of stellar structure, the thermal behavior of a spherical cloud of gas, isothermal gas spheres and the theory of thermionic currents [3]. Since the exact solution of the Lane–Emden equation does not exist in many cases, various methods [4,5,6,7,8,9,10] have been developed for solving such problem. The singular behavior is the main difficulty of the Lane–Emden equation.

In this work, we mainly consider systems of Lane–Emden equations. Such equations model several physical phenomenon such as chemical reactions, population evolution and so on [11]. In next section, we propose a numerical method for solving the following coupled Lane–Emden equation

$$\begin{aligned} \left\{ \begin{aligned}&u''(x)+\frac{r}{x}u'(x)=f_1(u(x),v(x)),\\&v''(x)+\frac{r}{x}v'(x)=f_2(u(x),v(x)), \end{aligned} \right. \end{aligned}$$

(1)

subject to

$$\begin{aligned} u'(0)=0,\quad u(1)=\beta _1,\quad v'(0)=0,\quad v(1)=\beta _2, \end{aligned}$$

(2)

where r is a real constant and $f_1(u(x),v(x))$ and $f_2(u(x),v(x))$ are arbitrary functions of u and v. Also, several numerical methods have been developed for solving systems of Lane–Emden equations. Rach et al. [3, 12] proposed a modified recursion scheme based on the Adomian decomposition method. Geng and Cui [13] provided homotopy perturbation reproducing kernel method. Lu [14] developed variational iteration method. Dehghan [15,16,17] presented homotopy perturbation method, sinc-collocation and cubic B-spline scaling function methods. Caglar [18] introduced B-spline method for solving linear systems.

This work is mainly based on Turkyilmazoglu’s works [19,20,21] and our previous work [22]. By using this method, a rapid convergent series solution can be obtained.

The reminder of this paper is organized as follows. A new numerical method is described in Sect. 2. In Sect. 3, convergence and an error estimate are presented. In Sect. 4, two BVPs are solved and our method is compared to existing numerical methods. Finally, our conclusions are made in Sect. 5.

2 A new algorithm

In this section we provide a new algorithm. Considering the base functions

$$\begin{aligned} \mathbf {X}=[\varphi _0(x),\varphi _1(x),\varphi _2(x),\varphi _3(x),\ldots ], \end{aligned}$$

which reside in the function space where the true exact of (1) exists, then the exact solution of (1) is

$$\begin{aligned} u(x)= & {} \sum _{k=0}^{\infty }a_{k}\varphi _k(x), \end{aligned}$$

(3)

$$\begin{aligned} v(x)= & {} \sum _{k=0}^{\infty }b_{k}\varphi _k(x), \end{aligned}$$

(4)

where $a_{k}$’s and $b_{k}$’s are coefficients to be determined.

By means of the definitions

$$\begin{aligned} \mathbf {X}_n=[\varphi _0(x),\varphi _1(x),\varphi _2(x),\ldots ,\varphi _n(x)], \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \mathbf {A}_{n}&=[a_{0},a_{1},a_{2},\ldots ,a_{n}]^{T},\\ \mathbf {B}_{n}&=[b_{0},b_{1},b_{2},\ldots ,b_{n}]^{T}, \end{aligned} \end{aligned}$$

thus we may approximate the solution at nth order by the product form

$$\begin{aligned} u_{n}(x)= & {} \sum _{k=0}^{n}a_{k}\varphi _k(x)=\mathbf {X}_n\mathbf {A}_{n}, \end{aligned}$$

(5)

$$\begin{aligned} v_{n}(x)= & {} \sum _{k=0}^{n}b_{k}\varphi _k(x)=\mathbf {X}_n\mathbf {B}_{n}, \end{aligned}$$

(6)

whose derivatives of N order are given by

$$\begin{aligned} u_{n}^{(N)}= & {} \mathbf {X}_n\mathbf {P}^N\mathbf {A}_{n},\quad N\ge 1, \end{aligned}$$

(7)

$$\begin{aligned} v_{n}^{(N)}= & {} \mathbf {X}_n\mathbf {P}^N\mathbf {B}_{n},\quad N\ge 1, \end{aligned}$$

(8)

where matrix $\mathbf {P}$ depends on the choice of $\mathbf {X}_{n}$. Having denoted the Hilbert space $H=L^2[0,1]$ with the inner product

$$\begin{aligned} \langle f,g\rangle =\int _0^1f(x)g(x)dx. \end{aligned}$$

(9)

Substituting (7) and (8) into (1),

$$\begin{aligned} x\mathbf {X}_n\mathbf {P}^{2}\mathbf {A}_{n}+2\mathbf {X}_n\mathbf {P}\mathbf {A}_{n}=xf_1(\mathbf {X}_n\mathbf {A}_{n},\mathbf {X}_n\mathbf {B}_{n}), \end{aligned}$$

(10)

$$\begin{aligned} x\mathbf {X}_n\mathbf {P}^{2}\mathbf {B}_{n}+2\mathbf {X}_n\mathbf {P}\mathbf {B}_{n}=xf_2(\mathbf {X}_n\mathbf {A}_{n},\mathbf {X}_n\mathbf {B}_{n}). \end{aligned}$$

(11)

Let $\mathbf {Q}=[\psi _0(x),\psi _1(x),\psi _2(x),\ldots ,\psi _n(x)]$ be a linearly independent set of functions in H, whose entries might be standard polynomials. Taking the inner product of (10) and (11) with the elements of $\mathbf {Q}$ , matrices $\mathbf {S}_{2(n+1)\times 1}$ and $\mathbf {T}_{2(n+1)\times 1}$ can be obtained, which satisfy

$$\begin{aligned} \mathbf {S}_{2(n+1)\times 1}=\mathbf {T}_{2(n+1)\times 1}. \end{aligned}$$

Notice that

$$\begin{aligned} \mathbf {S}_{q,1}= & {} \left\langle x\mathbf {X}_n\mathbf {P}^{2}\mathbf {A}_{n}+2\mathbf {X}_n\mathbf {P}\mathbf {A}_{n},\psi _{q-1}(x)\right\rangle ,\\ \mathbf {T}_{q,1}= & {} \left\langle xf_1(\mathbf {X}_n\mathbf {A}_{n},\mathbf {X}_n\mathbf {B}_{n}),\psi _{q-1}(x)\right\rangle , \end{aligned}$$

where $1\le q\le n+1$,

and

$$\begin{aligned} \mathbf {S}_{q,1}= & {} \left\langle x\mathbf {X}_n\mathbf {P}^{2}\mathbf {B}_{n}+2\mathbf {X}_n\mathbf {P}\mathbf {B}_{n},\psi _{q-(n+2)}(x)\right\rangle ,\\ \mathbf {T}_{q,1}= & {} \left\langle xf_2(\mathbf {X}_n\mathbf {A}_{n},\mathbf {X}_n\mathbf {B}_{n}),\psi _{q-(n+2)}(x)\right\rangle , \end{aligned}$$

where $n+2\le q\le 2n+2$.

Considering the initial or boundary conditions (2),

$$\begin{aligned} \begin{aligned}&\mathbf {X}_n(0)\mathbf {P}\mathbf {A}_{n}=0,\quad \mathbf {X}_n(1)\mathbf {A}_{n}=\beta _1\\&\mathbf {X}_n(0)\mathbf {P}\mathbf {B}_{n}=0,\quad \mathbf {X}_n(1)\mathbf {B}_{n}=\beta _2. \end{aligned} \end{aligned}$$

(12)

These 4 equations modify 4 number of entries of $\mathbf {S}_{2(n+1)\times 1}$ and the corresponding parts of $\mathbf {T}_{2(n+1)\times 1}$. The elements of $\mathbf {A}_{n}$ and $\mathbf {B}_{n}$ are determined uniquely, if the system of nonlinear algebraic equations $\mathbf {S}=\mathbf {T}$ is solved properly. Eventually, the concrete form of the approximate solution can be obtained

$$\begin{aligned} \begin{aligned} u_{n}(x)&=\sum _{k=0}^{n}a_{k}\varphi _k(x),\\ v_{n}(x)&=\sum _{k=0}^{n}b_{k}\varphi _k(x). \end{aligned} \end{aligned}$$

Note that when choosing base functions $\mathbf {X}_{n}$, continuous polynomials $\{x^k:k\in \mathbb {Z}\}$ are preferred. Since they are calculated efficiently and can represent various functions [19]. Then the entries of the matrix $\mathbf {P}$ are expressed as $\mathbf {P}_{i,i+1}=i$, $1\le i\le n$ and $\mathbf {P}_{ij}=0$ for other $1\le i,j\le n+1$, which means

(13)

3 Error estimate and convergence

In this section, the numerical analysis is presented. Let $H=L^2[0,1]$, $P_n=\{\phi _0,\phi _1,\ldots ,\phi _n\}$ be a set of polynomials of nth degree and $Y=span(P_n)$. The $L_2$-error can be obtained by the similar process which was shown in [20]. Since Y is a finite dimensional vector space, y has a unique best approximation in Y. Thus, there exists $\bar{u}, \bar{v}\in Y$ which satisfy

$$\begin{aligned} \begin{aligned}&\Vert u-\bar{u}\Vert _2\le \Vert u-h\Vert _2,\quad \forall h\in Y,\\&\Vert v-\bar{v}\Vert _2\le \Vert v-h\Vert _2,\quad \forall h\in Y.\\ \end{aligned} \end{aligned}$$

Let $\varvec{\Phi }=[\phi _0,\phi _1,\ldots ,\phi _n]^T$, there exists unique coefficients $\mathbf {A}=[a_0,a_1,\ldots ,a_n]$ and $\mathbf {B}=[b_0,b_1,\ldots ,b_n]$ such that

$$\begin{aligned} \begin{aligned}&u\simeq \bar{u}=\sum \limits _{i=0}^na_i\phi _i=\mathbf {A}\varvec{\Phi },\\&v\simeq \bar{v}=\sum \limits _{i=0}^nb_i\phi _i=\mathbf {B}\varvec{\Phi }, \end{aligned} \end{aligned}$$

where $\mathbf {A}$ and $\mathbf {B}$ can be obtained by the following process.

$$\begin{aligned} \begin{aligned}&\mathbf {A}\langle \varvec{\Phi },\varvec{\Phi }\rangle = \langle u,\varvec{\Phi }\rangle ,\\&\mathbf {B}\langle \varvec{\Phi },\varvec{\Phi }\rangle = \langle v,\varvec{\Phi }\rangle , \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&\langle u,\varvec{\Phi }\rangle \ = \int _0^1u(x)\varvec{\Phi }(x)^Tdx=[\langle u,\phi _0\rangle ,\langle u,\phi _1\rangle ,\ldots ,\langle u,\phi _n\rangle ],\\&\langle v,\varvec{\Phi }\rangle \ = \int _0^1v(x)\varvec{\Phi }(x)^Tdx=[\langle v,\phi _0\rangle ,\langle v,\phi _1\rangle ,\ldots ,\langle v,\phi _n\rangle ], \end{aligned} \end{aligned}$$

and $\langle \varvec{\Phi },\varvec{\Phi }\rangle$ is given by

$$\begin{aligned} \mathbf {C}= \langle \varvec{\Phi },\varvec{\Phi }\rangle \ = \int _a^b\varvec{\Phi }(x)\varvec{\Phi }(x)^Tdx. \end{aligned}$$

Then

$$\begin{aligned} \mathbf {A}= \langle u,\varvec{\Phi }\rangle \mathbf {C}^{-1}, \end{aligned}$$

(14)

and

$$\begin{aligned} \mathbf {B}= \langle v,\varvec{\Phi }\rangle \mathbf {C}^{-1}. \end{aligned}$$

(15)

Since the elements of $\mathbf {A}$ and $\mathbf {B}$ are uniquely determined by (14) and (15), the approximate solutions $\bar{u}$ and $\bar{v}$ can be obtained. Since the inner product in H is defined by $<f,g>\ =\int _0^1f(x)g(x)dx$ and $Y=span(P_n)$, then a $L_2$-error can be presented as

$$\begin{aligned} \Vert u-\bar{u}\Vert _2^2=\frac{\det \left[ \int _0^1\varvec{\Psi }(x)\varvec{\Psi }(x)^Tdx\right] }{\det \left[ \int _a^b\varvec{\Phi }(x)\varvec{\Phi }(x)^Tdx\right] }, \end{aligned}$$

and

$$\begin{aligned} \Vert v-\bar{v}\Vert _2^2=\frac{\det \left[ \int _0^1\varvec{\Omega }(x)\varvec{\Omega }(x)^Tdx\right] }{\det \left[ \int _a^b\varvec{\Phi }(x)\varvec{\Phi }(x)^Tdx\right] }, \end{aligned}$$

where $\varvec{\Phi }=[\phi _0,\phi _1,\ldots ,\phi _n]^T$, $\varvec{\Psi }=[u,\phi _0,\phi _1,\ldots ,\phi _n]^T$ and $\varvec{\Omega }=[v,\phi _0,\phi _1,\ldots ,\phi _n]^T$.

Next we will prove the convergence of the proposed method. Define $\omega (y,\delta )=\sup |y(x_1)-y(x_2)|$, where $x_1,x_2\in [a,b]\ and\ |x_1-x_2|\le \delta$. Assume that y(x) is bounded on interval [a, b], then $\Vert y-\sum \nolimits _{k=0}^ny\left( \frac{k}{n}\right) \phi _k\Vert _{\infty }\le \frac{3}{2}\omega (y,\sqrt{\frac{1}{n}})$ [23]. These lead to the following theorem.

Theorem 1

If u(x) and v(x) are bounded on interval [0, 1] and $Y=span\{P_n\}$, then

$$\begin{aligned} \Vert u-\mathbf {A}\varvec{\Phi }\Vert _2\le \frac{3}{2}\omega \left( u,\sqrt{\frac{1}{n}}\right) , \end{aligned}$$

(16)

and

$$\begin{aligned} \Vert v-\mathbf {B}\varvec{\Phi }\Vert _2\le \frac{3}{2}\omega \left( v,\sqrt{\frac{1}{n}}\right) , \end{aligned}$$

(17)

where $\mathbf {A}\varvec{\Phi }$ and $\mathbf {B}\varvec{\Phi }$ are the best approximations to u and v respectively in Y.

Proof

Since $\mathbf {A}\varvec{\Phi }$ and $\mathbf {B}\varvec{\Phi }$ are the best approximations to u and v respectively in Y, then

$$\begin{aligned} \Vert u-\mathbf {A}\varvec{\Phi }\Vert _2\le & {} \left\| u-\sum \limits _{k=0}^nu\left( \frac{k}{n}\right) \phi _k\right\| _{2}\le \left\| u-\sum \limits _{k=0}^nu\left( \frac{k}{n}\right) \phi _k\right\| _{\infty }\le \frac{3}{2}\omega \left( u,\sqrt{\frac{1}{n}}\right) ,\\ \Vert v-\mathbf {B}\varvec{\Phi }\Vert _2\le & {} \left\| v-\sum \limits _{k=0}^nv\left( \frac{k}{n}\right) \phi _k\right\| _{2}\le \left\| v-\sum \limits _{k=0}^nv\left( \frac{k}{n}\right) \phi _k\right\| _{\infty }\le \frac{3}{2}\omega \left( v,\sqrt{\frac{1}{n}}\right) . \end{aligned}$$

$\square$

If u(x) and u(x) are continuous on [0, 1], then we can get

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\omega \left( u,\sqrt{\frac{1}{n}}\right)= & {} 0,\\ \lim \limits _{n\rightarrow \infty }\omega \left( v,\sqrt{\frac{1}{n}}\right)= & {} 0, \end{aligned}$$

which shows that $\mathbf {A}\varvec{\Phi }$ and $\mathbf {B}\varvec{\Phi }$ are convergent to u and v respectively when $n\rightarrow \infty$. An error estimate is given in the following theorem.

Theorem 2

Suppose u(x) and v(x) are the true solutions to (1). Let $Y=span(P_n)$ and $u_n$ and $v_n$ be the best approximations to u and v in Y respectively. If $u,v\in C^{n+1}[0,1]$, then a $L_2$-error estimate is given by

$$\begin{aligned} \Vert u-u_{n}\Vert _2\le \frac{M_1}{\sqrt{2n+3}\cdot (n+1)!}, \end{aligned}$$

(18)

$$\begin{aligned} \Vert v-v_{n}\Vert _2\le \frac{M_2}{\sqrt{2n+3}\cdot (n+1)!}, \end{aligned}$$

(19)

where $M_1=\max _{x\in [0,1]}|u^{(n+1)}(x)|$ and $M_2=\max _{x\in [0,1]}|v^{(n+1)}(x)|$.

Proof

According to Taylor’s formula

$$\begin{aligned} u_n(x)=u(0)+u'(0)x+\frac{u''(0)}{2!}x^2+\cdots +\frac{u^{(n)}(0)}{n!}x^n+R_n(x), \end{aligned}$$

where $R_n(x)=\frac{u^{(n+1)}(\eta )}{(n+1)!}x^{n+1}$, $\eta \in (0,1)$. Also, consider the following polynomial

$$\begin{aligned} p(x)=u(0)+u'(0)x+\frac{u''(0)}{2!}x^2+\cdots +\frac{u^{(n)}(0)}{n!}x^n. \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned} \Vert u-u_{n}\Vert _2&\le \Vert u-p\Vert _2\le \sqrt{\int _0^1|u(x)-p(x)|^2dx}\le \sqrt{\int _0^1R_n^2(x)dx}\\&\le \frac{M_1}{\sqrt{2n+3}\cdot (n+1)!}, \end{aligned} \end{aligned}$$

where $M_1=\max _{x\in [0,1]}|u^{(n+1)}(x)|$. (19) can be proved by the similar process. $\square$

4 Applications of our method

In this section, two BVPs are solved to illustrate effectiveness of our method. As discussed in Section 2, we take $\mathbf {X}_n=\{1,x,x^2,\ldots ,x^n\}$. All the computations are performed by $Mathematica\ 8.0$. Moreover, if the exact solution does not exist, we compute the maximal error remainder parameters as the error analysis. The maximal error remainder parameters are

$$\begin{aligned} MER_n^{(1)}=\max \limits _{x\in [0,1]}\left| u_n''(x)+\frac{r}{x}u_n'(x)-f_1(u_n(x),v_n(x))\right| , \end{aligned}$$

(20)

and

$$\begin{aligned} MER_n^{(2)}=\max \limits _{x\in [0,1]}\left| v_n''(x)+\frac{r}{x}v_n'(x)-f_2(u_n(x),v_n(x))\right| . \end{aligned}$$

(21)

Example 1

Consider the following coupled Lane–Emden equations [3]

$$\begin{aligned} \left\{ \begin{aligned}&u''(x)+\frac{2}{x}u'(x)=k_{11}u^2(x)+k_{12}u(x)v(x),\\&v''(x)+\frac{2}{x}v'(x)=k_{21}v^2(x)+k_{22}u(x)v(x),\\&u'(0)=0,\quad u(1)=\beta _1,\quad v'(0)=0,\quad v(1)=\beta _2. \end{aligned} \right. \end{aligned}$$

(22)

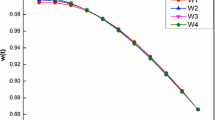
Such problem arises in catalytic diffusion reactions [11]. The parameters $\beta _1$, $\beta _2$, $k_{11}$, $k_{12}$, $k_{21}$ and $k_{22}$ can be specified for the actual chemical reactions. We take $\beta _1=1$, $\beta _2=2$, $k_{11}=1$, $k_{12}=2/5$, $k_{21}=1/2$ and $k_{22}=1$. There is no exact solution for such problem. So we compute the approximate solution by the proposed method. The comparisons on the maximal error remainder parameters between our method and modified ADM [3] are shown in Tables 1 and 2. It can be observed that our method performs better. Since the exact solution can not be found for this problem, the 12th order approximate solution results in an accuracy of order $O(10^{-11})$ by the proposed method which can be used in place of analytical solution. The theoretical error estimates (18) for the considered problems are shown in Tables 1 and 2 to visualize the convergence. The approximate solutions obtained by our method are listed in Tables 3 and 4 for various n. The logarithmic plots of $MER_n^{(1)}$ and $MER_n^{(2)}$ for $n=2$ through $n=11$ are displayed in Fig. 1. The dots in Fig. 1 are almost on straight line, which demonstrates an approximate exponential rate of convergence. The approximate solutions are plotted in Fig. 2 with $n=2,3,4$.

Table 1 Comparisons on $MER_n^{(1)}$ for Example 1

Table 2 Comparisons on $MER_n^{(2)}$ for Example 1

Table 3 The approximate solutions for various n

Table 4 The approximate solutions for various n

Fig. 1

Logarithmic plots of the maximal error remainder parameters for $n=2$–11

Fig. 2

Plots of the approximate solutions with $n=2,3,4$. a The curves of $u_n(x)$ for $n=2$ (dot line), $n=3$ (dash line), $n=4$ (solid line). b The curves of $v_n(x)$ for $n=2$ (dot line), $n=3$ (dash line), $n=4$ (solid line)

Example 2

Consider the following system of two coupled nonlinear differential equations which is subject to a set of Dirichlet boundary conditions and a mixed set of Neumann and Dirichlet boundary conditions [12]

$$\begin{aligned} \left\{ \begin{aligned}&u''(x)=\frac{\alpha _1u(x)v(x)}{1+\beta _1u(x)+\beta _2v(x)},\\&v''(x)+\frac{\alpha _2u(x)v(x)}{1+\beta _1u(x)+\beta _2v(x)},\\&u(0)=1,\quad u(1)=k,\quad v'(0)=0,\quad v(1)=1. \end{aligned} \right. \end{aligned}$$

(23)

Such equations describe the kinetics of the reaction between $\hbox {CO}_2$ and phenyl glycidyl ether (PGE) in solution. The functions u(x) and v(x) are the concentrations of $\hbox {CO}_2$ and PEG, respectively. x is the dimensionless distance as measured from the center and k is the dimensionless concentration of $\hbox {CO}_2$ at the surface of the catalyst. Next, we introduce the method for solving such problem. As we have discussed in Sect. 2, if the base functions are

$$\begin{aligned} \mathbf {X}=[\varphi _0(x),\varphi _1(x),\varphi _2(x),\varphi _3(x),\ldots ], \end{aligned}$$

then we can approximate the solution by the product form

$$\begin{aligned} u_{n}(x)= & {} \sum _{k=0}^{n}a_{k}\varphi _k(x)=\mathbf {X}_n\mathbf {C}_{n}, \end{aligned}$$

(24)

$$\begin{aligned} v_{n}(x)= & {} \sum _{k=0}^{n}b_{k}\varphi _k(x)=\mathbf {X}_n\mathbf {D}_{n}, \end{aligned}$$

(25)

where $\mathbf {C}_{n}=[c_{0},c_{1},c_{2},\ldots ,c_{n}]^{T}$, $\mathbf {D}_{n}=[d_{0},d_{1},d_{2},\ldots ,d_{n}]^{T}$ and $\mathbf {X}_n=[\varphi _0(x),\varphi _1(x),\varphi _2(x),\ldots ,\varphi _n(x)]$. $a_{k}$’s and $b_{k}$’s are coefficients to be determined. The derivatives are given by

$$\begin{aligned} u_{n}^{(N)}= & {} \mathbf {X}_n\mathbf {P}^N\mathbf {C}_{n},\quad N\ge 1, \end{aligned}$$

(26)

$$\begin{aligned} v_{n}^{(N)}= & {} \mathbf {X}_n\mathbf {P}^N\mathbf {D}_{n},\quad N\ge 1, \end{aligned}$$

(27)

where $\mathbf {P}$ is an operational matrix as we have discussed in Sect. 2. Substituting (26) and (27) into (23), we have

$$\begin{aligned} \mathbf {X}_n\mathbf {P}^{2}\mathbf {C}_{n}\cdot (1+\beta _1\mathbf {X}_n\mathbf {C}_{n}+\beta _2\mathbf {X}_n\mathbf {D}_{n})-\alpha _1\mathbf {X}_n\mathbf {C}_{n}\cdot \mathbf {X}_n\mathbf {D}_{n}= & {} 0, \end{aligned}$$

(28)

$$\begin{aligned} \mathbf {X}_n\mathbf {P}^{2}\mathbf {D}_{n}\cdot (1+\beta _1\mathbf {X}_n\mathbf {C}_{n}+\beta _2\mathbf {X}_n\mathbf {D}_{n})-\alpha _2\mathbf {X}_n\mathbf {C}_{n}\cdot \mathbf {X}_n\mathbf {D}_{n}= & {} 0. \end{aligned}$$

(29)

Similarly let $\mathbf {Q}=[\psi _0(x),\psi _1(x),\psi _2(x),\ldots ,\psi _n(x)]$ be a linearly independent set of functions in H. The working space and inner product are defined in Sect. 2. By taking the inner product of (28) and (29) with elements of $\mathbf {Q}$ respectively, matrices $\widetilde{\mathbf {S}}_{2(n+1)\times 1}$ and $\widetilde{\mathbf {T}}_{2(n+1)\times 1}$ can be obtained, which satisfy

$$\begin{aligned} \widetilde{\mathbf {S}}_{2(n+1)\times 1}=\widetilde{\mathbf {T}}_{2(n+1)\times 1}. \end{aligned}$$

Note that

$$\begin{aligned} \widetilde{\mathbf {S}_{q,1}}= \langle \mathbf {X}_n\mathbf {P}^{2}\mathbf {C}_{n}\cdot (1+\beta _1\mathbf {X}_n\mathbf {C}_{n}+\beta _2\mathbf {X}_n\mathbf {D}_{n})-\alpha _1\mathbf {X}_n\mathbf {C}_{n}\cdot \mathbf {X}_n\mathbf {D}_{n},\psi _{q-1}(x)\rangle , \end{aligned}$$

where $1\le q\le n+1$,

$$\begin{aligned} \widetilde{\mathbf {S}_{q,1}}= \langle \mathbf {X}_n\mathbf {P}^{2}\mathbf {D}_{n}\cdot (1+\beta _1\mathbf {X}_n\mathbf {C}_{n}+\beta _2\mathbf {X}_n\mathbf {D}_{n})-\alpha _2\mathbf {X}_n\mathbf {C}_{n}\cdot \mathbf {X}_n\mathbf {D}_{n},\psi _{q-(n+2)}(x)\rangle , \end{aligned}$$

where $n+2\le q\le 2n+2$,

and

$$\begin{aligned} \widetilde{\mathbf {S}_{q,1}}= 0, \end{aligned}$$

where $1\le q\le 2n+2$.

Considering the boundary conditions in (23),

$$\begin{aligned} \begin{aligned}&\mathbf {X}_n(0)\mathbf {C}_{n}=1,\quad \mathbf {X}_n(1)\mathbf {C}_{n}=k\\&\mathbf {X}_n(0)\mathbf {P}\mathbf {D}_{n}=0,\quad \mathbf {X}_n(1)\mathbf {D}_{n}=1. \end{aligned} \end{aligned}$$

(30)

These 4 equations modify 4 number of entries of $\widetilde{\mathbf {S}}_{2(n+1)\times 1}$ and the corresponding parts of $\widetilde{\mathbf {T}}_{2(n+1)\times 1}$. If we can solve nonlinear algebraic equations $\widetilde{\mathbf {S}}=\widetilde{\mathbf {T}}$ properly, then we can obtain the coefficients $\mathbf {C}_{n}=[c_{0},c_{1},c_{2},\ldots ,c_{n}]^{T}$ and $\mathbf {D}_{n}=[d_{0},d_{1},d_{2},\ldots ,d_{n}]^{T}$. Then the approximate solution of (23) can be obtained. It is reminded that the system of nonlinear algebraic equations can be solved numerically such as by Newton iteration method [24] or by any contemporary symbolic solver such as MATLAB and Mathematica. Since all the computations are performed by Mathematica, we can use ‘FindRoot’ or ‘NSolve’ command to solve such equations. Take $\alpha _1=1$, $\alpha _2=2$, $\beta _1=1$, $\beta _2=3$ and $k=1/2$. The comparisons on the maximal error remainder parameters are shown in Tables 5 and 6. It can be observed that our method performs better. As we have discussed in Example 1, the theoretical error estimates (18) are listed in Tables 5 and 6. The proposed method converges rapidly to the exact solution. The approximate solutions obtained by the proposed method are displayed in Tables 7 and 8.

Table 5 Comparisons on $MER_n^{(1)}$ for Example 2

Table 6 Comparisons on $MER_n^{(2)}$ for Example 2

Table 7 The approximate solutions for various n in Example 2

Table 8 The approximate solutions for various n in Example 2

Table 9 $\max _{x\in [0,1]}\left| u(x)-u_n(x)\right|$ for various n in Example 1

5 Conclusions

In this paper, we have provided a numerical method for solving coupled Lane–Emden boundary value problems in catalytic diffusion reactions and proved the convergence of the proposed method. Also, we give an error estimate. Finally, two BVPs are solved to demonstrate the high accuracy of our method. It is worthy to note that our method can be applied to solve other linear or nonlinear BVPs.

Table 10 $\max _{x\in [0,1]}\left| v(x)-v_n(x)\right|$ for various n in Example 1

Table 11 $\max _{x\in [0,1]}\left| u(x)-u_n(x)\right|$ for various n in Example 2

Table 12 $\max _{x\in [0,1]}\left| v(x)-v_n(x)\right|$ for various n in Example 2

6 Remarks

To show the efficiency of the present method, the BVPs in Example 1 and Example 2 are solved by a of selection of base functions such as Bessel polynomials [25], non-polynomial functions $\mathbf {X}_n=\{e^{\eta x},e^{\eta x}x,\ldots ,e^{\eta x}x^n\}$ [26], trigonometric functions $\mathbf {X}_n=\{1,\cos (x),\sin (x),\ldots ,\cos (\frac{n}{2}),\sin (\frac{n}{2})\}$ and our base functions. As we have discussed in Sect. 4, the 12th approximate solution is adequate for the practical purposes. The numerical results are shown in Tables 9, 10, 11 and 12. It can be obtained that non-polynomial functions converges to true solution faster. Certainly some other functions can be used as base function such as Chebyshev polynomials, Legendre polynomials and Bernstein polynomials [27, 28]. In our future work, more fast convergence basis will be considered and applied to solve many other BVPs.