1 Introduction

We consider the following class of two point nonlinear singular boundary value problems (SBVPs)

$$\begin{aligned} \left. \begin{aligned}&-u''-\frac{\alpha }{x}u'=f(x,u),\quad 0 < x < 1,\quad '\equiv \frac{d}{dx},\\&\quad u'(0)=B,\quad ~a_1 u(1)+b_1 u'(1)=c_1, \end{aligned}\right\} \end{aligned}$$
(1)

where \(\alpha , B, a_1,b_1,c_1\) are real constants and \(\alpha \ge 1\). We assume that f(x, u) is continuous and Lipschitz in \(D=\{(x,u)\in [0,1]\times \mathbb {R}\}\). Various real life problems [1–7] are governed by nonlinear singular boundary value problem (SBVP) (1). Below we mention few of these real life problems which are our test examples also.

  1. (i)

    Equilibrium of isothermal gas sphere:

    Chandrasekhar [1] derived the following two point nonlinear SBVP (\(\alpha =2\) and \(f(x,u)= u^\gamma \)), where \(\gamma \) is a physical constant. Here we consider the case, when \(\gamma =5\).

    $$\begin{aligned} \left. \begin{aligned}&-u''(x)-\frac{2}{x}u'(x)=u^5,~~~~~~0<x<1,\\&\quad u'(0)=0,~~~~u(1)=\sqrt{\frac{3}{4}}. \end{aligned}\qquad \qquad \right\} \end{aligned}$$
    (2)
  2. (ii)

    Thermal explosion in cylindrical vessel:

    Chamber [2] derived the following two point nonlinear SBVP, which arises in the thermal explosion

    $$\begin{aligned} \left. \begin{aligned}&-u''(x)-\frac{1}{x}u'(x)= e^u,\quad ~0<x<1,\\&\quad u'(0)=0,\quad u(1)=0. \end{aligned}~~~~~~~~~~\right\} \end{aligned}$$
    (3)
  3. (iii)

    Thermal distribution in the human head:

    Duggan and Goodman [5] derived the following two point nonlinear SBVP which describes the thermal distribution profile in the human head

    $$\begin{aligned} \left. \begin{aligned}&-u''(x)-\frac{2}{x}u'(x)= e^{-u},\quad ~0<x<1,\\&\quad u'(0)=0,\quad 2u(1)+u'(1)=0. \end{aligned}~~~~~~~~~~\right\} \end{aligned}$$
    (4)
  4. (iv)

    Radial stress on a rotationally symmetric shallow membrane cap:

    The following two point nonlinear SBVP arises in the study of radial stress on a rotationally symmetric shallow membrane cap [6, 7]

    $$\begin{aligned} \left. \begin{aligned}&-u''(x)-\frac{3}{x}u'(x)= \frac{1}{8 u^2}-\frac{1}{2},\quad ~0<x<1,\\&\quad u'(0)=0,\quad u(1)=1. \end{aligned}~~~~~~~~~~\right\} \end{aligned}$$
    (5)

Extensive literature is available for both analytical ([8–12] and the references their in) and numerical results ([13–20] and the references their in).

Recently, variational iteration method and its modified version have been studied by several researchers [21–25]. These methods give better results for linear problems but it suffers for most of the nonlinear problems [19, 31]. Wazwaz et al. [31] showed that VIM is more impractical for solving second kind Lane–Emden equation. To overcome this disadvantage, we propose this technique. It gives approximate solution in the form of a series. To increase the accuracy of the solution obtained by our technique we can compute more number of terms which is otherwise difficult. The convergence analysis and the error estimate of the proposed method are also discussed.

The prime motive of this work is to derive an effective numerical technique for a class of SBVP (1). The proposed technique is based on the concept of Variational Iteration Method (VIM) coupled with Homotopy perturbation method (HPM) [26, 27]. In VIM [25], an iterative scheme for nonlinear SBVPs

$$\begin{aligned} L(u)+N(u)=g(x) \end{aligned}$$
(6)

is defined as

$$\begin{aligned} u_{n+1}(x)=u_n(x)+\int \limits _{0}^{x} \lambda (t)\left[ Lu_n(t)+Nu_n(t)-g(t)\right] dt \end{aligned}$$
(7)

where L is a linear differential operator, N is a nonlinear operator, and g(x) is an inhomogeneous term. It is easy to see that we will get the best solution if

$$\begin{aligned} \int \limits _{0}^{x} \lambda (t)\left[ Lu_n(t)+Nu_n(t)-g(t)\right] dt, \end{aligned}$$
(8)

is minimized. For minimization we use Homotopy perturbation method [27].

2 Homotopy perturbation method (HPM)

Actually, Homotopy perturbation method (HPM) is combination of homotopy analysis and perturbation method, which mainly removes the restrictions on small parameter for perturbation methods. Homotopy plays an important role in differential topology, which is basically used to solve the nonlinear algebraic equations. In this analysis, a homotopy \(\mathcal {H}:[0,1]\times \mathbb {R} \rightarrow \mathbb {R}\) (see [28] and the references there in)

$$\begin{aligned} \mathcal {H}(x,p)=pf(x)+(1-p)(x-a)=0,~x\in R,~p\in [0,1], \end{aligned}$$

is constructed for nonlinear algebraic equation \(f(x)=0,\) where p is an imbedding parameter and \(x-a=0\) is a simple algebraic equation. It is clear that, when we vary p from 0 to 1, the homotopy \(\mathcal {H}(x,p)\) is varied from, \((x-a)\) to f(x), i.e., at \(p=1\), we get the solution of nonlinear algebraic equation \(f(x)=0.\) This process is called deformation, and we say that \( (x-a)~ \& ~f(x)\) are homotopic.

By using the homotopy analysis [28] and elimination of small parameter ([27] and the references there in), He [27] proposed a new perturbation method for nonlinear differential equations

$$\begin{aligned} A(u)-f(r)=0,\quad r\in \Omega , \end{aligned}$$
(9)

with boundary condition

$$\begin{aligned} B\left( u,\frac{\partial u}{\partial n}\right) =0, \quad r\in \Gamma , \end{aligned}$$
(10)

here \(A\equiv L + N\) is a general differential operator, where L and N are linear and nonlinear differential operators, respectively. B is a boundary operator, f(r) is a known analytic function and \(\Gamma \) is the boundary of the domain \(\Omega \). So, Eq. (9) can be written as

$$\begin{aligned} L(u)+N(u)-f(r)=0,~~r\in \Omega . \end{aligned}$$
(11)

Now we employ the ideas of homotopy analysis and construct the homotopy \(\nu (r,p):\Omega \times [0,1]\rightarrow \mathbb {R}\), which satisfies

$$\begin{aligned} H(\nu ,r,p)=(1-p)[L(\nu )-L(u_0)]+p[A(\nu )-f(r)]=0, ~~p\in [0,1],~r\in \Omega ,\nonumber \\ \end{aligned}$$
(12)

which is equivalent to

$$\begin{aligned} H(\nu ,r,p)=L(\nu )-L(u_0)+pL(u_0)+p[N(\nu )-f(r)]=0, \end{aligned}$$
(13)

where \(p\in [0,1]\) is an embedding parameter, and \(u_0\) is an initial guess of (9), satisfying the initial conditions. From (13), we have

$$\begin{aligned}&H(\nu ,r,0)=L(\nu )-L(u_0)=0, \end{aligned}$$
(14)
$$\begin{aligned}&H(\nu ,r,1)=L(\nu )+N(\nu )-f(r)=0. \end{aligned}$$
(15)

It is clear from (14) and (15), that \(L(\nu )-L(u_0)\) and \(L(\nu )+N(\nu )-f(r)\) are homotopic.

Now, we introduce perturbation and take p as a small parameter. We expand the solution of Eq. (13) as a power series of p given by

$$\begin{aligned} \nu =\nu _0+p\nu _1+p^2\nu _2+\cdots , \end{aligned}$$
(16)

where \(\nu _i,~i=0,1,2,\ldots \) are unknowns to be determined. At \(p=1\), we obtain the approximate solution of Eq. (9) given by

$$\begin{aligned} \nu (r,1)=u(r)=\nu _0+\nu _1+\nu _2+\cdots . \end{aligned}$$
(17)

Now, we write the nonlinear term in integral powers of parameter p given as

$$\begin{aligned} N(\nu )=\sum _{i=0}^{\infty } p^iH_i = H_0+pH_1+p^2H_2+\cdots , \end{aligned}$$
(18)

where \(H_n\)’s are defined as

$$\begin{aligned} H_n(\nu _0,\ldots ,\nu _n)=\frac{1}{n!}\frac{\partial ^n}{\partial p^n}N\left( \sum _{i=0}^{n} p^i\nu _i\right) \Bigg |_{p=0},~~n=0,1,2\ldots . \end{aligned}$$
(19)

In literature \(H_n\)’s are also known as He’s polynomial [29].

Finally, we substitute (16) and (18) into Eq. (13), collect coefficients of different powers of p and equating them to zero, we get

(20)

Now using the above system of equations we compute \(\nu _i,~i=0,1,2,\ldots \) and \(\sum _{i=0}^{\infty }\nu _i\) to get the solution \(\nu (r,1)=u(r)\) of the nonlinear equation (9).

2.1 Variational iteration method (VIM)

The iterative scheme for nonlinear SBVP (1) is given by (see [21])

$$\begin{aligned} u_{n+1}(x)=u_{n}(x)+\int \limits ^x_0 {\lambda \left( -\ddot{u}_n(t)-\frac{\alpha }{t} \dot{u}_n(t)-\tilde{f}(t,u_n)\right) dt}, \end{aligned}$$
(21)

where \(\dot{}\equiv \frac{d}{dt}\).

Following the analysis of [25], we arrive at stationary conditions given by

$$\begin{aligned}&1+\lambda _x(x)-\frac{\alpha \lambda (x)}{x}=0, \end{aligned}$$
(22)
$$\begin{aligned}&\lambda (x) =0, \end{aligned}$$
(23)
$$\begin{aligned}&-\lambda _{tt}(t) +\alpha \frac{(t\lambda _t(t)-\lambda (t))}{t^2}=0. \end{aligned}$$
(24)

By using the stationary conditions, the value of the Lagrange multipliers can be easily obtained. It is given as follows

$$\begin{aligned} \lambda (t) = \left\{ \begin{array}{ll} \displaystyle \frac{t^{\alpha }}{x^{\alpha -1}(1-\alpha )}-\frac{t}{(1-\alpha )}, &{} \forall ~\alpha >1, \\ \displaystyle \lim _{\alpha \rightarrow 1}\left[ \frac{t^{\alpha }}{x^{\alpha -1}(1-\alpha )}-\frac{t}{(1-\alpha )}\right] , &{} \mathrm {for}~\alpha =1. \end{array} \right. \end{aligned}$$

3 HPM & VIM

In this section we combine the two techniques HPM and VIM together and solve a class of two point nonlinear singular boundary value problems. Here we construct homotopy with the help of VIM. We follow an intuitive route [30] for the construction of the homotopy.

To get the solution of the nonlinear SBVP (1), we couple the concept of HPM with VIM, i.e., we consider the following homotopy (Appendix 7) for Eq. (21)

$$\begin{aligned} H(x,\nu ,p)=(1-p)[u_0-\nu ]+p\int \limits _{0}^{x} \lambda (t)[L\nu (t)+N\nu (t)-g(t)] dt=0, \end{aligned}$$
(25)

where \(p\in [0,1]\) is the embedding parameter, and \(u_0(x)\) is the initial guess satisfying the initial conditions. It follows from (25) that

$$\begin{aligned}&H(x,\nu ,0)= \nu -u_0=0, \end{aligned}$$
(26)
$$\begin{aligned}&H(x,\nu ,1)= \int \limits _{0}^{x} \lambda (t)[L\nu (t)+N\nu (t)-g(t)] dt=0. \end{aligned}$$
(27)

As embedding parameter p is varied from 0 to 1, \(\nu (p,x)\) changes from \(u_0(x)\) to the best approximation of Eq. (21).

We expand \(\nu (p,x)\) in a power series of p, where we take p as a small parameter,

$$\begin{aligned} \nu (p,x)=\sum _{i=0}^{\infty } p^i \nu _i. \end{aligned}$$
(28)

At \(p=1\), we get the best solution of nonlinear differential Eq. (6),

$$\begin{aligned} \nu (1,x)=u(x)=\sum _{i=0}^{\infty } \nu _i. \end{aligned}$$
(29)

Now using He’s polynomials, we decompose the nonlinear term [see Eq. (18)], i.e.,

$$\begin{aligned} N(\nu )=\sum _{i=0}^{\infty } p^iH_i. \end{aligned}$$
(30)

Substituting (28) and (30) into (25), and comparing the coefficients of same powers of p we get

$$\begin{aligned}&p^0: \nu _0=u_0(x)\nonumber \\&p^1: \nu _1=\int \limits _{0}^{x} \lambda (t)[L\nu _0+H_0-g(t)] dt,\nonumber \\&p^2: \nu _2=\nu _1+\int \limits _{0}^{x} \lambda (t)[L\nu _1+H_1] dt,\nonumber \\&\vdots \nonumber \\&p^{n+1}: \nu _{n+1}=\nu _{n}+\int \limits _{0}^{x} \lambda (t)[L\nu _{n}+H_n] dt,\nonumber \\&\vdots . \end{aligned}$$
(31)

We solve these set of equations to obtain the series solution

$$\begin{aligned} u=\lim _{n\rightarrow \infty }{u_n}=\displaystyle \sum _{i=0}^{\infty } \nu _i \end{aligned}$$
(32)

where \(u_n=\displaystyle \sum _{i=0}^{n} \nu _i\).

Additionally, for the nonlinear SBVP (1), we choose \(u_0=A\), where \(A=\sum ^{\infty }_{i=0}{A_i p^i}\), where p is a small parameter. Making use of this initial approximation, we can write the Eq. (25) as

$$\begin{aligned} (1-p)[A-\nu ]+p\int \limits _{0}^{x} \lambda (t)[L\nu (t)+N\nu (t)-g(t)] dt=0, \end{aligned}$$

where \(A=\sum ^{\infty }_{i=0}{A_i p^i}\) and \(\nu =\sum ^{\infty }_{i=0}{\nu _i p^i}\).

Now by collecting the coefficients of different powers of p and equate them to zero, we get

$$\begin{aligned} \left. \begin{aligned}&p^0:~~ \nu _0=u_0\\&p^1:~~ \nu _1=\nu _0+(A_1-A_0)+\int \limits _{0}^{x} \lambda (t)[L\nu _0(t)+H_0(t)-g(t)] dt,\\&p^2:~~ \nu _2=\nu _1+(A_2-A_1)+\int \limits _{0}^{x} \lambda (t)[L\nu _1(t)+H_1(t)] dt,\\&\qquad \quad \;\;\vdots \\&p^{n+1}:~~ \nu _{n+1}=\nu _{n}+(A_{n+1}-A_{n})+\int \limits _{0}^{x} \lambda (t)[L\nu _{n}(t)+H_n(t)] dt,\\&\qquad \quad \;\;\vdots . \end{aligned} \qquad \right\} \end{aligned}$$
(33)

We use equations labeled as Eq. (33) to compute our solution.

4 Accuracy and efficiency

The accuracy and efficiency of proposed technique are discussed in this section. Here, we study the existence and uniqueness of the solution of SBVP (1) and examine the convergence analysis and error estimate for the proposed technique.

We consider the norm

$$\begin{aligned} \Vert u\Vert =\max _{0\le x\le 1}|u(x)|,~~~~u\in \mathbb {X}, \end{aligned}$$

where \(\mathbb {X}=C[0,1]\) is a Banach space.

Further assume that there exist \(N_0\ge 0\) such that for all f(x, y), \(f(x,z)\in D\)

$$\begin{aligned} |f(x,y)-f(x,z)|\le N_0|y-z|, \end{aligned}$$
(34)

where \(D=\{(x,y)\in [0,1]\times \mathbb {R}\}\).

4.1 Existence and uniqueness of solutions

Theorem 4.1

The nonlinear singular boundary value problem SBVP (1) where f(x, u) satisfies the Lipschitz condition (34) and \(N_0<2(1+\alpha )\), has a unique solution.

Proof

Let \(y_1\) and \(y_2\) be two distinct solutions of nonlinear SBVP (1), so they will satisfy the Eq. (27) , i.e.,

$$\begin{aligned} \int \limits _{0}^{x} \lambda (t)[y''_1(t)+\frac{\alpha }{t}y'_1(t)+f(t,y_1)] dt=0, \end{aligned}$$
(35)

where \(L=-\frac{d^2}{dt^2}-\frac{\alpha }{t}\frac{d}{dt}\), \(N= -f(t,\_)\) and \(g(t)=0\). Similarly, we can define it for \(y_2\).

Now, Integration by parts and stationary conditions (22)–(24), yield

$$\begin{aligned} y_{1}(x)= \nu _0-\int \limits _{0}^{x} \lambda (t)f(t,y_1) dt. \end{aligned}$$
(36)

Similarly,

$$\begin{aligned} y_{2}(x)= \nu _0-\int \limits _{0}^{x} \lambda (t)f(t,y_2) dt. \end{aligned}$$
(37)

Making use of Eqs. (36)–(37), we get

$$\begin{aligned} \left| y_1-y_2\right|= & {} \left| \int \limits _{0}^{x} \lambda (t)\left[ f(t,y_1)-f(t,y_2)\right] dt\right| ,\\ \max _{0\le x\le 1}\left| y_1-y_2\right|= & {} \max _{0\le x\le 1}\left| \int \limits _{0}^{x} \lambda (t)\left[ f(t,y_1)-f(t,y_2)\right] dt\right| ,\\= & {} \max _{0\le t\le 1}\left| f(t,y_1)-f(t,y_2)\right| \max _{0\le x\le 1}\left| \int \limits _{0}^{x} \lambda (t)dt\right| ,\\ \left\| y_1-y_2\right\|\le & {} N_0\left\| y_1-y_2\right\| \max _{0\le x\le 1}\left| \frac{x^2}{2+2\alpha }\right| . \end{aligned}$$

Hence, we have

$$\begin{aligned} \left\| y_1-y_2\right\| \le \gamma \left\| y_1-y_2\right\| ,\\ \end{aligned}$$

where \(\gamma =\frac{N_0}{2+2\alpha }<1\). This gives that \(y_1=y_2\). Hence, the theorem is proved. \(\square \)

4.2 Convergence analysis

Now, to show the convergence of proposed technique, we use Eq. (21) and stationary conditions (22)–(24), and deduce,

$$\begin{aligned} u_{n+1}=u_n-\int \limits ^x_0 {\left( \left( -\lambda _t(t)+\frac{\alpha \lambda (t)}{t}\right) \dot{u}_n(t)+\lambda \tilde{f}(t,u_n)\right) dt}. \end{aligned}$$
(38)

Similarly, we have

$$\begin{aligned} u_{n}=u_{n-1}-\int \limits ^x_0 {\left( \left( -\lambda _t(t)+\frac{\alpha \lambda (t)}{t}\right) \dot{u}_{n-1}(t)+\lambda \tilde{f}(t,u_{n-1})\right) dt}. \end{aligned}$$
(39)

Now,

$$\begin{aligned} \left| u_{n+1}-u_n\right|= & {} \left| \int \limits ^x_0 \left( \left( -\lambda _{tt}(t) +\alpha \frac{(t \lambda _t(t)-\lambda )}{t^2}\right) (u_{n}-u_{n-1})\right. \right. \\&\qquad +\left. \left. \lambda (t)\left( \tilde{f}(t,u_n)-\tilde{f}(t,u_{n-1})\right) \right) dt\right| ,\\= & {} \left| \int \limits ^x_0 \left( \lambda (t)\left( \tilde{f}(t,u_n)-\tilde{f}(t,u_{n-1})\right) \right) dt\right| , \end{aligned}$$

or

$$\begin{aligned} \max _{0\le x\le 1}\left| u_{n+1}-u_n)\right|= & {} \max _{0\le x\le 1}\left| \int \limits ^x_0 \left( \lambda (t)\left( \tilde{f}(t,u_n)-\tilde{f}(t,u_{n-1})\right) \right) dt\right| ,\\\le & {} \max _{0\le t\le 1}|\tilde{f}(t,u_n)-\tilde{f}(t,u_{n-1})|\max _{0\le x\le 1}\left| \int \limits ^x_0 \lambda (t) dt\right| . \end{aligned}$$

As f satisfies the Lipschitz condition, so we get

$$\begin{aligned} \left\| u_{n+1}-u_n\right\|\le & {} N_0\max _{0\le t\le 1}|u_n - u_{n-1}|\max _{0\le x\le 1}\left| \frac{x^2}{2+2\alpha }\right| ,\\\le & {} \gamma \left\| u_n - u_{n-1}\right\| . \end{aligned}$$

Hence, we have

$$\begin{aligned} \left\| u_{n+1}-u_n\right\| \le \gamma \left\| u_n - u_{n-1}\right\| , \end{aligned}$$
(40)

where \(\gamma <1\).

Theorem 4.2

Let \(\nu _n(x),u(x)\in \mathbb {X}\) and further we assume that \(\Vert \nu _0\Vert \) is a finite, then we have \(\Vert \nu _{n+1}\Vert \le \gamma \Vert \nu _n\Vert ,~~~\gamma <1\), for \(n=0,1,2,\ldots \), and the sequence \(\{u_n=\sum _{i=0}^{n}{\nu _i}\}\) converges to the solution of SBVP (1).

Proof

As \(\{u_n\}\) is the sequence of partial sum of the series (32), i.e.,

$$\begin{aligned}&u_1=\nu _0+\nu _1,\\&u_2=\nu _0+\nu _1+\nu _2,\\&\vdots \\&u_n=\nu _0+\nu _1+\nu _2+\cdots +\nu _n,\\&\vdots \end{aligned}$$

which gives

$$\begin{aligned} \nu _{n+1}=u_{n+1}-u_n,~~~~~n=1,2,3,\cdots . \end{aligned}$$

Now with the help of (40), we can write

$$\begin{aligned} \Vert \nu _{n+1}\Vert =\Vert u_{n+1}-u_n\Vert \le \gamma \left\| u_n - u_{n-1}\right\| =\gamma \left\| \nu _n\right\| . \end{aligned}$$

Hence, we obtain

$$\begin{aligned} \Vert u_{n+1}-u_n\Vert =\Vert \nu _{n+1}\Vert \le \gamma \left\| \nu _n\right\| \le \gamma ^2\left\| \nu _{n-1}\right\| \le \cdots \le \gamma ^{n+1}\left\| \nu _0\right\| . \end{aligned}$$

To show the convergence of the sequence \(\{u_n\}\), we use Cauchy criterion

$$\begin{aligned} \left\| u_{n}-u_{m}\right\|&=\left\| (u_{n}-u_{n-1})+(u_{n-1}-u_{n-2})+\cdots +(u_{m+1}-u_{m})\right\| \\&\le \left\| (u_{n}-u_{n-1})\right\| +\left\| (u_{n-1}-u_{n-2})\right\| +\cdots +\left\| (u_{m+1}-u_{m})\right\| \\&\le \gamma ^{n}\left\| \nu _0\right\| +\gamma ^{n-1}\left\| \nu _0\right\| +\cdots +\gamma ^{m+1}\left\| \nu _0\right\| \\&\le \gamma ^{m+1}\left[ 1+\gamma +\gamma ^2+\cdots +\gamma ^{n-m-1}\right] \left\| \nu _0\right\| \\&\le \frac{ \gamma ^{m+1}\left( 1-\gamma ^{n-m}\right) }{1-\gamma }\left\| \nu _0\right\| . \end{aligned}$$

As \(0<\gamma <1\), we have

$$\begin{aligned} \left\| u_{n}-u_{m}\right\| \le \frac{ \gamma ^{m+1}}{1-\gamma }\left\| \nu _0\right\| . \end{aligned}$$
(41)

Now taking limit \(m\rightarrow \infty \), we get

$$\begin{aligned} \left\| u_{n}-u_{m}\right\| \rightarrow 0. \end{aligned}$$

Thus, the sequence \(\{u_n\}\) is a Cauchy sequence in Banach space \(\mathbb {X}\), so the series \(\sum _{i=0}^{n}{\nu _i}\) is convergent. \(\square \)

4.3 Error estimate

Theorem 4.3

The maximum absolute truncation error in the computation of the series solution (32) of SBVP (1) is given by

$$\begin{aligned} \max _{0\le x\le 1}\left| u(x)-\sum _{i=0}^{m}{\nu _i}\right| \le \frac{ \gamma ^{m+1}}{1-\gamma }\left\| \nu _0\right\| . \end{aligned}$$

Proof

From inequality (41), we have

$$\begin{aligned} \left\| u_{n}-u_{m}\right\| \le \frac{ \gamma ^{m+1}}{1-\gamma }\left\| \nu _0\right\| , \end{aligned}$$
(42)

where \(n\ge m\). If we fix m and varies \(n\rightarrow \infty \), then we get

$$\begin{aligned} \max _{0\le x\le 1}\left| u(x)-\sum _{i=0}^{m}{\nu _i}\right| \le \frac{ \gamma ^{m+1}}{1-\gamma }\left\| \nu _0\right\| . \end{aligned}$$

This completes the proof. \(\square \)

5 Numerical illustrations

5.1 Problem 1: Equilibrium of isothermal gas sphere

Consider the nonlinear SBVP (2). The exact solution of this problem is \(u(x)=(1+\frac{x^2}{3})^{-\frac{1}{2}}\). Using (33) and (2), we obtain the value of \(\nu _1, \nu _2,\ldots \) as

$$\begin{aligned} \left. \begin{aligned}&\nu _0=A_0,\\&\nu _1=A_1-\frac{1}{6} A_0^5 x^2,\\&\nu _2=\frac{1}{24} A_0^9 x^4-\frac{5}{6} A_1 A_0^4 x^2+A_2,\\&\nu _3=\frac{1}{432} (-5) A_0^{13} x^6+\frac{3}{8} A_1 A_0^8 x^4-\frac{5}{6} A_2 A_0^4 x^2-\frac{5}{3} A_1^2 A_0^3 x^2+A_3,\\&\nu _4=\frac{35 A_0^{17} x^8}{10368}-\frac{65}{432} A_1 A_0^{12} x^6+\frac{3}{8} A_2 A_0^8 x^4+\frac{3}{2} A_1^2 A_0^7 x^4\\&\qquad \;\,-\,\frac{5}{6} A_3 A_0^4 x^2-\frac{10}{3} A_1 A_2 A_0^3 x^2-\frac{5}{3} A_1^3 A_0^2 x^2+A_4,\\&\nu _5=-\frac{7 A_0^{21} x^{10}}{6912}+\frac{595 A_1 A_0^{16} x^8}{10368}-\frac{65}{432} A_2 A_0^{12} x^6- \frac{65}{72} A_1^2 A_0^{11} x^6+\frac{3}{8} A_3 A_0^8 x^4\\&\qquad \;\,+\,3 A_1 A_2 A_0^7 x^4 +\frac{7}{2} A_1^3 A_0^6 x^4-\frac{5}{6} A_4 A_0^4 x^2-\frac{5}{3} A_2^2 A_0^3 x^2- \frac{10}{3} A_1 A_3 A_0^3 x^2\\&\qquad \;\,-\,5 A_1^2 A_2 A_0^2 x^2-\frac{5}{6} A_1^4 A_0 x^2+A_5,\\ \vdots . \end{aligned}\right\} \nonumber \\ \end{aligned}$$
(43)

We have also computed other components, but due to lack of space we have not listed.

Using boundary conditions of (2), we get the values of \(A_i\) (Table 1)

Table 1 Numerical values of \(A_i\), where \(i=0,1,2,\ldots \)
Full size table

Hence, by using (43) and Table 1, we can write an approximate series solutions containing 15-terms i.e., \(u=\sum ^{15}_{i=0}{v_i}\).

In Table 2, we show the efficiency of this numerical technique. Here, we have discussed the approximated series solutions containing respectively 6, 10, 12 terms and their corresponding absolute errors, which shows a systematical decline in absolute errors. In Table 3 we compare our numerical results with the result of [25].

Table 2 Numerical solutions and absolute error for problem (2)
Full size table
Table 3 Numerical solutions and absolute error for problem (2)
Full size table
Table 4 Numerical values of \(A_i\), where \(i=0,1,2,\ldots \)
Full size table
Table 5 Numerical solutions and absolute error for (3)
Full size table

5.2 Problem 2: Thermal explosion in cylindrical vessel

Consider the nonlinear two point SBVP (3). The exact solution of this SBVP is \(u(x)=2~\ln \left( \frac{C+1}{C~ x^2 +1}\right) \), where \(C=3-2\sqrt{2}\). By employing the Eqs. (33) and (3), we obtain the components \(\{\nu _i\}\) of the series solutions of SBVP as

$$\begin{aligned} \left. \begin{aligned}&\nu _0=A_0,\\&\nu _1=A_1-\frac{1}{4} x^2 e^{A_0},\\&\nu _2=-\frac{1}{4} x^2 e^{A_0}+\frac{1}{64} x^2 \left( e^{A_0} \left( e^{A_0} x^2+16\right) -16 e^{A_0} A_1\right) +A_2,\\&\nu _3=-\frac{1}{4} x^2 e^{A_0}+\frac{1}{64} x^2 \left( e^{A_0} \left( e^{A_0} x^2+16\right) -16 e^{A_0} A_1\right) \\&\quad -\,\frac{e^{A_0} x^2 \left( x^2 e^{A_0} \left( x^2 \left( 2 e^{A_0}+e^{A_0}\right) +36\right) + 36 A_1 \left( x^2 \left( -\left( e^{A_0}+e^{A_0}\right) \right) +8 A_1-16\right) +576 A_2\right) }{2304}+A_3,\\&\nu _4=-\,\frac{1}{4} x^2 e^{A_0}+\frac{1}{64} x^2 \left( e^{A_0} \left( e^{A_0} x^2+16\right) -16 e^{A_0} A_1\right) \\&\qquad \;\, -\,\frac{e^{A_0} x^2 \left( x^2 e^{A_0} \left( x^2 \left( 2 e^{A_0}+e^{A_0}\right) +36\right) +36 A_1 \left( x^2 \left( -\left( e^{A_0}+e^{A_0}\right) \right) +8 A_1-16\right) +576 A_2\right) }{2304}\\&\qquad \;\, -\,\frac{e^{A_0} x^2}{147456} \left( -6 x^6 e^{3 A_0}-x^4 e^{2 A_0} \left( 11 e^{A_0} x^2-128 A_1+128\right) \right. \\&\qquad \left. \;\,-\,x^2 e^{A_0} \left( e^{2 A_0} x^4-64 e^{A_0} \left( 6 A_1-1\right) x^2 +1152 \left( \left( A_1-2\right) A_1+2 A_2\right) \right) \right. \\&\qquad \left. \;\,+\,64 \left( e^{2 A_0} A_1 x^4-18 e^{A_0} \left( A_1 \left( 3 A_1-2\right) +2 A_2\right) x^2\right. \right. \\&\qquad \left. \left. \;\,+\,96 \left( -6 A_2+A_1 \left( \left( A_1-3\right) A_1+6 A_2\right) +6 A_3\right) \right) \right) +A_4,\\ \vdots . \end{aligned}\right\} \nonumber \\ \end{aligned}$$
(44)

Making use of boundary conditions of (3), we obtain the values of \(A_0, A_1, A_2,\ldots \) (See Table 4). Hence, by using (44) and Table 4, we can write an approximate series solutions of SBVP, containing 9-terms i.e., \(u=\sum ^{8}_{i=0}{v_i}\). In Table 5, we have discussed the approximated series solution (containing different terms) for SBVP (3) and their corresponding absolute errors, which shows a systematical decline in absolute errors.

5.3 Problem 3: Thermal distribution in the human head

Consider the nonlinear SBVP (4). By employing the Eqs. (33) and (4), we obtain the components \(\{\nu _i\}\) of the series solutions of SBVP u as

$$\begin{aligned} \left. \begin{aligned}&\nu _0=A_0,\\&\nu _1=A_1-\frac{1}{6} e^{-A_0} x^2,\\&\nu _2=-\frac{1}{120} e^{-2 A_0} x^4+\frac{1}{6} e^{-A_0} A_1 x^2+A_2,\\&\nu _3=-\frac{1}{120} e^{-2 A_0} x^4+\frac{1}{6} e^{-A_0} A_1 x^2\\&\quad \quad -\frac{e^{-3 A_0} \left( -63 e^{A_0} \left( 2 A_1+1\right) x^4+630 e^{2 A_0} \left( A_1 \left( A_1+2\right) -2 A_2\right) x^2+4 x^6\right) }{7560}+A_3,\\&\nu _4=-\frac{1}{120} e^{-2 A_0} x^4+\frac{1}{6} e^{-A_0} A_1 x^2\\&\quad \quad -\frac{e^{-3 A_0} \left( -63 e^{A_0} \left( 2 A_1+1\right) x^4+630 e^{2 A_0} \left( A_1 \left( A_1+2\right) -2 A_2\right) x^2+4 x^6\right) }{7560}\\&\quad \quad -\frac{e^{-4 A_0}}{22680 x} \left( -12 e^{A_0} \left( 3 A_1+1\right) x^7+378 e^{2 A_0} \left( A_1^2+A_1-A_2\right) x^5\right. \\&\left. \quad \quad -\,630 e^{3 A_0} \left( -6 A_2+A_1 \left( A_1 \left( A_1+3\right) -6 A_2\right) +6 A_3\right) x^3+\frac{61 x^9}{72}\right) +A_4,\\ \vdots . \end{aligned}\right\} \end{aligned}$$
(45)

Making use of boundary conditions of (4), we obtain the values of \(A_0, A_1, A_2,\ldots \) (See Table 6).

Table 6 Numerical values of \(A_i\), where \(i=0,1,2,\ldots \)
Full size table

Hence, by using (45) and Table 6, we can write an approximate series solutions of SBVP, containing 11-terms, i.e., \(u=\sum ^{10}_{i=0}{v_i}\).

To check the efficiency of our technique for this problem we use absolute residual error because exact solution is not available. The absolute residual error measures that how well the approximate solution satisfies nonlinear SBVP (4).

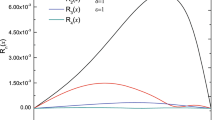
$$\begin{aligned} R_n=\left| -u_{n}''(x)-\frac{2}{x}u_{n}'(x)- e^{-u_{n}}\right| ,\quad ~0<x<1. \end{aligned}$$

Table 7 shows the numerical values of residual error \(R_n\), \(n=7,8,10\) and their systematical decay. We also compare our results with the results in [14] and [5].

Table 7 Numerical solutions and absolute residual error for (4)
Full size table

5.4 Problem 4: Rotationally symmetric shallow membrane cap

We consider the nonlinear SBVP (5). By employing the Eqs. (33) and (5), we obtain the components \(\{\nu _i\}\) of the series solutions of SBVP u as

$$\begin{aligned} \left. \begin{aligned}&\nu _0=A_0,\\&\nu _1=-\frac{x^2}{64 A_0^2}+A_1+\frac{x^2}{16},\\&\nu _2=\frac{x^4}{1536 A_0^3}-\frac{x^4}{6144 A_0^5}+\frac{A_1 x^2}{32 A_0^3}+A_2,\\&\nu _3=-\frac{x^6}{32768 A_0^4}+\frac{11 x^6}{589824 A_0^6}-\frac{13 x^6}{4718592 A_0^8}+\frac{5 A_1 x^4}{6144 A_0^6}\\&\quad \quad -\frac{A_1 x^4}{512 A_0^4}+\frac{A_2 x^2}{32 A_0^3}-\frac{3 A_1^2 x^2}{64 A_0^4}+A_3,\\&\nu _4=-\frac{x^6}{32768 A_0^4}+\frac{11 x^6}{589824 A_0^6}-\frac{13 x^6}{4718592 A_0^8}+\frac{5 A_1 x^4}{6144 A_0^6}\\&\quad \quad - \,\frac{A_1 x^4}{512 A_0^4}+\frac{A_2 x^2}{32 A_0^3}-\frac{3 A_1^2 x^2}{64 A_0^4}\\&\quad \quad + \,\frac{x^2}{1509949440 A_0^{11}}\left( 8 A_0^2 \left( 520 A_0 x^4+4160 A_1 x^4\right. \right. \\&\quad \quad \left. \left. -\, 320 A_0^3 x^2 \left( 480 A_1-480 A_2+11 x^2\right) \right. \right. \\&\quad \quad -\,6 A_0^2 \left( 320 A_1 x^2 \left( 240 A_1+11 x^2\right) +51 x^6\right) \\&\quad \quad +\,5760 A_0^5 \left( 64 A_1 \left( 24 A_1+x^2\right) -64 A_2 \left( 48 A_1+x^2\right) +x^4\right) \\&\quad \quad +\,288 A_0^4 \left( 80 A_1 \left( 32 A_1 \left( 16 A_1+x^2\right) +x^4\right) +x^6\right) \\&\quad \quad \left. \left. -\,5898240 A_0^6 \left( A_2-A_3\right) +101 x^6\right) -85 x^6\right) +A_4,\\ \vdots . \end{aligned}\right\} \end{aligned}$$
(46)

Making use of boundary conditions of (5), we obtain the values of \(A_0, A_1, A_2,\ldots \)(See Table 8).

Table 8 Numerical values of \(A_i\), where \(i=0,1,2,\ldots \)
Full size table

Hence, by using (46) and Table 8, we can write an approximate series solutions of SBVP, containing 10-terms, i.e., \(u=\sum ^{9}_{i=0}{v_i}\). Similar to above problem, exact solution of this problem (5) is also not known. So, again we check the efficiency of our technique with the use of absolute residual error.

$$\begin{aligned} R_n=\left| -u_n''(x)-\frac{3}{x}u_n'(x)-\frac{1}{8 u_n^2}+\frac{1}{2}\right| ,\quad ~0<x<1. \end{aligned}$$

Table 9 shows the numerical values of residual error \(R_n\), \(n=6,7,8,9\) and their systematical decay. Also we compare our result with the result of [25].

Table 9 Numerical solutions and absolute residual error for (5)
Full size table

6 Conclusion

In this paper, we have applied proposed Homotopy perturbation method coupled with Variational Iteration Method to nonlinear singular boundary value problems arising in chemistry and other branches. The proposed method is convergent and provides us approximate solutions which are very close to exact solution or best solution, known so far. This method can be preferred over finite difference method as it does not require matrix inversion. Using absolute and residual errors, we show the computational power of proposed method.