Thermal Functions of Diatomic Molecules Using Hulthén Plus Screened Kratzer Potential

Abstract

In the present paper, we have studied analytically the thermodynamic properties of diatomic molecules like LiH, HCl and H₂ and compared calculated properties with experimental data. In this regard, we have solved the Schrödinger equation with Hulthén plus screened Kratzer potential using the Nikiforov–Uvarov method and obtained energy eigenvalues. According to calculated the energy eigenvalues, we have deduced the partition function and thermodynamic properties of the molecules by applying the Poisson summation formalism. Our results show that the specific heat at constant pressure, Gibbs free energy and enthalpy are in good agreement with experimental data The average deviation of the specific heat at constant pressure, Gibbs free energy and enthalpy is $1.62 \%$, $3.57\%$ and $4.21\%$, respectively. It is obvious from the data that the potential model predicts well the thermodynamic properties of diatomic molecules.

1 Introduction

The theoretical prediction of the thermal properties of diatomic molecules is an interesting subject in physics, chemistry, material science and engineering. Examples of thermal properties are entropy, enthalpy, free energy, and specific heat [1,2,3,4,5,6]. The properties have important roles in phase transition, adsorption and synthesis of materials [7,8,9,10].

In the past few years, obtaining the thermodynamic properties of systems like diatomic molecules and semiconductors has been widely interested among scientists [2, 11,12,13,14,15]. The most important parameter that has played a great role in calculating the properties is the partition function which one can deduce it using energy eigenvalues. Applying calculated energy eigenvalues, we can obtain other thermodynamic properties such as entropy, mean energy, specific heat, and enthalpy. To this end, the first step to derive the energy spectrum is solving the Schrödinger equation [16,17,18] or using the path integral formalism [19, 20]. In this regard, different potential models have been studied in the literature [1, 21,22,23,24,25,26,27]. Among the considered potential, the Morse potential was the first experimental model that was greatly applied in physics and chemistry [28,29,30]. The potential is an interatomic model that generally uses the potential energy of a diatomic molecule. Therefore, many works considered other improved and generalized potentials and correspondingly derive thermodynamic properties for different systems like diatomic molecules [31,32,33] and nanostructures, i.e., quantum dots and quantum wires [34,35,36]. It is worthy to mention that the potential functions have been of growing interest because of their high application in fields like derive thermodynamic properties, calculating the molecular energy spectrum and simulation behavior of the molecular potential.

Nath and Roy [37] solved the Schrödinger equation with Deng-Fan potential using the Nikiforov–Uvarov method and obtained energy eigenvalues and thermodynamic properties for diatomic molecules such as H₂, LiH, HCl and CO. Okorie et al. [38] calculated analytically the fractional Schrödinger equation under Morse potential and derived the partition function and thermodynamic properties like internal energy, free energy, entropy and specific heat for diatomic molecules. Ding et al. [39] predicted thermodynamic properties for the sulfur dimer. They represented a new method with temperature and pressure as independent parameters for the Gibbs free energy and entropy of the sulfur dimer. Okon et al. [40] obtained the energy spectrum and thermodynamic properties of two molecules, namely CO and SeF, in the presence of Mobius square plus screened Kratzer potential. In this regard, we have considered the Hulthen and screened Kratzer potential model and deduce energy eigenvalues and have correspondingly obtained the partition function and thermodynamic properties of the diatomic molecules such as HCl, LiH and H₂.

As mentioned above, we combine Hulthén plus screened Kratzer (HSK) potential and have solved the Schrödinger equation applying Nikiforov–Uvarov (expressed in appendix) and series expansion method for the potential. The importance of combining potential models is obtaining a better result because potential models with more fitting quantities tend to give a better result [41, 42]. The HSK potential is defined as

$$V\left(r\right)=-\frac{{Z}_{1}{e}^{\nu r}}{1-{e}^{-\nu r}}-\frac{{Z}_{2}{e}^{-\nu r}}{r}+\frac{{Z}_{3}{e}^{-\nu r}}{{r}^{2}}$$

(1)

where ${Z}_{1}$ is the potential strength for Hulthén, and $\nu$ is the screening parameter. ${Z}_{2}\equiv 2{D}_{e}{r}_{e}$ and ${Z}_{3}\equiv {D}_{e}{{r}_{e}}^{3}$ where ${D}_{e}$ and ${r}_{e}$ are dissociation energy and equilibrium bond length, respectively. The behavior of the potential is plotted in Fig. 1.

Fig. 1

Hulthen plus screened Kratzer potential as a function of distance

2 Mathematical Framework

The Schrödinger equation with HSK potential is given as

$$\left(-\frac{{\hbar }^{2}}{2\mu }{\nabla }^{2}+V\left(r\right)\right){\Psi }_{nl}\left(r\right)={E}_{nl}{\Psi }_{nl}\left(r\right)$$

(2)

Where ${\Psi }_{nl}\left(r\right)$ denotes the eigen functions, ${E}_{nl}$ shows the energy eigenvalues, $\mu$ is the reduced mass, $\hbar$ is the reduced Plancks constant, and $r$ is radial distance from the origin. Inserting Eq. (1) into Eq. (2), we have the following equation

$$\frac{{d}^{2}{\Psi }_{nl}\left(r\right)}{d{r}^{2}}+\left[\frac{2\mu {E}_{nl}}{{\hbar }^{2}}+\frac{2\mu {Z}_{1}{e}^{-\nu r}}{{\hbar }^{2}(1-{e}^{-\nu r})}+\frac{2\mu {Z}_{2}{e}^{-\nu r}}{{\hbar }^{2}r}-\frac{2\mu {Z}_{3}{e}^{-\nu r}}{{\hbar }^{2}{r}^{2}}-\frac{l\left(l+1\right)}{{r}^{2}}\right]{\Psi }_{nl}\left(r\right)=0$$

(3)

To release the centrifugal term in Eq. (3), we use the Greene–Aldrich approximation scheme [43]. This scheme is a proper approximation to the centrifugal term which is valid for $\nu \ll 1$ and it is presented as

$$\frac{1}{{r}^{2}}\approx \frac{{\nu }^{2}}{{(1-{e}^{-\nu r})}^{2}}$$

(4)

Substituting Eq. (4) into Eq. (3), we have

$$\frac{{d}^{2}{\Psi }_{nl}\left(r\right)}{d{r}^{2}}+\left[\frac{2\mu {E}_{nl}}{{\hbar }^{2}}+\frac{2\mu {Z}_{1}{e}^{-\nu r}}{{\hbar }^{2}(1-{e}^{-\nu r})}+\frac{2\mu {Z}_{2}\nu {e}^{-\nu r}}{{\hbar }^{2}(1-{e}^{-\nu r})}-\frac{2\mu {Z}_{3}{\nu }^{2}{e}^{-\nu r}}{{\hbar }^{2}{(1-{e}^{-\nu r})}^{2}}-\frac{{\nu }^{2}l\left(l+1\right)}{{(1-{e}^{-\nu r})}^{2}}\right]{\Psi }_{nl}\left(r\right)=0$$

(5)

For simplicity, we use the following substitution

$$y={e}^{-\nu r}$$

(6)

Differentiating Eq. (6) and putting in Eq. (5), we have the following equation

$$\frac{{d}^{2}\Psi (y)}{d{y}^{2}}+\frac{1-y}{y(1-y)}\frac{d\Psi (y)}{dy}+\frac{1}{{y}^{2}{(1-y)}^{2}}\left[-\left(\varepsilon +{\eta }_{0}\right){y}^{2}+\left(2\varepsilon +{\eta }_{0}-{\eta }_{1}\right)y-(\varepsilon +\gamma )\right] \Psi \left(y\right)=0$$

(7)

where

$$-\varepsilon =\frac{2\mu {E}_{nl}}{{\nu }^{2}{\hbar }^{2}}; {\eta }_{0}=\frac{2\mu {Z}_{1}}{{\nu }^{2}{\hbar }^{2}}+\frac{2\mu {Z}_{2}}{\nu {\hbar }^{2}}; {\eta }_{1}=\frac{2\mu {Z}_{3}}{{\hbar }^{2}}; \gamma =l\left(l+1\right);$$

(8)

According to Eqs. (7) and (9) of ref. [44], we have

$$ \begin{gathered} \tilde{\tau } = 1 - y; { }\sigma \left( y \right) = y\left( {1 - y} \right);{ }\sigma^{\prime}\left( y \right) = 1 - 2y;{ }\sigma^{\prime\prime}\left( y \right) = - 2; \hfill \\ \tilde{\sigma }\left( y \right) = - \left( {\varepsilon + \eta_{0} } \right)y^{2} + \left( {2\varepsilon + \eta_{0} - \eta_{1} } \right)y - \left( {\varepsilon + \gamma } \right); \hfill \\ \end{gathered} $$

(9)

Inserting Eq. (9) into Eq. (11) of ref. [44], the following equation is obtained

$$\pi \left(y\right)=-\frac{y}{2}\pm \sqrt{\left({B}_{1}-K\right){y}^{2}+\left(K+{B}_{2}\right)y+{B}_{3}}$$

(10)

where

$${B}_{1}=\left(\frac{1}{4}+{\varepsilon }_{0}+{\eta }_{0}\right); {B}_{2}=-\left(2\varepsilon -{\eta }_{0}-{\eta }_{1}\right); {B}_{3}=\left(\varepsilon +\gamma \right); $$

(11)

In Eq. (11), we take the discrimination under the square root sign and solve for $K$. Here, we consider the negative root for the bound state as

$$K=-\left({B}_{2}+2{B}_{3}\right)-2\sqrt{{B}_{3}}\sqrt{{B}_{3}+{B}_{2}+{B}_{1}}$$

(12)

By inserting Eq. (12) into Eq. (10), we have the following relation

$$\pi \left(y\right)=-\frac{y}{2}-\left[\left(\sqrt{{B}_{3}}+\sqrt{{B}_{3}+{B}_{2}+{B}_{1}}\right)y-\sqrt{{B}_{3}}\right]$$

(13)

Applying Eqs. (9) and (12), we deduce $\tau (y)$ and $\tau^{\prime}\left( y \right)$ as below

$$\tau \left(y\right)=1-2y-2y\sqrt{{B}_{3}}-2y\sqrt{{B}_{3}+{B}_{2}+{B}_{1}}+2\sqrt{{B}_{3}}$$

(14)

$$ \tau^{\prime}\left( y \right) = - 2\left[ {1 + \sqrt {B_{3} } + \sqrt {B_{3} + B_{2} + B_{1} } } \right] $$

(15)

We define ${\lambda }_{n}$ and $\lambda$ by referring to Eqs. (10) and (13) of ref. [44] as

$${\lambda }_{n}={n}^{2}+n\left[1+2\sqrt{{B}_{3}}+2\sqrt{{B}_{3}+{B}_{2}+{B}_{1}}\right] n=0, 1, 2, \dots $$

(16)

$$\lambda =-\frac{1}{2}-\sqrt{{B}_{3}}-\sqrt{{B}_{3}+{B}_{2}+{B}_{1}}-\left({B}_{2}+2{B}_{3}\right)-2\sqrt{{B}_{3}}\sqrt{{B}_{3}+{B}_{2}+{B}_{1}}$$

(17)

Linking Eqs. (16) and (17) with the help of Eq. (8), we can calculate the energy eigenvalues for the HSK as

$${E}_{nl}=\frac{{\nu }^{2}{\hbar }^{2}l(l+1)}{2\mu }-\frac{{\nu }^{2}{\hbar }^{2}}{8\mu }{\left[\frac{{(n+\frac{1}{2}+\sqrt{{(l+\frac{1}{2})}^{2}+\frac{2\mu {D}_{e}{{r}_{e}}^{2}}{{\hbar }^{2}}})}^{2}-\frac{2\mu {Z}_{1}}{{\nu }^{2}{\hbar }^{2}}+\frac{4\mu {D}_{e}{r}_{e}}{\nu {\hbar }^{2}}+l(l+1)}{n+\frac{1}{2}+\sqrt{{(l+\frac{1}{2})}^{2}+\frac{2\mu {D}_{e}{{r}_{e}}^{2}}{{\hbar }^{2}}}}\right]}^{2}$$

(18)

According to the obtained energy spectrum, we calculated the partition function and thermodynamic properties of diatomic molecules. The partition function is derived by summation over all possible states of the system as

$$Q=\sum_{n=0}^{N}{e}^{-\beta {E}_{n}}$$

(19)

where $\beta =\frac{1}{{k}_{B}T}$, ${k}_{B}$ shows the Boltzmann constant, and $T$ is the temperature. Here, we have considered the s-wave state so $l=0$ and the maximum value of $N$ in Eq. (19) can be obtained by setting $\frac{d{E}_{n}}{dn}=0$. Therefore, we have

$$N=\frac{-\frac{1}{2}\nu \hbar -\frac{1}{2}\nu \hbar \sqrt{\frac{{\hbar }^{2}+8\mu {D}_{e}{{r}_{e}}^{2}}{{\hbar }^{2}}}+\sqrt{2\mu {Z}_{1}-4\mu {D}_{e}{r}_{e}\nu }}{\nu \hbar }$$

(20)

The partition function of the system with the help of Eqs. (19) and (20) has been calculated as

$$Q=\frac{({e}^{\frac{8\beta {\nu }^{2}{\hbar }^{2}\left[{\left(\frac{3}{2}+\frac{1}{2}\sqrt{1+\frac{8\mu {D}_{e}{{r}_{e}}^{2}}{{\hbar }^{2}}}\right)}^{2}-\frac{2\mu {Z}_{1}}{{\nu }^{2}{\hbar }^{2}}+\frac{4\mu {D}_{e}{r}_{e}}{\nu {\hbar }^{2}}\right]\left(3+\sqrt{1+\frac{8\mu {D}_{e}{{r}_{e}}^{2}}{{\hbar }^{2}}}\right)}{{\left(3+\sqrt{\frac{{\hbar }^{2}+8\mu {D}_{e}{{r}_{e}}^{2}}{{\hbar }^{2}}}\right)}^{2}}})}{{e}^{\left(-\frac{1}{2}\frac{{\nu }^{2}{\hbar }^{2}{\left[{(\frac{3}{2}\beta +\frac{1}{2}\sqrt{1+\frac{8\mu {D}_{e}{{r}_{e}}^{2}}{{\hbar }^{2}}})}^{2}-\frac{2\mu {Z}_{1}}{{\nu }^{2}{\hbar }^{2}}+\frac{4\mu {D}_{e}{r}_{e}}{\nu {\hbar }^{2}}\right]}^{2}}{\mu \beta {(3+\sqrt{\frac{{\hbar }^{2}+8\mu {D}_{e}{{r}_{e}}^{2}}{{\hbar }^{2}}})}^{2}}+-\frac{16{\nu }^{2}{\hbar }^{2}\beta {\left[{\left(\frac{3}{2}+\frac{1}{2}\sqrt{1+\frac{8\mu {D}_{e}{{r}_{e}}^{2}}{{\hbar }^{2}}}\right)}^{2}-\frac{2\mu {Z}_{1}}{{\nu }^{2}{\hbar }^{2}}+\frac{4\mu {D}_{e}{r}_{e}}{\nu {\hbar }^{2}}\right]}^{2}}{{\left(3+\sqrt{\frac{{\hbar }^{2}+8\mu {D}_{e}{{r}_{e}}^{2}}{{\hbar }^{2}}}\right)}^{3}}\right)}}$$

(21)

Also, the thermodynamic properties of diatomic molecules can be calculated applying the following formulas:

• Mean energy $U=-\frac{\partial \mathrm{ln}(Q)}{\partial \beta }$

• Entropy $S={k}_{B}\mathrm{ln}\left(Q\right)-{k}_{B}\beta \frac{\partial \mathrm{ln}(Q)}{\partial \beta }$

• Enthalpy $H=U+\mathrm{PV}$

• Specific heat in constant pressure ${c}_{P}=\frac{\partial H}{\partial T}$

• Specific heat in constant volume ${c}_{V}=\frac{\partial U}{\partial T}$

• Free energy $F=-{k}_{B}T \mathrm{ln}\left(Q\right)$

3 Results and Discussion

In this section, we have studied the energy spectrum and thermodynamic properties of diatomic molecules such as HCl, LiH and H₂ under the HSK potential model. The considered potential is plotted in Fig. 1. Also, we have compared our theoretical calculated data with experimental data in NIST [45]. To this end, the spectroscopic values of the molecules are presented in Table 1 and taken from ref. [46]. In our mathematical computations, we have used the following values: $\hbar c = 1973 eV$Å and $1 amu = 931.494028 eV$(Å)⁻¹ [46].

Table 1 Spectroscopic values of HCl, LiH and H₂

Table 2 represents the numerical calculation of the energy spectra of the HSK for HCl, LiH and H₂. We can observe from the data that for each vibrational quantum number, the energy increases with enhancement in the rotational quantum number.

Table 2 Bound state energy spectra ${E}_{nl}$ of HSKP for HCl, LiH and H₂

The specific heat at constant pressure, Gibbs free energy and enthalpy for HCl, LiH and H₂ are given in Tables 3, 4, and 5, respectively. The calculated data are obtained in the temperature range for HCl and H₂ at 300 K–6000 K and for LiH at $2000 K$–$6000 K$. For accuracy of our computations, we have compared the results with empirical data from the NIST database. It is worth noting that according to the NIST database, the empirical values of enthalpy are represented in the reduced form $H-{H}_{298.15}$. Moreover, we deduce the average absolute deviation (${\sigma }_{\mathrm{ave}}$) to quantitatively analyze the accuracy of the considered potential model. For this purpose, we apply the following formula

$${\sigma }_{ave}=\frac{100}{{N}_{p}}\sum \left|1-\frac{{X}_{\mathrm{theoreticl}}}{{X}_{\mathrm{experimental}}}\right|$$

where ${N}_{p}$ shows the number of data points. The average deviation of the specific heat at constant pressure, Gibbs free energy and enthalpy is $1.62 \%$, $3.57\%$ and $4.21\%$, respectively. It is obvious from the data that the potential model predicts well the thermodynamic properties of diatomic molecules.

Table 3 Thermodynamic properties for HCl using Hulthen-screened Kratzer potential compared with experimental data [45]

Table 4 Thermodynamic properties for LiH using Hulthen-screened Kratzer potential compared with experimental data [45]

Table 5 Thermodynamic properties for H₂ using Hulthen-screened Kratzer potential compared with experimental data [45]

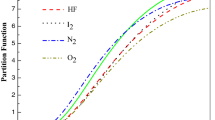
Figure 2 shows the partition function as a function of temperature for HCl, LiH and H₂. It is obvious from the figure that the partition function rises with increasing the temperature. The curves show a similar behavior, but LiH has higher values than the two others.

Fig. 2

Partition function for diatomic molecules using Hulthen-screened Kratzer potential

In Fig. 3, we have plotted the mean energy of diatomic molecules versus temperature. At low temperatures ($0<T<18 K$), they have different behavior but at higher temperatures ($T>18 K$) have similar behavior and show a smooth treatment. We can see a bow at the curves. For LiH, it occurs at ($5.63 K<T<9.1 K$), for HCl at ($6.86 K<T<10.11 K$) and for H₂ at ($9.89 K<T<15.52 K$). This behavior of diatomic molecules is due to their molecular structure. At $T<15 K$, we can see significant energy changes for three molecules but as temperature increases, they show less changes.

Fig. 3

Mean energy for diatomic molecules using Hulthen-screened Kratzer potential

Figure 4 presents the specific heat at constant volume for diatomic molecules. It can be seen that the curves show a peak structure at low temperature, so at special temperature, the probability of a transition to higher levels is occur. With enhancing temperature, the system reaches more thermal energy, and hence, the probability increases. In this regard, a peak occurs in the specific heat when the energy difference between two levels and thermal energy are equal to each other. For each molecule, the peaks appear at different values of specific heat and it is related to the structure of molecules.

Fig. 4

Specific heat at constant volume for diatomic molecules using Hulthen-screened Kratzer potential

In Fig. 5, we have plotted the entropy of diatomic molecules as a function of temperature. It is observed that the entropy for 3 cases is enhanced with increasing the temperature. It reflects the subject that the interaction potential increases the disorder of the system.

Fig. 5

Entropy for diatomic molecules using Hulthen-screened Kratzer potential

Figure 6 displays free energy of the diatomic molecules versus temperature. One can see that the curves show similar treatment. With increasing the temperature, first, they increase, and then, they decrease.

Fig. 6

Free energy for diatomic molecules using Hulthen-screened Kratzer potential

4 Conclusions

In this work, we have solved the SE with the Hulthén plus screened Kratzer potential model using a suitable approximation and have obtained the energy spectra of the model. Using the energy spectra of the potential, the partition function and other thermodynamic properties have been calculated using the Poisson summation formula. With these results, the specific heat at constant pressure, enthalpy and Gibbs free energy of diatomic molecules like HCl, LiH and H₂ have been studied graphically and compared with reported experimental data. There is a good agreement between them. Also, we have studied other thermodynamic properties such as mean energy, specific heat at constant volume, entropy and free energy for the diatomic molecules and show the behavior of the potential model.

Appendix: Nikiforov–Uvarov method

We use the Nikiforov–Uvarov method to solve the second-order differential equation with an appropriate transformation $S=S\left(r\right)$ [44]. It is given as follows

$$\frac{{d}^{2}{\Psi }_{n}\left(s\right)}{d{s}^{2}}+\frac{\widetilde{\tau }\left(s\right)}{\sigma \left(s\right)}\frac{d{\Psi }_{n}\left(s\right)}{ds}+\frac{\widetilde{\sigma }\left(s\right)}{{\sigma }^{2}\left(s\right)}{\Psi }_{n}\left(s\right)=0$$

(22)

where $\sigma \left(s\right)$ and $\widetilde{\sigma }\left(s\right)$ are second-degree polynomials and $\widetilde{\tau }\left(s\right)$ is a first-degree polynomial. By using the transformation ${\Psi }_{n}\left(s\right)=\Phi \left(s\right){y}_{n}\left(s\right)$ and considering separation of variables, Eq. (1) reduces to an equation of the hypergeometric function as

$$\sigma \left(s\right)\frac{{d}^{2}{y}_{n}\left(s\right)}{d{s}^{2}}+\tau \left(s\right)\frac{d{y}_{n}\left(s\right)}{ds}+\lambda {y}_{n}\left(s\right)=0$$

(23)

Here, ${y}_{n}\left(s\right)$ is the hypergeometric-type function. The polynomial solution of Eq. (23) is given by the Rodrigues relation

$${y}_{n}\left(s\right)=\frac{{B}_{n}}{\rho \left(s\right)}\frac{{d}^{n}}{d{s}^{n}}\left[{\sigma }^{n}\left(s\right)\rho \left(s\right)\right]$$

(24)

where ${B}_{n}$ is the normalization constant. The weight function, $\rho \left(s\right)$, must satisfy the following condition [44]

$$\frac{dw\left(s\right)}{ds}=\frac{\tau \left(s\right)}{\sigma \left(s\right)}w\left(s\right) ; w\left(s\right)=\sigma \left(s\right)\rho \left(s\right)$$

(25)

Also, $\Phi \left(s\right)$ is defined by its logarithmic derivative relation as

$$ \frac{{\Phi^{\prime}\left( s \right)}}{\Phi \left( s \right)} = \frac{\pi \left( s \right)}{{\sigma \left( s \right)}} $$

(26)

In this method, we need to define the function $\pi \left(s\right)$ and the parameter λ. So, we have

$$ \pi \left( s \right) = \frac{{\sigma^{\prime} - \tilde{\tau }}}{2} \pm \sqrt {\left( {\frac{{\sigma^{\prime} - \tilde{\tau }}}{2}} \right)^{2} - \tilde{\sigma } + k\sigma } $$

(27)

$$ \lambda = k + \pi^{\prime}\left( s \right) $$

(28)

To determine the value of $k$, the expression under the square root must be a square of a polynomial. Therefore, a new eigenvalue equation is given by

$$ \lambda = \lambda_{n} = - n\tau^{\prime} - \frac{{n\left( {n - 1} \right)}}{2}\sigma^{n} $$

(29)

where

$$\tau \left(s\right)=\widetilde{\tau }\left(s\right)+2\pi \left(s\right)$$

(30)