1 Introduction

In recent years, theoretical physics and chemistry have a wide application in explaining the behavior of the systems in different potentials. This approach has been possible through exact or approximate solutions of the relativistic or non-relativistic equations in D-dimension for different physical systems of interest (Hitler et al. (2017)). In non-relativistic quantum mechanics, exact solution of the SE is one of the interesting problems between scientists. For this purpose, a real potential such as pseudo harmonic potential (Ikhdair 2011), the Hulthen potential (Edet et al. 1909), the Morse potential (Khordad et al. 2019a), the Woods-Saxon potential (Abadi et al. 1910), the Kratzer-type potential (Kandirmaz 2018), the Badawi-Bessis-Bessis and Tietz potential (Khordad and Ghanbari 2019) and Maning-Rosen potential (Khordad et al. 2019b) and etc. is chosen to obtain eigenfunctions and energy eigenvalues of the SE. Several authors have calculated the SE and studied eigenfunctions and eigenvalues. Ishkhanyan (Ishkhanyan 2018) has solved the SE for a short-range exponential potential with inverse square root singularity. He used irreducible linear combinations of the Gauss hypergeometric functions. Sun et al. (Sun and Dong 2012) have obtained the bound state solutions with Tietz-wei (TW) diatomic molecular potential. Ikot et al. (Ikot et al. 2016) have solved the SE with improved ring-shaped non-spherical harmonic oscillator and coulomb potential. Hassanabadi et al. (Ikot et al. 2013) solved equation for Deng-Fan potential and obtained the spectra and eigenfunction for it. Le et al. (Le et al. 2018) solved equation using sextic double-well potential in two dimensions. Also, they give interesting rules to obtained exact analytical solutions. Dong et al. (Dong et al. 2016) express exact solution to solitonic profile mass Schrödinger problem. They used modified Pöscl-Teller potential. Hamzavi and Amirfakhrian (Hamzavi and Amirfakhrian 2012) solved Klein–Gordon equation for Deng-Fan potential in arbitrary N-dimension. They have used an approximation to the centrifugal term. Ahmadov et al. (Ahmadov et al. 2018) obtained bound-state solutions for the Manning-Rosen plus Hulthen potential. Rezaei Akbarieh and Mortazavi (Rezaei Akbarieh and Motavali 2008) have shown exact analytical solution for the Rosen-Morse type potential with equal scalar and vector potential. Ikhdair (Ikhdair 2009) has reported the approximate bound-state rotational-vibrational energy levels.

In this work, we have solved the SE for DLVO potential semi-exact. The DLVO theory can be used to explain stability and aggregation of aqueous dispersions quantitatively and describes the force between charged surface interacting through a liquid medium (B.v. Derjaguin, L. Landau 1993; Verwey 1947). Recently, researchers proposed that DLVO theory can also be employed to elucidate the interaction behavior between colloidal particles (Behrens et al. 2000; Celik and Bulut 1996; Oats et al. 2010; Elimelech et al. 2013; Yoon and Mao 1996). This paper is organized as follow: in Sect. 2, the SE with DLVO potential is solved. Section 3 contains theoretical method of optical properties and in Sect. 4, we show and discuss our results in detail. Finally, the corresponding calculation is given in Sect. 5.

2 Eigenfunctions and energy eigenvalues solution

Time-independent SE is written as

$$\left[ { - \frac{{h^{2} }}{2m}\nabla^{2} + V\left( r \right)} \right]\Psi \left( {r,\theta ,\varphi } \right) = E_{nl} \Psi \left( {r,\theta ,\varphi } \right)$$
(1)

By defining the wave function as \(\Psi \left( {r,\theta ,\varphi } \right) = \frac{1}{r}R\left( r \right)y\left( {\theta ,\varphi } \right)\), the radial SE obtain as (Flugge 1973)

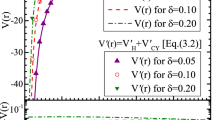
$$\left[ {\frac{{d^{2} }}{{dr^{2} }} - \frac{{l\left( {l + 1} \right)}}{{r^{2} }} + \frac{2m}{{h^{2} }}\left( {E_{nl} - V\left( r \right)} \right)} \right]R\left( r \right) = 0$$
(2)

where \(l\) is the angular momentum quantum number, \(m\) is the particle mass moving in the potential \(V\left( r \right)\) and \(E_{nl}\) is the nonrelativistic energy. Here, \(V\left( r \right)\) is DLVO potential that is given by (Poon and Andelman 2006)

$$V_{DLVO} = \left( {\frac{{Q exp\left( {kR} \right)}}{1 + kR}} \right)^{2} \frac{{exp\left( { - kr} \right)}}{\varepsilon r} - \frac{A}{6} \left[ {\frac{{2R^{2} }}{{r^{2} - 4R^{2} }} + \frac{{2R^{2} }}{{r^{2} }} + ln\left( {\frac{{r^{2} - 4R^{2} }}{{r^{2} }}} \right)} \right]$$
(3)

where \(r\) is the distance between the two charged colloids, \(Q\) is the charge of the colloid, \(R\) is hard-core radius, \(\varepsilon\) is the dielectric constant of the solvent, \(k\) is the inverse screening length that appears in the Debye–Huckel theory of electrolytes and \(A\) is the so-called Hamaker constant. Inserting Eq. (3) into Eq. (2), we obtain

$$\left\{ {\frac{{d^{2} }}{{dr^{2} }} - \frac{{l\left( {l + 1} \right)}}{{r^{2} }} + \frac{2m}{{h^{2} }}\left( {E_{nl} - B \frac{{exp\left( { - kr} \right)}}{\varepsilon r} + \frac{A}{6} \left[ {\frac{{2R^{2} }}{{r^{2} - 4R^{2} }} + \frac{{2R^{2} }}{{r^{2} }} + ln\left( {\frac{{r^{2} - 4R^{2} }}{{r^{2} }}} \right)} \right]} \right)} \right\}R\left( r \right) = 0$$
(4)

where \(B = \left( {\frac{{Q exp\left( {kR} \right)}}{1 + kR}} \right)^{2}\).

By defining the radial wave function as \(R\left( y \right) = y^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} \Phi \left( y \right)\) and changing variable \(= r^{2}\), Eq. (4) turns into

$$\left( {y\frac{{d^{2} }}{{dy^{2} }} - 3y\frac{d}{dy} + \beta_{1} y - \beta_{2} } \right) \Phi \left( y \right) = 0$$
(5)

We used the following abbreviations

$$\beta_{1} = \frac{1}{4} - \frac{{C_{1} }}{2} - \frac{{6mE_{nl} }}{{h^{2} }} + \frac{4mBk}{{\varepsilon h^{2} }} - \frac{{8AC_{2} R^{4} }}{3} - \frac{{AC_{3} }}{3}$$
(6)

and

$$\beta_{2} = \frac{1}{2}C_{1} + \frac{{2mE_{nl} }}{{h^{2} }} + \frac{4mB}{{\varepsilon h^{2} }} + \frac{{8AR^{4} }}{{3\left( {1 - 4R^{2} } \right)}} - \frac{{8AC_{2} R^{4} }}{3} - \frac{{AC_{3} }}{3} + \frac{{A ln\left( {1 - 4R^{2} } \right)}}{3}$$
(7)

In Eqs. (6) and (7), parameters \(C_{1}\), \(C_{2}\) and \(C_{3}\) express as

$$C_{1} = 2l\left( {l + 1} \right) + \frac{{4AR^{2} }}{3}$$
(8)
$$C_{2} = \frac{{\frac{1}{2} + \frac{1}{{4R^{2} - 1}}}}{{1 - 4R^{2} }}$$
(9)
$$C_{3} = \frac{{4R^{2} }}{{1 - 4R^{2} }} + \frac{3}{2} ln\left( {1 - 4R^{2} } \right)$$
(10)

According to these parameters, the solution of Eq. (5) is given by

$$\Phi \left( y \right) = w_{1} y KummerM\left( {\frac{{\sqrt { - 4\beta_{1} + 9} + \beta_{2} }}{{\sqrt { - 4\beta_{1} + 9} }},2,\sqrt { - 4\beta_{1} + 9} y} \right) exp\left( { - \frac{1}{2}y\left( {\sqrt { - 4\beta_{1} + 9} - 3} \right)} \right) + w_{2} y KummerU\left( {\frac{{\sqrt { - 4\beta_{1} + 9} + \beta_{2} }}{{\sqrt { - 4\beta_{1} + 9} }},2,\sqrt { - 4\beta_{1} + 9} y} \right) exp\left( { - \frac{1}{2}y\left( {\sqrt { - 4\beta_{1} + 9} - 3} \right)} \right)$$
(11)

Here, we take \(w_{1} = w_{2} = 1\) and kummer function is defined by

$$\Lambda _{n} \left( z \right) = \int\limits_{0}^{z} {\frac{{\log ^{{n - 1}} \left( t \right)}}{{1 + t}}} dt$$
(12)

In order to obtain finite wave function, it should be

$$\frac{{\sqrt { - 4\beta_{1} + 9} + \beta_{2} }}{{\sqrt { - 4\beta_{1} + 9} }} = n, \left( {n = 0,1,2, \ldots } \right)$$
(13)

Which gives single-valued wave functions. Inserting Eqs. (6) and (7) and Eqs. (8)-(10) into Eq. (13), the energy spectrum of the DLVO potential is obtained

$$E = \frac{{h^{2} }}{2m}\left[ { - 6 + 6n - \alpha_{2} + n\left( {6 - 6n + \sqrt \gamma } \right) - \sqrt \gamma } \right]$$
(14)

where

$$\gamma = 45 - 72n + 36n^{2} + 12\alpha_{2} + 4\alpha_{1}$$
(15)

Here, for simplicity in express energy spectrum, we rewrite Eqs. (6) and (7) as

$$\beta_{1} = - \frac{{6mE_{nl} }}{{h^{2} }} + \alpha_{1}$$
(16)

and

$$\beta_{2} = - \frac{{2mE_{nl} }}{{h^{2} }} + \alpha_{2}$$
(17)

3 Optical absorption coefficients and refractive index changes

In this section, we used density matrix formalism to obtain refractive index changes and optical absorption coefficients for GaAs corresponded to an optical intersubband transition. To this end, we discuss optical properties in theoretical framework. As we know, the corresponding system can be excited by an electromagnetic field of frequency ω, as

$$E\left( t \right) = \tilde{E} e^{{i{\omega t}}} + \tilde{E}^{*} e^{{ - i{\omega t}}}$$
(18)

We can write the time evolution of the matrix elements of one-electron density operator, ρ, as follow (Ünlü et al. 2006; Khordad 2011)

$$\frac{\partial \rho }{{\partial t}} = \frac{1}{ih}\left[ {H_{0} - q\chi E\left( t \right),\rho } \right] - \Gamma \left( {\rho - \rho^{\left( 0 \right)} } \right)$$
(19)

where \(H_{0}\) is the Hamiltonian for this system without the electromagnetic field \(E\left( t \right)\) and \(q\) is the electric charge. We use the symbol \(\left[ { , } \right]\) as the quantum mechanical commutator, \(\rho^{\left( 0 \right)}\) is the unperturbed density matrix operator and Γ is an operator corresponding for the damping due to the electron–phonon interaction, collisions among electrons, etc. We supposed that the elements of diagonal matrix of Γ are equal to the inverse of relaxation time \(T\). As we know, the electronic polarization \(P\left( t \right)\) and susceptibility \(\chi \left( t \right)\) are expressed by dipole operator \(M\) and density matrix ρ from below

$$P\left( t \right) = \varepsilon_{0} \chi \left( \omega \right)\tilde{E}e^{ - i\omega t} + \varepsilon_{0} \chi \left( { - \omega } \right)E ^{*} e^{i\omega t} = \frac{1}{V}Tr\left( {\rho M} \right)$$
(20)

where \(\varepsilon_{0}\) the permittivity of free space, the symbol is \(Tr\left( {trace} \right)\) denotes the summation over the diagonal elements of the matrix and ρ and \(V\) are the one-electron density matrix and the volume of the system, respectively.

By using Eq. (19), the analytical forms of the linear \(\chi^{\left( 1 \right)}\) and the third-order non-linear \(\chi^{\left( 3 \right)}\) susceptibility coefficients are obtained as

$$\varepsilon_{0} \chi^{\left( 1 \right)} \left( \omega \right) = \frac{{\sigma_{\nu } \left| {M_{21} } \right|^{2} }}{{E_{21} - h\omega - ih\Gamma_{12} }}$$
(21)
$$\varepsilon_{0} \chi^{\left( 3 \right)} \left( \omega \right) = - \frac{{\sigma_{\nu } \left| {M_{21} } \right|^{2} }}{{E_{21} - h\omega - ih\Gamma_{12} }} \left[ {\frac{{4\left| {M_{21} } \right|^{2} }}{{\left( {E_{21} - h\omega } \right)^{2} + \left( {h\Gamma_{12} } \right)^{2} }} - \frac{{\left( {M_{22} - M_{11} } \right)^{2} }}{{\left( {E_{21} - ih\Gamma_{12} } \right)\left( {E_{21} - h\omega - ih\Gamma_{12} } \right)}}} \right]$$
(22)

where \(\sigma_{\nu }\) is the carrier density. The refractive index changes are related to the susceptibility as (Kuhn et al. 1991)

$$\frac{\Delta n\left( \omega \right)}{{n_{r} }} = Re\left[ {\frac{\chi \left( \omega \right)}{{2n_{r}^{2} }}} \right]$$
(23)

where \(n_{r}\) is the refractive index and \(Re\) denotes the real part of relation. By using Eqs. (20–23), the linear and the third-order nonlinear refractive index changes can be obtained as (Kuhn et al. 1991)

$$\frac{{\Delta n^{\left( 1 \right)} \left( \omega \right)}}{{n_{r} }} = \frac{{\sigma_{\nu } \left| {M_{21} } \right|^{2} }}{{2n_{r}^{2} \varepsilon_{0} }}\left[ {\frac{{E_{21} - h\omega }}{{\left( {E_{21} - h\omega } \right)^{2} + \left( {h\Gamma_{12} } \right)^{2} }}} \right]$$
(24)

and

$$\frac{{\Delta n^{\left( 3 \right)} \left( \omega \right)}}{{n_{r} }} = - \frac{{\sigma_{\nu } \left| {M_{21} } \right|^{2} }}{{4n_{r}^{3} \varepsilon_{0} }} \frac{\mu cI}{{\left[ {\left( {E_{21} - h\omega } \right)^{2} + \left( {h\Gamma_{12} } \right)^{2} } \right]^{2} }} \left[ {4\left( {E_{21} - h\omega } \right)\left| {M_{21} } \right|^{2} - \frac{{\left( {M_{22} - M_{11} } \right)^{2} }}{{\left( {E_{21} } \right)^{2} + \left( {h\Gamma_{21} } \right)^{2} }}\left\{ {\left( {E_{21} - h\omega } \right)\left[ {E_{21} \left( {E_{21} - h\omega } \right) - \left( {h\Gamma_{21} } \right)^{2} } \right] - \left( {h\Gamma_{21} } \right)^{2} \left( {2E_{21} - h\omega } \right)} \right\}} \right]$$
(25)

where \(\mu\) is the permeability, \(M_{ij} = \left| {\Psi_{i} \left| {qr} \right|\Psi_{j} } \right|\) is the electric dipole moment matrix element and \(E_{ij} = E_{i} - E_{j}\). The parameter \(I\) is the optical intensity of the incident wave and define as (Khordad and Ghanbari 2017)

$$I = 2\sqrt {\frac{{\varepsilon_{R} }}{\mu }} \left| {E\left( \omega \right)} \right|^{2} = \frac{{2n_{r} }}{\mu c}\left| {E\left( \omega \right)} \right|^{2}$$
(26)

where \(c\) is the speed of light in free space. The total refractive index changes can be obtain from Eqs. (24–26)

$$\frac{\Delta n\left( \omega \right)}{{n_{r} }} = \frac{{\Delta n^{\left( 1 \right)} \left( \omega \right)}}{{n_{r} }} + \frac{{\Delta n^{\left( 3 \right)} \left( \omega \right)}}{{n_{r} }}$$
(27)

Accordingly, one can write the linear and third-order nonlinear absorption coefficients as follow (Ünlü et al. 2006; Aspnes 1976)

$$\alpha^{\left( 1 \right)} \left( \omega \right) = \omega \sqrt {\frac{\mu }{{\varepsilon_{R} }}} \left[ {\frac{{\sigma_{\nu } h\Gamma_{12} \left| {M_{21} } \right|^{2} }}{{\left( {E_{21} - h\omega } \right)^{2} + \left( {h\Gamma_{12} } \right)^{2} }}} \right]$$
(28)

and

$$\alpha^{\left( 3 \right)} \left( {\omega ,I} \right) = - \omega \sqrt {\frac{\mu }{{\varepsilon_{R} }}} \left( {\frac{I}{{2\varepsilon_{0} n_{r} c}}} \right)\frac{{\sigma_{\nu } h\Gamma_{12} \left| {M_{21} } \right|^{2} }}{{\left[ {\left( {E_{21} - h\omega } \right)^{2} + \left( {h\Gamma_{12} } \right)^{2} } \right]^{2} }} \left\{ {4\left| {M_{21} } \right|^{2} - \frac{{\left| {M_{22} - M_{11} } \right|^{2} \left[ {3E_{21}^{2} - 4E_{21} h\omega + h^{2} \left( {\omega^{2} - \Gamma_{12}^{2} } \right)} \right]}}{{E_{21}^{2} + \left( {h\Gamma_{12} } \right)^{2} }}} \right\}$$
(29)

One can deduce the total absorption coefficient, \(\alpha \left( {\omega ,I} \right)\) from Eqs. (28) and (29) as (Ünlü et al. 2006)

$$\alpha \left( {\omega ,I} \right) = \alpha^{\left( 1 \right)} \left( \omega \right) + \alpha^{\left( 3 \right)} \left( {\omega ,I} \right)$$
(30)

4 Results and discussion

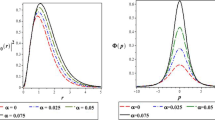
In this work, we have solved SE for DLVO potential. Figure 1 shows the DLVO potential qualitatively. As we see from Fig. 1, the DLVO potential has a deep minimum at short distances. At large distances, the coulomb repulsion dominates. This approach gives a local maximum in the curve. In Figs. 2 and 3, we have plotted several wave functions for different quantum numbers (\(n,l\)). It is found that there is a symmetry at \(r = 0\) in the wave function. For at \(l = 1\), there is a peak at \(r = 0\) and as \(l\) increases, the peak gets smoother. Table 1 indicates energy spectrum for quantum numbers (\(n,l\)). According to table, in constant \(l\), eigenvalues increase but in constant \(n\), eigenvalues decrease. To study the degeneracy and its relation to system symmetry, energy spectrum for two states (for example (\(n = 1,l = 0\)) and (\(n = 0,l = 1\))) show that the two states are not degenerate (\(\Delta E \ne 0\)).

Fig. 1
figure 1

The DLVO potential as a function of distance

Full size image
Fig. 2
figure 2

Variations of five eigenfunctions of DLVO potential for quantum numbers pairs ((5,0), (5,1), (5,2), (5,3), (5,4); in \(Q = k = \varepsilon =\) 1)

Full size image
Fig. 3
figure 3

Variations of four eigenfunctions of DLVO potential for quantum numbers pairs ((2,1), (3,1), (4,1), (5,1); in \(Q = k = \varepsilon =\) 1)

Full size image
Table 1 Energy eigenvalues of quantum number pairs \((n,l)\)
Full size table

Thereafter, we have calculated optical properties for GaAs. The used parameters in the calculation are \(n_{r} = 3.2\), \(T_{12} = 0.2 ps\), \(\Gamma_{12} = \frac{1}{{T_{12} }}\), \(\sigma_{\nu } = 3 \times 10^{16} cm^{ - 3}\) (Khordad 2011) and we take arbitrary parameters for potential constant. Figure 4 shows linear, nonlinear and total refractive index changes of GaAs as a function of photon energy with \(I = 0.1 {\raise0.7ex\hbox{${MW}$} \!\mathord{\left/ {\vphantom {{MW} {cm^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${cm^{2} }$}}\). The linear and nonlinear term are opposite in sign and expressed by \(\Delta n^{\left( 1 \right)}\) and \(\Delta n^{\left( 3 \right)}\) term. Therefore, the total refractive index change will be reduced.

Fig. 4
figure 4

The variations of linear, third-order and total refractive index changes with the photon energy for \(I = 0.1 {\raise0.7ex\hbox{${MW}$} \!\mathord{\left/ {\vphantom {{MW} {cm^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${cm^{2} }$}}\)

Full size image

Figure 5 displays the total refractive index changes as a function of photon energy for different \(I\) as 0.1, 0.2, 0.3 and \(0.4 {\raise0.7ex\hbox{${MW}$} \!\mathord{\left/ {\vphantom {{MW} {cm^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${cm^{2} }$}}\). It is clear that the refractive index change increase and shift towards higher energies with increasing intensity. In Fig. 6, the variations of linear, third-order nonlinear and total absorption coefficients are plotted as a function of the photon energy with \(I = 0.1 {\raise0.7ex\hbox{${MW}$} \!\mathord{\left/ {\vphantom {{MW} {cm^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${cm^{2} }$}}\). Figure 7 shows the total changes in the absorption coefficient as a function of the photon energy for different \(I\) as 0.1, 0.2, 0.3 and \(0.4 {\raise0.7ex\hbox{${MW}$} \!\mathord{\left/ {\vphantom {{MW} {cm^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${cm^{2} }$}}\). In this figure, we observed that the total changes in the absorption coefficient will be increases as \(I\) increases and shift toward higher energies. As we seen in Fig. 7, the radiation intensity does not effect on the peak position but increases the peaks. The physical reason is the increase in the number of electrons in the interband bandwidth. As we know, by increasing radiation intensity, more electron are excited.

Fig. 5
figure 5

The variations of total refractive index changes with the photon energy for different intensity

Full size image
Fig. 6
figure 6

The variations of linear, third-order and total absorption coefficients with the photon energy for \(I = 0.1 {\raise0.7ex\hbox{${MW}$} \!\mathord{\left/ {\vphantom {{MW} {cm^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${cm^{2} }$}}\)

Full size image
Fig. 7
figure 7

The variations of total absorption coefficients with the photon energy for different intensity

Full size image

5 Conclusion

In the present work, we have solved the radial Schrödinger equation for DLVO potential. We calculated energy spectrum and corresponding eigenfunction. By using the compact density matrix approach, the linear and third-order nonlinear optical properties for GaAs have been theoretically obtained. According to the results, it is found that the incident optical intensity has a rather great effect on the optical properties as it is expected from theoretical expressions. Here, we used arbitrary parameters for potential and hope that this study can make a significant contribution both to the experimental and theoretical investigations on this topic.