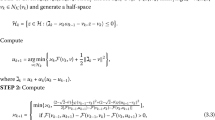An extragradient algorithm for quasiconvex equilibrium problems without monotonicity

Abstract

We attempt to provide an algorithm for approximating a solution of the quasiconvex equilibrium problem that was proved to exist by K. Fan 1972. The proposed algorithm is an iterative procedure, where the search direction at each iteration is a normal-subgradient, while the step-size is updated avoiding Lipschitz-type conditions. The algorithm is convergent to a $\rho$- quasi-solution with any positive $\rho$ if the bifunction f is semistrictly quasiconvex in its second variable, while it converges to the solution when f is strongly quasiconvex. Neither monotoniciy nor Lipschitz property is required. The main subprogram needed to solve at each iteration is a proximal regularized minimization problem whose objective function is the sum of a quasiconvex function and the one $\Vert .\Vert ^2$. We also discuss several cases where this global optimization problem can be solved efficiently.

1 Introduction

Let C be a nonempty closed convex set in $\mathbb {R}^n$ and $f: \mathbb {R}^n \times \mathbb {R}^n \rightarrow \mathbb {R}$ be a given bifunction such that $f(x,x) = 0$ for every $x \in C$. We consider the problem

In what follows we call Problem (EP) a convex (resp. quasiconvex) equilibrium problem if the function f(x, .) is convex (resp. quasiconvex) on C for any $x\in C$. The inequality appeared in Problem (EP) first was used by Nikaido and Isoda in 1955 [1] in a non-cooperative convex game. In recent years this problem attracted much attention of many authors as it contains a lot numbers of important problems such as optimization, variational inequality, Kakutani fixed point, Nash equilibrium problems and others as special cases, see e.g. the interesting monographs [2, 3], the papers [4,5,6,7,8,9,10,11,12] and the references cited therein.

Many algorithms have been developed for solving (EP) under the assumption that the bifunction is convex and subdifferentiable with respect to the second variable while the first one being fixed. Almost all of these algorithms are based upon the auxiliary problem principle, which states that when f(x, .) is convex, subdifferentiable on C, then the solution-set of (EP) coincides with that of the regularized problem

with any $\rho > 0$ (see [2, 8]). The main advantage of the latter problem is that the regularized bifunction $f_\rho$ is strongly convex in the second variable when the first one is fixed.

A basic method for solving Problem (REP) is the extragradient one, where at each iteration k, having $x^k\in C$, a main operation is of solving the mathematical subprogram

Thanks to convexity of the function $f(x^k,.)$ this problem is a strongly convex program, and therefore it is uniquely solvable. However, when f(x, .) is quasiconvex rather than convex, Problem (MP), in general, is not strongly convex, even not quasiconvex.

In the seminal paper [13] in 1972, K. Fan called Problem (EP) a minimax inequality and established solution existence results for it, when C is convex, compact and f is quasiconvex on C.

It worth mentioning that when f(x, .) is convex and subdifferentiable on C, the equilibrium problem (EP) can be reformulated as the following multivalued variational inequality

where $F(x^*) = \partial _2 f(x^*,x^*)$ with $\partial _2 f (x^*, x^*)$ being the diagonal subdifferential of f at $x^*$, that is the subdifferential of the convex function $f (x^*,.)$ at $x^*$. In the case f(x, .) is semi-strictly quasiconvex rather than convex, Problem (EP) can take the form of (MVI) with $F(x):= Na_{f(x,x)} {\setminus } \{0\}$, where $Na_{f(x,x)}$ is the normal cone of the adjusted sublevel set of the function f(x, .) at the level f(x, x), see [14]. More details about the links between equilibrium problems and variational inequalities can be found in [15].

Based upon the auxiliary principle, different methods such as the fixed point, projection, extragradient, regularization, gap function ones have been developed for solving equilibrium problem (EP) by using mathematical programming techniques, where the bifunction involved possesses certain monotonicity properties. Almost all of them require that the bifunction is convex with respect to its second variable, see e.g. the comprehensive monograph [2] and the references therein.

In [16], the authors studied an infeasible interior proximal algorithm for solving quasiconvex equilibrium problems with polyhedral constraints. At each iteration k of this algorithm, having $x^k$ it requires globally solving a nonconvex mathematical programming problem, where the objective function is the sum of $f(x^k,.)$ and a strongly convex function defined by a distance function. The convergence of this algorithm is proved under an assumption depending on the iterates $x^k$ and $x^{k+1}$. Very recently, Iusem and Lara [17] proposed an algorithm for solving quasiconvex equilibrium problem (EP). Their algorithm can be considered as a standard proximal point method for optimization problems applied to the quasiconvex function f(x, .). The convergence has been proved when f is pseudomonotone, Lipschitz-type and strongly quasi-convex.

In our recent papers [18, 19], by using the normal subdifferential of quasiconvex functions, we have proposed projection algorithms for Problem (EP) when the bifunction is pseudo and paramonotone.

In this paper, we continue our work by modifying the linesearch extragradient algorithm commonly used for convex equilibrium problem (EP) to solve quasiconvex equilibrium problems without requiring any monotonicity and Lipschitz-type properties of the bifunction involved. More precisely, after the next section that contains preliminaries on normal subdifferentials of a quasiconvex function, in the third section, we describe an extragradient linesearch algorithm for this quasiconvex equilibrium problem. Then by observing that the solution set of the regularized problem coincides with that of the Minty (dual) one for semi-strictly quasiconvex bifunction, we prove that the algorithm converges to a quasi (prox) solution when the bifunction involved is semi-strictly quasiconvex in its second variable, which is the unique solution when the bifunction is strongly quasiconvex in its second variable. As the algorithms in [17, 20], at each iteration of our algorithm, it requires globally solving a problem, whose objective function is the sum of a quasiconvex function and the one $\Vert .\Vert ^2$. We discuss several special cases where this subprogram can be solved efficiently. We close the paper by presenting some computational results showing the efficiency and behavior of the proposed algorithm.

2 Preliminaries on quasiconvexity, normal subdifferentials and monotonicity

Definition 1

([15, 21, 22]) Let C be a convex set in $\mathbb {R}^n$. Let $\varphi :\mathbb {R}^n \rightarrow \mathbb {R}\cup \{+\infty \}$ such that $C \subseteq \text {dom} \varphi$. The function $\varphi$ is said to be

• (i) Quasiconvex on C if and only if for every $x,y \in C$ and $\lambda \in \left[ 0,1\right]$, one has

  $$\begin{aligned} \varphi [(1-\lambda )x +\lambda y] \le \max [\varphi (x), \varphi (y)]. \end{aligned}$$

  (1)

• (ii) Semi-strictly quasi-convex on C if it is quasiconvex and for every $x,y \in C$ and $\lambda \in \left( 0,1\right)$, one has

  $$\begin{aligned} \varphi (x)<\varphi (y) \Rightarrow \varphi [(1-\lambda )x +\lambda y]< \varphi (y). \end{aligned}$$

  (2)

• (iii) Strongly quasiconvex on C with modulus $\gamma >0$ if for every $\lambda \in \left[ 0,1\right]$

  $$\begin{aligned} \varphi (\lambda x +(1-\lambda ) y) \le \max \{\varphi (x), \varphi (y)\} -\lambda (1-\lambda ) \frac{\gamma }{2}\Vert x-y\Vert ^2 \ \forall x, y \in C. \end{aligned}$$

• (iv) Pseudoconvex on on C if it is differentiable on an open set containing C and

  $$\begin{aligned} \langle \nabla \varphi (x), y-x\rangle \ge 0 \Rightarrow \varphi (y) \ge \varphi (x) \ \forall x, y \in C. \end{aligned}$$

• (v) Proximal convex on C with modulus $\alpha > 0$ (shortly $\alpha$-prox-convex) if there exists $\alpha > 0$ such that for any $z\in C$, $prox_{\varphi }(C,z) \not =\emptyset$ and

  $$\begin{aligned} p \in prox_{\varphi }(C,z) \Rightarrow \alpha \langle x-p, z-p\rangle \le \varphi (x)- \varphi (p) \ \forall x\in C, \end{aligned}$$

  where $prox_{\varphi }(C,z)$ is the proximal mapping of $\varphi$ at z on C, that is

  $$\begin{aligned} prox_{\varphi }(C,z):= \text {argmin}\{\varphi (y)+ \frac{1}{2}\Vert y-z\Vert ^2: y\in C\}. \end{aligned}$$

It is well known that strongly quasiconvex $\Rightarrow$ semi-strictly quasiconvex $\Rightarrow$ essentially quasiconvex $\Rightarrow$ quasiconvex but the converses are not true. Clearly, $\varphi$ is quasiconvex if and only if, for every $\alpha \in \mathbb {R}$, the strict level set at the level $\alpha$, that is

$$\begin{aligned} L_\alpha : =\{ y: \varphi (y) < \alpha \} \end{aligned}$$

is convex. The class of proximal-convex functions has recently been introduced in [21]. It is easy to see that when $\alpha =1$, it returns to the classical concept of convex functions. It can be seen from [21, Corollary 3.1] and [23, Proposition 7] that if $\phi$ is lower semicontinuous and strongly quasiconvex on C and $p\in prox_{\phi }(C,z)$ then $\phi$ is prox-convex on the complement of its sublevel set at level $\phi (p)$.

Recall that the (Hadamard) directional derivative of a function $\varphi$ at x with direction d is defined as

$$\begin{aligned} \varphi '(x,d):= \lim \inf _{t \searrow 0, u\rightarrow d} \frac{\varphi (x + tu) -f(x)}{t}. \end{aligned}$$

A point $x\in C$ is said to be a stationary point of $\varphi$ on C if $\varphi '(x,d) \ge 0$ for every d. A point is a minimizer of $\varphi$ on C then it is a stationary point. The converse direction is true when $\varphi$ is convex or pseudoconvex on C.

The Greenberg-Pierskalla subgradient of a quasiconvex function [24] is defined as

$$\begin{aligned} \partial ^{GP} \varphi (x):= \{ g \in \mathbb {R}^{n}: \langle g, y - x\rangle > 0 \Rightarrow \varphi (y) \ge \varphi (x)\}. \end{aligned}$$

A variation of this subdifferential is the star-subdifferential that is defined as

$$\begin{aligned} \partial ^*\varphi (x):= \{ g\in \mathbb {R}^{n}: \langle g,y-x\rangle < 0 \ \forall y\in L_\varphi (x)\}, \end{aligned}$$

where $L_\varphi (x)$ stands for the strict level set of $\varphi$ with level $\varphi (x)$. It is well known [24, 25] that if $\varphi$ is continuous on $\mathbb {R}^n$, then $\partial ^*\varphi (x)$ contains nonzero vector and

$$\begin{aligned} \partial ^*\varphi (x) \cup \{0\} = cl(\partial ^* \varphi (x) ) = \partial ^{GP}\varphi (x), \end{aligned}$$

where cl(A) stands for the closure of the set A. Thus the star-subdifferential is also called the normal-subdifferential. Various calculus rules for normal subdifferential can be found in [25]. The normal and Greenberg- Pierskalla subdifferentials are among the most commonly used types in quasiconvex analysis. They were used to design subgradient type methods for solving quasiconvex optimization problems (see [26,27,28,29]). It is worth mentioning that it is not an easy task to compute a subgradient for a general quasiconvex function. Fortunately, for some special classes of quasiconvex functions, a subset of these subdifferentials can be computed (for example, see [26]). The notion of the star subdifferential was also introduced by Penot ([30]), but it is not exactly the definition that we used in this paper.

The following concepts are commonly used in the field of equilibrium problem [2].

Definition 2

Let $f: C\times C \rightarrow \mathbb {R}$

• (i) f is said to be strongly monotone on C with modulus $\eta \ge 0$ (shortly $\eta$-strongly monotone) if

  $$\begin{aligned} f(x,y) + f(y,x) \le - \eta \Vert x-y\Vert ^2 \ \forall x, y \in C. \end{aligned}$$

  If $\eta = 0$ it is also called monotone on C.

• (ii) f is said to be paramonotone on C if x is a solution of (EP) and $y\in C$, $f(x,y) = f(y,x) = 0$ then y is also a solution of (EP).

• (iii) f is said to be pseudomonotone on C if $f(x,y) \ge 0$ then $f(y,x)\le 0$ for every $x,y \in C$.

• (iv) f is said to be Lipschitz-type on C if

  $$\begin{aligned} f(x,y) +f(y,z) \ge f(x,z) -L_1\Vert x-y\Vert ^2 - L_2\Vert y-z\Vert ^2 \ \forall x,y,z \in C. \end{aligned}$$

  Clearly, in the case of optimization when $f(x,y):= \varphi (y) - \varphi (x)$ it possesses both the paramonotonicity and Lipschitz-type property.

The following lemma will be used to prove our main theorem in the next section.

Lemma 1

(see e.g. [11]) Let $\{a_k \}$ and $\{b_k \}$ be nonnegative sequences of real numbers satisfying

$$\begin{aligned} a_{k+1} \le a_k + b_k \quad \forall k, \end{aligned}$$

with $\sum _{k=1}^{+\infty }b_k<+\infty$. Then the sequence $\{a_k\}$ is convergent.

3 Algorithm and its convergence

A problem closely related to Problem (EP) is the Minty (or dual) equilibrium one that is defined as

Let us denote by S and $S_d$ the solution set of (EP) and (DEP) respectively. It is clear that if f is pseudomonotone on C then $S\subseteq S_d$. Conversely, $S_d \subseteq S$ if f is upper semi-continuous with respect to the first variable and convex with respect to the second variable (see for example [31]).

In what follows we always suppose that f(., y) is upper semi-continuous for any $y\in C$.

In the following lemma, we prove that the inclusion $S_d \subseteq S$ still holds true when f is semi-strictly quasiconvex with respect to the second variable.

Lemma 2

Assume that f(x, .) is semi-strictly quasiconvex on C for any $x\in C$. Then $S_d \subseteq S$.

Proof

Let $z^*\in S_d$. If $z^*\not \in S$, then there would exist $y\in C$ such that $f(z^*,y)<0$.

For $\lambda \in (0,1)$, set $y_{\lambda }= \lambda z^*+(1-\lambda )y$. Since f(., y) is upper semi-continuous, there exists $0<\lambda <1$ such that $f(y_{\lambda },y)<0$. Since $z^*\in S_d$, $f(y_{\lambda }, z^*)\le 0$.

We consider two cases

• Case 1: $f(y_{\lambda }, z^*)< 0$. By the quasiconvexity of $f(y_{\lambda },.)$,

  $$\begin{aligned} 0=f(y_{\lambda }, y_{\lambda })\le \max \{f(y_{\lambda }, z^*), f(y_{\lambda }, y)\}<0. \end{aligned}$$

  This is a contradiction.

• Case 2: $f(y_{\lambda }, z^*)= 0$. By the semi-strictly quasiconvexity of $f(y_{\lambda },.)$ and the fact that $f(y_{\lambda },y)<0=f(y_{\lambda }, z^*)$, which would imply

  $$\begin{aligned} 0=f(y_{\lambda }, y_{\lambda })< \max \{f(y_{\lambda }, z^*), f(y_{\lambda }, y)\}=0. \end{aligned}$$

  This is also a contradiction.

When the bifunction is convex with respect to its second variable, the extragradient-type methods had been proposed for solving (EP) without monotonicity and Lipschitz properties (see for example [2, 10]). The following algorithm can be considered as a modification of the extragradient algorithm in [10] for solving Problem (EP) in the quasiconvex case. The conditions for the stepsizes are borrowed from the subgradient-projection algorithms for nonsmooth quasiconvex minimization problem (see [26]).

Algorithm 3.1

Take $\alpha ,\theta \in (0,1)$ and two sequences $\{\rho _k\}_{k\ge 0}$,$\{\sigma _k\}_{k\ge 0}$ of positive numbers such that

$$\begin{aligned} \rho _k \ \text { nonincreasingly converges to some} \ \overline{\rho } > 0, \nonumber \\ \quad \sum _{k=0}^{+\infty } \sigma _k=+\infty , \quad \sum _{k=0}^{+\infty } \sigma _k^2 <+\infty .\nonumber \end{aligned}$$

Initialization: Pick $x^0\in C$.

Iteration $k = 0,1...$

• Find $y^k$ such that

  $$\begin{aligned} y^k \in \text {argmin}_{y\in C} \left\{ f(x^k,y) +\frac{1}{2\rho _k} \Vert x^k-y\Vert ^2\right\} . \end{aligned}$$

  (3)

• If $y^k=x^k$, then stop: $x^k$ is a stationary point or a solution. If $y^k\not =x^k$, find the smallest positive integer m such that $z^{k,m}=(1-\theta ^m)x^k +\theta ^m y^k$ and

  $$\begin{aligned} f(z^{k,m},x^k) -f(z^{k,m},y^k) \ge \frac{\alpha }{2\rho _k} \Vert y^k-x^k\Vert ^2, \end{aligned}$$

  (4)

  and set $z^k=z^{k,m}$.

• Take

  $$\begin{aligned} g^k \in \partial ^*_2f(z^k,x^k):=\left\{ g\in \mathbb {R}^n: \langle g, y-x^k \rangle<0 \text { if } f(z^k,y)< f(z^k,x^k)\right\} , \end{aligned}$$

  (5)

  and normalize it to obtain $\Vert g^k\Vert =1$ ($g^k \not = 0$, see Proposition 3.2 below). Compute

  $$\begin{aligned} x^{k+1}=P_C(x^k -\sigma _k g^k). \end{aligned}$$

  (6)

If $x^{k+1}=x^k$ then stop: $x^k$ is a solution, else set $k:=k+1$.

Remark 1

• (i) The existence of solution for (3) can be guaranteed under the assumption that the function $f(x^k,.)$ is lower semicontinuous and $2-$weakly coercive (see [21]), i.e.,

  $$\begin{aligned} \liminf _{\Vert y \Vert \rightarrow +\infty } \frac{f(x^k,y)}{\Vert y\Vert ^2} \ge 0. \end{aligned}$$

  If C is bounded, the $2-$weakly coercivity assumption can be dropped. If f(x, .) is strongly quasiconvex on C, then it is $2-$weakly coercive (see [17] Lemma 2).

• (ii) The subproblem (3) may have more than one solution even in the case the function $f(x^k,.)$ is strongly quasiconvex. The uniqueness of the solution for this problem can be guaranteed under the assumption that $f(x^k,.)+\frac{1}{2\rho _k}\Vert x^k-.\Vert ^2$ is strongly quasiconvex (see [23]).

• (iii) The proximal operator has not only been extensively studied in the convex case but also in the nonconvex case (see [21, 32, 33]). This operator plays an important role in many algorithms (for example in [20, 32, 34]) for nonconvex and nonsmooth problems. Recently, in [23], the proximal point method for minimizing a strongly quasiconvex function has been implemented. When f is quasiconvex rather convex on C, problem (3), in general is not convex, even not quasiconvex. In general, it is not easy to solve this global optimization problem. However, in some special cases (see examples below) one can choose reqularization parameter $\rho _k$ such that problem (3) is strongly convex, and therefore it is uniquely solvable. In the paper [20], Attouch et al have developed an algorithm based upon the proximal method for solving a mixed equilibrium problem, when the subprogram defining the iterate $x^{k+1}$ at iteration k is the one that is the same as problem of type (3).

Example 1

Now we consider an example ([33]) in which the optimization problem (3) can be solved efficiently. Suppose that bifunction $f(x,y):= \max _{i\in I}g_i(x,y)$, where $I \subset \mathbb {R}$ is compact, and each $g_i(x,.)$ is quasiconvex on C for every fixed $x\in C$. Then f(x, .) is quasiconvex. Suppose that each $g_i(x,.)$ ($i\in I)$ is differentiable and its derivative is Lipschitz with constant $L_i(x)>0.$ Let $\rho <\frac{1}{L(x)}$ with $L(x):= \max _{i\in I}L_i(x)$ and

$$\begin{aligned} f_\rho (x,y):= f(x,y) +\frac{1}{2\rho }\Vert y-x\Vert ^2. \end{aligned}$$

Then $f_\rho (x,.)$ is strongly convex on C. Indeed, for any $u,v\in C$ and $i\in I$, consider the function $g_{i,\rho }(x,y):= g_i(x,y) +\frac{1}{2\rho }\Vert y-x\Vert ^2$. Then we have

$$\begin{aligned}{} & {} \langle \nabla _2 g_{i, \rho }(x,u) -\nabla _2 g_{i,\rho }(x,v),u-v\rangle \\{} & {} \quad = \langle \nabla _2 g_i(x,u) +\frac{1}{\rho } (u-x) -\nabla _2 g_i(x,v) - \frac{1}{\rho } (v-x),u-v\rangle \\{} & {} \quad \ge -L(x)\Vert u-v\Vert ^2 +\frac{1}{\rho }\Vert u-v\Vert ^2 = (\frac{1}{\rho }- L(x))\Vert u-v\Vert ^2. \end{aligned}$$

Hence $f_\rho (x,.)$ is strongly convex whenever $\rho <\frac{1}{L(x)}$. The above example belongs to the class of the lower -$C^2$ functions considered by some authors see e.g. [35,36,37].

In contrast to the convex case, in the algorithm, $y^k = x^k$ does not necessarily imply that $x^k$ is a solution. But, part (i) of the following proposition shows that it is a solution restricted to a part of C, while in the rest part it is only a stationary point.

Proposition 1

Assume that f(x, .) is semi-strictly quasiconvex on C for any $x\in C$ and $y^k=x^k$.

• (i) If $x^k$ is not a solution of (EP), that means

  $$\begin{aligned} \Omega (x^k):=\left\{ y\in C: f(x^k,y) <0\right\} . \end{aligned}$$

  is nonemty, then for any $y\in \Omega (x^k)$

  $$\begin{aligned} f'_{x^k}(x^k,y-x^k)=0, \end{aligned}$$

  where $f_{x^k}:= f(x^k,.)$.

• (ii) If $f(x^k,.)$ is pseudoconvex on C or strongly quasiconvex on C, then $x^k$ is a solution of (EP).

Proof

• (i) For $y\in \Omega (x^k)$, set $d=y-x^k$. For $\lambda \in \left( 0,1\right)$, set $y_{\lambda }= x^k +\lambda d = \lambda y +(1-\lambda )x^k$. Since $f(x^k,x^k) = 0$, by the semi-strictly quasiconvexity of $f(x^k,.)$, we have

  $$\begin{aligned} f(x^k, y_{\lambda })< 0. \end{aligned}$$

  So,

  $$\begin{aligned} \frac{f(x^k,x^k+\lambda d) -f(x^k,x^k)}{\lambda }<0. \end{aligned}$$

  (7)

  From

  $$\begin{aligned} x^k = y^k\in \text {argmin}\{ f(x^k,y) + \frac{1}{2\rho _k}\Vert y-x^k\Vert ^2: y\in C\}, \end{aligned}$$

  it follows that for any $y\in C$,

  $$\begin{aligned} f(x^k,y) +\frac{1}{2\rho _k} \Vert y -x^k\Vert ^2\ge 0. \end{aligned}$$

  Let $y=y_{\lambda }$, then

  $$\begin{aligned} f(x^k,y_{\lambda }) +\frac{1}{2\rho _k} \lambda ^2 \Vert y- x^k\Vert ^2\ge 0. \end{aligned}$$

  Therefore,

  $$\begin{aligned} \frac{f(x^k,x^k+\lambda d) -f(x^k,x^k)}{\lambda }\ge -\lambda \frac{1}{2\rho _k}\Vert d\Vert ^2. \end{aligned}$$

  (8)

  By combining (7), (8) and letting $\lambda \rightarrow 0^+$, we obtain $f'_{x^k}(x^k,d)=0.$

• (ii) Assume that $f(x^k,.)$ is pseudoconvex on C, then $f(x^k,.)$ is differentiable on an open set containing C and for any $y,y'\in C$, we have

  $$\begin{aligned} \nabla _2 f(x^k,y)(y'-y) \ge 0 \Rightarrow f(x^k,y') \ge f(x^k,y). \end{aligned}$$

  From $x^k=y^k$, it implies from part (i) that $\langle \nabla _2f(x^k,x^k),y-x^k \rangle \ge 0$ for every $y\in C$. Therefore, $f(x^k,y) \ge 0$ for $y\in C$. Now, we consider the case where $f(x^k,.)$ is strongly quasiconvex with modulus $\gamma >0$. Since $x^k =y^k$ with $y^k$ being the solution of subproblem (3), we have

  $$\begin{aligned} 0 \le f(x^k, y) + \frac{1}{2\rho _k} \Vert y-x^k\Vert ^2 \quad \forall y\in C. \end{aligned}$$

  (9)

  Let $y:= \lambda x + (1- \lambda )x^k$ with any $x\in C$ and $\lambda \in [ 0, 1]$. Then applying (9), by the strong quasiconvexity of $f(x^k,.)$, we obtain

  $$\begin{aligned}{} & {} 0\le f(x^k, \lambda x + (1- \lambda )x^k)+ \frac{1}{2\rho _k}\Vert \lambda x + (1- \lambda )x^k - x^k\Vert ^2 \\{} & {} \quad \le \max \{f(x^k,x^k), f(x^k,x) \} -\lambda (1-\lambda )\frac{\gamma }{2}\Vert x-x^k\Vert ^2 +\frac{1}{2\rho _k}\Vert \lambda x + (1- \lambda )x^k-x^k\Vert ^2. \end{aligned}$$

  Thus for any $\lambda \in [0,1]$ we have

  $$\begin{aligned} 0\le \max \{f(x^k,x),0\}+\Big [ \frac{\lambda ^2}{2\rho _k} - \gamma \frac{\lambda (1-\lambda )}{2} \Big ] \Vert x-x^k\Vert ^2\ \forall x\in C. \end{aligned}$$

  (10)

  The right hand side of (10) is a quadratic function on $\lambda$. At $\lambda =0$, this function takes value 0 and its derivative is negative, therefore

  $$\begin{aligned} 0<\max \{f(x^k,x),0\} \quad \forall x\in C. \end{aligned}$$

  Hence $f(x^k,x) > 0$ for every $x\in C$.

Proposition 2

Assume that f(., y) is continuous on C for any $y\in C$. If $y^k \not =x^k$ then the following statements hold:

• (i) There exists a positive integer m satisfying (4).

• (ii) If f(x, .) is semi-strictly quasiconvex on C for any $x\in C$, then $f(z^k,x^k) >0$.

• (iii) $0\not \in \partial ^*_2 f(z^k,x^k)$.

Proof

• (i) If there does not exist m satisfying (4), then for every positive integer m, we have

  $$\begin{aligned} f(z^{k,m},x^k) -f(z^{k,m},y^k) < \frac{\alpha }{2\rho _k}\Vert y^k-x^k\Vert ^2. \end{aligned}$$

  (11)

  Let $m \rightarrow +\infty$, we have $z^{k,m} \rightarrow x^k$ and (11) becomes

  $$\begin{aligned} -f(x^k,y^k) \le \frac{\alpha }{2\rho _k} \Vert y^k-x^k\Vert ^2. \end{aligned}$$

  (12)

  On the other hand, (3) means that for all $y\in C$,

  $$\begin{aligned} f(x^k,y^k) +\frac{1}{2\rho _k} \Vert y^k-x^k\Vert ^2 \le f(x^k,y) +\frac{1}{2\rho _k} \Vert y-x^k\Vert ^2. \end{aligned}$$

  By choosing $y=x^k$, we obtain

  $$\begin{aligned} f(x^k,y^k) +\frac{1}{2\rho _k} \Vert y^k-x^k\Vert ^2 \le 0. \end{aligned}$$

  (13)

  Combining (12) with (13), it follows that $\alpha \ge 1$. This is a contradiction because $\alpha \in \left( 0,1\right)$.

• (ii) From (4), $f(z^k,x^k)>f(z^k,y^k)$. By the semi-strictly quasiconvexity of $f(z^k,.)$ on C, it follows

  $$\begin{aligned} 0=f(z^k,z^k)< f(z^k,x^k). \end{aligned}$$

• (iii) It follows from part (ii) that

  $$\begin{aligned} 0=f(z^k,z^k)< f(z^k,x^k). \end{aligned}$$

  By the definition of $\partial ^*_2f(z^k,x^k)$, it is clear that $0\not \in \partial ^*_2f(z^k,x^k)$.

Proposition 3

If $x^{k+1}=x^k$ then $z^k$ is a solution of (EP) provided f(x, .) is semi-strictly quasiconvex on C for any $x\in C$.

Proof

By the algorithm, $x^{k+1}=x^k$ means that $x^k=P_C(x^k-\sigma _k g^k),$ which is equivalent to

$$\begin{aligned} \langle g^k, y-x^k\rangle \ge 0 \quad \forall y\in C. \end{aligned}$$

(14)

Remember that, by (5),

$$\begin{aligned} g^k \in \partial ^*_2f(z^k,x^k):=\left\{ g\in \mathbb {R}^n: \langle g, y-x^k \rangle<0 \text { if } f(z^k,y)< f(z^k,x^k)\right\} . \end{aligned}$$

Thus, by (14), $f(z^k,y) \ge f(z^k,x^k)$ for $y\in C$.

Note that, in part (ii) of Proposition 2, we have proved that if $x^k\not =y^k$, then $f(z^k,x^k )>0$. So, we can conclude that $f(z^k,y) \ge f(z^k,x^k) \ge 0$ for every $y\in C$, which means that $z^k$ is a solution of (EP).

Proposition 4

Suppose that f(x, .) is semi-strictly quasiconvex for any $x\in C$ and the solution-set $S_d$ of the Minty problem is nonempty. Let $z^* \in S_d$, then

$$\begin{aligned} \Vert x^{k+1}-z^*\Vert ^2 \le \Vert x^k-z^*\Vert ^2 +\sigma _k^2, \end{aligned}$$

(15)

and

$$\begin{aligned} \liminf _{k \rightarrow +\infty } \langle g^k, x^k -z^*\rangle =0. \end{aligned}$$

(16)

Proof

For $y\in C$, we have

$$\begin{aligned} \Vert x^{k+1} -y\Vert ^2= & {} \Vert P_C(x^k -\sigma _k g^k)-y\Vert ^2\\\le & {} \Vert x^k -\sigma _k g^k -y\Vert ^2\\\le & {} \Vert x^k -y\Vert ^2 +\sigma _k^2 + 2\sigma _k \langle g^k, y- x^k \rangle . \end{aligned}$$

With $y=z^*\in S_d$, we have

$$\begin{aligned} \Vert x^{k+1} -z^*\Vert ^2 \le \Vert x^k -z^*\Vert ^2 +\sigma _k^2 + 2\sigma _k \langle g^k, z^*- x^k \rangle . \end{aligned}$$

(17)

Since $f(z^k,z^*)\le 0< f(z^k,x^k)$ and $g^k \in \partial ^*_2f(z^k,x^k)$, it follows that

$$\begin{aligned} \langle g^k, z^*-x^k \rangle <0. \end{aligned}$$

Therefore,

$$\begin{aligned} \Vert x^{k+1}-z^*\Vert ^2 < \Vert x^k-z^*\Vert ^2 +\sigma _k^2. \end{aligned}$$

From (17), for any k, it holds that

$$\begin{aligned} \sigma _k\langle g^k, x^k-z^*\rangle \le \Vert x^k-z^*\Vert ^2-\Vert x^{k+1}-z^*\Vert ^2 +\sigma _k^2. \end{aligned}$$

By summing up over k, we obtain

$$\begin{aligned} \sum _{k=0}^{+\infty }\sigma _k\langle g^k, x^k-z^*\rangle \le \Vert x^0-z^*\Vert +\sum _{k=0}^{+\infty }\sigma _k^2. \end{aligned}$$

Note that $\sum _{k=0}^{+\infty }\sigma _k^2<+\infty$, $\sum _{k=0}^{+\infty }\sigma _k=+\infty$ and $\langle g^k, z^*-x^k \rangle <0$, hence

$$\begin{aligned} \liminf _{k \rightarrow +\infty } \langle g^k, x^k -z^*\rangle =0. \end{aligned}$$

Following [38] we say that a point $x \in C$ is $\rho$- quasi-solution (prox-solution) to Problem (EP) if $f(x,y)+\frac{1}{2\rho }\Vert y- x\Vert ^2 \ge 0$ for every $y\in C$.

For the convergence of the proposed algorithm we need the following assumptions.

• (A0) f is continuous jointly in both variables on an open set containing $C\times C$;

• (A1) f(x, .) is semistrictly quasiconvex on C for every $x\in C$;

• (A2) the solution-set $S_d$ of the Minty problem is nonempty;

• (A3) The sequence $\{y^k\}$ is bounded.

Theorem 1

Suppose that the algorithm does not terminate. Let $\{x^k\}$ be the infinite sequence generated by the algorithm. Under the assumptions (A0),(A1),(A2),(A3), there exists a subsequence of $\{x^k\}$ converging to a $\overline{\rho }$- quasi solution $\overline{x}$. If in addition, f(x, .) is strongly quasiconvex for every $x\in C$, then $\{x^k\}$ converges to the unique solution of (EP).

Proof of Theorem 1

Let $z^* \in S_d$. By part (i) Proposition 4 and $\sum _{k=1}^{+\infty } \sigma ^2_k<+\infty$, the sequence $\{\Vert x^k-z^*\Vert ^2\}$ is convergent by Lemma 1. Hence, $\{x^k\}$ is bounded.

Let $\{x^{k_j}\}$ be a subsequence of $\{x^k\}$ such that $x^{k_j}$ converges to some point $\overline{x}$ and

$$\begin{aligned} \lim _{j \rightarrow +\infty } \langle g^{k_j}, x^{k_j}-z^*\rangle =\liminf _{k \rightarrow +\infty } \langle g^k, x^k -z^*\rangle =0. \end{aligned}$$

(18)

Since the sequence $\{y^{k_j}\}_j$ is bounded. $\{z^{k_j}\}_j$ is bounded too. By taking subsequences if necessary, without loss of generality, we can assume that ${y^{k_j}}$ converges to $\overline{y}$ and ${z^{k_j}}$ converges to $\overline{z}$.

Step 1: We will prove that

$$\begin{aligned} f(\overline{z}, \overline{x})= 0. \end{aligned}$$

(19)

Indeed, from part (ii) Proposition 2, $f(z^k,x^k)>0$. In addition, by Assumption (A0), f(., .) is continuous on $C\times C$, we have

$$\begin{aligned} f(\overline{z}, \overline{x})= \lim _{j \rightarrow +\infty } f(z^{k_j},x^{k_j})\ge 0. \end{aligned}$$

Now, assume that $f(\overline{z}, \overline{x})=\epsilon >0$. Then there exists $j_0$ such that $f(z^{k_j},x^{k_j})>\frac{\epsilon }{2}$ for all $j\ge j_0$.

Since $z^*\in S_d$, we have $f(\overline{z}, z^*)\le 0$. Again by (A0), there exist $\epsilon _1, \epsilon _2 >0$ such that for all $z\in B(\overline{z}, \epsilon _1)$, $z'\in B(z^*,\epsilon _2)$:

$$\begin{aligned} f(z,z') <\frac{\epsilon }{2}. \end{aligned}$$

Since $\{z^{k_j}\}$ converges to $\overline{z}$, there exists $j_1$ such that for any $j\ge j_1$ we have $z^{k_j} \in B(\overline{z}, \epsilon _1)$, from which it follows that for $j \ge \max (j_0,j_1)$, and $z'\in B(z^*,\epsilon _2)$, we have

$$\begin{aligned} f(z^{k_j}, z') < f(z^{k_j},x^{k_j}). \end{aligned}$$

By taking $z'=z^*+\epsilon _2 g^{k_j}$ and thanks to (5), we have for $j \ge \max (j_0,j_1)$,

$$\begin{aligned} \langle g^{k_j}, x^{k_j} -z^* \rangle >\epsilon _2, \end{aligned}$$

which contradicts (18). Thus $f(\overline{z}, \overline{x})=0$.

Step 2: We prove that

$$\lim _{j\rightarrow +\infty }\Vert x^{k_j} -y^{k_j}\Vert =0.$$

From (4), we know that for any k

$$\begin{aligned} f(z^k,x^k) >f(z^k,y^k). \end{aligned}$$

So, $f(\overline{z}, \overline{y})\le f(\overline{z}, \overline{x})=0$ (by Step 1).

Let $\theta _j=\theta ^{m_j}$ such that $z^{k_j}= (1-\theta _j)x^{k_j}+\theta _j y^{k_j}$. Clearly, $0<\theta \le \theta _j<1$. Therefore, $\overline{z}$ is a convex combination of $\overline{x}$ and $\overline{y}$ and $\overline{z}\not = \overline{x}$.

Now if $f(\overline{z}, \overline{y})<0$, then $\overline{z}\not = \overline{y}$. By the semi-strictly quasiconvexity of $f(\overline{z},.)$, we have

$$\begin{aligned} 0=f(\overline{z}, \overline{z})< f(\overline{z}, \overline{x}), \end{aligned}$$

which is impossible. It implies that

$$\begin{aligned} f(\overline{z}, \overline{y})=0. \end{aligned}$$

From (4),

$$\begin{aligned} f(z^{k_j},x^{k_j}) -f(z^{k_j},y^{k_j}) \ge \alpha \rho _{k_j} \Vert y^{k_j}-x^{k_j}\Vert ^2. \end{aligned}$$

(20)

Let $j \rightarrow +\infty$, and note that $\lim _{k \rightarrow +\infty } \rho _k=\overline{\rho }>0$, we obtain

$$\begin{aligned} \lim _{j\rightarrow +\infty }\Vert x^{k_j} -y^{k_j}\Vert =0. \end{aligned}$$

This means $\overline{x}=\overline{y}$. Note that

$$\begin{aligned} y^{k_j} \in \text {argmin}_{y\in C} \left\{ f(x^{k_j},y) +\frac{1}{2\rho _{k_j}} \Vert x^{k_j}-y\Vert ^2\right\} . \end{aligned}$$

then for any $y\in C$, we have

$$\begin{aligned} f(x^{k_j},y^{k_j}) +\frac{1}{2\rho _{k_j} }\Vert x^{k_j}-y^{k_j}\Vert ^2\le f(x^{k_j},y) + \frac{1}{2\rho _{k_j}} \Vert x^{k_j}-y\Vert ^2. \end{aligned}$$

Let $j \rightarrow +\infty$, by the continuity of f and $\overline{x}=\overline{y}$, we obtain for any $y\in C$,

$$\begin{aligned} 0\le f(\overline{x},y) +\frac{1}{2\overline{\rho } }\Vert \overline{x}-y\Vert ^2. \end{aligned}$$

(21)

Assume, in addition, that f(x, .) is strongly quasiconvex on C with modulus $\gamma >0$. For any $x\in C$ and $\lambda \in [0,1]$, take $y=\lambda x + (1-\lambda ) \overline{x}$. By replacing it to (21) we obtain

$$\begin{aligned} 0\le f(\overline{x}, \lambda x+(1-\lambda ) \overline{x}) +\frac{1}{2\overline{\rho } }\Vert \overline{x}-(\lambda x+(1-\lambda ) \overline{x}\Vert ^2. \end{aligned}$$

Then using the definition of strong quasiconvexity, by the same argument as in the proof of part (ii) in Proposition 3.1, we can see that $f(\overline{x}, x) \ge 0$ for every $x\in C$.

Let

$$\begin{aligned} S_{\overline{\rho }}:= \{\overline{x}\in C: \quad f(\overline{x},y)+\frac{1}{2\overline{\rho }}\Vert \overline{x}-y\Vert ^2 \ge 0 \quad \forall y\in C\}. \end{aligned}$$

Remark 2

(i) In virtue of Lemma 2 we have $S_d\subseteq S$. Thus, if $S_{\overline{\rho }}=S_d$, then $\overline{x} \in S_d =S$. Remember that the sequence $\{\Vert x^k -\overline{x}\Vert ^2\}$ is convergent we can conclude that the whole sequence $\{x^k\}$ converges to $\overline{x}$ which is a solution of (EP).

(ii) Since for any $\overline{\rho }$, one can choose a sequence $\{\rho _k\}$ such that $\rho _k \rightarrow \overline{\rho }$. Thus, from $f(\overline{x},y) +\overline{\rho } \Vert \overline{x}-y\Vert ^2 \ge 0 \ \forall y\in C$, it can be seen that for any $\epsilon >0$, there exists $\overline{\rho } > 0$ small enough such that $f(\overline{x},y) \ge -\epsilon$ provided C is bounded. So one can consider $\overline{x}$ as an approximate solution.

In the case f is pseudomonotone, then by Lemma 2$S=S_d$. Clearly, $S\subseteq S_{\rho }$ for every $\rho > 0$. In addition, if f(x, .) is pseudoconvex and continuously differentiable for any $x\in C$, then $S = S_{\rho }$ for every $\rho >0$. Hence $\overline{x}$ is a solution.

(iii) Clearly, Assumption (A3) may be dropped if C is bounded (often in practice), moreover, one can see that this assumption is not needed if the optimization problem (3) admits a unique solution for every k.

The boundedness of $\{y^k\}$ can also be ensured under the following assumption:

(A3’) For any closed and bounded set $\Omega \subseteq C$, there exists a real number $\rho _0>0$ such that the function $f(x,y)+ \frac{\rho _0}{2}\Vert x-y\Vert ^2$ is bounded from below on $\Omega \times C$. That means there exists a real number c such that for any $x\in \Omega , y\in C$, one has

$$\begin{aligned} f(x,y)+ \frac{\rho _0}{2}\Vert x-y\Vert ^2 \ge c. \end{aligned}$$

Under Assumption (A3’), by choosing the sequence $\rho _k$ that converges to $\overline{\rho }>\rho _0$, one can ensure that $\{y^k\}$ is bounded. Indeed, if the sequence $\{y^k\}$ is unbounded, then there exists a subsequence $\{y^{k_j}\}$ of $\{y^k\}$ such that $\lim _{j \rightarrow +\infty } \Vert y^{k_j}\Vert =+\infty$. Since $\{x^k\}$ is bounded, there exists a closed and bounded set $\Omega \subseteq C$ such that $\{x^k\}\subset \Omega$. By assumption (A3’), there exists numbers $\rho _0>0$ and c such that for any $k\in \mathbb {N}$ and $y\in C$,

$$\begin{aligned} f(x^k,y)+ \frac{\rho _0}{2}\Vert x^k-y\Vert ^2 \ge c, \end{aligned}$$

with implies that, for any k,

$$\begin{aligned} f(x^k, y^k) +\frac{\rho _k}{2}\Vert x^k-y^k\Vert ^2 \ge c+\frac{\rho _k -\rho _0}{2} \Vert x^k-y^k\Vert ^2. \end{aligned}$$

Since $y^k$ is a solution of (3), we obtain

$$\begin{aligned} f(x^k, y^k) +\frac{\rho _k}{2}\Vert x^k-y^k\Vert ^2 \le f(x^k,x^k)=0. \end{aligned}$$

On the other hand, since $\{x^{k_j}\}$ is bounded and $\lim _{j \rightarrow +\infty } \Vert y^{k_j}\Vert =+\infty$, we have

$$\begin{aligned} \lim _{j\rightarrow +\infty } \big (c+\frac{\rho _k -\rho _0}{2} \Vert x^{k_j}-y^{k_j}\Vert ^2\big ) =+\infty , \end{aligned}$$

which leads to a contradiction.

The idea of Condition (A3’) comes from the prox-bounded property which is widely used to study the proximal mapping (see e.g. [13,32]). In the case of optimization when the bifunction f takes the form $f(x,y)=h(y)-h(x)$ with h being continuous on C, Condition (A3’) is ensured under the prox-boundedness of h on C.

This condition is also satisfied when f(x, .) is convex and its diagonal subdifferential $\partial _2 f(x,x)$ is bounded on any bounded set. It is worth to note that this assumption has been usually used in the field of equilibria.

The following simple example shows that a $\rho$- quasi-solution with any $\rho > 0$ may not be a solution.

Example 2

Let $C:= [-1, 0]$, $f(x,y):= y^3 -x^3$, Clearly, with $x^* =0$, we have $f(x^*,y) + \frac{1}{2\rho }(y-x^*)^2 = y^3 +\frac{1}{2\rho }y^2 \ge 0, \ \forall y\in C$ if $\rho >0$ small enough, for example $\rho < 1/2$. Thus, 0 is $\rho$- prox-solution, but $f(x^*,y) = y^3 < 0$ with $y=-1\in C$. So the auxiliary problem principle fails to appy to semi-strictly quasiconvex equilibrium problems.

4 Numerical experiments

We present here two examples to illustrate the behavior of our linesearch extragradient algorithm (for short LEQEP) for quasiconvex equilibrium problems. The algorithm is implemeted in Python 3 running on a Laptop with AMD Ryzen 7 5800 H with Radeon Graphics 3.20 GHz and 8GB RAM memory.

Example 3

We consider the following 1-dim strongly quasiconvex equilibrium problem ([17, Example 4.2])

$$\begin{aligned} C=\left[ 0, \delta \right] ;\\ f(x,y)=\sqrt{y}-\sqrt{x} +r x(y-x); \end{aligned}$$

where $\alpha , \delta >0$. It is easy to see that the solution set is $S=\{0\}.$

We test LEQEP on this example with $r= 2$ and $\delta =10$. We take $x^0=5$, $\rho =1$, $\alpha =0.5$, $\theta =0.5$ and stop the algorithm if $|x^k -y^k| <10^{-3}$ or $|x^{k+1}-x^{k}|<10^{-3}$. Our algorithm reach the unique solution $x^*=0$ after 84 iterations if we choose $\sigma _k=\frac{1}{k+1}$ and 8 iterations if we choose $\sigma _k=\frac{2}{k+1}$. Figure 1 illustrates the behavior of LEQEP for this example.

Fig. 1

Behavior of LEQEP in Example 3

Fig. 2

Behavior of LEQEP in Example 4 for $m=n=2$

Fig. 3

Behavior of LEQEP in Example 4 for $m=n=10$

Example 4

We consider the bifunction

$$\begin{aligned} f(x,y)=\max \{f_1(x,y),f_2(x,y)\}, \end{aligned}$$

where

$$\begin{aligned}{} & {} f_1(x,y)=\langle A_1x+b_1, \frac{E_1y+f_1}{c_1^Ty+d_1}- \frac{E_1x+e_1}{c_1^Tx+d_1}\rangle ,\\{} & {} f_2(x,y)=\langle A_2x+b_2, \frac{E_2y+f_2}{c_2^Ty+d_2}- \frac{E_2x+e2}{c_2^Tx+d_2}\rangle , \end{aligned}$$

with $A_1,A_2,E_1,E_2 \in \mathbb {R}^{m\times n}$, $b_1,b_2,e_1,e_2\in \mathbb {R}^m$, $c_1,c_2\in \mathbb {R}^n$ and $d_1,d_2 \in \mathbb {R}$. We also assume that

$$\begin{aligned} C\subset \{x: c_1^Tx+d_1>0\}\cap \{x: c_2^Tx+d_2>0\}. \end{aligned}$$

In this example, we test our algorithm with $m=n=2$ and 5, 10, 20, 50. In the first experiment, we take $m=n=2$ and

$$\begin{aligned}{} & {} A_1=A_2=I_2, \quad b_1=b_2 =0_2,\\{} & {} E_1=I_2, \quad e_1=1_2,\quad c_1=0_2,\quad d_1=1,\\{} & {} E_2=\begin{bmatrix} 1&{}2\\ 3&{}4 \end{bmatrix}, \quad e_2=c_2=1_2, \quad d_2=2,\\{} & {} C=\left[ 0,5\right] ^2. \end{aligned}$$

For any $x\in C$, the functions $f_1(x,.)$ and $f_2(x,.)$ are linear fractional functions and therefore strictly quasiconvex on C (see [26, Lemma 4]). Consequently, f(x, .) is strictly quasiconvex on C for any $x\in C$. We test LEQEP on this example with $x^0=\begin{bmatrix} 5&5 \end{bmatrix}^T$, $\rho =1$, $\alpha =0.5$, $\theta =0.8$ and stop the algorithm if $\Vert x^k -y^k\Vert <10^{-5}$ or $\Vert x^{k+1}-x^{k}\Vert <10^{-5}$. Our algorithm reach an approximate solution of $x^*=\begin{bmatrix}0&0 \end{bmatrix}^T$ after 129 iterations if we take $\sigma _k=\frac{1}{k+1}$ and after 13 iterations if we take $\sigma _k=\frac{3}{2(k+1)}$. Figure 2 illustrates the behavior of LEQEP in this example.

In the second experiment, we take $m=n=10$ and

$$\begin{aligned}{} & {} A_1=A_2=I_{10}, \quad b_1=b_2 =0_{10},\\{} & {} E_1=I_{10}, \quad f_1=1_{10},\quad c_1=0_{10},\quad d_1=1,\\{} & {} E_2=\begin{bmatrix} 4 &{}4 &{}2&{} 4&{} 2&{} 2&{} 3&{} 2&{} 1&{} 2\\ 1&{} 3&{} 0&{} 3&{} 0&{} 1&{} 1&{} 0&{} 2&{} 2\\ 2&{} 3&{} 0 &{} 2&{} 2&{} 2&{} 1&{} 1&{} 2&{} 2\\ 3&{} 2&{} 3&{} 0&{} 1&{} 1&{} 2&{} 4&{} 1&{} 1\\ 1&{} 4&{} 3&{} 0&{} 2&{} 1&{} 4&{} 3&{} 0&{} 3\\ 0&{} 4&{} 1&{} 4&{} 2&{} 3&{} 4&{} 3&{} 4&{} 2\\ 3&{} 0&{} 4&{} 4&{} 0&{} 4&{} 1&{} 1&{} 1&{} 2\\ 1&{} 2&{} 2&{} 3&{} 1&{} 0&{} 3&{} 0&{} 0&{} 0\\ 2&{} 0&{} 0&{} 3&{} 0&{} 3&{} 3&{} 4&{} 4&{} 2\\ 0&{} 2&{} 4&{} 4&{} 0&{} 4&{} 3&{} 0&{} 3&{} 1 \end{bmatrix}, \quad f_2=c_2=1_{10}, \quad d_2=2,\\{} & {} C=\left[ 0,5\right] ^2. \end{aligned}$$

We test LEQEP on this example with $x^0=5*1_{10}$, $\rho =1$, $\alpha =0.5$, $\theta =0.8$ and stop the algorithm if $\Vert x^k -y^k\Vert <10^{-5}$ or $\Vert x^{k+1}-x^{k}\Vert <10^{-5}$. Figure 3 illustrates the behavior of LEQEP in this example.

In the last experiment, each entry of the matrices $A_1,A_2,E_1,E_2$, vectors $b_1,b_2$, $c_1,c_2$, $f_1,f_2$ and number $d_1,d_2$ is randomly generated in the interval $\left[ 0,5\right]$. We test LEQEP for $m=n= 5,10,20,50$, $x^0=5*1_{n}$, $\rho =1$, $\alpha =0.5$, $\theta =0.8$ and stop the algorithm if $\Vert x^k -y^k\Vert <10^{-8}$ or $\Vert x^{k+1}-x^{k}\Vert <10^{-8}$ or the number of iterations exceed 1000. The average time and average error $\min (\Vert x^k-y^k\Vert , \Vert x^k -x^{k+1}\Vert )$ for each size are reported in Table 1 with different sizes, a hundred of problems have been tested for each size.

Table 1 Algorithm with $\alpha _k=\frac{n}{k+1}$

We also record the average errors of $\Vert x^k-y^k\Vert$ and $\Vert x^k -x^{k+1}\Vert$ in the first 1000 iterations in Fig. 4.

Fig. 4

Behavior of LEQEP for random input

5 Conclusion

We have proposed an extragradient linesearch algorithm for approximating a solution of equilibrium problems with quasiconvex bifunctions. The sequence of the iterates generated by the proposed algorithm converges to a proximal-solution when the bifunction is semi-strictly quasiconvex with respect to its second variable, which is an equilibrium solution provided the bifunction is strongly quasiconvex. Neither monotonicity nor Lischitz properties are required. From an efficient point of view, this algorithm needs an efficient algorithm for the typical problem of type (3).