A class of infeasible proximal bundle methods for nonsmooth nonconvex multi-objective optimization problems

Abstract

We propose a class of infeasible proximal bundle methods for solving nonsmooth nonconvex multi-objective optimization problems. The proposed algorithms have no requirements on the feasibility of the initial points. In the algorithms, the multi-objective functions are handled directly without any scalarization procedure. To speed up the convergence of the infeasible algorithm, an acceleration technique, i.e., the penalty skill, is applied into the algorithm. The strategies are introduced to adjust the proximal parameters and penalty parameters. Under some wild assumptions, the sequence generated by infeasible proximal bundle methods converges to the globally Pareto solution of multi-objective optimization problems. Numerical results shows the good performance of the proposed algorithms.

1 Introduction

In this paper we seek to solve the nonsmooth nonconvex multi-objective optimization problem:

$$\begin{aligned} \text{(MOP) }\qquad \qquad \begin{array}{ll} \min &{} F(x):=(f_1(x),\ldots ,f_p(x))\\ \mathrm{s.\ t.} &{} c(x)\le 0, \end{array} \end{aligned}$$

where the objective functions $f_i: R^n\rightarrow R, i=1,2,\ldots ,p$ and the constraint function $c: R^n\rightarrow R$ are locally Lipschitz continuous. Without loss of generality, we consider only one constraint function in (MOP). When dealing with multiple inequality constraints, one can utilize the maximum function to transform these finite constraints into one constraint.

The multi-objective optimization problem is to optimize several conflicting objectives at the same time, which has arisen in many real-life applications of finance, engineering, transportation, or mechanics, see [1, 4, 18, 21, 23] etc. Since these multiple objectives are conflict, the optimal solution in single objective optimization problems is not suitable for multi-objective optimization problems. The Pareto(efficient) solution of multi-objective optimization problems is proposed. The Pareto solution means that there does not exist another solution whose objective function value is the same or smaller than that of the Pareto solution, and at least one objective function value is strictly smaller. There are many Pareto solutions for multi-objective optimization problems. The set of all Pareto solutions is usually called the Pareto set and its corresponding multi-objective function value is called the Pareto frontier.

The theoretical research on multi-objective programming has achieved abundant results [24,25,26, 32], including various optimality conditions and stability results. The research on the numerical algorithms of multi-objective programming is relatively little. There are two main types of algorithms for solving multi-objective programming. One classical algorithm is based on the scalarization strategy [2, 3], which is to transform the multi-objective programming into its equivalent single-objective programming. This scalarization strategy has great influence on the efficiency of the algorithm and the convergence of the algorithm depends on the scalarization skill. The other kind of algorithms is to solve the multi-objective programming directly, without any scalarizations, see [6, 14, 19, 29]. This kind of multi-objective algorithms has its own special advantages and it can use all the information of the functions, which does not depend on any scalarization technologies.

It is universally acknowledged that the bundle method is a highly reliable and effective method for solving nonsmooth nonconvex optimization problems [7,8,9,10, 31]. In recent years, bundle methods are applied into various types of optimization problems, such as infinite programs [12, 27], control optimization problems [30], equilibrium problems [17, 22]. With the development of multi-objective optimization, the bundle methods are applied into solving nonsmooth multi-objective programs, refer to [13, 20]. However, the existing algorithms for solving nonsmooth multiobjective programming still have some limitations. The proximal bundle method proposed in [14] has the requirements on the feasibility of initial points, which makes great impact on the convergence of the algorithm. Obtaining a feasible initial point is very difficult because that finding a feasible initial point of multi-objective programming is almost the same as that of solving the whole problem. The paper [29] used the cutting-plane method to solve the multi-objective programming. The proposed auxiliary problem in [29], which adds the multi-objective functions to the constraint. The increasing number of constraints brings the result that the constraint qualification of the original problem may be hardly to satisfy, and it increases the difficulty of solving the subproblem of the cutting-plane model.

The aim of this paper is to utilize the proximal bundle method to seek Pareto solutions of multiobjective optimization problems. The multiple objective functions are handled individually without any scalarization procedure. By virtue of improvement functions and the bundle of information, we construct the subproblem of the multi-objective optimization problem. What difference from other existed multi-objective algorithms is that, in this paper, the proposed algorithm has no requirement on the feasibility of initial points, which means that the starting point is arbitrary and it may be infeasible. To further increase the convergent speed of the algorithm, an acceleration procedure is proposed, which is the penalty procedure. Some strategies are also put forward to adjust the penalty parameters. Under the wild assumptions, the sequence generated by penalized infeasible proximal bundle methods globally converges to the Pareto solution of multi-objective optimization problems.

The remainder of the paper is organized as follows. Section 2 gives some preliminaries about nonsmooth optimization and multiobjective optimization. Section 3 gives the infeasible proximal bundle method and the penalized infeasible proximal bundle method, moreover, the corresponding convergence results are provided. Section 4 is devoted to the numerical experiments illustrating the efficiency of the methods. Section 5 is the conclusion.

2 Preliminaries

In this section we give some preliminaries from the convex analysis and multi-objective optimization problems, which are needed in the following discussion.

Definition 2.1

[14] A function $f: R^n\rightarrow R$ is $f^\circ -$pseudoconvex, if it is locally Lipschitz continuous, and for all $x,y\in {R^n}$,

$$\begin{aligned} f(y)<f(x)\,\,\text {implies}\,\,f^\circ (x;y-x)<0. \end{aligned}$$

Definition 2.2

[14] For a locally Lipschitz continuous function $f: R^n\rightarrow R$ the Clarke generalized directional derivative at x in the direction $d\in R^n$ is defined by

$$\begin{aligned} f^\circ (x;d)=\limsup \limits _{\begin{array}{c} y\rightarrow x\\ t\downarrow 0 \end{array}}\frac{f(y+td)-f(y)}{t} \end{aligned}$$

and the Clarke subdifferential of f at x is

$$\begin{aligned} \partial f(x)=\{\xi \in {R^n}\,|\,f^\circ (x;d)\ge \xi ^Td,\forall d\in {R^n}\}. \end{aligned}$$

From the property of the Clarke subdifferential, it has $f^\circ (x;d)=\max \limits _{g\in {\partial f(x)}}g^Td$.

Next we present two assumptions which are used in the later theorems.

Assumption 2.1

For the given sequence $\{x^k\}\in {R^n}, \{y^l\}\in {R^n}$, the constant $M_0\ge 0$, the level set satisfies

$$\begin{aligned} L_0=\{x\in {R^n}\,|\,\max \{f_i(y^{l+1})-f_i(x^k),c(y^{l+1})-c(x^k)\,|\,i=1,2,\ldots ,p\}<M_0\}\subseteq \mathcal {O}, \end{aligned}$$

where $\mathcal {O}$ is an open and bounded set.

Definition 2.3

[15] The functions $f: R^n\rightarrow R$ is said to be subdifferentially regular at $x\in R^n$ if it is locally Lipschitz continuous at x and for all $d\in R^n$ the classical directional derivative

$$\begin{aligned} f^{'}(x;d)=\lim \limits _{t\downarrow 0}\frac{f(x+td)-f(x)}{t} \end{aligned}$$

exists and $f^{'}(x;d)=f^\circ (x;d)$.

The following theorems give the important properties of $f^\circ$-pseudoconvex function.

Theorem 2.1

[15] A $f^\circ$-pseudoconvex function f(x) attains its global minimum at $x^*$, if and only if $0\in \partial f(x^*).$

Theorem 2.2

[15] Let $f_i: R^n \rightarrow R$ be $f^\circ -$pseudoconvex for all $i=1,2,\ldots ,p$. Then the function

$$\begin{aligned} f(x)=\max \{f_i(x)\,|\,i=1,2,\ldots ,p\} \end{aligned}$$

is also $f^\circ -$pseudoconvex, and

$$\begin{aligned} \partial f(x)\subseteq \text {conv}\{\partial f_i(x) \,|\, f_i(x) = f(x), i = 1,\ldots ,p\}. \end{aligned}$$

Furthermore, if $f_i$ satisfies Definition 2.3, then

$$\begin{aligned} \partial f(x)=\text {conv}\{\partial f_i(x) \,|\, f_i(x) = f(x), i = 1,\ldots ,p\}. \end{aligned}$$

The ideal solution of (MOP) is:

$$\begin{aligned} x^*\in {C},\,\, f_i(x^*)\le f_i(x), \forall i=1,2,\ldots ,p, \end{aligned}$$

where C is the feasible set of (MOP). The ideal solution is hard to obtain because that these objectives are often balanced against each other. In the following we give the Pareto solution of (MOP).

Definition 2.4

[14] A vector $x^*$ is said to be a global Pareto solution of (MOP), if there does not exist $x\in C$ such that

$$\begin{aligned} f_i(x)\le f_i(x^*),\,\,\text {for all}\,\ i=1,2,\ldots ,p\,\,\,\text {and}\,\,\,f_j(x)< f_j(x^*)\,\,\text {for some}\,\,j. \end{aligned}$$

Vector $x^*$ is said to be a global weak Pareto solution of (MOP), if there does not exist $x\in C$ such that

$$\begin{aligned} f_i(x)< f_i(x^*),\,\,\text {for all}\,\ i=1,2,\ldots ,p. \end{aligned}$$

Definition 2.5

[14] A vector $x^*$ is called the local (weakly) Pareto solution of (MOP), if there exists $\delta >0$ such that $x^*$ is the (weakly) Pareto solution on $B(x^*,\delta )\cap C$. It can be seen that the Pareto solution must be the weakly Pareto solution.

The tangent cone and polar cone of set $K \subseteq R^n$ at x are defined as

$$\begin{aligned}&T_K(x)=\{d\in {R^n}\,|\,\text {there exist}\, t_i\rightarrow 0 \,\,\text {and}\,\, d_i\rightarrow d\,\,\text {with}\,\, x+t_id_i\in K\}, \\&K^{\le }=\{d\in {R^n}\,|\,w^Td\le 0, \forall w\in K\}. \end{aligned}$$

The convex hull and closure hull of K are denoted by $\text {conv}K$ and $\text {cl}K$. Denote

$$\begin{aligned} \text {ray}K=\{\lambda v\,|\,\lambda \ge 0, v\in {K}\}\,\,\,\text {and}\,\,\, \text {cone}K=\text {ray}\,\text {conv}K. \end{aligned}$$

Let $C:=\{x\in R^n\,|\, c(x)\le 0\}, K(x):=\partial c(x)$, and the constraint qualification

$$\begin{aligned} K^{\le }(x)\subseteq {T_C(x)} \end{aligned}$$

(2.1)

is posed to obtain optimality conditions.

The following theorem gives the optimality condition of (MOP).

Theorem 2.3

[15] $x^*$ is the local weakly Pareto solution of (MOP), and the constraint qualification (2.1) is satisfied, then

$$\begin{aligned} 0\in {\text {conv}\,\cup _{i=1}^{p}\, \partial f_i(x^*)+\text {cl}\,cone\,\partial c(x^*)}. \end{aligned}$$

(2.2)

Moreover, if $f_i,i=1,2,\ldots ,p, c$ are $f^\circ -$pseudoconvex, the condition (2.2) is the sufficient condition of that $x^*$ is the global weakly Pareto solution.

3 Infeasible multi-objective proximal bundle methods

In this section, firstly we give the infeasible multi-objective proximal bundle method(IMPB), the proposed method has an advantage that it has no requirement on the feasibility of initial points, which means that the algorithm can begin from any starting points.

To improve the speed of the IMPB method, we propose an acceleration procedure, which is the penalty skill, and, the strategy to adjust the penalty parameters is also given.

For both two algorithms, under wild assumptions, the sequences generated by the algorithms converge to the globally Pareto solutions of (MOP).

3.1 The infeasible multi-objective proximal bundle method

The IMPB method is the extension of proximal bundle methods into the multi-objective case, which is usually used to handle the nonconvex constrained problems [6, 16]. The idea of the IMPB method is to find the direction from any starting point, in which the values of all objective functions improve simultaneously. For the IMPB method, it still needs the scalarization to obtain the minimization function in the bundle. In this paper, we use the improvement function $H:R^n\times R^n\rightarrow R:$

$$\begin{aligned} H_{x^k}(y)=\max \{f_i(y)-f_i(x^k),c(y)\,|i=1,2,\ldots ,p\}. \end{aligned}$$

(3.1)

The following theorem gives the connection between the problem (MOP) and the improvement function.

Theorem 3.1

[14] A necessary condition for $x^* \in R^n$ to be a global weak Pareto solution of (MOP) is that

$$\begin{aligned} x^* =\arg \min \limits _{y\in R^n}H_{x^*}(y). \end{aligned}$$

(3.2)

Moreover, if $f_i, i = 1,\ldots ,p,c$ are $f^\circ$-pseudoconvex and the constraint qualification (2.1) is valid, then the condition (3.2) is sufficient for $x^*$ to be a global weak Pareto solution of (MOP).

Suppose that there are some reference points $x^j\in R^n$ from the past iterations and subgradients $g_{f_i}^j\in {\partial f_i(x^j)}$, $j\in {L_l^{f_i}}, L_l^{f_i}\subseteq \{1,2,\ldots ,l\}$ and $g_{c}^j\in {\partial c(x^j)}, j\in {L_l^{c}}, L_l^{c}\subseteq \{1,2,\ldots ,l\}$. The bundle of information are given as follows:

$$\begin{aligned} \begin{array}{l} B_k^{f_i}=\{(x^j,f_i(x^j),g_{f_i}^j):j\in {L_l^{f_i}}\}, L_l^{f_i}\subseteq \{1,2,\ldots ,l\};\\ B_k^{c}=\{(x^j,c(y^j),g_{c}^j):j\in {L_l^{c}}\}, L_l^{c}\subseteq \{1,2,\ldots ,l\}. \end{array} \end{aligned}$$

Let $x^k$ be the current approximation point of (MOP) at the iteration k. The linearization errors of $f_i(x)$ and c(x) at $y^j$ are defined as

$$\begin{aligned} \begin{array}{l} e_{f_{ij}}^k=f_i(x^k)-f_i(y^j)-\langle g_{f_i}^j,x^k-y^j\rangle ,j\in {L_l^{f_i}},\\ e_{c_{j}}^k=c(x^k)-c(y^j)-\langle g_c^j,x^k-y^j\rangle ,j\in {L_l^{c}}. \end{array} \end{aligned}$$

(3.3)

Because $f_i(x)$ and c(x) are nonsmooth nonconvex functions, the corresponding linearization errors $e_{f_{ij}}^k$ and $e_{c_{j}}^k$ may be negative. In order to make the linearization errors nonnegative, we consider the generalized linearization errors $\hat{e}_{f_{ij}}^k=e_{f_{ij}}^k+\eta _ld_j^k,\hat{e}_{c_j}^k+\eta _ld_j^k$, where $d_j^k=\frac{1}{2}\Vert y^j-x^k\Vert ^2$, $\eta _l$ is the convexificaton parameter [5]. In this paper, the minimal value of convexificaton parameter $\eta _l$ is chosen as

$$\begin{aligned} \eta _l^{\text {min}}=\max \limits _{1\le i\le p} \left\{ \max \limits _{j\in L_l^{f_i}/\{j_k\}}\frac{-2e_{f_{ij}}^k}{\Vert y^j-x^k\Vert ^2},\max \limits _{j\in L_l^{c}/\{j_k\}}\frac{-2e_{c_{j}}^k}{\Vert y^j-x^k\Vert ^2},0\right\} . \end{aligned}$$

(3.4)

When $\eta _l\ge \eta _l^{\text {min}}$, it has $\hat{e}_{f_{ij}}^k\ge 0,\hat{e}_{c_j}^k\ge 0$. For simplicity, denote $\Delta _j^k=y^j-x^k, c^+(x^k)=\max \{c(x^k),0\}$.

The piecewise approximation model of the objective function $f_i(x)$ at $y^j$ is

$$\begin{aligned} \begin{array}{rcl} \check{f}_{il}(y) &{} = &{} \max \limits _{j\in {L_l^{f_i}}}\{f_i(y^j)+\eta _ld_j^k+\eta _l\langle g_{f_i}^j+\eta _l\Delta _j^k,y-y^j\rangle \} \\ &{} = &{} f_i(x^k)+\max \limits _{j\in {L_l^{f_i}}}\{-\hat{e}_{f_{ij}}^k+\langle g_{f_i}^j+\eta _l\Delta _j^k,y-x^k\rangle \}. \end{array} \end{aligned}$$

The piecewise approximation model of the constraint function c(x) at $y^j$ is

$$\begin{aligned} \begin{array}{rcl} \check{c}_{l}(y) &{} = &{} \max \limits _{j\in {L_l^{c}}}\{c(y^j)+\eta _ld_j^k+\eta _l\langle g_{c}^j+\eta _l\Delta _j^k,y-y^j\rangle \} \\ &{} = &{} c(x^k)+\max \limits _{j\in {L_l^{c}}}\{-\hat{e}_{c_{j}}^k+\langle g_{c}^j+\eta _l\Delta _j^k,y-x^k\rangle \}. \end{array} \end{aligned}$$

Then the approximation of the improvement function (3.1) is

$$\begin{aligned} \check{H}_{l}(y)=\max \{\check{f}_{il}(y)-f_i(x^k),c_l(y)\,|i=1,2,\ldots ,p\}. \end{aligned}$$

(3.5)

Solve the following quadratic problem

$$\begin{aligned} y^{l+1}=\arg \min \limits _{y\in {R^n}}\{\check{H}_{l}(y)+\frac{u_l}{2}\Vert y-x^k\Vert ^2\} \end{aligned}$$

(3.6)

to get the candidate point $y^{l+1}$, where $x^k$ is called the proximal center and $u_l$ is the proximal parameter.

The quadratic problem (3.6) is equivalent to the problem

$$\begin{aligned} \qquad \qquad \begin{array}{ll} \min &{} r+ \frac{u_l}{2}\Vert y-x^k\Vert ^2\\ \mathrm{s.\ t.} &{} f_i(x^k)-\hat{e}_{f_{ij}}^k+\langle g_{f_i}^j+\eta _l\Delta _j^k,y-x^k\rangle \le r,j\in L_l^{f_i},i=1,2,\ldots ,p,\\ &{} c(x^k)-\hat{e}_{c_{j}}^k+\langle g_{c}^j+\eta _l\Delta _j^k,y-x^k\rangle \le r, j\in L_l^{c}. \end{array}~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$

(3.7)

The Lagrange function of (3.7) is

$$\begin{aligned} \begin{array}{rcl} L(y,r,\lambda ,u) &{}= &{} r+\frac{u_l}{2}\Vert y-x^k\Vert ^2+\sum \limits ^{p}_{i=1} \sum \limits _{j\in {L_l^{f_i}}}\lambda _{ij}[f_i(x^k)-\hat{e}_{f_{ij}}^k+\langle g_{f_i}^j+\eta _l\Delta _j^k,y-x^k\rangle -r]\\ &{} &{} + \sum \limits _{j\in {L_l^{c}}}u_{j}[c(x^k)-\hat{e}_{c_{j}}^k+\langle g_{c}^j+\eta _l\Delta _j^k,y-x^k\rangle - r]. \end{array} \end{aligned}$$

The dual problem of (3.7) is

$$\begin{aligned} \qquad \qquad \begin{array}{ll} \min \limits _{\lambda ,u\ge 0} &{} \frac{\Vert G^l\Vert ^2}{2}-\sum \limits ^{p}_{i=1} \sum \limits _{j\in {L_l^{f_i}}}\lambda _{ij}[f_i(x^k)-\hat{e}_{f_{ij}}^k] -\sum \limits _{j\in {L_l^{c}}}u_{j}[c(x^k)-\hat{e}_{c_{j}}^k] \\ \mathrm{s.\ t.} &{} \sum \limits _{i=1}^{p}\sum \limits _{j\in {L_l^{f_i}}}\lambda _{ij}+\sum \limits _{j\in {L_l^{c}}}u_{j}=1, \lambda _{ij}\ge 0, u_{j}\ge 0, \end{array}~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$

(3.8)

where $G^l=\sum \limits _{i=1}^{p}\sum \limits _{j\in {L_l^{f_i}}}\lambda _{ij}(g_{f_i}^j+\eta _l\Delta _j^k)+ \sum \limits _{j\in {L_l^{c}}}u_{j}(g_{c}^j+\eta _l\Delta _j^k)$.

Solve the dual problem (3.8) and obtain the solution $y^{l+1}$, which is

$$\begin{aligned} y^{l+1}=x^k-\frac{1}{u_l}G^l. \end{aligned}$$

(3.9)

The aggregate linearization function at $y^{l+1}$ is $\psi _l(y)=\check{H}_{l}(y^{l+1})+\langle G^l, y-y^{l+1}\rangle$. The function $\psi _l(y)$ is affine and $\psi _l(y^{l+1})=\check{H}_{l}(y^{l+1}), G^l=\nabla \psi _l(y)$, hence, we obtain $\psi _l(y)\le \check{H}_{l}(y), \forall y\in R^n$. The aggregate linearization error at $y^{l+1}$ is

$$\begin{aligned} \varepsilon _l^k=H_k(x^k)-\psi _l(y^{l+1}) =c^+(x^k)-\check{H}_l(y^{l+1})-u_l\Vert y^{l+1}-x^k\Vert ^2. \end{aligned}$$

Furthermore, the predicted decrease is

$$\begin{aligned} \delta _l=c^+(x^k)+\frac{\eta _l}{2}\Vert y^{l+1}-x^k\Vert ^2-\check{H}_l(y^{l+1}) =\varepsilon _l^k+R_l\Vert y^{l+1}-x^k\Vert ^2, \end{aligned}$$

(3.10)

where $R_l=u_l+\frac{\eta _l}{2}$.

Now we propose the infeasible multi-objective proximal bundle method.

The IMPB method

• Step 0 (Initialization) Choose a infeasible starting point $x^0 \in {C}$, and select a unacceptable functional increasing parameter $M_0$, a convex parameter $\Gamma _0$, a proximal parameter $\Gamma _1$, a stopping tolerance $\tau _{stop}$. Set $y_0^0=x^0$, compute $g_{f_i}^0\in {\partial f_i(y^0)}, i=1,2,\ldots ,p, g_c^0\in {\partial c(y^0)}$. Initialize $u_1, \eta _1, e_{f_{i0}}^0=e_{c_0}^0=d_0^0=\Delta _0^0=0$.

• Step 1 (Computing the candidat point) Solve the quadratic programming (3.6) and obtain the solution $y^{l+1}$. Compute the predicted decrease $\delta _l$ by (3.10).

• Step 2 (Stopping test) If $\delta _l\le \tau _{stop}$, then stop.

• Step 3 (Updating the bundle) Update the index set $L_{l+1}^{f_i}\supseteq \{l+1,i_k\}, L_{l+1}^{c}\supseteq \{l+1,i_k\}$. Compute $g_{f_i}^{l+1}\in {\partial f_i(y^{l+1})}, i=1,2,\ldots ,p,g_c^{l+1}\in {\partial c(y^{l+1})}$. Compute the bundle of information:

  $$\begin{aligned} \begin{array}{l} e_{f_{i,{l+1}}}^k=f_i(x^k)-f_i(y^{l+1})-\langle g_{f_i}^{l+1},x^k-y^{l+1}\rangle ,j\in {L_l^{f_i}},\\ e_{c_{l+1}}^k=c(x^k)-c(y^{l+1})-\langle g_c^{l+1},x^k-y^{l+1}\rangle ,j\in {L_l^{c}}. \end{array} \end{aligned}$$

• Step 4 (Testing the descent criterion) If the candidat point $y^{l+1}$ is good enough, i.e.,

  $$\begin{aligned} \left\{ \begin{array}{ll} \max \limits _{1\le i\le p}(f_i(y^{l+1})-f_i(x^k))\le -m\delta _l \,\,\text {and}\,\,c(y^{l+1}) \le 0, &{}\quad \text {if}\,\,c(x^k)\le 0;\\ c(y^{l+1})\le c(x^k)-m\delta _l,&{} \quad \text {if}\,\,c(x^k)>0. \end{array}\right. \end{aligned}$$

  (3.11)

  Update the stability center, and set $x^{k+1}=y^{l+1}$; otherwise, set $x^{k+1}=x^k$.

• Step 5 (Updating the convexification parameter) Compute $\eta _{l+1}^{min}$ by (3.4), and set

  $$\begin{aligned} \left\{ \begin{array}{ll} \eta _{l+1}=\eta _l, &{}\quad \text {if}\,\,\eta _{l+1}^{min}\le \eta _l;\\ \eta _{l+1}=\Gamma _0\eta _{l+1}^{min},&{}\quad \text {if}\,\,\eta _{l+1}^{min}>\eta _l. \end{array}\right. \end{aligned}$$

  (3.12)

• Step 6 (Updating the proximal parameter) If $\max \{f_i(y^{l+1})-f_i(x^k),c(y^{l+1})-c(x^k)\,|\,i=1,2,\ldots ,p\}>M_0$, set $u_{l+1}=\Gamma _1 u_l$; otherwise, set $u_{l+1}=u_l$, and go to Step 1.

There are some explanations about the IMPB method.

• (i) The descent criterion (3.11) has two distinct advantages: firstly, when the last stability center is not feasible, the second formula of (3.11) is used to reduce the infeasibility; secondly, when the last stability center is feasible, on the basis of maintaining the feasibility of candidate points, the value of objective functions is reduced.

• (ii) In Step 3, in order to find the new searching direction, it needs to reserve the information of new iteration points into the bundle. The size of the bundle increases with the number of iterations. When the number of iterations is large, due to the limited computer memory space, it is necessary to compress the bundle, which is called the aggregate technique. The readers can refer to [28] for more details about these aggregate technique.

• (iii) In Step 5, the updating manner of $\eta _l$ will finally make $\eta _l\ge \eta _{l+1}^{min}$, $\hat{e}_{f_{ij}}^k\ge 0, \hat{e}_{c_{j}}^k\ge 0$ after many iterations. In Step 6, in order to obtain $\{y^l\}\subseteq L_0$, it needs to increase the proximal parameter $u_l$ and adjust the piecewise approximation model, however, this may lead the infinite loop between Step 1 and Step 6. The following lemma proves that this loop will stop in finite steps.

Lemma 3.1

Suppose that the sequence of the candidate points generated by the IMPB method is bounded, i.e., $\{y^l\}\subseteq L_0$. Then there exists the iteration index $l^{'}>0$ such that $u_l=\bar{u}, \eta _l=\bar{\eta }$ for all $l>l^{'}$.

Proof

Because $L_0\subseteq O$, where O is an open bounded set, $L_0$ is a closed bounded set. The functions $f_i, i=1,2,\ldots ,p, c$ are Lipschitz continuous and there are Lipschizian constants $L_{il},i=1,2,\ldots ,p, L_c$. Take $L_f=\max \limits _{1\le i\le p}\{L_{il}\}, L=\max \{L_f,L_c\}, r=\frac{M_0}{L}$, for all $x\in {B_r(x^k)}$, we have

$$\begin{aligned} \begin{array}{l} \Vert f_i(x)-f_i(x^k)\Vert \le L\Vert x-x^k\Vert \le M_0, \\ \Vert c(x)-c(x^k)\Vert \le L\Vert x-x^k\Vert \le M_0. \end{array} \end{aligned}$$

Due to $g_{f_i}^j\in {\partial f_i(y^j)}, g_{c}^j\in {\partial c(y^j)},y^j\in {L_0}$, it has $\Vert g_{f_i}^j\Vert \le L, \Vert g_{c}^j\Vert \le L$. Take $i=i_k$, then $g_{h_k}^{i_k}\in {\partial \check{H}_l(x^k)}$, which is $\check{H}_l(y)\ge \check{H}_l(x^k)+\langle g_{h_k}^{i_k},y-x^k\rangle$. Moreover, it holds that

$$\begin{aligned} \begin{array}{l} \arg \min \limits _{y}\{\check{H}_l(y)+\frac{u_l}{2}\Vert y-x^k\Vert ^2\} \\ \subseteq \{y:\check{H}_l(x^k)+\langle g_{h_k}^{i_k},y-x^k\rangle +\frac{u_l}{2}\Vert y-x^k\Vert ^2\le \check{H}_l(x^k)\} \\ \subseteq \{y:-\Vert g_{h_k}^{i_k}\Vert \Vert y-x^k\Vert +\frac{u_l}{2}\Vert y-x^k\Vert ^2\le 0\} \\ \subseteq \{y:\Vert y-x^k\Vert \le \frac{2\Vert g_{h_k}^{i_k}\Vert }{u_l}\} \\ \subseteq \{y:\Vert y-x^k\Vert \le \frac{2T}{u_l}\}, \text {where}\, T=L_f+L_c. \end{array} \end{aligned}$$

When $l\rightarrow \infty$, $u_l$ becomes very large, then $\frac{2T}{u_l}$ becomes small. Moreover, the functions $f_i, i=1,2,\ldots ,p, c$ are Lipschitz, then $\max \limits _{1\le i\le p}\{f_i(y^{l+1})-f_i(x^k), c(y^{l+1})-c(x^k)\}>M_0$ does not hold, hence, there exists $l^{'}>0$, when $l>l^{'}$, it has $u_l=\bar{u}$.

The convexification parameter $\eta _l$ in Step 5 is nondecreasing during the iteration. In contrast, assume that $\eta _l$ does not converge to a stable value. After the iteration $l^{'}$, the generalized linearization errors are nonnegative, i.e., $\hat{e}^k_{f_{il}}\ge 0, \hat{e}^k_{c_{l}}\ge 0$. When $l>l^{'}$, it has that $\eta _l>\eta _k^{min}$. Hence, the parameter $\eta _l$ no longer updates, and $\eta _l=\bar{\eta }$. $\square$

Next we will give the convergence of the IMPB method. The set C is the feasible set of (MOP),i.e., $C=\{x\in {R^n}\,|\,c(x)\le 0\}$. k is the index of serious steps, and $L_s$ is the index set of all serious steps.

l(k) is the index when the candidate point $y^{l(k)}$ becomes the stability center $x^k$, i.e., $x^k=y^{l(k)}$. When the number of iterations becomes very large, the convexification parameter $\eta _l$ and the proximal parameter $u_l$ will finally remain unchanged. Let the stopping parameter $\tau _{\text {stop}}=0$ and the predicted decreasing $\delta _l>0$. Suppose that the algorithm generates two kinds of infinite steps, which are: (1) there are infinite serious steps; (2) there are many finite serious steps and then there are many infinite null steps. Before obtaining the convergence of the algorithm, a lemma is given.

Lemma 3.2

For any decreasing index $k_0>0$, the following conclusions are satisfied:

• (i) $x^k\in \{x\in {R^n}\,|\,c(x)\le {c^+(x^{k_0})}\}, \forall k\ge {k_0}$;

• (ii) if there exists $k_1$ satisfying $x^{k_1}\in {C}$, then $x^k\in {C}, \forall k\ge k_1.$

Proof

Fix the last decreasing index by $k_0$, i.e., all the iterate steps are null steps after $k_0$, the conclusion (i) holds clearly. Assume that there are $k_0+1$ serious steps, if $x^{k_0}\notin C$, by (3.11), we have $c(x^{k_0+1})<c^+(x^{k_0})=c(x^{k_0})$. Moreover, if $x^k\notin C, \forall k\ge k_0$, repeating the previous step, then $\{c(x^k)\}$ is nonincreasing, therefore, $c(x^{k})<c^+(x^{k_0})=c(x^{k_0}), k\ge k_0$.

Assume that it exists $k_1$ satisfying $x^{k_1}\in {C}$. If $k_1$ is the last serious step, the conclusion (ii) holds. Suppose that there are $k_1+1$ serious steps, by (3.11), it has $c(x^{k_1+1})\le 0=c^+(x^{k_1})$. Repeating the previous step, we obtain $c(x^{k})\le 0=c^+(x^{k_1}), \forall k\ge k_1$, which means $x^k\in {C}$. The conclusion holds.

$\square$

Lemma 3.2 shows that, no matter the initial point is feasible or infeasible, the proposed algorithm can be applied into both two cases. Once the iteration point is feasible, the algorithm becomes feasible and the speed of the algorithm is increased. It is of great practical significance for applying the algorithm into more general multi-objective optimization fields.

Lemma 3.3

Suppose that the IMPB method generates a infinite sequence of serious steps, and $L_s$ is the index set of all serious steps, then we have

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }\delta _k=0, \lim \limits _{k\rightarrow \infty }\varepsilon _l^k=0, \lim \limits _{k\rightarrow \infty }\Vert G^k\Vert =0, k\in {L_s}. \end{aligned}$$

Proof

We prove the conclusion from the following two cases. The first case is that the serious step satisfying the first condition of (3.11), i.e., $\exists \hat{k}\,\, s.t.\,\, c(x^{\hat{k}})\le 0, c(x^{k+1})\le 0, \forall k\ge \hat{k}, k\in {L_s}$, moreover, $\max \limits _{1\le i\le p}\{f_i(x^{k+1})-f(x^k)\}\le -m\delta _k$. Then we obtain $f_i(x^{k+1})-f(x^k)\le -m\delta _k, \forall i=1,2,\ldots ,p$, and $\{f_i(x^k)\}$ is nonincreasing. Because $f_i$ is bounded and $f^\circ -$pseudoconvex, there exists the limit of the function. Denoting $\{f_i(x^k)\}\rightarrow \hat{f}_i,i=1,2,\ldots ,p$, it has that

$$\begin{aligned} m\sum \limits _{k\in {L_s}}\delta _k\le \sum \limits _{k\in {L_s}}(f_1(x^k)-f_1(x^{k+1})), \forall k\ge \hat{k}, \end{aligned}$$

i.e.,

$$\begin{aligned} \sum \limits _{k\in {L_s}}\delta _k\le \frac{1}{m}\sum \limits _{k\in {L_s}}(f_1(x^k)-f_1(x^{k+1})),k\ge \hat{k}. \end{aligned}$$

Similarly,

$$\begin{aligned} \sum \limits _{k\in {L_s}}\delta _k\le \frac{1}{m}\sum \limits _{k\in {L_s}}(f_i(x^k)-f_i(x^{k+1})), i=1,2,\ldots ,p. \end{aligned}$$

After many infinite iterations, we obtain that

$$\begin{aligned} \sum \limits _{k\in {L_s}}\delta _k\le \frac{1}{m}\sum \limits _{k\in {L_s}}(f_i(x^{\hat{k}})-\hat{f}_i), i=1,2,\ldots ,p. \end{aligned}$$

Therefore,

$$\begin{aligned} \sum \limits _{k\in {L_s}}\delta _k\le \frac{1}{mp}(f_1(x^{\hat{k}})-\hat{f}_1+ f_2(x^{\hat{k}})-\hat{f}_2+\cdots +f_p(x^{\hat{k}})-\hat{f}_p), \end{aligned}$$

hence, we have $\lim \limits _{k\rightarrow \infty }\delta _k=0$.

The second case is that the serious step satisfying the second condition of (3.11), which is $c(x^k)>0$. From the second formula of (3.11), it has $c(x^{k+1})-c(x^k)\le -m\delta _k$, which means $0<\delta _k\le \frac{1}{m}(c(x^k)-c(x^{k+1}))$. Because c(x) is bounded and $f^\circ -$pseudoconvex, the limit of c(x) exists. Denoting $\{c(x^k)\}\rightarrow \hat{c}$, it holds that

$$\begin{aligned} \sum \limits _{k\in {L_s}}\delta _k\le \frac{1}{m}\sum \limits _{k\in {L_s}}(c(x^k)-c(x^{k+1})) =\frac{1}{m}(c(x^{\hat{k}})-\hat{c}). \end{aligned}$$

Therefore, we have $\lim \limits _{k\rightarrow \infty }\delta _k=0$. It follows from (3.10) that $0\le \varepsilon _l^k\le \delta _k$ and $\lim \limits _{k\rightarrow \infty }\varepsilon _l^k=0$. Due to $y^{l+1}=x^k-\frac{1}{u_l}G^k, \frac{1}{u_k}\ge \frac{1}{\bar{u}}$, it holds $\delta _k\ge \varepsilon _l^k+\frac{1}{u_k}\Vert G^k\Vert ^2$. Take the limit and we obtain $\lim \limits _{k\rightarrow \infty }\Vert G^k\Vert =0$. $\square$

Now we present the convergence of the IMPB method.

Theorem 3.2

Suppose that the IMPB method generates a infinite sequence of serious steps, then the accumulation point of $\{x^k\}$ is the weakly Pareto solution of (MOP).

Proof

For every $y\in {R^n}$, it has $H_{x^k}(y)\ge c^+(x^k)+\langle G^k, y-x^k\rangle -\varepsilon _l^k,l=l(k)\in {L_s}$. Due to $u_l\le \bar{u}$, by Lemma 3.2, it holds $\lim \limits _{k\rightarrow \infty } \varepsilon _l^k=0, \lim \limits _{l\rightarrow \infty }\Vert G^l\Vert =0$. The sequence $\{x^k\}$ is bounded and denote the subsequence by $\{x^{k_i}\}$. When $k\rightarrow \infty$, it has $x^{k_i}\rightarrow \bar{x}$. Moreover, there is $H_{\bar{x}}(y)\ge c^+(\bar{x})+\langle 0,y-\bar{x}\rangle -0=c^+(\bar{x})=H_{\bar{x}}(\bar{x})$. From the arbitrariness of y, it yields that $\min \{H_{\bar{x}}(y)\,|\,y\in {R^n}\}=H_{\bar{x}}(\bar{x})=c^+(\bar{x})$, i.e., $\bar{x}=\arg \min \limits _{y\in {R^n}}H_{\bar{x}}(y)$. In what follows, we prove that $H_{\bar{x}}(\bar{x})=c^+(\bar{x})=0$ by contradiction. Suppose that $c^+(\bar{x})>0$, by the local Lipschitz continuity of c, it holds that $c^+(y)=c(y)>f(y)-f(x), \forall y\in {B(\bar{x})}$. Because x is the local optimality solution, it has $c^+(\bar{x})>0$, which contradicts with the solution set being nonempty, hence, the relation $H_{\bar{x}}(\bar{x})=c^+(\bar{x})=0, 0\in {\partial }H_{\bar{x}}(\bar{x})$ is satisfied. By Theorem 3.1, we obtain that $\bar{x}$ is the weakly Pareto solution of (MOP). $\square$

Theorem 3.3

Suppose that the IMPB method generates an infinite sequence of null steps and $x^{k_{last}}$ is the last stability center, then $x^{k_{\text {last}}}$ is the weakly Pareto solution of (MOP).

Proof

Fix $H(\cdot )=H_{k_{last}}(\cdot )$, by Lemmas 3.2 and 3.3, it holds that $\lim \limits _{l\rightarrow \infty }y^l=\bar{y}$ and $\lim \limits _{l\rightarrow \infty }\check{H}_l(y^{l+1})=H(\bar{y})+ \frac{\bar{\eta }}{2}\Vert \bar{y}-x^{k_{last}}\Vert ^2$. Hence, the equality $H(\bar{y})+\frac{\bar{\eta }}{2}\Vert \bar{y}-x^{k_{last}}\Vert ^2\le c(x^{k_{last}})=H(x^{k_{last}})$ is satisfied. Because that ${k_{last}}$ is the index of the last stability center, when $l>{k_{last}}$, the decreasing criterion (3.11) is not satisfied, the following relations are satisfied.

• (i) If $c(x^{k_{last}})\le 0$, it has $\max \limits _{1\le i\le p}(f_i(y^{l+1})-f_i(x^{k_{last}}))>-m\delta _l$ and $c(y^{l+1})>0$. Hence,

  $$\begin{aligned} \begin{array}{l} H(y^{l+1})\ge \max \limits _{1\le i\le p}(f_i(y^{l+1})-f_i(x^{k_{last}}))>-m\delta _l=c^+(x^{k_{last}})-m\delta _l;\\ H(y^{l+1})\ge c(y^{l+1})>c^+(x^{k_{last}})- m\delta _l. \end{array} \end{aligned}$$

• (ii) If $c(x^{k_{last}})>0$, it has $c(y^{l+1})>c(x^{k_{last}})-m\delta _l, c^+(x^{k_{last}})= c(x^{k_{last}}),\lim \limits _{l\rightarrow \infty }\delta _l=0$.

Then $H(y^{l+1})\ge c(y^{l+1})>c^+(x^{k_{last}})-m\delta _l$ holds. Passing the limit to the above inequality and we get $H(\bar{y})\ge c^+(x^{k_{last}})$. Moreover, from $H(\bar{y})+\frac{\bar{\eta }}{2}\Vert \bar{y}-x^{k_{last}}\Vert ^2\le c^+(x^{k_{last}})$, we obtain that $\bar{y}=x^{k_{last}}$, i.e., $0\in {\partial H(x^{k_{last}})}$. According to Theorem 3.1, $x^{k_{last}}$ is the weakly Pareto solution of (MOP). The proof of the theorem is finished. $\square$

3.2 The penalized infeasible multi-objective proximal bundle method

In the improvement function of the IMPB algorithm, we use the functional value of testing points to approximate the optimal value of the objective function. This approach of the approximation is slow. The reason is that, the feasibility of the testing point in current iteration is not considered, and the number of iterations of the algorithm is increased. On the other hand, this approximation may make the algorithm fall into the infeasible local optimum, hence, the feasible optimality solution of the problem is hardly reached and the algorithm is invalid. For the above reasons, we make an improvement of the IMPB method. In the new algorithm, a penalty item is added into the improvement function, which considers the feasibility of testing points. The new algorithm is called the penalized infeasible multi-objective proximal bundle (PIMPB) method. In PIMPB algorithm, the feasibility of the current iteration point is considered, which not only reduces the risk of iteration points falling into the infeasible local optimal point, but also speeds up the process of approximating the optimal value of objective functions.

The new improvement function is $H:R^n \times R^n\rightarrow {R}$,

$$\begin{aligned} H_{x^k}(y)=\max \{f_i(y)-\theta _{i1}, c(y)-\theta _2\,|\,i=1,2,\ldots ,p\}, \end{aligned}$$

(3.13)

where $\theta _{i1}=f_i(x^k)+s_k\max \{0,c(x^k)\}, \theta _2=t_k\max \{0,c(x^k)\}$. The PIMPB algorithm is divided into two phases. The first phase is the infeasible iteration, in this phase, the iteration point is infeasible. The second phase is the feasible iteration, in this phase, the iteration point is feasible. Under this feasibility, the function value is decreased until the stopping criterion is satisfied.

Compared with the improvement function in the IMPB algorithm, the improvement function in the PIMPB algorithm is to subtract two penalty terms from the former. The penalty term only works in the first phase. In this phase, when the infeasibility of the constraint function is reduced, the objective function is allowed to have a slight increment, which can make the iteration point avoid becoming the infeasible local optimality solution. When the algorithm enters the second phase, the penalty term is zero, and the improvement function is the same as that in the IMPB algorithm. In addition, in numerical experiments, it is found that adding a penalty term can speed up the convergence of the algorithm.

In the following, we present the model of the PIMPB algorithm. The piecewise approximation models of objective functions and constraint function are the same as that in the IMPB algorithm. The new improvement function is

$$\begin{aligned} \begin{array}{rcl} \check{H}_l(y) &{} = &{} \max \{\check{f}_{il}(y)-\theta _{il},\check{c}_l(y)-\theta _2\,|\,i=1,2,\ldots ,p\} \\ &{} =&{} \max \{\check{f}_{il}(y)-f_i(x^k)-s_kc^+(x^k), \check{c}_l(y)-t_kc^+(x^k)\,|\,i=1,2,\ldots ,p\}. \end{array} \end{aligned}$$

(3.14)

Solve the following quadric programming problem

$$\begin{aligned} \min \limits _{y\in {R^n}}\,\,\check{H}_{l}(y)+\frac{u_l}{2}\Vert y-x^k\Vert ^2 \end{aligned}$$

(3.15)

to obtain the candidate point $y^{l+1}$. The equivalent problem of (3.15) is

$$\begin{aligned} \qquad \qquad \begin{array}{ll} \min &{} r+ \frac{u_l}{2}\Vert y-x^k\Vert ^2\\ \mathrm{s.\ t.} &{} -s_kc^+(x^k)-\hat{e}_{f_{ij}^k}+\langle g_{f_i}^j+\eta _l\Delta _j^k,y-x^k\rangle \}\le r,j\in L_l^{f_i},i=1,2,\ldots ,p,\\ &{} -t_kc^+(x^k)-\hat{e}_{c_{j}}^k+\langle g_{c}^j+\eta _l\Delta _j^k,y-x^k\rangle \le r, j\in L_l^{c}. \end{array} \end{aligned}$$

(3.16)

The following theorem gives the formula of the candidate point.

Theorem 3.4

Suppose that $y^{l+1}$ is the solution of (3.16), then

$$\begin{aligned} y^{l+1}=x^k-\frac{1}{u_l}G^l, \end{aligned}$$

(3.17)

where $G^l=\sum \nolimits _{i=1}^{p}\sum \nolimits _{j\in {L_l^{f_i}}}\lambda _{ij}(g_{f_i}^j+\eta _l\Delta _j^k)+ \sum \nolimits _{j\in {L_l^{c}}}u_{j}(g_{c}^j+\eta _l\Delta _j^k)$. Moreover, the following conclusions hold.

• (i) $G^l\in {\partial \check{H}_{l}(y^{l+1})}$;

• (ii) $\varepsilon _l^k=\sum \nolimits _{i=1}^{p}\sum \nolimits _{j\in {L_l^{f_i}}} \lambda _{ij}\hat{e}_{f_{ij}}^k+\sum \nolimits _{j\in {L_l^{c}}}u_{j}\hat{e}_{c_{j}}^k$, and $\varepsilon _l^k\ge 0$.

Proof

First we prove that (3.17) holds. The Lagrange function of (3.16) is

$$\begin{aligned} \begin{array}{rcl} L(y,r,\lambda ,u) &{}= &{}r+ \frac{u_l}{2}\Vert y-x^k\Vert ^2+\sum \limits _{i=1}^{p}\sum \limits _{j\in {L_l^{f_i}}} \lambda _{ij} [-s_kc^+(x^k)-\hat{e}_{f_{ij}^k}+ \langle g_{f_i}^j+\eta _l\Delta _j^k,y-x^k\rangle \}- r]\\ &{} &{} + \sum \limits _{j\in {L_l^{c}}}u_{j}[c(x^k)-t_kc^+(x^k)-\hat{e}_{c_{j}}^k+\langle g_{c}^j+\eta _l\Delta _j^k,y-x^k\rangle - r]. \end{array} \end{aligned}$$

Since the problem (3.16) is strongly convex, the optimal solution is unique and the dual gap is zero, then

$$\begin{aligned} \min \limits _{y,r}\max \limits _{\lambda ,u}L(y,r,\lambda ,u) =\min \limits _{\lambda ,u}\max \limits _{y,r}L(y,r,\lambda ,u). \end{aligned}$$

From $\frac{\partial L}{\partial r}=0$, it has $\sum \limits _{i=1}^{p}\sum \limits _{j\in {L_l^{f_i}}}\lambda _{ij}+\sum \limits _{j\in {L_l^{c}}}u_{j}=1$. Solve the following problem

$$\begin{aligned} \begin{array}{rl} \min \limits _{y} &{}r+ \frac{u_l}{2}\Vert y-x^k\Vert ^2+\sum \limits _{i=1}^{p}\sum \limits _{j\in {L_l^{f_i}}} \lambda _{ij} [-s_kc^+(x^k)-\hat{e}_{f_{ij}^k}+ \langle g_{f_i}^j+\eta _l\Delta _j^k,y-x^k\rangle \}]\\ &{} + \sum \limits _{j\in {L_l^{c}}}u_{j}[c(x^k)-t_kc^+(x^k)-\hat{e}_{c_{j}}^k+\langle g_{c}^j+\eta _l\Delta _j^k,y-x^k\rangle ] \end{array} \end{aligned}$$

to obtain $y^{l+1}$, taking the gradient on y, we obtain that $0=u_l(y^{l+1}-x^k)+G^l$, which is $y^{l+1}=x^k-\frac{1}{u_l}G^l$.

Next we prove the assertions (i) and (ii).

• (i) Since $y^{l+1}$ is the optimal solution of (3.15), it has $0\in {\partial \check{H}_{l}(y^{l+1})}+u_l(y^{l+1}-x^k)$, which is $G^l\in {\partial \check{H}_{l}(y^{l+1})}$, and the first assertion holds.

• (ii) Bring $y^{l+1}$ in the Lagrange function $L(y,r,\lambda ,u)$ and obtain

$$\begin{aligned} L(y^{l+1},r,\lambda ,u)= & {} \frac{u_l}{2}\Vert y^{l+1}-x^k\Vert ^2+\sum \limits _{i=1}^{p}\sum \limits _{j\in {L_l^{f_i}}} \lambda _{ij} [-s_kc^+(x^k)-\hat{e}_{f_{ij}^k}]\\&\quad +\sum \limits _{j\in {L_l^{c}}}u_{j}[c(x^k)-t_kc^+(x^k)-\hat{e}_{c_{j}}^k]-\frac{1}{u_l}\Vert G^l\Vert ^2. \end{aligned}$$

On the other hand, $L(y^{l+1},\lambda ,u)=\check{H}_{l}(y^{l+1})+\frac{u_l}{2}\Vert y^{l+1}-x^k\Vert ^2$, from the definition of (3.4), we have

$$\begin{aligned} \sum \limits _{i=1}^{p}\sum \limits _{j\in {L_l^{f_i}}} \lambda _{ij} \hat{e}_{f_{ij}^k} + \sum \limits _{j\in {L_l^{c}}}u_{j}\hat{e}_{c_{j}}^k=H_{x^k}(x^k) -\check{H}_l(y^{l+1})-u_l\Vert y^{l+1}-x^k\Vert ^2. \end{aligned}$$

Due to the aggregate linearization errors and $\hat{e}_{f_{ij}^k}\ge 0, \hat{e}_{c_{j}}^k\ge 0$ , it holds that $\varepsilon _l^k=\sum \limits _{i=1}^{p}\sum \limits _{j\in {L_l^{f_i}}} \lambda _{ij}\hat{e}_{f_{ij}}^k+\sum \limits _{j\in {L_l^{c}}}u_{j}\hat{e}_{c_{j}}^k\ge 0$. The second assertion is proven. $\square$

The aggregate linearization function is $\psi _l(y)=\check{H}_{l}(y^{l+1})+\langle G^l, y-y^{l+1}\rangle$. The function $\psi _l(y)$ is affine and $\psi _l(y^{l+1})=\check{H}_{l}(y^{l+1}), G^l=\nabla \psi _l(y)$, hence, we obtain $\psi _l(y)\le \check{H}_{l}(y), \forall y\in R^n$. The aggregate linearization error is

$$\begin{aligned} \varepsilon _l^k=H_l(x^k)-\psi _l(y^{l+1}) =H_k(x^k)-\check{H}_l(y^{l+1})-u_l\Vert y^{l+1}-x^k\Vert ^2. \end{aligned}$$

By the definition of subdifferentials, (3.17) and $\psi _l(y)\le \check{H}_{l}(y)$, we have

$$\begin{aligned} H_{x^k}(x^k)-\varepsilon _l^k\le \check{H}_l(y)+\langle G^k,x^k-y\rangle . \end{aligned}$$

(3.18)

The predicted decrease is

$$\begin{aligned} \delta _l=H_{x^k}(x^k)-\check{H}_l(y^{l+1}) =\varepsilon _l^k+u_l\Vert y^{l+1}-x^k\Vert ^2. \end{aligned}$$

(3.19)

Now we propose the PIMPB method.

The PIMPB method

• Step 0 (Initialization) Choose a infeasible starting point $x^0 \in {C}$ and a stopping tolerance $\tau _{stop}$. Select a convex parameter $\Gamma _0$, a proximal parameter $\Gamma _1$, a penalty parameter $\Gamma _2$ and an improvement parameter m. Set $y_0^0=x^0$ and compute $g_{f_i}^0\in {\partial f_i(y^0)}, i=1,2,\ldots ,p, g_c^0\in {\partial c(y^0)}$. Initialize $u_1, \eta _1, e_{f_{i0}}^0=e_{c_0}^0=d_0^0=\Delta _0^0=0$.

• Step 1 (Computing candidate points) Establish the piecewise linearization approximation model (3.15), and solve its dual problem (3.16) to obtain the dual parameters $\lambda ,u$. Compute $y^{l+1}$ by (3.17) and $\delta _l$ by (3.19).

• Step 2 (Stopping test) If $\delta _l\le \tau _{stop}$, then stop; otherwise, go to the next step.

• Step 3 (Updating the bundle) Update the index set $L_{l+1}^{f_i}\supseteq \{l+1,i_k\}, L_{l+1}^{c}\supseteq \{l+1,i_k\}$. Compute $g_{f_i}^{l+1}\in {\partial f_i(y^{l+1})}, i=1,2,\ldots ,p,g_c^{l+1}\in {\partial c(y^{l+1})}$. Compute the bundle of information:

  $$\begin{aligned} \begin{array}{l} e_{f_{i,{l+1}}}^k=f_i(x^k)-f_i(y^{l+1})-\langle g_{f_i}^{l+1},x^k-y^{l+1}\rangle ,j\in {L_l^{f_i}},\\ e_{c_{l+1}}^k=c(x^k)-c(y^{l+1})-\langle g_c^{l+1},x^k-y^{l+1}\rangle ,j\in {L_l^{c}}. \end{array} \end{aligned}$$

• Step 4 (Testing the descent criterion) If the candidate point $y_k^i$ is good enough, i.e.,

  $$\begin{aligned} \left\{ \begin{array}{ll} \max \limits _{1\le i\le p}(f_i(y^{l+1})-f_i(x^k))\le -m\delta _l \,\,\text {and}\,\,c(y^{l+1}) \le 0, &{}\quad \text {if}\,\,c(x^k)\le 0;\\ c(y^{l+1})\le c(x^k)-m\delta _l,&{} \quad \text {if}\,\,c(x^k)>0. \end{array}\right. \end{aligned}$$

  (3.20)

  then update the stability center, and set $x^{k+1}=y^{l+1}$; otherwise, set $x^{k+1}=x^k$.

• Step 5 (Updating the convexification parameter) Compute $\eta _{l+1}^{min}$ by (3.11), and set

  $$\begin{aligned} \left\{ \begin{array}{ll} \eta _{l+1}=\eta _l, &{}\quad \text {if}\,\,\eta _{l+1}^{min}\le \eta _l;\\ \eta _{l+1}=\Gamma _0\eta _{l+1}^{min},&{}\quad \eta _{l+1}^{min}>\eta _l. \end{array}\right. \end{aligned}$$

  (3.21)

• Step 6 (Updating the proximal parameter) If $y^{l+1}$ is the descent point, then set $u_{k+1}\le u_{max}<+\infty$; otherwise, set $u_{l+1}\in [u_l,u_{max}]$.

• Step 7 (Updating the penalty parameter)   Choose the penalty parameter $\Gamma _2$ satisfying

  $$\begin{aligned} 0\le t_k\le 1, s_k\ge 0, s_k-t_k\ge \Gamma _2>0, \end{aligned}$$

  (3.22)

  and set $k=k+1$, and go to Step 1.

Now we make the comparison between IMPB, PIMPB algorithms and other algorithms given in [14] and [19]. The main differences among them are as follows:

• (i) The first difference is the choice of the initial solution. The initial point of [14] and [19] is feasible. The initial point of this paper is arbitrary and it can be infeasible.

• (ii) The second difference is the descent criterion. Since the initial point of the algorithm is arbitrary, it needs to consider the feasibility of the testing points in the descent criterion. In the descent criterion, when the current stability center is feasible, the decrease of objective functions and the feasibility of the candidate point are considered. When the current stability center is infeasible, it needs to have a sufficient decrease for the constraint function.

• (iii) The third difference is the improvement function. To further guarantee the feasibility of the testing points, the penalty procedure is added to the improvement function. It not only reduces the risk of iteration points falling into the infeasible local optimum, but also speeds up the process of approximating the optimal value of objective functions.

Next we present several lemmas before giving the convergence of the PIMPB algorithm.

Lemma 3.4

The penalty parameter is updated according to (3.22), and the following conclusions hold.

• (i) If $c(x^k)\le 0$, it has $H_{x^k}(x^k)=0$. If $c(x^k)>0$, it has $H_{x^k}(x^k)=c(x^k)(1-t_k)$.

• (ii) When k is the index of null steps, it holds $H_{x^k}(y^{l+1})>H_{x^k}(x^k)-m\delta _k$.

Proof

• (i) If $c(x^k)\le 0$, it has $H_{x^k}(x^k)=0$. If $c(x^k)>0$, it follows from (3.22) that $H_{x^k}(x^k)=c(x^k)(1-t_k)\ge 0$ and (i) is proved.

• (ii) When k is the index of null steps, the descent criterion (3.19) doesn’t hold. We prove the conclusion from the following two cases. The first case is $c(x^k)>0$, and it has

$$\begin{aligned} \begin{array}{rcl} H_{x^k}(y^{k+1})&{} = &{}\max \{f_i(y^{k+1})-f_i(x^k)-s_kc(x^k),c(y^{k+1})-t_kc(x^k)\} \\ &{} \ge &{} c(y^{k+1})-t_kc(x^k) \\ &{} \ge &{} c(x^k)-m\delta _k-t_kc(x^k) \\ &{} =&{} (1-t_k)c(x^k)-m \delta _k\\ &{} = &{} H_{x^k}(x^k)-m \delta _k. \end{array} \end{aligned}$$

The second case is $c(x^k)\le 0$, then $\max \limits _{1\le i\le p}\{f_i(y^{k+1})-f_i(x^k)\}\ge -m\delta _k$ and $c(y^{k+1})>0$, hence,

$$\begin{aligned} \begin{array}{rcl} H_{x^k}(y^{k+1}) &{} = &{} \max \limits _{1\le i\le p}\{f_i(y^{k+1})-f_i(x^k),c(y^{k+1})\} \\ &{} \ge &{} \max \limits _{1\le i\le p}\{f_i(y^{k+1})-f_i(x^k)\}\\ &{}\ge &{}-m\delta _k\\ &{}=&{}H_{x^k}(x^k)-m \delta _k. \end{array} \end{aligned}$$

So we obtain $H_{x^k}(y^{k+1})\ge c(y^{k+1})>0\ge H_{x^k}(x^k)-m \delta _k$, and (ii) is proved. $\square$

Lemma 3.5

Suppose that the PIMPB algorithm generates an infinite sequence of serious steps, and $L_s$ is the index set of serious steps, then

• (i) $\lim \limits _{k\rightarrow \infty }\delta _k=0, \lim \limits _{k\rightarrow \infty }\varepsilon ^k_l=0, \lim \limits _{k\rightarrow \infty }\Vert G^k\Vert =0,k\in {L_s}$.

• (ii) $H_{x^k}(x^k)\le \check{H}_k(y)+o(1/k), k\in {L_s}$ when k is large enough.

Proof

• (i) The proof is similar with Lemma 3.3 and we omit the proof.

• (ii) Since $\lim \limits _{k\rightarrow \infty }\varepsilon ^k_l=0$, from (3.18), we obtain that $H_{x^k}(x^k)\le \check{H}_k(y)+o(1/k), k\in {L_s}$, when k is large enough. $\square$

Lemma 3.6

Suppose that the PIMPB algorithm generates an infinite sequence of null steps, and $L_s^{'}$ is the index set of null steps. $\hat{x}=x^{\hat{k}}$ is the last serious step, and there are all null steps after $\hat{k}$ steps. Then

• (i) $\lim \limits _{k\rightarrow \infty }\delta _k=0, \lim \limits _{k\rightarrow \infty }\varepsilon ^k_l=0, \lim \limits _{k\rightarrow \infty }\Vert G^k\Vert =0,k\in {L_s^{'}}$;

• (ii) when $k\in {L_s^{'}}$ is large enough, it has $y^k\rightarrow {\hat{x}}$;

• (iii) $H_{x^k}(x^k)\le \check{H}_k(y)+o(1/k), k\in {L_s^{'}}$ and k is large enough.

Proof

(i) From (3.17), it has $y^{k+1}=\hat{x}-\frac{1}{u_k}G^k, G^k=u_k(\hat{x}-y^{k+1})$, then

$$\begin{aligned} \begin{array}{rcl} 2\langle G^k, y-y^{k+1}\rangle &{} = &{}2u_k\langle \hat{x}-y^{k+1}, y-y^{k+1}\rangle \\ &{} = &{} u_k\langle \hat{x}-y^{k+1}, \hat{x}-y^{k+1}+y-\hat{x}\rangle +u_k\langle y-y^{k+1}+\hat{x}-y, y-y^{k+1}\rangle \\ &{} = &{} u_k\Vert y^{k+1}-\hat{x}\Vert ^2+u_k\Vert y-y^{k+1}\Vert ^2-u_k\Vert y-\hat{x}\Vert ^2. \end{array} \end{aligned}$$

By the aggregate linearization function, it yields

$$\begin{aligned} \begin{array}{rcl} \psi _k(y)&{} = &{} \check{H}_k(y^{k+1})+\langle G^k, y-y^{k+1}\rangle \\ &{} = &{} \check{H}_k(y^{k+1})+\frac{u_k}{2}\Vert y^{k+1}-\hat{x}\Vert ^2+\frac{u_k}{2}\Vert y-y^{k+1}\Vert ^2 -\frac{u_k}{2}\Vert y-\hat{x}\Vert ^2. \end{array} \end{aligned}$$

Denote $V_k=\check{H}_k(y^{k+1})+\frac{u_k}{2}\Vert y^{k+1}-\hat{x}\Vert ^2$, where $V_k$ is the optimal value of (3.15), then

$$\begin{aligned} \psi _k(y)+\frac{u_k}{2}\Vert y-\hat{x}\Vert ^2=V_k+\frac{u_k}{2}\Vert y-y^{k+1}\Vert ^2. \end{aligned}$$

When $y=\hat{x}$, there exists $\hat{M}>0$ satisfying $V_k+\frac{u_k}{2}\Vert \hat{x}-y^{k+1}\Vert ^2=\psi _k(\hat{x})\le \check{H}_k(\hat{x})\le \hat{M}$, then $V_k$ has the upper bound. Due to $\check{H}_{k+1}(y)\ge \psi _k(y)$, for $\forall y\in R^n$, it holds $\check{H}_{k+1}(y)+\frac{u_k}{2}\Vert y-\hat{x}\Vert ^2\ge V_k+\frac{u_k}{2}\Vert y-y^{k+1}\Vert ^2$. In a null step, from Step 6 of the PIMPB algorithm, it has $u_{k+1}\ge u_k$. Taking $y=y^{k+2}$, it holds $V_{k+1}\ge V_k-\frac{u_k}{2}\Vert y^{k+2}-y^{k+1}\Vert ^2$, and $\{V_k\}$ is nondecreasing, then $\{V_k\}$ is convergent and $V_{k+1}-V_k-\frac{u_k}{2}\Vert y^{k+2}-y^{k+1}\Vert ^2\rightarrow 0$. From Lemma 3.4, it has $H_{x^k}(y^{k+1})>H_{x^k}(x^{k})-m\delta _k$. Adding $\delta _k$ to the above inequality, we obtain

$$\begin{aligned} \begin{array}{rcl} 0\le (1-m)\delta _k &{} < &{} \delta _k +H_{x^k}(y^{k+1})-H_{x^k}(x^{k}) \\ &{} = &{} H_{x^k}(y^{k+1})-\hat{H}_{k}(y^{k+1}) \\ &{} = &{} H_{x^k}(y^{k+1})-\hat{H}_{k}(y^{k+2})+\hat{H}_{k}(y^{k+2})-\hat{H}_{k}(y^{k+1}). \end{array} \end{aligned}$$

Furthermore,

$$\begin{aligned} \begin{array}{rcl} \check{f}_{i,k+1}(y^{k+2}) &{} \ge &{} f_i(\hat{x})-\hat{e}_{f_{i,k+1}}^{k+1}+\langle g_{f_{i,k+1}}+\eta _{k+1}(y^{k+1}-\hat{x}),y^{k+2}-\hat{x}\rangle \\ &{} = &{} f_i(x^{k+1})+\langle g_{f_{i,k+1}},\hat{x}-y^{k+1}\rangle -\frac{\eta _{k+1}}{2}\Vert \hat{x}-y^{k+1}\Vert ^2\\ &{}&{}\quad +\,\langle g_{f_{i,k+1}}+\eta _{k+1}(y^{k+1}-\hat{x}),y^{k+2}-\hat{x}\rangle \\ &{} \ge &{} f_i(x^{k+1})+\langle g_{f_{i,k+1}},y^{k+2}-y^{k+1}\rangle +\eta _{k+1}\langle y^{k+1}-\hat{x} ,y^{k+2}-y^{k+1}\rangle \\ &{} = &{} f_i(x^{k+1})+\langle g_{f_{i,k+1}}+\eta _{k+1}\Delta _{k+1}^k,y^{k+2}-y^{k+1}\rangle . \end{array} \end{aligned}$$

Similarly, we have $\check{c}_{k+1}(y^{k+2})\ge c(x^{k+1})+\langle g_{c,k+1}+\eta _{k+1}\Delta _{k+1}^k,y^{k+2}-y^{k+1}\rangle$. Hence, it holds that

$$\begin{aligned} \begin{array}{rcl} \check{H}_{k+1}(y^{k+2}) &{} = &{}\max \{\check{f}_{i,k+1}(y^{k+2})-\theta _{i1},\check{c}_{k+1}(y^{k+2})-\theta _2\} \\ &{} \ge &{} \max \{f_i(x^{k+1})+\langle g_{f_{i,k+1}}+\eta _{k+1}\Delta _{k+1}^k,y^{k+2}-y^{k+1}\rangle -\theta _{i1},c(x^{k+1})\\ &{}&{}+\,\langle g_{c,k+1}+\eta _{k+1}\Delta _{k+1}^k,y^{k+2}-y^{k+1}\rangle -\theta _2\}. \end{array} \end{aligned}$$

Because $\{y^k\}$ is bounded, there exists $N>0$, $\forall k, \Vert \Delta _{k+1}^k\Vert \le N$. $f_i,i=1,2,\ldots ,p,c$ are Lipschitz functions, then it exists $L>0$ satisfying $\Vert g_{f_{i,k+1}}\Vert \le L, \Vert g_{c,k+1}\Vert \le L$. According to the Cauchy–Schwarz inequality, it has

$$\begin{aligned} \check{H}_{k+1}(y^{k+2})\ge {H}_{k}(y^{k+1})-(L+\eta _{k+1}N)\Vert y^{k+2}-y^{k+1}\Vert , \end{aligned}$$

then

$$\begin{aligned} \begin{array}{rcl} 0\le (1-m)\delta _k &{} < &{} \check{H}_{k+1}(y^{k+2})-{H}_{k}(y^{k+1})+(L+\eta _{k+1}N)\Vert y^{k+2}-y^{k+1}\Vert \\ &{} = &{} V_{k+1}-V_k-\frac{u_k}{2}\Vert y^{k+2}-\hat{x}\Vert ^2+\frac{u_k}{2}\Vert y^{k+1}-\hat{x}\Vert ^2\\ &{}&{}\quad +\,(L+\eta _{k+1}N)\Vert y^{k+2}-y^{k+1}\Vert \\ &{} = &{} \langle y^{k+2}-y^{k+1}, G^k\rangle +(L+\eta _{k+1}N)\Vert y^{k+2}-y^{k+1}\Vert \\ &{}&{}\quad +\,V_{k+1}-V_k-\frac{u_k}{2}\Vert y^{k+2}-y^{k+1}\Vert ^2 \\ &{} \le &{} (L+\eta _{k+1}N+\Vert G^k\Vert )\Vert y^{k+2}-y^{k+1}\Vert +V_{k+1}-V_k-\frac{u_k}{2}\Vert y^{k+2}-y^{k+1}\Vert ^2 \\ &{} \le &{} (2L+\eta _{k+1}N)\Vert y^{k+2}-y^{k+1}\Vert +V_{k+1}-V_k-\frac{u_k}{2}\Vert y^{k+2}-y^{k+1}\Vert ^2. \end{array} \end{aligned}$$

Due to $V_{k+1}-V_k-\frac{u_k}{2}\Vert y^{k+2}-y^{k+1}\Vert ^2\rightarrow 0,\Vert y^{k+2}-y^{k+1}\Vert \rightarrow 0$, it has $\lim \limits _{k\rightarrow \infty }\delta _k=0$. Because $0\le \varepsilon _l^k\le \delta _k$, it has that $\lim \limits _{k\rightarrow \infty }\varepsilon ^k_l=0$.

Furthermore, $\delta _k\ge \varepsilon ^k_l+\frac{1}{u_{max}}\Vert G^k\Vert ^2\ge 0$, it holds that $\lim \limits _{k\rightarrow \infty }\Vert G^k\Vert =0$, from (3.18), we obtain $H_{x^k}(x^k)\le \check{H}_k(y)+o(1/k), k\in {L_s^{'}}$ when k is large enough. $\square$

Now we give the convergence result of the PIMPB algorithm.

Theorem 3.5

Let $f_i, i=1,2\cdots ,p$ and g be $f^\circ$-pseudoconvex and the constraint qualification (2.1) be valid.

The penalty parameter of the PIMPB algorithm is updated according to (3.22). The PIMPB algorithm generates the sequence $\{x^k\}$, denoting $\{x^k\}\rightarrow \bar{x}, \{s_k\}\rightarrow \bar{s}, \{t_k\}\rightarrow \bar{t}$, then the following conclusions hold.

• (i) $\forall y\in {R^n}$, it has $\max \{\bar{c},0\}(1-\bar{t})\le \max \limits _{1\le i\le p}\{f_i(y)-\bar{f}_i-\bar{s}\max \{\bar{c},0\},c(y)-\bar{t}\max \{\bar{c},0\}\}$.

• (ii) If $\bar{c}>0$, it exists the constant $R_0$ satisfying $\bar{x}=\arg \min \limits _{y\in {R^n}}c(y)$ when $\bar{s}\ge R_0$.

• (iii) If $\bar{c}\le 0$, $\bar{x}$ is the weakly Pareto solution of (MOP).

Proof

Suppose that the PIMPB algorithm generates the infinite loops, denoting by $L_s, L_s^{'}$ the infinite serious steps and null steps, from Lemmas 3.4–3.6, there exists the subsequence K satisfying $\{x^k\}_{k\in {K}}\rightarrow \bar{x}$. When $K\subseteq L_s^{'}$, it has $\{y^k\}\rightarrow \bar{x}$, and the stability point $x^k=\bar{x}$ is unchanged. Moreover, it holds that

$$\begin{aligned} \forall y\in {R^n}, k\in {K}, H_{x^k}(x^k)=\max \{c(x^k),0\}(1-t_k)\le \check{H}_k(y)+o(1/k). \end{aligned}$$

Because $\check{H}_k(y)\le {H}_k(y)$, we have

$$\begin{aligned} \max \{c(x^k),0\}(1-t_k)\le \max \limits _{1\le i\le p}\{f_i(y)-\theta _{i1},c(y)-\theta _2\}+o(1/k), \end{aligned}$$

(3.23)

where $\theta _{i1}=f_i(x^k)+s_k\max \{c(x^k),0\}, \theta _2=t_k\max \{c(x^k),0\}$. When $\{x^k\}_{k\in K}\rightarrow \bar{x}$, denoting $\bar{f}_i=\lim \limits _{k\in {K}}f_i(x^k), \bar{c}=\lim \limits _{k\in {K}}c(x^k), \bar{s}=\lim \limits _{k\in {K}}s_k, \bar{t}=\lim \limits _{k\in {K}}t_k$, pass the limit to (3.23) and obtain

$$\begin{aligned} \forall y\in {R^n}, \max \{\bar{c},0\}(1-\bar{t})\le \max \limits _{1\le i\le p}\{f_i(y)-\bar{f}_i-\bar{s}\max \{\bar{c},0\},c(y)-\bar{t}\max \{\bar{c},0\}\}. \end{aligned}$$

The proof of (i) is finished.

(ii) When $\bar{c}>0$, take $R_0=\frac{1}{\bar{c}}\{\max \limits _{1\le i\le p}\{f_i(y)-\bar{f}_i\}-c(y)\}+\bar{t}$. If $\bar{s}\ge R_0$, it has

$$\begin{aligned} (\bar{s}-\bar{t})\bar{c}>\max \limits _{1\le i\le p}\{f_i(y)-\bar{f}_i\}-c(y)\Leftrightarrow f_i(y)-\bar{f}_i-\bar{s}\max \{\bar{c},0\}<c(y)-\bar{t}\max \{\bar{c},0\}. \end{aligned}$$

From (i), it holds $\bar{c}\le c(y), \forall y\in {R^n}$, which is $\bar{x}=\arg \min \limits _{y\in {R^n}}c(y)$, and (ii) holds. (iii) When $\bar{c}\le 0$, we have $H_{\bar{x}}(\bar{x})=0\le \max \limits _{1\le i\le p}\{f_i(y)-\bar{f}_i,c(y)\}, \forall y\in {R^n}$, so it has $0\in {\partial H_{\bar{x}}}(\bar{x})$, by Lemma 3.4, we know that $\bar{x}$ is the weakly Pareto solution of (MOP). $\square$

4 Numerical Results

In this section we give some numerical experiments to test the IMPB algorithm and the PIMPB algorithm for (MOP). The algorithms are completed in MATLAB 9.2. The subproblem is solved by quadratic-programming QuadProg.m which is available in the MATLAB optimization toolbox.

Example 1

The multiobjective optimization problem is defined by

$$\begin{aligned} \begin{array}{rl} \min &{} f_1(x)=\sqrt{\Vert x\Vert +2} \\ &{} f_2(x)=\max \{-x_1-x_2,-x_1-x_2+x_1^2+x_2^2-1\} \\ s.t. &{} g(x)=\max \{x_1^2+x_2^2-10,3x_1+x_2+1.5\}\le 0, \end{array} \end{aligned}$$

where $x=(x_1,x_2)^T\in {R^n}$. The function $f_1$ is $f^\circ -$pseudoconvex, $f_2$ is convex and the constraint function g is also convex.

Fig. 1

The mulobjective function

Figure 1 gives the images of objectives functions $f_1$ and $f_2$.

Since the IMPB algorithm has no requirement on the feasibility of the starting point, we choose the infeasible starting point $x^0=(1,1)^T$.

The parameters of the algorithm are given as follows: the increasing parameter $M_0=8$, the convex parameter $\Gamma _0=1.009$, the proximal parameter $\Gamma _1=1.005$, the stopping tolerance $\tau _{stop}=10^{-4}$, the improvement parameter $m=0.1$, the convex parameter $\eta _1=1$, the proximal parameter $u_1=1$, and the constraint tolerance is $10^{-3}$.

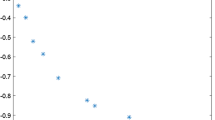
Figure 2 presents the variation of the constrained function during the iteration of the algorithm. From Fig. 2, it can be seen that the initial point is infeasible, and it leads to some initial iteration being infeasible.

When the iteration points are infeasible, the amplitude of the value of the constraint function is relatively large.

After nine iterations, the algorithm achieves the feasible point and executes the feasible solution mode.

The amplitude of the constraint function value is relatively small, and the Pareto optimal solution is found on the basis of keeping the feasibility.

Fig. 2

The constraint function

Fig. 3

The variation of the objective function

Figure 3 describes the changes of two objective functions during the iteration of the algorithm.

From Fig. 3, it can be seen that the two objective functions are non-monotonic. It is reasonable because the initial point is not feasible, and later some initial iteration are also not feasible. At this time, the values of functions are not necessarily reduced. The IMPB algorithm pays more attention to increasing the functional value to reduce the infeasibility, once the feasible point is reached, the values of two objective functions are reduced while the feasibility is maintained.

Table 1 shows that, at the same stopping criterion, after six iterations, the multiobjective proximal bundle(MPB) method provided by Karmitsa [14] reaches the Pareto optimal solution $x^*=(-0.4620,-0.1138)^T$, and the corresponding optimal value is $f^*=(1.5735,0.5759)^T$. The IMPB algorithm reaches the Pareto optimal solution $x^*=(-0.4486,-0.1544)^T$, the optimal value $f^*=(-0.4486, -0.1544)^T$ and the constraint function $g^*=-3.4931\times 10^{-4}$ after 33 iterations.

The IMPB algorithm is an infeasible algorithm and the initial point can be not feasible. Karmitsa’s MPB algorithm is a feasible algorithm, and it requires the feasibility of initial points and all the iterations need to be feasible. From this aspect, the number of iterations of the IMPB algorithm is more than that of Karmitsa’s MPB algorithm.

Table 1 The comparison of MPB and IMPB

To increase the speed of the IMPB algorithm, an acceleration procedure, i.e., the penalty procedure is added to the IMPB algorithm, which is called the PIMPB algorithm. In the PIMPB algorithm, set the penalty parameter $s_0=1$, the increasing penalty parameter $\Gamma _2=1.8$, and the other parameters are set the same with that in the IMPB algorithm.

Figures 4 and 5 describe the changes of the values of objective functions and the constraint function by using the PIMPB algorithm. Because that the penalty term of constraint function is added to the improvement function, the convergent speed of the PIMPB algorithm is obviously faster than that of the IMPB algorithm. It is follows from Table 2 that the IMPB algorithm performs 33 steps to achieve the stopping accuracy, while the PIMPB algorithm only needs 20 steps to achieve the same precision.

Table 2 The comparison of IMPB and PIMPB for Example 1

Fig. 4

The variation of the objective function

Fig. 5

The variation of the constraint function

Example 2

In this example we consider the Pentagon optimization problem [11]. There are three objective functions of 6-dimensions with 15 constraint functions in this nonsmooth nonconvex problem, which is

$$\begin{aligned} \begin{array}{rl} \min &{} f_1(x)=-\sqrt{(x_1-x_3)^2+(x_2-x_4)^2} \\ &{} f_2(x)=-\sqrt{(x_1-x_3)^2+(x_4-x_6)^2} \\ &{} f_3(x)=-\sqrt{(x_1-x_5)^2+(x_2-x_6)^2} \\ s.t. &{} g_{ij}(x)=x_i\cos (\frac{2\pi j}{5})+x_{i+1}\sin (\frac{2\pi j}{5})-1\le 0, \end{array} \end{aligned}$$

where $x=(x_1,x_2,\ldots ,x_6)^T$, $i=1,2,3; j=0,1,\ldots ,4$. Figure 6 gives the image of the objective function $f_1$.

We use the PIMPB method to solve this example and change the setting of parameters as follows: the proximal parameter $\Gamma _1=1.2$, the increasing penalty parameter $\Gamma _2=1.8$, the improvement parameter $m=0.08$, the stopping criterion $\tau _{stop}=10^{-3}$. Because the PIMPB method has no feasibility requirement on the starting point, we set the infeasible starting point $x^0=(-1,0.5,0.6,-1,0.9,1.8)^T$. At this starting point, the two constraint functions $g_{12}(x^0)=0.1029, g_{34}(x^0)=0.1365$ are infeasible, and the other 13 constraint functions are feasible .

Fig. 6

The objective function of $f_1$

Fig. 7

The maximum constraint function

Figure 7 shows the change of the maximum constraint function during iterations. From Fig. 7, it can be seen that the initial implementation of the PIMPB algorithm is infeasible. When the iteration point is infeasible, the value of the constraint function is larger. Fifteen times later, the feasible point is reached, and then the feasible solution mode is executed. At this time, the amplitude of the constraint function value is relatively small, and the Pareto optimal solution is found on the basis of keeping the feasibility. Figure 8 describes the changes of three objective functions during iterations.

Table 3 provides the comparison results of IMPB and PIMPB for this problem. The number of iterations by the PIMPB method is 55, about almost half of the IMPB method with 98 iterations. The CPU time of the PIMPB method is much less than that of the IMPB method.

To conclude, since the IMPB and PIMPB methods are infeasible algorithms, they are performed well for these two examples. The proposed algorithms reduces the requirements on the initial points of the problems, which decreases the computation of the algorithms. The overall behavior of the PIMPB algorithm is better than the IMPB method due to its distinctive penalty procedure, which is of great efficiency to solve constrained optimization problems.

Fig. 8

The three objective functions

Table 3 The comparison of IMPB and PIMPB for Example 2

5 Conclusion

We have presented two infeasible proximal bundle methods for nonsmooth nonconvex multiobjective optimization problems. In the algorithms, the multiobjective functions are handled individually without employing any scalarization. The proposed algorithm has no requirement on the feasibility of initial points. The penalty procedure is given to increase the speed of the convergence of the infeasible algorithm. Under some generalized convexity assumptions, we prove that the algorithm finds the global weakly Pareto optimal solutions of the problem.