Constrained incremental bundle method with partial inexact oracle for nonsmooth convex semi-infinite programming problems

Abstract

Semi-infinite problem (SIPs) are widely used in many control systems for solving complex control problem, such as polymerase chain reaction control system or other real time control system. In this paper, we present a bundle method for solving the nonsmooth convex SIPs, with the aim of working on the basis of “improvement function”, “inexact oracle” and “incomplete knowledge” of the constraints. The proposed algorithm, whenever a new stabilized center is refreshed, requires an evaluation within some accuracy for the value of constraints. Beyond that, by using the incremental technique, it does not require all information about the constraints, but only one component function value and one subgradient needed to be estimated to update the bundle information and generate the search direction. Thus the computational cost is significantly reduced. Global convergence of this method is established based on some mild assumptions. Numerical experiments show that the algorithm is efficient for solving nonsmooth convex SIPs.

1 Introduction

Semi-infinite problem (SIPs) can be used in polymerase chain reaction (PCR) control system for finding optimized complex control strategy. In this paper, we proposed an incremental bundle method for general nosmooth convex SIPs. One of basic motivation is to solve a large class of distributionally robust optimization problems, which can be rewritten as nonsmooth convex SIPs by an uncountable infinite dimensional set of probability distributions. In fact, the robust stochastic optimization for minimizing an expectation function is an important variety of decision problems with uncertainty data. An abstract form for such stochastic optimization problems is

$$\begin{aligned} \min _{x \in X} E_{W}[f(x,\xi )], \end{aligned}$$

where the expectation is taken concerning W which is supposed to be obtained. Unfortunately, in practical applications, such a distribution is not known precisely and has to be estimated from data. Just as in [4, 32], after defining a set $\mathcal {D}$ of possible probability distributions for the uncertain parameters is known; the objective function can be rewritten corresponding to the “worst” case expected cost over the choice of a distribution in $\mathcal {D}$. Therefore, the general distributionally robust optimization problem can be reformulated as follows:

$$\begin{aligned} \min _{x \in X} \max _{W \in \mathcal {D}} E_{W}[F(x)], \end{aligned}$$

where F is a disutility function or random cost we attempt to minimize in expectation. An equivalent expression is

$$\begin{aligned} \min _{x \in X} \max _{W \in \mathcal {D}} \int _{\xi \in \Pi } f(x,\xi )W(d \xi ) , \end{aligned}$$

where the support set $\Pi$ is closed and bounded, and $f(x,\xi )$ is a convex weight function in x that depends on parameter $\xi$. If the set X is a bounded set, the optimal objective function value can be lied in an interval $[\alpha _0,\alpha _1]$. Thus, the problem can be written as a nonsmooth convex SIP:

$$\begin{aligned} \begin{array}{lllll} \min &{}\alpha \\ s.t &{} \int _{\Pi } f(x,\xi )W(d \xi )-\alpha \le 0, \ \ W \in \mathcal {D}\\ &{} \alpha \in [\alpha _0,\alpha _1], \ \ x\in X. \end{array}\end{aligned}$$

(1.1)

In this paper, we consider the following general nonsmooth convex SIP:

$$\begin{aligned} \begin{array}{lll} \min \limits _{x} &{} f(x)\\ \ s.t. &{} c(x,y)\le 0, \ \forall \ y \in Y,\\ &{} x\in X, \end{array}\end{aligned}$$

(1.2)

where the functions f: $X\rightarrow \mathbf R$, c: $X \times Y \rightarrow \mathbf R$ satisfy the following conditions:

• X is a subset of $\mathbf R ^n$ and Y is a nonempty compact subset of $\mathbf R ^m$.

• The objective function f is a convex function, in general nondifferentiable.

• $c(\cdot ,y)$ is convex, in general nondifferentiable for all $y \in Y$, $c(x,\cdot )$ is upper semicontinuous on Y for all $x\in X$.

More broadly, such SIPs apply to optimal control, and diverse fields of engineering such as multiobjective optimization, resource allocation in decentralized systems, control systems design, and filter design in signal processing, decision making under competition, see the early literature [10, 13, 14, 30, 39, 54, 60].

The main difficulty for solving SIPs lies in that there are infinitely many constraints. The principal effort of existing methods is to reduce the infinite set Y to a finite one. The main proposed methods can be roughly divided into the following several types. Based on the KKT systems of SIPs, some semismooth Newton methods and smoothing Newton methods were presented in [17, 27, 29, 36, 41, 42, 56]. In every iteration only a system of linear equations needs to be solved, but they may not ensure the feasibility of the original, or the accumulation point is not necessarily an stationary point of the SIPs. The discretization methods, which based on the ideas of choosing a finite grid of Y, solve finite mathematical programs with Y replaced by the finite grid and updates the grid (see, e.g. [51, 53, 59]). The discretization methods are apt to implement, but the cost of per iteration increases rapidly as the cardinality of the finite grid of Y grows. The third common approach is the reduction-based method, which is to reduce the problem locally to a finite-dimensional nonlinear programming problem (see, e.g. [2, 3, 52, 58]). Unfortunately, the reduction-based method needs some highly strong assumptions including the conditions leading to the infiniteness of the set of active constraints. Another important method is the so-called exchange method (see, e.g. [6, 16, 26, 30, 55, 57, 60]). The new exchange method proposed in [60], does not require to solve a maximum problem over the index set at each iteration.

All methods above just apply to the smooth SIPs, where $f(\cdot )$ and $c(\cdot ,\cdot )$ all are smooth. The methods for solving nonsmooth SIPs are rare, and just only some excellent theoretical research. If the set Y is finite, necessary conditions of Karush–Kuhn–Tucker (KKT) condition for optimality can be established under various constraint qualifications. For example, Abadie, Zangwill, Guignard and Mangasarian–Fromovitz constraint qualification, are denoted by ACQ, ZCQ, GCQ and MFCQ. Puente et al. in [40], introduced the locally Farkas-Minkowski (LFM) property for linear SIPs, and its role as a constraint qualification was emphasized in many later papers. By using Clarke subdifferential, [19–21, 38] presented a nonsmooth analogue of the ACQ, ZCQ, GCQ and LFM property for locally Lipschitz SIPs. [28] introduced some new notions of constraint qualifications about the epigraphs of the conjugates of these functions for convex nonsmooth SIPs. [61] provided Lagrange multiplier rules for nonsmooth SIPs. [33] gave the subdifferential studies and applications of the supremum of uniformly Lipschitzian functions over arbitrary index sets with no topology. Furthermore, necessary and sufficient optimality conditions of KKT type for these problems are further researched in recent years.

In this paper, we proposed a bundle method for solving the nonsmooth convex SIP (1.2). By defining the following “max” function as

$$\begin{aligned} h(x):=\max \Big \{ c(x,y): \ y \in Y \Big \}, \end{aligned}$$

the (1) can be equivalently written as the following nonsmooth nonlinear problem:

$$\begin{aligned} \begin{array}{lll} &{}\min \limits _{x} \ f(x)\\ \ \ \ &{} s.t. \ \ h(x)\le 0, \ x \in X. \end{array}\end{aligned}$$

(1.3)

Various versions of the bundle method (see, e.g., [1, 12, 31, 35, 37, 47–49]) are recognized as one of the most stable and effective method for nonsmooth problems. However, in most of applications, it may be impossible to calculate $h(\cdot )$ accurately, but only controllable accuracy can be obtained [5, 45]. In fact, it may even be difficult to find a point $x \in X$ satisfying $h(x)\le 0$. Therefore, the bundle methodology cannot be used to (1.3) immediately.

Before continuing with our discussions, we introduce the improvement function associates with the problem (1.3):

$$\begin{aligned} \begin{array}{lll} H_{y}(x)=\max \Big \{ f(x)-f(y), h(x) \Big \}, \ \ \forall \ x \in \mathbf R ^n, \end{array}\end{aligned}$$

(1.4)

which is one of the most effective tools to handle constraints in this context, and plays a significant role in this paper. The constrained optimization problem can be rewritten as an unconstrained one. In fact, the point $x^*$ is a solution of (1.3) if and only if $x^*$ solves the unconstrained problem of minimizing $H_{x^*}(x)$ (see, e.g. [23, 46]). As the iteration progresses, the main motivations for our method include the improvement function, incomplete knowledge of the “max” function $h(\cdot )$ and the inexact oracle at some points. Based on these ideas, we introduce the improvement function to deal with the constraints, and propose an infeasible bundle method in this paper. Moreover, we introduce the so-called “incremental” conception, which stems from [22] and previously been applied for various problems (see, e.g. [5, 8, 9, 24, 34]). Now we expand the idea of “incremental” conception to the nonsmooth convex SIPs. At each iteration, we only need to compute one component function value c(x, y) and one respectively subgradient to update the bundles. Whenever a new stabilized center $\hat{x}$ is updated, we also need to evaluate $\max \limits _{y \in Y}c(\hat{x},y)$ within a given fixed accuracy. Fortunately, the process can be properly tackled by some excellent method (see, e.g. [7, 11, 25]).

This paper is organized as follows. In Sect. 2, we study the improvement function and introduce the corresponding bundle information. In Sect. 3, we propose a bundle method for solving problems (1.2). In Sect. 4, we establish the convergence property of our bundle method. In Sect. 5, we give some numerical results to see the performance of our bundle method.

2 Preliminaries

2.1 Concepts

Now we recall concepts and results of variational analysis that will be used in this paper. We shall make use of $\partial f(\bar{x})$ and $\partial _{x}c(\bar{x},y)$ to denote the subdifferential of $f(\cdot )$ and $c(\cdot ,y)$ at the point $\bar{x}$ as [44, Proposition 8.12], i.e.,

$$\begin{aligned} \begin{array}{lll} ~~\partial f(\bar{x}):=\Big \{ v \ | \ f(x)\ge f(\bar{x})+ \langle v,x-\bar{x} \rangle \Big \},\\ \partial _{x} c(\bar{x},y):=\Big \{ v \ | \ c(x,y)\ge c(\bar{x},y)+ \langle v,x-\bar{x} \rangle \Big \}. \end{array}\end{aligned}$$

Approximate subgradients in the Convex Analysis refer to the $\varepsilon$-subdifferential is defined as

$$\begin{aligned} \begin{array}{lll} \partial _{\varepsilon } f(\bar{x}):=\Big \{ v \ | \ f(x)\ge f(\bar{x})+ \langle v,x-\bar{x} \rangle -\varepsilon \Big \}, \end{array}\end{aligned}$$

whose central property is that $0\in \partial _{\varepsilon } f(\bar{x})$ implies $\varepsilon$-minimality of $\bar{x}$ for problem $\min f(x)$, i.e., $f(\bar{x})\le f(x)+\varepsilon$. The directional derivative, defined as [44] with respect to x in the direction $d \in \mathbf R ^n$, has an alternative representation

$$\begin{aligned} \begin{array}{llll} f'(x,d):= \max \limits _{g \in \partial f(x)} g^\mathrm{T}d\ \ \ \mathrm{and} \ \ \ c'_{y}(x,d):= \max \limits _{g \in \partial _x c(x,y)} g^\mathrm{T}d \ \ \mathrm{for } \ y \in Y. \end{array}\end{aligned}$$

According to [15, Theorem 4.4.2] and [19, Remark 3.6], it is known that Y is a nonempty compact subset, $c(\cdot , y)$ is convex on X for any $y\in Y$, and $c(x, \cdot )$ is upper semicontinuous on Y for each $x \in X$, then the subdifferential of $h(\cdot )$ can be represented as:

$$\begin{aligned} \partial h(x)=\mathrm{conv} \Big \{ \bigcup \partial _x c(x,y):\ y \in A(x) \Big \}, \end{aligned}$$

where the active index-set $A(x):=\{y \in Y : h(x)=c(x,y)\}$. The convexity of each $c(\cdot ,y)$, for any $y\in Y$ actually implies that $h(\cdot )$ is jointly upper semi-continuous on $X\times Y$. By the Carath$\acute{e}$odory’s Theorem [43, Theorem 17.1], a point x of $\mathbf R ^n$ lies in the convex hull of a set P, there is a subset $P'$ of P consisting of $n + 1$ or fewer points such that x lies in the convex hull of $P'$. Hence, for every $g \in \partial h(x)$, there exist the corresponding $\mu ^{g}_i$ and $y^g_i \in A(x)$, $i=1,\ldots , n+1$ such that

$$\begin{aligned} g= \sum \limits _{i=1}^{ n+1} \mu ^g_i g_{_{y^g_i}}, \ \mathrm{where} \ \mu ^g_i\ge 0, \ \sum \limits _{i=1}^{ n+1} \mu ^g_i=1,\ g_{_{y^g_i}}\in \partial _x c\left( x, y^g_i\right) , \ y^g_i \in A(x).\nonumber \\ \end{aligned}$$

(2.1)

Along iterations, the method keeps an stabilized center, denoted by $\hat{x}^k$, at the kth iteration. Then the kth improvement function is given as follows

$$\begin{aligned} \begin{array}{lll} H_{\hat{x}^k} (x)=\max \Big \{ f(x)-f(\hat{x}^k), h(x) \Big \}. \end{array}\end{aligned}$$

(2.2)

We introduce the following extended MFCQ (see [18, 50]) for this nonsmooth convex SIP.

Assumption 1

(EMFCQ) The extended MFCQ holds at the optimum point $x^*$. That is, there exists some feasible direction d of $\mathcal {F}:=\{ x\in X : c(x,y)\le 0, \ \mathrm{for\ all} \ y\in Y \}$ at $x^*$, satisfies

$$\begin{aligned} c_{y}'(x^*,d)<0, \ \mathrm{for \ all} \ y \in Y_{act}(x^*), \end{aligned}$$

(2.3)

where $Y_{act}(x^*)=\{ y \in Y \ | \ c(x^*,y)=0 \}$.

We now give the following necessary conditions for optimality.

Lemma 2.1

Suppose that Assumption 1 is satisfied. Then the following statements hold:

• (i) If $x^*$ is a solution to the problem (1), then

  $$\begin{aligned} \min \{ H_{x^*}(z) : \ z \in X \} = H_{x^*} (x^*) = 0. \end{aligned}$$

  (2.4)

• (ii) If the relation (2.4) holds, then $0 \in \partial H_{x^*}(x^*)+N_{X}(x^*)$, and the following conditions hold:

  $$\begin{aligned} \begin{array}{llll} &{} 0\in \partial f(x^*)+\mu \partial h(x^*)+N_{X}(x^*),\\ &{} \mu \ge 0, \ \mu h(x^*)=0, \ h(x^*)\le 0, \end{array}\end{aligned}$$

  (2.5)

  where $N_X (x^{*})$ denotes the normal cone of X at $x^*$.

• (iii) If the relations (2.5) holds, then there exist multipliers $\lambda ^*_i$ and $y_i^*\in Y_{act}(x^*)$, $i=1,\ldots , n+1$, satisfying

  $$\begin{aligned} \begin{array}{lll} &{} 0\in \partial f(x^*)+ \sum \limits _{i=1}^{ n+1} \lambda _i^* \partial _x c(x^*, y^*_i) +N_{X}(x^*),\\ &{} \lambda _i^* \ge 0,\ \lambda _i^* c(x^*, y^*_i)=0, \ \ i =1,\ldots , n+1. \end{array}\end{aligned}$$

  (2.6)

Proof

Suppose $x^*$ is a solution to the problem (1.2), i.e.,

$$\begin{aligned} f(z)\ge f(x^*) , \ \ \mathrm{for \ all} \ z \in \mathcal {F}, \end{aligned}$$

which implies that

$$\begin{aligned} \begin{array}{lll} H_{x^*} (z) &{} = \max \limits _{z\in \mathbf R ^n}\{ f(z)-f(x^*),\ h(z)\}\\ &{}\ge \max \limits _{z\in \mathcal {F}}\{ f(z)-f(x^*),\ h(z)\}\\ &{}\ge 0= H_{x^*}(x^*), \end{array}\end{aligned}$$

where the first inequality has used that $\mathcal {F}\subseteq \mathbf R ^n$, and the last equality is from $h(x^*)\le 0$. From here, the first item (i) follows.

From [23, Lemma 2.15], we obtain that $0 \in \partial H_{x^*}(x^*)+N_{X}(x^*)$, and $x^*$ is a FJ point of the problem (1.3). Then there exist some $\nu _{_0},\ \nu \ge 0$, such that

$$\begin{aligned} \begin{array}{llll} &{} 0\in \nu _{_0}\partial f(x^*)+\nu \partial h(x^*)+N_{X}(x^*),\\ &{} \nu _{_0}+\nu =1, \ \nu h(x^*)=0, \ h(x^*)\le 0. \end{array}\end{aligned}$$

(2.7)

Suppose that the EMFCQ holds, and $\nu _{_0}$ is zero in (2.7), we can obtain that $\nu =1$. Thus there exists a subgradient $\hat{g} \in \partial h(x^*)$ such that $-\hat{g} \in N_{X}(x^*)$. Furthermore, by using the complementary condition $\nu h(x^*)=0$, we conclude that $h(x^*)=0$. Then the definitions of $A(x^*)$ and $Y_{act}(x^*)$ yield $A(x^*)=Y_{act}(x^*)$.

Suppose d is a feasible direction of $\mathcal {F}$, from $-\hat{g}\in N_{X}(x^*)$ we have $\langle \hat{g}, d\rangle \ge 0$. By noting the relation (2.1) (Carath$\acute{e}$odory’s Theorem), there exist $\hat{y}_i \in A(x^*)$ and $\hat{\mu }_i\ge 0, \ i=1,\ldots ,n+1$ such that

$$\begin{aligned} \hat{g}= \sum \limits _{i=1}^{n+1} \hat{\mu }_i g_{_{\hat{y}_i}}, \ \mathrm{where} \ g_{_{\hat{y}_i}}\in \partial _x c(x^*, \hat{y}_i), \ \mathrm{for \ all }\ i=1,\ldots ,n+1. \end{aligned}$$

Besides, from the definition of the directional derivative, we can obtain

$$\begin{aligned} \langle g_{_{\hat{y}_i}},d\rangle \le \max \limits _{g \in \partial _x c(x,\hat{y}_i)} g^\mathrm{T}d =c_{_{\hat{y}_i}}'(x^*,d)<0, \ \ \mathrm{where}\ \ \hat{y}_i \in A(x^*). \end{aligned}$$

The second inequality the last inequality is from (2.3) and $A(x^*)=Y_{act}(x^*)$. Thus, it holds that

$$\begin{aligned} \begin{array}{llll} 0 \le \langle \hat{g}, d \rangle &{}=\sum \limits _{i=1}^{n+1} \hat{\mu }_i \langle g_{_{\hat{y}_i}},d\rangle \\ &{}\le \sum \limits _{i=1}^{n+1} \hat{\mu }_i c'_{\hat{y}_i}(x^*,d)<0. \end{array}\end{aligned}$$

Then that is an apparent contradiction. Thus $\nu _{_0}$ is strictly positive, and conditions (2.5) hold by setting $\mu =\frac{\nu }{\nu _{_0}}$. From here, the result item (ii) follows readily.

From the relations (2.5), then there exist a subgradient $g^*\in \partial h(x^*)$ such that

$$\begin{aligned} -\mu g^*\in \partial f(x^*)+N_{X}(x^*). \end{aligned}$$

(2.8)

By combining with (2.1), there are $\mu ^*_i\ge 0$, $y^*_i \in A(x^*)$ (for all $i=1,\ldots , n+1$) such that

$$\begin{aligned} \begin{array}{llll} g^*=\sum \limits _{i=1}^{ n+1} \mu ^*_i g_{_{y^*_i}}, \end{array}\end{aligned}$$

where $g_{_{y^*_i}}\in \partial _x c(x, y^*_i)$ for all $i=1,\ldots , n+1$. Now we can show that if $i_{1}\ne i_2$, then $y^*_{i_1}\ne y^*_{i_2}$, i.e., the different $g_{_{y^*_i}}$ contains in different $\partial _x c(x, y^*_i)$. Let $I:=\{j_{1},\ldots , j_{n-1}\}=\{1,2,\ldots , n+1\}/\{i_{1},i_{2}\}$. By contradiction, we suppose $i_{1}\ne i_2$ and $y^*_{i_1}=y^*_{i_2}$, then

$$\begin{aligned} \begin{array}{lllll} g^* &{}=\sum \limits _{i\in I} \mu ^*_i g_{_{y^*_i}} +\mu ^*_{i_1} g_{_{y^*_{i_1}}}+\mu ^*_{i_2} g_{_{y^*_{i_2}}}\\ &{}=\sum \limits _{i\in I} \mu ^*_i g_{_{y^*_i}} +\left( \mu ^*_{i_1}+\mu ^*_{i_2}\right) \left( \frac{\mu ^*_{i_1}}{\mu ^*_{i_1}+\mu ^*_{i_2}} g_{_{y^*_{i_1}}} +\frac{\mu ^*_{i_2}}{\mu ^*_{i_1}+\mu ^*_{i_2}} g_{_{y^*_{i_2}}}\right) . \end{array}\end{aligned}$$

Since $\partial _x c(x, y^*_{i_1})$ is a convex set and $g_{_{y^*_{i_1}}}, g_{_{y^*_{i_2}}} \partial _x c(x, y^*_{i_1})$, thus $\frac{\mu ^*_{i_1}}{\mu ^*_{i_1}+\mu ^*_{i_2}} g_{y^*_{i_1}} +\frac{\mu ^*_{i_2}}{\mu ^*_{i_1}+\mu ^*_{i_2}} g_{y^*_{i_2}} \in \partial _x c(x, y^*_{i_1})$. As a result, by setting $\hat{\lambda }_n=\mu ^*_{i_1}+\mu ^*_{i_2}$, $\hat{\lambda }_{n+1}=0$ and $\hat{\lambda }_{i}=\mu ^*_{j_{i}}$ (for all $i=1,\ldots , n-1$), we can obtain that the different $g_{_{y^*_i}}$ contains in different $\partial _x c(x, y^*_i)$. Thus it holds that

$$\begin{aligned} \begin{array}{llll} \mu g^* =\mu \sum \limits _{i=1}^{ n+1} \hat{\lambda }_i g_{_{y^*_i}} \in \mu \sum \limits _{i=1}^{ n+1} \hat{\lambda }_i \partial _x c(x, y^*_{i}), \end{array}\end{aligned}$$

which combines with (2.8), we can obtain that

$$\begin{aligned} 0\in \partial f(x^*)+\mu \sum \limits _{i=1}^{ n+1} \hat{\lambda }_i \partial _x c(x, y^*_{i})+N_{X}(x^*). \end{aligned}$$

By setting $\lambda ^*_i=\mu \times \hat{\lambda }_i$, the conditions (2.6) hold readily. In fact, (2.5) can be written as (2.6) equivalently. $\square$

By noting Lemma 2.1, we can obtain that (1.3) and its KKT condition are equivalent. In addition, if the Slater constraint qualification holds, i.e., there exists a point $\bar{x}\in X$ such that $c(\bar{x},y)<0$ for any $y\in Y$. Then the above three statements in Lemma 2.1 are equivalent.

2.2 Pretreatment for inner subproblem

In this subsection, we consider the inner subproblem, i.e.,

$$\begin{aligned} \max \limits _{y \in Y}c(\hat{x},y). \end{aligned}$$

(2.9)

We assume that the function value $h(\hat{x})$ can only be evaluated within a given fixed accuracy $\omega$. In fact, the assumption for fixed accuracy is realistic in many applications. The controllable accuracy may contain the following two cases: For each constant $\omega >0$, an $\omega$-optimal solution of (2.9) can be found; on the other hand, this may be possible only for some fixed (maybe unknown) $\omega < \infty$.

If $c(\hat{x},\cdot )$ is concave, then (2.9) can be rewritten as a constrained convex minimization programming, hence any inexact algorithms for constrained convex problems can be used; see, e.g., [25]. The method in [25] is just an inexact bundle method for minimizing a convex function over a closed convex set, which asymptotically evaluates the optimal value for (2.9) with accuracy $\omega$ and obtains $\omega$-optimal solutions $y(\hat{x})$. Even if $c(\hat{x}, \cdot )$ is not concave, just upper semicontinuous on Y, there are also some fine algorithms for estimating the problem (2.9). The method in [7] extended the classical cutting plane algorithm to tackle the unconstrained nonconvex nonsmooth optimizations, and whose parameters can be input for obtaining a solution with any given accuracy. Recently, W. Hare [11] proposed a proximal bundle method with inexact oracle for minimizing a nonconvex function over a closed compact set. For a class of nonconvex nonsmooth functions, an approximate critical point can be obtained, in the condition of inexact oracles.

Suppose that $\hat{x}$ is a current stabilized center. Let $y(\hat{x})\in Y$ denote a $\omega$-optimal solution to the maximum problem (2.9), that is

$$\begin{aligned} c(\hat{x},y(\hat{x}))\ge h(\hat{x})-\omega . \end{aligned}$$

The iterative rules in [7, 11, 25] can generate more and more accurate solutions to (2.9), until a $\omega$-optimal solution.

2.3 Bundle information

Bundle method are one of the most effective approaches for solving nonsmooth optimization problems. In this subsection, we introduce some essential elements for our bundle method. Suppose that $J_l^f$ and $J_l^c$ are the index sets for objective function and constrained functions at the iteration l respectively. The oracle outputs are collected along iterations to form the Bundle information.

$$\begin{aligned} \begin{array}{lll} &{} \mathcal {B}_{l}^f:=\Big \{(x^{j}, f(x^{j}), g_{f}^{j},\beta _{_j}) : \ j\in J_l^f \Big \}\ \ \ \ \ \mathrm{for} \ J_l^f\subset \{1,\ldots , l\};\\ &{} \mathcal {B}_l^c :=\Big \{(x^{j},c(x^{j},y^j), g_{c_{_j}}^{j},\nu _{_j}) : \ j\in J_l^c \Big \} \ \ \mathrm{for} \ J_l^c\subset \{1,\ldots , l\}, \end{array}\end{aligned}$$

(2.10)

where $y^j$ is a point in Y, $g_{c_{_j}}^{j} \in \partial _{x}c(x^{j},y^j)$, $g_f^j \in \partial f(x^j)$ and

$$\begin{aligned} \begin{array}{llllll} &{}\beta _{_j}:=f(x^j)+\langle g_f^j,\hat{x}^k-x^j \rangle , \ j \in J_l^f, \ \ &{}\hat{\beta }_{_k}:=f( \hat{x}^k), \\ &{}\nu _{_j}:= c(x^{j},y^j)+\langle g_{c_{_j}}^j,\hat{x}^k-x^j \rangle , \ j \in J_l^c, \ \ &{}\hat{\nu }_{_k}:=c( \hat{x}^k,y^j). \end{array}\end{aligned}$$

(2.11)

Having the information from (2.10), the kth improvement function is modelled by a convex function

$$\begin{aligned} \begin{array}{lll} &{} \mathcal {M}_l(x)=\max \{ \check{f}_{_l} (x)-f(\hat{x}^k), \check{c}_{_l} (x) \}, \\ \mathrm{where} &{} \left\{ \begin{array}{lll} \check{f}_{_l} (x)=\max \limits _{j\in J_l^f } \Big \{ f(x^j)+\langle g_f^j,x-x^j \rangle \Big \}, \\ \check{c}_{_l} (x)=\max \limits _{j\in J_l^c } \Big \{ c(x^{j},y^j)+\langle g_{c_{_j}}^j,x-x^j \rangle \Big \}. \end{array}\right. \end{array}\end{aligned}$$

(2.12)

An equivalent expression, better suited for implementation is

$$\begin{aligned} \begin{array}{lll}&\check{f}_l (\hat{x}^k+d)=\max \limits _{j\in J_l^f } \Big \{ \beta _{j}+\langle g_f^j, d \rangle \Big \}, \ \ \check{c}_{_l} (\hat{x}^k+d)=\max \limits _{j\in J_l^c } \Big \{ \nu _{_j}+\langle g_{c_{_j}}^j, d \rangle \Big \}, \end{array}\qquad \end{aligned}$$

(2.13)

where $d=x-\hat{x}^k$. Given a positive proximal parameter $\mu _{_l}$, each solution $d^{l}$ is generated by solving the following quadratic program

$$\begin{aligned} \min \limits _{d\in \mathcal {D}_k} \Big \{ \mathcal {M}_l(\hat{x}^k+d)+\frac{\mu _{_l}}{2}\Vert d\Vert ^2 \Big \}, \end{aligned}$$

(2.14)

where $\mathcal {D}_k:=X-\hat{x}^k$. With (2.14) as a QP with an extra scalar variable r as follows

$$\begin{aligned} \begin{array}{lll} &{}\min \limits _{(d,r)\in \mathcal {D}_k \times \mathbf R } r+\frac{\mu _{_l}}{2}\Vert d\Vert ^2,\\ QP(\mathcal {B}_l) &{} ~~s.t.~~~~~ \beta _{j}-f(\hat{x}^k)+\langle g_f^j, d \rangle \le r, \ \ j\in J_l^f,\\ &{}~~~~~~~~~~~ \nu _{j}+\langle g_{c_j}^j, d\rangle \le r, \ \ j\in J_l^c. \end{array}\end{aligned}$$

(2.15)

Let $(d^l, r_{_l})$ be the optimal solution to $QP(\mathcal {B}_l)$, we can obtain that $r_{_l}= \mathcal {M}_l(\hat{x}^k+d^l)$, and the new iterative point $x^{l+1}:=\hat{x}^k+d^l$. Furthermore, it is characterized by the following conditions:

$$\begin{aligned} \begin{array}{lll}&d^{l} =-\frac{1}{\mu _{_l}}(G^l+\alpha ^l),\ \ r_{_l}=m_{_l} +\langle G^l, d^l\rangle , \end{array}\end{aligned}$$

(2.16)

where

$$\begin{aligned} \begin{array}{llll} &{}m_{_l}:= \sum \limits _{j\in J_l^f} \lambda ^l_j (\beta _j-f(\hat{x}^k)) +\sum \limits _{j\in J_l^c} \gamma ^l_j \nu _j, \\ &{} \sum \limits _{j\in J_l^f} \lambda ^l_j +\sum \limits _{j\in J_l^c} \gamma ^l_j=1, \ \lambda ^l_j\ge 0,\ j \in J_l^f, \ \gamma ^l_j\ge 0, \ j \in J_l^c,\\ &{} G^l:= \sum \limits _{j\in J_l^f} \lambda ^l_j g_f^j +\sum \limits _{j\in J_l^c} \gamma ^l_j g_{c_j}^j \in \partial \mathcal {M}_l(x^{l+1}),\ \alpha ^l \in N_{X}(x^{l+1}). \end{array}\end{aligned}$$

(2.17)

The next lemma discusses the boundedness of the optimal value of the quadratic program QP($\mathcal {B}$).

Lemma 2.2

Let $w_{_l}$ denote the optimal value of QP($\mathcal {B}_l$), i.e.,

$$\begin{aligned} w_{_l}:=r_{_l}+\frac{\mu _{_l}}{2}\Vert d^l\Vert ^2. \end{aligned}$$

Then

$$\begin{aligned} w_{_l}\le m_{_l} \le H_{\hat{x}^k}(\hat{x}^k). \end{aligned}$$

(2.18)

Proof

By the definitions of $r_{_l}$, $d^l$ in (2.16), for all l, it holds that

$$\begin{aligned} \begin{array}{lll} r_{_l} &{} =m_{_l} +\langle G^l, d^l\rangle \\ &{}=m_{_l}-\mu _{_l}\Vert d^{l}\Vert ^2-\langle \alpha ^l, x^{l+1}-\hat{x}^k\rangle \\ &{}\le m_{_l}-\mu _{_l}\Vert d^{l}\Vert ^2, \end{array}\end{aligned}$$

where the last inequality has used the fact $\alpha ^l \in N_{X}(x^{l+1})$. Therefore, it is obvious that

$$\begin{aligned} w_{_l}\le m_{_l}-\frac{\mu _{_l}}{2}\Vert d^{l}\Vert ^2< m_{_l}. \end{aligned}$$

Besides, by noting (2.11) and the convexity of f and c, then

$$\begin{aligned} \beta _j-f(\hat{x}^k)=f(x^j)+\langle g_f^j,\hat{x}^k-x^j \rangle -f(\hat{x}^k)\le 0, \ \ \forall \ j\in J_l^f, \end{aligned}$$

and

$$\begin{aligned} \nu _{j} = c(x^{j},y^j)+\langle g_{c_{_j}}^j,\hat{x}^k -x^j \rangle \le c(\hat{x}^k,y^j)\le h(\hat{x}^k), \ \ \forall \ j\in J_l^c. \end{aligned}$$

Hence, we conclude that the inequality $m_{_l}\le H_{\hat{x}^k}(\hat{x}^k)$ holds. From here the result has been proved.

The following lemma can be used to establish an approximate optimality condition.

Lemma 2.3

The vector $G^l$ satisfies the following relation

$$\begin{aligned} H_{\hat{x}^k}(x)\ge H_{\hat{x}^k}(\hat{x}^k)+\langle G^l, x-\hat{x}^k\rangle -\epsilon _{_l}, \end{aligned}$$

(2.19)

where $\epsilon _{_l}:=H_{\hat{x}^k}(\hat{x}^k)-m_{_l}\ge 0$. That is $G^l\in \partial _{\epsilon _{_l}} H_{\hat{x}^k}(\hat{x}^k)$.

Proof

By (2.11) and the convexity of f, it follows that for all $j \in J_{l}^f$

$$\begin{aligned} \begin{array}{lll} f(x) &{}\ge f(x^j)+\langle g_f^j, x-x^j\rangle \\ &{}=f(x^j)+\langle g_f^j, \hat{x}^k-x^j\rangle +\langle g_f^j, x-\hat{x}^k\rangle \\ &{}=f(\hat{x}^k)+\langle g_f^j, x-\hat{x}^k\rangle -f(\hat{x}^k)+\beta _j. \end{array}\end{aligned}$$

Similarly we can obtain that

$$\begin{aligned} \begin{array}{lll} h(x) &{}\ge c(x,y^j)\ge c(x^j,y^j)+\langle g_{c_j}^j,x-x^j \rangle \\ &{}= c(x^j,y^j)+\langle g_{c_{_j}}^j,\hat{x}^k-x^j \rangle +\langle g_{c_{_j}}^j,x-\hat{x}^k \rangle \\ &{}=\nu _{_j}+\langle g_{c_{_j}}^j,x-\hat{x}^k \rangle , \end{array}\end{aligned}$$

for all $j \in J_{l}^c$. By combining with above two inequalities, and using the definition of $H_{\hat{x}^k}(\cdot )$, we have

$$\begin{aligned} \begin{array}{lllll} H_{\hat{x}^k}(x)&{}=\max \{ f(x)-f(\hat{x}^k), h(x) \}\\ &{} \ge \sum \limits _{j\in J_l^f} \lambda ^l_j ( f(x)-f(\hat{x}^k)) +\sum \limits _{j\in J_l^c} \gamma ^l_j h(x)\\ &{} \ge \langle G^l, x-\hat{x}^k\rangle +\sum \limits _{j\in J_l^f} \lambda ^l_j (\beta _j-f(\hat{x}^k)) +\sum \limits _{j\in J_l^c}\gamma ^l_j\nu _{_j}\\ &{}\ge H_{\hat{x}^k}(\hat{x}^k)+\langle G^l, x-\hat{x}^k\rangle -(H_{\hat{x}^k}(\hat{x}^k)-m_{_l}). \end{array}\end{aligned}$$

(2.20)

Furthermore, by noting the fact that $\beta _j-f(\hat{x}^k)\le 0$, $\nu _{_j}\le c(\hat{x}^k,y^j)\le h(\hat{x}^k)$, as well as the definition of $m_{_l}$, we can obtain that

$$\begin{aligned} \epsilon _{_l}=H_{\hat{x}^k}(\hat{x}^k)-m_{_l}\ge 0. \end{aligned}$$

(2.21)

From here the thesis can be readily proved.

Remark 1

Lemma 2.1 and Lemma 2.3 play a critical role in establishing an approximate optimality condition. Since $G^l \in \partial _{\epsilon _{_l}} H_{\hat{x}^k}(\hat{x}^k)$, we can obtain that

$$\begin{aligned} G^l+\alpha ^l \in \partial _{\epsilon _{_l}} (H_{\hat{x}^k}(\hat{x}^k)+ i_X (\hat{x}^k)), \end{aligned}$$

where $i_X (\cdot )$ stands for the indicator function of the set X. Therefore, if $\Vert G^l+\alpha ^l\Vert$ and $\epsilon _{_l}$ are small enough, the current stabilized center $\hat{x}^k$ can be accepted as an approximate optimal solution.

3 A constrained incremental bundle method

Now we are ready to introduce an incremental bundle method for solving the SIP problem (1). Setting the following global parameters for the execution of our method:

• the optimality tolerance $\varepsilon >0$ and the subgradient approximation measure $\eta > 0$;

• the increase parameter $\sigma > 1$.

Three positive parameters subject to possible modifications are also needed, that is the descent parameter $\delta$, the proximity parameter $\mu$ and the inner precision parameter $\omega$. In addition, the initial parameters are set, respectively, as $\delta :=\delta _0$, $\mu :=\mu _0>1$ and $\omega :=\omega _0$ with $\omega _0<\varepsilon$. For convergence analysis, the following condition should be satisfied

$$\begin{aligned} \eta ^2>\frac{2\mu _{_0}\delta _{_0}}{\iota -0.5}, \ \ \ \omega _{_0}=\frac{\eta ^2}{4 \mu _{_0}}, \ \ \ \iota \in (0.5,1), \end{aligned}$$

which imply that

$$\begin{aligned} \eta ^2>\frac{2\mu _0(\delta _0+\omega _0)}{\iota }. \end{aligned}$$

(3.1)

Algorithm 1

Step 0 (Input and Initialization).

Select an initial starting point $x^0$, a point $y^0 \in Y$, $\iota \in (0,1)$, the optimality tolerance $\varepsilon >0$, the subgradient approximation measure $\eta >0$, and the increase parameter $\sigma >1$. Call oracle to compute $f(x^0)$, $c(x^0,y^0)$, as well as $g_f^0\in \partial f(x^0)$, $g_{c_{_0}}^0 \in \partial _{x}c(x^0,y^0)$. Initialize the iteration counter $k=l=0$, choose the bundle index set $L^f_0:=\{0\}$, $L^c_0:=\{0\}$, the first stabilized center $\hat{x}^0=x^0$, the starting prox-parameter $\mu _{_0}$ as well as $\delta _{_0}$, $\omega _{_0}$.

The main iteration

Step 1 (Model Generation and QP Subproblem)

Having the current stabilized center $\hat{x}^k$, the bundle $\mathcal {B}_l$, the prox-parameter $\mu _{_l}$. Solve QP($\mathcal {B}_l$) (2.15), or the corresponding dual problem DP($\mathcal {B}_l$), and obtain both the optimal primal and dual solutions $(d^{l},r_{_l})$ and $\lambda ^l$, $\gamma ^l$. Let $x^{l+1}:=\hat{x}^k+d^l$. Select a point $y^{l+1} \in Y$, and call oracle to compute $f(x^{l+1})$, $c(x^{l+1},y^{l+1})$, as well as $g_f^{l+1}$, $g_{c_{l+1}}^{l+1}$. If

$$\begin{aligned} \Vert G^l+\alpha ^l\Vert >\eta , \end{aligned}$$

(3.2)

then go to Step 3.

Step 2 (Approximate optimality test)

Estimate the $c(\hat{x}^k,y(\hat{x}^k))$, and let $c^+(\hat{x}^k,y(\hat{x}^k)):=\max \{0, c(\hat{x}^k,y(\hat{x}^k))\}$. If

$$\begin{aligned} c^+(\hat{x}^k,y(\hat{x}^k)) \le m_{_l}+\varepsilon -\omega , \end{aligned}$$

(3.3)

where

$$\begin{aligned} m_{_l}:= \sum \limits _{j\in J_l^f} \lambda ^l_j (\beta _j-f(\hat{x}^k)) +\sum \limits _{j\in J_l^c} \gamma ^l_j \nu _j, \end{aligned}$$

then an approximate optimal solution has been found, then stops.

Else set $\mu _{_{l+1}}:= \sigma \mu _{_l}$, $\delta _{_{l+1}}:=\delta _{_{l}}/\sigma$, $\omega _{_{l+1}}:=\eta ^2/4\mu _{_{l+1}}$, and perform a bundle restoration procedure, that is delete one or more elements from the bundle, while keeping at least the element referred to the stability center $\hat{x}^k$, i.e.,

$$\begin{aligned} J_f^l:=\{1\},\ J_c^l:=\{1\}, \ \mathcal {B}_f^l:=\{\hat{x}^k,f(\hat{x}^k),\hat{g}_f^k,\hat{\beta }_k \},\ \mathcal {B}_c^l:=\{\hat{x}^k,c(\hat{x}^k,y(\hat{x}^k)),\hat{g}_{c_k}^k, \hat{\nu }_k \}, \end{aligned}$$

where $\hat{\beta }_k=f(\hat{x}^k)$, $\hat{g}_f^k\in \partial f(\hat{x}^k)$, $\hat{\nu }_k=c(\hat{x}^k ,y(\hat{x}^k))$, $\hat{g}_{c_k}^k \in \partial _{x} c(\hat{x}^k ,y(\hat{x}^k))$. Set $l:=l+1$ and return to Step 1.

Step 3. (Noise Attenuation Test)

As soon as

$$\begin{aligned} f(x^{l+1})-f(\hat{x}^k) > \iota r_{_l} +(1-\iota )m_{_l}+\delta , \end{aligned}$$

(3.4)

update the bundle

$$\begin{aligned} \mathcal {B}_{l+1}^f:=\mathcal {B}_l^f \bigcup \Big \{x^{l+1}, f(x^{l+1}), g_{f}^{l+1},\beta _{l+1} \Big \},\ \ \mathcal {B}_{l+1}^c:=\mathcal {B}_l^c. \end{aligned}$$

(3.5)

Next update the bundle index set $l:=l+1$, and return to Step 1.

Otherwise, estimate a point $\bar{y}:=y(x^{l+1})\in Y$, and launch the oracle to compute $c(x^{l+1},\bar{y})$, $g_{c_{\bar{y}}}^{l+1} \in \partial _x c(x^{l+1},\bar{y})$. If it fulfills another cut property

$$\begin{aligned} c\left( x^{l+1},\bar{y}\right) >\omega +\delta , \end{aligned}$$

(3.6)

then we set $y^{l+1}=\bar{y}$, $g_{c_{_{l+1}}}^{l+1}=g_{c_{_{\bar{y}}}}^{l+1}$, and $\nu _{_{l+1}} := c(x^{l+1},\bar{y})+\langle g_{c_{_{\bar{y}}}}^{l+1},\hat{x}^k-x^{l+1} \rangle$, and update the bundle as follows

$$\begin{aligned} \mathcal {B}_{l+1}^c:=\mathcal {B}_l^c \bigcup \Big \{x^{l+1},c(x^{l+1},y^{l+1}), g_{c_{_{l+1}}}^{l+1},\nu _{_{l+1}} \Big \},\ \ \mathcal {B}_{l+1}^f:=\mathcal {B}_l^f. \end{aligned}$$

(3.7)

Next update the bundle index set $l:=l+1$, and return to Step 1. Otherwise, set $\hat{x}^{k+1}=x^{l+1}$, and exit the main iteration and go to Step 4.

Step 4 (Bundle update)

Update the index $k:=k+1$ and the bundle with respect to the new stabilized center, and return to Step 1.

We now add some another comments of Algorithm 1. Step 2 aims to test the approximate optimality condition introduced in Lemma 2.3. If our algorithm stops at Step 2, namely, the termination of Algorithm 1, takes place when

$$\begin{aligned} \Vert G^l+\alpha ^l\Vert \le \eta , \ \ c^+(\hat{x}^k,y(\hat{x}^k))\le m_{_l}+\varepsilon -\omega . \end{aligned}$$

By noting the fact that $h(\hat{x}^k)\le c(\hat{x}^k,y(\hat{x}^k))+\omega$ and combining with (2.2), we have

$$\begin{aligned} \begin{array}{lll} H_{\hat{x}^k}(\hat{x}^k) &{}\le c^{+}(\hat{x}^k,y(\hat{x}^k))+\omega \\ &{}\le m_{_l}+\varepsilon . \end{array}\end{aligned}$$

Using (2.21), it holds that

$$\begin{aligned} \epsilon _{_l}=H_{\hat{x}^k}(\hat{x}^k)-m_{_l}\le \varepsilon . \end{aligned}$$

In short, Algorithm 1 stops if and only if

$$\begin{aligned} \Vert G^l+\alpha ^l\Vert \le \eta \ \ \mathrm{and} \ \ \epsilon _{_l}\le \varepsilon , \end{aligned}$$

which implies, by combining with Lemma 2.1 and Lemma 2.3, that the current stabilized center $\hat{x}^k$ satisfies KKT conditions (2.5) and (2.6) approximatively. Otherwise, the proximal parameter $\mu$ will increase, and parameters $\delta$ and $\omega$ decrease properly. In the meantime, bundle information will be reset, or rather the elimination of all the elements but the stabilized center, whose related information will be fixed after the initial bundle reset. Accordingly, along with the increase of $\mu$, the step length $d^l$ will become less and less, that means the trial points will be closer to the stabilized center.

It is worth noting that in Step 3, the reduction has been achieved, whenever the decrease property and the condition (3.2) are satisfied. Therefore, whenever Algorithm 1 exits from the main iteration, a new stabilized center has been obtained, and this correlative information is needed to update before a new execution of the main iteration is entered.

4 Convergence results

Now it is well known that each new trial point should provide either a better point of the current estimate of the minimum of $f(\cdot )$, or at least a better point of the approximation properties of the model $\mathcal {M}_l(\cdot )$. The following Lemmas 4.1, 4.2 will give two simple properties named the decrease property and the cut property, respectively.

Lemma 4.1

Let $\delta$ be any positive scalar and $\iota \in (0,1)$. If

$$\begin{aligned} \begin{array}{lll} &{}f(x^{l+1})-f(\hat{x}^k)\le \iota r_{_l} +(1-\iota )m_{_l}+\delta ,\\ &{}~c(x^{l+1},y(x^{l+1})) \le \omega +\delta \end{array}\end{aligned}$$

(4.1)

hold, then $x^{l+1}$ is the serious point, and the following decrease property holds:

$$\begin{aligned} f\left( x^{l+1}\right) \le f(\hat{x}^k)-\mu _{_l}\iota \Vert x^{l+1}-\hat{x}^k\Vert ^2+2(\omega +\delta ). \end{aligned}$$

(4.2)

Proof

If the first relation in (4.1) holds, we can obtain that

$$\begin{aligned} \begin{array}{lllll} &{}f\left( x^{l+1}\right) -f(\hat{x}^k) \le \iota r_{_l} +(1-\iota )m_{_l} +\delta \\ &{} \quad =\sum \limits _{j \in J_l^f} \lambda ^l_j (\beta _j-f(\hat{x}^k)) +\sum \limits _{j\in J_l^c}\gamma ^l_j \nu _j +\iota \langle G^l, d^{l}\rangle +\delta , \end{array}\end{aligned}$$

(4.3)

where the last equality has used the definitions in (2.16) and (2.17). Observe that the serious point $\hat{x}^k$ satisfies (4.1), we can obtain that

$$\begin{aligned} c(\hat{x}^k,y(\hat{x}^k))\le \omega +\delta . \end{aligned}$$

In view of (2.11), and the convexity of $f(\cdot )$ and $c(\cdot , y)$, it holds that

$$\begin{aligned} \beta _j-f(\hat{x}^k) \le 0,\ \mathrm{for \ all} \ j \in J_l^f, \end{aligned}$$

and

$$\begin{aligned} \nu _{_j}\le c(\hat{x}^k,y^j) \le h(\hat{x}^k) \le 2\omega +\delta , \ \mathrm{for \ all} \ j \in J_l^c, \end{aligned}$$

where the second inequality has used the fact that $h(\hat{x}^k)\le c(\hat{x}^k,y(\hat{x}^k))+\omega$. By noting $\sum \limits _{j\in J_l^f} \lambda ^l_j +\sum \limits _{j\in J_l^c} \gamma ^l_j=1$, and combining with the relation (4.3), we have

$$\begin{aligned} f(x^{l+1}) \le f(\hat{x}^k) +\iota \langle G^l, x^{l+1}-\hat{x}^k\rangle +2\omega +2\delta . \end{aligned}$$

Following (2.16), we can observe that

$$\begin{aligned} \begin{array}{lll} \langle G^l, x^{l+1}-\hat{x}^k\rangle =-\mu _{_l} \Vert x^{l+1}-\hat{x}^k\Vert ^2 -\langle \alpha ^l, x^{l+1}-\hat{x}^k\rangle \le -\mu _{_l} \Vert x^{l+1}-\hat{x}^k\Vert ^2, \end{array}\qquad \end{aligned}$$

(4.4)

where the last inequality has used the fact that $\alpha ^l \in N_{X}(x^{l+1})$. As a result,

$$\begin{aligned} f(x^{l+1}) \le f(\hat{x}^k)-\mu _{_l} \iota \Vert x^{l+1} -\hat{x}^k\Vert ^2+2\omega +2\delta . \end{aligned}$$

From here the result has been proved.

Lemma 4.2

Let $\delta$ be any positive scalar and $\iota \in (0,1)$.

• (i) If

  $$\begin{aligned} f(x^{l+1})-f(\hat{x}^k) > \iota r_{_l} +(1-\iota )m_{_l}+\delta \end{aligned}$$

  holds, then $(d^{l},r_{_l})$ is not feasible for problem QP($\mathcal {B}_{l+1}$) by resetting the bundle, such as

  $$\begin{aligned} \mathcal {B}_{l+1}^f :=\mathcal {B}_l^f \bigcup \Big \{x^{l+1}, f(x^{l+1}), g_{_f}^{l+1},\beta _{l+1}\Big \}, \ \ \mathcal {B}_{l+1}^c:=\mathcal {B}_l^c. \end{aligned}$$

  (4.5)

• (ii) If the point $y^{l+1} \in Y$ satisfying

  $$\begin{aligned} c\left( x^{l+1},y^{l+1}\right) >\omega +\delta , \end{aligned}$$

  then $(d^{l},r_{_l})$ is not feasible for problem QP($\mathcal {B}_{l+1}$) by resetting the bundle, such as

  $$\begin{aligned} \mathcal {B}_{l+1}^c:=\mathcal {B}_l^c \bigcup \Big \{x^{l+1},c(x^{l+1},y^{l+1}), g_{c_{_{l+1}}}^{l+1}, \nu _{_{l+1}}\Big \}, \ \ \mathcal {B}_{l+1}^f:=\mathcal {B}_l^f. \end{aligned}$$

  (4.6)

Proof

If the first condition holds, i.e., $f(x^{l+1})-f(\hat{x}^k) >\iota r_{_l}+(1-\iota )m_{_l} +\delta$. By using (2.11) and (2.16), we can obtain that

$$\begin{aligned} \begin{array}{lll} &{} \beta _{l+1}-f(\hat{x}^k)+\langle g_f^{l+1}, d^{l}\rangle \\ &{} =f(x^{l+1})-f(\hat{x}^k)\\ &{}>\iota r_{_l} +(1-\iota )m_{_l}+\delta \\ &{}=r_{_l}+\mu _{_l}(1-\iota )\Vert d^l\Vert ^2 -(1-\iota )\langle \alpha ^l, \hat{x}^k-x^{l+1} \rangle +\delta \\ &{}\ge r_{_l}+\delta , \end{array}\end{aligned}$$

where the last inequality follows from $\alpha ^l \in N_{X}(x^{l+1})$ and $\iota \in (0,1)$. Thus $(d^{l},r_{_l})$ is not feasible for problem QP($\mathcal {B}_{l+1}$).

Since f and $c(\cdot ,y)$ for any $y\in Y$ are convex, by noting (2.11), we have

$$\begin{aligned} \beta _{j}-f(\hat{x}^k)+\langle g_f^j, 0 \rangle \le 0, \ \ \mathrm{for \ all } \ j\in J_{l}^f, \end{aligned}$$

and

$$\begin{aligned} \begin{array}{lll} &{}\nu _{_j}+\langle g_{c_{_j}}^j,0 \rangle \le c(\hat{x}^k,y^j)\\ &{}\le h(\hat{x}^k)\le c(\hat{x}^k,y(\hat{x}^k))+\omega \\ &{}\le 2\omega +\delta , \end{array}\end{aligned}$$

for all $j\in J_l^c$, where the last inequality has used $c(\hat{x}^k,y(\hat{x}^k))\le \omega +\delta$. Thus, $(0,2\omega +\delta )$ is a feasible point of the corresponding quadratic program. Using (2.16) and noting $(d^l,r_{_l})$ is the solution of the corresponding quadratic program, then the optimal values $w_{_l}$ is smaller than $2\omega +\delta$, i.e.,

$$\begin{aligned} r_{_l}+\frac{1}{2\mu _{_l}}\Vert G^l+\alpha ^l\Vert ^2 = r_{_l}+\frac{\mu _{_l}}{2}\Vert d^{l}\Vert ^2\le 2\omega +\delta , \end{aligned}$$

which, taking into account $\Vert G^l+\alpha ^l\Vert >\eta$ and $\omega =\eta ^2/4 \mu _{_l}$, implies that

$$\begin{aligned} r_{_l}\le 2\omega +\delta -\frac{1}{2\mu _{_l}}\Vert G^l+\alpha ^l\Vert ^2 = \delta . \end{aligned}$$

(4.7)

Moreover, if the condition (ii) holds, by using the above inequality, we can obtain

$$\begin{aligned} \begin{array}{lll} &{} \nu _{_{l+1}}+\langle g_{c_{_{l+1}}}^{l+1}, d^{l} \rangle \\ &{}=c(x^{l+1},y^{l+1})\\ &{}>\omega +\delta \\ &{} \ge r_{_l}+\omega , \end{array}\end{aligned}$$

where the first inequality follows from (3.6), and the last one has used the (4.7). It follows that $(d^{l},r_{_l})$ is not feasible for QP($\mathcal {B}_{l+1}$). Thus the thesis easily follows.

We now give a preliminary result for the global convergence of Algorithm 1.

Lemma 4.3

Suppose that $w_{_l}$ and $w_{_{l+1}}$ are, respectively, the optimal values of QP($\mathcal {B}_{l}$) and QP($\mathcal {B}_{l+1}$). Then

$$\begin{aligned} w_{_{l+1}} \ge w_{_l}+\frac{\mu _{_l}}{2}\Vert d^{l+1}-d^{l}\Vert ^2. \end{aligned}$$

(4.8)

Proof

Suppose that $(\bar{d},\bar{r})$ is any feasible point for QP($\mathcal {B}_{l}$), then it fulfils the following inequalities

$$\begin{aligned} \begin{array}{lll} &{} \beta _{j}-f(\hat{x}^k)+\langle g_f^j, \bar{d}\rangle \le \bar{r}, \ \ j\in J_l^f,\\ &{}\nu _{_j}+\langle g_{c_{_j}}^j, \bar{d} \rangle \le \bar{r}, \ \ j\in J_l^c. \end{array}\end{aligned}$$

By combining with (2.17), we obtain that

$$\begin{aligned} m_{_l}+\langle G^l, \bar{d}\rangle \le \bar{r}. \end{aligned}$$

Observe that $(d^{l+1},r_{_{l+1}})$ is a feasible point for QP($\mathcal {B}_{l}$), then one gets

$$\begin{aligned} m_{_l}+\langle G^l, d^{l+1}\rangle \le r_{_{l+1}}. \end{aligned}$$

Since $(d^{l},r_{_l})$ is the optimal solution of QP($\mathcal {B}_{l}$), it follows from (2.16) that

$$\begin{aligned} m_{_l}+\langle G^l,d^l \rangle = r_{_l}. \end{aligned}$$

By the above two relations, thus

$$\begin{aligned} \langle G^l, d^{l+1}-d^{l}\rangle \le r_{_{l+1}}-r_{_l}. \end{aligned}$$

(4.9)

Observe further that

$$\begin{aligned} \begin{array}{llll} w_{_{l+1}}&{}=r_{_{l+1}}+\frac{\mu _{_{l+1}}}{2}\Vert d^{l+1}\Vert ^2\\ &{}\ge r_{_{l+1}}-r_{_{l}}+r_{_{l}}+\frac{\mu _{_{l}}}{2}\Vert d^{l+1}-d^l+d^l\Vert ^2\\ {} &{}\ge \langle G^l, d^{l+1}-d^{l}\rangle +w_{_l} +\frac{\mu _{_{l}}}{2}\Vert d^{l+1}-d^{l}\Vert ^2 +\mu _{_l}\langle d^{l+1}-d^{l}, d^{l} \rangle , \end{array}\end{aligned}$$

(4.10)

where the last inequality has used (4.9) and the definition of $w_{_l}$. By noting the fact that $d^l =-\frac{1}{\mu _{_l}}(G^l+\alpha ^l)$ and $\alpha ^l \in N_{X}(x^{l+1})$, it obtains that

$$\begin{aligned} \begin{array}{llll} &{} \mu _{_l}\langle d^{l+1}-d^{l}, d^{l} \rangle \\ &{}=-\langle G^l, d^{l+1}-d^{l}\rangle -\langle \alpha ^l, x^{l+2}-x^{l+1}\rangle \\ &{}\ge -\langle G^l, d^{l+1}-d^{l}\rangle , \end{array}\end{aligned}$$

which implies, together with (4.10), that (4.8) holds.

Lemma 4.4

Suppose that $(d^{l},r_{_l})$ is the optimal solution to QP($\mathcal {B}_l$). Let $j(k)\in J_{l}^f$ denote an iteration index yielding a serious step: $\hat{x}^{k}=x^{j(k)}:=\hat{x}^{k-1}+d^{j(k)-1}$. The following properties hold:

• (1) $r_{_l}\le H_{\hat{x}^{k}} (\hat{x}^{k})$ ;

• (2) $r_{_l}\le H_{\hat{x}^{k}} (x^{l+1})$ ;

• (3) $d^{l} \in V_{R_{_{l(k)}}} (0)$ (a neighbourhood of 0 with radius $R_{l(k)}$), where

  $$\begin{aligned} R_{_{l(k)}} =\left\{ \begin{array}{ll} ~~~~~~~~~~~\frac{2\Vert g_f^{j(k)}\Vert }{\mu _{_l}}, \ &{}\mathrm{if} \ m_{_l}\le 0;\\ \frac{\Vert G^l\Vert +\sqrt{\Vert G^l\Vert ^2+2\mu _{_l}H_{\hat{x}^k}(\hat{x}^k)}}{\mu _{_l} }, \ &{}\mathrm{if} \ m_{_l}> 0.\end{array}\right. \end{aligned}$$

  (4.11)

Proof

• (1) Since f is convex, by (2.11) and (2.15), one gets

  $$\begin{aligned} \begin{array}{llll} &{}\beta _{l}-f(\hat{x}^k)+\langle g_f^l,0 \rangle \\ &{}=-(f(\hat{x}^k)-f(x^l)-\langle g_f^l, \hat{x}^k-x^l \rangle )\\ &{}\le 0. \end{array}\end{aligned}$$

  On the other hand, by noting the convexity of $c(\cdot , y^l$), we can obtain that

  $$\begin{aligned} \begin{array}{lll} &{} \nu _{_l}+\langle g_{c_l}^l, 0 \rangle \\ &{}=c(x^l,y^l)+\langle g_{c_l}^l, \hat{x}^k-x^l \rangle \\ &{}\le c(\hat{x}^k,y^l). \end{array}\end{aligned}$$

  Recalling the definition of $H_{\hat{x}^k}(\cdot )$, we can obtain that $(0,H_{\hat{x}^k}(\hat{x}^k))$ is a feasible point of QP($\mathcal {B}_l$). Thus,

  $$\begin{aligned} r_{_l}\le r_{_l} +\frac{\mu _{_l}}{2} \Vert d^l\Vert ^2\le H_{\hat{x}^k}(\hat{x}^k). \end{aligned}$$

• (2) It follows by observing that $r_{_l}=\mathcal {M}_{l} (\hat{x}^k+d^{l})\le H_{\hat{x}^k} (\hat{x}^k+d^{l}).$

• (3) Suppose now that $m_{_l}\le 0$, it follows from (2.16) that

  $$\begin{aligned} r_{_l}\le \langle G^l, d^l\rangle =-\mu _{_l}\Vert d^l\Vert ^2-\langle \alpha ^l, x^{l+1}-\hat{x}^k \rangle <0. \end{aligned}$$

  Thus (0, 0) is the feasible point for QP($\mathcal {B}_l$).

By noting the relation (2.11), it holds that

$$\begin{aligned} \begin{array}{lll} \beta _{j(k)}&{}:=f(x^{j(k)})+\left\langle g_f^{j(k)},\hat{x}^k-x^{j(k)} \right\rangle \\ &{}=f(\hat{x}^{k})=\hat{\beta }_k. \end{array}\end{aligned}$$

Notice that (0, 0) is the feasible point for QP($\mathcal {B}_l$), then the optimal value $w_{_l}=r_{_l}+\frac{\mu _{_l}}{2}\Vert d^{l}\Vert ^2$ is smaller than 0. Thus we can obtain that

$$\begin{aligned} \begin{array}{llll} 0&{}\ge r_{_l}+\frac{\mu _{_l}}{2}\Vert d^{l}\Vert ^2\\ &{} \ge \beta _{j(k)}-f(\hat{x}^k)+\langle g_f^{j(k)}, d^l \rangle +\frac{\mu _{_l}}{2}\Vert d^{l}\Vert ^2\\ &{}=\langle g_f^{j(k)}, d \rangle +\frac{\mu _{_l}}{2}\Vert d^{l}\Vert ^2\\ &{}\ge \frac{\mu _{_l}}{2}\Vert d^l\Vert ^2-\Vert g_f^{j(k)}\Vert \Vert d^l\Vert , \end{array}\end{aligned}$$

where the second inequality has used the fact that $r_{_l}\ge \beta _{j(k)}-f(\hat{x}^k)+\langle g_f^{j(k)}, d^l \rangle$. Thus, we can obtain that

$$\begin{aligned} \Vert d^l\Vert \le \frac{2\Vert g_f^{j(k)}\Vert }{\mu _{_l}}. \end{aligned}$$

On the other hand, if $m_{_l}>0$ holds, then by noting the fact that $(0,H_k(\hat{x}^k))$ is feasible point for QP($\mathcal {B}_l$), we obtain that the optimal value $w_{_l}= r_{_l}+\frac{\mu _{_l}}{2}\Vert d^l\Vert ^2$ is smaller than $H_k(\hat{x}^k)$, i.e.,

$$\begin{aligned} H_{\hat{x}^k}(\hat{x}^k)\ge r_{_l}+\frac{\mu _{_l}}{2}\Vert d^l\Vert ^2. \end{aligned}$$

Furthermore, by noting (2.16), we obtain that

$$\begin{aligned} \begin{array}{llll} 0&{} \ge \frac{\mu _{_l}}{2}\Vert d^l\Vert ^2 +\langle G^l, d^l\rangle + m_{_l}-H_{\hat{x}^k}(\hat{x}^k)\\ &{}\ge \frac{\mu _{_l}}{2}\Vert d^l\Vert ^2 -\Vert G^l\Vert \Vert d^l\Vert -H_{\hat{x}^k}(\hat{x}^k). \end{array}\end{aligned}$$

Thus

$$\begin{aligned} \Vert d^l\Vert \le \frac{\Vert G^l\Vert +\sqrt{\Vert G^l\Vert ^2+2\mu _{_l}H_{\hat{x}^k}(\hat{x}^k)}}{\mu _{_l}}, \end{aligned}$$

From here all the items have been proven.

To prove global convergence of Algorithm 1, it is necessary to obtain the finite termination of the “main iteration”. The finiteness of the “main iteration” corresponds to prove that one of the following cases can occur:

• either there are finitely many passages through Step 2, or

• the “main iteration” passes finitely many times through Step 3.

In what follows, we suppose that $f(\cdot )$ and $c(\cdot ,y)$ for any $y\in Y$ are boundedness from below on subset X, which is a standing assumption in nonsmooth optimization. Moreover, let L denote the Lipschitz constant of $f(\cdot )$ and $c(\cdot ,y)$ for any $y\in Y$ on subset X, then we can obtain that $\Vert g_f^l\Vert \le L$, $\Vert g_{c_{y}}^l\Vert \le L$ for all $y\in Y$, and then $\Vert G^l\Vert \le L$.

In the following two lemmas, we can obtain that the “main iteration” is well defined.

Lemma 4.5

There are finitely many passages through Step 2. That is only finite loops between Step 1 and Step 2 are executed.

Proof

For a contradiction, we assume there are infinitely many passages through Step 2. For convenience, let $\hat{x}^k$ and t denote, respectively, the current fixed stabilized center and the index of the tth passage through Step 2. Furthermore, let $(\tilde{d}^{t},\tilde{r}_t)$, $(\tilde{\lambda }^t, \tilde{\gamma }^t)$, $\tilde{R}_{_t}$, $\tilde{\mu }_{t}$ and $\tilde{\omega }_{t}$ denote, respectively, the primal solution of the current quadratic program, the matching multipliers, the upper bound of $\tilde{d}^t$, the prox-parameter and the inner precision parameter.

Infinitely many passages through Step 2 imply the following conditions:

$$\begin{aligned} \Vert \tilde{G}^t+\tilde{\alpha }^t\Vert \le \eta , \end{aligned}$$

and

$$\begin{aligned} c^+(\hat{x}^k,y(\hat{x}^k)) > \tilde{m}_{_t}+\varepsilon -\tilde{\omega }_{t} \ \ \end{aligned}$$

(4.12)

are simultaneously satisfied infinitely many times. Observe that the bundle will be always restored, which ensures the elements

$$\begin{aligned} \begin{array}{llll} \mathcal {B}_f^l:=\{\hat{x}^k,f(\hat{x}^k),\hat{g}_f^k,\hat{\beta }_k \},\ &{}\mathrm{where} \ \hat{\beta }_k=f(\hat{x}^k),\\ \mathcal {B}_c^l:=\{\hat{x}^k,c(\hat{x}^k,y(\hat{x}^k)),\hat{g}_{c_k}^k, \hat{\nu }_k \}, \ &{}\mathrm{where} \ \hat{\nu }_{_k}=c(\hat{x}^k ,y(\hat{x}^k)) \end{array}\end{aligned}$$

are always preserved in the bundle. By noting (4.11) in Lemma 4.4, we get that

$$\begin{aligned} \Vert \tilde{d}^{t}\Vert \le \tilde{ R}_{_t}\le \max \left\{ \frac{2L }{\tilde{\mu }_{_t}},\ \frac{2L+\sqrt{2\tilde{\mu }_{_t}H_{\hat{x}^k}(\hat{x}^k)}}{\tilde{\mu }_{_t} }\right\} . \end{aligned}$$

By noting $\tilde{\mu }_{_t}\rightarrow \infty$, we can obtain that $\Vert \tilde{d}^{t}\Vert$ tends to 0 as $t\rightarrow \infty$. Since $(\tilde{d}^{t},\tilde{r}_{_t})$ is the solution of QP($\mathcal {B}$), then it is of course a feasible point of the problem, namely,

$$\begin{aligned} \tilde{r}_{_t}\ge \hat{\beta }_k -f(\hat{x}^k)+\langle \hat{g}_f^k,\tilde{d}^{t} \rangle \ge -L\Vert \tilde{d}^{t}\Vert , \end{aligned}$$

and

$$\begin{aligned} \tilde{r}_{_t}\ge \hat{\nu }_k+\langle \hat{g}_{c_k}^k, \tilde{d}^{t} \rangle \ge c(\hat{x}^k ,y(\hat{x}^k)) -L\Vert \tilde{d}^{t}\Vert , \end{aligned}$$

which imply that

$$\begin{aligned} \tilde{r}_{_t} \ge c^+(\hat{x}^k,y(\hat{x}^k))-L\Vert \tilde{d}^{t}\Vert . \end{aligned}$$

Besides, since f and $c(\cdot ,y)$ for any $y\in Y$ are convex, by noting (2.11), we have

$$\begin{aligned} \begin{array}{llll} \beta _{j}-f(\hat{x}^k)+\langle g_f^j, 0 \rangle \le 0, \ \ \mathrm{for \ all } \ j\in \tilde{J}_{t}^f, \end{array}\end{aligned}$$

and

$$\begin{aligned} \begin{array}{llll} \nu _{_j}+\langle g_{c_j}^j,0 \rangle \le c(\hat{x}^k,y^j)\le h(\hat{x}^k)\le c(\hat{x}^k,y(\hat{x}^k))+\tilde{\omega }_{t}, \ \ \mathrm{for \ all } \ j\in \tilde{J}_t^c, \end{array}\end{aligned}$$

which imply that $(0,c^+(\hat{x}^k,y(\hat{x}^k))+\tilde{\omega }_{t})$ is the feasible point of the matching quadratic program. Observe that $(\tilde{d}^{t}, \tilde{r}_{_t})$ is the solution of the matching quadratic program, then the corresponding optimal values $\tilde{w}_{_t}$ is smaller than $c^+(\hat{x}^k,y(\hat{x}^k))+\tilde{\omega }_{t}$, i.e.,

$$\begin{aligned} \tilde{w}_{_t}:=\tilde{r}_{_t} +\frac{\tilde{\mu }_{_t}}{2} \Vert \tilde{d}^{t}\Vert ^2\le c^+(\hat{x}^k,y(\hat{x}^k))+\tilde{\omega }_{t}. \end{aligned}$$

Hence we have that

$$\begin{aligned} c^+(\hat{x}^k,y(\hat{x}^k))+\tilde{\omega }_{t}\ge \tilde{r}_{_t} \ge c^+(\hat{x}^k,y(\hat{x}^k))-L\Vert \tilde{d}^{t}\Vert . \end{aligned}$$

Now, by noting the fact that $\lim \limits _{t\rightarrow \infty } \tilde{\omega }_{t}=0$ and $\lim \limits _{t\rightarrow \infty }\Vert \tilde{d}^{t}\Vert =0$, we have

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }\tilde{r}_{_t}= c^+(\hat{x}^k,y(\hat{x}^k)). \end{aligned}$$

Moreover, by using (2.16), we obtain that $\tilde{m}_{_t}\rightarrow c^+(\hat{x}^k,y(\hat{x}^k))$ as $t\rightarrow \infty$, which is a contradiction with (4.12). From here the result has been proved.

Lemma 4.6

The “main iteration” is impossible to loop infinitely many times between Step 1 and Step 3.

Proof

Suppose first, for a contradiction, there are infinitely many passages through Step 3. Note the quadratic program QP($\mathcal {B}$) will be solved infinitely many times, with the cut property (3.4) or (3.6) holds. For convenience, let $\hat{x}=\hat{x}^k$, $\tilde{\mu }$ and $\tilde{\omega }$ denote, respectively, the current fixed stabilized center, the current fixed prox-parameter and the fixed inner precision parameter. Let t, $(\tilde{d}_{_t}, \tilde{r}_{_t})$ and $(\tilde{\lambda }^t, \tilde{\gamma }^t)$ stand for, respectively, the index of the tth passage through Step 3, the primal solution and the matching multipliers of the current quadratic program.

Then the matching optimal values can be denoted as

$$\begin{aligned} \tilde{w}_{_t}:=\tilde{r}_{_t}+\frac{\tilde{\mu }}{2}\Vert \tilde{d}^{t}\Vert ^2. \end{aligned}$$

According to Lemma 2.2 and Lemma 4.3, we obtain that $\{\tilde{w}_{_t} \}$ is monotonously nondecreasing and bounded, thus convergent. The latter implies, again by Lemma 4.3, that

$$\begin{aligned} \Vert \tilde{d}^{t+1}-\tilde{d}^{t}\Vert ^2\rightarrow 0 \ \ \mathrm{as}\ t\rightarrow \infty , \end{aligned}$$

which combines with the boundedness of $\{ \Vert \tilde{d}^t\Vert \}$, it holds that $\{\tilde{d}^{t}\}$ is convergent. As a consequence, by noting that $\tilde{r}_{_t}=\frac{\tilde{\mu }}{2}\Vert \tilde{d}^{t}\Vert ^2-\tilde{w}_{_t}$, then the sequence $\{\tilde{r}_{_t}\}$ is also convergent.

Infinitely many passages through Step 3 imply the following conditions hold infinitely many times

$$\begin{aligned} \Vert \tilde{G}^t+\tilde{\alpha }^t\Vert >\eta , \end{aligned}$$

and either

$$\begin{aligned} f(\tilde{x}^{t+1})-f(\hat{x}) > \iota \tilde{r}_{_t} +(1-\iota )\tilde{m}_{_t}+\delta , \end{aligned}$$

(4.13)

or

$$\begin{aligned} c(\tilde{x}^{t+1},y(\tilde{x}^{t+1})) > \tilde{\omega }+\delta . \end{aligned}$$

(4.14)

If the inequality (4.13) holds infinitely many times. Observe that $(\tilde{d}^{t+1}, \tilde{r}_{_{t+1}})$ is the solution of QP($\mathcal {B}_{t+1}$), thus it is of course the feasible point of the current quadratic program, namely,

$$\begin{aligned} \begin{array}{llll} \tilde{r}_{_{t+1}} &{}\ge \tilde{\beta }_{t+1}-f(\hat{x})+\langle \tilde{g}_f^{t+1}, \tilde{d}^{t+1} \rangle \\ &{}=f\left( \tilde{x}^{t+1}\right) -f\left( \hat{x}\right) +\langle \tilde{g}_f^{t+1},\tilde{d}^{t+1}-\tilde{d}^{t} \rangle \\ &{}>\iota \tilde{r}_{_t} +(1-\iota )\tilde{m}_{_t}+\delta +\langle \tilde{g}_f^{t+1},\tilde{d}^{t+1}-\tilde{d}^{t} \rangle , \end{array}\end{aligned}$$

where the last inequality follows from (4.13). Thus, we can obtains that

$$\begin{aligned} \begin{array}{llll} &{} \delta +\langle \tilde{g}_f^{t+1}, \tilde{d}^{t+1}-\tilde{d}^{t}\rangle \\ &{} \le (\tilde{r}_{_{t+1}}-\tilde{r}_{_{t}})+(1-\iota )(\tilde{r}_{_{t}}-\tilde{m}_{_t})\\ &{} = (\tilde{r}_{_{t+1}}-\tilde{r}_{_{t}})+(1-\iota )\langle \tilde{G}^t,\tilde{d}^t\rangle \\ &{} \le \tilde{r}_{_{t+1}}-\tilde{r}_{_{t}}, \end{array}\end{aligned}$$

(4.15)

where the last inequality has used the relation (4.4), and the equality follows from (2.16). Passing to the limit and noting the boundedness of $\tilde{g}_f^{t+1}$, it holds that $\delta \le 0$, which is a contradiction.

On the other hand, if (4.14) holds infinitely many times, by noting $(\tilde{d}^{t+1}, \tilde{r}_{_{t+1}})$ is the solution of the matching quadratic program, we can obtain that

$$\begin{aligned} \begin{array}{lll} \tilde{r}_{_{t+1}} &{}\ge \tilde{\nu }_{_{t+1}}+\langle \tilde{g}_{c_{_{t+1}}}^{t+1}, \tilde{d}^{t+1} \rangle \\ &{} = c(\tilde{x}^{t+1},y(\tilde{x}^{t+1}))+\langle \tilde{g}_{c_{_{t+1}}}^{t+1},\tilde{d}^{t+1}-\tilde{d}^{t} \rangle \\ &{} \ge \tilde{\omega }+\delta -L \Vert \tilde{d}^{t+1}-\tilde{d}^{t} \Vert \\ &{} \ge \tilde{\omega }+\tilde{r}_{_{t}}-L\Vert \tilde{d}^{t+1}-\tilde{d}^{t}\Vert , \end{array}\end{aligned}$$

where the last inequality has used the fact $\delta \ge \tilde{r}_{_t}$ in (4.7). Thus it holds that

$$\begin{aligned} \begin{array}{lll} \tilde{r}_{_{t+1}} -\tilde{r}_{_{t}} \ge \tilde{\omega } -L \Vert \tilde{d}^{t+1}-\tilde{d}^{t} \Vert . \end{array}\end{aligned}$$

Passing to the limit as $t\rightarrow \infty$, we obtain that $\tilde{\omega }\le 0$, which is a contradiction. $\square$

Lastly, we can prove global convergence of Algorithm 1.

Theorem 4.1

Consider solving the nonsmooth convex SIPs (1.2) with Algorithm 1. For any $\varepsilon >0$ and $\eta >0$, Algorithm 1 stops after finitely many executions of the “main iteration” at an approximate optimum point $\tilde{x}$, satisfying the following approximate optimality condition:

$$\begin{aligned} \Vert \tilde{G}+\tilde{\alpha }\Vert \le \eta \ \ \mathrm{and} \ \ \tilde{\epsilon }:=H_{\tilde{x}}(\tilde{x})-\tilde{m}\le \varepsilon , \end{aligned}$$

where $\tilde{m}$ has been defined in (2.17).

Proof

For a contradiction, we assume there are an infinite number of “main iteration” executions, which mean that the stabilized center is updated infinitely. Let k, $(\hat{d}^{k},\hat{r}_{_k})$ and $(\hat{\lambda }^k,\hat{\gamma }^k)$ denote the index of the kth “main iteration”, the primal solution of the current QP and the matching multipliers, and $\hat{J}_k^f$, $\hat{J}_k^c$ stand for the matching index sets.

We observe that the stabilized center $\hat{x}^k$ should be updated only if

$$\begin{aligned} \Vert \hat{G}^k+\hat{\alpha }^k\Vert > \eta \end{aligned}$$

holds. Let $p_{k}$ denote number of bundle resets carried out during the kth “main iteration”. It follows from Lemma 4.5 that $p_{k}$ is always is bounded. Moreover, by Lemma 4.1, we can obtain that

where the first equality has used (2.16) and the last equality is from Step 2 in Algorithm 1. Therefore, by summing up the above relation, we can obtain that

$$\begin{aligned} f(\hat{x}^{k+1})-f\left( \hat{x}^0\right) \le a \sum \limits _{j=0}^k \frac{1}{(\sigma )^{p_{j}}}, \end{aligned}$$

where $a:= -\frac{\iota \eta ^2}{\mu _0}+2\delta _0+2\omega _0$, which is negative follows from (3.1). By noting the boundness of $p_j$, then $\frac{1}{(\sigma )^{p_{j}}}$ is uniformly bounded away from zero. As a result, passing to the limit, we can obtain

$$\begin{aligned} \lim _{k\rightarrow \infty }f\left( \hat{x}^{k+1}\right) -f(\hat{x}^0) \le a \lim _{k\rightarrow \infty } \sum \limits _{j=0}^k \frac{1}{(\sigma )^{p_{j}}} \le -\infty , \end{aligned}$$

which is a contradiction, since f is bounded from below.

Therefore, Algorithm 1 will eventually stop at Step 2, and output an approximate point $\tilde{x}$, which satisfies the following conditions:

$$\begin{aligned} \Vert \tilde{G}+\tilde{\alpha }\Vert \le \eta , \end{aligned}$$

(4.16)

and

$$\begin{aligned} H_{\tilde{x}}(\tilde{x})-\omega \le c^+(\tilde{x},y(\tilde{x}))\le \tilde{m}+\varepsilon -\omega , \end{aligned}$$

implies that $H_{\tilde{x}}(\tilde{x})-\tilde{m}\le \varepsilon$. By Lemmas 2.1 and 2.3, it holds that

$$\begin{aligned} \tilde{G}+\tilde{\alpha } \in \partial _{\varepsilon } H_{\tilde{x}}(\tilde{x})+N_{X}(\tilde{x}), \end{aligned}$$

which, combining with (4.16), implies that $\tilde{x}$ satisfies the approximate optimality conditions.

5 Computational results

We complete Algorithm 1 in MATLAB and the numerical experiments were done by using a PC with 1.80GHz CPU. Quadratic programming solver is QuadProg.m, which is available in the Optimization Toolbox. In our experiments, we choose the values for all the parameters as follows:

$$\begin{aligned} \varepsilon =10^{-3}, \ \eta =10^{-3},\ \delta _0=10^{-6}, \ \iota =0.56, \ \sigma =10, \ \mu _0=10. \end{aligned}$$

Now we try to handle the maximum problem (2.9), i.e.,

$$\begin{aligned} \max \limits _{y \in Y}c(\bar{x},y), \end{aligned}$$

where $\bar{x}$ is the current iterative point. There are a few excellent methods for solving both convex and nonconvex optimization, and the solution with any accuracy can be returned [7, 11]. In particular, [11] proposed an inexact nonconvex bundle if the Y is a compact set and simple enough. If the objective function $c(\tilde{x},\cdot )$ is concave, then (2.9) is a constrained concave maximization program. Therefore, any standard algorithms for minimizing constrained convex problem are suitable for our algorithm.

5.1 Computational results for nosmooth convex semi-infinite problems

In this subsection, we tested 8 nonsmooth convex semi-infinite examples, namely, Examples 1-8.

Example 1

$$\begin{aligned} \begin{array}{lllll} &{} \min &{} f(x):=1.21 \exp (|x_1|)+ \exp (|x_2|) ,\\ &{} s.t. &{} c(x,y):=y - \exp (x_1 + x_2)\le 0, \\ &{} &{} y\in [-10,1]. \end{array}\end{aligned}$$

Example 2

$$\begin{aligned} \begin{array}{lllll} &{} \min &{} f(x):=\frac{1}{3} |x_1|+\frac{1}{2} |x_1|+|x_2|,\\ &{} s.t. &{} c(x,y):=(1-x_1^2y^2)^2-x_1y^2-|x_2|+x_2\le 0, \\ &{} &{} y\in [-1,1]. \end{array}\end{aligned}$$

Example 3

$$\begin{aligned} \begin{array}{lllll} &{} \min &{} f(x):= |x_1-2x_2+5x_2^2-x_2^3-13|+|x_1-14x_2+x^2_2+x_2^3-29|,\\ &{} s.t. &{} c(x,y):=|x_1|+2x_2y^2+\exp (x_1+x_2)-\exp (y)\le 0, \\ &{} &{} y\in [0,1]. \end{array}\end{aligned}$$

Example 4

$$\begin{aligned} \begin{array}{lllll} &{} \min &{} f(x):= |x_1-2|+|x_2|,\\ &{} s.t. &{} c(x,y):=|x_1|\cos (y_1)-x_2 \sin (y_2)-4 \le 0, \\ &{} &{} y\in [0,2\pi ]\times [0,2\pi ]. \end{array}\end{aligned}$$

Example 5

$$\begin{aligned} \begin{array}{lllll} &{} \min &{} f(x):= |x_1|+|x_2|+|x_3|,\\ &{} s.t. &{} c(x,y):=x_1 + x_2 \exp (x_3y) -\exp (2x_1 y) + \sin (4y) \le 0, \\ &{} &{} y\in [0,1]. \end{array}\end{aligned}$$

Example 6

$$\begin{aligned} \begin{array}{lllll} &{} \min &{} f(x):= |x_1|+|x_2|+|x_3|,\\ &{} s.t. &{} c(x,y):=x_1 + x_2 \exp (x_3y_1) -\exp (2y_2) +\sin (4y_1) \le 0, \\ &{} &{} y\in [0,1]\times [0,1]. \end{array}\end{aligned}$$

Example 7

$$\begin{aligned} \begin{array}{lllll} &{} \min &{} f(x):=\frac{1}{2} (|x_1|+|x_2|+|x_3|+|x_4|),\\ &{} s.t. &{} c(x,y):=\sin (y_1 y_2)-x_1-x_2 y_1- x_3 y_2 -x_4 y_1 y_2 \le 0, \\ &{} &{} y\in [0,1]\times [0,1]. \end{array}\end{aligned}$$

Example 8

$$\begin{aligned} \begin{array}{lllll} &{} \min &{} f(x):=\frac{1}{2} (|x_1|+|x_2|+|x_3|+|x_4|+|x_5|+|x_6|),\\ &{} s.t. &{} c(x,y):=\exp \left( y_1^2+ y_2^2\right) -x_1-x_2 y_1- x_3 y_2 -x_4 y_1^2-x_5 y_1 y_2-x_6 y_2^2 \le 0, \\ &{} &{} y\in [0,1]\times [0,1]. \end{array}\end{aligned}$$

The numerical results are listed in Tables 1 and 2, and notations are used as follows:

$$\begin{aligned} \begin{array}{lllllll} &{} \mathrm{stop}_{\eta _{_\mathrm{k}}}:=\Vert \hat{\mathrm{G}}^\mathrm{k}+\hat{\alpha }^\mathrm{k}\Vert , \\ &{} \mathrm{stop}_{\varepsilon _{_\mathrm{k}}}:= \mathrm{c}^+(\hat{\mathrm{x}}^\mathrm{k},\mathrm{y}(\hat{\mathrm{x}}^\mathrm{k}))-\hat{\mathrm{m}}_{_\mathrm{k}} \\ &{} (x_0, y_0)-- \mathrm{the \ initial \ point,}\\ &{} f^{*} -- \mathrm{the \ final \ objective\ value,}\\ &{}h^{*}--\mathrm{the \ final \ constrained \ value,}\\ &{} \mathrm{Ni} -- \mathrm{the \ number \ of \ null \ iterations,}\\ &{} k -- \mathrm{the \ number \ of \ serious \ iterations,}\\ &{} \mathtt{Time_{max}} -- \mathrm{the \ CPU \ time \ for \ solving \ (2.9) (sec.)},\\ &{} \mathtt{Time} -- \mathrm{the \ CPU \ time (sec.)}. \end{array}\end{aligned}$$

Table 1 The last three iterates generated by Algorithm 1 for Examples 1–8

Table 2 Test results by Algorithm 1 for Examples 1–8

The test results are summarized in Tables 1 and 2, and show that Algorithm 1 performs well for Examples 1–8. From Table 1, we can note the value of stop$_{\eta _k}$ and stop$_{\varepsilon _k}$ drop to zero fast in the last three iterations, which means that Algorithm 1 is convergent quickly. From Table 2, the value of $h^*$ shows that Algorithm 1 can ensure the feasibility for all the test examples. Also, we can note the CPU time for estimating (2.9) (Time $_{max}$) is extremely short, which shows the inexact oracle idea is reasonable. Above all, the Time shows that our method is efficient for solving nonsmooth SIP problem (1).

5.2 Comparison of Algorithm 1 with classic algorithms

In this subsection, we first test performance on the following five classical convex SIPs (Examples 9–13). We compare the performance of Algorithm 1 with that of the central cutting plane algorithm (CCPA) as detailed in [26] and the SIP solver fseminf in MATLAB toolbox.

Example 9

Consider the following convex SIP problem, which satisfies the Slater CQ and the feasible set is bounded.

$$\begin{aligned} \begin{array}{lllll} \min &{} f(x)=(x_1-2)^2+(x_2-0.2)^2,\\ s.t. &{} c(x,y)=(5sin(\pi \sqrt{y})/(1+y^2))x^2_1-x_2 \le 0, \\ &{} x_{1}\in [0,1], \ x_{2}\in [0,1] \ \mathrm{and} \ Y=[0, 1]. \end{array}\end{aligned}$$

The problem is stemmed from Tichatschke and Nebeling [54], and was also tested by Kortanek and No [26]. Obviously, it satisfies the Slater CQ, and its objective function is strictly convex

Example 10

This problem is convex SIP problem, and the objective function is strictly convex.

$$\begin{aligned} \begin{array}{lllll} \min &{} f(x)=x_1^2+x_2^2,\\ s.t. &{} c(x,y)=\cos (y)x_{1}+\sin (y)x_{2}- (1+\cos (y)+\sin (y))\le 0, \\ &{} Y=[\pi , \frac{3}{2}\pi ], \end{array}\end{aligned}$$

which is discussed by Goberna and López [10], and Zhang and Wu [60]. Although the feasible set is not bounded, the objective function is level bounded on the feasible set.

Example 11

Consider the following convex SIP problem, and has been tested by Kortanek and No [26].

$$\begin{aligned} \begin{array}{lllll} \min &{} f(x)=x_1^2+x_2^2+x_2^3,\\ s.t. &{} c(x,y)= x_1+x_2 \exp (x_3 y)+\exp (2y)-2\sin (4y)\le 0, \\ &{} x_{1}\in [-2,2], \ x_{2}\in [-2,2], \ x_{3}\in [-2,2], \ Y=[0,1], \end{array}\end{aligned}$$

where the objective function is strictly convex, and the problem satisfies the Slater CQ.

Example 12

The problem is a convex SIP problem with multidimensional index set, and has been tested by Kortanek and No [26].

$$\begin{aligned} \begin{array}{lllll} \min &{} f(x)=x_1^2+x_2^2,\\ s.t. &{} c(x,y)= (x_1^2+ x_2^2-4)y_{1}+((x_1-2)^2 + (x^2-2)^2-4)y_{2}\le 0, \\ &{} x_{1}\in [0,2], \ x_{2}\in [0,2], \ Y=[0,1]\times [0,1]. \end{array}\end{aligned}$$

Observe that the problem satisfies the Slater CQ and has strictly convex objective function, the feasible set is bounded.

Example 13

Consider the following quadratically constrained convex quadratic SIP problem, which stems from linear-phase FIR digital filter design with weighted peak-constrained least-square error. The convex SIP problem has been tested by Zhang and Wu [60].

$$\begin{aligned} \begin{array}{lllll} \min f(x)&{}=x^\mathrm{T}Hx-2c^\mathrm{T}x,\\ s.t. \quad c_{1}(x,y)&{}=|\varphi (y)^{T}x-1|-0.05\le 0, \ \mathrm{for} \ y\in Y_1=[0,0.05], \\ c_{2}(x,y)&{}=|\varphi (y)^{T}x|-0.01\le 0, \ \mathrm{for} \ y\in Y_2=[0.1,0.5], \end{array}\end{aligned}$$

where

$$\begin{aligned} \varphi (y)= & {} (2\cos (2\pi y(n-1)), 2\cos (2\pi y(n-2)), \ldots , 2\cos (2\pi y), 1)^{T}, \ \ n= 18.\\ H= & {} \int _{0}^{0.05} \varphi (y)\varphi (y)^{T}dy+1000\int _{0.1}^{0.5} \varphi (y)\varphi (y)^{T}dy, \ \ c=\int _{0}^{0.05} \varphi (y)dy \end{aligned}$$

Algorithm 1 will obtain the solution of this problem after 21 iterations, where

$$\begin{aligned} \begin{array}{lll}x^*=&{}(0.0053, 0.0033, 0.00067,-0.0034,-0.0083,-0.01343,\\ &{}-0.0211,-0.0223,-0.0219,-0.0149,-0.0007, 0.0199,\\ &{}0.0447, 0.0737, 0.1002, 0.1232, 0.1382, 0.1436)^{T}. \end{array}\end{aligned}$$

Comparative computational results are summarized in Table 3.

Table 3 Comparison of results for Examples 9–13

It is worth noting that our algorithm is much more effective than CCPA and SIP solver fseminf. Specifically, the SIP solver fseminf cannot obtain the optimal solution when it is used to solve Example 10. Besides, perhaps because of the dimension of Example 13 is too large, both of the CCPA and fseminf need too much time for solving Example 13, thus they are obliged to stop running. The solution of Example 13 has been reported in itself.

Example 14

Consider the following unconstrained SIP [32]:

$$\begin{aligned} \min \limits _{x\in [-1,1]^{n}}\max \limits _{t\in [0,1]}\sum \limits _{i=1}^{n} (i x_{i}-i/n-\sin (2\pi t+i))^2, \end{aligned}$$

which is a classic SIPs.

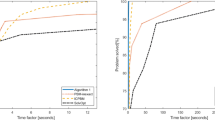
We compared the performance of Algorithm 1 on Example 14 with the new exchange method (EXM) in [60] and the SIP solver fseminf in Matlab toolbox. By setting $n=2,5,10,15,20,25,30$, the numerical results are summarized in Table 4.

Table 4 Comparison of Algorithm 1, the new EXM and fseminf for Example 14

Table 4 shows, the fseminf is acceptable for lower dimension problems, but it takes too much time for $10\le n\le 20$, Besides, we have to give up running fseminf for $n\ge 25$, since it spends too much time to stop, or did not converge. The performance of the EXM is excellent for Example 14, but it needs much more time than Algorithm 1 for most problems.

5.3 Computational results for moment robust optimization

To test the efficiency of Algorithm 1 for solving the moment robust optimization, we compute the following robust stochastic constraints optimization problem as [32].

Example 15

$$\begin{aligned} \begin{array}{lllll} \min &{} f(x):=(x_1-2)^2+(x_2-0.2)^2,\\ s.t. &{} E_{W} \left[ \frac{5 sin\pi \sqrt{\xi }}{1 + \xi ^2}x_1^2-x_2\right] \le 0, \ \ W \in \mathcal {D}, \\ &{}x_1 \in [-1, 1], \ x_2 \in [0, 0.2], \end{array}\end{aligned}$$

where $\mathcal {D}:=\Big \{ W: E_{W}[\xi ^i]=\frac{1}{i+1},\ i = 0,\ 1, . . . m\Big \}$.

In our numerical experiment, we set the initial point $x^0=(1.3,0.7)$, the increase parameter $\sigma =2.5$, the initial parameters $\mu _0=4.5$, $\delta _0=10^{-6}$, $\iota =0.08$, the optimality tolerance $\varepsilon =10^{-3}$.

By setting different moment constraints $m=1,2,3,4,5,6,\infty$, Example 15 gives various classical robust optimization model of the problem. It should be noted that the solutions for solving Example 15 for increasing values of t correspond to fewer and fewer conservative solutions. The objective value increases along with the increasing values of t. Fortunately, the inner subproblem (2.9) can be solved effectively, which implies the inexact oracle idea is reasonable. All in all, the numerical results show that Algorithm 1 can solve the robust stochastic constraints optimization problem effectively.

The numerical results are listed in the following Table 5.

Table 5 The numerical results gave by Algorithm 1 for Example 15 with different moment constraints