Multiple instance classification via quadratic programming

Abstract

Multiple instance learning (MIL) is a variation of supervised learning, where data consists of labeled bags and each bag contains a set of instances. Unlike traditional supervised learning, labels are not known for the instances in MIL. Existing approaches in the literature make use of certain assumptions regarding the instance labels and propose mixed integer quadratic programs, which introduce computational difficulties. In this study, we present a novel quadratic programming (QP)-based approach to classify bags. Solution of our QP formulation links the instance-level contributions to the bag label estimates, and provides a linear bag classifier along with a decision threshold. Our approach imposes no additional constraints on relating instance labels to bag labels and can be adapted to learning applications with different MIL assumptions. Unlike existing specialized heuristic approaches to solve previous MIL formulations, our QP models can be directly solved to optimality using any commercial QP solver. Also, kindly confirm Our computational experiments show that proposed QP formulation is efficient in terms of solution time, overcoming a main drawback of previous optimization algorithms for MIL. We demonstrate the classification success of our approach compared to the state-of-the-art methods on a wide range of real world datasets.

1 Introduction

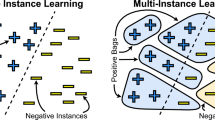
Most data mining approaches focus on solving classification problems using machine learning and pattern recognition techniques. Classification tasks require input samples with given outputs, known as the class labels. In multiple instance learning (MIL), instances are grouped into bags and a class label is known for each bag, whereas the instance labels are not fully provided. The data representation and learning setup of MIL are in alignment with many real world applications. Current research areas of MIL include image classification, drug activity prediction, text mining and many others [5]. In these applications, global descriptions of the objects are decomposed into multiple parts. When objects are represented by multiple parts, only some parts may be relevant for classification. In addition, it is expensive and time consuming to collect true labels of parts individually. MIL paradigm provides an opportunity to solve classification problem under these circumstances.

For instance, consider sample images from Corel image classification dataset [6] in Fig. 1. Under MIL scenario, images correspond to bags and patches sampled from the images correspond to the instances. In this example, images are classified either as positive or negative based on the presence of a horse on its patches as shown in Fig. 1. Only some patches of an image are informative for classification and it is sufficient to label the whole image instead of the individual instances.

Fig. 1

An illustration of MIL setting for image classification. Images on the left with located horses inside the red rectangles are classified as positive whereas the other images form the negative class

Unknown instance labels and uncertainty on the bag formations contribute to the difficulty of MIL problem. Success of the MIL algorithms depends on their capability of capturing the internal structures of bags. The most common way of relating bag labels to the individual instance labels is introduced as standard MIL assumption in the first MIL application [8] and is widely used in several methods. The standard MIL assumption states that label of a bag is positive if and only if it contains at least one positive instance, otherwise the bag is negatively labeled. In Fig. 2, a regular input data with 12 instances and 3 features is used to form a MIL data with 3 bags following the standard MIL assumption.

Although it is embraced by many methods, standard assumption is considered to be restrictive for some MIL applications. For example, consider a document retrieval application, where the bags are articles and multiple sections extracted from them are the instances. The aim is to detect whether an article is about a specific subject (e.g. finance) or not. A section including the predetermined words and word combinations makes this section a positive instance. However, articles that are not relevant may also contain these words in a particular section (e.g. including financial terms in the introduction). Thus, standard MIL assumption is not well suited to this problem. Generalized MIL [1, 12, 34] is formalized to describe MIL scenarios other than the standard MIL under various constraints [34]. Under generalized MIL, collective MIL assumption [12] models equal contribution of instances to the bag label. The idea is to derive a bag-level classifier from an instance-level decision function by averaging the learning results in underlying instance-feature space.

Fig. 2

Multiple instance data representation of one positive bag and 2 negative bags with 3 features

We propose a novel Quadratic Programming-based Multiple Instance Learning (QP-MIL) framework. Our proposal is based on the idea of determining a simple linear function for discriminating positive and negative bag classes. We model MIL problem as a QP problem using the input data representation. An optimal solution of our QP formulation returns an instance-level scoring function. For an unlabeled bag, instance-level scores are averaged to assess the bag-level score. Finally, class label of the bag is determined according to the predetermined threshold value. Rather than selecting bag representatives as in standard MIL, QP-MIL regards collective MIL assumption because of its modeling capability of the standard assumption and coverage on other MIL assumptions by means of the smooth average of instance-level decisions [13].

The remainder of the paper is organized as follows: Sect. 2 summarizes the existing MIL methods and mathematical programming formulations of MIL. Sect. 3 introduces formal description of the MIL problem and provides an existing SVM-based MIL formulation, MIHLSVM as a background. Sect. 4 describes the proposed QP-MIL framework. Sect. 5 provides insights resulting from the numerical comparisons of QP-MIL with MIHLSVM and presents the classification success and computational efficacy of QP-MIL with the experiments on a wide-range of MIL datasets. Conclusions and future extensions are discussed in Sect. 6.

Table 1 The comparison of MIL formulations

2 Related work

Previously, various data-mining and machine learning algorithms have been devised to solve the MIL problem. These approaches are heuristic algorithms and optimality of their solutions cannot be guaranteed. In this study, we focus on optimization-based approaches to solve MIL problem, and we refer the reader to comprehensive surveys [1, 5] for other categories of MIL methods.

SVM classification is extended to MIL setting previously [2, 20, 22, 23, 25, 37]. Table 1 describes and compares the Multiple Instance Support Vector Machine (MISVM) models in the literature. The level of the formulations indicates whether the misclassification penalties are incurred for bags or not. The assumptions are qualified as weak if only the standard MIL assumption holds. Otherwise, if there are additional restrictions reflected to the mathematical model, assumption status is entitled as strong.

In MISVM models, an instance is selected from a positive bag as a witness to represent that bag. Figure 3 illustrates standard SVM classification in instance space and bag-level separation. To classify bags, a witness instance is selected from a positive bag as shown in Fig. 3. Witness instances are considered to be responsible from bag positivity and must be correctly classified.

Fig. 3

An illustration of witness selection in MISVM models. Red circles indicate instances in negative bags. In positive bags, instances are represented with blue triangles and witness instances are enclosed in dashed circles

In mi-SVM and MI-SVM formulations [2], two types of constraints are added to the SVM formulation satisfying at least one sample in each positive bag has a label of one in mi-SVM and a witness instance is present for positive bags in MI-SVM. MissSVM [37] is formulated upon MI-SVM [2] with additional constraints on the positive bags. Minimizing the misclassification error at either extreme, an instance of a positive bag is either positively or negatively labeled. Another method KI-SVM [22] selects witnesses from positive bags as key instances.

Sparse transductive MIL formulation (stMIL) [4] has an additional constraint that pulls all the negative instances in the bag closer to the hyperplane. An $\ell _1$-norm SVM-based formulation [23] incorporating the assumption “arbitrary convex combination of instances in the positive bags represents each positive bag” is a linear program with bilinear constraints.

MIL problem is formulated as a mixed 0–1 quadratic programming problem in [20], where MIL is reduced to instance-level learning, disregarding the bag information. Hard margin and soft margin maximization formulations of MIL, MIHMSVM and MIHLSVM [25] have additional bag-level misclassification penalties. A penalty is incurred if all instances in a positive bag are misclassified or at least one instance in the negative bag is misclassified. The resulting formulations are mixed integer quadratic programs (MIQPs), which are known to be NP-hard problems [20].

Most of the aforementioned MISVM models are analyzed in a recent survey [9]. It is emphasized in [9] that local convergence of the heuristic solution approaches for solving non-convex MISVM formulations leads to a sacrifice from the classification performance. The authors also discuss scalability of MISVM methods: Increased number of instances and bags affect model dimensionality and therefore increase both hyperparameter selection and model solution times.

When SVMs are tailored for MIL, specifically devised SVM solvers [11] can only be used solving subproblems of various heuristic solution algorithms [2, 20, 22, 23, 26, 37]. We propose a simplified QP formulation, which can be directly solved to optimality using any commercial QP solver. Instead of utilizing an iterative heuristic procedure, we are able to report exact solutions of each problem instance. Thus, repetition of the performed classification task is possible and the resulting classifier is reproducible in this way.

Our study explores the utility of QP-MIL compared to the previous state-of-the-art MIL approaches. Leading methods in MIL literature are various machine learning-based approaches. We select several MIL algorithms as baseline methods to demonstrate success of the MIL classifiers. We carry out another comparison of QP-MIL considering SVM-based MIL, in terms of model building and classifier testing. We experimented direct solution of a mixed integer quadratic programming (MIQP) formulation proposed in [25] for comparison.

3 Background

3.1 Problem statement

Let $\mathbf {x}_i$ be a d-dimensional feature vector of instance i and $X = \{\mathbf {x}_i:i=1,\ldots ,n\}$ be a set of instances. Also let $y_i$ be a single, discrete-valued feature, specifically the label of instance i. Then, instance set $X = \{\mathbf {x}_i :i=1,\ldots ,n \}$ forms the training set. This set can be labeled with $y_i$, $i=1,\ldots ,n$ or can be unlabeled. A bag $B_j$ consists of a set of instances $I_j$ formed by $\mathbf {x}_i$’s and $n_j$ is the number of the instances in $B_j$. Therefore, $\upchi = \{(B_j,l_j):j=1,\ldots ,m\}$ is a training bag set containing instances and a label $l_j$ of each bag. Let an instance-based classifier be a function from instances to labels $f(\mathbf {x}_i) \rightarrow y_i$, and let $g(B_j) \rightarrow l_j$ be the function of a bag-based single classifier. Concisely, given a training set of bags with given label information $\upchi = \{(B_j,l_j):j=1,\ldots ,m\}$, our MIL task is to learn a classifier $g(B_j)$ to predict the labels of input bags.

The sets, parameters and decision variables used in models are given as follows.

Indices:

• $i=1,2,\ldots ,n$: index for the instances

• $j=1,2,\ldots ,m$: index for the bags

Sets:

• $I_j$: set of instances in bag

• $J^+ = \{j : l_j = 1\}$: set of positive bags

• $J^- = \{j : l_j = -1\}$: set of negative bags

• $I^+ = \{i : i \in I_j \wedge j \in J^+\}$: set of instances in positive bags

• $I^- = \{i : i \in I_j \wedge j \in J^-\}$: set of instances in negative bags

• $I = I^+ \cup I^-$: set of all instances

Parameters:

• $\mathbf {x}_i \in \mathfrak {R}^d$, $i=1,2,\ldots ,n$: instance vectors

• $l_j$: bag labels

• C: trade-off parameter

Decision variables of QP-MIL:

• $\mathbf {w}$: d-dimensional feature weight vector

• $m_i$, $i=1,2,\ldots ,n$: instance pseudo class memberships

• $\beta _j$, $j=1,2,\ldots ,m$: bag class memberships

• $\delta _j^+, \delta _j^-$: slack variables for the positive and negative bag deviations

• $\tau$: decision threshold for bag classification

Decision variables of MIHLSVM [25]:

• $\mathbf {w}$: d-dimensional feature weight vector

• b: bias term

• $\beta _j$, $j=1,2,\ldots ,m$: bag class memberships

• $\eta _i$, $i=1,2,\ldots ,n$: variables identifying witness instances

• $z_i$, $i=1,2,\ldots ,n$: auxiliary variables replacing $\xi _i \eta _i$, $i=1,2,\ldots ,n$.

3.2 A previous MIQP formulation: MIHLSVM [25]

Multiple Instance Hinge Loss Support Vector Machines (MIHLSVM) [25] extends traditional SVM for MIL. Unlike earlier SVM-based approaches to MIL, MIHLSVM defines bag-level hinge loss to penalize bag misclassifications. The proposed model handles the situation of nonlinearly seperable classes and the resulting formulation is a MIQP. The authors propose direct solution of MIHLSVM in [25] and do not present a heuristic algorithm as those in other MISVM studies [2, 20, 22, 23, 37]. Still, it is difficult to get an exact solution to a MIHLSVM problem instance. We present our comparisons with MIHLSVM in Sect. 5.4.1.

A MIQP formulation of the described problem [25] is given as below

$$\begin{aligned} \text {(MIHLSVM)} \mathop {\text {min}}_{\mathbf {w},b,\varvec{\xi },\varvec{\xi }^+,\varvec{\xi }^-,\varvec{\eta }, \varvec{z}} \frac{1}{2}||\mathbf {w}||^2&+ C\left( \sum _{j \in J^-}\xi _j^- + \sum _{j \in J^+}\xi _j^+ \right) \end{aligned}$$

(1a)

$$\begin{aligned} \text {st} -\left( \langle \mathbf {w},\mathbf {x}_i \rangle + b\right)&\ge 1-\xi _i \forall i \in I^- \end{aligned}$$

(1b)

$$\begin{aligned} \langle \mathbf {w},\mathbf {x}_i \rangle + b&\ge 1-\xi _i \forall i \in I^+ \end{aligned}$$

(1c)

$$\begin{aligned} \sum _{i \in I_j} \eta _i&= 1 \forall j \in J^+ \end{aligned}$$

(1d)

$$\begin{aligned} \xi _i&\le \xi _j^- \forall j \in J^-, \forall i \in I_j \end{aligned}$$

(1e)

$$\begin{aligned} \xi _j^+&= \sum _{i \in I_j}z_i \forall j \in J^+ \end{aligned}$$

(1f)

$$\begin{aligned} z_i&\ge \xi _i - M(1-\eta _i) \forall i \in I^+ \end{aligned}$$

(1g)

$$\begin{aligned} z_i&\le \xi _i \forall i \in I^+ \end{aligned}$$

(1h)

$$\begin{aligned} z_i&\le M\eta _i \forall i \in I^+ \end{aligned}$$

(1i)

$$\begin{aligned} z_i&\ge 0 \forall i \in I^+ \end{aligned}$$

(1j)

$$\begin{aligned} \xi _i&\ge 0 \forall i \in I \end{aligned}$$

(1k)

$$\begin{aligned} \eta _i&\in \lbrace 0,1 \rbrace \forall i \in I^+ . \end{aligned}$$

(1l)

In addition to maximization of the margin between bag classes, the objective function (1a) also minimizes bag misclassifications where a selected constant C controls the trade-off between two objectives. Constraints (1b) and (1c) are margin constraints enabling penalization of misclassification using slack variables $\xi _i$ for misclassified instances. The weight vector $\mathbf {w}$ and the offset parameter b defines the instance-level separating hyperplane. Constraint (1d) forces a positive bag to have a positive instance as a witness. Negative bag misclassifications are represented by constraint (1e) using slack variables $\xi _j^-, \forall j \in J^-$. It is assumed that a negative bag is misclassified if all of its instances are misclassified.

Constraints (1g)–(1i) with the auxiliary variables $z_i \ge 0, \forall i \in I^+$ determine misclassification of a witness instance in a positive bag. Constraint (1f) assesses the misclassification of a positive bag as misclassification of its selected witness instance. Constraint (1l) imposes binary restrictions on witness variables and nonnegativity restrictions on slack variables are introduced by constraint (1k).

After solving MIQP formulation, the following classifier can be used for bag classification

$$\begin{aligned} \text {sgn}\left( \mathop {\text {max}}_{i\in I_j}\left( \langle \mathbf {w},\mathbf {x}_i\rangle + b \right) \right) , \qquad j \in J. \end{aligned}$$

(2)

We know that the MIHLSVM formulation given in (1) is a mixed integer quadratic program, and therefore, can be solved directly by commercial MIQP solvers. The efficiency of this approach along with QP-MIL is compared in Sect. 5.4.1 to verify the modeling and solution quality of the proposed MIL framework.

4 Quadratic programming for multiple instance learning

A bag classification rule can be found by solving the following optimization model:

$$\begin{aligned} \text {(QP)} \mathop {\text {min}}_{\mathbf {w},\varvec{\beta },\mathbf {m},\tau ,\varvec{\delta }^+,\varvec{\delta }^-} \frac{1}{2}||\mathbf {w}||^2&- C\left( \frac{1}{m^+} \sum _{j \in J^+}\delta _j^+ + \frac{1}{m^-} \sum _{j \in J^-}\delta _j^- \right) \end{aligned}$$

(3a)

$$\begin{aligned} \text {s.t.} \langle \mathbf {w},\mathbf {x}_i \rangle&= m_i \forall i \in I \end{aligned}$$

(3b)

$$\begin{aligned} \beta _j&= \frac{1}{n_j} \sum _{i \in I_j} m_i \forall j \in J \end{aligned}$$

(3c)

$$\begin{aligned} \beta _j&\ge \tau + \delta _j^+ \forall j \in J^+ \end{aligned}$$

(3d)

$$\begin{aligned} \beta _j&\le \tau - \delta _j^- - \varepsilon \forall j \in J^- \end{aligned}$$

(3e)

$$\begin{aligned} 0 \le&m_i \le 1 \forall i \in I \end{aligned}$$

(3f)

$$\begin{aligned} 0 \le&\delta _j^+ \le 1 \forall j \in J^+ \end{aligned}$$

(3g)

$$\begin{aligned} 0 \le&\delta _j^- \le 1 \forall j \in J^- \end{aligned}$$

(3h)

$$\begin{aligned} 0 \le&\tau \le 1 \end{aligned}$$

(3i)

Regularization processes are introduced to supervised learning problems for recovering the important features and for satisfying model generalizability. The quadratic objective function (3a) performs maximization of bag class membership margin together with a regularization of feature weights. In the first term of the objective function (3a), standard $\ell _2$-norm of the weight coefficients $\mathbf {w}$ are minimized. Therefore, effect of redundant or uninformative features can also be controlled. The second term of the objective function (3a) maximizes the margin of bag class estimates formed by the threshold variable $\tau$. In order to handle potential problems due to class imbalances, summations of the nonzero slack variables $\delta _j^+$, $\forall j \in J^+$ and $\delta _j^-$, $\forall j \in J^-$ in the objective function (3a) are normalized with the number of positive bags $m^+$, and the number of negative bags $m^-$, respectively. The hyperparameter C in the objective function (3a) tunes the trade-off between regularization of $\mathbf {w}$ and maximization of bag class membership estimate margin.

For each instance, an estimate of the class label is obtained as a pseudo class membership value. Constraint (3b) determines instance pseudo class memberships $m_i, \forall i=1,\ldots ,n$ using the coefficient vector $\mathbf {w}$ entry of which corresponds to the weight assigned to a feature of the input data. For each instance, Constraint (3c) maps bag-level class estimates $\beta _j, \forall j=1,\ldots ,m$ onto the [0, 1] interval by averaging instance-level scores, which are forced to be between 0 and 1 by Constraint (3f). Constraints (3d) and (3e) ensure that absolute difference between class membership estimate $\beta _j$ and the threshold $\tau$ are maximized in the objective function for both positive and negative bags. Constraint (3i) restricts the decision threshold $\tau$ to be between 0 and 1. Similarly, slack variables $\delta _j^+$, $\forall j \in J^+$ and $\delta _j^-$, $\forall j \in J^-$ are restricted to be between 0 and 1 by Constraints (3g) and (3h). We set $\varepsilon$ in Equation (3e) to a small positive value ($10^{-6}$) so that class membership value of a negative bag is strictly below the threshold $\tau$.

QP-MIL models the contributions of all instances in a bag to the bag label collectively. Averages of pseudo-class membership estimates for instances determine the class membership estimates for the bags. A bag is positively labeled if its class membership value is above decision threshold $\tau$, and negatively labeled otherwise. An optimal value of $\tau$ is adaptively identified in QP-MIL during the optimization process. This threshold is also applicable to the test bags. After solving the QP formulation in (3) on the training set, instance scores are calculated by Equation (3b) for each instance in a test bag and simply averaged in Equation (3c) to compute the bag-level score. If the output is below the optimal value of $\tau$, the classifier produces a negative label, else a positive label.

The resulting bag-level classifier can be defined as

$$\begin{aligned} g(B_j) = {\left\{ \begin{array}{ll} 1 &{} \quad \text {if} \beta _j \ge \tau , \\ -1 &{} \quad \text {otherwise}, \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} \beta _j = \frac{1}{n_j}\sum _{i \in I_j} m_i , \end{aligned}$$

and

$$\begin{aligned} m_i = \left\langle \mathbf {w},\mathbf {x}_i\right\rangle \forall i \in I_j . \end{aligned}$$

Our proposed MIL framework is independent of the underlying MIL assumptions. We seek to model bag structures by taking into account the reflection of instance scores to the bag labels. Since all instances contribute to the bag-level scoring, this paradigm resembles the collective MIL assumption [12]. It is shown in [13] that if an instance level separation can be performed in an embedding space $\mathcal {H}$ with a classifier f in a standard MIL problem, then the bags can also be separated in another embedding space $\mathcal {H}'$, which has a higher dimensionality than $\mathcal {H}$, by scoring each bag with the average of its instance-level estimates as $g(B_j) = \frac{1}{n_j}\sum _{i \in I_j} f(\mathbf {x}_i)$. Therefore, various MIL assumptions can be handled with a proper data representation and collective modeling of the bag structures.

In order to perform class separation by correct classification, having class membership values above the threshold for positive bags and below the threshold for negative bags is desirable. Therefore, we maximize summation of the absolute differences between bag class membership estimates. This paradigm defines the margin between positive and negative class membership estimates, as well. Thus, optimal value of decision threshold $\tau$ leaves the maximum margin between bag class membership estimates. Figure 4 illustrates a possible solution to the QP model (3). The selected value for decision threshold $\tau$ is 0.55 and the class memberships estimates for 3 positive and 3 negative bags are consistent with this threshold.

Fig. 4

An illustration of a solution to QP model (3). Instance level scores are symbolized with red circles and blue triangles, for negative and positive bags, respectively. The vertical green line indicates the decision threshold and each dashed line maps bag class membership of a bag. For a positive and a negative bag, class membership margins are indicated with horizontal arrows

5 Experiments

5.1 Data representation

In MIL, a specific data region representing the positive instance class is named as a concept. The concept instances are informative for class discrimination. Based on this idea, representative sets can be derived in many ways as prototypes to capture the informative instance relationships. Several MIL methods benefit from the dissimilarities to selected prototypes to represent the bags [6, 7, 10, 14, 21]. Moreover, a number of similar algorithms [31, 38] utilize clustering to learn a target concept in MIL problems. Inspired by success of aforementioned methods, we attempt to perform MIL classification in a newly represented feature space. QP model (3) produces a linear classifier and success of this classifier is limited only to linearly separable data.

In QP-MIL, the relationships between instances can be implicitly modeled by preprocessing the input data. Instead of building a classifier in the original instance feature space, we attempt to represent the instances using dissimilarities to the selected prototypes. Aim of the representation is building a linear classifier, which is capable of class separation in a different space. We pool instances in bags and then group them by k-means clustering algorithm into an appropriate number of clusters. Then, the cluster centers are taken as the prototypes. The new features are simply constructed by calculating the Euclidean distances of each instance to these cluster centers. This way, protoypes are derived as a summarized representation of the original data and the linear classifier becomes applicable to the new features.

5.2 Multiple instance datasets

We evaluate our approach in image classification, molecular activity prediction, text categorization and audio classification tasks. The datasets are categorized in Table 2 based on their application domain and the dataset characteristics are also provided. The first category includes famous drug activity prediction tasks on Musks and Mutagenesis’ datasets and a protein identification task. Image classification datasets constitute the second category containing the Corel image datasets, UCSB breast cancer dataset and other smaller sized benchmarks Elephant, Fox and Tiger. Positive class is considered as the target images and the remaining images determine the negative bag class.

Another dataset category covers web mining tasks on Newsgroups and Web recommendation datasets. In Newsgroups, blog posts are categorized into 20 groups based on their subjects where a bag is formed by a collection of multiple posts (i.e. the instances). In the positive class, the terms about a specific subject appears in a number of posts, and the bags with posts about other subjects constitute the negative bags. In Web recommendation, a web page in the user history is a bag and the web pages linked to that web page are the instances. Recommendations of a specific user form the positive class and the bags constituted by the remaining eight users are negatively labeled.

The last category is the bird song recordings from 13 different classes of birds, where a recording is bag and segments of recording are the instances. The target bird class is considered as positive, whereas the bags from the other classes are labeled as negative. We follow an effective experimentation strategy. Cross validation folds are generated by splitting the original dataset into the training set and the test set. We utilize the same splitting indices across both our proposed and the state-of-the-art methods from the literature to perform a comprehensive comparison. All the datasets and cross validation indices are available online at [19].

5.3 Experimental setting and performance criteria

Our experiments use a Windows 10 PC with 16 GB RAM, dual core CPU (Intel Core i7-7700HQ 2.8 GHz). For each dataset, a stratified cross validation scheme is conducted to assess the generalizability of the classifiers. Initially, we scale each feature to zero mean and unit variance. We obtain data representations in QP-MIL via the implementation in Python that uses scikit-learn [24] library. We model QP formulations using Gurobi Python interface and solve using barrier QP solver of Gurobi 8.0 [15]. The default parameters are accepted for the barrier algorithm except for the convergence tolerance, which is set to 0.01. QP-MIL has two parameters: number of clusters, $\kappa$ in data representation and cost parameter C of QP model (3). In k-means clustering, necessarily enough number of clusters, $\kappa$ is determined by using elbow approach [18]. Briefly, within cluster variance after k-means clustering is plotted along with increasing values of $\kappa$ and the position of the elbow is identified to assign the corresponding value to $\kappa$. We run a nested cross-validation with an inner cross-validation loop to choose hyperparameter C from the set $\{0.01,0.1,1,10,100,1000\}$. All of the instances of MIHLSVM formulation are also executed using Gurobi 8.0 [15].

Table 2 Common MIL datasets

The baseline MIL approaches selected for comparison are MILES [6], MInD [7] with bag dissimilarity representation $\text {D}_{\mathrm{meanmin}}$ and miFV [33]. MILES iteratively measures similarities of bags to the training instances, and builds a linear SVM classifier along with $\ell _1$-norm regularization at the same time. MInD defines a bag-level feature representation by using the bag-to-bag dissimilarity measure $\text {D}_{\mathrm{meanmin}}$. miFV benefits from Fisher vectorial coding to map each bag to a single vector. Both MInD and miFV build a linear SVM classifier to classify bag vectors. We execute MILES [6] and MInD [7] using the MIL toolbox [29], and use a MATLAB [32] implementation to run miFV [33]. We accept the default parameters in the original paper for MILES [6]. We use the parameter setting proposed in [7] for MInD [7]. Following the authors’ advice, we employ an inner ten-fold cross-validation to select the three parameters of miFV [33], which are enumerated as PCA energy, number of components and cost parameter of linear SVM. PCA energy attains values from the set $\{0.8, 0.9, 1\}$. The alternatives for the number of Gaussian components is selected from $\{1, 2, 3, 4, 5\}$. The cost parameter of the linear SVM classifier are $\{0.05, 1, 10\}$.

A receiver operation characteristics (ROC) curve visualizes the trade-off between percentage of true positive predictions and percentage of false positive predictions. Area under the ROC curve (AUC) is asserted to be a reliable metric for classification [16]. Larger AUC values indicate a better classifier. Another measure for classifier performance in MIL problems is classification accuracy. For a specific decision threshold value, such as the value of $\tau$ in QP-MIL after optimization, the bag classes are predicted and the accuracy of the classifier is computed. The class imbalance problem is seen in MIL tasks such as Corel, Web recommendation and Birds benchmarks. The value of $\tau$ is optimized on the training bags, and suffers from misleading accuracy when the bag classes are imbalanced. AUC is more effective under class imbalance since all possible thresholds are evaluated to report the classifier performance. Additionally, given the consistent performance of AUC on MIL datasets [30], we qualify AUC as a primary comparison metric in our study.

Table 3 Model size summary of QP-MIL and MIHLSVM on problem instances of 4 datasets

Table 4 Comparison of QP-MIL and MIHLSVM on problem instances of 4 datasets. 10 models of each formulation are built for each dataset, and the average values are reported

5.4 Experimental results

5.4.1 Comparison of QP-MIL with MIHLSVM

In this section, we present a comparison between QP-MIL and MIHLSVM formulation given in Sect. 1 in terms of computational efficiency and other indicators related to classification performance of the derived solutions. The clustering-based data representation described in Sect. 5.1 is considered as the input of all compared formulations.

Table 3 presents the overview of problem sizes on four moderate sized MIL datasets. All datasets are modelled using QP-MIL formulation in (3) and the MIHLSVM formulation in (1). For each dataset in Table 3, ten separate models of QP-MIL and MIHLSVM are built, where ten different partitioning of the original dataset form the input in each model. The averages of problem dimension properties for ten models are reported in Table 3. Formulations in (3) and (1) have quadratic objective functions and number of the quadratic terms are equal for both. Since we solve the formulations on a cluster center-based data representation, the number of quadratic terms is equal to the dimensionality of this representation.

In Table 4, we compare the performance of QP-MIL with the MIHLSVM. MIHLSVM is an MIQP and can be directly solved by standard MIQP solvers. We solve the MIHLSVM formulation in (1) and set the cost parameter C in the objective function (1a) to 1. It is plausible to tune up the appropriate value for C by a cross-validation procedure. However, the computation time of parameter selection in MIHLSVM is a limitation [25].

We are unable to report overall results for MIHLSVM since each cross-validation fold lasts longer than one day for relatively small datasets such as Elephant and Fox. Therefore, we do not carry out a cross-validation loop, and manifest only the model solution time for $C=1$. In contrast with the described procedure in Sect. 4, we do not embed parameter selection into QP-MIL during comparisons of this section and the predetermined value of C is 1. The results in Table 4 are based on one repeat of a ten-fold cross validation. All methods are executed within a time limit of 1800 seconds. First column is the number of problem instance from each dataset that is solved to optimality until the time limit is reached. The mean percentage optimality gap [(upper bound- lower bound)/upper bound] is reported for each algorithm and the corresponding average model solution time in seconds is also presented. To observe generalizability of the learner, we evaluate obtained solutions on the test bags. Average accuracy and AUC values over ten experiments are reported for all three approaches.

Table 5 AUC and accuracy results of four MIL methods with standard errors ($\times$ 100)

Computational study demonstrates that QP-MIL is significantly more efficient and provides accurate solutions compared to the MIHLSVM formulation. All instances of QP-MIL can be solved exactly without a sacrifice in classification success as demonstrated by AUC and accuracy results in Table 4. Being the largest dataset in this comparison, Musk 2 requires an average solution time of 3 seconds to solve QP model (3) to optimality. On the other hand, only one MIHLSVM instance of Musk 1 dataset can be solved to optimality within the time limit. Except for Musk 1, Gurobi is unable to reduce the optimality gap below 90%. For the sake of fairness, we do not include MIHLSVM in the overall comparison results in Sect. 5.4.2 due to the requirements of a higher runtime even for small/moderate sized datasets.

5.4.2 Comparison to baseline methods

Table 5 summarizes the performance of our proposed QP-MIL approach with MILES [6], MInD [7] with bag dissimilarity representation $\text {D}_{\mathrm{meanmin}}$ and miFV [33] on four different MIL application categories. Their descriptions and implementation details are provided in Sect. 5.3.

AUC and accuracy results of MIL classifiers in Table 5 are the averages of a ten-fold cross validation repeated for five times. The best result for each dataset is in boldface. In molecular activity prediction, the highest AUC results are obtained by QP-MIL in Musk 1, and by $\text {D}_{\mathrm{meanmin}}$ in Musk 2. Fisher vector based bag representation suits on Mutagenesis 1 dataset, where second best AUC and accuracy results are obtained by QP-MIL and miFV, respectively. In Protein, the leading method is MILES, which is followed by QP-MIL.

QP-MIL has the best image classification success in Elephant, Tiger and USCB Breast cancer datasets. The implicit instance selection mechanism of MILES is effective on Fox dataset and QP-MIL follows MILES on this dataset. In Corel image datasets, $\text {D}_{\mathrm{meanmin}}$ has the highest average performance, and QP-MIL performs very close to $\text {D}_{\mathrm{meanmin}}$. Results of QP-MIL and $\text {D}_{\mathrm{meanmin}}$ are very close to each other on the average on 20 Newsgroups datasets. In Web recommendation, performance of QP-MIL falls behind miFV and $\text {D}_{\mathrm{meanmin}}$. QP-MIL has the highest AUC and accuracy results in almost all Birds datasets.

The average testing results based on problem categories are reported in Table 6. For each problem category, results of the best method are in boldface. Average AUC and accuracy results in Table 6 demonstrate that QP-MIL is competitive with other algorithms across all application categories and provides the best classification results on some datasets. QP-MIL achieves the best or the second best average AUC and accuracy performance on molecular activity prediction datasets.

Table 6 Average AUC and accuracy results of four MIL methods based on problem categories

Table 7 Average time results of QP-MIL

Image classification results in Table 6 reveal that QP-MIL is broadly comparable with the competitors in all benchmarks. In text categorization, performance of QP-MIL is competitive in Newsgroups datasets and miFV is the leading method in Web recommendation datasets. QP-MIL yields the best average AUC and accuracy results in audio recording classification as verified by the reported results on Birds competition. Finally, QP-MIL has the best overall average AUC and accuracy results.

Both miFV and $\text {D}_{\mathrm{meanmin}}$ are bag-level methods and they are mostly tuned for computer vision and bioinformatics applications of MIL. However, QP-MIL is not tailored for a certain MIL application and overall results of this section confirm generalizability of our approach to various application domains. Without forcing the standard MIL assumption, QP-MIL matches or outperforms the state-of-the-art algorithms on a broad range of applications.

Table 7 shows the time taken up by experiments of QP-MIL on 71 datasets. Again, reported results are the averages after 5 repeats of a ten-fold cross validation. We divide the total time spent by QP-MIL into three main parts: representation learning (RL) time, inner cross-validation (CV) time and model solution time. At first, we obtain clustering-based data representation. We determine the required number of clusters on the training instances and use the resulting cluster centers to represent the training bags. Compared to the computational time on the training instances, RL time for the test bags is negligible. Therefore, we only report the RL time consumed on the training set. As described in Sect. 5.3, we report classification results after a nested cross-validation procedure. The time spent for inner cross-validation loop is the CV time. After parameter selection, we solve QP model and record execution time of barrier algorithm as the model solution time.

Table 7 reveals that QP models are solved efficiently regardless of the dataset dimensionality. Due to the repeated solution of the QP model within each inner fold, significant amount of time is spent on parameter selection. However, RL times are considerably longer compared to CV times in Web datasets since large number of features complicates the dissimilarity calculations in data representation phase. In Mutagenesis datasets, predetermined value of the threshold controlling parameter $\varepsilon$ may cause infeasibility in QP models. If infeasibility is detected, we solve an auxiliary optimization problem to deal with this situation. Specifically, by keeping the original constraints of (3), we convert $\varepsilon$ into a decision variable and maximize its value. This way, a suitable value of $\varepsilon$ is derived. Then, QP model (3) is solved after stating the selected $\varepsilon$ value. This process increases both the CV time and model solution time on these datasets as seen in Table 7. QP-MIL provides an efficient learning approach concerning different MIL application categories. In the light of parameter sensitivity discussions in Sect. 5.4.4, QP-MIL can be implemented without parameter selection to gain from the execution time.

5.4.3 Contribution of threshold selection to model robustness

To make classification more robust, QP-MIL selects the decision threshold automatically. After each experiment, optimal decision threshold is returned with the QP solution as the value of variable $\tau$. To observe the robustness of accuracy results of QP-MIL, we conduct a comparison via solving an extra alternative formulation. We describe another QP, QP without $\tau$, where only variable $\tau$ is excluded and the remaining variables and constraints are the same with the original QP. After solving QP without $\tau$, optimal decision threshold is selected on the training set. Then, testing accuracy is calculated using this threshold value.

Table 8 shows the testing accuracy results after solving both formulations for 3 different datasets. These results imply that including $\tau$ as a variable in QP elicits only negligible differences on accuracy and hence the resulting classifier. We also compare solutions of the original QP formulation and QP without $\tau$ in terms of variance. In Fig. 5, the boxplots of testing accuracies on 3 datasets are provided. Figure 5 demonstrates that QP solutions with a threshold have lower variance compared to QP solutions without $\tau$. Namely, QP-MIL results with similar accuracy and lower variance than QP without $\tau$. Overall, QP with $\tau$ generates robust results and the embedded threshold selection is a particular advantage of the proposed method.

Table 8 Comparison of the testing accuracy results on 3 datasets computed with two different QP solutions depending on whether threshold parameter $\tau$ is included in the model or not

Fig. 5

Boxplots of pairwise accuracy comparison of QP solution with a threshold variable $\tau$, and QP solution without $\tau$ on 3 datasets

5.4.4 Parameter sensitivity

In this section, we conduct experiments on four real-world datasets to examine the sensitivity of QP-MIL to C setting. Six different values of C are tested with 50 replicates of the experiments. We select the tuning set of C as $\{0.01,0.1,1,10,100,1000\}$. We execute data representation and model solving as described in Sect. 5.3 except for the inner cross validation. For each level of C, we solve QP model (3) and record the classification results for the test bags. Figure 6 presents the behavior of the QP-MIL classifier on four datasets. For each dataset, boxplots show the AUC values for different levels of C. For Musk 2, value of C does not have a significant effect on the AUC performance. Corresponding boxplots in Fig. 6 show that smaller C values yield slightly better AUC results in Elephant dataset. Finally, analysis with the boxplots in Fig. 6 demonstrates that changing value of C does not significantly affect the AUC performance for other datasets.

The reported results of the comparisons with baseline approaches are provided after a cross-validation procedure in Sect. 5.4.2. The trade-off between maximization of bag class membership margin and sparsity of the weighting vector can be considered as a practically dispensable criterion for learning. Since most of the computation time is consumed by parameter selection as reported in Table 4, value of C can be fixed initially for run-time considerations. Setting a higher value of C introduces potential risk of overfitting, and therefore may reduce generalization to unknown objects. As shown in the boxplots of Fig. 6, small C values yield higher AUC values in both Musk 2 and Elephant. Therefore, if the parameter selection phase is skipped, we suggest to use small values of C to obtain satisfactory results.

Fig. 6

Sensitivity of the QP-MIL to different values for C on 4 real-world datasets

6 Conclusions

In this paper, we propose an optimization-based method, QP-MIL, to solve multiple instance classification problem, where a bag of instances are classified instead of single instances. Our algorithm is based on a quadratic programming (QP) formulation, which performs classification without imposing additional constraints on relating instance labels to the bag labels. Solving QP problem produces a decision function, which computes a bag class membership score by aggregating instance-level scores. Instance-level scores are obtained by a linear function of feature values. This way, all instances contribute to the bag label and their contributions are modeled by specifying the feature weights. The optimization process outputs a bag-level decision threshold to classify new bags together with the decision function. Distances of bag class memberships to the threshold value are maximized and the sparseness of feature weight vector is controlled by a cost parameter.

We have tested our approach on a wide range of datasets from various categories such as drug activity prediction, image categorization, text mining and audio recording classification. In order to support further research on this area, we serve the used datasets, codes and configurations on our supporting page [19]. We compared the performance of our approach to state-of-the-art machine learning based approaches. To model instance relationships, cluster centers are selected as prototypes and input features are the instance-to-prototype distances. For each dataset, generated problem instances can be easily solved to optimality in seconds. Our experiments on 71 datasets indicate that QP-MIL is competitive with the recent successful heuristic algorithms, and provides the best classification results on a variety of datasets.

Since this study focuses on optimization-based MIL, we also performed comparisons with a recent method MIHLSVM in terms of problem size and computation time. MIHLSVM solves mixed integer quadratic programs to learn a bag classifier. Our comparisons between QP-MIL and MIHLSVM indicate that MIHLSVM problem instances have difficulties to scale to large datasets. Our computational results show that direct solution of MIHLSVM is not able to retrieve satisfactory solutions to MIL problem within a reasonable amount of time. Finally, we examined the effect of the cost parameter and illustrated that the classification performance does not excessively depend on adjustment of the cost parameter. Our MIL approach offers an efficient solution to MIL problem in terms of classification accuracy and model solution time, and can be extended to large real-world challenges as a future work.