Dynamics Complexity of Generalist Predatory Mite and the Leafhopper Pest in Tea Plantations

Abstract

The tea green leafhopper Empoasca onukii is one kind of insect pest threatening the tea production, and the mite Anystis baccarum has been used as an agent for pest control. In this paper, we introduce a generalist predator-prey model to study the dynamics for informing biological control. There have been some bifurcation studies of the generalist predator-prey model in the last few years. Except for the bifurcations include saddle-node bifurcation of codimension 1 and 2, Hopf bifurcations, and Bogdanov-Takens bifurcation of codimension 2 and 3, we also present the bifurcations of nilpotent singularities of elliptic and focus type of codimension 3. We find that the nilpotent singularities are associated with a cubic Liénard system, and the nilpotent bifurcations are three-parameter bifurcations of a codimension 4 nilpotent focus. Furthermore, we show that the nilpotent focus serves as an organizing center to connect all the codimension 3 bifurcations in the system. We also present the bifurcation diagrams to unfold the nilpotent singularities of codimension 3. One interesting observation is that we show numerically the existence of three limit cycles in the system .

1 Introduction

Tea is a popular drink around the world with an estimation of 25000 cups consumed every second, about 2.16 billion cups per day worldwide. Tea consumption is seeing an annual growth of 2.8 percent and is expected to becoming higher in the future [1]. Hence, tea has been an important commercial crop which has been planted in more than 48 countries and regions, and by 2018 the global gross production value reached 16.75 billion US dollars [2]. However, the tea production has been damaged by insects and mite pests, causing on average a 5–55% yield loss (approximately U.S. $500 million and $1 billion) [3] .

To mitigate the damage of tea pests, various pest control techniques have been developed and applied, including cultural (like pruning and plucking, trap crop, resistance breeding) [4, 5], mechanical and physical (hand destruction, barriers, light traps, sticky traps) [5], chemical pesticide [5] and biological control (natural enemies, bio-pesticides, and botanical pesticides) [3, 4]. Cultural and physical method is simple and safe but requires lots of manpower. Commonly used pesticides are effective, however it will cause the pest resistance, pest resurgence, and the undesirable pesticide residues on brewed tea [6]. The use of natural enemies for pest control is effective, safe, and economical. Therefore, the biological control methods have received much attention in recent years [4, 7], especially by improving the influence of natural enemies on pest population via conservation biological control method [8]. Understanding the basis of interactions of tea pests and natural enemies is essential not only for an eco-friendly tea production system [3, 7], but help to control the tea pests while reduce or even eliminate the use of pesticide.

Mathematical models have been made to understand the population dynamics in ecology for many years since the pioneering work of Lotka and Volterra [9]. However, there are less modeling studies on the dynamics of tea garden ecosystems which can be more complicated with thousands of different species, providing a relatively steady microclimate and food supply of insect and mite communities [3]. Among many species, the E. onukii is one of the most important pests threatening the tea production in China and other countries in Asia [5]. The total loss of tender tea shoots caused by Empoasca onukii may account for 15-50% [5, 11]. Some tea plants may cease to grow due to the severe damages.

Among many of the natural enemies of E. onukii, the Anystis baccarum is a predatory mite which is beneficial to the tea plantations [12, 13]. It is a whirligig mite causing no damage to fruit, and it can move rapidly over the branches and foliage of the trees [13]. Also, it shows a level of compatibility with several chemical fungicides [13]. Hence, it may be used for pest suppression, however, unlike specialist predators, A. baccarum is a generalist predator that can feed on a range of invertebrate prey [4, 13], buffering the fluctuation of population from the absence of any one of preys [15]. The role of generalist predators in controlling pests has also been explored in some cropping systems through field experiments [16, 17]. Therefore, we will explore the interaction between generalist predator and its preys to find ways to optimize the beneficial synergies of pest control [16]. In particularly, we will study the dynamics of E. onukii and A. baccarum for seeking a sustainable way for pest suppression in tea plantations.

Fig. 1

Average abundance (standard error) of E. onukii and A. baccarum per 1 $m^2$ in tea canopies in the tea plantations in the Wuyi mountain area from May 2006 until April 2008

To understand the interaction of E. onukii and A. baccarum, Chen et al. [18, 19] carried out field studies in the Wuyi mountain area, the north of Fujian province of China. The abundance data for the two species were collected over a two-year period and presented in Figure 1. One can see from the figure that in the first year, there is a negative correlation between the two species. However, it did not show the same trend in the second year. A significant decrease in the population of E. onukii was not detectable despite the greater abundance of A. baccarum in the second year [19]. One can also observe that when E. onukii is abundant, ideally the A. baccarum mainly feed on E. onukii or may feed on other preys as well, so that the number of E. onukii is reduced to only a certain extent. Therefore, the control of the target pest E. onukii using A. baccarum is much more complicated as A. baccarum is a generalist predator.

It is not difficult to directly make up a predator-prey type of model for the pest and predator mite. However, to understand the population dynamics between these two species and to promote the use of A. baccarum to control E. onukii, we will use the results of field studies [18, 19] and build a simpler dynamical model to study the interaction of the adults population, which will allow us to explore the factors and reason leading to complex dynamics using bifurcation theory, and to find threshold conditions for controlling E. onukii using its generalist natural enemy.

Let us consider a tea plantation with fixed area where tea trees grow. We are interested in the fresh tender leaves which can be measured by the weight or equivalently transformed single-side surface area of leaves. Let K be the total tea leaves surface area ($m^2$) and E(t) denote the adult population of E. onukii, the number of E. onukii per unit tea leaves surface area ($m^2$) at time t. We assume that the average number of E. onukii that per unit tea leaves surface area can carry is $n_e$. Hence, it is plausible to assume that E. onukii satisfy a logistic growth with an intrinsic reproduction rate $r_1>0$ and the carrying capacity $K_1=K n_e>0$ in the absence of A. baccarum.

Let M(t) denote the adult population of A. baccarum, the number of A. baccarum per unit tea leaves surface area ($m^2$) at time t and the average number of A. baccarum per unit tea leaves surface area is $n_m$. As a generalist predator, A. baccarum can prey on other pests and maintain its population without E. onukii. Hence, we assume that the A. baccarum reproduces also following a logistic growth with a constant intrinsic growth rate $r_2>0$ and a carrying capacity $K_2=Kn_m>0$ in the absence of E. onukii. In fact, the generalist predators are more common in ecosystems than the specialist predator. We observe that the euryphagous nature of A. baccarum is conducive to maintaining its population to suppress the E. onukii when the outbreak occurs even when the density of E. onukii is relatively low. If the A. baccarum are monophagous, there may not be enough to control the E. onukii due to the decreasing of E. onukii population. Hence, we will develop a predator prey model considering A. baccarum as a generalist predator.

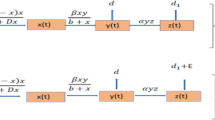
In order to describe the predator-prey relationship between the E. onukii and the A. baccarum, we look at it from a micro perspective. Since each species of insect will be active for certain amount of time per day, we assume that E. onukii and A. baccarum spend $T_e$ and $T_m$ hours foraging per day ($0<T_m,T_e<24 h$) [12, 20]. During the period of $T_m$, each A. baccarum can attack $N_E$ number of E. onukii. The factors affecting $N_E$ are: the area and time needed to search E. onukii, the successful search rate of A. baccarum, attack rate of A. baccarum and the number of E. onukii. If searching is successful, A. baccarum needs $T_h$ time on average to handle the prey (pursue, capture, kill and eat) [12]. Hence, the number of E. onukii attacked by one A. baccarum equals $N_E=spT_sKE$, where s is the successfully searching rate of A. baccarum per unit area per unit of time. p is the capture probability of A. baccarum after search. $T_s$ is the time per day that A. baccarum spend for searching, K is the total tea leaves surface area, and E is the number of E. onukii per unit tea leaves surface area ($m^2$). Note that we have $T_s=T_m-T_hN_E$. Then, we have

$$\begin{aligned} N_E=P(E)=\frac{spT_mKE}{1+spT_hKE} =\frac{\frac{T_m}{T_h}E}{\frac{1}{spT_hK}+E}=\frac{mE}{a+E} \end{aligned}$$

where $m=\frac{T_m}{T_h}$, which is the maximum number of E. onukii that A. baccarum can handle in the time period $T_m$ for foraging. Another important parameter $a=\frac{1}{spT_hK}$, describes the number of E. onukii handled by A. baccarum in the average time period that A. baccarum successfully search and capture one E. onukii. Each A. baccarum on average preys $N_E$ number of E. onukii. And P(E) is the widely used functional response, Holling type II, in the predator prey model. We derive the process to determine the meaning of the parameters in our model, which will help the model analysis incorporating our field experimental data in future work. Hence we have the following model

$$\begin{aligned} \left\{ \begin{array}{rcl} \displaystyle \frac{dE}{dt}&{}=&{} r_1E(1-\displaystyle \frac{E}{K_1}) - \displaystyle \frac{mEM}{a+E},\\ \displaystyle \frac{dM}{dt} &{}=&{} r_2M(1-\displaystyle \frac{M}{K_2}) + \displaystyle \frac{cmEM}{a+E}, \end{array} \right. \end{aligned}$$

(1.1)

where all the parameters $r_1, r_2, K_1, K_2, a, m$ are positive constants as defined above, and c is the conversion rate.

For the model (1.1), we can rewrite as

$$\begin{aligned} \left\{ \begin{array}{rcl} \displaystyle \frac{dE}{dt}&{}=&{} E(r_1-\displaystyle \frac{r_1}{K_1}E - \displaystyle \frac{m}{a+E}M),\\ \displaystyle \frac{dM}{dt} &{}=&{} M(r_2-\displaystyle \frac{r_2}{K_2}M+ \displaystyle \frac{cm}{a+E}E). \end{array} \right. \end{aligned}$$

(1.2)

It turns out that system (1.2) is a model on the bookshelf. One can see that system (1.2) can be regarded as a generalized Lotka-Volterra model with a fractional response function. Recall that for a quadratic Lotka-Volterra system, it is well-known that it has relative simple dynamics, and in particular the system does not even have a limit cycle [21]. As far as we can tell that Alexeev (1973) [22] and Bazykin (1974) [23] are among the first researchers considered the predator competition for resources other than prey and studied the following model,

$$\begin{aligned} \left\{ \begin{array}{rcl} \displaystyle \frac{dx}{dt}&{}=&{} ax-\displaystyle \frac{bxy}{1+Ax}-ex^2,\\ \displaystyle \frac{dy}{dt} &{}=&{} -cy+\displaystyle \frac{dxy}{1+Ax}-hy^2, \end{array} \right. \end{aligned}$$

(1.3)

where a is the reproduction rate of prey population in the absence of the predator. b is the per capita rate of the consumption of prey by the predators. The parameter $c>0$ is the natural mortality rate of the predator, $\frac{d}{b}$ reflects the fraction of prey biomass that is converted into predator biomass. $\frac{1}{A}$ is the prey population density at which the predator’s consumption is half the maximum value or half saturation level. e is the coefficient of competition among prey. h is the coefficient of competition for resources other than prey [10]. The system (1.3) depends on four parameters after rescaling and the related dynamics are well discussed in Bazykin (1998) [10]. But the predator in this model is a specialist predator that only relies on the prey population. When $c<0$, that the predator also has the reproduction rate, the system (1.3) is consistent with the model (1.1). It is worth mentioning that Magal et al. [24] also used the model to explore the spatial dynamics of host and generalist parasitoids with logistic growth, and investigated the biological control of the leaf miner population. Their non-spatial model is the same as (1.1). Recently, Seo and Wolkowicz [25] identified some cases missed in the non-spatial model analysis of Magal et al. [24], and they gave a more detailed bifurcation analysis and presented a bifurcation diagram using $K_1$ and $K_2$ as bifurcation parameters, they analyzed the impact of different $K_1$ and $K_2$ on pest control and proposed possible pest reduction strategies. More recently, Xiang et al. [26] also studied the nilpotent singularity of the model and presented the bifurcations associated with the nilpotent singularity of elliptic and focus type. Here we suggest and use the terms and classification given by Dumortier et al. [27] and in Zhu and Rousseau [28] in classifying the non-cusp type of nilpotent singularities.

The dynamics of generalist predator-prey model (1.2) are much more complicated then most of the specialist predator-prey models. The model can undergo Hopf bifurcation, degenerate Hopf bifurcation, and Bogdanov-Takens (BT) bifurcations of codimension 2 and 3, bifurcations of nilpotent focus and elliptic point. The three types of codimension 3 bifurcations of nilpotent singularities were presented in the study of Xiang et al. [26], but how these codimension 3 bifurcations are organized in the system are not discussed. From the available studies, the system can have two limit cycles [25, 26, 29], just like the specialist predator-prey model with other Holling types of response function studied in [30]. Currently, the available bifurcation studies are only partial unfolding of the complex dynamics from the degenerate nilpotent singularity, the understanding of the local dynamics still remains incomplete, not to say the global dynamics of the system.

The model exhibits three boundary equilibria and up to three coexistence equilibria, and the complicated dynamics involves Bogdanov-Takens bifurcation of codimension 2 and 3, and bifurcations of nilpotent singularity of focus and elliptic type of codimension 3 or 4. As described by Xiao and Zhu [35], the predator-prey system of the form (1.2) can be locally transformed into a generalized Liénard-type system. There have been extensive global analysis of Liénard system involving the nilpotent singularities. For the related bifurcation studies, we only refer to Dangelmayr and Guckenheimer [36], Khibnik et al. [37] and a recent work of Chen and Zhu [38] and references therein. In this paper, we will present a full bifurcation analysis of the system (1.2). Using normal form theory we will show that it is the nilpotent focus of codimension 4 that serves as an organizing center of the codimension 3 nilpotent bifurcations. We will also present the bifurcation diagrams near the nilpotent singularities of focus and elliptic type of codimension 3 using $r_1$, $r_2$, $K_1$ and $K_2$ as bifurcation parameters. For system (1.2), one interesting observation is that we numerically show the existence of three limit cycles in the generalist predator-prey systems.

The paper is organized as the following. We present the existence and number of equilibria and local stability in Sect. 2. In Sect. 3, we study the bifurcation and complex dynamics of the system. We prove the existence of saddle-node bifurcation of codimension 1 and 2, Hopf bifurcation, BT bifurcation and nilpotent singularity of codimension 3 and 4. We also provide the one and two-parameter bifurcation diagrams and the bifurcation diagram near the nilpotent singularity of codimension 3. Section 4 contains the phase portraits of system (1.1) with different parameters. We present an example numerically to show the existence of three limit cycles. Our numerical simulation illustrates the different types of coexistence of A. baccarum and E. onukii and the large amplitude oscillation of this two species population is possible. Finally, in Sect. 5, we summarize our results and discuss the implications for pest control based on our dynamical findings. Some of the calculations were assisted by the use of Maple [39]. The phase portraits and one and two-parameter bifurcation diagrams were produced by the Matlab [40].

2 Equilibrium States and Local Stability

2.1 Existence and Number of Equilibria

Our model (1.1) always has three boundary equilibria, $S_{00}(0,0)$, $S_{10}(K_1, 0)$ and $S_{01}(0, K_2)$, which represent three trivial equilibrium states respectively. For co-existence equilibrium state, one can verify that any positive equilibrium ${\bar{S}}({\bar{E}}, {\bar{M}})$, if it exists, is the intersection of the two curves

$$\begin{aligned} \begin{aligned} U_1(E)&=\frac{r_1(K_1-E)(a+E)}{K_1m} =\frac{r_1E}{P(E)}(1-\frac{E}{K_1}), \\ U_2(E)&=K_2\left[ \frac{mcE}{r_2(a+E)}+1\right] =K_2[\frac{c}{r_2}P(E)+1], \end{aligned} \end{aligned}$$

(2.1)

and its E coordinate satisfies

$$\begin{aligned} \begin{aligned} U(E)=E^3-(K_1-2a)E^2 +\left[ a^2-2aK_1+\frac{K_1K_2cm^2}{r_1r_2} +\frac{mK_1K_2}{r_1}\right] E -a^2K_1+\frac{maK_1K_2}{r_1}=0.\nonumber \end{aligned}\\ \end{aligned}$$

(2.2)

The cubic equation (2.2) has at most 3 positive solutions. We are only interested in the non-negative solutions of equation (2.2).

We first use $K_1$ and $K_2$ as parameters to discuss the number of positive equilibria. The equation (2.2) has at least one positive solution when $K_2<\frac{r_1a}{m}$. For the case of $K_2>\frac{r_1a}{m}$, some calculations and results can be found in [25, 26]. Using the formula of Fan in [31], we can compute the discriminant of (2.2) to get

$$\begin{aligned} \begin{aligned} \Delta =B^2-4AC, \end{aligned} \end{aligned}$$

(2.3)

where

$$\begin{aligned} A&=(K_1+a)^2-\frac{3mK_1K_2\delta }{r_1r_2},\\ B&=2a(K_1+a)^2-\frac{3mK_1K_2[K_1\delta +a(7r_2-cm)]}{r_1r_2},\\ C&=\left[ a^2-2aK_1+\frac{K_1K_2cm^2}{r_1r_2} +\frac{mK_1K_2}{r_1}\right] ^2+3(K_1-2a)(-a^2K_1+\frac{maK_1K_2}{r_1}), \end{aligned}$$

and $\delta =r_2+cm$. Collecting in terms of $r_1$, $\Delta$ becomes

$$\begin{aligned} \begin{aligned} \Delta =\tilde{A}r_1^2+\tilde{B}r_1+\tilde{C}, \end{aligned} \end{aligned}$$

(2.4)

where $\tilde{C}=4m\delta ^3$ and

$$\begin{aligned} \tilde{A}&=\frac{4ac(K_1+a)^3r_2^2}{K_1^2K_2^2},\\ \tilde{B}&=-\frac{(K_1+a)^2 r_2^3 +2K_2cm(K_1+a)(K_1+10a)r_2^2 +c^2m^2(K_1^2+20K_1a-8a^2)r_2}{K_1K_2}. \end{aligned}$$

The sign of $\Delta$ decides the number of real roots of (2.2). The equation $\Delta =0$ may have two real roots if $\Delta _r>0$ which are denoted as $r_{1i}=r_{1i}(K_1,K_2)(i=1,2)$:

$$\begin{aligned} r_{11}(K_1,K_2)=\frac{-B+\sqrt{\Delta _r}}{2A}, \ \ r_{12}(K_1,K_2)=\frac{-B-\sqrt{\Delta _r}}{2A}, \end{aligned}$$

where $\Delta _r =\frac{r_2^2[K_1\delta +ar_2][K_1\delta +a(r_2-8cm)]^3}{K_1^2K_2^2}$.

Fig. 2

Existence of positive equilibria (number and position) of system (1.1) with $K_{1}$ and $K_{2}$ as parameters. The light blue curve is $U_1(E)$; the orange curve is $U_2(E)$ (Color figure online)

For $r_2<8cm,K_2<\frac{r_1a}{m}$ and $K_1>\frac{a}{8}(8cm-r_2)$, $r_{1i}=r_{1i} (K_1,K_2) (i=1,2)$ defines two curves $C_1$ and $C_2$ in $(K_1,K_2)$ plane

$$\begin{aligned} \begin{array}{rcl} C_1&{}=&{} \left\{ (K_1,K_2) \Big | r_1=r_{11} (K_1,K_2), \ K_1>\dfrac{a}{\delta }(8cm-r_2), K_2< \dfrac{r_{1}a}{m} \right\} , \\[2ex] C_2&{} = &{} \left\{ (K_1, K_2)\Big | r_1=r_{12} (K_1,K_2), K_1> \dfrac{a}{\delta }(8cm-r_2), K_2< \dfrac{r_{1}a}{m} \right\} , \end{array} \end{aligned}$$

and they subdivide the nonnegative cone of $(K_1, K_2$ plane into three open regions (see Fig. 2):

$$\begin{aligned} V_1=&\left\{ (K_1,K_2), \Delta >0 \right\} ,\\ V_2=&\left\{ (K_1,K_2), C_{1}\cup C_{2} \right\} ,\\ V_3=&\left\{ (K_1,K_2), \Delta <0 \right\} . \end{aligned}$$

In $V_1, V_2$ and $V_3$, system (1.1) has one, two (except for the intersection point) and three positive equilibria respectively.

2.2 Local Stability of Equilibria

The equilibrium $S_{00}$ has two positive eigenvalues $r_1$ and $r_2 >0$, it is a unstable node. $S_{10}(K_1,0)$ is always a saddle which means that as a generalist predator, the A. baccarum will never go extinction.

For the pest free equilibrium point $S_{01}(0,K_2)$, it has two eigenvalues, one is $-r_2<0$, the other is $r_1-\frac{mK_2}{a}$. Hence it is locally asymptotically stable if $K_2>\frac{r_1a}{m}$, is a saddle if $\frac{r_1a}{m}>K_2$, and it will be a saddle-node when $K_2=\frac{r_1a}{m}$. In later section, we will see that $S_{01}$ can be a saddle-node of codimension 2.

Now, we discuss the local stability of the coexistence or positive equilibria. Using the expressions of $U_1(E)$ and $U_2(E)$, we can rewrite the system (1.1) as

$$\begin{aligned} \left\{ \begin{array}{rcl} \displaystyle \frac{dE}{dt} &{}=&{} P(E)[U_1(E)-M],\\ \displaystyle \frac{dM}{dt} &{}=&{} \dfrac{r_2}{K_2}M[U_2(E)-M]. \end{array} \right. \end{aligned}$$

(2.5)

The Jacobian matrix of system (2.5) is

$$\begin{aligned} \left. \begin{array}{rcl} J(E)=\begin{pmatrix} P(E)U'_1(E)+P'(E)[U_1(E)-M]&{} -P(E)\\ \frac{r_2}{K_2}MU'_2(E)&{}- \frac{r_2}{K_2}M+\frac{r_2}{K_2}[U_2(E)-M] \end{pmatrix}. \end{array} \right. \end{aligned}$$

(2.6)

For any positive equilibrium, if exists, the characteristic equation at the equilibrium $\overline{S}(\overline{E}, \overline{M})$ is of the form

$$\begin{aligned} \begin{aligned} \lambda ^2-\left[ P(E)U'_1(E)-\frac{r_2}{K_2}\overline{M}\right] \lambda +P(E)\frac{r_2}{K_2}\overline{M}\big [U'_2(E)-U'_1(E)\big ]=0. \end{aligned} \end{aligned}$$

(2.7)

If $\lambda _1$ and $\lambda _2$ are the two eigenvalues, then we have the trace and determinant of J(E) are

$$\begin{aligned} \begin{array}{rcl} T(J(\overline{S}))&{}=&{}\lambda _{1}+\lambda _{2}=P(\overline{E})U'_1(E) -\frac{r_2}{K_2}\overline{M},\\ D(J(\overline{S}))&{}=&{}\lambda _{1}\lambda _{2} =P(\overline{E})\frac{r_2}{K_2}\overline{M}\big [U'_2(\overline{E})-U'_1(\overline{E})\big ], \end{array} \end{aligned}$$

(2.8)

where

$$\begin{aligned} U'_1(\overline{E})= \frac{r_1(-a - 2\overline{E} + K_1)}{K_1m},\ \ \ \ U'_2(\overline{E})=\frac{K_2acm}{r_2(a + \overline{E})^2}. \end{aligned}$$

For any $\overline{S}$, sign of the $D(\overline{E})$ is determined by the slope difference of the two curves $M=U_1(E)$ and $M=U_2(E)$ at the intersection. As shown in Fig. 3, if we denote $k_i=U'_i(\overline{E})$ ($i=1,2$) then when $k_1>k_2$, $D(J(\overline{S}))<0$, the equilibrium point is a saddle. If $k_1<k_2$, then $D(J(\overline{S}))>0$, and the real part of the eigenvalues will be both positive or negative depending on the sign of $T(J(\overline{S}))$.

Fig. 3

The existence and stability of the three positive equilibria $S_1$, $S_2$ and $S_3$ for $(K_1, K_2)\in V_3$

It follows from (2.8) that a Hopf bifurcation may occur at $\overline{S}$ if $T(J(\overline{S}))=0$. Also, if $k_1=k_2$, $D(J(\overline{S}))=0$, a saddle-node bifurcation may occur. Furthermore, the equilibrium will be nilpotent if $T(J(\overline{S}))=D(J(\overline{S}))=0$.

To summarize, as shown in Figs. 2 and 3, we have the following proposition on the number and local stability of positive equilibria.

Proposition 2.1

Consider the system (1.1) with parameters $K_1$ and $K_2< \dfrac{r_{1}a}{m}$. For any $r_1$, $r_2$, a, c, $m>0$, we have

• (1) If  $(K_{1}, K_{2})\in V_{1}$ ($\Delta >0$), system has a unique positive equilibrium $S_{1}$, it is a non-saddle.

• (2) If  $(K_{1},K_{2})\in V_{2}$, ($\Delta =0$),

  • (2.1) If $r_2<8cm$, $K_1>2a$, $\Delta _{r}=0$ and $(K_1,K_2)=K^*(K_1^*,K_2^*)=C_1\cap C_2$ with

    $$\begin{aligned} K_1^*=\frac{a(8cm-r_2)}{\delta }, \ \ K_2^*=\frac{27r_1r_2c^2ma}{\delta ^2(8cm-r_2)}, \end{aligned}$$

    (2.9)

    then, system has a unique degenerate positive equilibrium which we denote it as $S_{123}=(E_{123}, M_{123})$ with

    $$\begin{aligned} E_{123}=\frac{K_1^*-2a}{3}, \ \ M_{123}=\frac{2r_1(K_1^*+a)^2}{9K_1^*m}. \end{aligned}$$

    (2.10)

  • (2.2) If $\Delta _{r}>0$ or when $(K_1, K_2)\in C_1\cup C_2/(K_1^*, K_2^*)$, system has two positive equilibria.

    • (i) When $(K_{1},K_{2})\in C_{1}/(K_1^*,K_2^*)$, system has the two positive equilibria are $S_{1}(E_1,M_1)$ and $S_{23}(E_{23},M_{23})$, and $S_{23}$ is of multiplicity 2 and a saddle-node if $T(S_{23})\ne 0$.

    • (ii) When $(K_{1},K_{2})\in C_{2}/(K_1^,K_2^*)$, the system has two positive equilibria $S_{12}(E_{12},M_{12})$ and $S_{3}(E_{3},M_{3})$, and $S_{12}$ is of multiplicity 2 and a saddle- node if $T(S_{12}) \ne 0$.

• (3) If $(K_{1},K_{2})\in V_3$ ($\Delta <0$), system has three distinct positive equilibria. We denote these three equilibria as $S_i (E_i,M_i)$ with $i=1,2,3$ and $E_1< E_2< E_3$. The middle one $S_2$ ($E_2, M_2$) is always a saddle.

3 Bifurcation and Complex Dynamics

For system (1.1), when $K_1$ and $K_2$ change, it can have up to three positive equilibria which will undergo various type of bifurcations. Among the rest of 5 model parameters $r_1$, $r_2$, a, c, m, we will select to add the parameters $r_1$ and $r_2$ to study the bifurcations, hence we will use $K_1,K_2$ and $r_1, r_2$ to present the bifurcations in the parameter space $(K_1, K_2, r_1, r_2)$.

3.1 Saddle-Node Bifurcations

System may undergo saddle-node bifurcations at a positive equilibrium and boundary equilibrium $S_{01}(0,K_2)$.

It follows from the Prop. 2.1 that $S_{1}$ and $S_{2}$ coalesce at $S_{12}$ if $(K_{1}, K_{2})\in C_{2}$. Note that $U'_2(E)=\frac{acmK_{2}}{r_{2}(a+E)^2}>0$, hence when exists, $S_{12}$ is always located to the left of the hump of the parabola. From (2.8), we have $D(J(S_{12}))=0$, and the associated eigenvalues, one is zero, and the other

$$\begin{aligned} \begin{aligned} \lambda _{2}&=T_{\Delta }=P(E_{12})U'_1(E_{12})-\frac{r_2}{K_2}M_{12}\\&=-\frac{2r_1E_{12}^2 +[(\delta -r_1)K_1+r_1a]E_{12}+K_1ar_2}{K_1(a+E_{12})} =-\frac{h(E_{12})}{K_1(a+E_{12})}, \end{aligned} \end{aligned}$$

here we define that

$$\begin{aligned} h(\overline{E})=2r_1\overline{E}^2 +[\delta K_1+r_1(a-K_1)]\overline{E}+K_1r_2a, \end{aligned}$$

(3.1)

with $\overline{E}=E_{12}$, $0<E_{12}<\frac{K_1-a}{2}$.

Note that $\frac{d h(E_{12})}{d r_1}=E_{12}(2E_{12}-K_1+a)< 0$, therefore $\lambda _{2}$ will change sign at most once, and $h(r_{11})<h(r_{12})$. Hence, we only need to find the nilpotent equilibria that $T_{\Delta }=0$, which separate the stable and unstable saddle-node bifurcation.

For the equilibrium $S_{12}$, if $T_{\Delta }=T(J(S_{12}))\ne 0$, we can linearize the system at $S_{12}$ and diagonalize the linear part to obtain

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x}&{}=&{} A_{20}x^2+xO(y)+O(|y|^2,|x,y|^3),\\ \dot{y}&{}=&{}T_{\Delta }y+O(|x,y|^2), \end{array} \right. \end{aligned}$$

(3.2)

where

$$\begin{aligned} \begin{aligned} A_{20}&= \frac{E_{12}(\delta E_{12}+r_2a)}{r_2(a+E_{12})^3h(E_{12})}\{r_1r_2(K_1+a)(a+E_{12})^2+K_1K_2m[a(cm-2r_2)-2\delta E_{12}]\},\\ E_{12}&=\frac{m\delta K_1^2K_2+am(7r_2-2cm)K_1K_2-2ar_1r_2(K_1+a)^2}{2r_1r_2(K_1+a)^2-6m\delta K_1K_2}. \end{aligned} \end{aligned}$$

Obviously, $A_{20}$ determines the codimension of the saddle-node bifurcation if $T_{\Delta }\ne 0$. If $A_{20}\ne 0$, then it follows from (3.2) that $S_{12}$ is a saddle-node (for $S_{23}$, the calculation is similar).

If $A_{20}=0$, we have

$$\begin{aligned} \begin{array}{ll} &{}r_1r_2\delta ^2 K_1^3K_2 -4m\delta ^3 K_1^2K_2^2+2ar_1r_2\delta (10cm+r_2)K_1^2K_2\\ &{} \ \ \ \ \ \ +a^2r_1r_2(r_2^2+20cmr_2-8c^2m^2)K_1K_2-4acr_1^2r_2^2(K_1+a)^3=0. \end{array} \end{aligned}$$

(3.3)

One can verify that for any positive model parameters, if $K_1= K_1^*, K_2= K_2^*$, then $A_{20}=0$, which corresponds to the case $S_{12}=S_{23}=S_{123}$.

Substituting the expressions (2.9) for $K_1= K_1^*, K_2= K_2^*$ into $T_{\Delta }=0$, we can solve to get a unique solution

$$\begin{aligned} r_1=r_1^*=\frac{2\delta (8cm-r_2)}{3(2cm-r_2)}. \end{aligned}$$

Therefore, $T_\Delta$ changes sign at $(K_1^*,K_2^*, r_1^*)$. When $(K_1,K_2,r_1)=( K_1^*,K_2^*, r_1^*)$, $S_{123}$ becomes a nilpotent equilibrium which will be discussed further in Section 3.4.

Proposition 3.1

For the system (1.1) with $(K_1,K_2) \in C_1\cup C_2/(K_1^*,K_2^*)$ ( $\Delta =0$ and $T_{\Delta }\ne 0$), we have

• (1) When exist, $S_{12}$ and $S_{23}$ are saddle-nodes of codimension 1 for $(K_1,K_2)$ on $C_2$ and $C_1$ respectively.

• (2) If $K_1= K_1^*, K_2= K_2^*$ but $r_1\ne r_1^*$, the unique positive equilibrium $S_{12}=S_{23}=S_{123}$ will be a saddle-node of codimension 2.

Now we study the bifurcation of the boundary equilibrium $S_{01}(0,K_2)$. When $K_2=\frac{r_1a}{m}$, one can calculate to verify that $S_{01}$ has two eigenvalues 0 and $-r_2$, hence it is a saddle-node. Translate the $S_{12}(0,K_{2})$ into the origin by letting $x=E,y=M-\frac{r_1a}{m}$, we obtain

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x}&{}=&{} \dfrac{r_1(K_1-a)}{K_1a}x^2-\dfrac{m}{a}xy+\dfrac{m}{a^2}x^2y -\dfrac{r_1}{a^2}x^3+O(|x,y|^4),\\[1ex] \dot{y}&{}=&{}cr_1x-r_2y-\dfrac{cr_1}{a}x^2+\frac{cm}{a}xy- \frac{r_2m}{r_1a}y^2-\frac{cm}{a^2}x^2y+ \dfrac{cr_1}{a^2}x^3+O(|x,y|^4). \end{array} \right. \end{aligned}$$

(3.4)

If we make a change of variables as $u=x$, $v=\frac{cr_1}{r_2}x+y$, then system (3.4) becomes

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{u}&{}=&{} \tilde{a}_{20}u^2+\tilde{a}_{11}uv +\tilde{a}_{30}u^3+\tilde{a}_{21}u^{2}v+O(|u,v|^4),\\[1ex] \dot{v}&{}=&{}-r_2v+\tilde{b}_{20}u^2+\tilde{b}_{11}uv +\tilde{b}_{02}v^2+O(|u,v|^3), \end{array} \right. \end{aligned}$$

(3.5)

where

$$\begin{aligned}&\tilde{a}_{20}= \frac{r_1((r_2-cm)K_1 - r_2a)}{ar_2K_1}, \ \ \tilde{a}_{11}=-\dfrac{m}{a},\ \ \ \ \tilde{a}_{30}=\dfrac{r_1(cm - r_2)}{a^2r_2},\ \ \ \ \tilde{a}_{21}=\dfrac{m}{a^2},\ \ \ \ \\&\tilde{b}_{20}=-\dfrac{((r_1(cm - r_2) - r_2^2)K_1 + r_1r_2a)r_1c}{aK_1r_2^2},\ \ \ \ \tilde{b}_{11}=\dfrac{cm(r_1-r_2)}{ar_2}, \ \ \ \ \tilde{b}_{02}=-\dfrac{r_2m}{r_1a}. \end{aligned}$$

Therefore, $S_{01}$ is a saddle-node of codimension 1 when $\tilde{a}_{20}\ne 0$.

When $S_{12}=S_{01}$, we have $K_1=\frac{r_{2}a}{r_{2}-cm}$ ($r_2>cm$), and we can verify that $\tilde{a}_{20}=0, \tilde{a}_{30}\ne 0$. Also, when $S_{123}=S_{01}$, we have $K_1=2a, r_2=2cm$, and $\tilde{a}_{20}=0, \tilde{a}_{30}\ne 0$. Unlike in [26], this is a more degenerate case which may involve canard cycles and deserves further investigation [32].

Summarizing the above discussion, we have the following proposition.

Proposition 3.2

For the pest free equilibrium $S_{01}(0,K_2)$, if $K_2=\frac{r_1a}{m}$,

• (1) it is a saddle-node of codimension 1.

• (2) when $K_1=\frac{r_{2}a}{r_{2}-cm}$, and $(r_2>cm)$, $S_{01}$ is a saddle-node of codimension 2.

3.2 Hopf Bifurcations

Though the Hopf bifurcations were analyzed in Seo and Wolkowicz in details [25], but their analysis did not capture all the possible cases, we will present the Hopf bifurcation analysis and add the other two types of $(K_1,K_2)$ plane bifurcation diagrams which were missing in their analysis. From the Prop. 2.1, when exists, the equilibria $S_{1}$ and $S_{3}$ may undergo Hopf bifurcation(s) if

$$\begin{aligned} \begin{aligned} T(J(\overline{S}))&=k_1P(\overline{E})-\frac{r_2}{K_2}\overline{M} =-\frac{h(\overline{E})}{K_1(a+\overline{E})}=0, \end{aligned} \end{aligned}$$

(3.6)

where $h(\overline{E})$ is defined in (3.1).

Denote the discriminant of equation $h(\overline{E})=0$ as $\Delta _1$, and collect in terms of parameter $K_1$,

$$\begin{aligned} \Delta _1=(\delta -r_1)^2K_1^2+2r_1a(cm - r_1 - 3r_2)K_1+a^2r_1^2, \end{aligned}$$

with its discriminant denoted as $\Delta _2=-32a^2r_1^2r_2(cm - r_1 - r_2)$. The equation $h(\overline{E})=0$ may have two roots if $\Delta _1>0$ which we denote them respectively as

$$\begin{aligned} H_1=\frac{r_1(K_1-a)-K_1\delta +\sqrt{\Delta _1}}{4r_1}, \ \ \ \ H_2=\frac{r_1(K_1-a)-K_1\delta -\sqrt{\Delta _1}}{4r_1}. \end{aligned}$$

For $H_{1,2}$ to be real numbers, it also requires

$$\begin{aligned} K_1>\frac{r_1a}{r_1-\delta }\quad (0<r_1<\delta ). \end{aligned}$$

When $\Delta _2<0$, then $r_1<cm-r_2$, $\Delta _1$ is always greater than 0. When $\Delta _2\ge 0$, then $r_1\ge cm-r_2$, $\Delta _1>0$ when $K_1\ge K_1^{+}$ or $K_1\le K_1^{-}$, with

$$\begin{aligned} K_1^{+}=\frac{2r_1a( r_1 + 3r_2-cm)+\sqrt{\Delta _2}}{2(r_1-\delta )^2}, \quad K_1^{-}=\frac{2r_1a( r_1 + 3r_2-cm)-\sqrt{\Delta _2}}{2(r_1-\delta )^2}. \end{aligned}$$

To ensure $K_1^{\pm }$ are positive, it requires

$$\begin{aligned} r_1\ge cm-r_2=\text {max}\{cm-r_2, cm-3r_2\}. \end{aligned}$$

Also, one can easily find that $K_1^{+}>\frac{r_1a}{r_1-\delta }$. Hence, we have the following condition to ensure $\Delta _1>0$,

$$\begin{aligned} \begin{aligned} K_1&>\frac{r_1a}{r_1-\delta },\quad 0<r_1<cm-r_2,\\ K_1&\ge K_1^{+},\quad cm-r_2\le r_1<\delta . \end{aligned} \end{aligned}$$

(3.7)

Substituting $H_1$ and $H_{2}$ into $U(\overline{E})$ yields the set of Hopf bifurcation which is defined by a curve $H(K_1,K_2,r_1)=0$ given by

$$\begin{aligned} \begin{aligned} K_2=\frac{p_3\pm p_2\sqrt{\Delta _1}}{4(p_1\mp \delta \sqrt{\Delta _1})mr_1K_1} \end{aligned} \end{aligned}$$

(3.8)

where

$$\begin{aligned} p_1&=\delta (\delta -r_1)K_1+r_1a(\delta -4r_2),\\ p_2&=-r_2[(r_1^2-\delta ^2)K_1^2+2ar_1(\delta +2r_1+r_2)K_1-a^2r_1^2],\\ p_3&=-r_2[(\delta +r_1)(\delta -r_1)^2K_1^3 -ar_1[-3r_1^2+2(\delta +r2)r_1+\delta (\delta +6r_2)]K_1^2\\&\ \ \ -a^2r_1^2(\delta -11r_1-10r_2)K_1+a^3r_1^3]. \end{aligned}$$

On the other hand, for Hopf bifurcation to occur, we need $D(J(\overline{S}))>0$ ($k_1<k_2$), which is equivalent to

$$\begin{aligned} 2r_1r_2\overline{E}^3 - r_1r_2(K_1 - 5a)\overline{E}^2 - 2ar_1r_2(K_1 - 2a)\overline{E} + a(K_1K_2cm^2 - K_1ar_1r_2 + a^2r_1r_2)>0 \end{aligned}$$

(3.9)

Substituting $H_{1,2}$ into the (3.9) and we obtain

$$\begin{aligned} K_2>\frac{r_2(\hat{p}_1-\hat{p}_2\sqrt{\Delta _1})}{8K_1acm^2r_1^2}\ \ (\text {for}\ \ H_1), K_2>\frac{r_2(\hat{p}_1+\hat{p}_2\sqrt{\Delta _1})}{8K_1acm^2r_1^2}\ \ (\text {for}\ \ H_2), \end{aligned}$$

(3.10)

where

$$\begin{aligned} \hat{p}_1=&\delta (\delta - r_1)^2K_1^3 - 2r_1a[(-cm - 2r_2)r_1 - \delta (cm + 4r_2)]K_1^2 + r_1^2a^2(cm + 4r_1 + 15r_2)K_1 \\&- 4a^3r_1^3,\\ \hat{p}_2=&\delta (\delta - r_1)K_1^2 - r_1a(3cm + 5r_2)K_1 + 4a^2r_1^2. \end{aligned}$$

Therefore, under condition of (3.7) and (3.10), a Hopf bifurcation may occur at $\overline{E}=H_1$, $\overline{E}=H_2$ or at $\overline{E}=H_1=H_2$ when $\Delta _1=0$, except when $\overline{E}=E_{12}$ or $\overline{E}=E_{23}$ or $\overline{E}=E_{12}=E_{23}=E_{123}$ where the degenerate equilibrium point occurs and the Hopf bifurcation curve is given by (3.8).

Next, we verify the transversality condition. Let $\gamma$ be the real part of the eigenvalue of $S_1$ or $S_3$, then

$$\begin{aligned} \gamma =\frac{1}{2}T(\overline{E}) =-\frac{2r_1\overline{E}^2+[\delta K_1+r_1(a-K_1)]\overline{E}+K_1r_2a}{2K_1(a+\overline{E})}. \end{aligned}$$

A straightforward calculation gives

$$\begin{aligned} \frac{\partial \gamma }{\partial K_2} =\frac{\partial \gamma }{\partial \overline{E}} \frac{\partial \overline{E}}{\partial K_2} =\frac{-2r_1\overline{E}^2-4r_1a\overline{E} -r_1a^2+K_1(r_1-cm)a}{2K_1(a+\overline{E})^2} \frac{\partial \overline{E}}{\partial K_2 }, \end{aligned}$$

where

$$\begin{aligned} \frac{\partial \overline{E}}{\partial K_2 } =\frac{-K_1m[(cm+r_2)\overline{E}+r_2a]}{(K_1K_2cm^2+K_1K_2mr_2-2K_1ar_1r_2 -2K_1r_1r_2\overline{E}+a^2r_1r_2+4ar_1r_2\overline{E} +3r_1r_2\overline{E}^2)}. \end{aligned}$$

Since $\overline{E}$, $K_1$, $r_2$, c, m, a are all positive, $\frac{\partial \overline{E}}{\partial K_2 }\ne 0$. Also, we find $\frac{\partial \gamma }{\partial \overline{E}}=0$ only when $\overline{E}=\hat{E}=\frac{-2r_1a+\sqrt{2r_1a[K_1(r_1-cm)+r_1a]}}{2r_1}$ and the coordinate $\hat{E}$ does not satisfy $U(\hat{E})=0$. For the positive equilibrium $\overline{S}(\overline{E},\overline{M})$, $\frac{\partial \gamma }{\partial \overline{E}}\ne 0$. Hence, $\frac{\partial \gamma }{\partial K_2}\ne 0$, the transversality condition is satisfied.

Moreover, we can find the point that $D(J(\overline{S}))=0$, which is the intersection of Hopf and saddle-node bifurcation curves. It separates the Hopf bifurcation and neutral saddle curves. We now plot the curves $\Delta =0$ and $H(K_1, K_2, r_1)=0$ in $(K_1,K_2)$ plane when $r_1=r_1^*$ for different $r_2$. A numerical generated partial bifurcation diagram contains both Hopf and saddle-node bifurcations is presented in $(K_1,K_2)$ plane in Fig. 4. This is the slices of the bifurcation diagram near the degenerate equilibrium point when $r_1$ is fixed. Also, the bifurcation diagram with $r_1$ varying are presented in Figs. 8 and  9. In this paper, we discussed the bifurcation diagram involving four parameters through the slices.

Different cases can happen with the two curves are tangent at different positions (Fig. 4a, b, c) which corresponds to different type of nilpotent singularities. The curve in blue is for saddle-node bifurcation, $\Delta =0$, which has two parts of stable and unstable saddle-node bifurcation separated by a point associated with nilpotent equilibrium point (Fig. 4a, b) or Bogdanov-Takens point (Fig. 4c; while the curve in red, $H=0$ is composed of curves segment of Hopf bifurcation curve and neutral saddle curve which are separated by the point corresponding to the nilpotent equilibrium (Fig. 4a, b) or Bogdanov-Takens point (Fig. 4c).

Fig. 4

The diagram of Hopf and saddle-node bifurcations in $(K_1,K_2)$ plane when $r_1=r_1^*$ with different $r_2$. $SN^{\pm }$ is the unstable (blue dot line) and stable (blue solid line) saddle node bifurcation curve respectively; NS is the neutral saddle curve (red dot line); H is the Hopf bifurcation curve (red solid line); NFP is the nilpotent focus point of codimension 3; NEP is the nilpotent elliptic point of codimension 3; CP is the cusp point; BT is the Bogdanov-Takens point (Color figure online)

3.3 Bogdanov-Takens Bifurcation

The analysis of Bogdanov-Takens bifurcation of codimension 2 was not included in the studies of Seo and Wolkowicz [25] and Xiang et al. [26], we will briefly present the bifurcation for the purpose of completeness.

Theorem 3.3

Suppose

$$\begin{aligned} K_2=\widetilde{K_2}=\frac{r_2(a + \overline{E})^2(r_2a + \overline{E}\delta )}{m^2ac\overline{E}},\ \ \ \ r_1=\widetilde{r_1}=\frac{K_1(r_2a + \delta \overline{E})}{\overline{E}(-a - 2\overline{E} + K_1)}, \end{aligned}$$

$K_1>a + 2\overline{E}$ and $\hat{m}_{20}\ne 0$, $\hat{m}_{11}\ne 0$, system (1.1) localized at $\overline{S}$ is topologically equivalent to

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x}&{}=&{} y,\\ \dot{y}&{}=&{} sgn(\hat{m}_{20})x^2+sgn(\hat{m}_{11})xy+O(|x,y|^3). \end{array} \right. \end{aligned}$$

(3.11)

Proof

Firstly, we bring the co-existence equilibrium point $\overline{S}$ to the origin by the translation [33, 34] $X=E-\overline{E}, Y=M-\overline{M}$ and we obtain

$$\begin{aligned} \left. \begin{array}{rcl} \begin{pmatrix} \dot{X}\\ \dot{Y} \end{pmatrix} =J(\overline{S})\begin{pmatrix} X\\ Y\\ \end{pmatrix} + \begin{pmatrix} l_{20}X^2+l_{11}XY+l_{21}X^2Y+l_{30}X^3\\ m_{20}X^2+m_{11}XY+m_{02}Y^2+m_{21}X^2Y+m_{30}X^3\\ \end{pmatrix} +O(|X,Y|^4), \end{array} \right. \nonumber \\ \end{aligned}$$

(3.12)

where

$$\begin{aligned}&J(\overline{S})=\begin{pmatrix} l_{10}&{}{}l_{01}\\ l_{10}&{}{}l_{01}\\ \end{pmatrix} ,\ \ \ \ l_{10}=\frac{\widetilde{r_1}\overline{E}(K_1-a-2\overline{E})}{K_1(a+\overline{E})},\ \ \ \ l_{01}=-\frac{m\overline{E}}{a+\overline{E}}, \ \ \ \ \\&m_{10}= \frac{\widetilde{K_2}acm(r_2a+\delta \overline{E})}{r_2(a+\overline{E})^3},m_{01}=-\frac{r_2a+\delta \overline{E}}{a+\overline{E}},\ \ \ \ l_{11} = -\frac{m\overline{E}}{(a+\overline{E})^2},\ \ \ \ \ \\&l_{20} =-\frac{\widetilde{r_1}(\overline{E}^2+3a\overline{E}+a^2-K_1a)}{K_1(a+\overline{E})^2},\ \ \ \ l_{21}=\frac{am}{(a+\overline{E})^3}, l_{30}=\frac{\widetilde{r_1}a(\overline{E}-K_1)}{K_1(a+\overline{E})^3}, \ \ \ \ m_{11}=\frac{acm}{(a+\overline{E})^2}, \ \ \ \ \\&m_{20}=-\frac{\widetilde{K_2}acm(r_2a+\delta \overline{E})}{r_2(a+\overline{E})^4}, \ \ \ \ m_{02}=-\frac{r_2}{\widetilde{K_2}},m_{21}=-\frac{acm}{(a+\overline{E})^3}, \ \ \ \, m_{30}=\frac{\widetilde{K_2}acm(r_2a+\delta \overline{E})}{r_2(a+\overline{E})^5}. \end{aligned}$$

Then under following transformation

$$\begin{aligned} \begin{pmatrix}X\\ Y\end{pmatrix}=\widetilde{P}\begin{pmatrix}x\\ y\end{pmatrix},\ \ \ \ \widetilde{P}=(\widetilde{V}_{1}, \widetilde{V}_{2}), \end{aligned}$$

where

$$\begin{aligned} \widetilde{V}_{1}=\begin{pmatrix}1\\ k_1\end{pmatrix}, \ \ \ \ \widetilde{V}_{2}=\begin{pmatrix}\frac{1}{P(\overline{E})k_1}\\ 0\end{pmatrix}, \end{aligned}$$

and $|\widetilde{P}|\ne 0$, then we have

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x}&{}=&{} y+\overline{l}_{20}x^{2}+\overline{l}_{11}xy+\overline{l}_{02}y^2+O(|x,y|^3),\\ \dot{y}&{}=&{}\overline{m}_{20}x^{2}+\overline{m}_{11}xy+\overline{m}_{02}y^2+O(|x,y|^3), \end{array}\right. \end{aligned}$$

(3.13)

where

$$\begin{aligned} \overline{l}_{20}&=-\frac{r_2a+\delta \overline{E}}{(a+\overline{E})^2},\ \ \ \ \overline{l}_{11}=\frac{acm-2r_2a-2\delta \overline{E}}{(r_2a+\delta \overline{E})(a+\overline{E})},\ \ \ \overline{l}_{02}=-\frac{1}{r_2a+\delta \overline{E}},\\ \overline{m}_{20}&=\frac{(K_1-2a-3\overline{E})(r_2a+\delta \overline{E})^2}{(a+\overline{E})^3(K_1-a-2\overline{E})}, \ \ \ \ \overline{m}_{02}=\frac{(K_1-a-3\overline{E})}{\overline{E}(K_1-a-2\overline{E})},\\ \overline{m}_{11}&=\frac{-6\delta \overline{E}^3+[2K_1\delta -4a(3r_2+cm)]\overline{E}^2+r_2a(3K_1-7a)\overline{E}+r_2a^2(K_1-a)}{\overline{E}(-a-2\overline{E}+K_1)(a+\overline{E})^2}. \end{aligned}$$

Then we use the following near-identity transformation

$$\begin{aligned} u=x,\ \ \ \ v=y+\overline{l}_{20}x^{2}+\overline{l}_{11}xy+\overline{l}_{02}y^2+O(|x,y|^3), \end{aligned}$$

and if we change u, v into x, y, we obtain

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x}&{}=&{} y,\\ \dot{y}&{}=&{} \hat{m}_{20}x^2 +\hat{m}_{11}xy +O(|x,y|^3), \end{array} \right. \end{aligned}$$

(3.14)

where

$$\begin{aligned} \hat{m}_{20}&=\overline{m}_{20}=\frac{(K_1-2a-3\overline{E})(r_2a+\delta \overline{E})^2}{(a+\overline{E})^3(K_1-a-2\overline{E})},\\ \hat{m}_{11}&=\overline{m}_{11}+2\overline{l}_{20} =\frac{-2\delta \overline{E}^2-4r_2a\overline{E}-r_2a(K_1-a)}{\overline{E}(a+\overline{E})(K_1-a-2\overline{E})}. \end{aligned}$$

If $\hat{m}_{20}\ne 0$ $(K_1\ne \frac{K_1-2a}{3})$ and $\hat{m}_{11}\ne 0$, and we make a rescaling of coordinates and time by

$$\begin{aligned} X=\frac{\hat{m}_{20}}{\hat{m}_{11}^2}x,\ \ \ \ Y=\frac{\hat{m}_{20}^2}{\hat{m}_{11}^3}y,\ \ \ \ \tau =\frac{\hat{m}_{11}}{\hat{m}_{20}}t, \end{aligned}$$

and rewrite $X, Y, \tau$ into x, y, t, the system (3.14) is topologically equivalent to system (3.11). Also, we can verify that $\hat{m}_{20}=0$ when $\overline{S}=S_{123}$. We will discuss it in details in the Sect. 3.4. $\square$

And if $T^{'}(J(\overline{S}))=0$, we have

$$\begin{aligned} K_1=\frac{2\delta \overline{E}^2+r_2a(4\overline{E}+a)}{r_2a}. \end{aligned}$$

(3.15)

When $K_1, K_2, r_1$ satisfy the condition in theorem 3.3 and 3.15, we can verify that

$$\begin{aligned} \hat{m}_{11}=0, \ \ \hat{m}_{20}=\frac{(r_2a+\delta \overline{E})(2\delta \overline{E}^2+r_2a\overline{E}-r_2a^2)}{2\overline{E}(a+\overline{E})^3}\ne 0. \end{aligned}$$

Hence, $\overline{S}$ is a cusp point at least codimension 3. To determine its codimension, we need to calculate the coefficient of $x^3y$ term in the normal form 3.11. We will not do the computation here as Xiang et al. [26] showed that the existence of cusp type Bogdanov-Takens bifurcation of codimension 3.

3.4 Bifurcations for the Nilpotent Singularity

Though the relative bifurcations called focus and elliptic type of BT bifurcation of codimension 3 were carried out in Xiang et al. [26], we present the analysis of bifurcations for the nilpotent singularity followed the terms and classification given by Dumortier et al. [27] and in Zhu and Rousseau [28], to find the organizing center for the system (1.1). Also, we present the bifurcation diagram near the focus and elliptic type of nilpotent singularity of codimension 3 based on the analysis of Dumortier et al. [27], which is not included in Seo and Wolkowicz [25] and Xiang et al. [26].

It follows from the Prop. 2.1 and 3.1 and the discussion about Hopf bifurcations, a straightforward calculation can conclude that the system (1.1) has a unique positive equilibrium $S_{123}$ which can now be written and denoted as $S^*=(E^*,M^*)$ with

$$\begin{aligned} E^*=\frac{a(2cm-r_2)}{\delta }, \ \ \ M^*=\frac{12mc^2a}{2cm-r_2}, \end{aligned}$$

if

$$\begin{aligned} \begin{aligned} K_1=K_1^*=\frac{a(8cm-r_2)}{\delta },\ \ \ \ K_2=K_2^*=\frac{18r_2ac^2m}{(2cm-r_2)\delta },\ \ \ \ r_1=r_1^*=\frac{2\delta (8cm-r_2)}{3(2cm-r_2)}. \end{aligned}\nonumber \\ \end{aligned}$$

(3.16)

Theorem 3.4

For system (1.1) with all positive parameters and $(K_1,K_2,r_1)$ satisfying (3.16), the equilibrium $S^*(E^*,M^*)$ is a nilpotent singularity of codimension at least 3, and the system (1.1) localized at $S^*$ is topologically equivalent to

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x}&{}=&{} y,\\ \dot{y}&{}=&{} -x^3+bxy-x^2 y+y^2Q_{12}(x,y), \end{array} \right. \end{aligned}$$

(3.17)

where $b=\frac{7r_2-8cm}{2(2cm-r_2)}$.

Furthermore, if we fix the parameters a, c, m, and depending on the value of $r_2$, we have

• (1) When $\frac{24\sqrt{2}-8}{17}cm<r_2<2cm$, $S^*$ is a codimension 3 nilpotent sigularity of elliptic type.

• (2) When $0<r_2<\frac{8}{7}cm, \frac{8}{7}cm< r_2<\frac{24\sqrt{2}-8}{17}cm$, $S^*$ is a nilpotent singularity of the focus type of codimension 3.

• (3) when $r_2=\frac{8}{7}cm$ or $\frac{24\sqrt{2}-8}{17}cm$, the equilibrium $S^*$ is nilpotent point of codimension $\ge 4$.

Proof

Firstly, we translate the degenerate equilibrium $S^*$ to the origin by $X=E-E^*$, $Y=M-M^*$ and expand system (1.1) in the neighborhood of the new origin, we will have

$$\begin{aligned} \left. \begin{array}{rcl} \begin{pmatrix} \dot{X}\\ \dot{Y} \end{pmatrix} =J(S^*)\begin{pmatrix} X\\ Y\\ \end{pmatrix} + \begin{pmatrix} a_{20}X^2+a_{11}XY+a_{21}X^2Y+a_{30}X^3 \\ b_{20}X^2+b_{11}XY+b_{02}Y^2+b_{21}X^2Y+b_{30}X^3\\ \end{pmatrix} +Q_1(X,Y), \end{array} \right. \nonumber \\ \end{aligned}$$

(3.18)

where $Q_1(X,Y)=O(|X,Y|^4)$ and

$$\begin{aligned}&J(S^*)=\begin{pmatrix} a_{10}&{}a_{01}\\[1ex] b_{10}&{}b_{01}\\ \end{pmatrix} ,a_{10}=\frac{2\delta }{3},a_{01}=\frac{(-2cm+r_2)}{3c},b_{10}= \frac{4c\delta ^2}{3(2cm-r_2)}, b_{01}=-\frac{2\delta }{3},\\&a_{11} = -\frac{\delta ^2}{9amc^2},a_{20} =\frac{-2(cm-2r_2)\delta ^2}{9mca(2cm-r_2)},a_{21}=\frac{\delta ^3}{27a^2m^2c^3}, a_{30}= -\frac{4\delta ^4}{27a^2c^2m^2(2cm-r_2)}, \\&b_{11}=\frac{(\delta ^2}{9acm},b_{20}= -\frac{4\delta ^3}{9am(2cm-r_2)}, b_{02}= -\frac{(2cm-r_2)\delta }{18amc^2},b_{21}=-\frac{\delta ^3}{27a^2c^2m^2},\\&b_{30}= \frac{4\delta ^4}{27a^2cm^2(2cm-r_2)}. \end{aligned}$$

Next we transform the linear part of the system (3.18) to the Jordan canonical form and find that $J(S^*)$ is nilpotent. Note that the generalized eigenvectors associated with the zero eigenvalues are $V_1=(\frac{2cm-r_2}{2c},\delta )',\ \ V_2=(0,-\frac{3}{2})'$ which satisfy $J(S^*)V_1=0,J(S^*)V_2=V_1$. Let $P=(V_1,V_2)$, then under the non-singular linear transformation

$$\begin{aligned} \begin{pmatrix}X\\ Y\end{pmatrix}=P\begin{pmatrix}x\\ y\end{pmatrix}, \end{aligned}$$

with $|P|=-\frac{3(2cm-r_2)}{4c}<0$, system (3.18) becomes

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x}&{}=&{} y+\widetilde{a}_{20}x^2+\widetilde{a}_{30}x^3 +y(\widetilde{a}_{11}x+\widetilde{a}_{21}x^2) +\widetilde{Q}_{11}(x,y),\\[1ex] \dot{y}&{}=&{}\widetilde{b}_{30}x^3+y(\widetilde{b}_{11}x +\widetilde{b}_{21}x^2)+\widetilde{b}_{02}y^2+\widetilde{Q}_{12}(x,y), \end{array}\right. \end{aligned}$$

(3.19)

where $\widetilde{Q}_{1i}(x,y)=O(|x,y|^4)$, $(i=1,2)$, and

$$\begin{aligned}&\widetilde{a}_{20}=\frac{-2c^3m^3-3c^2m^2r_2+r_2^3}{9ac^2m},\ \ \ \ \widetilde{a}_{30}=-\frac{\delta ^4(2cm-r_2)}{54a^2c^4m^2},\ \ \ \ \widetilde{a}_{11}=\frac{\delta ^2}{6ac^2m},\\ {}&\widetilde{a}_{21}=-\frac{\delta ^3(2cm-r_2)}{36a^2c^4m^2},\ \ \ \ \widetilde{b}_{30}=-\frac{\delta ^4(4cm+r_2)(2cm-r_2)}{162a^2c^4m^2},\\ {}&\widetilde{b}_{11}=\frac{r_2\delta ^2}{6ac^2m},\ \ \ \ \widetilde{b}_{21}=-\frac{\delta ^3(4cm+r_2)(2cm-r_2)}{108a^2c^4m^2},\ \ \ \ \widetilde{b}_{02}=\frac{\delta (2cm-r_2)}{12ac^2m}. \end{aligned}$$

Thirdly, we use the following near-identity transformation

$$\begin{aligned} u=x,\ \ \ \ v=y+\widetilde{a}_{20}x^2+\widetilde{a}_{30}x^3+y(\widetilde{a}_{11}x+\widetilde{a}_{21}x^2)+\widetilde{Q}_{11}(x,y) \end{aligned}$$

and if we change u, v into x, y, we obtain

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x}&{}=&{} y,\\ \dot{y}&{}=&{} -\hat{b}_{30}x^3 +y(\hat{b}_{11}x -\hat{b}_{21}x^2)+y^2\hat{Q}_{12}(x,y), \end{array} \right. \end{aligned}$$

(3.20)

where

$$\begin{aligned}&\hat{b}_{30}=\frac{\delta ^4(2cm-r_2)^2}{81a^2c^4m^2},\ \ \ \ \hat{b}_{11}=-\frac{\delta ^2(8cm-7r_2)}{18ac^2m},\ \ \ \ \hat{b}_{21}=\frac{\delta ^3(2cm-r_2)(4cm+7r_2)}{108a^2c^4m^2}. \end{aligned}$$

If we make a rescaling of coordinates and time by

$$\begin{aligned}&X=\frac{\hat{b}_{21}}{\sqrt{\hat{b}_{30}}}x,\ \ \ \ Y=\frac{\hat{b}_{21}^2}{\hat{b}_{30}^{\frac{3}{2}}}y,\ \ \ \ \tau =\frac{\hat{b}_{30}}{\hat{b}_{21}}t \end{aligned}$$

and rewrite $X, Y, \tau$ into x, y, t, system (3.20) becomes

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x}&{}=&{} y,\\ \dot{y}&{}=&{} -x^3+bxy-x^2 y+y^2Q_{12}(x,y), \end{array} \right. \end{aligned}$$

(3.21)

where $b=\frac{7r_2-8cm}{2(2cm-r_2)}$.

It follows from the classification criteria for the nilpotent singularity in [27, 28], we have that if $\frac{24\sqrt{2}-8}{17}cm$ $<r_2<$ 2cm, then $b>2\sqrt{2}$, $S^*$ is a nilpotent elliptic point of codimension 3. It is a nilpotent point of focus type of codimension 3 when $0<b$ $<2\sqrt{2}$ or $(\frac{8}{7}cm$ $<r_2<\frac{24\sqrt{2}-8}{17}cm)$. If $r_2=\frac{8}{7}cm$ ($b=0$) or $r_2=\frac{24\sqrt{2}-8}{17}cm$ ($b=2\sqrt{2}$), it is a nilpotent singularity of codimension $\ge 4$. $\square$

In Fig. 5, we simulate and present the 3 types of nilpotent singularity classified in Theorem 3.4 with parameters selected for each of the cases. Fig. 5a and b represent the two cases of nilpotent focus, nilpotent elliptic point of codimension 3 is presented in Fig. 5c, and the most degenerate case of nilpotent focus of codimension 4 is presented in Fig. 5d).

Fig. 5

The phase portrait of different type of nilpotent singularity when fixed $a=1,c=1,m=1$. (a) Nilpotent focus of codimension 3 ($b<0$): $r_2=0.5$, $K_1=5,K_2=4,r_1=5$; (b) Nilpotent focus of codimension 3 ($0<b<2\sqrt{2}$): $r_2=1.2$, $K_1=3.0909, K_2=12.2727, r_1=12.4667$; (c) Nilpotent elliptic point of codimension 3 ($b>2\sqrt{2}$): $r_2=1.6$, $K_1=2.3333,K_2=27.6923,r_1=27.7334$; (d) Nilpotent focus of codimension 4 ($b=0$), $r_2=\frac{8}{7}$,$K_1=3.2,K_2=11.2,r_1=\frac{80}{7}.$

It is worth pointing out that the most degenerate case occurs when $r_2=\frac{8}{7}cm$, and then the system (1.1) localized at $S^*$ is topologically equivalent to

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x}&{}=&{} y,\\ \dot{y}&{}=&{} -x^3-x^2 y. \end{array} \right. \end{aligned}$$

(3.22)

System (3.22) is the 3-jet of nilpotent focus of codimension 4. This is also the cubic Liénard equations. In the work of Khibnik et al. [37], they called it doubly degenerate Bogdanov-Takens point with no quadratic terms in the normal form. There are different type of unfolding of this nilpotent singularity of codimension 4, which is analyzed by the Dangelmayr and Guckenheimer (1987) [36] and Khibnik et al. (1998) [37]. From their analysis, we can obtain that three different types of codimension 3 bifurcation, Cusp type Bogdanov-Takens bifurcations of codimension 3, focus type and elliptic type of nilpotent singularity of codimension 3 can bifurcate from this nilpotent singularity of codimension 4. This nilpotent focus of codimension 4 serves as an organizing center for the complex dynamics of the system (1.1).

We summary the above bifurcation analysis in the Table 1.

Table 1 The summary of different type of bifurcations

As in the available bifurcation studies [25, 26, 29] where $K_1$ and $K_2$ were commonly used as bifurcation parameters, here we will add $r_1$ as the third parameter, namely we will study system (1.1) for parameters $(K_1, K_2, r_1)$ in a neighborhood of $(K_1^*, K_2^*, r_1^*)$ to explore the complex dynamics which can be bifurcated from the codimension 3 nilpotent singularity $S^*$.

Let

$$\begin{aligned} K_1=K_1^*+\epsilon _1, \ K_2=K_2^*+\epsilon _2,\ r_1=r_1^*+\epsilon _3, \end{aligned}$$

where $\epsilon =(\epsilon _1,\epsilon _2,\epsilon _3)$ and $|\epsilon |$ is sufficiently small. Then we will study the bifurcation of the following unfolding system

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{rcl} \displaystyle \frac{dE}{dt}&{}=&{} \displaystyle \left( r_1^*+\epsilon _3\right) E\left( 1-\displaystyle \frac{E}{K_1^*+\epsilon _1}\right) - \displaystyle \frac{mEM}{a+E},\\ \displaystyle \frac{dM}{dt} &{}=&{} r_2M\left( 1-\displaystyle \frac{M}{K_2^*+\epsilon _2}\right) + \displaystyle \frac{cmEM}{a+E}. \end{array} \right. \end{aligned} \end{aligned}$$

(3.23)

Theorem 3.5

For parameters $|\epsilon |$ sufficiently small and any other positive parameters a, c, m, system (3.23) is a generic unfolding of the codimension 3 nilpotent singularity of elliptic type when $\frac{24\sqrt{2}-8}{17}cm<r_2<2cm$, of focus type when $0<r_2<\frac{8}{7}cm$ and $\frac{8}{7}cm< r_2<\frac{24\sqrt{2}-8}{17}cm$.

Proof

It has been shown by Dumortier et al. [27] that a generic unfolding with the parameters $(\mu _{1},\mu _{2},\mu _{3})$, of codimension 3 nilpotent singularity is $C^{\infty }$ equivalent to

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x}&{}=&{}y,\\ \dot{y}&{}=&{}\mu _{1}+ \mu _{2}x-x^{3}+y(\mu _{3} +bx-x^2+O(x^3))+y^2Q(x,y). \end{array} \right. \end{aligned}$$

(3.24)

We will show that system (3.23), with parameters $\epsilon =(\epsilon _1,\epsilon _2,\epsilon _3)$, is also a generic unfolding of codimension 3 singularity by showing that there exist smooth coordinate change which take (3.23) into (3.24) with $\frac{D(\mu _{1},\mu _{2},\mu _{3})}{D(\epsilon _1,\epsilon _2,\epsilon _3)}|_{\epsilon =(0,0,0)}\ne 0$.

When $\epsilon =0$, the system (1.1) has a nilpotent equilibrium $S^*(E^*,M^*)$. Let $x=E-E^*$, $y=M-M^*$. When $|\epsilon |$ is sufficient small, the system (3.23) becomes

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x}&{}=&{} L_{11}(x)+yL_{12}(x),\\ \dot{y}&{}=&{}L_{21}(x)+yL_{22}(x)+Q_{2}y^2, \end{array} \right. \end{aligned}$$

(3.25)

where

$$\begin{aligned} L_{11}(x)=&\frac{a(2cm-r_2)\big (2\delta ^2\epsilon _1 +18acm\epsilon _3+3\delta \epsilon _1\epsilon _3\big )}{3\delta \big (\epsilon _1\delta +a(8cm-r_2)\big )}\\&+\frac{6\delta ^2\epsilon _1+3a(4cm+r_2)\epsilon _3 +3\delta \epsilon _1\epsilon _3 +2a\delta (8cm-r_2)}{3\big (\epsilon _1\delta +a(8cm-r_2)\big )}x\\&+\frac{4\delta ^4\epsilon _1-9acm(2cm-r_2)\delta \epsilon _3 -2a\delta ^2(8cm-r_2)(cm-2r_2)}{9acm(2cm-r_2)\big (\epsilon _1\delta +a(8cm-r_2)\big )}x^2\\ {}&-\frac{4\delta ^4}{27a^2c^2m^2(2cm-r_2)}x^3+O(x^4),\\ L_{12}(x)=&-\frac{2cm-r_2}{3c} -\frac{\delta ^2}{9ac^2m}x+\frac{\delta ^3}{27a^2c^3m^2}x^2 -\frac{\delta ^4}{81a^3c^4m^3}x^3+O(x^4),\\ L_{21}(x)=&\frac{8ac^2m\delta ^2\epsilon _2}{18ac^2mr_2 +(2cm-r_2)\delta \epsilon _2}+\frac{4c\delta ^2}{3(2cm-r_2)}x -\frac{4\delta ^3}{9am(2cm-r_2)}x^2\\ {}&+\frac{4\delta ^4}{27a^2cm^2(2cm-r_2)}x^3+O(x^4),\\ L_{22}(x)=&\frac{-36ac^2mr_2\delta +2(2cm-r_2)\delta ^2\epsilon _2}{54ac^2mr_2 +3(2cm-r_2)\delta \epsilon _2}+\frac{\delta ^2}{9acm}x +\frac{-\delta ^3}{27a^2c^2m^2}x^2\\ {}&+\frac{\delta ^4}{81a^3c^4m^3}x^3+O(x^4),\\ Q _{2}=&\frac{-r_2(2cm-r_2)\delta }{18ac^2mr_2+(2cm-r_2)\delta \epsilon _2}. \end{aligned}$$

Then, we make the following transformation

$$\begin{aligned} x_{1}=x,\ \ \ \ y_{1}=L_{11}(x)+yL_{12}(x). \end{aligned}$$

System (3.25) can be transformed into

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x_{1}}&{}=&{}y_{1},\\ \dot{y_{1}}&{}=&{}\overline{L}_{21}(x_{1}) +y_{1}\overline{L}_{21}(x_{1})+y_{1}^2\overline{Q}_{2}(x_{1}), \end{array}\right. \end{aligned}$$

(3.26)

where

$$\begin{aligned} \overline{L}_{21}(x_{1}) =&d_{00}+d_{10}x_{1}+d_{20}x_{1}^2+d_{30}x_{1}^3+O(x_{1}^4),\\ \overline{L}_{22}(x_{1}) =&d_{01}+d_{11}x_{1}+d_{21}x_{1}^2+d_{31}x_{1}^3+O(x_{1}^4), \end{aligned}$$

with

$$\begin{aligned} d_{00}=&\frac{4(2cm-r_2)\delta ^2}{27cr_2(8cm-r_2)} \left[ 3cr_2\epsilon _1-(8cm-r_2)\epsilon _2 +\frac{27ac^2mr_2}{\delta ^2}\epsilon _3+O(|\epsilon |^2)\right] ,\\ d_{10}=&\frac{2\delta ^3}{27acmr_2(8cm-r_2)} \left[ r_2(14cm-r_2)\epsilon _1-2m(8cm-r_2)\epsilon _2 +\frac{54ac^2m^2r_2}{\delta ^2}\epsilon _3+O(|\epsilon |^2)\right] ,\\ d_{20}=&\frac{\delta ^4(2cm-r_2)^2}{81a^2c^3m^2r_2(8cm-r_2)(2cm-r_2)} \Bigr [\frac{2cr_2(26c^2m^2-2cmr_2-r_2^2)}{(2cm-r_2)^2}\epsilon _1 +(8cm-r_2)\epsilon _2\\ {}&-\frac{27ac^2mr_2}{\delta ^2}\epsilon _3 +O(|\epsilon |^2)\Bigr ],\ \ \ \ d_{30}=-\frac{4\delta ^4}{81a^2c^2m^2}+O(|\epsilon |),\\ d_{01}=&\frac{(2cm-r_2)^2\delta ^2}{27ac^2mr_2(8cm-r_2)} \left[ \frac{18c^2mr_2}{2cm-r_2}\epsilon _1 +(8cm-r_2)\epsilon _2-\frac{27ac^2mr_2}{\delta ^2}\epsilon _3 +O(|\epsilon |^2)\right] ,\\ d_{11}=&-\frac{(8cm-7r_2)\delta ^2}{9acm(2cm-r_2)}+O(|\epsilon |),\ \ \\ d_{21}=&-\frac{(4cm+7r_2)\delta ^3}{27a^2c^2m^2(2cm-r_2)}+O(|\epsilon |),\\ d_{31}=&-\frac{(8cm+11r_2)\delta ^4}{81a^3c^3m^3(2cm-r_2)}+O(|\epsilon |). \end{aligned}$$

Then, we reduce the $\overline{L}_{21}(x_{1})$ to $-x_{1}^3+u_2x_{1}+u_1$ [30]. Note that for $\epsilon$ sufficiently small, $d_{30}(\epsilon ) =\frac{\partial ^3\overline{L}_{21}}{\partial x_{1}^3}(0)=-\frac{4(cm+r_2)^4}{81a^2c^2m^2}+O(|\epsilon |)\ne 0$, we make the translation

$$\begin{aligned} x_{2}=x_{1}+\frac{d_{20}}{3d_{30}},\ \ \ \ y_{2}= y_{1} \end{aligned}$$

which brings the system into

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x_{2}}&{}=&{}y_{2},\\ \dot{y_{2}}&{}=&{}\widetilde{L}_{21}(x_{2}) +y_{2}\widetilde{L}_{22}(x_{2})+y_{2}^2\widetilde{Q}_{2}(x_{2}), \end{array} \right. \end{aligned}$$

(3.27)

where

$$\begin{aligned} \widetilde{L}_{21}(x_{2})= & {} \widetilde{d}_{00}+\widetilde{d}_{10}x_{2} -\widetilde{d}_{30}x_{2}^3+O(x_{2}^4),\\ \widetilde{L}_{22}(x_{2})= & {} \widetilde{d}_{01} +\widetilde{d}_{11}x_{2}+\widetilde{d}_{21}x_{2}^2+O(x_{2}^3), \end{aligned}$$

Then, if we rescale $y_2$ and time t using

$$\begin{aligned} x_{3}=x_{2},\ \ \ \ y_{3}=\frac{y_{2}}{\sqrt{\widetilde{d}_{30}}},\ \ \ \ \widetilde{t}=\sqrt{\widetilde{d}_{30}}t \end{aligned}$$

the coefficient of $x_{3}^3$ becomes $1+O(|\epsilon _2|)$. We have

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x_{3}}&{}=&{}y_{3},\\ \dot{y_{3}}&{}=&{}\widetilde{\widetilde{L}}_{21}(x_{3}) +y_{3}\widetilde{\widetilde{L}}_{22}(x_{3}) +y_{3}^2\widetilde{\widetilde{Q}}_{2}(x_{3}), \end{array} \right. \end{aligned}$$

(3.28)

where

$$\begin{aligned} \widetilde{\widetilde{L}}_{21}(x_{3})=&\widetilde{\widetilde{d}}_{00}+\widetilde{\widetilde{d}}_{10}x_{3}-x_{3}^3+O(x_{3}^4),\\ \widetilde{\widetilde{L}}_{22}(x_{3}) =&\widetilde{\widetilde{d}}_{01} +\widetilde{\widetilde{d}}_{11}x_{3} -\widetilde{\widetilde{d}}_{21}x_{3}^2+O(x_{3}^3), \end{aligned}$$

with

$$\begin{aligned} \widetilde{\widetilde{d}}_{00}&=\frac{3a^2cm^2(2cm-r_2)}{r_2(8cm-r_2)\delta ^2} \left[ 3cr_2\epsilon _1-(8cm-r_2)\epsilon _2+\frac{27ac^2mr_2}{\delta ^2}\epsilon _3+O(|\epsilon |^2)\right] ,\\ \widetilde{\widetilde{d}}_{10}&=\frac{3acm}{2r_2(8cm-r_2)\delta } \left[ r_2(14cm-r_2)\epsilon _1-2m(8cm-r_2)\epsilon _2 +\frac{54ac^2m^2r_2}{\delta ^2}\epsilon _3+O(|\epsilon |^2)\right] ,\\ \widetilde{\widetilde{d}}_{01}&=\frac{1}{24cr_2(8cm-r_2)} \Bigr [-\frac{2cr_2(64c^3m^3-54c^2m^2r_2-30cmr_2^2+7r_2^3)}{(2cm-r_2)^2}\epsilon _1+(8cm-r_2)^2\epsilon _2\\&-\frac{27ac^2mr_2^2}{\delta ^2}\epsilon _3+O(|\epsilon |^2)\Bigr ],\\ \widetilde{\widetilde{d}}_{11}&=\frac{7r_2-8cm}{2(2cm-r_2)} +O(|\epsilon |),\ \ \ \ \ \widetilde{\widetilde{d}}_{21}= \frac{(4cm+7r_2)\delta }{6acm(2cm-r_2)}+O(|\epsilon |). \end{aligned}$$

Using the Malgrange preparation theorem, we can reduce the $\widetilde{\widetilde{L}}_{21}(x_{3})$ to $\widetilde{\widetilde{d}}_{00}+\widetilde{\widetilde{d}}_{10}x_{3}-x_{3}^3$.

For system (3.28), $\widetilde{\widetilde{d}}_{21}(0)= \frac{(4cm+7r_2)\delta }{6acm(2cm-r_2)}>0$. Thus, we reduce the $\widetilde{\widetilde{L}}_{22}(x_{3})$ to $u_{3}+bx_{3}-x_{3}^2+O(x_{3}^3)$ by rescaling the $x_3$, $y_3$, $\widetilde{t}$ using $x_{4}=\widetilde{\widetilde{d}}_{21}x_{3},\ \ y_{4}=\widetilde{\widetilde{d}}_{21}^2y_{3},\ \ \tau =\frac{1}{\widetilde{\widetilde{d}}_{21}}\widetilde{t}.$ Now if we rewrite $x_4$ ,$y_4$ ,$\tau$ into x, y, t, then the system becomes

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x}&{}=&{}y,\\ \dot{y}&{}=&{}\hat{d}_{00} +\hat{d}_{10}x-x^3+y[\hat{d}_{01}+\hat{d}_{11}x-x^2+O(x^3)] +y^2\hat{Q}_{2}(x), \end{array} \right. \end{aligned}$$

(3.29)

where

$$\begin{aligned} \hat{d}_{00}&=\frac{(4cm+7r_2)^3\delta }{72ac^2mr_2(8cm-r_2)(2cm-r_2)^2}\left[ 3cr_2\epsilon _1-(8cm-r_2)\epsilon _2 +\frac{27ac^2mr_2}{\delta ^2}\epsilon _3+O(|\epsilon |^5)\right] ,\\ \hat{d}_{10}&=\frac{(4cm+7r_2)^2\delta }{36acmr_2(8cm-r_2)(2cm-r_2)^2}\Bigr [r_2(14cm-r_2)\epsilon _1 -2m(8cm-r_2)\epsilon _2+\frac{54ac^2m^2r_2}{(\delta ^2}\epsilon _3\\&\quad \ \ \ +O(|\epsilon |^4)\Bigr ],\\ \hat{d}_{01}&=\frac{(4cm+7r_2)\delta }{144ac^2mr_2(8cm-r_2)(2cm-r_2)} \Bigr [-\frac{2cr_2(64c^3m^3-54c^2m^2r_2-30cmr_2^2+7r_2^3)}{(2cm-r_2)^2}\epsilon _1\\&\quad \ \ \ +(8cm-r_2)^2\epsilon _2-\frac{27ac^2mr_2^2}{\delta ^2}\epsilon _3 +O(|\epsilon |^3)\Bigr ],\ \ \ \ \hat{d}_{11}=\frac{7r_2-8cm}{2(2cm-r_2)}+O(|\epsilon |). \end{aligned}$$

Then, if we denote $\hat{d}_{00}=\mu _{1}(\epsilon _1,\epsilon _2,\epsilon _3),\ \ \ \ \hat{d}_{10}=\mu _{2}(\epsilon _1,\epsilon _2,\epsilon _3),\ \ \ \ \hat{d}_{01}=\mu _{3}(\epsilon _1,\epsilon _2,\epsilon _3),\ \ \ \ \hat{d}_{11}=b(\epsilon _1,\epsilon _2,\epsilon _3),$ since $r_2<2cm$, we can verify that

$$\begin{aligned} \left| \frac{\partial (\mu _{1},\mu _{2},\mu _{3})}{\partial (\epsilon _1,\epsilon _2,\epsilon _3)}\right| _{\epsilon =0} =\frac{\delta (4cm+7r_2)^6}{2304a^2c^3m^2r_2(8cm-r_2)(2cm-r_2)^4}>0. \end{aligned}$$

(3.30)

Thus, the transformation of parameters is nonsingular. The system (3.23) with parameters $\epsilon =(\epsilon _1,\epsilon _2,\epsilon _3)$, is a generic family unfolding the codimension 3 nilpotent singularity. $\square$

3.5 Bifurcation Diagram

Based on the bifurcation analysis of Dumortier et al. [27], we present the bifurcation diagrams in the following two figures, Figs. 6 and 7. The bifurcation set is a topological cone with vertex at $0\in {\mathbb {R}}^3$, composed of surfaces and lines which are transversal to the spheres $\mathbb S =\{(\mu _{1},\mu _{2},\mu _{3}|\mu _{1}^2+\mu _{2}^2+\mu _{3}^2)=\sigma ^2$, $0<\sigma \ll 1\}$ by removing one point outside the bifurcation set, on the hemisphere $\mu _{2}<0$. The vertical coordinate is $\mu _{3}$; the horizontal coordinate is $\mu _{1}$ oriented to the left.

In the bifurcation diagrams shown in Figs. 6 and 7, there are three points labeled as Cusp for cusp point, BT for Bogdanov-Takens point and DH for degenerate Hopf bifurcation point. The bifurcation curves presented include the curves of saddle-node bifurcations (SN), Hopf bifurcations (H), Homoclinic bifurcation (Hom) and saddle-node bifurcation of limit cycles ($SN_{lc}$).

Fig. 6

The bifurcation diagram of focus type nilpotent singularity of codimension 3

Fig. 7

The bifurcation diagram of elliptic type nilpotent singularity of codimension 3

In order to understand the dynamics for the interaction of the two species in different sizes of tea garden, we will numerically investigate and present the bifurcation diagrams in $(K_1,K_2)$ plane with different value of $r_1$ for both the focus and elliptic cases. (Tables 2 and 3)

3.5.1 Focus Type

From the Theorem 3.4, we know that the nilpotent singularity of codimension 3 is focus type when we fix four parameters $a=1,c=1,m=1$ and $r_2=0.5$. Then, we plot the bifurcation diagram in $(K_1,K_2)$ plane with different $r_1$ by choosing $r_2=0.5$. From Fig. 8a – e, we can see the changing trend of relative position between the Hopf bifurcation curve and saddle-node bifurcation curve. When $r_1$ decreases from 6 to 4, the Hopf curve moves toward rightward from the outside of saddle-node bifurcation curve to the inside, without changing the structure in Fig. 8a. When $r_1$ keeps decreasing, the Hopf bifurcation curve changes the shape as show in Fig. 8e.

Table 2 Collections of phase portraits for the system in the elliptic case when the parameters vary in subregions , referring to Fig. 6

Table 3 Collections of phase portraits for the system in the elliptic case when the parameters vary in subregions, referring to Fig. 7

The saddle-node bifurcation curve is composed of the upper part, the lower part and the intersection point cusp point, while the Bogdanov-Takens point separates the saddle-node bifurcation curve into two part with stable saddle-node bifurcation curve and unstable bifurcation curve. The Hopf bifurcation curve is tangent to the lower part of saddle-node bifurcation curve in Fig. 8e ($r_1=3.5$) and 8d ($r_1=4$), while the Hopf bifurcation curve is tangent to the upper part of saddle-node bifurcation curve in Fig. 8a and b ($r_1=6$). In Fig. 8c ($r_1=5$), the parameters satisfy the condition (3.16) in Theorem 3.4 at which the nilpotent point of codimension 3 occurs when cusp point and Bogdanov-Takens point of codimension 2 coincide. In this case, the Hopf bifurcation curve is tangent to both stable saddle-node bifurcation curve and unstable saddle-node bifurcation curve. Also, the number of degenerate Hopf point is changed from 0 to 2 when $r_1$ changes from 3.5 to 6 pass through $r_1=r_1^*=5$. We simulate the bifurcation curve of saddle-node bifurcation of limit cycle near the degenerate Hopf bifurcation point. In the region c between the bifurcation curve of subcritical Hopf and saddle-node of limit cycle, the system (1.1) can have two limit cycle, one stable and the other is unstable, which is verified by the numerical simulations as whow in Fig. 12c.

3.5.2 Elliptic Type

As the same with focus type, we fix four parameters $a=1,c=1,m=1$ and $r_2=1.6$, and the nilpotent singularity of codimension 3 is of elliptic type according to the Theorem 3.4. Then, we plot the bifurcation diagram in $(K_1,K_2)$ plane with different $r_1$. Compare to focus type we can see the similar changing trend of relative position between the Hopf bifurcation curve and saddle-node bifurcation curve and the number of degenerate Hopf point, from Fig. 9a–e. The Hopf curve moves rightward with decreasing $r_1$, and it finally changes the shape. However, the most part of parameters are in the region $K_2>\frac{r_1a}{m}$ where $S_1$ is in the negative quadrant in Fig. 9d and e. In order to show the moving trend of Hopf curve, we still present the bifurcation diagram which contains the parameters in the region $K_2>\frac{r_1a}{m}$.

Another difference is that the Hopf bifurcation curve is tangent to the upper part of saddle-node bifurcation curve when $r_1<r_1^*$ instead of the lower part of saddle-node bifurcation curve in focus type. Whereas $r_1>r_1^*$, the Hopf bifurcation curve is tangent to the lower part of saddle-node bifurcation curve. We did not present it in Fig. 9 due to the redundancy. Also, in elliptic type bifurcation diagram in $(K_1,K_2)$ plane, there are two Bogdanov-Takens points, we omit the one in the region of $K_2>\frac{r_1a}{m}$.

Next, we plot the one-parameter bifurcation diagram to explain the model dynamics. First, we present bifurcation diagram in $(E, K_1)$ plane with different $K_2$ as shown in Fig. 10 and bifurcation diagram in $(E, K_2)$ plane with different $K_1$ as shown in Fig. 11. In general, reducing the carrying capacity of E. onukii population in the tea plantation to a certain low level, the low level of E. onukii population state can be stable under different carrying capacities of A. baccarum, and pest suppression is possible. With the decreasing of carrying capacity of E. onukii, one can see that the system may go through a stable state of high E. onukii to the gradual excitation of oscillations around the unique equilibrium, and a stable state of low E. onukii (Fig. 10a). For an environment that is not suitable for E. onukii, the pest E. onukii can be effectively controlled, yet this may not always work. For some level of the capacity for A. baccarum, the E. onukii population can still outbreak even though the capacity of E. onukii is reduced when the initial capacity of E. onukii is relatively high (Fig. 10b–f). Also, the initial condition plays an important role. Different initial states can lead to different equilibrium states, low level of E. onukii or the large-amplitude oscillation of E. onukii population (Fig. 10f).

When we fixed the carrying capacity of E. onukii, increasing the capacity of A. baccarum may be effective to control E. onukii (Fig. 11d, h). However, in other cases, increasing the capacity of A. baccarum may not be effective from the beginning. On the contrary, it may induce a large amplitude oscillation of E. onukii population. Small increases in the carrying capacity of A. baccarum may lead to an opposite effect. The initial state of the E. onukii is also important for the pest control (Fig. 11d).

Fig. 8

Bifurcation diagram for the nilpotent focus of codimension 3 in $(K_1,K_2)$ plane with different $r_1$ when $a, c, m=1$ and $r_2=0.5$. The green solid and dot lines are the stable and unstable saddle-node bifurcation respectively; red solid and dot line represents the supercritical and subcritical Hopf bifurcation; cyan line stands for the saddle-node of limit cycle; magenta line is neutral saddle curve not the bifurcation curve. DH is the degenerate Hopf point; CP is the cusp point; BT is the Bogdanov-Takens point (Color figure online)

Fig. 9

Bifurcation diagram of the codimension 3 nilpotent elliptic point in $(K_1,K_2)$ plane with different $r_1$ and $a=c=m=1$, $r_2=1.6$. The line colors and points explanation are the same as in Fig.12 (Color figure online)

Fig. 10

Bifurcation diagrams in $(E,K_1)$ plane shown different scenarios of changing $K_2$. We fixed $a=1,c=1,m=1$, and a–d $r_2=0.5,r_1=6$ (focus type), e–f $r_2=1.6,r_1=26$ (elliptic type). H is the Hopf point; SN is the saddle node; NS is the neutral saddle point. The blue and red color represent the equilibrium is stable and unstable, respectively (Color figure online)

Fig. 11

Bifurcation diagram in $(E,K_2)$ plane with different $K_1$. We fixed $a=1,c=1,m=1$, and a–d $r_2=0.5,r_1=6$ (focus type), e–h $r_2=1.6,r_1=26$ (elliptic type). H is the Hopf point; SN is the saddle node; NS is the neutral saddle point. The blue and red color represent the equilibrium is stable and unstable, respectively. Note that we did not present the cases of elliptic type which is similar to focus type due to redundancy (Color figure online)

4 Numerical Simulations and Existence of Three Limit Cycles

In this section, we will carry out numerical simulations and plot phase portraits by choosing different parameter values in the subregion of bifurcation diagram to explain the complexity of the dynamics.

Fig. 12

The phase portrait of system (1.1) with a nilpotent singularity of focus type. Here when fixed $r_2=0.5, r_1=6$ in the generic regions of parameters $(K_1,K_2)$. The regions $(a)-(j)$ correspond to the regions of bifurcation diagram in Fig. 8. The blue line represents that the solution is stable, while the red line stands for unstable solution. Also, we use red dot line to clarify the situation that $S_1$ is unstable and $S_3$ is stable (Color figure online)

Fig. 13

The phase portrait of system (1.1) with a nilpotent elliptic singularity when fixed $r_2=1.6, r_1=26$ in the generic regions of parameters $(K_1,K_2)$. The regions $(a)-(j)$ are correspond to the regions of bifurcation diagram in Fig. 9. The blue line represents that the solution is stable, while the red line stands for unstable solution. Also, we use red dot line to clarify the situation that $S_1$ is stable and $S_3$ is unstable. In case e and i, the $S_1$ and $S_3$ are stable (Color figure online)

4.1 Focus Type

When the parameters $(K_1, K_2)$ in region from a to j in Fig. 8, all the phase portraits are presented in Fig. 12. It contains all the possible solutions of system (1.1) when the nilpotent singularity of codimension 3 is of focus type.

In the case 12a–c , the system has one unique positive equilibrium, and it goes through from a stable node to an unstable node through a Hopf bifurcation, then becomes a stable node again. The system (1.1) has three equilibria in case 12d–12j which happens when the parameter $(K_1, K_2)$ are in the inside of saddle-node bifurcation curve. The $S_3$ is always stable while $S_1$ changes from stable node to unstable node through a Hopf bifurcation as shown in the case 12d–f. In the case 12h–j , $S_1$ is always an unstable node while $S_3$ goes through stable node to unsatble node, and the system always has a large amplitude stable limit cycle outside the three equilibrium points.

4.2 Elliptic Type

For system (1.1) with a nilpotent singularity of elliptic type, we present the phase portraits when the parameters are in the corresponding regions from a to i in Fig. 9. In the case 13a–c, the phase portrait of the system shows the same structure as in focus type.

The system has one unique positive equilibrium, and it has one stable limit cycle in Fig. 13b and two limit cycles in Fig. 13c. The system (1.1) has three equilibria in the case 13d–i which happens when the parameter $(K_1, K_2)$ are in the inside of saddle-node bifurcation curve. The $S_1$ is always stable while $S_3$ changes from a stable node to an unstable node through a Hopf bifurcation, then to a stable node again in the case Fig. 13e–i. But we did not find the large amplitude stable limit cycle outside the three equilibrium points in the elliptic type, which also proved in the studies of Dumortier et al. [27].

4.3 Three Limit Cycles in the System with Singularity of Elliptic Type

We want to point out is that we find a special case that for the system (1.1) with a nilpotent elliptic equilibrium, the system can have three distinct limit cycles when $K_1=2.5868,K_2=27.78, r_1=27.78333334$, $r_2=1.6$, $a=1$, $c=1$, $m=1$, a case corresponds to the region c in Fig. 9c. The largest limit cycle shows that the slow-fast pattern. And the period is around 150 days which is close to the life span of the A. baccarum (81-114 days [14], varied with local climate).

This case of three limit cycles may occur in parameters between the homoclinic bifurcation and the limit point of limit cycle bifurcation, a case similar to Shan et. al (2016) [34], where they numerically showed the existence of the three limit cycles when the system has three positive equilibrium in the most degenerate case of nilpotent singularity. The existence of three limit cycles also is presented in the global analysis of the cubic Liénard equation in Khibnik et al. (1998) [37]. Also, the number of limit cycle in system (1.1) may be at least 4 when consider the bifurcation of the most degenerate case $r_2=\frac{8}{7}cm$, the nilpotent focus of codimension 4 [37]. As for the exact number of limit cycles which can be bifurcated from the nilpotent focus of codimension 4 in the system, it still remains an open problem which is associated with the bifurcation of a Liénard systems and even with the famous Hilbert sixteenth problem for planar polynomial systems. This existence of three limit cycles also manifests that the complexity of the dynamics of the generalist predator A. baccarum and prey E. onukii in tea plantation can be much more complicated with bi-stability and even tri-stability.

5 Conclusion and Discussion

In this paper, we established a predator-prey model for the tea green leafhopper pest E. onukii and their predatory mite A. baccarum as a generalist predator. The euryphagous nature is crucial for the predator to survival in nature, and it is a very important characteristic of the species which leads to easier coexistence of the two species. The look-simple two dimension model exhibits very complex dynamics. Through bifurcation analysis, we have shown that there can be different equilibrium states (see Figs. 12 and 13) when the parameters vary in tea plantations, and the associated bifurcations and dynamics of these equilibria reveal the possible scenarios.

The eradication of the pest E. onukii is difficult. Even though when the carrying capacity of the predatory mite A. baccarum is high enough ($K_2>\frac{r_1a}{m}$), the pest-free equilibrium is locally stable. But it still exists the stable equilibrium state of high E. onukii population. The pest eradication also depends on the initial condition of E. onukii population, as observed in Seo and Wolkowicz (2020) [25]. Hence, it is plausible to suppress the pest rather than eradicate it. The analysis of the coexistence equilibrium is also crucial for the pest suppression strategy.

It turns out that the co-existence of these two species is always possible. We can classify the phase portraits of the system (1.1) when $(K_1, K_2)$ is in different regions while $r_1$ is varied. By the local stability and bifurcation analysis of all the equilibrium states, we summarize the different possible types equilibrium state in Table 4, varying from single equilibrium, single limit cycle, two equilibria, two equilibria and limit cycle, equilibrium and limit cycle with the number of 1 , 2, even 3. And it may have more types of coexistence state when the growth rate of generalist predator ($r_2$) varied. There are many different combinations and types of coexistence of the two species E. onukii and A. baccarum when the external condition changes. Also, it is possible to have a stable coexistence of E. onukii and A. baccarum in different states for the same external conditions.

Table 4 The classification of the phase portraits of the system (1.1) with a nilpotent singularity

Mathematically there are several different types of multi-stability. When the parameters are all fixed, the system can have two stable fixed points, a stable fixed point and a stable limit cycle, two stable fixed point and a stable limit cycle, a stable fixed point and two stable limit cycles. Also, biologically the behavior of the system is much different in the case of two stable equilibria, equilibrium and a limit cycle. This result is different from the finding of Colling et.al (1990) [41] due to the existence of a large amplitude periodic solution in our model. Moreover, the phenomenon is much more complicated with the A. baccarum as a generalist predator. The phenomenon of two different stable states has been well studied [10, 41], however, as far as we know that it is not common to see the existence of three different stable states, or triple-stability in a biological system. When the reproduction rate $r_2$ varies in the interval $\frac{24\sqrt{2}-8}{17}cm<r_2<2cm$, the system can have three different stable states for the same parameters, two stable fixed point and one stable limit cycle (Fig. 15).

Fig. 14

The most special case that the system have three limit cycles when $K_1=2.5868,K_2=27.78, r_1=27.783333334$, and $r_2=1.6,a=1,c=1,m=1$. The initial conditions for solution curves in black, red and blue are $(x_0,y_0)=(0.5316,33.81)$; (0.5164, 33.69) and $(x_0,y_0)=(0.2931,31.01)$, respectively (Color figure online)

Fig. 15

The different stable states under different initial condition with parameter fixed at $K_1=2.57,K_2=25.996, r_1=26, r_2=1.6, a=1, c=1, m=1$. The black line: $(x_0,y_0)=(0.2,32)$; the red line: $(x_0,y_0)=(0.3,30)$; the blue line: $(x_0,y_0)=(0.45,31)$. (Color figure online)

As we described in the introduction, the different phenomena are observed in the field study. Hence, it is possible that there are different coexistence states of A. baccarum and E. onukii in different levels of population sizes. In addition to the growth and development rules of A. baccarum itself, the extensive appetite of A. baccarum may generate that there are a variety of possible coexistence phenomena between A. baccarum and E. onukii, which may correspond to many stable states presented in the model.

We claim that $S_1$ is the equilibrium with low E. onukii and low A. baccarum population, while $S_3$ is the equilibrium with high E. onukii and high A. baccarum population. The multistability allows the system to model the E. onukii population outbreak in response to population perturbations, like the increase in predator by artificially releasing or the deceasing caused by the pesticide. If the populations are at a stable state with high E. onukii and high A. baccarum population, the population perturbations will force the populations to move to the state with low E. onukii and low A. baccarum population. The release of predator and the application of pesticide can effectively take control of E. onukii population. However, it can also cause the populations to jump to the oscillations that the A. baccarum can not effectively control E. onukii. Even worse, the population perturbations may lead the populations to move from low E. onukii and A. baccarum population to high E. onukii and A. baccarum population, which make the problem worse. But the introduction of A. baccarum always reduces the abundance of E. onukii below the carrying capacity and may have some effects on pest suppression.

Fig. 16

The type of nilpotent singularity when $r_2$ varied (Color figure online)

Referring to different tea plantations, where $K_1, K_2$ and $r_1$ are all fixed, the system may have different biological behaviors as different growth rates of A. baccarum ($r_2$). Increasing $r_2$ may also be helpful to control E. onukii. Mathematically, different $r_2$ manifests themselves as different types of degenerate singularities, the focus type and the elliptic type and more degenerate focus case. With the increase of $r_2$, the type of degenerate equilibrium changes from the focus ($0<r_2<\frac{8}{7}cm, \frac{8}{7}cm< r_2<\frac{24\sqrt{2}-8}{17}cm$) to elliptic $(\frac{24\sqrt{2}-8}{17}cm,2cm)$, and the large amplitude oscillation of E. onukii population may disappear. We may observe the slow-fast oscillation of E. onukii population. When the growth rate of A. baccarum is relatively high, the abundance of E. onukii may maintain a low level the most of time. Even though when the E. onukii increase significantly in a short time, the A. baccarum will increase fast and then control the E. onukii (Fig. 14). This shows the possibility of pest suppression by using the generalist predatory mite, A. baccarum. (Fig. 15)

Also, we notice that our analysis can extend to when the predator is a specialist predator with intraspecific competition, the system (1.3) ($r_2<0$, Fig. 16). All types of coexistence states analyzed in our study can also occur between specialist predators and prey. Competition within the predator may be more conducive to the coexistence of predator and prey.

We close by noting that the dynamical behavior of this generalist predator-prey system is complicated. We analyze the change of dynamics using four different parameters. The nilpotent focus of of codimension 4 serves as an organizing center for the complex dynamics of the model. We find that it can have three limit cycles around one of the positive equilibrium and even 4 limit cycles. Moreover, various coexistence phenomena can happen. Not only the bistability, but also the tri-stability can happen too.