Abstract
We develop a global Hopf bifurcation theory for differential equations with a state-dependent delay governed by an algebraic equation, using the \(S^1\)-equivariant degree. We apply the global Hopf bifurcation theory to a model of genetic regulatory dynamics with threshold type state-dependent delay vanishing at the stationary state, for a description of the global continuation of the periodic oscillations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Consider the following system of differential-algebraic equations (DAEs) with state-dependent delay,
where we assume that
- (S1):
-
The map f: \(\mathbb {R}^N\times \mathbb {R}^N\times \mathbb {R}\ni (\theta _1,\theta _2,\sigma ) \mapsto f(\theta _1,\theta _2,\sigma )\in \mathbb {R}^N\) is \(C^2\) (twice continuously differentiable).
- (S2):
-
The map g: \(\mathbb {R}^N\times \mathbb {R}^N\times \mathbb {R}\ni (\gamma _1,\,\gamma _2,\,\sigma )\mapsto g(\gamma _1,\,\gamma _2,\,\sigma )\in \mathbb {R}\) is \(C^2\).
- (S3):
-
\((\frac{\partial }{\partial \theta _1}+\frac{\partial }{\partial \theta _2})f(\theta _1,\,\theta _2,\,\sigma )|_{\sigma =\sigma _0,\,\theta _1=\theta _2=x_{\sigma _0}}\) is nonsingular, where \(\sigma _0\in \mathbb {R}\), and where \((x_{\sigma _0},\tau _{\sigma _0})\) (or, for simplicity, \((x_{\sigma _0},\tau _{\sigma _0},\,\sigma _0)\)) is a stationary state of (1.1). That is,
$$\begin{aligned}&f(x_{\sigma _0},\,x_{\sigma _0},\,\sigma _0)=0,\quad g(x_{\sigma _0},\,x_{\sigma _0},\,\sigma _0)=\tau _{\sigma _0}. \end{aligned}$$
(S3) implies that there exists \(\epsilon _0>0\) and a \(C^1\)-smooth curve \((\sigma _0-\epsilon _0,\,\sigma _0+\epsilon _0)\ni \sigma \mapsto (x_{\sigma },\,\tau _{\sigma })\in \mathbb {R}^{N+1}\) such that \((x_{\sigma },\,\tau _{\sigma })\) is the unique stationary state of (1.1) in a small neighborhood of \((x_{\sigma _0},\,\tau _{\sigma _0})\) for \(\sigma \) close to \(\sigma _0.\) In the following, we write \(\partial _i f=\frac{\partial }{\partial \theta _i}f\) for \(i=1,\,2\), and similarly we define \(\partial _i g\) for \(i=1,\,2\).
The state-dependent delay of system (1.1) arises in several applications. To mention a few, in the model of turning processes [7], the delay \(\tau \) is the time duration for one around of cutting, in the echo control model [18], the state-dependent delay is the echo traveling time between the object’s positions when the sound is emitted and received. See [4] for a review. To model diffusion processes in genetic regulatory dynamics with time delay, we considered in [5] the following system:
where \(f_0,\,g_0: \mathbb {R}\rightarrow \mathbb {R}\) are three times continuously differentiable functions; \(\mu _m\), \(\mu _p\), c and \(\epsilon _0\) are positive constants. The time delay \(\tau (t)=\epsilon _0+c(x(t)-x(t-\tau (t)))\) models the homogenization time of the substances produced in the regulatory processes. Since the equation for \(\tau \) can be written as
we call \(\tau \) a threshold type state-dependent delay and we have shown in [5] that using the time transformation \(t\mapsto \int _{0}^t(1-c\dot{x}(s))\mathrm {d}s\) inspired by [15, 16], system (1.2) can be transformed into a system with constant delay and distributed delay under certain conditions. In such a case, the theory we developed in [1] is applicable to system (1.2) for a local and global Hopf bifurcation theory. However, if \(\epsilon _0=0\) in (1.2), then the integral equation for \(\tau \) becomes
which cannot be employed to remove the state-dependent delay using the time transformation \(t\mapsto \int _{0}^t(1-c\dot{x}(s))\mathrm {d}s\). Thus the global Hopf bifurcation theory developed in [1] is no longer applicable. We remark that if we obtain a differential equation of \(\tau \) from \(\tau (t)=\epsilon _0+c(x(t)-x(t-\tau ))\) by taking derivatives on both sides, the resulting system will have a foliation of equilibria and at least one zero eigenvalue. Thus the global Hopf bifurcation theory developed in [6] is not applicable either. With these facts, we are motivated to develop a global Hopf bifurcation theory for system (1.1) and apply it to an extended three dimensional Goodwin’s model with state-dependent delay where the delay vanishes at the stationary state. [See system (5.1) at Sect. 5 for a brief description of the model.]
To start the discussion, we denote by \(C(\mathbb {R};\,\mathbb {R}^N)\) the normed space of bounded continuous functions from \(\mathbb {R}\) to \(\mathbb {R}^N\) equipped with the usual supremum norm \(\Vert x\Vert =\sup _{t\in \mathbb {R}}|x(t)|\) for \(x\in C(\mathbb {R};\,\mathbb {R}^N)\), where \(|\cdot |\) denotes the Euclidean norm. We also denote by \(C^1(\mathbb {R};\,\mathbb {R}^N)\) the normed space of continuously differentiable bounded functions with bounded derivatives from \(\mathbb {R}\) to \(\mathbb {R}^N\) equipped with the usual \(C^1\) norm
for \( x\in C^1(\mathbb {R};\,\mathbb {R}^N).\)
We wish to drop the algebraic equation in (1.1) for the application of \(S^1\)-equivariant degree. We have
Lemma 1
Assume that (S2) holds. The following statements are true:
- \(\mathrm{(i)}\) :
-
For every \((x,\,\sigma )\in C(\mathbb {R};\mathbb {R}^N)\times \mathbb {R}\), where x is periodic, there exists a function \(\tau : \mathbb {R}\rightarrow \mathbb {R}\) such that \(\tau (t)=g(x(t),\,x(t-\tau (t)),\,\sigma ).\)
- \(\mathrm{(ii)}\) :
-
Let \(\sigma \in \mathbb {R}\) be fixed and \(x_0\) be a constant function in \(C(\mathbb {R};\mathbb {R}^N).\) There exists an open ball \(O(\epsilon )\subset C^1(\mathbb {R};\mathbb {R}^N)\) centered at \(x_0\) with radius \(\epsilon >0\) such that for every periodic \(x\in O(\epsilon )\) with period \(p>0\), there exists a unique periodic \(\tau \in C^1(\mathbb {R};\mathbb {R})\) with period p such that \(\tau (t)=g(x(t),\,x(t-\tau (t)),\,\sigma ),\,t\in \mathbb {R}.\) Moreover, \(\tau \) depends on x continuously under the supremum norm.
Proof
Fix an arbitrary \(t\in \mathbb {R}\) and let \(a=\tau (t)\). Consider the graphs of \(h=a\) and \(h=g(x(t),\,x(t-a),\,\sigma )\) in the h-a plane. The graphs must have an intersection since \(x\in C(\mathbb {R};\mathbb {R}^N)\) is periodic and \(h=g(x(t),\,x(t-a),\,\sigma )\) is continuous and bounded with respect to a. Since t is arbitrary, there exists a function \(\tau : \mathbb {R}\rightarrow \mathbb {R}\) with \(a=\tau (t)\) such that \(\tau (t)=g(x(t),\,x(t-\tau (t)),\,\sigma ).\)
Define \(F:\mathbb {R}^2\rightarrow \mathbb {R}\) by \(F(a,\,t)=a-g(x(t),\,x(t-a),\,\sigma )\) where \(x\in C^1(\mathbb {R};\mathbb {R}^N)\) is periodic. By (S2) F is continuously differentiable in \((a,\,t)\in \mathbb {R}^2\). Moreover, \(a=\tau (t)\) is such that \(F(a,\,t)=0\). Note that we have
Since by (S2) \(\partial _2 g(\gamma _1,\,\gamma _2,\,\sigma )\) is continuous, there exists an open ball \(O(\epsilon )\subset C^1(\mathbb {R};\mathbb {R}^N)\) near \(x_0\) with \(\epsilon >0\), such that for every \(x\in O(\epsilon )\) with x periodic, we have \(\frac{\partial F}{\partial a}\ne 0\). Indeed, we can choose \(\epsilon >0\) small enough so that \(\frac{\partial F}{\partial a}\) assumes values in a small neighborhood of 1 in \(\mathbb {R}\). By the Implicit Function Theorem, the solution \(a=\tau (t)\) of \(a=g(x(t),\,x(t-a),\,\sigma )\) for a is continuously differentiable with respect to t. Moreover, by taking derivatives on both sides of \(\tau (t)=g(x(t),\,x(t-\tau (t)),\,\sigma )\) we know that \(\dot{\tau }\) is bounded in \(\mathbb {R}\). That is, \(\tau \in C^1(\mathbb {R};\mathbb {R})\).
Next we show that we can choose \(\epsilon >0\) small enough so that \(\tau \) is unique. Suppose not. Then for every \(\epsilon >0\), there exists \(x\in O(\epsilon )\) with period p such that \(\tau \) is not unique. That is, there exists \(\tau _0\ne \tau \) such that \(\tau _0(t)=g(x(t),\,x(t-\tau _0(t)),\,\sigma ).\) Let \(\epsilon _1>0\) and \(L>0\) be such that
Then by the Integral Mean Value Theorem, for \(x\in O(\epsilon )\subset O(\epsilon _1)\), we have
which leads to \(L\epsilon \ge 1\) for every \(\epsilon \in (0,\,\epsilon _1)\). This is a contradiction. Therefore, \(\tau \) is uniquely determined by x with \(\tau (t)=g(x(t),\,x(t-\tau (t)),\,\sigma ),\,t\in \mathbb {R}\).
Next, we show that \(\tau \) is p-periodic. Indeed, we have for every \(t\in \mathbb {R}\),
which combined with \(\tau (t)=g(x(t),\,x(t-\tau (t)),\,\sigma )\) and the uniqueness of the solution for \(\tau \) leads to \(\tau (t)=\tau (t+p),\,t\in \mathbb {R}\).
Lastly, we show that \(\tau \) depends on x continuously. Suppose that x and \(\bar{x}\) both lie in \(O(\epsilon )\subset C^1(\mathbb {R};\mathbb {R}^N)\) and that \(\tau \) and \(\bar{\tau }\) are the corresponding solutions of \(\tau (t)=g(x(t),\,x(t-\tau (t)),\,\sigma ),\,t\in \mathbb {R}\) for \(\tau \). Let \(L_1>0\) and \(L_2>0\) be the supremum of \(|\partial _1g|\) and \(|\partial _2g|\) when x is in \(O(\epsilon )\), respectively. We have
Take \(\epsilon >0\) so that \(0<L_2\epsilon <1\). We have \(|\tau (t)-\bar{\tau }(t)|<\frac{(L_1+L_2)\Vert x-\bar{x}\Vert }{1-L_2\epsilon }\) and
which shows the continuous dependency of \(\tau \) on x under the supremum norm. \(\square \)
By Lemma 1, we notice that if \(x\in C(\mathbb {R};\mathbb {R}^N)\) is periodic, the function \(\tau \) satisfying \(\tau (t)=g(x(t),\,x(t-\tau (t)),\,\sigma )\) is not necessarily continuous and neither is \(f(x(t),\,x(t-\tau (t)),\,\sigma )\), while continuity is crucial for applying topological degree theory for a Hopf bifurcation. However, if \(x\in C^1(\mathbb {R};\mathbb {R}^N)\) is periodic and is in a small neighborhood of a constant function, \(\tau \) is continuously differentiable. The complexity is caused by the implicitly given \(\tau \) in the algebraic equation of system (1.1). If we replace the delayed term \(x(t-\tau (t))\) with \(x(t-\tau _\sigma )\) in the algebraic equation where \(\tau _\sigma \) is the stationary state of \(\tau \) defined after (S3), we obtain the following system with state-dependent delay,
where \(\tau \) is continuous if x is continuous. We notice that system (1.5) shares the same set of stationary states of system (1.1) and it has interest on its own right since it also represents a class of differential-algebraic equations with state-dependent delay. Due to the similarities between systems (1.5) and (1.1), we are interested in developing global Hopf bifurcation theories for both systems, while for systems (1.5) we use the state space of \(C(\mathbb {R};\mathbb {R}^N)\) and for system (1.1) we use \(C^1(\mathbb {R};\mathbb {R}^N)\). Moreover, we show that if system (1.5) undergoes Hopf bifurcation at \((x_{\sigma _0},\,\tau _{\sigma _0})\), then system (1.1) also undergoes Hopf bifurcation at the same bifurcation point. Namely, we show that systems (1.5) and (1.1) share the same set of Hopf bifurcation points.
We organize the remaining part of the paper as following: Using the framework for a Hopf bifurcation theory established in [6], we develop a local Hopf bifurcation theory for system (1.5) in Sect. 2 and for system (1.1) in Sect. 3. We develop global Hopf bifurcation theories for both systems (1.1) and (1.5) in Sect. 4. In Sect. 5 we apply the developed local and global Hopf bifurcation theories to the prototype system (1.2) with \(\epsilon _0=0\). We conclude the discussion in Sect. 6.
2 Local Hopf Bifurcation for System (1.5)
We begin with definitions of notations. We denote by \(V=C_{2\pi }(\mathbb {R};\,\mathbb {R}^{N})\) the space of \(2\pi \)-periodic continuous functions from \(\mathbb {R}\) to \(\mathbb {R}^{N}\) equipped with the supremum norm. We denote by \(C_{2\pi }^1(\mathbb {R};\,\mathbb {R}^{N})\) the Banach space of \(2\pi \)-periodic and continuously differentiable functions equipped with the \(C^1\) norm.
Note that if \(x\in C(\mathbb {R};\mathbb {R}^N)\) is p-periodic, then \(\tau (t)=g(x(t),\,x(t-\tau _\sigma ),\,\sigma ),\,t\in \mathbb {R}\) is continuous and p-periodic. We call x a solution if \((x,\,\tau )\) satisfies system (1.5). For a stationary state \(x_{\sigma _0}\) of system (1.5) with the parameter \(\sigma _0\), we say that \((x_{\sigma _0},\,\sigma _0)\) is a Hopf bifurcation point of system (1.5), if there exist a sequence \(\{(x_k,\,\sigma _k,\,T_k)\}_{k=1}^{+\infty }\subseteq C(\mathbb {R}; \mathbb {R}^{N})\times \mathbb {R}^2\) and \(T_0> 0\) such that
and \((x_k,\,\sigma _k)\) is a nonconstant \(T_k\)-periodic solution of system (1.5).
Due to the nature of the same approach of using the \(S^1\)-equivariant degree, the presentation of the remaining part of this section is similar to that of [6], even though the systems in question are different. We study Hopf bifurcation of (1.5) through the system obtained through the formal linearization [2]. Namely, we freeze the state-dependent delay in system (1.5) at its stationary state and linearize the resulting differential equation of x with constant delay at the stationary state. For \(\sigma \in (\sigma _0-\epsilon _0,\,\sigma _0+\epsilon _0)\), the following system is called the formal linearization of system (1.5) at the stationary point \(x_{\sigma }\):
where
Letting \(x(t)=e^{\omega t}\cdot C+x_\sigma \) with \(C\in \mathbb {R}^{N}\), we obtain the following characteristic equation of the linear system corresponding to the inhomogeneous linear system (2.1),
where \(\varDelta _{(x_\sigma ,\,\sigma )}(\omega )\) is an \(N\times N\) complex matrix defined by
A solution \(\omega \) to the characteristic equation (2.2) is called a characteristic value of the stationary state \((x_{\sigma },\,\sigma )\). If zero is not a characteristic value of \((x_{\sigma _0},\,\sigma _0)\), \((x_{\sigma _0},\, \sigma _0)\) is said to be a nonsingular stationary state. We say that \((x_{\sigma _0},\,\sigma _0)\) is a center if the set of nonzero purely imaginary characteristic values of \((x_{\sigma _0},\,\sigma _0)\) is nonempty and discrete. \((x_{\sigma _0},\,\sigma _0)\) is called an isolated center if it is the only center in some neighborhood of \((x_{\sigma _0},\,\sigma _0)\) in \(\mathbb {R}^{N}\times \mathbb {R}\).
If \((x_{\sigma _0}, \,\sigma _0)\) is an isolated center of (2.1), then there exist \(\beta _0>0\) and \(\delta \in (0,\,\epsilon _0)\) such that
and
for any \(\sigma \in (\sigma _0-\delta ,\,\sigma _0+\delta )\) and any \(\beta \in (0,\,+\infty )\setminus \{\beta _0\}\). Hence, we can choose constants \(\alpha _0=\alpha _0(\sigma _0,\,\beta _0)>0\) and \(\varepsilon =\varepsilon (\sigma _0,\,\beta _0)>0\) such that \(\det \varDelta _{ (x_{\sigma _0},\, \sigma _0)}(\cdot )\) has no zeros in \(\partial \Omega \) where \( \Omega :=(0,\,\alpha _0)\times (\beta _0-\varepsilon ,\,\beta _0+\varepsilon )\subset \mathbb {R}^2\cong \mathbb {C}\). We note that \(\det \varDelta _{ (x_{\sigma }, \, \sigma )}(\omega )\) is analytic in \(\omega \) and is continuous in \(\sigma \). If \(\delta >0\) is small enough, then there is no zero of \(\det \varDelta _{(x_{{\sigma _0\pm \delta }}, \, {\sigma _0\pm \delta })}(\omega )\) in \(\partial \Omega \). So we can define the number
and the crossing number of \((x_{\sigma _0},\, \sigma _0, \,\beta _0)\) as
where \(\deg _B\) is the Brouwer degree in finite-dimensional spaces. See, e.g., [8] for details.
To formulate the Hopf bifurcation problem as a fixed point problem in \(C_{2\pi }(\mathbb {R};\mathbb {R}^N)\), we normalize the period of a \(2\pi /\beta \)-periodic solution x of (1.5) and the associated \(\tau \in C(\mathbb {R};\mathbb {R})\) by setting \((x(t),\tau (t))=(y(\beta t),\,z(\beta t))\) and obtain
where \((y_{\sigma },\,z_{\sigma })=(x_{\sigma },\,\tau _{\sigma })\).
Define \(N_0: V \times \mathbb {R}\times (0,\,+\infty )\ni (y,\,\sigma ,\,\beta )\mapsto N_0(y,\,\sigma ,\,\beta )\in V\) by
where z is chosen to satisfy the second line of (2.6) in light of Lemma 1.
Then the differential equation part of system (2.6) is rewritten as
Correspondingly, (2.1) is transformed into
where \(\tilde{N}_0: V \times \mathbb {R}\times (0,\,+\infty )\ni (y,\,\sigma ,\,\beta )\mapsto \tilde{N}_0(y,\,\sigma ,\,\beta )\in V\) is defined by
We note that y is \(2\pi \)-periodic if and only if x is \((2\pi /\beta )\)-periodic.
Let \(L_0: C_{2\pi }^1(\mathbb {R};\,\mathbb {R}^{N})\rightarrow V\) be defined by \(L_0 y(t)=\dot{y}(t), t\in \mathbb {R}\) and \(K: V\rightarrow \mathbb {R}^{N}\) be defined by
Define the map \(\tilde{\mathcal {F}}: V\times \mathbb {R}\times (0,\,+\infty )\rightarrow V\) by
We call the set defined by
a special neighborhood of \(\widetilde{\mathcal {F}}\), if it satisfies
-
(i)
\(\widetilde{\mathcal {F}}(y,\,\sigma ,\,\beta )\ne 0\) for every \((y,\,\sigma ,\,\beta )\in \overline{B(y_0,\,\sigma _0,\,\beta _0; r,\,\rho )}\) with \(|(\sigma ,\,\beta )-(\sigma _0,\,\beta _0)|=\rho \) and \(\Vert y-y_\sigma \Vert \ne 0\);
-
(ii)
\((y_0,\,\sigma _0,\,\beta _0)\) is the only isolated center of (2.9) in \(\overline{B(y_0,\,\sigma _0,\,\beta _0; r,\,\rho )}\).
We cite some technical Lemmas from [6] with necessary notational adaptations, before we state and prove the local Hopf bifurcation theorem for system (1.5).
Lemma 2
([6]) Let \(L_0: C_{2\pi }^1(\mathbb {R};\,\mathbb {R}^{N})\rightarrow V\) be defined by \(L_0 y(t)=\dot{y}(t), t\in \mathbb {R}\) and let \(K: V\rightarrow \mathbb {R}^{N}\) be defined at (2.10). Then \(L_0+K\) has a compact inverse \((L_0+K)^{-1}: V\rightarrow V\).
Lemma 3
([6]) For any \(\sigma \in \mathbb {R}\) and \(\beta >0\), the map \(N_0(\cdot ,\,\sigma ,\,\beta ): V\rightarrow V\) defined by (2.7) is continuous.
Lemma 4
([6]) If system (2.1) has a nonconstant periodic solution with period \(T>0\), then there exists an integer \(m\ge 1,\,m\in \mathbb {N}\) such that \(\pm im\,2\pi /T\) are characteristic values of the stationary state \((x_{\sigma },\,\tau _{\sigma },\,\sigma )\).
For the purpose of establishing the \(S^1\)-degree on some special neighborhood near the stationary state, we have
Lemma 5
Assume \((\text{ S1 })\)–\((\text{ S3 })\) hold. Let \(L_0\) and K be as in Lemma 2 and \(\tilde{N}_0:V\times \mathbb {R}\times (0,\,+\infty )\rightarrow V\) be as in (2.9). Let \(\tilde{\mathcal {F}}: V\times \mathbb {R}\times (0,\,+\infty )\rightarrow V\) be defined at (2.11). If \(B(y_0,\,\sigma _0,\,\beta _0; r,\,\rho )\) is a special neighborhood of \(\widetilde{\mathcal {F}}\) with \(0<\rho <\beta _0\), then there exists \(r'\in (0,\, r]\) such that the neighborhood
satisfies
for \((y,\,\sigma ,\,\beta )\in \overline{B(y_0,\,\sigma _0,\,\beta _0; r',\,\rho )}\) with \(y\ne y_\sigma \) and \(|(\sigma ,\,\beta )-(\sigma _0,\beta _0)|=\rho \).
Proof
We prove by contradiction. Suppose the statement is not true, then for any \(0<r'\le r\), there exists \((y,\,\sigma ,\,\beta )\) such that \(0<\Vert y-y_\sigma \Vert <r',\,|(\sigma ,\,\beta )-(\sigma _0,\,\beta _0)|=\rho \) and
Then there exists a sequence of nonconstant periodic solutions \(\{(y_k,\,\sigma _k,\,\beta _k)\}_{k=1}^{\infty }\) of (2.12) such that
and
where \(z_k\) is determined by \(y_k\) by the second line of system (2.6).
Note that \(0<\rho <\beta _0\) implies that \(\beta _k\ge \beta _0-\rho >0\) for every \(k\in \mathbb {N}\). Also, since the sequence \(\{\sigma _k,\,\beta _k\}_{k=1}^{\infty }\) belongs to a bounded neighborhood of \((\sigma _0,\,\beta _0)\) in \(\mathbb {R}^2\), there exists a convergent subsequence, still denoted by \(\{(\sigma _k,\,\beta _k)\}_{k=1}^{\infty }\) for notational simplicity, that converges to \((\sigma ^*,\,\beta ^*)\) so that \(|(\sigma ^*,\,\beta ^*)-(\sigma _0,\,\beta _0)|=\rho \) and \(\beta ^*>0\). Then we have
and
In the following we show that the system
has a nonconstant periodic solution which contradicts the assumption that \((y_{\sigma _0},\,\sigma _0,\,\beta _0)\) is the only center of (2.9) in \(\overline{B(y_0,\,\sigma _0,\,\beta _0; r,\,\rho )}\).
By (S1), f: \(\mathbb {R}^N\times \mathbb {R}^N\times \mathbb {R}\ni (\theta _1,\theta _2,\sigma ) \rightarrow f(\theta _1,\theta _2,\sigma )\in \mathbb {R}^N\) is \(C^2\) in \((\theta _1,\,\theta _2)\). It follows from the Integral Mean Value Theorem that
where
Put
Then we have
We claim that there exists a convergent subsequence of \(\{v_k\}_{k=1}^{+\infty }\). Indeed, by (2.13) and system (2.6), we know that \(\{z_k,\,\beta _k\}_{k=1}^{+\infty }\) is uniformly bounded in \(C(\mathbb {R};\mathbb {R})\times \mathbb {R}\) and hence \(\lim _{t\rightarrow +\infty } [t-\beta _k z_k(t)] =+\infty \). Then by (2.19) and (2.20), we have
Recall that \(\partial _i f(\sigma ^*)\) and \(\partial _i g(\sigma ^*)\), \(i=1,\,2\), are defined in (2.1). By (2.15), we know that \((y_{\sigma _k}+s(y_k(t)-y_{\sigma _k}),y_{\sigma _k}+s(y_k(t-z_k(t))-y_{\sigma _k}),\,\sigma _k)\) converges to the stationary state \((y_{\sigma ^*},\,y_{\sigma ^*},\,\sigma ^*)\) in \(C(\mathbb {R};\mathbb {R}^{2N})\times \mathbb {R}\) uniformly for all \(s \in [0,1 ]\). By (S1) we know that \(f(\theta _1,\,\theta _2,\,\sigma )\) is \(C^2\) in \((\theta _1,\,\theta _2,\,\sigma )\) and \(\partial _1 f(\theta _1,\,\theta _2,\,\sigma )\) is \(C^1\) in \(\sigma \). Also, by (2.13), the sequence \(\{u_k,\,\beta _k,\,\sigma _k\}_{k=1}^{+\infty }\) is uniformly bounded in \(C(\mathbb {R};\mathbb {R}^{N+1})\times \mathbb {R}^2\). Then there exists a constant \(\tilde{L}_1>0\) so that
for all \(t\in \mathbb {R}\), \(k\in \mathbb {N}\) and \(s\in [0,\,1]\). Therefore, we have \(\lim _{k\rightarrow +\infty }\Vert \partial _1 f_k(\sigma _k,\,s)-\partial _1 f(\sigma ^*)\Vert =0\) uniformly for \(s\in [0, 1]\). By the same argument we obtain that
uniformly for \(s\in [0, 1]\). From (2.22) we know that \(\Vert \partial _1 f_k(\sigma _k,\,s)\Vert \) and \(\Vert \partial _2 f_k(\sigma _k,\,s)\Vert \) are both uniformly bounded for all \(k\in \mathbb {N}\) and \(s\in [0,\,1]\). Then it follows from (2.21) that there exists a constant \(\tilde{L}_2>0\) such that \(\Vert \dot{v}_k\Vert <\tilde{L}_2\) for any \(k\in \mathbb {N}\). By the Arzela–Ascoli Theorem, there exists a convergent subsequence \(\{v_{k_j}\}_{j=1}^{+\infty }\) of \(\{v_k\}_{k=1}^{+\infty }\). That is, there exists \(v^*\in \{v\in V: \Vert v\Vert =1\}\) such that
By the Integral Mean Value Theorem, we have
Therefore, it follows from (2.23) and (2.25) that
It follows from (2.15), (2.22), (2.23) and (2.26) that the right hand side of (2.21) converges uniformly to the right hand side of (2.17). Therefore, \(v^*\) is differentiable and we have
and
Since by (S3) the matrix \( \partial _1 f(\sigma ^*)+\partial _2 f(\sigma ^*), \) is nonsingular, \(v=0\) is the only constant solution of (2.27). Also, we have \(v^*\in \{v\in V: \Vert v\Vert =1\}\), \(\Vert v^*\Vert \ne 0\). Therefore, \((v^*(t),\,\sigma ^*,\,\beta ^*)\) is a nonconstant periodic solution of the linear equation (2.27). Then by Lemma 4\((y_{\sigma ^*},\,\sigma ^*,\,\beta ^*)\) is also a center of (2.9) in \(\overline{B(y_0,\,\sigma _0,\,\beta _0; r,\,\rho )}\). This contradicts the assumption that \(B(y_0,\,\sigma _0,\,\beta _0; r,\,\rho )\) is a special neighborhood of (2.6). This completes the proof. \(\square \)
To apply the homotopy argument of \(S^1\)-degree, we show the following
Lemma 6
Assume (S1)–(S3) hold. Let \(L_0\), K, \(\tilde{N}_0\), \(\tilde{\mathcal {F}}\) be as in Lemma 5 and \(N_0: V\times \mathbb {R}\times (0,\,+\infty )\rightarrow V\) be as in (2.6). Define the map \(\mathcal {F}: V\times \mathbb {R}\times (0,\,+\infty )\rightarrow V\) by
If \(\mathcal {U}=B(y_0,\,\sigma _0,\,\beta _0; r,\,\rho )\)\(\subseteq V\times \mathbb {R}\times (0,\,+\infty )\) is a special neighborhood of \(\tilde{\mathcal {F}}\) with \(0<\rho <\beta _0\), then there exists \(r'\in (0,\,r]\) such that \(\mathcal {F}_{\theta }=(\mathcal {F},\,\theta )\) and \(\tilde{\mathcal {F}}_{\theta }=(\tilde{\mathcal {F}},\,\theta )\) are homotopic on \(\overline{B(y_0,\,\sigma _0,\,\beta _0; r',\,\rho )}\), where \(\theta \) is a completing function (or Ize’s function) defined on \(\overline{B(y_0,\,\sigma _0,\,\beta _0; r',\,\rho )}\) which satisfies
-
(i)
\(\theta (y_\sigma ,\,\sigma ,\,\beta )=-|(\sigma ,\,\beta )-(\sigma _0,\,\beta _0)|\) if \((y_\sigma ,\,\sigma ,\,\beta )\in \bar{\mathcal {U}};\)
-
(ii)
\(\theta (y,\,\sigma ,\,\beta )=r'\) if \(\Vert y-y_\sigma \Vert =r'\).
Proof
Since \(\mathcal {U}=B(y_0,\,\sigma _0,\,\beta _0; r,\,\rho )\)\(\subseteq V\times \mathbb {R}\times (0,\,+\infty )\) is a special neighborhood of \(\tilde{\mathcal {F}}\) with \(0<\rho <\beta _0\), then by Lemma 5, both \(\mathcal {F}_{\theta }=(\mathcal {F},\,\theta )\) and \(\tilde{\mathcal {F}}_{\theta }=(\mathcal {F},\,\theta )\) are \(\mathcal {U}\)-admissible. That is, the \(S^1\) degrees of \(\mathcal {F}_{\theta }\) and \(\tilde{\mathcal {F}}_{\theta }\) are well-defined on \(\mathcal {U}\). Note that we introduce the completing function \(\theta \) in order to distinguish nontrivial solutions from trivial ones. See [8] for details.
Suppose, for contradiction, that the conclusion is not true. Then for any \(r'\in (0,\,r]\), \(\mathcal {F}_{\theta }=(\mathcal {F},\,\theta )\) and \(\tilde{\mathcal {F}}_{\theta }=(\tilde{\mathcal {F}},\,\theta )\) are not homotopic on \(\overline{B(y_0,\,\sigma _0,\,\beta _0; r',\,\rho )}\). That is, any homotopy map between \(\mathcal {F}_{\theta }\) and \(\tilde{\mathcal {F}}_{\theta }\) has a zero on the boundary of \(\overline{B(y_0,\,\sigma _0,\,\beta _0; r',\,\rho )}\). In particular, the linear homotopy \(h(\cdot ,\,\alpha ):=\alpha \mathcal {F}_{\theta }+(1-\alpha )\tilde{\mathcal {F}}_{\theta }=(\alpha \mathcal {F} +(1-\alpha )\tilde{\mathcal {F}},\theta ) \) has a zero on the boundary of \(\overline{B(y_0,\,\sigma _0,\,\beta _0; r',\,\rho )}\), where \(\alpha \in [0,\,1]\).
Note that \(\theta (y,\,\sigma ,\,\beta )>0\) if \(\Vert y-y_\sigma \Vert =r'\). Then, there exist \((y,\,\sigma ,\,\beta )\) and \(\alpha \in [0,\,1]\) such that \(\Vert y-y_\sigma \Vert <r',\,|(\sigma ,\,\beta )-(\sigma _0,\,\beta _0)|=\rho \) and
Since \(r'>0\) is arbitrary in the interval \((0,\,r]\), there exists a nonconstant sequence \(\{(y_k,\,\sigma _k,\,\beta _k,\,\alpha _k)\}_{k=1}^{\infty }\) of solutions of (2.28) such that
and
Note that \(0<\rho <\beta _0\) implies that \(\beta _k\ge \beta _0-\rho >0\) for every \(k\in \mathbb {N}\). From (2.29) we know that \(\{(\sigma _k,\,\beta _k,\,\alpha _k)\}_{k=1}^{\infty }\) belongs to a compact subset of \(\mathbb {R}^3\). Therefore, there exist a convergent subsequence, denoted for notational simplicity by \(\{(\sigma _k,\,\beta _k,\,\alpha _k)\}_{k=1}^{\infty }\) without loss of generality, and \((\sigma ^*,\,\beta ^*,\,\alpha ^*)\in \mathbb {R}^3\) such that \(\beta ^*\ge \beta _0-\rho >0\), \(\alpha ^*\in [0,\,1]\) and
Similarly as in the proof of Lemma 5, we show that the system
with \(\partial _i f(\sigma ^*),\, \partial _i g(\sigma ^*), i=1,\,2,\) defined at (2.1), has a nonconstant periodic solution which contradicts the assumption that \(B(u_0,\,\sigma _0,\,\beta _0; r,\,\rho )\) is a special neighborhood which contains an isolated center of (2.9).
By (2.30), we know that the subsequence \(\{(y_k,\,\sigma _k,\,\beta _k,\,\alpha _k)\}_{k=1}^{\infty }\) satisfies
By (S1), f: \(\mathbb {R}^N\times \mathbb {R}^N\times \mathbb {R}\ni (\theta _1,\theta _2,\sigma ) \rightarrow f(\theta _1,\theta _2,\sigma )\in \mathbb {R}^N\) is \(C^2\) in \((\theta _1,\,\theta _2)\). Then it follows from the Integral Mean Value Theorem and from (2.33) that
where
Put
Then we have
We show that there exists a convergent subsequence of \(\{v_k\}_{k=1}^{+\infty }\). Indeed, by (2.29) we know that \(\{z_k,\,\beta _k\}_{k=1}^{+\infty }\) is uniformly bounded in \(C(\mathbb {R};\mathbb {R})\times \mathbb {R}\). Therefore we have
By (2.35), (2.36) and (2.38), we have \(\Vert v_k\Vert =1,\,\Vert v_k(\cdot -\beta _k z_k)\Vert =1\). By (S1) and (2.31) and by a similar argument yielding (2.22), we know that
uniformly for \(s\in [0, 1]\). We know from (2.39) that \(\Vert \partial _1 f_k(\sigma _k,\,s)\Vert \), \(\Vert \partial _2 f_k(\sigma _k,\,s)\Vert \), are both uniformly bounded for every \(k\in \mathbb {N}\) and \(s\in [0,\,1]\). It follows from (2.37) that there exists \(\tilde{L}_3>0\) such that \(\Vert \dot{v}_k\Vert <\tilde{L}_3\) for every \(k\in \mathbb {N}\). By the Arzela–Ascoli Theorem, there exists a convergent subsequence \(\{v_{k_j}\}_{j=1}^{+\infty }\) of \(\{v_k\}_{k=1}^{+\infty }\). That is, there exists \(v^*\in \{v\in V: \Vert v\Vert =1\}\) such that
By the Integral Mean Value Theorem, we obtain for all \(t\in \mathbb {R}\),
Then by (2.31) and (2.41) we have
From (2.40) and (2.42) we have
It follows from (2.31), (2.39), (2.40) and (2.43) that the right hand side of (2.37) converges uniformly to the right hand side of (2.32). Therefore,
and
Noticing that \(v^*\in \{v: \Vert v\Vert =1\}\), we have \(\Vert v^*\Vert \ne 0\). Since the matrix \(\partial _1 f(\sigma ^*)+\partial _2 f(\sigma ^*)\) is nonsingular, \(v^*\) is a nonconstant periodic solution of (2.45). Then by Lemma 4\((y_{\sigma ^*},\,\sigma ^*,\,\beta ^*)\) is also a center of (2.9) in \(\overline{B(y_0,\,\sigma _0,\,\beta _0; r,\,\rho )}\). This contradicts the assumption that \(B(y_0,\,\sigma _0,\,\beta _0; r,\,\rho )\) is a special neighborhood of (2.9) which contains only one center \((y_0,\,\sigma _0,\,\beta _0)\). This completes the proof. \(\square \)
Now we are in the position to prove a local Hopf bifurcation theorem for system (1.5).
Theorem 1
Assume (S1)–(S3) hold. Let \((x_{\sigma _0},\, \sigma _0)\) be an isolated center of system (2.1). If the crossing number defined by (2.5) satisfies
then there exists a bifurcation of nonconstant periodic solutions of (1.5) near \((x_{\sigma _0}, \,\sigma _0)\). More precisely, there exists a sequence \(\{(x_n, \,\sigma _n, \beta _n)\}\) such that \(\sigma _n\rightarrow \sigma _0\), \(\beta _n\rightarrow \beta _0\) as \(n\rightarrow \infty \), and \(\lim _{n\rightarrow \infty }\Vert x_n-x_{\sigma _0}\Vert =0\), where
is a nonconstant \(2\pi /\beta _n\)-periodic solution of system (1.5).
Proof
Let \((x,\,\tau )\) be a solution of system (1.5) with x being \(2\pi /\beta \)-periodic and \(\beta >0\). Let \((x(t),\tau (t))=(y(\beta t),\,z(\beta t))\). Then system (1.5) is transformed to
Let \(V=C_{2\pi }(\mathbb {R};\,\mathbb {R}^{N})\). For any \(\xi =e^{i\nu }\in S^1\), \(u\in V\), \((\xi u)(t):=u(t+\nu )\). Recall that \(\delta \) and \(\varepsilon \) are defined before (2.5). Let \(\mathscr {D}(\sigma _0,\,\beta _0)=(\sigma _0-\delta ,\,\sigma _0+\delta )\times (\beta _0-\varepsilon ,\,\beta _0+\varepsilon )\) and define the maps
where \((\sigma ,\,\beta )\in \mathscr {D}(\sigma _0,\,\beta _0)\) and \(t\in \mathbb {R}\), and \((y_{\sigma },\,z_{\sigma })\) is the stationary state of the system at \(\sigma \) such that \(y_{\sigma _0}=x_{\sigma _0}\). The space V is a Banach representation of the group \(G=S^1\).
Define the operator \(K: V\rightarrow \mathbb {R}^{N}\) by
By Lemma 2, the operator \(L_0+K: C_{2\pi }^1(\mathbb {R};\mathbb {R}^{N})\rightarrow V\) has a compact inverse \((L_0+K)^{-1}: V\rightarrow V\). Then, finding a \(2\pi /\beta \)-periodic solution for the system (1.5) is equivalent to finding a solution of the following fixed point problem:
where \((y,\,\sigma ,\,\beta )\in V\times \mathbb {R}\times (0,\,+\infty )\).
Define the following maps \(\mathcal {F}: V\times \mathbb {R}\times (0,\,+\infty )\rightarrow V\) and \(\tilde{\mathcal {F}}: V\times \mathbb {R}\times (0,\,+\infty )\rightarrow V\) by
Finding a \({2\pi }/{\beta }\)-periodic solution of system (1.5) is equivalent to finding the solution of the problem
By results in [6], it is sufficient to verify the following conditions:
-
(A1)
V has an \(S^1\)-isotypical decomposition \(V=\overline{\oplus _{k=0}^\infty V_k}\) and for each integer \(k=0,\,1,\,2\ldots ,\) the subspace \(V_k\) is of finite dimension.
-
(A2)
There exists a compact resolvent K of \(L_0\) such that for every fixed parameter \((\sigma ,\,\beta )\in \mathbb {R}^2\), \((L_0+K)^{-1}\circ [N_0(\cdot ,\,\sigma ,\,\beta )+K]: V\rightarrow V\) is a condensing map.
-
(A3)
There exists a 2-dimensional submanifold \(M\subset V_0\times \mathbb {R}^2\) such that i) \(M\subset \mathcal {F}^{-1}(0)\); ii) if \((y_0,\,\sigma _0,\,\beta _0)\in M\), then there exists an open neighborhood \(U_{(\sigma _0,\,\beta _0)}\) of \((\sigma ,\,\beta )\) in \(\mathbb {R}^2\) , an open neighborhood \(U_{y_0}\) of \(U_0\) in \(V_0\), and a \(C^1\)-map \(\eta : U_{(\sigma _0,\,\beta _0)}\rightarrow U_{y_0}\) such that \(M\cap (U_{y_0}\times U_{(\sigma _0,\,\beta _0)})=\{(\eta (\sigma ,\,\beta ),\,(\sigma ,\,\beta )): (\sigma ,\,\beta )\in U_{(\sigma _0,\,\beta _0)}\}\).
-
(A4)
\(M\subset \widetilde{\mathcal {F}}^{-1}(0)\) and for every fixed parameter \((\sigma ,\,\beta )\in \mathbb {R}^2\), \((L_0+K)^{-1}\circ [\tilde{N}_0(\cdot ,\,\sigma ,\,\beta )+K]: V\rightarrow V\) is a condensing map.
-
(A5)
There exist \(r>0\) and \(\rho >0\) so that \(B(y_0,\,\sigma _0,\,\beta _0; r,\,\rho )\) is a special neighborhood of \(\widetilde{\mathcal {F}}\) and there exists \(r'\in (0,\, r]\) such that \(\mathcal {F}(y,\,\sigma ,\,\beta )\ne 0\) for \((y,\,\sigma ,\,\beta )\in \overline{B(y_0,\,\sigma _0,\,\beta _0; r',\,\rho )}\) with \(y\ne \eta (\sigma ,\,\beta )\) and \(|(\sigma ,\,\beta )-(\sigma _0,\beta _0)|=\rho \).
-
(A6)
\(D_u\widetilde{\mathcal {F}}(y_0,\,\sigma _0,\,\beta _0): V_0\rightarrow V_0\) is an isomorphism.
By (S1) we know that the linear operator \(\tilde{N}_0\) is continuous. By Lemma 3, we know that \(N_0(\cdot ,\,\sigma ,\,\beta ): V\rightarrow V\) is continuous. Moreover, by Lemma 2 the operator \((L_0+K)^{-1}: V\rightarrow V\) is compact and hence \((L_0+K)^{-1}\circ (\frac{1}{\beta }N_0(\cdot , \alpha , \beta )+K): V\rightarrow V\) and \((L_0+K)^{-1}\circ (\frac{1}{\beta }\tilde{N}_0(\cdot , \alpha , \beta )+K): V\rightarrow V\) are completely continuous and hence are condensing maps. That is, (A2) and (A4) are satisfied.
Since \((x_{\sigma _0}, \,\sigma _0)=(y_{\sigma _0},\,\sigma _0)\) is an isolated center of system (2.1) with a purely imaginary characteristic value \(i\beta _0\), \(\beta _0>0\), \((y_{\sigma _0},\,\sigma _0,\,\beta _0)\in V\times \mathbb {R}\times (0,\,+\infty )\) is an isolated V-singular point of \(\tilde{\mathcal {F}}\). That is, \((y_{\sigma _0},\,\sigma _0,\,\beta _0)\) is the only point in V such that the derivative \(D_y\mathcal {F}(y_{\sigma _0},\,\sigma _0,\,\beta _0)\) is not an automorphism of V. We define the following two-dimensional submanifold \(M\subset V_0\times \mathbb {R}\times (0,\,+\infty )\) by
such that the point \((y_{\sigma _0},\,\sigma _0,\,\beta _0)\) is the only V-singular point of \(\tilde{\mathcal {F}}\) in M. M is the set of trivial solutions to the system (2.1) and satisfies the assumption (A3).
Since \((y_{\sigma _0},\,\sigma _0,\,\beta _0)\in V\times \mathbb {R}\times (0,\,+\infty )\) is an isolated V-singular point of \(\tilde{\mathcal {F}}\), for \(\rho >0\) sufficiently small, the linear operator \(D_u \tilde{\mathcal {F}}(y_\sigma ,\,\sigma ,\,\beta ): V\rightarrow V\) with \(|(\sigma ,\,\beta )-(\sigma _0,\,\beta _0)|<\rho \), is not an automorphism only if \((\sigma ,\,\beta )=(\sigma _0,\,\beta _0)\). Then, by the Implicit Function Theorem, there exists \(r>0\) such that for every \((y,\,\sigma ,\,\beta )\in V\times \mathbb {R}\times (0,\,+\infty )\) with \(|(\sigma ,\,\beta )-(\sigma _0,\,\beta _0)|=\rho \) and \(0<\Vert y-y_\sigma \Vert \le r\), we have \(\tilde{\mathcal {F}}(y,\,\sigma ,\,\beta )\ne 0\). Then the set \(B(x_0,\,\sigma _0,\,\beta _0; r, \rho )\) defined by
is a special neighborhood for \(\tilde{\mathcal {F}}\).
By Lemma 5, there exists a special neighborhood \(\mathcal {U}=B(y_{\sigma _0},\,\sigma _0,\,\beta _0;r', \rho )\) such that \(\mathcal {F}\) and \(\tilde{\mathcal {F}}\) are nonzero for \((y,\,\sigma ,\,\beta )\in \overline{B(y_{\sigma _0},\,\sigma _0,\,\beta _0;r', \rho )}\) with \(y\ne y_\sigma \) and \(|(\sigma ,\,\beta )-(\sigma _0,\,\beta _0)|=\rho \). That is, (A5) is satisfied.
Let \(\theta \) be a completing function on \(\mathcal {U}\). It follows from Lemma 6 that \( (\mathcal {F},\,\theta ) \) is homotopic to \((\tilde{\mathcal {F}},\,\theta )\) on \(\mathcal {U}\).
It is known that V has the following isotypical direct sum decomposition
where \(V_0\) is the space of all constant mappings from \(\mathbb {R}\) into \(\mathbb {R}^{N}\), and \(V_k\) with \(k>0\), \(k\in \mathbb {N}\) is the vector space of all mappings of the form
where \(x,\,y\in \mathbb {R}^{N}\). Then \(V_k\), \(k>0,\,k\in \mathbb {N}\), are finite dimensional. Then, (A1) is satisfied.
For \((\sigma ,\,\beta )\in \mathscr {D}(\sigma _0,\,\beta _0)\), we denote by \(\varPsi (\sigma ,\,\beta )\) the map \(D_y\widetilde{\mathcal {F}}(y(\sigma ),\,\sigma ,\,\beta ): V\rightarrow V\). Then we have \(\varPsi (\sigma ,\,\beta )(V_k)\subset V_k\) for all \(k=0,\,1,\,2,\,\ldots \). Therefore, we can define \(\varPsi _k: \mathscr {D}(\sigma _0,\,\beta _0)\rightarrow L(V_k,\,V_k)\) by
We note that \(V_k\), \(k\ge 1,\,k\in \mathbb {N}\), can be endowed with the natural complex structure \(J: V_k\rightarrow V_k\) defined by
By extending the linearity of J to the vector space spanned over the field of complex numbers by \(e^{ik\cdot }\cdot \epsilon _j:\mathbb {R}\ni t\rightarrow e^{ik t}\cdot \epsilon _j\in \mathbb {C}^{N},\,j=1,\,2,\,\ldots ,\,N\), we know that
is a basis of \(V_k\), where \(\{\epsilon _1,\,\epsilon _2,\,\ldots ,\epsilon _{N}\}\) denotes the standard basis of \(\mathbb {R}^{N}\). Then we identify \(V_k\) with the vector space over the complex numbers spanned by \(e^{ik\cdot }\cdot \epsilon _j,\,j=1,\,2,\,\ldots ,\,N\).
Then we have for \(v_k\in V_k\), \(k\in \mathbb {Z}\), \(k\ge 1\),
where \((v_k)_{\beta z_{\sigma }}=v_k(\cdot -\beta z_{\sigma })\). Then we have, for \(e^{ik\cdot }\epsilon _j\in V_k\),
where the last equality follows from (2.3). Therefore, the matrix representation \([{\varPsi }_k]\) of \({\varPsi }_k(\sigma ,\,\beta )\) with respect to the ordered \(\mathbb {C}\)-basis \(\{e^{ik\cdot }\epsilon _j\}_{j=1}^{N}\) is given by
Next we show that there exists some \(k\in \mathbb {Z}\), \(k\ge 1\), such that \(\mu _k(y_{\sigma _0},\,\sigma _0,\beta _0):=\deg _B(\det _\mathbb {C}[\varPsi _k])\ne 0\).
Define \(\varPsi _H: \mathscr {D}(\sigma _0,\,\beta _0)\rightarrow \mathbb {R}^2\simeq \mathbb {C}\) by
The number \(\mu _1(y_{\sigma _0},\,\sigma _0,\,\beta _0)\) can be written as follows (see Theorem 7.1.5 of [8]):
where \(\epsilon =\mathrm {sign}\det \varPsi _0(\sigma ,\,\beta )\) for \((\sigma ,\beta )\in \mathscr {D}(\sigma _0,\,\beta _0)\). For a constant map \(v_0\in V_0\),
Then, by (S3), we have \(\epsilon \ne 0\) and therefore (A6) is satisfied.
Note that \(\alpha _0,\,\beta _0,\,\delta \) and \(\varepsilon \) are chosen at (2.5). Define the function \(H: [\sigma _0-\delta ,\,\sigma _0+\delta ]\times \overline{\Omega }\rightarrow \mathbb {R}^2\simeq \mathbb {C}\) by
where \(\Omega =(0,\,\alpha _0)\times (\beta _0-\varepsilon ,\,\beta _0+\varepsilon )\), \(\alpha _0=\alpha _0(\sigma _0,\,\beta _0)>0\). By the same argument for (2.4) and (2.5), we know that H satisfies all the conditions of Lemma 2.1 of [6] (or Lemma 7.2.1 of [8]) by the choice of \(\alpha _0,\,\beta _0,\,\varepsilon \) and \(\delta \). So we have
Thus, \(\mu _1(y_{\sigma _0},\,\sigma _0,\,\beta _0)\ne 0\) which, by Theorem 2.4 of [6], implies that \( (y_{\sigma _0},\,\sigma _0,\,\beta _0)\) is a bifurcation point of the system (2.46). Consequently, there exists a sequence of non-constant periodic solutions \((x_n,\,\sigma _n,\,\beta _n)\) such that \(\sigma _n\rightarrow \sigma _0\), \(\beta _n\rightarrow \beta _0\) as \(n\rightarrow \infty \), and \(x_n\) is a \(2\pi /\beta _n\)-periodic solution of (1.5) such that the associated pair \((x_n,\,\tau _n)\) with \(\tau _n(t)=g(x_n(t),\,x_n(t-\tau _n(t)),\,\sigma _n)\) satisfies (1.5) with \(\lim _{n\rightarrow +\infty }\Vert (x_n,\,\tau _n)-(x_{\sigma _0},\,\tau _{\sigma _0})\Vert =0\). \(\square \)
3 Local Hopf Bifurcation for System (1.1)
Now we consider the local Hopf bifurcation problem of system (1.1). By Lemma 1, we know that if \(x\in C^1(\mathbb {R};\mathbb {R}^N)\) is p-periodic and is in a small neighborhood \(O(\epsilon )\) of \(x_\sigma \), there exists a unique p-periodic \(\tau \in C^1(\mathbb {R};\mathbb {R})\) such that \(\tau (t)=g(x(t),\,x(t-\tau (t)),\,\sigma ),\,t\in \mathbb {R}\). We call x a solution if \((x,\,\tau )\) satisfies system (1.1).
For a stationary state \(x_{\sigma _0}\) of system (1.1) with the parameter \(\sigma _0\), we say that \((x_{\sigma _0},\,\sigma _0)\) is a Hopf bifurcation point of system (1.1), if there exist a sequence \(\{(x_k,\,\sigma _k,\,T_k)\}_{k=1}^{+\infty }\subseteq C^1(\mathbb {R}; \mathbb {R}^{N})\times \mathbb {R}^2\) and \(T_0> 0\) such that
and \((x_k,\,\sigma _k)\) is a nonconstant \(T_k\)-periodic solution of system (1.1).
We freeze the state-dependent delay in system (1.1) at its stationary state and linearize the resulting differential equation of x with constant delay at the stationary state. For \(\sigma \in (\sigma _0-\epsilon _0,\,\sigma _0+\epsilon _0)\), the following formal linearization of system (1.1) at the stationary point \(x_{\sigma }\):
where
Notice that the system (3.1) is the same as system (2.1) and hence they share the same characteristic equations.
Let \((x_{\sigma _0}, \,\sigma _0)\) be an isolated center of (2.1) and let \(O(\epsilon ^*)\subset C^1(\mathbb {R};\mathbb {R}^N)\) be a neighborhood of \(x_{\sigma _0}\). In the following we confine the discussion with \(x\in O(\epsilon ^*)\subset C^1(\mathbb {R};\mathbb {R}^N)\), where by Lemma 1, \(\epsilon ^*>0\) is chosen so that every p-periodic \(x\in O(\epsilon ^*)\subset C^1(\mathbb {R};\mathbb {R}^N)\) determines a unique continuously differentiable p-periodic \(\tau \).
Now we formulate the Hopf bifurcation problem as a fixed point problem in \(C^1(\mathbb {R};\mathbb {R}^N)\). We normalize the period of the \(2\pi /\beta \)-periodic solution \(x\in O(\epsilon ^*)\) of (1.5) and the associated \(\tau \in C^1(\mathbb {R};\mathbb {R})\) by setting \((x(t),\tau (t))=(y(\beta t),\,z(\beta t))\). We obtain
Let \(W=O(\epsilon ^*)\cap C^1_{2\pi }(\mathbb {R};\mathbb {R}^N)\). Define \(N_1: W\ni (y,\,\sigma ,\,\beta ) \times \mathbb {R}^2\rightarrow N_1(y,\,\sigma ,\,\beta )\in C^1_{2\pi }(\mathbb {R};\mathbb {R}^N)\) by
where z is chosen according to y in light of Lemma 1 so that \((y,\,z)\) is a solution of the second line of (3.2). Then the equation for \(\dot{y}\) in system (3.2) is rewritten as
Correspondingly, (3.1) is transformed into
where \(\tilde{N}_1: W\ni (y,\,\sigma ,\,\beta ) \times \mathbb {R}^2\rightarrow \tilde{N}_1(y,\,\sigma ,\,\beta )\in C^1_{2\pi }(\mathbb {R};\mathbb {R}^N)\) is defined by
with \((y_{\sigma },\,z_{\sigma })=(x_{\sigma },\,\tau _{\sigma })\). We note that y is \(2\pi \)-periodic if and only if x is \((2\pi /\beta )\)-periodic.
Let \(L_0: C_{2\pi }^1(\mathbb {R};\,\mathbb {R}^{N})\rightarrow C_{2\pi }(\mathbb {R};\,\mathbb {R}^{N})\) be defined by \(L_0 y(t)=\dot{y}(t), t\in \mathbb {R}\) and \(K: C^1_{2\pi }(\mathbb {R};\mathbb {R}^N)\rightarrow \mathbb {R}^{N}\) be defined by
Define the map \(\tilde{\mathcal {F}}: W\times \mathbb {R}^2\rightarrow C^1_{2\pi }(\mathbb {R};\mathbb {R}^N)\) by
We suppose that the set defined by
is a special neighborhood of \(\widetilde{\mathcal {F}}\) which satisfies
-
(i)
\(\widetilde{\mathcal {F}}(y,\,\sigma ,\,\beta )\ne 0\) for every \((y,\,\sigma ,\,\beta )\in \overline{B(y_0,\,\sigma _0,\,\beta _0; r,\,\rho )}\) with \(|(\sigma ,\,\beta )-(\sigma _0,\,\beta _0)|=\rho \) and \(\Vert y-y_\sigma \Vert _{C^1}\ne 0\);
-
(ii)
\((y_0,\,\sigma _0,\,\beta _0)\) is the only isolated center in \(\overline{B(y_0,\,\sigma _0,\,\beta _0; r,\,\rho )}\).
Before we state and prove the local Hopf bifurcation theorem for system (1.1), we need the following technical Lemmas.
Lemma 7
Let \(L_0: C_{2\pi }^1(\mathbb {R};\,\mathbb {R}^{N})\rightarrow C_{2\pi }(\mathbb {R};\,\mathbb {R}^{N})\) be defined by \(L_0 y(t)=\dot{y}(t), t\in \mathbb {R}\) and let \(K: C_{2\pi }^1(\mathbb {R};\,\mathbb {R}^{N})\rightarrow \mathbb {R}^{N}\) be defined at (3.6). Then the inverse \((L_0+K)^{-1}: C_{2\pi }(\mathbb {R};\,\mathbb {R}^{N})\rightarrow C_{2\pi }^1(\mathbb {R};\,\mathbb {R}^{N})\) exists and is continuous.
Proof
By the proof of Lemma 3.1 in [6], \(L_0+K: C_{2\pi }^1(\mathbb {R};\,\mathbb {R}^{N})\rightarrow C_{2\pi }(\mathbb {R};\,\mathbb {R}^{N})\) is one-to-one and onto. Moreover, \((L_0+K)^{-1}: C_{2\pi }(\mathbb {R};\,\mathbb {R}^{N})\rightarrow C_{2\pi }^1(\mathbb {R};\,\mathbb {R}^{N})\) is continuous. \(\square \)
Lemma 8
For any \(\sigma \in \mathbb {R}\) and \(\beta >0\), the map \(N_1(\cdot ,\,\sigma ,\,\beta ): W\rightarrow C_{2\pi }^1(\mathbb {R};\,\mathbb {R}^{N})\) defined by (3.3) is continuous.
Proof
Let \(\{y_n\}_{n=1}^\infty \subset W\) be a convergent sequence with limit \(y_0\in W\). By Lemma 1, \(\{y_n\}_{n=1}^\infty \subset W\) uniquely determines a sequence \(\{z_n\}_{n=1}^\infty \subset C_{2\pi }^1(\mathbb {R};\,\mathbb {R})\) satisfying
Moreover, there exists \(z_0\in C_{2\pi }^1(\mathbb {R};\,\mathbb {R})\) such that \(z_0(t)=g(y_0(t),\,y_0(t-\beta z_0(t)),\,\sigma ),\,t\in \mathbb {R}\) and by Lemma 1 we have,
By taking derivatives on both sides of \(z_n(t)=g(y_n(t),\,y(t-\beta z_n(t),\,\sigma )\) we obtain that
Notice that, we have
Using the Triangle Inequality and the Integral Mean Value Theorem, and noticing from (S2) that g is \(C^2\), we can show that
Therefore, by (3.9) and (3.10) we have \(\lim _{n\rightarrow \infty }\sup _{t\in [0,\,2\pi ]}|\dot{z}_n(t)-\dot{z}_0(t)|=0\) which combined with (3.8) leads to \(\lim _{n\rightarrow \infty }\Vert z_n- z_0\Vert _{C^1}=0.\)
Next we show that \(N_1: W\rightarrow C_{2\pi }^1(\mathbb {R};\,\mathbb {R}^{N})\) defined by \( N_1(y,\,\sigma ,\,\beta )(t)=f(y(t),\,y(t-\beta z(t)),\,\sigma ) \) is continuous. That is,
By the proof of Lemma 3.2 in [6], we know that the restriction  is a continuous map from \(C_{2\pi }(\mathbb {R};\,\mathbb {R}^{N})\) to \(C_{2\pi }(\mathbb {R};\,\mathbb {R}^{N})\). Therefore, we have
is a continuous map from \(C_{2\pi }(\mathbb {R};\,\mathbb {R}^{N})\) to \(C_{2\pi }(\mathbb {R};\,\mathbb {R}^{N})\). Therefore, we have
Moreover, since \(\lim _{n\rightarrow \infty }\Vert y_n- y_0\Vert _{C^1}=0\) and \(\lim _{n\rightarrow \infty }\Vert z_n- z_0\Vert _{C^1}=0.\) We can use the Triangle Inequality and the Integral Mean Value Theorem to obtain that
By (3.13) and (3.14), \(N_1: W\rightarrow C_{2\pi }^1(\mathbb {R};\,\mathbb {R}^{N})\) is continuous. \(\square \)
To establish the \(S^1\)-degree on some special neighborhood near the stationary state , we have
Lemma 9
Assume \((\text{ S1 })\)–\((\text{ S3 })\) hold. Let \(L_0\) and K be as in Lemma 7 and \(\tilde{N}_1:W\times \mathbb {R}\times (0,\,+\infty )\rightarrow C_{2\pi }^1(\mathbb {R};\mathbb {R}^N)\) be as in (3.5). Let \(\tilde{\mathcal {F}}: W\times \mathbb {R}\times (0,\,+\infty )\rightarrow C_{2\pi }^1(\mathbb {R};\mathbb {R}^N)\) be defined at (2.11). If \(B(y_0,\,\sigma _0,\,\beta _0; r,\,\rho )\) is a special neighborhood of \(\widetilde{\mathcal {F}}\) with \(0<\rho <\beta _0\), then there exists \(r'\in (0,\, r]\) such that the neighborhood
satisfies
for \((y,\,\sigma ,\,\beta )\in \overline{B(y_0,\,\sigma _0,\,\beta _0; r',\,\rho )}\) with \(y\ne y_\sigma \) and \(|(\sigma ,\,\beta )-(\sigma _0,\beta _0)|=\rho \).
Proof
We prove by contradiction. Suppose the statement is not true, then for any \(0<r'\le r\), there exists \((y,\,\sigma ,\,\beta )\) such that \(0<\Vert y-y_\sigma \Vert _{C^1}<r',\,|(\sigma ,\,\beta )-(\sigma _0,\,\beta _0)|=\rho \) and
Then there exists a sequence of nonconstant periodic solutions \(\{(y_k,\,\sigma _k,\,\beta _k)\}_{k=1}^{\infty }\) of (3.15) such that
and
where \(z_k\) is chosen according to \(y_k\) in light of Lemma 1 so that \((y_k,\,z_k)\) is a solution of system (3.2).
Note that \(0<\rho <\beta _0\) implies that \(\beta _k\ge \beta _0-\rho >0\) for every \(k\in \mathbb {N}\). Also, since the sequence \(\{\sigma _k,\,\beta _k\}_{k=1}^{\infty }\) belongs to a bounded neighborhood of \((\sigma _0,\,\beta _0)\) in \(\mathbb {R}^2\), there exists a convergent subsequence, still denoted by \(\{(\sigma _k,\,\beta _k)\}_{k=1}^{\infty }\) for notational simplicity, that converges to \((\sigma ^*,\,\beta ^*)\) so that \(|(\sigma ^*,\,\beta ^*)-(\sigma _0,\,\beta _0)|=\rho \) and \(\beta ^*>0\). Then we have
and
We need to show that the system
has a nonconstant periodic solution which contradicts the assumption that \((y_{\sigma _0},\,\sigma _0,\,\beta _0)\) is the only center of (3.5) in \(\overline{B(u_0,\,\sigma _0,\,\beta _0; r,\,\rho )}\). But (3.18) implies that
Then by the same argument in the proof of Lemma 5, (3.20) has a nonconstant periodic solution. This completes the proof. \(\square \)
To apply the homotopy argument of \(S^1\)-degree, we show the following
Lemma 10
Assume (S1)–(S3) hold. Let \(L_0\), K, \(\tilde{N}_1\), \(\tilde{\mathcal {F}}\) be as in Lemma 9 and \(N_1: W\times \mathbb {R}^2\rightarrow C_{2\pi }^1(\mathbb {R};\mathbb {R}^N)\) be as in (3.2). Define the map \(\mathcal {F}: W\times \mathbb {R}\times (0,\,+\infty )\rightarrow C_{2\pi }^1(\mathbb {R};\mathbb {R}^N)\) by
If \(\mathcal {U}=B(y_0,\,\sigma _0,\,\beta _0; r,\,\rho )\)\(\subseteq W\times \mathbb {R}\times (0,\,+\infty )\) is a special neighborhood of \(\tilde{\mathcal {F}}\) with \(0<\rho <\beta _0\), then there exists \(r'\in (0,\,r]\) such that \(\mathcal {F}_{\theta }=(\mathcal {F},\,\theta )\) and \(\tilde{\mathcal {F}}_{\theta }=(\tilde{\mathcal {F}},\,\theta )\) are homotopic on \(\overline{B(y_0,\,\sigma _0,\,\beta _0; r',\,\rho )}\), where \(\theta \) is a completing function (or Ize’s function) defined on \(\overline{B(y_0,\,\sigma _0,\,\beta _0; r',\,\rho )}\) which satisfies
-
(i)
\(\theta (y_\sigma ,\,\sigma ,\,\beta )=-|(\sigma ,\,\beta )-(\sigma _0,\,\beta _0)|\) if \((y_\sigma ,\,\sigma ,\,\beta )\in \bar{\mathcal {U}};\)
-
(ii)
\(\theta (y,\,\sigma ,\,\beta )=r'\) if \(\Vert y-y_\sigma \Vert _{C^1}=r'\).
Proof
Since \(\mathcal {U}=B(y_0,\,\sigma _0,\,\beta _0; r,\,\rho )\)\(\subseteq W\times \mathbb {R}^2\) is a special neighborhood of \(\tilde{\mathcal {F}}\) with \(0<\rho <\beta _0\), then by Lemma 9, both \(\mathcal {F}_{\theta }=(\mathcal {F},\,\theta )\) and \(\tilde{\mathcal {F}}_{\theta }=(\mathcal {F},\,\theta )\) are \(\mathcal {U}\)-admissible. For contradiction, suppose that the conclusion is not true. Then for any \(r'\in (0,\,r]\), \(\mathcal {F}_{\theta }=(\mathcal {F},\,\theta )\) and \(\tilde{\mathcal {F}}_{\theta }=(\tilde{\mathcal {F}},\,\theta )\) are not homotopic on \(\overline{B(y_0,\,\sigma _0,\,\beta _0; r',\,\rho )}\). That is, any homotopy map between \(\mathcal {F}_{\theta }\) and \(\tilde{\mathcal {F}}_{\theta }\) has a zero on the boundary of \(\overline{B(y_0,\,\sigma _0,\,\beta _0; r',\,\rho )}\). In particular, the linear homotopy \(h(\cdot ,\,\alpha ):=\alpha \mathcal {F}_{\theta }+(1-\alpha )\tilde{\mathcal {F}}_{\theta }=(\alpha \mathcal {F} +(1-\alpha )\tilde{\mathcal {F}},\theta ) \) has a zero on the boundary of \(\overline{B(y_0,\,\sigma _0,\,\beta _0; r',\,\rho )}\), where \(\alpha \in [0,\,1]\).
Note that \(\theta (y,\,\sigma ,\,\beta )>0\) if \(\Vert y-y_\sigma \Vert _{C^1}=r'\). Then, there exist \((y,\,\sigma ,\,\beta )\) and \(\alpha \in [0,\,1]\) such that \(\Vert y-y_\sigma \Vert _{C^1}<r',\,|(\sigma ,\,\beta )-(\sigma _0,\,\beta _0)|=\rho \) and
Since \(r'>0\) is arbitrary in the interval \((0,\,r]\), there exists a nonconstant sequence \(\{(y_k,\,\sigma _k,\,\beta _k,\,\alpha _k)\}_{k=1}^{\infty }\) of solutions of (3.22) such that
and
Note that \(0<\rho <\beta _0\) implies that \(\beta _k\ge \beta _0-\rho >0\) for every \(k\in \mathbb {N}\). From (3.23) we know that \(\{(\sigma _k,\,\beta _k,\,\alpha _k)\}_{k=1}^{\infty }\) belongs to a compact subset of \(\mathbb {R}^3\). Therefore, there exist a convergent subsequence, denoted for notational simplicity by \(\{(\sigma _k,\,\beta _k,\,\alpha _k)\}_{k=1}^{\infty }\) without loss of generality, and \((\sigma ^*,\,\beta ^*,\,\alpha ^*)\in \mathbb {R}^3\) such that \(\beta ^*\ge \beta _0-\rho >0\), \(\alpha ^*\in [0,\,1]\) and
By the same token for the proof of Lemma 5, we show that the system
with \(\partial _i f(\sigma ^*),\, \partial _i g(\sigma ^*), i=1,\,2,\) defined at (2.1), has a nonconstant periodic solution which contradicts the assumption that \(B(u_0,\,\sigma _0,\,\beta _0; r,\,\rho )\) is a special neighborhood which contains an isolated center of (3.5). Since (3.23) implies \( \lim _{k\rightarrow +\infty }\Vert y_k-y_{\sigma _k}\Vert =0\), by the same argument in the proof of Lemma 10 we know that system (3.26) has a nonconstant periodic solution. This is a contradiction. \(\square \)
Now we are in the position to prove the local Hopf bifurcation theorem for system (1.1).
Theorem 2
Assume (S1)–(S3) hold. Let \((x_{\sigma _0},\, \sigma _0)\) be an isolated center of system (2.1). If the crossing number defined by (2.5) satisfies
then there exists a bifurcation of nonconstant periodic solutions of (1.1) near \((x_{\sigma _0}, \,\sigma _0)\). More precisely, there exists a sequence \(\{(x_n, \,\sigma _n, \beta _n)\}\) such that \(\sigma _n\rightarrow \sigma _0\), \(\beta _n\rightarrow \beta _0\) as \(n\rightarrow \infty \), and \(\lim _{n\rightarrow \infty }\Vert x_n-x_{\sigma _0}\Vert _{C^1}=0\), where
is a nonconstant \(2\pi /\beta _n\)-periodic solution of system (1.1).
Proof
Let \((x,\,\tau )\) be a solution of system (1.1) with x being \(2\pi /\beta \)-periodic and \(\beta >0\). Let \((x(t),\tau (t))=(y(\beta t),\,z(\beta t))\). Then system (1.1) is transformed to
Let \(W=O(\epsilon ^*)\cap C_{2\pi }^1(\mathbb {R};\,\mathbb {R}^{N})\). For any \(\xi =e^{i\nu }\in S^1\), \(u\in W\), \((\xi u)(t):=u(t+\nu )\). By results in [6], it is sufficient to verify the following conditions (A1)-(A6) listed in the proof of Theorem 1.
Recall that \(\delta \) and \(\varepsilon \) are defined before (2.5). Let \(\mathscr {D}(\sigma _0,\,\beta _0)=(\sigma _0-\delta ,\,\sigma _0+\delta )\times (\beta _0-\varepsilon ,\,\beta _0+\varepsilon )\) and define the maps
where \((\sigma ,\,\beta )\in \mathscr {D}(\sigma _0,\,\beta _0)\) and \(t\in \mathbb {R}\), and \((y_{\sigma },\,z_{\sigma })\) is the stationary state of the system at \(\sigma \) such that \(y_{\sigma _0}=x_{\sigma _0}\). The space \(C_{2\pi }^1(\mathbb {R};\,\mathbb {R}^{N})\) is a Banach representation of the group \(G=S^1\).
Define the operator \(K: C_{2\pi }^1(\mathbb {R};\,\mathbb {R}^{N})\rightarrow \mathbb {R}^{N}\) by
By Lemma 2, the operator \(L_0+K: C_{2\pi }^1(\mathbb {R};\mathbb {R}^{N})\rightarrow C_{2\pi }(\mathbb {R};\,\mathbb {R}^{N})\) has a compact inverse \((L_0+K)^{-1}\). Then, finding a \(2\pi /\beta \)-periodic solution for the system (1.1) is equivalent to finding a solution of the following fixed point problem:
where \((y,\,\sigma ,\,\beta )\in W\times \mathbb {R}\times (0,\,+\infty )\).
By (S1) we know that the linear operator \(\tilde{N}_1\) is continuous. By Lemma 8, we know that \(N_1(\cdot ,\,\sigma ,\,\beta ): W\rightarrow C_{2\pi }^1(\mathbb {R};\mathbb {R}^{N})\) is continuous. Moreover, by Lemma 7 the operator \((L_0+K)^{-1}: C_{2\pi }(\mathbb {R};\mathbb {R}^{N}) \rightarrow C_{2\pi }^1(\mathbb {R};\mathbb {R}^{N})\) is continuous. Noticing that the embedding \(j: C_{2\pi }^1(\mathbb {R};\mathbb {R}^{N})\hookrightarrow C_{2\pi }(\mathbb {R};\mathbb {R}^{N})\) is compact, we obtain that \((L_0+K)^{-1}\circ (\frac{1}{\beta }N_1(\cdot , \alpha , \beta )+K): W\rightarrow C_{2\pi }^1(\mathbb {R};\mathbb {R}^{N})\) and \((L_0+K)^{-1}\circ (\frac{1}{\beta }\tilde{N}_1(\cdot , \alpha , \beta )+K): W\rightarrow C_{2\pi }^1(\mathbb {R};\mathbb {R}^{N})\) are completely continuous and hence are condensing maps. That is, (A2) and (A4) are satisfied.
Define the following maps \(\mathcal {F}: W\times \mathbb {R}\times (0,\,+\infty )\rightarrow C_{2\pi }^1(\mathbb {R};\mathbb {R}^{N})\) and \(\tilde{\mathcal {F}}: W\times \mathbb {R}\times (0,\,+\infty )\rightarrow C_{2\pi }^1(\mathbb {R};\mathbb {R}^{N})\) by
which are equivariant condensing fields. Finding a \({2\pi }/{\beta }\)-periodic solution of system (1.1) is equivalent to finding the solution of the problem
Since \((x_{\sigma _0}, \,\sigma _0)=(y_{\sigma _0},\,\sigma _0)\) is an isolated center of system (2.1) with a purely imaginary characteristic value \(i\beta _0\), \(\beta _0>0\), \((y_{\sigma _0},\,\sigma _0,\,\beta _0)\in W\times \mathbb {R}\times (0,\,+\infty )\) is an isolated singular point of \(\tilde{\mathcal {F}}\). That is, \((y_{\sigma _0},\,\sigma _0,\,\beta _0)\) is the only point in W such that the derivative \(D_y\mathcal {F}(y_{\sigma _0},\,\sigma _0,\,\beta _0)\) is not an automorphism of \(C_{2\pi }^1(\mathbb {R};\mathbb {R}^{N})\). One can define the following two-dimensional submanifold \(M\subset V_0\times \mathbb {R}\times (0,\,+\infty )\) by
such that the point \((y_{\sigma _0},\,\sigma _0,\,\beta _0)\) is the only singular point of \(\tilde{\mathcal {F}}\) in M. M is the set of trivial solutions to the system (2.1) and satisfies the assumption (A3).
Since \((y_{\sigma _0},\,\sigma _0,\,\beta _0)\in W\times \mathbb {R}\times (0,\,+\infty )\) is an isolated singular point of \(\tilde{\mathcal {F}}\), for \(\rho >0\) sufficiently small, the linear operator \(D_u \tilde{\mathcal {F}}(y_\sigma ,\,\sigma ,\,\beta ): W\rightarrow C_{2\pi }^1(\mathbb {R};\mathbb {R}^{N})\) with \(|(\sigma ,\,\beta )-(\sigma _0,\,\beta _0)|<\rho \), is not an automorphism only if \((\sigma ,\,\beta )=(\sigma _0,\,\beta _0)\). Then, by the Implicit Function Theorem, there exists \(r>0\) such that for every \((y,\,\sigma ,\,\beta )\in W\times \mathbb {R}\times (0,\,+\infty )\) with \(|(\sigma ,\,\beta )-(\sigma _0,\,\beta _0)|=\rho \) and \(0<\Vert y-y_\sigma \Vert \le r\), we have \(\tilde{\mathcal {F}}(y,\,\sigma ,\,\beta )\ne 0\). Then the set \(B(x_0,\,\sigma _0,\,\beta _0; r, \rho )\) defined by
is a special neighborhood for \(\tilde{\mathcal {F}}\).
By Lemma 9, there exists a special neighborhood \(\mathcal {U}=B(y_{\sigma _0},\,\sigma _0,\,\beta _0;r', \rho )\) such that \(\mathcal {F}\) and \(\tilde{\mathcal {F}}\) are nonzero for \((y,\,\sigma ,\,\beta )\in \overline{B(y_{\sigma _0},\,\sigma _0,\,\beta _0;r', \rho )}\) with \(y\ne y_\sigma \) and \(|(\sigma ,\,\beta )-(\sigma _0,\,\beta _0)|=\rho \). That is, (A5) is satisfied.
Let \(\theta \) be a completing function on \(\mathcal {U}\). It follows from Lemma 10 that \( (\mathcal {F},\,\theta ) \) is homotopic to \((\tilde{\mathcal {F}},\,\theta )\) on \(\mathcal {U}\). It is known that \(C_{2\pi }^1(\mathbb {R};\mathbb {R}^{N})\) has the following isotypical direct sum decomposition
where \(V_0\) is the space of all constant mappings from \(\mathbb {R}\) into \(\mathbb {R}^{N}\), and \(V_k\) with \(k>0\), \(k\in \mathbb {N}\) is the vector space of all mappings of the form
where \(x,\,y\in \mathbb {R}^{N}\). Then \(V_k\), \(k>0,\,k\in \mathbb {N}\), are finite dimensional. Then, (A1) is satisfied.
The verification of (A6) and the computation of the crossing number \(\gamma (y_{\sigma _0},\,\sigma _0,\,\beta _0)\ne 0\) is the same as that in the proof of Theorem 1. We omit the details here. Then by Theorem 2.4 of [6], \( (y_{\sigma _0},\,\sigma _0,\,\beta _0)\) is a bifurcation point of the system (3.27). Consequently, there exists a sequence of non-constant periodic solutions \((x_n,\,\sigma _n,\,\beta _n)\) such that \(\sigma _n\rightarrow \sigma _0\), \(\beta _n\rightarrow \beta _0\) as \(n\rightarrow \infty \), and \(x_n\) is a \(2\pi /\beta _n\)-periodic solution of (1.1) such that \(x_n\) satisfies (1.1) with \(\lim _{n\rightarrow +\infty }\Vert x_n-x_{\sigma _0}\Vert _{C^1}=0\). \(\square \)
4 Global Bifurcation of DAEs with State-Dependent Delays
In this section we use a Rabinowitz-type global Hopf bifurcation theorem (Theorem 2.5 developed in [6]) to describe the maximal continuation of bifurcated periodic solutions with large amplitudes when the bifurcation parameter \(\sigma \) is far away from the bifurcation value. Note that systems (1.1) and (1.5) share the same differential equation for x and differ only in the algebraic equation for the state-dependent delay \(\tau \). Moreover, by Theorems 1 and 2, both systems share the same set of Hopf bifurcation points. In the following, we state results in terms of system (1.1), which are also applicable to system (1.5).
Lemma 11
(Vidossich [17]) Let X be a Banach space, \(v: \mathbb {R}\rightarrow X\) be a \(\mathsf {p}\)-periodic function with the following properties:
-
(i)
\(v\in L_{loc}^1(\mathbb {R},\, X)\);
-
(ii)
there exists \(U\in L^1([0,\,\frac{\mathsf {p}}{2}];\mathbb {R}_+)\) such that \(|v(t)-v(s)|\le U(t-s)\) for almost every (in the sense of the Lebesgue measure) \(s,\,t\in \mathbb {R}\) such that \(s\le t\), \(t-s\le \frac{\mathsf {p}}{2}\);
-
(iii)
\(\int _0^{\mathsf {p}} v(t)\,\mathrm {d}t=0\).
Then
We make the following assumption on f:
-
(S4)
There exists constant \(L_f>0\) such that
$$\begin{aligned} |f(\theta _1,\,\theta _2,\,\sigma )-f(\overline{\theta }_1,\,\overline{\theta }_2,\,\sigma )|\le L_f (|\theta _1-\overline{\theta }_1|+|\theta _2-\overline{\theta }_2|), \end{aligned}$$for every \(\theta _1,\,\theta _2,\,\overline{\theta }_1,\,\overline{\theta }_2,\, \sigma \in \mathbb {R}\).
Lemma 12
Suppose that system (1.1) satisfies the assumption (S4) and x is a nonconstant periodic solution. The following statements are true.
-
(i)
If \(\Vert \tau \Vert _{L^{\infty }}<\frac{1}{2L_f}\), then the minimal period \(\mathsf {p}\) of x satisfies
$$\begin{aligned} \mathsf {p}\ge \frac{2}{1-2L_f\Vert \tau \Vert _{L^{\infty }}} . \end{aligned}$$ -
(ii)
If \(\tau \) is continuously differentiable in \(\mathbb {R}\), then the minimal period \(\mathsf {p}\) of x satisfies
$$\begin{aligned} \mathsf {p}\ge \frac{4}{L_f(2+\Vert \dot{\tau }\Vert _{L^{\infty }})}. \end{aligned}$$ -
(iii)
Suppose there exists a constant \(L_g>0\) such that
$$\begin{aligned} |g(\theta _1,\,\theta _2,\,\sigma )-g(\overline{\theta }_1,\,\overline{\theta }_2,\,\sigma )|\le L_g (|\theta _1-\overline{\theta }_1|+|\theta _2-\overline{\theta }_2|), \end{aligned}$$for every \(\theta _1,\,\theta _2,\,\overline{\theta }_1,\,\overline{\theta }_2,\, \sigma \in \mathbb {R}\). If \(\Vert \dot{x}\Vert _{L^{\infty }}<\frac{1}{L_g}\), then the minimal period \(\mathsf {p}\) of x satisfies
$$\begin{aligned} \mathsf {p}\ge \frac{2(1-L_g\Vert \dot{x}\Vert _{L^{\infty }})}{L_f}. \end{aligned}$$
Proof
Assume that x is a nonconstant periodic solution with minimal period \(\mathsf {p}\). Let \(v(t)=\dot{x}(t)\). Then we have \(\int _0^\mathsf {p} v(t)\mathrm {d}t=0\). For \(s\le t\), by (S4) and the Integral Mean Value Theorem, we have
-
(i)
By (4.1) we have
$$\begin{aligned}&|v(t)-v(s)| \le L_f\Vert \dot{x}\Vert _{L^{\infty }}(t-s)+ L_f\Vert \dot{x}\Vert _{L^{\infty }}(t-s+|\tau (t)-\tau (s)|)\\&\quad \le 2L_f \Vert \dot{x}\Vert _{L^{\infty }} (t-s)+2L_f \Vert {\tau }\Vert _{L^{\infty }} \cdot \Vert \dot{x}\Vert _{L^{\infty }}. \end{aligned}$$Let
$$\begin{aligned} U(t)= 2L_f \Vert \dot{x}\Vert _{L^{\infty }} t+2L_f \Vert {\tau }\Vert _{L^{\infty }} \cdot \Vert \dot{x}\Vert _{L^{\infty }}. \end{aligned}$$Then, by Lemma 11, we obtain
$$\begin{aligned} \mathsf {p}\Vert \dot{x}\Vert _{L^{\infty }}&\le 2 \int _0^{\frac{\mathsf {p}}{2}}U(t)\mathrm {d}t=\frac{\mathsf {p}^2}{4} \cdot 2L_f \Vert \dot{x}\Vert _{L^{\infty }} +\mathsf {p}\cdot 2L_f \Vert {\tau }\Vert _{L^{\infty }} \cdot \Vert \dot{x}\Vert _{L^{\infty }}. \end{aligned}$$If \(\Vert \tau \Vert _{L^{\infty }}<\frac{1}{2L_f}\), then
$$\begin{aligned} \mathsf {p}\ge \frac{2}{ (1-2L_f \Vert {\tau }\Vert _{L^{\infty }})}. \end{aligned}$$ -
(ii)
If \(\tau \) is continuously differentiable in \(\mathbb {R}\), then we have \(\Vert \dot{\tau }\Vert _{L^{\infty }}<\infty \). Moreover, by (4.1) we have
$$\begin{aligned} |v(t)-v(s)|&\le L_f\Vert \dot{x}\Vert _{L^{\infty }}(t-s)+ L_f\Vert \dot{x}\Vert _{L^{\infty }}(t-s+|\tau (t)-\tau (s)|)\\&\le (2 +\Vert \dot{\tau }\Vert _{L^{\infty }}) L_f\cdot \Vert \dot{x}\Vert _{L^{\infty }}(t-s). \end{aligned}$$Let
$$\begin{aligned} U(t)= (2 +\Vert \dot{\tau }\Vert _{L^{\infty }})L_f \cdot \Vert \dot{x}\Vert _{L^{\infty }}t. \end{aligned}$$Then, by Lemma 11, we obtain
$$\begin{aligned} \mathsf {p}\Vert \dot{x}\Vert _{L^{\infty }}&\le 2 \int _0^{\frac{\mathsf {p}}{2}}U(t)\mathrm {d}t=\frac{\mathsf {p}^2}{4} \cdot (2 +\Vert \dot{\tau }\Vert _{L^{\infty }}) L_f\cdot \Vert \dot{x}\Vert _{L^{\infty }}. \end{aligned}$$Therefore,
$$\begin{aligned} \mathsf {p}\ge \frac{4}{ L_f(2 +\Vert \dot{\tau }\Vert _{L^{\infty }})}. \end{aligned}$$ -
(iii)
If g is Lipschitz continuous, then we have
$$\begin{aligned}&|\tau (t)-\tau (s)| \le L_g |x(t)-x(s)|+L_g |x(t-\tau (t))-x(s-\tau (s))|\\&\quad \le L_g\Vert \dot{x}\Vert _{L^{\infty }}(t-s)+L_g \Vert \dot{x}\Vert _{L^{\infty }}(t-s+|\tau (t)-\tau (s)|). \end{aligned}$$If \(\Vert \dot{x}\Vert _{L^{\infty }}<\frac{1}{L_g}\), then we have
$$\begin{aligned} |\tau (t)-\tau (s)| \le \frac{2L_g\Vert \dot{x}\Vert _{L^{\infty }}(t-s)}{1-L_g\Vert \dot{x}\Vert _{L^{\infty }}}. \end{aligned}$$(4.2)$$\begin{aligned} |v(t)-v(s)|&\le L_f\Vert \dot{x}\Vert _{L^{\infty }}(t-s)+ L_f\Vert \dot{x}\Vert _{L^{\infty }}(t-s+|\tau (t)-\tau (s)|)\\&\le 2L_f\cdot \Vert \dot{x}\Vert _{L^{\infty }}(t-s)+ \frac{2L_fL_g\Vert \dot{x}\Vert _{L^{\infty }}^2(t-s)}{1-L_g\Vert \dot{x}\Vert _{L^{\infty }}}\\&=\frac{2L_f \Vert \dot{x}\Vert _{L^{\infty }}}{1-L_g\Vert \dot{x}\Vert _{L^{\infty }}}(t-s). \end{aligned}$$Let
$$\begin{aligned} U(t)= \frac{2L_f \Vert \dot{x}\Vert _{L^{\infty }}}{1-L_g\Vert \dot{x}\Vert _{L^{\infty }}}t. \end{aligned}$$We obtain
$$\begin{aligned} \mathsf {p}\Vert \dot{x}\Vert _{L^{\infty }}&\le 2 \int _0^{\frac{\mathsf {p}}{2}}U(t)\mathrm {d}t=\frac{\mathsf {p}^2}{4} \cdot \frac{2L_f \Vert \dot{x}\Vert _{L^{\infty }}}{1-L_g\Vert \dot{x}\Vert _{L^{\infty }}}, \end{aligned}$$and
$$\begin{aligned} \mathsf {p}\ge \frac{2(1-L_g\Vert \dot{x}\Vert _{L^{\infty }})}{L_f}. \end{aligned}$$\(\square \)
To describe the minimal periods of the periodic solutions near the bifurcation point, we need the following result which was first established in [9] for ordinary differential equations and was extended to other types of delay differential equations in [6, 19].
Lemma 13
Suppose that system (1.1) satisfies (S1–S4). Assume further that there exists a sequence of real numbers \(\{\sigma _k\}_{k=1}^{\infty }\) such that:
-
(i)
For each k, system (1.5) with \(\sigma =\sigma _k\) has a nonconstant periodic solution \(x_k\in C(\mathbb {R};\mathbb {R}^{N+1})\) with the minimal period \(T_k>0,\) and one of the conditions (i), (ii) and (iii) at Lemma 12 is satisfied by \((x_k,\,\tau _k)\);
-
(ii)
\(\lim \limits _{k\rightarrow \infty }\sigma _k=\sigma _0\in \mathbb {R}\), \(\lim \limits _{k\rightarrow \infty }T_k=T_0<\infty \), and \(\lim \limits _{k\rightarrow \infty }\Vert x_k-x_0\Vert =0\), where \(x_0:\mathbb {R}\rightarrow \mathbb {R}^{N}\) is a constant map with the value \(x_{0}\).
Then \(x_0\) is a stationary state of (1.1) and there exists \(m\ge 1,\,m\in \mathbb {N}\) such that \(\pm im\,{2\pi }/{T_0}\) are the roots of the characteristic equation (2.2) with \(\sigma =\sigma _0\).
Proof
By Lemma 12 and the uniform convergence of \(\{(x_k,\,\sigma _k,\,T_k)\}_{k=1}^\infty \) we conclude that there exists \(T^*>0\) such that \(T_k\ge T^*\) and therefore \(T_0\ge T^*\). We can show that \((x_0,\,\sigma _0)\) is a stationary state of (1.5), and that the following linear system
has a nonconstant periodic solution, the proofs of which are just simplified versions of the proof for Lemma 4.3 in [6] without the equations for \(\tau _k\). Hence we omit the details here. Then by Lemma 4, there exists \(m\ge 1,\, m\in \mathbb {N}\), such that \(\pm im\,2\pi /T_0\) are characteristic values of (2.2). This completes the proof. \(\square \)
Now we can describe the relation between \(2\pi /\beta _k\) and the minimal period of \(u_k\) in Theorem 1.
Theorem 3
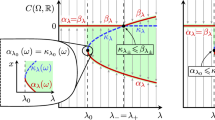
Assume (S1–S4) hold and every point in the sequence \(\{(x_k,\,\tau _k)\}_{k=1}^\infty \) at Theorem 1 satisfies one of the conditions among (i), (ii) and (iii) at Lemma 12, then every limit point of the minimal period of \(x_k\) as \(k\rightarrow +\infty \) is contained in the set
Moreover, if \(\pm i\,m\,n\beta _0\) are not characteristic values of \((x_0,\,\sigma _0)\) for any integers \(m,\, n\in \mathbb {N}\) such that \(m\,n>1\), then \(2\pi /\beta _k\) is the minimal period of \(u_k(t)\) and \(2\pi /\beta _k\rightarrow 2\pi /\beta _0\) as \(k\rightarrow \infty \).
Proof
Let \(T_k\) denote the minimal period of \(x_k(t)\). Then there exists a positive integer \(n_k\) such that \(2\pi /\beta _k=n_k T_k\). Since \(T_k\le 2\pi /\beta _k\rightarrow 2\pi /\beta _0\) as \(k\rightarrow \infty \), there exists a subsequence \(\{T_{k_j}\}_{j=1}^{\infty }\) and \(T_0\) such that \(T_0=\lim _{j\rightarrow \infty }T_{k_j}\). Since \(2\pi /\beta _{k_j}\rightarrow 2\pi /\beta _0\), \(T_{k_j}\rightarrow T_0\) as \(j\rightarrow \infty ,\)\(n_{k_j}\) is identical to a constant n for k large enough. Therefore, \(2\pi /\beta _0=n T_0\). Thus \(T_{k_j}\rightarrow 2\pi /(n\beta _0)\) as \(j\rightarrow \infty \). By Lemma 13, \(\pm im\,{2\pi }/{T_0}=\pm im\,n\beta _0\) are characteristic values of \((x_0,\,\sigma _0)\) for some \(m\ge 1,\,m\in \mathbb {N}\).
Moreover, if \(\pm i\,m\,n\beta _0\) are not characteristic values of \((u_0,\,\sigma _0)\) for any integers \(m\in \mathbb {N}\) and \(n\in \mathbb {N}\) with \(mn>1\), then \(m=n=1\). Therefore, for k large enough \(n_{k_j}=1\) and \(2\pi /\beta _k=T_k\) is the minimal period of \(x_k(t)\) and \(2\pi /\beta _k\rightarrow 2\pi /\beta _0\) as \(k\rightarrow \infty \). This completes the proof. \(\square \)
The following lemma shows that we can locate all the possible Hopf bifurcation points of system (1.1) with state-dependent delay at the centers of its corresponding formal linearization. Since the proof is similar to that for Lemma 4.5 in [6], we omit the details here.
Lemma 14
Assume (S1–S3) hold. If \((x_0,\,\sigma _0)\) is a Hopf bifurcation point of system (1.1), then it is a center of (2.1).
Now we are in the position to consider the global Hopf bifurcation problem of system (1.1). Letting \((x(t),\tau (t))=(y(\frac{2\pi }{\mathsf {p}}t),\,z(\frac{2\pi }{\mathsf {p}}t))\), we can reformulate the problem as a problem of finding \(2\pi \)-period solutions to the following equation:
where the z satisfies the algebraic equation \(z(t)=g(y(t),y(t-\frac{\mathsf {p}}{2\pi }z(t)),\,\sigma )\). Accordingly, the formal linearization (2.1) becomes
Using the same notations as in the proof of Theorem 1, we can define
Then the following system
is equivalent to (4.4) and
is equivalent to (4.5). Let \(\mathcal {S}\) denote the closure of the set of all nontrivial periodic solutions of system (4.6) in the space \(V\times \mathbb {R}\times \mathbb {R}_+\), where \(\mathbb {R}_+\) is the set of all nonnegative reals. It follows from Lemma 12 that the constant solution \((x_0,\,\sigma _0,\,0)\) does not belong to this set if the sequence \(\{(x_k,\,\tau _k)\}_{k=1}^\infty \) in Theorem 1 satisfies one of the conditions among i), ii) and iii) at Lemma 12. Consequently, we can assume that problem (4.6) is well posed on the whole space \(V\times \mathbb {R}^2\), in the sense that if \(\mathcal {S}\) exists in \(V\times \mathbb {R}^2\), then it must be contained in \(V\times \mathbb {R}\times \mathbb {R}_+\).
Then by the global Hopf bifurcation theorem 2.5 developed in [6] and with similar arguments leading to Theorem 4.6 in [6], we obtain the following global Hopf bifurcation theorem for system (1.1) with state-dependent delay.
Theorem 4
Suppose that system (1.1) satisfies (S1–S4) and (S3) holds at every center of (4.7). Assume that all the centers of (4.7) are isolated and every periodic solution x of system (1.1) satisfies one of the conditions among (i), (ii) and (iii) at Lemma 12. Let \(\mathcal {M}\) be the set of trivial periodic solutions of (4.6) and assume that \(\mathcal {M}\) is complete. If \((x_0,\,\sigma _0,\,\mathsf {p}_0)\in \mathcal {M}\) is a bifurcation point, then either the connected component \({C}(x_0,\,\sigma _0,\,\mathsf {p}_0)\) of \((x_0,\,\sigma _0,\,\mathsf {p}_0)\) in \(\mathcal {S}\) is unbounded, or
where \(\mathsf {p}_i\in \mathbb {R}_+\), \((x_i,\,\sigma _i,\,\mathsf {p}_i)\in M\), \(i=0,\,1,\,2,\ldots , q\). Moreover, in the latter case, we have
where \(\gamma (x_i,\,\sigma _i,\,2\pi /\mathsf {p}_i)\) is the crossing number of \((x_i,\,\sigma _i,\,\mathsf {p}_i)\) defined by (2.5) and
5 Global Hopf Bifurcation of a Model of Regulatory Dynamics
We consider the following extended Goodwin’s model for regulatory dynamics:
where x is the concentration of mRNA, y is the concentration of the related protein; z is the concentration of an active enzyme which controls the level of the metabolite functioning as repressor at the DNA level; \(\mu _m\), \(\mu _p\) and \(\mu _e\) are nonnegative degradation rates; \(\alpha _m\), \(\alpha _p\) and \(\alpha _e\) are positive coefficients for the inhibition/activation terms; c and \(\tilde{z}\) are positive constants; h is an even positive integer. The Goodwin’s model [3] without delay (\(\tau =0\)) has been extensively studied in system biology modeling various regulatory dynamics. Note that if we freeze the delay \(\tau \) at the stationary state in system (5.1), it becomes the classic Goodwin’s model without delay.
We are interested in the onset and termination of each Hopf bifurcation branch of periodic solutions which are described as one of the alternatives given in Theorem 4. To be specific, we need to obtain the boundedness or unboundedness of the connected component of the pairs of nonconstant periodic solution and parameter in the product space of the state and the parameter space. In the following, we first analyze the local Hopf bifurcation of system (5.1) and then consider the boundedness of periodic solutions of system (5.1) for a global Hopf bifurcation in light of Theorem 4.
5.1 Local Hopf Bifurcation
Note that h is an even positive integer. Every stationary point \((x,\,y,\,z)\) of System (5.1) satisfies that
and \((x,\,y,\,z)=\left( x_0,\,\frac{\alpha _p}{\mu _p} x_0,\,\frac{\alpha _e\alpha _p}{\mu _e\mu _p} x_0\right) \), where by Descartes’ rule of signs we know that \(x=x_0\) is the unique solution of
Freezing the delay of system (5.1) at \(\tau =0\) and linearizing the resulting nonlinear system at the stationary state \((x,\,y,\,z)=\left( x_0,\,\frac{\alpha _p}{\mu _p} x_0,\,\frac{\alpha _e\alpha _p}{\mu _e\mu _p} x_0\right) \) leads to the characteristic polynomial
which has a unique negative root and a pair of imaginary roots. In the following, we discuss the existence of purely imaginary eigenvalues as the parameter \(\alpha _m\) varies. We have
Lemma 15
Let \((x,\,y,\,z)\) be a stationary state of system (5.1). Then the following equation of \((x,\,\alpha _m)\)
has a unique solution for \((x,\,\alpha _m)=(x^*,\,\alpha _m^*)\).
Proof
Noticing that by the second equation of (5.4), \(\frac{\alpha _m}{x}=\mu _m\left( 1+\left( \frac{\alpha _e\alpha _p}{\mu _e\mu _p\tilde{z}}x\right) ^{h}\right) \), we rewrite the first equation of (5.4) into
which has a unique positive solution for \(x^h\) and hence for x with \(x=x^*\) for some \(x^*>0\). Then \(\alpha _m=\alpha _m^*\) with \(\alpha _m^*=x^*\mu _m\left( 1+\left( \frac{\alpha _e\alpha _p}{\mu _e\mu _p\tilde{z}}x^*\right) ^{h}\right) \). The solution of (5.4) is \((x,\,\alpha _m)=(x^*,\,\alpha _m^*)\). \(\square \)
Lemma 16
Let \(\alpha _m^*\) be as in Lemma 15 and \(\lambda =u\pm iv\) be the imaginary roots of the characteristic polynomial at (5.3). Then u and v are continuously differentiable with respect to \(\alpha _m\) and \(u=0\) if and only if \(\alpha _m=\alpha _m^*\). Moreover,

Proof
Let \((x,\,y,\,z)=\left( x_0,\,\frac{\alpha _p}{\mu _p} x_0,\,\frac{\alpha _e\alpha _p}{\mu _e\mu _p} x_0\right) \) be a stationary state of System (5.1) and let
Noticing that \(z=\frac{\alpha _e\alpha _p}{\mu _e\mu _p} x_0\) and
we know that F is continuously differentiable with respect to \((\lambda ,\,\alpha _m)\). Let \((\lambda ,\,\alpha _m)\) be such that \(F(\lambda ,\,\alpha _m)=0\). Then we have
Next we show that \(\frac{\mathrm {d}F}{\mathrm {d}\lambda }\ne 0\) at every solution of \(F(\lambda ,\,\alpha _m)=0\). Otherwise, F has a repeated root and the root satisfies
which leads to two distinct negative roots:
This is a contradiction. Then by the Implicit Function Theorem, \(\lambda \) is continuously differentiable with respect to \(\alpha _m\).
Next we bring \(\lambda =u+iv\) into the characteristic polynomial at (5.3) we have
where \(c_0=\frac{h\alpha _m{z}^{h-1}}{\tilde{z}^h\left( 1+\left( \frac{z}{\tilde{z}}\right) ^h\right) ^2}=\frac{h\alpha _m^3}{\tilde{z}^h\mu _m^2}\cdot \left( \frac{\alpha _e\alpha _p}{\mu _e\mu _p}\right) ^{h-1}{x}^{h-3}.\) If \(u=0\), then (5.5) leads to
where x satisfies \(\mu _mx= \frac{\alpha _m}{1+\left( \frac{\alpha _e\alpha _p}{\mu _e\mu _p\tilde{z}}x\right) ^{h}}.\) By Lemma 5.4, we have \(\alpha _m=\alpha _m^*.\) By the uniqueness of \(\alpha _m^*\), \(u=0\) if and only if \(\alpha _m=\alpha _m^*\).
To compute \(\frac{\mathrm {d}u}{\mathrm {d}\alpha _m}\) at \(\alpha _m=\alpha _m^*\), we take derivatives with respect to \(\alpha _m\) on both sides of the equations at (5.5) and then letting \(u=0\), we obtain
Then we have

By the second equation of (5.6), we have

Noticing that
can be regarded as a fourth order polynomial of \(x^h\) with positive coefficients, and that \(\frac{\mathrm {d}x_0}{\mathrm {d}\alpha _m}=\frac{1}{\mu _m+\mu _m(h+1)\left( \frac{\alpha _e\alpha _p}{\mu _e\mu _p\tilde{z}}\right) ^hx_0^h}>0\), we have

hence  . \(\square \)
. \(\square \)
Notice that  implies the crossing number at the stationary point \((x(\alpha _m^*),\,y(\alpha _m^*),\,z(\alpha _m^*))\) satisifes:
implies the crossing number at the stationary point \((x(\alpha _m^*),\,y(\alpha _m^*),\,z(\alpha _m^*))\) satisifes:
Moreover, we can check that conditions (S1–S3) for Theorem 1 are satisfied. Then we have the following local Hopf bifurcation theorem for system (5.1).
Theorem 5
Let \(\alpha _m^*\) be as in Lemma 15. Then system (5.1) undergoes Hopf bifurcation near the stationary point \((x(\alpha _m^*),\,y(\alpha _m^*),\,z(\alpha _m^*))\) as \(\alpha _m\) varies near \(\alpha _m^*\).
5.2 Global Hopf Bifurcation
In this section, we develop a global Hopf bifurcation theory for system (5.1). By Lemma 5.4 and Theorem 5, we know that \((x(\alpha _m^*),\,y(\alpha _m^*),\,z(\alpha _m^*))\) is the only Hopf bifurcation point and is an isolated center. To apply the global Hopf bifurcation Theorem 4, it remains to check condition (S4) and one of the conditions among (i), (ii) and (iii) at Lemma 12. We first consider the boundedness of periodic solutions.
Theorem 6
Let \((x,\,y,\,z)\) be a periodic solution of system (5.1). Then \((x,\,y,\,z)\) satisfies for every \(t\in \mathbb {R}\),
Proof
Note that \(h>0\) is an even integer. We have \(\dot{x}(t)\le -\mu _m x(t)+\alpha _m\), which by Gronwall’s inequality leads to
Since x is periodic, there exists \(p>0\) such that \(x(t)=x(t+p)\) for every \(t\in \mathbb {R}\) and for every \(n\in \mathbb {N}\), we have \(x(t)=x(t+np)\). Then for every \(t\in \mathbb {R}\) we have \(x(t)=x(t+np)\le e^{-\mu _m(t+np)}x(0)+\frac{\alpha _m}{\mu _m}\left( 1-e^{-\mu _m (t+np)}\right) \rightarrow \frac{\alpha _m}{\mu _m}\) as \(n\rightarrow \infty .\) Therefore, we have \(x(t)\le \frac{\alpha _m}{\mu _m}\) for every \(t\in \mathbb {R}\).
By the same token, with \(x(t-\tau )\le \frac{\alpha _m}{\mu _m}\), we obtain from the second equation of system (5.1) that \(y(t)\le \frac{\alpha _p\alpha _m}{\mu _p\mu _m}\), \(t\in \mathbb {R}\), and subsequently from the third equation of system (5.1) that \(z(t)\le \frac{\alpha _e\alpha _p\alpha _m}{\mu _e\mu _p\mu _m}\) for every \(t\in \mathbb {R}\).
To obtain lower bounds of \(x,\,y\) and z, let \(\bar{x}=-x\), \(\bar{y}=-y\) and \(\bar{z}=-z\). Then system (5.1) becomes
We have \(\dot{\bar{x}}(t) < -\mu _m \bar{x}(t)\), which leads to
Note that \(\bar{x}\) is also p-periodic. For every \(t\in \mathbb {R}\) we have
Therefore, we have \(\bar{x}(t)\le 0\) for every \(t\in \mathbb {R}\). By the same token, with \(\bar{x}(t-\tau )\le 0\), we obtain from the second equation of system (5.8) that \(\bar{y}(t)\le 0\), \(t\in \mathbb {R}\), and subsequently from the third equation of system (5.8) that \(\bar{z}(t)\le 0\) for every \(t\in \mathbb {R}\). Then by the definition of \((\bar{x},\,\bar{y},\,\bar{z})\), we obtain that for every \(t\in \mathbb {R}\), \(x(t)\ge 0,\,y(t)\ge 0,\,z(t)\ge 0.\)
If there exists \(t_0\in \mathbb {R}\) such that \(x(t_0)=0\), then by the first equation of system (5.1) we have \(\dot{x}(t_0)>0\). By the continuity of \(\dot{x}\), there exists \(\delta >0\) such that x is strictly increasing in \((t_0-\delta ,\,t_0+\delta )\). so that \(x(t)<0\) for \(t\in (t_0-\delta ,\,t_0)\). This is a contradiction. By the same token we have \(y(t)>0\) and \(z(t)>0\) for every \(t\in \mathbb {R}\). \(\square \)
Lemma 17
Let \(f_0: \mathbb {R}^3\times \mathbb {R}^3\times \mathbb {R}\rightarrow \mathbb {R}^3\) be defined by
where \(\theta _1=(x_1,\,y_1,\,z_1)\) and \(\theta _2=(x_2,\,y_2,\,z_2)\). Then \(f_0\) is Lipschitz continuous with a Lipschitz constant
where \(h_0=\frac{h\left( 1-\frac{2}{h+1}\right) ^{\frac{h-1}{h}}}{\left( 1+\frac{h-1}{h+1}\right) ^2}.\)
Proof
We use the Mean Value theorem for integrals to obtain a Lipschitz constant. Let \(\tilde{\theta _1}=(\tilde{x}_1,\,\tilde{y}_1,\,\tilde{z}_1)\) and \(\tilde{\theta _2}=(\tilde{x}_2,\,\tilde{y}_2,\,\tilde{z}_2)\). Then we have
We have
Noticing that the map \(\mathbb {R}\ni t\rightarrow \frac{t^{h-1}}{(1+t^h)^2}\) vanishes at \(t=0\) and \(t=\infty \) and that
if and only if \(t=\pm \left( 1-\frac{2}{h+1}\right) ^{\frac{1}{h}}\), we obtain that \(\sup _{z_2}\left| \frac{\mathrm {d}}{\mathrm {d}z_2}\frac{\alpha _m}{1+\left( \frac{z_2}{\,\tilde{z}}\right) ^h}\right| =\frac{\alpha _mh_0}{\tilde{z}}\) with
and the supremum is achieved at \(\frac{z_2}{\,\tilde{z}}=\left( 1-\frac{2}{h+1}\right) ^{\frac{1}{h}}\). Then by (5.10) \(f_0\) is Lipschitz continuous with a Lipschitz constant \(L_f=\max \left\{ \mu _m,\,\mu _p,\,\mu _e,\,\alpha _p,\,\alpha _e,\,\frac{\alpha _mh_0}{\tilde{z}}\right\} .\)\(\square \)
To apply the global Hopf bifurcation theorem, we also use Lemma 12 to show the closure of all nontrivial periodic solutions bifurcating from the stationary point \((x(\alpha _m^*),\,y(\alpha _m^*),\,z(\alpha _m^*))\) will not include constant solution with zero period.
Lemma 18
Let \((x,\,y,\,z)\) be a periodic solution of system (5.1). If \(\alpha _m<\frac{1}{c}\), then \(\tau :\mathbb {R}\rightarrow \mathbb {R}\) given by \(\tau (t)=c(x(t)-x(t-\tau (t)))\) exists and is continuously differentiable.
Proof
The existence and continuity of \(\tau \) follows from Lemma 1. Let \(f_1: \mathbb {R}^2\rightarrow \mathbb {R}\) be defined by
Then \(f_1\) is continuously differentiable with respect to \((\tau ,\,t)\). Moreover, by (5.11) we have
By the first equation of system (5.1) and by Lemma 6 we have for every \(t\in \mathbb {R}\), \(\dot{x}(t)<\alpha _m\) and
Then we have \(|\dot{x}|<\alpha _m\) and by (5.11) we have
By the Implicit Function Theorem, \(\tau \) is continuously differentiable at \(t\in \mathbb {R}\). \(\square \)
It follows from Lemma 18 and (ii) of Lemma 12 that if \(\alpha _m<\frac{1}{c}\), then the period \(\mathsf {p}\) of every nonconstant periodic solution satisfies \(\mathsf {p}\ge \frac{4}{L_f(2+\Vert \dot{\tau }\Vert _{L^\infty })}>0\).
Now we are in the position to state the global Hopf bifurcation theorem.
Theorem 7
Let \(\alpha _m^*\) be as in Lemma 15 and \(p^*=\frac{2\pi }{v^*}\) where \(v^*>0\) is the imaginary part of eigenvalue of the formal linearization of system (5.1) at \(\alpha _m=\alpha _m^*\). Suppose that \(\alpha _m^*<\frac{1}{c}\). There exists a connected component \(\mathcal {C}\) of the closure of all nonconstant periodic solution of system (5.1) bifurcating from \((\alpha _m^*,\,p^*,\,x(\alpha _m^*),\,y(\alpha _m^*),\,z(\alpha _m^*))\in \mathbb {R}^2\times C(\mathbb {R};\mathbb {R}^3)\), which satisfies that
- \(\mathrm{(i)}\) :
-
either the projection of \(\mathcal {C}\) onto the parameter space of the period \(\mathsf {p}\) is unbounded.
- \(\mathrm{(ii)}\) :
-
or the projection of \(\mathcal {C}\) onto the parameter space of \(\alpha _m\) does not cross \(\alpha =0\) but is not contained in any compact subset of the interval \((0,\,\frac{1}{c})\).
Proof
We first show that if \(\alpha _m=0\), system (5.1) has no nonconstant periodic solutions. Otherwise, let \((x,\,y,\,z)\) be a nonconstant periodic solution with \(\alpha _m=0\). Then from system (5.1) \(\dot{x}=-\mu _mx\) implies that \(x=0\) and subsequently \(y=z=0\). This is a contradiction. \(\square \)
In the following we consider \(\alpha _m\) in \((0,\,\frac{1}{c})\) and introduce the following change of variables:
where q is an increasing function of \(\alpha \) with \(\lim _{\alpha \rightarrow -\infty }q(\alpha )=0\) and \(\lim _{\alpha \rightarrow +\infty }q(\alpha )=\frac{1}{c}\). Then system (5.1) is rewritten as
with \(\alpha \in \mathbb {R}\) and \(\alpha ^*=q^{-1}(\alpha _m^*)\) the critical value of \(\alpha \) for a unique Hopf bifurcation point. By Theorem 5 There exists a connected component \(\mathcal {C}_0\) of the closure of all nonconstant periodic solution of system (5.13) bifurcating from the stationary point \((\alpha ^*,\,p^*,\,x(\alpha ^*),\,y(\alpha ^*),\,z(\alpha ^*))\in \mathbb {R}^2\times C(\mathbb {R};\mathbb {R}^3)\).
By Lemma 17, condition (S4) is satisfied by system (5.13). By Lemma 18, the function \(\tau \) defined by \(\tau (t)=c(x(t)-x(t-\tau (t)))\) for a nonconstant periodic solution \((x,\,y,\,z)\) of system (5.13) is continuously differentiable. Hence by Lemma 12, the period \(\mathsf {p}\) of every nonconstant periodic solution \((x,\,y,\,z)\) of system (5.13) is positive. Notice that \((\alpha ^*,\,p^*,\,x(\alpha ^*),\,y(\alpha ^*),\,z(\alpha ^*))\) is the only bifurcation point of system (5.13), by Theorem 4, the connected component \(\mathcal {C}_0\) is unbounded in \(\mathbb {R}^2\times C(\mathbb {R};\mathbb {R}^3)\).
Notice that by Theorem 6, the projection of \(\mathcal {C}_0\) onto the space of \((x,\,y,\,z)\in C(\mathbb {R};\mathbb {R}^3)\) is bounded. The unboundedness of \(\mathcal {C}_0\) is either because of the unbounded projection onto the parameter space of the period \(\mathsf {p}\), or the projection of \(\mathcal {C}\) onto the parameter space of \(\alpha \).
Notice that q induces a homeomorphism \((q,\,id): \mathbb {R}^2\times C(\mathbb {R};\mathbb {R}^3)\rightarrow \mathbb {R}^2\times C(\mathbb {R};\mathbb {R}^3)\) defined by
The image \(\mathcal {C}=(q,\,id)(\mathcal {C}_0)\) of \(\mathcal {C}_0\) under \((q,\,id)\) is a connected component of the closure of all nonconstant periodic solution of system (5.1) bifurcating from the bifurcation point
which satisfies that either the projection of \(\mathcal {C}\) onto the parameter space of the period \(\mathsf {p}\) is unbounded, or the projection of \(\mathcal {C}\) onto the parameter space of \(\alpha _m\) does not cross the hyperplane \(\alpha _m=0\) but is not contained in any compact subset of the interval \((0,\,\frac{1}{c})\). \(\square \)
6 Concluding Remarks
Motivated by the extended Goodwin’s model with a state-dependent delay governed by an algebraic equation, we developed global Hopf bifurcation theories for differential-algebraic equations with state-dependent delay, using the \(S^1\)-equivariant degree. This is based on the framework described in [6] where the technique of formal linearization is employed to obtain auxiliary linear systems at the stationary states which indicate local and global Hopf bifurcation using a homotopy argument. We remark that the work discussed two types of state-dependent delays: the one in system (1.5) depends on the state variable explicitly and the other in system (1.1) depends on the state variable implicitly. We also remark that the local and global Hopf bifurcation theory we developed for system (1.5) is also applicable for systems with the delay given by \(\tau (t)=h(x_t)\) where h is a function of \(x_t(s)=x(t+s), -r\le s\le 0,\,r>0\), provided that \(\tau \) is continuous.
The local and global Hopf bifurcation theories are applied to the extended Goodwin’s model which describes intracellular processes in the genetic regulatory dynamics. We obtained two alternatives for the connected component \(\mathcal {C}\) of periodic solutions in the Fuller space \(\mathbb {R}^2\times C(\mathbb {R};\mathbb {R}^3)\). Namely, the projection of \(\mathcal {C}\) onto the parameter space of the period \(\mathsf {p}\) is unbounded, or the projection onto the parameter space of \(\alpha _m\) is not contained in any compact subset of the interval \((0,\,\frac{1}{c})\). We remark that in the previous case, there exists a sequence of periodic solutions with periods going to \(\infty \). From (4.6), system (5.1) can be represented as
where x is normalized to be \(2\pi \)-periodic. Notice from the definition of \(\mathscr {N}_0\) at (2.7) that \(\mathsf {p}\) appears only in the time domain of \(\mathscr {N}_0\). Note also that the periodic solutions are uniformly bounded with \(\alpha _m\in (0,\,\frac{1}{c})\). Then with \(\mathsf {p}\rightarrow \infty \), this alternative implies the possibility that the system has a sequence of nonconstant periodic solutions with the limiting profile satisfying the algebraic equation \(\mathscr {N}_0(x,\,\alpha _m,\,\mathsf {p})=0.\) See ([10,11,12]) for a discussion of limiting profiles for differential equations with state-dependent delays.
If the projection of \(\mathcal {C}\) onto the parameter space of the period \(\mathsf {p}\) is bounded, we have the latter alternative that the projection of \(\mathcal {C}\) onto the parameter space of the period \(\alpha _m\) is not contained in any compact subset of the interval \((0,\,\frac{1}{c})\). Since \(\mathcal {C}\) will not cross the hyperplane \(\alpha _m=0\), and will not blow up at \(\alpha _m=\frac{1}{c}\) with the boundedness of the solutions and periods, \(\mathcal {C}\) must cross the hyperplane \(\alpha _m=\frac{1}{c}\) leaving the solutions at \(\alpha _m\ge \frac{1}{c}\) out of the scope of the discussion.
We also remark that the state-dependent delay in system (1.5) may be negative or positive and is not a priori advanced or retarded type delay differential equations. It remains open to investigate this type of systems in general settings for a qualitative theory including existence and uniqueness of solutions. For systems with mixed type constant delays, see, among many others [13, 14].
References
Balanov, Z., Hu, Q., Krawcewicz, W.: Global Hopf bifurcation of differential equations with threshold-type state-dependent delay. J. Differ. Equ. 257, 2622–2670 (2014)
Cooke, K., Huang, W.: On the problem of linearization for state-dependent delay differential equations. Proc. Am. Math. Soc. 124(5), 1417–1426 (1996)
Goodwin, B.: Oscillatory behavior in enzymatic control processes. Adv. Enzym. Regul. 3, 425–438 (1965)
Hartung, F., Krisztin, T., Walther, H.-O., Wu, J.: Chapter 5: Functional differential equations with state-dependent delays: theory and applications. In: CaÑada, P.D.A., Fonda, A. (eds.) Handbook of Differential Equations: Ordinary Differential Equations, vol. 3, pp. 435–545. North-Holland, Amsterdam (2006)
Hu, Q.: A model of regulatory dynamics with threshold type state-dependent delay. Math. Biosci. Eng. (2017, accepted)
Hu, Q., Wu, J.: Global Hopf bifurcation for differential equations with state-dependent delay. J. Differ. Equ. 248(12), 2801–2840 (2010)
Insperger, T., Stépán, G., Turi, J.: State-dependent delay in regenerative turning processes. Nonlinear Dyn. 47, 275–283 (2007)
Krawcewicz, W., Wu, J.: Theory of Degrees with Applications to Bifurcations and Differential Equations, Canadian Mathematical Society Series of Monographs and Advanced Texts. Wiley, New York (1997)
Mallet-Paret, J., Yorke, A.J.: Snakes: oriented families of periodic orbits, their sources, sinks, and continuation. J. Differ. Equ. 43, 419–450 (1982)
Mallet-Paret, J., Nussbaum, R.: Boundary layer phenomena for differential-delay equations with state-dependent time lags, I. Arch. Ration. Mech. Anal. 120(2), 99–146 (1992)
Mallet-Paret, J., Nussbaum, R.: Boundary layer phenomena for differential-delay equations with state dependent time lags: II. J. Reine Angew. Math. 477, 129–197 (1996)
Mallet-Paret, J., Nussbaum, R.: Boundary layer phenomena for differential-delay equations with state-dependent time lags: III. J. Differ. Equ. 189(2), 640–692 (2003)
Mallet-Paret, J.: The Fredholm alternative for functional differential equations of mixed type. J. Dyn. Differ. Equ. 11, 1–47 (1999)
Rustichini, A.: Hopf bifurcation for functional differential equations of mixed type. J. Dyn. Differ. Equ. 1, 145–177 (1989)
Smith, H.: Structured population models, threshold-type delay and functional-differential equations. Delay Differ. Equ. AMS, IA 1992, 52–64 (1991)
Smith, H.L.: Reduction of structured population models to threshold-type delay equations and functional differential equations: a case study. Math. Biosci. 113(1), 1–23 (1993)
Vidossich, V.: On the structure of periodic solutions of differential equations. J. Differ. Equ. 21, 263–278 (1976)
Walther, H.: Stable periodic motion of a system using echo for position control. J. Dyn. Differ. Equ. 15(1), 143–223 (2003)
Wu, J.: Global continua of periodic solutions to some differential equations of neutral type. Tôhoku Math. J. 45, 67–88 (1993)
Acknowledgements
The author would like to thank an anonymous referee for the detailed and constructive comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hu, Q. Global Hopf Bifurcation for Differential-Algebraic Equations with State-Dependent Delay. J Dyn Diff Equat 31, 93–128 (2019). https://doi.org/10.1007/s10884-017-9640-0
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10884-017-9640-0