1 Introduction

The two-sided assembly lines appear commonly in plants which produce large-sized products, such as automobiles and domestic products, replacing traditional one-sided assembly lines. They use both (left and right) sides of the line in parallel, making it possible to decrease the line length, reduce the throughput time, cut down the cost of tools and fixtures, and lessen material handling.

The two-sided assembly line balancing problem (TALBP) belongs to the class of job scheduling problems (Huang and Yin 2004; Huang and Wang 2006) and has proven to be NP-hard (Scholl and Becker 2006). Thus, there does not exist polynomial time exact algorithm for solving it unless \(P=NP\). During the last two decades, a large number of researchers have extensively studied the TALBP problem. For example, Bartholdi first studied the TALBP problem in 1993, considering minimizing the number of stations as the objective based on a simple assignment rule (Bartholdi 1993). Lee et al. (2001) developed a group assignment procedure for TALBP, assigning task groups instead of individual tasks with the objective of maximizing work relatedness and work slackness. Hu et al. developed a station-oriented enumerative assignment procedure based on the Hoffman heuristic to solve the TALBP (Hu et al. 2008). The experimental results verified that the proposed procedure performed well. Özcan and Toklu (2009c) presented a pre-emptive goal programming model for precise goals and fuzzy goals, respectively, for TALBP. The proposed mathematical model aims to minimize the number of mated-stations and the secondary objective is to minimize the number of stations for a given cycle time with zoning constraints.

Meanwhile, metaheuristic based heuristics have shown to be a feasible way to find high quality solutions with a reasonable time for the TALBP. Simaria and Vilarinho proposed an ant colony optimization algorithm to address the mixed-model of TALBP with the precedence, zoning, capacity, side and synchronism constraints and the objective of minimizing the number of workstations (Simaria and Vilarinho 2009). The results showed that the proposed procedure is superior to the procedure of Lee et al. (2001) for a single model for TALBP. Kim et al. (2000) addressed the TALBP using the genetic algorithm (GA). The objective was to minimize the number of stations within a given cycle time with positional constraints. Özcan and Toklu (2009a) proposed a tabu search algorithm for the TALBP with the objective of minimizing the number of stations and the smoothness index. Özcan and Toklu presented a simulated annealing algorithm for the mixed-model of TALBP with the main objective of minimizing the number of mated-stations and the secondary objective of minimizing the number of operators, considering two performance criteria simultaneously: maximizing the weighted line efficiency and minimizing the weighted smoothness index (Özcan and Toklu 2009b). Özbakyr and Tapkan presented a bees algorithm to solve TALBP with and without zoning constraints in order to minimize the number of stations for a given cycle time. The results showed that the proposed bees algorithm outperformed the compared reference algorithms for most of the tested problems (Özbakir and Tapkan 2011). Taha et al. developed a genetic algorithm (GA) to solve TALBP, where a station oriented procedure was proposed to assign tasks to mated-stations and these rules were shown to be effective especially for large problem instances. The results showed that the proposed GA found the best solution for more than 90 % of the test problems (Taha et al. 2011). Khorasanian et al. (2013) suggested a performance criterion called assembly line tasks consistency to calculate the average relationship between the tasks assigned to the stations. They proposed a simulated annealing algorithm to solve TALBP with and without considering the relationships between tasks. The computational results showed that the proposed simulated annealing algorithm outperformed the compared reference algorithms and found five new best solutions for the number of stations performance criterion and ten new best solutions for the number of mated-stations performance criterion for the tested public benchmark instances (Khorasanian et al. 2013).

A new family of assembly line balancing problems, called Time and Space constrained Assembly Line Balancing Problem (TSALBP), considers space limitations in addition to the common constraints in Simple Assembly Line Balancing Problem (SALBP) (Bautista and Pereira 2007). Although the acronym TSALBP is very similar to TALBP, they possess very different natures.

Recently, the general path relinking (PR) framework (Glover 1997; Glover et al. 2000) has attracted increasing attention in the community of combinatorial optimization, and shows outstanding performances in solving a number of hard problems, such as unconstrained binary quadratic optimization (Wang et al. 2012), multiple-level warehouse layout (Zhang and Lai 2006), capacitated clustering (Deng and Bard 2013), and multi-depot periodic vehicle routing (Rahimi-Vahed et al. 2013). In this paper, we introduce an effective path relinking algorithm for solving the TALBP which relies on both a solution relinking procedure and a local search procedure. To the best of our knowledge, this is the first path relinking algorithm for solving the TALBP problem. Assessed on a set of 45 benchmark instances commonly used in the literature, the proposed algorithm proves highly effective compared to the state-of-the-art algorithms in the literature, by improving the best solutions for one instance, and obtaining comparable or even competitive results compared with four state-of-the-art reference algorithms in the literature.

The rest of the paper is organized as follows. In Sect. 2, we describe in detail the TALBP problem. In Sect. 3, our proposed MN-PR algorithm is given and each main component of the algorithm is described in details. In Sect. 4, we show our computational results and comparisons with the current best performing algorithms in the literature. In Sect. 5, we investigate the significance of some key ingredients of our MN-PR algorithm, before concluding the paper in Sect. 6.

2 Problem description

Different from the single assembly line, a two-sided assembly line has a mated station for each cycle time. Thus, there are two operators working at the opposite sides of the line simultaneously performing different tasks of the same individual product. The tasks are performed on the mated-stations according to certain sequence dependence of tasks and may have restrictions on the operation directions. Some assembly operations can only be performed on a specified side, while others could be performed at either side of the line. Therefore, the tasks are classified into three types: Left (L), Right (R), and Either (E) tasks. A task can only be assigned to a station if the following two constraints are both satisfied: (1) the sum of the task time and the total task times of the tasks performed before that task in the same station is less than or equal the cycle time; (2) the sum of the task time and the finishing time of its predecessor in the opposite-side of that mated-station is less than or equal the cycle time.

The task precedence relationships can be defined by a precedence diagram, where the operation time t and the operation direction (R, L or E) are shown for each task. For example, Fig. 1 shows the precedence diagram of the tasks needed to assemble a product on a two-sided assembly line. In this diagram, each node represents a task and each directed arrow between nodes i and j indicates that task i immediately precedes task j. There is a label (\(t_i\), \(d_i\)) above each node i. The first element of this label indicates the time required for performing task i, and the second element designates the side on which task i can be performed. For the second element, there are three types named R, L, and E. The type R(L) for a task implies that the task can only be performed on the right (left) side of the line. If a task has the type E, it can be performed on either side of the line. The TALBP studied in this paper follows the general assumptions of the TALBP with deterministic operation times and without assignment restrictions except the precedence constraints.

Fig. 1
figure 1

An example of the TALBP problem

Full size image

The objective of the TALBP is thus to optimize the numbers of the mated-station and stations, which are respectively denoted as NM and NS. Note that NM is the main objective while NS is a side objective when the main objective NM ties.

3 Multi-neighborhood based path relinking for TALBP

In this section, we present our multi-neighborhood based path relinking algorithm (MN-PR) for solving the TALBP. Our proposed MN-PR algorithm integrates several distinguishing features which ensure its effectiveness, including two complementary neighborhoods, a path relinking operator to generate new solutions and an infeasible solution fixing strategy.

3.1 Search space and evaluation function

The solution of the TALBP can be represented as a sequence of all the tasks. By running a procedure, called feasible solution building procedure as described in Sect. 3.3, we can obtain a unique solution from a given sequence. Thus, for the TALBP, the search space \(\varOmega \) explored by our MN-PR algorithm is composed of all feasible task sequences. The size of the search space \(\varOmega \) is bounded by O(n!), where n is the number of tasks in the instance. We say a sequence is feasible if for any task, all its preceding tasks are before it in the sequence.

To evaluate the quality of a candidate solution \(s \in \varOmega \), we adopt an evaluation function which is defined by considering the two objectives simultaneously: (i) minimizing the number of mated-stations, (ii) minimizing the number of stations. Formally, it is stated as:

$$\begin{aligned} f = NM + \frac{{NS}}{{2*NM + 1}} \end{aligned}$$
(1)

where NS and NM are the numbers of stations and mated stations in the solution, respectively.

3.2 Main framework

Path relinking algorithms are known to be highly effective for solving a large number of constraint satisfaction and optimization problems. By combining the more global relinking procedure and the more intensive local search, the path relinking framework offers a useful balance between intensification and diversification as a means of exploiting the search space.

In principle, our multi-neighborhood based path relinking algorithm (MN-PR) repeatedly alternates between a path relinking operator that is used to generate new offspring solutions and a local search procedure that optimizes the newly generated offspring solutions. As soon as an offspring solution is improved by local search, the population is accordingly updated based on two criteria: solution quality and population diversity.

The general architecture of the MN-PR algorithm is described in Algorithm 1. Notice that we use a simplified description of the PR framework here compared with the traditional path relinking, which can be considered as a hybrid evolutionary algorithm where the recombination operator is replaced by a path relinking operator. The proposed MN-PR algorithm is composed of four main components: population initialization, a local search procedure, a path relinking operator and a population updating rule.

Starting from an initial random population, MN-PR uses the local search procedure to optimize each individual to reach a local optimum (lines 4–6). Then, the path relinking operator is employed to generate new offspring solutions (line 8), whereupon a new round of local search is again launched to optimize the objective function. Subsequently, the population updating rule decides whether such an improved solution should be inserted into the population and which existing individual should be replaced (line 10). In the following subsections, the main components of our MN-PR algorithm are described in details.

Several stopping criteria are possible for the above MN-PR algorithm, such as a maximum number of iterations, the number of times of updating the population, and so on. In this work, our MN-PR algorithm terminates when the maximum number of population updatings is reached.

figure a

3.3 Building a feasible solution from a sequence

Since our solution is represented as a sequence of all the tasks, we need to build a feasible solution from a given sequence. Specifically, we use a side assignment rule proposed by Taha et al. (2011) to generate a feasible solution from a sequence. The main idea is that tasks are assigned to stations according to a station-oriented heuristic. For a given sequence, a new mated station is firstly opened. Then, tasks are selected according to their positions in the sequence and their preferred operation direction to fill this mated station as much as possible while considering the cycle time. This procedure is repeated until all the tasks are assigned. Interested readers are referred to Taha et al. (2011) for more details.

3.4 Population initialization

In our MN-PR algorithm, the individuals of the initial population are randomly generated. To generate our initial population, we apply the following procedure as described in Algorithm 2. In this manner, each of the generated individuals in the population is a feasible solution.

figure b

3.5 Local search procedure

A simple descent local search is employed in our proposed MN-PR algorithm. At each iteration, the best neighboring solution is selected to be compared with the current solution. If the objective value of the best neighboring solution is better than that of the current solution, this neighboring solution is used to replace the current solution. This procedure is repeated to iteratively improve the current solution until no improving solutions can be found in the current neighborhood.

In our MN-PR algorithm, our local search method employs two complementary neighborhoods. Given a sequence as the starting point of our local search, the first neighborhood is first explored. When no improving solution can be found using the first neighborhood, we switch to the second neighborhood and optimize the objective function further until it also reaches the local optimum solution too.

In local search, a neighborhood is typically defined by a move operator mv, which transforms a solution X to generate a neighboring solution \(X'\), denoted by \(X' = X \oplus mv\). Let M(X) be the set of all possible moves which can be applied to X, then the neighborhood N of X is defined by \(N(X) = \{X' : X' = X \oplus mv, mv \in M(X) \}\).

To move from one solution to another in the search space, our local search procedure employs two different neighborhood structures:

The first neighborhood is defined by moving a ask from its original position in the sequence to another position. Note that the new position of the moved task should be feasible such that its new position is between all its predecessors and all its successors. This neighborhood move is called insert move, denoted as \(N_{1}\). Figure 2 gives an example of this neighborhood, where task 5 can be inserted before task 3 and task 4, as well as being inserted after task 6.

Fig. 2
figure 2

Neighborhood structure \(N_{1}\)

Full size image

Our second neighborhood is called swap move neighborhood, denoted as \(N_{2}\). It consists of swapping the positions of two tasks in the given sequence. In order to get a feasible solution after this neighborhood move, we impose a restriction that the new positions of the swapped tasks are both between all its predecessors and all its successors. In addition, for the purpose of reducing the size of the search space, we restrict the distance between the positions of the two swapped tasks to be no more than 3, which can also be verified by the fact in our experiments that long distance swap moves usually deteriorate the solution quality especially for high quality solutions. Figure 3 illustrates an example of this swap neighborhood.

Fig. 3
figure 3

Neighborhood structure \(N_{2}\)

Full size image

According to our experiments, these two neighborhoods are complementary to each other and can enhance the search effectiveness by combining them together, although the insert neighborhood has been widely used in the literature and can be considered as the basic neighborhood in our local search procedure.

3.6 Path relinking operator

The path relinking operator aims to generate new solutions by creating paths connecting two high-quality (parent) solutions, and it is composed of two main operations. The first one is to construct a path connecting two parent solutions, where the parent solutions located at the beginning and the end of the path are respectively called the initiating solution and the guiding solution, while other solutions are called intermediate ones. Another operation is to choose one solution as the reference solution from the constructed path for further improvement. In order to describe our path relinking procedure, we first give some primary definitions, denoting the initiating solution by \(s^a\) and the guiding solution by \(s^b\) :

  • LCS: The longest common subsequence of \(s^a\) and \(s^b\)

  • NC: The set of tasks not included in the LCS of solutions \(s^a\) and \(s^b\)

  • HD: The Hamming moving distance from \(s^a\) to \(s^b\)

In this work, we present two path relinking operators respectively called the greedy path relinking (GPR) operator and the random path relinking (RPR) operator. For the GPR operator, the procedure of creating a path connecting two parent solutions is described in Algorithm 3, where a solution sequence (i.e., a path) of length \(HD+1\) (s(0), s(1), \(s(2),\ldots , s(HD)\)) is generated in a step by step way by starting from s(0). Note that s(m) differs from \(s(m-1)\) by the relative position of only one task, \(m = 1, 2, \ldots , HD\). In addition, s(0) and s(HD) correspond respectively to the initiating solution \(s^{a}\) and the guiding solution \(s^{b}\), while other solutions are intermediate (or path) solutions. Moreover, at each step, a best insert move is always chosen to generate the next intermediate solution. In Algorithm 3, \(s(r+1) \leftarrow s(r) \oplus l^*\) (line 19) means that the task in the \(l^*\)th position of s(r) is moved to the position as the guiding solution \(s^b\) and this generated solution is denoted as \(s(r+1)\).

figure c

After the creation of the path, we choose one solution from this path such that the chosen solution is far enough from the initiating and guiding solutions and has a good objective value (Wang et al. 2012). Specifically, we construct a candidate solution list (CSL) that consists of the intermediate solutions having a distance of at least \(\xi \cdot HD\) (where \(\xi \) is a predetermined parameter value between 0 and 1.0 and is empirically set to be 0.4 in our experiments) from both the initiating and guiding solutions. Then, the solution having the best objective value in CSL is chosen as the reference solution.

For the RPR operator described in Algorithm 4, the intermediate solutions are generated from \(s^{a}\) to \(s^{b}\) in a random way. The only difference with the GPR operator is that at each step it chooses a random move towards the guiding solution \(s^b\) regardless of the objective function. This process is repeated until NC becomes empty.

The reference solution selection strategy is the same as the GPR operator. However, one should notice that the intermediate solutions on the generated path from \(s^a\) to \(s^b\) may not be feasible solutions for the RPR operator. In this case, we just use the infeasible solution fixing strategy as described in Sect. 3.7 to fix this solution into a feasible one.

Finally, with a consideration of efficiency (see Sect. 5.2 for a comparison between the GPR and RPR operators), our MN-PR algorithm employs the RPR operator as its path relinking operator, and the GPR operator is designed just for the purpose of comparison and analysis.

figure d

3.7 Infeasible solution fixing strategy

One should notice that not all the path solutions \(s(1),\ldots , s(r)\) constructed from \(s^{a}\) to \(s^{b}\) are feasible ones, since the precedence constraint of the TALBP is very strong and the generated intermediate solutions may not be feasible. For this reason, we use an infeasible fixing strategy fix those infeasible solutions into feasible ones.

If a solution is infeasible, it must violate some of the task precedence constraints. For example, if task A is the predecessor of task B, but task B is in front of task A in the sequence, an infeasible solution is generated. In this case, we need to remove this conflict by moving task A to a position after task B or moving task B to a position before task A. However, if there are several conflicts in a sequence, it is possible that a new conflict occurs while solving a previous conflict. In order to avoid this situation and improve the fixing efficiency, two rules are considered as follows:

  1. 1.

    Each time the task involved in the largest conflict (defined as the largest distance of the two conflicting tasks) is selected to move;

  2. 2.

    If a task is once moved to remove a conflict, this task cannot be moved any more.

With these two rules, our infeasible solution fixing strategy can quickly fix an infeasible solution into a feasible one, based on which our local search can then further optimize it to a local optimum.

3.8 Population updating

In our MN-PR algorithm, we use a simple population updating criterion to decide if a newly generated offspring solution should be inserted into the population and which solution should be replaced if yes. Specifically, when an offspring \(s^{0}\) is obtained by the path relinking procedure, we optimize \(s^0\) by the local search procedure. If the improved \(s^0\) is better than the worst solution in the population according to the objective value and is not the same as any solution in the population, the worst solution in the population is replaced by the improved solution \(s^0\). This population updating strategy can help to maintain an elite population with certain population diversities.

4 Computational results

In this section, experiments are carried out to evaluate the performance of our proposed MN-PR algorithm.

4.1 Test instances

To ensure a fair comparison, we test our proposed algorithm on the same set of TALBP instances as those used by the reference algorithms in the literature. The benchmark problems include: P12 and P24 are taken from Kim et al. (2000), P16, P65, and P205 are taken from Lee et al. (2001), and P148 is taken from Bartholdi (1993) and modified by Lee et al. (2001).

4.2 Experimental protocol and reference algorithms

Our algorithm is programmed by using the C# programming language of Visual Studio 2010 and the experiments are conducted on a PC with an Intel(R) Core(TM) i3-2310M CPU 2.10 GHz and 4 GB of RAM. For each instance, our MN-PR algorithm is independently run for 5 times and each run is limited to be 100 times of population updating. The following results report the best results of these 5 runs.

Our results are compared with four state-of-the-art algorithms for solving the TALBP in the literature, which include: a tabu search algorithm (TSA) proposed by Özcan and Toklu (2009a), a bee colony algorithm (BA) proposed by Özbakir and Tapkan (2011), a genetic algorithm (GA) proposed by Taha et al. (2011) and a simulated annealing algorithm (mSA) proposed by Khorasanian et al. (2013).

4.3 Results and comparisons with reference algorithms

The computational results of our MN-PR algorithm and comparisons with four high-performance reference algorithms are presented in Table 1. The first two columns give the problem name and the cycle time (CT) for each instance. In the third column, the lower bounds of both the number of stations (NS) and mated stations (NM) are presented. The next four columns illustrate the computational results of the four reference algorithms where the TSA and BA algorithms only report their NS values, while the results of our MN-PR algorithm are provided in the last two columns. In addition, the last three rows provide the summarized comparison between our MN-PR algorithm and the four reference algorithms, which respectively represent the number of instances for which our MN-PR algorithm can get better, equal and worse results than the corresponding reference algorithms. In the table, “x” denotes that the reference algorithm does not report the result for the corresponding instance.

Table 1 Computational results of our MN-PR algorithm and comparisons with the reference algorithms for the public TALBP instances
Full size table

From Table 1, one observes that when our MN-PR algorithm is compared with TSA, the results are very close with each other for the small-sized problems. However, our MN-PR outperforms TSA for large instances. For all the ten P205 problems, our MN-PR algorithm can obtain better results than TSA. In total, our MN-PR algorithm can get 13 better results than TSA, while no worse results are obtained. As for the BA algorithm, our MN-PR algorithm also obtains better results. Specifically, our MN-PR algorithm can get 6 better results while one worse result is obtained. When compared with GA, our MN-PR algorithm can get better or equal results for all the 45 tested instances. Particularly, our MN-PR algorithm can get better NS and NM values for 5 and 4 instances, respectively. Finally, compared with mSA, the best performing algorithm in the literature for TALBP, although our MN-PR algorithm obtains worse NS and NM values for 4 and 3 instances, our MN-PR algorithm can get better NS value for one instance (P65_326) and equal results for all the remaining instances.

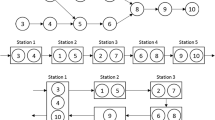
It is worthy to notice that our MN-PR algorithm improves the upper bound for the NS value of instance P65_326. Two different best solutions for instance P65_326 are shown in Figs. 4 and 5. Interested readers are referred to Lee et al. (2001) for detailed information about instance P65_326.

5 Analysis and discussion

Now we turn our attention to analyzing some important features of the MN-PR algorithm, including the importance of the proposed path relinking operator and the multi-neighborhood strategy.

Fig. 4
figure 4

A solution of \(NS=16, NM=9\) for instance P65_326

Full size image
Fig. 5
figure 5

Another solution of \(NS=16, NM=9\) for instance P65_326

Full size image

5.1 Importance of multi-neighborhood strategy

In this section, we try to figure out which neighborhood is the most essential one in our MN-PR algorithm. The experiments are performed by comparing the original MN-PR algorithm with simplified versions of our MN-PR algorithm. Specifically, we consider two variants of the MN-PR algorithm respectively with neighborhoods \(N_1\) and \(N_2\).

Table 2 shows the results of the above mentioned variants of the MN-PR algorithm for 22 large size instances, since small size problem instances are very easy to solve for all the variants of our algorithms. For each variant of our MN-PR algorithm, the best NS and NM values as well as the computational time to reach this best solution are reported.

Table 2 Comparison among the MN-PR algorithms with neighborhood \(N_1\), \(N_2\) and \(N_1+N_2\) in terms of the best solution found on the 22 large instances
Full size table

From Table 2 one finds that the original MN-PR algorithm outperforms other variants. The MN-PR algorithm with neighborhood \(N_2\) performs worse than the other two variants of our MN-PR algorithm, showing that neighborhood \(N_1\) is the basic neighborhood in our algorithm. One also obverses that with both neighborhoods, our MN-PR algorithm can obtain better results the other two variants with just one neighborhood respectively for 5 and 11 instances, indicating the importance of combining the two neighborhoods.

From the experiments we can observe that each neighborhood is important in our MN-PR algorithm. The combination of these different neighborhoods make the algorithm more powerful and each neighborhood is meaningful in the proposed MN-PR algorithm.

5.2 Comparison between the Path Relinking Operators

The relinking operator is one of the fundamental ingredients of our MN-PR algorithm. In order to analyze the influence of the relinking operator on the performance of the MN-PR algorithm, we compare our GPR and RPR relinking operators, and the corresponding MN-PR algorithms are respectively denoted by GPR and RPR. The experiment is carried out on the same set of benchmarks as mentioned in Sect. 5.1. The computational results are summarized in Table 3. The first two columns give the instance name and the cycle time. Columns 3 gives the lower bound. Computational results of GPR and RPR are respectively listed in the following columns, including the best NS and NM values, as well as the computing time to reach the best solution (t(s) in seconds).

Table 3 Comparison between the MN-PR algorithms with GPR and RPR operators
Full size table

In comparison with GPR, RPR obtains better results for nine instances in terms of NS or NM values and no worse results are obtained, which implies that the RPR operator is more robust than the GPR operator. On the other hand, the computing time of RPR is comparable to that of GPR. Therefore, it can be concluded that the search capability of the random relinking operator is better than the greedy relinking operator, which can be explained by the fact that the random relinking operator may bring more diversification into the search and it is more appropriate to be integrated with the intensive local search procedure.

6 Conclusion

In this paper, we propose a multi-neighborhood based path relinking algorithm for solving the two-sided assembly line balancing problem. The proposed MN-PR algorithm includes a number of distinguishing features, such as a multi-neighborhood based local search strategy, a dedicated path relinking procedure to generate new solutions and a strategy to fix an infeasible solution created by the path relinking procedure to a feasible one.

We test the proposed MN-PR algorithm on a set of 45 benchmark instances commonly used in the literature. Computational results show that our algorithm is highly effective in comparison with the state-of-the-art algorithms in the literature. For most instances, our proposed MN-PR algorithm is able to find the optimal or near optimal solutions in a reasonable time. Specifically, it improves the best known NS value for instance P65_326.

We studied some essential ingredients of the proposed algorithm which shed light on the following points. First, the multi-neighborhood strategy plays a crucial role in the high performance of the MN-PR algorithm. Second, the random path relinking (RPR) operator is generally better than the greedy path relinking (GPR) operator for TALBP.

There are several directions to extend this work. One immediate possibility is to introduce new diversification strategies in the path relinking procedure, such as exterior path relinking, to increase the diversity of the algorithm. The other possibility is to develop more advanced local search procedures, such as tabu search (Lü and Huang 2009; Huang et al. 2013). Finally, it is important to consider problem specific knowledge to enhance the performance of the present MN-PR algorithm.