Hybrid meta-heuristic algorithms for U-shaped assembly line balancing problem with equipment and worker allocations

Abstract

In this paper, a new U-shaped assembly line balancing problem is studied. For the first time, the criteria such as equipment cost, number of stations and activity performing quality level are considered to be optimized simultaneously by activity to station and worker to station decisions. For this aim, a multi-objective nonlinear formulation is proposed and its linearized version is also presented. Since, according to the literature, the U-shaped assembly line balancing problem with equipment requirements is an NP-hard problem, the problem of this study is NP-hard too. Because of this complexity, the classical algorithms like simulated annealing, variable neighborhood search, and classical genetic algorithm with a novel encoding/decoding scheme are used as solution approaches. As an extension, two hybrid versions of the proposed classical algorithms are proposed according to the characteristics of the problem. In order to evaluate the proposed meta-heuristics, because the problem is new, some test problems are generated randomly. Computational study of the paper, including sensitivity analysis of the proposed meta-heuristics and final experiments on the test problems, proves the superiority of the hybrid versions of the classical algorithms.

1 Introduction

Assembly lines are one of the most widely used traditional manufacturing systems for mass and high volume production, which help to increase the efficiency and speed of production systems as well as reduce the production costs and timely respond to fluctuations in demands of competitive markets. These lines were first introduced by Henry Ford at Ford automobile factories, and since that time various researches have been done to improve the performance of the assembly lines (Yuan et al. 2015; Saif et al. 2017; Make et al. 2017; Zhou and Tan 2018; Pattanaik and Jena 2019). An assembly line consists of a set of several workstations located along with a transportation system with a flow of materials between them. Each of the stations performs a set of activities. Materials and product parts flow continuously on the line by the transportation system, and after the operations of a station are performed, they are transferred to the next station until they reach the end of the line. Each station performs a set of activities from the required activities for completing the product. Regarding the production cycle time, a number of activities are assigned to each workstation. According to the assembly line balancing problem, the assignment should be done in a way that one or more objectives is optimized subject to the cycle time of the line and precedence relationships of the activities. The objectives could be minimizing the number of workstations, minimizing cycle time, minimizing total costs, etc. (see Scholl and Klein (1999), Ozcan and Toklu (2009) for the number of workstation minimization, Ozcan and Toklu (2009) Foroughi et al. (2016) for cycle time minimization, and Foroughi and Gökçen (2018), Yavari et al. (2019), Li et al. (2019) for cost minimization).

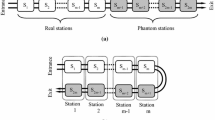
Due to the type and characteristics of the products, the layout of the line, as well as the technical and operational requirements, different classifications are presented by the researchers for assembly line balancing problems. The most well-known classifications provided by Baybars (1986) have divided assembly line balancing problems into two categories. The first group is called the simple assembly line balancing problem, and the second one is called the general assembly line balancing problems. The simple assembly balancing problem considers some simple assumptions so that the balance problem can easily be solved. Assembly line balancing problems that remove one or more of the assumptions of simple assembly balancing problems are in the category of general assembly line balancing problem. Also, in a different classification, assembly lines can be divided based on the layout of stations. The assembly lines can be divided into four types according to the layout (Hadi-Vencheh and Mohamadghasemi, 2013) of the stations such as straight assembly lines, U-shaped assembly lines, parallel assembly lines, and two-sided assembly lines (Saif et al. 2014). In straight assembly lines, all stations are placed on a direct path and the pieces or materials pass through the stations from the beginning to the end of the line. An important condition is that an activity can be assigned to a station if all of its predecessors are assigned to that station or earlier stations. U-shaped assembly lines generalize straight assembly lines in which the stations are located in such a way that entry and exit of the materials are carried out from one position and operations of two or more stations can be performed by one operator (Saif et al. 2014; Delice et al. 2017; Aigbedo and Monden, 1997). An important condition is that an activity can be assigned to a station if either all of its predecessors or all of its successors are assigned to that station or earlier stations (see Fig. 1). In these lines, the time of worker’s unemployment is reduced. Moreover, the number of stations required for U-shaped lines is never greater than the number of stations required for straight assembly lines (Baykasoglu 2006; Ajenblit and Wainwright 1998).

Fig. 1

A precedence graph, its simple balancing, and its U-shaped balancing (Source: Khorram 2018)

In recent years, many studies have been done on assembly line balancing problems, and various algorithms have been used to solve them. In the assembly line balancing problems, depending on the type of line and the type of problem, different objectives can be considered. For example, studies of Chica et al. (2011) and Hamta et al. (2013) have been done to reduce the cycle time as a variable. The studies of Ponnambalam et al. (2000) and Nourmohammadi and Zandieh (2011) have met the goals of minimizing the number of workstations and the smoothness index in assembly line balancing problems. Also, various meta-heuristic algorithms have been used to solve these problems. The genetic algorithm was used by Miltenburg (2002), Rabbani et al. (2012), Alavidoost et al. (2017), and Zhang and Gen (2011) to solve a variety of the assembly line balancing problems. The U-shaped assembly line was first studied by Miltenburg and Wijngaard (1994). Subsequently, many studies have been done to develop the formulation and solution approaches to this problem. Kim, et al. (2000), for the first time, considered the U-shaped assembly line balancing problem with the sequencing problem simultaneously. Kara et al. (2009) proposed a fuzzy goal programming and fuzzy binary programming model for this problem. Hamta et al. (2014) provided an integer nonlinear mathematical model for this problem. On the other hand, some researches were carried out by Agpak et al. (2012) and Ogan and Azizoglu (2015) to improve and develop the mathematical model of the U-shaped assembly line balancing problem. Alavidoost et al., (2017) solved straight and U-shaped assembly line balancing problems using an improved genetic algorithm with consideration of fuzzy values for activity performing times. Also, Ogan and Azizoglu (2015) proposed a mathematical model for the U-shaped assembly line balancing problem by considering activities required equipment. Then they used a typical branch and bound algorithm to solve this problem. Li et al. (2017) presented a new mixed-integer linear programming model with the goal of minimizing the number of workstations for balancing the U-shaped assembly lines. In this model, one constraint is used to represent the precedence relationship constraint instead of two constraints in the studies of the literature. Li et al. (2018) proposed a branch, bound and remember algorithm for the U-shaped assembly line balancing problem. Li et al. (2021) proposed an enhanced beam search heuristic for U-shaped assembly line balancing problems.

There are a few researches employing the simulated annealing algorithm to solve the assembly line balancing problems. One is the study of Suresh and Sahu (1994) which used the simulated annealing algorithm to solve the assembly line balancing problem. Also, McMullen and Frazier (1998) used this algorithm to solve the multi-objective assembly line balancing problem with parallel workstations, random task times, and multiple products. In addition, Roshani et al. (2012) used the simulated annealing algorithm to solve a two-sided assembly line balancing problem. Baykasoglu (2006) used this algorithm to solve U-shaped assembly line balancing problem with the objectives of maximizing line performance and line smoothness index. Erel et al. (2001) used this algorithm to solve a typical U-shaped assembly line balancing problem. In addition, Manavizadeh et al. (2013) investigated the U-shaped assembly line balancing problem with the aim of minimizing the number of workstations through balancing workload and maximizing the weighted efficiency with the simulated annealing algorithm.

In this study, an approach consisting of mathematical formulation and meta-heuristic algorithms is developed to solve a new U-shaped assembly balancing problem. Compared to the literature, a new nonlinear multi-objective formulation (Hadi-Vencheh 2011; Kovács et al. 2017) for the U-shaped assembly line balancing problem is presented and linearized. This problem for the first time considers the criteria such as equipment purchasing cost, number of stations, and activity performing quality simultaneously and optimizes them by activity and worker allocations. Since the U-shaped assembly line balancing problem with equipment requirements is an NP-hard problem (Ogan and Azizoglu, 2015), the use of meta-heuristic algorithms for the problem of this study is inevitable. As a solution approach, the classical simulated annealing and classical variable neighborhood search algorithms with a novel encoding/decoding scheme are used and hybridized according to the characteristics of the problem. In order to evaluate the proposed meta-heuristics, because the problem is new, some test problems are generated randomly. Computational study of the paper including sensitivity analysis of the proposed meta-heuristics and final comparison of them proves the effectiveness of the hybrid versions of the classical simulated annealing for the problem of this study.

The remainder of this paper has four sections. Section 2 presents the problem description and its formulation. Section 3 develops the meta-heuristic solution approaches. Section 4 includes the computational study of the problem and the solution approaches. The paper ends with the concluding remarks of Sect. 5.

2 Problem description and formulation

The problem of this study is a typical U-shaped assembly line balancing problem. This problem has some properties and assumptions which are explained as follow.

• A set of activities with their given precedence relationships are to be assigned to a set of given stations in order to produce a single product.

• A set of workers is available where each of them is able to perform all of the activities at a known quality level.

• Cycle time of the line is known.

• There is a set of equipment where one or some of them is used to perform each activity.

• For each established station, the set of required equipment and a worker should be allocated.

• For each station, after allocating its activities and workers, the lowest quality among its activities determines the quality level of that station. Accordingly, the dis-quality level of each station is one minus its quality level.

• The following objectives are considered simultaneously,

  • Minimization of the equipment purchasing cost.

  • Minimization of the number of established stations.

  • Minimization of the average of the dis-quality level of the line.

For this problem, the following notations are considered,

Sets

$PR_{i}$ The set of predecessors for activity

$SC_{i}$ The set of successors for activity i.

$TL_{i}$ The set of equipment used for activity i.

Indexes

$i,p$ Indexes used for activities $i,p \in \left\{ {1,2,...,I} \right\}$.

$k,r$ Indexes used for stations $k,r \in \left\{ {1,2,...,K} \right\}$.

$u$ Index used for workers $u \in \left\{ {1,2,...,U} \right\}$.

$l$ Index used for equipment $l \in \left\{ {1,2,...,L} \right\}$.

Parameters

$t_{i}$ The time to perform activity i.

$ec_{l}$ The purchasing cost of equipment l.

$q_{iu}$ The quality level of worker u for performing activity i.

$ct$ Cycle time.

Variables

$U_{i}$ A binary variable. It takes value of 1 if activity i is assigned to the front leg of the U-shaped line, it takes value of zero if activity i is assigned to the behind leg (the front leg is the first leg passing by the product).

$X_{ik}$ A binary variable. It takes value of 1 if activity i is assigned to station k, otherwise, its value is zero.

$S_{k}$ A binary variable. It takes value of 1 if station k includes at least one activity, otherwise, its value is zero.

$Z_{lk}$ A binary variable. It takes value of 1 if equipment l is assigned to station k, otherwise, its value is zero.

$W{}_{uk}$ A binary variable. It takes value of 1 if worker u is assigned to station k, otherwise, its value is zero.

$Q_{k}$ The quality level of station k.

According to the above-mentioned notations and assumptions, the following mathematical formulation is proposed to optimize the proposed U-shaped assembly line balancing problem.

Objective function 1

$$ OF_{1} = \min \sum\limits_{l = 1}^{L} {\sum\limits_{k = 1}^{K} {ec_{l} Z_{lk} } } $$

(1)

Objective function 2

$$ OF_{2} = \min \sum\limits_{k = 1}^{K} {S_{k} } $$

(2)

Objective function 3

$$ OF_{3} = \min \frac{{\sum\limits_{k = 1}^{K} {1 - Q_{k} } }}{{\sum\limits_{k = 1}^{K} {S_{k} } }} $$

(3)

subject to

$$ \sum\limits_{k = 1}^{K} {kX_{pk} } - \sum\limits_{k = 1}^{K} {kX_{ik} } \le K\left( {1 + U_{p} - 2U_{i} } \right),\;\forall \left( {p,i} \right)|p \in PR_{i} $$

(4)

$$ \sum\limits_{k = 1}^{K} {kX_{sk} } - \sum\limits_{k = 1}^{K} {kX_{ik} } \le KU_{i} ,\;\forall \left( {i,s} \right)|s \in SC_{i} $$

(5)

$$ \sum\limits_{k = 1}^{K} {X_{ik} = 1} ,\forall i $$

(6)

$$ S_{k} \ge X_{ik} ,\;\forall i,k $$

(7)

$$ S_{k} \le \sum\limits_{i = 1}^{I} {X_{ik} } ,\forall k $$

(8)

$$ \sum\limits_{i = 1}^{I} {t_{i} X_{ik} \le ct} ,\;\forall k $$

(9)

$$ \sum\limits_{u = 1}^{K} {W_{uk} = S_{k} } ,\forall k $$

(10)

$$ \sum\limits_{k = 1}^{K} {W_{uk} \le 1} ,\;\forall u $$

(11)

$$ \left( {1 - q_{iu} } \right)W_{uk} X_{ik} \le 1 - Q_{k} ,\;\forall i,k,u $$

(12)

$$ X_{ik} \le \frac{{\sum\limits_{{l \in Tl_{i} }} {Z_{lk} } }}{{\left| {Tl_{i} } \right|}},\forall i,k $$

(13)

$$ X_{ik} ,Z_{lk} ,S_{k} ,W_{uk} \in \left\{ {0,1} \right\},\forall i,k,l,u $$

(14)

$$ Q_{k} \ge 0,\forall k $$

(15)

Objective function (1) minimizes total equipment purchasing cost for all stations. Objective function (2) minimizes the number of established stations. Objective function (3) minimizes average dis-quality level of the established stations. Constraints (4)-(5) respect the precedence relationships of the activities. These constraints also respect to the concept of U-shaped assembly line, which says an activity can be assigned to a station if either all of its predecessors or all of its successors have been assigned to earlier stations. Constraint (6) assigns each activity to only one station. Constraints (7)-(8) consider a station as an established station if it contains at least one activity. Constraint (9) respects to the cycle time for each station. Constraints (10)-(11) assign workers to established stations. Constraint (12) determines the dis-quality level of each station. Constraint (13) determines the required equipment for the activities of each station, where, $\left| {Tl_{i} } \right|$ is the cardinality of set $Tl_{i}$. Finally, constraints (14)-(15) are sign constraints.

The proposed formulation (1)-(15) is a nonlinear formulation because of objective function (3) and constraint (12). In the rest of this section, this formulation is linearized. For this aim, some steps are followed. These steps are explained in the rest of this section.

• Step 1

  Linearize constraint (12) by the following conversion, where, $Y_{iuk}$ is a binary variable.

  $$ \left( {1 - q_{{iu}} } \right)W_{{uk}} X_{{ik}} \le 1 - Q_{k} \Leftrightarrow \left\{ \begin{gathered} \left( {1 - q_{{iu}} } \right)Y_{{iuk}} \le 1 - Q_{k} \hfill \\ W_{{uk}} + X_{{ik}} \ge 2Y_{{iuk}} \hfill \\ W_{{uk}} + X_{{ik}} \le 1 + Y_{{iuk}} \hfill \\ \end{gathered} \right.,\;\forall i,k,u $$

  (16)

• Step 2

  Use a typical Charnes and Cooper (1962) conversion method for objective function (3) as follow, where T is a non-negative variable.

  $$ OF_{3} = \min \frac{{\sum\limits_{{k = 1}}^{K} {1 - Q_{k} } }}{{\sum\limits_{{k = 1}}^{K} {S_{k} } }} \Leftrightarrow \left\{ {\begin{array}{*{20}l} {OF_{3} = \min \sum\limits_{{k = 1}}^{K} {T - T\left( {Q_{k} } \right)} } \hfill \\ {subject\;to} \hfill \\ {\sum\nolimits_{{k = 1}}^{K} {S_{k} } = \frac{1}{T} \Rightarrow \sum\nolimits_{{k = 1}}^{K} {T\left( {S_{k} } \right)} = 1} \hfill \\ \end{array} } \right. $$

  (17)

• Step 3 In the conversion (17), the nonlinear term $\sum\nolimits_{k = 1}^{K} {T\left( {S_{k} } \right)} = 1$ is linearized as follow, where $V_{k} = T\left( {S_{k} } \right)$ is a non-negative variable.

  $$ \sum\nolimits_{{k = 1}}^{K} {T\left( {S_{k} } \right)} = 1 \Leftrightarrow \left\{ {\begin{array}{*{20}l} {\sum\nolimits_{{k = 1}}^{K} {V_{k} } = 1,\forall k} \hfill \\ {V_{k} \le S_{k} } \hfill \\ {V_{k} \le T} \hfill \\ {V_{k} \ge T - \left( {1 - S_{k} } \right)} \hfill \\ \end{array} } \right. $$

  (18)

• Step 4 In the conversion (17), the nonlinear term $T\left( {Q_{k} } \right)$ is linearized as follow, where $R_{k} = T\left( {Q_{k} } \right)$ is a non-negative variable. In this conversion, the inequality $\left( {1 - q_{iu} } \right)Y_{iuk} \le 1 - Q_{k}$ obtained in Step 1 also is influenced.

  $$ OF_{3} = \min \sum\limits_{k = 1}^{K} {T - T\left( {Q_{k} } \right)} \Leftrightarrow OF_{3} = \min \sum\limits_{k = 1}^{K} {T - R_{k} } $$

  (19)
  $$ \left( {1 - q_{iu} } \right)Y_{iuk} \le 1 - Q_{k} \Leftrightarrow \left( {1 - q_{iu} } \right)Y_{iuk} T \le T - R_{k} ,\;\forall i,k,u $$

  (20)

• Step 5 The nonlinear term $Y_{iuk} T$ of inequality (20) is replaced by a non-negative variable $B_{iuk} = Y_{iuk} T$, and the inequality is linearized as follow,

  $$ \left( {1 - q_{{iu}} } \right)Y_{{iuk}} T \le T - R_{k} \Leftrightarrow \left\{ {\begin{array}{*{20}l} {\left( {1 - q_{{iu}} } \right)B_{{iuk}} \le T - R_{k} ,\forall i,k,u} \hfill \\ {B_{{iuk}} \le Y_{{iuk}} } \hfill \\ {B_{{iuk}} \le T} \hfill \\ {B_{{iuk}} \ge T - \left( {1 - Y_{{iuk}} } \right)} \hfill \\ \end{array} } \right. $$

  (21)

According to the obtained linearized constraints and objective functions of the above steps, the nonlinear formulation (1)-(15) is equivalent to the below linear formulation.

Objective function 1

$$ OF_{1} = \min \sum\limits_{l = 1}^{L} {\sum\limits_{k = 1}^{K} {ec_{l} Z_{lk} } } $$

(22)

Objective function 2

$$ OF_{2} = \min \sum\limits_{k = 1}^{K} {S_{k} } $$

(23)

Objective function 3

$$ OF_{3} = \min \sum\limits_{k = 1}^{K} {T - R_{k} } $$

(24)

subject to

$$ \sum\limits_{k = 1}^{K} {kX_{pk} } - \sum\limits_{k = 1}^{K} {kX_{ik} } \le K\left( {1 + U_{p} - 2U_{i} } \right),\forall \left( {p,i} \right)|p \in PR_{i} $$

(25)

$$ \sum\limits_{k = 1}^{K} {kX_{sk} } - \sum\limits_{k = 1}^{K} {kX_{ik} } \le KU_{i} \forall \left( {i,s} \right)|s \in SC_{i} $$

(26)

$$ \sum\limits_{k = 1}^{K} {X_{ik} = 1} ,\forall i $$

(27)

$$ S_{k} \ge X_{ik} ,\;\forall i,k $$

(28)

$$ S_{k} \le \sum\limits_{i = 1}^{I} {X_{ik} } ,\;\forall k $$

(29)

$$ \sum\limits_{i = 1}^{I} {t_{i} X_{ik} \le ct} ,\;\forall k $$

(30)

$$ \sum\limits_{u = 1}^{K} {W_{uk} = S_{k} } ,\;\forall k $$

(31)

$$ \sum\limits_{k = 1}^{K} {W_{uk} \le 1} ,\;\forall u $$

(32)

$$ \left( {1 - q_{iu} } \right)B_{iuk} \le T - R_{k} ,\;\forall i,k,u $$

(33)

$$ W_{uk} + X_{ik} \ge 2Y_{iuk} ,\;\forall i,k,u $$

(34)

$$ W_{uk} + X_{ik} \le 1 + Y_{iuk} ,\;\forall i,k,u $$

(35)

$$ \sum\nolimits_{k = 1}^{K} {V_{k} } = 1 $$

(36)

$$ V_{k} \le S_{k} ,\;\forall k $$

(37)

$$ V_{k} \le T,\,\forall k $$

(38)

$$ V_{k} \ge T - \left( {1 - S_{k} } \right)\;\forall k $$

(39)

$$ B_{iuk} \le Y_{iuk} \;\forall i,k,u $$

(40)

$$ B_{iuk} \le T,\;\forall i,k,u $$

(41)

$$ B_{iuk} \ge T - \left( {1 - Y_{iuk} } \right),\;\forall i,k,u $$

(42)

$$ X_{ik} \le \frac{{\sum\limits_{{l \in Tl_{i} }} {Z_{lk} } }}{{\left| {Tl_{i} } \right|}},\;\forall i,k $$

(43)

$$ X_{ik} ,Z_{lk} ,S_{k} ,W_{uk} ,Y_{iuk} \in \left\{ {0,1} \right\},\;\forall i,k,l,u $$

(44)

$$ T,V_{k} ,R_{k} ,B_{iuk} \ge 0,\;\forall k $$

(45)

In the next section of the paper, some meta-heuristic approaches are developed to solve the formulation (22)-(45) effectively.

3 Solution methodology

Generally, the assembly line balancing problems in their simple form are of the NP-hard class of combinatorial optimization problems (see Ogan and Azizoglu 2015). Therefore, we conclude that the linearized formulation (22)-(45) which contains many variables and constraints in addition to classical assembly line balancing problems of the literature, has a high degree of complexity to be solved exactly by optimization solvers. For this aim, first, the classical simulated annealing (SA) and the classical variable neighbourhood search (VNS) algorithms are proposed to solve the formulation (22)-(45). In continue, these algorithms are hybridized by a local search algorithm in order to obtain better solutions. In the rest of this section, first, an encoding/decoding scheme is proposed to construct and evaluate the solutions of the proposed meta-heuristic algorithms. Then the proposed meta-heuristic algorithms are explained.

3.1 Encoding/decoding scheme

A special encoding/decoding scheme is proposed to construct and evaluate a feasible solution for the formulation (22)-(45). The proposed meta-heuristic approaches of this study are mainly based on this scheme. This encoding/decoding scheme follows three steps as represented by Fig. 2 and its steps are detailed in continue.

Fig. 2

The proposed encoding/decoding scheme

Step 1. Activity to station assignment. According to the concept of U-shaped lines, either all of the predecessors or all of the successors of an eligible activity for being assigned to a candidate station should be assigned to earlier stations or that station. On the other hand, for each activity, a set of eligible stations is defined to assign it to one of them. Starting from Station 1, the last station contains one of the predecessors or successors of an activity, and the later stations are eligible for that activity. For example, if we consider Station 6 for assigning an activity and the last station containing its predecessors or successors is Station 3, the set of eligible stations for this activity contains stations 3, 4, 5, and 6. In the beginning, all of the stations, respectively from 1 to K are eligible. Now, to perform this step, the below sub-steps are followed.

Step 1.1. A permutation of the activities is generated randomly as a solution vector.

Step 1.2. A set of eligible activities starting from the beginning of the solution vector are obtained, respectively. Also, a set of eligible stations is obtained for each eligible activity.

Step 1.3. The first eligible activity is assigned to its earliest possible eligible station. The condition for this assignment is that the operating time of the stations does not exceed the cycle time. If an eligible activity is assigned to a station, it is removed from the solution vector, and also it is removed from the predecessor and successor lists of the remaining activities of the solution vector.

Step 1.4. The last two steps are repeated until the solution vector becomes empty.

Step 2. Equipment to station assignment. In this step, according to the activity assignment plan obtained by Step 1, the required equipment of each opened station is determined from the required equipment of the activities of that station. For the cases that more than one activity from a station requires an equipment, just one unit of that equipment is assigned to that station.

Step 3. Worker to station assignment. A random permutation of the available workers is generated. Starting from the beginning of the permutation, the workers are assigned to the opened stations, respectively. Therefore, some of the workers are unassigned if all of the potential stations are not opened.

Step 4. Solution evaluation. The solution obtained by steps 1–3 is evaluated in this step. For this aim, the multi-objective function of the formulation (22)-(45) is converted to a single objective function by a typical global criterion. For this aim, the following sub-steps are followed.

Step 4.1. For the obtained solution, the objective functions of the formulation (22)-(45) are obtained easily by the Eqs. 1-3. For this aim, the variables $Z_{lk}$, $S_{k}$, and $Q_{k}$ are calculated easily from the obtained solution.

Step. 4.2. Calculate the following single objective function, which is a typical global criterion. According to the minimization type objective functions (1)-(3), smaller values of OF are favoured.

$$ OF = \frac{{\sum\limits_{l = 1}^{L} {\sum\limits_{k = 1}^{K} {ec_{l} Z_{lk} } } }}{{UB_{{OF_{1} }} }} + \frac{{\sum\limits_{k = 1}^{K} {S_{k} } }}{{UB_{{OF_{2} }} }} + \frac{{{\raise0.5ex\hbox{$\scriptstyle {\sum\limits_{k = 1}^{K} {1 - Q_{k} } }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\sum\limits_{k = 1}^{K} {S_{k} } }$}}}}{{UB_{{OF_{3} }} }} $$

(46)

In this equation, $UB_{{OF_{1} }}$ is a proposed upper bound for the value of objective function (1). In this global criterion, each objective function value is converted to a scale between 0 and 1. Therefore, their summation has more sense and gives a more accurate evaluation. Regardless of the obtained solution, the following upper bounds are proposed in this study.

$$ UB_{{OF_{1} }} = K\sum\limits_{l = 1}^{L} {ec_{l} } $$

(47)

$$ UB_{{OF_{2} }} = K $$

(48)

$$ UB_{{OF_{3} }} = K\mathop {\max }\limits_{i,u} \left\{ {1 - q_{iu} } \right\} $$

(49)

In Eq. 47, it is assumed that all of the equipment are assigned to all of the potential stations. In Eq. 48, it is assumed that all potential stations are opened. In Eq. 49, it is assumed that the highest possible dis-quality level appears in all of the potential stations.

In order to explain the calculations of this step, the example of Fig. 1 is considered. Some data from the example is shown in Table 1 and others are given below,

• Number of stations is considered $K = 5$.

• Three types of equipment are available where all of them are required for any of the

• activities. We consider $ec_{1} = 1000$, $ec_{2} = 2000$, and $ec_{3} = 3000$.

Table 1 Data of the illustrative example

Based on the given data and the U-shaped configuration of Fig. 1, the following calculations are done to obtain the value of the objective function (46).

• $UB_{{OF_{1} }}$ is calculated as $UB_{{OF_{1} }} = K\mathop \sum \limits_{l = 1}^{L} ec_{l} = 5 \times \left( {1000 + 2000 + 3000} \right) = 30000$.

• $UB_{{OF_{2} }} = K = 5$.

• $UB_{{OF_{3} }} = K\mathop {\max }\limits_{i,u} \left\{ {1 - q_{iu} } \right\} = 5 \times \max \left\{ {1 - 0.8, 1 - 0.8, \ldots , 1 - 0.9} \right\} = 4 \times 0.4 = 2$.

• In the U-shaped configuration, all 5 stations are established and all of the equipment are assigned to each station because it has been assumed that each activity needs all of the equipment. Therefore, the total equipment cost of the U-shaped configuration is calculated as$\mathop \sum \limits_{l = 1}^{K} \mathop \sum \limits_{k = 1}^{K} ec_{l} Z_{lk} = \left( {1000 + 2000 + 3000} \right) + \left( {1000 + 2000 + 3000} \right) + \left( {1000 + 2000 + 3000} \right) = 18000$ On the other hand, it is assumed that workers 1 to 5 are assigned to stations 1 to 5, respectively. Therefore, based on the activities and workers of the stations,

• $1 - Q_{1} = \max \left\{ {1 - q_{31} , 1 - q_{41} , 1 - q_{10,1} } \right\} = 0.3$, $1 - Q_{2} = 0.4$, $1 - Q_{3} = 0.4$, $1 - Q_{4} = 0.4$, and $1 - Q_{5} = 0.4$.ss

• Finally, the objective function (46) is calculated as below,

• $$ \begin{aligned} OF & = \frac{{\mathop \sum \nolimits_{{l = 1}}^{K} \mathop \sum \nolimits_{{k = 1}}^{K} ec_{l} Z_{{lk}} }}{{UB_{{OF_{1} }} }} + \frac{{\mathop \sum \nolimits_{{k = 1}}^{K} S_{k} }}{{UB_{{OF_{2} }} }} \\ & \quad + \frac{{{\raise0.7ex\hbox{${\mathop \sum \nolimits_{{k = 1}}^{K} 1 - Q_{k} }$} \!\mathord{\left/ {\vphantom {{\mathop \sum \nolimits_{{k = 1}}^{K} 1 - Q_{k} } {\mathop \sum \nolimits_{{k = 1}}^{K} S_{k} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\mathop \sum \nolimits_{{k = 1}}^{K} S_{k} }$}}}}{{UB_{{OF_{3} }} }} \\ & = \frac{{18000}}{{30000}} + \frac{5}{5} + \frac{{{\raise0.7ex\hbox{${0.3 + 0.4 + 0.4 + 0.4 + 0.4}$} \!\mathord{\left/ {\vphantom {{0.3 + 0.4 + 0.4 + 0.4 + 0.4} 5}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$5$}}}}{2} = 1.83 \\ \end{aligned} $$

3.2 Meta-heuristic solution approaches

3.2.1 Classical simulated annealing (SA-1)

Simulated annealing (SA) is a meta-heuristic algorithm for complex optimization problems based on a single solution, which is introduced by Kirkpatrick et al. (1983) (see also Niroomand and Vizvari, 2015). The objective function of the algorithm is like the energy of materials that should be decreased by decreasing the temperature. The search starts with the initial temperature ($T_{0}$) and the initial solution ($x_{0}$). The initial solution is changed to a new solution or neighbor.

solution ($x^{\prime}$). If this change decreases the objective function (energy), the new solution is accepted, otherwise, it can be accepted by the probability of $\exp \left( {\tfrac{ - \Delta OF}{{T_{0} }}} \right)$ where $\Delta OF = OF\left( {x^{\prime}} \right) - OF\left( {x_{0} } \right)$. The changing procedure is repeated several times for the accepted solution, and in each repetition, the accepted solution may be replaced by the new solution. After that, the initial temperature is cooled down and the whole procedure is repeated until reaching a stopping criterion like a final temperature, running time, etc. In the end, the best solution is reported. The SA is detailed by the pseudo-code of Fig. 3.

Fig. 3

The classical SA used for the formulation (22)-(45)

Some clarifications for applying the classical SA to the formulation (22)-(45) are as follow,

• The encoding/decoding scheme of classical SA is exactly the same as Sect. 3.1.

• In the beginning of the algorithm, a random permutation of the workers is generated and it is used in all of the generated solutions. Therefore, the common set of workers is used in all of the generated solutions.

• The neighbourhood search operator is the swap. In the swap operator, the current solution vector is considered. Two integer random numbers from 1 to I are generated. The activities of the positions of these generated numbers are interchanged and a new solution vector is obtained.

3.2.2 SA algorithm with random worker assignment (SA-2)

The proposed classical SA of Sect. 3.2.1 is hybridized here in order to obtain a better solution. For this aim, at any generated solution during the SA, a random permutation of the workers is generated and applied to that solution. Therefore, the difference of this version of the SA with the SA of the previous sub-section is that just a common set of workers is not used for the generated solutions, and for each generated solution, a specific set of workers is generated randomly.

3.2.3 SA algorithm with local search for worker assignment (SA-3)

In this sub-section, another hybrid version of the classical SA is proposed to improve the solutions found for the formulation (22)-(45). For this aim, the SA of Sect. 3.2.2 is considered and improved. The improvement is done by applying a local search in each worker assignment step of the encoding/decoding scheme (Step 3). For this aim, the following are done in the worker assignment step when a new solution (neighbor solution) is generated,

• The worker assignment step of the encoding/decoding scheme (Step 3) is repeated for a number of iterations ($n_{w}$).

• As in each iteration, a random permutation of the workers is generated, this permutation is changed by a swap (similar to the swap operator used in the classical SA) operator for a number of iterations ($n_{it}$) in order to improve the worker assignment as much as possible.

• Among the $n_{w} n_{it}$ generated set of workers, the set that results in less value of objective function (3) obtained by formulation ${\raise0.5ex\hbox{$\scriptstyle {\sum\limits_{k = 1}^{K} {1 - Q_{k} } }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\sum\limits_{k = 1}^{K} {S_{k} } }$}}$ is selected for worker assignment of the neighbor solution.

3.2.4 Classical variable neighbourhood search (VNS-1)

The VNS is a single solution meta-heuristic algorithm to solve the combinatorial optimization problems effectively (see Niroomand and Vizvari, 2015). It contains a set of neighbourhood search structures (this set is shown by NS). The procedure starts with an initial solution and takes one of the neighbourhood search structures (NSS) and tries to improve the initial solution for a number of iterations. The improved solution (if improved) or initial solution (if not improved) is transferred to the next neighbourhood search structure (NSS). The procedure is repeated for all neighbourhood search structures (NSS). The whole procedure may be repeated for a number of iterations. Finally, the best-obtained solution is reported.

Some clarifications for applying the classical VNS to the formulation (22)-(45) are as follow,

• The encoding/decoding scheme is exactly the same as Sect. 3.1.

• At the beginning of the algorithm, a random permutation of the workers is generated and it is used in all of the generated solutions. Therefore, the common set of workers is used in all of the generated solutions.

• Three neighbourhood search structure are used as follow,

• NSS-1: In the solution vector, an activity is selected randomly and all activities before the selected activity is transferred to the end of the vector in the same order.

• NSS-2: In the solution vector, an activity is selected randomly and is transferred to another randomly selected position.

• NSS-3: The neighbourhood search structure is the swap introduced in Sect. 3.2.1.

The pseudo-code of the VNS-1 is shown in Fig. 4.

Fig. 4

The classical VNS used for the formulation (22)-(45)

3.2.5 VNS algorithm with random worker assignment (VNS-2)

The proposed classical VNS of Sect. 3.2.4 is hybridized here in order to obtain a better solution. For this aim, at any generated solution during the VNS, a random permutation of the workers is generated and applied to that solution. Therefore, the difference of this version of the VNS with the VNS-1 is that just a common set of workers is not used for the generated solutions, and for each generated solution, a specific set of workers is generated randomly.

3.2.6 VNS algorithm with local search for worker assignment (VNS-3)

In this sub-section, another hybrid version of the classical VNS is proposed to improve the solutions found for the formulation (22)-(45). For this aim, the VNS-2 is considered and improved. The improvement is done by applying a local search in each worker assignment step of the encoding/decoding scheme (Step 3). For this aim, the followings are done in the worker assignment step when a new solution (neighbor solution) is generated,

• The worker assignment step of the encoding/decoding scheme (Step 3) is repeated for a number of iterations ($n_{w}$).

• As in each iteration, a random permutation of the workers is generated, this permutation is changed by a swap (similar to the swap operator used in the classical VNS) operator for a number of iterations ($n_{it}$) in order to improve the worker assignment as much as possible. Among the $n_{w} n_{it}$ generated set of workers, the set that results in less value of objective function (3) obtained by formulation ${\raise0.5ex\hbox{$\scriptstyle {\sum\limits_{k = 1}^{K} {1 - Q_{k} } }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\sum\limits_{k = 1}^{K} {S_{k} } }$}}$ is selected for worker assignment of the neighbor solution.

3.2.7 Classical genetic algorithm and its improved versions

For more comparison of the proposed algorithms, the GA is also considered in this study (similar to the GA applied by Gen et al. (1997) and Niroomand et al. (2016)). The classical and modified versions of the GA is briefly explained as below,

• GA-1: In this GA, a population of solutions is generated randomly (the number of solutions of the population is denoted by N). Each solution is generated and evaluated by the encoding–decoding scheme of Sect. 3.1. A roulette wheel mechanism (see Gen et al. 1997) is used and two solutions (parents) from the population are selected. The partial mapped crossover (PMX) (see Niroomand et al. 2016) is applied to the sequences of the first step of the solutions to form a new solution (offspring). Then, with a mutation rate ($p_{r}$) a swap operator (see Niroomand et al. 2016) is applied on the sequence of the first step of the new solution for possible improvement. The remaining $N - 2$ solutions of the population are regenerated randomly and are added to the population. The new solution is also added to the population while the parents remain in the population. Then the best N solutions among all solutions of the population are selected to form a new population. The procedure is repeated for a number of iterations ($n_{max}$) and the best-obtained solution among the last population is introduced as the best solution of the GA. Some clarifications for applying the classical SA to the formulation (22)-(45) are as follow,

• The encoding/decoding scheme of the GA-1 is exactly the same as Sect. 3.1.

• At the beginning of the algorithm, a random permutation of the workers is generated and it is used in all of the generated solutions. Therefore, the common set of workers is used in all of the generated solutions.

• GA-2: The proposed GA-1 is hybridized here in order to obtain a better solution. For this aim, in any generated solution during the procedure of GA-1, a random permutation of the workers is generated and applied in that solution. Therefore, the difference of this version of the GA with the GA-1 is that just a common set of workers is not used for the generated solutions, and for each generated solution, a specific set of workers is generated randomly.

• GA-3: In this sub-section, another hybrid version of the GA-1 is proposed to improve the solutions found for the formulation (22)-(45). For this aim, the GA-2 is considered and improved. The improvement is done by applying a local search in each worker assignment step of the encoding/decoding scheme (Step 3). For this aim, the followings are done in the worker assignment step when a new solution (neighbor solution) is generated,

• The worker assignment step of the encoding/decoding scheme (Step 3) is repeated for a number of iterations ($n_{w}$).

• As in each iteration, a random permutation of the workers is generated, this permutation is changed by a swap (similar to the swap operator used in the GA-1) operator for a number of iterations ($n_{it}$) in order to improve the worker assignment as much as possible. Among the $n_{w} n_{it}$ generated set of workers, the set that results in less value of objective function (3) obtained by formulation ${\raise0.5ex\hbox{$\scriptstyle {\sum\limits_{k = 1}^{K} {1 - Q_{k} } }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\sum\limits_{k = 1}^{K} {S_{k} } }$}}$ is selected for worker assignment of the neighbor solution.

4 Computational study

The formulation (22)-(45) and the proposed meta-heuristic solution approaches are numerically evaluated in this section. For this aim, some test problems are generated. Using these test problems, the behavior of the parameters of the meta-heuristic algorithms is studied experimentally and the best value for each parameter is determined. Then the final experiments using the obtained values of the parameters are performed. It is notable to mention that the meta-heuristic solution approaches are coded in MATLAB and are run on a computer Core i7- 16.00 GB RAM—3.88 GHz CPU. The rest of this section describes the details of the computational study.

4.1 Test problems

As mentioned earlier, some test problems are generated to evaluate the proposed meta-heuristic solution approaches. In this section, some characteristics of these test problems are detailed. The interested readers can contact the corresponding author for the complete set of data of the test problems.

Except the characteristics represented by Table 2, the following data are also considered for the test problems which are not reported in the paper.

• Activity operating time, which is randomly generated between 1 and CT.

• Equipment purchasing cost, which is randomly generated for each equipment.

• Quality level of performing each activity by each worker which is randomly generated between 0 and 1.

• Set of equipment used for each activity.

Table 2 Some characteristics of the test problems

In order to study the performance of the proposed meta-heuristics deeply, the size of the test problems are considered from a small size to a large size.

4.2 Parameter tuning

A very important step in implementing any meta-heuristic algorithm is to determine the best value of its parameters. A very simple but time-consuming and even impossible way is to consider all possible values of the parameters of a meta-heuristic algorithm and determine all of the combinations of the parameters. These combinations determine the number of experiments to be performed for studying the effect of the parameters on the performance of the algorithm.

As an effective method to deal with such difficulty and reduce the number of required experiments, Taguchi (1986) proposed Taguchi experimental design method which has been used in many optimization-based studies like Taassori et al. (2015), Niroomand et al. (2015), Mirzaei et al. (2016), Niroomand et al. (2016), Sanei et al. (2016), Boros et al. (2016), Salehi et al. (2020), etc. The process of the Taguchi method divides the parameters into two groups of uncontrollable and controllable parameters. During the process, it tries to decrease the impact of uncontrollable parameters and find the best value of the controllable parameters. For this aim, the Taguchi method uses orthogonal arrays to decrease the number of required experiments. The number of rows (experiments) of the orthogonal array of an algorithm with four parameters and three levels in each parameter is at least $\left( {4 \times \left( {3 - 1} \right)} \right) + 1 = 9$. If there is no orthogonal array with exactly nine number of rows, the larger arrays are modified. The result of experiments of the orthogonal array is a signal-to-noise ratio (S/N ratio) to be minimized in the case of best values of the parameters. For a minimization type objective function, this ratio is as follow,

$$ S/N = - 10\left( {\log_{10} \left( {objective \, function} \right)^{2} } \right) $$

(50)

For the meta-heuristics of this study, two or three values for each parameter is proposed which are mainly taken from the literature. These values are reported in Table 3 and the total required number of experiments is also obtained there to show the complexity of simple parameter tuning for these algorithms. For the algorithms based on SA, in final temperature, only one value is considered, which means that this parameter is not studied for tuning purposes. On the other hand, the most suitable orthogonal array for each meta-heuristic is obtained and its experiments using values of Table 3 are designed.

Table 3 The levels considered for the parameters of the proposed meta-heuristics

The experiments of the orthogonal arrays are performed on TP6 test problem. Each experiment is run five times to obtain more reliable results. The average objective function values is used to obtain the S/N ratio of each parameter level and finally, the best value of each parameter is obtained and reported by Table 4.

Table 4 The best level obtained for the parameters of the proposed meta-heuristics

4.3 Final experiments

The best level of the parameters obtained by Sect. 4.2 are used to run the proposed algorithms for all test problems. In order to have a fair comparison among the proposed algorithms, the following conditions are considered when running the proposed meta-heuristic algorithms,

• A common CPU time equal to the CPU time of the longest algorithm in each test problem is considered to run that test problem by all of the algorithms. This issue considers two points, (1) all algorithms are run for equal CPU time, and (2) as the considered CPU time is depended on the size of the test problems, for larger test problems, larger CPU time is considered.

• In order to obtain more reliable results, each test problem is solved by each algorithm 20 times.

In addition, the problem (22)-(45) is solved by CPLEX solver of GAMS for obtaining the optimal solution of each test problem. For this aim, each objective function is divided by its upper bound explained by Eqs. (47)-(49) and the obtained fractions are summed up. The obtained single objective function is identical to the objective function (46), which is used to evaluate the solutions generated by the meta-heuristic solution approaches. The CPU running time of 30,000 s is considered for all test problems while they are solved by GAMS. The obtained results by exact experiments is depicted in the last column of Table 5. It can be seen that only test problems TP1 to TP6 can be solved exactly in the given CPU running time. For other test problems, no optimal solution is obtained at that running time.

Table 5 The results obtained for the test problems by the proposed meta-heuristic approaches SA-1, SA-2, and SA-3

The results obtained by final experiments are reported in Table 5, Figs. 5,  6, and 7. In these table and figures, the minimum, maximum and average of the objective function values obtained by each meta-heuristic algorithm for each test problem are reported.

Fig. 5

Minimum objective function values obtained by the metaheuristic algorithms for all test problems

Fig. 6

Maximum objective function values obtained by the metaheuristic algorithms for all test problems

Fig. 7

Average of objective function values obtained by the metaheuristic algorithms for all test problems

The results of Table 5 are represented based on the average of the objective function values obtained by each meta-heuristic algorithm. The graphs of the objective function values are depicted in Figs. 5,  6, and  7 where minimum obtained value, maximum obtained value, and average of values of all 20 runs of each meta-heuristic algorithm for each test problem are represented, respectively. According to the obtained results, the following conclusions are drawn from the results of Table 5 and Figs. 5, 6, 7.

• In all test problems, among the SA-based algorithms, the best average of the obtained objective function values is related to the SA-3 algorithm. After this algorithm, the SA-2 algorithm results in a better average of the obtained objective function values compared to the SA-1 algorithm for most of the test problems. Among the VNS-based algorithms, the VNS-3 performs better than the VNS-2 and VNS-1 algorithms. Among the GA-based algorithms, the GA-3 performs better than the GA-2 and GA-1 algorithms.

• In all test problems, the best minimum value of the obtained objective function values is related to either GA-3 or SA-3 algorithms. After these algorithms, the SA-2 and GA-2 algorithms result in better minimum value of the obtained objective function values compared to others.

• In all test problems, the best maximum value of the obtained objective function values is related to either SA-3 or GA-3 algorithms. After these algorithms, the SA-2 algorithm results in a better maximum value of the obtained objective function values compared to the SA-1 algorithm is most of the test problems. Among the VNS-based algorithms, the VNS-3 performs better than the VNS-2 and VNS-1 algorithms.

• In the case of the minimum obtained objective function value, the GA-3 algorithm performs definitely better than the other algorithms.

• The obtained results prove the superiority of the SA-3, VNS-3, and GA-3 algorithms over others. This means that, applying a local search on the worker assignment step in the classical algorithms, makes them a powerful solution approach compared to the classical SA, VNS, and GA (the SA-1, VNS-1, and GA-1 algorithms).

For more exact comparison of the obtained results of Table 5, a one-way ANOVA is used to statistically compare them in 0.05 $\alpha$-level. The result of ANOVA shows that there is a significant difference among the average of objective function values of Table 5. In continue, the Tukey test is performed to exactly compare the algorithms based on the average of objective function values of Table 5. The result of the Tukey test is shown by Table 6 where the sign “ < / = / > ” means that the algorithm of row performs better/equal/worse than the algorithm of column in 0.05 $\alpha$-level. According to the results of Table 6, the SA-1, VNS-1, and GA-1 algorithms are strongly worse than the others while the algorithms SA-3, VNS-3, and GA-3 are strongly better than the others. Interestingly, the algorithms SA-3, VNS-3, and GA-3 are equal in all of the test problems. This means that, applying a local search on the worker assignment step in the classical algorithms makes them a powerful solution approach compared to the classical SA, VNS, and GA (the SA-1, VNS-1, and GA-1 algorithms).

Table 6 The results of one-way ANOVA for comparison of the algorithms overall test problems (the sign “ < / = / > ” means that the algorithm of row performs better/equal/worse than the algorithm of the column in 0.05 $\alpha$-level)

4.4 Managerial insights

The mathematical formulation, solution procedure, and obtained results show the following implications from the managerial point of view,

• For industrial holdings, the formulation and solution approaches can be used to establish the assembly line of a new product for the first time.

• The proposed solution approaches can help the managers to overcome multi-objective nature of real-world multi-objective optimization problems.

• The proposed improvement procedure of the proposed algorithms can be modified for other assembly line balancing problems.

5 Conclusions

In this paper, a new U-shaped assembly line balancing problem was studied. Comparing to the literature, a new multi-objective formulation for U-shaped assembly line balancing problem was presented. The problem considers the criteria such as equipment purchasing cost, number of stations, and activity performing quality simultaneously and optimizes them by activity and worker allocations. Since the proposed U-shaped assembly line balancing problem is an NP-hard problem, the use of meta-heuristic algorithms for the problem is inevitable. As solution approach, the classical simulated annealing (SA), variable neighborhood search (VNS), and genetic algorithm (GA) with a novel encoding/decoding scheme were used and hybridized according to the characteristics of the problem. In order to evaluate the proposed meta-heuristics, because the problem is new, some test problems were generated randomly. Computational study of the paper including sensitivity analysis of the proposed meta-heuristics and final comparison of them, proved the effectiveness of the hybrid versions of the SA, VNS, and GA comparing to other approaches. It means that in the problem of this study applying the local search on the worker assignment phase (the hybrid algorithms SA-3, VNS-3, and GA-3) dramatically improved the obtained solutions (Table 7).

Table 7 CPU running times of the algorithms and common run time used for the final experiments in seconds

As the future study on the problem of this paper, the problem can be tackled by multi-objective meta-heuristic solution approaches. Furthermore, considering the problem in an uncertain environment and applying the methods such as stochastic programming, fuzzy programming, interval programming, etc. can be of interest.