1 Introduction

Simulation of biological dynamics has a long history over the last few decades, one of which is a quantitative approach to tumor therapy. Many mathematical models, physical computational, and engineering computational have been applied to various aspects of tumor therapy, that the main goal of understanding tumor response to clinical intervention. Simulations of the dynamics model of tumor therapy are known as in silico trials which aim to predict a patient’s specific response to various treatments or treatment combinations. The simulation of tumor therapy becomes an invaluable tool for optimizing patient care. Therefore, this study aims to describe the simulation of the biological dynamics of tumor cell growth and the interaction between tumor cells with combination treatment.

Mathematical models are powerful tools for testing hypotheses and confirming experiments using simulations of complex system dynamics. Through these models, we can also understand the basic mechanisms of complex biological dynamic systems in a relatively fast time without sacrificing large laboratory experiment time. Variations of the biological system dynamics model can be adapted to the experiment to be reviewed. In tumor therapy simulations, the model can be validated using data from clinical experiments, but if clinical experimental data are not available, then the simulation results can be used as a hypothesis of the tumor growth in the presence of therapy in a patient. Quantitative models have been developed as an experimental approach to tumor therapy. In the last 2 decades, many models have been developed in the form of ordinary differential equations based on the rate of division of individual cells; thus, this will pave the way for research in the field of quantitative tumor modeling. Since this study can develop a tumor therapy model that model can be used to simulate tumor growth in response to treatment.

One of the tumors in the brain is glioma, while glioblastoma is the most aggressive type of cancer in the brain. It is one of the most feared cancers because more than two-thirds of adults who have been diagnosed with this cancer will die within 2 years after being diagnosed. Treatment of this cancer is a challenge for doctors and researchers because of the biological nature of this cancer. First, this cancer can infiltrate the brain which is one of the most important organs of the body, so skilled neurosurgeons often have difficulty reaching it. Second, this cancer is located behind the blood–brain barrier; it is a transport protein junction system that protects delicate nerve tissue from exposure factors, so it will also inhibit exposure to chemotherapy therapy. Third, the genetic and epigenetic development of this cancer is in the unique microenvironment of the brain, so it often makes cancer resistant to conventional treatment [1]. Patients with glioblastoma have an estimated 5-year survival of only about 5% after the diagnosis time. Patients with gliomas that have spread within the brain typically do not survive more than 5 years; this is due to this cancer progressing to higher stages [2].

Glioblastoma is rare cancer because every year, only 6 patients are diagnosed out of every 100,000 people. This cancer is in the central nervous system (CNS) originating from (precursor) glial cells. Most of this cancer arise characterized by infiltrative growth by diffusion into the surrounding CNS parenchyma of the brain [3]. Most glioblastomas are thought to originate from glial cells or their precursors, and 30–40% comprise all intracranial neoplasms. Many studies have developed an understanding of the mechanisms triggering and regulating glioblastoma invasion [4]. The results of the model developed in this study are expected to obtain a more effective and better therapeutic strategy and can reduce clinical toxicity.

Sturrock and co-workers [5] have developed mathematical models based on the facts of post-diagnostic glioma cell evolution. The main difference between their model and those of previous researchers is that diagnosed glioma cells have an association between glioma growth and changes in the concentration of blood glucose and serum glucose in the brain. In addition, based on the diagnosis, the cause of the slow growth of tumors in some cases is made possible by the action of the immune system affecting the tumor growth. In the early stages of tumor growth, post-diagnosis has also been shown that tumor-associated antigens can be found on tumor cells. These cells have diffused deep into the interior of the tumor cells so that these cells will accumulate in the tumor tissue. These immune cells will be active; this is caused by the growth of tumor tissue. Ayala-Hernández and co-workers [6] have also developed these mathematical models to be used to analyze glioma behavior and the concentration of blood glucose and serum glucose in the brain with the parameters involved being randomly assigned. The determination of these parameters was based on the analysis of the greatest effect on glioma growth and the decrease in the concentration of blood glucose and serum glucose in the brain. Their model is a system of coupled nonlinear ordinary differential equations that can be analyzed for stability.

Traditional cancer therapies, such as surgery, chemotherapy, and radiation, are still considered to have low efficacy and high toxicity for patients. Currently, researchers are intensively discovering new cancer treatments developed based on advances in genetic engineering, that is, virotherapy. This therapy uses genetically modified viruses that can specifically infect, replicate, and destroy cancer cells without causing damage to healthy cells. Currently, virotherapy is a promising cancer treatment, but this therapy has challenges because the virus can be destroyed by immune cells before infecting cancer cells. Wodarz [7, 8] has formulated a basic model of tumor growth affected by virotherapy treatment. The basic model describes the interaction between three variables uninfected tumor cells by the virus, infected tumor cells by the virus, and free virus. Based on this basic model, several mathematical models have been developed to explain the interaction mechanism between tumor cells and oncolytic viruses to gain a more detailed understanding of the dynamics of virotherapy. The development of mathematical models in this study will use the virotherapy process based on the model equations that have been introduced by Wodarz [7, 8].

Friedman and co-workers [9] have formulated and analyzed a mathematical model of a spherical glioma injected with the oncolytic virus hrR3 (mutant of herpes simplex virus (HSV)) in its center. Their model described both uninfected and infected tumor cells, necrotic cells, free virus cells, and innate immune cells. Their parameter estimates were in agreement with experimental results for gliomas, and some of these parameters were also based on the much more aggressive glioma. Vasiliu and Tian [10] have also focused on developing the interaction dynamics of these five cell populations. They studied periodic solutions and Hopf bifurcations of important biological parameters of viral burst size. Their version of the model is composed of ordinary differential equations to analyze the Hopf bifurcation and periodic solutions.

Iarosz and co-workers [11] have introduced a system of coupled ordinary differential equations to model chemotherapy-treated glioma that considers interactions between glial cells, gliomas, neurons, and chemotherapeutic agents. Their model can analyze the process of inhibiting glioma growth and identify the parameter values of the glioma growth inhibition that can be obtained from the model, and it can minimize the loss of healthy cells. Researchers have also shown that chemotherapy treatment has the potential to be combined with an antitumor, namely, an oncolytic virus, to be more efficacious. An overview of the combination treatment strategy of chemotherapy and viral induction used to optimize tumor destruction was also carried out by Nguyen and co-workers [12]. They focus on discussing the therapeutic context of the synergistic combination effect and its implications for clinical use in the future.

De Pillis and co-workers have developed and analyzed a mathematical model of the ordinary differential equations that regulate tumor growth at the cell population level with a combination of treatments using immune cells and chemotherapy. This model helps to guide the development of combination therapy. The numerical simulation results of the combination therapy illustrate some situations where neither chemotherapy nor immunotherapy alone is sufficient to control tumor growth, but combination therapy can eliminate the entire tumor. Therefore, this study will use the chemotherapy model equation that has been applied in the research of De Pillis and co-workers [13].

Urenda-Cázares and co-workers [14] have introduced a mathematical model of the treatment combination of chemotherapy and oncolytic virotherapy as an alternative treatment against glioma. They built a model of the dynamics system based on the interaction between glial cells, glioma cells, chemotherapeutic agents, and virotherapy that injects a specific virus and only attacks tumor cells. They have used three different types of viruses. The process of virotherapy against tumor cells is divided into healthy cells and infected cells; it is assumed that the infected cells cannot multiply. Their results show that the proposed treatment can reduce the number of chemotherapy sessions and also that virotherapy is recommended to select the type of virus according to the type of cancer. The conclusions of their model reinforce and claim that the use of combination chemotherapy and virotherapy treatments is more efficacious against tumors.

Therefore, a treatment combination of chemotherapy and virotherapy has been used widely as clinical treatment and has shown synergistic properties and the potential to kill tumors. So, in this study, we will develop a mathematical model of chemotherapy that has been widely applied for tumor destruction and combined with virotherapy to optimize the treatment process and then analyze its implications. These model development results are expected to provide an overview of glioma or glioblastoma treatment in the future.

This study will present the development of mathematical models describing the interaction between glioma cells, blood glucose, and immune cells that was combined with chemotherapy and virotherapy as an alternative treatment for glioma. Section 2 presents the development of mathematical models in detail, and the value of the parameters of this model is also presented in detail. Section 3 presents the results and analysis of the simulations that have been carried out. Finally, conclusions are presented in Sect. 4.

2 Formulation of mathematical models of combination therapy

2.1 Mathematical model of glioma growth based on blood glucose levels

This study begins with the model development from the equations proposed by Sturrock and co-workers [5]. The equations have also been used by Ayala-Hernández and co-workers [6] to demonstrate the dynamics of small glioma growing in the brain that elicit a response from the host immune system in a simplified form. Their model assumes that both the host’s immune system and gliomas need energy to maintain their function, and the energy source is glucose, which can be in the brain or blood. Their mathematical model consisted of four variables: (1) the symbol \(T\) defines the glioma concentration; (2) the symbol \({\sigma }_{brain}\) represents the glucose concentration in the brain; (3) the symbol \(I\) defines the concentration of the immune system; and (4) the symbol \({\sigma }_{serum}\) represents the serum glucose concentration. Their model is expressed in the system of ordinary differential equations as follows:

$$\frac{dT}{dt}=\underbrace{{ \alpha _T \sigma _{brain}T\left(1-\frac{T+{T}_{i}}{{K}_{T}}\right)}}_{Production}-\underbrace{d_{T}T}_{Apoptosis}-\underbrace{d_{TI}TI}_{Immune \ response},$$
(1)
$$\frac{d\sigma_{brain}}{dt}=\underbrace{\alpha_{\sigma}(\sigma_{serum}-\sigma_{brain})}_{Glucose \ exchange}-\underbrace{d_{T\sigma}T\sigma_{brain}}_{Glioma \ consumption}-\underbrace{(d_{\sigma 1}+\alpha_{s}(\nu+I))\sigma_{brain}}_{Natural \ consumption},$$
(2)
$$\frac{dI}{dt}=\underbrace{\alpha_{s}(\nu+I)\sigma_{brain}+\alpha_{TI}TI}_{Producion}-\underbrace{d_{I}I}_{Natural \ decay}-\underbrace{d_{TT}TI}_{Glicoma \ response},$$
(3)
$$\frac{d{\sigma }_{serum}}{dt}=\underbrace{{{\alpha }_{\sigma }\left({\sigma }_{brain}-{\sigma }_{serum}\right)}}_{Glucose\ exchange}+\underbrace{{F\left(t\right)}}_{Glucose\ intake}-\underbrace{{{d}_{\sigma 2}{\sigma }_{serum}}}_{Natural\ consumption} ,$$
(4)

where

$$F\left(t\right)=\mathrm{max}\left\{{\sigma }_{min},{\sigma }_{0}\mathrm{sin}\left(6\pi t\right)\right\}$$

All of the Eqs. (1)–(4) above are time-dependent \(t > 0\). Equation (1) defines the time evolution of glioma growth, Eq. (2) represents the rate of glucose concentration in the brain, Eq. (3) defines the rate of immune system activity in the brain, and Eq. (4) represents the rate of glucose concentration in serum. Table 1 shows the set of parameter values from Eqs. (1)–(4).

Table 1 Description and values of the estimated parameters of Eqs. (1)–(4) from the literature [5] and [6]
Full size table

Many mathematical models have been developed to describe and understand the dynamics of combination therapy of chemotherapy and virotherapy, so it is of interest to us to build and analyze coupled nonlinear ordinary differential equations to describe and understand the dynamics model of glioma therapy, when chemotherapy, virotherapy, and the two combinations of these therapies are performed. Our proposed model is a dynamic model of small gliomas growing in the brain, and the tumor's growth will cause a response from the immune system. This model also assumes that the immune system and brain tumors need energy, and the energy source is glucose, to maintain their function in the brain. Then, this above model will be combined with the process of chemotherapy and the virus injection so that tumor cells exposed to chemotherapy and tumor cells that are uninfected and infected with the virus can be described and also analyzed. The development of this model is expected to demonstrate the effect of chemotherapy and virotherapy which is determined by the important variables, such as the level of immune cells, blood glucose, and glucose in the brain, during the therapy process. The simulation results are also expected to show which treatment is more efficacious for reducing tumor cells in the brain, monotherapy, or a combination of the two therapies.

2.2 Mathematical model of chemotherapy

De Pillis and co-workers [15] have introduced a mathematical model of the tumor-immune interaction with chemotherapy to obtain an optimal treatment strategy. Their numerical results of the dynamics model are used to analyze and control drug therapy to get optimal results. Their model also makes it possible to test and compare various control strategies in linear and nonlinear cases. In the linear control case, the tumor cells were completely killed, but in the nonlinear control case, the tumor cells would rapidly move to a small value, then gradually decrease; this corresponds to the amount of drug delivered to the patient. A nonlinear control has the added benefit of keeping the tumor under control when the tumor becomes small so that the most vigorous tumor treatment is not required. A nonlinear controller allows for minimizing harmful side effects while allowing the system to maintain a small tumor size.

De Pillis and co-workers [13] have also presented a chemo-immunotherapy model that detects three compartments, that is, immune cells, tumor cells, and chemotherapy drugs in the bloodstream. The tumor cells in the blood concentration are assumed to be constant throughout the bloodstream. The chemotherapy drug prescribed is doxorubicin, because the parameters allow it to be determined more precisely. The chemotherapy model includes the chemotherapeutic drug-killing term in each cell population. Because chemotherapy drugs, such as doxorubicin, are only effective during certain phases of the cell cycle, pharmacokinetics will show limited efficacy in chemotherapy. Equation \(1-{e}^{-kQ}\) to represent fractional cell killing of chemotherapy. The mathematical model used to reflect the curve leading to tumor cell death induced by dose–response induction of chemotherapy is defined by the equation:

$$F\left(T,\ Q\right)={-K}_{T}\left(1-{e}^{-{\delta }_{T}Q}\right)T$$
(5)

where the parameters KT and δT define the rate of tumor death due to chemotherapy and the drug efficacy coefficient, while the variable Q defines the chemotherapeutic agent. While the mathematical model that will be used to reflect the curve of immune cell death due to drug poisoning when chemotherapy is defined by the equation:

$$F\left(I,\ Q\right)={-K}_{I}\left(1-{e}^{-{\delta }_{T}Q}\right)I$$
(6)

where a parameter KI defines the killing rate of chemotherapeutic agents to immune cells.

2.3 Mathematical model of virotherapy

The characteristics of the virus to combat tumor cells are carried out selectively. The virus will infect tumor cells using viral replication and viral cytotoxicity and induce a specific viral and tumor response, so this will benefit the patient. Although the immune response can slow the rate of viral replication, this must be avoided, so that the virus does not integrate into the human genome. The interaction equations between the tumor growth, the population of replicating viruses, and the antiviral immune response are presented in the form of coupled nonlinear ordinary differential equations. Wodarz [7] has introduced a mathematical model to describe the interactions between tumor cells, viruses, and the immune system. This model has been used to show the characteristics of viruses used to reduce tumor cells; this is to evaluate the efficacy of anticancer therapy carried out by viruses. The therapeutic efficacy was assessed by examining the interaction between the tumor cells and the specific viral response; then, this model was extended to include not only specific viruses but also specific tumors.

Wodarz [7] has presented the model composed of three variables, namely, (1) uninfected tumor cells (T), (2) virus-infected tumor cells (Ti), and (3) viruses with specific cytotoxic T lymphocytes (CTL) (V), so the coupled ordinary differential equations are given as follows:

$$\frac{dT}{dt}=rT\left(1-\frac{T+{T}_{i}}{k}\right)-dT-\beta T{T}_{i}$$
(7)
$$\frac{d{T}_{i}}{dt}=\beta T{T}_{i}+s{T}_{i}\left(1-\frac{T+{T}_{i}}{k}\right)-a{T}_{i}-{p}_{v}{T}_{i}V$$
(8)
$$\frac{dV}{dt}={c}_{v}{T}_{i}V-bV$$
(9)

where parameter r defines the growth rate of tumor cells logistically, parameter d defines the death rate of tumor cells, and parameter k defines the carrying capacity which is the maximum size or space that can be occupied by tumor cells. Whereas the parameter β defines the spread rate of the virus to tumor cells (this parameter can also be seen as the rate of viral replication), the parameter a defines the rate of infected tumor cells and then killed by the virus, and the parameter s defines the growth rate of infected tumor cells logistically. This assumes that the infected division of tumor cells produces two daughter cells that carry the virus. This would certainly be the case with viruses that integrate into the tumor cell genome, but with viruses that do not integrate, the probability of transmission upon cell division must be high enough to justify this assumption. Parameter cv defines the virus-specific CTL that develops in response to the antigen, parameter b defines the viral laxative, and parameter pv defines the CTL for killing infected tumor cells.

The dynamics model of predator–prey is an inspiration for CTL response after exposure to antigen, so CTL proliferates and kills tumor cells. The amount of antigen (Ti) and CTL (V) is directly proportional to the proliferation of CTL, representing a relatively strong and efficient response. The model assumes that infected tumor cells can only infect their closest neighbors. Therefore, the simulation results of the model yield are qualitatively very similar to those obtained from the model of the simple mass conservation. This model is the first valid model to investigate the basic dynamics of viruses infecting tumor cells.

2.4 Mathematical model of combination therapy

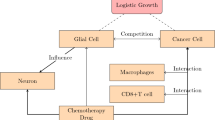
The new dynamic model of the combination therapy system that will be applied for glioma therapy is based on the dynamics model of glioma tumor growth that has been proposed by Sturrock and co-workers [5] consisting of four main variables, namely, glioma cells (T), glucose in the brain (σbrain), immune cells (I), and serum glucose or blood glucose (σserum). Their equations are expressed in the form of coupled nonlinear ordinary differential equations. In this study, the equations describe blood glucose intake that takes into account homeostatic glucose absorption using the equation that has been proposed by Quiroz and Femat [16]. The model development resulted in 7 variables consisting of the following: (1) T defines healthy glioma cells, (2) Ti defines virus-infected glioma cells, (3) σserum defines blood glucose, (4) σbrain defines glucose in the brain, (5) I defines immune cells, (6) Q defines chemotherapeutic agent, and (7) V defines virus. Each variable is expressed in units of g/ml, but chemotherapeutic agents are expressed in units of mg.

$$\frac{dT}{dt}=\underbrace{{ \sigma _T \sigma _{brain}T\left(1-\frac{T+{T}_{i}}{{K}_{T}}\right)}}_{Production}-\underbrace{{d}_{T}{T}}_{Apoptosis}-\underbrace{{{d}_{TI}TI}}_{{Immune\ response}}-\underbrace{{{K}_{T}\left(1-{e}^{-kQ}\right)T}}_{Chemotherapy\ response}-\underbrace{{\beta TV}}_{Virotherapy\ response}$$
(10)
$$\frac{d{T}_{i}}{dt}=\underbrace{{\beta TV}}_{Infected\ glioma}-\underbrace{{{d}_{{T}_{i}}{T}_{i}}}_{Infected\ glioma\ death}-\underbrace{{{d}_{TiI}{T}_{i}I}}_{Glioma\ death\ by\ immune}$$
(11)
$$\frac{d{\sigma }_{brain}}{dt}=\underbrace{{{\alpha }_{\sigma }\left({\sigma }_{serum}-{\sigma }_{brain}\right)}}_{Glucose\ exchange}-\underbrace{{{d}_{T\sigma }T{\sigma }_{brain}}}_{Glioma\ consumption}-\underbrace{{\left({d}_{\sigma 1}+{\alpha }_{s}\left(v+I\right)\right){\sigma }_{brain}}}_{Natural\ consumption}$$
(12)
$$\frac{dI}{dt}=\underbrace{{{\alpha }_{s}\left(v+I\right){\sigma }_{brain}{+\alpha }_{TI}TI }}_{Production}+\underbrace{{s{T}_{i}I}}_{Stimulation}-\underbrace{{{d}_{I}I}}_{Natural decay}-\underbrace{{{d}_{TT}TI}}_{Glioma response}-\underbrace{{{d}_{ITi}I}}_{Immune death}-\underbrace{{{K}_{I}\left(1-{e}^{-kQ}\right)I}}_{Chemotherapy}$$
(13)
$$\frac{d{\sigma }_{serum}}{dt}=\underbrace{{{\alpha }_{\sigma }\left({\sigma }_{brain}-{\sigma }_{serum}\right)}}_{Glucose\ exchange}+\underbrace{{\frac{r\left(I,G\right)}{PBF}}}_{Glucose\ intake}-\underbrace{{{d}_{\sigma 2}{\sigma }_{serum}}}_{Natural\ consumption}$$
(14)

where [16]

$$\begin{aligned}& \qquad \qquad \quad r\left(G,I\right)={M}_{I}\left(I\right){M}_{G}\left(G\right){r}_{B}\\& {M}_{I}\left(I\right)=7.03+6.52\tanh\left(0.333{ I}^{N}-1.9672\right) \\& \qquad \qquad\qquad \quad \;{M}_{G}\left(G\right)={G}^{N}\end{aligned}$$
$$\frac{dQ}{dt}=\underbrace{{P\left(t\right)}}_{ Injection\ of\ chemotherapy\ agent}-\underbrace{{{d}_{Q}Q}}_{Degradation\ of\ chemotherapeutic\ agent}$$
(15)
$$\frac{dV}{dt}=\underbrace{{U\left(t\right)}}_{Injection\ of\ virus}+\underbrace{{b{d}_{Ti}{T}_{i}}}_{Increase\ of\ virus}-\underbrace{{\rho\ TV}}_{Lost virus}-\underbrace{{bV}}_{Death\ of\ the\ virus}$$
(16)

Equation (10) defines the concentration dynamics of healthy glioma cells describing the production of healthy glioma cells, the natural death of healthy glioma cells (apoptosis), the response of immune cells to glioma cells, and the response to chemotherapy and virotherapy. Equation (11) defines the concentration dynamics of infected glioma cells due to virotherapy describing an increase of infected glioma cells, natural death of infected glioma cells, and death of infected glioma cells caused by the immune response. Equation (12) defines the concentration dynamics of glucose in the brain that describes the exchange of glucose between the blood and the brain, the consumption of glucose in the brain by glioma cells, and the consumption of glucose by the brain normally. Equation (13) defines the concentration dynamics of immune cells describing the production of immune cells, stimulation of immune cells due to the presence of infected glioma cells, natural immune cell death, immune cell response due to the presence of glioma cells, and death of immune cells responsible for the infection and the response of immune cells to chemotherapy. Equation (14) describes the concentration dynamics of glucose in the blood describing glucose exchange, glucose intake, and natural glucose consumption. Equation (15) defines the dynamics of a chemotherapeutic agent describing the injection of a chemotherapeutic agent and the degradation of a chemotherapeutic agent. Equation (16) defines the viral concentration by describing the dose of virus injection, the increase of virus due to rupture of infected glioma cells, the possibility of virus loss during the infection process, and the natural death of the virus. The parameter values that will be used in numerically simulated can be seen in Tables 1 and 2.

Table 2 Parameter, description, value (unit), and references
Full size table

This study shows a glucose exchange between blood glucose and glucose in the brain. Glucose in the brain will be a supplier of nutrients for immune cells and glioma cells so that glioma cells and immune cells will suppress each other. The chemotherapy process will suppress immune cells and glioma cells; this refers to the nature of chemotherapy agents that cannot distinguish cell types. Viruses from the virotherapy process will infect glioma cells and turn glioma cells into infected glioma cells. Infected glioma cells will stimulate or trigger immune cells, while immune cells will inhibit or kill glioma cells. In this infected process, there is a possibility of the virus missing caused by immune cells.

In this study, numerical simulations were carried out using the numerical method of the Runge Kutta order 45. Numerical simulations were carried out using initial values referring to studies [5, 6], especially for healthy glioma cells (T), glucose in the brain (σbrain), immune cells (I), and serum glucose or blood glucose (σserum). The initial values of chemotherapeutic agents and viruses in virotherapy are zero, so the initial values for each of these variables are as follows:

$$({T}_{s};\ {\sigma }_{brain};\ I;\ {\sigma }_{serum};\ Q;V) \approx (0.14;\ 3.92\ \times\ {10}^{-4};\ 2.84\ \times\ {10}^{-4};\ 4.39 \times {10}^{-4};0;0)$$

In this study, the scenario of the numerical simulation consists of three scenarios based on the therapy to be carried out. In the first scenario, chemotherapy is given 30 days after the patient is diagnosed with glioma. A chemotherapy dose of 560 mg was injected every day for 5 days, or a total dose of 2800 mg was injected with a chemotherapy agent in the form of cyclophosphamide, which can be seen in Fig. 1. The dose was taken according to the regulations of The United States Food and Drug Administration [https://www.accessdata.fda.gov/drugsatfda_docs/label/2013/] which recommends that cyclophosphamide be applied at a dose of 50 mg/kg body weight and the patient’s body weight is assumed to be around 70 kg. In the first scenario, all variables related to virotherapy, such as U(t), V, and Ti, were deactivated. In the second scenario, the virotherapy process was applied 30 days after the patient was diagnosed with glioma. The injected virus concentration was 5 × 10−7 g/ml. The given viral injection concentrations were referred to in the literature [33]. During this virotherapy process, all variables related to chemotherapy, such as P(t) and Q, were deactivated. In the third scenario, the combination therapy process, virotherapy was applied 30 days after the patient was diagnosed with glioma. An injection dose of a chemotherapy agent of 560 mg every day for 5 days then continued with the application of the virotherapy process by injecting the virus on the 16th day after injection of recent chemotherapy. The therapeutic time for combination therapy was referred to in the literature [14].

Fig. 1
figure 1

The process of giving chemotherapy doses of 560 mg was injected every day for 5 days, and a total dose of 2800 mg was injected with chemotherapeutic agents

Full size image

Cyclophosphamide is a bifunctional alkylating agent as well as a prodrug that requires metabolic transformation to produce mustard phosphoramide, the active alkylating species. This is because, in the experimental system, cyclophosphamide has shown a steep log-linear relationship between dose and cytotoxicity. Based on clinical studies, cyclophosphamide has also shown activity against various tumors. Based on clinical trials, cyclophosphamide has been combined with oncolytic viruses as a therapy for cancer. Clinical trials have shown that brain tumors treated with oncolytic viruses, which are derived from live herpes simplex virus (HSV), can reduce cancer cells significantly when cyclophosphamide is applied before the oncolytic virus application process [47].

Oncolytic virotherapy is a unique antitumor, in which the virus selectively kills tumor cells, then replicates and spreads through the tumor while inducing an antitumor immune response. Talimogen laherparepvec (T-Vec) is a genetically engineered oncolytic virus based on the herpes simplex virus-1 (HSV) which is the most prominent virus and the only oncolytic virus approved by the Food and Drug Administration (FDA) used to treat gliomas. In June 2021, the oncolytic virus received conditional and time-limited approval for the treatment of malignant gliomas in Japan. Therefore, oncolytic viruses can selectively infect and kill tumor cells while activating the immune system. The general mechanism of virotherapy can be described as follows [48,49,50]:

  1. 1.

    Tumor cells can be selectively infected by oncolytic viruses. This will also cause the virus to induce tumor lysis directly due to the inhibition of the antiviral innate immune pathway in most tumor cells.

  2. 2.

    Due to viral infection, tumor cell lysis can lead to the release of tumor-associated antigens. This is a pattern of cell-derived damage-related molecules. Viruses can recruit dendritic cells and innate lymphoid cells (e.g., NK cells) to clear virus-infected cells early.

  3. 3.

    The release of tumor-associated antigens, pro-inflammatory cytokines, and chemokines by tumor cells, lysis, and innate immune cells can enhance antigen presentation and antigen-specific adaptive immune response.

  4. 4.

    The immune response will also kill infected tumor cells.

  5. 5.

    The oncolytic virus can promote the recruitment of tumor-infiltrating lymphocytes to the tumor site so that it will make it immunosuppressive in the microenvironment. This process is following immunotherapy.

3 Results and discussion

3.1 Simulation results of chemotherapy

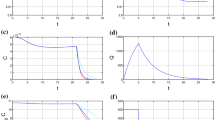
The simulation results of Eqs. (9)–(15) using only the chemotherapy process are given in four graphs that describe the glioma concentration, glucose concentration in the brain, immune concentration, and blood glucose concentration. The red line represents the simulation result without therapy, while the green line represents the simulation result using chemotherapy. All the graphs of the simulation results can be seen in Fig. 2.

Fig. 2
figure 2

The red and green lines indicate without and with chemotherapy. Blue and black dotted lines represent the highest and lowest basal blood glucose levels

Full size image

In Fig. 2, the simulation results show that the chemotherapy process for glioma has no significant effect. This can be seen from the concentration decrease of the glioma at the time of application of chemotherapy which is not so large for 0 to 9 years; the glioma concentration still increased to about 0.56 g/ml. In a without therapy case, the glioma concentration could reach a concentration of about 0.91 g/ml. This is consistent with the fact that gliomas are relatively resistant to chemotherapy and gliomas are self-repairing [17]. Most cancer cells (malignant tumors) have stem cell properties, namely, the ability or very high potential to develop into many different cell types, the ability to resist drugs, and the ability to remain inactive for a long time if there is still a treatment process [18, 19]. The chemotherapy process is still less effective in reducing glioma cells; this is possible because most chemotherapeutic agents utilize apoptosis induction to kill cancer cells, while apoptosis induction is less effective against cancers that have similar properties to stem cells [20, 21].

In Fig. 2, the chemotherapy process also has an impact on the concentration of immune cells. The concentration of immune cells will decrease during the application of chemotherapy; this is because chemotherapy cannot differentiate cell types [22]. In addition, chemotherapy agents are often used to suppress immune cells (immunosuppressants) [23]. However, after the chemotherapy process was applied, immune cells had the same pattern as without therapy. The concentration of immune cells will be higher. This is due to the suppression of glioma cell growth during the chemotherapy process. Therefore, during this process, the suppression of glioma cells against immune cells also becomes less than when without chemotherapy. The suppression process of immune cells by glioma cells occurs in most cancer microenvironments that are immunosuppressive [24,25,26].

In Fig. 2, changes in the concentration of glioma cells and immune cells are also accompanied by changes in the concentration of blood glucose and glucose in the brain. This is because glucose is a source of food or nutrition for the growth of glioma cells. During the chemotherapy process, the concentration of blood glucose and glucose in the brain had a higher concentration than without chemotherapy. When chemotherapy is applied, the concentration of blood glucose and glucose in the brain increases; this is due to the suppression of glioma cells and immune cells which results in reduced glucose intake in the brain. After the application of chemotherapy, the pattern of decreasing concentrations of blood glucose and glucose in the brain corresponded to the pattern of decreasing concentrations of blood glucose and glucose in the brain without chemotherapy, but the concentrations of blood glucose and glucose in the brain had a larger value. This pattern of decline occurs due to the reactivation of glioma cells for growth and also the reactivation of immune cells triggered by glioma growth.

3.2 Simulation results of virotherapy

The simulation results of the virotherapy process are shown in Fig. 3. The simulation results show that virotherapy can reduce the growth of glioma cells for a long time even though the concentration of glioma cells fluctuates, while the simulation results of glioma concentrations without therapy still increase the concentration to around 0.9 g/ml (red line). This is very different from the simulation results of virotherapy (green line); the maximum concentration of glioma cells was 0.2 g/ml even though the concentration fluctuated. Virotherapy can inhibit glioma growth consistently; this is consistent with the fact that virotherapy can kill cancer stem cells (CSC) in brain cancer [27]. Even virotherapy can diminish the ability to repair CSC [28, 29]. The mechanism of virotherapy inhibiting the growth of cancer cells (malignant tumors) involves two things, namely, directly destroying cancer cells and stimulating immune cells to inhibit the growth of cancer cells.

Fig. 3
figure 3

The red and green lines indicate without and with virotherapy. The blue and black dotted lines represent the highest and lowest basal blood glucose levels

Full size image

In Fig. 3, the simulation results of the concentration of immune cells during the virotherapy process showed that the concentration of immune cells fluctuated, but the values tended to be more stable ranging from 2.4 × 10−3 to 2.9 × 10−3 g/ml. This is different from the simulation results of the concentration of immune cells without therapy. If without therapy, the concentration of immune cells will be stimulated by the concentration of glioma cells. Immune cells will decrease due to the growth of glioma cells because it will inhibit the increase in immune cells. When the concentration of immune cells increases, the concentration of glioma cells decreases; this indicates that there is a viral infection of glioma cells caused by the virotherapy process. This also causes the process of suppression of the growth of glioma cells. The virotherapy process can also increase immune cells, such as white blood cells and neutrophils [30, 31].

In Fig. 3, the changing concentrations of glioma cells and immune cells were fluctuating which was followed by the concentrations of blood glucose and glucose in the brain. During the virotherapy process is applied, there is an increase in the concentrations of blood glucose and glucose in the brain even though both concentrations fluctuate. Fluctuations in the concentrations of blood glucose and glucose in the brain are associated with glucose uptake by immune cells and glioma cells. This occurs when glioma cells decrease while immune cells increase so that glucose intake for glioma cells decreases and glucose intake for immune cells increases. Conversely, when glioma cells increase, immune cells decrease, so glucose intake for glioma cells increases, and intake for immune cells decreases. Glioma cells prefer to consume glucose compared to normal cells; this is because cancer cells undergo metabolic changes that cause an increase in the need for glucose intake [32]. In the virotherapy process, simulation results of blood glucose concentration showed that blood glucose was still in the normal range even though the values fluctuated. This was different from the simulation results of blood glucose concentrations without therapy which tended to decrease.

The simulation results of the virotherapy process show fluctuating results. This fluctuation is made possible by several things. First, it is related to infection rate parameters and virus burst size. The infection rate and burst size of each virus were different based on the study results of two parameters referring to the literature [33]. This literature decided to take the infection rate and virus burst size due to consideration of several references which stated that the occurrence of infection speed and virus burst size was still unable to fight the growth rate of glioma cells, but the virus was still able to keep up with it. The effectiveness of virotherapy is influenced by the infectiousness and spread of the virus [34]. Second, it is a possibility of re-infection from the virus; this can be seen in Fig. 4 which illustrates the simulation results of virus injection, virus concentration, and the concentration of infected glioma cells.

Fig. 4
figure 4

Numerical simulation results of the virus injection process, virus concentration, and infected glioma cells in the application of virotherapy

Full size image

Figure 4 shows the iterative process of viral infection and infected glioma cells during the simulation. This repeated viral infection of glioma cells can provide the advantage that the application of virotherapy can be carried out with only one injection and without repeated injections for a long time, but this has not been explained and is still under debate. However, there are clinical studies conducted by Russell and co-workers [35] and Russel [36] which demonstrate this possibility, and this has been shown by a clinical study conducted on 49-year-old women with myeloma who were given virotherapy with a single high-dose viral injection which can destroy myeloma cells so that for 5 years it does not show signs of systemic myeloma cell recurrence. The pattern of infected glioma cells indicates latent infection by the virus. Latent infection is characterized by the absence of viral infection among repeated infections [37]. Latent infections can be found in several groups of viruses, such as adenovirus and herpes simplex virus, which can be latent for a long time in the human body to defend themselves from the immune system [38]. Both groups of viruses are candidate viruses for virotherapy against glioma cells.

3.3 Simulation results of the combination of chemotherapy and virotherapy

The results of the combination therapy simulation consisting of the chemotherapy process and the virotherapy process can be seen in Fig. 5. The simulation results of this combination therapy show that the concentration of glioma cells during the application of chemotherapy decreased and then fluctuated glioma cells caused by the application of virotherapy. Simulation results fluctuate more visibly from the application of combined therapy than from virotherapy alone. Concentrations of glioma cells from this combination therapy ranged from 0.1 to 0.2 g/ml. This combination therapy is also able to inhibit the growth of glioma cells for a long time because virotherapy can reduce the concentration of glioma cells more markedly than chemotherapy alone.

Fig. 5
figure 5

The red and green lines indicate without and with combination chemotherapy and virotherapy. Blue and black dotted lines represent the highest and lowest basal blood glucose levels

Full size image

Figure 6 describes viral injection, virus concentration, and concentration of infected glioma cells from the simulation results of combination therapy. Figure 6 also shows a higher concentration of infected glioma cells (up to about 0.008 g/ml) than the concentration of infected glioma cells from virotherapy alone (about 0.004 g/ml).

Fig. 6
figure 6

Numerical simulation results of the virus injection process, virus concentration, and infected glioma cells in the application of combination chemotherapy and virotherapy

Full size image

Figure 5 also shows the concentration of blood glucose, and glucose in the brain increases during the application of chemotherapy; it is because glucose intake is reduced for glioma cells and immune cells caused to the suppression of chemotherapy agents. Then, the concentration of both fluctuated due to virotherapy. Concentrations of blood glucose and glucose in the brain tend to be more stable ranging from 0.7 × 10−3 to 0.78 × 10−3 g/ml. The concentrations of blood glucose and glucose in the brain were still within normal concentration intervals and did not show a tendency to decrease in concentration as shown in the blood glucose concentration without therapy.

This study not only describes the impact of the therapy on the concentration of glioma cells, blood glucose, immune cells, and glucose in the brain, but this study also looks at the effectiveness of chemotherapy, virotherapy, and combination therapy against glioma growth by comparing the concentration of glioma cells for each year. The effectiveness results are shown in Table 3. The concentration range of glioma cells with virotherapy ranged from 141.6 × 10−3 to 191.6 × 10−3 g/ml, and the concentration range of glioma cells with combination therapy ranged from 126.9 × 10−3 to 208.2 × 10−3 g/ml. The previous therapy had a concentration range that was smaller than the concentration range of glioma with chemotherapy alone which was in the range between 147.8 × 10−3 and 571.6 × 10−3 g/ml. The mean value of the difference in glioma concentrations each year between no therapy and each therapy (chemotherapy, virotherapy, and combination therapy) was 174.4 × 10−3 g/ml, 359.3 × 10−3 g/ml, and 351.3 × 10−3 g/ml. Based on these results in Table 3, it can be seen that virotherapy and combination therapy have a higher effectiveness than chemotherapy alone.

Table 3 Comparison of glioma cell concentrations with and without therapy for several years
Full size table

4 Conclusions

Based on the simulation results that have been obtained, this study can conclude that chemotherapy alone only inhibits the growth of gliomas when this therapy is applied; after completion of therapy, glioma cells increased again. In addition, the concentration of immune cells decreased during the application of chemotherapy. After the application of chemotherapy, the concentrations of blood glucose and glucose in the brain became higher. The concentrations of both showed a decrease in the same pattern as the simulation results without therapy. Virotherapy and combination therapy were able to inhibit the growth of glioma cells in the long term. The concentrations of immune cells, blood glucose, and glucose in the brain were more stable when compared with without therapy. Blood glucose is still within the normal range of basal glucose. Parameters in the form of infection rate and viral burst size are important parameters in the success of therapy involving virotherapy. The effectiveness of virotherapy and the combination therapy (chemotherapy and virotherapy) has a greater effectiveness value than the effectiveness of chemotherapy alone when viewed from the difference in concentrations of glioma cells each year and the average value of differences in concentrations of glioma cells with and without therapy.