Effects of CCN1 and Macrophage Content on Glioma Virotherapy: A Mathematical Model

Abstract

Oncolytic virus (OV) is a genetically engineered virus that can selectively replicate in and kill tumor cells while not harming normal cells. OV therapy has been explored as a treatment for numerous cancers including glioblastoma, an aggressive and devastating brain tumor. Experiments show that extracellular matrix protein CCN1 limits OV therapy of glioma by orchestrating an antiviral response and enhancing the proinflammatory activation and migration of macrophages. Neutralizing CCN1 by antibody has been demonstrated to improve OV spread and tends to increase the time to disease progression. In this paper, we develop a mathematical model to investigate the effects of CCN1 on the treatment of glioma with oncolytic herpes simplex virus. We show that numerical simulations of the model are in agreement with the experimental results and then use the model to explore the anti-tumor effects of combining antibodies with OV therapy. Model simulations suggest that the macrophage content of the tumor is a critical factor to the success of OV therapy and to the reduction in tumor volume gained with the CCN1 antibody.

1 Introduction

Glioblastoma multiforme (GBM) is the most devastating brain tumor. Despite aggressive therapy involving tumor resection, radiation and chemotherapy, the median survival time from diagnosis is 15 months (Stupp et al. 2005). Oncolytic virus (OV) is a genetically manipulated virus that can selectively replicate in and kill tumor cells, while not harming normal, healthy cells (Msaouel et al. 2009). Upon lysis of an infected tumor cell, the newly formed viruses burst out and infect other tumor cells.

Oncolytic viral therapy has been explored as an approach to combat aggressive tumors, including glioblastoma (Freeman et al. 2006; Haseley et al. 2009; Lun et al. 2005). The efficacy and toxicity of OV are being investigated in clinical trials (Heo et al. 2013; Hwang et al. 2011; Markert et al. 2009; Nakao et al. 2011), but achieving therapeutic efficacy remains a challenge (Patel and Kratzke 2013; Vähä-Koskela and Hinkkanen 2014). One of the factors that limits OV therapy is the antigenicity of the infected tumor cells; the immune system recognizes these cells and destroys them together with the viruses inside. Past and ongoing studies consider the combination of OV therapy with immune suppressive drugs (Fulci et al. 2006; Thorne et al. 2010).

Another factor that reduces the efficacy of OV therapy is the adhesiveness of the extracellular matrix (ECM) in the tumor microenvironment, which slows the free movement of extracellular viruses. Treatment of glioma with chondroitinase ABC I (Chase ABC) to ‘loosen’ the ECM scaffold in order to increase the efficacy of OV therapy was explored by Dmitrieva et al. (2011) and Kim et al. (2014).

Still another factor that limits the efficacy of OV treatment in glioma is CCN1, an extracellular matrix protein known to be involved in angiogenesis, cell migration and inflammation (Emre and Imhof 2014; Lau 2012). Kurozumi et al. (2008) showed that CCN1 is upregulated during oncolytic herpes simplex (HSV-1) infection of glioma. Haseley et al. (2012) subsequently found that exogenous CCN1 orchestrated a type I interferon (IFN) antiviral response that reduced viral replication and limited cytolytic efficacy. The effect was mediated by the binding of CCN1 to the cell surface integrin $\alpha _6\beta _1$; consequent secretion of IFN-$\alpha$ was essential for the innate antiviral effect (Haseley et al. 2012). OV-induced CCN1 also increased migration of macrophages toward virus-infected cells by direct stimulation through binding integrin $\alpha _\mathrm{M}\beta _2$ and by the induction of monocyte chemoattractant protein-1 (MCP-1) in glioma cells. It further also increased the proinflammatory activation of macrophages which caused secretion of factors, such as IFN-$\gamma$ and IL1-$\beta$ (Thorne et al. 2014). In this study, HSV-1 was injected into tumor-bearing nude mice and neutralizing CCN1 treatment with antibody indicated a reduction in tumor volume and a strong trend toward an increase in time to disease progression.

In the present paper, we develop a mathematical model that corresponds to the experimental setup of Thorne et al. (2014). The model, presented in Sect. 2, is represented by a system of partial differential equations. Parameter estimation is provided in Appendix 7.1; numerical results follow in Sect. 4. We show that the model simulations are in agreement with the experimental results and then use the model to propose an explanation for the large variation in response to treatment observed in Thorne et al. (2014). Based on this explanation, we can gain insight into which tumors will respond most significantly to a neutralizing CCN1 antibody.

2 Mathematical Model

The mathematical model is based on the network shown in Fig. 1. The model variables are listed in Table 1 together with their units. Descriptions of model parameters are given in Table 2.

Fig. 1

Model interaction network. Uninfected tumor cells become infected upon entry of a free virus. Infected cells undergo lysis resulting in release of free viruses. Infected cells produce proteins CCN1 and MCP-1 which are chemoattractants for macrophages. CCN1 orchestrates an antiviral response and also inhibits tumor growth. CCN1 further causes proinflammatory activation of macrophages and induces killing of infected cells and virus by macrophages. Macrophages activated by CCN1 signal infected glioma cells to increase production of MCP-1

Table 1 Model variables and units

Table 2 Model parameter descriptions

Tumor cells ($x$) become infected ($y$) by extracellular virus ($v$). Upon lysis, infected cells become dead cells ($n$) while releasing their newly formed viruses to the ECM. The infected tumor cells secrete protein CCN1 and macrophages are attracted to the tumor by CCN1 and MCP-1. The presence of MCP-1 in the tumor microenvironment was established by Thorne et al. (2014). We assume MCP-1 is produced by the infected cells and that the production is enhanced by macrophages, both of which are supported by Thorne et al. (2014). Finally, macrophage killing of both extracellular viruses and infected tumor cells is enhanced by CCN1 (Thorne et al. 2014).

We proceed to develop a dynamical system based on the network shown in Fig. 1. The system of differential equations includes diffusion for cells, viruses and proteins, as well as advection of cells with the same velocity $\mathbf {u}$ for all the cells. Although clinical GBM can have very complex geometries, the subcutaneous rear flank tumors in mice, as in Thorne et al. (2014), are typically close to an oblate spheroid in shape; in some rare cases, the tumors can be very nearly spherical. Therefore, for computational purposes, we assume the tumor is spherical and the radius grows in time in a radially symmetric manner; we denote the radius by $R(t)$. We additionally assume all the variables are spherically symmetric, so that $\mathbf {u}=u(r,t)\frac{z}{r}$, where $z$ is a point in the 3d space $\mathbb {R}^3$ with $|z|=r$.

Uninfected tumor cells (x) Proliferation of uninfected tumor cells occurs at rate $\lambda _\mathrm{x}$, and we assume proliferation is inhibited in the presence of CCN1 due to upregulation of mediators of the type I interferon (IFN) response (Li et al. 2013). The cells become infected with virus at a rate proportional to $\beta$ which takes into account the probability of successful viral entry upon contact with a cell. The equation for uninfected tumor cell density, $x(r,t)$, is then given by

$$\begin{aligned} \dfrac{\partial {x}}{\partial {t}}+\underbrace{\dfrac{1}{r^2}\dfrac{\partial }{\partial r}\left( r^2ux\right) }_{\text {advection}}-\underbrace{D\dfrac{1}{r^2}\dfrac{\partial {}}{\partial {r}}\left( r^2\dfrac{\partial {x}}{\partial {r}}\right) }_{\text {diffusion}} =\underbrace{\dfrac{\lambda _x}{1+k_xC} x}_{\text {proliferation}}-\underbrace{\beta _\mathrm{x} x v}_{\text {infection}}. \end{aligned}$$

(1)

The source of diffusion (or dispersion) of cells is the random motion of particles that tend to move from high concentrations to low concentrations.

Infected tumor cells (y) Infected tumor cells undergo lysis at a rate $d_\mathrm{y}$ due to high viral replication which causes the cells to burst. Lysis is inhibited by CCN1 due to activation of the cellular antiviral defense response (Haseley et al. 2012). Infected cells can also be killed by macrophages; we assume the rate of killing is enhanced by the presence of CCN1 (Thorne et al. 2014). Thus, the evolution of the infected tumor cell density, $y(r,t)$, is determined by the equation

$$\begin{aligned} \dfrac{\partial {y}}{\partial {t}}+\underbrace{\dfrac{1}{r^2}\dfrac{\partial }{\partial r}\left( r^2uy\right) }_{\text {advection}}- \underbrace{D\dfrac{1}{r^2}\dfrac{\partial {}}{\partial {r}}\left( r^2\dfrac{\partial {y}}{\partial {r}}\right) }_{\text {diffusion}}= & {} \underbrace{\beta _\mathrm{x} x v}_{\text {infection}}-\underbrace{\delta _\mathrm{y}y M\left( 1+\dfrac{\alpha _\mathrm{C}C}{k_\mathrm{C}+C}\right) }_{\text {killing by macrophage}}\nonumber \\&-\underbrace{\dfrac{d_y}{1+k_yC} y}_{\text {lysis}}. \end{aligned}$$

(2)

Dead tumor cells (n) We account for the presence of cells that have been killed by macrophage or lysis by incorporating the density of dead tumor cells, $n(r,t)$. We assume that these dead cells are removed at a rate $d_\mathrm{n}$. The equation for $n(r,t)$ is then

$$\begin{aligned} \dfrac{\partial {n}}{\partial {t}} +\underbrace{\dfrac{1}{r^2}\dfrac{\partial }{\partial r}\left( r^2un\right) }_{\text {advection}}- \underbrace{D\dfrac{1}{r^2}\dfrac{\partial {}}{\partial {r}}\left( r^2\dfrac{\partial {n}}{\partial {r}}\right) }_{\text {diffusion}}= & {} \underbrace{\delta _\mathrm{y}y M\left( 1+\dfrac{\alpha _\mathrm{C}C}{k_\mathrm{C}+C}\right) }_{\text {killing by macrophage}}\nonumber \\&+\underbrace{\dfrac{d_y}{1+k_yC} y}_{\text {lysis}}-\underbrace{d_\mathrm{n} n}_{\text {removal}}. \end{aligned}$$

(3)

Macrophages (M) The density of proinflammatory macrophages, $M(r,t)$, is determined by the equation

$$\begin{aligned}&\dfrac{\partial {M}}{\partial {t}}+ \underbrace{\dfrac{1}{r^2}\dfrac{\partial }{\partial r}\left( r^2uM\right) }_{\text {advection}} - \underbrace{D\dfrac{1}{r^2}\dfrac{\partial {}}{\partial {r}}\left( r^2\dfrac{\partial {M}}{\partial {r}}\right) }_{\text {diffusion}} =-\underbrace{\dfrac{1}{r^2}\dfrac{\partial {}}{\partial {r}}\left( r^2\chi _\mathrm{P}M\dfrac{\partial {P}}{\partial {r}}\right) }_{\text {chemotaxis by P}}\nonumber \\&\qquad -\underbrace{\dfrac{1}{r^2}\dfrac{\partial {}}{\partial {r}}\left( r^2\chi _\mathrm{C}M\dfrac{\partial {C}}{\partial {r}}\right) }_{\text {chemotaxis by C}}+\underbrace{\lambda _\mathrm{M}\left( 1+\dfrac{\alpha _\mathrm{MC}C}{k_\mathrm{MC}+C}\right) }_{\text {activation}} -\underbrace{d_\mathrm{M} M}_{\text {death}}. \end{aligned}$$

(4)

In addition to advection and diffusion, macrophages undergo directed movement via chemotaxis. While MCP-1 is a known chemoattractant for macrophages, recent evidence shows that CCN1 can also induce direct migration in macrophages (Thorne et al. 2014). The first two terms on the right-hand side of Eq. (4) take into account chemotaxis by MCP-1 and CCN1, respectively.

Glioblastoma cells secrete various cytokines that attract tumor-associated macrophages (TAM); GBM biopsy specimens showed TAM infiltrated and located within the tumor with no difference between central and peripheral tumor areas (Roggendorf et al. 1996). Therefore, for simplicity, we choose the source of macrophages, $\lambda _\mathrm{M}$, to be constant. We also assume that CCN1 enhances the proinflammatory activation of macrophages (Thorne et al. 2014).

Free virus (v) The density of free virus in the interstitial space, $v(r,t)$, is modeled according to the equation

$$\begin{aligned} \dfrac{\partial {v}}{\partial {t}} -\underbrace{D_\mathrm{v}\dfrac{1}{r^2}\dfrac{\partial {}}{\partial {r}}\left( r^2\dfrac{\partial {v}}{\partial {r}}\right) }_{\text {diffusion}} = \underbrace{\dfrac{bd_y}{1+k_yC} y}_{\text {lysis}}-\underbrace{\delta _\mathrm{v}vM\left( 1+\dfrac{\alpha _\mathrm{C}C}{k_\mathrm{C}+C}\right) }_{\text {killing by macrophage}} -\underbrace{\beta _\mathrm{v} xv}_{\text {infection}}-\underbrace{d_\mathrm{v} v}_{\text {clearance}}. \end{aligned}$$

(5)

Free viruses are released through lysis of infected cells with burst size $b$. We assume that macrophages ingest free virus at the rate $\delta _\mathrm{v}$, and CCN1 further enhances this killing as it does for the infected cells. Free virus is lost through viral entry into a tumor cell (upon infection) as well as through viral clearance mechanisms.

MCP-1 (P) Monocyte chemotactic protein-1 (MCP-1), also commonly referred to as CCL2, is produced by infected glioma cells (Thorne et al. 2014). We assume that there is also a constant source of MCP-1, $\sigma _\mathrm{P}$, but do not explicitly include expression of MCP-1 by healthy glioma cells. This assumption is supported by the experimental results of Thorne et al. (2014) which show that MCP-1 is significantly overexpressed, as much as ninefold, in infected glioma cells compared to control glioma cells. The same work also suggests that CCN1 activates macrophages which then signal glioma cells to secrete more MCP-1 (Thorne et al. 2014). The evolution of the concentration of MCP-1, $P(r,t)$, is therefore determined by the equation

$$\begin{aligned} \dfrac{\partial {P}}{\partial {t}} - \underbrace{D_\mathrm{P}\dfrac{1}{r^2}\dfrac{\partial {}}{\partial {r}}\left( r^2\dfrac{\partial {P}}{\partial {r}}\right) }_{\text {diffusion}} =\underbrace{\sigma _\mathrm{P}}_{\text {source}}+\underbrace{\lambda _\mathrm{P}y\left( 1+\dfrac{\alpha _\mathrm{M}M}{k_\mathrm{M}+M}\right) }_{\text {production}}-\underbrace{d_\mathrm{P} P}_{\text {degradation}} \end{aligned}$$

(6)

where the production term on the right-hand side takes into account the crosstalk between macrophages and glioma cells.

CCN1 (C)

CCN1 is produced primarily by tumor cells within the growing tumor mass. Results of Haseley et al. (2012, Figure 1) indicate that, although there is some CCN1 gene expression in glioma cells in the absence of oncolytic virus, the expression is significantly upregulated following infection with oncolytic virus. Therefore, we assume there is a constant production of CCN1, $\sigma _\mathrm{C}$, as well as production of CCN1 by infected cells at rate $\lambda _\mathrm{C}$. The equation determining the dynamics of the concentration of CCN1, $C(r,t)$, is thus given by

$$\begin{aligned} \dfrac{\partial {C}}{\partial {t}} - \underbrace{D_\mathrm{C}\dfrac{1}{r^2}\dfrac{\partial {}}{\partial {r}}\left( r^2\dfrac{\partial {C}}{\partial {r}}\right) }_{\text {diffusion}} = \underbrace{\sigma _\mathrm{C}}_{\text {source}}+\underbrace{\lambda _\mathrm{C} y}_{\text {production}}-\underbrace{d_\mathrm{C} C}_{\text {degradation}}. \end{aligned}$$

(7)

Advection velocity (u)

We model the tumor as an incompressible fluid in which a velocity field arises due to proliferation and removal of tumor cells.

We assume that the total density of macrophages and tumor cells is constant, denoted by $\theta$, that is,

$$\begin{aligned} x+y+n+M = \theta \end{aligned}$$

(8)

throughout the tumor. Summing Eqs. (1)–(4), we get

$$\begin{aligned} \dfrac{\theta }{r^2}\dfrac{\partial }{\partial r}\left( r^2u\right)&=\dfrac{\lambda _x}{1+k_xC} x-d_\mathrm{n}n-\dfrac{1}{r^2}\dfrac{\partial {}}{\partial {r}}\left( r^2\chi _\mathrm{P}M\dfrac{\partial {P}}{\partial {r}}\right) -\dfrac{1}{r^2}\dfrac{\partial {}}{\partial {r}}\left( r^2\chi _\mathrm{C}M\dfrac{\partial {C}}{\partial {r}}\right) \\&\qquad +\lambda _\mathrm{M}\left( 1+\dfrac{\alpha _\mathrm{MC}C}{k_\mathrm{MC}+C}\right) -d_\mathrm{M} M, \end{aligned}$$

and by integration, we derive the following equation for $u$, the advection velocity:

$$\begin{aligned} u= & {} \dfrac{1}{\theta r^2}\int _0^r s^2\left( \dfrac{\lambda _x}{1+k_xC} x-d_\mathrm{n}n+\lambda _\mathrm{M}\left( 1+\dfrac{\alpha _\mathrm{MC}C}{k_\mathrm{MC}+C}\right) -d_\mathrm{M}M\right) ds\nonumber \\&-\dfrac{\chi _\mathrm{P}}{\theta }M\dfrac{\partial {P}}{\partial {r}}-\dfrac{\chi _\mathrm{C}}{\theta }M\dfrac{\partial {C}}{\partial {r}}. \end{aligned}$$

(9)

2.1 Boundary Conditions:

We assume that the tumor radius changes at the rate of the local velocity, that is,

$$\begin{aligned} \dfrac{dR}{dt} = u \qquad \text {at }\,\, r=R(t). \end{aligned}$$

(10)

Boundary conditions at the tumor center follow from the assumed spherical symmetry:

$$\begin{aligned} \dfrac{\partial {x}}{\partial {r}} = \dfrac{\partial {y}}{\partial {r}} = \dfrac{\partial {n}}{\partial {r}} = \dfrac{\partial {M}}{\partial {r}} = \dfrac{\partial {v}}{\partial {r}} = \dfrac{\partial {P}}{\partial {r}} = \dfrac{\partial {C}}{\partial {r}} = 0 \qquad \text {at }\,\, r=0. \end{aligned}$$

(11)

In the experimental method of Thorne et al. (2014), mice were injected in the rear right flank with glioblastoma cells. When tumors reached an average size of $200\,mm^3$, mice were injected intratumorally with oncolytic virus in the same spatial coordinate as tumor cell implant; the virus is assumed to be in the center as the tumor grows around the injection site. By their design, oncolytic viruses are not able to replicate in normal cells (i.e. outside the tumor). In addition, bioluminescent imaging does not indicate virus present outside of the presumed tumor volume (Thorne et al. 2014, Figure 1c). Thus, we take a no-flux boundary condition for the free virus density at the tumor boundary,

$$\begin{aligned} \dfrac{\partial {v}}{\partial {r}}=0 \qquad \text {at } \,\, r=R(t). \end{aligned}$$

(12)

We assume that the tumor is in a pre-metastatic state, and therefore, cancer cells do not shed out of the tumor. Since the proteins MCP-1 and CCN1 are produced by the tumor cells, we further assume that the proteins, like the tumor cells, follow a no-flux boundary condition. These assumptions result in the following boundary conditions for the tumor cells densities and protein concentrations at the tumor boundary,

$$\begin{aligned} \dfrac{\partial {x}}{\partial {r}}=\dfrac{\partial {y}}{\partial {r}}=\dfrac{\partial {n}}{\partial {r}}=\dfrac{\partial {P}}{\partial {r}} =\dfrac{\partial {C}}{\partial {r}} =0 \qquad \text {at }\,\, r=R(t). \end{aligned}$$

(13)

Experimental results of Desbaillets et al. (1994) showed that monocyte chemoattraction to glioblastoma cells in an in vitro assay was neutralized by anti-MCP-1 antibodies. Hence, we assume that macrophages in blood vessels outside the tumor, where macrophage density is $\tilde{M}$, are infiltrating the tumor due to attraction by MCP-1. This attraction on the boundary is expressed by

$$\begin{aligned} \dfrac{\partial {M}}{\partial {r}}+\alpha (M-\tilde{M})&= 0 \qquad \text {at }\,\, r=R(t) \end{aligned}$$

(14)

with the functional form

$$\begin{aligned} \alpha (P) = \tilde{\alpha }\dfrac{P}{k_\mathrm{P}+P}; \end{aligned}$$

we have not included a dependence on $C$, assuming that MCP-1 is a stronger attractant of monocytes from the blood than CCN1.

3 Parameter Estimation and Macrophage Content

Full details of the parameter estimation for the model are provided in Appendix 7.1. We highlight here the estimation of parameters affected by the macrophage content of the tumor, a parameter that is shown in Sect. 4 to play a significant role in determining treatment outcome.

We denote by $m$ the macrophage content of the tumor, i.e., the ratio of macrophages density to total cells density in the tumor. Then the density of macrophages in a tumor, $M_0$, is given by

$$\begin{aligned} M_0=m\theta \end{aligned}$$

(15)

where $\theta$ is the total density of tumor cells and macrophages (Eq. (8)). Badie and Schartner (2000) found that macrophage content ranged from 5 to 12 % in rat glioma models while studies of human glioblastoma samples indicate macrophage content ranges of 1.5–15 % (Parney et al. 2009) and 8–78 % (Morantz et al. 1979). Since we compare our model to experiments in mice glioma, we take the default value of $m$ to be 0.10. All model parameters and concentrations used in the default case, as estimated in Appendix 7.1, can be found in Tables 3 and 4, respectively, including corresponding references.

Table 3 Model parameter values and references

Table 4 Protein concentrations and cell densities

In Sect. 4, we will also explore model simulations with varying values of $m$ from 0.01 to 0.3. The parameters for activation of macrophages, $\lambda _\mathrm{M}$, and macrophage saturation for MCP-1 production, $k_\mathrm{M}$, are those model parameters that are affected by changing the value of $m$. Both $\lambda _\mathrm{M}$ and $k_\mathrm{M}$ increase linearly with $m$ as indicated by Eqs. (15), (19) and (21). The corresponding values of $\lambda _\mathrm{M}$ and $k_\mathrm{M}$ used for simulations in Sect. 4 are provided in Table 5.

Table 5 Parameter values (dimensionalized) varying with $m$

4 Numerical Results

We first nondimensionalize the model and make a transformation to fix the moving boundary, as described in Appendix 7.2. Numerical simulations of the nondimensionalized system (22–32) with fixed boundary are then performed via an adaptive finite difference upwind scheme, as described in Appendix 7.3.

According to the experimental method of Thorne et al. (2014), we assume that the oncolytic virus is injected into the center of the tumor at time $t=0$. Therefore, we model the initial virus profile $v_0(r) := v(r,0)$ with a Guassian distribution centered at $r=0$:

$$\begin{aligned} v_0(r) = a\exp \left( \dfrac{-r^2}{2\sigma ^2}\right) \end{aligned}$$

(16)

where $a=2.5$ and $\sigma =0.48$. The other initial conditions are given by

$$\begin{aligned} x_0(r) = 1-\tilde{M}, y_0(r) = 0, M_0(r)=\tilde{M}, P_0(r) = 1, C_0(r)=1, R(0)=3\,\hbox {mm}; \end{aligned}$$

(17)

i.e., we assume that initially there are no infected or dead tumor cells.

4.1 Spatio-temporal Evolution of Variables

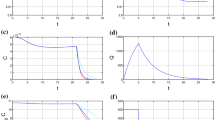
Figures 2 and 3 show the spatio-temporal evolutions of the model variables for the cases of intermediate macrophage content, $m=0.1$, and low macrophage content, $m=0.01$, respectively. Resulting from the injection of virus at time $t=0$, there are early increases in the proportions of infected and dead cells as well as MCP-1 and CCN1 concentrations (Figs. 2 and 3b, c, f, g). Corresponding to the increases in protein concentrations, there is a delayed response by the macrophage population which peaks on days 13 and 19 for $m=0.1$ and $m=0.01$, respectively (Figs. 2d and 3d). As expected, we see a higher proportion of macrophages for $m=0.1$, and accordingly, since the macrophages hinder the propagation of virus through the tumor, there is a higher proportion of uninfected cells at later time points. When $m=0.01$, on the other hand, the infiltrating macrophage population is significantly smaller, thus allowing the system to stabilize at higher proportions of infected and dead cells. Ultimately, the success or failure of therapy is driven by the advection velocity, $u$ (Eq. 28), at the tumor boundary which determines the growth or decay of the tumor radius (Eq. 29). For intermediate macrophage content, $m=0.1$, the advection velocity at the boundary, $r=1$, decreases initially, but following the infiltration of macrophages and consequent elimination of infected cells, the velocity eventually increases approximately linearly (Fig. 3h). However, for $m=0.01$, the advection velocity eventually stabilizes (Fig. 2h).

Fig. 2

(Color online) Spatio-temporal evolution of model variables versus time and $r$, the transformed distance from the tumor center (i.e. scaled by tumor radius $R(t)$) for $m=0.1$. Shown are proportions of a uninfected cells, x b infected cells, y c dead cells, n and d macrophages, M e free virus density, v f MCP-1 concentration, P g CCN1 concentration, C and h advection velocity, u

Fig. 3

(Color online) Spatio-temporal evolution of model variables versus time and $r$, the transformed distance from the tumor center (i.e. scaled by tumor radius $R(t)$) for $m=0.01$. Shown are proportions of a uninfected cells, x b infected cells, y c dead cells, n d macrophages, M e free virus density, v f MCP-1 concentration, P g CCN1 concentration C and h advection velocity, u

4.2 Tumor Volume with OV Therapy

We compare the tumor volume profile for our model with experimental data from two mice studies. The first, a study by Yoo et al. (2012, Figure 5a) measuring the growth of untreated subcutaneous glioma tumors, is simulated by setting $v_0(r)=0$ and $R(0)=3.9\,\hbox {mm}$ to match the initial tumor radius in the experiment. The second set of data, for OV-treated subcutaneous glioma tumors from Thorne et al. (2014, Figure 7), is simulated by taking the initial conditions as given by Eqs. (16) and (17). Our model provides a good fit to both the untreated and OV-treated tumor volume data as seen in Fig. 4. Note that the individual mice display a wide range of responses to the OV treatment (from the least effective (blue and yellow) to complete response (black)), and we can make our simulations fit with these diverse responses by varying the macrophage content, $m$. Corresponding to the differences in advection velocity seen in Figs. 2h and 3h, we see in Fig. 4 that tumors with intermediate to high macrophage content eventually grow exponentially while tumors with low macrophage content, such as $m=0.01$, respond much better to treatment and demonstrate tumor decay and stabilization.

Fig. 4

Simulation of the model for untreated tumor with $m=0.1$ (dashed) and for OV-treated tumor with varying values of $m$ (solid). Open points represent the average experimental data for a group of untreated mice (Yoo et al. 2012). The set of filled points of each color corresponds to the experimental data for an individual OV-treated mouse (Thorne et al. 2014) (Color figure online)

4.3 Tumor Volume with OV Therapy and Antibodies

Experimental data indicate that neutralizing CCN1 with an anti-CCN1 antibody leads to a reduction in tumor volume and a significant increase in time to progression of disease (Thorne et al. 2014). We consider this case by setting $\sigma _\mathrm{C}=\lambda _\mathrm{C}=0$ in Eq. (27), effectively blocking any production of CCN1. Figure 5 shows the results of these simulations for varying values of $m$. The experimental data for mice treated with the antibody (Thorne et al. 2014), to which the model fits well, are also shown.

In addition to using the CCN1 neutralizing antibody, it is also possible to block the macrophage integrin $\alpha _\mathrm{M}\beta _2$ which has been shown to play an important role in initiating the cross talk between glioma cells and macrophages through interaction with CCN1 (Thorne et al. 2014). We simulate the use of this antibody by setting $\alpha _\mathrm{C}=\alpha _\mathrm{MC}=0$ in Eqs. (23), (24) and (25). The three treatment scenarios are compared in Fig. 6, where lines of the same color corresponds to a single $m$ value with OV alone (solid), OV with CCN1 neutralizing antibody (dashed) or OV with $\alpha _\mathrm{M}\beta _2$ antibody (dot dashed). Our model reflects the experimentally observed reduction in tumor volume in the presence of the CCN1 antibody and further suggests that the $\alpha _\mathrm{M}\beta _2$ antibody can lead to even more tumor reduction for large values of $m$. We also observe that the antibodies are most effective for intermediate values of $m$ and only provide a very slight tumor reduction for $m=0.01$.

Fig. 5

Simulation for OV-treated tumors with CCN1 neutralizing antibody for varying values of $m$. The set of filled points of each color corresponds to the experimental data for an individual mouse treated with OV and CCN1 neutralizing antibody (Thorne et al. 2014) (Color figure online)

Fig. 6

(Color online) Simulation for tumors treated with OV alone (solid), OV and CCN1 antibody (dashed), and OV and $\alpha _\mathrm{M}\beta _2$ antibody (dot dashed) for varying values of $m$

4.4 Profiles of Cell Proportions, Virus Density, and Protein Concentrations

Figure 7 shows the spatial averages of proportion of tumor volume occupied by uninfected cells, infected cells, macrophages and dead cells and the average virus density and protein concentrations throughout the duration of treatment (until $t=60$ days) for the three treatment scenarios (OV alone, OV with CCN1 antibody and OV with $\alpha _\mathrm{M}\beta _2$ antibody) with $m=0.1$. Following injection, the free virus population decreases. Correspondingly, as with the detailed spatio-temporal simulations in Figs. 2 and 3, we see early peaks in the infected cells, the dead cells, MCP-1 and CCN1 which cause a delayed peak in the macrophage population. When CCN1 neutralizing antibody is also introduced (dashed), the infected cells and the dead cells increase and the macrophage population is reduced, in agreement with the experimental results (Haseley et al. 2012; Thorne et al. 2014). Although there is a decreased activation of macrophages when CCN1 is blocked, the average MCP-1 concentration eventually becomes higher, which is due to the presence of more infected cells. With the use of the $\alpha _\mathrm{M}\beta _2$ antibody (dot dashed), the proportion of macrophages is smaller at earlier times which is consistent with the larger infected cell population and this results in the increased reduction in tumor volume as seen in Fig. 6.

Fig. 7

(Color online) Model simulation of treatment with OV alone (solid), OV and CCN1 antibody (dashed), and OV and $\alpha _\mathrm{M}\beta _2$ antibody (dot dashed) for $m=0.1$. Shown are the spatial averages of proportion of tumor volume occupied by uninfected cells (a), infected cells (b), macrophages (c), and dead cells (d) and the average virus density (free virus, e), MCP-1 concentration (f) and CCN1 concentration (g) throughout the tumor

5 Sensitivity Analysis

Latin hypercube sampling was performed according to the sensitivity analysis method described by Marino et al. (2008). Table 6 gives the parameters with their ranges, baselines and units. We generated 1000 samples and calculated the partial rank correlation coefficients (PRCC) and p values with respect to the tumor radius at 60 days, i.e. $R(60)$. Figure 8 plots PRCC by parameter in order of increasing p value (shown by color). A positive PRCC value indicates that an increase in the parameter of interest correlates with an increase in tumor size, while a negative PRCC means that a decrease in tumor size results. The parameters that are significantly positively correlated with tumor growth (i.e. with $p<0.01$) are $d_\mathrm{v}$, $\lambda _\mathrm{x}$, $\lambda _\mathrm{M}$ and $\alpha _\mathrm{MC}$, while those that are significantly negatively correlated with tumor growth are $\beta _\mathrm{x}$, $d_\mathrm{y}$, $d_\mathrm{n}$, $d_\mathrm{C}$, $d_\mathrm{M}$ and $k_\mathrm{MC}$. We note that $d_\mathrm{v}$ and $\lambda _\mathrm{x}$ are the most positively correlated parameters; as the viral clearance rate, $d_\mathrm{v}$, or the proliferation rate of uninfected cancer cells, $\lambda _\mathrm{x}$, increases, the tumor volume will increase. The two most negatively correlated parameters are $\beta _\mathrm{x}$ and $d_\mathrm{y}$; as the infection rate of cancer cells, $\beta _\mathrm{x}$, increases or the lysis rate of infected tumor cells, $d_\mathrm{y}$, increases, more virus will enter into tumor cells and begin to multiply fast or, upon increased lysis rate, the newborn virus will be able to re-enter and infect more uninfected tumor cells, thus resulting in decrease of tumor volume. We can similarly interpret the effect of the other positively and negatively correlated parameters. In particular, we note that $\lambda _\mathrm{M}$, the parameter which increases as macrophage content increases, is also highly positively correlated; this observation, in agreement with the results of Sect. 4, is to be expected since macrophages reduce the effect of the viral therapy.

Table 6 Parameters with their ranges, baselines and units for Latin hypercube sampling

Fig. 8

(Color online) Partial rank correlation coefficient (PRCC) values for each of the model parameters resulting from Latin hypercube sampling sensitivity analysis, with respect to tumor radius at $t=60$ days. Bar color corresponds to p value; asterisk indicates $p<0.01$

6 Discussion

In the present work, we have developed a mathematical model which describes the effects of CCN1 on HSV-1 virotherapy of glioma. The model provides good fit to the experimental data of Haseley et al. (2012, 2014) and is in agreement with their conclusion that blocking CCN1 with a neutralizing antibody increases time to progression of disease. The model predicts that tumors with intermediate macrophage content respond most effectively to the antibody. It also indicates that using an alternative antibody which blocks the macrophage integrin $\alpha _\mathrm{M}\beta _2$ could provide increased anti-tumor efficacy. Other combination treatments could be tested with the model, such as blocking or upregulating MCP-1, as well as the effects of varying treatment schedules.

Our model also puts forward an hypothesis to the intriguing question of why seemingly identical mice, as those in the experiments by Thorne et al. (2014), demonstrate such a wide range of responses to OV treatment. We suggest that the variation can be attributed to differences in macrophage content of the tumors. Badie and Schartner (2000) found that macrophage content ranged from 5 to 12 % in rat glioma, while studies of human glioblastoma samples indicate macrophage content ranges of 1.5–15 % (Parney et al. 2009) and as large as 8–78 % (Morantz et al. 1979). While the methods used in Morantz et al. (1979) may have been limited in their ability to distinguish between macrophages and microglia, it is clear from these studies that macrophage content can differ greatly between tumors. In our model, by varying the macrophage content, $m$, we obtained a good fit to experimental data from mice demonstrating a range of treatment responses. The macrophage content significantly affects estimation of the parameter for activation of macrophage, $\lambda _\mathrm{M}$, which captures the complex dynamics of how the immune system of the mouse responds to the OV infection. Simulations indicate that small $m$, i.e., a low macrophage content or, analogously, limited activation of macrophages, corresponds to more effective treatment. This result is in agreement with experimental work which shows that depleting macrophages allows for increased OV titers (Fulci et al. 2007). While perhaps this result is intuitive, the usefulness of the model is in casting the result in quantitative terms. For example, it suggests that even a difference of only a few percent in macrophage content can have a large effect on treatment outcome. This result further emphasizes the important role of CCN1 as an OV-induced activator of macrophages and the clinical potential of combining OV therapy with CCN1 neutralizing antibodies.

Invasion is a hallmark of aggressive glioblastoma, and a great deal of research in the field is moving toward eradicating invading cells in addition to the bulk tumor mass (Xie et al. 2014; Vehlow and Cordes 2013). Unfortunately, the rear flank tumor mice models of Thorne et al. (2014) do not model the invasive nature of glioma as the injected cancer cells are trapped subcutaneously. Therefore, the mathematical model in the present work assumes the tumor to have the constituency of a solid mass and does not consider the dynamics of invasion. However, we can speculate that, by blocking CCN1 and, subsequently, the antiviral immune response, the presence of the oncolytic HSV vector could be prolonged and, theoretically, allow a greater number of distal cancer cells to be infected and killed. Developing models that take these important dynamics of invasion into account would be interesting, but for this, new experimental methods would be necessary that adequately model invasion while allowing for appropriate administration of antibody therapy.

In this paper, we have demonstrated that the significant variations in the OV treatment results for seemingly identical mice can be explained by the different immune responses of the individual mice in terms of attracting macrophages into the tumor microenvironment. But of course there may be other “mice-personalized” parameters that give rise to variances in response to treatment. It would be interesting to determine such potential parameters, but this will also require new experiments.

Appendix

1.1 Parameter Estimation for the Dimensionalized Model

1.1.1 Diffusion and Chemotactic Coefficients

We assume that the diffusion coefficients of all tumor and immune cells are equal and take them to be $8.64\times 10^{-5}$ $\hbox {mm}^2\hbox {day}^{-1}$ (Hao and Friedman 2014; Kim et al. 2011). We assume that the diffusion coefficient, $D_\mathrm{p}$, for a protein $p$ can be calculated from its molecular weight, $M_\mathrm{p}$, by the formula $D_\mathrm{p}=KM_\mathrm{p}^{2/3}$ where $K=0.325~\hbox {mm}^2\hbox {day}^{-1}\hbox {dalton}^{-2/3}$, as explained in Hao and Friedman (2014). The molecular weight of CCN1 is 42027 daltons (Jay et al. 1997). Hence, the diffusion coefficient of CCN1 is estimated by

$$\begin{aligned} D_\mathrm{C} = K\times M_{\mathrm{CCN1}}^{2/3} = 0.325 \times (42027)^{2/3} = 392.9 ~\hbox {mm}^2\hbox {day}^{-1}. \end{aligned}$$

The sensitivity of macrophage to chemoattractants is difficult to estimate and values in the literature include the range from $8.64 \times 10^{4}$ to $1.73\times 10^9$ $\hbox {mm}^5\hbox {g}^{-1}\hbox {day}^{-1}$ (Hao and Friedman 2014; Kim and Friedman 2010). We choose an intermediate value of $\chi _\mathrm{C}=\chi _\mathrm{P}=10^6\,\hbox {mm}^5\hbox {g}^{-1}\hbox {day}^{-1}$.

1.1.2 Estimate of $d_\mathrm{C}$, $\lambda _\mathrm{C},\mu _\mathrm{C}$ from Eq. (7)

We assume that the half-life of extracellular CCN1 is 30 h (Yang and Lau 1991) and accordingly take

$$\begin{aligned} d_\mathrm{c}=\frac{\ln 2}{30} \,h^{-1}=0.55\,\hbox {day}^{-1}. \end{aligned}$$

CCN1 is highly overexpressed in glioma so we consider a typical concentration of CCN1 in tumor to be $C_0=10^{-9}\hbox {g}\,\hbox {mm}^{-3}$ (Zhang et al. 2012). The steady-state of Eq. (7) is

$$\begin{aligned} \sigma _\mathrm{c}+\lambda _\mathrm{c}y-d_cC=0. \end{aligned}$$

(18)

We assume that with no virus present, CCN1 reaches the steady-state concentration $C_0$; therefore, we take

$$\begin{aligned} \sigma _\mathrm{c}=d_cC_0=5.5\times 10^{-10}\,\hbox {g}\,\hbox {mm}^{-3}\,\hbox {day}^{-1}. \end{aligned}$$

Furthermore, we take the density of tumor cells and macrophages (Eq. (8) to be $\theta = 10^6\,\hbox {cells}/\hbox {mm}^3$ (Friedman et al. 2006) and assume that approximately one-tenth of the tumor cells are infected by the virus (Fulci et al. 2006). Hence, we take a typical concentration of infected tumor cells to be $y_0 = 10^5\, \hbox {cells}/\hbox {mm}^3$. Experimental evidence shows that in the presence of oncolytic virus, CCN1 gene expression is approximately three times higher than without virus (Haseley et al. 2012; Fig. 1a). Accordingly, we let $C_1=3C_0$ and from Eq. (18), we deduce that

$$\begin{aligned} \lambda _\mathrm{c}=\dfrac{d_\mathrm{c}C_1-\sigma _\mathrm{c}}{y_0}=1.1\times 10^{-14}\,\hbox {g}\,\hbox {day}^{-1}\,\hbox {cell}^{-1}. \end{aligned}$$

1.1.3 Estimate of $b,d_\mathrm{y},k_\mathrm{y}, d_\mathrm{v},\delta _\mathrm{y},\delta _\mathrm{v}$ from Eqs. (2) and (5)

The lytic cycle of HSV-1 is approximately 12–16 h (Kurozumi et al. 2008). Accordingly, we take $d_\mathrm{y}$, the lysis rate of infected tumor cells, to be $1.5\,\hbox {day}^{-1}$. CCN1 has been shown to induce a cellular antiviral response that reduces viral replication; experimental data measuring luciferase-encoded virus indicates that the quantity of infectious particles is significantly reduced in the presence of CCN1 (Haseley et al. 2012; Figs. 2, 3). Therefore, we estimate that $k_\mathrm{y}=0.1/C_0=10^8\,\hbox {mm}^3\hbox {g}^{-1}$. For oncolytic HSV-1, the burst size ranges from 10 to 100 (Friedman et al. 2006). We choose the burst size, $b$, to be $50\, \hbox {viruses}/\hbox {cell}$. Friedman et al. (2006) estimated the clearance rate of free HSV-1 to be $0.6\,\hbox {day}^{-1}$ in a model that studied the affects of cyclophosphamide on virotherapy of glioma. We take the clearance rate of virus, $\delta _\mathrm{v}$, to be $0.5\,\hbox {day}^{-1}$.

Friedman et al. (2006) did not consider particular immune cell populations and estimated the average immune killing rate of infected cells to be $4.8\times 10^{-7}\,\hbox {mm}^3\,\hbox {cell}^{-1}\,\hbox {day}^{-1}$. We take the killing rate of infected cells by macrophage, $\delta _\mathrm{y}$, to be $4.8\times 10^{-8}\,\hbox {mm}^3\,\hbox {cell}^{-1}\,\hbox {day}^{-1}$. We make the assumption that the rate of macrophage-mediated killing is proportional to the surface area of the target. We assume the tumor cells to be spherical with a diameter of $40\mu m$ (Tönjes et al. 2013). HSV-1 is an icosahedral virus with a diameter of approximately $200\,nm$ (Rochat et al. 2011). Therefore, the ratio of the surface area of a tumor cell to surface area of a virus is approximately $4\times 10^4$, and we accordingly take

$$\begin{aligned} \delta _\mathrm{v} =\dfrac{\delta _\mathrm{y}}{4\times 10^4} = 1.2\times 10^{-12}\,\hbox {mm}^3\,\hbox {cell}^{-1}\,\hbox {day}^{-1}. \end{aligned}$$

1.1.4 Estimate of $\alpha _\mathrm{C},k_\mathrm{C}$ from Eqs. (2) and (5) and $m$

As explained in Sect. 3, we take the default value of the macrophage content, $m$, to be 0.10 and, according to Eq. (15), take the density of macrophage in a typical tumor to be $M_0= 10^5\,\hbox {cells}\,\hbox {mm}^{-3}$. As supported by experimental evidence (Thorne et al. 2014, Figure 3b), we assume the macrophage density under OV treatment, $M_1$, is 1.5 times higher than in a typical tumor. Cytotoxicity experiments by Haseley et al. (unpublished) suggest that macrophage-mediated killing resulted in 1.2 times more cell death in glioma cells overexpressing CCN1 compared to control glioma cells. Therefore, considering the term for macrophage killing of infected cells in Eq. (2), we estimate that

$$\begin{aligned} M_1\delta _\mathrm{y}y_1\left( 1+\dfrac{\alpha _\mathrm{C}C_1}{k_\mathrm{C}+C_1}\right) = 1.2M_0\delta _\mathrm{y}y_0\left( 1+\dfrac{\alpha _\mathrm{C}C_0}{k_\mathrm{C}+C_0}\right) \!. \end{aligned}$$

Here we assume that the number of infected cells is inversely proportional to the number of macrophages, so that $y_1=\frac{y_0}{1.5}$ since $M_1=1.5M_0$. We take $k_\mathrm{C}=2C_0$ and thus solve for $\alpha _\mathrm{C}$ to get $\alpha _\mathrm{C}=1$.

1.1.5 Estimate of $\lambda _\mathrm{x}$, $k_\mathrm{x}$, and $\beta _\mathrm{x}$ from Eq. (1)

Since high expression of CCN1 correlates with poor prognosis, we assume that the inhibition of tumor growth due to the IFN response orchestrated by CCN1 is not as strong as the inhibition of viral replication in Eq. (5). Therefore, we estimate $k_\mathrm{x}=0.01/C_0=10^7\,\hbox {mm}^3\hbox {g}^{-1}$, so that $k_\mathrm{x}=0.1k_\mathrm{y}$. We take the proliferation rate of uninfected glioma cells to be $\lambda _\mathrm{x}=0.2\,\hbox {day}^{-1}$ based on data measuring the growth of subcutaneous glioma tumors in a control group of mice treated with phosphate-buffered saline (Yoo et al. 2012). We choose the infection rate of cells by virus to be $\beta _\mathrm{x}=1.7\times 10^{-8}\,\hbox {mm}^3\hbox {day}^{-1}\hbox {virus}^{-1}$ as estimated by Friedman et al. (2006).

1.1.6 Estimate of $\lambda _\mathrm{M}, \alpha _\mathrm{MC}, k_\mathrm{MC}$ from Eq. (4)

Experimental results by Thorne et al. Thorne et al. (2014) indicate that OV-induced CCN1 significantly increases macrophage migration and enhances the proinflammatory activation of macrophages. Accordingly, we take $\alpha _\mathrm{MC}=2$. We also take $k_\mathrm{MC}=C_0$. The death rate of macrophages, $d_\mathrm{M}$, is taken to be $0.015\,\hbox {day}^{-1}$ (Hao and Friedman 2014; Friedman et al. 2008).

To estimate the constant source of macrophages, $\lambda _\mathrm{M}$, we consider the dynamics of the macrophage density at a spatially homogeneous steady-state without virus. In that case, there is a nonnegative advection velocity, $u$, and Eq. (1) implies that

$$\begin{aligned} \dfrac{1}{r^2}\dfrac{\partial {}}{\partial {r}}(r^2u) = \dfrac{\lambda _\mathrm{x}}{1+k_\mathrm{x}C}. \end{aligned}$$

Substituting this expression into the homogeneous steady state of Eq. (4) gives

$$\begin{aligned} M\left( \dfrac{\lambda _\mathrm{x}}{1+k_\mathrm{x}C}\right) = \lambda _\mathrm{M}\left( 1+\dfrac{\alpha _\mathrm{MC}C}{k_\mathrm{MC}+C}\right) -d_\mathrm{M}M, \end{aligned}$$

so that

$$\begin{aligned} \lambda _\mathrm{M}=\dfrac{\left( \dfrac{\lambda _\mathrm{x}}{1+k_\mathrm{x}C_0}+d_\mathrm{M}\right) M_0}{1+\dfrac{\alpha _\mathrm{MC}C_0}{k_\mathrm{MC}+C_0}}=1.07\times 10^4\,\hbox {cells}\,\hbox {mm}^{-3}\,\hbox {day}^{-1}. \end{aligned}$$

(19)

1.1.7 Estimate of $\lambda _\mathrm{P}, \alpha _\mathrm{M}, k_\mathrm{M}$ from Eq. (6)

We assume that in normal healthy tissue, the concentration of MCP-1 is $P_0=3\times 10^{-13}\hbox {g}\,\hbox {mm}^{-3}$ (Rhodes et al. 2009) and that the degradation rate of MCP-1 is $d_\mathrm{P}=1.7$ $\hbox {day}^{-1}$ (Chen et al. 2012). According to Eq. (6), the steady-state concentration of MCP-1 satisfies the equation

$$\begin{aligned} \sigma _\mathrm{P}+\lambda _\mathrm{P}y\left( 1+\dfrac{\alpha _\mathrm{M}M}{k_\mathrm{M}+M}\right) -d_\mathrm{P}P=0 \end{aligned}$$

(20)

and, therefore, with $y=0$ and $P=P_0$,

$$\begin{aligned} \sigma _\mathrm{P}=d_\mathrm{P}P_0=5.1\times 10^{-13}\,\hbox {g}\,\hbox {mm}^{-3}\,\hbox {day}^{-1}. \end{aligned}$$

Experimental data show that, compared to uninfected glioma cells, MCP-1 expression is approximately 2.5 times larger in infected glioma cells without macrophages present and about 13 times higher in infected glioma cells cultured with macrophages (Thorne et al. 2014, Figure 5a). Accordingly, we let $P_1=2.5P_0$ and $P_2=13P_0$. By Eq. (20), we can estimate $\lambda _\mathrm{P}$, the rate of MCP-1 production by infected glioma cells, by

$$\begin{aligned} \lambda _\mathrm{P} = \dfrac{d_\mathrm{P}P_1-\sigma _\mathrm{P}}{y_0} =7.65\times 10^{-18}\,\hbox {g}\,\hbox {cell}^{-1}\,\hbox {day}^{-1} \end{aligned}$$

and $\alpha _\mathrm{M}$, corresponding to further production of MCP-1 due to macrophage signaling, by

$$\begin{aligned} \alpha _\mathrm{M} = \dfrac{k_\mathrm{M}+M_1}{M_1}\left( \dfrac{d_\mathrm{P}P_2-\sigma _\mathrm{P}}{\lambda _\mathrm{P}y_0}-1\right) = 11.7 \end{aligned}$$

where we assumed that

$$\begin{aligned} k_\mathrm{M} = M_0. \end{aligned}$$

(21)

1.1.8 Estimate of $\tilde{\alpha },k_\mathrm{P},\tilde{M}$ from Boundary Condition Eq. (14)

The density of macrophages in the blood ranges from $2\times 10^4$ to $10^5$ $\hbox {cells}/\hbox {mL}$ (Tietz 1995). Accordingly, we choose $\tilde{M} = 50\,\hbox {cells}\,\hbox {mm}^{-3}$. We also take $\tilde{\alpha } = 1$ and $k_\mathrm{P}=P_0$.

1.2 Nondimensionalized Model with Fixed Boundary

We nondimensionalize the cell and virus densities by $\overline{x} = x/\theta$, $\overline{y} = y/\theta$, $\overline{n} = n/\theta$, $\overline{M} = M/\theta$, $\overline{v}=\frac{v}{b\theta }$. The protein concentrations are nondimensionalized by $\overline{P}=P/P_0$ and $\overline{C}=C/C_0$ where $P_0$ and $C_0$ are the reference concentrations given in Table 4. Correspondingly, other parameters are nondimensionalized:

$$\begin{aligned} \overline{\beta _\mathrm{x}}= & {} b\theta \beta _\mathrm{x}, \overline{\beta _\mathrm{v}}=\beta _\mathrm{v}\theta , \overline{\delta _\mathrm{y}}=\delta _\mathrm{y}\theta , \overline{\delta _\mathrm{v}}=\delta _\mathrm{v}\theta ,\\ \overline{\chi _\mathrm{P}}= & {} \chi _\mathrm{P}P_0, \overline{\chi _\mathrm{C}}=\chi _\mathrm{C}C_0, \overline{k_\mathrm{x}} = k_\mathrm{x}C_0, \overline{k_\mathrm{y}} = k_\mathrm{y}C_0,\\ \overline{\lambda _\mathrm{M}}= & {} \dfrac{\lambda _\mathrm{M}}{\theta }, \overline{\alpha _\mathrm{MC}}=\dfrac{\alpha _\mathrm{MC}}{\theta }, \overline{k_\mathrm{M}}=\dfrac{k_\mathrm{M}}{\theta }, \overline{\tilde{M}}=\dfrac{\tilde{M}}{\theta },\\ \overline{\sigma _\mathrm{p}}= & {} \dfrac{\sigma _\mathrm{p}}{P_0}, \overline{\lambda _\mathrm{p}}=\dfrac{\lambda _\mathrm{p}\theta }{P_0}, \overline{k_\mathrm{P}}=\dfrac{k_\mathrm{P}}{P_0},\\ \overline{\sigma _\mathrm{C}}= & {} \dfrac{\sigma _\mathrm{C}}{C_0}, \overline{\lambda _\mathrm{C}}=\dfrac{\lambda _\mathrm{C}\theta }{C_0}, \overline{k_\mathrm{C}}=\dfrac{k_\mathrm{C}}{C_0}, \overline{k_\mathrm{MC}}=\dfrac{k_\mathrm{MC}}{C_0}. \end{aligned}$$

We eliminate the equation for dead cells by Eq. (8) and fix the moving boundary by making the transformation $\overline{r}=r/R(t)$. Dropping the bar notation for simplicity, we obtain the following nondimensionalized model for $r \in (0,1)$ and $t > 0$:

$$\begin{aligned} \dfrac{\partial {x}}{\partial {t}}&=\dfrac{D}{r^2}\dfrac{\partial {}}{\partial {r}}\left( \dfrac{r^2}{R^2}\dfrac{\partial {x}}{\partial {r}}\right) -\dfrac{1}{r^2}\dfrac{\partial }{\partial r}\left( r^2\dfrac{ux}{R}\right) +\dfrac{r}{R}\dfrac{dR}{dt}\dfrac{\partial {x}}{\partial {r}} + \dfrac{\lambda _x}{1+k_xC} x-\beta _\mathrm{x} x v, \end{aligned}$$

(22)

$$\begin{aligned} \dfrac{\partial {y}}{\partial {t}}&= \dfrac{D}{r^2}\dfrac{\partial {}}{\partial {r}}\left( \dfrac{r^2}{R^2}\dfrac{\partial {y}}{\partial {r}}\right) -\dfrac{1}{r^2}\dfrac{\partial }{\partial r}\left( r^2\dfrac{uy}{R}\right) \nonumber \\&\qquad +\dfrac{r}{R}\dfrac{dR}{dt}\dfrac{\partial {y}}{\partial {r}} + \beta _\mathrm{x} x v-\delta _\mathrm{y}y M\left( 1+\dfrac{\alpha _\mathrm{C}C}{k_\mathrm{C}+C}\right) -\dfrac{d_y}{1+k_yC} y, \end{aligned}$$

(23)

$$\begin{aligned} \dfrac{\partial {M}}{\partial {t}}&= \dfrac{D}{r^2}\dfrac{\partial {}}{\partial {r}}\left( \dfrac{r^2}{R^2}\dfrac{\partial {M}}{\partial {r}}\right) - \dfrac{1}{r^2}\dfrac{\partial }{\partial r}\left( r^2\left( \dfrac{uM}{R}+\dfrac{\chi _\mathrm{P}M}{R^2}\dfrac{\partial {P}}{\partial {r}}+\dfrac{\chi _\mathrm{C}M}{R^2}\dfrac{\partial {C}}{\partial {r}} \right) \right) \nonumber \\&\qquad +\dfrac{r}{R}\dfrac{dR}{dt}\dfrac{\partial {M}}{\partial {r}} +\lambda _\mathrm{M}\left( 1+\dfrac{\alpha _\mathrm{MC}C}{k_\mathrm{MC}+C}\right) -d_\mathrm{M} M, \end{aligned}$$

(24)

$$\begin{aligned} \dfrac{\partial {v}}{\partial {t}}&= \dfrac{D_\mathrm{v}}{r^2}\dfrac{\partial {}}{\partial {r}}\left( \dfrac{r^2}{R^2}\dfrac{\partial {v}}{\partial {r}}\right) +\dfrac{r}{R}\dfrac{dR}{dt}\dfrac{\partial {v}}{\partial {r}} +\dfrac{d_y}{1+k_yC} y\nonumber \\&\qquad -\delta _\mathrm{v}vM\left( 1+\dfrac{\alpha _\mathrm{C}C}{k_\mathrm{C}+C}\right) -\beta _\mathrm{v} xv-d_\mathrm{v} v, \end{aligned}$$

(25)

$$\begin{aligned} \dfrac{\partial {P}}{\partial {t}}&=\dfrac{D_\mathrm{P}}{r^2}\dfrac{\partial {}}{\partial {r}}\left( \dfrac{r^2}{R^2}\dfrac{\partial {P}}{\partial {r}}\right) +\dfrac{r}{R}\dfrac{dR}{dt}\dfrac{\partial {P}}{\partial {r}} +\sigma _\mathrm{P}+\lambda _\mathrm{P}y\left( 1+\dfrac{\alpha _\mathrm{M}M}{k_\mathrm{M}+M}\right) -d_\mathrm{P} P, \end{aligned}$$

(26)

$$\begin{aligned} \dfrac{\partial {C}}{\partial {t}}&= \dfrac{D_\mathrm{C}}{r^2}\dfrac{\partial {}}{\partial {r}}\left( \dfrac{r^2}{R^2}\dfrac{\partial {C}}{\partial {r}}\right) +\dfrac{r}{R}\dfrac{dR}{dt}\dfrac{\partial {C}}{\partial {r}} +\sigma _\mathrm{C}+\lambda _\mathrm{C}y-d_\mathrm{C} C, \end{aligned}$$

(27)

$$\begin{aligned} u&= \dfrac{R}{r^2}\int _0^r s^2\left( \dfrac{\lambda _x}{1+k_xC} x-d_\mathrm{n}(1-x-y-M)\right. \nonumber \\&\qquad \quad \left. +\, \lambda _\mathrm{M}\left( 1+\dfrac{\alpha _\mathrm{MC}C}{k_\mathrm{MC}+C}\right) -d_\mathrm{M}M\right) \,ds\nonumber \\&\qquad -\dfrac{\chi _\mathrm{P}}{R}M\dfrac{\partial {P}}{\partial {r}}-\dfrac{\chi _\mathrm{C}}{R}M\dfrac{\partial {C}}{\partial {r}}, \end{aligned}$$

(28)

$$\begin{aligned} \dfrac{dR}{dt}&= u(1,t). \end{aligned}$$

(29)

With this transformation, the moving boundary condition (Eq. (10)) becomes Eq. (29). The boundary conditions at the tumor center remain unchanged so that

$$\begin{aligned} \dfrac{\partial {x}}{\partial {r}} = \dfrac{\partial {y}}{\partial {r}} = \dfrac{\partial {n}}{\partial {r}} = \dfrac{\partial {M}}{\partial {r}} = \dfrac{\partial {v}}{\partial {r}} = \dfrac{\partial {P}}{\partial {r}} = \dfrac{\partial {C}}{\partial {r}} = 0 \qquad \text {at } r=0, \end{aligned}$$

(30)

while the boundary conditions at the boundary of the tumor, Eqs. (13), (14), become

$$\begin{aligned} \dfrac{\partial {x}}{\partial {r}}=\dfrac{\partial {y}}{\partial {r}}=\dfrac{\partial {n}}{\partial {r}}=\dfrac{\partial {v}}{\partial {r}}=\dfrac{\partial {P}}{\partial {r}} =\dfrac{\partial {C}}{\partial {r}}&=0 \qquad \text {at } r=1, \end{aligned}$$

(31)

$$\begin{aligned} \dfrac{1}{R}\dfrac{\partial {M}}{\partial {r}}+\tilde{\alpha }\dfrac{P}{k_\mathrm{P}+P}(M-\tilde{M})&= 0 \qquad \text {at } r=1. \end{aligned}$$

(32)

1.3 Numerical Scheme

We rewrite the nondimensionalized model (22)–(29) as

$$\begin{aligned} \dfrac{\partial {z}}{\partial {t}} + A_z\dfrac{\partial {z}}{\partial {r}}- \dfrac{D_z}{R^2}\dfrac{\partial {^2z}}{\partial {r^2}}&= F_z, \qquad \qquad z = x,y,M,v,P,C \end{aligned}$$

(33)

$$\begin{aligned} \dfrac{1}{Rr^2}\dfrac{\partial {}}{\partial {r}}(r^2u)&= F, \end{aligned}$$

(34)

$$\begin{aligned} \dfrac{dR}{dt}&= u(1,t) \end{aligned}$$

(35)

where $D_z = D$ for $z = x,y,M$. The advection coefficients are given by

$$\begin{aligned} A_z&= \dfrac{u}{R}-\dfrac{r}{R}\dfrac{dR}{dt}-\dfrac{2D_z}{R^2r},&\qquad \quad z = x,y,M \end{aligned}$$

(36)

$$\begin{aligned} A_z&= -\dfrac{r}{R}\dfrac{dR}{dt} -\dfrac{2D_z}{R^2r},&\qquad \quad z = v,P,C \end{aligned}$$

(37)

and the reaction terms are given by

$$\begin{aligned} F&= \dfrac{\lambda _x}{1+k_xC} x-d_\mathrm{n}(1-x-y-M)+\lambda _\mathrm{M}\left( 1+\dfrac{\alpha _\mathrm{MC}C}{k_\mathrm{MC}+C}\right) -d_\mathrm{M}M \end{aligned}$$

(38)

$$\begin{aligned}&\qquad \qquad -\dfrac{1}{r^2}\dfrac{\partial {}}{\partial {r}}\left( \dfrac{\chi _\mathrm{P}}{R^2}r^2M\dfrac{\partial {P}}{\partial {r}}\right) -\dfrac{1}{r^2}\dfrac{\partial {}}{\partial {r}}\left( \dfrac{\chi _\mathrm{C}}{R^2}r^2M\dfrac{\partial {C}}{\partial {r}}\right) , \nonumber \\ F_\mathrm{x}&= \dfrac{\lambda _x}{1+k_xC} x-\beta _\mathrm{x} x v-xF, \end{aligned}$$

(39)

$$\begin{aligned} F_\mathrm{y}&= \beta _\mathrm{x} x v-\delta _\mathrm{y}y M\left( 1+\dfrac{\alpha _\mathrm{C}C}{k_\mathrm{C}+C}\right) -\dfrac{d_y}{1+k_yC} y-yF,\end{aligned}$$

(40)

$$\begin{aligned} F_\mathrm{M}&=\lambda _\mathrm{M}\left( 1+\dfrac{\alpha _\mathrm{MC}C}{k_\mathrm{MC}+C}\right) -d_\mathrm{M} M-\dfrac{1}{r^2}\dfrac{\partial {}}{\partial {r}}\left( \dfrac{\chi _\mathrm{P}}{R^2}r^2M\dfrac{\partial {P}}{\partial {r}}\right) \nonumber \\&\qquad -\dfrac{1}{r^2}\dfrac{\partial {}}{\partial {r}}\left( \dfrac{\chi _\mathrm{C}}{R^2}r^2M\dfrac{\partial {C}}{\partial {r}}\right) -MF,\end{aligned}$$

(41)

$$\begin{aligned} F_\mathrm{v}&= \dfrac{d_y}{1+k_yC} y-\delta _\mathrm{v}vM\left( 1+\dfrac{\alpha _\mathrm{C}C}{k_\mathrm{C}+C}\right) -\beta _\mathrm{v} xv-d_\mathrm{v} v,\end{aligned}$$

(42)

$$\begin{aligned} F_\mathrm{P}&= \sigma _\mathrm{P}+\lambda _\mathrm{P}y\left( 1+\dfrac{\alpha _\mathrm{M}M}{k_\mathrm{M}+M}\right) -d_\mathrm{P} P,\end{aligned}$$

(43)

$$\begin{aligned} F_\mathrm{C}&= \sigma _\mathrm{C}+\lambda _\mathrm{C}y-d_\mathrm{C} C. \end{aligned}$$

(44)

We formulate a finite difference upwind scheme to solve (30)–(35). Determining an upper bound for $A_z$ in order to calculate the CFL condition (Gustafsson et al. 2013) is not analytically feasible. Thus, we use an adaptive scheme to ensure stability of the numerical method.

The mesh is defined as follows. Let

$$\begin{aligned} r_i = (i-1)\Delta r \end{aligned}$$

for $i=1,\ldots ,N$ where $\varDelta r = \frac{1}{N-1}$; thus $r_1=0$ and $r_\mathrm{n}=1$. We take $N=50$. Let $t_1=0$ and

$$\begin{aligned} t_{n+1} = t_{n}+\varDelta t_{n}, \end{aligned}$$

for $n = 1,2,\ldots$ where $\varDelta t_{n}$ is chosen according to Eq. (47) below. Let $z^n_i$ denote the numerical solution approximating $z(r_i,t_\mathrm{n})$ for $z = x,y,M,v,P,C,u$ and let $R^n$ denote $R(t_\mathrm{n})$.

According to (16) and (17), the initial conditions are $x_i^1 = 1-\tilde{M}$, $y_i^1=0$, $M_i^1 = \tilde{M}$, $v_i^1 = a\exp (r_i^2/(2\sigma ^2))$, $P_i^1 = C_i^1 = 1$ for $i=1,\ldots ,N$ and $R^1 = 3$.

Given $R^{n}$ and $z^{n}$ for $z = x,y,M,v,P,C$ we calculate $R^{n+1}$ and $z^{n+1}$ according to the following scheme:

• 1. Compute $F^{n}, F^{n}_z$ for $z = x,y,M,v,P,C$ according to Eqs. (38)–(44) where the chemotaxis terms in $F$ and $F_\mathrm{M}$ are approximated by the form:

  $$\begin{aligned}&\dfrac{\chi _\mathrm{P}}{(R^n)^2}\dfrac{1}{r_i^2\varDelta r^2}\left( r_{i+\frac{1}{2}}^2\left( \dfrac{M^n_{i+1}+M^n_{i}}{2}\right) (P^n_{i+1}-P^n_{i})\right. \nonumber \\&\quad \left. -r_{i-\frac{1}{2}}^2\left( \dfrac{M^n_{i}+M^n_{i-1}}{2}\right) (P^n_{i}-P^n_{i-1})\right) \end{aligned}$$

  (45)

  for $i=2,...,N-1$ where $r_{i+\frac{1}{2}} = r_i +\frac{\varDelta r}{2}$.

• 2. Compute the advection velocity $u^{n}$, according to Eq. (34), with the trapezoidal rule:

  $$\begin{aligned} u_i^n = \dfrac{1}{r_i^2}\left( r_{i-1}^2u^n_{i-1}+\dfrac{R^n\varDelta r}{2}(r_i^2F^n_i+r^2_{i-1}F^n_{i-1})\right) \end{aligned}$$

  (46)

  for $i=2,\ldots ,N$ where $u^n_1 = 0$.

• 3. Compute $A_z^{n}$ for $z = x,y,M,v,P,C$ according to Eqs. (36) and (37).

• 4. Compute $\Delta t_{n}$ as follows:

  $$\begin{aligned} \Delta t_\mathrm{n} = \dfrac{0.1\Delta r}{\max (|A_\mathrm{x}^n|,|A_\mathrm{v}^n|,|A_\mathrm{P}^n|,|A_\mathrm{C}^n|)} \end{aligned}$$

  (47)

  in order to satisfy the CFL condition.

• 5. Compute $z_i^{n+1}$ for $z = x,y,M,v,P,C$ and $i=2,\ldots ,N-1$ using the upwind scheme:

  $$\begin{aligned} z_i^{n+1}= & {} z_i^n + \Delta t_\mathrm{n}\left[ \dfrac{D_z}{(R^n)^2}\dfrac{1}{\varDelta r^2}\left( z^n_{i+1}-2z^n_i+z^n_{i-1}\right) \right. \nonumber \\&\quad \left. -\left( [A_z^+]_i^n[z_r^-]_i^n+[A_z^-]_i^n[z_r^+]_i^n\right) + [F_z]_i^n \right] \end{aligned}$$

  (48)

  where $A_z^+=\max (A_z,0)$, $A_z^-=\min (A_z,0)$, $[z_r^-]_i^n = \dfrac{z_i^n-z_{i-1}^n}{\Delta r}$, and $[z_r^+]_i^n = \dfrac{z_{i+1}^n-z_{i}^n}{\Delta r}$. Use the boundary conditions (30)–(32) to calculate $z_i^n$ for $i=1,N$.

• 6. Compute $R^{n+1}$, according to Eq. (29), by

  $$\begin{aligned} R^{n+1} = R^{n} + \Delta t_{n} u_\mathrm{n}^{n}. \end{aligned}$$

  (49)