1 Introduction

Various growth curve models such as logistic [1], Richards [2], von Bertalanffy [3], Gompertz [4], and extended Gompertz [5, 6] have been developed over a long time. The growth models have important applications in a wide range of disciplines, including the fields of biology, ecology [7], demography [8], population dynamics, finance, econometrics. When growth curves are applied in real-life problems, usually, a class of growth curves is chosen for the data. The best model is selected from the class of growth curves, based on some ‘model selection criteria’ such as AIC [9] and BIC [10,11,12]. Selection of the suitable model(s) is challenging from the sigmoidal size–time relationship.

Relative growth rate (RGR) [13] plays an important role in understanding the rate of growth associated with the growth process. Let X(t) be the size of the growth process at time t and R(t) be the RGR at time t. Mathematically, R(t) is defined by

$$\begin{aligned} R(t) = \frac{1}{X(t)} \frac{\mathrm {d}X(t)}{\mathrm {d}t} = \frac{\mathrm {d}\ln X(t)}{\mathrm {d}t}. \end{aligned}$$
(1)

Research under the growth curve domain involves formulating and identifying growth curves, and RGR is the yardstick for evaluating growth rates [5, 7, 14]. For an exponential growth curve model, RGR is theoretically constant for all mutually exclusive and exhaustive time intervals. However, the case is not the same for more sophisticated laws where RGR is not constant. When the RGR is linearly decreasing as a function of size, the growth process is logistic. Unfortunately, it is impossible to obtain a perfectly linear shape from real data, which makes it difficult to choose an appropriate model [15]. Likewise, if RGR decreases, we cannot determine whether the growth process is logistic, Gompertz, or something else. For sigmoidal growth curves, RGR usually takes two possible shapes: decreasing and bell-shaped, and its asymptotic value is 0. A variety of growth models makes the identification of a growth law inconclusive in most cases.

Recently, Bhowmick et al. [16] proposed a growth metric, namely interval-specific rate parameter (ISRP), which is defined as follows. Let the relative growth of any growth law be of the following form

$$\begin{aligned} \frac{1}{X(t)} \frac{\mathrm {d}X(t)}{\mathrm {d}t} = b \mathrm {g}(t) ~~~\text{ or }~~~ \mathrm {g}(X(t)). \end{aligned}$$
(2)

The authors defined the ISRP or \(b(\Delta t)\) specific to a model as the weighted sum of RGR over the unit time interval which can be expressed as

$$\begin{aligned} b(\Delta (t)) = \frac{1}{\Delta t} \int _{t_1}^{t_2} w(t) \frac{1}{X(t)} \frac{\mathrm {d}X(t)}{\mathrm {d}t} \mathrm {d}t \end{aligned}$$
(3)

where w(t) is \(\mathrm {g}(t)^{-1} ~\text{ or }~ \mathrm {g}(X(t))^{-1}\) given in Eq. (2). In contrast to the RGR, the ISRP remains constant for true growth laws based on the data being analyzed. It is important to note that the ISRP form is model-dependent, and we need to check separately for each possible model. There are several studies [17,18,19] which developed a ‘goodness of fit test’ to test a growth model. However, there is no such model-independent growth metric to guide about which model should be selected and which should not. A new model invariant growth metric is therefore necessary, which can be model invariant like RGR and distinguish growth curves clearly.

This article proposes a parallel measure of RGR, called instantaneous maturity rate (IMR), which allows us to distinguish one growth curve family from another and characterize growth curves. Additionally, we have explained how IMR can be used to select models step by step. We provide the estimation technique of IMR and derive the asymptotic distribution of IMR. Finally, we illustrate the estimation technique and its performance using simulation and real data.

The organization of the paper is as follows. We formulate a new growth rate measure and derive the IMR of various growth models in Sect. 2. We provide a step by step model selection techniques using IMR in Sect. 2.2. The estimation procedure of IMR and the distribution of IMR are given in Sect. 3. In Sect. 4.1, we provide simulation study to show the applicability of IMR. Section 4.2 is devoted to illustrate the application of IMR in the identification of growth curves using real data. Concluding remarks are given in Sect. 5.

2 Instantaneous maturity rate

According to the definition (Eq. 1), RGR is the growth rate for a specific time period relative to the current size. The RGR function does not depend on any information regarding the entire growth process or the asymptotic size. For any time point, an experimenter needs to know how much RGR a species needs to reach the usual size. The hazard function in survival analysis is similar to this, but in a reverse fashion. In survival analysis, the experimenter is interested in the instantaneous failure rate or hazard rate at time point t. The hazard rate is the probability density function of the conditional distribution that the system will fail in the interval \((t,t+\Delta t)\) given that it has survived up to the time point t.

For a specific time point t, we define the instantaneous maturity rate as the ratio of two quantities. The numerator is the instantaneous relative growth rate (RGR) at time t. The denominator is the cumulative relative growth rate (CRGR) yet to reach asymptotic size. So mathematically, IMR m(t) at time t is defined as

$$\begin{aligned} m(t) = \frac{R(t)}{\int \limits _{t}^{\infty }R(u)\mathrm {d}u}, \end{aligned}$$
(4)

where R(t) is RGR at time t. For growth model which has a parameter representing the asymptotic size (K), the denominator can be written as \(\int \limits _{t}^{\infty }R(u)\mathrm {d}u = \int \limits _{t}^{\infty }\frac{1}{X(u)}\frac{\mathrm {d}X(u)}{\mathrm {d}u}\mathrm {d}u = \int \limits _{X(t)}^{K}\mathrm {d} \ln (X(u)) = \ln K - \ln X(t)\). Hence, IMR at time t can also be written as \(m(t) = \frac{R(t)}{\ln K - \ln X(t)}\). If the asymptotic size is infinite, for example, exponential growth, then \(m(t)=0\) for all time point t. For the exponential growth, RGR at any time is constant and the RGR required to reach the asymptotic size is infinite. Hence, the ratio of the two quantities in Eq. (4) will be zero.

Another important remark about IMR is that it is a scale-invariant measure of growth. To understand this, let us consider a scale transformation of X(t) by \(Z(t) = a X(t)\). Also, let \(R_Z(t)\), \(R_X(t)\) be the RGR of Z(t) and X(t), respectively. Since RGR is a scale-invariant measure, we have, \(R_Z(t) = R_X(t)\). Hence, the invariance of IMR follows from Eq. (4). Let us consider the growth process, \(Y(t) = \frac{X(t)}{K}\). The IMR of Y(t) is given by \(-\frac{1}{\ln Y(t)} \frac{\mathrm {d}\ln Y(t)}{\mathrm {d}t}\). So in this case, IMR is the RGR of \(\ln Y(t)\) with a negative sign. Recently, Chakraborty et al. [20] proposed a unification function for a broad class of growth models using RGR, which is given by

$$\begin{aligned} R(t) = \frac{r}{b^d} y^a(1-y^b)^d t^{c-1}. \end{aligned}$$
(5)

The class of models can also be represented uniquely by IMR and which is given by

$$\begin{aligned} m(t) = \frac{r}{b^d} y^a\frac{(1-y^b)^d}{-\ln (y)} t^{c-1}. \end{aligned}$$
(6)

We shall discuss the IMR of various growth curves and their properties later. IMR can take various shapes like increasing, decreasing, constant, sigmoidal, bell-shaped, bathtub. If IMR is decreasing/constant, then RGR takes decreasing shape. We have \(R(t) = m(t) \times (\ln K - \ln X(t))\). R(t) is a decreasing function since \(\ln K - \ln X(t)\) is always a decreasing function of time and given that IMR is decreasing or constant. However, the converse is not true. For example, in the case of logistic RGR decreases, while IMR increases. Thus, the RGR profile may fail to identify the underlying growth curve model that essentially is a limitation of characterizing various growth laws using RGR. In comparison, IMR has that advantage. Now, we demonstrate how IMR can be more advantageous in identifying growth curves in comparison with RGR.

We consider two different growth laws Richards and Gompertz, for this purpose. We see from Fig. 1 that for both curves, shape of RGR is a decreasing function of both size and time. However, the shape of IMR over time of Gompertz growth is constant, while the shape of the IMR of Richards is sigmoidal over time. Hence, the identification of growth curves using IMR is relatively easier in comparison with RGR.

Fig. 1
figure 1

Plot of RGR over size (Column-1), RGR over time (Column-2), and IMR over time (Column-3) for Gompertz and Richards model. Sub-figures I-III are given for Gompertz growth, and sub-figures IV-VI are given for Richards growth. The plots of RGR over both time and size do not distinguish the growth laws clearly. However, if we compare the IMR over time, we can easily distinguish between Gompertz and Richards growth

Full size image

2.1 Characterization of growth curves using IMR

Theorem 1

IMR uniquely characterizes a growth law.

Proof

The IMR of a growth curve at time t is denoted by m(t) and defined by

$$\begin{aligned} m(t) = \frac{R(t)}{\ln K - \ln {X(t)}}. \end{aligned}$$
(7)

Let \(X_0\) be the initial size. From the definition of IMR, we get

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}\ln {X(t)}}{\ln K - \ln {X(t)}}&= m(t) \mathrm {d}t \\ \implies \frac{\ln K - \ln {X(t)}}{\ln K - \ln {X_0}}&= e^{-\int \limits _0^t m(u) \mathrm {d}u} \end{aligned} \end{aligned}$$
(8)
$$\begin{aligned} \implies R(t) = \left( \ln K - \ln {X_0}\right) e^{-\int \limits _0^t m(u) \mathrm {d}u} m(t) \end{aligned}$$
(9)

Again from Eq. (8), we get

$$\begin{aligned} \begin{aligned}\frac{\ln X(t) - \ln {X_0}}{\ln K - \ln {X_0}}&= 1- e^{-\int \limits _0^t m(u) \mathrm {d}u}\\ \implies X(t)&= X_0 e^{\left[ \ln {\frac{K}{X_0}} \left( 1- e^{-\int \limits _0^t m(u) \mathrm {d}u}\right) \right] } \\ \implies X(t)&= X_0 e^{\left[ b' \left( 1- e^{- M(t)}\right) \right] }\end{aligned} \end{aligned}$$
(10)

where \(M(t) = \int \limits _0^t m(u) \mathrm {d}u\) and \(b' = \ln {\frac{K}{X_0}}\). So if we have any two growth process X(t) and Y(t) with IMR \(m_X(t)\), and \(m_Y(t),\) respectively, then \(m_X(t) = m_Y(t)\) if and only if \(X(t)= Y(t)\) for all t. Hence, IMR can uniquely characterize a growth process.\(\square\)

Table 1 Shapes of IMR for various growth laws
Full size table

2.1.1 Characterization of some popular growth laws

There are a lot of applications for the logistic and Gompertz growth models. The von Bertalanffy growth curve can also be used to describe growth in a number of fields. Note that RGR only admits decreasing shapes for these growth curves. This calls for considering the relatively complex extended Gompertz model, which enables us to capture other possible shapes of RGR. We believe it will be worthwhile to focus on analyzing these four familiar growth curves, which should be of interest to many readers. In order to provide a thumb rule for experimental scientists regarding the characterization of the above-mentioned growth curves, we suggest three corollaries.

Corollary 1.1

The IMR of Gompertz growth curve with \(R(t) = r (\ln K-\ln X(t))\) is given by \(m(t) = r\). Again if \(m(t) = r\), then we get the Gompertz growth law. Hence, any growth process is Gompertz if and only if IMR is constant over time, which characterizes the Gompertz growth law.

Corollary 1.2

Consider the logistic growth curve with RGR \(R(t) = r\left( 1-\frac{X(t)}{K}\right)\). The IMR of logistic growth is an increasing function of time. It is a sigmoidal curve. The maximum value of IMR is r, which is the upper horizontal asymptote of IMR. The minimum value of IMR is \(\frac{R_0}{\ln K - \ln X_0},\) where \(X_0\) is the initial size and \(R_0\) is the initial RGR.

Corollary 1.3

Let us consider the von Bertalanffy growth curve whose RGR is given by \(R(t) = rX(t)^{-1/3}\left( 1-\left( \frac{X(t)}{K}\right) ^{1/3}\right)\). The IMR of von Bertalanffy growth is a decreasing function of time. It is a reversed sigmoidal curve. The minimum value of IMR is \(\frac{r}{3}\), which is the lower horizontal asymptote of IMR.

Table 1 shows the expressions of IMR for various growth laws derived from Eq. (10). A detailed derivation is available in Supplementary Material. In particular, we provide the following theorem concerning the Gompertzian family of growth curves, for the extended Gompertz growth model (hereafter EGM) proposed by Chakraborty et al. [6].

Theorem 2

The RGR of the EGM is

$$\begin{aligned} R(t) = be^{-at^c}t^{c-1}, ~~~~~b,a,c > 0. \end{aligned}$$
(11)

The EGM can be characterized as follows:

  1. 1.

    A growth process is EGM if and only if its IMR is proportional to \(t^{c-1}\). In case of EGM, we have \(m(t) = act^{c-1}\).

  2. 2.

    IMR is increasing (decreasing) \(\iff\) \(\ln \left[ \frac{K-X(t)}{K-X_0}\right]\) is concave (convex) \(\iff\) \(c>1\) \((c \le 1)\) \(\iff\) RGR is bell-shaped (decreasing) function of time.

  3. 3.

    For any four time points \(t_1, t_2, t_3\) and \(t_4\), such that \(\frac{t_1}{t_2} = \frac{t_3}{t_4}\)

    $$\frac{m(t_1)}{m(t_2)} = \frac{m(t_3)}{m(t_4)}.$$

Remark 1

For other sophisticated growth curves, a variety of theorems can be derived. It is important to note that, in many cases, experimental scientists describe a family of growth curves instead of a unique model based on the IMR function. For them, the best-fitted model should be chosen based on a set of model selection criteria such AIC and BIC.

2.2 Proposed model selection scheme

  • Step 1: Empirically estimate IMR based on the given data. The formula for estimation of IMR from data is given in Sect. 3.

  • Step 2: Plot the IMR over time.

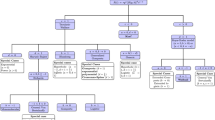
  • Step 3: Identify the possible model(s) based on the shape of IMR and asymptotic size. The shapes are given in Fig. 2.

    1. (a)

      If the IMR is constant, then the underlying model is Gompertz.

    2. (b)

      If IMR decreases with parabolic shape (positive x and y can be major axis), the associated growth model can be any one of extended Gompertz, extended logistic, Korf, Weibull, and general Gompertz.

    3. (c)

      If IMR increases with parabolic shape, the underlying growth model can be extended Gompertz, extended logistic, and general Gompertz.

    4. (d)

      If IMR is sigmoidal, then we can say that the growth model is Richards.

    5. (e)

      If IMR is reversed-sigmoidal, then the suitable growth models can be monomolecular or von Bertalanffy.

    6. (f)

      If the IMR is bell-shaped, then the underlying growth model can be Tsoularis–Wallace. If IMR is bell-shaped, then the corresponding growth model is Weibull.

  • Step 4: If we have more than one possible model, use AIC/BIC to find the best fit model.

Note that the model selection criteria, AIC, and BIC are relative measures. If we choose a class of models none of which are appropriate for approximating the true model, AIC or BIC will still give us the best model. The proposed scheme will be useful in such cases, and based on the shape of the IMR, we can determine the class of growth equations.

Fig. 2
figure 2

According to the shapes of IMR over time, this flowchart shows the classification of the growth curves. There are five different types of IMR shapes. Using these shapes, it is possible to classify and identify the underlying model into a unique specific category of growth law or a family of growth curves

Full size image

2.3 An alternative interpretation of IMR

We explore another interpretation of IMR in this section, as it is an extended measure of growth rate. In the following, the first two theorems explain the relationship between RGR and IMR for two specific growth curves, and the third theorem describes the relationship between RGR and IMR for any growth curve for large t values.

Theorem 3

In the Gompertz growth model, IMR is the relative growth rate of RGR (i.e., RGR of RGR) with a negative sign, at any point in time.

Proof

Differentiating the RGR of Gompertz \(R(t)=r(\ln K - \ln X(t))\) with respect to t and then replacing \(\frac{1}{X(t)}\frac{dX(t)}{dt}\) with R(t), the required result follows.\(\square\)

Theorem 4

In case of EGM, the following relation between RGR and IMR holds true:

$$\frac{1}{R(t)}\frac{\mathrm {d}R(t)}{\mathrm {d}t} + m(t) =\frac{c-1}{t}.$$

Proof

Let us consider the RGR of the EGM proposed by Chakraborty et al. [6].

Taking logarithm of both sides of Eq. (11), we get

$$\begin{aligned} \ln R(t) = \ln b -at^c+(c-1) \ln t. \end{aligned}$$

Differentiating, we get

$$\begin{aligned} \begin{aligned} \frac{1}{R(t)}\frac{\mathrm {d}R(t)}{\mathrm {d}t}&= -act^{c-1} +\frac{c-1}{t} \\ \implies \frac{1}{R(t)}\frac{\mathrm {d}R(t)}{\mathrm {d}t}&= -m(t) + \frac{c-1}{t}, \end{aligned} \end{aligned}$$
(12)

where \(m(t) =act^{c-1}\) is the IMR at time t.\(\square\)

Theorem 5

Let R(t) and m(t) be the RGR and IMR of any growth law at time t, respectively. We define RGR of RGR as \(\frac{1}{R(t)}\frac{\mathrm {d}R(t)}{\mathrm {d}t}\). If the limiting value of RGR of RGR exists, then it must be equal to the limiting value of IMR with a negative sign, i.e., \(\lim \limits _{t \rightarrow \infty }m(t) = -\lim \limits _{t \rightarrow \infty }\frac{1}{R(t)}\frac{\mathrm {d}R(t)}{\mathrm {d}t}\).

Proof

We have \(m(t) = \frac{R(t)}{\ln K - \ln X(t)}\). Note if we find the limiting value of IMR, we get \(\frac{0}{0}\) form, since \(\lim \limits _{t \rightarrow \infty } R(t) = 0\) and \(\lim \limits _{t \rightarrow \infty } [\ln K -\ln X(t)] = 0\). Now applying L’Hospital’s rule, we have

$$\begin{aligned} \lim \limits _{t \rightarrow \infty } m(t) = \lim \limits _{t \rightarrow \infty } \frac{R(t)}{\ln K - \ln X(t)} = -\lim \limits _{t \rightarrow \infty } \frac{1}{R(t)} \frac{\mathrm {d}R(t)}{\mathrm {d}t}. \end{aligned}$$
(13)

\(\square\)

Remark 2

The cumulative relative growth rate can find the time point at which an individual reaches a certain proportion of logarithmic size. In other words, it gives some proportion of maturity. This measure can be used to compare two growth curves. In the case of asymptotic growth, an individual never reaches its asymptotic size in a finite time. So in case, we find that when the individual reaches \(p\%\) of its asymptotic size. For example, to find when an individual reaches its 99% size, we take \(p=0.99\).

Remark 3

In extended growth curves, an individual grows at different rates from the rate of standard growth curves. However, to determine how faster or slower the process grows for extended growth curves with respect to the standard growth curves, we find the ratio of the RGR of extended growth and the standard growth at the same time point. For example, this measure for Gompertz growth can be defined as \(\frac{R(t)}{R_G(t)}\), where R(t) is RGR of any growth curve at time t and \(R_G(t)\) is the same of Gompertz growth. The quantity \(\frac{R(t)}{R_G(t)}\) is proportional to IMR.

Remark 4

It is important to note that IMR is also helpful in unifying a class of growth equations. The unification is an alternative route to characterization. The main idea is to generate many growth equations from a single compact formula. Using the Box-Cox transformation, Garcia [22] proposed a single growth equation that unifies many of the existing sigmoid growth curves. Recently, Chakraborty et al. [20] proposed a novel unification method to characterize a broad class of growth curve models using RGR. Recently, Peckham et al. [23] studied a class of growth equations in which a suitable transformation of the size variable is written as an exponentially weighted average of the transformed initial size and transformed asymptotic size. This idea was further utilized to study the growth equation in a stochastic environment. A key difference between the study of Garcia [22], Chakraborty et al. [20] and Peckham et al. [23] is that the former strategies have advantages in selecting the correct model. Given a set of training data points, the estimated IMR essentially gives the idea of which class of models would be appropriate for drawing inference. In the latter case, studied in Peckham et al. [23], it does not give any advantage in model selection. Moreover, such affine transformation may not be obtainable or difficult to compute for several other growth equations.

2.4 Synergy between IMR and hazard rate in survival analysis

In actuarial sciences and demography, the hazard rate (or force of mortality) provides the most intuitive way to introduce analysts’ assumptions and knowledge in mortality laws [24]. Failure rate/hazard rate is frequently used in survival analysis to measure the frequency of failure of a system or component. Failure rate is defined as the probability of failure in finite interval of time say \((t, t + \Delta t)\), given the age of the component, say t. If F(t) denotes the failure distribution, then the failure rate in the interval \((t, t + \Delta t)\) is \(\frac{F(t+\Delta t) - F(t)}{1 - F(t)}\), for t such that \(F(t) < 1\) [25, 26]. If we divide this quantity by \(\Delta t\) and let \(\Delta t \rightarrow 0\), then we get instantaneous failure rate or hazard rate at time t, say h(t). So \(h(t) = \frac{f(t)}{1 - F(t)}\) or \(\frac{1}{1-F(t)}\frac{\mathrm {d}F(t)}{\mathrm {d}t}\), where f(t) is failure density. Hazard rate is the probability density function of the conditional distribution that the system will fail in \((t, t + \Delta t)\) given that it has survived at time t.

The hazard rate is constant for exponentially distributed failure density. It can also be increasing or decreasing function of time. For example, if failure density follows Weibüll distribution, then the hazard function takes increasing, decreasing, and constant shape depending upon \(c>1\), \(c<1\), and \(c=1\), respectively. A decreasing failure rate (DFR) describes a phenomenon where the probability of an event in a fixed time interval in the future decreases over time. A decreasing failure rate can describe a period of “infant mortality” where earlier failures are eliminated or corrected and correspond to the situation where h(t) is a decreasing function. Increasing failure rate is an intuitive concept caused by components wearing out. Decreasing failure rate describes a system that improves with age.

We consider the following definitions to establish the synergy of IMR with hazard rate.

Definition 1

The cumulative relative growth rate at time t is defined by \(\int \limits _{0}^{t}\frac{\mathrm {d}\ln X(s)}{\mathrm {d}s}\mathrm {d}s = \ln X(t) - \ln X_0\).

Note that the minimum and maximum value cumulative relative growth rate is 0 and \(\ln {K} - \ln {X_0}\), respectively. To relate this with cumulative distribution, we standardize the cumulative relative growth rate by dividing \(\ln {K} - \ln {X_0}\).

Definition 2

Standardized cumulative relative growth rate: The standardized cumulative relative growth rate, S(t), is defined by \(S(t) = \frac{\ln X(t) - \ln X_0}{\ln {K} - \ln {X_0}}\). So S(t) lies between 0 and 1, and S(t) is an increasing function of time t as \(X_t\) is increasing function.

The hazard rate of \(S(t) = \frac{\ln X(t) - \ln X_0}{\ln K - \ln X_0}\) is given by

$$h(t)=\frac{S'(t)}{1-S(t)} = \frac{\frac{1}{X(t)}\frac{\mathrm {d}X(t)}{\mathrm {d}t}}{\ln K - \ln X(t)}.$$

So m(t) has synergy in mathematical form with the hazard rate of S(t). For illustration purposes, we compute the cumulative RGR, S(t) for the Gompertz growth curve. In the case of Gompertz growth, size at time t is given by

$$\begin{aligned} X(t) = X_0 e^{\frac{b}{a}(1-e^{-at})}. \end{aligned}$$
(14)

Also, the relative growth rate of Gompertz growth is \(be^{-at}\), which is proportional to probability density function of exponentially distributed random variable, and the asymptotic size K is \(X_0 e^{\frac{b}{a}}\). For Gompertz growth \(S(t) = 1-e^{-at}\), which is also cumulative distribution function of exponentially distributed random variable. So the standardized cumulative relative growth rate of Gompertz growth is same as cumulative distribution function of exponentially distributed random variable. In case of growth curves IMR reflects how fast the system grows in comparison with Gompertz growth process.

Although the conceptual framework of the two functions is same, the objectives are defined in an opposite sense. The hazard rate is applicable in lifetime distributions where the focus is on modeling the failure pattern of any system. In comparison, IMR is relevant in growth curve modeling. The experimenter is interested in knowing the present maturity status of some biological organisms. IMR is a ratio of two random quantities (RGR and log(size)). It has a distributional structure, unlike the hazard rate. We will discuss the IMR under random environment in Sect. 3.

3 Estimation of IMR in stochastic environment

We have already mentioned that the hazard rate has similarity in mathematical form with the IMR. Hazard rate is applicable in lifetime distributions where the main focus is on modelling the failure pattern of any system. But in comparison IMR is relevant in growth curve modelling where the experimenter is interested to know present maturity status of any species. Note that in case of IMR maturity rate is an indicator of species growth. Although the conceptual framework of two functions is same, the objectives of two problems are defined in opposite sense. Besides this unlike hazard rate, IMR has some distributional structure under the stochasticity of size/RGR variable.

In this section, we study the statistical properties of the empirical estimator of IMR. In the previous sections, we have used the variable X(t) to denote the size at time t, which is typically written in a deterministic differential equation setup. We use the notation \(X_t\) to distinguish a random variable whose realizations are the observed data. We consider \(X_t\) to be the magnitude of a suitably measured size variable at time point t, where \(t=t_1, t_2,\ldots ,t_q,\) and denote \(\mathbf {X}=\left( X(t_1),X(t_2),\ldots , X(t_q)\right) '\) to be the vector of the observations. Suppose that at each time point data are collected on n individuals. Thus, we have n independent and identically distributed (iid) observations at each time point \(t_j\), and the data matrix is given by:

$$\begin{aligned} \mathbf {X}_{n\times q} = \begin{bmatrix} X_{1t_1} &{} X_{1t_2} &{} \cdots &{} X_{1t_q} \\ X_{2t_1}&{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} \ddots &{} \ddots &{} \vdots \\ X_{nt_1} &{}X_{nt_2}&{} \cdots &{} X_{nt_q} \end{bmatrix}, \end{aligned}$$
(15)

where \(\mathbf {X}_{it}\) is the size of the i-th individual on t-th time point; \(i = 1,2,\cdots ,n\) and \(t = t_1,t_2,\cdots ,t_q\). Rows (vector) of the matrix \(\mathbf {X}\) are independent and identically distributed random vector of order q. Let us fix any particular column of \(\mathbf {X}\). Each component of this column vector is independent and identically distributed. Different statistical assumptions regarding the distribution of the data are available in the literature depending on the nature of the problems under study [27,28,29,30,31]. Following Pal et al. [32], we consider the assumption of multivariate normality on the data matrix; that is, \(\mathbf {X}\) follows multivariate normal distribution whose mean is specified by the underlying deterministic growth equation and a symmetric positive definite matrix as its variance–covariance matrix. The further assumption on the structure of the variance–covariance matrix will be explained in a later section. In the following, we consider the Gompertz growth equation as a test bed and develop the estimate of IMR and study its statistical properties. The methodology can be easily extended for other growth equations as well.

3.1 Estimation of IMR for Gompertz growth

We start with the solution of the Gompertz growth equation, which is given by

$$\begin{aligned} X(t) = X_0 e^{\left[ \frac{b}{a}\left( 1-e^{-at}\right) \right] }. \end{aligned}$$
(16)

Let us consider that we have observed the size at 3 equi-spaced time points \(t_1\), \(t_2\), \(t_3\). Let h be the distance between any two time points. Simply putting \(t_1\), \(t_2\), \(t_3\) and taking logarithm in Eq. (16) will lead us to the following system of equations:

$$\begin{aligned} \ln X(t_i) = \ln X_0 -\frac{b}{a}\left( 1-e^{-at_i}\right) ~~~~~ \text{ for }~ i=1,2,3. \end{aligned}$$
(17)

Solving the above three equations for a and b, we get

$$\begin{aligned} a = \frac{1}{h}\ln \left[ \frac{\ln {\left( \frac{X(t_2)}{X(t_1)}\right) }}{\ln \left( \frac{X(t_3)}{X(t_2)}\right) }\right] \end{aligned}$$
(18)

The IMR of Gompertz growth is equal to a. So, based on the data matrix \(\mathbf {X}\), we now write the sample analogue of the estimate of IMR at time \(t_1\) is given by

$$\begin{aligned} \widehat{m(t_1)} = \hat{a} = \frac{\ln \left[ \frac{\ln {\left( \frac{\overline{X_{t_2}}}{\overline{X_{t_1}}} \right) }}{\ln \left( \frac{\overline{X_{t_3}}}{\overline{X_{t_2}}}\right) }\right] }{t_2-t_1}, \end{aligned}$$
(19)

where \(\overline{X_{t_1}} = \frac{1}{n}\sum \limits _{i=1}^n X_{i t_1}\); similarly \(\overline{X_{t_1}}\) and \(\overline{X_{t_2}}\) are defined. It is worth mentioning that similar to the proposal of Modified RGR by Pal et al. [32], IMR also requires three consecutive and equi-spaced time points \(\{t_1, t_2, t_3\}\). IMR of Gompertz growth can be viewed as the RGR of RGR between two consecutive time points, which follows from Eq. (18).

Remark 5

Pal et al. [32] studied in detail the statistical properties of the RGR (both Fisher’s and Modified RGR) for the Gompertz growth equation. This paper aims to devise a new growth measure that would perform better than RGR to identify the underlying growth law. Thus, the Gompertz growth equation is a natural choice for us to study for comparison and link with the existing literature.

3.1.1 Asymptotic distribution

In this section, we obtain the asymptotic distribution of the sample estimate of IMR. Note that \(\widehat{m(t)}\) is a highly nonlinear function of the three random quantities \(\overline{X_{t_i}},~i=1,2,3\), whose joint distribution is multivariate normal. (Hence, each \(\overline{X_{t_i}}\) has marginal normal distribution.) The following lemma gives the key idea to derive the asymptotic distribution [33].

Lemma 1 The Multivariate Delta Method:

Let \(Y_n = \left( Y_{n1}, Y_{n2},\cdots ,Y_{nk}\right) ' \in \mathbb {R}^k\) be a sequence of random vectors such that

$$\sqrt{n} \left( Y_n - \mu \right) \xrightarrow {d} \mathcal {N}\left( \mathbf {0}, \Sigma \right) ,$$

where \(\mu \in \mathbb {R}^k\). Let \(g: \mathbb {R}^k \rightarrow \mathbb {R}\) have derivative \(\Delta _g(\mu )\) at \(\mu \in \mathbb {R}^k,\) and derivatives are nonzero. Then,

$$\sqrt{n} \left[ g\left( Y_n\right) - g(\mu )\right] \xrightarrow {d} \mathcal {N}\left( 0, \Delta _g(\mu )' \Sigma \Delta _g(\mu )\right) .$$

The symbol \(\xrightarrow {d}\) represents the convergence in distribution.

Theorem 6

Let \(\mathbf {X}_{it}\) be the size of the i-th individual on t-th time point; \(i = 1,2,\cdots ,n\) and \(t = 1,2,\cdots ,q\) which follows multivariate normal distribution with mean structure from Gompertz distribution and the specified dispersion matrix \(\Sigma\). Let \(\overline{X_{t}}\) be the mean size at t-th time point. Let us consider the estimate of IMR \(\widehat{m(t)} = \ln \left[ \frac{\ln {\left( \frac{\overline{X_{t+2}}}{\overline{X_{t+1}}} \right) }}{\ln \left( \frac{\overline{X_{t+3}}}{\overline{X_{t+2}}}\right) }\right]\). The sampling distribution of \(\widehat{m(t)}\) is given by \(\mathcal {N}\left( 0, \Delta ' \Sigma \Delta \right) ,\) where

\(\Delta ' = \frac{1}{b \mu _0 \left( e^{-a}-1\right) }\left( \frac{a e^{at}}{\exp \left[ \frac{b}{a}(1-e^{-at})\right] }, \frac{a\left( 1+e^{-a}\right) e^{a(t+1)}}{\exp \left[ \frac{b}{a}(1-e^{-a(t+1)})\right] }, \frac{a}{e^{-a(t+1)} \exp \left[ \frac{b}{a}\left( 1-e^{-a(t+2)}\right) \right] }\right)\).

Proof

For simplicity in notations, let \(\theta = (a,b)'\) denote the parameters from the Gompertz model which are involved in the estimate of IMR and \(\mu _t\) be the Gompertz mean function. We also denote \(\overline{X_{t}}\), \(\overline{X_{t+1}}\) and \(\overline{X_{t+2}}\) as U, V, and W, respectively, and they are normally distributed random variables, by multivariate central limit theorem. So, the estimate of IMR at time t is given by \(\widehat{m(t)} = -\ln \left( \frac{\ln (W/V)}{\ln (V/U)}\right)\). Let us assume \(\phi (U,V,W) = -\ln \left( \frac{\ln (W/V)}{\ln (V/U)}\right)\). Considering the real variable counterpart, differentiating \(\phi (u,v,w)\) partially with respect to u, v, and w we obtain

$$\begin{aligned} \begin{aligned} \frac{\partial \phi }{\partial u}\bigg |_{\theta =\hat{\theta }}&= \frac{1}{u \ln \left( u/v\right) }\bigg |_{\theta =\hat{\theta }} \\&= -\frac{1}{\mu _t \ln \left( \mu _{t+1}/\mu _{t}\right) } \\&= - \frac{1}{\mu _0 \exp \left[ \frac{b}{a}\left( 1-e^{-at}\right) \right] \frac{b}{a}e^{-at}\left( 1-e^{-a}\right) } \\&= \frac{a e^{at}}{b \mu _0 \left( e^{-a}-1\right) \exp \left[ \frac{b}{a}(1-e^{-at})\right] }, \end{aligned} \end{aligned}$$
(20)
$$\begin{aligned} \begin{aligned} \frac{\partial \phi }{\partial v}\bigg |_{\theta =\hat{\theta }}&= \frac{1}{v} \frac{\ln \left( w/u\right) }{\ln \left( v/u\right) \ln \left( w/v\right) }\bigg |_{\theta =\hat{\theta }} \\&= \frac{\ln \left( \mu _{t+2}/\mu _{t}\right) }{\mu _{t+1} \ln \left( \mu _{t+1}/\mu _{t}\right) \ln \left( \mu _{t+2}/\mu _{t+1}\right) } \\&= \frac{1}{\mu _0 \exp \left[ \frac{b}{a}\left( 1-e^{-a(t+1)}\right) \right] } \frac{1-e^{-2a}}{ \frac{b}{a}e^{-a(t+1)}\left( 1-e^{-a}\right) ^2} \\&= \frac{a\left( 1+e^{-a}\right) e^{a(t+1)}}{b\mu _0 \left( 1-e^{-a}\right) \exp \left[ \frac{b}{a}(1-e^{-a(t+1)})\right] }, \end{aligned} \end{aligned}$$
(21)

and

$$\begin{aligned} \begin{aligned} \frac{\partial \phi }{\partial w}\bigg |_{\theta =\hat{\theta }}&= \frac{1}{w \ln \left( v/w\right) }\bigg |_{\theta =\hat{\theta }} \\&= -\frac{1}{\mu _{t+2} \ln \left( \mu _{t+2}/\mu _{t+1}\right) } \\&= - \frac{1}{\mu _0 \exp \left[ \frac{b}{a}(1-e^{-a(t+2)})\right] \frac{b}{a}e^{-a(t+1)}\left( 1-e^{-a}\right) } \\&= \frac{a}{b \mu _0\left( e^{-a}-1\right) e^{-a(t+1)} \exp \left[ \frac{b}{a}\left( 1-e^{-a(t+2)}\right) \right] }, \end{aligned} \end{aligned}$$
(22)

Using multivariate delta method, we obtain \(\sqrt{n}\left[ \widehat{m(t)} - m(t)\right] \sim \mathcal {N}\left( 0, \Delta ' \Sigma \Delta \right) ,\) where \(\Delta ' = \left( \frac{\partial \phi }{\partial u}, \frac{\partial \phi }{\partial v}, \frac{\partial \phi }{\partial w}\right) \bigg |_{\theta =\hat{\theta }}\) and \(\Sigma\) is the variance–covariance matrix of the random variables U, V, and W. It is worth noting that convergence to normality is not really unexpected, as the delta method is essentially considered as an extension of the central limit theorem [34].\(\square\)

3.2 General estimator of IMR

Having obtained an estimate of IMR for a specific growth model, we now provide an estimator of IMR for a general growth model. Since IMR is a function of RGR itself, we start our discussion with \(\widehat{R_t}\) which is an estimate of RGR at \(t^{th}\) time point for \((t=1,2,\ldots ,q-1)\). Then, we consider the empirical estimate of IMR as \(\widehat{m(t)} = \frac{\widehat{R_t}}{\widehat{R_t} + \widehat{R_{t+1}} +\cdots + \widehat{R_{q-1}}}\). The construction of the estimator is intuitively clear from the definition IMR itself, in which the integral \(\int \limits _t^{\infty }R(u)\mathrm {d}u\) in the denominator is empirically approximated by summation. Although it appears model-independent estimate (like RGR), it would give a serious problem when the number of time points in which the observations are available is small in number. In addition, at the last time point, the estimate automatically goes to 1. So, we consider another estimator of IMR as follows:

$$\begin{aligned} \widehat{m(t)}=\frac{\ln \left( \frac{\overline{X_{t+1}}}{\overline{X_t}}\right) }{\ln \widehat{K}-\ln \overline{X_t}}, \end{aligned}$$
(23)

where \(\widehat{K}\) is an estimate of asymptotic size K, which is specific to the growth model. In particular, \(\widehat{K}\) can be taken as the nonlinear least-squares estimate of K as well. So, the second estimator is model-dependent.

It is essential to mention that model-dependent measures may perform better than a model-independent measure of growth, as shown by Pal et al. [32]. In the following paragraph, we shall illustrate the estimation procedure in detail and derive the asymptotic distribution of the estimator for another extended Gompertz model discussed by Chakraborty et al. [6]. The computations can be carried out for other growth models in a similar manner.

According to the data setup, we have q observations \((t_i, X_i), i=1,2,\cdots ,q\) and we are interested in fitting the nonlinear Gompertz growth model proposed by Chakraborty et al. [6]

$$\begin{aligned} X_i = X_0 \exp \left[ \frac{b}{ac}\left( 1-e^{-at_i^c}\right) \right] + \epsilon _i,~~ i=1,2,\ldots ,q. \end{aligned}$$
(24)

where \(\mathbb {E}(\epsilon _i)=0\) for all \(i=1,2,\ldots ,n\). Let \(\theta = (a,b,c)'\) and \(\hat{\theta }=\left( \hat{a},\hat{b},\hat{c}\right) '\) be the nonlinear least square estimator of \(\theta\). The estimate of \(\widehat{K}\) is given by \(\widehat{X_0} \exp \left( \frac{\hat{b}}{\hat{a}\hat{c}}\right)\). If we have more replicated observations at each time point, then \(X_i\) will be replaced by the average value \(\overline{X_i}\) before fitting. Under the appropriate regularity conditions and for large values of n, we have

$$(\hat{\theta } - \theta ) \sim \mathcal {N}_3\left( \mathbf {0}, \sigma ^2(F_{\theta }'F_{\theta })^{-1}\right) ,$$

where \(F_{\theta } = \left( \frac{\partial f}{\partial a}, \frac{\partial f}{\partial b}, \frac{\partial f}{\partial c}\right) '\bigg |_{\theta }\) and \(\mathcal {N}_p\) represents a p-variate normal distribution. Now applying Delta method, we can obtain the asymptotic distribution of \(\widehat{K}\) as \(\mathcal {N}\left( K, \sigma ^2 F_1'(F_{\theta }'F_{\theta })^{-1}F_1\right)\) where \(F_1=\left( -\frac{b}{a^2c}, \frac{1}{ac}, \frac{-b}{ac^c}\right) K\). Let us call the asymptotic variance of \(\widehat{K}\) as \(\sigma _{K}^2 = \sigma ^2 F_1'(F_{\theta }'F_{\theta })^{-1}F_1)\).

3.2.1 Asymptotic distribution of IMR under extended Gompertz model

Theorem 7

Let us consider the EGM and \(\widehat{m(t)}\) be the estimate of IMR at time t using general estimator of IMR given in Eq. (23). The asymptotic sampling distribution of \(\widehat{m(t)}\) is given by:

$$\sqrt{n}\left( \widehat{m(t)}-m(t)\right) \sim \mathcal {N}(0,\Delta '\Sigma \Delta ),$$

where

$$\Delta ' = \left( - \frac{\exp (2at^c - a(t+1)^c)}{b \mu _0 \exp \left( \frac{b}{ac}(1-e^{-at^c})\right) }, \frac{a^2c^2 \exp (2at^c)}{b^2 \mu _0 \exp \left( \frac{b}{ac}(1-e^{-a(t+1)^c})\right) }, - \frac{ac (e^{-at^c} - e^{-a(t+1)^c})}{b \mu _0 \exp \left( \frac{b}{ac} - 2at^c\right) }\right)$$

and

$$\Sigma = \frac{1}{n} \left( \begin{array}{ccc} \sigma ^2 &{} \rho \sigma ^2 &{} 0 \\ \rho \sigma ^2 &{} \sigma ^2 &{} 0\\ 0 &{} 0 &{} \sigma _K^2 \\ \end{array} \right).$$

Proof

To obtain the asymptotic distribution of \(\widehat{m(t)}\), we require the joint distribution of \(\overline{X_t}\), \(\overline{X_{t+1}}\) and \(\widehat{K}\). K (\(X_{\infty }\)) is the asymptotic size which is achieved at a very large time point. In growth studies as the time difference increases, the correlation between the random variables decreases; that is, the correlation between \(X_t\) and \(X_{t+M}\) is almost negligible for large M. Thus, the correlation between \(\overline{X_t}\) and \(\widehat{K}\) is negligible. Thus, the joint distribution of \(\overline{X_t}\), \(\overline{X_{t+1}},\) and \(\widehat{K}\) can be given by

$$\begin{aligned} \left( \begin{array}{c} \overline{X_t} \\ \overline{X_{t+1}} \\ \widehat{K} \end{array} \right) \sim \mathcal {N}_3 \left( \left( \begin{array}{c} {\mu _t} \\ {\mu _{t+1}} \\ K \end{array} \right) , \frac{1}{n} \left( \begin{array}{ccc} \sigma ^2 &{} \rho \sigma ^2 &{} 0 \\ \rho \sigma ^2 &{} \sigma ^2 &{} 0\\ 0 &{} 0 &{} \sigma _K^2 \\ \end{array} \right) \right) . \end{aligned}$$
(25)

In the above expression, equality of variance of \(X_t\) and \(X_{t+1}\) is due to the homoscedasticity assumption of the error variance. For simplicity in notation, we consider, \(\overline{X_t} =X\), \(\overline{X_{t+1}}=Y\) and \(\widehat{K}=Z\), and then, estimate of IMR at time t is given by \(\widehat{m(t)} = \frac{\ln (Y/X)}{\ln (Z)-\ln (X)} = \psi (X,Y,Z)\). Differentiating \(\psi (x,y,z)\) partially with respective to x, y, and z, we get

$$\begin{aligned} \begin{aligned} \frac{\partial \psi }{\partial x}&= \frac{1}{x} \frac{\ln y - \ln (z)}{(\ln z- \ln x)^2} \\ \implies \frac{\partial \psi }{\partial x}\bigg |_{\theta =\hat{\theta }}&= -\frac{1}{\mu _t} \frac{\ln (K/\mu _{t+1})}{(\ln (K/\mu _t))^2} \\&= - \frac{\exp (2at^c - a(t+1)^c)}{b \mu _0 \exp \left( \frac{b}{ac}(1-e^{-at^c})\right) } \end{aligned} \end{aligned}$$
(26)
$$\begin{aligned} \begin{aligned} \frac{\partial \psi }{\partial y}&= \frac{1}{y}\frac{1}{(\ln K- \ln x)^2} \\ \implies \frac{\partial \psi }{\partial y}\bigg |_{\theta =\hat{\theta }}&= \frac{1}{\mu _{t+1}} \frac{1}{(\ln (K/\mu _t))^2} \\&= \frac{a^2c^2 \exp (2at^c)}{b^2 \mu _0 \exp \left( \frac{b}{ac}(1-e^{-a(t+1)^c})\right) } \end{aligned} \end{aligned}$$
(27)
$$\begin{aligned} \begin{aligned} \frac{\partial \psi }{\partial z}&= -\frac{1}{z} \frac{\ln y- \ln x}{(\ln K- \ln x)^2} \\ \implies \frac{\partial \psi }{\partial z}\bigg |_{\theta =\hat{\theta }}&= - \frac{1}{K} \frac{\ln (\mu _{t+1}/\mu _t)}{(\ln (K/\mu _t))^2} \\&= - \frac{ac (e^{-at^c} - e^{-a(t+1)^c})}{b \mu _0 \exp \left( \frac{b}{ac} - 2at^c\right) } \end{aligned} \end{aligned}$$
(28)

Now applying delta method, we obtain the distribution of \(\widehat{m(t)}\) for extended Gompertz growth model which is given as follows:

$$\sqrt{n}\left( \widehat{m(t)}-m(t)\right) \sim \mathcal {N}(0,\Delta '\Sigma \Delta ),$$

where \(\Delta ' = \left( \frac{\partial \psi }{\partial x}, \frac{\partial \psi }{\partial y}, \frac{\partial \psi }{\partial z}\right) \bigg |_{\theta = \hat{\theta }}\) and \(\Sigma\) is the variance–covariance matrix as specified in Eq. (25).\(\square\)

4 Illustration with data

In this section, we use simulated and real data sets to identify a suitable model using IMR.

4.1 Simulation study

We consider the simulation setup which is given by

$$\begin{aligned} X_t = \mu _{t} + \epsilon _t,~~~~t=1,2,\cdots ,q. \end{aligned}$$
(29)

The random vector \(\epsilon = (\epsilon _1, \epsilon _2, \cdots , \epsilon _q)'\) is assumed to follow multivariate normal distribution with mean \(\mathbf {0}\) and dispersion matrix \(\Sigma\). In growth studies, it is a common assumption that observations at closer time points are highly correlated, and as the difference increases, correlations between them diminish [31, 32]. In this case, the choice of Koopman structure of the covariance matrix is considered as it closely mimics the decaying correlation for time points far apart [35]. So, we consider the following covariance structure for \(\epsilon\).

$$\Sigma = \sigma ^2 \left( \begin{array}{cccc} 1 &{} \rho &{} \ldots &{} \rho ^{q-1} \\ \rho &{} 1 &{} \ldots &{} \rho ^{q-2} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \rho ^{q-1} &{} \rho ^{q-2} &{} \ldots &{} 1 \\ \end{array} \right) .$$

It can be easily observed that for large q, entries away from the main diagonal would be almost zero. The form of the dispersion matrix has been used in many studies [36]. It is clear that the covariance between \(X_t\) and \(X_{t+j}\) will be higher for small j and close to zero for large j. We generate the size variable \(X_t\) at \(q =20\) time points for \(n=20\) different individuals from multivariate normal distribution using the mean structure \((\mu _1,\mu _2, \cdots ,\mu _q)'\) and the dispersion matrix as noted above. So the final data matrix consists of 20 rows and 20 columns where each row is a realization from a multivariate normal distribution and each column is a realization of a univariate normal distribution. The simulation study was carried out for three different growth models, elaborated separately below.

4.1.1 Gompertz

We consider the following form of size to simulate the growth process originated from Gompertz model

$$\begin{aligned} \mu _t = X_0e^{\left[ \ln \frac{b}{a}\left( 1-e^{-at}\right) \right] } \end{aligned}$$
(30)

with \(b=1, a=0.25\) and the dispersion matrix with \(\sigma =0.1, \rho =0.5\). We compute the mean size at 20 time points using \(\overline{X_t} = \frac{1}{20}\sum \limits _{i=1}^{20} X_{it}\). We estimate RGR by \(\widehat{R(t)} = \log \left( \frac{\overline{X_{t+1}}}{\overline{X_{t}}}\right)\) at \(t=1,2,\cdots ,19\) from the mean size at 20 time points. The estimated RGR is depicted in Fig. 3a. We estimate the IMR using the estimator discussed in Eqs. (19) and (23). We plot the theoretical and estimated values of IMR for the Gompertz growth curves in Fig. 3. Note that here theoretical IMR is constant at each time points, which is easily understood from the estimated IMR. Again from Fig. 3a, we cannot identify the growth model using RGR, whereas using IMR we can recognize that the true growth model is Gompertz since IMR is constant.

Fig. 3
figure 3

The simulation results for Gompertz growth model for the parameter value \(b=1, a=0.25, \sigma =0.1, \rho =0.5\). In the first figure, we have given the estimated value of RGR and from the estimated value, we cannot recognize the growth curve. However, from the second figure, we can easily say that the growth process is Gompertz. We have also given the theoretical value of IMR to show the performances of the various estimators of IMR. IMR(1) and IMR(2) are the estimators of IMR given in Eqs. (19) and (23), respectively

Full size image

4.1.2 Logistic

Now, we simulate the of 20 individuals at 20 time points from the logistic distribution

$$\begin{aligned} X(t) = \frac{K}{1+e^{-at+b}} \end{aligned}$$
(31)

with \(a=0.25; b=0; K=20; \sigma =0.001, \rho =0.5.\) We calculate the RGR for \(t=1,2,\ldots ,19\) using the mean of the simulated size variable. The RGR is displayed in Fig. 4a, which decreases over time. We also calculate the IMR for the time points \(t=1,2,\ldots ,18\) using the estimate given in Eq. (23). The estimated IMR is displayed in Fig. 4b which is sigmoidal, and we can easily identify that the growth process is originated from logistic or Richards growth.

Fig. 4
figure 4

Sub-figure a depicts the empirical RGR of a simulated data for logistic growth model (\(a=0.25, b=0, K=20, \sigma =0.001, \rho =0.5\)). The trend of RGR is decreasing and suggests the associated growth model can be logistic, Gompertz, or some other models. The sub-figure b shows the corresponding RGR. Here, the trend of estimated IMR shows sigmoidal shape. So the corresponding growth model is logistic

Full size image

4.1.3 Extended Gompertz model

In this section, we perform the simulation study where the observations are generated from the EGM with the mean function as

$$\begin{aligned} \mu _t = X_0e^{\left[ \ln \frac{b}{ac}\left( 1-e^{-at^c}\right) \right] } \end{aligned}$$
(32)

where \(X_0\) is the initial size, and b, a, and c are positive constants. Note that the shape of RGR curve is decreasing for \(c \le 1\) and bell-shaped for \(c>1\). Hence, we simulate two sets of parameter values, one for \(c<1\) and the other for \(c>1\) to cover the two distinct possible shapes of RGR. First, we simulate X(t) for \(t=1,2,3,\ldots ,20\) for the parameter values \(X_0=3\), \(b=1, a=0.5, c=0.5, \sigma =0.1, \rho =0.5\). The RGR is estimated using the estimator, as noted previously. The estimated values are displayed in Fig. 5a. The shape RGR decreases, and the growth model can be Gompertz, logistic, Richards, extended Gompertz, extended logistic, etc. However, suppose we plot the estimated value of IMR. In that case, we observe that the growth process cannot be logistic, Gompertz, Richards, etc. We also plot the theoretical value of IMR using the extended Gompertz growth model (see Fig. 5b). From the figure, we observe that the general estimator of IMR discussed in this paper performs well.

Again, we simulate the size for 20 time points with \(X_0=3\), \(b=0.1, a=0.01, c=2, \sigma =0.1\), and \(\rho =0.5\). The RGR and IMR are displayed in Fig. 6. In this case, RGR is bell-shaped, and the growth process can be recognized using RGR as well as IMR. Again, in this case, we observe that the estimated IMR values are pretty close to the theoretical IMR.

Fig. 5
figure 5

Sub-figure a represents the RGR over time from the simulated data from RGM for \(c=0.5, b=1, a=0.5, \sigma =0.1\), and \(\rho =0.5\). The sub-figure b depicts the empirical IMR over time for the same data using general estimator of IMR. The plot of IMR shows how the estimated IMR is close to the theoretical IMR

Full size image
Fig. 6
figure 6

The sub-figure a shows the empirical RGR of simulated data from the EGM for \(c=2, b=0.1, a=0.01, \sigma =0.1\), and \(\rho =0.5\). Sub-figure b depicts the estimated and theoretical RGR for the simulated data from EGM. Here, we see that the estimated MR values are close to the theoretical RGR

Full size image

4.2 Real data applications

In this section, we use two real data sets to illustrate the applicability of IMR. A real-life experiment was performed in a pond of the Indian Statistical Institute (ISI), Kolkata, to study the adaptability of fish against various stressors under natural conditions. There were four locations in a circular layout model, namely A, B, C, and D. Four hoopnets were placed in each location [6]. The sizes (length) of twelve fishes for twelve consecutive time points were collected in a constant interval of time, i.e., once a week (four times a month). A detailed description of the experiment is available in several articles [5, 16, 37]. For illustration purposes, we investigate the performance of IMR and RGR in two locations, A and C, only. In locations B and D, the shapes of RGR are the same as in location A. Here for each location, we have 12 observations at 12 time points. We computed the average length at each time point, and then, we estimated RGR at time t using \(\hat{R_t}=\ln \left( \frac{\overline{X_{t+1}}}{\overline{X_t}}\right)\). We plot the mean RGR against time for each location in the left panel of Figs. 7 and 8. We also estimate the IMR in locations A and C using the procedure discussed in Sect. 3. The estimated values of IMR are displayed right panel of Figs. 7 and 8.

For illustration, we fit fish length using various growth models like Gompertz, logistic, EGM, extended logistic model (ELM) [6], and Bhowmick–Bhattacharya extended Gompertz model (BBEGM) [5]. More details about mathematical expression of EGM, ELM, and BBEGM are available in Supplementary Material. We consider BBEGM for the parameter c=1 and c=2 as it has explicit expression of size for integral values of c. We aim to select suitable models using RGR and IMR and justify using the model selection criterion. We estimate the model parameters for Location A and Location C using nonlinear least squares and provide the estimated values in Tables 2 and 3, respectively. The observed and estimated values of size are displayed in Fig. 9. We consider two possible shapes of RGR as follows.

RGR decreasing

The decreasing RGR is observed in Location C. Let us consider the model identification using RGR. Since RGR is decreasing, Gompertz, logistic, ELM, EGM models can be considered as possible models. The BBEGM models are not considered here since RGR is decreasing.

Now, consider the model selection using IMR. In this location, IMR is decreasing (Fig. 8). The Gompertz model is not suitable here since a model is Gompertz if and only if IMR is constant. The logistic model is not suitable here since the theoretical IMR of logistic is sigmoidal. The BBEGM (1) and BBEGM (2) are not suitable here since the IMR of BBEGM (1) and BBEGM (2) is increasing. So using the shape of IMR, we can say that ELM and EGM are suitable in this location. So IMR reduces the list of possible models.

Now, choose the best model using the AIC criterion. Now from Table 3, we notice that the best model ELM and EGM perform better than logistic and Gompertz, which we can understand from the shape of IMR without fitting the growth curves.

RGR bell-shaped

The bell-shaped RGR is observed in Location A. First, we consider logistic and Gompertz as possible models. We observe (ref. Table 2) that all the model parameters are statistically significant, and logistic is the best model since it has lower AIC compared to the Gompertz model. But suppose we justify the models in light of IMR. In that case, we observe that none of the models is suitable to capture the estimated IMR (increasing). Now based on shape of IMR, we should consider ELM \((c>1)\), EGM \((c>1)\), and BBEGM \((c>0)\). All the models give a better fit than Gompertz and logistic. Again, if we select the logistic or Gompertz model, we will have maximum RGR at the beginning. However, we see from Fig. 7 that RGR attains its maximum in the middle of the experimental time window. We also compute the time point \(\hat{t}=4.526, SE = 0.4005\). Hence, identifying the wrong model can lead us to get incorrect results about the important characteristic of the growth curve.

From the above discussion, we observe that IMR reduces the model search space. It also reduces the probability of the selection of the wrong model. After selecting the possible model, we can go the model testing procedure based on ISRP or some goodness of fit test for the chosen model [17, 32, 36].

Fig. 7
figure 7

The scatter plot of empirical RGR for Location A has been displayed in the left panel. The scatter plot shows bell-shaped trend. The scatter plot of empirical IMR for Location A and the fitted IMR has been displayed in the right panel. The fitted IMR shows an increasing parabolic shape, which suggests that the possible growth model can be EGM, ELM, or BBEGM

Full size image
Fig. 8
figure 8

The plot of empirical RGR for Location C has been displayed in the sub-figure (a). The plot of RGR shows decreasing trend from which we can say that the model can be Gompertz, logistic, EGM, ELM, BBEGM, etc. The plot of empirical IMR for Location C and the fitted IMR has been displayed in (b). The fitted IMR shows a decreasing shape, which suggests that the possible growth model cannot be Gompertz or logistic. So IMR has advantageous in model identification

Full size image
Table 2 Estimated value of parameters of various models in Location A
Full size table
Table 3 Estimated value of parameters of various models in Location C
Full size table
Fig. 9
figure 9

The sub-figure given in a depicts the scatter plot of size over time in Location A and the estimated growth curves using various models. The sub-figure given in b shows the plot of size over time in Location C and the estimated growth curves using different growth equations

Full size image

5 Conclusion

To conclude our findings in the manuscript, we emphasize developing a new metric in growth curve literature. Studies suggest that the use of relative growth rate (logged difference of size, devised by Fisher [13]) is more advantageous in applications than fitting the equations to the size data. Since then, RGR has been predominantly used in the statistical inference of growth models. The limitations of RGR were identified recently in 2014 by Bhowmick et al. [16] in which the authors proposed the concept of interval-specific rate parameter (ISRP) and revised the estimates of RGR. The authors have further established that the use of modified RGR estimates performs better than Fisher’s RGR in selecting the underlying growth equation [32]. The research community accepts both the above methods, and many researchers have adopted these methods.

RGR is important for the formulation, identification, and unification of growth curves. However, the RGR has limited applications due to its only two shapes: decreasing and bell-shaped. In addition, RGR’s asymptotic value is zero for all sigmoidal growth curves. Due to its wide variety of shapes, the newly developed growth measure, IMR, is more flexible in identifying growth laws, making it a valuable tool for identifying growth curves. The Gompertz IMR can be viewed as the relative rate of change of RGR with a negative sign. For any growth curve, IMR is approximately equal to the RGR of the RGR (with a negative sign) for large values of t. In addition, the standardized relative growth rate (SRGR) can be used to compare the level of maturity of any system irrespective of its asymptotic size.

Generally, it is difficult to estimate the IMR because the asymptotic size is unknown. We have also proposed a method to estimate IMR based on a data set in order to overcome this difficulty. The method can be applied to other growth equations, and the distribution of IMR can be derived using the delta method. This will allow us to narrow down our choice of competing models to analyze real data sets.