1 Introduction

Plenty of growth curve models are available in the existing literature (Gompertz 1825; Verhulst 1838; Richards 1959; von Bertalanffy 1960; Tsoularis and Wallace 2002; Koya and Goshu 2013; Crescenzo and Spina 2016), which were developed over a century. The evolution of novel growth equations can be classified into two notable directions: generalization and Unification. By generalization, we refer to the process in which we start with a simple equation to understand the growth mechanism of a specific biological process. Then to generate more flexible shapes and increase its applications for a wide range of research areas, more parameters are incorporated within the model. Naturally, the original equation, from which the process started, becomes a special case of the generalized equation that contains more parameters. Unification refers to a compact representation of different growth curve models. This is usually achieved by proposing a single function to represent a larger class of growth models. Unification allows a better mathematical tractability as it deals with a particular function with some fundamental (key) parameters.

Recently, there have been some innovations in growth curve literature, which deals with these two concepts. Two notable generalizations were proposed by Tsoularis and Wallace (2002) and Koya and Goshu (2013). Tsoularis and Wallace (2002) introduced a generalized form of the logistic growth equation (henceforth, TW model) which included many common growth laws as special cases. Koya and Goshu (2013) proposed an eight parameter growth function (henceforth, KG model) which accommodates several commonly known growth models such as logistic, Gompertz, Brody, Monomolecular, Mitscherlich, Von Bertalanffy, Richards, generalized Weibull. The TW model contains three more parameters in comparison with Gompertz and logistic growth and two extra parameters in comparison with Richards’ growth function. Similarly, the KG model (Koya and Goshu 2013) contains a total of five additional parameters in comparison with the logistic, Gompertz and Weibull growth functions. Although the generalized equations offer a better flexibility in shapes, these models are difficult to fit real data sets as the model complexity increases significantly due to the presence of a large number of parameters. The estimators of the model parameters, which are to be estimated from data, often lack many desirable statistical properties.

The unification of the growth curves has also attracted many researchers (Garcia 2005; Martinez et al. 2008, 2009; Tjørve and Tjørve 2010, 2017). Using the Box–Cox transformation Garcia (2005) proposed a single growth equation that unifies many of the existing sigmoid growth curves. Martinez et al. (2008, 2009) obtained the one-parameter generalization of the logarithmic and exponential functions to unify a great majority of growth models. An important feature of the unification of growth curves is that it formulates a relationship between different models, which is useful in visualizing various growth functions in a single mathematical framework. The unification usually enhances the generality of software, facilitating the development of more widely applicable software, and identification of suitable statistical procedures (Garcia 2005). The unification function for different growth curves is more appealing because of its compactness in terms of a reduced number of parameters. For instance, the unification function described by Garcia (2005) contains only two shape parameters. So for the advancement of growth curve analysis, a further research and development of unification would be more useful than the generalization.

Recently, there have been significant innovations going on to analyze the real data using growth functions that explicitly involve the relative growth rate (henceforth, RGR). RGR is expressed either as a function of size (state variable) or time or both in this model set up. We refer such models as “RGR growth curves” in rest of the manuscript. We shall elaborate it in later sections. A number of research papers are available in which the utilities of RGR growth curves are well discussed (Bhattacharya et al. 2009; Bhowmick et al. 2014; Bhowmick and Bhattacharya 2014; Mukhopadhyay et al. 2016; Chakraborty et al. 2017; Pal et al. 2018). The unification functions proposed by Garcia (2005) and Martinez et al. (2008) are developed on the pillars of two arbitrary chosen mathematical functions that apparently do not provide much useful insight about the underlying biological process. It is necessary to mention that these existing unification approaches do not offer functions, which are able to combine the RGR growth curves which are functions of both size and time, respectively.

Therefore, the present study is aimed to investigate the existence of further unification functions that offer a simple but compact mathematical expression to unify the RGR growth curves. In addition, the proposed candidate should be able to derive the existing unification approaches by Garcia (2005) and Martinez et al. (2009) as special cases. In this article, we propose a novel unification function that possesses the above two existing unifications. The unification is achieved by introducing size and time allometry together into the basic Richards’ equation. Although the existing mathematical form of the Richards’ equation can capture most of the monotonic shapes of RGR, but due to the joint impact of both time and size, the proposed framework integrates a much bigger class of growth models. Moreover, the proposed unification function can be well interpreted as it is originated from a basic RGR equation which is not the case for Garcia (2005) and Martinez et al. (2008).

The organization of the rest of the paper is as follows. We first describe the existing unification methods in Sect. 2. We provide a short description RGR to facilitate a smooth transition between unification and RGR functions. Then, we develop unification technique based on RGR in Sect. 3. The various shapes of RGR expressed by the proposed unification are studied in Sect. 4.

2 Literature Survey: Existing Unification

We describe two existing unification approaches proposed by Garcia (2005) and Martinez et al. (2008) in this section. Garcia (2005) used the Box–Cox transformation to unify a larger class of sigmoidal growth curves. The Box–Cox transformation, given by

$$\begin{aligned} x^{(a)} = {\left\{ \begin{array}{ll} \frac{(x^a-1)}{a} &{} \hbox { if}\; a \ne 0,\\ \ln (x) &{} \hbox { if}\; a = 0, \end{array}\right. } \end{aligned}$$
(1)

is a way to transform an approximately normal random variables into a normal random variable (Box and Cox 1964). Normality is an important assumption for many statistical techniques. However, if the underlying random variable is not normal, applying the Box–Cox transformation, one can transform an approximately normal variable into a normal variable, which can enable to run a broader number of tests. Not only in Statistics, the Box–Cox transformation has a nice application to unify many sigmoidal growth curves. Garcia (2005) used the Box–Cox transform to unify the growth curves such as logistic (Verhulst 1838; Gompertz 1825; Richards 1959; Korf 1939; Weibull 1951), etc. The unified growth equation is given by

$$\begin{aligned} B(B(y,a),b) = t, \end{aligned}$$
(2)

where a and b are the parameters. Note that \(B(y,a)=-y^{(a)},\) where \(y^{(a)}\) is the Box–Cox transformation of y (Eq. 1) and y is the proportion of size with respect to asymptotic size, that is, if x(t) denotes the size at time t and \(x_{\infty }\) is the size at \(t\rightarrow \infty \), then \(y(t) = x(t)/x_{\infty }\). For different parameter values of a and b, various growth curves are obtained such as logistic (\(a=-1\), \(b=0\)), Gompertz \((a \rightarrow 0, b=0)\), Richards / \(\theta -\)logistic \((a = -\theta , b= 0)\).

The one-parameter generalization of the logarithmic and exponential functions is used to unify a great majority of growth models by Martinez et al. (2008, 2009). The one-parameter generalization of the logarithm function is given by

$$\begin{aligned} \ln _{q}(x) = \int _{1}^{x} \frac{\mathrm {d}t}{t^{1-q}} = \lim _{p \rightarrow q} \frac{x^p-1}{p}, \end{aligned}$$
(3)

which is the natural logarithm for \(q=0\). It is important to note that \(\ln _{q}(x)\) is same as \(- B(x,q)\). The unified growth equation of Martinez et al. (2008) is given by

$$\begin{aligned} \frac{\mathrm {d}\ln _{q}(y)}{\mathrm {d}t} = k [-\ln _{p}(y)]^\gamma , \end{aligned}$$
(4)

which contains many growth curves as a special case. It includes logistic (\(q=0, p=1, \gamma =1\)), Gompertz (\(q=0, p \rightarrow 0, \gamma =1\)), Richards (\(q=0, p=-\theta , \gamma =1\)), Von Bertalanffy (\(q=-\frac{1}{3}, p=\frac{1}{3}, \gamma =1\)), etc. like Garcia’s unified equation. It also contains the general logistic model proposed by Tsoularis and Wallace (2002), which cannot be obtained from Garcia’s unified equation. More precisely, if we take \(a \rightarrow 0\) in case of Garcia’s unification, we get \(\frac{1}{y}\frac{\mathrm {d}y}{\mathrm {d}t}= [-\ln (y)]^{(1-b)}\), whereas if we take \(p \rightarrow 0\) for Matrinez et. al.(2008) unification, we get \(\frac{1}{y}\frac{\mathrm {d}y}{\mathrm {d}t}= k y^{1-q} [ -\ln (y)]^\gamma \).

3 Proposed Unification Method

3.1 Relative Growth Rate

Relative growth rate (RGR) (Fisher 1921) plays an important role to understand the rate of growth associated with the growth process. The RGR is defined as the per unit rate of change in the value of the variable. Let X(t) be the size of the growth process at time \(t, t \ge 0\), and R(t) be the RGR at time t. Mathematically, R(t) is defined by

$$\begin{aligned} R(t) = \frac{1}{X(t)} \frac{\mathrm {d}X(t)}{\mathrm {d}t} = \frac{\mathrm {d}\ln X(t)}{\mathrm {d}t}. \end{aligned}$$
(5)

The simplest growth equation is exponential growth where size is unbounded and RGR is constant (Malthus 1798). However, in reality, unrestricted growth is rare and RGR must be density dependent. The logistic law is the first member of this bounded density-dependent family, where RGR is linearly dependent on density. The simplest nonlinear extension of this growth law was due to von Bertalanffy (1949), which was further extended to negative power by Richards (1959) (Garcia 2008).

As pointed out by Bhowmick et al. (2014) sometimes it is not easy, and even misleading, for an experimenter to identify the suitable underlying model by studying the shape of the size profile curves among the available growth curves. However, in comparison, if we plot the empirical estimate of RGR against time or size, we can at least guess and identify the growth curves that are appropriate for the given data based on the monotonic structure of RGR. So the identification of the proper model is comparatively easy for RGR profile than the size profile curves. In addition, RGR contains a reduced number of parameters, which may be appeared to be advantageous in model fitting exercises using real data (Eberhardt et al. 2008). This is particularly important when growth profile curves look similar to common and existing growth curves, but the RGR is not monotonically decreasing with time (Gompertz), size (logistic, Richards, Von Bertalanffy, etc.), or constant (exponential). This observation has also motivated us to search for a unification function based on RGR rather than the size variable.

3.2 RGR and Unification

We shall ignore any linear transformations of the size variable X(t) and time t in the development of novel unification function, and we consider \(y(t) = \frac{X(t)}{K}\) or simply y, where X(t) is the size at time t, and K is the asymptotic size. So y has been scaled to the interval \(0 \le y \le 1\). Thus, disregarding differences in location and scale, the various models correspond to specific values of two essential shape parameters.

We shall start our development with the Richards’ growth equation. Basically, Richards growth law is that fundamental growth which can capture three shapes of RGR, namely linear, monotonic convex and monotonic concave. The Box–Cox transformation is a tool by which we can convert an approximately normal random variable to another random variable following a normal distribution. Garcia (2005) used this transformation to build a unified growth equation. The Richards’ growth equation is given by \(R(t) = r(1-y^b)\), which implies that \(R(t) \propto B(y,b)\). Starting with a single parameter, the proposed unification is followed by the following three steps.

I::

Mathematically, RGR is proportional to a polynomial of density with constant and the higher-order terms only in Richards’ growth. A more general density-dependent growth curve can be obtained by considering RGR proportional to \(B(y,b)^d\). Note that the modified RGR equation \(\left[ R(t) \propto B(y,b)^d\right] \) includes additional terms of polynomial in comparison with the original Richards equation.

II::

Again the RGR R(t) is proportional to \(y^a\) in case of size allometry. Combining all these factors, we can get \(R(t) = ry^a B(y,b)^d\) (Ross 2009), r is the constant of proportionality.

III::

RGR is also assumed to be proportional to a time-dependent factor f(t) (say) to capture the time allometry form. Hence, the modified unification equation can be written as \(R(t) = ry^a B(y,b)^d f(t)\), where \(y^a B(y,b)^d\) is the size-dependent factor and f(t) is the time-dependent factor which can control the species fitness. One of the simplest but important time-dependent factors is given by the allometric power of time i.e., to \(t^{c-1}\) (Bhowmick and Bhattacharya 2014).

We propose the following unification equation based on the above discussion

$$\begin{aligned} R(t) = r y^a [B(y,b)]^d t^{c-1} = r y^a \left[ \frac{1-y^b}{b}\right] ^d t^{c-1}, \end{aligned}$$
(6)

where r, a, b, c and d real numbers. Note that the last term of Eq. (6) is only valid for \(b\ne 0\), otherwise it involves a logarithm. This is the usefulness of the Box–Cox transformation in the context of growth models. Alternatively, the unification equation can also be written as

$$\begin{aligned} \frac{\mathrm {d}B(y,-a)}{\mathrm {d}t} = - r \left[ B(y,b)\right] ^d t^{c-1}. \end{aligned}$$
(7)

We shall demonstrate that existing unification approaches proposed by Garcia (2005) and Martinez et al. (2008) are special cases of the proposed unified growth equation.

3.3 Relationship with Existing Unification

The unification of Garcia (2005) can be obtained as a special case of our proposed unification equation Eq. (6). Garcia (2005) assumed \(B(B(y,p),q)=t\), so they got a general age invariant growth equation as follows: Differentiating the yield equation we get,

$$\begin{aligned}&\frac{\mathrm {d}B(B(y,p),q)}{\mathrm {d}t} =1 \nonumber \\&\quad \Rightarrow B'(B(y,p),q) \frac{\mathrm {d}B(y,p)}{\mathrm {d}t} = 1 \nonumber \\&\quad \Rightarrow - (B(y,p))^{q-1} \frac{\mathrm {d}B(y,p)}{\mathrm {d}t} = 1 \end{aligned}$$
(8)
$$\begin{aligned}&\quad \Rightarrow \frac{\mathrm {d}B(y,p)}{\mathrm {d}t} = - (B(y,p))^{1-q} \nonumber \\&\quad \Rightarrow \frac{\mathrm {d}y}{\mathrm {d}t} = y^{1-p}(B(y,q))^{1-q} \nonumber \\&\quad \Rightarrow \frac{1}{y} \frac{\mathrm {d}y}{\mathrm {d}t} = y^{-p}(B(y,p))^{1-q}. \end{aligned}$$
(9)

So, Garcia (2005)’s unification equation is given by

$$\begin{aligned} \frac{1}{y}\frac{\mathrm {d}y}{\mathrm {d}t} = y^{-p} \left( \frac{1 - y^p}{p}\right) ^{1-q}. \end{aligned}$$
(10)

It is easy to follow that Eq. (10) is a special case of Eq. (6), where \(a=-p, b=p, d=1-q, c=1\).

The unification of Martinez et al. (2008) can be obtained as a special case of our proposed unification equation Eq. (6). The convenience of generalizing the logarithmic and exponential functions is an important tool to unify many growth curves. The one-parameter generalizations of the logarithmic and exponential functions can unify the great majority of growth models (Martinez et al. 2008, 2009).

The unification of Martinez et al. (2008) (Eq. 4) can be written as

$$\begin{aligned} R(t) = k y^{1-q}[B(y,p)]^\gamma . \end{aligned}$$
(11)

We observe from Eq. (11) that the unification of Martinez et al. (2008) is a special case of our proposed unification Eq. (6) for \((c=1)\).

3.4 Utility of the Proposed Unification

The above two unification techniques (given in Sect. 3.3) unify a large number of growth curves. However, there are a number of growth models, which are not possible to describe by these two methods. Few examples are: KG model (Koya and Goshu 2013), extended Gompertz (Bhowmick and Bhattacharya 2014), extended logistic (Chakraborty et al. 2017), modified Gompertz using Korf law (Crescenzo and Spina 2016). Our proposed function can be regarded as a unified version of these models. As an example, the generalized growth models of Koya and Goshu (2013) can be obtained as a special case of the proposed unification equation Eq. (6). The KG growth equation after ignoring the time and size location and scale parameters is given by

$$\begin{aligned} y = \left[ 1-B \mathrm {e}^{-kt^\gamma }\right] ^m. \end{aligned}$$
(12)

So the growth equation in RGR form can be described as

$$\begin{aligned} R(t) = r y^{-\frac{1}{m}}(1-y^\frac{1}{m})t^{\gamma -1}, \end{aligned}$$
(13)

when \(m>0\) and

$$\begin{aligned} R(t) = r (1-y^{-\frac{1}{m}})t^{\gamma -1}, \end{aligned}$$
(14)

when \(m<0\). Equation (13) is a special case of our proposed unified growth equation (6) with \(a = -\frac{1}{m}, b=\frac{1}{m}, d=1\) and \(c=\gamma \). Similarly, Eq. (14) is a special case of Eq. (6) with \(a=0, b={-\frac{1}{m}}, d=1,\) and \(c=\gamma \).

The proposed model of Crescenzo and Spina (2016) is given by

$$\begin{aligned} R(t) = \alpha (1+t)^{-(\beta +1)}, \end{aligned}$$
(15)

where \(\alpha >0\) and \(\beta >0\). It can be easily verified with a simple algebra that the proposed model by Crescenzo and Spina (2016) is a special case of unifying Eq. (6) with the values of the unifying parameters being \(a=0, b \rightarrow 0, d>1,\) and \(c=1\). The size variable X(t) at time t corresponding to Eq. (15) is given by

$$\begin{aligned} X(t) = K \mathrm {e}^{-\frac{\alpha }{\beta }(1+t)^{-\beta }}, \end{aligned}$$
(16)

where K is the asymptotic size. Let \(y(t) = \frac{X(t)}{K}\). The RGR equation Eq. (15) can be expressed as follows

$$\begin{aligned} R(t) = r (-\ln y)^{d}, \end{aligned}$$
(17)

where \(d=\frac{\beta +1}{\beta }\). Clearly, \(d>1\). So, our proposed model also unifies growth equation proposed by Crescenzo and Spina (2016) with \(a=0, b \rightarrow 0, d>1,\) and \(c=1\). Note that the model is a particular case of generalized Gompertz (\(d>0\)) model. The model was developed by combining Gompertz and Korf laws, which can be recovered for the limiting parameter values. For example, for large values of \(\beta \), d tends to 1 and we obtain the Gompertz growth model. It is also to be noted that the model of Crescenzo and Spina is the same as the model of Korf, except the shift \(t\rightarrow t+1\).

The list of growth models which can be obtained as a special case of the proposed unification equation is given in Table 1. We provide a flowchart in Fig. 1 to show the relationship between the growth curves.

Table 1 Unification of growth curves using Eq. (6) and the parameter values
Full size table
Fig. 1
figure 1

Flowchart of the various growth curves from the proposed unified growth equation

Full size image

3.5 Non uniqueness of Forms of RGR

It is often overlooked that the differential form of a growth curve is not unique. For any (smooth) growth function \(y = f(t)\), there is a unique derivative \(\frac{\mathrm {d}y}{\mathrm {d}t} = f(t)\) and a unique autonomous differential equation \(\frac{\mathrm {d}y}{\mathrm {d}t} = g(y)\), but there is an infinity of forms \(\frac{\mathrm {d}y}{\mathrm {d}t} = h(y, t)\) containing both y and t. For instance, in h(y, t) one can substitute \(y\rightarrow y^p f(t)^{(1-p)}\) and/or \(t \rightarrow t^q f^{-1}(y)^{(1-q)}\), for any real p and q. For example, Garcia (2011) illustrated five differential forms of the Schumacher growth curve, for which the absolute growth rate \(\frac{\mathrm {d}y}{\mathrm {d}t}\) is of the form h(y, t). The same is the case with Korf, Gompertz, Extended logistic and Weibull, etc.

Note that in the above case, the absolute growth rate was written as the model equation. So a similar discussion with RGR is of immense importance in this regard. As a consequence, the representation of RGR in terms of size and time will not be unique and there can be several forms \(R(t) = h(y, t)\) containing both y and t. Hence, a growth having two different RGR forms may be regarded as two different growth laws. For example, Crescenzo–Spina and generalized Gompertz were regarded as two different growth laws. This motivated us to inspect the presentation of the possible occurrence of various growth models. We kept our discussion restricted to Korf, Gompertz, Richards, Weibull and Extended logistic models only. Some alternative forms of RGR for these models are presented in Table 2.

From the above discussion, it is clear that the RGR column in Table 1 shows only one of many possibilities. We would like to emphasize that the proposed form of RGR as a function of size and time is not arbitrary, rather it was motivated by important biological phenomena such as density-dependent decay (generally considered as \((1-y^b )^d\)) and the size allometry reflected through \((y^a)\) and the time allometry \((t^{c-1})\). Hence, the proposed unification can explain three different aspects of growth law. In particular, the proposed unification provides a platform to chose a RGR equation to start with.

Table 2 The mathematical expressions of RGR for different growth models
Full size table

It is worth noting that the equivalence is only valid in a fully deterministic setting. In case of stochastic setup, after any disturbance, the drift forms of stochastic differential equation follow different trajectories (Garcia 2011). Donnet et al. (2010) and Garcia (1983, 2018) used deterministically equivalent forms of the Bertalanffy–Richards model that have different stochastic properties.

Remark

The proposed unified growth equation can combine a large class of growth curves. However, the extended Gompertz model proposed by Bhowmick and Bhattacharya (2014) cannot be unified with Eq. 6. Instead of considering \(f(t) = t^{c-1}\), if we consider \(f(t) = e^{-st}t^{c-1}\) then the model developed in Bhowmick and Bhattacharya (2014) can be covered. But, in that situation, we will have one extra parameter. Note that Gompertz growth has two forms \(R(t) = r \text{ e }^{-st}\) and \(R(t) = r (-\ln y)\). We only consider the size-dependent form, \(R(t) = r (-\ln y)\). The size-dependent extension of Gompertz growth has additional advantages such as closed-form solution of RGR equation exists for all parameter values.

3.6 Generalized RGR: An Alternative Interpretation of the Proposed Unification

We study the relationship between the unifying functions of Garcia (2005) and the one-parameter generalized logarithm with RGR in this section. We define \(\gamma \)-generalized relative growth rate at time t, \(\left[ R_{\gamma }(t)\right] \), as the ratio of rate of change of growth in per unit time and the \(\gamma ^{\text{ th }}\) power of size at time t, i.e.,

$$\begin{aligned} R_{\gamma }(t) = \frac{1}{x^\gamma } \frac{\mathrm {d}x}{\mathrm {d}t}. \end{aligned}$$

Note that \(R_{\gamma }(t)\) is the per capita growth rate when \(\gamma =1\). Generalized RGR is not a scale invariant quantity unless \(\gamma =1\).

The unified growth equation using generalized RGR is expressed as

$$\begin{aligned} R_{(a+1)}(t) = r \left[ B(y,b)\right] ^d t^{c-1}. \end{aligned}$$
(18)

Recall that

$$\begin{aligned} B(x,c) = {\left\{ \begin{array}{ll} \frac{(1-x^c)}{c} &{} \hbox { if}\ c \ne 0\\ -\ln (x) &{} \text {if } c = 0. \end{array}\right. } \end{aligned}$$

Now, differentiating B(x, c) with respect to t, we get \(\frac{\mathrm {d}B(x,c)}{\mathrm {d}t} = - x^{c-1}\frac{\mathrm {d}x}{\mathrm {d}t} = - R_{1-c}(t)\). The \(\gamma \)-generalized relative growth rate at time t, \(R_{\gamma }(t)\) is nothing but \(-\frac{\mathrm {d}B(x,1-\gamma )}{\mathrm {d}t}\) and the relative growth rate is \(-\frac{\mathrm {d}B(x,0)}{\mathrm {d}t}\).

Again we have the one-parameter generalization of logarithm function as

$$\begin{aligned} \ln _{c}(x) = \int _{1}^{x} \frac{\mathrm {d}t}{t^{1-c}} = \lim _{p \rightarrow c} \frac{x^p-1}{p}. \end{aligned}$$
(19)

Differentiating, we get \(\frac{\mathrm {d}\ln _{c}(x)}{\mathrm {d}t} = x^{c-1}\frac{\mathrm {d}x}{\mathrm {d}t} = R_{1-c}(t)\). So the \(R_{\gamma }(t)\) is the growth rate of \(\ln _{1-\gamma }(x)\), i.e., \(R_{\gamma }(t) = \frac{\mathrm {d}\ln _{1-\gamma }(x) }{\mathrm {d}t }\). The usual relative growth rate is \(\frac{\mathrm {d}\ln _{c}(x) }{\mathrm {d}t }\) for \(c=0\).

If the functional form of generalized RGR is given then the functional form of size is derived as follows:

We have,

$$\begin{aligned} \frac{\mathrm {d}\ln _{1-\gamma }(x) }{\mathrm {d}t }= & {} R_{\gamma }(t)\nonumber \\\Rightarrow & {} \int _0^{t} \mathrm {d}\ln _{1-\gamma }(x) = \int _0^{t} R_{\gamma }(s) \mathrm {d}s \nonumber \\\Rightarrow & {} \ln _{1-\gamma }X(t) - \ln _{1-\gamma }X(0) = \int _0^{t} R_{\gamma }(s)\mathrm {d}s \nonumber \\\Rightarrow & {} X(t) = X(0) \left[ 1 + \frac{1-\gamma }{{X(0)^{1-\gamma }}}\int _0^{t} R_{\gamma }(s)\mathrm {d}s \right] ^{1/(1-\gamma )} \nonumber \\\Rightarrow & {} X(t) = X(0) e_{1-\gamma }\left( {\frac{1}{X(0)^{1-\gamma }}\int _0^{t} R_{\gamma }(s)\mathrm {d}s}\right) , \end{aligned}$$
(20)

where \(e_{c}(x)\) is the one-parameter generalized exponential function and defined as \(e_{c}(x)=\lim _{q \rightarrow c}(1+qx)^{\frac{1}{q}}\). If \(1+qx\) is negative then \(e_{c}(x)\) is defined as 0.

3.6.1 Example-I

Garcia’s unification \(B(B(y, p), q) = t\) is equivalent to saying \((1-q)^{th}\) generalized RGR of B(y, p) is constant. As already mentioned, the yield equation of Garcia (2005) is given by \(B(B(y, p), q) = t\), and we observe that \(\frac{\frac{\mathrm {d}B(y, p)}{\mathrm {d}t}}{B(y,p)^{1-q}}= -1\) (Eq. 9). So \((1-q)^{\text{ th }}\) generalized RGR of B(y, p) is a constant for the growth laws that obey Garcia (2005)’s unification, namely logistic, Gompertz and Richard’s. Few more interesting observations in characterizing growth curves are listed below:

  1. 1.

    If \(p \rightarrow 0\) and \(q=0\) then we get the Gompertz growth law. But when \(p \rightarrow 0\), \(B(y, p) = - \ln y\) and \(-\frac{\mathrm {d}B(y, p)}{\mathrm {d}t}=\frac{\mathrm {d}\ln y}{\mathrm {d}t}\). Hence, RGR of logarithmic of size variable is constant in case of the Gompertz growth.

  2. 2.

    We have \(p = -1\) and \(q=0\) in case of the logistic growth law. But when \(p =-1\), B(y, p) is \(1-\frac{1}{y}\). So in case of the logistic growth model RGR of (\(1-y^{-1}\)) is constant.

  3. 3.

    We put \(p =1\) and \(q=0\) to get the Monomolecular growth law. So in this case, \(-\frac{\mathrm {d}B(y, p)}{\mathrm {d}t}\) is the absolute growth rate and B(y, p) is \(1-y\). Hence, the RGR of (\(1-y\)) is constant in case of the Monomolecular growth.

  4. 4.

    If we put \(q=0\) and \(0<p<1\), we get general Von Bertalanffy growth model. So for the general Von Bertalanffy growth model, we have RGR of \(1-y^p\) is constant.

3.6.2 Example-II

The Martinez’s unified growth equation using generalized RGR is expressed as

$$\begin{aligned} R_{(a+1)}(t) = r \left[ B(y,b)\right] ^d. \end{aligned}$$
(21)

4 Illustration of the Proposed Unification

We demonstrate that how our proposed unification function can be used for a large family of growth functions in this section. The identification of growth curves is relatively easier if we consider the shapes of RGR instead of size (Bhowmick and Bhattacharya 2014), which motivated us to study the various shapes of RGR of growth curve models in light of the unified growth equation. The unified growth model is given by

$$\begin{aligned} R(t)=\frac{r}{b^d} y^a (1-y^b)^d t^{c-1}. \end{aligned}$$
(22)

Differentiating with respect to t, we get,

$$\begin{aligned} \frac{\mathrm {d}R(t)}{\mathrm {d}t}= & {} \frac{r}{b^d} \left[ y^a (1-y^b)^d (c-1) t^{c-2} + y^{a-1} (1-y^b)^{d-1}t^{c-1} [a - (a+bd)y^b] \frac{\mathrm {d}y}{\mathrm {d}t} \right] \nonumber \\= & {} \frac{r}{b^d} y^{a-1} (1-y^b)^{d-1} t^{c-2} \left[ (c-1) y (1-y^b) + t \left[ a- (a+bd)y^b\right] \frac{\mathrm {d}y}{\mathrm {d}t} \right] .\nonumber \\ \end{aligned}$$
(23)
Fig. 2
figure 2

(Color figure online) RGR profile of the members of Tsoularis–Wallace model is shown in the panels (a)–(d). We see from the panel (a) that RGR can take both the decreasing as well as bell shapes depending on the values of a. The RGR profile of Richards family of growth curves \((R(t) = r (1-y^b))\) over size and time is depicted in the panels (b) and (c), respectively. We assume \(r=-1\) for first three graphs of the panels (b) and (c) where b is negative and \(r=1\) elsewhere. We get various RGR curves for different values of b such as Monomolecular \((b=-1)\), Von Bertalanffy \((b=-0.33)\), general Von Bertalanffy \((b=-0.2)\), and logistic \((b=1)\). We observe that RGR can take only decreasing shapes for any values of d, which is depicted in the subfigure (d)

Full size image
  1. 1.

    Tsoularis and Wallace: If we put \(c=1\) in the unified growth equation, we get the Tsoularis and Wallace (2002) model

    $$\begin{aligned} R(t)=\frac{r}{b^d} y^a (1-y^b)^d, \end{aligned}$$
    (24)

    and

    $$\begin{aligned} \frac{\mathrm {d}R(t)}{\mathrm {d}t} = \frac{r}{b^d} y^{a-1}(1-y^b)^{d-1}\left[ a-(a+bd)y^b\right] \frac{\mathrm {d}y}{\mathrm {d}t}. \end{aligned}$$

    We know y is size at time t and \(\frac{\mathrm {d}y}{\mathrm {d}t}\) is the growth rate. So \(\frac{\mathrm {d}y}{\mathrm {d}t}\) is non negative. The term \(y^{a-1}(1-y^b)^{(d-1)}\) is also non negative. If \(a \le 0\), then \(\frac{\mathrm {d}R(t)}{\mathrm {d}t}\) is negative for all y. Hence, R(t) is a decreasing function when \(a \le 0\).

    If \(a > 0\) then \(\frac{\mathrm {d}R(t)}{\mathrm {d}t}\) is non-monotonous as it does not take same sign for all \(0 \le y \le 1\). RGR is bell shaped in this case. RGR is increasing for \(0 \le y \le (\frac{a}{a+b})^{1/b}\) and decreasing otherwise. Now we consider the following special cases of TW model.

    1. (a)

      Marusic–Bajzer growth\((d=1)\): The Marusic and Bajzer (1993) model takes both monotone and non-monotone shapes. It takes decreasing shapes when \((a \le 0)\) and bell shapes when \((a>0)\). The various possible shapes of RGR are depicted in Fig. 2a.

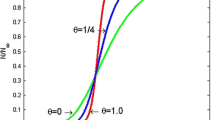
      Now if we put \(a=0\), we get Richards growth model for \(b\ge -1\). Since \(a=0\), RGR takes decreasing shapes only. Hence, the special cases of this model such as Monomolecular \((b=-1, r<0)\), general Von Bertalanffy \((0<b<1, r<0)\), Von Bertalanffy \((b=-\frac{1}{3}, r<0)\) (von Bertalanffy 1960), logistic \((b=1)\) (Verhulst 1838), Gompertz \((b \rightarrow 0)\) (Gompertz 1825) models take only decreasing shapes. The shapes of RGR for different values of b are shown in Fig. 2b, c.

    2. (b)

      Blumberg\((b =1)\): The Blumberg (1968) model takes both monotone and non-monotone shapes depending on the values of a. If \(a \le 0\) then it takes decreasing shapes and bell shapes when \(a>0\). The shapes of RGR for different values of d are shown in Fig. 2d.

    3. (c)

      General Gompertz\((a=0, b \rightarrow 0)\): The RGR function takes only decreasing shapes since \(a=0\). The shapes of RGR are shown in Fig. 3. The figure also includes its particular cases Gompertz \((d=1)\) and second-order exponential polynomial \((d=\frac{1}{2})\) growth curves. Note that the RGR of second exponential polynomial decreases linearly over time.

    4. (d)

      Generic \([a=b(1-d)]\): The generic model (Turner et al. 1976) takes decreasing shape when \(a \le 0\) i.e., \(d \ge 1\). RGR is bell shaped when \(0<d<1\). The hyperbolic growth model is a special case of the generic growth when \(a=-\frac{1}{n}\). RGR takes only decreasing shapes for hyperbolic growth since a is always negative.

Fig. 3
figure 3

(Color figure online) Profile plot of RGR of generalized Gompertz growth over size and time. \(d=\frac{1}{2}\) represents the second-order exponential growth model, and \(d=1\) represents the Gompertz growth models. Note that RGR is always decreasing for different values of d. Also, note that for second-order exponential polynomial RGR decreases linearly over time

Full size image
  1. 2.

    Korf: We have \(a=0, d=0, c<0\), in case of Korf (1939) model and \(\frac{\mathrm {d}R(t)}{\mathrm {d}t} = r(c-1) t^{c-2}<0\). Hence, RGR takes only decreasing shapes. The shapes of RGR over time and size are depicted in Fig. 4.

  2. 3.

    Koya–Goshu Model: Koya and Goshu (2013) proposed a generalized growth model as a solution of the ordinary differential equation that quantifies the growth phenomena. The eight parameter generalization is given by the following equation:

    $$\begin{aligned} y(t) = y_0 - [K- y_0]\left[ 1 - B e^{-k{\left( \frac{t-\mu }{\delta }\right) }^\gamma }\right] ^{m}, \end{aligned}$$
    (25)

    where y(t) is size at time t. The interpretation of the parameters are as follows: \(y_0\): initial size, K: asymptotic size, \(B= 1 - \left[ \frac{\theta -y_0}{K-y_0}\right] ^{\frac{1}{m}}\), \(\mu :\) time shift parameter, \(\delta :\) time scale parameter, \(\gamma , m:\) shape parameters of the growth function. The growth equation after ignoring the location and scale parameters is given in Eq. 12. The RGR equations are given in Eqs. (13) and (14). It can be shown that if \(a=0\) (14) then

    $$\begin{aligned} \frac{\mathrm {d}R(t)}{\mathrm {d}t}= & {} \frac{R(t)}{t}(c-1 - ry^bt^c). \end{aligned}$$
    (26)

    Here, RGR can take decreasing shape \((c \le 1)\) and bell shape \((c>1)\). If \(a=-b<0\) (13) then

    $$\begin{aligned} \frac{\mathrm {d}R(t)}{\mathrm {d}t}= & {} \frac{R(t)}{t}(c-1 - ry^{-b}t^c), \end{aligned}$$
    (27)

    and RGR can take both decreasing and bell shapes. Different parameter choices lead to different growth models, which are described as follows:

    1. (a)

      Weibull: The Weibull (1951) growth model is obtained by putting \(a=-1, b=1, d=1\). Putting the values of a, b, d in (23) we get

      $$\begin{aligned} \frac{\mathrm {d}R(t)}{\mathrm {d}t} = r y^{-2} t^{c-2}\left[ (c-1)y(1-y) - t \frac{\mathrm {d}y}{\mathrm {d}t}\right] . \end{aligned}$$

      If \(c \le 1\), then \(\frac{\mathrm {d}R(t)}{\mathrm {d}t}<0\) and RGR is a decreasing function.

      $$\begin{aligned} \frac{\mathrm {d}R(t)}{\mathrm {d}t}= & {} \frac{r R(t)}{t}\left[ \frac{c-1}{r} - \frac{t^c}{y}\right] \\= & {} \frac{r R(t)}{t}\left[ \frac{c}{r}- \frac{t^c}{y} - \frac{1}{r}\right] . \end{aligned}$$

      It can be shown that \(r t^c \ge cy\) using the size–time relationship, and hence, \(\frac{\mathrm {d}R(t)}{\mathrm {d}t}<0\) when \(c>1\). So RGR is always a decreasing function. We have depicted the various possible shapes of RGR in Fig. 5.

    Fig. 4
    figure 4

    (Color figure online) Profile plot of RGR of Korf growth over size and time. For various possible values of c, we get only different decreasing shapes of RGR

    Full size image
    Fig. 5
    figure 5

    (Color figure online) Profile plot of RGR of Weibull growth over size and time. Note that in the case of Weibull growth RGR takes only decreasing shapes over both size and time

    Full size image
    Fig. 6
    figure 6

    (Color figure online) RGR profile of the extended Gompertz growth over size and time. Here, the RGR can take both decreasing and bell shapes over both size and time depending on the parameter c. \(c=1\) represents the Gompertz growth. If \(c < 1\) RGR takes decreasing shapes, the maximum value of RGR is observed at the initial time point, and the initial value of RGR is more than the initial RGR of Gompertz growth. If \(c>1\) RGR is bell shaped, the maximum value of RGR is observed after the initial time point, and the initial RGR is smaller in comparison with the Gompertz growth

    Full size image
    Fig. 7
    figure 7

    (Color figure online) RGR profile of extended logistic growth over size and time. The extended logistic model also captures both decreasing and bell shapes over both size and time like extended Gompertz model depending on the parameter c. \(c=1\) represents the logistic growth. When \(c < 1\) RGR takes decreasing shapes, the maximum value of RGR is observed at the initial time point, and the initial value of RGR is more than the initial RGR of the logistic growth. When \(c>1\) RGR is bell shaped, the maximum value of RGR is observed after the initial time point, and the initial RGR is smaller in comparison with the logistic growth

    Full size image
    1. (b)

      Extended Gompertz Model: The RGR equation of extended Gompertz model proposed by Chakraborty et al. (2017) is given by

      $$\begin{aligned} \frac{1}{X(t)}\frac{\mathrm {d}X(t)}{\mathrm {d}t}=ac (\ln K -\ln X(t)) t^{c-1}, \end{aligned}$$
      (28)

      where \(a > 0\) and \(c > 0\). Integrating the above equation (Eq. 28), we obtain the following relation of size and time

      $$\begin{aligned} \ln {\frac{X(t)}{X_0}}=\ln \frac{K}{X_0}\left( 1-e^{-at^c}\right) , \end{aligned}$$
      (29)

      where \(X_0\) is the size at \(t=0\). Differentiating Eq. (28), we get,

      $$\begin{aligned} \frac{\mathrm {d}R(t)}{\mathrm {d}t}= & {} bt^{c-2}e^{-at^c}(c-1 - act^c). \end{aligned}$$
      (30)

      If \(c \le 1\), then RGR is a decreasing function of time. If \(c>1\) RGR initially increases up to the time point \((\frac{c-1}{ac})^{\frac{1}{c}}\) and decreases there after. The shapes of RGR are illustrated in Fig. 6.

    2. (b)

      Extended logistic Model: The extension of logistic model proposed by Chakraborty et al. (2017) is given by

      $$\begin{aligned} \frac{1}{X(t)}\frac{\mathrm {d}X(t)}{\mathrm {d}t}=\frac{r}{K} (K - X(t)) t^{c-1}, \end{aligned}$$
      (31)

      where \(r > 0\) and \(K > 0\). Integrating the above equation (Eq. 31), we obtain the following relation of size and time

      $$\begin{aligned} X(t) = \frac{K}{1 + \ln \left( \frac{K}{X_0}-1\right) e^{-at^c}}, \end{aligned}$$
      (32)

      where \(X_0\) is the initial size. Differentiating Eq. (31), we get

      $$\begin{aligned} \frac{\mathrm {d}R(t)}{\mathrm {d}t}= & {} \frac{R(t)}{t}(c-1 - ryt^c). \end{aligned}$$
      (33)

      If \(c \le 1\), then RGR is a decreasing function of time. On the other hand, if \(c>1\) RGR is bell shaped. The possible shapes of RGR are shown in Fig. 7.

Various shapes of RGR are summarized in Table 1.

4.1 Some Important Points

  1. 1.

    If \(c=1\) then RGR is a function of size only and all the models take decreasing shapes when \(a \le 0\) and bell shapes when \(a>0\).

  2. 2.

    The RGR form of general Von Bertalanffy growth is \(R(t) = r y^{-a}(1-y^a) = -r (1-y^{-a})\), where \(0<a<1\). Note that the Von Bertalanffy growth can be considered as the form of the Richards growth with \(-1<b<0\) and \(r<0\). Hence, we can conclude that Monomolecular \((b=-1)\), Von Bertalanffy \((-1<b<0, r<0)\), Bertalanffy \((b=-\frac{1}{3}, r<0)\), Gompertz \((b \rightarrow 0)\), logistic \((b=1)\) are special cases of Richards’ growth.

  3. 3.

    Korf growth can be interpreted as a special case of generalized Gompertz growth, and it converges to Gompertz growth for large values of c.

  4. 4.

    Weibull is time covariate generalization of the Monomolecular growth model. Weibull is one of the growth curves with \(c>0\) where RGR takes only decreasing shape for any values of c.

  5. 5.

    The KG model is the time covariate generalization of the Richards’ growth model, whereas the extended logistic and extended Gompertz models (Chakraborty et al. 2017) are time covariate generalization of logistic and Gompertz models, respectively.

4.2 Allee Effect and Unified Growth Equation

Conceptually, a much wider range of growth models are retrieved from the unified equation as special cases. We have already discussed such cases in Sect. 3 of this article. In particular, increasing shape of RGR at low size is of special importance in ecology. Such profiles indicate the presence of Allee effect. In ecology, Allee effect in a natural population refers to the density-mediated drop in population fitness when they are small in numbers. The evidence of Allee effect in real data is generally detected by positive correlation between per capita growth rate and populations size. Some of the ecological factors that lead to the Allee effects are mate limitation, cooperative breeding, high predation, etc. (Courchamp et al. 2008; Bhowmick et al. 2015). In this manuscript, RGR and density (size) have positive association in some of these models, namely Tsoularis–Wallace (\(a>0\)) and Koya–Goshu \((c>1)\). Many flexible shapes, offered in this manuscript, represent an Allee growth profile. For example, in Fig. 2a (\(a=1\) or \(a = \frac{1}{2}\)) RGR increases at small sizes. Similar cases are observed in Figs. 6a and Fig. 7a for \(c=2\) and \(c=3\), respectively. More precisely, these designated growth profiles demonstrate the weak Allee effect, in which, RGR is small at low abundance, but is never negative. On the other hand, a strong Allee effect refers to the situation where RGR is negative below a critical threshold populations size. A detailed discussion on this can be found in Courchamp et al. (2008). The proposed unification may aid in identifying the weak Allee effect by identifying the correct growth profile. Thus, the proposed unification method can additionally integrate a family of weak Allee effect model with the existing density-dependent growth equation.

5 Conclusion

Mathematical modeling of growth processes has a long history, and its applications are widespread. However, substantial evidence on the unification of growth equations is still lacking in this vast growth literature. Garcia (2005) and Martinez et al. (2008) are two significant contributions in the literature that unify a large class of existing growth models. Recently, a rich family of growth curves has been developed, which is characterized by the RGR function of both time and size. The exiting unification approaches are not sufficient to represent such RGR growth curves. We developed a unification approach based on this generalized RGR function that is capable of covering the limitation of existing unification.

RGR has immense practical value in biological growth curve analysis, which has been amplified by the construction of RGR curves in the literature. The said unification method is originally motivated to explain the growth process by RGR, which is more appropriate than the original size variable in data analysis. Thus, the proposed mathematical framework enjoys a better biological rationale compared to existing unification, which was achieved by selecting some arbitrary function mechanistically. Consequently, the unification of RGR curves reinforces greater utility in real-life applications.

Due to a large number of models, considerable misunderstanding is there in the growth curve literature because many models are presented as parameterization or re-parameterization of the other models (Tjørve and Tjørve 2010). Our proposed unification might be useful in reducing the number of growth models and facilitate searching for the best model for a given data set more efficiently. Thus, it is expected to reduce the confusion by comparing two similar rival models (often containing a large number of parameters) by appropriate selection of unification parameters only. This would also allow a better performance in the statistical fitting of growth functions by nonlinear regression analysis.