Dynamical behaviour of a two-predator model with prey refuge

Abstract

A three-component model consisting on one-prey and two-predator populations is considered with a Holling type II response function incorporating a constant proportion of prey refuge. We also consider the competition among predators for their food (prey) and shelter. The essential mathematical features of the model have been analyzed thoroughly in terms of stability and bifurcations arising in some selected situations. Threshold values for some parameters indicating the feasibility and stability conditions of some equilibria are determined. The range of significant parameters under which the system admits different types of bifurcations is investigated. Numerical illustrations are performed in order to validate the applicability of the model under consideration.

1 Introduction

Ecological traits that describe animal behaviours such as habitat usage and foraging strategies are the objects and results of natural selection. Therefore, studies on the stability of an ecological system considering evolutionary perturbation are extremely important. When a system contains many interacting species, the fitness of one will depend on its own ecotype as well as on those of the other interacting individuals that coexist in this ecosystem (cf. Cressman and Garay [1]).

The Hoogly–Matla estuarine complex, with its luxuriant mangroves is a unique ecosystem. This ecosystem is considered as one of the best detritus-based ecosystems (cf. Ray and Straskraba [2]). One of the important biological components in the estuary is the detritivorous fish community. This mangrove ecosystem is composed of several islands, which are criss-crossed by numerous creeks originating from the main rivers. These creeks are supplied with rich detritus loads originating from an adjacent mangrove litter. The rich detritus of these creeks supports the most important detritivorous fish, namely Liza parsia. In these creeks, two important predator fish of these detritivorous fish are also abundant, viz. Sciaena miles and Otolithoides pama. These two species are in competition for food and shelter and feed mainly on the same detritivorous fish, viz. Liza parsia. These two competing predators can coexist because they exploit their environment differently. The prey species also exist in the same environment by avoiding predation pressure in two ways. Firstly, the competition between two predators indirectly helps the prey species survive, and secondly, the most important part of the prey’s survival strategy is the refuge phenomenon. The mangrove plants are extended from the supra-littoral zone to the lower-littoral zone up to the creek bed. To avoid predation pressure during high tide (as the predator species only visit these creeks during high tide), the prey species takes refuge into the bushy part of the submerged mangrove plants. One of the more relevant behavioral traits that affects the dynamics of the predator–prey system is the use of spatial refuge by the prey. This spatial refuge is noticed where environmental heterogeneity provides less accessible sights for the predator, which can be exploited/utilized by a given number of prey. For this reason, certain portions of the prey species are partially protected against predators (cf. Gonzalez-Olivares and Ramos-Jiliberto [3]).

The use of refuge has been shown to enhance predator–prey coexistence by preventing prey extinction (cf. Connell [4], Murdoch and Oaten [5]). The study of the consequences of prey refuge on the dynamics of predator–prey interactions can be recognized as a major but rather challenging issue in applied mathematics and theoretical ecology (cf. Hassell and May [6], Hassell [7], Holling [8, 9], Hoy [10], Huang et al. [11], Smith [12]). Some of the empirical and theoretical works based on prey refuge have concluded that the refuge used by prey has a stabilizing effect on predator–prey interactions and also the prey species can be prevented from extinction by using this policy (cf. Gonzalez-Olivares and Ramos-Jiliberto [3], Collings [13], Freedman [14], Hochberg and Holt [15], Kar [16], Krivan [17], May [18], McNair [19], Ruxton [20], Sih [21], Taylor [22]). The presence of a constant proportion of prey refuge does not change the nature of the dynamical stability of the neutrally stable Lotka–Volterra model, while a constant refuge of any size can replace the neutrally stable behavior with a stable equilibrium (cf. Smith [12]). Hassell and May [6] have shown that the addition of a large refuge to a model, which in the absence of prey refuge exhibits a divergent oscillation, can replace the oscillatory behavior with a stable equilibrium. Based on the above, an attempt is made in the present investigation to study a three-component predator–prey model in which one prey species takes refuge and two predator species feed on the same prey species with competition among themselves.

The present investigation has been carried out sequentially as follows: basic assumptions and the model formulation are proposed in Section 2. Section 3 deals with some preliminary results. We discuss the local stability and Hopf bifurcation of the boundary equilibria and persistence of system (3) in Sections 4 and 5, respectively. Simulation results are exhibited in Section 6 while a final discussion and interpretation of the results are included in the concluding Section 7.

2 One-prey and two-predator model

The model considered is based on the one-prey and two-predator system

$$ \label{eq1} \left\{ {{\begin{array}{*{20}c} \hfill {\displaystyle\frac{dx_1 }{dt}=\alpha x_1 \left( {1-\frac{x_1 }{k}} \right)-\displaystyle\frac{\beta_1 x_1 x_2 }{1+a_1 x_1 }-\displaystyle\frac{\beta_2 x_1 x_3 }{1+a_2 x_1 }} \\[7pt] {{\kern-37.5pt}\displaystyle\frac{dx_2 }{dt}=-d_1 x_2 +\displaystyle\frac{c_1 \beta_1 x_1 x_2 }{1+a_1 x_1 }-\sigma_1 x_2 x_3 } \\[7pt] {{\kern-37.5pt}\displaystyle\frac{dx_3 }{dt}=-d_2 x_3 +\displaystyle\frac{c_2 \beta_2 x_1 x_3 }{1+a_2 x_1 }-\sigma_2 x_2 x_3 } \\ \end{array} }} \right. $$

(1)

where x ₁ is the prey population size, and x ₂ and x ₃ are the population sizes of the first and second predator species, respectively, at any time t. Here α, k are respectively the growth rate and the environmental carrying capacity of the prey species, d ₁ and d ₂ are the predators’ death rates, and σ ₁ and σ ₂ are the rates at which the growth rate of the first predator is annihilated by the second predator and vice versa. $\frac{\beta _1 }{a_1 }$, $\frac{\beta_2 }{a_2 }$ are the respective maximum numbers of prey that can be eaten by the first and second predators per unit time, while c ₁, c ₂ are the conversion factors, denoting the number of newly born first and second predators for each captured prey species, where 0 < c ₁, c ₂ < 1. All the system parameters are assumed to be positive constants. The terms $\frac{\beta_1 x_1 }{1+a_1 x_1 }$ and $\frac{\beta_2 x_1 }{1+a_2 x_1 }$ denote the first and second predators’ response to the prey species, respectively. This type of predator response function is known as the Holling type II response function (cf. Holling [23]).

The above model has been updated by incorporating prey refuges proportionally to the prey density viz. m ₁ x ₁ and m ₂ x ₁ from the first and second predator species, respectively, where 0 ≤ m ₁, m ₂ < 1. It is considered that the first and second predator species are in competition for food and other essential resources such as shelter. Incorporation of prey refuges leaves the factors (1 − m ₁)x ₁ and (1 − m ₂)x ₁ of the prey population open to be hunted by the first and second predators, respectively, and the competitive effect reduces the growth rate of both predator species. Under these additional effects, system (1) reduces to the following modified form:

$$ \label{eq2} \left\{ {{\begin{array}{*{20}c} {\displaystyle\frac{dx_1 }{dt}=\alpha x_1 \left( {1-\frac{x_1 }{k}} \right)-\displaystyle\frac{\beta_1 \left( {1-m_1 } \right)x_1 x_2 }{1+a_1 \left( {1-m_1 } \right)x_1 }-\displaystyle\frac{\beta_2 \left( {1-m_2 } \right)x_1 x_3 }{1+a_2 \left( {1-m_2 } \right)x_1 }} \\[6pt] {{\kern-75pt}\displaystyle\frac{dx_2 }{dt}=-d_1 x_2 +\displaystyle\frac{c_1 \beta_1 \left( {1-m_1 } \right)x_1 x_2 }{1+a_1 \left( {1-m_1 } \right)x_1 }-\sigma_1 x_2 x_3 } \\[6pt] {{\kern-75pt}\displaystyle\frac{dx_3 }{dt}=-d_2 x_3 +\displaystyle\frac{c_2 \beta_2 \left( {1-m_2 } \right)x_1 x_3 }{1+a_2 \left( {1-m_2 } \right)x_1 }-\sigma_2 x_2 x_3 } \\ \end{array} }} \right. $$

(2)

with initial conditions,

$$ x_{1}(0)=x^{0}_{1}>0, x_{2}(0)=x^{0}_{2}>0, x_{3}(0)=x^{0}_{3}>0. $$

By making use of the transformations given by x ₁ = kS, $x_2 =\frac{\alpha ka_1 P_1 }{\beta_1 }$, $x_3 =\frac{\alpha ka_2 P_2 }{\beta_2 }$, and t ^′ = αt, the present improved dynamical system (2) reduces to the following non-dimensional system (using t instead of t ^′ for notational convenience)

$$ \label{eq3} \left\{ {{\begin{array}{*{20}c} {\displaystyle\frac{dS}{dt}=S\left({1-S} \right)-\displaystyle\frac{SP_1}{A_1 +S}-\displaystyle\frac{SP_2 }{A_2 +S}} \\[8pt] {{\kern-15pt}\displaystyle\frac{dP_1 }{dt}=-\delta_1 P_1 +\displaystyle\frac{\epsilon_1 SP_1 }{A_1 +S}-\gamma_1 P_1 P_2 } \\[8pt] {{\kern-15pt}\displaystyle\frac{dP_2 }{dt}=-\delta_2 P_2 +\displaystyle\frac{\epsilon_2 SP_2 }{A_2 +S}-\gamma_2 P_1 P_2 } \\ \end{array} },} \right. $$

(3)

where $\epsilon_1 =\frac{c_1 \beta_1 }{\alpha a_1 }$, $\epsilon_2 =\frac{c_2 \beta _2 }{\alpha a_2 }$, $\gamma_1 =\frac{\sigma_1 ka_2 }{\beta_2 }$, $\gamma _2 =\frac{\sigma_2 ka_1 }{\beta_1 }$, $\delta_1 =\frac{d_1 }{\alpha }$, $\delta_2 =\frac{d_2 }{\alpha }$, $A_1 =\frac{1}{a_1 \left( {1-m_1 } \right)k}$, $A_2 =\frac{1}{a_2 \left( {1-m_2 } \right)k}$. For ecological reasons, model (3) is considered only in ${\rm Int}(\mathbf{R}^{\mathbf{3}}_{+})=\{(S, P_{1}, P_{2}); S > 0, P_{1} > 0, P_{2} > 0\}$.

The corresponding model in the absence of refuges (m ₁ = 0, m ₂ = 0) is analogous to that of (3) with differences in the non-dimensional parameters A ₁ and A ₂ only, where $A_{\,1}^{\,0} =\left. {A_1 } \right|_{m_1 =0} =\frac{1}{a_1 k} \;\mbox{and}\;A_{\,2}^{\,0} =\left. {A_2 } \right|_{m_2 =0} = \frac{1}{a_2 k} .$

3 Some preliminary results

3.1 Existence and positive invariance

For t > 0, letting X ≡ ($S, P_{1}, P_{2})^{T}$, F:ℝ³→ℝ³, F = ($F_{1}, F_{2}, F_{3})^{T}$ , system (3) can be rewritten as $\frac{dX}{dt}=F\left( X \right)$. Here $F_i \in C^\infty \left(\mathbb{R} \right)$ for i = 1, 2, 3, where $F_1 =S\left( {1-S} \right)-\frac{SP_1 }{A_1 +S}-\frac{SP_2 }{A_2 +S}$, $F_2 =-\delta_1 P_1 +\frac{\epsilon_1 SP_1 }{A_1 +S}-\gamma_1 P_1 P_2$ and $F_3 =-\delta_2 P_2 +\frac{\epsilon_2 SP_2 }{A_2 +S}-\gamma_2 P_1 P_2$. Since the vector function F is a smooth function of the variables (S, P ₁, P ₂) in the positive octant $\Omega =\left\{ {\left( {S,P_1 ,P_2 } \right);S>0,\,P_1 >0,\,P_2 >0} \right\}$, the local existence and uniqueness of the solution hold.

3.2 Boundedness

Boundedness implies that the system is biologically well-behaved. The following propositions ensure the boundedness of system (3).

Proposition 1

The prey population is always bounded from above.

Proof

From the first sub-equation of (3), the following inequality is found

$$ {\begin{array}{*{20}c} {\displaystyle\frac{dS}{dt}\le S\left( {1-S} \right),} \hfill & {_{t\to +\infty }^{\lim \,\sup \;S\left( t \right)\le 1} } \hfill \\ \end{array} }. $$

□

Proposition 2

If max $\left\{ {R_{P_1 } ,R_{P_2 } } \right\}<1$ , where $R_{P_1 } =\frac{\epsilon_1 }{\delta_1 A_1 }$ and $R_{P_2 } =\frac{\epsilon_2 }{\delta_2 A_2 }$ , then the total predator population goes into extinction.

Proof

From the second and third sub-equations of (3) and recalling Proposition 1, it can be easily shown that

$$ \frac{dP_1 }{dt}+\frac{dP_2 }{dt}\le -\delta_1 P_1 \left( {1-R_{P_1 } } \right)-\delta_2 P_2 \left( {1-R_{P_2 } } \right). $$

Thus, if max $\left\{ {R_{P_1 } ,R_{P_2 } } \right\}<1$, then the predator population will go into extinction. The parameter combinations $R_{P_1 }$ and $R_{P_2 }$ are similar to the reproduction ratios in epidemic theory (cf. Hethcote et al. [24], Inaba and Nishiura [25], and Haque and Venturino [26]).□

Proposition 3

The solutions of (3) starting in Ω are uniformly bounded with an ultimate bound.

Proof

Define a function $X=S+\frac{P_1 }{\epsilon_1 }+\frac{P_2 }{\epsilon_2 }$. Taking its time derivative along the solutions of (3), we have

$$ \frac{d\chi }{dt}+\phi \chi \le S\left( {1+\phi -S}\, \right)+\frac{1}{\epsilon_1 }\left( {\phi -\delta_1 } \right)P_1 +\frac{1}{\epsilon_2 }\left( {\phi -\delta _2 } \right)P_2. $$

Now we choose ϕ in such a way that ϕ < min {δ ₁, δ ₂}, so that the above inequality reduces to

$$ \begin{array}{rll} \frac{d\chi }{dt}+\phi \chi &\le& S\left( {1+\phi -S}\, \right)\\ &\le& \frac{\left( {1+\phi } \right)^2}{4}\equiv \rho. \end{array} $$

Integrating the differential inequality between the limits t ₀ and t, (cf. Birkhoff and Rota [27] and Haque and Venturino [28]), we find

$$ \label{eq4} \chi \left( t \right)\le e^{-\phi t}\chi \left( {t_0 } \right)+\frac{\rho }{\phi }\left( {1-e^{-\phi t}} \right)\le \max \left( {\chi \left( {t_0 } \right),\frac{\rho }{\phi }} \right)\;\mbox{and}\;_{t\to +\infty }^{\lim \,\sup } \;\chi \left( t \right)\le \frac{\rho }{\phi }, $$

(4)

with the last bound independent of the initial condition. Hence, all the solutions of (3) starting in ${\rm {\bf R}}_+^3$ for any θ > 0 evolve with respect to time in the compact region

$$ \label{eq5} \overline \Omega =\left\{ {\left( {S,P_1 ,P_2 } \right)\in {\rm {\bf R}}_+^3 :S+\frac{P_1 }{\epsilon_1 }+\frac{P_2 }{\epsilon 2}\le \frac{\rho }{\phi }+\theta } \right\}. $$

(5)

□

3.3 Equilibria and their feasibility

Equilibria

The equilibria of (3) are the origin (i) E ₀ ≡ (0, 0, 0); the boundary points (ii) E ₁ ≡ (1, 0, 0), (iii) E ₂ ≡ (S ₂, P ₁₂, 0), (iv) E ₃ ≡ (S ₃, 0, P ₂₃), (v) E ₄ ≡ (0, P ₁₄, P ₂₄) and the interior equilibrium (vi) $E^{\,\ast} \equiv \left( {S^{\,\ast} ,P_1^{\,\ast} ,P_2^{\,\ast} } \right)$, where

$$ \begin{array}{rll} S_2 &=&\displaystyle\frac{\delta_1 A_1 }{\epsilon_1 -\delta_1 },\;P_{12} =\displaystyle\frac{A_1 \epsilon_1 \left( {\epsilon_1 -\delta_1 \left( {1+A_1 } \right)} \right)}{\left( {\epsilon_1 -\delta_1 } \right)^2};\\ S_3 &=&\displaystyle\frac{\delta_2 A_2 }{\epsilon_2 -\delta_2}, \;P_{23} =\displaystyle\frac{A_2 \epsilon_2 \left( {\epsilon_2 -\delta_2 \left( {1+A_2 } \right)} \right)}{\left( {\epsilon_2 -\delta_2 } \right)^2};\\ P_{14} &=&-\displaystyle\frac{\delta_2 }{\gamma_2 },\;P_{24} =-\displaystyle\frac{\delta_1 }{\gamma _1 };\,P{\kern1pt}_1^* =\displaystyle\frac{S{\kern1pt}^{*} \left( {\epsilon_2 -\delta_2 } \right)-\delta_2 A_2 }{\gamma_2 \left( {A_2 +S{\kern1pt}^{*} } \right)},\;P{\kern1pt}_2^{*} =\displaystyle\frac{S{\kern1pt}^{*} \left( {\epsilon_1 -\delta_1 } \right)-\delta_1 A_1 }{\gamma_1 \left( {A_1 +S{\kern1pt}^{*}} \right)};\\ \end{array} $$

in which S ^∗ is the positive root of the cubic equation given by

$$ \begin{array}{rll} \label{eq6} &&\gamma_1 \gamma_2 S{^{\,\ast}}^3+\gamma_1 \gamma_2 \left( {-1+A_1 +A_2 } \right)S{^{\,\ast}}^2+\left( \gamma_1 \left( {\epsilon_2 -\delta_2 } \right)+\gamma _2 \left( {\in_1 - \delta_1 } \right)\right.\notag\\ &&{\kern12pt}\left.-\,\gamma_1 \gamma_2 \left( {A_1 +A_2 -A_1 A_2 } \right) \right)S{^{\,\ast}} -\left( {\gamma_1 \gamma_2 A_1 A_2 +\delta_2 \gamma_1 A_2 +\delta_1 \gamma_2 A_1 } \right)=0 . \end{array} $$

(6)

Therefore, according to Descartes’ rule of sign, cubic (6) has exactly one positive real root irrespective of the sign of the coefficient of S ^∗ if A ₁ + A ₂ > 1.

Feasibility

It is clear that the equilibria E ₀, E ₁ are obviously feasible. The equilibrium point E ₄ is always infeasible. E ₂ is feasible under the condition ϵ ₁ > δ ₁(1 + A ₁) and E ₃ is feasible under the condition ϵ ₂ > δ ₂(1 + A ₂). The interior equilibrium E ^∗ is feasible if the conditions (i) $\epsilon_1 >\delta_1 \left( {1+\frac{A_1}{S{^{\,\ast}} }} \right)$ and (ii) $\epsilon_2 >\delta_2 \left( {1+\frac{A_2 }{S{^{\,\ast}}}} \right)$ simultaneously hold.

4 Stability and bifurcation analysis

The Jacobian of (3) at any arbitrary point $\left({\tilde{{S}},\tilde{{P}}_1 ,\tilde{{P}}_2 } \right)$ is J ≡ DF (X) = (b _ij ) ∈ R ^{3 ×3} with

$$ J=\left( {b_{ij} } \right)\!=\!\left[\!\!{{\begin{array}{*{20}c} {1\!-\!2\tilde{{S}}\!-\!\dfrac{A_1 \tilde{{P}}_1 }{\left({A_1 \!+\!\tilde{{S}}}\right)^2}\!-\!\dfrac{A_2 \tilde{{P}}_2 }{\left({A_2 \!+\!\tilde{{S}}} \right)^2}} \hfill & {\dfrac{\tilde{{S}}}{A_1 \!+\!\tilde{{S}}}} \hfill &{\dfrac{\tilde{{S}}}{A_2 \!+\!\tilde{{S}}}} \hfill \\ {\dfrac{\epsilon_1 A_1 \tilde{{P}}_1 }{\left( {A_1 \!+\!\tilde{{S}}} \right)^2}} \hfill & {-\delta_1 \!+\!\dfrac{\epsilon_1 \tilde{{S}}}{A_1 \!+\!\tilde{{S}}}-\gamma_1 \tilde{{P}}_2 } \hfill & {-\gamma_1 \tilde{{P}}_1 } \hfill \\ {\dfrac{\epsilon_2 A_2 \tilde{{P}}_2 }{\left( {A_2 \!+\!\tilde{{S}}} \right)^2}} \hfill & {-\gamma_2 \tilde{{P}}_2 } \hfill & {-\delta_2 \!+\!\dfrac{\epsilon_2 \tilde{{S}}}{A_2 \!+\!\tilde{{S}}}\!-\!\gamma_2 \tilde{{P}}_1 } \hfill \\ \end{array} }} \!\!\right]\!. $$

Let this be denoted by $J_k =J\left( {E_k } \right)=\left( {b_{ij}^{\left[ k \right]} } \right)$ at the equilibrium E _k , k = 0, ..., 4 and $J{\kern1pt}^{\ast} =\left( {b_{ij}^{\left[ \ast \right]} } \right)$ at E *. Its characteristic equation is $\Delta (\lambda )\equiv \lambda^3+\kappa_1 \lambda^2+\kappa_2 \lambda +\kappa_3 =0$, where κ ₁ = −tr(J ), κ ₂ = M and κ ₃ = − det(J ); M being the sum of the principal minors of order two of J.

Note that the conditions for Hopf bifurcation to occur are that there exists a certain bifurcation parameter ζ = ζ _h such that $C_2 \left( {\zeta_h } \right)=\kappa_1 \left( {\zeta_h } \right)\kappa_2 \left( {\zeta_h } \right)-\kappa_3 \left( {\zeta_h } \right)=0$ with κ ₂ > 0 and $\frac{d}{d\zeta }\left. {\left( {Re\left( {\lambda \left( \zeta \right)} \right)} \right)} \right|_{\zeta =\zeta_h } \ne 0$, where λ is given by the characteristic equation Δ(λ) = 0.

Stability

The eigenvalues of the Jacobian matrix J ₀ are 1, − δ ₁ and − δ ₂. Hence E ₀ is unstable along the S axis. The eigenvalues of the Jacobian matrix J ₁ are −1, $-\delta_1 +\frac{\epsilon_1 }{1+A_1 }$ and $-\delta_2 +\frac{\epsilon_2 }{1+A_2 }$. Hence the equilibrium E ₁ is locally asymptotically stable if the conditions (i) ϵ ₁ < δ ₁(1 + A ₁) and ϵ ₂ < δ ₂(1 + A ₂) are satisfied.

Remark

The existence of local stability of system (3) around E ₁ eliminates the feasibilities of E ₂ as well as E ₃. Furthermore, it is observed that E ₂ →E ₁ as $\epsilon_1 =\delta_1 \left( {1+A_1 } \right)$ and E ₃→E ₁ as $\epsilon_2 =\delta_2 \left( {1+A_2 }\right)$.

4.1 Existence of transcritical bifurcation around E ₁

Theorem 4

The system (3) does not experience any saddle-node, pitch-fork, or Hopf bifurcation but admits a transcritical bifurcation at the equilibrium point E ₁ as the parameter ϵ ₁ crosses the critical value $\epsilon_1 =\delta_1 \left( {1+A_1 } \right)$ .

Proof

One of the eigenvalues of J ₁ will be zero iff $\det (J_2 )=b_{11}^{\left[ 1 \right]} b_{22}^{\left[ 1 \right]} b_{33}^{\left[ 1 \right]} =0$, i.e., $b_{22}^{\left[ 1 \right]} =0$ or $b_{33}^{\left[ 1 \right]} =0$, which respectively gives $\epsilon_1 =\delta_1 \left( {1+A_1 } \right)=\epsilon_1^{\left[ {tc} \right]}$ or $\epsilon_2 =\delta_2 \left( {1+A_2 } \right)=\epsilon_2^{\left[ {tc} \right]}$. Now when $\epsilon_1 =\epsilon_1^{\left[ {tc} \right]}$, the other two eigenvalues are given by ς ₁ = −1, $\zeta_2 =\delta_2 +\frac{\epsilon_2 }{1+A_2 }$. These eigenvalues will be of same sign if $\epsilon_2 <\epsilon_2^{\left[ {tc} \right]}$ or of opposite sign if $\epsilon_2 >\epsilon_2^{\left[ {tc} \right]}$. Now we have obtained that $\Xi =\left( {\theta ,-\left( {1+A_1 } \right)\theta ,0} \right)^T$, $\Upsilon =(0,\hbar_2 ,0)^T$, where Ξ, Υ are the eigenvectors corresponding to the eigenvalue ς ₁ = 0 of the matrices J ₁ and $J_1^T$ respectively and θ, h are any two non-zero real numbers. Note that $\Upsilon ^T\left[ {F_{\epsilon 1} \left( {E_1 ,\epsilon_1^{\left[ {tc} \right]} } \right)} \right]=0$ when E ₁ = (1, 0, 0) and hence system (3) does not experience any saddle-node bifurcation (cf. Sotomayor [29]). Again $\Upsilon^T\left[ {DF_{\epsilon 1} \left( {E_1 ,\;\epsilon_1^{\left[ {tc} \right]} } \right)\Xi } \right]=\hbar_2 \theta \ne 0$ and $\Upsilon^T\left[ {D^{\,2}F\left( {E_1 ,\;\epsilon_1^{\left[ {tc} \right]} } \right)\left( {\Xi ,\Xi } \right)} \right]=-\frac{\left( {1+\epsilon_1 } \right)}{\left( {1+A_1 } \right)}A_1 \theta^2\hbar \ne 0$, where $\left[ {DF_{\epsilon_1 } \left( {E_1 ,\epsilon _1^{\left[ {tc} \right]} } \right)} \right]=\left( {\alpha_{ij} } \right)_{3\times 3}$ and $\alpha_{11} = \alpha _{12} = \alpha_{13} = 0, \alpha_{21} = 0, \alpha_{22} =\frac{1}{1+A_1 }, \alpha_{23} = 0, \alpha_{31} = \alpha_{32} = \alpha_{33} = 0$ and $\left[ {D^{\,2}F\left( {X,\epsilon_1 } \right)} \right]=\left[ {{\begin{array}{*{20}c} {\nabla \frac{\partial F_1 }{\partial S}} \hfill & {\nabla \frac{\partial F_2 }{\partial S}} \hfill & {\nabla \frac{\partial F_3 }{\partial S}} \hfill \\ {\nabla \frac{\partial F_1 }{\partial P_1 }} \hfill & {\nabla \frac{\partial F_2 }{\partial P_1 }} \hfill & {\nabla \frac{\partial F_3 }{\partial P_1 }} \hfill \\[3pt] {\nabla \frac{\partial F_1 }{\partial P_2 }} \hfill & {\nabla \frac{\partial F_2 }{\partial P_2 }} \hfill & {\nabla \frac{\partial F_3 }{\partial P_2 }} \hfill \\[3pt] \end{array} }} \right]\in {\rm {\bf R}}^{3\times 3\times 3}$ , $\nabla \frac{\partial F_i }{\partial S}=\left( {\frac{\partial^2F_i }{\partial S^2},\;\frac{\partial^2F_i }{\partial P_1 S},\;\frac{\partial^2F_i }{\partial P_2 S}} \right)^T$, $\nabla \frac{\partial F_i }{\partial P_1 }=\left( {\frac{\partial^2F_i }{\partial SP_1 },\;\frac{\partial^2F_i }{\partial P_1^{\,2} },\;\frac{\partial^2F_i }{\partial P_2 P_1 }} \right)^T$, $\nabla \frac{\partial F_i }{\partial P_2 }=\left( {\frac{\partial^2F_i }{\partial SP_2 },\;\frac{\partial^2F_i }{\partial P_1^{P_2} },\;\frac{\partial^2F_i }{\partial P_2^{\,2} }} \right)^T$ for i = 1, 2, 3. The expressions for DF (U), D ² F (U, U) and D ³ F (U, U, U) can be obtained analytically (cf. Rudin [30]). Thus the system possesses a transcritical bifurcation around E ₁ (cf. Sotomayor [29]).

Again, since $\Upsilon^T\left[ {D^{\,2}F\left( {E_1 ,\epsilon_1^{\left[ {tc} \right]} } \right)\left( {\Xi ,\Xi } \right)} \right]\ne 0$, by the same theorem in Sotomayor [29], the system does not have any pitch-fork bifurcation. Furthermore, as the characteristic polynomial for the Jacobian J ₁ has three linear factors, no Hopf bifurcation can arise.

In a similar fashion, one can show that for $\epsilon_1 =\epsilon_1^{\left[ {tc} \right]}$, system (3) possesses a transcritical bifurcation but does not attain any saddle-node, pitch-fork, or Hopf bifurcation at $\epsilon_2 =\epsilon _2^{\left[ {tc} \right]}$.□

4.2 Local stability of system (3) around the boundary equilibria

At E ₂, the quadratic factor of the characteristic polynomial corresponding to J ₂ gives

$$ {\begin{array}{*{20}r} {\lambda^2-b_{11}^{\left[ 2 \right]} \lambda -b_{12}^{\left[ 2 \right]} b_{21}^{\left[ 2 \right]} =0,} \\[6pt] {\Rightarrow \lambda^2-\left( {-S_2 +\dfrac{S_2 P_{12} }{\left( {A_1 +S_2 } \right)^2}} \right)\lambda +\left( {\dfrac{\epsilon_1 A_1 +S_2 }{\left( {A_1 +S_2 } \right)^2}} \right)=0.} \\ \end{array} } $$

and one explicit eigenvalue, $b_{33}^{\left[ 2 \right]} \!=\!- \delta_2 \!+\!\frac{\epsilon_2 S_2 }{A_2 +S_2 }-\gamma_2 P_{12}$, with $b_{11A}^{\left[ 2 \right]} =\frac{2S_2 }{A_1 +S_2 } \big(S_2 -$ $\frac{1-A1}{2}\big)$. Therefore, the conditions for stability are: (i) $\delta_2 >\frac{\epsilon_2 S_2 }{A_2 +S_2 }-\gamma_2 P_{12}$ and (ii) $S_2 >\frac{1-A_1 }{2}$, i.e., . Otherwise if $A_{1} < \frac{(\epsilon_1 - \delta_1)}{(\epsilon_1 + \delta_1)} \equiv A_{[1H]}$, then system (3) is unstable around E ₂.

In a similar way, it can be found that at E ₃ another quadratic factor of the characteristic polynomial corresponding to J ₃ gives

$$ \lambda^2 - b^{[3]}_{11} \lambda - b^{[3]}_{13}b^{[3]}_{31} = 0, $$

and one eigenvalue is explicitly $b^{[3]}_{22} = -\delta_1 + \frac{\epsilon_1 S_3}{A_1+S_3} - \gamma_1 P_{23}$ with $b^{[3]}_{13} = -\frac{S_3}{A_2 + S_3} < 0$, $b^{[3]}_{31} = \frac{\epsilon_2 A_2 P_{23}}{(A_2 + S_3)^2} > 0$ and $b^{[3]}_{11} = -\frac{2S_3}{A_2 + S_3}(S_3 - \frac{1-A_2}{2})$.

Hence, E ₃ is locally asymptotically stable if the conditions (i) $\delta_1>\frac{\epsilon_1 S_3 }{A_1 +S_3 }-\gamma_1 P_{23}$ and (ii) $S_3 > \frac{1-A_2 }{2}$, i.e., $A_2 > \frac{(\epsilon_2 - \delta_2)}{(\epsilon_2 + \delta_2)} \equiv A_{[2H]}$ hold. Otherwise if A ₂ < A _[2H], then system (3) is unstable around E ₂.

Theorem 5

E ₁ is globally asymptotically stable if $\min \left\{ {\frac{\delta_1 A_1 }{\epsilon_1 },\frac{\delta_2 A_2 }{\epsilon_2 }} \right\}>2$ .

Proof

Let $\mathbf{R}^3_{+S} = \{(S, P_1, P_2): S > 0, P_1 \geq 0, P_2 \geq 0\}$ and consider the scalar function $L_S :{\rm {\bf R}}_{+S}^3 \to {\rm {\bf R}}$ as

$$ \begin{array}{rll}\label{eq7a} L_s(t) = \frac{1}{2}(S-1)^2 + \frac{1}{\epsilon_1}P_1 + \frac{1}{\epsilon_2}P_2. \end{array} $$

(7)

□

The derivative of (7) along the solutions of system (3) is

$$ \begin{array}{rll} \label{eq7} \par \frac{dL_2}{dt}&=&-S\left(S-1\right)^2-\left(\frac{P_1}{A_1 + S}+\frac{P_2}{A_2 + S}\right)S^2 + \left(\frac{2}{A_1}-\frac{\delta_1}{\epsilon_1}\right)P_1 \\ &&+\left( \frac{2 }{A_2} - \frac{\delta_2}{\epsilon_2}\right)P_2-\left(\frac{\gamma_1}{\epsilon_1}+\frac{\gamma_2}{\epsilon_2}\right)P_1 P_2 \\ &&< 0, \,\,\, \mbox{if~min}\left\{\frac{\delta_1 A_1}{\epsilon_1}, \frac{\delta_2 A_2}{\epsilon_2}\right\} > 2. \par \end{array} $$

(8)

Theorem 6

E ₂ is globally asymptotically stable if conditions ( $i) \frac{\gamma_1 \left( {A_1 +S_2 } \right)^2\left( {1-S_2 } \right)}{\epsilon_1 A_1 }+\frac{S_2 }{A_2 }<\frac{\delta_2 }{\epsilon_2 }$ and (ii) S ₂ > 1 – A ₁ hold.

Proof

Let us consider the scalar function $L_2 :{\rm {\bf R}}_+^3 \to {\rm {\bf R}}$ as

$$ \label{eq8} L_2 \left( t \right)=\left( {S-S_2 -S_2 \ln \left( {\frac{S}{S_2 }} \right)} \right)+\frac{A_1 +S_2 }{\epsilon_1 A_1 }\left( {P_1 -P_{1_2 } -P_{1_2 } \ln \left( {\frac{P_1 }{P_{1_2 } }} \right)} \right)+\frac{P_2 }{\epsilon_2 }. $$

(9)

The time derivative of L ₂(t) along the solutions of system (3) is

$$ \begin{array}{rll} \label{eq7} \dfrac{dL_2 }{dt}&=&-\left( {1-\dfrac{1-S_2 }{A_1 +S}} \right)\left( {S-S_2 } \right)^2-\left( {\dfrac{A_1 +S_2 }{\epsilon_1 A_1 }+\dfrac{\gamma_2 }{\epsilon_2 }} \right)P_1 P_2 \\[3pt] &&+\left( {\dfrac{S_2 }{A_2 +S}+\dfrac{\gamma_1 \left( {A_1 +S_2 } \right)P_{12} }{\epsilon_1 A_1 }-\dfrac{\delta_2 }{\epsilon_2 }} \right)P_2 \\[3pt] &&<-\left( {1-\dfrac{1-S_2 }{A_1 }} \right)\left( {S-S_2 } \right)^2+\left( {\dfrac{S_2 }{A_2 }+\dfrac{\gamma_1 \left( {1-S_2 } \right)\left( {A_1 +S_2 } \right)^2}{\epsilon_1 A_1 }-\dfrac{\delta_2 }{\epsilon_2 }} \right)P_2\\[3pt] &&<0,\;\mbox{by}\;\mbox{condition}\;\left( \mbox{i} \right)\;\mbox{and}\;\left( {\mbox{ii}} \right). \end{array} $$

(10)

Moreover, $\frac{dL_s}{dt}|{_{E_1}} = 0$. The proof follows from (9) and Lyapunov-LaSalle’s invariance principle (cf. Hale [31]).

Hence proved.□

Theorem 7

E ₃ is globally asymptotically stable if conditions ( $i)~\frac{\gamma_2 \left( {A_2 +S_3 } \right)^2\left( {1-S_3 } \right)}{\epsilon_2 A_2 }+\frac{S_3 }{A_1 }<\frac{\delta_1 }{\epsilon_1 }$ and (ii ) S ₃ > 1 − A ₂ hold.

Proof

The proof is similar to the proof of Theorem 6.□

4.3 Local stability analysis of the system around E ^∗

Proposition 8

System (3) around the interior equilibrium E ^∗ is not stable.

Proof

Interested readers are referred to Theorem 2 of Gakkhar et al. [32].□

4.4 Existence of Hopf bifurcation of system (3) around the boundary equilibria

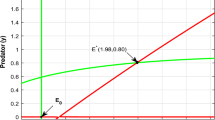
In order to have Hopf bifurcation around the equilibria E ₂, E ₃, it is sufficient to show that the coefficient of λ in the quadratic factor of the characteristic polynomial of J _k (k = 2, 3) is zero and the constant term is positive. The conditions for which annihilation of the linear terms in the quadratic factors of the characteristic polynomials of J ₂ and J ₃ can be made possible are $b_{11}^{\left[ {12} \right]} =0, b_{11}^{\left[ 3 \right]} =0$ and eventually we obtain the critical values for Hopf bifurcation as A ₁ = A _[1H] and A ₂ = A _[2H] for E ₂ and E ₃, respectively, as shown in Figs. 1 and 2.

Fig. 1

a Hopf bifurcation behavior of the dynamical system around E ₂. b System (3) emits a limit cycle near E ₂ for A ₁ = 0.6226216216 > A _[1H] = 0.6216216216, other parameters are: ϵ ₁ = 0.9, ϵ ₂ = 0.6, A ₂ = 0.9, δ ₁ = 0.21, δ ₂ = 0.81, γ ₁ = 1.0 and γ ₂ = 0.4. c Projection of the phase portrait on different planes. d Local stability around E ₂ for larger A ₁ = 0.7226216216 > A _[1H]

Fig. 2

a The Hopf bifurcation behavior of the dynamical system around E ₃. b System (3) emits a limit cycle near E ₃ for A ₂ = 0.7787777778 > A _[2H] = 0.7777777778, other parameters are: ϵ ₁ = 0.6, ϵ ₂ = 0.8, A ₁ = 0.5, δ ₁ = 0.1, δ ₂ = 0.1, γ ₁ = 0.5 and γ ₂ = 0.3. c Projection of the phase portrait on different planes. d Local stability around E ₃ for larger A ₂ = 0.9777777778 > A _[2H]

4.5 Non-existence of periodic solutions around E ^∗

In this section, we prove that under some suitable conditions, there are no periodic solutions of the system around the positive interior equilibrium E ^∗.

To prove this, the criterion by Li and Muldowney [33] can be applied. Consider the general autonomous ordinary differential equation

$$ \begin{array}{rll}\label{eq11a} \frac{dX}{dt} = F(X\,), \end{array} $$

(11)

where F is a C ¹ function in some open subset of ${\mathbb R}^N$. Let $J=\left( {\frac{\partial F}{\partial X}} \right)$ be the Jacobian matrix of system (10). Denote by J ^[2], the $\left( {_2^n } \right)\times \left( {_2^n } \right)$ matrix, which is the second compound matrix of J (cf. Appendix A). Recalling $X\in {\mathbb R}^N$, then the corresponding logarithmic norm of J ^[2], denoted by μ $_{\infty }(J{\kern1pt}^{[2]})$, endowed by the vector norm ∣ X ∣ _∞ = sup ∣ X _i  ∣ , is given by

$$ \label{eq9} \mu_\infty \left( {J^{\,\left[ 2 \right]}} \right)=\sup \left\{ {\frac{\partial F_r }{\partial x_r }+\frac{\partial F_s }{\partial x_s }+\sum\limits_{j\,\ne r,s} {\left( {\left| {\frac{\partial F_r }{\partial x_j }} \right|+\left| {\frac{\partial F_s }{\partial x_j }} \right|} \right):1\le r<s\le N} } \right\}, $$

(12)

where ${\mu }_{\infty }(J{\kern1pt}^{\,[2]})< 0$ implies the diagonal dominance by row matrix J ^[2] (cf. Appendix B). Therefore, we have the following theorem:

Theorem 9

A simple closed rectifiable curve that is invariant under system (3) cannot exist if μ _∞(J ^[2]) < 0.

Let us apply Li-Muldowney’s criterion for the non-existence of periodic solutions of system (3). The logarithmic norm μ _∞, endowed by the norm ∣ X ∣ _∞ of the second additive compound matrix J ^[2], associated with the Jacobian J ^∗, is negative if the suprema of the following functions satisfy

$$ \begin{array}{rll} \label{eq10} &&1-\delta_1 +S\left( {\frac{\epsilon }{A_1 +S}+\frac{1}{A_2 +S}-2} \right)+P_1 \left( {\gamma_1 -\frac{A_1 }{\left( {A_1 +S} \,\right)^2}} \right)\\ &&P_2 \left( {\gamma_1 +\frac{A_2 }{\left( {A_2 +S}\, \right)^2}} \right)<0, \end{array} $$

(13)

$$ \begin{array}{rll} \label{eq11} &&1-\delta_2+S\left( {\frac{\epsilon }{A_2 +S}+\frac{1}{A_1 +S}-2} \right)+P_2 \left( {\gamma_2 -\frac{A_2 }{\left( {A_2 +S} \,\right)^2}} \right)\\ &&P_1 \left( {\gamma_2 +\frac{A_1 }{\left( {A_1 +S}\,\right)^2}} \right)<0, \end{array} $$

(14)

$$ \begin{array}{rll} \label{eq12} &&\delta_1 -\delta_2 +\epsilon S\left( {\frac{1}{A_1 +S}+\frac{1}{A_2 +S}} \,\right)-P_1 \left( {\gamma_2 -\frac{\epsilon A_1 }{\left( {A_1 +S}\,\right)^2}} \right)\\ &&P_2 \left( {\gamma_1 +\frac{\epsilon A_2 }{\left( {A_2 +S}\,\right)^2}} \right)<0. \end{array} $$

(15)

The sufficient conditions to satisfy (13), (14), and (15) are respectively,

$$ \label{eq13} \delta_1 >1,\,2A_1 A_2 >A_1 +\epsilon A_2 ,\;\mbox{and}\;\gamma_1 <\frac{A_1 }{1+A_1 }; $$

(16)

$$ \label{eq14} \delta_2 >1,\,2A_1 A_2 >\epsilon A_1 +A_2 ,\;\mbox{and}\;\gamma_2 <\frac{A_2 }{1+A_2 }; $$

(17)

$$ \label{eq15} \max \left\{ {\epsilon_1 ,\epsilon_2 } \right\}=\epsilon_1 <\min \left\{ {A_1 \gamma_2 ,A_2 \gamma_1 ,\frac{A_1 A_2 \left( {\delta_1 +\delta_2 } \right)}{A_1 +A_2 }} \right\}. $$

(18)

A direct application of Li-Muldowney’s method ensures that system (3) has no periodic solution under the conditions stated in (16)–(18). However, the periodic solution for system (3) may exist for a set of parameters not satisfying the conditions (16)–(18) as evident from Fig. 3b.

Fig. 3

a Existence of a periodic solution of the dynamical system around E ₂ for A ₁ = 0.006. b The periodic solution of the dynamical system around E ^∗ for A ₁ = 0.10. c The periodic solution of the dynamical system around E ₃ for A ₁ = 0.40. The remaining parameters are: ϵ ₁ = 3.80, ϵ ₂ = 0.3, A ₁ = 0.1, A ₂ = 0.3, δ ₁ = 1.9, δ ₂ = 0.1, γ ₁ = 0.2 and γ ₂ = 0.02

5 Persistence of the system

Proposition 10

System (3) is not persistent.

Proof

Since system (3) is unconditionally unstable around the interior equilibrium E ^∗, stability of coexistence equilibrium E ^∗ is never possible (cf. Gakkhar et al. [32] and Freedman and Waltman [34]).□

6 Numerical simulation

For the purpose of making a quantitative analysis of the present investigations, numerical simulations have been carried out by making use of MATLAB-R2010a and Maple-12. The analytical findings of the present study are summarized and presented schematically in Table 1. All of these results are verified by means of numerical illustrations, some of which are exhibited in the figures. In order to compare the results of the present updated model (3) with those of the existing one in the absence of refuge (m ₁ = 0, m ₂ = 0), the respective values of $A_{\,1}^{\,0} \left( {=\frac{1}{a_1 k}} \right)$ and $A_{\,2}^{\,0} \left( {=\frac{1}{a_2 k}} \right)$ have been taken to be 0.5 and 0.8 from Kar [16]. Global stability of system (3) at E ₁ is observed (not reported here) for the set of parameters: ϵ ₁ = 0.011, ϵ ₂ = 0.01, A ₁ = 0.6, A ₂ = 0.6, δ ₁ = 0.2, δ ₂ = 0.1, γ ₁ = 0.1 γ ₂ = 0.2, which satisfies the condition $\min \left\{ {\frac{\delta_1 A_1 }{\epsilon_1 },\;\frac{\delta_2 A_2 }{\epsilon_2 }} \right\}>2$. This set of parameters also satisfies the conditions for global stability of the system around E ₁ (cf. Theorem 5). In fact, this set of parameter values also satisfies the conditions ϵ ₁ < δ ₁(1 + A ₁) and ϵ ₂ < δ ₂(1 + A ₂) for local asymptotic stability of system (3) around E ₁. The critical parameters A _[1H] and A _[2H] have been determined in terms of other system parameters as: $A_{\left[ {1H} \right]} =\frac{\left( {\epsilon_1 -\delta_1 } \right)}{\left( {\epsilon_1 +\delta_1 } \right)}$ and $A_{\left[ {2H} \right]} =\frac{\left( {\epsilon_2 -\delta_2 } \right)}{\left( {\epsilon_2 +\delta_2 } \right)}.$ When the parameter A ₁( = 0.6226216216) exceeds the critical value A _[1H]( = 0.6216216216), the present system experiences Hopf bifurcation around E ₂ as displayed in Fig. 1a–c, however, the local stability around E ₂ attains for larger values of A ₁( = 0.7216216216) (cf. Fig. 1d), which may be justified in the sense that with the increase of A ₁, the behavior around the boundary equilibrium E ₂ changes viz. from Hopf bifurcation to local stability. In conformity with our analytical findings (cf. Theorem 6), we found a figure (not reported here), demonstrating the independence of initial data on the behavior of global stability. System (3) leads to E ₃ (the figure is not reported here) for various initial data (cf. Theorem 7). The system experiences Hopf bifurcation around E ₃ when the parameter A ₂( = 0.7787777778) exceeds the critical value A _[2H] ( = 0.7777777778) (cf. Fig. 2a–c), however, the local stability around E ₃ attains for larger values of A ₂( = 0.9777777778) (cf. Fig. 2d), which may be justified in the sense that with the increase of A ₂, the behavior around the boundary equilibrium E ₃ changes as E ₂. The periodic solutions of the system around E ₂, E ^∗ and E ₃ with the increasing values of m ₁ (i.e., A ₁) are clearly depicted in Fig. 3a–c.

Table 1 Schematic representation of our analytical findings: LAS = Locally asymptotically stable; GAS = Globally asymptotically stable

7 Conclusions and comments

Fundamental areas of ecological research include the processes by which the population varies in abundance in space and time and identifying the mechanism through which such processes operate, which is crucial for understanding population dynamics (cf. Anderson [35]). The prey may avoid being killed by predators in two ways: either by defending themselves or by escaping. One of the most important ways to escape is to move into a refuge, where the predation risk is reduced. Different studies have shown that the contribution of refuges to the stability of prey–predator interactions depends on numerous factors. These factors are the relative part of the population, i.e., protected, the refuge gives guaranteed protection against predators on the basis of predator density, i.e., absolute versus partial refuge, whether the prey can reproduce when they are in refuge or not, and also the density dependence on prey reproduction and mortality (cf. Magalhaes et al. [36]). Many studies have focused on that the habitat complexity enhances the refuge of predators that reduces the predation pressure. Menezes et al. [37] focused on that the predators interacting with prey in the absence of refuge could not change their prey consumption dynamics as more prey were offered. Sometimes during prey refuge, predation is drastically reduced and predators also seek refuge to increase the predation pressure. In the mangrove ecosystem, Ray and Straskraba [2] showed that detritivorous fish, the prey species, and different predator fish coexist and their co-existence depends mainly on the minimum required abundance of detritivorous fish.

In this paper, we consider a prey–predator system with the Holling type II response function incorporating a constant proportion of prey refuge. Incorporation of prey refuge and the competition effect among predator species into system (2) make it more realistic. The smell, color, injection of some poisonous agent, size, skin, body cover, etc., may be used as different forms of refuge, which can be used to save the prey species from their predator. We see that many prey–predator population species face competition amongst themselves for the limited resources of food, shelter, and other biological needs. A refuge can be an important factor in the biological control of pests, though a higher amount of refuge can increase prey density and lead to prey population outbreak. For example, Hoy [10] showed that ‘hotspots’ of high spider mite densities in almond orchards can trigger orchard-wide outbreaks. We derived the conditions for the existence of local and global stabilities of the boundary equilibria and persistence criteria and in addition we found some critical values of some parameters at which the system undergoes bifurcations around some selective equilibria. Finally, a set of numerical simulations has been performed to validate some of the important results obtained.

In the present numerical study, it is found that the principle of competitive exclusion holds good for our present system, i.e., the fittest predator will survive and others will face extinction. When the second predator species, viz. Otolithoides pama becomes extinct from the system due to competition and the prey species viz. Liza parsia shows no refuge, the system creates an unstable oscillation around the boundary equilibrium position E ₂ (cf. Fig. 4, blue curve). However, in reality, when the prey species shows refuge up to a certain limit (viz. Liza parsia shows refuge within the range 15 to 74 %), the system converges to the stable equilibrium point from the unstable oscillation. By keeping the value of m ₂ (coefficient of refuge of the prey species corresponding to the second predator species) fixed, if the refuged value of the prey resource viz. Liza parsia corresponding to the first predator viz. Sciaena miles, is increased and exceeds the critical value (75 %), the system appears to break down and the total predator species is eliminated from the system, i.e., the boundary equilibrium E ₂ is changed to the predator free axial equilibrium E ₁ (cf. Fig. 4a, red and black curves). On the contrary, in the case when the refuge value used by Liza parsia corresponding to second predator, viz. Otolithoides pama is gradually increased to a certain level, the system experiences no change from unstable oscillatory behavior (cf. Fig. 4b, all curves). As the second predator species is absent in E ₂, the increment of the m ₂ value to any extent does not affect the stability of the system and the system always shows oscillatory behavior around E ₂ (cf. Fig. 4b). When the refuges of Liza parsia for both the predator species are enhanced, then the equilibrium E ₂ of the system shows a stable nature up to a certain level of refuges (viz. m ₁ = 60% and m ₂ = 60 %) (cf. Fig. 4c) and in this case, further increment of m ₁( ≥ 75 %) can cause the system to break down (cf. Fig. 4c). In this case, when the level of refuge of the prey species increases, the predator species becomes eradicated from the system as the level of refuge used by the prey exceeds 75 % (cf. Fig. 4a, c). Similar observations can be made for equilibrium E ₃ from Fig. 5a, c. Furthermore, one important result observed in Fig. 5b is that when the prey species Liza parsia shows refuge for the second predator viz. Otolithoides pama and increases gradually, the oscillatory nature of system (3) immediately becomes stable around E ₃ and it remains up to the refuge value m ₂ = 61.5 %. However, further increment of the refuge value m ₂ (very small) makes system (3) oscillatory (unstable) around E ₂, which was not found by Sarwardi et al. [38]. All these percentages of refuge values used for Figs. 4 and 5 are calculated in tabular form (cf. Tables 2 and 3).

Fig. 4

a Different solution plots as m ₁ increases, i.e., A ₁ increases (cf. Table 2) keeping the other parameters unchanged. b Different solution plots as m ₂ increases, i.e., A ₂ increases (cf. Table 2) keeping the other parameters unchanged. c Different solution plots as both m ₁ and m ₂ increase, i.e., A ₁ and A ₂ increase. The remaining parameters are: ϵ ₁ = 0.6, ϵ ₂ = 0.7, δ ₁ = 0.2, δ ₂ = 0.8, γ ₁ = 1.0, γ ₂ = 0.4

Fig. 5

a Different solution plots as m ₁ increases, i.e., A ₁ increases (cf. Table 3) keeping the other parameters unchanged. b Different solution plots as m ₂ increases, i.e., A ₂ increases (cf. Table 3) keeping the other parameters unchanged. c Different solution plots as both m ₁ and m ₂ increase, i.e., A ₁ and A ₂ increase. The remaining parameters are: ϵ ₁ = 0.6, ϵ ₂ = 0.9, δ ₁ = 0.11, δ ₂ = 0.1, γ ₁ = 0.5, γ ₂ = 0.3

Table 2 The parameter values of A ₁ and A ₂ corresponding to the values of m ₁ and m ₂ used in Fig. 4a–c

Table 3 The parameter values of A ₁ and A ₂ corresponding to the values of m ₁ and m ₂ used in Fig. 5a–c

From the above numerical observations, it is found that the coefficient of refuge (m ₁) of prey species viz. Liza parsia corresponding to the first predator species viz. Sciaena miles plays a more crucial role in stabilizing the boundary equilibrium E ₂. Again the coefficient of refuge (m ₂) of prey species viz. Liza parsia corresponding to the second predator species viz. Otolithoides pama plays a more crucial role in stabilizing the boundary equilibrium E ₃. The survey report (cf. Roy et al. [39]) corroborates the present findings of the numerical results of this investigation. It is very difficult to validate the model results with realistic data so far as the refuge is concerned in the natural field.

Appendices

Appendix A

The definition of the second additive compound matrix can be found in the paper of Li and Muldowney [33]. Let A = (a _ij ) be an n ×n matrix. The second additive compound A ^[2] is the $\left( {_2^n } \right)\times \left( {_2^n } \right)$ matrix defined as follows:

For any integer $i = 1, {\ldots}, \left( {_2^n } \right)$, let (i) = (i ₁, i ₂) be the ith member in the lexicographic ordering of integer pairs (i ₁, i ₂), such that, 1 ≤ i ₁ < i ₂ ≤ n.

Then the element in the ith row and jth column of A ^[2] is

• $a_{i_{1}}{_{i_{1}}} +a_{i_{2}}{_{i_{2}}},$   if (i) = (j )

• $\left( {-1} \right)^{r+s}a_{i_{r}j_{\,s}},$   if exactly one entry i _r of (i) doesn’t occur in (j ) and j _s doesn’t occur in (j )

• 0,   if neither entry from (i) occurs in (j )

For n = 3

$$ \label{eq16} A=\left( {\alpha_{ij} } \right)_{3\times 3}=\left[ {{\begin{array}{*{20}c} {\alpha_{11} } & {\alpha_{12} } & {\alpha_{13} } \\ {\alpha_{21} } & {\alpha_{22} } & {\alpha_{23} } \\ {\alpha_{31} } & {\alpha_{32} } & {\alpha_{33} } \\ \end{array} }} \right], $$

(19)

its second additive compound matrix is

$$ \label{eq17} A_{\,3\times 3}^{\,\left[ 2 \right]} =\left[ {{\begin{array}{*{20}c} {\alpha_{11} +\alpha_{22} } \hfill & {\alpha_{23} } \hfill & {-\alpha_{13} } \hfill \\ {\alpha_{32} } \hfill & {\alpha_{11} +\alpha_{33} } \hfill & {\alpha_{12} } \hfill \\ {-\alpha_{31} } \hfill & {\alpha_{21} } \hfill & {\alpha_{22} +\alpha_{23} } \hfill \\ \end{array} }} \right]. $$

(20)

In this case, (1) = (1, 2), (2) = (1, 3), (3) = (2, 3).

Appendix B

Theorem 11

Bendixson’s criterion in R ⁿ (cf. Arino et al. [40]): A simple closed rectifiable curve that is invariant with respect to (11) cannot exist if any one of the following conditions is satisfied in R ⁿ :

• (i) ${\sup \left\{ {\dfrac{\partial F_r }{\partial x_r }+\dfrac{\partial F_s }{\partial x_s }+\displaystyle\sum\limits_{j\,\ne\, r,s} {\left( {\left| {\dfrac{\partial F_j }{\partial x_r }} \right|+\left| {\dfrac{\partial F_j }{\partial x_s }} \right|} \right):1\le r<s\le n} } \right\}<0,}$

• (ii) ${\sup \left\{ {\dfrac{\partial F_r }{\partial x_r }+\dfrac{\partial F_s }{\partial x_s }+\displaystyle\sum\limits_{j\,\ne\, r,s} {\left( {\left| {\dfrac{\partial F_r }{\partial x_j }} \right|+\left| {\dfrac{\partial F_s }{\partial x_j }} \right|} \right):1\le r<s\le n} } \right\}<0,}$

• (iii) λ ₁ + λ ₂ < 0,

• (iv) ${\inf \left\{ {\dfrac{\partial F_r }{\partial x_r }+\dfrac{\partial F_s }{\partial x_s }+\displaystyle\sum\limits_{j\,\ne\, r,s} {\left( {\left| {\dfrac{\partial F_j }{\partial x_r }} \right|+\left| {\dfrac{\partial F_j }{\partial x_s }} \right|} \right):1\le r<s\le n} } \right\}<0,}$

• (v) ${\inf \left\{ {\dfrac{\partial F_r }{\partial x_r }+\dfrac{\partial F_s }{\partial x_s }+\displaystyle\sum\limits_{j\,\ne\, r,s} {\left( {\left| {\dfrac{\partial F_r }{\partial x_j }} \right|+\left| {\dfrac{\partial F_s }{\partial x_j }} \right|} \right):1\le r<s\le n} } \right\}<0,}$

• (vi) λ _n − 1 + λ _n  < 0,

where λ ₁ ≥ λ ₂ ≥ ⋯ ≥ λ _n are eigenvalues of $\frac{1}{2}\left( {\left( {{\partial F} \mathord{\left/ {\vphantom {{\partial F} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}} \right)^\ast +\left( {{\partial F} \mathord{\left/ {\vphantom {{\partial F} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}} \right)} \right)$ . ${{\partial F} \mathord{\left/ {\vphantom {{\partial F} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}$ is the Jacobian matrix of F and the asterisk denotes the transposition.