A predator–prey model with prey refuge: under a stochastic and deterministic environment

Abstract

This study aims to thoroughly investigate the dynamics of a predator–prey model with a Beddington-De Angelis functional response. We assume that the prey refuge is proportional to both species. We establish the standard properties of boundedness, permanence, and local stability. We show that under certain parameter conditions, transcritical bifurcation and Hopf bifurcation occur. To understand the nature of the limit cycle, we determine the direction of the Hopf bifurcation. We focus on the significant ranges of the predators’ prey capturing rate and examine how the level of prey fear and the predator’s mutual interference affect the system’s stability. Through numerical analysis, we study the behavior of the Lyapunov exponent and observe multiple self-repeating shrimp-shaped patterns that indicate periodic attractors in discrete-time predator–prey system. These structures appear across a broad region associated with chaotic dynamics. Additionally, if the intensity of white noise is kept below a specific threshold, the deterministic control approach is equally effective in environmental fluctuation. Numerical simulations support these findings.

1 Introduction

One main objective of ecology is understanding the dynamic relationship between predator and prey. There are two methods for capturing the impact of the predator on the prey in a predator–prey system. Predators use their initial approach path to hunt and eat their prey, as observed in nature. In the second strategy, the presence of a predator may drastically change the behaviour of the prey because of their fear of predation. A relatively novel perspective states that indirect impact can similarly affect a predator–prey system’s dynamics [1]. When predation is a concern, prey populations may change their grazing zones to a safer area, renouncing their areas of highest intake; they can increase their alertness, change their reproductive strategies, and so on. This type of survival tactic results in a decrease in the reproductive capacity of the prey subject to predator pressure [2].

Although the fear effect has been investigated for a long time, it is reported in [3] that in 2016, prey populations’ birth rates decreased due to fear of predators. While the level of fear has no effect on the dynamical behaviour, expressed by the Holling I functional response, it can instead stabilise the entire system by preventing periodic solutions when the Holling II response function is adopted in the model formulation. Following this discovery, many predator–prey models incorporating the“level of fear” term in the growth function of the prey have been investigated. In [4], a predator–prey model is proposed and the impact of level of fear is examined to show how it stabilises the dynamics at high predator density. Two alternative “level of fear” terms in the growth function of prey and middle predator in a three species food chain are presented in [2]. Their findings suggest that fear can stabilise a chaotic system.

In addition to the level of fear, dynamic system behavior is significantly influenced by several other crucial factors, including prey refuge [5, 6], Allee effect, harvesting and the availability of additional food [7].

The study of a prey-predator system with prey refuge has been a hot topic in biomathematics, numerous achievements and essential advancements are being attained in this field [8,9,10,11]. In their analyses, the majority of authors see, for instance [12,13,14], assumed that the prey refuge is either constant or related to the prey volume.

Our starting point here is much different. Indeed, we assume that the prey refuge size is directly proportional to both prey and predator densities [15,16,17]. This scheme is more adherent to reality than previous refuge schemes. According to [8], in a food chain model, the prey refuge threshold can impact all species’ chances for long-term survival. The findings of the predator–prey model incorporating a prey refuge and additional food for the predator explored in [18] indicate that somewhat higher prey refuge values allow sustained species coexistence. However, the predator becomes extinct when the prey refuge attains a significant level.

The primary factor in the prey-predator relationship is the predator’s rate of prey consumption, sometimes referred to as the predator’s functional response [19]. The dynamics of interacting populations in ecology contain various response functions. The Beddington-De Angelis response function, a variation of the Holling type II functional response was proposed in [20,21,22] to describe interference among predators in the prey hunting process.

In biology, however, the deterministic approach has some drawbacks. It is hard to precisely foresee the system’s future. In comparison to its deterministic counterpart, a stochastic model reflects a natural system more accurately. In some studies, Gaussian white noise is included in a model of environmental fluctuations to assess the impact of noise on dynamical systems. To our knowledge, no one has explored such a model using Gaussian white noises, and color noise which have been shown to be particularly beneficial in modelling fast fluctuating phenomena in the presence of refuge, fear factor and mutual predator interference in system. In this paper, following Wiener processes, these fluctuations are expressed as white noises [20]. Recently, a stochastic delay predator–prey model with fear effect and diffusion for prey explored in [23,24,25].

This study examines the combined effects of hunting, fear effect, and predator interference. To our knowledge, no previous research incorporates the joint impact of the three above factors. The salient features of the model are as follows. Fear of predator hunting is here assumed to decrease the prey birth rate. Prey refuge and predator interference are incorporated into the proposed model.

Specifically, the goal of this work is to investigate the following biological question: What impact does the prey capture rate have on the dynamics of the prey-predator system?

The paper is organized as follows. The construction of a mathematical model based on the above set of assumptions is performed in Sect. 2. The main analytical findings and mathematical details are summarized in the next section. In Sect. 4, existence of stochastic stability and some properties are explained in presence of white noise. Sections 5 and 6 contain the numerical simulations and briefly summarize discussions.

2 Basic assumptions and model formulation

We develop a predator–prey model with the following characteristics:

• 1. The response function of Beddington-De Angelis [26].

• 2. The prey grows logistically.

• 3. The prey refuge is a function of both prey (x) and predator (y) population sizes.

• 4. The prey exhibits fear, according to the anti-predator behavior.

The intrinsic growth rate and the intra-species competition rate of prey are denoted by r and $r_1$, respectively. When a predator is present, the prey’s intrinsic growth rate depends on the density of the predator, F(y; K); where y represents the density of the predator population, and K denotes the level of prey fear due to anti-predator reaction.

Based on ecological grounds the assumptions for F(y; K) are

• 1. $F(y;0)=r$: the prey reproduction rate remains unchanged without the fear effect.

• 2. $F(0; K)=r$: the prey reproductive rate remains unchanged without predators.

• 3. $\lim \limits _{K\rightarrow \infty }F(y; K)=0$: fearful prey under strong fear pressure cannot reproduce.

• 4. $\lim \limits _{y\rightarrow \infty }F(y; K)=0$: prey cannot reproduce when predator density is exceedingly high.

• 5. with a high level of fear, the prey reproduction rate decreases:

  $$\begin{aligned} \frac{\partial F(y;K)}{\partial K}<0. \end{aligned}$$

• 6. with a high predator density, the prey reproduction rate decreases.

  $$\begin{aligned} \frac{\partial F(y;K)}{\partial y}<0. \end{aligned}$$

Denoting by K the level of prey fear due to anti-predator reaction; we can explicitly write

$$\begin{aligned} F(y;K)=\frac{r}{1+Ky}. \end{aligned}$$

The function $F(y;K)=\frac{r}{1+Ky}$ has been selected to depict the adverse effect of predator density on the prey population’s growth rate. With an increase in predator density denoted by $(1+Ky)$, the fraction’s denominator rises accordingly. Consequently, the value of $F(y; K)=\frac{r}{1+Ky}$ decreases, causing a reduction in the growth rate of the prey population. The parameter r is a fixed value associated with the inherent growth rate of the prey population when not influenced by predation. This function F(y; K) elucidates how changes in the growth rate of the prey population are influenced by both predator density (y) and the level of prey fear (K). Higher values of K indicate heightened prey apprehension towards predators, intensifying the negative impact on their growth rate.

In what follows, let $\delta _1$ be the refuge coefficient. Then $\delta _1 x y$ represents the amount of prey that finds refuge. We only consider values of $\delta _1$ that satisfy the inequality $1-\delta _1 y\ge 0$. Realistic ecosystem allowable ranges of refuge are $0\le \delta _1 \le 1$ and $0\le 1-\delta _1 y\le 1$, [16, 17]. Thus there is an upper bound for which this amount should be sufficiently small, i.e., $\delta _1\le \frac{1}{y}$. In view of (3) below, the inequality that $\delta _1$ must ultimately satisfy is

$$\begin{aligned} \delta _1 < \frac{\zeta }{\Gamma +\zeta }. \end{aligned}$$

(1)

Therefore, the remaining $x-\delta _1 xy$ prey species are exposed to predation by predators.

Here, $m_1$, $a_1$, $b_1$, $c_1$ respectively represent the rates of prey capture by the predator, the half-saturation constant for prey, the handling time on the feeding rate effort, the mutual interference among the predators, while $e_1$ is the conversion coefficients for turning prey into new predators, and $d_1$ is the predator’s natural mortality. Nonnegative initial conditions are naturally assumed. By incorporating intra-species competition of prey and prey fear in [17], the model takes the form

$$\begin{aligned} \frac{dx}{dt}&= \frac{rx}{1+Ky}-r_1x^2-\frac{m_1(x-\delta _1xy)y}{a_1+b_1(x-\delta _1xy)+c_1y}\nonumber \\&\equiv G_1(x,y)\nonumber \\ \frac{dy}{dt}&=\frac{e_1m_1(x-\delta _1xy)y}{a_1+b_1(x-\delta _1xy)+c_1y} - d_1y\equiv G_2(x,y). \end{aligned}$$

(2)

The predator–prey model presented incorporates various ecological dynamics, including prey response to predator presence, logistic prey growth, prey refuge as a function of both prey and predator populations, and anti-predator behavior. The model’s applicability stems from its ability to capture these complex interactions and dynamics within ecological systems.

Key features contributing to its applicability include:

• Beddington-De Angelis Response Function: This response function accounts for the impact of predator density on prey growth rate, reflecting realistic predator–prey interactions.

• Logistic Prey Growth: The model integrates logistic growth dynamics for prey populations, acknowledging carrying capacity constraints within ecosystems.

• Prey Refuge Mechanism: By incorporating prey refuge as a function of both prey and predator populations, the model considers spatial and behavioral strategies adopted by prey to avoid predation.

• Anti-predator Behavior: The model incorporates prey fear as an adaptive response to predator presence, influencing prey reproduction rates.

Additionally, parametrization of the model includes ecological relevance, such as prey capture rates, handling time, mutual interference among predators, conversion coefficients, and predator natural mortality, enhancing its applicability to real-world ecosystems.

In summary, the model’s comprehensive representation of predator–prey dynamics, incorporating biological and ecological principles, underpins its applicability in understanding and predicting dynamics within ecological systems.

In the next section, we summarize the mathematical findings.

The results that we outline below are preliminary in that they assess properties that are needed from the biological viewpoint.

3 System analysis and preliminary results

3.1 Boundedness

Proposition 3.1

All non negative solutions (x(t), y(t)) of the system (2) initiating in $R^2_+-\{0,0\}$ are uniformly bounded.

Proof

Let us choose the total system population $\Theta =x+y$. Therefore,

$$\begin{aligned} \frac{d\Theta }{dt}= & {} \frac{dx}{dt}+\frac{dy}{dt} =\frac{rx}{1+Ky}-r_1x^2\\{} & {} -\frac{m_1(x-\delta _1xy)y}{a_1+b_1(x-\delta _1xy)+c_1y}\\{} & {} +\frac{e_1m_1(x-\delta _1xy)y}{a_1+b_1(x-\delta _1xy)+c_1y}-d_1y. \end{aligned}$$

Let us consider a positive constant $\zeta$ such that $\zeta \le d_1$. It follows

$$\begin{aligned} \frac{d\Theta }{dt}+\zeta \Theta\le & {} rx-r_1x^2+\zeta x\\{} & {} -\frac{m_1(1-e_1)(x-\delta _1xy)y}{a_1+b_1(x-\delta _1xy)+c_1y}\\{} & {} -y(d_1-\zeta ) \\\le & {} (r+\zeta )x-r_1x^2\le \frac{(r+\zeta )^2}{4r_1}. \end{aligned}$$

By choosing $\Gamma =\frac{(r+\zeta )^2}{4r_1}$, we obtain

$$\begin{aligned} 0\le & {} \Theta (x(t),y(t))\le \frac{\Gamma }{\zeta }(1-e^{-\zeta t})\\{} & {} +\Theta (x(0),y(0))e^{-\zeta t}, \end{aligned}$$

which indicates that $0\le \Theta (x(t),y(t))\le \frac{\Gamma }{\zeta }$ as $t\rightarrow \infty$. Therefore, all nonnegative solutions of the system (2) originating in $R^2_+-\{0,0\}$ will be restricted to lie in the region $\nabla =\{(x,y)\in R_+^2:x(t)+y(t)\le \frac{\Gamma }{\zeta }+\varepsilon \}$. $\square$

Boundedness is crucial because it indicates that the ecological system has reasonable behaviour. Indeed boundedness of the system implies that none of the two interacting species undergoes an unexpected or long-term exponential growth, which, given limited resources, would not be ecologically sustainable. In particular, using the boundedness result shown above, namely

$$\begin{aligned} y(t)\le \frac{\Gamma }{\zeta }+\varepsilon , \quad \varepsilon <1, \end{aligned}$$

we have immediately

$$\begin{aligned} \frac{1}{y} > \frac{\zeta }{\Gamma +\zeta }. \end{aligned}$$

(3)

3.2 Persistence of the system (2)

It is necessary to demonstrate the positivity of the system (2) since it suggests that the population will thrive in the long run. The system is said to be persistent if a compact set $D_1\subset \Psi _1=\{(x,y):x>0, y>0\}$ exists in which the solutions of the system (2) ultimately enter and remain in the region.

Proposition 3.2

The system (2) is persistent if the following conditions hold

$$\begin{aligned}{} & {} r>d_1, \end{aligned}$$

(4)

$$\begin{aligned}{} & {} m_1>\frac{1}{e_1} \left[ \frac{a_1d_1r_1}{r}+b_1d_1 \right] . \end{aligned}$$

(5)

Proof

We follow the approach of [16] to demonstrate persistence. Take a Lyapunov function candidate $V_1(x,y)=x^{\zeta _1} y^{\zeta _2}$ where $\zeta _1$ and $\zeta _2$ are real constants. As a result, the average Lyapunov function looks as follows:

$$\begin{aligned} \Gamma (x,y)= & {} \frac{\dot{V_1}}{V_1}=\zeta _1\frac{\dot{x}}{x}+\zeta _2\frac{\dot{y}}{y}\\= & {} \zeta _1\left( \frac{r}{1+Ky}-r_1x\right. \\{} & {} \left. -\frac{m_1(1-\delta _1y)y}{a_1+b_1(x-\delta _1xy)+c_1y}\right) \\+ & {} \zeta _2\left( \frac{e_1m_1(x-\delta _1xy)}{a_1+b_1(x-\delta _1xy)+c_1y} - d_1\right) . \end{aligned}$$

Now, we have to show that the function is positive at each boundary equilibrium.

At $E_0$, the trivial equilibrium, we find the value $\Gamma (0,0)=\zeta _1 r-\zeta _2 d_1$. Let $\zeta _1=\zeta _2=\zeta$, then $\Gamma (0,0)=\zeta (r-d_1)>0$ if the condition (4) holds.

Similarly, at the predator-free equilibrium $E_1$, we have

$$\begin{aligned} \Gamma \left( \frac{r}{r_1},0 \right) =\zeta \left( \frac{e_1m_1r}{ar_1+b_1r}-d_1 \right) >0 \end{aligned}$$

if the condition (5) is satisfied. These findings show that $\Gamma (x,y)$ is positive at each boundary equilibrium. Thus the system (2) is persistent. As the system is uniformly persistent there exist $\rho _1>0$ and $t>t_1$ such that $x(t)>\rho _1$ and $y(t)>\rho _1$ $~\forall t >t_1.$ $\square$

3.3 Nonexistence of periodic solution

Let us write the system (2) as $\dot{X}=G(X)$, where $X=(x,y)$ and $G=(G_1, G_2)$. Here, $G_1, G_2 \in C^{\infty }({\mathbb {R}}_+^2)$, where $G_1=\frac{rx}{1+Ky}-r_1x^2-\frac{m_1(x-\delta _1xy)y}{a_1+b_1(x-\delta _1xy)+c_1y}$ and $G_2=\frac{e_1m_1(x-\delta _1xy)y}{a_1+b_1(x-\delta _1xy)+c_1y} - d_1y$. Let us explore a continuously differentiable function, denoted as ${\hat{H}}(x,y)=\frac{1}{xy}$, defined over the domain $(x,y)\in \Omega .$ Here,

$$\begin{aligned}{} & {} \nabla .({\hat{H}}G)\nonumber \\{} & {} \quad =\frac{\partial }{\partial x}\left( \frac{\frac{r}{1+Ky}-r_1x}{y}-\frac{m_1(1-\delta _1y)y}{a_1+b_1(x-\delta _1xy)+c_1y}\right) \nonumber \\{} & {} \quad + \frac{\partial }{\partial y}\left( \frac{e_1m_1(x-\delta _1xy)y}{a_1+b_1(x-\delta _1xy)+c_1y}-d_1y\right) \nonumber \\{} & {} \quad =-\left( \frac{r_1}{y}+\frac{m_1[e_1(c_1+a_1\delta )-b_1(1-\delta _1y)^2]}{[a_1+b_1(x-\delta _1xy)+c_1y]^2}\right) \nonumber \\{} & {} \quad <0, \forall y \in \left( \frac{1}{\delta _1}(1-\sqrt{\frac{e_1(c_1+a_1\delta _1)}{b_1}},\frac{1}{\delta _1}\right) \end{aligned}$$

(6)

where $e_1(c_1+a_1\delta _1)>b_1$. Hence, we can deduce that $\nabla .({\hat{H}}G)<$ within the subdomain ${\hat{D}}$ of $\Omega$, defined by ${\hat{D}}{=}\left\{ (x,y)\in \Omega : \frac{1}{\delta _1}\left( 1{-}\sqrt{\frac{e_1(c_1+a_1\delta _1)}{b_1}}\right)< y< \frac{1}{\delta _1}\right\} .$ Applying Bendixson-Dulac’s criterion, as outlined in [27], we can infer that no periodic orbits exist in the specified subdomain ${\hat{D}}$ for the present system.

3.4 Equilibria: feasibility and stability

Here, all possible equilibria have been determined. The system (2) allows only three possible equilibrium states. The system disappearance is expressed by the point $E_0=(0,0)$. Then we find the predator-free equilibrium $E_1=(rr_1^{-1},0)$ and finally the coexistence equilibrium $E^*=(x^*,y^*)$. In it, we have

$$\begin{aligned} y^*=\frac{(e_1m_1-b_1d_1)x^*-a_1d_1}{\delta _1(e_1m_1-b_1d_1){{\textbf {x}}}^*+c_1d_1}. \end{aligned}$$

The value of $x^*$ is obtained by solving the quartic algebraic equation

$$\begin{aligned} \sum _{n=0}^{4} B_n X^{n} = 0 \end{aligned}$$

(7)

whose coefficients are:

$$\begin{aligned} B_4= & {} r_1e_1\delta _1(e_1m_1-b_1d_1)^2(\delta _1+K),\\ B_3= & {} d_1(e_1m_1-b_1d_1)\{\delta _1(c_1\delta _1-Ka_1)\\{} & {} +c_1(\delta _1+K)\}r_1e_1-e_1r\delta ^2_1(e_1m_1-b_1d_1)^2,\\ B_2= & {} (e_1m_1-b_1d_1)^2(\delta _1+K)d_1\\{} & {} +r_1e_1c_1d^2_1(c_1\delta _1-Ka_1)\\{} & {} -2\delta _1(e_1m_1-b_1d_1)c_1d_1e_1r,\\ B_1= & {} (e_1m_1-b_1d_1)[c_1\delta _1-2Ka_1-a_1\delta _1]d^2_1\\{} & {} -c^2_1d^2_1e_1r,\\ B_0= & {} -a_1d^3_1(c_1\delta _1-Ka_1). \end{aligned}$$

Now, this algebraic equation is investigated, and the conditions for the roots being positive are assessed under some parameter restrictions. Figure 1 shows that the coexistence equilibrium can indeed be achieved.

Fig. 1

Mutual position of prey-nullclines (green) and predator-nullclines (red) of the system for the reference parameter values given in Table 1

To assess the coexistence equilibrium, we must find at least one positive root of the equation (7). In general, the equation (7) has at most four complex roots. Let us assume that one pair of complex roots exists, namely ${\widehat{\alpha }}$ and its conjugate $\widehat{\alpha ^*}$. The following quadratic equation

$$\begin{aligned}{} & {} X^2+\widehat{\theta _1}X+\widehat{\theta _2}=(X-{\widehat{\alpha }})(X-\widehat{\alpha ^*})\\{} & {} \quad =X^2 -2Re({\widehat{\alpha }})X+|{\widehat{\alpha }}|^2 \end{aligned}$$

is formed by a conjugate pair in which ${\widehat{\theta }}_1=-2Re({\widehat{\alpha }})$, ${\widehat{\theta }}_2=|{\widehat{\alpha }}|^2$. Assuming that there are two real roots $x_1^*$ and $x_2^*$ of $x^*$ of the equation (7) such that $(x_1^*+x_2^*)=-{\widehat{p}}_r$, and $x_1^*x_2^*={\widehat{q}}_s$. Consequently, the factorization of equation (7) becomes:

$$\begin{aligned}{} & {} \sum _{n=0}^{4} B_n X^{n} = B_4(X^2+{\widehat{\theta }}_1X+{\widehat{\theta }}_2)(X^2+{\widehat{p}}_rX+{\widehat{q}}_s)\nonumber \\{} & {} \quad =B_4\left[ X^4+({\widehat{p}}_r+{\widehat{\theta }}_1)X^3+({\widehat{\theta }}_2+{\widehat{q}}_s+{\widehat{\theta }}_1{\widehat{p}}_r)X^2\right. \nonumber \\{} & {} \qquad \left. +({\widehat{\theta }}_1{\widehat{q}}_s+{\widehat{\theta }}_2{\widehat{p}}_r)X+{\widehat{\theta }}_2{\widehat{q}}_s\right] . \end{aligned}$$

(8)

Comparing coefficients on both sides, we discover that

$$\begin{aligned} {\widehat{p}}_r=\frac{B_3}{B_4}+2Re({\widehat{\alpha }}), \quad {\widehat{q}}_s=\frac{B_0}{B_4|{\widehat{\alpha }}|^2}. \end{aligned}$$

We now discuss the two cases that can arise.

Fig. 2

(a, b) The system exhibits transcritical bifurcation at $m_1=0.1529.$

Case 1: If ${\widehat{q}}_s>0,$, i.e., if $c_1<\frac{Ka_1}{\delta _1}$ then both real roots are positive if satisfy the following conditions ${\widehat{p}}_r<0$ and ${\widehat{p}}^2_r-4{\widehat{q}}_s>0.$ Therefore, there exist two positive real roots

$$\begin{aligned} x_1^*=\frac{-{\widehat{p}}_r+\sqrt{{\widehat{p}}^2_r-4{\widehat{q}}_s}}{2}, \, x_2^*=\frac{-{\widehat{p}}_r-\sqrt{{\widehat{p}}_r^2-4{\widehat{q}}_s}}{2}, \end{aligned}$$

only if ${\widehat{p}}_r^2-4{\widehat{q}}_s>0$ holds since as $B_3<0$.

Case 2: If ${\widehat{q}}_s<0,$ i.e. if $c_1>\frac{Ka_1}{\delta _1}$ then one root is obviously positive satisfying the above conditions. Thus the condition for the existence of the coexistence equilibrium point $E^* (x^*,~y^*)$ is given by,

$$\begin{aligned}{} & {} (a): ~x^*>\frac{a_1d_1}{e_1m_1-b_1d_1}, \quad (b): ~m_1>\frac{b_1d_1}{e_1},\nonumber \\{} & {} \quad (c): ~{\widehat{p}}^2_r-4{\widehat{q}}_s>0, \quad (d): ~c_1>\frac{Ka_1}{\delta _1}. \end{aligned}$$

(9)

As for stability, we need the general form of the Jacobian matrix at ${\overline{E}}=({\overline{x}},{\overline{y}})$. It is explicitly defined as

$$\begin{aligned} {\overline{J}}=\left[ \begin{array}{cc} {\overline{a}}_{11} &{} {\overline{a}}_{12} \\ {\overline{a}}_{21} &{} {\overline{a}}_{22} \end{array} \right] \end{aligned}$$

(10)

where

$$\begin{aligned}{} & {} {\overline{a}}_{11}=\frac{r}{(1+K{\overline{y}})}-2r_1{\overline{x}}-\frac{m_1(a_1+c_1{\overline{y}})(1-\delta _1{\overline{y}}){\overline{y}}}{[a_1+b_1({\overline{x}}-\delta _1{\overline{x}}~{\overline{y}})+c_1{\overline{y}}]^2},\\{} & {} {\overline{a}}_{12}=-\frac{r{\overline{x}}K}{(1+K {\overline{y}})^2}-\frac{m{\overline{x}}[(a_1+c_1{\overline{y}})(1-2\delta _1{\overline{y}})+(1-\delta _1{\overline{y}})(b_1{\overline{x}}-b_1\delta _1{\overline{x}}~ {\overline{y}}-c_1{\overline{y}})]}{[a_1+b_1(\overline{(}x-\delta _1 {\overline{x}}~{\overline{y}})+c_1{\overline{y}}]^2},\\{} & {} {\overline{a}}_{21}=\frac{e_1m_1(a_1+c_1{\overline{y}})(1-\delta _1{\overline{y}}){\overline{y}}}{[a_1+b_1({\overline{x}}-\delta _1{\overline{x}}~{\overline{y}})+c_1{\overline{y}}]^2},\\{} & {} {\overline{a}}_{22}=\frac{e_1m_1{\overline{x}}[(a_1+c_1{\overline{y}})(1-2\delta _1{\overline{y}})+(1-\delta _1 {\overline{y}})(b_1{\overline{x}}-b_1\delta _1 {\overline{x}}~{\overline{y}}-c_1{\overline{y}})]}{[a_1+b_1({\overline{x}}-\delta _1{\overline{x}}~{\overline{y}})+c_1{\overline{y}}]^2}-d_1. \end{aligned}$$

The trivial equilibrium $E_0$ of the system (2) is always unstable since one eigenvalue of (10) is here $r>0$. The system (2) at $E_1$ is unstable if $R_1=\frac{e_1m_1r}{d_1(a_1r_1+b_1r)}>1$.

Note that the Jacobian at $E^*$ has one simplification,

$$\begin{aligned} {\widehat{a}}_{11}=-r_1x^*+\frac{m_1b_1x^*y^*(1-\delta _1y^*)^2}{[a_1+b_1(x^*-\delta _1x^*y^*)+c_1y^*]^2}. \end{aligned}$$

Its eigenvalues, in this case, are obtained as roots of the quadratic $\lambda ^2-{\text {tr}}(J^*)+\det (J^*)=0$, with

$$\begin{aligned} {\text {tr}}(J^*)=-({\widehat{a}}_{11}+{\widehat{a}}_{22}), \quad \det (J^*)= {\widehat{a}}_{11}{\widehat{a}}_{22}-{\widehat{a}}_{12}{\widehat{a}}_{21}. \end{aligned}$$

Now if ${\text {tr}}(J^*)<0$ as well as $\det (J^*)>0$ then according to the Routh-Hurwitz criterion $E^*$ is locally asymptotically stable. This result depends upon system parameters. Therefore, we investigate the above conditions by numerical simulations.

Thus, the stability of the above equilibrium points is investigated, showing that both $E_1$ and $E^*$ are conditionally stable. Local bifurcation analysis shows a transcritical bifurcation between these points. Figure 2a, b illustrates our analytical results at $m_1=m^{TC}_{1}=0.1529.$

Further, we observe the onset of persistent oscillations. These limit cycles arise in view of a Hopf bifurcation, whose direction is also assessed.

3.5 Hopf-Bifurcation

Proposition 3.3

The necessary and sufficient conditions for Hopf bifurcation of (2) at $E^*$ for $m_1=m^c_1$ are

$$\begin{aligned}{} & {} [{\text {tr}}(J^*)]_{m_1=m^c_1}=0, \quad [\det (J^*)]_{m_1=m^c_1}\\{} & {} \quad >0, \quad \frac{d}{dm_1}[tr(J^*)]_{m_1=m^c_1}\ne 0. \end{aligned}$$

Proof

Annihilating the Jacobian trace gives

$$\begin{aligned}{} & {} \frac{e_1m_1x^*[(a_1+c_1y^*)(1-2\delta _1y^*)+(1-\delta _1y^*)(b_1x^*-b_1\delta _1x^*y^*-c_1y^*)]}{[a_1+b_1(x^*-\delta _1x^*y^*)+c_1y^*]^2}\\{} & {} \quad + \frac{m_1b_1x^*y^*(1-\delta _1y^*)^2}{[a_1+b_1(x^*-\delta _1x^*y^*)+c_1y^*]^2} =d_1+r_1x^*. \end{aligned}$$

Now $[\det (J^*)]_{m_1=m^c_1}>0$ is equivalent to the characteristic equation $\lambda ^2+[\det (J^*)]_{m_1=m^c_1}=0$ whose roots are purely imaginary. For $m_1=m^c_1$, the characteristic equation can indeed be written as

$$\begin{aligned} \chi ^2+\omega =0, \quad \omega =[\det (J^*)]_{m_1=m^c_1}>0. \end{aligned}$$

(11)

Therefore, the above equation has two roots, $\chi _1=+i \sqrt{\omega }$ and $\chi _2=-i \sqrt{\omega }$. At any neighboring point $m_1$ of $m^c_1$, we can express the above roots in general form as $\chi _{1,2}=\lambda _1(m_1)+\pm i\lambda _2(m_1)$, where

$$\begin{aligned} \lambda _1(m_1)=\frac{tr(J^*)}{2}, \quad \lambda _2(m_1)=\sqrt{det(J^*)-\frac{tr(J^*)}{4}}. \end{aligned}$$

Now the transversality condition

$$\begin{aligned} \frac{d}{dm_1}(Re(\chi _j(m_1)))_{m_1=m^c_1}\ne 0, \quad j=1,2, \end{aligned}$$

needs to be verified. Substituting $\chi _1=\lambda _1(m_1)+i\lambda _2(m_1)$ in (11) and calculating the derivative, we have

$$\begin{aligned}{} & {} 2\lambda _1(m_1) \lambda '_1(m_1)- 2\lambda _2(m_1) \lambda '_2(m_1)+\omega '=0,\nonumber \\{} & {} \quad 2\lambda _2(m_1) \lambda '_1(m_1)+ 2\lambda _1(m_1) \lambda '_2(m_1)=0. \end{aligned}$$

(12)

Solving (12), we get

$$\begin{aligned} \frac{d}{dm_1}(Re(\chi _j(m_1)))_{m_1=m^c_1}=\frac{-2\lambda _1\omega '}{2(\lambda ^2_1+\lambda ^2_2)}\ne 0, \end{aligned}$$

i.e.

$$\begin{aligned} \frac{d}{dm_1}[tr(J^*)]_{m_1=m^c_1}\ne 0, \end{aligned}$$

which satisfies the transversality condition. This implies that the system undergoes a Hopf-bifurcation at $m_1=m^c_1$. Figures 11a, b show the sign switching of the eigenvalues and the verification of the condition for Hopf bifurcation at $H^*$ when $m_1=m^c_1$. $\square$

The bifurcation analysis, in particular, indicates an important finding: When the prey capture rates are high, there is a risk that both species oscillate. However, even with a predator’s high rate of prey capture, there is no chance for oscillations if the fear level is low. A similar situation occurs when the refuge coefficient is high.

3.6 Direction of Hopf Bifurcation

By taking $m_1$ as a bifurcation parameter, the previous theorem indicates that the system (2) exhibits a Hopf bifurcation. The direction and stability aspects of bifurcating periodic solutions arising from the coexisting equilibrium point, $E^*$ via this Hopf bifurcation is now discussed.

We first calculate the Lyapunov coefficient and explore the stability and direction of the Hopf bifurcation.

First, we translate the coexistence equilibrium of (2) $E^*(x^*,y^*)$ into the origin by setting ${\widehat{z}}_1=x-x^*$, ${\widehat{z}}_2=y-y^*$. Then the system (2) becomes

$$\begin{aligned} \frac{d{\widehat{z}}_1}{dt}= & {} \frac{r({\widehat{z}}_1+x^*)}{1+K({\widehat{z}}_2+y^*)}-r_1({\widehat{z}}_1+x^*)^2\\{} & {} -\frac{m_1({\widehat{z}}_1+x^*)(1-\delta _1({\widehat{z}}_2+y^*))({\widehat{z}}_2+y^*)}{a_1+b_1({\widehat{z}}_1+x^*) (1-\delta _1({\widehat{z}}_2+y^*))+c_1({\widehat{z}}_2+y^*)},\\ \frac{d{\widehat{z}}_2}{dt}= & {} \frac{e_1m_1({\widehat{z}}_1+x^*)(1-\delta _1({\widehat{z}}_2+y^*)) ({\widehat{z}}_2+y^*)}{a_1+b_1({\widehat{z}}_1+x^*)(1-\delta _1({\widehat{z}}_2+y^*))+c_1({\widehat{z}}_2+y^*)}\\{} & {} - d_1({\widehat{z}}_2+y^*). \end{aligned}$$

The following system is obtained by expanding on Taylor’s series up to terms of order 3 at $({\widehat{z}}_1, {\widehat{z}}_2) = (0, 0)$ the above system:

$$\begin{aligned} \dot{{\widehat{z}}_1}= & {} {\overline{c}}_{10}{\widehat{z}}_1+{\overline{c}}_{01}{\widehat{z}}_2+{\overline{c}}_{20}{\widehat{z}}^2_1+{\overline{c}}_{11}{\widehat{z}}_1{\widehat{z}}_2+{\overline{c}}_{02}{\widehat{z}}^2_2+{\overline{c}}_{30}{\widehat{z}}^3_1\nonumber \\{} & {} +{\overline{c}}_{21}{\widehat{z}}^2_1{\widehat{z}}_2+ {\overline{c}}_{12}{\widehat{z}}_1{\widehat{z}}^2_2+{\overline{c}}_{03}{\widehat{z}}^3_2+ {\mathcal {O}}( |{\widehat{z}}|^4),\nonumber \\ \dot{{\widehat{z}}_2}= & {} {\overline{d}}_{10}{\widehat{z}}_1+{\overline{d}}_{01}{\widehat{z}}_2+{\overline{d}}_{20}{\widehat{z}}^2_1+{\overline{d}}_{11}{\widehat{z}}_1{\widehat{z}}_2+{\overline{d}}_{02}{\widehat{z}}^2_2+{\overline{d}}_{30}{\widehat{z}}^3_1\nonumber \\{} & {} +{\overline{d}}_{21}{\widehat{z}}^2_1{\widehat{z}}_2+{\overline{d}}_{12}{\widehat{z}}_1{\widehat{z}}^2_2+{\overline{d}}_{03}{\widehat{z}}^3_2+ {\mathcal {O}}( |{\widehat{z}}|^4), \end{aligned}$$

(13)

where

$$\begin{aligned} {\overline{c}}_{10}= & {} \frac{r}{1+Ky^*}-2r_1x^*-\frac{m_1c_{11}y^*}{A}\\{} & {} +\frac{m_1c^2_{11}b_1x^*y^*}{A^2},\\ {\overline{c}}_{01}= & {} \frac{m_1c_{11}x^*y^*(c_1-b_1\delta _1x^*)}{A^2}-\frac{r K x^*}{(1+Ky^*)^2}\\{} & {} -\frac{m_1(c_{11}x^*-\delta _1 x^*y^*)}{A},\\ {\overline{c}}_{20}= & {} -r_1+\frac{m_1c^2_{11}b_1y^*}{A^2}-\frac{m_{1}A_{11}c_{11}x^*y^*}{A^3},\\ {\overline{c}}_{11}= & {} \frac{m_{1}c_{11}\sigma _{11}}{A^2} -\frac{rK}{(1+Ky^*)^2}\\{} & {} -\frac{m_1(c_{11}-\delta _1y^*)}{A}-\frac{m_1c_{11}A_{12}x^*y^*}{A^3},\\ {\overline{c}}_{02}= & {} \frac{rK^2x^*}{(1+Ky^*)^3}+\frac{m_1\delta _1x^*}{A}\\{} & {} +\frac{m_{1}(c_{11}x^*-\delta _1 x^*y^*)(c_1-b_1\delta _1x^*)}{A^2}\\{} & {} -\frac{A_{22}m_1c_{11}x^*y^*}{A^3},\\ {\overline{c}}_{30}= & {} -\frac{m_1c_{11}y^*A_{11}}{A^3}+\frac{m_1b_1c^2_{11}x^*y^*}{A^4},\\ {\overline{c}}_{21}= & {} \frac{m_1c_{11}b_{1}(c_{11}-2\delta _1y^*)}{A^2}+\frac{m_1c_{11}p_{23}x^*y^*}{A^4} \\{} & {} -\frac{m_{1}\sigma _{12}}{A^3},\\ {\overline{c}}_{12}= & {} \frac{rK^2}{(1+Ky^*)^3}+\frac{m_1c_{11}p_{24}x^*y^*}{A^4}\\{} & {} +\frac{m_1\delta _1}{A}+\frac{m_{1}\sigma _{13}}{A^2} -\frac{m_{1}\sigma _{14}}{A^3},\\ {\overline{c}}_{03}= & {} -\frac{rK^3x^*}{(1+Ky^*)^3}+\frac{m_1\delta _1x^*(c_1-b_1\delta _1x^*)}{A^2}\\{} & {} -\frac{m_1(c_{11}x^*-\delta _1x^*y^*)A_{22}}{A^3}+\frac{m_1c_{11}p_{22}x^*y^*}{A^4},\\ {\overline{d}}_{10}= & {} \frac{e_1m_1c_{11}y^*}{A}\left[ 1-\frac{b_1c_1x^*}{A}\right] ,\\ {\overline{d}}_{01}= & {} e_1m_1 \left[ \frac{c_{11}x^*-\delta _1x^*y^*}{A}\right. \\{} & {} \left. -\frac{c_{11}x^*y^*(c_1-b_1\delta _1x^*)}{A^2}-\frac{d_1}{e_1m_1}\right] ,\\ {\overline{d}}_{20}= & {} e_1m_1c_{11} \left[ \frac{A_{11}x^*y^*}{A^3} -\frac{b_1c_{11}y^*}{A^2}\right] ,\\ {\overline{d}}_{11}= & {} e_1m_1 \left[ \frac{c_{11}A_{12}x^*y^*}{A^3} + \frac{c_{11}-\delta _1 y^*}{A} -\frac{\sigma _{15}}{A^2} \right] ,\\ {\overline{d}}_{02}= & {} e_1m_1 \left[ -\frac{\delta _1x^*}{A}-\frac{(c_{11}x^*-\delta _1x^*y^*)(c_1-b_1\delta _1x^*)}{A^2}\right. \\{} & {} \left. +\frac{c_{11}A_{22}x^*y^*}{A^3} \right] ,\\ {\overline{d}}_{30}= & {} e_1m_1 \left[ \frac{c_{11}y^*A_{11}}{A^3}-\frac{b_1c^2_{11}x^*y^*}{A^4}\right] ,\\ {\overline{d}}_{21}= & {} e_1m_1\left[ -\frac{\sigma _{16}}{A^2} \right. \\{} & {} +\frac{(c_{11}x^*-\delta _1x^*y^*)A_{11}+c_{11}y^*A_{12}-2b_1^2\delta _1C^2_{11}x^*y^*}{A^3}\\{} & {} \left. -\frac{c_{11}p_{23}x^*y^*}{A^4} \right] ,\\ {\overline{d}}_{12}= & {} e_1m_1 \left[ -\frac{\sigma _{17}}{A^2} -\frac{\delta _1}{A}\right. \\{} & {} \left. +\frac{c_{11}A_{22}y^*+A_{32}c_{11}x^*y^*+A_{12}(c_{11}x^* -\delta _1x^*y^*)}{A^3}\right. \\{} & {} \left. -\frac{c_{11}P_{24}x^*y^*}{A^4} \right] ,\\ {\overline{d}}_{03}= & {} e_1m_1[-\frac{\delta _1x^*(c_1-b_1\delta _1x^*)}{A^2} + \frac{(c_{11}x^*-\delta _1x^*y^*)A_{22}}{A^3}\\{} & {} -\frac{c_{11}p_{22}x^*y^*}{A^4}],\\ \sigma _{11}= & {} b_{1}(c_{11}x^*-b_1x^*y^*)+y^*(c_1-b_1\delta _1x^*)\\{} & {} -b_1\delta _1x^*y^*,\quad \\ \sigma _{12}= & {} (c_{11}x^*-\delta _1x^*y^*)A_{11}+c_{11}y^*A_{12}-2b_1^2\delta _1c^2_{11}x^*y^*,\\ \sigma _{13}= & {} (c_{11}-\delta _1y^*)(c_1{-}b_1\delta _1x^*){-}2c_{11}b_1\delta _1x^*{+}b_1\delta ^2_1x^*y^*,\\ \sigma _{14}= & {} c_{11}A_{22}y^*+A_{32}c_{11}x^*y^*+(c_{11}x^*-\delta _1x^*y^*)A_{12},\\ \sigma _{15}= & {} b_1c_{11}(c_{11}x^*-b_1x^*y^*)+c_{11}y^*(c_1-b_1\delta _1x^*)\\{} & {} -c_{11}b_1d_1x^*y^*,\\ \sigma _{16}= & {} b_1c_{11}(c_{11}-\delta _1y^*)-b_1\delta _1c_1y^*,\\ \sigma _{17}= & {} (1-2\delta _1y^*)(c_1-b_1\delta _1x^*)-b_1\delta _1c_1x^*\\{} & {} -b_1\delta _1(c_{11}x^* -\delta _1x^*y^*)\\ A= & {} a_1+b_1x^*-b_1\delta _1x^*y^*+c_1y^*,\quad \\{} & {} c_{11}=1-\delta _1y^*, \quad \\ A_{11}= & {} b^2_1+b_1^2\delta ^2_1y^*-2b^2_1\delta _1y^*,\\ A_{12}= & {} 2b^2_1\delta ^2_1x^*y^*-2b^2_1\delta _1x^*-2b_1\delta _1c_1y^*+2b_1c_1,\quad \\ A_{22}= & {} b_1^2\delta ^2_1x^{*2}+c_1^2-2b_1\delta _1c_1x^*,\\ A_{32}= & {} 2b_1^2\delta _1^2x^*-2b_1\delta _1c_1,\quad p_{22}=(c_1-b_1\delta _1x^*)^3,\quad \\ p_{23}= & {} 3b_1^2c^2_{11}(c_1-b_1\delta _1x^*),\\ p_{24}= & {} 3b_1c_{11} (c_1-b_1\delta _1x^*). \end{aligned}$$

If the higher-order terms are ignored, system (13) can be restated in the following form:

$$\begin{aligned} \dot{{\widehat{Z}}}=J_E^*{\widehat{Z}}+{\widehat{H}}({\widehat{Z}}), \quad {\widehat{Z}}=\left( \begin{array}{c} {\widehat{z}}_1 \\ {\widehat{z}}_2 \\ \end{array} \right) , \end{aligned}$$

(14)

where

$$\begin{aligned} {\widehat{H}}= & {} \left( \begin{array}{c} {\widehat{H}}_1 \\ {\widehat{H}}_2 \\ \end{array} \right) =\left( \begin{array}{c} {\overline{c}}_{20}{\widehat{z}}^2_1+{\overline{c}}_{11}{\widehat{z}}_1{\widehat{z}}_2+{\overline{c}}_{02}{\widehat{z}}^2_2+{\overline{c}}_{30}{\widehat{z}}^3_1+{\overline{c}}_{21}{\widehat{z}}^2_1{\widehat{z}}_2+{\overline{c}}_{12}{\widehat{z}}_1{\widehat{z}}^2_2+{\overline{c}}_{03}{\widehat{z}}^3_2 \\ {\overline{d}}_{11}{\widehat{z}}_1{\widehat{z}}_2+{\overline{d}}_{02}{\widehat{z}}^2_2+{\overline{d}}_{30}{\widehat{z}}^3_1+{\overline{d}}_{21}{\widehat{z}}^2_1{\widehat{z}}_2+{\overline{d}}_{12}{\widehat{z}}_1{\widehat{z}}^2_2+{\overline{d}}_{03}{\widehat{z}}^3_2\\ \end{array} \right) . \end{aligned}$$

The eigenvector ${\widehat{v}}$ of the community matrix $J_E^*$ corresponding to the eigenvalues $i\omega _0$ at $m_1=m^c_1$ is ${\widehat{v}}=\left( {\overline{c}}_{01}, i\omega _0-{\overline{c}}_{10} \right) ^T$. Now, let us define

$$\begin{aligned} S=(Re({\widehat{v}}), -Im({\widehat{v}}))=\left( \begin{array}{cc} {\overline{c}}_{01} &{} 0 \\ -{\overline{c}}_{10} &{} -\omega _0 \\ \end{array} \right) . \end{aligned}$$

Let ${\widehat{Z}}=SY$ or $Y=S^{-1}{\widehat{Z}},$ where $Y=(y_1, ~y_2)^T$. As a result of this transformation, the system (14) becomes $\dot{Y}=(S^{-1}J_E^*S)Y+S^{-1}{\widehat{H}}(SY)$. This can be written as

$$\begin{aligned}\left( \begin{array}{c} \dot{y_1} \\ \dot{y_2} \\ \end{array} \right)= & {} \left( \begin{array}{cc} 0 &{} -\omega _0 \\ \omega _0 &{} 0 \\ \end{array} \right) \left( \begin{array}{c} y_1 \\ y_2 \\ \end{array} \right) \\{} & {} \quad +\left( \begin{array}{c} {\widehat{Q}}^1(y_1,y_2;m_1=m^c_1) \\ {\widehat{Q}}^2(y_1,y_2;m_1=m^c_1) \\ \end{array} \right) , \end{aligned}$$

where ${\widehat{Q}}^1$ and ${\widehat{Q}}^2$ are nonlinear functions in $y_1$ and $y_2$. Explicitly, they are given by

$$\begin{aligned} {\widehat{Q}}^1(y_1,y_2;m_1=m^c_1)= & {} \frac{1}{{\overline{c}}_{01}}{\widehat{H}}_1,\\{} & {} {\widehat{Q}}^2(y_1,y_2;m_1=m^c_1)\\= & {} -\frac{1}{\omega _0 {\overline{c}}_{01}}({\overline{c}}_{10}{\widehat{H}}_1+{\overline{c}}_{01}{\widehat{H}}_2), \end{aligned}$$

with

$$\begin{aligned} {\widehat{H}}_1= & {} ({\overline{c}}_{20}{\overline{c}}^2_{01}-{\overline{c}}_{11}{\overline{c}}_{01}{\overline{c}}_{10} +{\overline{c}}_{02}{\overline{c}}_{10}^2)y^2_1\\{} & {} +\omega _0(2{\overline{c}}_{02}{\overline{c}}_{10} -{\overline{c}}_{11}{\overline{c}}_{01})y_1y_2+\omega ^2_0{\overline{c}}_{02}y^2_2\\{} & {} +({\overline{c}}_{12}{\overline{c}}_{01}{\overline{c}}^2_{10}-{\overline{c}}_{03}{\overline{c}}^3_{10} +{\overline{c}}_{30}{\overline{c}}^3_{01}-{\overline{c}}_{21}{\overline{c}}^2_{01}{\overline{c}}_{10})y^3_1\\{} & {} -\omega ^3_0{\overline{c}}_{03}y^3_2+\omega _0(2{\overline{c}}_{12}{\overline{c}}_{10}{\overline{c}}_{01}\\{} & {} -{\overline{c}}_{21}{\overline{c}}^2_{01}-3{\overline{c}}_{03}{\overline{c}}^2_{10})y^2_1y_2 +\omega ^2_0({\overline{c}}_{12}{\overline{c}}_{01}\\{} & {} -3{\overline{c}}_{03}{\overline{c}}_{10})y_1y^2_2, \end{aligned}$$

and

$$\begin{aligned} {\widehat{H}}_2= & {} ({\overline{d}}_{20}{\overline{c}}^2_{01}-{\overline{d}}_{11}{\overline{c}}_{01}{\overline{c}}_{10} +{\overline{d}}_{02}{\overline{c}}_{10}^2)y^2_1\\{} & {} +\omega _0(2{\overline{d}}_{02}{\overline{c}}_{10} -{\overline{d}}_{11}{\overline{c}}_{01})y_1y_2+\omega ^2_0{\overline{d}}_{02}y^2_2\\{} & {} +({\overline{d}}_{12}{\overline{c}}_{01}{\overline{c}}^2_{10}-{\overline{d}}_{03}{\overline{c}}^3_{10}\\{} & {} +{\overline{d}}_{30}{\overline{c}}^3_{01}-{\overline{d}}_{21}{\overline{c}}^2_{01}{\overline{c}}_{10})y^3_1 -\omega ^3_0{\overline{d}}_{03}y^3_2\\{} & {} +\omega _0(2{\overline{d}}_{12}{\overline{c}}_{10}{\overline{c}}_{01} -{\overline{d}}_{21}{\overline{c}}^2_{01}-3{\overline{d}}_{03}{\overline{c}}^2_{10})y^2_1y_2\\{} & {} +\omega ^2_0({\overline{d}}_{12}{\overline{c}}_{01}-3{\overline{d}}_{03}{\overline{c}}_{10})y_1y^2_2. \end{aligned}$$

To evaluate the stability and direction of a periodic solution, we compute the first Lyapunov coefficient:

$$\begin{aligned} l_1= & {} \frac{1}{16}\left[ {\widehat{Q}}^1_{111}+{\widehat{Q}}^1_{122}+{\widehat{Q}}^2_{112}+{\widehat{Q}}^2_{222}\right] \\{} & {} +\frac{1}{16\omega _0}\left[ {\widehat{Q}}^1_{12}({\widehat{Q}}^1_{11}+{\widehat{Q}}^1_{22})-{\widehat{Q}}^2_{12}({\widehat{Q}}^2_{11}+{\widehat{Q}}^2_{22})\right. \\{} & {} \left. -{\widehat{Q}}^1_{11}{\widehat{Q}}^2_{11}+{\widehat{Q}}^1_{22}{\widehat{Q}}^2_{22}\right] , \end{aligned}$$

where

$$\begin{aligned} {\widehat{Q}}^k_{ij}= & {} \frac{\partial ^2{\widehat{Q}}^k}{\partial y_i \partial y_j}\mid _{(y_1,y_2;m_1)=(0,0;m^c_1)},\\ {\widehat{Q}}^k_{ijl}= & {} \frac{\partial ^3{\widehat{Q}}^k}{\partial y_i \partial y_j \partial y_l}\mid _{(y_1,y_2;m_1)=(0,0;m^c_1)}, \quad \\{} & {} i,j,k,l\in \{1,2\}. \end{aligned}$$

If $l_1<0$, the Hopf bifurcation is supercritical; if $l_1>0$, it is subcritical.

3.6.1 A normal form of the Bogdanov-Takens bifurcation

We consider a planar vector field described as follows:

$$\begin{aligned} \dot{{{\textbf {x}}}}=f({{\textbf {x}}},{\hat{\mu }}), {{\textbf {x}}}\in {\mathbb {R}}^2, {\hat{\mu }} \in {\mathbb {R}}^2, \end{aligned}$$

(15)

where f is smooth a smooth function. Assuming that the origin ${\textbf{x}} = 0$ in (15) corresponds to an equilibrium with two zero eigenvalues, i.e., $\lambda _{1,2}=0$ at ${\hat{\mu }}=0$, and the Jacobian ${\textbf{J}}_{{\textbf{x}}} f (0, 0)$ is both nilpotent and different from the null matrix. We can express equation (15) at ${\hat{\mu }}= 0$ as:

$$\begin{aligned} \dot{x}=\hat{{{\textbf {J}}}}_{{\textbf {x}}} f(0,0){{\textbf {x}}}+\hat{{{\textbf {F}}}}({{\textbf {x}}}), \end{aligned}$$

(16)

where the function $\hat{{\textbf{F}}}({\textbf{x}})$ includes all terms of quadratic and higher order, denoted as $O(||{\textbf{x}}||^2)$.

The matrix $\hat{{\textbf{J}}}_{{\textbf{x}}} f(0,0)$ has one linearly independent eigenvector, denoted as $\hat{{\textbf{v}}_1}$, corresponding to the repeated eigenvalue of 0. Furthermore, it is possible to identify a generalized eigenvector $\hat{{{\textbf {v}}}}_2$ that satisfies the equation $\hat{{{\textbf {J}}}}_{{\textbf {x}}} f(0,0)\hat{{{\textbf {v}}}}_2=\hat{{{\textbf {v}}}}_1$. Let $\hat{{\textbf{V}}} = [\hat{{\textbf{v}}}_1, \hat{{\textbf{v}}}_2]$ denote the matrix with columns $\hat{{\textbf{v}}}_1$ and $\hat{{\textbf{v}}}_2$, both being linearly independent vectors.

Therefore, by utilizing the change of coordinates defined as:

$$\begin{aligned} {{\textbf {y}}}=\hat{{{\textbf {V}}}}^{-1}{{\textbf {x}}} \end{aligned}$$

(17)

the vector field f undergoes a transformation to a $C^{\infty }$ -conjugated system, defined as

$$\begin{aligned} g=\hat{{{\textbf {V}}}}^{-1}ofo \hat{{{\textbf {V}}}}. \end{aligned}$$

(18)

In particular, at ${\hat{\mu }} = 0$, system (16) undergoes a transformation to the following form, as illustrated:

$$\begin{aligned} \dot{{{\textbf {y}}}}=\hat{{{\textbf {J}}}}_{{\textbf {y}}}g(0,0)y+(\hat{{{\textbf {V}}}}^{-1}o\hat{{{\textbf {F}}}}o\hat{{{\textbf {V}}}})(y), \end{aligned}$$

(19)

where

$$\begin{aligned} \hat{{{\textbf {J}}}}_{{\textbf {y}}}g(0,0)=\left( \begin{array}{cc} 0 &{} 1 \\ 0 &{} 0 \\ \end{array} \right) . \end{aligned}$$

Expanding (18) in a Taylor series around $(y_1, y_2) = (0, 0)$ with respect to ${\textbf{y}} = (y_1, y_2)$ yields the following expressions:

$$\begin{aligned} \dot{y_1}= & {} y_2+{\hat{a}}_{00}({\hat{\mu }})+{\hat{a}}_{10}({\hat{\mu }})y_1+{\hat{a}}_{01}({\hat{\mu }})y_2\\{} & {} +\frac{1}{2}{\hat{a}}_{20}({\hat{\mu }})y^2_1 +{\hat{a}}_{11}({\hat{\mu }})y_1y_2 \\{} & {} +\frac{1}{2}{\hat{a}}_{02}({\hat{\mu }})y^2_2+O(||y||^3),\\ \dot{y_2}= & {} {\hat{b}}_{00}({\hat{\mu }})+{\hat{b}}_{10}({\hat{\mu }})y_1+{\hat{b}}_{01}({\hat{\mu }})y_2\\{} & {} +\frac{1}{2}{\hat{b}}_{20}({\hat{\mu }})y^2_1 +{\hat{b}}_{11}({\hat{\mu }})y_1y_2\\{} & {} +\frac{1}{2}{\hat{b}}_{02}({\hat{\mu }})y^2_2+O(||y||^3), \end{aligned}$$

where the coefficients ${\hat{a}}{ij}({\hat{\mu }})$ and ${\hat{b}}{ij}({\hat{\mu }})$ are smooth functions that can be determined using (15), (17), and (18). Specifically, at ${\hat{\mu }} = 0$, derived from (16) and (19), we obtain ${\hat{a}}{00}(0) = {\hat{a}}{10}(0) = {\hat{a}}{01}(0) = {\hat{b}}{00}(0) = {\hat{b}}{10}(0) = {\hat{b}}{01}(0) = 0$. With this context, we proceed to establish the subsequent outcome regarding the normal form of the Bogdanov-Takens bifurcation.

Proposition 3.4

Consider the planar system (15) and suppose, ${\hat{\mu }} = 0$, let the system have an equilibrium at the origin denoted as $x = 0$, with a double zero eigenvalue $\lambda _{1,2}(0) = 0$. We further assume the validity of the following genericity conditions:

• 1. The Jacobian ${{\textbf {J}}}_{{\textbf {x}}} f (0, 0)$ is not the null matrix;

• 2. ${\hat{a}}_{20}(0) + {\hat{b}}_{11}(0) \ne 0$;

• 3. ${\hat{b}}_{20}(0) \ne 0;$

• 4. The map $({{\textbf {x}}},{\hat{\mu }}) \mapsto (f({{\textbf {x}}},{\hat{\mu }}), tr {{\textbf {J}}}_{{\textbf {x}}}f({{\textbf {x}}},{\hat{\mu }}), det {{\textbf {J}}}_{{\textbf {x}}}f({{\textbf {x}}},{\hat{\mu }}))$ is regular at $({{\textbf {x}}},{\hat{\mu }}) = (0, 0)\in {\mathbb {R}}^4$. In this scenario, a smooth and invertible change of parameters can be made such that, within a sufficiently small neighborhood of $({{\textbf {x}}},{\hat{\mu }}) = (0, 0)$, the vector field f is topologically equivalent to one of the prescribed normal forms:

  $$\begin{aligned} \left. \begin{aligned} \dot{\zeta }_1=&\zeta _2,\\ \dot{\zeta }_2=&\alpha _1 + \alpha _2 \zeta _2 + \zeta ^2_ 2+ {\hat{s}} \zeta _1\zeta _2, \end{aligned} \right\} \end{aligned}$$

  (20)

  where ${\hat{s}} = {\hat{b}}_{20}(0)({\hat{a}}_{20}(0) + {\hat{b}}_{11}(0)) = \pm 1$.

The normal form (20) was initially devised by Bogdanov, while an equivalent form was concurrently introduced by Takens. Further details and the proof of this theorem can be found in [28].

Due to space constraints, we omit the detailed calculation for proving the existence of a germ of a Bogdanov-Takens bifurcation in system (2). However, it’s important to note that the specified conditions (1)-(4) guarantee local topological equivalence to the normal form of the Bogdanov-Takens bifurcation. Numerical verification is also conducted to ensure satisfaction of the Bogdanov-Takens bifurcation (cf. Figure 10).

Therefore, a smooth, invertible coordinate transformation, an orientation-preserving time rescaling, and a reparametrization can be applied. This ensures that within a sufficiently small neighborhood of $(x, y, m_1, d_1) = (0,0, m_1^*, d_1^*)$, system (2) is topologically equivalent to one of the specified normal forms of a Bogdanov-Takens bifurcation, represented by (21):

$$\begin{aligned} \left. \begin{aligned} \dot{\zeta }_1=&\zeta _2,\\ \dot{\zeta }_2=&\alpha _1 +\alpha _2 \zeta _2 + \zeta ^2_ 2\pm \zeta _1\zeta _2. \end{aligned} \right\} \end{aligned}$$

(21)

In (21), the sign of the term $\zeta _1\zeta _2$ is determined by the sign of ${\hat{b}}_{20}(0)({\hat{a}}_{20}(0) + {\hat{b}}_{11}(0))$.

3.7 Transcritical bifurcation

Proposition 3.5

When the system bifurcation parameter $m_1$ crosses the critical threshold $m_1=m^{TC}_{1}$, the system (2) undergoes a transcritical bifurcation.

Proof

The Jacobian matrix $J_1$ of the system (2) at $E_1$ has one vanishing eigenvalue for $m_1=m^{TC}_{1}$. Let $U_1$ and $V_1$, respectively, be the eigenvectors of the matrices $J_1$ and $(J_1)^T$ corresponding to zero eigenvalues. As a result, we get

$$\begin{aligned} U_1=\left( -(\frac{rK}{r_1}+\frac{m_1}{a_1r_1+b_1r}~~1\right) ^T, \quad V_1=(0~~ 1)^T. \end{aligned}$$

We have then

$$\begin{aligned}{} & {} F_{m_1}(x,y)=\left( \begin{array}{cc} -\frac{(x-\delta _1 x y)y}{a_1+b_1(x-\delta _1xy)+c_1y}&\;\frac{e_1(x-\delta _1 x y)y}{a_1+b_1(x-\delta _1xy)+c_1y} \end{array} \right) ^T, \\{} & {} F_{m_1}\left( E_1;m_1=m^{TC}_1\right) =\left( \begin{array}{cc} 0&\;\; 0 \end{array} \right) ^T, \end{aligned}$$

and

$$\begin{aligned} \left( V_1\right) ^T F_{{k_1}}\left( E_1;m_1=m^{TC}_1\right) = 0. \end{aligned}$$

Also,

$$\begin{aligned} DF_{m_1}\left( E_1;m_1=m^{TC}_1\right) U_1 = (0 \;\;-1)^T. \end{aligned}$$

We therefore obtain

$$\begin{aligned} \left( V_1\right) ^T\left[ DF_{m_1}\left( E_1;m_1=m^{TC}_1\right) (U_1)\right] =\frac{e_1r}{a_1+b_1r}. \end{aligned}$$

Further,

$$\begin{aligned}{} & {} \left( V_1\right) ^TD^2 F\left( E_1;m_1= m^{TC}_1\right) (U_1,U_1)\\{} & {} \quad =-\frac{e_1m_1r^2_1}{(a_1r_1+b_1r)^2}\left[ \frac{2a_1rK}{r_1}+\frac{2a_1m_1}{a_1r_1+b_1r}\right. \\{} & {} \quad \left. +\frac{(2\delta _1a_1+c_1)r}{r_1}\right] <0. \end{aligned}$$

By applying Sotomayor’s theorem [29], we may conclude that the system experiences a transcritical bifurcation at $E_1$ when $m_1$ crosses the threshold $m^{TC}_{1}$. $\square$

Fig. 3

Sensitivity analysis of various estimated parameters respectively for prey (left) and predators (right)

3.8 Global sensitivity analysis

We used global sensitivity analysis (GSA) employing Latin Hypercube Sampling (LHS) with partial rank correlation coefficient (PRCC) sensitivity analysis to examine the sensitivity of each parameter. Each parameter’s sensitivity is represented in a bar graph and assessed regarding bar length. If a parameter’s PRCC value is larger than $\pm 0.3$, it is considered sensitive to a variable. The parameters r, K, $m_1$ and $d_1$ are all found to be sensitive for the system (2), as shown in Fig. 3.

4 The stochastic model with white noise

We analyze our system by studying environmental characteristics and their fluctuations. Throughout time t, we treat all parameters as constants. Specifically, we explore the stochastic stability of the coexistence equilibrium.

There are two approaches to introduce stochasticity into a deterministic system. First, by substituting one of the environmental characteristics with random parameters. Second, by integrating a randomly fluctuating driving force into deterministic equations, while keeping the parameters unchanged [30]. In this present study, we choose the second strategy. Utilizing Gaussian white noise-type stochastic perturbations on state variables around their stable values $\hat{E}^*$ proves to be an effective approach for modeling rapid fluctuations. These fluctuations are directly related to the distances between each population’s equilibrium values, $x^*$ and $y^*$ [31]. The deterministic system (2) can be expanded to the stochastic model below based on the aforementioned assumption.

$$\begin{aligned} dx= & {} G_1(x,y)dt+\sigma _1(x-x^*)d\xi _t^1,\nonumber \\ dy= & {} G_2(x,y)dt+\sigma _2(y-y^*)d\xi _t^2, \end{aligned}$$

(22)

where the real constant parameters $\sigma _1$, $\sigma _2$ are the intensities of environmental fluctuations and $\xi _t^i=\xi _i(t)$, $i=1, 2$ are the standard Wiener processes that are independent of each other [32].

The stochastic system (22) can be expressed as an It$\bar{\text {o}}$ stochastic differential system in a compact form

$$\begin{aligned} dX_t=G(t,X_t)dt+g(t,X_t)d\xi _t, \hspace{1em} X_{t0}=X_0, \end{aligned}$$

(23)

The It$\bar{\text {o}}$ process is the solution of the preceding equation $X_t=(x,y)^T$ for $t>0$. The drift coefficient, denoted as G, can be described as a slowly varying continuous component. Here, $g = \text {diag}[\sigma _1(x - x^*), \sigma _2(y - y^*)]$ denotes the diffusion coefficient, representing the rapidly fluctuating continuous random component in the diagonal matrix. Here, $\xi _t=(\xi _t^1,\xi _t^2)^T$ is a two-dimensional stochastic process with scalar Wiener process components that have increments $\Delta \xi _t^j=\xi _j(t+\Delta t)-\xi _j(t)$ which are free Gaussian random variables $\textbf{N}(0,\Delta t)$. The system (22) is classified as a multiplicative noise system due to the dependence of the diffusion matrix g on the solution of $X_t$.

4.1 Stochastic stability of the coexistence equilibrium

The coexistence equilibrium in the stochastic differential system (22) acts as a central point. $\hat{E}^*$ is derived by introducing the perturbation vector $u(t) = (u_1(t), u_2(t))^T$, where $u_1 = x - x^*$ and $u_2 = y - y^*$.

To establish mean square asymptotic stability using Lyapunov functions in the context of the complete nonlinear equations (22), we can follow the approach outlined in [33]. However, for simplicity, we focus on the stochastic differential equations obtained by linearizing (22) around the coexistence equilibrium $E^*$. The linearized version of (23) around $E^*$ is given by

$$\begin{aligned} du(t)=F_L(u(t))dt+g(u(t))d\xi (t), \end{aligned}$$

(24)

where now $g(u(t))={\text {diag}} [ \sigma _1u_1, \sigma _2u_2 ]$ and $F_L(u(t))=\left[ \begin{array}{c} -a_{11}u_1-a_{12}u_2 \\ a_{21}u_1-a_{22}u_2 \end{array} \right] = M u,$

$$\begin{aligned}{} & {} a_{11}=-{\widehat{a}}_{11}=r_1x^*-\frac{m_1b_1x^*y^*(1-\delta _1y^*)^2}{[a_1+b_1(x^*-\delta _1x^*y^*)+c_1y^*]^2},\\{} & {} a_{12}=-{\widehat{a}}_{12}=\frac{rx^*K}{(1+Ky^*)^2}+\frac{m_1x^*[(a_1+c_1y^*)(1-2\delta _1y^*)+(1-\delta _1y^*)(b_1x^*-b_1\delta _1x^*y^*-c_1y^*)]}{[a_1+b_1(x^*-\delta _1x^*y^*)+c_1y^*]^2},\\{} & {} a_{21}=-{\widehat{a}}_{21}=\frac{e_1m_1(a_1+c_1y^*)(1-\delta _1y^*)y^*}{a_1+b_1(x^*-\delta _1x^*y^*)+c_1y^*]^2},\\{} & {} a_{22}=-{\widehat{a}}_{22}=d_1-\frac{e_1m_1x^*[(a_1+c_1y^*)(1-2\delta _1y^*)+(1-\delta _1y^*)(b_1x^*-b_1\delta _1x^*y^*-c_1y^*)]}{[a_1+b_1(x^*-\delta _1x^*y^*)+c_1y^*]^2}. \end{aligned}$$

and the coexistence equilibrium corresponds now to the origin $(u_1, u_2=(0, 0)$. Let $\Omega =\left[ (t\ge t_0)\times R^3, t_0\right. \in \left. R^+\right]$ and let $\Theta (t,X)\in C^{(1,2)}(\Omega )$ be a differentiable function of time t and twice differentiable function of X. Let further

$$\begin{aligned} L_{\Theta }(t,u)= & {} \frac{\partial \Theta (t,u(t))}{\partial t} + f^T ( u(t))\frac{\partial \Theta (t,u)}{\partial u} \nonumber \\{} & {} + \frac{1}{2}{\text {tr}}\left[ g^T(u(t))\frac{\partial ^2\Theta (t,u)}{\partial u^2}g(u(t))\right] , \quad \end{aligned}$$

(25)

where

$$\begin{aligned} \frac{\partial \Theta }{\partial u}= & {} \left( \frac{\partial \Theta }{\partial u_1},\frac{\partial \Theta }{\partial u_2}\right) ^T, \quad \frac{\partial ^2\Theta (t,u)}{\partial u^2}\\= & {} \left( \frac{\partial ^2\Theta }{\partial u_j \partial u_i}\right) _{i,j=1,2}. \end{aligned}$$

With these positions, we now recall the following result, [34].

Proposition 4.1

Assume that the functions $\Theta (u,t)\in C_2(\Omega )$ and $L_{\Theta }$ satisfy the inequalities

$$\begin{aligned}{} & {} \hat{r}_1|u|^{\beta }\le \Theta (u,t) \le \hat{r}_2|u|^{\beta }, \end{aligned}$$

(26)

$$\begin{aligned}{} & {} L_{\Theta }(u,t)\le -\hat{r}_3|u|^{\beta }, \hspace{1em} \hat{r}_i>0, \hspace{.5em} i=1,2,3, \hspace{.5em} \beta >0.\nonumber \\ \end{aligned}$$

(27)

Then the trivial solution of (24) is exponentially $\beta$-stable for all time $t\ge 0$.

Remark 1

For $\beta =2$ in (26) and (27), the trivial solution of (24) is exponentially mean square stable; furthermore, the trivial solution of (24) is globally asymptotically stable in probability, [34].

Proposition 4.2

Assume $a_{ij}<0$, $i,j=1,2$, and that for some positive real values of $\omega _1$, the following inequality holds. Then if $\sigma _1^2<2a_{11}$, it follows that

$$\begin{aligned} \sigma _2^2<2a_{22},\quad \end{aligned}$$

(28)

where

$$\begin{aligned} {\omega _1}=\frac{a_{12}}{a_{21}},\quad \quad a_{11}>0,~ \quad a_{22}>0. \end{aligned}$$

(29)

and the zero solution of system (22) is asymptotically mean square stable.

Table 1 Description of the parameters, used in the model system (2) with their units/dimensions: V stands for volume of the species and T for time

Proof

We consider the Lyapunov function

$$\begin{aligned} \Theta (u(t))=\frac{1}{2}\left[ u_1^2 + \omega _1u_2^2 \right] , \end{aligned}$$

(30)

where real positive constants $\omega _1$ to be define later. Verifying the validity of inequalities (26) for $\beta =2$ is a straightforward process. Moreover,

$$\begin{aligned} L_{\Theta }(u(t))= & {} (-a_{11}u_1-a_{12}u_2)u_1\nonumber \\{} & {} +(a_{21}u_1-a_{22}u_2)\omega _1u_2\nonumber \\{} & {} +\frac{1}{2}{\text {tr}} \left[ g^T(u(t))\frac{\partial ^2\Theta }{\partial u^2}g(u(t))\right] . \end{aligned}$$

(31)

Now we evaluate that

$$\begin{aligned} \frac{\partial ^2 \Theta }{\partial u^2}=\left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} \omega _1 \\ \end{array} \right] \end{aligned}$$

and $g^T(u(t))\frac{\partial ^2\Theta }{\partial u^2}g(u(t))=\left[ \begin{array}{cc} \sigma _1^2u_1^2 &{} 0 \\ 0 &{} \omega _1\sigma _2^2u_2^2 \\ \end{array} \right]$ so that we can estimate the trace term as

$$\begin{aligned} {\text {tr}}\left[ g^T(u(t))\frac{\partial ^2\Theta }{\partial u^2}g(u(t))\right] = \sigma _1^2{u_1}^2 + \omega _1\sigma ^2{u_2}^2. \end{aligned}$$

Hence from (31), we obtain $L_{\Theta }(u(t))=-(a_{11}-\frac{\sigma ^2_1}{2})u^2_1-(a_{12}-a_{21}\omega _1)u_1u_2-(a_{22}-\frac{\sigma _2^2}{2})\omega _1u^2_2.$ If we choose $\omega _1=\frac{a_{12}}{a_{21}},$ then we get

$$\begin{aligned} L_{\Theta }(u(t))= & {} -(a_{11}-\frac{\sigma _1^2}{2})u^2_1\nonumber \\{} & {} -(a_{22}-\frac{\sigma ^2_2}{2})\omega _1u^2_2=-u^TQu, \end{aligned}$$

(32)

where $Q=diag[(a_{11}-\frac{\sigma _1^2}{2}), (a_{22}-\frac{\sigma ^2_2}{2})\omega _1]$ and the diagonal matrix Q is a real symmetric positive definite matrix and hence its eigenvalues $\lambda _1$ and $\lambda _2$ become positive real quantities if the following conditions holds: $\sigma _1^2<2a_{11}$ with $a_{11}>0$ and $\sigma _2^2<2a_{22}$ and $a_{22}>0$. If $\lambda _m$ stands for the minimum of two positive eigenvalues $\lambda _1$ and $\lambda _2$ for the diagonal matrix. Then the previous inequality for $L_{\Theta }(u(t))$ we thus get

$$\begin{aligned} L_{\Theta }(u(t)) \le -\lambda _m|u(t)|^2, \end{aligned}$$

thus completing the proof. $\square$

Remark 2

Proposition 4.2 provides the necessary conditions for the stochastic stability of the coexistence equilibrium $\hat{E}^*$ in the presence of environmental fluctuations, as discussed in [35]. Consequently, the model’s internal parameters, combined with the intensities of environmental fluctuations, contribute to upholding the stability of the stochastic system.

5 Numerical simulations

Utilizing MATLAB, we run numerical simulations over the parametric value set to visualize the analytical findings, see Table 1.

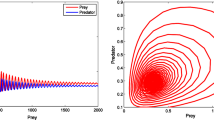
In particular, it is found that the system (2) exhibits a stable behaviour around $E^*=(1.98,0.80)$, see Fig. 4a.

Fig. 4

a The plot is generated for the values of the reference parameters given in Table 1 showing the stability of the coexistence equilibrium. b The plot is obtained with $m_1=0.97$ and the other values of the reference parameters in Table 1 giving rise to a stable limit cycle

Fig. 5

a, b For $m_1$, the trajectory illustrates the various dynamical behaviours of prey (left) and predator (right). c The trajectory shows a set of stable limit cycles generated from the Hopf (H) point, taking $m_1$ as the bifurcation parameter. d Bifurcation diagram as function of the bifurcation parameter $m_1$ for the prey (left) and predators (right)

Fig. 6

a When $m_1=0.97$, the figure shows oscillatory behavior around $E^*$ (continuous line) for $K=2$ and a stable behaviour for $K=0.2$ (bold continuous line). b When $m_1=0.97$, the picture displays oscillatory behaviour around $E^*$ (continuous line) for $\delta _1=0.05$ and a stable behaviour for $\delta _1=0.5$ (bold continuous line)

Fig. 7

a Bifurcation diagram for $m_1$ when $K=0.2$. b Bifurcation diagram for $m_1$ when $\delta _1=0.5$. In both frames, the prey is on the left, and the predators are on the right

Fig. 8

a, b For $c_1$, the trajectory illustrates the various dynamical behaviours respectively of prey (left) and predators (right). c The trajectory depicts a set of stable limit cycles generated from the Hopf (H) point in the $c_1-x-y$ bifurcation space taking $c_1$ as bifurcation parameter. d Bifurcation diagram in terms of $c_1$: prey (left), predators (right)

Fig. 9

a–d Two parameters bifurcation diagram in the $m_1-K$, $m_1-d_1$, $m_1-c_1$, and $m_1-\delta _1$ parameter spaces, respectively

5.1 Effect of $m_1$

When the predator’s hunting rate $m_1$ is high, the dynamical system switches to unstable behavior, specifically for $m_1=0.96$. This is illustrated in Fig. 4b. For the parameter $m_1$, the behaviour of the coexistence equilibrium is shown in Fig. 5a, b. The Hopf bifurcation point (H) is found at $m_1=0.946987$ with eigenvalue $\pm 0.770711i$ and a branch point (BP) at $m_1=0.152917$, with eigenvalue $(0,-3)$.

Figure 5c shows that the system undergoes a supercritical bifurcation after a sequence of stable limit cycles from the Hopf point, the first Lyapunov exponent is $-3.208284e^{-02}$. The results above prove that increasing $m_1$ can reduce both prey and predator densities and that when $m_1=0.946987$, the system (2) switches from being stable to limit cycles.

The symbol (BP) shows a transcritical bifurcation at the branch point.

5.2 Combined effect of K and $m_1$

As noted above, when $m_1 = 0.97$ and $K=2$, the system exhibits a persistent oscillatory behavior around $E^*$. The system trajectories settle to the coexistence equilibrium $E^*$ for low values of K, such as $K = 0.2$, see Fig. 6a.

5.3 Combined effect of $\delta _1$ and $m_1$

As reported in Fig. 4b, when $m_1 = 0.97$ and $\delta =.05$, the system attains oscillatory behavior near $E^*$. Taking the higher value of the prey refuge, $\delta _1=0.5$, the system trajectories settle to the coexistence equilibrium $E^*$ once more (cf. Figure  6b).

5.4 Effect of $c_1$

The mutual interference among predators $c_1$ is a key factor in switching the prey and predator behaviors, as shown in Fig. 8a, b. We have a Hopf point at $c_1=0.201944$ with eigenvalues $\pm 0.770711i$. The system undergoes a supercritical bifurcation with the first Lyapunov exponent $-1.442495e^{-02}$ at that point, and each population starts to oscillate persistently. A family of stable limit cycles is thus created from the H point in the $c_1-x-y$ parameter space (cf. Figure 8c).

5.5 Bifurcations

The bifurcation diagrams of Figs.  5d,  7a, b and  8d fully describe the whole dynamic nature of the system (2) in terms of the parameters $m_1$ and $c_1$ respectively. To visualise the relationship between the predator capture rate with prey fear level and refuge size separately, we have respectively plotted bifurcation diagrams with $m_1$ as the bifurcation parameter for $K =2$ and $K=0.2$, Fig. 5d and 7a and for $\delta _1=0.05$ as well as $\delta _1=0.5$, Figs. 5d and  7b.

Figure 9a–d display the two parameters bifurcation diagram for $m_1-K$, $m_1-d_1$, $m_1-c_1$, and $m1-\delta _1$ respectively. A Bogdanov-Takens bifurcation is shown in the dynamical system (2) arising at the critical values of the bifurcation parameters as $m_{1[bt]}=0.729046$ and $d_{1[bt]}=0$, at which both eigenvalues vanish (cf. Fig. 10). Table 2 provides a summary of the nature of equilibrium points as discussed in the above study.

5.6 Environmental fluctuations

Following that, we will look at the system’s dynamical behaviour in the presence of environmental perturbations. We employ the Euler Maruyama (EM) method using MATLAB software to numerically simulate the stochastic differential Eq. (22). Using a suitable Lyapunov function (30), we established the condition for asymptotic stability of $\hat{E}^*$ in mean square sense for the system (22). These conditions are determined by $\sigma _1$ and $\sigma _2$ and model system parameters. Using, $\sigma _1=0.01$ and $\sigma _2=0.015$, as the intensities of environmental perturbations with parameters set as apply in deterministic system, each species coexist and stochastically stable ((cf. Figure 12)a). Next, we set the environmental fluctuation values to $\sigma _1=0.08$ and $\sigma _2=0.08$, coexistence equilibrium becomes unstable ((cf. Figure 12)b).

Table 2 Natures of equilibrium points

5.7 Two parameters, Lyapunov exponent and basin of attractions

In this section, the system (2) can be transform into the following discrete-time system by using Euler’s method

Fig. 10

Two parameters Bogdanov-Takens bifurcation diagram in the $m_1-d_1$ parameter space

$$\begin{aligned} \left. \begin{aligned} x_{n+1}&= x_n+h\left[ \frac{r x_n}{1+K y_n}-r_1 x_n^2\right. \\&\quad \left. -\frac{m_1(x_n-\delta _1 x_n y_n)y_n}{a_1+b_1(x_n-\delta _1 x_n y_n)+c_1 y_n}\right] ,\\ y_{n+1}&=y_n+h\left[ \frac{e_1m_1(x_n-\delta _1x_ny_n)y_n}{a_1+b_1(x_n-\delta _1 x_n y_n)+c_1y_n} - d_1y_n\right] , \end{aligned} \right\} \nonumber \\ \end{aligned}$$

(33)

where h is the step size. Here, we delve into the numerical exploration of the two-parameter dynamics outlined in model (33), specifically emphasizing stability and chaos. We bypass the analytical examination of local stability, deeming it self-evident. Our primary focus lies on the investigation of stability and chaos in the context of the two-parameter dynamics and the numerical exploration of the basin of attraction. We use Python for this purpose. Since they enable us to examine stable periodic patterns embedded in the chaotic zone, the bi-parameter dynamics are essential to our understanding. By doing this, we can then ascertain the complex transitional patterns underlying their dispersion in the chaotic sea. Moreover, the bi-parameter dynamics can show how multistability has emerged in the system. First, we will discuss the Lyapunov exponent (LE). Recently, many scholars have addressed this type of behavior in different models (see [38]). We choose the step size $h = 0.01$. We chose two parameters for this: the prey reproduction rate (r) and the level of fear (K). Through constructing the LE between these two parameters, we can dynamically analyze how the fear level affects the reproduction rate of the prey species. In Fig. 13, the LE is plotted between these two parameters. The LE can be calculated from the eigenvalues of the Jacobian matrix.

Fig. 11

The figures depict the change of sign of real part (left column) and imaginary part (right column) of $\lambda _1$ (top frames) and $\lambda _2$ (bottom frames) respectively

Fig. 12

a The figures depict solution of system is stochastically stable for $\sigma _1=0.01$ and $\sigma _2=0.015$. b The figures depict solution of system is stochastically unstable for $\sigma _1=0.08$ and $\sigma _2=0.08$

Fig. 13

a The maximum Lyapunov exponent plot is in the parameter space $K \times r \in [0.01, 4]\times [0.01, 8]$. The other parameter values are: ${r_1=0.01, m_1=0.96, \delta _1=0.03, a_1=0.05, b_1=0.07, c_1=0.24, e_1=0.21, d_1=0.54}$. bThe logarithmic lyapunov exponent plot for $r\times K \in [0.01, 10]\times [0.01, 10]$ with $\{r_1=0.04, m_1=0.99, \delta _1=0.05, a_1=0.08, b_1=0.08, c_1=0.28, e_1=0.23, d_1=0.94\}$

The Jacobian matrix of model (2) has two different eigenvalues. The average of the real part of the eigenvalues determines the LE. For simplicity, we use various Python libraries to calculate the LE numerically. In Fig. 13a, the multiple values of the LE have been labeled in the color bar, which is represented by different colors in the plot. The white color in the plot represents the non-existence of the solution. The positive values of the LE represent a chaotic regime, the negative values represent stable or stable periodic behavior, and the Lyapunov value equal to zero means the bifurcation in the system (2). For the LE diagrams in Fig. 13a, we examined model (2) dynamics by adjusting K and r while keeping other parameters constant at $r_1=0.01, m_1=0.96, \delta _1=0.03, a_1=0.05, b_1=0.07, c_1=0.24, e_1=0.21, d_1=0.54$. Here, we fixed the initial conditions as (0.6, 0.8). We explored 1000 combinations of K and r, resulting in a grid of $1000$ equispaced points in $K \times r=[0.01, 4]\times [0.01, 8]$. At each of these $1000$ parameter points, we computed the LE and periodicity of the orbit by iterating model (2) for 100 iterations. Since there is no positive value in the plot, the system is not chaotic for this bi-parameter space with other fixed parameter values. The color scheme changing from $-35$ to $-5$ represents the combined behavior of stable and stable periodic behavior, whereas the brown color in the plot represents the bifurcation regime in the system (2). From plot Fig. 13a, we conclude that when the prey reproduction rate is low, the fear effect causes bifurcation in the system. In contrast, the high reproduction rate demands a high level of fear to maintain the stability of the ecosystem. A similar discussion can be had for the LE in plot 13b. Plot 13b represents the logarithmic LE with parameter values:

$$\begin{aligned}{} & {} \{r_1=0.04, m_1=0.99, \delta _1=0.05, a_1=0.08, \\{} & {} b_1=0.08, c_1=0.28, e_1=0.23, d_1=0.94\} \end{aligned}$$

and initial conditions (0.9, 0.9). We choose $K \times r=[0.01, 10]\times [0.01, 10]$ for plot 13b. The basin of attraction of model (2) is examined in a prey-predator model. It speaks of the starting points (sets of population values) from which the system develops to reach a specific stable equilibrium or limit cycle. The period of the system is determined iteratively for a range of initial condition combinations, offering insights into the stability and periodicity of the ecological dynamics. A Fig. 14 is used to depict the complex dynamics. The graph illustrates how changes in $x_0$ and $y_0$ affect the predator–prey model’s periods. To distinguish different periods, a custom colormap is utilized, assigning distinct colors to each period. We fix $r=3, r_1=0.22, m_1=0.97, \delta _1=0.01, a_1=2.0, b_1=0.1, c_1=0.02, e_1=0.01, d_1=0.02,\text { and } K=0.5.$

Fig. 14

a The basin of attraction in the space $[0.5, 9.5]\times [0.5, 9.5]$. The different color boxes in the color bar represent different periods in the chosen space. Plot b and c are the local amplifications of plot (a)

6 Discussion

This paper incorporates the features of prey refuge and the fear effect in an ecosystem. We study their impact on a predator–prey interaction model.

In this study, we have considered the concepts presented in the earlier paper [1, 16], but with a modification to the functional response form. Instead of using the Holling types II counterparts utilized in their work, we incorporate the Beddington-De Angelis functional response model. Further, we consider fear terms built directly into the growth equations of prey, according to anti-predator behavior.

Prey populations grow logistically but are preyed upon by predators, interfering among them. This phenomenon is modeled via a Beddington-De Angelis response function. The equilibria’ feasibility and stability are assessed after showing the boundedness of the solution trajectories. There are three possible feasible equilibrium points for the system (2), trivial $E_0$, prey-only $E_1$ and coexistence $E^*$, of which only the last two are conditionally stable, a transcritical bifurcation relating them.

To address the first question stated in the Introduction, we concentrate on the effects of changing the parameter $m_1$ expressing the predator’s rate of prey capture. It is crucial to show the onset of the Hopf bifurcation and the stability switching behaviour. The system exhibits oscillatory behaviour when $m_1>m_{1c}=0.946987$, but it settles to stable coexistence in the range $0.152917<m_1<0.946987$. When $m_1$ crosses the value 0.152917, the predator vanishes and the coexistence equilibrium $E^*$ migrates into the predator-free equilibrium $E_1$.

Our focus lies on the refuge coefficient, which determines how the changes influence the system dynamics in the refuge function. From a mathematical perspective, our observations revealed that the characteristics of the behavioral policy regarding prey refuge have a stabilizing impact on the dynamics of predator–prey interactions [16]. When the predation process follows the Beddington-De Angelis response function, our observation reveals an opposing relationship between the fear factor and prey capture by the predator, significantly influencing the system’s stability. However, the study above did not address in [1, 16, 26]. The comparison of our results indicates that the distinct assumptions regarding the response functions lead to significantly contrasting behaviors of the system.

The switching phenomenon of both populations has also been observed under the influence of mutual interference coefficient among predators. Similar phenomena have been identified in [26]. A pair of two-parameter bifurcations are shown in two different parameter spaces. Each exhibits different stability characteristics. Based on the findings, we can deduce that the predator’s prey capture rate and the mutual interference coefficient’s influence, as well as fear level and prey refuge should be kept within a certain range to avoid either predator extinction and possible system instability. This in case the predators are considered as a population to be preserved. In case instead they represent a threat for the ecosystem, e.g. as invasive alien species, the mathematical and numerical findings should be reversed in order to ensure their eradication.

Environmental noise has a profound impact on ecological systems, introducing randomness and unpredictability to the dynamics. In the predator–prey model context, noise reflects the unpredictable variations in environmental factors like resource availability, predation pressure, or habitat quality. These fluctuations affect the growth rates of predator and prey populations, leading to unpredictable changes in population sizes over time.

By accounting for noise effects, we acknowledge the inherent uncertainty in ecological processes. Deterministic models may overlook this complexity, but stochastic simulations offer a more realistic portrayal of ecosystem dynamics. They enable us to explore a spectrum of possible outcomes and evaluate the resilience of model predictions to environmental variability.

When the model incorporates environmental noise with low intensity, it can lead to stochastic asymptotic stability. High-intensity noise, on the other hand, has the potential to induce oscillations with significant amplitudes, leading to unpredictable behavior in the system. When meeting defined constraints on random variations in the environment and model parameters, the model achieves stochastic stability.

By exploring two distinct parameter sets, the study presents numerical results for a dissipative standard map in discrete-time predator–prey system. The introduction of dissipation induces a modification in the phase space structure, leading to the replacement of elliptic fixed points with attracting fixed points. Examining the Lyapunov exponent reveals a highly diverse parameter space (K, r) containing numerous self-similar shrimp-shaped structures. These structures, corresponding to periodic attractors, emerge within a large region associated with chaotic dynamics.

The study introduces innovative elements in several key areas:

• Integration of Prey Refuge and Fear: This study innovatively incorporates prey refuge and fear effects into the predator–prey model, diverging from traditional approaches. By considering these elements, the model reflects subtle prey responses to predators, ultimately improving predictive precision.

• Adoption of Beddington-De Angelis Model: Unlike conventional Holling type II models, this research adopts the Beddington-De Angelis functional response model. This selection provides a more detailed depiction of predator–prey interactions, enhancing the model’s realism.

• Analysis of Stability and Equilibrium: Through a comprehensive examination of stability and equilibrium points, this study offers insights into system dynamics. Pinpointing critical thresholds and bifurcations illuminates conditions for stable coexistence and the factors contributing to instability.

• Exploration of Parameter Sensitivity and Bifurcation: This research delves into the system’s sensitivity to crucial parameters, such as the predator’s prey capture rate. Investigation of bifurcation phenomena reveals pivotal thresholds that govern population dynamics and ecosystem stability.

• Consideration of Environmental Noise: Furthermore, this study evaluates the impact of environmental noise on system stability. Through the analysis of stochastic processes, it provides valuable insights into the resilience of ecological systems to external disturbances.

The study of dissipative structures holds great importance in modern theoretical biology. These structures encompass temporal or spatial anomalies that can arise in systems solely influenced by dissipation under certain conditions. We will specifically delve into the analysis of spatial dissipative patterns. Furthermore, the dissipative elements being studied in this scenario primarily arise from the effects of diffusion, positioning this research as an exploration of dissipative structure. The manuscript also discusses predator–prey models with quadratic interactions and weak dissipation, showing that with seasonal forcing, these models can coexist with multiple periodic attractors. It highlights that these dynamics are most evident in the conservative case with zero dissipation, where a mix of regular and chaotic motions is observed. Moving away from the conservative scenario leads to transient chaos, the destruction of invariant tori, and a shift to stable limit cycles. This change results in complex basins of attraction that can be influenced by stochastic perturbations, causing shifts in system behavior. Biologically, weak dissipation signifies predators effectively controlling prey density below carrying capacity. The potential existence of dissipative structures in ecological systems akin to those observed in chemical interactions. It references prior studies on slime mold aggregation as an example of such structures in ecological contexts. While these studies initially suggested instability due to noise. The current paper then describes attempts to identify purely dissipative structures by modifying predator–prey equations with noise terms to simulate random motion effects. The focus shifts to exploring scenarios where uneven geographic distributions of predators and prey could be mutually beneficial, highlighting that cooperative prey behaviors could lead to faster reproduction rates, benefiting both prey and predators through increased prey populations ”diffusing” into predator-concentrated areas. This analysis seeks to understand the dynamics of predator–prey systems and the potential for cooperative interactions to influence population dynamics in ecological settings.

In essence, this study propels the comprehension of predator–prey interactions by integrating innovative components like prey refuge and fear effects, utilizing novel functional response models, and conducting thorough stability and sensitivity analyses. These advancements enhance ecological models’ precision and predictive capabilities, aiding in ecosystem management and conservation initiatives.

Ecologically, random disturbances can significantly impact population dynamics, potentially leading to the extinction of both prey and predator populations, especially when the disturbance is significant. Simulations show that increasing the fear effect (K) reduces predator density, while the impact on prey density is unclear. Furthermore, increasing the amount of refuge (m) benefits prey populations but is detrimental to the persistence of predator populations. These findings highlight the complex interplay between various ecological factors such as disturbance, fear effects, and refuge availability in shaping population dynamics in predator–prey systems.

The current paper discusses the impacts of environmental fluctuations on a predator–prey system, highlighting that lower intensities of environmental noises lead to fluctuations near deterministic system trajectories. However, as noise intensities increase, so do fluctuations, with very high amplitudes occurring at larger intensities. Lowering noise intensity could minimize fluctuations in prey and predator densities, promoting system stability. The text also explores stochastic dynamics in systems exhibiting bistability behavior, noting that increased noise intensity can induce transitions rarely seen in stochastic predator–prey systems. The study underscores the importance of controlling environmental disturbances for species survival. It introduces future research directions examining the combined effects of seasonality and stochasticity on predator–prey systems with fear effects and Beddington-functional response. Overall, the research demonstrates the reliability of the proposed predator–prey models in ecological contexts, emphasizing the interplay between noise, system dynamics, and environmental stability.

These are compelling areas for future research. One aspect involves integrating additional environmental noises like colored noise, Poisson noise, and more into the model. Additionally, exploring the impact of impulsive perturbations and delays can enhance the model’s realism. These aspects are reserved for future exploration.