Introduction

Models of the flow curves of hot-deformed austenite of microalloyed medium carbon steels have been extensively studied to understand the mechanisms of flow softening that occur during hot deformation, as well as to predict the loads required for hot rolling (or hot forging) [1–6]. Flow stress rapidly increases during the initial period of deformation due to the dominant effect of work hardening (WH), and the rate of increase slows down until reaching a saturation stress level, resulting from a balance between work hardening and flow softening from dynamic recovery. In most microalloyed medium carbon steels, additional flow softening usually occurs due to dynamic recrystallization (DRX). Thus, the modeling of the flow curves of hot-deformed austenite comprised of two parts, the modeling of WH (and dynamic recovery) and of flow softening due to DRX.

Concerning the modeling of WH (and dynamic recovery), Jonas et al. [4] have recently established a description of the WH curve showing the saturation behavior. The description is based on the evolution equation developed by Kocks, Mecking and others, [7–10] and takes into account the accumulation and annihilation of dislocations by work hardening and dynamic recovery.

To model the kinetics of flow softening due to DRX, the Avrami kinetics is conventionally applied to the softening data measured from the experimental flow curves. The softening fraction X is usually expressed in terms of t 1/2 as X = 1−exp [−0.692(t/t 1/2)n], where t 1/2 is a time corresponding to X = 1/2. Earlier work by Laasraoui and Jonas [1] used the peak strain ε p, instead of the critical strain ε c, to calculate t 1/2. Cabrera et al. [3] have modeled the t 1/2, in a traditional form, as t 1/2 = Kd m0 \( {\dot{{\varepsilon }}} \) n′exp(Q/RT), where the authors have also used the peak strain ε p to calculate t 1/2, i.e., t = (ε−ε p)/\( {\dot{{\varepsilon }}} \); the time exponent n was taken as a constant independent of temperature and strain rate. Fernandez et al. [11] experimentally measured the DRX fractions in hot-torsion experiments and analyzed the data via Avrami equation expressed in log(ε−ε c), rather than in log(t), to determine the Avrami constants; the authors, however, have not tried to model the Avrami constants with deformation conditions. Some authors [12, 13] have utilized a form of log [(ε−ε c)/ε p] to evaluate the Avrami constants; however, in this form, the temperature dependency of the rate constant cannot be properly assessed because of the temperature dependency of peak strain (ε p). Jonas et al. [4] have extensively analyzed the Avrami kinetics of the softening fraction due to DRX in various microalloying carbon steels, using a traditional t 1/2 method, this time in terms of the critical strain εc, i.e., t = (ε−ε c)/ \( {\dot{{\varepsilon }}} \); the authors, however, have not tried to model the n and t 1/2 as a function of strain rate and temperature. Recently, Quelennec et al. [5] and Quelennec and Jonas [6] have proposed a physical DRX model utilizing the “physical softening parameter” instead of the conventional “empirical softening parameter.” The results of their extensive modeling efforts have shown that the t 1/2 cannot be fitted to a simple relationship but could only be fitted to complicated functions of strain rate and temperature [6].

In the present work, we propose a simple method which can model the Avrami equation with a single variable, i.e., the temperature-compensated strain rate Z (Z = \( {\dot{{\varepsilon }}} \)exp(Q def/RT)) and which can be used to calculate the flow curves at various deformation conditions by utilizing the work-hardening curve proposed by Jonas et al. [4]; the new method relies on describing the Avrami kinetics in terms of the ε1/2 rather than the conventional t1/2. In addition, we further propose a new method using grain size distribution (GSD) to estimate the DRX fraction in partially recrystallized grain structure, where it is typically difficult to distinguish DRX grains from initial grains.

Experiments

Ingots of V-microalloyed medium carbon steel (having compositions of 0.45C–0.26Si–1.21Mn–0.16Cr–0.014Al–0.13 V–0.006 N) of 350-mm thickness were cast in a vacuum induction furnace through a customer service of POSCO. After homogenizing (1 h at 1250 °C) and hot size rolling to a 100-mm hot slab, the slab was further hot rolled to finally produce a plate of 20-mm thickness. The final plate was machined into rod-shaped specimens of 10-mm diameter and 15 mm-length for Gleeble testing.

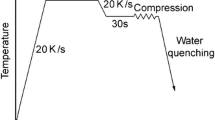
The specimens were heated (heating rate, 10°C s−1) to 1200 °C in a Gleeble 1500 (Dynamic systems Inc., NY) chamber under Ar atmosphere, held for 3 min, and then cooled (cooling rate, 5 °C s−1) to various deformation temperatures for hot compression testing under strain rates from 0.01 to 5 s−1; some of the selected specimens were ice-brine quenched in Gleeble immediately after deformation with various strains to observe the evolution of recrystallized grain structure.

To minimize friction during Gleeble testing, carbon and Ta foils were inserted between the specimen and compression anvil. To correct for minor friction effects, a series of hot compression tests at various strains were carried out in Gleeble to calculate barreling factors [14]. The measured flow curves were corrected for the friction effect using the friction coefficients obtained from the barreling factors. The friction-corrected flow curves have been used for all the analyses of flow curves in the present work.

In order to observe the prior austenite grain structure, the ice-brine quenched specimens were mechanically polished and chemically etched using picric acid. The prior austenite grain size and GSD were measured using an image analyzer via Inspector, in which one measures the area of each grain on optical images and estimates an equivalent size of circle. The number of grains measured for each condition varied from about 150–600.

Results

Figure 1 shows the true stress–strain curves of V-microalloyed (S45CVMn) medium carbon steels at various temperatures and strain rates. The flow curves at temperatures below 1000 °C and high strain rate (5 s−1) first increase rapidly and the increasing rate gradually decreases to approach a saturation stress at large strain, suggesting that softening mostly occurs by dynamic recovery. However, at temperatures above 1000 °C and strain rates lower than 5 s−1, the flow curves, after displaying pronounced peaks, gradually decrease to approach steady-state stresses, suggesting that in addition to dynamic recovery, the softening occurs through DRX. The peak stress and strain increase either with a decreasing deformation temperature or with an increasing strain rate in accordance with the DRX behavior.

Fig. 1
figure 1

True stress–strain curves of V-microalloyed medium carbon steel at various temperatures: a 1150 °C; b 1050 °C; c 950 °C; d 850 °C. The dotted curves represent the flow curves calculated by modeling the Avrami kinetics as a function of Z

Full size image

Since the softening occurs by dynamic recovery and DRX, one first needs to construct the flow curve arising from WH and dynamic recovery (DRV) in order to study the kinetics of DRX. The WH-DRV curve (designated here as WH curve) is known to show a saturation behavior at large strain due to a competition between WH and DRV [7–10]. Once the WH curve is constructed, one can estimate the fraction of softening due to dynamic recrystallization X (Fig. 2) by

Fig. 2
figure 2

The calculated work-hardening curve and experimentally measured flow curve at 1050 °C, έ0.1: a calculated work-hardening curve; b calculation of the recovery rate (r) and saturation stress (σ sat). The figure b also shows the critical stress σ c and peak stress σ p in the plot

Full size image
$$ X = \frac{{\sigma_{\text{wh }} - \sigma }}{{\sigma_{\text{sat}} - \sigma_{\text{ss}} }}, $$
(1)

where σ sat is the saturation stress in WH curve and σ ss is the steady-state stress under DRX condition.

In order to construct the WH curve (σ wh), we have adopted the equation recently developed by Jonas et al. [4] based on the concept of the competition between storage and annihilation of dislocations during deformation [8]:

$$ \sigma_{\text{wh}} = \sqrt { \sigma_{\text{sat}}^{2} - \left( {\sigma_{\text{sat}}^{2} - \sigma_{0}^{2} } \right)\exp ( - r(\varepsilon - \varepsilon_{0} ))} $$
(2)
$$ 2\sigma \frac{{{\text{d}}\sigma }}{{{\text{d}}\varepsilon }} = r\sigma_{\text{sat}}^{2} - r\sigma^{2} , $$
(3)

where σ 0 is the yield stress.

The plot 2σ(dσ/dε) versus σ 2 allows one to determine the recovery rate r from the slope and σ sat from the intercept. Here one has to use a linear portion of the data, i.e., stresses less than σ c (which is the critical stress for the initiation of DRX); the critical stress is determined by applying the method proposed by Poliak and Jonas [15]. Figure 2 shows an example of determining the recovery rate r and saturation stress σ sat by applying Eq. (3) to the measured stress–strain data.

One can then calculate the WH curve (σ wh) as a function of strain according to Eq. (2); a typical example of such calculation is shown in Fig. 2, together with the corresponding experimental flow curve (σ). The fraction of softening can be then calculated as a function of strain, using Eq. (1) and experimentally measured σ ss as seen in Fig. 2; the steady-state stress is taken as 0.82 σ p if the steady state is not apparent in the experimental curve.

Figure 3 displays the results of the calculation of softening fraction X from the measured flow curves (Fig. 1) as a function of strain, using Eqs. (1) and (2), at various temperatures (under the strain rate 5 s−1). It should be noted that strain scales with time at a constant strain rate. The softening fraction increases slowly at an initial stage and then rapidly rises at an intermediate stage, before slowly approaching a saturation value at the last stage. This variation in behavior of the softening fraction with strain closely resembles a sigmoidal rate curve, which can be best described by the Avrami kinetics [16].

Fig. 3
figure 3

The variation of softening fraction due to DRX as a function of strain at various temperatures (strain rate 5 s−1): a 1150 °C; b 1050 °C; c 950 °C; d 850 °C. Continuous line indicates the data obtained from the flow curves; the open circle the experimentally measured data; the open square the data evaluated from grain size distribution (GSD) method

Full size image

Since the flow softening is believed to occur by DRX, the microstructures of some selected specimens were examined using optical microscopy, to study the evolution of GSD under the DRX condition (Fig. 4). A well-developed necklace grain structure, which is a characteristic of DRX grain structure, appears when the deformation temperature is lower than 1000 °C (Fig. 4e, f). However, such well-developed necklace grain structure becomes increasingly less evident as the deformation temperature increases to above 1000 °C (Fig. 4a, c). As a result, the measurement of the DRX fraction appears to be increasingly difficult to carry out at high deformation temperatures (above about 1000 °C), although the measurements can be easily performed at low deformation temperatures.

Fig. 4
figure 4

Optical microstructures showing partially (or fully) recrystallized austenite grain structures during deformation at various temperatures (strain rate 5 s−1) and strains: a 1150 °C, ε0.6; b 1150 °C, ε1.2; c 1050 °C, ε0.6; d 1050 °C, ε1.0; e 950 °C, ε0.6; f 850 °C, ε1.0

Full size image

Figure 5 shows the measurements of GSDs for some selected deformation conditions. The GSD of the initial condition (not shown here) showed a typical lognormal distribution, with a peak near 100 μm, showing positively skewed distribution (long right tail). As the deformation (at the strain rate 5 s−1) proceeds, the GSD evolves with strain in a distinctively different manner depending on temperature. To examine the details of the evolution behavior of GSD, the measured GSDs were fitted to lognormal distribution function (LDF) given as [17]:

Fig. 5
figure 5

Grain size distributions of partially (or fully) recrystallized grain structures at high (1150 °C) and low temperatures (950 °C) for small and large strains (strain rate 5 s−1): a 1150 °C, ε0.4; b 1150 °C, ε1.2; c 950 °C, ε0.4; d 950 °C, ε1.2

Full size image
$$ F = \frac{1}{{\sqrt {2\pi \sigma^{2} } }} \frac{1}{D}\exp \left[ { - \frac{{\left( {\ln D - \mu } \right)^{2} }}{{2\sigma^{2} }}} \right], $$
(4)

where D is the grain size, μ is the average of ln D, and σ is the standard deviation. The LDF’s constructed at different levels of strain were plotted together in the same scale (frequency vs. grain size) to compare the variation of GSD’s as a function of strain. The results (Fig. 6) clearly show a distinctively different variation in GSD behavior for high and low deformation temperatures. At high deformation temperatures (above about 1000 °C), the peak of lognormal function is progressively shifted towards smaller grain size with increasing strain before undergoing a complete recrystallization. In contrast, at temperatures below about 1000 °C, the peak suddenly appears at small grain size and, thereafter, the frequency of the peak (remaining at a similar size) tends to increase with the increasing strain. This particular evolution behavior of distribution function at low temperatures is related to a sudden appearance of numerous fine DRX grains at low deformation temperatures, as seen in Fig. 4e, f.

Fig. 6
figure 6

Variation of lognormal distribution functions (LDF’s) as a function of strain at two different temperatures (strain rate 5 s−1): a 1050 °C; b 950 °C

Full size image

As deformation proceeds (Fig. 6a), the LDF starts to deviate from that of the initial structure and the LDF progressively shifts, with the increasing strain, toward the LDF of fully recrystallized grain structure at strain 1.2. If one assumes that the recrystallized grains in a partially recrystallized grain structure conform, for all levels of strain ε, to a GSD given by a fully recrystallized grain structure, the LDF of a fully recrystallized grain structure defines a maximum probability of each class of recrystallized grain sizes in a partially recrystallized grain structure (at a given strain ε). The amount of DRX grains in a partially recrystallized grain structure (at strain ε) can then be related to the area A(ε) (Fig. 7a), which is defined by the area belonging simultaneously to the two LDF curves of partially recrystallized grain distribution (at strain ε) and of fully recrystallized grain distribution (at strain 1.2). The fraction of DRX can then be estimated by normalizing the area A(ε) by the area A 0, which is the area defined by the LDF curve of fully recrystallized grain distribution (Fig. 7b). A more detailed examination (Fig. 7b), however, shows that a significant fraction of A 0 is overlapped by the LDF curve of initial grain distribution (ε = 0). The overlapped area (designated as A i (0)) should belong to un-recrystallized grains at the beginning of deformation and will progressively turn into recrystallized grains with the increasing amount of strain, before finally becoming fully recrystallized grains at strain 1.2.

Fig. 7
figure 7

Schematic diagrams of LDF’s of partially recrystallized (ε), fully recrystallized (ε = 1.2), and un-recrystallized (ε = 0) grain structures, showing how one can estimate the recrystallized fraction from the three areas A(ε) (a), A 0 and A i (0) (b) defined by the three LDF’s

Full size image

It is clear that the amount of recrystallized grains in the distribution (overlapped) A i (0) evolves from 0 at ε = 0 to A i (0) at ε = 1.2 (Fig. 7b). We now assume that the recrystallization kinetics of the grains belonging to A i (0) follow the same Avrami kinetics as the grains belonging to the other distribution. Namely, the recrystallized fraction at strain ε, y (= A i (ε)/A i(0)) = 1−exp (−k(ε−ε c)n), where A i (ε) is a hypothetical area which, among the area A i (0), has undergone recrystallization at strain ε. If we take n as 2 (from the present softening data), we get the following expression, as for the area corresponding to un-recrystallized grains in the distribution A i (0) (at strain ε):

$$ {{\Delta }}A_{i} \left( \varepsilon \right) \, \left( { = \, A_{{i}} \left( 0 \right) \, - \, A_{{i}} \left( \varepsilon \right)} \right) \, = \, A_{{i}} \left( 0 \right) \, \exp \left( { - k\left( {\varepsilon \, {-} \, \varepsilon_{\text{c}} } \right)^{2} } \right) $$
(5)

The constant k is determined by imposing the experimentally observed limiting conditions; for example, we get k = 2 at high temperatures as we apply the condition y = 0.95 at ε = 1.2. A true DRX fraction X can be now evaluated by subtracting, from the area A(ε) (Fig. 7a), the un-recrystallized area ΔA i(ε) in the distribution A i(0) as

$$ X = \frac{{A\left( \varepsilon \right) - {{\Delta }}A_{i} (\varepsilon )}}{{A_{0} }} $$
(6)

The DRX fractions, estimated using Eq. (6), are shown in Fig. 3 and compared with the experimentally measured data. (It can be noted that the experimental measurements at high temperatures are difficult but not impossible; extensive measurements are required to ensure sufficient accuracy.) The results show that the data obtained using the GSD method, i.e., Eq. (6), are in good agreement with the experimentally measured data (except at 850 °C), suggesting that the currently proposed GSD method is useful for evaluating the DRX fraction from a partially recrystallized grain structure especially at high temperatures, where recrystallized grains are difficult (although not impossible) to distinguish from un-recrystallized grains.

The evaluation at 850 °C tends to significantly overestimate the DRX fraction as compared to the experimentally measured values. The discrepancy is largely due to the fact that the LDF of fully recrystallized grain distribution (A 0) is evaluated from the GSD, which is measured, not in fully recrystallized grain distribution, but in partially recrystallized grain distribution; as a result, the LDF is extremely narrow and may not represent a true LDF for fully recrystallized grain distribution. At such low temperature, however, the recrystallized grains are easily recognizable (Fig. 4e, f) and the DRX fraction can be experimentally measured with confidence.

In order to study the DRX mechanisms and also to calculate the flow curves, one has to analyze and model the Avrami kinetics. The traditional method is to express the Avrami equation in terms of time, t as [4]:

$$ X = 1 - \exp \left( { - kt^{n} } \right) = 1 - \exp \left[ { - 0.693\left( {\frac{t}{{t_{1/2} }}} \right)^{n} } \right], $$
(7)

where time t is given by t = (ε−ε c)/\( {\dot{{\varepsilon }}} \) and t 1/2 = A \( {\dot{{\varepsilon }}} \) −q exp(Q/RT) (dropping the initial grain size effect). Although this equation can properly describe the rate of DRX softening (by 1/t 1/2), the expression makes it difficult to model the flow curves in terms of deformation conditions, i.e., temperature-compensated strain rate, Z (Z = \( {\dot{{\varepsilon }}} \)exp(Qdef/RT)) [6].

To solve this difficulty, we introduce a new method of expressing and analyzing the Avrami kinetics. The basic idea of the new method relies on expressing the softening fraction X (due to DRX) in terms of strain (which scales with time at a constant strain rate) rather than in terms of time, as

$$ X = 1 - {\text{e}}^{{ - [k(\varepsilon - \varepsilon_{\text{c}} )]^{n} }} $$
(8)

The time exponent n can be obtained, as in the traditional method, by plotting log[ln(1/(1−X))] against log(ε−ε c) and by finding the slope at each strain rate. The results (Fig. 8) show that a good linear relationship is generally obeyed at each temperature and strain rate. The time exponent n is evaluated from the slope at various conditions and the logarithm of n is plotted against the logarithm of Z (= \( {\dot{{\varepsilon }}} \)exp(Q def/RT)); the value of Q def (= 350 kJ mol−1) was determined from the peak stress data (Fig. 1) using a similar method as in the literature [1]. The result (Fig. 9) clearly shows, despite what is frequently assumed in the literature [3, 4], that the time exponent n is not a constant, but surely decreases with increasing Z: the value of n is about 2.3 at low Z and becomes about 1.4 at high Z. From linearity, the time exponent n can be described as a function of Z as

Fig. 8
figure 8

Variation of the softening fraction (log[ln(1/(1−X))]) as a function of strain (log(ε−ε c)) at various strain rates and temperatures: a 1150 °C; b 950 °C. Note the slope (n) is decreasing with the increasing strain rate

Full size image
Fig. 9
figure 9

Variations of the Avrami constant n as a function of Z (a) and of the (ε−ε c)1/2 as a function of temperature at various strain rates (b) and as a function of strain rate at various temperatures (c). Here Z is a temperature-compensated strain rate, i.e., Z = έexp(Q def/RT)

Full size image
$$ n = 1.14 \times 10Z^{ - 0.056} $$
(9)

The rate constant k 1/2 can be calculated by determining (ε−ε c)1/2 for X = 1/2 in Fig. 8 and using the following expression from Eq. (8):

$$ k_{1/2} = \frac{{(\ln 2)^{1/n} }}{{(\varepsilon - \varepsilon_{\text{c}} )_{1/2} }}, $$
(10)

where (ε−ε c)1/2 scales with time (t 1/2) required for X = 1/2. To find an expression for the rate constant k 1/2, an expression for (ε−ε c)1/2 is sought as a function of temperature and strain rate. Figure 9b shows that log(ε−ε c)1/2 linearly increases with (1/T) in accordance with Eq. (10), since the rate constant k 1/2,i.e., logk 1/2 is expected to be inversely proportional to (1/T). From the slope, one can estimate the activation energy Q and the figure indicates that the activation energies are similar at various strain rates; the average value is estimated to be 56 kJ mol−1, which is similar to that determined in the traditional t 1/2 method [4]. However, unlike in the traditional t 1/2 method, log(ε−ε c)1/2 is found to also increase with the increase in log\( {\dot{{\varepsilon }}} \) at constant temperature (Fig. 9c), exhibiting a positive slope rather than a negative slope, as reported in the traditional t 1/2 method [4]. The slopes being more or less similar at various temperatures, the positive strain rate quotient is found to be +0.17 from the average of the slopes. Combining these results together, (ε−ε c)1/2 can be expressed as

$$ (\varepsilon - \varepsilon_{\text{c}} )_{1/2} = 2.0 \times 10^{ - 3} {\acute {\varepsilon}}^{0.17} \exp \left( {\frac{56,000}{\text{RT}}} \right) $$
(11)

Then, similarly to the conventional t 1/2 method (Eq. 7), the softening fraction X can be calculated in terms of (ε−ε c)1/2 by

$$ X = 1 - \exp \left[ { - 0.693\left( {\frac{{\varepsilon - \varepsilon_{\text{c}} }}{{\left( {\varepsilon - \varepsilon_{\text{c}} } \right)_{1/2} }}} \right)^{n} } \right] $$
(12)

The rate constant k 1/2 can now be calculated using Eqs. (9–11) as in the traditional t 1/2 method. An alternative method is to directly estimate the rate constant k 1/2 using the experimentally measured values of n, (ε−ε c)1/2 and using Eq. (10). The directly estimated values of k 1/2 are plotted as log(k 1/2) versus log(Z) in Fig. 10; the figure shows a good linear relationship between log(k 1/2) and log(Z), which definitively differs from the traditional t 1/2 method: log(t 1/2) (and thus log(k)) was impossible to curve fit to the log(Z) in the traditional t 1/2 method [6]. The reason that log(k 1/2) can be linearly fitted to log(Z) is because log(ε−ε c)1/2, unlike log(t 1/2), can be linearly fitted to log(Z), as shown in Fig. 10b. From a direct curve fitting in the figure (Fig. 10a), the rate constant k 1/2 is expressed in terms of Z as

Fig. 10
figure 10

Variation of the rate constant k((ε−ε c)1/2) (a) and (ε−ε c)1/2 (b) as a function of Z. Compare with the variation behaviors of t 1/2 (c) and k(t 1/2) (d) as a function of Z

Full size image
$$ k_{1/2} = 7.35 \times 10^{2} Z^{ - 0.18}. $$
(13)

Using Eqs. (8), (9), and (13), one thus can calculate the softening fraction X due to DRX as a function of strain ε at various strain rates and temperatures. The calculated curves (not shown here) generally showed a good agreement with the curves estimated from the flow curves at various deformation conditions. Once the softening fraction X is calculated, one then can calculate the variation of flow stress as a function of strain ε, using Eqs. (1) and (2), at various strain rates and temperatures. The results of the calculation were compared with the experimental results in Fig. 1 and show a good agreement to one another at various deformation conditions. The calculation further showed that very much similar results can be obtained using the (ε−ε c)1/2 method, i.e., using Eqs. (9), (11), and (12); however, the direct k 1/2 method is expected to be more reliable because of the smaller number of fitting procedures involved in the calculation.

Discussion

The present method of modeling the Avrami kinetics, which may be called the ε 1/2 (i.e., (ε−ε c)1/2) method (as opposed to the traditional t 1/2 method), provides a simple and useful tool to model the flow curves of V-microalloyed medium carbon steel as shown in Fig. 1. The current method allows the prediction of flow curves at various deformation conditions using the Avrami kinetic equation (Eq. 8) expressed by two simple exponential functions of a single variable, Z (Eqs. 9, 13); or by employing Eq. (12) and by fitting (ε−ε c)1/2 in a simple exponential function of Z (see Fig. 10b). The reason for the successful modeling using a single variable Z in the current ε 1/2 method is because, unlike the traditional t 1/2 method, the temperature and strain rate dependencies of ε 1/2 (Eq. 11) exhibit the same sense as those of Z, whereas the t 1/2 shows an opposite dependency on \( {\dot{{\varepsilon }}} \) and T as compared to that of Z. This can be clearly seen by noting the relationship between t 1/2 and ε 1/2, i.e., t 1/2 = ε 1/2/\( {\dot{{\varepsilon }}} \). Thus, t 1/2 can be simply obtained from Eq. (11), as

$$ t_{1/2} = 2.0 \times 10^{ - 3} {\acute {\varepsilon}}^{ - 0.83} \exp \left( {\frac{56,000}{\text{RT}}} \right) $$
(14)

One can immediately notice that the only difference is in the dependency on the strain rate \( {\dot{{\varepsilon }}} \) and that the sense of its dependency is reversed; as a result of the reversed sense now, the dependency of t 1/2 on \( {\dot{{\varepsilon }}} \) and T becomes opposite to that of Z. It should be noted here that the quotient (−0.83) of the strain rate, as well as the activation energy, is actually very close to that (−0.84) obtained by the conventional t 1/2 method in the literature [4]. The problem with this opposite sense of temperature and strain rate dependencies is clearly manifested in the plot of t 1/2 (or ln(t 1/2)) against Z(or ln(Z)) (Fig. 10c, d), where a unified relationship is impossible to find between t 1/2 and Z (and likewise between k(t 1/2) and Z), in agreement with a previous report [6].

An examination of literature data [4–6] showed that a linear relationship between lnε 1/2 and lnZ similarly holds in various low-to-medium carbon microalloyed steels, indicating that the ε 1/2 method is a general method which can be used to model the Avrami kinetics of most microalloyed carbon steels in terms of the single variable Z.

It should be mentioned here that the current ε 1/2 method (Eq. 11) has a limitation, in that it cannot properly represent the recrystallization rate with the variation of strain rate, whereas the traditional t 1/2 method (Eq. 14) (actually the reciprocal of t 1/2) properly exhibits the recrystallization rate as a function of strain rate. However, the current ε 1/2 method correctly represents the recrystallization rate in terms of the variation of temperature, in exactly the same way as the t 1/2 method (compare Eqs. 11 and 14). The activation energy obtained in the current analysis (56 kJ mol−1) is distinctively low as compared to that generally known in the static recrystallization kinetics [18]; small activation energy is actually similar to the activation energy for the rate of boundary migration [19]. It may be possible that the kinetics of boundary migration is rate controlling in the necklace recrystallization, unlike the static recrystallization, because the driving force for growth is small in the DRX [10].

The current result (Fig. 9a; Eq. 9) shows that the time exponent “n” is not a constant, as is usually assumed in the literature [2, 3] but definitively varies depending on Z, although its dependency is weak. It is worth noting that a similar tendency was also evident in a previous study of plain carbon steels [20]. A seemingly small change in the value of “n” (from 2.3 to 1.4) (which can be easily overlooked in the flow curve modeling) actually can imply an important shift in the mode of necklace recrystallization according to a simulation result of Thomas et al. [21]. Recently, Thomas et al. [21] studied the kinetics of microstructure evolution by modeling a geometrical aspect of necklace recrystallization. The modeling results showed that the time exponent “n” in the Avrami kinetics strongly depends on the strain rate (at const. temperature); n = 1 at a high strain rate; n = 3 at a low strain rate. This was because nucleation is responsible for the most of the necklace recrystallization at high strain rates, whereas most of the necklace recrystallization is due to boundary migration at low strain rates.

The evidence of such a shift between the nucleation dominant mode and boundary migration dominant mode can be clearly observed in Figs. 4 (and 6), by recalling that a similar transition is expected to also occur depending on the value of Z. Extremely fine recrystallized (through necklace recrystallization) grains are formed at high Z (at low temperature) due to the difficulty of boundary migration (Fig. 4f), whereas a necklace grain structure is difficult to distinguish from un-recrystallized grain structure at low Z’s (Fig. 4a, c), most probably due to a significant boundary migration rather than a repeated nucleation. Furthermore, the n value corresponding to each microstructure is in good agreement with the prediction of Thomas et al.’s model, i.e., n = 1.4 at high Z and n = 2.3 at low Z (Fig. 9a). The current result (Fig. 9a), however, shows that the value of n is continuously varying with the variation of Z. This is believed to suggest that a mixed mode is operating in most deformation conditions but that necklace recrystallization proceeds increasingly in a nucleation dominant mode as the deformation carries out at increasingly high Z (or vice versa).

In high Z conditions, where the necklace grain structure is apparent, the LDF peak appears from the early stage of deformation at the peak position of the fully recrystallized grain structure (Fig. 6b), and the frequency of the recrystallized peak progressively increases with the progress of deformation. This is because necklace recrystallization occurs in a nucleation dominant mode (i.e., by repeated nucleation) and the GSD is little affected by the level of strain at which nuclei form because of a severely limited boundary migration (growth).

In contrast, in low Z conditions (where necklace grain structure is not apparent, Fig. 6a), the peak of LDF is progressively shifted with increasing strain (ε) from its initial position to a fully recrystallized position. This would suggest the occurrence of continuous recrystallization in addition to discontinuous recrystallization. However, since a necklace grain structure is clearly observed with high Z conditions and the time exponent “n” is in good agreement with the boundary migration dominant mode, we believe that the peak shifts because of a significant boundary migration (i.e., growth) that occurs during necklace recrystallization at low Z’s, in accordance with the model of Thomas et al. [21]. The peak can shift when significant boundary migration is possible because the recrystallized grain sizes, in such conditions, are likely to be determined by the balance between the growth rate (G) and nucleation rate (N). Derby and Ashby [22], in their model of dynamically recrystallized grain sizes, showed that the steady-state grain sizes can be expressed as proportional to (G/N)1/3. If one assumes that a similar relation holds all along the deformation strain, the recrystallized grain sizes are expected to depend on the strain and to decrease with an increase in the deformation strain; this is because the nucleation rate N is expected to increase exponentially with strain, whereas the growth rate G increases mildly with the increasing strain.

In our GSD model, it is assumed that recrystallized grains at various levels of strain (namely in partially recrystallized structures) conform to the LDF of fully recrystallized grain structure. Namely, each class of recrystallized grains formed at each level of strain is assumed to exhibit the same probability (maximum) of distribution as that of the same class in fully recrystallized grain structure. The reasoning for this assumption relies on the same argument advanced above, based on the model of Derby and Ashby [22], that the grain size at each level of strain is likely to be determined by (G/N)1/3 at each level of deformation strain.

The recrystallization fractions estimated from the current GSD method were compared with those experimentally measured in Fig. 3 to verify the validity of the current GSD method. The result shows good agreement as long as a reference GSD (i.e., A 0 in Fig. 7) is accurately measurable, and this is believed to support the feasibility of the current GSD method. It is noted here again that the experimental measurements at low Z’s (i.e., high temperatures) are not impossible, although the measurements appear to be difficult because of the similarity with recrystallized grain structures (as seen in Fig. 4a, c). Careful comparison with the initial (prior to deformation) grain structure makes it possible to recognize the recrystallized grains in partially recrystallized grain structures.

The softening fractions (estimated from the flow curves) are generally in good agreement with the DRX fractions up to an intermediate stage of deformation, i.e., to a strain of about 0.6 (Fig. 3). At a later stage of deformation, however, the softening fraction tends to overestimate the DRX fraction at high temperatures and the overestimation appears to arise from an apparent retardation (or delay) of DRX kinetics at a later stage of deformation (Fig. 3a, b). Although the cause of the overestimation is not clearly understood at present, the overestimation could arise if a dynamic recovery is significantly delayed (simultaneously with a delay of DRX) for some reason; in such a situation, the WH and recovery equation employed in the present calculation (Eq. 2) would particularly underestimate σ sat in Eq. 1, since Eq. 2 is derived for a situation where dynamic recovery occurs purely through dislocation dynamics in the absence of any obstacles [4, 8].

One of the possible causes for a delay of recovery and DRX would be a dynamic precipitation of carbonitride particles in the present V-microalloyed steel. The calculation using the solubility products in the literature [23] shows that the solution temperatures of AlN and VC(N) are about 1050 and 960 °C, respectively, in the present microalloyed steel. Thus, AlN particles would be a possible reason for the delay of the propagation of DRX at 1050 °C. As for VC(N) particles, although it is thermodynamically possible for VC(N) particles to form abundantly at 850 °C, it is highly unlikely that they can actually precipitate at a strain rate as fast as 5 s−1 [24].

Conclusions

A new method of modeling the Avrami kinetics, based on the ε 1/2 method, is proposed to express the kinetics of flow softening due to DRX, which is, unlike the conventional t 1/2 method, capable of modeling the softening fractions and flow curves with a single variable, i.e., Z (= \( {\dot{{\varepsilon }}} \)exp(Q def/RT)). The time exponent of the Avrami kinetics decreases from n = 2.3 to 1.4 with increasing Z, which results from a shift in the mode of necklace recrystallization, from boundary migration dominant mode to nucleation dominant mode. A GSD method of modeling the evolution of GSD with LDF is also proposed as a new method for estimating the DRX fraction in deformation conditions where the recrystallized grains are difficult to distinguish from un-recrystallized grains. The softening fraction evaluated from the flow curves tends to overestimate the DRX fraction at a later stage of deformation, when the recrystallization and recovery appear to be retarded by dynamic precipitation.