Introduction

The medium carbon Nb-V microalloyed steel, as a typical non-quenched and tempered steel, has been widely used for cutting shaft parts in machine tool and other machinery industry (Ref 1, 2).This steel can be directly used for cutting products after shaped into parts, as the mechanical properties are obtained at the end of the forming process. So an important saving of costs and energy can be reached by reducing the number of operations (such as heat treatment, and straightening.) (Ref 3-6). Recently, more and more attention has been paid on this kind of steel.

This steel is produced by thermo-mechanical controlled processing consisting of controlled rolling and controlled cooling. The rolling temperature is from about 850 to 1200 °C. Several interconnect metallurgical phenomena such as WH, DRV, and DRX inevitably occur during hot deformation process (Ref 7). The hot deformation process directly affects the microstructure evolution of the material and the mechanical properties of the formed product. So, in order to improve the properties of this steel, parameters of the hot forming process must be controlled carefully and the hot deformation behavior of this steel must be investigated clearly (Ref 8, 9).

In the past, some researches about microalloyed steel have already been done. Xie et al. (Ref 10), Bao et al. (Ref 11), Cho et al. (Ref 12), etc., have studied the DRX, static recrystallization (SRX), and metadynamic recrystallization (MDRX) behavior of Nb microalloyed steel. Wei et al. (Ref 13) and Zhao et al. (Ref 14) investigated the DRX behavior of V microalloyed steel. Lan et al. (Ref 15) studied the DRX and SRX behavior of Nb-Ti microalloyed steel. There are also some studies about the flow behavior of V microalloyed steel (Ref 4, 16-20). However, for hot deformation behavior of the medium carbon Nb-V microalloyed steel, few studies have been reported, especially for systematic researches about both DRX behavior and flow behavior of the steel.

In this paper, the isothermal hot compression tests of a medium carbon Nb-V microalloyed steel in a wide range of strain rates and deformation temperatures were conducted. Based on the experiment data, the DRX behavior of this steel was investigated. The constitutive equation to predict the flow stress of the tested steel was also developed and flow stress predicted by the developed constitutive equation was compared with the experimental ones.

Experimental Procedures

The chemical composition of the tested steel in this paper is given in Table 1. In order to perform the isothermal hot compression tests, cylindrical specimens with a diameter of 8 mm and a height of 12 mm were machined. To reduce the friction between the anvils and the end faces of the specimens during the compression process, tantalum foils with thickness of 0.05 mm were placed between anvils and specimens.

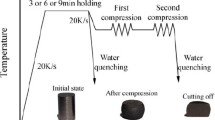
Table 1 Chemical composition of the tested steel (wt.%)
Full size table

Isothermal hot compression tests were conducted on a Gleeble-1500 thermo-mechanical simulator. Figure 1 shows the schematic of the isothermal hot deformation process. Before compression, the specimens were heated to 1523 K at the rate of 20 K/s and held for 300 s to make the alloyed elements completely dissolve and ensure uniform temperature, during this process the initial ferrite and pearlite phases transformed to single austenite phase. Then, the specimens were cooled to the testing temperatures (from 1123 to 1473 K with an interval of 50 K) at the rate of 20 K/s and held for 30 s to eliminate the temperature gradient. Subsequently, the specimens were compressed to a strain of 0.8 at the testing temperatures with the constant strain rates (0.01, 0.1, 1, and 10 s−1). After compression, the specimens were water quenched immediately to room temperature. The initial austenite grain size of the steel after austenite homogenization is shown in Fig. 2.

Fig. 1
figure 1

Schematic of the isothermal hot deformation process

Full size image
Fig. 2
figure 2

The initial austenite grain size of the steel after austenite homogenization

Full size image

Results and Discussion

Analysis of Flow Stress Curves

A series of typical true strain-stress curves obtained from the hot compression tests are shown in Fig. 3. It can be seen that the flow stress was greatly influenced by the deformation temperature and strain rate. The flow stress increases with the increase of strain rate and the decrease of temperature. This is because that lower strain rates and higher temperatures provide longer time for energy accumulation and higher mobility at boundaries for the nucleation and growth of dynamically recrystallized grains and dislocation annihilation (Ref 21). Meanwhile, all the curves obtained can be ranged into three types depending on the relationship between stress and strain, as shown in Fig. 4: WH, characterized by increasing stress with strain (like curve 1123 K, 1 s−1); DRV, characterized by saturation stress with increasing strain (like curve 1223 K, 0.1 s−1); and DRX, characterized by an observed peak stress (like curve 1473 K, 0.01 s−1) (Ref 22). Besides, compared to the C-Mn steel (Ref 17) and V microalloyed steel (Ref 4, 18, 19), the flow stress of this medium carbon Nb-V microalloyed steel is about 10-40 MPa higher than them. This may due to the high solute strengthening and precipitation strengthening effect of microalloyed element Nb (Ref 23).

Fig. 3
figure 3

Flow stress curves of the tested steel obtained under different strain rates (a) 0.01 s−1 (b) 0.1 s−1 (c) 1 s−1 and (d) 10 s−1

Full size image
Fig. 4
figure 4

Three types of the flow stress curves

Full size image

As shown in Fig. 4, the typical true strain-stress curves of DRX of the tested steel can be divided into two stages by critical strain εc. In stage I, the true stress increases rapidly with the increasing strain at initial deformation process and then the increasing rate decreases. This is because that the WH caused by the dislocation generation and multiplication is greater than the DRV caused by the dislocation climbing, sliding, and cross-slip. In stage II, the true stress is influenced by the interaction of WH, DRV, and DRX. At the beginning of this stage, the true stress increases to a peak stress with a decreased increasing rate. Because in this region, the WH is dominant until the balance of hardening and softening, including DRV and DRX, is reached. Then, the true stress gradually decreases to a steady value. The reason is that in this region the hardening is weaker than softening until a new balance of them is reached.

Constitutive Analysis of DRX Behavior

Zener-Hollomon Parameter and Hot Working Equation

Hot deformation of metals is a thermally activated process, and the flow stress is mainly affected by deformation temperature, strain rate, and stain. Recently, the Arrhenius equation is widely used to analysis the relationship between deformation temperature, strain rate, and flow stress, particularly at high temperature (Ref 24):

$$\dot{\upvarepsilon } = AF\left( \upsigma \right)\exp \left( {{{ - Q} \mathord{\left/ {\vphantom {{ - Q} {RT}}} \right. \kern-0pt} {RT}}} \right),$$
(1)

where

$$F\left( \upsigma \right) = \left\{ {\begin{array}{*{20}l} {\upsigma^{{n_{1} }} } \hfill & {\upalpha \upsigma < 0.8} \hfill \\ {\exp \left( {\upbeta \upsigma } \right)} \hfill & {\upalpha \upsigma > 1.2} \hfill \\ {\left[ {\sinh \left( {\upalpha \upsigma } \right)} \right]^{n} } \hfill & {{\text{for all }}\upsigma } \hfill \\ \end{array} } \right. ,$$

in which, \(\dot{\upvarepsilon }\) is the strain rate, Q is the activation energy of hot deformation, R is the universal gas constant, T is the absolute temperature, \(\upsigma\) is the flow stress, and A, α, β, n 1, and n are material constants, α = β/n 1.

The effects of the temperatures and strain rate on the deformation behaviors can be represented by Zener-Hollomon parameter (Z) in an exponential equation (Ref 25). Z parameter is written as follows:

$$Z = \dot{\upvarepsilon }\exp \left( {Q/RT} \right).$$
(2)

In order to determine the parameters in the equations, the peak stress is employed to the linear regression process. Equation 1 can be expressed as power law equation and exponential law equation at low and high stress levels, respectively. Then the following equations can be obtained,

$$\dot{\upvarepsilon } = A_{1} \upsigma_{\text{p}}^{{n_{1} }},$$
(3)
$$\dot{\upvarepsilon } = A_{2} \exp (\upbeta \upsigma_{\text{p}} ),$$
(4)

where A 1 and A 2 are material constant. Taking the logarithm of both sides of Eq 3 and 4, respectively, then Eq 5 and 6 can be gained,

$$\ln \dot{\upvarepsilon } = n_{1} \ln \upsigma_{\text{p}} + \ln A_{1},$$
(5)
$$\ln \dot{\upvarepsilon } = \upbeta \upsigma_{\text{p}} + \ln A_{2} .$$
(6)

Substituting the value σP and \(\dot{\upvarepsilon }\) into the Eq 5 and 6. Then the relationships between strain rate and stress can be obtained in Fig. 5. The value of β and n 1 can be obtained from the mean slopes of \(\ln \dot{\upvarepsilon }\) − σp and \(\ln \dot{\upvarepsilon }\) − lnσp, respectively. The value of β is 0.0915 MPa−1 and n 1 is 6.8195. So, the value of α is derived, α = β/n 1 = 0.01342 MPa−1.

Fig. 5
figure 5

The relationships of (a) \(\ln \dot{\upvarepsilon }\) − lnσp and (b) \(\ln \dot{\upvarepsilon }\) − σp

Full size image

The hyperbolic sine law of F(σ) has been verified that it can accurately describe hot deformation behavior at both low stress and high stress level (Ref 26, 27). Therefore, the following equations can be derived,

$$\dot{\upvarepsilon } = A\sinh \left( {\upalpha \upsigma_{\text{p}} } \right)^{n} \exp \left( { - Q/RT} \right).$$
(7)

By taking the logarithm of both sides of Eq 7 give

$$\ln \dot{\upvarepsilon } = \ln A + n\ln \left[ {\sinh \left( {\upalpha \upsigma_{\text{p}} } \right)} \right] - Q/RT.$$
(8)

Then the following equations can be derived,

$$\frac{1}{n} = \left[ {\frac{{\partial \ln \left[ {{\rm sinh}\left( {\upalpha \upsigma_{\text{p}} } \right)} \right]}}{{\partial \ln \dot{\upvarepsilon }}}} \right],$$
(9)
$$Q = Rn\left[ {\frac{{\partial \ln \left[ {{\rm sinh}\left( {\upalpha \upsigma_{\text{p}} } \right)} \right]}}{\partial (1/T)}} \right].$$
(10)

The relationships of \(\ln \dot{\upvarepsilon }\) − ln[sinh(ασP)] and ln[sinh(ασP)] − 1/T are shown in Fig. 6(a) and (b), respectively. It is easy to obtain the value of n and Q from the slops of the plots as 5.10 and 318.31 kJ/mol, respectively. Activation energy Q is an important material constant which can reflect the deformation difficulty degree in hot deformation. Medina and Hernandez (Ref 28) have investigated that the value of Q of 0.36C-Mn steel and C-Mn-0.043 V steel are 271 and 275 kJ/mol, respectively. And they are lower than the value of tested steel in this paper. This indicates that vanadium addition has no obvious effect on the activation energy, and the microalloyed element Nb can increase the activation energy dramatically. The reason may be that activation energy varied with atomic volumes of the microalloyed elements, which occupy substitutional sites (V V < V Nb). And the atomic radius of V is slightly greater than that of Fe, therefore, the influence of V is much lower than that of Nb.

Fig. 6
figure 6

The relationships of (a) \(\ln \dot{\upvarepsilon }\) − ln[sinh(ασp)] and (b) ln[sinh(ασp)] − 1/T

Full size image

According to the obtained parameters, the material constant A in Eq 1 is calculated as 6.9 × 1010. Then the hot working equation can be expressed as

$$\dot{\upvarepsilon } = 6.9 \times 10^{10} \sinh \left( {0.0134\upsigma_{\text{p}} } \right)^{5.10} \exp \left( { - 318310/RT} \right).$$
(11)

Critical Strain, Kinetics Model, and Microstructure of DRX

The critical strain of material is the prerequisite for the research of DRX. According to the previous researches (Ref 4, 14), the relationship between εc and Z is showed as below

$$\upvarepsilon_{c} = A_{3} Z^{k},$$
(12)

then substituting the values of εc obtained from the flow stress curves and Z into the Eq 12, and the relationship between critical strain and Z parameter can be obtained as shown in Fig. 7. It can be seen that the lnεc and lnZ relation is linear and the slop and interrupt of the regressed curve are 0.164 and 0.002997, respectively. So the relationship between εc and Z can be expressed as below

$$\upvarepsilon_{\text{c}} = 2.997{ \times }10^{ - 3} Z^{0.164}.$$
(13)
Fig. 7
figure 7

The relationship between lnεc and lnZ

Full size image

In this research, the modified Avrami equation (Ref 29-31) which incorporates an empirical time constant for 50% recrystallization t 0.5 is used to describe the DRX volume fraction X of the tested steel. The DRX volume fraction X is expressed as

$$X = 1 - \exp \left[ { - 0.693(t/t_{0.5} )^{{k_{\text{d}} }} } \right],$$
(14)
$$t_{0.5} = A_{4} \dot{\upvarepsilon }^{{A_{5} }} \exp \left( {\bar{Q}/RT} \right),$$
(15)

where t is the deformation time after the critical strain, and k d, A 4, A 5, and \(\bar{Q}\) are constants.

As seen from Fig. 3, DRX is an important softening mechanism. But it is difficult to determine the DRX volume fraction X by microstructural observations directly. In this research, the DRX volume fraction X is derived from the flow curves, which is defined as the following (Ref 32-35).

$$X = \frac{{\upsigma_{\text{p}} - \upsigma }}{{\upsigma_{\text{p}} - \upsigma_{\text{s}} }},$$
(16)

where σp is the peak stress and σs is the steady state stress. The σp − σs term represents the maximum achievable softening fraction, and the σp − σ represents the flow softening from peak to the stress of σ. Note that the effect of DRV on flow softening is not considered and the initiation of DRX is considered occurred from σp. This assumption simplifies the Avrami analysis with acceptable level of accuracy (Ref 36, 37).

Equations 14 and 15 can be written as Eq 17 and 18, respectively.

$$\ln [ - \ln \left( {1 - X} \right)] = \ln 0.693 + k_{\text{d}} \ln (t/t_{0.5} ),$$
(17)
$$\ln t_{0.5} = \ln A_{4} + A_{5} \ln \dot{\upvarepsilon } + \bar{Q}/RT.$$
(18)

The relationship between ln[−ln(1 − X)] and ln(t/t 0.5) is shown in Fig. 8. The value of k d can be determined by the linear slope of the curve as 2.012. Then, the values of A 4, A 5 and \(\bar{Q}\) can be obtained from the linear regression according to Eq 18. And the mean value of A 4, A 5, and \(\bar{Q}\) are 0.0257, −0.857 and 29315.62, respectively. So the kinetic model of DRX for the tested steel can be established as follows,

$$X = 1 - \exp \left[ { - 0.693\left( {{t \mathord{\left/ {\vphantom {t {t_{0.5} }}} \right. \kern-0pt} {t_{0.5} }}} \right)^{2.012} } \right],$$
(19)
$$t_{0.5} = 0.0257\dot{\upvarepsilon }^{ - 0.857} \exp (29315.62/RT).$$
(20)
Fig. 8
figure 8

Relationship between ln[−ln(1 − X)] and ln(t/t 0.5)

Full size image

Based on the derived DRX kinetic model, the effect of deformation temperature, strain rate, and strain on the DRX volume fraction X is shown in Fig. 9. It can be seen that with the true strain increasing X increases slowly at first and then the increasing rate gradually increased, and reduced in the end. Moreover, the increasing rate of X increases with increasing temperature and decreasing strain rate. Comparisons between predicted and experiment results are also presented. The predicted results agree with experimental ones, which indicate that the developed model can give a accurate results of DRX of the tested steel.

Fig. 9
figure 9

Experimental and predicted DRX volume fraction X with strain rate of (a) 0.01 s−1 and (b) 0.1 s−1

Full size image

Some researchers have verified that the DRX grain size is influenced by Z parameter. The DRX grain size increases with the decreasing Z, i.e., the DRX grain size increases with the increasing deformation temperature and decreasing strain rate. Figure 10 and 11 show the recrystallized austenite grain size after hot isothermal compression at different conditions. It can be seen that the DRX grain size increases from strain rate of 1-0.01 s−1 with the same temperature of 1373 K, and the DRX grain size increases obviously with the increasing of temperature with the same strain rate of 1 s−1. In order to model the dependence of the grain size on Z parameter, the following equation is used,

$$D_{\text{s}} = BZ^{ - k}.$$
(21)
Fig. 10
figure 10

The recrystallized austenite grain size after hot isothermal compression at the temperature of 1373 K and strain rates of (a) 1 s−1 (b) 0.1 s−1 and (c) 0.01 s−1

Full size image
Fig. 11
figure 11

The recrystallized austenite grain size after hot isothermal compression at the strain rate of 1 s−1 and temperatures of (a) 1423 K and (b) 1473 K

Full size image

Although regression analysis, as shown in Fig. 12, the value of B and k can be obtained as 12751.222 and 0.211. So the DRX grain size model can be expressed as below,

$$D_{\text{s}} = 12751.222Z^{ - 0.211} .$$
(22)
Fig. 12
figure 12

The relationship between lnD s and lnZ

Full size image

Constitutive Analysis of Flow Stress Behavior

The flow stress in steel during hot temperature has two softening mechanisms: dynamic recovery (DRV) and dynamic recrystallization (DRX). When the strain fails to reach the critical strain, DRV is the only softening mechanism. When the strain exceeds the critical strain, DRX occurs (Ref 22, 38).

When no DRX occurring, the dislocation density supposed to be the coupled effects of generation by WH and annihilation by DRV. The dependence of the dislocation density on strain can be written as follows:

$$\frac{d\uprho }{d\upvarepsilon } = U - \Upomega \uprho ,$$
(23)

where ρ is the dislocation density, and U and Ω are the parameters related to the strain that represent the work hardening and softening terms, respectively.

The relationship between flow stress and dislocation density can be described as follows (Ref 39):

$$\upsigma = \upalpha \upmu b\sqrt \uprho ,$$
(24)

where α, μ, and b are constants with the value of 0.7, 8.1 × 104, and 2.6 × 10−10, respectively.

Utilizing Eq (23) and (24), the constitutive equation for flow stress during DRV process can be obtained:

$$\upsigma_{r} = [(\upalpha \upmu b)^{2} \uprho_{0} e^{ - \Upomega \upvarepsilon } + (\upalpha \upmu b)^{2} (U/\Upomega ) ( 1 { - }e^{ - \Upomega \upvarepsilon } )]^{0.5} ,$$
(25)

where σr is the flow stress during DRV process, ρ0 is the initial dislocation density, 1.0 × 10−12 m−2.

The parameters Ω and (αμb)2 U are depends on the deformation temperature and strain rate, the following typical equation are used to describe the relationships:

$$\Upomega = A_{\Upomega } \dot{\upvarepsilon }^{{{\text{m}}_{\Upomega } }} exp( - Q_{\Upomega } /RT),$$
(26)
$$(\upalpha \upmu b)^{2} U = A_{U} \dot{\upvarepsilon }^{{m_{U} }} exp\left( {{{Q_{U} } \mathord{\left/ {\vphantom {{Q_{U} } {RT}}} \right. \kern-0pt} {RT}}} \right).$$
(27)

In order to regress the constants in Eq 26 and 27, several groups of stress and strain values were obtained from the flow stress curves. Although multiple linear regression, the values of A Ω, m Ω, and Q Ω are 280, −0.1, and 35966.4 J/mol. The values of m U and Q U /R are the slopes of the plots in the ln[(αμb)2 U] versus ln \(\dot{\upvarepsilon }\) and ln[(αμb)2 U] versus 1/T, as shown in Fig. 13(a) and (b). Then the values of A U , m U , and Q U can be obtained as 344.5, 0.19, and 63269.5 J/mol.

Fig. 13
figure 13

The relationship between ln[(αμb)2 U] and ln\(\dot{\upvarepsilon }\)(a); ln[(αμb)2 U] and 1/T (b)

Full size image

When DRX occurring, dislocation density decreases with the DRX fraction increasing. The flow stress can be described as following:

$$\upsigma_{\text{d}} = \sqrt {\upsigma_{\text{r}}^{2} - X\left( {\upsigma_{\text{r}}^{2} - \upsigma_{\text{ss}}^{2} } \right)} ,$$
(28)

where σd is the flow stress during the DRX period. σss is the stead state stress after DRX. The stead state stress can be defined as following:

$$\upsigma_{\text{ss}} = A_{\text{ss}} \left[ {\dot{\upvarepsilon }\exp \left( {Q_{\text{ss}} /RT} \right)} \right]^{{m_{\rm ss} }} ,$$
(29)

where A ss, m ss, and Q ss are constants, and they can be regressed by the experimental data. The values of A ss, m ss, and Q ss are 0.938, 0.172, and 301.4 kJ/mol, respectively.

Then, the constitutive equation for DRV can be obtained as follows:

$$\upsigma_{\text{r}} = [217.3\exp ( - \Upomega \upvarepsilon ) + 1.23 \times \dot{\upvarepsilon }^{0.29} {\text{exp(11937/T)(1}} - \exp ( - \Upomega \upvarepsilon )]^{0.5} .$$
(30)

The constitutive equation for DRX can be obtained as follows:

$$\upsigma_{\text{d}} = \left\{ \begin{aligned} \upsigma_{\text{r}} \, \upvarepsilon \le \upvarepsilon_{c} \hfill \\ \sqrt {\upsigma_{\text{r}}^{2} - X(\upsigma_{\text{r}}^{2} - 0.88 \times \dot{\upvarepsilon }^{0.344} exp\left( {{{301440} \mathord{\left/ {\vphantom {{301440} {RT}}} \right. \kern-0pt} {RT}}} \right)^{0.344} } \, \upvarepsilon \text{ > }\upvarepsilon_{c} \hfill \\ \end{aligned} \right.$$
(31)

In order to evaluate the accuracy of the developed constitutive equation in predicting the flow stress during hot deformation, standard statistical parameters of correlation coefficient (R) is used to quantify the predictability of the constitutive equation. It can be expressed as:

$$R = \frac{{\sum\nolimits_{i = 1}^{N} {\left( {E_{i} - \overline{E} } \right)\left( {P_{i} - \overline{P} } \right)} }}{{\sqrt {\sum\nolimits_{i = 1}^{N} {\left( {E_{i} - \overline{E} } \right)^{ 2} \sum\nolimits_{i = 1}^{N} {\left( {P_{i} - \overline{P} } \right)^{ 2} } } } }},$$
(32)

where E i is the experimental data and P i is the predicted value obtained from the constitutive equation. \(\bar{E}\) and \(\bar{P}\) are the mean values of E and P, respectively. N is the total number of data employed in the investigation. As is shown in Fig. 14, a good correlation (R = 0.973) is obtained, which indicates that the developed constitutive equation is appropriate to predict the flow stress of the steel during hot deformation.

Fig. 14
figure 14

Correlation between the experimental and predicted flow stress data

Full size image

Conclusions

Isothermal hot compression experiments of a medium carbon Nb-V microalloyed steel were performed in a wide range of temperatures (1123-1473 K) and strain rates (0.01-10 s−1). DRX behavior and constitutive equation of flow stress of the tested steel was carried out. The following conclusions can be obtained:

  1. (1)

    Deformation temperature and strain rate have great influence on flow stress of the steel. The flow stress increases with the increase of strain rate and the decrease of temperature. All the flow curves obtained can be ranged into three principal types: WH, characterized by increasing stress with strain; DRV, characterized by saturation stress with increasing strain; and DRX, characterized by an observed peak stress.

  2. (2)

    The hot working equation of the tested steel was obtained as \(\dot{\upvarepsilon } = 6.9 \times 10^{10} \sinh \left( {0.0134\upsigma_{\text{p}} } \right)^{5.10} \exp \left( { - 318310/RT} \right).\) Activation energy Q is calculated as 318.310 kJ/mol which is higher than C-Mn steel and V microalloyed steel due to the addition of microalloyed element Nb.

  3. (3)

    The DRX behavior of the tested steel was investigated. The relationship of critical strain on Z was obtained as \(\upvarepsilon_{c} = 2.997{ \times }10^{ - 3} Z^{0.164}.\) The kinetics model was developed as \(X = 1 - \exp [ - 0.693(t/t_{0.5} )^{2.012} ],\) \(t_{0.5} = 0.02566\dot{\upvarepsilon }^{ - 0.857} \exp (29315.62/RT),\) and the predicted DRX volume fraction X agree with experimental ones. The relationship of DRX grain size D s on Z was obtained as \(D_{\rm s} = 12751.222Z^{ - 0.211}.\)

  4. (4)

    Constitutive equation for flow stress of the tested steel was established. The correlation coefficient R of the experimental and predicted flow stress is 0.973 which indicates that the developed constitutive equation can accurately predict the flow stress of tested steel.