A Stochastic Multi-layer Algorithm for Semi-discrete Optimal Transport with Applications to Texture Synthesis and Style Transfer

Abstract

This paper investigates a new stochastic algorithm to approximate semi-discrete optimal transport for large-scale problem, i.e., in high dimension and for a large number of points. The proposed technique relies on a hierarchical decomposition of the target discrete distribution and the transport map itself. A stochastic optimization algorithm is derived to estimate the parameters of the corresponding multi-layer weighted nearest neighbor model. This model allows for fast evaluation during synthesis and training, for which it exhibits faster empirical convergence. Several applications to patch-based image processing are investigated: texture synthesis, texture inpainting, and style transfer. The proposed models compare favorably to the state of the art, either in terms of image quality, computation time, or regarding the number of parameters. Additionally, they do not require any pixel-based optimization or training on a large dataset of natural images.

1 Introduction

Since its original formulation by Monge [38], the theory of optimal transportation has been very widely developed [52, 63] and has found many applications in computational sciences [45]. Given two probability distributions $\mu$ (source) and $\nu$ (target), the optimal transport (OT) problem consists in finding a way to transfer the source mass $\mu$ onto the target mass $\nu$ while minimizing a transportation cost. The solution then defines a distance between $\mu$ and $\nu$ that is truly sensitive to the distances in the underlying spaces. Thus, OT provides a natural way to compare probability distributions.

Therefore, OT has been used for numerous applications in imaging science. First, applying OT in the color space permits to evaluate the distance between the color distributions of two images, which was used in [51] for image retrieval. The corresponding OT maps provide candidates to transfer the colors from one image to the other, but must be regularized to produce the visually plausible results [48]. Similarly, from two images, one can transfer the colors to a kind of averaged color distribution, which was coined as midway image equalization in [7]. Both problems of color transfer and color equalization have found a variational formulation in [44]. In these color applications, the transport maps act on a three-dimensional space for RGB images and on a one-dimensional space for gray-level images. Even before that, a one-dimensional OT distance was used to compare angular descriptors identified as probability distributions on the circle, in order to address image matching [47].

In a higher-dimensional setting, several authors propose to use OT distances to compare images identified as probability distributions. For example, a Kantorovich–Rubinstein norm was used in the data-fidelity term for image denoising in [30]. Transportation maps acting on images can then be used to perform image warping [1, 12, 22, 35, 43], which is relevant for images that reflect some kind of density of material. Notice that similar tools can also be used to process shapes identified as probability distributions which allows to perform shape interpolation [57] and shape registration [10] with applications in brain imaging [11].

Several other imaging applications require to use optimal transport in a feature space. Indeed, gathering several features defined around a pixel gives information on the regularity or textural aspect of the image in the neighborhood. Such a point of view was already developed in [51] for image retrieval. The authors of [49] proposed to address image segmentation by constraining the distribution of features (color and derivatives norms) in the segmented regions. More generally, it is possible to use OT distances between feature distributions, or even image distributions, for texture modeling. In [64], the OT distance between Gaussian texture models was related to the distance between Fourier transform modulii, which led to an elegant formulation of Gaussian texture mixing. The authors of [58] proposed to use OT distances between distributions of linear and nonlinear features (e.g., wavelet responses or dictionary-based features) to address texture synthesis and restoration. In the present paper, considering that the textural aspect is encoded in the patch distribution, we will exploit OT between patch distributions to address texture synthesis.

A common bottleneck with many imaging applications of the OT framework is that, except in one dimension, solving an OT problem is usually difficult and computationally expensive. Indeed, in the case of two discrete distributions, the OT problem is equivalent to a linear programming problem. If the distributions support have the same number of points n, this problem can be solved with the Hungarian algorithm [28] which has complexity $\mathcal {O}(n^3)$ and thus scales quite badly with n. One possibility to overcome this numerical issue is to add an entropic penalization in the OT problem, leading to the definition of Sinkhorn distances [6, 27, 50]. Such regularized OT distances can be computed with a fixed point algorithm that is geometrically convergent. However, for some imaging applications, the entropic regularization may deteriorate the OT plan. And besides, the computational gain is only available for the case of two discrete distributions with n points, whereas for high-dimensional OT problems, the discretization of the underlying space is prohibited (representing 100-dimensional distributions with ten bins in each direction would require to store a discrete vector of size $10^{100}$).

In this paper, we will focus on the semi-discrete case of OT, meaning that the source distribution $\mu$ is assumed to have a density with respect to the Lebesgue measure, while the target distribution $\nu$ is discrete. The authors of [2] have shown that in this case, the OT map takes the form of a weighted nearest neighbor (NN) assignment where the weight parameters solve a differentiable concave optimization problem. Since [2], several numerical solutions have been proposed to solve the semi-discrete OT problem [25, 26, 31, 37], but they often require the exact computation of a gradient which amounts to computing the $\mu$-measure of polytopes. In a high-dimensional setting, computing such integrals may be intractable. Thus, one may turn to stochastic gradient algorithms to approximate the OT maps, as proposed in [19] and later studied in [3]. But when the number J of points in the target distribution is large, this stochastic algorithm converges slowly [15].

A classical way to improve the practical convergence of optimization methods is to exploit a multiscale representation of the data. For which concerns optimal transport, numerous multiscale strategies have already been proposed which essentially consists in working on simplified versions of the measures $\mu$ and $\nu$. Several authors [5, 21, 42] have proposed to discretize the measures on a grid and then use a grid refinement strategy to target the true OT map. They propose different arguments to demonstrate the stability of the refined transport plans (which exploits directly or indirectly the sparsity of the true OT plan when $\mu$ and $\nu$ are absolutely continuous). In the case of large-scale discrete OT, the author of [53, 54] proposed multiscale algorithms for unregularized and regularized OT problems that exploit a hierarchical representation of the supports of the source and target distributions in order to drastically diminish the number of variables in the dual formulation of OT. This coarse-to-fine strategy was also used in [11] to accelerate computations on very large datasets. However, for semi-discrete OT in a high-dimensional setting, these multiscale schemes are hardly tractable.

Another strategy is to consider a multiscale decomposition $(\nu ^{\ell })_{0 \leqslant \ell < L}$ of the measure $\nu$, meaning that $\nu ^{\ell }$ is an approximation of $\nu$ with a fixed budget of $J^{\ell }$ points, $J^0> J^1> \cdots > J^{L-1}$ (and similarly for the source $\mu$). This approach was proposed in [37] to solve richer and richer semi-discrete OT problem by initializing the optimization algorithm at one scale with an extrapolation of the solution at the previous scale. A similar approach (with decomposition of both the source and target measures) was followed by [20] to solve large-scale discrete OT problems.

In this paper, we propose a different multiscale approach to approximately solve the semi-discrete OT problem. The main idea is to consider so-called multi-layer transport maps that can be roughly understood as a composition of weighted NN assignments that solve restricted OT problems between $\mu$ and the simplified measures $\nu ^{\ell }$ (obtained with a hierarchical clustering of $\nu$ at different resolutions). In general, such a multi-layer transport map may not exactly solve the OT problem because a simple weighted NN assignment may not be decomposed as a multi-layer map. In other words, restricting to such multi-layer maps induces a bias that can be related to the geometry of the hierarchical clustering of $\nu$. However, optimizing such a multi-layer transport map amounts to solving many semi-discrete OT problems with much smaller target distributions. For that reason, when using stochastic algorithms for semi-discrete OT, we demonstrate that nearly optimal cost can be attained in a faster way with multi-layer transport maps (even if the total number of parameters of a multi-layer map is slightly larger than a weighted NN assignment).

Such a multi-layer approach thus helps to efficiently solve high-dimensional semi-discrete OT problems linked to imaging applications. In particular, we will be able to improve a texture model [15] based on semi-discrete OT in the patch space. The initial model presented in [15] was limited to target distributions of 1000 patches of size $3 \times 3$. Using multi-layer transport maps will allow to consider richer distributions of patches with larger size, thus enriching the class of well-reproduced texture. We will see that these new texture models can also be used for texture inpainting and style transfer.

The rest of the paper is organized as follows. In Sect. 2, we recall the framework of semi-discrete optimal transport. Section 3 is devoted to multi-layer transport maps. First, we define multi-layer transport maps and analyze their optimality conditions. And then, we propose a stochastic algorithm to optimize multi-layer transport maps and examine its behavior on a simple one-dimensional example. In Sect. 4, we demonstrate that such multi-layer transport maps can be used to improve a texture model based on semi-discrete OT. We also show that this texture model can be used to address textural inpainting. Finally, in Sect. 5, we propose to extend the framework used in texture synthesis to address style transfer. Let us mention that a preliminary version of this work has been published as a conference paper [29]. Compared to the conference version, we contributed with a more thorough study of optimality conditions for multi-layer transport maps, a more extensive study of the performance of these models in texture synthesis and new applications on textural inpainting and style transfer. The experiments shown in this paper can be reproduced with the MATLAB implementation available at https://www.math.u-bordeaux.fr/~aleclaire/texto/multilayer.php.

2 Semi-discrete Optimal Transport

Let ${\mu , \nu }$ be two probability measures on $\mathbb {R}^D$. For the sake of simplicity, we will restrict to the case of the quadratic cost, even if some of the concepts developed in this paper could be used with other cost functions. For the quadratic cost, Monge’s formulation of OT consists in solving

$$\begin{aligned} \inf _T \int _{\mathbb {R}^D} \Vert x - T(x)\Vert ^2 \mathrm{d}\mu (x) , \end{aligned}$$

(OT-M)

where the infimum is taken over all measurable functions $T : \mathbb {R}^D \rightarrow \mathbb {R}^D$ for which $T_{\sharp } \mu = \nu$, where $T_{\sharp } \mu$ is the push-forward measure defined by $T_{\sharp }\mu (A) = \mu (T^{-1}(A))$ for every Borel set $A \subset \mathbb {R}^d$. The Monge problem admits a convex relaxation due to Kantorovich

$$\begin{aligned} W^2(\mu ,\nu ) = \inf _{\varPi } \int _{\mathbb {R}^D \times \mathbb {R}^D} \Vert x - y\Vert ^2 \mathrm{d}\varPi (x,y) , \end{aligned}$$

(OT-K)

where the infimum is taken on all probability distributions $\varPi$ on $\mathbb {R}^D \times \mathbb {R}^D$ with marginal $\mu , \nu$. If (OT-M) admits a solution T, then $(\mathrm {Id} \otimes T)_{\sharp } \mu$ is a solution to (OT-K). But the Kantorovich problem is more general in the sense that they may exist no map T such that $T_{\sharp } \mu = \nu$. Besides, under some conditions (that will be satisfied in the semi-discrete case), one can show that (OT-M) admits a solution which is uniquely defined almost everywhere. In such a case, the solution will be denoted by $T^*$. We refer the reader to the books [52, 63] for an exhaustive presentation of the OT framework.

In this paper, we only consider the semi-discrete case of optimal transportation. Indeed, we assume that $\mu$ is absolutely continuous with respect to the Lebesgue measure on $\mathbb {R}^D$ with density $\rho$ and that $\nu$ is supported on a finite set Y

$$\begin{aligned} \nu = \sum _{y \in Y} \nu (y) \delta _{y} . \end{aligned}$$

(1)

As proved in [2, 26, 31], the solution of (OT-M) has the form of a weighted NN assignment. Indeed, for $v \in \mathbb {R}^Y$, one can define $T_{Y,v}$ by

$$\begin{aligned} T_{Y,v}(x) := \mathop {\mathrm{argmin}}_{y \in Y} \Vert x - y \Vert ^2 - v(y) . \end{aligned}$$

(2)

This map is defined almost everywhere (i.e., at all points where the previous argmin is uniquely defined). The preimages

$$\begin{aligned} \mathcal {L}_v(y) = T_{Y,v}^{-1}(\{y\}) \end{aligned}$$

(3)

are called the Laguerre cells and form a partition of $\mathbb {R}^D$ up to a negligible set called the Laguerre tessellation (or also power diagram).

Then, it is known [2, 26] that $T_{Y,v}$ is a solution of (OT-M) as soon as v maximizes the concave function

$$\begin{aligned} H(v) := \mathbb {E}_{X \sim \mu } \left[ h(X,v) \right] \end{aligned}$$

(4)

where

$$\begin{aligned} h(x,v) = \left( \min _{y \in Y} \Vert x-y\Vert ^2 - v(y) \right) + \sum _{y \in Y} v(y) \nu (y) . \end{aligned}$$

(5)

One can see that for all $v \in \mathbb {R}^J$ and for almost all $x \in \mathbb {R}^D$,

$$\begin{aligned} \partial _{v(y)} h(x,v) = - \mathbb {1}_{\mathcal {L}_v(y)}(x) + \nu (y) \end{aligned}$$

(6)

where $\mathbb {1}_{\mathcal {L}_v(y)}$ is the indicator function of $\mathcal {L}_v(y)$, and that

$$\begin{aligned} \partial _{v(y)} H(v)&= \mathbb {E}_{X \sim \mu } \left[ \partial _{v(y)} h(X,v)\right] \nonumber \\&= -\mu (\mathcal {L}_v(y)) + \nu (y) . \end{aligned}$$

(7)

Several authors [2, 26, 31, 37] have proposed exact gradient-based methods or quasi-Newton schemes in order to optimize the weights v when the distributions $\mu$ and $\nu$ are defined on $\mathbb {R}^D$ for $D=2$ or $D=3$ dimensions, in cases where the $\mu$-measure of the Laguerre cells needed in (7) is tractable. However, in a high-dimensional framework where such integrals are not tractable, one may turn to the average stochastic gradient descent (ASGD) Algorithm 1 to solve it. One can show [3, 15, 19] that this algorithm has a convergence guarantee in $\mathcal {O}(\frac{\log k}{\sqrt{k}})$ (in expectation). Numerical experiments also confirm its slow convergence rate, especially when the number J of points in the target distribution gets very large.

3 Multi-layer Semi-discrete Transport Maps

In order to cope with the slow convergence of the stochastic algorithm used to estimate the semi-discrete OT map, we propose to approximate the optimal map with hierarchical applications of several weighted NN assignments that are tuned to solve simpler semi-discrete OT problems (i.e., with smaller target distributions). These smaller problems are related to a multiscale decomposition $\nu ^{0}, \ldots , \nu ^{L-1}$ of the target measure, that is, a collection of measures that “summarizes” $\nu$ from fine ($\ell =0$) to coarse ($\ell = L$) resolution.

As already mentioned in the introduction, a multiscale algorithm for semi-discrete OT has already been proposed in [37]. However, as reported in [29] and illustrated in experimental Sect. 3.6, it is not straightforward to design an “upscaling” scheme that gives a good initial guess for the variable v at one scale from the solution found at the previous scale. In the following, we thus propose a new strategy which consists in:

• 1. modeling the OT map itself as a multiscale hierarchical operator;

• 2. optimizing at all scales simultaneously.

In order to avoid confusion with aforementioned multiscale techniques, we refer to the proposed hierarchical model as a multi-layer transport map.

3.1 Decomposition of the Target Measure

In all this section, we will work with a decomposition

$$\begin{aligned} \nu ^{0}, \ldots , \nu ^{L-1}, \nu ^L \end{aligned}$$

(8)

of the target measure. By convention, $\nu ^0=\nu$ and $\nu ^L$ will be supported on a singleton, so that there are only L non-trivial scales. At scale $\ell \in \{0, \ldots , L\}$, we will use a measure

$$\begin{aligned} \nu ^{\ell } = \sum _{y \in Y^{\ell }} \nu ^{\ell }(y) \delta _{y} \end{aligned}$$

(9)

supported by a finite set $Y^{\ell }$ of cardinal $J^{\ell }$ (which is a prescribed budget of points at scale $\ell$, with $J^0 = J$, and $J^L = 1$).

Following [37], this decomposition is built recursively: the measure $\nu ^{\ell +1}$ should be a close approximation of $\nu ^{\ell }$ with a budget of $J^{\ell +1}$ points. More precisely, given $\nu ^{\ell }$, $\nu ^{\ell +1}$ is built as an approximate solution of

$$\begin{aligned} \min _{m} W^2(\nu ^{\ell },m) \end{aligned}$$

(10)

where the min is taken on all discrete measures m on $\mathbb {R}^D$ whose support has $J^{\ell +1}$ points.

This non-convex problem is known to be equivalent to a weighted K-means problem, which we approximately solve with Lloyd’s algorithm. At the end of this algorithm, we get a set $Y^{\ell +1} \subset \mathbb {R}^D$ of $J^{\ell +1}$ centroids corresponding to a partition

$$\begin{aligned} Y^\ell = \bigsqcup _{y \in Y^{\ell +1}} C_y^{\ell } \end{aligned}$$

(11)

and the associated masses

$$\begin{aligned} \forall \, y \in Y^{\ell +1}, \quad \nu ^{\ell +1}(y) = \nu ^\ell (C_y^\ell ). \end{aligned}$$

(12)

Additionally, we consider normalized distributions per cluster

$$\begin{aligned} \forall \, y \in Y^{\ell +1} , \forall \, z \in C_y^\ell \quad {\tilde{\nu }}_y^{\ell }(z) = \frac{\nu _y^{\ell }(z)}{\nu _y^{\ell }(C^{\ell }_y)}. \end{aligned}$$

(13)

With the convention $J^L = 1$, the clustering of $Y^{L-1}$ is trivial with only one cluster, and the corresponding centroid (the only point of $Y^L$) is the $\nu ^{L-1}$-barycenter of $Y^L$.

An illustration of such a multiscale decomposition is given in Fig. 1. Let us emphasize that the previous decomposition algorithm (based on K-means) can be called hierarchical in the sense that there exists a tree structure on the elements of the sets $Y^{\ell }$, (Each $y \in Y^{\ell }$ has exactly one parent in $Y^{\ell +1}$.) This hierarchical structure will be crucial for the construction of multi-layer transport maps.

Fig. 1

Illustration of the multiscale approximation of the discrete target distribution $\nu$ in the 1D case and the multi-layer transport map T(x) applied sequentially with $L=3$ layers. See the text for more details about notation

3.2 Multi-layer Transport Maps

Now, we can define multi-layer transport maps by using a hierarchical tree search based on weighted NN assignments.

Definition 1

Let us denote by $\mathbf {Y}$ the hierarchical clustering of Y composed of the sets $(Y^0, Y^1, \ldots , Y^L)$ and the clusters $(C_y^{\ell })_{0 \leqslant \ell < L, y \in Y^{\ell +1}}$ satisfying (11). Let us also consider the multi-layer parameters

$$\begin{aligned} \mathbf {v}= {\left( v^{\ell }_y \right) }_{0\leqslant \ell < L, y \in Y^{\ell }} \in \prod _{\ell =0}^{L-1} \mathbb {R}^{Y^{\ell }} . \end{aligned}$$

(14)

Then, we can define a multi-layer map $T_{\mathbf {Y},\mathbf {v}}$ recursively as follows. Let us fix $x \in \mathbb {R}^d$. We set $T^{L}(x) = y^L$ (only point in $Y^{L}$). And then, for $\ell = L-1, \ldots , 0$, denoting $y = T^{\ell +1}(x)$, we set

$$\begin{aligned} T^{\ell }(x) = T_{C_y^{\ell },v_y^{\ell }}(x) = \mathop {\mathrm{argmin}}_{z \in C_y^{\ell }} \Vert x-z\Vert ^2 - v_y^{\ell }(z) . \end{aligned}$$

(15)

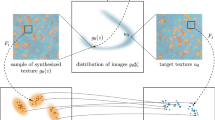
Then, $T_{\mathbf {Y},\mathbf {v}}(x) = T^0(x)$ (Fig. 2).

Fig. 2

Illustration of a multi-layer map ( for $L=2$ layers). Here the source distribution $\mu$ is chosen to be a Gaussian mixture model with 4 components (in gray levels). For each layer $\ell$, the arrows illustrate $T^{\ell }(x)$ (arrows) the multi-layer mapping of samples x drawn from $\mu$ (circle points on the left) to the points of the discrete distribution $\nu ^\ell$ (diamonds for layer $\ell =1$ and square for layer $\ell = 0$)

3.3 Optimal Multi-layer Maps

Let $T_{\mathbf {Y},\mathbf {v}}$ be a multi-layer map, and we recall the definition $T^{\ell }$ ($\ell = L, \ldots , 0$) of the intermediate maps. Notice that applying these intermediate maps at a point x amounts to tracing back a hierarchy of Laguerre cells to which x belongs. Therefore, the sets ${\mathcal {L}^{\ell }_y = (T^{\ell })^{-1}(\{y\})}$ provide a decomposition

$$\begin{aligned} \mathbb {R}^D = \bigsqcup _{y \in Y^{\ell }} \mathcal {L}^{\ell }_y \end{aligned}$$

(16)

which is a partition up to a negligible set. These subsets are obtained by intersecting Laguerre cells in a nested way; therefore the $\mathcal {L}_y^{\ell }$ will be called the nested cells.

In the following, we denote by $\mu _{|A}$ the restriction of the measure $\mu$ to the Borel set A.

Definition 2

A multi-layer map $T_{\mathbf {Y},\mathbf {v}}$ associated with the hierarchical clustering $\mathbf {Y}$ is said to be optimal if, for all $0 \leqslant \ell < L$ and all $y \in Y^{\ell +1}$, $T_{C_y^{\ell },v_y^{\ell }}$ realizes the semi-discrete OT from $\mu _{|\mathcal {L}_y^{\ell +1}}$ to $\nu ^{\ell }_{|C_y^{\ell }}$.

Remark

Let us emphasize that this optimality condition must be understood in a coarse to fine manner. Indeed, for a given scale $0 \leqslant \ell < L$, the conditions $\mu (\mathcal {L}_y^{\ell +1}) = \nu ^{\ell }(C_y^{\ell })$, i.e., $\mu (\mathcal {L}_y^{\ell +1}) = \nu ^{\ell +1}(y)$ are ensured for all $y \in Y^{\ell +1}$ if and only the map $T^{\ell +1}$ realizes the semi-discrete OT at the previous scale. By uniqueness of optimal semi-discrete OT maps, it follows that there exists a unique optimal multi-layer map (up to a $\mu$-negligible set).

Alternately, for a given nested cell ${\mathcal {L}_y^{\ell +1}, y \in Y^{\ell +1}}$ at the previous scale, one can consider the normalized measure

$$\begin{aligned} {\tilde{\mu }}_y^{\ell +1} = \frac{\mu _{|\mathcal {L}_y^{\ell +1}}}{\mu (\mathcal {L}_y^{\ell +1})} . \end{aligned}$$

(17)

Then, from the last remark, we get that a multi-layer map $T_{\mathbf {Y},\mathbf {v}}$ is optimal if and only if for all $0 \leqslant \ell < L$ and all $y \in Y^{\ell +1}$, $T_{C_y^{\ell },v_y^{\ell }}$ realizes the semi-discrete OT from ${\tilde{\mu }}_y^{\ell +1}$ to ${\tilde{\nu }}_y^{\ell }$.

Fig. 3

Bias due to the hierarchical clustering. In this figure, we illustrate the bias which is induced by the hierarchical clustering and quantized by (27). Here, $\mu$ is the uniform distribution on the largest square, and $\nu$ the discrete uniform distribution on the eight blue crosses. The red points form a possible clustering at level 1. We draw the optimal Laguerre cells with blue boundaries and the optimal Laguerre cells at level 1 with red boundary. For the very particular case of the left diagram, the OT map is exactly the optimal multi-layer map. However, on the right diagram, the hierarchical induces a bias at level 1 that can be measured by the area of the region colored in green (Color figure online)

It is also possible to express the optimality of multi-layer maps in terms of the variables $\mathbf {v}$: For all $0 \leqslant \ell < L$ and all $y \in Y^{\ell +1}$, the weights $v_y^{\ell }$ should maximize the function

$$\begin{aligned} H_y^{\ell }(v_y^{\ell })&= \int _{\mathcal {L}_y^{\ell +1}} \min _{z \in C_y^{\ell }} (\Vert x-z\Vert ^2 - v_y^{\ell }(z)) \mathrm{d}\mu (x) \nonumber \\&\quad + \sum _{z \in C_y^{\ell }} v_y^{\ell }(z) \nu ^{\ell }(z) \end{aligned}$$

(18)

Notice that the weights $\mathbf {v}$ should solve, at each layer $\ell$, $J^{\ell +1}$ subproblems of semi-discrete OT where the nested cells $\mathcal {L}_y^{\ell +1}$ intervene.

Proposition 1

The multi-layer map $T_{\mathbf {Y},\mathbf {v}}$ solves the semi-discrete OT problem between $\mu$ and $\nu$ if and only if

$$\begin{aligned} \forall y \in Y, \quad \mathcal {L}_y^0 = (T^*)^{-1}(\{y\}) \end{aligned}$$

(19)

up to a $\mu$-negligible set. In this case, at each scale $\ell$, all the nested cells $\mathcal {L}_y^{\ell }$ can be written as a reunion of Laguerre cells associated with the OT map $T^*$, up to a $\mu$-negligible set.

Proof

First of all, let us recall that with the adopted assumptions on $\mu$, the OT map $T^*$ is uniquely defined $\mu$-almost everywhere. It follows that $T_{\mathbf {Y},\mathbf {v}} = T^*$ a.e. is equivalent to (19). The last statement holds because, by construction of the maps $T^{\ell }$, for all $0 \leqslant \ell < L$ and all $y \in Y^{\ell +1}$,

$$\begin{aligned} \mathcal {L}_y^{\ell +1} = \bigcup _{z \in C_y^{\ell }} \mathcal {L}_z^{\ell } . \end{aligned}$$

(20)

$\square$

One practical consequence of Proposition 1 is that, if $T_{\mathbf {Y},\mathbf {v}}$ is optimal, then the boundary of a nested cell $\mathcal {L}_y^{\ell }$ is included in the reunion of boundaries of $(T^*)^{-1}(\{z\})$ for all $z \in Y$ that are children of y. But, except for very particular cases (see Fig. 3), this has no reason to happen because each face composing the boundary of $\mathcal {L}_y^{\ell }$ is orthogonal to one of the segments joining two points of $Y^{\ell }$. Therefore, the geometry of the partition $(\mathcal {L}_y^{\ell })_{y \in Y^{\ell }}$ at scale $\ell$ is very much impacted by the positions of the centroids $y \in Y^{\ell }$. In other words, the choice of hierarchical clustering imposes a bias that cannot be coped with by the optimization of the weights $\mathbf {v}$.

In dimension $D=1$, the situation is much simpler, as shown by the next proposition.

Proposition 2

Assume that the dimension $D=1$. Let us also assume that the hierarchical clustering is increasing in the following sense: For all $0 \leqslant \ell < L$, for all $y_1,y_2 \in Y^{\ell +1}$ such that $y_1<y_2$ then we have $z_1<z_2$ for all $z_1 \in C_{y_1}^{\ell }$ and $z_2 \in C_{y_2}^{\ell }$. Then, the optimal multi-layer map realizes the semi-discrete OT from $\mu$ to $\nu$.

Proof

Let us show by induction on $\ell =L-1, \ldots , 0$ that $T^{\ell }$ is non-decreasing and realizes the semi-discrete OT between $\mu$ and $\nu ^{\ell }$. By Definition 2 and since there is only one point in $Y^L$ (for which $\mathcal {L}_y^L = \mathbb {R}^D$ and $C_y^{L-1} = Y$), $T^{L-1}$ is the OT map between $\mu$ and $\nu ^{L-1}$. Next, assume that $T^{\ell +1}$ is non-decreasing and realizes the OT between $\mu$ and $\nu ^{\ell +1}$. Again, from Definition 2, and for all $y \in Y^{\ell +1}$, on $\mathcal {L}_y^{\ell +1}$, $T^{\ell }$ coincides with $T_{C_y^{\ell },v_y^{\ell }}$ which realizes the OT from $\mu _{|\mathcal {L}_y^{\ell +1}}$ to $\nu ^{\ell }_{|C_y^{\ell }}$, and which is thus non-decreasing. Thus, $T^{\ell }$ is a non-decreasing map such that for each $z \in Y^{\ell }$, $\mu ((T^{\ell })^{-1}(\{z\})) = \nu ^{\ell }(z)$. This implies that $T^{\ell }$ is the semi-discrete OT map between $\mu$ and $\nu ^{\ell }$. $\square$

Remark

The above discussion shows that, except in dimension 1, fixing a hierarchical clustering of $\nu$ imposes constraints on the shapes of the optimal nested cells. Optimizing both the multi-layer maps and the hierarchical clustering of $\nu$ seem worth of interest, but it would probably lead to a much more complex non-convex problem.

3.4 Stochastic Optimization

As already said, finding an optimal multi-layer map amounts to compute in a coarse-to-fine manner many semi-discrete OT maps, by solving the restricted semi-dual problems (18). If we have optimality at the previous scales $\ell '>\ell$, then the OT problem at scale $\ell$ is well-defined. Then, going back to the Monge formulation of these separates subproblems, the map $T^{\ell }$ actually minimizes

$$\begin{aligned} \int _{\mathbb {R}^D} \Vert T^{\ell }(x) - x\Vert ^2 \mathrm{d}\mu (x) = \sum _{y \in Y^{\ell +1}} \int _{\mathcal {L}^{\ell +1}_y} \Vert T^{\ell }(x) - x\Vert ^2 \mathrm{d}\mu (x)\nonumber \\ \end{aligned}$$

(21)

but with marginal constraints on each of the Laguerre cells $\mathcal {L}^{\ell +1}_y$.

If we consider the concave problem (18), the gradient of $H_y^{\ell }$ can still be computed

$$\begin{aligned} \frac{\partial H_y^{\ell }}{\partial v_y^{\ell }(z)} = - \mu (\mathcal {L}_y^{\ell +1} \cap \mathcal {L}_z^{\ell }) + \nu ^{\ell }(z) \end{aligned}$$

(22)

where we kept the notation $\mathcal {L}_y^{\ell +1} \cap \mathcal {L}_z^{\ell }$ for $\mathcal {L}_z^{\ell }$ to emphasize that $\mathcal {L}_z^{\ell }$ is a subset of $\mathcal {L}_y^{\ell +1}$ which is fixed by the previous layer. If $v_y^{\ell }$ is a critical point of $H_y^{\ell }$, then

$$\begin{aligned} \forall z \in C_y^{\ell }, \quad \mu (\mathcal {L}_y^{\ell +1} \cap \mathcal {L}_z^{\ell }) = \nu ^{\ell }(z) \end{aligned}$$

(23)

which implies that $\mu (\mathcal {L}_y^{\ell +1}) = \nu ^{\ell }(C_y^{\ell })$. However, this last condition is not guaranteed if we do not have optimality at the previous scales. In this case, $H_y^{\ell }$ have no critical point and thus no maximum.

For that reason, we can only propose a heuristic algorithm to optimize the multi-layer map $T_{\mathbf {Y},\mathbf {v}}$. It consists in performing gradient ascent to simultaneously increase the values of all functions $H_y^{\ell }$ for all layers $0 \leqslant \ell < L$ and all $y \in Y^{\ell +1}$. However, in order to cope with the fact that the OT maps are not optimal at the previous layers, we consider instead the cost adapted to the normalized measures defined in (17) and (13)

$$\begin{aligned} {\tilde{H}}_y^\ell (v_y^{\ell }) := \mathbb {E}_{X \sim {\tilde{\mu }}_y^{\ell +1}} \left[ {\tilde{h}}^\ell _y(X,v_y^{\ell }) \right] \end{aligned}$$

(24)

with

$$\begin{aligned} {\tilde{h}}^\ell _y(x,v_y^{\ell }) = \left( \min _{z \in C_y^{\ell }} \Vert x-z\Vert ^2 - v^\ell _y(z) \right) + \sum _{z \in C_y^{\ell }} v^\ell _y(z) {{\tilde{\nu }}}_y^\ell (z).\nonumber \\ \end{aligned}$$

(25)

The corresponding gradient

$$\begin{aligned} \frac{\partial {\tilde{h}}_y^\ell }{\partial v_y^{\ell }(z)}(x,v_y^{\ell }) = - \mathbb {1}_{\mathcal {L}^{\ell }_z}(x) + {{\tilde{\nu }}}^\ell _y(z) \end{aligned}$$

(26)

is normalized as well (i.e., it has zero sum after taking the expectation) and is used in lieu of the former gradient estimate Eq. (22). The corresponding optimization procedure is summarized in Algorithm 2.

3.5 Aggregating the Errors

In order to measure how much a multi-layer map drifts from the true OT map $T^*$, one may essentially distinguish two types of errors. The first one is the bias that is induced by a fixed hierarchical clustering and which cannot be coped with the optimization of $\mathbf {v}$, as discussed in Sect. 3.3. Denoting by $\mathcal {L}_y^{* \ell }$ the nested cells of the optimal multi-layer map, it is possible to quantize this bias at level $\ell$ by

$$\begin{aligned} \text {bias}(\ell ) = \sum _{y \in Y^{\ell }} \mu \left( \mathcal {L}_y^{* \ell } \, \mathrm {\varDelta } \bigcup _{z \in C(y)} (T^*)^{-1}(\{z\}) \right) \end{aligned}$$

(27)

where $A \mathrm {\varDelta } B$ refers to the symmetric difference between the sets A, B, and where C(y) is the set of children of y at scale 0. In Fig. 3, we illustrate this bias on a simple two-dimensional example. In general, computing this bias is a difficult problem since it requires to know the optimal nested cells $\mathcal {L}_y^{*\ell }$, which is equivalent to know the optimal multi-layer map. However, in dimension 1, this bias is known to be zero by Proposition 2.

Another source of error comes from the suboptimality of the elementary transport maps $T_{C_y^{\ell },v_y^{\ell }}$ parameterized by the vectors $v_y^{\ell }$. Of course, one could directly consider the values of the functions $H_y^{\ell }$. But it is certainly more revealing to consider the $L^1$-norm of their gradients (22) and to aggregate them. Therefore, we obtain an error

$$\begin{aligned} E = \sum _{\ell =0}^{L-1} \sum _{z \in Y^{\ell }} |\mu (\mathcal {L}_z^{\ell }) - \nu ^{\ell }(z)| . \end{aligned}$$

(28)

Analogously to the single-layer case, this corresponds to the amount of mistransported mass at all scales. Given a hierarchical clustering $\mathbf {Y}$, then $\min E = 0$ which, by definition, is attained only for the optimal multi-layer map. Notice also that, contrary to (27), the error (28) can be estimated by a Monte Carlo method.

3.6 1D Experiments

Experimental setting In this section, we propose a simple one-dimensional experiment to evaluate the convergence speed of the Algorithm 2 to approximate the optimal multi-layer map. For all the experiments shown in this section,

• $\mu$ is he standard Gauss distribution $\mathcal {N}(0,1)$,

• $\nu$ is the uniform discrete distribution on J equally spaced points between $-1$ and 1.

The benefit of such a one-dimensional setting is that the OT map between $\mu$ and $\nu$ can be computed (using the quantiles of $\mu$), and besides, it is easy to compute distances between a transported measure $T_{\sharp } \mu$ and $\nu$. In the following, we will focus on the Kolmogorov distance $d_{\text {KOL}}(T_{\sharp } \mu ,\nu )$, which is defined as the $L^{\infty }$ distance between cumulative distribution functions. Another benefit of the one-dimensional setting is that, as shown by Proposition 2, the bias (27) induced by the monotone hierarchical clustering is zero. Therefore, the optimal multi-layer map targeted by Algorithm 2 is exactly the optimal transport map $T^*$. The budget $J^{\ell }$ of points at scale $\ell$ is chosen manually (see more explanation below), and the hierarchical clustering is computed with Lloyd’s algorithm.

Let us mention that in the multi-layer setting, the comparison cannot be fairly performed at a fixed number of iterations since one iteration of ASGD for the one-layer transport has not the same cost as one iteration of ASGD for multi-layer transport. Therefore, the comparison will be based on the true computational time (in seconds).

Multi-layer versus one layer First, let us compare the multi-layer framework with $L=2$ (Algorithm 2) with the single-layer framework (Algorithm 1) with $J = 10^3$ and $10^4$ points in the target distribution. The number of clusters for the 2-layer transport is $J^1 = \lfloor \sqrt{J} \rfloor$ (integer part of $\sqrt{J}$). We also compare to a naive multiscale variant of Algorithm 2 that consists in exploiting another decomposition $\nu ^{\ell }$ of the target measures (with more scales) and estimating the semi-discrete OT from $\mu$ to $\nu ^{\ell }$ in a coarse-to-fine manner by initializing the weights v with an extrapolation of the weights found at the previous scale (for example, simply propagating the values from parent to children in the hierarchical clustering). Such an extrapolating rule was also presented in [37] for a deterministic framework (based on an efficient second-order optimization scheme which is not implemented here).

The results can be seen in Fig. 4. One can see that the bilayer algorithm reaches a good value for the distance $d_{\text {KOL}}(T_{\sharp } \mu ,\nu )$ in a faster way than the single-layer algorithm, especially when J gets very large. However, in the case of $J=1000$ points, it is interesting to notice that, up to a certain time, the single-layer algorithm attains a better cost (even if the bias induced by the hierarchical clustering is exactly zero). This reflects the fact that Algorithm 2 is only a heuristic optimization scheme, and it is expected to have a more oscillatory behavior than the single-layer algorithm. In particular, we observed that the convergence at the fine layers is slower because the current cells at this layer depend on those obtained at the coarsest scales (and setting the cells at the coarsest scale is an instance of a stable convex stochastic optimization algorithm). Thus, it is especially interesting to turn to the multi-layer algorithm if J is very large with a constrained computational time. Notice also that, in the stochastic setting, the naive multiscale procedure does not help much in terms of convergence speed. Besides, in this naive procedure, one should choose a budget of iterations per scale, which is less trivial in the stochastic setting than in the deterministic quasi-Newton setting of [37] (where only $\approx 10$ iterations are needed to obtain the solution with very good precision).

Fig. 4

Two-layer versus one-layer. We compare with the multi-layer Algorithm 2) (two-layer) with the single-layer algorithm (one-layer) and with the naive multiscale procedure (naive-multiscale). We monitor the Kolmogorov distance between $T_{\sharp } \mu$ and $\nu$ . The horizontal axis represents the computational time (in seconds) and the vertical axis the Kolmogorov distance between the current transported measure $T_{\sharp } \mu$ and the target measure $\nu$. When J is very large, the two-layer approach leads to a better transport map in a reasonable time

Setting the number of clusters We first assume here for simplicity that Y can be decomposed into L scales with balanced clusters. We denote by $n_L$ the number of NN comparison required to evaluate the L-layer transport map $T_{\mathbf {Y},\mathbf {v}}$ (15) at a given point; $p_L$ is the number of weight parameters $v_y^\ell (z)$ describing $T_{\mathbf {Y},\mathbf {v}}$.

For $L=1$, we have $n_1 = J$ and $p_1 = J$.

For $L=2$ layers with $J_1$ balanced clusters and a total of J points, $n_2=J_1+\frac{J}{J_1}$: the minimum number of comparison is then $n_2 = 2\sqrt{J}$ for $J_1=\sqrt{J}$. The corresponding number of parameters is $p_2=J_1+J_1\times \frac{J}{J_1}= \sqrt{J} + J$.

For $L=3$ layers with $J_1$ and $J_2$ balanced clusters at each layer respectively, the number of points comparison per iteration for J points is $n_3=J_1+J_2+\frac{J}{J_1 J_2}$: the minimum number of comparison is then $n_3 = 3\root 3 \of {J} < n_2$ for $J_2=J_1=\root 3 \of {J}$. The number of parameters is then $p_3=J_1+J_1 \times J_2+J_1 J_2 \times \frac{J}{J_1 J_2}= \root 3 \of {J} + \root 3 \of {J^2} + J > p_2$.

Thus, from the sole perspective of computation load indicated by $n_L$, one should use a hierarchical representation where the number of clusters per scale is close to $\root L \of {J}$. One could then hope that such a choice would provide a faster convergence, since the number of iteration per second is maximized. This is confirmed empirically in Fig. 5, where we consider the same experimental setting as before, with $J=10^4$ (Fig. 5a), $J=10^5$ (Fig. 5b) and $J=10^6$ (Fig. 5c). In these experiments, the optimal number of clusters for convergence corresponds approximately to $\root L \of {J}$.

Fig. 5

Comparison of convergence speed for estimating the multi-layer transportation plan, according to the number L of layers and the number $J^\ell = K$ of clusters. Increasing the number of layers accelerates convergence when the number of clusters is optimal ($K\approx \root L \of {J}$). (Note: each curve is displayed every $10^4$ iterations; the initial offset corresponds to the amount of time required to reach such a number of iterations, increasing with K.)

Fig. 6

Comparison of convergence speed for estimating the multi-layer transportation plan for a large number J of points. We see here that increasing the number of layers can improve the convergence speed when J is very large, but it may increase the bias due to hierarchical clustering.

Setting the number of layers Observe now that the number of comparisons $n_L$ decreases much faster than the number of parameters $p_L$ increases when using perfectly balanced clusters. Moreover, it is interesting to notice that, while the number of parameters grows with the number of layers, the maximum number of parameters is actually bounded by 2J. Indeed, even if the following geometric sum is divergent

$$\begin{aligned} p_L = \sum _{\ell =1}^{L} J^{\tfrac{\ell }{L}} = \frac{1 - J^{\tfrac{1+L}{L}} }{1 - J^{\tfrac{1}{L}}} - 1 \xrightarrow [L \rightarrow \infty ]{} + \infty \end{aligned}$$

the worst practical case, i.e., the deepest possible search tree that can be built, corresponds to the binary classification tree, for which we have (setting $J= 2^L$)

$$\begin{aligned} p_L = \sum _{\ell =1}^{L} 2^{\ell } = 2^{1+L} - 2 = 2 (J-1) < 2J \end{aligned}$$

but only $n_L = 2L$ comparisons.

Setting aside questions about complexity (such as optimization of memory access, data structure and parallel computing), one would be tempted to conclude that, as the number of layers does not impact much the number of parameters of the model while providing an interesting speed-up, one should use the highest possible number of layers. However, increasing the number of layers makes it more difficult for the estimated transport map to get close to the optimal one. Hence, there is a trade-off between using more layers to reduce the computation time and less layers to reduce the complexity of the model.

Figures 5 and 6 illustrate the impact of increasing the number of layers on convergence speed for $L \in \{1, 2,3\}$ layers and from $J=10^4$ to $J=10^7$. The comparison of performance shows that, even if a larger number of layers allows for more samples to be drawn during optimization, the bias error caused by clustering discussed previously in Sect. 3.5 is more difficult to cope with. Nevertheless, the benefit of increasing the number of layers is yet overwhelming when considering a large number of points J (Fig. 6).

4 Application to Texture Synthesis

In this section, we show how the optimal multi-layer maps introduced above can be used to enrich a texture model based on OT in the patch space [15]. One main interest of semi-discrete OT maps for patch-based texture synthesis is that the transport maps project onto patches seen in the exemplar texture while maintaining a global statistical consistency. The main limitation of the model of [15] was that the discrete target patch distributions were constrained to have $\approx 10^3$ points (otherwise, the ASGD algorithm would converge too slowly), which prevents one from using patches larger than $3 \times 3$ (e.g., the $7 \times 7$ patch distribution of a natural texture needs much more than $10^3$ patches to be accurately represented). As was shown in the previous sections, the multi-layer strategy allows to approximate the transport map with larger discrete target distributions and thus to extend our texture model to $7 \times 7$ patches, which greatly enlarges the class of well-reproduced textures. Let us emphasize that one must not confound the layers of the multi-layer OT maps of the previous section and the image resolutions; the model here defined will indeed be multiscale in both these aspects.

In all the following, we denote by $u : \varOmega \rightarrow \mathbb {R}^d$ the original texture (with d channels, $d=1$ for gray-level images, and $d=3$ for color images). We also denote by $\omega = \{0,\ldots ,w-1\}^2$ the patch domain and by $\mathbb {R}^D$ the patch space (where $D = d w^2$).

Fig. 7

Single-resolution model, synthesis results. For several original textures shown in the first column, we compare several synthesis results obtained by the single-resolution transformed random field (30), where T is either a monolayer or bilayer transport map and where the patch size w ranges from 3 to 7. Even if the visual differences between the monolayer and bilayer map are subtle in terms of geometric content, one can see that the patch statistics (and in particular the color distribution) are better respected with the bilayer transport maps

Fig. 8

Single-resolution model, output patch distributions. In this figure, we examine the output patch distributions after the monolayer and bilayer transport maps for the single-resolution model with patch size $w=5$, for the textures shown in the two first rows of Fig. 7. Each diagram represents the one-dimensional distribution obtained after projecting on a principal axis in the patch space, and the corresponding patch principal component is displayed just below. On each diagram, the black curve is the reference distribution, the blue curve is the distribution after multi-layer transport, and the yellow curve is the distribution after monolayer transport. This experiment reflects again the fact that in a large-scale setting, multi-layer maps provide better transportation maps which here help to better preserve patch distributions compared to monolayer maps

4.1 Single-Resolution Model

The texture model [15] consists in transforming a stationary Gaussian random field by applying patch transport maps at several resolutions. First, we recall the construction of the texture model for a single resolution.

The single resolution model is built on the Gaussian random field U defined by

$$\begin{aligned} \forall \, a \in \mathbb {Z}^2, \ U(a) = \bar{u} + \sum _{b \in \mathbb {Z}^2} t_u(b) W(a-b) , \end{aligned}$$

(29)

where $\bar{u} = \frac{1}{|\varOmega |} \sum _{a \in \varOmega } u(a)$, W is a normalized centered Gaussian random field (i.e., the W(a) are independent with standard $\mathcal {N}(0,1)$ distribution), and where $t_u = \frac{1}{\sqrt{|\varOmega |}} (u-\bar{u}) \mathbf {1}_{\varOmega }$. Then, we extract all patches $U_{|a+\omega }$ of U, apply to all these patches the same map ${T : \mathbb {R}^D \rightarrow \mathbb {R}^D}$ and then aggregate the transformed patches with a simple average. In other words, we define the transformed random field by

$$\begin{aligned} \forall a \in \mathbb {Z}^2, \quad V(a) = \frac{1}{|\omega |} \sum _{b \in \omega } T(U_{|a-b+\omega })(b). \end{aligned}$$

(30)

In order to reimpose geometric structures of the exemplar texture in a statistically coherent way, the patch map T should solve (at least approximately) the OT between the distribution $\mu$ of a patch $U_{|\omega }$ of U (which is a Gaussian distribution with explicit parameters) and the empirical distribution $\nu$ of the patches of u. Such a transformed random field is still stationary and possesses some properties that were listed in [15], for example a covariance control and long-range independence.

Therefore, $\mu$ is absolutely continuous and $\nu$ is discrete so that the OT between $\mu$ and $\nu$ is actually a weighted NN assignment as in Eq. (2). In our previous work [15], we used such a weighted NN assignment, estimated with Algorithm 1. But again, the estimation step was then very slow for $J \gg 1000$ and so we restricted to $J=1000$ patches in the target distribution, which constrained us to work only with $3 \times 3$ patches. The rest of this section aims at replacing the weighted NN assignment by a multi-layer map and precisely assessing the benefit of such multi-layer maps when working with larger target distributions and larger patches.

Before presenting the results, let us give the details about the remaining parameters of the model. In contrast to our previous work, the target distribution $\nu$ is here given by all patches of u. Thus, the monolayer transport map $T_v$ is parameterized by a single $v \in \mathbb {R}^J$ where J is the number of patches in u (for example, for a $128 \times 128$ image, we have $J \approx 16000$). For the multi-layer transport, we use only $L=2$ layers (thereby defining bilayer transport maps) and perform a two-scale hierarchical clustering with $J^1 = 40$. (The clusters are found using Lloyd’s k-means algorithm.)

In Fig. 7, in the single-resolution case, we compare the synthesized images obtained with a monolayer patch transport and a bilayer patch transport, with patch size $w = 3, 5, 7$. One can first remark that the visual quality of the synthesized texture is very limited with this model working at a single resolution. Indeed, increasing the patch size allows to retrieve larger geometric structures from the exemplar, but $w=7$ is not large enough to capture all structures of the textures shown in Fig. 7. We will cope with this strong restriction in Sect. 4.2.

However, beyond the geometric content, the patch statistics are better retrieved with a bilayer map than a monolayer map. This reflects again that Algorithm 2 allows to better approximate the transport map in a more reasonable time. Indeed, in this experiment, the number of iterations was set to $10^5$ for monolayer transport, and $10^6$ for bilayer transport, and yet, the required computational time was much lower in the bilayer case.

The statistical benefit is confirmed by the patch distributions shown in Fig. 8. Since the patch space is high-dimensional ($D=75$ for color $5 \times 5$ patches), we only represent the one-dimensional distributions obtained after projecting on a few principal components of the patch space. In general, on the most important principal components, the multi-layer map will perform at least as good as the monolayer map, (Even if, in some cases, the approximation is not perfect.) Actually, applying the same methodology on a larger set of textures and principal components (not shown here) allows to do draw the following conclusions:

• On a wide majority of components, the multi-layer and monolayer maps perform nearly equally.

• On few main principal components (that will dominate in the visual perception), the multi-layer map better approximates the reference distribution.

• Sometimes (for example, on the last principal components with less energy), the monolayer map performs better.

These remarks correlate the visual differences observed in Fig. 7.

4.2 Multi-resolution Model

In this section, we define a texture model using multi-layer maps at several image resolutions. We will work with S subsampled versions $u_{s}$, $(0 \leqslant s\leqslant S-1$) of the original image at different resolutions, $u_{s}$ being defined on a subdomain $\varOmega _{s} \subset 2^{s} \mathbb {Z}^2$. We will also denote by $\nu _s$ the empirical distribution of $w\times w$ patches of $u_{s}$.

Fig. 9

Multi-resolution model, synthesis results. For several exemplar textures displayed in the middle column, we present several synthesis results obtained with a multi-resolution model exploiting multi-layer transport maps working on $7 \times 7$ patches at each resolution. We compare with the previous model [15] based on single-layer transport on $3 \times 3$ patches. See the text for comments

Fig. 10

Preserving fine scale details. This figure illustrates that the multi-layer model retrieves geometric structures of the exemplar in a cleaner way. In particular, applying the single-layer model on patches $7\times 7$ is not sufficient to produce relevant structures. Also, one can see that the last $3 \times 3$ transport applied at resolution 0 is important to retrieve fine scale structures

Fig. 11

Comparison. For each row, we display, from left to right, an original texture, the result of the model based on two-layer patch transport, the result of the feed-forward network of [59], the result of the neural optimization procedure of [16] and the results of the patch-based method of [46]. See the text for comments

Fig. 12

In this figure, we compare the synthesis results obtained with the model based on bilayer OT and with the models of [59] and [16]. The first and fifth rows contain images synthesized with these three models. In the second row, we display the output color distributions visualized with [33]. The patch distributions obtained with the different models are displayed in the third and seventh rows (summarized by the one-dimensional distribution of the projections on the principal components shown in fourth and eighth rows). In the sixth row, we display the Fourier spectrum of images of the fifth row. See the text for comments

Fig. 13

Innovation capacity. In this figure, we illustrate the capacity of innovation of three texture models by looking for several patches of the exemplar texture (marked with red, green and blue squares) the 50 NN in the synthesis (marked with squares with corresponding color). Compared to other recent texture synthesis algorithms, our texture model generates patterns which are more similar to those of the exemplar texture (because multi-layer maps projects of patches seen in the exemplar), but always with some local variations due to patch averaging

The model is defined by successive patch transport and exemplar-based upsampling as summarized in Algorithm 3. The estimation of the model can be done during one initial pass of synthesis (that can be performed offline). At the coarsest resolution $s= S-1$, as in the previous section, the model is initialized with the Gaussian random field $U_{S-1}$ associated with $u_{S-1}$. Then, for every scale $s= S-1, \ldots , 1$, a patch transform $T_s$ is applied to all patches of the current synthesis. This transformation is computed during the estimation stage with the two following steps:

• Fit a GMM distribution $\mu _{s}$ to the patches of $U_{s}$.

• Compute the patch transformation $T_{s}$ that realizes the OT from $\mu _{s}$ to $\nu _{s}$.

Once estimated, all patches are transformed with $T_{s}$ and averaged, which defines a transformed random field

$$\begin{aligned} V_s(a) = \sum _{b \in 2^s\omega } T_s(U_{s|a-b+2^s\omega })(b) ,\ x \in 2^s\mathbb {Z}^2. \end{aligned}$$

(31)

Since $T_{s}$ is actually a patch assignment, there is a “coordinate map” ${C_s: 2^s\mathbb {Z}^2 \rightarrow \varOmega _s}$ which allows to express $V_s$ as

$$\begin{aligned} V_s(a) = \sum _{b \in 2^s\omega } u_s\big (C_s(a-b)+b\big ) , \ x \in 2^s\mathbb {Z}^2. \end{aligned}$$

(32)

Then, an exemplar-based upsampling step allows to initialize the synthesis at the next resolution. It consists in taking twice larger patches at the same positions. This is equivalent to set for all $a \in 2^s\mathbb {Z}^2$ and for all $t \in \{0,2^{s-1}\}^2$,

$$\begin{aligned} U_{s-1}(a+t) = \sum _{b \in 2^s\omega } u_{s-1}\big (C_s(a-b)+b+t\big ). \end{aligned}$$

(33)

An illustration of this coarse-to-fine synthesis procedure is available in [15].

Here again, instead of taking a single-layer transport map for $T_s$, we propose to use a bilayer transport map that better approximates the semi-discrete OT between $\mu _s$ and $\nu _s$, even for larger patches. Therefore, in contrast to [15] (referred to as a single-layer model or “1-layer” in the captions), the model will not be limited to ${3 \times 3}$ patches anymore. Indeed, in the experiments shown in this section, the bilayer maps are defined on $7 \times 7$ patches.

Let us give the parameters of the used bilayer maps. In all the examples shown below, we used $S=4$ scales for images smaller than $500 \times 500$ and $S=6$ scales for larger images. Since the target patch distribution $\nu _s$ of the exemplar texture has a more complex structure for coarse scales, the number of clusters $J^1$ is adapted to the scale, i.e., we take $J^1 = 10$ for $s=S-1$, $J^1 = 20$ for $s=S-2$, and $J^1 = 40$ for $s<S-2$. The hierarchical clustering is again found using the k-means algorithm; however, in order to keep a reasonable complexity even if the exemplar texture is very large, we fix a budget B of patches in each cluster. If the number of patches in a cluster $C_y^0$ exceeds B, then we randomly select B patches in this cluster. This budget also depends on the scale: $B = 100$ for $s=S-1$, $B = 200$ for $s=S-2$ and $B = 400$ for $s<S-2$. At the finest scales, the global budget is thus $40 \times 400 = 16000$; this selection step amounts to simplifying $\nu$ with only 16000 patches. For which regards the source distribution, during the estimation phase, a GMM distribution $\mu _s$ with 10 components is fitted to the current patch distribution of $U_s$ using the Expectation Maximization algorithm [36]. Using 10 Gaussian components to model the $7 \times 7$ patch distribution of a texture seems relevant in comparison with [15] where 4 components were used to model the $3 \times 3$ patch distribution of a texture and also to [65] where $\approx 20$ components were used to model the $8 \times 8$ patch distribution of a natural image. Finally, in order to reimpose details at the finest resolution, we apply on $V_0$ a last bilayer transport map on $3 \times 3$ patches to get the output image V.

Let us emphasize on the fact that the overall algorithm can be decoupled into an estimation and synthesis step. In other words, the estimation of bilayer transport maps at all resolutions (which is quite costly) can be done once and for all. Once estimated, these transport maps can be applied to all patches and also be used to synthesize many images with arbitrary size. For this reason, if the model is pre-estimated, then the synthesis algorithm has a very low computational time, comparable to methods based on pre-estimated feed-forward networks like [59].

Several synthesis results obtained with the multi-layer model are displayed in Fig. 9. Compared to the previous model [15], it is clear that working on $7 \times 7$ patches (instead of $3 \times 3$ patches) allows to capture larger geometric structures of the exemplar texture. This is not surprising since the semi-discrete transport maps that are used are essentially weighted NN assignments that use patches seen in the exemplar texture. But still, combining the Gaussian initialization at coarse resolution and the patch averaging procedure at all resolutions permits to create new patches which are not seen in the exemplar. This is where the model gets its capacity of innovation. The copy-paste effect will be discussed below. Let us also mention that the new model is able to better respect fine details, thanks to the last $3 \times 3$ transport map applied at the finest resolution, see Fig. 10.

In Fig. 11, we compare the multi-resolution model with other state-of-the-art texture models. The model of Gatys et al. [16] consists in optimizing the image (starting from a white noise) in order to match some spatially averaged second-order responses obtained in a pre-learned neural network. The model of Ulyanov et al. [59] consists in learning a feed-forward neural network that mimicks the optimization procedure of Gatys’ method. Finally, the model of Raad et al. [46] consists in progressively growing the texture using patch conditional sampling (also working in a coarse-to-fine manner so that one resolution is conditioned by the previous coarser resolution).

One can see that the visual quality is comparable to the one attained by the model of Gatys et al. [16] and is clearly higher than the one obtained by the other models (should it be in terms of details, frequency content, or spectrum). However, compared to [16], the images generated with our model are often smoother; this is probably due to the averaging step used to merge patches at all resolutions. Also, the unstructured texture of the fifth row of Fig. 11 is worth of comment; on this example, both models fail to preserve the frequency content of the texture, but the failure of our model can be avoided by properly setting the parameter S. Indeed, one should set the number S resolutions depending on the size of structures present in the exemplar image, keeping in mind that the receptive field is of size $2^{S-1} w \times 2^{S-1} w$ (for example, with $S=4$ resolutions and $7 \times 7$ patches, the receptive field is $56 \times 56$). For a texture with no salient structure (like the one shown in the 5th row of Fig. 11), taking a single-resolution model (i.e., $S=1$) is sufficient to obtain a perfect result. Observe that pseudo-periodic patterns are often not well reproduced by neural network methods, while long correlations can be captured by our multiscale model. This phenomenon can be circumvented by adding other terms to the considered loss function, adding Fourier spectrum information [34] or spatial correlation [55].

Additionally, it is interesting to compare the results by looking at the resulting patch distributions, as is proposed in Fig. 12. Since the patch distribution is very high-dimensional, for that, one can plot the one-dimensional distributions obtained after projections in the principal components of the patch space (the principal component analysis being led on the patches of the original texture). Curiously, even if our model is inherently designed to preserve the patch distribution, one can see that the model by Gatys et al. often outperforms it in terms of proximity to the original patch distribution. Again, this may be caused by the averaging step, or also by the fact that the multi-layer maps do not attain exactly the target empirical patch distributions. However, this is very difficult how some observed drifts on the patch distributions (on some principal components) will impact the visual perception. Complementing the study by looking at the color distribution or the spectrum helps to understand the failure/success of the different algorithms.

Let us also remark that, even if our model does not reach the visual quality of Gatys’ model, it reaches a very good compromise between visual quality and synthesis time (since, again, the model estimation can be performed offline). In contrast, the model by Ulyanov et al. [59], which can also be estimated offline and has a comparable synthesis time, produces the results with curious visual artifacts that can be analyzed in the patch distribution or the spectrum.

Finally, we propose one last experiment that aims at evaluating the capacity of innovation of the previous models. For several large patches in the original texture, we propose to single out their NN in the synthesis. The results can be seen in Fig. 13. Since the bilayer transport maps project onto patches seen in the original texture, it is expected that some pieces of the synthesis are quite close to the original. However, one can see that there are always small differences thanks to the patch averaging step.

4.3 Textural Inpainting

To close this section, we propose to show briefly that the texture model defined in the previous section can also be used to address textural inpainting. Indeed, if the original texture $u : \varOmega \rightarrow \mathbb {R}$ is known outside a mask $M \subset \varOmega$, one can define the target patch distribution as the empirical distribution of available patches. Working with several resolutions is not an issue either since one can compute subsampled versions $u_s : \varOmega _s \rightarrow \mathbb {R}$ and define an adapted mask $M_s$ at resolution s (for example, by thresholding the bilinear reduction in the indicator function of M).

Fig. 14

Multiscale Textural inpainting. The proposed textural inpainting consists in using a Gaussian conditional sampling at the coarsest scale (first row, third column) and then adding details with bilayer patch transport maps

Fig. 15

Textural inpainting results. For several masked textures (first and third rows), we display the inpainting result obtained with the model based on two-layer patch transport. Notice that the inpainted content blends quite nicely with the rest of the image, even if a residual blur is sometimes perceived due to patch averaging

Fig. 16

Textural inpainting comparison. In this figure, we compare our approach for textural inpainting with the one of Newson et al.[40]. (Their result was obtained with the online demo [41].) Notice that our approach blends the synthesized content with more blur, but also in a way that is less oblivious of the surrounding content. In contrast, with [40], the generated content often disagrees with the context at the boundary of the mask

Fig. 17

Textural inpainting comparison. In this example, we compare our approach with Deep image prior [61] (which optimizes a deep neural network with skipping connection to generate the masked image using Mean Square Error criterion) and with [4], where patches from the uncovered part of the image are used to fill in the masked domain and blended to avoid blocking artifacts. Notice that the available textural content is better represented with our approach since it is inherently designed to respect the patch distribution

However, at the coarsest scale, the synthesized Gaussian texture should agree with the unmasked content. Fortunately, in the Gaussian case, the inpainting problem can be formulated as a conditional Gaussian model estimated outside the mask as proposed in [14]. The benefit of such a conditional simulation is that, at the coarsest scale, the synthesized content will extend the long-range correlations that can be observed outside the mask. Then, using this Gaussian inpainting of the coarsest scale, one can apply the bilayer transport maps at several resolutions in order to reimpose geometric structures, as shown in Fig. 14. The model is estimated in the same way than for the case of pure synthesis, except that the target patch distributions contain only patches which do not overlap the mask. (The number of scales should be sometimes reduced in order to find enough available patches at the coarsest resolution.) Also, a crucial difference lies in the patch recomposition: One should apply the transport maps to all patches that overlap the mask boundary (and average them to get an image).

Some textural inpainting results can be seen in Figs. 14, 15 and 16. As can be observed in Figs. 14 and 15, this inpainting model allows to inpainting structured textures in a reasonable way. However, for complex sharp textures, some blur can be perceived at the boundary of the mask (for example, in the second example of Fig. 16). Also, the comparison of Fig. 16 highlights the benefit of considering the patch distributions. Indeed, constraining the patch distribution allows to avoid inpainting failures that are undesirable optima when optimizing functionals based only on the distance to the patch NN.

Figure 17 compares our approach with two other inpainting techniques [4, 61] that have a limited amount of artifacts at the boundary of the mask. On the one hand, deep image prior [61] consists in training a fully convolutional neural network (in this specific case, with skipping connections) to generate the masked image from a (fixed) noise input using a mean square error loss function outside the masked domain. Due to the continuous nature of the generative network, this technique gives sometimes surprisingly good results with a seamless transition at the border of the mask. On the other hand, we compare to the greedy patch-based copy method of [4], where an efficient blending technique is proposed to avoid block artifacts when combining locally patches from different locations in the image. Again, our approach compares favorably to those methods, despite introducing some noticeable blur at the finest resolution due to the averaging of patches.

5 Application to Style Transfer

5.1 A Short Review on Image Stylization

The principle of image stylization or style transfer (see, e.g., [8, 9, 13, 16, 23, 24, 59, 66]) is to give a source image the artistic look of an example (or style) image, such as a painting, a texture or another picture with the desired visual features (e.g., color or dynamic range). The most important aspect of this problem is that the synthesized image should at the same time have similar visual features than the style image and preserve the geometrical content of the original image.

Until recently, most successful approaches consisted in patch-based methods that are largely based on texture synthesis [8, 23]. Often, the only main difference is that the initialization, instead of using random noise, is the image to be modified itself. However, there is no guarantee that the resulting image will keep most of its important geometrical structures. In order to cope with this issue, other methods rely on a variational formulation that balances the two objectives: An objective function comparing style features to the style image, linearly combined with a second objective comparing other geometric features to the original image. Such formulations are usually used to drive an optimization algorithm that iteratively updates the pixel values of the synthesized image.

As was already discussed in the introduction, textural or style features can be based on patch representations [9, 13]. However, a more popular way to extract features is to use a visual representation of images that is learned on a large dataset of natural images, as initiated in [16]. In practice, most techniques use features extracted from layers of the deep convolutional neural network VGG-19 [56] trained on ImageNet, but random representations could be used as well [62]. Note that learned representations for image classification are known to be heavily biased toward textural information [18, 39]. In order to use such a network for style transfer, spatial information linked to geometrical features of the input must be kept while the style features must be extracted with spatially averaged statistics (often with second-order statistics, like Gram matrices). Although using deep representations makes the optimization more involved (as it requires backward propagation through a deep network), it improves greatly the visual quality [17].

The authors of [24] have shown that this optimization process could be performed offline by training a deep network to achieve a given type of stylization on a dataset (MS-COCO with 80k training images). After training, the corresponding stylization of a new source image is simply done by a single forward propagation through the neural network. Afterward, the authors of [59] demonstrated that such a technique can be used for texture synthesis as well, or for multiple styles [66]. While image quality might not be on par with deep optimization technique [17], the speed-up is of several orders of magnitude, as it requires less computations than for a single iteration which involves forward & backward propagation through a deep descriptive network.

5.2 Feed-Forward Texture Transfer

We propose here to adapt the multi-resolution texture synthesis algorithm of the last section to perform style transfer in a “feed-forward” fashion. More precisely, we estimate the multi-resolution texture model associated with the style image, and then, we directly apply the multi-layer transport maps to the source image in a coarse-to-fine manner, without any optimization. The main difference is the following: At each scale, the upscaled output from the previous scale is now blended with geometric features from the source image. For simplicity, we use only edges as geometric features. Note that, as for the “perceptual loss” in [16, 24, 59], style features do not encode spatial information in our case (patch distribution) but geometrical features do. The method is summarized in Algorithm 4 and detailed in the next paragraphs. Contrary to other aforementioned approaches, our algorithm is not optimizing the input image nor trained on a dataset.

Fig. 18

Illustration of contour extraction and blending for texture transfer. This figure contains the style image u (a), the source image w (b), the mask $M_w$ (c) defined from Eq. (35), the preprocessed image $\tilde{w}$ (d) defined from Eq. (34), the contour image $M_w \tilde{w}$ (e), the result of multiscale blending (f) obtained from Alg. 4, the result with naive blending (g), and the synthesis without blending (h). Note that the direct blending of the contours in the synthesized texture is not sufficient (g). Using blending directly during the multi-resolution synthesis (f) gives more satisfying results

Preprocessing We denote by w the input image to be processed and u the style image. In order to ensure that the patch distribution of w at the coarsest resolution $s = S-1$ is close to the one of u (which serves to estimate the transport maps), we first preprocess w to match the patch second-order statistical properties of u. Namely, the preprocessed image $\tilde{w}$ is constructed by overlapping transformed patches:

$$\begin{aligned} {\tilde{w}}(a) = \frac{1}{|\omega |} \sum _{b \in \omega } A(w_{ |a-b+\omega })(b) , \end{aligned}$$

(34)

where A is an affine transform that imposes the patch mean and patch covariance of u. Because the reconstructed image ${\tilde{w}}$ may have out of range values, a local histogram equalization of the intensity channel in Lab color space is performed. An example illustrating this preprocessing is shown in Fig. 18d.

Blending geometric and texture information Geometric features are based on contour extraction. A mask is first computed from the gradient intensity on the smoothed input image and normalized using a sigmoid function:

$$\begin{aligned} M_{w}(x) = S_t \left( \Vert \nabla (w *g_\gamma ) (x) \Vert \right) \end{aligned}$$

(35)

where $*$ indicates the discrete convolution with the Gaussian density function $g_\gamma$ of standard deviation $\gamma$ (controlling the detection scale), and

$$\begin{aligned} S_\tau (w) = \frac{1}{1 + e^{-10 \frac{w-\tau }{\tau }}} \end{aligned}$$

(36)

parameterized by $\tau$, which controls the detection intensity. Figure 18c shows the mask computed at the largest resolution.

The blending of texture synthesis with geometric features is performed with a convex combination between the current upsampled image (33) and the preprocessed image ${\tilde{w}}_s$ (34) (Fig. 18e)

$$\begin{aligned} {\tilde{U}}_s(x) = \left( 1- M_{w_s}(x) \right) U_s(x) + M_{w_s}(x) {\tilde{w}}_s(x). \end{aligned}$$

(37)

Once blended, we can apply the pre-learned multi-layer transport map as in (31). Figure 18 shows that applying the blending before the transport map (Fig. 18g) rather than after (Fig. 18h) gives a much better result.

In practice, as shown in Fig. 19, decreasing the threshold $\tau$ adds details with less contrast from the input, and decreasing $\gamma$ keeps only fine details.

Remark

Observe that, as we blend the preprocessed input image with textures, the patch distribution of the stylized image does not follow the GMM that served as the source of the transport maps. However, as we change patches only at some edges of the texture image, the difference is practically negligible for this application.

Fig. 19

Illustration of contour extraction and blending parameters $\gamma$ and $\tau$ for texture transfer. The same random seed is used to generate the style on the first two lines. The last row shows the effect of changing the random seed used to initialize the algorithm Gaussian random field (29), where $\tau =0.02$ and $\gamma =0.8$ (as fixed throughout the rest of experiments)

Additionally, Fig. 19 shows the stylization results with different random initializations. It should be noted that we do not have any of the diversity problems reported for feed-forward networks in [60] and [32] for instance.

Fig. 20

Image stylization comparison of the proposed approach with other feed-forward techniques requiring learning over a dataset. We display the style image (a), the source image (b), the result of Johnson et al. [24] (c), the result of Zhang et al. [66], the result of our approach for several values of the blending parameter $\tau$ (e, g, i), and the result of Gatys et al. [17] for several values of the weighting parameter $\lambda$ (f, h, j). See the text for comments

5.3 Stylization Results

First, Fig. 20 gives a comparison of our image stylization approach (Fig. 20g) with the gold standard technique of deep image optimization introduced by Gatys et al. [17] (Fig. 20f). As already mentioned, the optimization process is based on an objective function, linearly combining a style loss with a content loss function weighted by a parameter $\lambda$. The interesting aspect of using deep image representation is that it enables a more liberal definition of the content of the image to be preserved than ours, resulting in mixing the content of both images in intricate patterns (see, for instance, the posts becoming curved like the branches in the source image). However, as already reported in previous work (see, e.g., [34]), some features are not well preserved, such as color, and checkerboard artifacts may also appear. On the other hand, as previously demonstrated, our technique aims at matching the patch distribution from the style image, hence being better at preserving color and reproducing tiny details from the exemplar image. For a complete comparison, we display stylization with our method when incorporating only geometric details at low resolution (by setting $\tau =0$ after the third scale, and referred to as low in Fig. 20e) or with all details at high resolution (by setting $\tau =1$ after the third scale, referred to as high in Fig. 20i).

Fig. 21

Feed-forward multi-layer style transfer. Note that the same random seed (i.e., used to generate the Gaussian texture sample at the coarsest scale) is used for all examples, showing how incorporating geometric features in Algorithm 4 changes the outcome. Stylization parameters are fixed throughout all experiments as well ($\gamma = 0.8$ and $\tau = 0.02$) but could be adapted depending on the geometric content of the source image

Comparing our technique to other feed-forward approaches from the literature [24, 66] (that still require training on a large dataset of natural images) is interesting as well. Both techniques (Johnson et al. [24] in Fig. 20c, Zhang et al. [66] in Fig. 20d) do not manage to preserve the main features of the style image, thus highlighting the benefit of our statistical framework. Quite interestingly, unlike Gatys et al. [17], these methods have automatically learned to preserve the contours from the source image, as we choose to do explicitly.

Figure 21 shows various stylization results for different types of source image. In these experiments, all stylization parameters are fixed (same random seed, $\tau =0.02$ and $\gamma =0.8$) and the same parameters have been used for learning all bilayer transportation maps from the style image (as detailed in Sect. 4.2). To start with, observe that our method is better suited for style images which are textures, which is the main hypothesis of our statistical framework. When it is not the case, we observed that the multi-layer model has more trouble to match statistics with the same set of parameters, requiring more iterations during training, and more sampled patches, more GMM components, etc. Yet, it is still providing interesting results on non-stationary style examples (such as rows 1, 4 and 8 of Fig. 21).

6 Conclusion

In this paper, we have proposed to approximate a semi-discrete OT map with multi-layer transport maps that exploit a hierarchical clustering of the target discrete distribution. After studying the optimality condition for such multi-layer maps, we have shown that they can be optimized with a heuristic stochastic optimization approach. The corresponding algorithm performs better than the usual stochastic algorithm for semi-discrete OT, especially when the target discrete distribution has a very large support. However, we have shown that, except in dimension 1, the hierarchical clustering of the target distribution induces a bias that cannot be coped with by the optimization procedure.

Such multi-layer transport maps, therefore, can be used for applications that rely on a large-scale OT setting (both in terms of dimensions of the underlying space and in terms of support of the target distribution). In particular, we proposed to exploit this multi-layer approach to tackle OT in the patch space, which is useful for several imaging applications, and we gave the results in texture synthesis, texture inpainting and style transfer. For texture synthesis, the multi-layer approach allowed us to consider larger patches in a previous texture model, which considerably enrich the class of well-reproduced textures. We thus obtained a texture model that is comparable to state-of-the-art models in terms of visual quality, while maintaining several mathematical properties (like long-range independence), and a good empirical control on visual statistics (like the color distribution of the spectrum). Besides, once estimated, such a texture model can be sampled in a fast manner (since it consists only in recursive weighted NN patch assignments) and thus has a competitive computational time compared to recent neural network techniques.

This texture model can also be used to address texture inpainting (by relying on a Gaussian conditional sampling scheme for the coarse resolution) or style transfer (with a feed-forward approach that blends the source image with a synthesized texture and which does not need pixel-based optimization). For both these problems, this model produces the visual results that compare well to other competing methods, with the benefit of a good statistical control, in the sense that all the textural content visible in the input texture (or the style image) will be fairly represented in the output image. For inpainting, this statistical control allows to avoid trivial solutions of patch-based approach (for example, flat areas obtained by repeating a flat available patch).

The main limitation of this texture model lies in its constrained architecture. While the number of scales is easily tuned, the patch recomposition strategy is here fixed as a simple average. Although this linear strategy helps to preserve the covariance structure of the random field, it inexorably produces some blur in the synthesized images, which is often the main explication for the failure cases encountered in this article. This issue would certainly be solved by constraining the patch distribution after the patch recomposition strategy. But this would require a radical change of the model architecture that we leave for further investigation.