Wasserstein Generative Models for Patch-Based Texture Synthesis

Abstract

This work addresses texture synthesis by relying on the local representation of images through their patch distributions. The main contribution is a framework that imposes the patch distributions at several scales using optimal transport. This leads to two formulations. First, a pixel-based optimization method is proposed, based on discrete optimal transport. We show that it generalizes a well-known texture optimization method that uses iterated patch nearest-neighbor projections, while avoiding some of its shortcomings. Second, in a semi-discrete setting, we exploit differential properties of Wasserstein distances to learn a fully convolutional network for texture generation. Once estimated, this network produces realistic and arbitrarily large texture samples in real time. By directly dealing with the patch distribution of synthesized images, we also overcome limitations of state-of-the-art techniques, such as patch aggregation issues that usually lead to low frequency artifacts (e.g. blurring) in traditional patch-based approaches, or statistical inconsistencies (e.g. color or patterns) in machine learning approaches.

This study has been carried out with financial support from the French Research Agency through the GOTMI project (ANR-16-CE33-0010-01). The authors also acknowledge the French GdR ISIS through the support of the REMOGA project.

1 Introduction

General Context. Among the boiling topic of image synthesis, exemplar-based texture synthesis aims at generating large textures from a small sample. This is of great interest in various fields ranging from computer graphics for cinema or video games to image or artwork restoration. The exemplar texture is often assumed to be perceptually stationary, i.e. with no large geometric deformations nor lighting changes.

Representing an image with its set of patches, which are small sub-images of size $s\times s$, is particularly well suited in this stationary setting. Patches take profit of the self-similarities contained in natural images, and are at the core of efficient image restoration methods [2, 8, 13]. Patch representation has proven to be fruitful for designing texture synthesis methods ranging from simple iterative copy/paste or nearest-neighbor procedures [3, 12] to methods that aim at imposing the patch distribution using optimal transport [4, 7, 14].

These patch-based approaches generally suffer from three main practical limitations. First, the patches are often processed independently and then combined to form a recomposed image [4, 14]. The overlap between patches leads to low frequency artifacts such as blurring. Second, the optimization has to be performed sequentially in a coarse-to-fine manner (both in image resolution and patch size) starting from a good initial guess. Last, global patch statistics must be controlled along the optimization to prevent strong visual artifacts [7, 10].

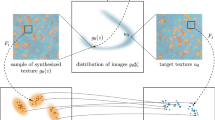
In this work, we circumvent these limitations and introduce a framework for synthesizing a texture such that its patch distributions at different scales are close, in an optimal transport sense, to the one of the exemplar image. We demonstrate that patches are sufficient features for texture synthesis when used in an appropriate optimal transport framework, as illustrated in Fig. 1. Actually, even if deep features representations have shown impressive performances for image synthesis [5, 9], patch-based methods are still competitive when only a single image is available for training [1, 17], both considering the computational cost and the visual performance. Moreover, deep learning methods are still difficult to interpret, whereas patch-based models offer a better understanding of the synthesis process and its cases of success and failure.

Our framework is naturally adapted to the training of a generative network with the semi-discrete formulation of optimal transport. To this end, we rely on feed-forward convolutional neural networks proposed in [1, 17, 19] for texture and image generation. Training a texture generator with our optimal transport approach allows to generate on-the-fly arbitrarily large textures. Finally, an interesting by-product of the proposed method is that it defines a discrepancy measure between two textures by computing the mean of the optimal transport cost between patch distributions at various scales.

Fig. 1.

Two synthesis examples illustrating the drawbacks that are overcome with our optimal transport framework on patches (Algorithm 1). Contrary to the method TexOptim from [12], our method respects the statistics from the exemplar image and unlike the method of Gram-VGG from [5], it does not suffers from color inconsistency artifacts.

Overview of the Paper. The goal of the method is to synthesize a texture whose multi-scale patch distributions are close in an optimal transport sense to the ones of the target texture. Consider a target texture image $v \in {\mathcal K}^m$ with m pixels taking values in ${\mathcal K}\subset {\mathbf{R}}^d$ bounded¹. We define the collection of its patches $\{P_1v,\ldots , P_mv\}$ as the set of all sub-images of size $p= s \times s$ extracted from v. For the sake of simplicity, we use periodic boundary conditions so that the number of patches is exactly m. Then we define the empirical patch distribution of v by $\nu = \frac{1}{m}\sum _{i=1}^m \delta _{P_i v}$. Our objective is therefore to prescribe the statistics of the patch distribution of the synthesized textures, in order to match the target distribution $\nu$. To do so, we propose one framework for synthesizing a single texture image u (Sect. 3) and one for learning a generative model $g_\theta \sharp \zeta$ (Sect. 4), where the push-forward of a measure $\zeta$ is defined by $g_\theta \sharp \zeta (B) =\zeta (g_\theta ^{-1}(B))$ for any borel set B. In both cases, we force the patch distribution $\mu _t$ of the synthesized textures (depending on a variable t which is either the image u or the parameters $\theta$) to be close to the empirical patch distribution $\nu$ for the optimal transport cost

$$\begin{aligned} \mathrm {OT}_c(\mu _t,\nu ) = \inf _{\pi \in \varPi (\mu _t,\nu )} \int c(x,y)d\pi (x,y), \end{aligned}$$

(1)

where $c :{\mathcal K}^p\times {\mathcal K}^p \rightarrow {\mathbf{R}}$ is a Lipschitz cost function and $\varPi (\mu _t,\nu )$ is the set of probability distributions on ${\mathcal K}^p\times {\mathcal K}^p$ having marginals $\mu _t$ and $\nu$. When using $c(x,y) = \Vert x-y\Vert ^2$, as done for experiments in this work, $\mathrm {OT}_c$ corresponds to the square of the Wasserstein-2 distance. Minimizing with respect to t the optimal transport cost from Eq. (1) appears to be a hard task. Therefore, considering the discrete nature of $\nu$, we propose to take advantage of the semi-discrete formulation of the optimal transport cost (see [16])

$$\begin{aligned} \mathrm {OT}_c(\mu _t,\nu ) = \max _{\psi \in {\mathbf{R}}^m} F(\psi ,t) := \int \psi ^{c}(x) d \mu _t(x) + \frac{1}{m}\sum _{j=1}^m \psi _j \end{aligned}$$

(2)

where the c-transform of $\psi$ writes in this case $\psi ^{c}(x) = \min _{j} \left[ c(x,P_jv) - \psi _j\right]$. Estimating the variable t, i.e. the image u or the generator’s parameters $\theta$, amounts to solving the following minimax problem

$$\begin{aligned} \min _t \max _\psi F(\psi ,t). \end{aligned}$$

(3)

For fixed t, the function $\psi \mapsto F(\psi ,t)$ is concave and an optimal $\psi ^*$ can be approximated with an averaged stochastic gradient ascent as proposed in [6].

When the variable t is an image, we propose in Sect. 3 to perform a gradient descent, which outcome is illustrated in Fig. 1. A stochastic gradient-based algorithm is then proposed in Sect. 4 to learn a generative model using a convolutional neural network. Both approaches exploit the property, demonstrated in Sect. 2, that the gradient of the optimal transport $\nabla _t \mathrm {OT}_c(\mu _t,\nu )$ coincides with the gradient $\nabla _t F(\psi ^*,t)$ of the function F at an optimal value $\psi ^*$.

2 Gradient of Optimal Transport

This section is devoted to the computation of the gradient with respect to the parameter t of the optimal transport cost $\mathrm {OT}_c(\mu _t,\nu )$ in the considered semi-discrete case. We show, under hypotheses on the patch distribution $\mu _t$, that $\nabla _t \mathrm {OT}_c(\mu _t,\nu ) = \nabla _t F(\psi ^*,t)$ with $\psi ^*\in \mathop {\text {arg max}}\nolimits _\psi F(\psi ,t)$, when both terms exist. More precisely, we consider $\mu _t = \frac{1}{n}\sum _{i=1}^n (P_i\circ g_t)\sharp \zeta$ to be the patch distribution of a generative model $g_t\sharp \zeta$, where $\zeta$ is a fixed probability measure on ${\mathcal Z}\subset {\mathbf{R}}^r$ and $g_t(\cdot ) = g(t,\cdot )$ is defined with a measurable function $g:{\mathcal T}\times {\mathcal Z}\rightarrow {\mathcal K}^n$ where ${\mathcal T}\subset {\mathbf{R}}^q$ is the open set of parameters. For a given z, $g_t(z)$ is an image whose patches are $P_ig_t(z)=(P_i\circ g_t)(z)$. This encompasses the image optimization problem of Sect. 3 using $g_t\sharp \zeta = \delta _t$. The function F defined in (2) then becomes

$$\begin{aligned} F(\psi , t) =\frac{1}{n}\sum _{i=1}^n \mathbf {E}_{Z\sim \zeta }\left[ \psi ^c(P_i \circ g_t(Z))+ \frac{1}{m}\sum _{j=1}^m \psi _j \right] . \end{aligned}$$

(4)

In order to solve the related minimax problem (3), we need the gradients of F with respect to $\psi$ and t. The function F is concave in $\psi$ and its gradient has been studied in [6]. To compute the gradient with respect to t, one has to deal with the points of non-differentiability of $\psi ^c(x)$, that reads $\psi ^c(x) = \min _j\left[ c(x,P_jv) - \psi _j\right]$ in the semi-discrete case. To that end, we introduce the open Laguerre cells

$$\begin{aligned} L_j(\psi ) = \left\{ x ~|~\forall k\ne j, ~c(x,P_jv) - \psi _j < c(x,P_kv) - \psi _k \right\} . \end{aligned}$$

(5)

The set of points where $\psi ^c$ is differentiable coincides with $\cup _j L_j(\psi )$, whose complement is negligible if c is a $\ell _p$ cost. In order to avoid points living in this complementary set, we introduce the following hypothesis.

Hypothesis 1

g satisfies Hypothesis 1 at $(t, \psi )$ if $\zeta \left( (P_i\circ g_{t})^{-1}\{ \cup _j L_j(\psi ) \}\right) =1$ for any patch position i, that is, for a given variable t, the generated patches are almost surely within the Laguerre cells defined by $\psi$.

Note that Hypothesis 1 is satisfied for any $\psi$ if $c(x,y)=\Vert x-y\Vert _p^p$ and if, for any i, $(P_i\circ g_{t})\sharp \zeta$ is absolutely continuous with respect to the Lebesgue measure.

We also introduce a regularity hypothesis for the generative model $g_t$ to control its variations and differentiate under expectation.

Hypothesis 2

There exists $K:{\mathcal T}\times {\mathcal Z}\rightarrow {\mathbf{R}}_+$ such that for all t, there exists a neighborhood V of t such that $\forall \ t' \in V$ and $\forall \ z \in {\mathcal Z}$

$$\begin{aligned} \Vert g(t, z) - g(t',z)\Vert \le K(t,z)\Vert t-t'\Vert \end{aligned}$$

(6)

with K verifying for all t, $\mathbf {E}_{Z\sim \zeta }\left[ K(t,Z)\right] < \infty$.

Now, we show the following theorem that ensures the differentiability of F with respect to the parameter t.

Theorem 1

Assume c to be $\mathscr {C}^1$. Let g satisfy Hypothesis 2. Let $t_0$ be a point where $t\rightarrow g_t(z)$ is differentiable $\zeta (z)$-a.e. and let g satisfy Hypothesis 1 at $(t_0,\psi )$. Then $t \mapsto F(\psi , t)$ is differentiable at $t_0$ and

$$\begin{aligned} \nabla _t F(\psi , t_0) =\frac{1}{n}\sum _{i=1}^n \mathbf {E}_{Z\sim \zeta }\left[ ( \partial _t g(t_0,Z))^T \nabla \psi ^c(P_ig(t_0,Z)) \right] \end{aligned}$$

(7)

with $\nabla \psi ^c(P_ig(t_0,z)) = \nabla _x c(P_ig(t_0,z), P_{\sigma (i)}v)$ where $\sigma (i)$ is the unique index such that $P_ig(t_0,z) \in L_{\sigma (i)}(\psi )$ (which exists $\zeta (z)$-almost surely).

Proof

Since $\psi ^c$ is differentiable on $\cup _jL_j(\psi )$, Hypothesis 1 implies that for any i, $\psi ^c(P_i g_t(z))$ is differentiable at $t_0$ for $\zeta$-almost every z with gradient $\partial _t g(t_0,z))^T \nabla \psi ^c(P_ig(t_0,z))$. Since the derivatives of c are bounded by a constant C and since g satisfies Hypothesis 2, we get a neighborhood V of $t_0$ such that for any $t\in V$ and any z, $\Vert (\partial _t g(t,z))^T \nabla \psi ^c(P_ig(t,z))\Vert \le K(t_0,z) C$ with $\mathbf {E}[K(t_0,Z)] <\infty$. Differentiating under the expectation yields the final result.    $\square$

Finally, we relate the gradient of F to the gradient of the optimal transport.

Theorem 2

Let $t_0$ such that $t \mapsto \text {OT}_c(\mu _t, \nu )$ and $t \mapsto F(\psi ^*, t)$ are differentiable at $t_0$ with $\psi ^*\in \mathop {\text {arg max}}\nolimits _\psi F(\psi , t_0)$ then

$$\begin{aligned} \nabla _t\text {OT}_c(\mu _{t_0}, \nu ) = \nabla _t F(\psi ^*, t_0) \end{aligned}$$

(8)

Proof

Let fix $\psi ^*\in \mathop {\text {arg max}}\nolimits _\psi F(\psi , t_0)$. The function $h(t) = F(\psi ^*, t) - \mathrm {OT}_c(\mu _t, \nu )$ is differentiable at $t_0$ and maximized at $t_0$, therefore we get $\nabla _t h(t_0) = 0$.    $\square$

3 Image Optimization

In this section we introduce a pixelwise optimization algorithm that minimizes a optimal transport cost between patch distributions. This discrete optimal transport problem is covered by the framework of Sect. 2 by taking $g_u(z) = z - u$ for all z and $\zeta = \delta _0$, so that $g_u\sharp \delta _0 = \delta _u$. Then we relate this algorithm to the texture optimization framework of [12] and propose a multi-scale extension to account for different scales in the sample texture to synthetize. Finally, we illustrate the experimental stability and convergence of the proposed framework.

3.1 Mono-Scale Texture Synthesis Algorithm

Let $u \in {\mathbf{R}}^n$ be the image to synthesize with n pixels and $\mu _u= \frac{1}{n}\sum _{i=1}^n \delta _{P_i u}$ its patch distribution. In order to prescribe to u the patch distribution $\nu$ of the exemplar image v, we aim at solving

$$\begin{aligned} \min _{u \in {\mathbf{R}}^n} \mathrm {OT}_c\left( \mu _{u}, \nu \right) = \min _{u \in {\mathbf{R}}^n} \max _{\psi \in {\mathbf{R}}^m} F(\psi , u), \end{aligned}$$

(9)

where

$$\begin{aligned} F(\psi , u) = \frac{1}{n} \sum _{i=1}^n \psi ^c(P_iu) + \frac{1}{m}\sum _{j=1}^m\psi _j \text { and } \psi ^c(P_iu) = \min _j\left[ c(P_iu, P_jv) -\psi _j\right] . \end{aligned}$$

Note that the problem is quite similar to [7] where the primal formulation of optimal transport between discrete patch distributions is however considered. As in [12], the authors resort to an alternative minimization scheme requiring to solve an optimal assignment problem at each step, which turns out to be computationally prohibitive. To solve the minimax problem (9), we also propose an iterative alternate scheme in u and $\psi$, starting with an initial image $u^0$. However, for the discrete case of optimal transport being considered, the authors of [6] show that an optimal potential $\psi ^*$ can be estimated with a gradient ascent on $\psi$. Therefore, for a fixed $u^k$, we perform a gradient ascent with respect to $\psi$ to obtain an approximation $\psi ^{k+1}$ of $\psi ^*\in \mathop {\text {arg max}}\nolimits _\psi F(\psi , u^{k})$. A gradient descent step is then realized on u, using the gradient of F with respect to u given in Theorem 1. Note that if $\psi ^*$ is an optimal potential and if we are at a point of differentiability of the $\mathrm {OT}_c$, Theorem 2 relates this gradient of F to the gradient of $\mathrm {OT}_c$. Realizing a gradient step in this direction thus corresponds to performing a gradient descent step for the optimal transport.

Using the quadratic cost $c(x,y) = \frac{1}{2}\Vert x-y\Vert ^2$, as in the experiments, we have

$$\begin{aligned} \nabla _u F(\psi ^{k+1},u^k) = \frac{1}{n} \left( \sum _{i=1}^nP_i^TP_iu^k - \sum _{i=1}^nP_i^TP_{\sigma ^{k+1}(i)}v\right) , \end{aligned}$$

(10)

at a point $(\psi ^{k+1},u^k)$ where we can uniquely define

$$\begin{aligned} \sigma ^{k+1}(i) = \mathop {\text {arg min}}\limits _j \frac{1}{2}\Vert P_iu^k-P_jv \Vert ^2 - \psi ^{k+1}_j . \end{aligned}$$

(11)

Notice that $P_j$ is a linear operator whose adjoint $P_j^T$ maps a given patch q to an image whose j-patch is q and is zero elsewhere. Therefore $\sum _{i=1}^nP_i^T$ corresponds to an uniform patch aggregation. To simplify, we consider periodic conditions for patch extraction, so that $\sum _{i=1}^nP_i^TP_i = p\mathrm {I}$, where $p=s\times s$ denotes the number of pixels in the patches. Hence, from (10) and considering a step size $\eta \frac{n}{p}$, $\eta >0$, the update of u through gradient descent writes

$$\begin{aligned} u^{k+1} = (1-\eta ) u^{k} + \eta v^{k}, \end{aligned}$$

(12)

where $v^{k} = \frac{1}{p}\sum _{i=1}^nP_i^TP_{\sigma ^{k+1}(i)}v$ is the image formed with patches from the exemplar image v which are the nearest neighbors to the patches of $u^k$ in the sense of (11). The gradient step then mixes the current image $u^k$ with $v^k$. In the case $\psi = 0$, the minimum in (11) is reached by associating to each patch of $u^k$ its $\ell _2$ nearest neighbor in the set $\{P_1v,\ldots , P_nv\}$, as similarly done in [12].

This image synthesis process is illustrated in Fig. 2, with a comparison of image synthesis for various patch sizes. As expected, this method cannot take into account variations that may occur at scales larger than s. We therefore propose a multi-scale extension in the next section.

Fig. 2.

Influence of patch-size s for the pixel optimization method Alg. 1 with $L=1$.

3.2 Multi-scale Texture Synthesis

In order to deal with various texture scales, we extend our method in a multi-scale fashion. In [7], a coarse-to-fine greedy strategy is used, where the optimization is performed iteratively at a smaller resolution, before upscaling the solution to the next scale. This strategy is employed on both image resolution and patch size in [12]. In this work, we propose to solve the optimal transport problem at different scales simultaneously.

We first create a pyramid of down-sampled and blurred images. For each scale $l = 1, \ldots , L$, we use a linear blurring and down-sampling operator $S_l$ that computes a reduced version $u_l = S_l u$ of u of size $n/2^{l-1}\times n/{2^{l-1}}$. The multi-scale texture synthesis is obtained by minimizing

$$\begin{aligned} \mathcal {L}(u) = \sum _{l=1}^{L} \max _{\psi _l}F_{v_l}(u_l, \psi _l), \end{aligned}$$

(13)

where $F_{v_l}(u_l, \psi _l) = \frac{1}{n} \sum _{j=1}^n \min _i\left[ c(P_ju_l ,P_iv_l) - (\psi _l)_i\right] + \frac{1}{m}\sum _{i=1}^m(\psi _l)_i$. As for the single-scale case, an alternate scheme is considered to minimize $\mathcal {L}$. The gradient descent update of u combines gradient at multiple scales: $\nabla _u\mathcal {L}(u) = \sum _{l=1}^{L}S_l^T\nabla _u F_{v_l}(u_l, \psi _{l})$. The multi-scale process is summarized in Algorithm 1.

3.3 Experiments

In all experiments, we consider $L=4$ scales and patches of size $s=4$. We use auto-differentiation from the Pytorch package and gradient descent is performed with the Adam optimizer [11] with learning rate 0.01. We use $N_\psi = 10$ iterations for the estimation of $\psi$ at each step. The process takes approximately 3 min to run 500 iterations for synthesizing a $256 \times 256$ image on a GPU Nvidia K40m.

Figure 1 shows examples of synthesized textures with Algorithm 1 and comparisons with a patch-based method [12] and the state-of-the art method [5] prescribing deep neural features from VGG-19 [18]. While it is already known that the approach of [5] might have color inconsistencies [15], it mostly suffers here from the small resolution of the input, which makes difficult the extraction of deep features.

Contrary to our method and [5], the approach of [12] does not rely on statistics and does not respect the distribution of features from the original sample. Therefore, it must be initialized with a good guess (permutation of patch) instead of any random image. Additionally, it requires to sample large patches (from $s=32$ to $s=8$) on a sub-grid to enforce local copy and avoid blurring. We illustrate in Fig. 3 the stability of our method with respect to the initialization. Faithful textures are obtained from any initialization (column b): random image (first row) or another texture (second row).

With our Algorithm 1, the optimization nevertheless has to be done each time a new image is synthesized. In order to define a versatile algorithm that generates new samples on-the-fly, we rely on generative models in the next section.

Fig. 3.

Algorithm 1 is run for the same $100\times 100$ sample (a) with two initial images (b). Both results in faithful $200\times 200$ synthesis (c) in $k=500$ iterations and the loss $\mathcal {L}(u_k)$ (13) shows a monotone convergence behaviour (d).

4 Training a Convolutional Generative Network

In this section, we consider the problem of training a network to generate images that have a prescribed patch distribution at multiple scales. Then we present some visual results together with a comparison with existing methods. Finally we discuss quantitative evaluation of texture synthesis methods and we propose a framework to derive a multi-scale optimal transport loss between patch distributions that can be used as an evaluation score for texture synthesis.

4.1 Proposed Algorithm for Semi-discrete Formulation

We now consider a generator $g_\theta$ defined through a function g that is assumed to satisfy Hypothesis 2, which guarantees the existence of gradients in Theorem 1. The optimal transport formulation is now semi-discrete (in comparison with the previous discrete case). We then propose a stochastic alternate algorithm for training the generator $g_\theta$.

From Theorem 2, the gradient of the optimal transport can be expressed with the gradient of the function F. Since this gradient writes as an expectation from Theorem 1, we perform a stochastic gradient descent considering the term inside the expectation in (7) as a stochastic gradient. In the semi-discrete case, an optimal potential $\psi ^*$ can also be approximated with an averaged stochastic gradient ascent [6]. This leads us to propose Algorithm 2 for minimizing the following loss w.r.t. parameters $\theta$:

$$\begin{aligned} L(\theta ) = \sum _{l=1}^{L} \max _{\psi _l} \mathbf {E}_{z\sim \zeta } \left[ F_{v_l}(\psi _l,\left( g_\theta (z)\right) _l)\right] . \end{aligned}$$

(14)

In practice, for each iteration k and at each layer l we first update the corresponding potential $\psi _l$ with an averaged stochastic gradient ascent as proposed in [6]. Then we sample an image and perform a stochastic gradient step in $\theta$. In order to test our framework, the function $g_\theta$ has the same convolutional architecture as the one used for texture generation in [19]. This network has been designed to synthesize textures by minimizing the Gram-VGG loss introduced in [5]. We next demonstrate that we are able to learn the parameters of such a generative network by only enforcing the patch distributions at various scales.

In our PyTorch implementation , we use the Adam optimizer [11] to estimate the parameters $\theta$. We run the algorithm for 10000 iterations with a learning-rate $\eta _{\theta } = 0.01$. An averaged stochastic gradient ascent with 100 inner iterations is used for computing $\psi ^*$. In this setting, 30 min are required to train our generator with a GPU Nvidia K40m.

Fig. 4.

Texture synthesis from a generative network trained on a single $256\times 256$ sample (a). Comparison of our multi-scale approach (b) using $4\times 4$ patches (see Alg. 2) with TexNet [19] (using VGG-19 features), SinGAN [17], PSGAN [1] and TexTo [14].

4.2 Experimental Results and Discussions

Figure 4 gives a comparison of our results with four relevant synthesis methods from the literature. We first consider the Texture Networks (TexNet) method [19], which trains a generative network using VGG-19 feature maps computed on a sample texture. Note that the very same convolutional architecture has been used for our model. We also compare to SinGAN [17] (a recent generative adversarial newtork (GAN) technique generating images from a single example relying on patch sampling), to PSGAN [1] (a previous approach that similarly adapts the GAN framework to the training of a single image) and to TexTo [14] (which also constrains patch distributions with optimal transport but in an indirect way). We used Pytorch implementations of SinGAN, PSGAN, and TexNet, with their default parameters.

The results obtained with our Alg. 2 are visually close to the ones from TexTo [14]. However, the patch-aggregation step from TexTo makes the results blurrier than our method which inherently deals with the aggregation issue. Although TexNet [19] produces textures that look sharper than our results, it may fail to reconstruct larger structures as in the fourth image. Observe that patch-based networks TexTo and SINGAN create less visual artifacts (checkerboard patterns due to VGG pooling, false colors, etc.). Dealing with patch distributions can lead to local copy of large-scale structures as we can easily see in the second row of Fig. 4. Although similar large scale structures are copied, they are not exact copy/pastes of the same area from the exemplar texture and local changes can be observed within these similar patterns. Moreover, this phenomenon also appears for other methods, particularly in SINGAN and PSGAN.

4.3 Evaluation of Texture Synthesis Methods

Evaluating texture synthesis methods is a complex and open question. The visual quality is subjective and for now, there is no widely accepted perceptual metric. For quantitative evaluation, several metrics have been proposed, such as SIFID [17] (Single Image Fréchet Inception Distance) or the metric given by the feature correlations of VGG [5]. Using our framework, we also propose a new evaluation metric that measures the Wasserstein distance between patch distributions at each scale. Table 1 presents the scores for these three metrics for textures from Fig. 4.

Table 1. Evaluation of texture synthesis from Fig. 4 for various discrepancy measures, emphasizing best result and second best (lower is better). The average score (Avg) is computed over all images. SIFID [17] is computed from first max pooling Inception features. VGG Gram norm [5] is computed from cross-correlation of VGG features as used by [19]. The proposed distance is based on multi-scale patch optimal transport.

As expected, each method performs better for its associated metric. Our two algorithms and TexTo present the lowest scores for the proposed optimal transport loss, whereas TexNet [19] obtains the best results with the metric based on VGG features or the inception network. Our algorithms reach competitive scores for all these metrics and achieve the best results for two of the four proposed textures with Alg. 1. Let us mention however that the considered metrics are not always directly correlated to perception: in the last texture of Fig. 4, TexNet presents smaller values for both SIFID and VGG scores, whereas the synthesized texture does not match the input one in term of large-scale coherence.