1 Introduction

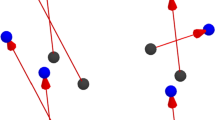
Single-View Geometry (SVG) is concerned with how cameras form images of the world geometrically. More precisely, SVG deals with the geometry and algebra of the warp, a mapping that exists between a model of the world and a model of the image, as illustrated by Fig. 1. SVG endeavors to (i) establish the existence and form of such mappings, (ii) study their characteristics and (iii) estimate them numerically. For rigid bodies, SVG uses simple geometric primitives such as points and an algebraic projective framework, which led to a deep understanding of points (i), (ii) and (iii) [6, 9, 13]. Point (i) merely uses the body’s pose and the camera’s pinhole projection model and leads to the projective camera represented by a (\(3\times 4\)) matrix, point (ii) studies what properties make a (\(3\times 4\)) matrix valid as a camera and point (iii) solves the so-called camera resection or pose estimation problem. The case of deformable bodies forms an open and challenging research challenge, owing to the deformation causing the model and observed body shapes to be different. Deformable SVG is important because it will form the mathematical framework for and deepen our understanding of the Shape-from-Template (SfT) problem [12, 18, 23]. In order to define deformable SVG more specifically, we start with the informal definition of an important mapping, the embedding. The embedding maps points from the body’s model to its deformed state in camera coordinates and thus extends the notion of relative body–camera pose from the rigid case as it also holds the body’s deformation. As in the rigid case, the projection mapping represents the camera, mapping points from the deformed body to its observed image. The warp is then defined as the composition of the projection with the embedding. It maps points from the body’s model to the observed image of the deformed body. This informal definition of the warp already provides a simple and generic answer to point (i). In contrast, point (ii) is much more involved, but tremendously important to understand, for two main reasons. The first reason is to understand the theoretical possibility of characterizing the observations forming valid images independently of the body’s deformed state. It contrasts with the rigid case where the body’s state is already known: In the deformable case, the observed shape is unknown because deformation occurred between the body’s state in the model and the body’s state as observed in the image. The second reason is that the theoretical characteristics of the warp may be used to improve point (iii). For deformable bodies, it is indeed very common to estimate the warp using a derivative-penalizing regularizer, as in the Thin-Plate Spline [3] and optic flow computation [10]. An understanding of point (ii) can provide physically sound regularizers, with the potential to improve warp estimation. Importantly, these regularizers are independent of the observed shape and thus insensitive to reconstruction ambiguities. These considerations, however, require further assumptions on the embedding, for, by definition, the warp is so far just a mere locally smooth mapping.

Fig. 1
figure 1

Geometric setup used in studying SVG. The mapping to be studied is the warp, which exists between the body’s model and the body’s image. In the rigid case, the image shows the body’s model up to pose and perspective projection. In the deformable case, the body’s shape changes between the model and image with much higher complexity and the setup uses the embedding-projection framework. The 1D setup is simpler to study that the 2D setup yet provides valuable theoretical and practical insights for both cases

Full size image

We propose to study deformable SVG for locally rational projective embeddings. Locally rational means that the embeddings resemble a rational function of some degree in the infinitesimal vicinity of any smooth point. A rational function is formed by the ratio of two polynomials and thus naturally includes simple polynomial functions. It is simple to see that the locally rational embeddings lead to locally rational warps, as the projection mapping is essentially a ratio. A noteworthy consequence is that the polynomial embeddings do not lead to a simplified form of the warp and thus of the SVG. Our motivations for choosing these embeddings are threefold. Our first motivation is genericity: The chosen embeddings can represent the surface of thin or thick objects, whether they deform isometrically or in more complex ways. Indeed, any embedding can be locally approximated to a good extent by its Taylor or Padé approximation [21] at some finite order. Understanding the limits of using such an extremely generic prior, slightly stronger than mere local smoothness, forms a fundamental research question. A locally linear embedding was successfully used in isometric deformable reconstruction [17]. The chosen embeddings generalize this concept, as they can behave locally as polynomials of a fixed but arbitrary degree, beyond linearity. Our experimental results show that in terms of warp estimation, the quadratic and cubic locally rational models outperform the linear model, so that the proposed generalization brings a practical improvement. Our second motivation is simplicity and stability of the representation. A global embedding model would have to adjust its complexity to the actual deformation. Therefore, coping with complex deformations would come at the price of a higher degree, potentially causing instabilities. In contrast, the chosen embeddings are locally constrained to behave similarly to rational functions of low degree. Our third motivation is that this representation allows us to truly model perspective projection without ever approximating it. Indeed, perspective projection is simply expressed by rationality, which is perfectly respected by the proposed invariants.

Our methodology is to first study point (ii) for strictly rational embeddings, establishing differential invariants on the warp. Because the existence and study of such invariants for an arbitrary degree were not previously established, except for the special case of linear rational functions [15], this forms a main contribution of our work. We specifically studied the differential invariants though other non-differential invariants may exist. We then study point (iii), deriving warp regularizers from our differential invariants. We use these regularizers as soft penalties in warp estimation in place of the usual derivative-penalizing regularizers. Concretely, we have chosen to work with a 1D setup, for which the deformable body is a plane curve, the camera a projection from 2D to 1D and the warp a 1D mapping. Our motivations are twofold. Our first motivation is that the 1D warp case forms a necessary step to establish the 2D warp case, where the deformable body is a surface and the camera a usual pinhole. The 1D case is simpler than the 2D case, yet conveys valuable insights on the theoretical form of the sought invariants, their use in warp estimation and their practical impact. Indeed, our experimental results show that in terms of warp estimation, the locally rational representation substantially outperforms the locally polynomial representation assumed by the existing derivative-penalizing regularizers, when used in a compound cost exploiting point correspondences. Our second motivation is that the 1D warp invariants already give a subset of the 2D warp invariants. We show this fact by constructing a virtual 1D setup from the 2D setup. The main result is that the 1D invariants hold for a 1D warp along any rational curve chosen in the 2D model and for any 1D projection of the 2D image.

We first review previous work in §2 and give background material in §3. We then give our theoretical results on the invariants of univariate rational functions in §4 and show how this applies to deformable 1D SVG in §5. We give experimental results on warp estimation in §6 and a conclusion in §7. Finally, a first appendix discusses the extension of our 1D framework to higher dimensions, in particular to form a basis for 2D deformable SVG, and a second appendix gives the proof of our proposition regarding the invariants.

2 Previous Work

We split our review of previous work into four parts: deformable SVG, the 1D camera, rational functions and the embedding-projection framework.

Deformable SVG. SVG has been well studied for rigid bodies [6, 9, 13] and very scarcely for deformable bodies. Most of the work in SfT, whose geometric setup is modeled by SVG, focuses on computing the body’s 3D deformation and not on characterizing the warp’s properties [12, 18, 23]. The estimation of rigid SVG and Multiple-View Geometry (MVG) from images of algebraic curves was thoroughly studied [14, 24]. The deformable case of multiview reconstruction was specifically studied for isometric curves [6]. A comprehensive differential framework was given in [5]. There are two main differences between these works and ours. First, they use a rigid or an isometric prior, while we use a locally rational model, which is a much more generic and thus much weaker constraint. Second, they study the differential relationships between space and image curves for quantities such as speed, curvature and torsion, while we establish generic invariants at any order.

The 1D camera. We use the 1D camera as a simplified case of the regular 2D camera. The 1D camera was introduced in [22] for line-based affine Structure-from-Motion but can be also derived by analogy to the usual 2D camera. It has a total of five parameters which are two intrinsics (the focal length f and the principal point \(q_0\), both expressed in number of pixels) and three extrinsics (a rotation angle and two translation parameters). The strategy of using the 1D camera to simplify a 2D problem was used in the rigid case; for instance, the 1D trifocal tensor is much easier to understand and work with than the 2D trifocal tensor [7, 8]. We defined the 1DSfT problem and showed that it makes expressing a constraint such as isometry much easier than in the usual 2D formulation [11]. We showed that, in general configuration, 1DSfT has a discrete number of solutions if the isometric prior is used, but an infinite number of ambiguities otherwise. Solutions derived in the 1D case can sometimes be used directly in the 2D case. For instance, the geometry of a 2D camera in planar motion is equivalent to a 1D camera on the trifocal plane of the 2D cameras [8].

Rational functions. Rational functions are used in several areas of applied mathematics such as data interpolation via the Padé approximation [21] and the Non-Uniform Rational B-Spline (NURBS) [19]. Their properties were studied for instance in [25, 26]. The closest fundamental result to ours is probably the Schwarzian derivative [16], a differential version of the cross-ratio which we showed may be directly used in warp estimation [20]. The Schwarzian is also the solution of the ODE \(2\mu ^{(1)}\mu ^{(3)}-3{\mu ^{(2)}}^2=0\) [15], where \(\mu ^{(k)}\) represents the kth derivative of \(\mu \). In the context of SVG, it is derived by considering a linear projective embedding, or equivalently, making the assumption that the curve is locally flat. Our theory generalizes the Schwarzian by considering rational projective embeddings of an arbitrary degree and has the Schwarzian as a special case.

The embedding-projection framework. The embedding-projection framework has been extensively used to model SfT. In the 2D setup, differential solutions were found to resolve reconstruction for the isometric and conformal models [1]. The framework has more recently been used in the 1D setup to study isometric reconstruction [11]. These works and their extensions use differential equations giving the reconstruction in terms of the warp. However, none of them studied deformable SVG. They thus assume that the warp is computed in a preliminary step, independently of the reconstruction, thereby neglecting valuable constraints. In contrast, our study of deformable SVG shows that the warp strongly depends on the assumptions made on the embedding. Deriving these warp invariants by marginalizing the embedding is far from trivial, but using them in warp estimation then brings substantial improvements.

3 Background

3.1 Notation

We write logical equivalence as \(\Leftrightarrow \). We use \(C^\infty (\mathbb {R} ^c,\mathbb {R} ^d)\) for the set of smooth functions from \(\mathbb {R} ^c\) to \(\mathbb {R} ^d\) and use the shortcut \(C^\infty {\mathop {=}\limits ^{{\mathrm{def}}}}C^\infty (\mathbb {R},\mathbb {R})\). We write \({\mathcal {U}}=[a,b]\) the set of natural numbers in the interval [a, b], for \(a,b\in \mathbb {N}\). For a set \({\mathcal {U}}\subset \mathbb {N}\), \({\mathcal {U}}= [u_1,u_{|{\mathcal {U}}|}]\), we define \(\mu ^{({\mathcal {U}})} {\mathop {=}\limits ^{{\mathrm{def}}}}( \mu ^{(u_1)} \,\,\,\cdots \,\,\,\mu ^{(u_{|{\mathcal {U}}|})} )^\top \) as a multivalued function giving the orders of derivatives of \(\mu \) from \({\mathcal {U}}\). We use \(\mathbb {R} ^*\) to denote the set of nonzero real numbers and \(\mathbb {N}^*\) to denote the set of nonzero natural numbers.

3.2 Univariate Polynomial Functions

Let \({\mathcal {P}}_{n}\) be the set of univariate polynomials of degree n and \({\bar{{\mathcal {P}}}}_n {\mathop {=}\limits ^{{\mathrm{def}}}}{\mathcal {P}}_0 \cup \cdots \cup {\mathcal {P}}_n\) the set of univariate polynomials of degree at most n. For instance, \({\mathcal {P}}_0\) is the set of constant functions, \({\mathcal {P}}_1\) the set of linear functions and \({\bar{{\mathcal {P}}}}_1={\mathcal {P}}_0 \cup {\mathcal {P}}_1\) the set of constant and linear functions. We have:

$$\begin{aligned} \delta \in {\mathcal {P}}_{n}\Rightarrow & {} \{ \delta ^{(e)} = 0 ~|~ e>n \} \end{aligned}$$
(1)
$$\begin{aligned} \delta ^{(e)} = 0\Rightarrow & {} \{ \delta \in {\mathcal {P}}_{n} ~|~ n<e \} \end{aligned}$$
(2)
$$\begin{aligned} \delta ^{(e)} = 0\Leftrightarrow & {} \delta \in {\bar{{\mathcal {P}}}}_{e-1}. \end{aligned}$$
(3)

3.3 Univariate Rational Functions

A univariate rational function \(\mu \) is a fraction of two polynomials of degrees \(a,b\in \mathbb {N}\), respectively. We define \(\mu \)’s degree as the pair \((a,b)\in \mathbb {N}^2\). Formally, a function \(\mu \) is a univariate rational function if and only if \(\exists a,b \in \mathbb {N}\text {~s.t.~ }{\mathcal {R}}_{a,b}[\mu ]\) with:

$$\begin{aligned} {\mathcal {R}}_{a,b}[\mu ]\,\,\,{\mathop {\Leftrightarrow }\limits ^{{\mathrm{def}}}}\,\,\, \left( \exists \alpha \in {\mathcal {P}}_{a},\gamma \in {\mathcal {P}}_{b},\gcd (\alpha ,\gamma )\in \mathbb {R} ^* \text {~s.t.~ }\mu = \frac{\alpha }{\gamma } \right) , \nonumber \\ \end{aligned}$$
(4)

where \(\gcd (\alpha ,\gamma )\) is the polynomial greatest common divisor of \(\alpha \) and \(\gamma \). The condition on \(\gcd (\alpha ,\gamma )\) means that the fraction cannot be simplified to a lower degree. The domain of \(\mu \) is \(\Omega \subset \mathbb {R} \) with \(\Omega = \{ x\in \mathbb {R} ~|~\gamma (x)\not =0 \}\). A function \(\mu \) is a univariate rational function of degree at most (a, b) if \({\bar{{\mathcal {R}}}}_{a,b}[\mu ]\) holds with:

$$\begin{aligned} {\bar{{\mathcal {R}}}}_{a,b}[\mu ]\,\,\,{\mathop {\Leftrightarrow }\limits ^{{\mathrm{def}}}}\,\,\, \left( \exists \alpha \in {\bar{{\mathcal {P}}}}_{a},\gamma \in {\bar{{\mathcal {P}}}}_{b} \text {~s.t.~ }\mu = \frac{\alpha }{\gamma } \right) . \end{aligned}$$
(5)

Abusing notation, we write \(\mu \in {\mathcal {R}}_{a,b}\) and \(\mu \in {\bar{{\mathcal {R}}}}_{a,b}\) equivalently to \({\mathcal {R}}_{a,b}[\mu ]\) and \({\bar{{\mathcal {R}}}}_{a,b}[\mu ]\), respectively. The set of univariate rational functions forms a field, meaning that the addition, subtraction, multiplication and division of rational functions is a rational function.

4 Canonical Invariants of Univariate Rational Functions

We show that a univariate rational function \(\mu \) of degree (a, b) satisfies differential invariants. These invariants form an infinite set for a given degree (a, b), as function \(\mu \) also satisfies the invariants of higher degrees. We here define and study the canonical invariant of degree (a, b). Importantly, when applied to a function \(\mu \in C^\infty \), the canonical invariant constrains \(\mu \) to be a univariate rational function of degree at most (a, b). It is straightforward to see that the canonical invariant thus implies all the invariants of higher degrees.

Our key result is given in the next proposition. It is an equivalence between the set of univariate rational functions of some maximal degree and the canonical differential invariant of that degree. The proof of this proposition is given as Appendix B.

Proposition 1

(Canonical invariants) A function \(\mu \) is a univariate rational function of degree at most (a, b) if and only if it satisfies the canonical invariant \({\mathcal {I}}_{a,b}\). Formally:

$$\begin{aligned} \forall \mu \in C^\infty ,a,b\in \mathbb {N}\quad \quad {\bar{{\mathcal {R}}}}_{a,b}[\mu ] \,\,\,\Leftrightarrow \,\,\, {\mathcal {I}}_{a,b}[\mu ] \end{aligned}$$

with:

$$\begin{aligned} {\mathcal {I}}_{a,b}[\mu ] \,\,\,{\mathop {\Leftrightarrow }\limits ^{{\mathrm{def}}}}\,\,\, \left( \sum _{s \in {\mathcal {S}}_{b+1}} {{\,\mathrm{sgn}\,}}(s) \prod _{i=1}^{b+1} { a+i \atopwithdelims ()s_i-1 } \mu ^{(a+i-s_i+1)} = 0 \right) .\nonumber \\ \end{aligned}$$
(6)

We use \({\mathcal {S}}_{b+1}\) to generate all permutations of the set \([1,b+1]\) and \({{\,\mathrm{sgn}\,}}(s)\in \{-1,1\}\) to compute the signatureFootnote 1 of permutation \(s=\{s_1,\dots ,s_{b+1}\}\). \({\mathcal {I}}_{a,b}[\mu ]\) is an homogeneous polynomial ODE of degree \(b+1\). The lowest and greatest orders it involves are \(\max (a-b+1,0)\) and \(a+b+1\), respectively.

Examples. We give four examples of univariate rational functions and canonical invariants and discuss the general case and advanced examples. An important case is the one of linear fractional functions, which are univariate rational functions of degree (1, 1). Any univariate rational function \(\mu \) of degree (1, 1) can be written as \(\mu (x)=\frac{a_1x+a_0}{b_1x+b_0}\) for \(a_0,a_1,b_0,b_1\in \mathbb {R} \). Proposition 1 says that such functions are also characterized by the following differential canonical invariant:

$$\begin{aligned} {\mathcal {I}}_{1,1}[\mu ] \,\,\,\Leftrightarrow \,\,\, \left( -2\mu ^{(1)}\mu ^{(3)}+3\mu ^{(2)}\mu ^{(2)} = 0 \right) . \end{aligned}$$

This can be easily verified. This invariant is the ODE from which the Schwarzian derivative was derived [15], and as expected, it corresponds to linear fractional functions, called homographies in the context of projective geometry. The same reasoning leads to the differential canonical invariant for the quadratic fractional functions, using \((a,b)=(2,2)\), as:

$$\begin{aligned} {\mathcal {I}}_{2,2}[\mu ]\Leftrightarrow & {} \Big ( -12\mu ^{(1)}\mu ^{(3)}\mu ^{(5)}+15\mu ^{(1)}\mu ^{(4)}\mu ^{(4)} \\&\,\, + \, 18\mu ^{(2)}\mu ^{(2)}\mu ^{(5)} -30\mu ^{(2)}\mu ^{(4)}\mu ^{(3)}\\&\,\, + \, 40\mu ^{(3)}\mu ^{(3)}\mu ^{(3)}-30\mu ^{(3)}\mu ^{(2)}\mu ^{(4)} = 0 \Big ). \end{aligned}$$

The numerator’s and denominator’s degrees need not be equal, and we can for instance derive the canonical invariants for the constant-quadratic or the quadratic-linear fractional functions as:

$$\begin{aligned} {\mathcal {I}}_{0,2}[\mu ]\Leftrightarrow & {} \Big ( \mu ^{(0)}\mu ^{(0)}\mu ^{(3)}-3\mu ^{(0)}\mu ^{(2)}\mu ^{(1)}\\&\,\, + \, 6\mu ^{(1)}\mu ^{(1)}\mu ^{(1)}-3\mu ^{(1)}\mu ^{(0)}\mu ^{(2)} = 0 \Big ), \end{aligned}$$

and:

$$\begin{aligned} {\mathcal {I}}_{2,1}[\mu ] \,\,\,\Leftrightarrow \,\,\, \left( -3\mu ^{(2)}\mu ^{(4)}+4\mu ^{(3)}\mu ^{(3)} = 0 \right) . \end{aligned}$$

We observe that the order of the invariants increases with a, while the number of terms and degrees increase with b.

Generally speaking, any rational plane curve induces a rational warp which thus satisfies the proposed invariants. For example, the warp \(\mu \) induced by a cubic B-spline satisfies \({\mathcal {I}}_{3,3}[\mu ]\), while the warp \(\mu \) induced by a cubic NURBS satisfies \({\mathcal {I}}_{9,9}[\mu ]\), as shown in §5.3.

Polynomial kernel of the canonical invariants. The kernel of the simple derivative invariant of order e is formed by the polynomials of degree \(e-1\), see Eq. 3. The canonical invariant of order (a, b) also includes polynomials in its kernel, forming the polynomial kernel of the canonical invariant. Their degree is now derived in terms of a, b. As can be seen from Eq. 6 and from the examples above, the canonical invariant \({\mathcal {I}}_{a,b}[\mu ]\) is a sum where each term has partial derivatives of \(\mu \) as factors. Therefore, using Eq. 1, there must exist a polynomial \(\hat{\mu }\) so that \({\mathcal {I}}_{a,b}[\hat{\mu }]\) holds. We call \(\hat{\mu }\in {\bar{{\mathcal {P}}}}_{d}\) the polynomial kernel of \({\mathcal {I}}_{a,b}\), and define the polynomial kernel’s degreed as the greatest natural number so that \(\forall \hat{\mu }\in {\bar{{\mathcal {P}}}}_{d}\), \({\mathcal {I}}_{a,b}[\hat{\mu }]\) holds. It is easy to show that \(d=a\). This is obtained by considering that each term in \({\mathcal {I}}_{a,b}[\mu ]\) must vanish. Because a term is a product of derivatives, what matters is thus the greatest order involved in the term, as the derivative at this order vanishes with a higher degree polynomial than the other derivatives. Overall, for all terms to vanish, we must thus select \(d+1\) as the minimum over the terms in \({\mathcal {I}}_{a,b}[\mu ]\) of the greatest order involved in each term. By examining Eq. 6, we can compute the sum of orders on each term as \(\sum _{i=1}^{b+1} (a+i-s_i+1) = (a+1)(b+1)\), which is a constant value. Additionally, there is a term in \({\mathcal {I}}_{a,b}[\mu ]\) where all orders are equal. Together, these imply that \(d+1\), the minimum over the terms of the greatest order per term, is given by the order of the term where all factors have the same order. Because we have \(b+1\) factors per term, we obtain \(d=\frac{(a+1)(b+1)}{b+1}-1=a\). For the four examples above, we have \(d=1\), \(d=2\), \(d=0\) and \(d=2\). In the first example, it says that the polynomial kernel is made of linear functions \(\hat{\mu }\in {\mathcal {P}}_1\), for which \(\hat{\mu }^{(2)}=0\). Of course, the canonical invariant does not only have polynomials in its kernel, but also univariate rational functions, according to Proposition 1. The polynomial kernel is indeed included in the general kernel, as \(\hat{\mu }\in {\bar{{\mathcal {P}}}}_a \Rightarrow {\bar{{\mathcal {R}}}}_{a,0}[\hat{\mu }] \Rightarrow {\bar{{\mathcal {R}}}}_{a,b}[\hat{\mu }]\) for \(b\ge 0\).

5 Deformable Single-View Geometry

We first give our notation and show how the warp is derived for a generic embedding and perspective projection. We then specialize the derivation to rational embeddings, showing that the warp is then itself rational. We finally show how to estimate the warp under a locally rational regularization constructed from the canonical invariants.

5.1 Notation

We denote the deformed plane curve as \({\mathcal {C}}\) in the projective plane \(\mathbb {P}^2\). We represent \({\mathcal {C}}\) by a projective embedding \(\varphi :\Omega \rightarrow \mathbb {P}^2\) where \(\Omega \subset \mathbb {R} \) is the curve parameterization’s domain, leading to \({\mathcal {C}}=\varphi (\Omega )\). In other words, we have that \({\mathcal {C}}\) is the set of points of the projective plane \(\mathbf Q = \varphi (p) \in \mathbb {P}^2\) obtained by embedding any point \(p\in \Omega \). The camera is given by a function \(\Pi :\mathbb {P}^2\rightarrow \mathbb {R} \) representing a 1D projective camera [22], and the warp is simply \(\eta {\mathop {=}\limits ^{{\mathrm{def}}}}\Pi \circ \varphi \). We require \(\eta \in C^\infty (\Omega ,\mathbb {R})\), meaning that the warp must be a smooth function, except at some points where the invariants may not be evaluated. This is implied by requiring that \({\mathcal {C}}\) is a smooth curve lying entirely in the open projective half-plane representing the front or the back of the camera, but, however, forms a weaker requirement.

5.2 The Warp for a Generic Embedding

The general 1D projective camera \(\Pi \) can be defined as the composition of a 2D homography \(h:\mathbb {P}^2\rightarrow \mathbb {P}^2\) and the canonical perspective projection as:

$$\begin{aligned} \Pi (\mathbf Q ) \,\,\,{\mathop {=}\limits ^{{\mathrm{def}}}}\,\,\,\frac{\mathbf{h _{1}}^\top \mathbf{Q }}{\mathbf{h _{2}}^\top \mathbf{Q }}, \end{aligned}$$
(7)

with \(\mathbf h _1,\mathbf h _2\in \mathbb {R} ^3\) and not both identically zero. These six parameters are defined up to scale, meaning that only five of them are independent and contain the camera’s two intrinsics and three extrinsics. Whether the camera is calibrated or not does not change the way deformable SVG is defined in this context. Using Eq. 7, we derive the warp as:

$$\begin{aligned} \eta \,\,\,=\,\,\,\Pi \circ \varphi \,\,\,=\,\,\,\frac{\mathbf{h _{1}}^\top \varphi }{\mathbf{h _{2}}^\top \varphi }. \end{aligned}$$
(8)

5.3 The Warp for a Locally Rational Embedding

We denote the three components of the projective embedding as \(\varphi ^\top = [\varphi _1 \,\, \varphi _2 \,\, \varphi _3 ]\). We first assume that the embedding is rational, meaning that we have \(\varphi _i \in {\bar{{\mathcal {R}}}}_{a_i,b_i}\), and so that there exist \(\alpha _i\in {\bar{{\mathcal {P}}}}_{a_i}\), \(\gamma _i\in {\bar{{\mathcal {P}}}}_{b_i}\), \(i\in \{1,2,3\}\) with \(\varphi _i = \frac{\alpha _i}{\gamma _i}\). We analyze the numerator and denominator of \(\eta \) in Eq. 8 by letting \(l\in \{1,2\}\) as:

$$\begin{aligned} \mathbf h _l^\top \varphi= & {} h_{l1}\varphi _1+h_{l2}\varphi _2+h_{l3}\varphi _3 \\= & {} h_{l1}\frac{\alpha _1}{\gamma _1} + h_{l2}\frac{\alpha _2}{\gamma _2} + h_{l3}\frac{\alpha _3}{\gamma _3} \\= & {} \frac{h_{l1}\alpha _1\gamma _2\gamma _3 + h_{l2}\alpha _2\gamma _3\gamma _1 + h_{l3}\alpha _3\gamma _1\gamma _2}{\gamma _1\gamma _2\gamma _3}. \end{aligned}$$

We thus have:

$$\begin{aligned} \frac{\mathbf{h }_{1}^\top \varphi }{\mathbf{h }_{2}^\top \varphi } \,\,\,=\,\,\,\frac{h_{11}\alpha _1\gamma _2\gamma _3 + h_{12}\alpha _2\gamma _3\gamma _1 + h_{13}\alpha _3\gamma _1\gamma _2}{h_{21}\alpha _1\gamma _2\gamma _3 + h_{22}\alpha _2\gamma _3\gamma _1 + h_{23}\alpha _3\gamma _1\gamma _2}. \end{aligned}$$

Since \(\delta _1\in {\bar{{\mathcal {P}}}}_a,\delta _2\in {\bar{{\mathcal {P}}}}_b \Rightarrow \delta _1\delta _2 \in {\bar{{\mathcal {P}}}}_{a+b}, \delta _1+\delta _2\in {\bar{{\mathcal {P}}}}_{\max (a,b)}\) we have \(\eta \in {\bar{{\mathcal {R}}}}_{a,b}\) with:

$$\begin{aligned} a = b = \max (a_1+b_2+b_3,a_2+b_3+b_1,a_3+b_1+b_2), \end{aligned}$$

where we recall that \((a_i,b_i)\) is the degree of \(\varphi _i\), \(i\in \{1,2,3\}\). Therefore, we have \(\eta \in {\bar{{\mathcal {R}}}}_{a,a}\), and we can use Proposition 1 to state that \({\mathcal {I}}_{a,a}[\eta ]\) must hold. This way, we have obtained constraints that the warp must satisfy in order to be geometrically valid for a rational embedding. This brings an answer to point (ii) of SVG, which we defined in Introduction as a study of the warp’s characteristics, independently of the embedding and projection. Our target assumption, however, is that the embedding is locally rational, meaning that it is rational in an infinitesimal neighborhood of each point \(p\in \Omega \). Consequently, the warp is also locally rational. The key advantage is that representing a non-trivial curve with a globally rational embedding requires one to use high-degree polynomials for its numerator, its denominator or both of them, whereas using high-degree polynomials is not stable in practice [21]. In contrast, a locally rational warp is a flexible and stable warp, which will be constrained to behave similarly to a low-degree rational warp on a local basis. A similar reasoning may be found in the definition of B-spline curves, which are both flexible and stable thanks to the use of local low-degree polynomials [19]. In practice, we use a stable generic deformable model for the warp and perform warp estimation using a regularizer constructed from the canonical invariants. When used as a penalty term in warp estimation, this regularizer makes the warp behave locally like a rational map. This process is described in the next section, where we use a simple Gaussian radial basis function to model the warp.

5.4 Estimating the Warp from Correspondences

We describe how the canonical invariants fit into a framework to estimate the warp from point correspondences. This framework preserves the generic warp model’s natural flexibility while making it locally rational. It is different from using an explicit rational embedding which would make the warp globally rational.

General methodology We want to estimate the warp \(\eta \) from m point correspondences \(\{p_j,q_j\}\), \(p_j\in \Omega \), \(q_j\in \mathbb {R} \), \(j\in [1,m]\). The general methodology is to define a correspondence cost functional \(C[\eta ] = \frac{1}{m} \sum _{j=1}^m {\left( \eta (p_j)-q_j \right) }^2\) and a regularizer \(R[\eta ]\), and to solve the following variational problem:

$$\begin{aligned} \min _\eta C[\eta ] + \lambda R[\eta ], \end{aligned}$$
(9)

where \(\lambda \in \mathbb {R} ^+\) is the regularization weight, controlling the relative influence of the two terms in relationship to the intrinsic scale of each term.

Regularization weight The value of \(\lambda \) is important. We choose it by splitting the correspondences into a training set, a validation set and a test set. We then sample \(\lambda \) on a predefined range, solve problem 9 for each value of \(\lambda \) using the training set and finally keep the warp with the lowest validation residual. The sampling range is chosen such that outside it the resulting warp does not exhibit significant changes. We use 30 samples in our experiments.

Regularizer In the literature, the regularizer is often derived from the \(L_2\) norm of the warp’s partial derivatives integrated over the domain. For example, the B-spline [19] and the Thin-Plate Spline [4] were constructed by penalizing second-order derivatives. We call these the polynomial regularizers because they constrain the warp to be locally polynomial. We use a low order \(k\in \{1,2,3\}\) because the regularizers are differential, thus measured very locally. This already allows significant flexibility on the warp. They are defined as:

$$\begin{aligned} R_{\mathrm{POL}\ k}[\eta ] \,\,\,{\mathop {=}\limits ^{{\mathrm{def}}}}\,\,\,\int _\Omega { \left( \eta ^{(k)}(p) \right) }^2 \mathrm{d}p. \end{aligned}$$

We, however, show in §5.3 that a locally polynomial or rational embedding leads to a locally rational warp with degree (a, a). We thus use the canonical rational invariant \({\mathcal {I}}_{a,a}\) given in Proposition 1 to construct new regularizers, for \(a\in \{1,2,3\}\), as:

$$\begin{aligned} R_{{\mathrm{RAT}}\ a}[\eta ] \,\,\,{\mathop {=}\limits ^{{\mathrm{def}}}}\,\,\,\int _\Omega { \left( {\mathcal {I}}_{a,a}[\eta ](p) \right) }^2 \mathrm{d}p. \end{aligned}$$

The regularizers are applied to the whole warp. However, they are constructed as integrals over the domain \(\Omega \). Importantly, the integrands measure the warp’s closeness to a polynomial or a rational function at point \(p\in \Omega \). The regularizers thus measure the extent to which the warp is everywhere locally similar to a polynomial or a rational function. In other words, the lower the regularizer, the closer the warp to a local polynomial or rational function on each and every point of its domain.

Minimization In order to solve problem 9, we introduce a flexible parametric representation of the warp using a Gaussian radial basis function [2]. The l Gaussian bases are uniformly spread across the domain \(\Omega \), which we define as \(\Omega = \{ p \in \mathbb {R} ~|~ 0\le p\le 1\}\) by default. Their position is defined as \(c_1,\dots ,c_l\in \Omega \) and thus given by \(c_k=\frac{k-1}{l-1}\), \(k\in [1,l]\). Their standard deviation \(\sigma \) is fixed. The parameters to estimate are thus contained in a set \({\varvec{\omega }}\in \mathbb {R} ^l\) of l weights, one for each Gaussian basis. We use \(l=50\) Gaussian bases with \(\sigma = \frac{5}{l}\) in our experiments. The parametric warp representation is thus \(\eta (p;{\varvec{\omega }}) {\mathop {=}\limits ^{{\mathrm{def}}}}\sum _{k=1}^l \omega _k \exp \left( - \frac{(p-c_k)^2}{2\sigma ^2}\right) \). We use gradient descent starting from the identity warp.

Results Each estimated warp is tied to a regularizer and thus denoted accordingly, as POL1, POL2, POL3, RAT1, RAT2 and RAT3. As a baseline, we also used the radial basis function representation fitted without a regularizer, by setting \(\lambda =0\) in problem 9. The resulting warp is denoted PLAIN.

Fig. 2
figure 2

Results of simulated data experiments. From left to right, the object is slanted, curved and both slanted and curved. From top to bottom, the simulated camera and object with the observed point shown in black, individual plots and joint plot with normalization of the six measured quantities

Full size image

6 Experimental Results

Our two main goals are (i) to assess to which extent the invariants hold on an independent warp and (ii) to assess their contribution to the stability of warp estimation when used to form regularizers. We report two sets of experiments to evaluate these two main goals, both using simulated and real data.

6.1 Assessing the Invariants on Independent Warps

We want to compare the value of the invariants estimated for independent warps, in order to objectively find the ability of each invariant to capture the warp’s behavior. This is because, even if theoretically the rational invariants use a more physically valid representation of the warp than the simple warp derivatives, their dependency on higher order derivatives may cause instabilities. For simulated data, we use the true warp, while for real data, we use the PLAIN warp. We first describe the measured quantities.

6.1.1 Measured Quantities

We measured six quantities related to the six regularizers defined in §5.4. These are the first three derivatives of the warp, namely \(|\eta ^{(1)}|\), \(|\eta ^{(2)}|\) and \(|\eta ^{(3)}|\), related to the classical polynomial regularizers, and the first three canonical invariants, namely \(|{\mathcal {I}}_{1,1}[\eta ]|\), \(|{\mathcal {I}}_{2,2}[\eta ]|\) and \(|{\mathcal {I}}_{3,3}[\eta ]|\), related to the rational regularizers. We use the absolute value as only the magnitude of these quantities matters, not their sign. However, because they are of different orders of magnitude, they cannot be cross-compared individually. We thus also report a normalized version of these six quantities achieved by dividing by the maximum over a set of values.

6.1.2 Simulated Data

Simulation setup We simulated a 1D perspective camera with a 1 unit focal length observing a 1D flat object of size 4 units whose midpoint is located 10 units from the center of projection. The flat object is then deformed, which is represented by simulating its embedding from the template domain \(\Omega \). By projecting the object, we arrive at a simulated image. Because the warp \(\eta \) is the composition of the known projection and embedding functions, as shown by Eq. 8, we can estimate the warp’s target value and its derivatives analytically at any point in \(\Omega \). We use a fixed point shown in black on the simulated shape in Fig. 2 to monitor the six measured quantities. We then did three types of basic transformations of the object: slanting, curving and a combination of both. The embedding is rational for the former but not for the last two transformations, as it involves trigonometric functions. This way, our measurements depend directly on the basic transformations of slanting and curving and can be plotted according to the amount of perspective, of curvature and of their combination.

Perspective The default fronto-parallel view of the object does not contain perspective. In order to increase the perspective effect, we slanted the object by rotating it around its midpoint with an angle \(\theta \) varying between 0\(^{\circ }\) and 45\(^{\circ }\). The results are shown in the left column of Fig. 2. We observe that the warp derivatives are sensitive to perspective. More precisely, \(|\eta ^{(2)}|\) and \(|\eta ^{(3)}|\) vanish at \(\theta =0\), when the object is exactly fronto-parallel, but then quickly increase with perspective, while \(|\eta ^{(1)}|\) does not even vanish at \(\theta =0\). On the other hand, all three canonical invariants \(|{\mathcal {I}}_{1,1}[\eta ]|\), \(|{\mathcal {I}}_{2,2}[\eta ]|\) and \(|{\mathcal {I}}_{3,3}[\eta ]|\) vanish independently of the amount of perspective.

Fig. 3
figure 3

Results of real data experiments. The top row shows the input 2D images from which the 1D images were constructed. The middle and bottom rows show the six measured quantities individually and in a joint plot with normalization, respectively

Full size image

Curvature. The default flat-shaped object does not contain curvature. In order to increase curvature, we curved the object by linearly morphing its shape with an arc of radius 4 units. Importantly, the resulting shape is not described by a polynomial or a rational function. The results are shown in the middle column of Fig. 2. We make the same observation on the warp derivatives as in the increasing perspective case: These are sensitive to curvature. On the other hand, contrarily to the case of perspective, the canonical invariants also show sensitivity to curvature. We observe that the sensitivity decreases with the order. More precisely, \(|{\mathcal {I}}_{1,1}[\eta ]|\) performs very similarly to \(|\eta ^{(2)}|\) and \(|\eta ^{(3)}|\), while \(|{\mathcal {I}}_{2,2}[\eta ]|\) and \(|{\mathcal {I}}_{3,3}[\eta ]|\) show better performance, \(|{\mathcal {I}}_{3,3}[\eta ]|\) having a flat regime approximately twice as long as \(|{\mathcal {I}}_{2,2}[\eta ]|\). We observe that \(|{\mathcal {I}}_{2,2}[\eta ]|\) and \(|{\mathcal {I}}_{3,3}[\eta ]|\) have a large intrinsic scale, exhibiting larger values than the other four invariants. The intrinsic scale of an invariant is arbitrary. Importantly however, it does not influence the results of warp estimation, thanks to the cross-validation mechanism selecting the regularization weight automatically.

Combined perspective and curvature. We increased both perspective and curvature by combining slanting and curving of the object as above described. The results are shown in the right column of Fig. 2. We make the same observations as in the increasing curvature case: All six measured quantities are sensitive to the combined effect of perspective and curvature. There are two important differences, however. First, there is a larger gap between the group formed by the warp derivatives and \(|{\mathcal {I}}_{1,1}[\eta ]|\) and the group formed by \(|{\mathcal {I}}_{2,2}[\eta ]|\) and \(|{\mathcal {I}}_{3,3}[\eta ]|\). Second, there is a smaller gap between \(|{\mathcal {I}}_{2,2}[\eta ]|\) and \(|{\mathcal {I}}_{3,3}[\eta ]|\).

Synthesis. Our experimental observations perfectly confirm the theory. First, we have that the warp derivatives are not invariant to camera perspective and object curvature. Second, we have that all canonical invariants are insensitive to camera perspective and have various sensitivities to object curvature. The first-order canonical invariant is very sensitive to object curvature while the second- and third-order canonical invariants have a good tolerance. This is sensible because a higher order canonical invariant models a higher order rational embedding able to represent the object’s local curvature.

6.1.3 Real Data

Data acquisition and result presentation We emulated a 1D camera by slicing space along a plane containing the center of projection of a 2D camera. Concretely, we created a 1D template with 30 regularly spaced black tick marks which we printed on a paper sheet. We then selected a horizontal line crossing the ticks on the 2D image of the deformed paper sheet. The ticks were manually marked in the 2D image and these locations projected on the line. The 1D coordinates of the ticks along this line define the 1D image obeying the geometry of a 1D camera. Each tick thus gives a 1D correspondence between the template and the image. The interest of this dataset lies in the noise distribution on the data, which is more realistic than on simulated data, in the realism of the 2D shape and in the realism of the physical imaging process, to which the pinhole camera is just an approximation. We fitted the warp PLAIN to the correspondences. We then chose 100 points uniformly spread in the template and used the warp to estimate their location in the image and their derivatives. From these, we estimated the value of the six measured quantities, sorted them and plotted them individually and jointly with normalization, as for the simulated data. For a particular quantity, the plotted curve thus starts with the lowest values, obtained for the points where the warp best minimizes the quantity and increases toward the highest values, obtained for the points where the warp is least compatible with the quantity.

Results The results obtained for three images are shown in Fig. 3. The first-order derivative \(|\eta ^{(1)}|\) does clearly not do a good job, as it has a steady logarithmic or linear increase. The second- and third-order derivatives \(|\eta ^{(2)}|\) and \(|\eta ^{(3)}|\) perform better, but also show an increase at all points. Similarly, the first-order canonical invariant \(|{\mathcal {I}}_{1,1}[\eta ]|\) shows an increase at all points, performing worse than \(|\eta ^{(2)}|\) and \(|\eta ^{(3)}|\). The second- and third-order canonical invariants \(|{\mathcal {I}}_{2,2}[\eta ]|\) and \(|{\mathcal {I}}_{3,3}[\eta ]|\), however, both have a flat part starting at the beginning of their curves. This flat part means that these two quantities, and thus the corresponding invariants, form a better model of the warp than the other quantities. The third-order canonical invariant \(|{\mathcal {I}}_{3,3}[\eta ]|\) is significantly better than the second-order one \(|{\mathcal {I}}_{2,2}[\eta ]|\). These results agree with the synthetic data experiments to some extent. Indeed, as predicted by theory, we have that the canonical invariants perform better than the mere derivatives, because they model the effect of perspective. The results also differ from the synthetic data experiments as for the canonical invariants, the larger the degree, the better the results. This is explained by the fact that the local shape is probably of higher complexity in the real data case and thus requires a more complex warp to be accurately captured.

6.2 Assessing the Invariants in Warp Estimation

We want to evaluate the performance of the six regularizers defined in §5.4 in warp estimation from point correspondences.

6.2.1 Simulated Data

We describe the simulation setup and then the results obtained when varying the amount of noise, the number of points and when creating an extrapolation area.

Fig. 4
figure 4

Results of simulated data experiments. The top row shows an example of simulated configuration. From left to right, the noise, number of points and extrapolation domain are varied. From the second to fourth row, the zeroth-, first- and second-order errors are shown for the seven tested warps

Full size image

Simulation setup We used the same simulation setup as in §6.1.2 with a more complex shape obtained by combining sines and cosines with a global rotation and translation. An example of shape is shown in Fig. 4. We generated a finite number of point correspondences which we corrupted with noise following a Gaussian distribution whose standard deviation controls the noise level. We used a default noise level of 0.5% of the object’s image size and number of points of 20. We split the correspondence set equally in training and validation sets. We used the true warp to assess the estimated warps by measuring the discrepancy at 1000 regularly sampled test points at the zeroth-, first- and second-orders. The zeroth-order discrepancy is the distance between the position predicted by the true and the estimated warp. The first- and second-order discrepancies are the differences between the first- and second-order derivatives predicted by the true and the estimated warp. The results are averages over 50 trials.

Noise We vary the noise level between 0 to 1% of the object’s image size. The results are shown in the left column of Fig. 4. We observe that the overall accuracy does not show the typical trend of degrading with noise. This is explained by the fact that regularization smoothes out noise. We observe that the POL1 warp gives the poorest performance. It is followed by a group comprising the PLAIN, POL2 and POL3 warps, with POL2 performing slightly better in terms of first-order error. We next find the RAT2 and RAT3 warps followed by the RAT1 warp. These three warps are on par in terms of zeroth-order error but the RAT1 warp performs clearly best in terms of the first- and second-order errors.

Fig. 5
figure 5

Results of real data experiments. The top row shows the input 2D images from which the 1D images were constructed. The other three rows show the result of the mild interpolation, strong interpolation and extrapolation experiments, respectively

Full size image

Number of points We vary the number of points between 10 and 50. The results are shown in the middle column of Fig. 4. We observe that the accuracy increases with the number of points for all warps at zeroth and first order. However, this increase becomes very shallow for the POL1, POL2, POL3 and PLAIN warps at second order. The POL1 warp has the worst performance, followed by a group with the POL2, POL3 and PLAIN warps. The RAT2 and rat3 warps perform better and the RAT1 warp outperforms, except for lower numbers of points. The differences between the warps increase with the order.

Extrapolation We created an extrapolation domain by removing input correspondences in a localized part on the side of the object. We observe that the accuracy degrades with the size of the extrapolation domain. The POL1 warp has the worst performance, and the RAT1 warp has the best performance. We find in between the five other warps with performances depending on the order and the size of the extrapolation domain. In particular, the RAT3 warp always outperforms at zeroth and first orders. It outperforms at second order when the extrapolation domain is smaller than 10% of the object.

Synthesis Our experimental observations show that there is a real benefit in using a rational regularizer over a regular polynomial regularizer in warp estimation. We have that the first-order rational regularizer outperforms in almost all cases. It is closely followed by the second- and third-order rational regularizers and then by the second- and third-order polynomial regularizers. Interestingly, the plain Gaussian radial basis function is on par with the second- and third-order rational regularizers. Finally, the first-order polynomial regularizer underperforms in almost all cases. The differences across the warps generally increase with the order of the estimated derivatives. The reason for these results is that the first-order rational regularizer forms the optimal trade-off in terms of local shape capture capability and local constraint strength. Indeed, the higher the degree, the more flexible the modeling capability but the weaker the constraint. The powerful modeling capability of the second- and third-order rational regularizers is thus impaired by the weakened local constraint they exert on the warp, compared to the first-order rational regularizer.

6.2.2 Real Data

In the case of real data, we do not have access to ground truth. We followed the estimation methodology described in §5.4 and three cases of splitting the 30 input point correspondences into training, validation and test sets. This allowed us to emulate mild and strong interpolation and extrapolation. The results are the test residuals given in Fig. 5. They are averages over 50 trials for each configuration in each case.

Mild interpolation The mild interpolation case emulates the non-uniformity of data by changing the size of the training set, without creating overly large areas of missing data. We used a fixed size of ten points for each of the validation and test sets while varying the number of training points from 10 to 5. These points are all chosen randomly at each trial. The results are shown in the second row of Fig. 5. We observe that all warps follow the same trend of nicely degrading for a decreasing number of training points. The PLAIN warp always performs worst while the RAT2 warp always performs best, except for the convex shape where the RAT3 warp performs slightly better for larger numbers of training points. The second worst is the POL1 warp. It is followed by the POL2 and then the POL3 warps. The POL3 warp has performances close to the RAT1 warp, which is itself below the RAT2 warp. Overall, the RAT2 warp has the best performance. This is because the RAT2 warp has increased modeling capabilities compared to the RAT1 warp from its higher degree. However, because the interpolation range is limited, the extra modeling capabilities of the RAT3 warp did not compensate its lower constraining strength on the warp.

Strong interpolation The strong interpolation case emulates the lack of data in possibly large areas surrounded by available data by changing the size of the test set within the domain. We split the input points into three parts. The left and right parts are used to sample the training and validation sets while the middle part forms the test set. We use a fixed number of ten points for each of the training and validation sets and ensure that five of each lies in the left and right parts. The number of test points is then varied from 1 to 9. It represents the size of the gap that the warp has to interpolate. The results are shown in the third row of Fig. 5. We observe that all warps roughly follow the same trend of degrading for an increasing interpolation range. The PLAIN and POL1 warps are the worst, except for the convex shape where the POL2 and RAT1 warps also perform poorly. The POL3 and RAT3 warps show better performances. The RAT1 warp is on par, except for the convex shape. The RAT2 warp performs better in all cases, except a single configuration with one point on the concave shape. Overall, the RAT2 warp has the best performance. The explanation for these results are similar to the mild interpolation case. Even though the interpolation range is larger, this remains a relatively easy task for the warps, and the extra modeling capability of the RAT3 warp is not needed.

Extrapolation The extrapolation case emulates the lack of data on the boundary of the domain by changing the size of the test set. We vary the number of test points from 1 to 9 and choose them as the leftmost points in the input points. We use a fixed number of ten points for each of the training and validation sets. They are chosen randomly in the remaining input points. The results are shown in the fourth row of Fig. 5. We observe a mild error increase or a slight error decrease, depending on the shape, for all warps but the POL1 warp, for an increasing extrapolation range. Indeed, the POL1 warp quickly degrades dramatically in all three shapes. It is then difficult to give a general ordering of the warps, as their performance changes significantly across the configurations and shapes. Nonetheless, we observe that the PLAIN warp does well as compared to the two previous cases of interpolation. While the best results are generally achieved by the RAT3 warp, the POL2 and POL3 warps outperform on the concave shape for smaller extrapolations. Overall, the RAT3 warp has the best performance. This is explained by the fact that the rat3 warp has the highest modeling capabilities of all the tested warps, and that extrapolation is fundamentally a more difficult task than interpolation, in the sense that the model must capture the structure of the data to a very good extent in order to make reliable predictions.

7 Conclusion

We have proposed a theoretical framework based on locally rational embeddings and univariate rational functions to formulate the SVG of a deformable body observed by a 1D projective camera. This framework is generic in the sense that it does not impose a specific deformation constraint, but uses mere local smoothness represented by a locally rational embedding. Our work is theoretic and includes experimental results showing the ability of the proposed invariants to improve the estimation of warps. Our framework fits in the recent and fascinating research topic of understanding the visual geometry of a deformable body. We now discuss two possibilities of future work based on our framework: deformable MVG and higher dimensions.

A natural question when working on deformable SVG is whether the framework would form a basis for deformable MVG. Local smoothness surely forms a good basis for deformable MVG because locally smooth warps have a local group structure. Concretely for two images, deformable SVG studies the smooth warps \(\eta _i \in C^\infty \) from the parameterization space defined from the embeddings as \(\eta _i = \Pi \circ \varphi _i\), \(i=1,2\), while deformable MVG studies the smooth inter-image warp \(\eta _{1,2} \in C^\infty \). By construction, we have \(\eta _{1,2} = \eta _2 \circ {\eta }^{-1}_1 = \Pi \circ \varphi _2\circ {\eta }^{-1}_1\). We can thus construct a smooth embedding \(\varphi _{1,2}\) by using image 1 as a parameterization space for image 2 as \(\varphi _{1,2} {\mathop {=}\limits ^{{\mathrm{def}}}}\varphi _2\circ {\eta }^{-1}_1\). Therefore, one could use local smoothness to define the warps and exploit the proposed deformable SVG.

Extending our 1D framework to higher dimensions also forms an appealing idea. The extension to 2D is particularly interesting, as it will allow one to handle the 2D images of surfaces taken by regular cameras.