General Deformations of Point Configurations Viewed By a Pinhole Model Camera

Abstract

This paper is a theoretical study of the non-rigid structure from motion problem: what can be computed from a monocular view of a parametrically deforming set of points? We treat various variations of this problem for 3D affine and general smooth deformations (under some mild technical restrictions) with either a calibrated or an uncalibrated camera. We show that in general at least three images related by quasi-identical deformations are needed to have a finite set of solutions to the points’ structure.

1 Introduction

Non-rigid structure from motion (NRSfM) from a monocular camera has been addressed in several papers. The setup is a camera tracking a deforming object. As the general problem is unconstrained there have been many papers addressing certain specifications of the general case, for example using a weak perspective or an affine camera, [1, 3, 4, 6, 13] or when the deformation of the object is restricted to be a linear combination of k rigid shapes [10]. Some papers constrain the deformation of the object to a physical model or a parameterized family of deformations which they then attempt to solve for in an optimization framework [12] or [28, 31] based on [29]. A review of much of the relevant literature can be found in [21]. A review of non-rigid 3d registration can be found in [30].

The general case of deforming configurations of points has also received attention, but with some restrictions. Some authors consider configurations of points moving with constrained motions [18, 26]. Other papers treat general motion but restrict their analysis to the case of a single point [2, 14,15,16]. There has not been much published on the theoretical underpinnings of the recovery of the structure of deforming configurations of points.

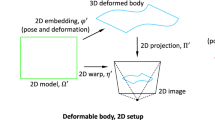
In this paper, we analyze, for the first time, the complexity and ambiguities of a fixed perspective camera tracking a parametrically set of deforming points in 3D. When the points move rigidly, this is the classic structure from motion (SfM) [11].

The specific deformations we analyze are affine and more generally smooth deformations under mild restrictions. We first focus on affine deformations, since general deformations are affine at the first order in a sense that will be detailed in Sect. 4. Therefore, when considering general deformations, we will essentially approximated them by successive affine deformations, as explained in details in Sect. 4.

The paper is organized as described in the following paragraphs.

We show that when the camera is calibrated and the body undergoes an affine deformation, a matching constraint similar to the classical epipolar geometry can be formulated. We show that from two images one cannot recover the deformation or the original points. When three images (i.e., two deformations) are available, we show that in a generic situation, the remaining ambiguity is still three-dimensional. However, when the two deformations are quasi-identical (see below for a complete definition), there is exactly one solution.

We also show that an invariant shape description can be recovered from 3 images. The recovery of this invariant does not require camera calibration.

Then, we turn our attention to the case of complete reconstruction (deformation and structure) for general smooth deformations. We show that if the deformation is slow with respect to the time frame and its spatial variations are small with respect to the mutual distances between the points, it can be calculated from a calibrated camera and 3 images, i.e., from the first view and a two other images coming from the same deformation repeated twice, like the affine distortion.

3D projective transformations are not treated as their images, at least in the 2 image case, are indistinguishable from those of affine transformations;

$$\begin{aligned} {[}I;0] \begin{pmatrix} A_{3 \times 4} \\ a \,b \,c \,d \end{pmatrix} = [I;0] \begin{pmatrix} A \\ 0\, 0\, 0\,1\end{pmatrix} \end{aligned}$$

We are mainly interested in the theoretical possibilities both as to the number of corresponding points and images needed. We present complete algebraic solutions. It will be seen that the theory for multiview deformation from a calibrated camera theory often resembles the multiview rigid body theory.

In order to illustrate our theoretical results, we have implemented most of the algorithms in Python. A Jupyter notebook is available at https://drive.google.com/file/d/16AcnSh_e-_9Nuam-QDkDub7ttAUa0F-A/view.

2 Affine Deformations: Motion and Shape

We start with the study of point correspondences undergoing affine deformations. This has both a practical and a theoretical impact. On the practical side, we shall see that one can write a matching constraint which is the classical epipolar geometry. Thus, finding correspondences between two images of an affinely deforming object can be done with the same machinery as in the classical case of images of rigidly moving bodies. We consider only invertible affine deformations to avoid degenerate situations where distinct points collapse to a single point after the deformation.

Fig. 1

The perspective image of the vertices of a cube, in black, deforming affinely to the blue points, the arrows are correspondences, epipolar lines

On the theoretical front, we shall use this result extensively in the sequel.

2.1 Fundamental Matrix

Let us consider a set of deforming points being imaged with a calibrated camera which we take WLOG as [I; 0]. The projection of a 3D point P in homogeneous coordinates into the first image is $q=[I;0]P$, while the projection into the second image is $q'=[I;0]\begin{pmatrix} A &{} t \\ 0 &{} 1\end{pmatrix} P$. Eliminating P from these two sets of equations leads to a bilinear constraint over the corresponding image points $q,q'$, the so-called fundamental matrix E where, $q'^t E q = 0$.

Lemma 1

When $t \ne 0$, the fundamental matrix of this pair of images is: $E \equiv [t]_{\times } A$, where $[t]_{\times }$ is the matrix of the cross product with t in the standard basis of ${\mathbb {R}}^3$.

Proof

Consider a point P in ${\mathbb {P}}^3$, not at infinity, projected to q in the first image. Then, $q \equiv [I;0]P$, thus $P = [\lambda q, 1]^t$, for some $\lambda \in {\mathbb {R}}$. [A; t]P is projected into the second image as $q' \equiv [A;t]P$. Thus, $q' \equiv (\lambda A q + t)$. Then, $[t]_{\times } q' \equiv [t]_{\times } Aq$ as $[t]_{\times } t=0$. This yields $q'^t [t]_{\times } A q=0$ giving $E \equiv [t]_{\times } A$. $\square$

If $t = 0$, E is not defined as $t_x$ $[t]_{\times }=0$.

We denote by $\equiv$ equality modulo multiplication by a nonzero scalar.

If there are corresponding pairs of points between the two images: $(q_i,q_i')_{i=1, \cdots ,n}$, the following equations hold:

$$\begin{aligned} q_i'^t E q_i = 0 \end{aligned}$$

(1)

for each i and rank E is 2 as rank $[t]_{\times }$ is 2. Indeed, the deformation is assumed to be invertible, i.e., $\det (A) \ne 0$. E can thus be computed from 7 pairs of corresponding points in general position or linearly from at least 8 pairs of points.

However, since E is rank 2 and is defined modulo multiplication by a nonzero scalar, the knowledge of it can only provide up to 7 over the 12 parameters that define an affine transformation. This implies that several images are necessary to compute the deformation. A more precise analysis is presented below. However, before we proceed, let us first investigate the relation with the classical multiple view geometry.

2.2 The Relation with Classical Multiview Imaging

As

$$\begin{aligned}{}[M;m]\left( \begin{pmatrix} A &{} t \\ 0 &{} 1\end{pmatrix}P \right) = [MA;Mt+m] P \end{aligned}$$

the images of affinely deforming points are equivalent to imaging a fixed structure with multiple cameras. Thus, relying on [11], from two images an affinely distorting object, O (and $\begin{pmatrix} A &{} t \\ 0 &{} 1\end{pmatrix}O$ ), can be reconstructed going through the fundamental matrix, with the uncertainty up to a 3d projective transformation.

Likewise, the recovery of the affine deformation from 3 images, as will be presented in v 2.3, is equivalent to autocalibration of a changing camera for the specific family of three cameras with parameters, $[I;0],[M;m],[M^2,Mm+m]$ with the extra caveat that the setup in the affine deformation case is not homogeneous. To our best knowledge, there is no specific algorithm for this configuration and every general autocalibration algorithm will produce a result modulo the group of projective transformations, which is not adapted to our purpose to compute the affine deformations.

Starting from the next section, we will present a more precise and in depth analysis of the case of interest for us, that is the case of affine deformations.

2.3 Deformation Recovery

Once the fundamental matrix $E \equiv [t]_{\times }A$ is computed, deformation can be recovered up to a 4-parameter ambiguity. To show this, we recall a lemma from [11] (page 255): If a rank 2 matrix F can be decomposed in two different ways as $F = [t]_{\times } A = [{\tilde{t}}]_{\times } {\tilde{A}}$, then there exists a constant $\lambda \ne 0$ and $v \in {\mathbb {R}}^3$, such that: ${\tilde{t}} = \lambda t$ and $\lambda {\tilde{A}} = A + tv^t$. Notice that since the matrix E is defined modulo ${\mathbb {R}}^*$ (multiplication by a nonzero scalar), there are 5 and not 4 degrees of freedom related to the extraction of the deformation from E.

Can more than two images help? Let us consider the situation where the deformation between the first and the second image is (A, a) and between the second and the third (B, b). We now have three distinct fundamental matrices: $E_{12} \equiv [a]_{\times } A$, $E_{23} \equiv [b]_{\times }B$ and $E_{13} \equiv [Ba+b]_{\times }BA$.

From $E_{12}$, we can compute $a_0$ and $A_0$ such that $\exists \alpha \ne 0, a = \alpha a_0$ and $\exists v_1, A = \frac{1}{\alpha }(A_0 + a_0 v_1^t)$. From $E_{23}$, we can compute $b_0$ and $B_0$ such that $\exists \beta \ne 0, b = \beta b_0$ and $\exists v_2, B = \frac{1}{\beta }(B_0 + b_0 v_2^t)$. From the third fundamental matrix $E_{13}$, we can compute $c_0$ and $C_0$ such that:

$$\begin{aligned} \exists \gamma \ne 0, Ba+b = \gamma c_0 \end{aligned}$$

(2)

and

$$\begin{aligned} \exists v_3, BA = \frac{1}{\gamma }(C_0 + c_0v_3^t) \end{aligned}$$

(3)

From Eqs. (2) and (3), we get the following system:

$$\begin{aligned} \left\{ \begin{aligned}&\alpha (B_0 + b_0 v_2^t) a_0 + \beta ^2 b_0 - \beta \gamma c_0 = 0\\&\gamma (B_0 + b_0 v_2^t) (A_0 + a_0 v_1^t) - \alpha \beta (C_0 +c_0v_3^t) = 0 \end{aligned} \right. \end{aligned}$$

(4)

Furthermore, one has to enforce the constraint that none of $\alpha ,\beta$ nor $\gamma$ vanishes. Formally, this is equivalent to computing in the localization of the polynomial ring with respect to these variables [7]. Concretely, one must introduce new variables: x, y, z and the equations: $\alpha x - 1 = \beta y - 1 = \gamma z -1 = 0$.

Eventually, the number of unknowns is $N = 9+3+3 = 15$ and we have exactly 15 equations. They define a real algebraic variety X of ${\mathbb {R}}^{15}$. By [19], it is known that real algebraic varieties are stratified manifolds. Roughly speaking a stratified manifold has a dense open set which is a smooth manifold and whose complement is a stratified manifold of strictly smaller dimension. Further technical conditions are needed to fully define a stratified manifold. These conditions are satisfied in the case of real algebraic varieties. See [19] for more details.

Our concern now is to determine the dimension of X. X is a finite set only if the dimension is zero. In this case, its degree is useful to estimate the number of solutions. We prove here that X has a strictly positive dimension.

Theorem 2

For two unrelated non-singular deformations, such that Ba and b are linearly independent, X is a three-dimensional manifold diffeomorphic to $\{-1,1\} \times {\mathbb {R}}^3$.

Proof

Let $\alpha _0, \beta _0, \gamma _0, x_0, y_0, z_0, v_{10}, v_{20}, v_{30}$ be a point on X. X cannot be empty since at least the actual deformations must satisfy the equations defining X. Let $a = \alpha _0 a_0$, $A = 1/\alpha _0(A_0 + a_0 v_{10}^t)$, $b = \beta _0 a_0$, $B = 1/\beta _0(B_0 + b_0 v_{20}^t)$. Then we know that $Ba+b = \gamma _0 c_0$ and $BA = 1/\gamma _0(C_0 + c_0 v_{30}^t)$. Consider the variety Y defined by the following system:

$$\begin{aligned} \left\{ \begin{aligned}&\alpha ' (B + b v_2'^t) a + \beta '^2 b - \beta ' \gamma ' (Ba+b) = 0\\&\gamma ' (B + b v_2'^t) (A + a v_1'^t) - \alpha ' \beta ' (BA + (Ba+b)v_3'^t) = 0 \\&\alpha ' x' - 1 = 0 \\&\beta ' y' - 1 = 0 \\&\gamma ' z' - 1 = 0 \end{aligned} \right. \end{aligned}$$

The varieties X and Y are easily seen to be isomorphic by the affine mapping:

$$\begin{aligned} \begin{aligned}&(\alpha ,\beta ,\gamma ,x,y,z,v_1^t,v_2^t,v_3^t) \mapsto \\&\quad (\alpha ',\beta ',\gamma ',x',y',z',v_1'^t,v_2'^t,v_3'^t) \\&\qquad =(\alpha /\alpha _0, \beta /\beta _0, \gamma /\gamma _0, \alpha _0 x, \beta _0 y, \gamma _0 z, \\&\qquad 1/\alpha _0^2 (v_1^t - v_{10}^t), 1/\beta _0^2 (v_2^t - v_{20}^t), 1/\gamma _0^2 (v_3^t - v_{30}^t)) \end{aligned} \end{aligned}$$

For the sake of clarity and simplicity, we shall drop the prime in all variables. For instance, we shall continue to write $\alpha$ while we intend $\alpha '$ and similarly for all variables.

Assume that (A, a, B, b) is given and satisfies the assumptions of the theorem. The first equation yields $(\alpha - \beta \gamma )Ba + (\alpha (v_2^ta) + \beta ^2 - \beta \gamma )b = 0$. Since the vectors Ba, b are linearly independent, we have:

$$\begin{aligned} \alpha - \beta \gamma = 0 \end{aligned}$$

(5)

and

$$\begin{aligned} \alpha (v_2^ta) + \beta ^2 - \beta \gamma =0 \end{aligned}$$

(6)

The second equation yields $(\gamma - \alpha \beta )BA + Ba(\gamma v_1^t - \alpha \beta v_3^t) + b(\gamma v_2^tA + \gamma (v_2^ta)v_1^t - \alpha \beta v_3^t) = 0$. Since $\text{ rank }(BA) = 3$ and $\text{ rank }(Ba(\gamma v_1^t - \alpha \beta v_3^t) + b(\gamma v_2^tA + \gamma (v_2^ta)v_1^t - \alpha \beta v_3^t)) \le 2$, we have

$$\begin{aligned} \gamma -\alpha \beta = 0 \end{aligned}$$

(7)

and

$$\begin{aligned} Ba(\gamma v_1^t - \alpha \beta v_3^t) + b(\gamma v_2^tA + \gamma (v_2^ta)v_1^t - \alpha \beta v_3^t) = 0 \end{aligned}$$

(8)

Relying on Eqs. 5 and 7, we get that $\beta \in \{-1,1\}$.

If $\beta = 1$, we get $\alpha = \gamma$ and so by Eq. 8, we have $Ba(\alpha v_1^t - \alpha v_3^t) + b(\alpha v_2^tA + \alpha (v_2^ta)v_1^t - \alpha v_3^t) = 0$. Again, since Ba and b are linearly independent, we get $v_1 = v_3$ and $v_2^t A + (v_2^ta) v_1^t - v_1^t=0$. Equation 6 yields $v_2^ta = \frac{\alpha -1}{\alpha }$. Hence, $v_2 = \frac{1}{\alpha } A^{-t}v_1$. Then, by $v_2^ta = \frac{\alpha -1}{\alpha }$, we finally get $\alpha = 1 +v_1^t A^{-1} a$. Proving that given $v_1$, one can compute linearly $v_2,v_3,\alpha ,\gamma$. Therefore, the connected component of Y on which $\beta = 1$ is indeed a manifold diffeomorphic to ${\mathbb {R}}^3$.

Now if $\beta = -1$, the same technique yields a similar conclusion. Indeed here $\gamma = -\alpha$, which leads to $Ba(-\alpha v_1^t - \alpha v_3^t) + b(-\alpha v_2^tA - \alpha (v_2^ta)v_1^t - \alpha v_3^t) = 0$. The linear independence of Ba and b provides us with the following constraints: $v_3 = -v_1$ and $v_2^t A + (v_2^ta) v_1^t - v_1^t=0$. The latter one is identical to the constraint in the $\beta = 1$ case. Therefore, we have a similar conclusion and the connected component of Y for which $\beta = -1$ is a manifold diffeomorphic to ${\mathbb {R}}^3$ too.

From these two cases, the conclusion of the theorem follows. $\square$

Concerning the discussion above, one can check that in the neighborhood of each real solution, there are infinitely other real solutions. For example, provided that (A, a), (B, b) is a solution, $(\lambda A,a),(B,b)$ for $\lambda \in {\mathbb {R}} \backslash \{0\}$ is also a solution, since the fundamental matrices remains unchanged up to a scale.

The practical consequence of this theorem is that one cannot hope to recover deformations from three images in the general case.

Numerical experiments confirm the theoretical result. When two random affine transformations are chained, the Jacobian matrix of the system (4) has rank 9 in the vicinity of the solution, as expected, since we have 12 unknown variables ($\alpha , \beta , \gamma , v_1, v_2, v_3$).

When the same deformation is repeated twice the system of equations is simplified.

Before we proceed more in depth, let us make the following observation. The deformations (A, a) and $(\lambda A, \lambda a)$ for $\lambda \ne 0$ produce the same image. Therefore, one could conclude that whatever the number of images, one can only expect to recover the deformation modulo this equivalence. However, observe that if multiples $(\lambda A, \lambda a)$ and $(\mu A, \mu a)$ of the same deformation are applied consecutively we get the following overall deformation $(\mu \lambda A^2, \mu \lambda Aa + \mu a)$ which is equivalent to $(A^2, Aa + a)$ only if $\mu \lambda = \mu$ or equivalently $\lambda = 1$. Therefore, if the same deformation is repeated twice, one can hope to be able to fully recover it. This is the conclusion the analysis below exhibits.

Consider the fundamental matrices $E_{12}$ and $E_{13}$. $E_{23}$ is the same as $E_{12}$ because the same deformation is repeated twice. We compute $A_0,a_0,C_0,c_0$ as previously and for the actual deformation A, a there exist $\alpha \ne 0$, $v_1 \in {\mathbb {R}}^3$, $\gamma \ne 0$ and $v_3 \in {\mathbb {R}}^3$, such that:

$$\begin{aligned} \left\{ \begin{aligned}&a = \alpha a_0 \\&A = 1/\alpha (A_0 + a_0 v_1^t) \\&Aa + a = \gamma c_0 \\&A^2 = 1/\gamma (C_0 + c_0 v_3^t) \end{aligned} \right. \end{aligned}$$

This results in the following system of equations:

$$\begin{aligned} \left\{ \begin{aligned}&(A_0 + a_0 v_1^t) a_0 + \alpha a_0 - \gamma c_0 = 0\\&\gamma (A_0 + a_0 v_1^t)^2 - \alpha ^2 (C_0 + c_0 v_3^t) = 0 \\&\alpha x - 1 = 0 \\&\gamma z - 1 = 0 \end{aligned}\right. \end{aligned}$$

(9)

Theorem 3

For a generic affine deformation, such that the three following conditions hold (i) $\text{ rank }(A) = 3$, (ii) 1 is not an eigenvalue of A and (iii) Aa, a are linearly independent, repeated twice, one can recover this deformation from the three images.

Proof

Here, X designates the sub-variety of ${\mathbb {R}}^{10}$ defined by the system (9). Let $\alpha _0, \beta _0, x_0, z_0, v_{10}, v_{30}$ be a point on X. Let $a = \alpha _0 a_0$, $A = 1/\alpha _0(A_0 + a_0 v_{10}^t)$. Then, we know that $Aa+a = \gamma _0 c_0$ and $A^2 = 1/\gamma _0(C_0 + c_0 v_{30}^t)$. Consider the variety Y defined by the following system:

$$\begin{aligned} \left\{ \begin{aligned}&(A + a v_1'^t) a + \alpha ' a - \gamma ' (Aa+a) = 0\\&\gamma ' (A + a v_1'^t)^2 - \alpha '^2(A^2 + (Aa+a)v_3'^t) = 0 \\&\alpha ' x' - 1 = 0 \\&\gamma ' z' - 1 = 0 \end{aligned}\right. \end{aligned}$$

(10)

The varieties X and Y are easily seen to be isomorphic. Indeed the following affine mapping: $(\alpha ,\gamma ,x,y,z,v_1^t,v_3^t) \mapsto (\alpha ',\gamma ',x',z',v_1'^t,v_3'^t) = (\alpha /\alpha _0, \gamma /\gamma _0, \alpha _0 x, \beta _0 y, \gamma _0 z, 1/\alpha _0^2 (v_1^t - v_{10}^t), 1/\gamma _0^2 (v_3^t - v_{30}^t))$ is an isomorphism from X and Y. Therefore, $\dim (X) = \dim (Y)$.

As before, we shall drop the prime from all variables in order to ease the expressions.

The first equation yields

$$\begin{aligned} (1-\gamma )Aa + ((v_1^ta) + \alpha - \gamma )a = 0. \end{aligned}$$

(11)

Since Aa and a are linearly independent, we get $\gamma =1$ and $v_1^t a = 1-\alpha$. The second equation yields $(1-\alpha ^2)A^2 + Aa(v_1^t - \alpha ^2 v_3^t) + a(v_1^t A + (v_1^ta) v_1^t - \alpha ^2 v_3^t) = 0$. Since $\text{ rank }(A^2) = 3$ and $\text{ rank }(Aa(v_1^t - \alpha ^2 v_3^t) + a(v_1^t A + (v_1^ta) v_1^t - \alpha ^2 v_3^t)) \le 2$, this yields $1-\alpha ^2 = 0$ and $v_1^t - \alpha ^2 v_3^t = v_1^t A + (v_1^ta) v_1^t - \alpha ^2 v_3^t = 0$ (because Aa and a are linearly independent). Hence, $v_1 = \alpha ^2 v_3$ and $v_1^t A + (v_1^ta) v_1^t - v_1^t= 0$. Since $v_1^t a = 1-\alpha$, we get $A^t v_1 = \alpha v_1$. Since $1 \not \in spec(A^t) = spec(A)$, $\alpha \ne 1$ and then $\alpha = -1$. Then, $v_1$ is an eigenvector of $A^t$ with respect to $-1$. Together with $v_1^t a = 1-\alpha = 2$, one can compute $v_1$ and then there is a unique solution to the system, since the other variables can be computed from $\alpha$ and $v_1$. $\square$

The unique solution is real since this is the actual deformation that the points have undergone.

Randomly simulating this setup, Eq. 9, by least squares recovers the original affine transformation almost exactly using scipy.optimize.least_squares.

There are cases, other than two identical transformations, where the deformations are also solvable.

For example, when $B = \lambda A$ and $b = \mu a$ for unknown, nonzero scalars $\lambda , \mu$. The system of Eqs. 4 reduces to:

$$\begin{aligned} \left\{ \begin{aligned}&\lambda (A_0 + a_0 v_1^t) a_0 + \alpha \mu a_0 - \gamma c_0 = 0\\&\lambda \gamma (A_0 + a_0 v_1^t)^2 - \alpha ^2 (C_0 +c_0v_3^t) = 0 \end{aligned}\right. \end{aligned}$$

(12)

This system is similar but still different, from system (9). Of course, as previously, one has to add the two further equations $\alpha x - 1 = \gamma z - 1 = 0$. Now we shall prove the following result.

System (12) defines a discrete variety. As a consequence,

Theorem 4

If (A, a) is the first deformation and $(\lambda A, \mu a)$ the second deformation ($\lambda \ne 0$ and $\mu \ne 0$), one can recover the two deformations and the structure provided that Aa, a are linearly independent and $\frac{\mu }{\lambda } \not \in spec(A)$ is known.

Proof

We proceed as in the previous theorem. Here X designates the sub-variety of ${\mathbb {R}}^{10}$ defined by system (12) (together with equations $\alpha x - 1 = \gamma z - 1 = 0$). Note that $\lambda , \mu$ are not unknowns but parameters. Let $\alpha _0, \gamma _0, x_0, z_0, v_{10}, v_{30}$ be a point on X. Let $a = \alpha _0 a_0$, $A = 1/\alpha _0(A_0 + a_0 v_{10}^t)$. Then, we know that $\lambda Aa + \mu a = \gamma _0 c_0$ and $\lambda A^2 = 1/\gamma _0(C_0 + c_0 v_{30}^t)$. Consider the variety Y defined by the following system:

$$\begin{aligned} \left\{ \begin{aligned}&\lambda (A + a v_1'^t) a + \alpha ' \mu a - \gamma ' (\lambda Aa+ \mu a) = 0\\&\lambda \gamma ' (A + a v_1'^t)^2 - \alpha '^2(\lambda A^2 + (\lambda Aa + \mu a)v_3'^t) = 0 \\&\alpha ' x' - 1 = 0 \\&\gamma ' z' - 1 = 0 \\ \end{aligned}\right. \end{aligned}$$

(13)

Again the two varieties X and Y are easily seen to be isomorphic. And as before, we shall drop the prime from all variables.

Form the second equation, we get $\lambda (1-\gamma )Aa + (\lambda v_1^t a + \alpha \mu - \gamma \mu ) a = 0$. Therefore, $\gamma = 1$ and $v_1^t a = \frac{\mu }{\lambda }(1-\alpha )$.

From the second equation we get: $\lambda (1-\alpha ^2)A^2 + \lambda Aav_1^t + \lambda a v_1^t A + \lambda (v_1^t a) a v_1^t - \alpha ^2 \lambda Aa v_3^t - \alpha ^2 \mu a v_3^t = 0$.

Relying on a rank argument, as above, we get $1-\alpha ^2 = 0$ and $\lambda Aa (v_1^t - \alpha ^2 v_3^t) + a (\lambda v_1^t A + \lambda (v_1^t a) v_1^t - \alpha ^2 \mu v_3^t) = 0$.

The linear independence of Aa and a again implies that $v_1^t - \alpha ^2 v_3^t = 0$ and $\lambda v_1^t A + \lambda (v_1^t a) v_1^t - \alpha ^2 \mu v_3^t = 0$. This yields $v_3 = \frac{1}{\alpha ^2}v_1$ and $A^t v_1 = \frac{\mu \alpha }{\lambda } v_1$. If $\alpha = 1$, then $v_1$ would be an eigenvector of $A^t$ with respect to $\frac{\mu }{\lambda }$, which contradicts the assumption. Then, $\alpha = -1$ and then one can compute $v_1$ relying on $A^t v_1 = \frac{\mu \alpha }{\lambda } v_1$ and $v_1^t a = \frac{\mu }{\lambda }(1-\alpha )$. From this, one gets $v_3$. Thus, there is a unique solution. $\square$

Randomly simulating this setup, Eq. 12 together with the localization equations, by least squares recovers the original affine transformation almost exactly using scipy.optimize. least_squares.

On the practical side, since the ratio $\frac{\mu }{\lambda }$ must be known for the computation to be carried out, one can assume that $\mu = \lambda$. This situation will be formalized in definition 5.

2.4 Beyond Fundamental Matrices

Consider now the computation of both the deformation and the structure without computing the fundamental matrix. Let $P_1, \cdots , P_n$ be n points in ${\mathbb {R}}^3$ that undergo an affine deformation $\left( \begin{matrix} A &{} t \\ 0 &{} 1 \end{matrix} \right)$. Before the deformation the image points are $q_i = (u_i,v_i,1)^t$ and after the deformation are denoted $q_i' = (u_i',v_i',1)^t$. The camera matrix is still [I, 0]

With these notations, there exists for each i, $\lambda _i \in {\mathbb {R}} \backslash \{0\}$, such that $P_i = \lambda _i q_i$. Hence, we have the following set of equations:

$$\begin{aligned} q_i' \equiv \lambda _i A q_i + t \end{aligned}$$

(14)

First, notice that this equation is an equality in the projective plane. From a set of such equations, one cannot expect to fully compute the deformation.

However, we shall show that one can compute the deformation modulo an overall scale and fully recover the structure, provided $t \ne 0$ and 4 points are known in ${\mathbb {R}}^3$.

If $t = 0$, equality (14) reads $q_i' \equiv A q_i$ and one cannot recover the structure (i.e., $\lambda _i$) at all. Therefore, we assume in the sequel that $t \ne 0$.

Definition 5

Two affine deformations (A, a) and (B, b) are said to be homothety equivalent if there exists a nonzero real $\lambda$ such that $B = \lambda A$ and $b = \lambda a$.

Lemma 6

Assume n image correspondences $q_i \leftrightarrow q_i'$, before and after deformation, are given. Assume that the initial structure is known, that is $\lambda _1, \cdots , \lambda _n$ are known. Then the set of deformations that can be computed in this setting is a one-dimensional linear space, provided that $n \ge 4$ and the points $\{P_i = \lambda _i q_i\}_{1 \le i \le n}$ are in a generic position.

Proof

Equation (14) is says that $AP_i + t$ lies in the ray defined by the camera center and the image point $q_i'$.

Let $\phi _1(P) = AP+a$ and $\phi _2(P) = BP +b$ be two invertible affine deformations that are compatible with Eq. (14) for $i=1, \cdots , n$. Then there is an affine transformation h that maps $\phi _1(P_i)$ to $\phi _2(P_i)$ for each i, say $h = \phi _2 \circ \phi _1^{-1}$. More precisely $h(Q) = BA^{-1}Q - BA^{-1}a + b$. Let $Q_i = \phi _1(P_i)$. For each i, the origin, $Q_i$ and $h(Q_i)$ are aligned. Then, provided that $n \ge 4$ and points are in a generic configuration, h is an homothety, that is $b = BA^{-1}a$ and $BA^{-1} = \sigma I$ for some $\sigma \ne 0$. Indeed let $v_i$ be the vector $\overrightarrow{OQ_i}$, such that $v_1,v_2,v_3$ form a basis of ${\mathbb {R}}^3$. Then, we have $h(v_i) = \sigma _i v_i$ for $1 \le i \le 3$ and some nonzero scalars $\sigma _1,\sigma _2,\sigma _3$. Now let $v_4 = \overrightarrow{OQ_4}$, so that $v_4$ is a linear combination of $v_1,v_2,v_3$: $v_4 = \alpha _1 v_1 + \alpha _2 v_2 + \alpha _3 v_3$. Then, $h(v_4) = \sigma _4 v_4 = \alpha _1 \sigma _1 v_1 + \alpha _2 \sigma _2 v_2 + \alpha _3 \sigma _3 v_3$, so that $\sigma _1 = \sigma _2 = \sigma _3 = \sigma _4$ and h is an homothety as expected.

Hence, $B = \sigma A$ and $b = \sigma a$. Therefore, under the assumptions of the lemma, two deformations that are compatible with Eq. (14) are homothety equivalent.

Now consider the three first points that define a non-degenerate triangle. For the sake of simplicity, denote them $P_1, P_2, P_3$. The plane defined by these point, say H, intersects the rays defined by $q_1',q_2',q_3'$ in three points $Q_1,Q_2,Q_3$. The correspondences $P_i \mapsto Q_i$ provide 9 linear independent constraints on the deformation (A, a).

Now consider a fourth point $P_4$ not lying on H. Saying that $AP_4+a$ lies in the rays defined by $q_4'$ adds two linear constraints independent of the previous ones.

We end up with 11 linear independent constraints. This allows computing an element in the equivalent class of the actual deformation, say $(A_0,a_0)$. As mentioned previously the two deformations (A, a) and $(A_0,a_0)$ are homothety equivalent.

The group of homotheties centered at the origin is a one-dimensional linear space, which yields the conclusion. $\square$

Now equation (14) implies

$$\begin{aligned} \left\{ \begin{aligned}&\lambda _i a_1^t q_i + t_1 - u_i' (\lambda _i a_3^t q_i + t_3) = 0 \\&\lambda _i a_2^t q_i + t_2 - v_i' (\lambda _i a_3^t q_i + t_3) = 0 \end{aligned}\right. , \end{aligned}$$

(15)

where we denote by $a_1^t,a_2^t,a_3^t$ the line of A and $t_1,t_2,t_3$ the coordinates of t. Since the points are assumed to be in ${\mathbb {R}}^3$ and therefore do not lie at infinity, the coefficients $(\lambda _i a_3^t q_i + t_3)$ do not vanish, since affine transformations do not send points to infinity. Therefore, the implication is an equivalence.

For each i, let us consider the following function $f_i: {\mathbb {R}}^{12} \times {\mathbb {R}} \longrightarrow {\mathbb {R}}^2$ that maps $(a_{11}, \cdots , a_{33}, t_1, t_2, t_3, \lambda _i)$ to $(\lambda _i a_1^t q_i + t_1 - u_i' (\lambda _i a_3^t q_i + t_3), \lambda _i a_2^t q_i + t_2 - v_i' (\lambda _i a_3^t q_i + t_3))$. The Jacobian matrix of $f_i$ is:

$$\begin{aligned} \left[ \begin{array}{ccccccccccccc} \lambda _i u_i &{} \lambda _i v_i &{} \lambda _i &{} 0 &{} 0 &{} 0 &{} - \lambda _i u_i u_i' &{} - \lambda _i v_i u_i' &{} \\ - \lambda _i u_i'&{} 1 &{} 0 &{} -u_i' &{} a_1^tq_i - u_i' a_3^t q_i \\ 0 &{} 0 &{} 0 &{} \lambda _i u_i &{} \lambda _i v_i &{} \lambda _i &{} - \lambda _i u_i v_i' &{} - \lambda _i v_i v_i' &{} \\ - \lambda _i v_i' &{} 0 &{} 1 &{} -v_i' &{} a_2^tq_i - v_i' a_3^t q_i \end{array} \right] \nonumber \\ \end{aligned}$$

(16)

This matrix has always rank 2 and $f_i$ is therefore a submersion from ${\mathbb {R}}^{12} \times {\mathbb {R}}$ to ${\mathbb {R}}^2$. The level set over 0 is not empty since the actual deformation and structure define a point in it. Therefore, the $f_i^{-1}(0)$ is actually a smooth manifold of dimension $13-2=11$.

Now let us consider for each k in $\{1, \cdots , n\}$, the injection $i_k^n: {\mathbb {R}}^{12} \times {\mathbb {R}} \longrightarrow {\mathbb {R}}^{12} \times {\mathbb {R}}^n$, such that $i_k^n(a_{11}, \cdots , a_{33},t_1,t_2,t_3,\lambda _k) = (a_{11}, \cdots , a_{33},t_1,t_2,t_3,0, \cdots , 0, \lambda _k, 0, \cdots , 0)$, where $\lambda _k$ is sent to the position k in the second factor in the product ${\mathbb {R}}^{12} \times {\mathbb {R}}^n$. Let $\pi _k^n$ be the left inverse of $i_k^n$, that is the projection from ${\mathbb {R}}^{12} \times {\mathbb {R}}^n$ to ${\mathbb {R}}^{12} \times {\mathbb {R}}$, where the $k-$copy of ${\mathbb {R}}$ is the only factor that is kept.

If we stack together all equations $f_i = 0$ for $1 \le i \le n$, we get a closed set in ${\mathbb {R}}^{12} \times {\mathbb {R}}^n$, since each function $f_i$ introduces a new variable $\lambda _i$. This closed set is precisely $\cap _{i=1}^n (f_i \circ \pi _i^n)^{-1}(0)$.

Proposition 7

For $n \in \{1,\cdots ,7\}$, the set $\cap _{i=1}^n (f_i \circ \pi _i^n)^{-1}(0)$ is a smooth manifold of dimension $12-n$.

In order to grasp the idea behind the following proof, let us write the Jacobian matrix of the system $\{f_1 \circ \pi _1^2 = 0, f_2 \circ \pi _2^2 = 0\}$:

$$\begin{aligned} \left[ \begin{array}{cccccccccccccc} \lambda _1 u_1 &{} \lambda _1 v_1 &{} \lambda _1 &{} 0 &{} 0 &{} 0 &{} - \lambda _1 u_1 u_1' &{} \\ - \lambda _1 v_1 u_1' &{} - \lambda _1 u_1'&{} 1 &{} 0 &{} -u_1' &{} a_1^tq_1 - u_1' a_3^t q_1 &{} 0 \\ 0 &{} 0 &{} 0 &{} \lambda _1 u_1 &{} \lambda _1 v_1 &{} \lambda _1 &{} - \lambda _1 u_1 v_1' &{} \\ - \lambda _1 v_1 v_1' &{} - \lambda _1 v_1' &{} 0 &{} 1 &{} -v_1' &{} a_2^tq_1 - v_1' a_3^t q_1 &{} 0 \\ \lambda _2 u_2 &{} \lambda _2 v_2 &{} \lambda _2 &{} 0 &{} 0 &{} 0 &{} - \lambda _2 u_2 u_2' &{} \\ - \lambda _2 v_2 u_2' &{} - \lambda _2 u_2'&{} 1 &{} 0 &{} -u_2' &{} 0 &{} a_1^tq_2 - u_2' a_3^t q_2 \\ 0 &{} 0 &{} 0 &{} \lambda _2 u_2 &{} \lambda _2 v_2 &{} \lambda _2 &{} - \lambda _2 u_2 v_2' &{} \\ - \lambda _2 v_2 v_2' &{} - \lambda _2 v_2' &{} 0 &{} 1 &{} -v_2' &{} 0 &{} a_2^tq_2 - v_2' a_3^t q_2 \\ \end{array} \right] \nonumber \\ \end{aligned}$$

(17)

This explicitly shows that adding a new point adds two new rows and one column to the matrix, which becomes a $4 \times 14$ matrix of rank 4. This process continues until $n=7$, with no alteration, as the proposition argues. The proof formalizes this idea.

Proof

The proposition holds for $n=1$ according to the above analysis. Assume that it is true for some $n \le 6$, let us prove it for $n+1$. By the induction assumption we have $\dim (\cap _{i=1}^n (f_i \circ \pi _i^n)^{-1}(0)) = 12-n$.

Since we now add a point, a direction is added and now we shall look at $M = \cap _{i=1}^{n} (f_i \circ \pi _i^{n+1})^{-1}(0)$ in place of $\cap _{i=1}^{n} (f_i \circ \pi _i^n)^{-1}(0))$. Therefore, $\dim (M) = 12-n+1$.

Now let N be $(f_{n+1} \circ \pi _{n+1}^{n+1})^{-1} (0)$. By the above analysis, N is a smooth manifold of dimension $12+n+1 - 2 = 12+n-1$. Indeed $f_{n+1} \circ \pi _{n+1}^{n+1}$ is a smooth function from ${\mathbb {R}}^{12} \times {\mathbb {R}}^{n+1}$ to ${\mathbb {R}}^2$, which is a submersion.

The two manifolds M and N are transverse, since for each $x \in M \cap N$, we have $T_x M + T_x N = T_x ({\mathbb {R}}^{12} \times {\mathbb {R}}^{n+1})$.

Indeed, if $\{e_i\}_{1 \le i \le 12+n+1}$ denotes the standard basis of ${\mathbb {R}}^{12+n+1}$ then for $x = (a_{11}, \cdots , a_{33}, t_1, t_2, t_3, \lambda _1, \cdots , \lambda _{n+1})$, the vectors:

$$\begin{aligned} \begin{aligned} z_1&= e_{12+n+1}, \\ z_2&= -\prod _{i=1}^n (a_1^t q_{i} - u'_{i}a_3^t q_{i}) e_{10} \\&\quad + \sum _{k=1}^n \prod _{i \ne k} (a_1^t q_{i} - u'_{i}a_3^t q_{i}) e_{12+k} \end{aligned} \end{aligned}$$

are linearly independent and lie in $T_x M$, but not in $T_x N$.

Therefore, $T_x N + {\mathbb {R}} z_1 + {\mathbb {R}} z_2 = T_x ({\mathbb {R}}^{12} \times {\mathbb {R}}^{n+1}) \subset T_x N + T_x M$.

Then, $M \cap N = \cap _{i=1}^{n+1} (f_i \circ \pi _i^{n+1})^{-1}(0)$ is a manifold, which dimension is $12-n+1 + 12+n-1 - (12 + n + 1) = 12 - n -1$ as expected. This completes the induction. $\square$

Adding further points does not decrease the dimension. More precisely, we now prove the following result.

Theorem 8

Given $n \ge 7$ correspondences $q_i \leftrightarrow q_i'$ of points that are in a generic configuration (see Sect. 2.6 for more details), the set $\cap _{i=1}^n (f_i \circ \pi _i^n)^{-1}(0)$ is a smooth submanifold of ${\mathbb {R}}^{12+n}$ of dimension 5.

Proof

For the sake of simplicity, let us denote $\cap _{i=1}^n (f_i \circ \pi _i^n)^{-1}(0)$ by M. Consider the canonical projection $\pi : {\mathbb {R}}^{12+n} \rightarrow {\mathbb {R}}^{12}$ on the 12 first coordinates. The image of M by $\pi$ is obtained by eliminating $\lambda _i$ for each i from the two equations each correspondence provides. Thus, $\pi (M)$ is defined by the following equations:

$$\begin{aligned} (a_1^t q_i - u_i' a_3^t q_i)(v_i' t_3 - t_2) = (a_2^t q_i - v_i' a_3^t q_i)(u_i' t_3 - t_1), \end{aligned}$$

for i in $\{1, \cdots , n\}$. After simplification, this yields:

$$\begin{aligned}{} & {} v_i' t_3 a_1^t q_i - t_2 a_1^t q_i + t_2 u_i' a_3^t q_i \\{} & {} \quad = u_i' t_3 a_2^t q_i - t_1 a_2^t q_i + t_1 v_i' a_3^t q_i, \end{aligned}$$

which is a bi-linear relation on $q_i$ and $q_i'$. This relation can also be written in a matrix form:

$$\begin{aligned} q_i'^t [t]_{\times } A q_i = 0. \end{aligned}$$

So with no surprise, we roll back to the fundamental matrix, which was obtained by eliminating the 3d points, while here we eliminated $\lambda _i$, which is equivalent. From the beginning of Sect. 2.1 it appears clearly that, provided the points are in a generic configuration that allows the computation of E, the set $\pi (M)$ is indeed a five-dimensional smooth manifold parametrized by $({\mathbb {R}}^*)^2 \times {\mathbb {R}}^3$ and embedded into ${\mathbb {R}}^{12}$.

Now let us consider the fiber of $\pi$ over a point $z = (a_1^1,a_2^t,a_3^t,t_1,t_2,t_3) \in \pi (M)$. For each i, one has two consistent equations on $\lambda _i$ (Eq. (15)). Therefore, the fiber is a discrete set parametrized by the n values $\lambda _1, \cdots , \lambda _n$. More precisely, around each point $z \in \pi (M)$, there is a neighborhood $U_z$, so that if it is chosen small enough there are no two identical fibers and the parametrization of the fiber remains the same for all points of $U_z$.

Therefore, each fiber is a zero-dimensional manifold, diffeomorphic to $\{1, \cdots , n\}$. Around each point $z \in \pi (M)$, there is an open neighborhood $U_z \subset \pi (M)$ and a bijection $\phi _z: \pi ^{-1}(U_z) \rightarrow U_z \times \{1, \cdots , n\}$ that satisfies:

• 1. $\text {pr}_1 \circ \phi _z = \pi _{\mid \pi ^{-1}(U_z)}$ (where $\text {pr}_1: U_z \times \{1, \cdots , n\} \rightarrow U_z$ is the projection on the first factor),

• 2. for each $z' \in U_z$, the fiber over $z'$, $\pi ^{-1}(z')$, is diffeomorphic to $\{1, \cdots , n\}$.

Therefore, the set M is in fact a smooth manifold, with dimension $5 + 0 =5$ (see, for example, Proposition 1.1.14 in [22]). $\square$

The practical implication of this theorem is that all the information, one can expect to extract is already contained in the fundamental matrix.

Here again, numerical computations exhibit the expected result. When considering a random affine transformation and $n \ge 7$ points, the Jacobian matrix of the system formed by 2n equations of the form (15), evaluated at the true solution, has rank $12 + n - 5$, showing the manifold has indeed dimension 5.

2.5 Shape Recovery

Once the deformation is known the shape before and after deformation is easily calculated. Indeed from the first image, each point is known up to a scalar multiplication (depth). From the second image, this scalar for each point is computed linearly. The complicated part is to compute the deformation and this is our focus.

2.6 Critical Surface

Are there point configurations that do not allow the recovery of the fundamental matrix? It turns out the situation is similar to the classical case.

Assume that the projected points before and after deformation do not constrain the fundamental matrix uniquely. Therefore, there exists more than one solution (homogeneous) to the system: $q_i^t E p_i = 0$. One is the correct solution $E_1 = [t]_\times A$, while another solution $E_2$ would have another decomposition. Therefore, if there exists another solution, the points must satisfy:

$$\begin{aligned} q_i^t E_2 p_i = P_i^t \left[ \begin{array}{c} A^t \\ t^t \end{array} \right] E_2 [I;0] P_i = 0. \end{aligned}$$

(18)

Let $M = \left[ \begin{array}{c} A^t \\ t^t \end{array} \right] E_2 [I;0]$. Then, Eq. (18) simply means that the points $P_i$ lie on the quadric defined by $\frac{1}{2}(M+M^t)$.

In other words, this means that the original points in space lie on a quadric, whose equation involves the affine motion that we are looking for. In this case, the recovery presents an additional layer of ambiguity. There exist several fundamental matrices and for each fundamental matrix, the corresponding affine motion is recovered up to the ambiguity described above.

3 Affine Deformations: Invariant Shape

The shape of a deforming object is by definition changing but there are descriptions invariant to the transformations, we shall show when these descriptions can be recovered from a sequence of images of a deforming object.

3.1 Equations

Let $P_0,P_1,P_2,P_3,\ldots ,P_{n-1}$ be 3d points in homogeneous coordinates with 1 as the last coordinate. Here and through all Sect. 3, the points $P_0,P_1,P_2,P_3$ are assumed to define an affine basis of the three-dimensional affine space ${\mathbb {R}}^3$.

If a point P satisfies $P=\alpha P_0+\beta P_1+\gamma P_2+(1-\alpha -\beta -\gamma ) P_3$, when it is affinely transformed by T then,

$$\begin{aligned} TP=\alpha TP_0+\beta TP_1+\gamma TP_2+(1-\alpha -\beta -\gamma ) TP_3. \end{aligned}$$

Thus, $(\alpha ,\beta , \gamma )$ is an affine invariant and $\alpha ,\beta , \gamma$ and $1-\alpha -\beta -\gamma$ are the affine invariant coordinates of P. In this section, we aim at computing this affine invariant. The transformation itself is not recovered here. We deal with the simultaneous recovery of the transformation and the point coordinates in Sect. 2.4.

The real advantage of this affine invariant is that it does not require camera calibration, while full recovery of deformation and structure requires it. On the other hand, the affine invariant description only provides structure up to an unknown affine deformation.

Let us write down the equations for the two image point sets $\{q_i\}$ and $\{q_i'\}$ of an affinely changing point set where $\begin{pmatrix}A &{} t \\ 0 &{} 1\end{pmatrix}$ is the affine transformation and C the unknown camera matrix.

• For the first image, before the deformation, for each i, we have: $q_i \equiv C [\alpha _i P_0+\beta _i P_1+\gamma _i P_2+(1-\alpha _i-\beta _i-\gamma _i) P_3]$. Thus, each image point gives two equations.

• After the deformation, in the second image, for each i, we have: $q_i' \equiv C \begin{pmatrix}A &{} t \\ 0 &{} 1 \end{pmatrix} P_i \equiv C \begin{pmatrix}A &{} t \\ 0 &{} 1 \end{pmatrix} [\alpha _i P_0+\beta _i P_1+\gamma _i P_2+(1-\alpha _i-\beta _i-\gamma _i) P_3]$. Again this yields two equations per point.

The system has $2\times 2n = 4n$ equations, where n is the number of points. As for the unknowns, there are $4\times 3+3(n-4)+ 12 + 12 = 3n+24$ unknowns namely $P_0,P_1,P_2,P_3$, $\{\alpha _i, \beta _i,\gamma _i\}_{i \ge 4}$, the camera matrix C and the affine transformation $\begin{pmatrix}A &{} t\\ 0 &{} 1\end{pmatrix}$.

There are still ambiguities as, for any full rank V a $4\times 4$ matrix with last row [0, 0, 0, 1], $CP=(CV) (V^{-1}P)$, (new camera $\times$ new points) and $C\begin{pmatrix}A &{} t\\ 0 &{} 1\end{pmatrix}P = (CV)\left( V^{-1}\right. \left. \begin{pmatrix}A t\\ 0 1\end{pmatrix}V\right) (V^{-1}P)$, (new camera $\times$ new affine transformation $\times$ new points). Since, in the context of this section where we want to compute an invariant of the shape, the only unknowns that are relevant are $\{\alpha _i, \beta _i,\gamma _i\}_{i \ge 4}$, we can assume $C=[I;0]$, removing 12 unknowns. This formally makes the computation identical to the case of a calibrated camera, while calibration is not required here.

To make things more explicit, let us introduce new variables $\lambda _0,\lambda _1,\lambda _2,\lambda _3$, such that $P_i = \lambda _i q_i$ for $0 \le i \le 3$. Then, the equations can be written as follows:

$$\begin{aligned}&q_i \wedge [\alpha _i (\lambda _0 q_0) +\beta _i (\lambda _1 q_1) + \gamma _i (\lambda _2 q_2) + \delta _i (\lambda _3 q_3)] = 0 \end{aligned}$$

(19)

$$\begin{aligned}&q_j' \wedge [A;t] \begin{bmatrix}\lambda _j q_j \\ 1 \end{bmatrix} = 0 \end{aligned}$$

(20)

$$\begin{aligned}&q_i' \wedge [A;t] \begin{bmatrix} \alpha _i (\lambda _0 q_0) +\beta _i (\lambda _1 q_1) + \gamma _i (\lambda _2 q_2) + \delta _i (\lambda _3 q_3) \\ 1 \end{bmatrix} = 0 \end{aligned}$$

(21)

where $0 \le j \le 3$ and $4 \le i \le n-1$ and $\delta _i = 1-\alpha _i-\beta _i-\gamma _i$, $\wedge$ being the cross product.

These equations define a real algebraic variety in ${\mathbb {R}}^{12} \times {\mathbb {R}}^{4} \times {\mathbb {R}}^{3(n-4)}$ (we discarded $\delta _i$ in this counting).

Since none of $\{\lambda _0,\lambda _1,\lambda _2,\lambda _3\}$ should be zero, we need to compute in the localization of the polynomial ring with respect to each $\lambda _i$ [7]. Here again, this is done by adding new variables $\{\mu _0,\mu _1,\mu _2,\mu _3\}$ and the equations:

$$\begin{aligned} \lambda _i \cdot \mu _i - 1 = 0 \end{aligned}$$

(22)

We end up with a real algebraic variety embedded in ${\mathbb {R}}^{12} \times {\mathbb {R}}^{4} \times {\mathbb {R}}^4 \times {\mathbb {R}}^{3(n-4)}$. Since $\{\lambda _0,\lambda _1,\lambda _2,\lambda _3,\mu _0,\mu _1,\mu _2,\mu _3\}$ and $\{a_{ij},t_k\}_{1 \le i,j,k \le 3}$ are not of interest, we eliminate them from the system and get a system involving only $\{\alpha _i,\beta _i,\gamma _i\}_{4 \le i \le n-1}$. This is equivalent to projecting X over ${\mathbb {R}}^{3(n-4)}$. Notice that we are concerned with the case $n \ge 5$. The question now is: does this define a zero-dimensional variety or in other words can the affine invariant describing each point be computed up to a finite fold ambiguity? We address this question in the following subsection.

3.2 Dimension Analysis

3.2.1 The case of two images

The variety X defined here is isomorphic to the set $\cap _{i=1}^n (f_i \circ \pi _i^n)^{-1}(0)$ that appears in theorem 8. Indeed both express the same constraints on the same data in slightly different parametrizations. Therefore, X has dimension 5. Given this fact, can the projection of X on ${\mathbb {R}}^{3(n-4)}$ be a finite variety? By analyzing the fibers of the projection, we shall prove that the image of X by the projection has a positive dimension.

Indeed consider a point in the projection of X on ${\mathbb {R}}^{3(n-4)}$. Let us denote this point $w = (\alpha _i,\beta _i,\gamma _i)_{4 \le i \le n-1}$. And let $\pi : {\mathbb {R}}^{12} \times {\mathbb {R}}^{4} \times {\mathbb {R}}^4 \times {\mathbb {R}}^{3(n-4)} \rightarrow {\mathbb {R}}^{3(n-4)}$ be the canonical projection. We shall determine the fiber of $\pi$ over w in several steps.

Lemma 9

Provided $n \ge 6$ and the points are in a generic position, the Eq. (19), where $\lambda _0, \lambda _1, \lambda _2, \lambda _3$ are considered as the only unknowns, define a one-dimensional linear space.

Proof

The geometric signification of these equations is that the point $\alpha _i (\lambda _0 q_0) + \beta _i (\lambda _1 q_1) + \gamma _i (\lambda _2 q_2) + \delta _i (\lambda _3 q_3)$ lie in the ray defined by the camera center and the pixel $q_i$. This yields two independent homogeneous linear conditions on $\lambda _0, \lambda _1, \lambda _2, \lambda _3$ for each i. If we stack all together these equations, we get a homogeneous linear system whose rank has to be less than 4, unless there is no non-trivial solution, which is impossible since the initial structure of the points $P_0,P_1,P_2,P_3$ is actually a non-trivial solution. On the other hand, the system has at least rank 3, unless the affine invariants $(\alpha _i,\beta _i,\gamma _i)_{4 \le i \le n-1}$ satisfy a set of algebraic constraints (the vanishing of all $3 \times 3$ sub-determinant), which contradicts the genericity assumption. Eventually, we found that the system has exactly rank 3 and the set of solutions is a linear one-dimensional space. $\square$

Lemma 10

Provided $\lambda _0, \lambda _1, \lambda _2, \lambda _3$ are known, Eq. (20) define a four-dimensional sub linear of the space of all affine transformations.

Proof

Each of Eq. (20) means that the point $[A,t] \begin{bmatrix} \lambda _j q_j \\ 1 \end{bmatrix}$ lie in the ray $L_i$ generated by $q_i'$ and the camera center. Therefore, for each $i \in \{0,1,2,3\}$, we get two independent homogeneous linear equations on (A, t).

To check that by stacking together the 8 equations obtained for $i=0,1,2,3$, we get a four-dimensional linear space, consider the choice of four points $Q_0,Q_1,Q_2,Q_3$, each $Q_i$ lying on $L_i$. For each such sequence, there is a unique affine transformation that maps $P_i$ to $Q_i$, since the points $P_i$ form an affine basis of ${\mathbb {R}}^3$. The transformations that satisfy Eq. 20 are precisely those obtained by this procedure.

Therefore, the set of solutions is a four-dimensional linear subspace of ${\mathbb {R}}^{12}$. $\square$

Lemma 11

Provided $n \ge 6$ and $\lambda _0, \lambda _1, \lambda _2, \lambda _3$ are known, Eq. (20) and (21) define a one-dimensional linear subspace of the affine group of ${\mathbb {R}}^3$.

Proof

In lemma 10, we proved that Eq. (20) define a four-dimensional linear subspace of ${\mathbb {R}}^{12}$. For each point $P_i$, $i \ge 4$, Eq. (21) yields two independent homogeneous linear equations on (A, t). Provided we have at least two such points, we get a linear homogeneous system on (A, t) with at least 12 equations.

The rank of the system cannot be full, since there is a non-trivial solution, i.e., the actual transformation undergone by the points. The rank of the system will be at least 11, unless the points $P_i$, for $i \ge 4$ satisfy one or more algebraic relations, which contradicts here again the genericity assumption. This completes the proof. $\square$

Corollary 12

Under the assumption that the points $\{P_i\}_{0 \le i \le n-1}$ are in a generic configuration and provided that $n \ge 6$, the fiber of $\pi$ over $w \in \pi (X)$ is a two-dimensional smooth manifold. Therefore, $\pi (X)$ cannot be a finite set so two images are not enough to compute the affine invariant coordinates of the points $P_i$ for $4 \le i \le n-1$.

Proof

The dimension of the fiber is a direct consequence of the lemmas proven just above. Indeed, by lemma 9, there is a one-dimensional ambiguity on $\lambda _0, \lambda _1, \lambda _2, \lambda _3$ and by lemma 11, given $\lambda _0, \lambda _1, \lambda _2, \lambda _3$, there is a one-dimensional ambiguity of the transformation (A, t). This yields the fact that the fiber is indeed a two-dimensional manifold.

Assume that $\pi (X)$ is finite. Then, it is a zero-dimensional smooth manifold. In that case, the restriction of $\pi$ to X is a surjective submersion and the fibers have dimension $\dim (X) - 0 =5$, which is a contraction. $\square$

One can wonder if some prior knowledge of the world can help to get a finite set of solutions. It turns out that even the knowledge of $\{P_0,P_1,P_2,P_3\}$ cannot fully allow the computation of the affine invariant coordinates as shown in the following theorem.

Theorem 13

If the 4 points $\{P_0,P_1,P_2,P_3\}$ are known and $n \ge 6$, the variety of affine invariant coordinates of the other points $\{P_i\}_{4 \le i \le n-1}$ from two images from a single non-calibrated camera has dimension 3, even if the scene undergoes a general affine deformation and the points are in generic position.

Proof

Since the 4 points $\{P_0,P_1,P_2,P_3\}$ are known, Eq. (20) define a four-dimensional linear subspace of ${\mathbb {R}}^{12}$. Let us write the points of this space as linear combinations $\eta _1 [A_1,t_1] + \eta _2 [A_2,t_2] + \eta _3 [A_3,t_3] + \eta _4 [A_4,t_4]$, where $[A_i,t_i]$ are linearly independent affine transformations that satisfies Eq. (20).

Let us plug this representation into Eq. (21), we get quadratic equations on $\eta _1,\eta _2,\eta _3,\eta _4,\alpha _i,\beta _i,\gamma _i$ for $4 \le i \le n-1$:

$$\begin{aligned} \sum _{j=1}^4 \eta _j q_i'&\wedge [A_j,t_j] \\&\quad \begin{bmatrix} \alpha _i (\lambda _0 q_0) +\beta _i (\lambda _1 q_1) + \gamma _i (\lambda _2 q_2) + \delta _i (\lambda _3 q_3) \\ 1 \end{bmatrix} \nonumber \\&= 0,\nonumber \end{aligned}$$

(23)

for $4 \le i \le n-1$. Together with Eq. (19), this defines a real algebraic variety in Y in ${\mathbb {R}}^4 \times {\mathbb {R}}^{3(n-4)}$ (4 variables $\eta _1,\eta _2,\eta _3,\eta _4$ and $3(n-4)$ variables $\alpha _i,\beta _i,\gamma _i$ for $4 \le i \le n-1$), which is a smooth manifold of dimension 4, as we shall prove now.

First, observe that Eq. (19) merely mean that for each $i \ge 4$, there exists $\lambda _i \in {\mathbb {R}}$, such that $\alpha _i (\lambda _0 q_0) + \beta _i (\lambda _1 q_1) + \gamma _i (\lambda _2 q_2) + \delta _i (\lambda _3 q_3) = \lambda _i q_i$, which is equivalent to write $\alpha _i(P_0-P_3) + \beta _i(P_1 - P_3) + \gamma _i (P_2 - P_3) = \lambda _i q_i - P_3$. Let $\Delta$ be the $3 \times 3$ matrix, which columns are $P_0 - P_3, P_1-P_3, P_2 - P_3$. Then $\Delta$ is non-singular and:

$$\begin{aligned} \left[ \begin{array}{c} \alpha _i \\ \beta _i \\ \gamma _i \end{array} \right] = \lambda _i \Delta ^{-1}q_i - \Delta ^{-1}P_3. \end{aligned}$$

(24)

Plugging this expression into Eq. (23) yields:

$$\begin{aligned} \sum _{j=1}^4 \eta _j q_i' \wedge [A_j,t_j] \begin{bmatrix} \lambda _i q_i \\ 1 \end{bmatrix} = 0, \end{aligned}$$

which can also be written $\lambda _i q_i' \wedge \left( \left( \Sigma _{j=1}^4 \eta _j A_j \right) q_i \right) + q_i' \wedge \left( \Sigma _{j=1}^4 \eta _j t_j \right) = 0$. Let $U_i$ be the open dense set of ${\mathbb {R}}^4$, for which when $\eta = (\eta _1,\eta _2,\eta _3,\eta _4) \in U_i$, we have: $q_i' \wedge \left( \left( \Sigma _{j=1}^4 \eta _j A_j \right) q_i \right) \ne 0$. Over $U_i$, we have: $\lambda _i = \frac{\parallel q_i' \wedge \left( \Sigma _{j=1}^4 \eta _j t_j \right) \parallel }{\parallel q_i' \wedge \left( \left( \Sigma _{j=1}^4 \eta _j A_j \right) q_i \right) \parallel }$. Thus, $\lambda _i$ is a smooth function of $\eta$ on $U_i$ and so are $\alpha _i, \beta _i, \gamma _i$ by Eq. (24).

Let $U = \cap _{i=4}^{n-1} U_i$, which is also a dense open of ${\mathbb {R}}^4$. Let $f: U \rightarrow {\mathbb {R}}^{3(n-4)}$ be the smooth function that maps $\eta$ to $(\alpha _4,\beta _4,\gamma _4, \cdots , \alpha _{n-1},\beta _{n-1},\gamma _{n-1})$. Therefore, Y is the graph of f and is, therefore, a smooth embedded sub-manifold of ${\mathbb {R}}^4 \times {\mathbb {R}}^{3(n-4)}$ of dimension 4 (see [17], Proposition 5.7).

Now, let us consider the projection of Y on ${\mathbb {R}}^{3(n-4)}$ that we shall denote Z. Let $\pi : Y \rightarrow Z$ be this projection. Over each point of $(\alpha _i,\beta _i,\gamma _i)_{4 \le i \le n-1} \in Z$, the fiber of $\pi$ is a one-dimensional linear space, provided $n \ge 6$ and the points are in generic position. Indeed, Eq. (23) define an homogeneous system on $\eta = [\eta _1, \cdots , \eta _4]$, which matrix is $M_i = \left[ q_i' \wedge [A_1,t_1] P_i, q_i' \wedge [A_2,t_2] P_i, q_i' \wedge [A_3,t_3] P_i, q_i' \wedge \right. \left. [A_4,t_4] P_i \right] ,$ where we denote $P_i = \begin{bmatrix} \alpha _i (\lambda _0 q_0) +\beta _i (\lambda _1 q_1) + \gamma _i (\lambda _2 q_2) + \delta _i (\lambda _3 q_3) \\ 1 \end{bmatrix}$ for the sake of simplicity. The matrix $M_i$ has rank 2, since its four columns are in the plane perpendicular to $q'_i$ and the transformation $\{[A_i,t_i]\}_{1 \le i \le 4}$ are linearly independent. For $k \ne l$, the columns of the matrices $M_k$ and $M_l$ define a three-dimensional space, as they span the whole space ${\mathbb {R}}^3$. Indeed since $k \ne l$, the columns of these matrices lie in two un-parallel planes in ${\mathbb {R}}^3$. Therefore, a third point will not bring any further constraint on $\eta$, since the columns the matrix defines are linear combinations of the columns of $M_k$ and $M_l$. Eventually, we get that Eq. (23) define a one-dimensional linear space for $\eta _1, \eta _2, \eta _3, \eta _4$ over each point $(\alpha _i,\beta _i,\gamma _i)_{4 \le i \le n-1} \in Z$.

Now we shall analyze the variety Z. Equation (23) can be seen as a homogeneous linear system on $\eta$. More precisely, let M be the $3(n-4) \times 4$ matrix. obtained by stacking together all matrices $M_i$ for $4 \le i \le n-1$. The variety Z is a determinantal algebraic variety (see [8]) defined by the vanishing of all $4 \times 4$ minors of M and by Eq. (19). We don’t know if Z is smooth, but at least let V be the complement of its possible singular locus. Then V is a dense open set in Z and a smooth manifold. Let us consider the restriction of the projection $\pi : Y \rightarrow Z$ to $V_0 = \pi ^{-1}(V)$. It is a surjective smooth map in which fibers are all one-dimensional linear spaces. Moreover, for each point $z \in V$, there is a neighborhood W such that the columns of M that are independent will remain the same for all point $z' \in W$. Then, over W, all points of the inverse image $\pi ^{-1}(W)$ will be given by the same parametrization, so that $\pi ^{-1}(W)$ is diffeomorphic to $W \times {\mathbb {R}}$. Hence, the projection $\pi :V_0 \rightarrow V$ is a fiber bundle (in fact a vector bundle). Therefore, it is a surjective submersion and $\dim (Z) = \dim (Y) - 1 = 3$. $\square$

The system defined by Eqs. (19), (20) and (21) defines a four-dimensional manifold provided $\lambda _0,\lambda _1,\lambda _2,\lambda _3$ are known, as proven in the proof of theorem 13. In order to illustrate this fact numerically, one can compute the dimensional of the kernel of the Jacobian matrix of the system at the actual true solution. As expected, the results is indeed 4, or equivalently the rank is actually $12+3(n-4)-4$.

3.2.2 Three images

In this section, we investigate the case of three images. Two configurations are possible, either the same deformation is repeated twice or two different deformations are performed.

The case of two distinct deformations is quickly dealt with, relying on theorem 2, one can prove the following result:

Theorem 14

When the points undergo two unrelated generic affine deformations, the affine invariants $(\alpha _i,\beta _i,\gamma _i)$ cannot be computed up to a finite fold ambiguity.

Proof

If we stack Eqs. (19), (20), (21) and (22) with the equations coming from a third image generated by a generic distinct affine deformations, we get a real algebraic variety X embedded in ${\mathbb {R}}^{12} \times {\mathbb {R}}^{12} \times {\mathbb {R}}^8 \times {\mathbb {R}}^{3(n-4)}$. Projecting this variety over ${\mathbb {R}}^{12} \times {\mathbb {R}}^{12}$, we get the variety defined by the fundamental matrices. As known from theorem 2, this variety is a three-dimensional smooth manifold, that we shall denote Y. Since once the deformations are known the structure can be uniquely computed by triangulation so that the points are smooth functions of the deformations. Therefore, the projection $\pi _1: X \rightarrow Y$, which is surjective and smooth by construction, has a smooth left inverse $\sigma$ and is, therefore a diffeomorphism. Thus, X is actually a smooth submanifold of ${\mathbb {R}}^{12} \times {\mathbb {R}}^{12} \times {\mathbb {R}}^8 \times {\mathbb {R}}^{3(n-4)}$ and $\dim (X) = 3$.

Consider now the projection over ${\mathbb {R}}^{3(n-4)}$: $\pi _2: X \rightarrow {\mathbb {R}}^{3(n-4)}$. The image of X is a constructible set, that is a finite union of locally closed sets in the Zariski topology.

Therefore, there is a dense open set in the subspace topology for the classical topology, which is a smooth manifold. Let V be this open set and let us restrict the co-domain of $\pi _2$ to V, so that $\pi _2$ is seen as a smooth map from $V_0 = \pi _2^{-1}(V)$ to V.

Then $\pi _2 \mid _{V_0}$ is a fiber bundle with ${\mathbb {R}}^2$ as generic fiber. Indeed consider a point $z \in V$. Equation (19) will define $\lambda _0,\lambda _1,\lambda _2,\lambda _3$ up to a one-dimensional ambiguity, as shown in lemma 9, and the parametrization of the solution space will remain valid for all points $z' \in W_1$, a neighborhood of z.

Then, Eqs. (20) and (21), given $\lambda _0,\lambda _1,\lambda _2,\lambda _3$, will define the first affine deformation, i.e., (A, a), modulo a one-dimensional ambiguity, as in lemma 11.

Here again, the parametrization of the solution space will remain valid in a neighborhood $W_2$ of z. Of course, this parametrization also depend on $\lambda _0,\lambda _1,\lambda _2,\lambda _3$.

Equations similar to  (20) and (21) for the third image, allows computing the composition of the two affine deformations, i.e., $(BA,Ba+b)$, modulo a one-dimensional ambiguity, with a parametrization that stays stable in some neighborhood of z and that also depends on $\lambda _0,\lambda _1,\lambda _2,\lambda _3$.

Once the scale of $(BA,Ba+b)$ is fixed, the first deformation (A, a) is fully determined.

This shows that the fiber over z is a two-dimensional manifold, the parametrization of which is valid in a neighborhood of z.

Hence, this construction shows that $\pi _2 \mid _{V_0}$ is locally trivial, which makes it a fiber bundle, whose standard fiber is two-dimensional. Therefore, $\dim (V) = 1$ and the affine invariant coordinates cannot be computed up to a finite fold ambiguity. $\square$

Let us now turn our attention to the case where the points undergo the same deformations twice. Here the unknowns are exactly the same as in the case of two images: $\{\lambda _0,\lambda _1,\lambda _2,\lambda _3\}$, $\{a_{ij},t_k\}_{1 \le i,j,k \le 3}$, $t = [t_1,t_2,t_3]^t$ and $\{\alpha _i,\beta _i,\gamma _i\}_{4 \le i \le n-1}$. The equations involved in this situation also contain those of the case of two images and in addition equations similar to (20) and (21). Finally, with $P_i = \alpha _i (\lambda _0 q_0) +\beta _i (\lambda _1 q_1) + \gamma _i (\lambda _2 q_2) + \delta _i (\lambda _3 q_3)$, we get:

$$\begin{aligned}&q_i \wedge P_i = 0 \end{aligned}$$

(25)

$$\begin{aligned}&q_j' \wedge [A;t] \begin{bmatrix} \lambda _j q_j \\ 1 \end{bmatrix} = 0 \end{aligned}$$

(26)

$$\begin{aligned}&q_i' \wedge [A;t] \begin{bmatrix} P_i \\ 1 \end{bmatrix} = 0 \end{aligned}$$

(27)

$$\begin{aligned}&q_j'' \wedge [A^2;At+t] \begin{bmatrix} \lambda _j q_j \\ 1 \end{bmatrix} = 0 \end{aligned}$$

(28)

$$\begin{aligned}&q_i'' \wedge [A^2;At+t] \begin{bmatrix} P_i \\ 1 \end{bmatrix} = 0 \end{aligned}$$

(29)

As above, we add to these equations, the localization constraints expressed in 22. All together we get a variety $X \subset {\mathbb {R}}^{12} \times {\mathbb {R}}^8 \times {\mathbb {R}}^{3(n-4)}$. Again, we are interested in the projection of this variety into the factor ${\mathbb {R}}^{3(n-4)}$. However, here we are in a position to prove the following result.

Theorem 15

If the points undergo the same deformation twice, one can compute the affine invariant structure, i.e., $\{\alpha _i,\beta _i,\gamma _i\}_{4 \le i \le n-1}$ up to a finite fold ambiguity from the three images.

Proof

The proof is quite clear and works with the same scheme as the previous proofs. By eliminating from the equations the variables other than the affine deformations, we get the same equations of the fundamental matrices. From theorem 3, we know that there is a single solution for the affine deformation. Then the other variables are uniquely determined. As a consequence, $\dim (X) = 0$. Therefore, if one first eliminates the variables related to the deformation and the $\lambda _i$, a discrete variety for the affine invariant $(\alpha _i,\beta _i,\gamma _i)$ is left. $\square$

On the practical side, from Eq. (19), for $i \ge 4$, we can express any vector of affine coordinates $[\alpha _i,\beta _i,\gamma _i]$ as a linear function of the single parameter $\lambda _i$ as done in Eq. (24).

Similarly from Eq. (9), one can extract a representation of [A, t] as a point in a four-dimensional linear space. These representations can be plugged into the system made of Eq. (27) (or equivalently (21)) and (29).

This yields a nonlinear system that can solved numerically using scipy.optimize.least_squares.

4 General Smooth Deformations

Consider a non-singular complete vector field on ${\mathbb {R}}^3$, denoted X. Let $\Phi : {\mathbb {R}}^3 \times {\mathbb {R}} \rightarrow {\mathbb {R}}^3$ be the flow of X, i.e., $\forall x \in {\mathbb {R}}^3, \frac{\partial \Phi }{\partial t}(x,t) \mid _{t=0} = X_x$. Let $\delta t$ be a small duration and $\delta x$ a small vector, we have:

$$\begin{aligned} \begin{aligned}&\Phi (x + \delta x,t+\delta t) \\&\quad \approx \Phi (x,t) + \delta t \frac{\partial \Phi }{\partial t} (x,t) + \frac{\partial \Phi }{\partial x} (x,t) \delta x \\&\quad = \Phi (x,t) + \delta t X_{\Phi (x,t)} + \left( \frac{\partial X}{\partial x}\right) _{\Phi (x,t)} \delta x \end{aligned} \end{aligned}$$

where $\left( \frac{\partial X}{\partial x}\right) _{\Phi (x,t)}$ is the Jacobian matrix of X computed at $\Phi (x,t)$. In this equation, we used the canonical identification between a vector space and its tangent space at any point.

If the time separation between consecutive frames is small in comparison to values of the vector field X and if the distance between the points $\{P_i\}_{i=1, \ldots , n}$ is small in comparison with the spatial variability of X, the transformation between consecutive frames can be approximated by an affine deformation [A, a], where

$$\begin{aligned} \left\{ \begin{aligned} A&= \left( \frac{\partial X}{\partial x}\right) _{\Phi (x,t)} \\ a&= \delta t X_{\Phi (x,t)} \end{aligned}\right. \end{aligned}$$

In that scenario, the motion can be described by a sequence of affine deformations. If the video frequency is high enough, two consecutive deformations are quite similar and by theorems 3 and 4, one can recover the deformation and the structure, or by theorem 15 one can recover the affine invariant coordinates.

By this approach, one can recover a complex deformation by successive approximations.

5 Conclusion

We introduced a new problem in multiple-view geometry, i.e., the recovery of structure and deformation from a single perspective camera, where the deformation is either an affine transformation or a general smooth deformation defined as the flow of slowly varying vector field and the camera is either calibrated or not. We showed several theoretical results and in the course of the theoretical analysis provided concrete algorithms, many of which we have implemented in the Jupyter notebook available to the reader. This paves the way for further theoretical and practical research about deformable configurations of points viewed from a monocular sequence.