Abstract
A number of methods, both algebraic and iterative, have been developed recently for the fitting of concentric circles. Previous studies focus on first-order analysis for performance evaluation, which is appropriate only when the observation noise is small so that the bias is insignificant compared to variance. Further studies indicate that the first-order analysis does not appear sufficient in explaining and predicting the performance of an estimator for the fitting problem, especially when the noise level becomes significant. This paper extends the previous study to perform the second-order analysis and evaluate the estimation bias of several concentric circle estimators. The second-order analysis exposes important characteristics of the estimators that cannot be seen from the first-order studies. The insights gained in the theoretical study have led to the development of a new estimator that is unbiased and performs best among the algebraic solutions. An adjusted maximum likelihood estimator is also proposed that can yield an unbiased estimate while maintaining the KCR bound performance.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Various objects appear concentric in images. Examples include a compact disk, an iris and the cross section of a transmission pipe. Perhaps, the simplest concentric pattern is formed by circles that have a common center. A set of concentric circles are characterized by the center and the radii. The estimation of the concentric circle parameters is a challenging problem due to the nonlinear relationship between the observed data points and the unknown parameters. It has been an active research and has applications in biometrics such as iris recognition [26], commercial electronics such as camera calibration [15], and industry, such as, steel coils quality control.
Many concentric circle estimators have been developed over the years, including the preliminary solution by Dampegama [10], the suboptimum method by Benko et al. [4], the conic fitting solution by O’Leary et al. [19] and the algebraic solution by Ma and Ho [17]. Recently, Al-Sharadqah and Ho [3] have revisited previously proposed methods and developed new ones for the problem of fitting concentric circles. Both algebraic and iterative methods were investigated, and the first-order analysis was performed. The analytical results indicate that the algebraic solutions are easy to apply, but the performance is suboptimum. The iterative solutions, namely the maximum likelihood estimator (MLE), the gradient weighted algebraic fit (GRAF) and the Renormalization method (RM), can yield the KCR bound [7, 14, 20] performance. Furthermore, the MLE, using the Levenberg–Marquardt implementation, is much more computationally efficient than the GRAF and the RM. Under the first-order analysis, these estimators all have zero bias [3].
The first-order analysis is appropriate when the signal-to-noise ratio (SNR) of the measurements is high, so that the bias is negligible compared to variance. It is not uncommon in many practical scenarios where the SNR is not sufficient. In such cases, the first-order analysis will not be a reasonable indication in predicting the performance of an estimator. The first-order analysis also is not adequate to explain the behaviors of different estimators.
This paper continues the previous study [3] to analyze in the second-order performance of various algebraic and iterative concentric circle fitting methods. The second-order analysis is quite challenging and more involved than the first order. Nevertheless, it reveals very interesting results among different estimators. In particular, the concentric circle center estimate has zero essential bias for both the algebraic (except the simple fit method) and iterative solutions. Regarding the radii, the algebraic solutions have essential bias four times higher than that of the MLE and the GRAF and RM two times.
The insights gained from the second-order analysis have led us to develop a hyper-accurate estimator that is among most accurate for an algebraic solution while having zero essential bias up to second order. It is computationally efficient. Although its performance is unable to achieve the KCR bound, it can serve as a promising initial guess for the iterative methods. We also propose the adjusted MLE that has zero bias up to second order and maintains the KCR bound performance.
We shall process a realistic data set to support the analysis and the performance of the proposed algorithms. The data are obtained from an image of a CD/DVD, where the Canny edge detection method [5] is applied to obtain the data sample points for the fitting of two concentric circles. The results verify very well the theoretical studies.
For ease of illustration, as shown in Fig. 1, we shall consider two concentric circles. It is straightforward to extend the study to more than two concentric circles. Let us denote \(n_i\) to be the number of data points on the ith component of the concentric circles, where \(i = 1, 2\). The data from the concentric circles are modeled as
where \(\mathbf {s}_{ij} = (x_{ij}, y_{ij})^\mathrm{T}\) represents the \(2\times 1\) vector containing the Cartesian coordinates of the jth point observed around the ith circle. Also, \(\tilde{\mathbf {s}}_{ij} = (\tilde{x}_{ij}, \tilde{y}_{ij})^\mathrm{T}\) is the true value, and \(\mathbf {n}_{ij} = (\delta _{ij},\epsilon _{ij})^\mathrm{T}\) is the observation noise of \(\mathbf {s}_{ij}\). In this paper, we use the common notations that bold capital letters denote matrices and bold lower case letters represent vectors. \(\mathbf {1}_m\) and \(\mathbf {0}_m\) are length m vectors of ones and zeros. Also, the symbol tilde represents the true value, and \(\bullet ^-\) is the Moore–Penrose pseudoinverse of \(\bullet \). For an unknown parameter \(\bullet \) to be estimated, \(\hat{\bullet }\) is an estimate of it while \(\bullet \) itself is viewed as a variable for optimization.
Concentric circles fitting problem lies under the umbrella of Errors-in-Variables (EIV) model. Here, we shall adopt the functional model in which the true points \(\tilde{\mathbf {s}}_{ij}\)’s are fixed, but they are unknown and satisfy the following relation
for each \(i=1,2\), and \(j=1,\ldots ,n_i\). Here, the four-dimensional vector \(\tilde{{\varvec{\theta }}}\) is the unknown \(\tilde{{\varvec{\theta }}}=(\tilde{\mathbf {c}}^\mathrm{T},\tilde{R}_1,\tilde{R}_2)^\mathrm{T} \) to be estimated, and \( \tilde{\mathbf {c}}= (\tilde{a}, \tilde{b})^\mathrm{T}\) is the center of the common concentric circles. \(\tilde{R}_1\) and \(\tilde{R}_2\), with \(\tilde{R}_1<\tilde{R}_2\), are the two circle radii, and \(\Vert \cdot \Vert \) is the Euclidean norm.
Expanding the square in Eq. (2) and denoting \(\Vert \tilde{\mathbf {s}}_{ij} \Vert ^2\) as \(\tilde{z}_{ij}\), Eq. (2) can be expressed as
where \({\tilde{{\varvec{\phi }}}}=(\tilde{A},\tilde{B},\tilde{C},\tilde{D}_1,\tilde{D}_2)^\mathrm{T}\) is the algebraic parameter vector. Thus, one might alternatively estimate the algebraic parameter vector and then recover the natural parameters through the relationships between the two parametric spaces
where
Note here that Eq. (3) can be expressed in a compact form as \(P_i={\tilde{{\varvec{\phi }}}}^\mathrm{T}\tilde{\mathbf {z}}_{ij}\), where
For notation simplicity, we shall collect all \(n = n_1 + n_2\) measurement data points together as \(\mathbf {s}= \tilde{\mathbf {s}}+ \mathbf {n}\) with \(\mathbf {s}=(\mathbf {s}_1^\mathrm{T},\mathbf {s}_2^\mathrm{T})^\mathrm{T}\), \(\tilde{\mathbf {s}}=(\tilde{\mathbf {s}}_1^\mathrm{T},\tilde{\mathbf {s}}_2^\mathrm{T})^\mathrm{T}\), and \(\mathbf {n}=(\mathbf {n}_1^\mathrm{T},\mathbf {n}_2^\mathrm{T})^\mathrm{T}\), where \(\mathbf {s}_i = (\mathbf {s}_{i1}^\mathrm{T}, \ldots , \mathbf {s}_{in_i}^\mathrm{T})^\mathrm{T}\), \(\mathbf {n}_i = (\mathbf {n}_{i1}^\mathrm{T}, \ldots ,\mathbf {n}_{in_i}^\mathrm{T})^\mathrm{T}\). Here, \(\mathbf {s}\) and \(\mathbf {n}\) are \(2n \times 1\) vectors of the observed points and the noise vectors, respectively, while \(\tilde{\mathbf {s}}\) is the true value of \(\mathbf {s}\).
The noise vector \(\mathbf {n}\) is modeled as a Gaussian random vector with mean zero and covariance matrix \(\mathbf {Q}\). It is often reasonable to assume \(\mathbf {n}_{ik}\) and \(\mathbf {n}_{jl}\), for \(k \ne l\) or \(i\ne j\), are independent so that \(\mathbf {Q}\) is a diagonal matrix. Here, we look at the specific case that \(\mathrm{cov}(\mathbf {n}_{ij},\mathbf {n}_{il})=\sigma ^2\hat{\delta }_{jl}\) for all \(l,j=1,\ldots , n_i\) and \(i=1,2\), where \(\hat{\delta }_{jl}\) represents the Kronecker delta function. Finally, it is worth mentioning here that in all numerical experiments we have conducted, the condition \(\zeta _i>0\), for each i, has fulfilled. In our experiments, we were carefully monitoring this condition. If a single case did appear, then its estimation would not be considered in our calculations.
The paper is organized as follows. Section 2 reviews the existing methods that will be analyzed. Section 3 briefly summarizes the first-order analysis results for completeness. Section 4 focuses on the second-order analysis of the MLE and introduces the adjusted MLE that has zero essential bias. Section 5 is dedicated to the second-order analysis of the algebraic fits. It also develops the new Hyper-accurate fitting method that works best among other algebraic solutions. Section 6 performs the second-order analysis for the iterative methods. The studies in Sects. 4–6 are supported with numerical examples.
Section 7 gives three comprehensive numerical simulations and a practical experimental study with realistic and Sect. 7 summarizes our conclusion. The technical details of this paper are included in “Appendix.”
2 Background
In this section, we briefly introduce the methods discussed in this paper. A full description of these methods can be found in Al-Sharadqah and Ho [3].
2.1 The MLE
Based on our statistical assumptions, the MLE, \(\hat{{\varvec{\theta }}}_\mathrm{m}\), turns out to be the minimizer of \(\mathscr {F}_1({\varvec{\theta }})=\sum _{i=1}^2\sum _{j=1}^{n_i}\Vert \mathbf {s}_{ij}-\tilde{\mathbf {s}}_{ij} \Vert ^2\), subject to a system of equations given in Eq. (2). Al-Sharadqah and Ho [3] proved that, under the isotropic and homogeneity of the noisy errors that are also adopted in this paper, the MLE is equivalent to orthogonal distance regression (ODR), or the so-called the geometric fit. The geometric fit minimizes the sum of the squares of the orthogonal distances of the observed points \(\mathbf {s}_{ij}\) to the fitted circles indexed by \((a,b,R_1)\) and \((a,b,R_2)\); i.e.,
where \(\mathbf {r}_{ij}=\mathbf {s}_{ij}-\mathbf {c}\). The signed distance \(d_{ij}\) stands for the distance from \(\mathbf {s}_{ij}\) to the circle \(P_i\). i.e., for each \(i=1\), 2, and \(j=1\),\(\ldots ,n_i\),
This is a nonlinear least squares problem, and it needs an iterative procedure to obtain its solution \(\hat{{\varvec{\theta }}}_\mathrm{m}\). In [3], two Levenberg–Marquardt (LM)-based algorithms were proposed to compute its solution.
2.2 Gradient Weighted Algebraic Fit
Al-Sharadqah and Ho [3] implemented the so-called gradient weighted algebraic fit (GRAF), a well-known method in estimating the parameters for many subjects, to concentric circles fitting [8, 16, 22]. The GRAF \({\hat{{\varvec{\phi }}}}_\mathrm{g}\) is the estimator that minimizes the objective function
where
As an immediate consequence of our statistical assumption \(\mathrm{cov}(\mathbf {n}_{ij} )=\sigma ^2\mathbf {I}_2\), the objective function \(\mathscr {G}\) in Eq. (9) has the formal expression
where
and
where
Note that in Eq. (11) the objective function \(\mathscr {G}\) represents the sum of the ratios of two homogeneous quadratic polynomials of degree 2; hence, if \({\hat{{\varvec{\phi }}}}_\mathrm{g}\) is the solution of Eq. (11), then \(c{\hat{{\varvec{\phi }}}}_\mathrm{g}\) is also another solution for any nonzero constant c. To remove the indeterminacy, we restrict the domain of the solution \({\hat{{\varvec{\phi }}}}_\mathrm{g}\) on the unit ball; i.e., \(\Vert {\hat{{\varvec{\phi }}}}_\mathrm{g}\Vert =1\). Moreover, the solution is invariant under translation, rotation, and scaling.
Differentiating \(\mathscr {G}\) in Eq. (11) with respect to \({\varvec{\phi }}\), we obtain the so-called variational equation; i.e.,
where,
and \(\gamma _{ij}={\hat{{\varvec{\phi }}}}_\mathrm{g} ^\mathrm{T}\mathbf {V}_{ij}{\hat{{\varvec{\phi }}}}_\mathrm{g} \). Its solution \({\hat{{\varvec{\phi }}}}_\mathrm{g }\) is the generalized eigenvector of the matrix pencil \((\mathbf {\mathscr {M}},\mathbf {\mathscr {L}})\) associated with the unity eigenvalue. Since both \(\mathbf {\mathscr {M}}\) and \(\mathbf {\mathscr {L}}\) depend on \({\varvec{\phi }}\), Eq. (15) can only be solved by iterative procedures. Two numerical schemes that appear in many computer vision literature were used to solve Eq. (15). Chojnacki et al. [8] proposed the Fundamental Numerical Scheme (FNS), while Leedan and others [16, 18] proposed the Heteroscedastic-Error-In-Variables Scheme (HEIV).
2.3 Renormalization and Generalized GRAF
Kanatani developed the Renormalization method [12, 13], which took a prominent position in solving many practical problems in geometric fitting and computer vision before GRAF was developed. Al-Sharadqah and Ho extended the Renormalization method to the concentric circles. In our context, the Renormalization fit \({\hat{{\varvec{\phi }}}}_\mathrm{R}\) solves
where \(\mathbf {\mathscr {N}}=\sum _{i=1}^2\sum _{j=1}^{n_i} \gamma _{ij}^{-1}\mathbf {V}_{ij}\). Then, one finds \({\varvec{\phi }}\) as a generalized eigenvector for the matrix pencil \((\mathbf {\mathscr {M}}, \mathbf {\mathscr {N}})\). That is, we solve the generalized eigenvalue problem and choose the generalized eigenvector associated with the smallest positive eigenvalue \(\lambda \). However, both of the matrices \(\mathbf {\mathscr {M}}\) and \(\mathbf {\mathscr {N}}\) depend on \({\varvec{\phi }}\); thus, Kanatani proposed an iterative algorithm to find the solution. More details about all these numerical schemes can be found in the surveys [6, 9]. Since the Renormalization method can be considered as an approximation for GRAF and it is a special case of Eq. (17), we will call the solution of the general equation (17) by the generalized GRAF.
2.4 Algebraic Fits
Here, we discuss the all non-iterative algebraic methods that will be analyzed in this paper. They are called algebraic, because they minimize the sum of the squares of the algebraic distances \(\sum _{i=1}^2\sum _{j=1}^{n_i}\Vert P_i({\varvec{\theta }},\mathbf {s}_{ij}) \Vert ^2\). Alternatively, the problem can be rewritten in terms of the algebraic parameter \({\varvec{\phi }}\) by expressing \(P_i({\varvec{\phi }},\mathbf {s}_{ij})\) as \({\varvec{\phi }}^\mathrm{T}\mathbf {z}_{ij}\). Since \(\mathbf {M}_{ij}=\mathbf {z}_{ij}\mathbf {z}_{ij}^\mathrm{T}\) and the matrix of the moments \(\mathbf {M}=\sum _{i=1}^2 \sum _{j=1}^{n_i} \mathbf {M}_{ij}\), the objective function we are seeking to minimize is \({\varvec{\phi }}^\mathrm{T}\mathbf {M}{\varvec{\phi }}\). To avoid the trivial solution, we restrict our domain to \(\Vert {\varvec{\phi }}\Vert =1\), but this does not remove the indeterminacy entirely. To address this issue, a quadratic constraint in the parametric subspace of \({\mathbb R}^5\) must be imposed. That is, we generally use \({\varvec{\phi }}^\mathrm{T}\mathbf {N}{\varvec{\phi }}=c\), for some constant c. This converts our problem to the minimization problem
This objective function depends on the constraint matrix \(\mathbf {N}\), and as such its minimizer’s behavior depends upon \(\mathbf {N}\). Different choices of \(\mathbf {N}\) lead to new estimators. For instance, \(\mathbf {N}_\mathrm{K}=\mathbf {e}_1'\mathbf {e}_1'^\mathrm{T}\) with \(\mathbf {e}_1'=(1,0,0,0,0)^\mathrm{T}\) is the constraint matrix of the simple fit, the Taubin method has the constraint matrix \(\mathbf {N}_\mathrm{T}=\mathbf {V}\), while the constraint matrices \(\mathbf {N}_{\mathbf {A}}=\mathbf {A}\) and \(\mathbf {N}_{\mathbf {B}}=\mathbf {B}\) for Type-A and Type-B direct methods, respectively, are presented shortly. In this paper, we will investigate these four choices of \(\mathbf {N}\). A brief description of each method is presented shortly, while details about these methods together with their properties and implementations have been thoroughly discussed in [3].
All algebraic fits share a common aspect. They minimize (18), and as such, one finds the solution by differentiating the objective function (18) with respect to \({\varvec{\phi }}\) and equating its derivatives with zero. Therefore, the minimization problem reduces to solving the generalized eigenvalue problem
The matrix of the moments \(\mathbf {M}\) is positive definite in general. The only exceptional case that \(\mathbf {M}\) becomes singular when all the points for fitting lie exactly on the concentric circles, but the chance of having this situation is near zero. \(\lambda \) is the generalized eigenvalue for the pencil of matrices \((\mathbf {M},\mathbf {N})\), and \({\varvec{\phi }}\) is the corresponding generalized eigenvector. Because \(\Vert {\varvec{\phi }}\Vert =1\), we pick the solution as the unit generalized eigenvector associated with the eigenvalue \(\lambda \). The choice of \(\lambda \) depends on the structure of the constraint matrix \(\mathbf {N}\).
2.4.1 Simple Algebraic Fit
Perhaps, the simplest approach is to minimize the sum of the squares of the algebraic errors. That is,
Equivalently, one minimizes (18) subject to \(A=1\). This constraint can be written as \({\varvec{\phi }}^\mathrm{T}\mathbf {N}_\mathrm{K}{\varvec{\phi }}=1\), where \(\mathbf {N}_\mathrm{K}=\mathbf {e}_1'\mathbf {e}_1'^\mathrm{T}\). This method is called the simple fit (SF) and it is the fastest method. Moreover, it works well if data are distributed along long concentric circular arcs. However, this feature attribute disappears when data are sampled along short concentric circular arcs. In this paper, we will investigate this issue, and we will explain its behavior analytically.
2.4.2 The Taubin Method
The Taubin method is one of the most accurate algebraic method [3]. Its solution \({\hat{{\varvec{\phi }}}}_\mathrm{T}\) minimizes the objective function
with
The matrix \(\mathbf {V}_{ij}\) is defined in Eq. (13). Since \(\mathbf {N}_\mathrm{T}\) is positive semidefinite, \({\hat{{\varvec{\phi }}}}_\mathrm{T}=\mathrm{argmin}_{\Vert {\varvec{\phi }}\Vert =1} \mathscr {F}_\mathrm{T}({\varvec{\phi }})\) is the generalized eigenvector of the matrix pencil \((\mathbf {M},\mathbf {V})\) corresponding to the smallest positive eigenvalue \(\lambda \). This solution is an approximation of the GRAF when the double summation is distributed over both of the numerator and the denominator of \(\mathscr {G}\) [cf. Eq. (11)]. Furthermore, regardless of its losses for the optimality criterion, the Taubin fit behaves—in some prospect—like the GRAF. This observation will be investigated analytically in our second-order error analysis.
2.4.3 Type-A Direct Method
Another algebraic method that was also proposed as an approximation of GRAF is the Type-A direct fit [3]. It results by presumably assuming that the observed points are close enough to the true curves. Then, \({\varvec{\phi }}^\mathrm{T}\mathbf {z}_{ij}\approx 0\). Therefore, \({\varvec{\phi }}^\mathrm{T}\mathbf {V}{\varvec{\phi }}= n_1\zeta _1+n_2\zeta _2 \), where \(\zeta _i\) is defined in Eq. (5). Thus, Eq. (11) can be approximated by
with
For this method, \({\hat{{\varvec{\phi }}}}_\mathrm{A}=\mathrm{argmin_{\Vert {\varvec{\phi }}\Vert =1}}\, \mathscr {F}_\mathrm{A}({\varvec{\phi }})\) is the generalized eigenvector that corresponds to the smallest nonnegative generalized eigenvalue \(\lambda \).
2.4.4 Type-B Direct Method
This method is stemmed from the two geometric constraints of concentric circles. That is, \({\varvec{\phi }}\) must satisfy \(\zeta _i>0\) for each \(i=1,2\). If these two constraints are combined together, we have the constraint \( \zeta _1+\zeta _2>0\). Note that this is a single homogeneous constraint of degree 2. Therefore, we can set \(2B^2+2 C^2 -4A(D_1+D_2)=1\); i.e., \({\varvec{\phi }}^\mathrm{T}\mathbf {N}_{\mathbf {B}}{\varvec{\phi }}=1\), where
and then we minimize
With a very similar analysis to the Type-A direct fit, one can show that the new estimator \({\hat{{\varvec{\phi }}}}_\mathrm{B}=\mathrm{argmin}_{\Vert {\varvec{\phi }}\Vert =1} \mathscr {F}_\mathrm{B}({\varvec{\phi }})\) is the unit generalized eigenvector of the smallest positive eigenvalue of \((\mathbf {M},\mathbf {B})\). The matrix \(\mathbf {B}\) does not depend on \(n_1\) or \(n_2\), and it coincides with the Type-A direct fit only whenever \(n_1=n_2\). Because of this similarity in its structure to the Type-A direct fit, this method is called the Type-B direct method (or Type-B for short).
3 Results of First-Order Error Analysis
To demonstrate the performance of the methods mentioned above, we turn our attention to the statistical error analysis. In general, the accuracy of an estimator \(\hat{\varvec{\varTheta }}\) of the parameter vector \(\varvec{\varTheta }\) is measured by its mean squared error.
where \(\Delta \hat{\varvec{\varTheta }}= \hat{\varvec{\varTheta }}-\tilde{\varvec{\varTheta }}\). Evaluating the MSE, however, is not possible to our problem. However, if the noise level \(\sigma \) is not significant—as a realistic assumption in many research subjects in signal and image processing—then we can ignore the higher-order noise terms and approximate the mean squared error by
where \(\sigma ^2 \varXi _1\) is the first leading term of the covariance matrix of \(\hat{\varvec{\varTheta }}\) and it is the only term of order \(\sigma ^2\). In [3], the statistical analysis was restricted to the first leading term of the MSE, which is also the main term of the covariance matrix.
This leading term has a natural lower bound known by the Kanatani–Cramér–Rao (KCR) lower bound [7]. If the leading term of an estimator achieves this bound, then the estimator is optimal. The optimality issue was one of the main goals of [3]. Al-Sharadqah and Ho evaluated the leading term for each of the methods: the MLE, the GRAF, the Renormalization, and the algebraic fits and they showed that all the iterative methods are optimal in this sense. Indeed, for the MLE, it was shown in [3] that its linear approximation is \(\tilde{{\varvec{\theta }}}+ \Delta _1 \hat{{\varvec{\theta }}}_\mathrm{m}\), where the first-order error term \(\Delta _1 \hat{{\varvec{\theta }}}_\mathrm{m}= \tilde{\mathbf {K}}\mathbf {f}_1\) and \(\mathbf {f}_1\) presented in Eq. (34) and \(\tilde{\mathbf {K}}=\tilde{\mathbf {R}}\tilde{\mathbf {W}}^\mathrm{T}\). Here, \(\tilde{\mathbf {R}}=(\tilde{\mathbf {W}}^\mathrm{T}\tilde{\mathbf {W}})^{-1}\) with \(\tilde{\mathbf {W}}^\mathrm{T}=[\tilde{\mathbf {W}}_1^\mathrm{T}\,\,\, \tilde{\mathbf {W}}_2 ^\mathrm{T}]\) and
and
Moreover, the linear approximation of the MLE is normally distributed with mean \(\tilde{{\varvec{\theta }}}\) and covariance matrix \(\sigma ^2\tilde{\mathbf {R}}\). This first leading term of the covariance of the MLE is expressed in terms of the natural parameters \({\varvec{\theta }}=(a,b,R_1,R_2)\) and it coincides with the KCR of \(\varvec{\varTheta }={\varvec{\theta }}\), which was derived by Ma and Ho [17]; i.e., \(\mathrm{KCR}(\hat{{\varvec{\theta }}})=\sigma ^2\tilde{\mathbf {R}}\). This shows why the MLE is optimal.
Al-Sharadqah and Ho [3] also applied the perturbation theory to the two other iterative methods and showed that the leading terms of their covariances are identical and equal to
where \(\tilde{\mathbf {\mathscr {M}}}= \sum _{i=1}^2 \sum _{j=1}^{n_i}\tilde{\zeta }_{i}^{-1}\tilde{\mathbf {z}}_{ij}\tilde{\mathbf {z}}_{ij}^\mathrm{T}\) and \(\tilde{\zeta }_{i}\) is the true value of \(\zeta _i\) [cf. Eq. (5)].
This leading term of the covariances for the GRAF and the generalized GRAF is expressed in terms of the algebraic parameters \(\varvec{\varTheta }={\varvec{\phi }}\) and it coincides with the KCR lower bound [7]. That is, the KCR of \({\hat{{\varvec{\phi }}}}\) is \(\mathrm{KCR}({\hat{{\varvec{\phi }}}})=\sigma ^2\tilde{\mathbf {\mathscr {M}}}^-.\)
It is worth mentioning here that the relationship between the lower bounds in the two parametric spaces is \(\mathrm{KCR}(\hat{{\varvec{\theta }}})=\tilde{\mathbf {E}}\,\mathrm{KCR}({\hat{{\varvec{\phi }}}})\,\tilde{\mathbf {E}}^\mathrm{T} \) where \(\mathbf {E}\) is a \(4\times 5\) “Jacobian” matrix that comes from taking partial derivatives in Eq. (4), see [3] for more details. This shows that the leading term of the covariance matrices for both the Renormalization and GRAF equal to the KCR lower bound, and hence, we conclude that they are statistically optimal.
Finally, it was shown in [3] that the leading terms of the covarainces of all algebraic fits are the same and equal to
where \(\tilde{\mathbf {M}}= \sum _{i=1}^2 \sum _{j=1}^{n_i}\tilde{\mathbf {z}}_{ij}\tilde{\mathbf {z}}_{ij}^\mathrm{T}\). Moreover, this covariance matrix does not achieve the KCR lower bound, and this proves that the algebraic methods are suboptimal.
4 Second-Order Analysis of MLE
The leading term of the covariance matrix of any algebraic fit does not depend on the constraint matrix \(\mathbf {N}\). Therefore, all algebraic concentric circle fits have the same covariance matrix (to the leading order). This is because their linear approximations, say \(\hat{\varvec{\varTheta }}_\mathrm{L}=\tilde{\varvec{\varTheta }}+{\Delta }_1\hat{\varvec{\varTheta }}\), are equal. Moreover, the leading term of the covariance matrices of algebraic fits do not achieve the KCR lower bound; i.e., they are not statistically optimal. However, the algebraic methods behave differently in practice. For instance, the Taubin method always outperforms the Type-A direct fit. The same observation appears among the iterative (optimal) methods. Some fits always perform better than others, even though they belong to the same class.
To shed more light about their behaviors, we shall trace the second most important terms in their MSEs that come from the bias. That is, we shall expand our analysis by including the second-order error term \({\Delta }_2\hat{\varvec{\varTheta }}\) and study the quadratic approximations of \(\hat{\varvec{\varTheta }}\)
We only need to evaluate \({\Delta }_2\hat{\varvec{\varTheta }}\), which is a quadratic form of the noisy error vector \(\mathbf {n}\). This refines Eq. (26) to
here, \(\sigma ^2 \varXi _1\) and \(\sigma ^4 \varXi _2\) are the first and the second leading terms of the covariance matrix of \(\hat{\varvec{\varTheta }}\) and their orders of magnitudes are \(\sigma ^2/n\) and \(\sigma ^4/n\), respectively. The term \(\sigma ^4 \tilde{\mathbf {b}}\tilde{\mathbf {b}}^\mathrm{T}\) comes as the outer product of the second-order error bias \({\mathbb E}({\Delta }_2\hat{\varvec{\varTheta }})=\sigma ^2\tilde{\mathbf {b}}\) with itself. We shall show later that \(\mathscr {O}(\sigma ^2)\) -bias, \(\sigma ^2\tilde{\mathbf {b}}\), can be decomposed into \(\tilde{\mathbf {b}}=\tilde{\mathbf {b}}_1+\tilde{\mathbf {b}}_2\). The most important part, \(\sigma ^2\tilde{\mathbf {b}}_1\sim \sigma ^2\), is referred as the essential bias and the least important part, \(\sigma ^2\tilde{\mathbf {b}}_2\sim \sigma ^2/n\), is called the nonessential bias.
It is worth mentioning that we are studying here the quadratic approximation of \(\hat{\varvec{\varTheta }}\) and its MSE, which coincides with the MSE of \(\hat{\varvec{\varTheta }}\) up to order of magnitude \(\sigma ^4/n\). That is, there are other \(\mathscr {O}(\sigma ^4/n)\)—terms in the full MSE expression that were not included. Those terms are the expected value of the outer product of first- and the third-order errors terms, which are discarded in our analysis. However, if \(n_i\)’s are fairly large, say 20–100, then those ignored terms together with the less important part in \(\sigma ^4(\tilde{\mathbf {b}}_2\tilde{\mathbf {b}}^\mathrm{T}+\tilde{\mathbf {b}}\tilde{\mathbf {b}}_2^\mathrm{T})\) become negligible. Accordingly, the only terms are persisted in orders of magnitudes \(\sigma ^4\). They are free of n and they come only from the essential bias.
The MLE is often considered as one of the best estimators available. We shall begin with the second-order analysis of the MLE.
4.1 Second-Order Bias of MLE
If we restrict the error analysis to the first leading term, then the MLE will be an unbiased and efficient estimator of \(\hat{{\varvec{\theta }}}_\mathrm{m}\). Higher-order analysis reveals the bias of the MLE persists even for very large sample size. Therefore, we address here the bias of the MLE \(\hat{{\varvec{\theta }}}_\mathrm{m}\), and find the MSE of its quadratic approximation. This can be accomplished by computing its second-order error term, \({\Delta }_2\hat{{\varvec{\theta }}}_\mathrm{m}\), and evaluating its expectation. Including all terms of order \(\mathscr {O}_\mathrm{P}(\sigma ^2)\) of \(d_{ij}\) shows that, for each \( i=1,2\) and \(j=1,\ldots , n_i\),
where
and
where \(f_{1ij}=\tilde{u}_{ij} \delta _{ij} + \tilde{v}_{ij} {\epsilon }_{ij}\) and
We also have defined
and \( \check{\mathbf {n}}_{ij}=(\delta _{ij},{\epsilon }_{ij},0,0)^\mathrm{T}\). The derivations of Eqs. (32)–(35) are long and their details can be found in “Appendix.”
The quantity \(q_{ij}\) includes all terms up to order \(\mathscr {O}_\mathrm{P}(\sigma ^2)\) and it can be expressed in the vector notations as \(\mathbf {q}_i= \mathbf {l}_i +\mathbf {f}_{2i}\), where the vector \(\mathbf {f}_{2i} = (f_{2i1}, \ldots , f_{2in_i})^\mathrm{T}\). Next, minimizing \(\mathscr {F}({\varvec{\theta }})\) to the second-order term is equivalent to minimizing
This least squares problem turns into \(\tilde{\mathbf {W}}{\Delta }_2\hat{{\varvec{\theta }}}_\mathrm{m}=\mathbf {l}+\mathbf {f}_2\), where concatenated vectors are \(\mathbf {l}=(\mathbf {l}_1^\mathrm{T}\, ,\mathbf {l}_2^\mathrm{T})^\mathrm{T}\) and \(\mathbf {f}_2=(\mathbf {f}_{21}^\mathrm{T} , \mathbf {f}_{22}^\mathrm{T})^\mathrm{T}\). Thus, \( {\Delta }_2\hat{{\varvec{\theta }}}_\mathrm{m}= \tilde{\mathbf {K}}\mathbf {l}+\tilde{\mathbf {K}}\mathbf {f}_2=\tilde{\mathbf {K}}\mathbf {f}_2,\) and the quadratic approximation of \(\hat{{\varvec{\theta }}}_\mathrm{m}\) becomes \(\hat{{\varvec{\theta }}}_\mathrm{Q}=\tilde{{\varvec{\theta }}}+ \tilde{\mathbf {K}}(\mathbf {f}_1+\mathbf {f}_2)\), where \(\mathbf {f}_1=(\mathbf {f}_{11}^\mathrm{T},\mathbf {f}_{12}^\mathrm{T})^\mathrm{T}\).
As a simple numerical experiment to validate the linear and the quadratic approximations, we positioned \(n_1=10\) and \(n_2=20\) equidistant points on the concentric circular arcs with center (0, 0) and radii \(\tilde{R}_1\)=1 and \(\tilde{R}_2=2\). Both arcs have the same initial angle 0. The terminal angle for the smaller circle is \(\omega _1=90^\circ \) and for the larger circle is \(\omega _2=120^\circ \). The true points were contaminated by white Gaussian noise with standard deviation 0.2. \(N=10^5\) ensemble runs were performed and for each run the estimate of \(\hat{R}_1\) is recorded. The linear and the quadratics approximations of \(\hat{R}_1\) are computed using \(\hat{{\varvec{\theta }}}_\mathrm{L}\) and \(\hat{{\varvec{\theta }}}_\mathrm{Q}\), while the MLE is computed by the LM algorithm. The kernel densities of these estimates are shown in Fig. 2. As Fig. 2 shows, the kernel density of the linear approximation (dashed curve) significantly differs from the identical kernel densities of the MLE (solid curve) and its quadratic approximation (dotted curve). This example also demonstrates the importance of the second-order error analysis discussed in this paper.
Evaluating the expressions of the bias and the MSE of \({\Delta }_2\hat{{\varvec{\theta }}}_\mathrm{Q}\) involves lengthy calculations. To simplify our calculations, let us denote the \(n_i\)-dimensional vectors whose \(j^\mathrm{th}\) entities are
by \(\mathbf {a}_i\), \(\mathbf {b}_i\), \(\mathbf {c}_i\), and \(\tilde{\mathbf {h}}_i\), respectively. These vectors play a key role later, so some of their relevant identities are presented in the following lemma. The proof is deferred to “Appendix.”
Lemma 1
For each \(i,k=1,\) 2, and \(j=1,\ldots ,n_i\), let \(\tilde{\mathbf {H}}_{ik}\) be a \(n_i\times n_k\) matrix with \(jl^\mathrm{th}\) entities \(\tilde{h}_{ijkl}=\tilde{\mathbf {t}}_{ij}^\mathrm{T}\tilde{\mathbf {R}}\tilde{\mathbf {t}}_{kl}\) and \(\tilde{\mathbf {D}}_{\tilde{\mathbf {h}}_i}=\mathrm{diag}\left( \tilde{\mathbf {h}}_i\right) \). Then,
Moreover, for each i, \(k=1,2\), one has
while \({\mathbb E}(\mathbf {a}_i\mathbf {b}_k^\mathrm{T})={\mathbb E}(\mathbf {b}_i\mathbf {c}_k^\mathrm{T})={\mathbf {0}}_{n_i\times n_k} \) and
The first advantage of these identities appears in the evaluation the bias of \(\hat{{\varvec{\theta }}}_\mathrm{Q}\). Since \({\mathbb E}({\Delta }_1\hat{{\varvec{\theta }}}_\mathrm{m})={\mathbf {0}}\) we only need \({\mathbb E}({\Delta }_2\hat{{\varvec{\theta }}}_\mathrm{m})=\tilde{\mathbf {K}}\,{\mathbb E}(\mathbf {f}_2)\), where \( \mathbf {f}_{2i}=\frac{1}{2\tilde{R}_i}(\mathbf {a}_i+\mathbf {b}_i+\mathbf {c}_i)\), it is sufficient to find \({\mathbb E}(\mathbf {a}_i)\), \({\mathbb E}(\mathbf {b}_i)\), and \({\mathbb E}(\mathbf {c}_i)\). From now on, the appearance of the notation \((\,\check{}\,)\) over a vector means that the vector is divided by \(\frac{1}{2\tilde{R}_i}\). For instance, \(\check{\mathbf {a}}_i\) and \(\check{\tilde{\mathbf {h}}}_i\) are equal to \(\frac{1}{2\tilde{R}_i}\mathbf {a}_i\) and \(\frac{1}{2\tilde{R}_i}\tilde{\mathbf {h}}_i\), respectively; but in the case of matrices, we define the matrices \(\check{\tilde{\mathbf {D}}}_{\tilde{\mathbf {h}}_i}=\frac{1}{4\tilde{R}_i^2}\tilde{\mathbf {D}}_{\tilde{\mathbf {h}}_i}\) and \(\check{\tilde{\mathbf {H}}}_{ik}=\frac{1}{4\tilde{R}_i\tilde{R}_k}\tilde{\mathbf {H}}_{ik}\). With these notations, we decompose \(\mathbf {f}_{2i}\) into \( \mathbf {f}_{2i}=\check{\mathbf {a}}_{i}+\check{\mathbf {b}}_{i}+\check{\mathbf {c}}_{i}\), for each \(i=1,2\). Based on Lemma 1,
Premultiplying \({\mathbb E}(\mathbf {f}_2)\) by \(\tilde{\mathbf {K}}\) gives
where
and \(\check{n}_i=\frac{n_i}{2\tilde{R}_i}\). Since \(2\tilde{R}_i \tilde{\mathbf {w}}_i\) is the \((2+i)^\mathrm{th}\) column of \(\tilde{\mathbf {W}}^\mathrm{T}\tilde{\mathbf {W}}\), then
and
Accordingly,
where \(\check{\mathbf {e}}_3= \frac{1}{2\tilde{R}_1}\mathbf {e}_3\) and \(\check{\mathbf {e}}_4= \frac{1}{2\tilde{R}_2}\mathbf {e}_4\). The essential bias of the MLE, \(\sigma ^2(\check{\mathbf {e}}_3+\check{\mathbf {e}}_4)\), depends upon \(\tilde{R}_1\) and \(\tilde{R}_2\) only and it does not rely on the actual data. The second part is of order \(\sigma ^2/n_i\)’s, and it represents the nonessential bias. It is worth mentioning here that the MLE of the center does not have essential bias while amounts of the essential bias of \(\hat{R}_i\)’s are \(\frac{\sigma ^2}{2\tilde{R}_i}\).
Finally, our thorough analysis shows that the MSE of \(\hat{{\varvec{\theta }}}_\mathrm{Q}\) is
where
and
The complete derivations of Eqs. (41)–(43) are in “Appendix.”
4.2 Adjusted MLE
The MLE has second-order bias, which can be adjusted to improve the MLE [cf. Eq. (40)]. Then one can remove the bias to improve estimating the parameters by computing the \(\hat{{\varvec{\theta }}}_\mathrm{m}=(\hat{a},\hat{b},\hat{R}_1,\hat{R}_2)\) first and then removing the realization of its bias through
where \(\hat{\mathbf {K}}\), \(\hat{\check{\mathbf {h}}} \), and \({\hat{\sigma }}^2=\mathscr {F}(\hat{{\varvec{\theta }}}_\mathrm{m})/(n-4)\) are the estimating version of \(\tilde{\mathbf {K}}\), \(\check{\tilde{\mathbf {h}}}\), and \(\sigma ^2\), respectively. One can show that these statistics are unbiased estimators for their true versions up to the first leading term. Accordingly, the verification that \(\hat{{\varvec{\theta }}}_\mathrm{adj}\) is unbiased estimator of \(\tilde{{\varvec{\theta }}}\) (up to order \(\sigma ^4\)) becomes straightforward.
5 Second-Order Analysis of Algebraic Fits
The performance of all algebraic fits in the MSE sense depends on their variances and their biases. It is remarkable to note that the leading term of the covariance matrix of any algebraic fit does not depend on the constraint matrix \(\mathbf {N}\). This observation implies that all algebraic circle fits have the same variance (to the leading order). However, this leading term does not attain the KCR lower bound. Consequently, all algebraic fits are suboptimal. This fact reveals a big departure from the analysis of the single circle fitting by Al-Sharadqah and Chernov [1, 2].
Evaluating the bias is an essential step in parametric estimation in order to obtain a good estimator, especially that the iterative methods, such as the MLE, need a good initial guess in order to guarantee their convergence. Besides, in the cases where the noise level is large, all iterative methods, including the MLE, diverge. This makes algebraic fits the only plausible solutions at our hand. Therefore, this section is devoted to analyze the bias of the algebraic fits, such as the simple fit, the Type-A fit, the Type-B fit, and the Taubin fit. The algebraic method proposed in [19] will not be included there. Indeed, its mechanism is not only unclear, but also the quality of its performance is insufficient as demonstrated in [3].
The \(\mathbf {z}_{ij}\) is a quadratic form of the random vector \(\mathbf {s}_{ij}=(x_{ij},y_{ij})^\mathrm{T}\), which can be written as
The first-order error \(\Delta _1\mathbf {z}_{ij}\) is a linear combination of \((\delta _{ij},{\epsilon }_{ij})\). That is,
where \(\tilde{\mathbf {a}}_{ij}=(2\tilde{x}_{ij},1,0,0,0)^\mathrm{T}\) and \(\tilde{\mathbf {b}}_{ij}=(2\tilde{y}_{ij},0,1,0,0)^\mathrm{T}\). Accordingly, for each \(j=1,\ldots ,n_i\),
where \(\tilde{\mathbf {V}}_{ij}=\tilde{\mathbf {a}}_{ij}\tilde{\mathbf {a}}_{ij}^\mathrm{T}+\tilde{\mathbf {b}}_{ij}\tilde{\mathbf {b}}_{ij}^\mathrm{T}\). Moreover, the second-order error term is \({\Delta }_2\mathbf {z}_{ij}=(\delta _{ij}^2+{\epsilon }_{ij}^2)\mathbf {e}_1'\) and \({\mathbb E}({\Delta }_2\mathbf {z}_{ij})=2\mathbf {e}_1'\), where \(\mathbf {e}_1'= (1,0,0,0,0)^\mathrm{T}\).
Now, using Taylor series expansion, we can decompose \({\Delta }{\hat{{\varvec{\phi }}}}={\hat{{\varvec{\phi }}}}-{\tilde{{\varvec{\phi }}}}\) as
where \(\Delta _1{\hat{{\varvec{\phi }}}}\) is a linear form of \(\delta _{ij}\)’s and \({\epsilon }_{ij}\)’s and \(\Delta _2{\hat{{\varvec{\phi }}}}\) is a quadratic form of \(\delta _{ij}\)’s and \({\epsilon }_{ij}\)’s, and all other higher-order terms are represented by \(\mathscr {O}_P(\sigma ^3)\). To assess the bias, we need to evaluate \({\mathbb E}({\Delta }_2{\hat{{\varvec{\phi }}}})\) because \({\mathbb E}({\Delta }_1{\hat{{\varvec{\phi }}}})={\mathbf {0}}\). Since all algebraic fits solve the equation \(\mathbf {M}{\varvec{\phi }}=\lambda \mathbf {N}{\varvec{\phi }}\), then if we apply matrix perturbation to \(\lambda \), \({\hat{{\varvec{\phi }}}}\), \(\mathbf {M}\) and \(\mathbf {N}\), then \(\mathbf {M}{\hat{{\varvec{\phi }}}}=\lambda \mathbf {N}{\hat{{\varvec{\phi }}}}\) becomes
From the first-order analysis [3], it was shown that \(\tilde{\lambda }=\Delta _1\lambda =0\), and
and
Hence, equating all \(\mathscr {O}_P(\sigma ^2)\)-terms in Eq. (46) yields
where
and \(\mathscr {S}\) is the symmetrization operator; i.e., \(\mathscr {S}(\bullet )= (\bullet +\bullet ^\mathrm{T} )/2 \). Next, we find \({\Delta }_2\lambda \). Premultiplying Eq. (48) and using Eq. (47) lead to
Since \(\Delta _2 {\hat{{\varvec{\phi }}}}\) is not orthogonal to \({\tilde{{\varvec{\phi }}}}\), we decompose \(\Delta _2 {\hat{{\varvec{\phi }}}}= \Delta _2^{\parallel } {\hat{{\varvec{\phi }}}}+ \Delta _2^\perp {\hat{{\varvec{\phi }}}}\) into the components that are parallel and orthogonal to \({\tilde{{\varvec{\phi }}}}\). Then, \(\Delta _2^{\parallel } {\hat{{\varvec{\phi }}}}= -\tfrac{1}{2}\, \Vert \Delta _1 {\hat{{\varvec{\phi }}}}\Vert ^2 {\tilde{{\varvec{\phi }}}}\) and \({\mathbb E}(\Delta _2^{\parallel } {\hat{{\varvec{\phi }}}}) = -\tfrac{1}{2}\, \sigma ^2(\mathrm{tr}\,\tilde{\mathbf {M}}^-){\tilde{{\varvec{\phi }}}}\), which really accounts for the curvature of the unit sphere \(\Vert {\hat{{\varvec{\phi }}}}\Vert =1\) rather than represents the bias of \({\hat{{\varvec{\phi }}}}\). Our goal is to evaluate \({\mathbb E}(\Delta _2^\perp {\hat{{\varvec{\phi }}}})\), and we will suppress the \(\perp \) sign for brevity. Therefore, Eqs. (48)–(49) lead to
with
If \(\mathbf {R}\) is decomposed into \(\mathbf {R}_1-\mathbf {R}_2\) with \(\mathbf {R}_1={\Delta }_2\mathbf {M}\) and \(\mathbf {R}_2=\Delta _1\mathbf {M}\tilde{\mathbf {M}}^-\Delta _1\mathbf {M}\), then
Moreover, analogous to [2, 21], a thorough analysis here shows that
where \(\tilde{\psi }_{ij}^{(a)}=\tilde{\mathbf {z}}_{ij}^\mathrm{T}\tilde{\mathbf {M}}^-\tilde{\mathbf {z}}_{ij}\).
It is worth mentioning here that \({\mathbb E}(\mathbf {R}_1)\sim n\sigma ^2\) and \({\mathbb E}(\mathbf {R}_2)\sim \sigma ^2\). Since \(\tilde{\mathbf {M}}^-\sim \mathscr {O}(n^{-1})\), then the contributions of \({\mathbb E}(\mathbf {R}_1)\) and \({\mathbb E}(\mathbf {R}_2)\) to their biases are of orders of magnitudes \(\sigma ^2\) and \(\sigma ^2/n\), respectively. Therefore, the most important term of \(\mathbf {R}\) is \(\mathbf {R}_1\), which has a key role in our analysis, while \(\mathbf {R}_2\) has a less significant contribution to the MSE. Now, combining Eqs. (52) and (53) with Eq. (49) forms
Furthermore, since \(\tilde{\mathbf {z}}_{ij}^\mathrm{T}{\tilde{{\varvec{\phi }}}}=0\) and \({\tilde{{\varvec{\phi }}}}^\mathrm{T}\mathbf {e}_1'=\tilde{A}\), we obtain
This simplifies the general form of the algebraic fits to
Equation (55) provides the general expression of the bias for any algebraic fit. Each algebraic fit has its specific matrix \(\mathbf {N}\), and as such, each method has its own bias.
Bias of the Taubin fit In this case, recall that \(\tilde{\mathbf {N}}= \tilde{\mathbf {V}}=\sum _{i}^2\sum _{j}^{n_i}\tilde{\mathbf {V}}_{ij}\) [cf. Eq. (13)] and \(\tilde{\gamma }_{ij}={\tilde{{\varvec{\phi }}}}^\mathrm{T}\tilde{\mathbf {V}}_{ij}{\tilde{{\varvec{\phi }}}}=\tilde{\zeta }_i\). Thus, a thorough analysis shows that
where
Bias of Type-A direct fit \({\hat{{\varvec{\phi }}}}_\mathrm{A}\) The matrix \(\mathbf {N}=\mathbf {A}\) is free of data. Thus, \(\tilde{\mathbf {N}}=\mathbf {A}\) and
Now, the very helpful relation
reduces the expression of \({\mathbb E}({\Delta }_2{\hat{{\varvec{\phi }}}}_{A})\) to
where \(\alpha =\sum _{i=1}^2\sum _{j=1}^{n_i} \tilde{\zeta }^{-1}\tilde{\zeta }_i \tilde{\psi }_{ij}^{(a)}\). The only terms in Eqs. (56) and (59) with order of magnitude \(\sigma ^2\) are \(\sigma ^2\,I_{{\tilde{{\varvec{\phi }}}}}\) and \(2\sigma ^2\, I_{{\tilde{{\varvec{\phi }}}}}\).
Bias of Type-B direct fit \({\hat{{\varvec{\phi }}}}_\mathrm{B}\) The matrix \(\mathbf {N}=\mathbf {B}\) is free of data. In this case, \(\tilde{\mathbf {N}}=\mathbf {B}\) and
where \(\bar{\tilde{\psi }}_i=\frac{1}{n_i}\sum _{j=1}^{n_i}\tilde{\psi }_{ij}^{(a)}\).
Bias of simple algebraic fit The same approach applies here to derive the bias the simple fit, in which its constraint matrix \(\mathbf {N}=\mathbf {e}_1'\mathbf {e}_1'^\mathrm{T}\). Then, after direct algebraic manipulations, we obtain
5.1 Comparisons Between Algebraic Fits
From the error analysis, the second-order biases of the Taubin fit, the Type-A direct fit, the Type-B direct fit, and the simple algebraic fit have been derived. For comparison purpose, it is more appropriate to convert their bias expressions to the natural geometric parameters \({\varvec{\theta }}\). They are related by \({\mathbb E}({\Delta }_2\hat{{\varvec{\theta }}})=\tilde{\mathbf {E}}{\mathbb E}({\Delta }_2{\hat{{\varvec{\phi }}}})+\mathscr {O}(\sigma ^3)\), where \(\tilde{\mathbf {E}}\) is the Jacobian matrix. To simplify the comparisons, we shall decide that the smaller the essential bias, the better the estimator. For fairly large n, only the essential bias in each of Eqs. (56) and (59) persist.
The essential bias of the Taubin fit in term of its natural geometric parameter \({\varvec{\theta }}\) is
implying its center has a zero essential bias while the radii have data-free essential biases. Consequently, we can see now that the Type-A fit has essential bias twice as much as the bias of the Taubin fit. This answers why and by how much the Taubin fit outperforms the Type-A direct fit. The essential bias for the two other fits is listed in Table 1, and they depend on the true values of the parameters and the observations.
To analytically investigate their performances, we plotted both parts of the normalized bias (NB) of \(\hat{R}_1\); i.e., \(\mathrm{NB}(\hat{R}_1)\) \(=\frac{{\mathbb E}(\hat{R}_1)}{\sigma ^2}\) and the normalized bias of \(\hat{{\varvec{\theta }}}\); i.e., \(\mathrm{NB}(\hat{{\varvec{\theta }}})=\frac{\Vert {\mathbb E}({\Delta }_2\hat{{\varvec{\theta }}})\Vert }{\sigma ^2}\). Firstly, we positioned \(n_1=50\) and \(n_2=100\) equidistant points on concentric circular arcs with central angles initiated at \(0^\circ \) and terminated at \(\omega ^\circ \) (i.e., \(\frac{\pi }{180^\circ }\omega ^\circ \) radiant). The center of the concentric circles is (0, 0), and the radii are \(\tilde{R}_1=1\) and \(\tilde{R}_2=2\), see Fig. 3. Then, we repeated the process with \(n_1=100\) and \(n_2=50\) and the results are shown in Fig. 4. The \(x-\)axis represents the length of the arcs \(\omega \), which varies from \(\pi /2\) to \(2\pi \).
Normalized bias of the radius \(\hat{R}_1\), i.e., \(\mathrm{NB}(\hat{R}_1)= \sigma ^{-2}{\mathbb E}(\hat{R}_1)\), and the normalized bias of \(\hat{{\varvec{\theta }}}\), i.e., \(\mathrm{NB}(\hat{{\varvec{\theta }}})=\sigma ^{-2}\Vert {\mathbb E}({\Delta }_2 \hat{{\varvec{\theta }}})\Vert \), for the four algebraic fits whenever \(n_1=50\) and \(n_2=100\). The tested methods are the Type-A direct fit (blue), the Type-B direct fit (gold), the simple fit (green), and the Taubin fit (red). a Normalized bias of \(\hat{R}_1\), \(\mathrm{NB}(\hat{R}_1)\), whenever \(n_1=50\) and \(n_2=100\). b Normalized bias of \(\hat{{\varvec{\theta }}}\), \(\mathrm{NB}(\hat{{\varvec{\theta }}})\), whenever \(n_1=50\) and \(n_2=100\) (Color figure online)
Figures 3 and 4 reveal the behaviors of the normalized essential biases (represented by the solid lines) and the normalized nonessential biases (represented by the dotted lines). The first subfigure in each figure represents the normalized bias of \(\hat{R}_1\), \(\mathrm{NB}(\hat{R}_1)\), and the second subfigure represents the total normalized bias of \(\hat{{\varvec{\theta }}}\), \(\mathrm{NB}(\hat{{\varvec{\theta }}})\). Our pack includes the Type-A direct fit (blue), the Type-B direct fit (gold), the simple fit (green), and the Taubin fit (red). The figures show how the essential biases dominate the nonessential biases that are quite close to zero. This observation remains valid, even if \(n_i\)’s were chosen much smaller than our choice, provided that \(\omega \) is relatively large, say \(\omega =\pi \).
As Figs. 3 and 4 show, the normalized essential biases of \(\hat{R}_1\) and \(\hat{{\varvec{\theta }}}\) for each of the Type-A fit and the Taubin fit are always 2 and 1, respectively. On the other hand, the two other fits have much more involved situations.
Normalized bias of the radius \(\hat{R}_1\), i.e., \(\mathrm{NB}(\hat{R}_1)= \sigma ^{-2}{\mathbb E}(\hat{R}_1)\), and the normalized bias of \(\hat{{\varvec{\theta }}}\), i.e., \(\mathrm{NB}(\hat{{\varvec{\theta }}})=\sigma ^{-2}\Vert {\mathbb E}({\Delta }_2 \hat{{\varvec{\theta }}})\Vert \), for the four algebraic fits whenever \(n_1=100\) and \(n_2=50\). The tested methods are the Type-A direct fit (blue), the Type-B direct fit (gold), the simple fit (green), and the Taubin fit (red). a Normalized bias of \(\hat{R}_1\), \(\mathrm{NB}(\hat{R}_1)\), whenever \(n_1=100\) and \(n_2=50\). b Normalized bias of \(\hat{{\varvec{\theta }}}\), \(\mathrm{NB}(\hat{{\varvec{\theta }}})\), whenever \(n_1=100\) and \(n_2=50\). (Color figure online)
The simple fit has the same essential bias as the Taubin fit for \(\omega \ge 4.5 \) radiant, but its tendency of giving smaller radii appears for short circular arcs when \(\omega \le 3.5\) radiant. The bias in radius estimate becomes the smallest among all other methods whenever \(\omega \in (3.5,4.5)\), but this does not mean that the simple fit returns the best estimator over this zone. The reason behind this is that the bias of center estimate becomes very large. One can verify this phenomenon by plotting the analytic expression of the magnitude of the normalized bias of the center or by investigating the behavior of the normalized bias of \(\hat{{\varvec{\theta }}}\) as shown in Figs. 3b and 4b. Accordingly, we conclude that the simple fit coincides with the Taubin fit whenever observations are sampled along large concentric circular arcs. This resemblance behavior disappears whenever \(\omega \) becomes smaller and satisfies \(\omega <4.5\). Meanwhile, the simple fit continues to behave better than the Type-A direct fit over the zone \(\omega \in (3.5,4.5)\). As \(\omega \) reduces, the simple fit increases the bias considerably and its performance becomes the worst.
On the other hand, the Type-B direct fit has three scenarios depending on the difference \(n_1-n_2\).
-
1.
The simplest case appears whenever \(n_1=n_2\). In this case, the two direct fits coincide.
-
2.
The most practical scenario that Fig. 3 shows the case of \(n_1\ll n_2\). The normalized essential biases of \(\hat{R}_{1}\) and \(\hat{{\varvec{\theta }}}\) obtained by the Type-B direct fit reach their horizontal asymptotes that equal 2.8 whenever \(\omega \ge 3\), but they blow out as \(\omega \) becomes smaller. This makes the Type-B fit the second worst fit, after the simple fit, for short arc and the worst fit in case of long circular arcs.
-
3.
Figure 4 demonstrates the third scenario that appears whenever \(n_1\gg n_2\). In this case, the horizontal asymptotes of the normalized essential bias of \(\hat{R}_1\) and \(\hat{{\varvec{\theta }}}\) for the Type-B direct fit equal to 1.8. Moreover, on the zone \(\omega \in (2,2.6) \) the normalized bias of \(\hat{R}_1\) becomes the smallest among all other fits but the magnitude of the normalized bias of the center increases, which makes the normalized total bias of \(\hat{{\varvec{\theta }}}\) larger as shown in Fig. 4b. Lastly, for \(\omega \in (0,2)\), both of the center and the bias have heavy biases.
5.2 Hyper-Accurate Fit
A pertinent approach to the analysis of Al-Sharadqah and Chernov, this rigorous analysis allows us to propose a new algebraic method that its estimator has zero essential bias and it possesses translation and rotation invariance properties. Since the essential bias of the Type-A direct fit is two times the essential bias of the Taubin fit, one can design a new constraint matrix \(\mathbf {H}\) such that its noiseless version is \(\tilde{\mathbf {H}}= 2\tilde{\mathbf {V}}-\tilde{\mathbf {A}}\). That is, if \(\tilde{\mathbf {H}}\) is substituted in the general formula of the bias in Eq. (55), then the new estimator, say \({\hat{{\varvec{\phi }}}}_\mathrm{H}\) will have zero essential bias. The constraint matrix \(\mathbf {H}\) can be defined as
The generalized eigenvalue problem \(\mathbf {M}{\varvec{\phi }}=\lambda \mathbf {H}{\varvec{\phi }}\) has 5 pairs of solutions \((\lambda ,{\hat{{\varvec{\phi }}}})\) that also give zero essential biases, but the solution must also minimize the sum of the squares of the algebraic distances \({\varvec{\phi }}^\mathrm{T}\mathbf {M}{\varvec{\phi }}\), subject to a quadratic constraint in \({\varvec{\phi }}\). Since \(\mathbf {A}{\tilde{{\varvec{\phi }}}}=\tilde{\mathbf {V}}{\tilde{{\varvec{\phi }}}}-2\tilde{A}\sum _{i=1}^2\sum _{j=1}^{n_i} \tilde{\mathbf {z}}_{ij}\), then
and \({\tilde{{\varvec{\phi }}}}^\mathrm{T}\tilde{\mathbf {H}}{\tilde{{\varvec{\phi }}}}=\tilde{\zeta }\). The quantity \(\tilde{\zeta }=n_1\tilde{\zeta }_1+n_2\tilde{\zeta }_2\) is positive because \(\tilde{\zeta }_i=\tilde{B}^2+\tilde{C}^2-4\tilde{A}\tilde{D}_i>0\) for each i. This means that the new estimator
must possess the property \({\varvec{\phi }}^\mathrm{T}\mathbf {H}{\varvec{\phi }}>0\). Therefore, one can set the constraint \({\varvec{\phi }}^\mathrm{T}\mathbf {H}{\varvec{\phi }}=1\).
The constraint matrix \(\mathbf {H}\) is a symmetric but not a positive definite. It has one zero eigenvalue, three positive eigenvalues, and one negative eigenvalue. Therefore, its solution is the unit generalized eigenvector of the pencil \((\mathbf {M},\mathbf {H})\) that associates with the smallest positive eigenvalue \(\lambda \). However, the matrix \(\mathbf {H}\) is singular; thus, it is a numerically stable strategy to alternatively solve the problem by choosing the unit generalized eigenvector of the pencil \(( \mathbf {H},\mathbf {M})\) that associates with the largest positive eigenvalue.
The solution of this problem can be found by some built-in functions in many software packages, such as MATLAB. Alternatively one can use the following trick. Since the matrix of the moments \(\mathbf {M}\) can be written in terms of the so-called design matrix \(\mathbf {Z}\), i.e., \(\mathbf {M}=\mathbf {Z}^\mathrm{T}\mathbf {Z}\), then we can compute the “economic size” SVD of \(\mathbf {Z}\) by \(\mathbf {Z}=\mathbf {U}_0\mathbf {D}_0\mathbf {V}_0^\mathrm{T}\). Now we define \({\varvec{\phi }}'=\mathbf {V}_0^\mathrm{T}{\varvec{\phi }}\) and choose the eigenvector \({\hat{{\varvec{\phi }}}}'\) of the largest positive eigenvalue \(\eta \) that solves \((\mathbf {D}_0^{-2}\mathbf {V}_0^{T}\mathbf {H}\mathbf {V}_0) {\hat{{\varvec{\phi }}}}_\mathrm{\mathbf {H}}'=\eta {\hat{{\varvec{\phi }}}}_\mathrm{\mathbf {H}}' \), and finally replicate the solution back to \({\hat{{\varvec{\phi }}}}_\mathrm{\mathbf {H}}=\mathbf {V}_0{\hat{{\varvec{\phi }}}}_\mathrm{\mathbf {H}}'\).
We note that the new estimator is invariant under translations and rotations because the constraint matrix \(\mathbf {H}\) is a linear combination of two others, \(\mathbf {V}\) and \(\mathbf {A}\), that satisfy the invariance requirements. Finally, we call this method hyper-accurate algebraic method (or Hyper method for short).
Remark 1
In the case that the observation belongs to the more general Gaussian assumptions, such as \(cov(\mathbf {n}_{ij},\mathbf {n}_{kl})=\sigma ^2\hat{\delta }_{ik}\hat{\delta }_{jl}\mathbf {Q}_{ij}\), then the Hyper method still has the constraint matrix \(\mathbf {H}=2\mathbf {V}-\mathbf {A}\), where \(\mathbf {V}=\sum _{i=1}^2\sum _{j=1}^{n_i} \mathbf {V}_{ij}\) and \(\mathbf {V}_{ij}\) in Eq. (13) will be replaced by
5.3 Numerical Experiments
Next we turn our attention to run some numerical experiments and validate our second-order biases. We shall adopt the same models discussed in Sect. 5.1, and we shall examine the performances of each of the MLE and the algebraic methods. We examine firstly long concentric arcs with \(\omega =240^\circ \) whenever \(n_1=50\) and \(n_2=100\) (Table 2) and \(n_1=100\) and \(n_2=50\) (Table 4). Then, we repeat this process again for short circular arcs with \(\omega =120^\circ \) as listed in Tables 3 and 5.
The true points were contaminated by zero-mean white Gaussian noise with standard deviation \(\sigma =.05\). A total of \(N=10^5\) ensemble trials were performed. Tables 2, 3 and 5 summarize the normalized values of the biases of each component of \(\hat{{\varvec{\theta }}}=(\hat{a},\hat{b},\hat{R}_1,\hat{R}_2)^\mathrm{T}\). It also exhibits the normalized total bias of \(\hat{{\varvec{\theta }}}\), i.e., \(\mathrm{NB}(\hat{{\varvec{\theta }}})\), as well as the normalized mean squared error (NMSE) of \(\hat{{\varvec{\theta }}}\), which were estimated by
where \(\hat{{\varvec{\theta }}}^{(k)}\) is the estimate of \({\varvec{\theta }}\) in the kth trial. The tables include all of the four algebraic fits and the MLE. Note that the latter is the only method that its first-order variance achieves the KCR lower bound.
First, we observe that the normalized bias of radius estimates \((\hat{R}_1,\hat{R}_2)\) for the MLE is close to the theoretical normalized essential biases \((\frac{1}{2\tilde{R}_1},\frac{1}{2\tilde{R}_2} )=(0.5,0.25)\) as listed in Tables 2 and 4. The tables also show that this bias is half of the bias of the Taubin method, which is half of the bias from the Type-A fit. Since these algebraic methods have the same first-order covariance matrix, the MSE of the Taubin fit is smaller than the Type-A method. On the other hand, it is clear that the Hyper fit has the smallest bias among all experimented fits and its NMSE is smaller than all other algebraic fits. Note that for short-arc cases these conclusions remain valid even though their results are slightly different. These differences comes from the contributions of the nonessential biases (\(\approx \)10–15 % of the essential biases).
Second, the following observations regarding the simple fit validate our theoretical analysis. Tables 2 and 4 show how well behaved the simple fit is for long circular arcs. Its biases for \(\hat{R}_1\) and \(\hat{R}_2\) are the smallest compared with other estimators (MLE, Type-A, Type-B, Taubin). However, its center estimate in this case is the worst, and as such, this makes the simple fit have similar performance as the Taubin fit. On the other hand, if the observations are clustered along short circular arcs, then the simple method will return a much smaller concentric circles. This attenuation behavior for the radii is clearly listed in Tables 3 and 5.
Third, in the regard of the behavior of the normalized bias of Type-B fit, Tables 2, 3, 4 and 5 show an excellent agreement with our conclusions presented in Sect. 5.1. Tables 2 and 4 show that the normalized bias of \(\hat{R}_1\) for the Type-B fit approaches its theoretical limit 2.8 and 1.8 (respectively) \(\omega \) becomes large. Whenever \(n_2=100\) and \(n_1=50\), Table 4 shows that the total normalized bias of Type-B method is smaller than the Type-A method, and as such, the NMSE of \(\hat{{\varvec{\theta }}}_\mathrm{B}\) is smaller than the NMSE of \(\hat{{\varvec{\theta }}}_\mathrm{A}\). Note that this situation is reversed whenever \(n_1=50\) and \(n_2=100\) as listed in Table 2. In the latter case, \(\mathrm{NB}(\hat{R}_1)\) for the Type-B method approaches its theoretical limit 2.8 as \(\omega \) increases, and its \(\mathrm{NB}(\hat{{\varvec{\theta }}}_\mathrm{B})\) becomes larger than all other algebraic methods. Consequently, it becomes the worst in this case (recall that the simple fit behaves like the Taubin fit for large concentric circular arcs).
Another excellent agreement between the numerical experiments and the theoretical results occurs again in our last observation regarding the behavior of the Type-B fit in case of short concentric circular arcs (Tables 3 and 5). Here, the bias of the center estimate is relatively large for the Type-B if compared with the other methods (excluding the simple fit) but its radius depends on the difference \(n_1-n_2\). For \(n_1=50\) and \(n_2=100\), its \(\mathrm{NB}(\hat{R}_i)\) is also much larger than the others, and as a result, its has the highest bias among other fits (except the simple fit). This demonstrates why it falls behind the Type-A fit but it is still better than the simple fit in the MSE sense. Finally, for \(n_1=100\) and \(n_2=50\), \(\mathrm{NB}(\hat{R}_i)\)’s are negative, but with small magnitudes if compared with the other fits (excluding the simple fit). This makes the Type-B method the second worst method after the simple method, when data are sampled along short circular arcs with \(n_1\gg n_2\).
6 Second-Order Analysis of Iterative Methods
In this section, we will evaluate the bias of the GRAF and the generalized GRAF. We will show why the GRAF has a smaller bias than the Renormalization method. We first start with the GRAF. To apply the perturbation analysis to GRAF \({\hat{{\varvec{\phi }}}}_{g}\), we express \( {\hat{{\varvec{\phi }}}}_\mathrm{g} -{\tilde{{\varvec{\phi }}}}=\Delta _1{\hat{{\varvec{\phi }}}}_\mathrm{g} +\Delta _2{\hat{{\varvec{\phi }}}}_\mathrm{g}+\mathscr {O}_\mathrm{P}(\sigma ^3)\), where \(\Delta _2{\hat{{\varvec{\phi }}}}_\mathrm{g} \) is a quadratic form of \(\delta _{ij}\)’s and \({\epsilon }_{ij}\)’s and all other higher-order terms are represented by \(\mathscr {O}_P(\sigma ^3)\). Here \(\Delta _1{\hat{{\varvec{\phi }}}}_\mathrm{g} \) and \(\Delta _2{\hat{{\varvec{\phi }}}}_\mathrm{g} \) can be obtained by applying the Taylor expansion of \(\gamma _{ij}^{-1} = ({\hat{{\varvec{\phi }}}}_\mathrm{g} ^\mathrm{T}\mathbf {V}_{ij}{\hat{{\varvec{\phi }}}}_\mathrm{g} )^{-1}\) around its true value \(\tilde{\gamma }_{ij}^{-1}\), where \(\tilde{\gamma }_{ij}={\tilde{{\varvec{\phi }}}}^\mathrm{T}\tilde{\mathbf {V}}_{ij}{\tilde{{\varvec{\phi }}}}\) can be simplified further—after some straightforward algebraic manipulations—to
where \(\tilde{\zeta }_i\) is the true value of \(\zeta _i\) [cf. Eq. (5)]. Therefore, if we use the Taylor series expansion of \(\gamma _{ij}^{-1} = ({\hat{{\varvec{\phi }}}}_\mathrm{g}^\mathrm{T}\mathbf {V}_{ij}{\hat{{\varvec{\phi }}}}_\mathrm{g})^{-1}\) around \(\tilde{\gamma }_{ij}^{-1}\), then we obtain
Accordingly,
where \(\Delta _1^j \mathbf {\mathscr {M}}\) and \(\Delta _2^k \mathbf {\mathscr {M}}\), for \(j=1,2\) and \(k=1,2,3\) denote the various “parts” of \({\Delta }_1\mathbf {\mathscr {M}}\) and \({\Delta }_2\mathbf {\mathscr {M}}\), respectively. Their formal definitions are listed below.
here, \( \Delta _2\gamma _{ij}\) is irrelevant because \(\Delta _2^3\mathbf {\mathscr {M}}{\tilde{{\varvec{\phi }}}}={\mathbf {0}}\) and its expression is omitted, while
where \(\Delta _1\mathbf {V}_{ij}=\tilde{\mathbf {T}}_{ij}\delta _{ij}+\tilde{\mathbf {S}}_{ij}{\epsilon }_{ij}\), with
Now, perturbating Eq. (15) leads to
Since \({\hat{{\varvec{\phi }}}}_\mathrm{g}^\mathrm{T}\mathbf {M}_{ij}{\hat{{\varvec{\phi }}}}_\mathrm{g}= (\mathbf {z}_{ij}^\mathrm{T}{\hat{{\varvec{\phi }}}}_\mathrm{g})^2\) and \(\tilde{\mathbf {z}}_{ij}^\mathrm{T}{\tilde{{\varvec{\phi }}}}=0\), we have \({\hat{{\varvec{\phi }}}}_\mathrm{g}^\mathrm{T}\mathbf {M}_{ij}{\hat{{\varvec{\phi }}}}_\mathrm{g} \sim \mathscr {O}_P(\sigma ^2)\), and hence \(\tilde{\mathbf {\mathscr {L}}}=\Delta _1\mathbf {\mathscr {L}}={\mathbf {0}}\), thus \(\mathbf {\mathscr {L}}= {\Delta }_2\mathbf {\mathscr {L}}+\mathscr {O}_\mathrm{P}(\sigma ^3)\), where
Thus, equating all \(\mathscr {O}(\sigma )\)-terms in Eq. (65) yields \(\Delta _1 {\hat{{\varvec{\phi }}}}_\mathrm{g} =-\tilde{\mathbf {\mathscr {M}}}^{-}\Delta _1^1\, \mathbf {\mathscr {M}}{\tilde{{\varvec{\phi }}}}\), and further,
Note here that \(\Vert {\hat{{\varvec{\phi }}}}_\mathrm{g} \Vert = \Vert {\tilde{{\varvec{\phi }}}}\Vert =1\) implies \(\Delta _1 {\hat{{\varvec{\phi }}}}_\mathrm{g} \) is orthogonal to \({\tilde{{\varvec{\phi }}}}\). Also, it is worth mentioning here that \({\tilde{{\varvec{\phi }}}}\) is in the null space of \({\Delta }_1^2\mathbf {\mathscr {M}}\).
To find the second-order error bias, we first equating all \(\mathscr {O}(\sigma ^2)-\) terms and obtain
Since \(\Delta _1^2\mathbf {\mathscr {M}}{\tilde{{\varvec{\phi }}}}=\Delta _2^3\mathbf {\mathscr {M}}{\tilde{{\varvec{\phi }}}}={\mathbf {0}}\), we have
where we denote for brevity
and
and \(\mathbf {R}_3^{*}=\bigl (\Delta _1^1\mathbf {\mathscr {M}}+ \Delta _1^2\mathbf {\mathscr {M}}\bigr )\tilde{\mathbf {\mathscr {M}}}^-\Delta _1^2\mathbf {\mathscr {M}}\). Note that \({\mathbb E}(\mathbf {R}_3^*){\tilde{{\varvec{\phi }}}}={\mathbf {0}}\), so it be will discarded in our analysis. Accordingly, we present the following identities and we moved its derivation to “Appendix”; i.e.,
where
and \( \tilde{\psi }_i=\tilde{\mathbf {z}}_{ij}^\mathrm{T}\tilde{\mathbf {\mathscr {M}}}^-\tilde{\mathbf {z}}_{ij}\). Also,
Here we have defined
where \(\tilde{\mathbf {a}}_{ij}\) and \(\tilde{\mathbf {b}}_{ij}\) are the first and the second columns of \(\nabla \mathbf {z}_{ij}\).
Furthermore, the interesting identity \(\tilde{\varvec{\varGamma }}_{ij}{\tilde{{\varvec{\phi }}}}=4\tilde{A}\tilde{\zeta }_i\tilde{\mathbf {z}}_{ij}\) simplifies \(\tilde{\mathbf {G}}_2{\tilde{{\varvec{\phi }}}}\); i.e.,
To find the bias of the GRAF, then we need to compute \({\mathbb E}(\Delta _2\mathbf {\mathscr {L}})\), which was already computed by Kanatani [20, pp. 181–182] and Al-Sharadqah and Chernov[2] for conic fitting; thus, after simple algebraic manipulations, we obtain
Hence, \({\mathbb E}({\Delta }_2{\hat{{\varvec{\phi }}}}_\mathrm{g})=-\sigma ^2\tilde{\mathbf {\mathscr {M}}}^{-}\tilde{\mathbf {G}}_2 {\tilde{{\varvec{\phi }}}}\). Thus
Since \( \sum _{j=1}^{n_i}\tilde{\zeta }_{i}^{-1}\tilde{\mathbf {z}}_{ij}\) is the \((3+i)\)th column of \(\tilde{\mathbf {\mathscr {M}}}\) for each \(i=1,2\), then the bias of GRAF is reduced to
For large \(n=n_1+n_2\), we have \(\tilde{\mathbf {\mathscr {M}}}= \mathscr {O}(n)\); hence both of \(\tilde{\mathbf {\mathscr {M}}}^-\) and \(\tilde{\psi }_{ij} \) are of order of magnitude \(\mathscr {O}(1/n)\). Therefore, the essential bias of the GRAF is \(-\sigma ^2I_{{\tilde{{\varvec{\phi }}}}}\), which is the negative of the essential bias of the Taubin fit as revealed by Table 1. Now, premultiplying Eq. (76) by \(\tilde{\mathbf {E}}\) expresses the bias of the GRAF in terms of its geometric parameters \({\varvec{\theta }}\). Most importantly, we notice that the center has only nonessential bias while its radii have both parts, from which the essential part is \(\sigma ^2(\frac{-1}{\tilde{R}_1},\frac{-1}{\tilde{R}_1})\). This essential bias is the negative of the essential bias of the Taubin fit. Hence, the GRAF and the Taubin fit—in absolute value—have essential biases for the two radii twice as much as the MLE have. In other words, the GRAF tends to return concentric circles with smaller radii, while the MLE and the Taubin method have the opposite tendency.
6.1 Analysis of Generalized GRAF
Here, we analyze the bias of the generalized GRAF that solves the generalized eigenvalue problem in Eq. (17). This can be done by applying matrix perturbation to \(\mathbf {\mathscr {M}}\), \(\mathbf {\mathscr {N}}\), \({\hat{{\varvec{\phi }}}}\), and \(\lambda \) in Eq. (17) and using the same approach implemented in the second-order analysis of the algebraic fits. That is, perturbating
Then, one can show that \(\tilde{\lambda }=\Delta _1\lambda =0\). Therefore, \({\Delta }_1{\hat{{\varvec{\phi }}}}\) is the same as Eq. (67) and its covariance also equals to \(\sigma ^2\tilde{\mathbf {\mathscr {M}}}^-\) [cf. Eq. (29)].
To evaluate the bias, we first equate all \(\mathscr {O}_\mathrm{P}(\sigma ^2)\) in Eq. (46) and obtain
From Eq. (67), we conclude \(\Delta _2\mathbf {\mathscr {M}}{\tilde{{\varvec{\phi }}}}+ \Delta _1\mathbf {\mathscr {M}}\Delta _1{\hat{{\varvec{\phi }}}}\)
To find \({\Delta }_2\lambda \), we premultiply Eq. (78) with \({\tilde{{\varvec{\phi }}}}^\mathrm{T}\) and obtain \({\tilde{{\varvec{\phi }}}}^\mathrm{T} \tilde{\mathbf {\mathscr {M}}}= {\mathbf {0}}^\mathrm{T}\). Hence, \(\Delta _2\lambda =\frac{{\tilde{{\varvec{\phi }}}}^\mathrm{T}\mathbf {R}^*{\tilde{{\varvec{\phi }}}}}{{\tilde{{\varvec{\phi }}}}^\mathrm{T} \tilde{\mathbf {\mathscr {N}}}{\tilde{{\varvec{\phi }}}}}\), and \(\Delta _2{\hat{{\varvec{\phi }}}}\) can be written as
where the symmetrization operator \(\mathbf {S}_{\bullet }\) is defined in Eq. (51). Now, premultiplying Eq. (70) by \({\tilde{{\varvec{\phi }}}}^\mathrm{T}\) and recalling that \(\tilde{\zeta }_i={\tilde{{\varvec{\phi }}}}^\mathrm{T}\tilde{\mathbf {V}}_{ij}{\tilde{{\varvec{\phi }}}}\) yield \({\tilde{{\varvec{\phi }}}}^\mathrm{T}{\mathbb E}(\mathbf {R}^*){\tilde{{\varvec{\phi }}}}=\sigma ^2 \sum _{i}^2\sum _{j}^{n_i}(1-\tilde{\zeta }_i^{-1}\tilde{\psi }_{ij})\). Also, since kernel\((\tilde{\mathbf {\mathscr {M}}})=\,\)span\((\tilde{\mathbf {A}})\), which is a one-dimensional subspace of \({\mathbb R}^5\), we have the identity
Thus,
The Renormalization scheme [13, 14] is a special case of the generalized GRAF \(\mathbf {\mathscr {N}}=\sum _{i=1}^2\sum _{j=1}^{n_i}\gamma _{ij}^{-1}\mathbf {V}_{ij}\). In this case, \({\tilde{{\varvec{\phi }}}}^\mathrm{T}\tilde{\mathbf {\mathscr {N}}}{\tilde{{\varvec{\phi }}}}=n\), hence
where
Note here that \(\tilde{\mathbf {\mathscr {M}}}^-\tilde{\mathbf {G}}_1^*=\mathscr {O}(1/n)\) and \(\tilde{\mathbf {\mathscr {M}}}^-\tilde{\mathbf {G}}_1 = \mathscr {O}(1)\). Thus, the Renormalization scheme suppresses \(\tilde{\mathbf {G}}_1\) to a matrix of a smaller order, while GRAF eliminates it completely. Finally, combining Eqs. (74) and (76) with (80) and (81) gives the final expression of the second-order bias of the Renormalization method.
To demonstrate our results on these two iterative methods and their connection with the MLE and the Taubin method, we experimented the same settings as before that \(\tilde{{\varvec{\theta }}}=(0,0,1,2)\) with \(n_1=50\), \(n_2=100\), and \(\omega =180^\circ \). Table 6 shows the NMSE and the normalized bias (NB) of \(10^5\) estimates of \(\hat{{\varvec{\theta }}}\) computed based on Eq. (61).
As listed in Table 6, \(\mathrm{NB}( \hat{a})\) and \(\mathrm{NB}( \hat{b})\) are negligible. Also, for each \(i=1,2\), we clearly see that \(\mathrm{NB}( \hat{R}_i)\) is close to \(\tilde{R}_i^{-1}\) for the Taubin fit and it is near \( -\tilde{R}_i^{-1}\) for each of the GRAF and the Renormalization methods. It is about \( (2\tilde{R}_i)^{-1}\) for the MLE. In total, we notice that the normalized biases of \(\hat{{\varvec{\theta }}}\) for the GRAF, the Renormalization fit, and the Taubin fit are equal, while the normalized bias of \(\hat{{\varvec{\theta }}}_\mathrm{m}\) is approximately equal to \(\frac{1}{\sqrt{2}}\) of the normalized biased of the GRAF and the others. Moreover, the adjusted MLE has the smallest normalized MSE, as being a refinement for the MLE, whose performance is superior to all other methods.
7 Numerical Experiments
We shall examine our theoretical results through some numerical experiments using synthetic data and real image data.
7.1 Experiments on Synthetic Data
In this section, we present results of experiments obtained from synthetic data. We considered the estimators obtained from the five algebraic fits: The simple fit (S), Taubin fit (T), Type-A direct fit (A), Type-B direct fit (B), and Hyper fit (H). Also, we included the iterative methods: GRAF based on the FNS scheme (F), the Renormalization (R) method, the MLE (M), and its refinement (AM), after supplying them with the solution of the Hyper fit as the initial guess. We define \(n_1=50\) and \(n_2=100\) equidistant points on the concentric circular arcs with center (0, 0) and radii \(\tilde{R}_1\)=1 and \(\tilde{R}_2=2\). Both arcs have the same initial angle 0 and terminal angle \(\omega \). Three cases were considered here with \(\omega =240^\circ \), \(\omega =120^\circ \), and \(\omega =60^\circ \). The true points were contaminated by zero-mean white Gaussian noise with standard deviation \(\sigma \). For each \(\sigma \), \(N=10^4\) ensemble trials were performed and for each trial the estimates are computed. We plotted (a) the NMSE of \(\hat{{\varvec{\theta }}}\) and (b) the NB of \(\hat{{\varvec{\theta }}}\), as the noise level \(\sigma \) increases from 0. In Figs. 5, 6 and 7a, the horizontal dashed line represents the normalized KCR, which is computed by taking the sum of the diagonal elements of \(\tilde{\mathbf {R}}=(\tilde{\mathbf {W}}^\mathrm{T}\tilde{\mathbf {W}})^{-1}\).
Figures 5, 6 and 7 exhibit the NMSE and the normalized bias NB for each of the fitting methods in the three cases. As a general observation, whenever \(\sigma \) is approaching 0, the NMSE of all iterative methods approach the \(\sigma ^{-2}\mathrm{KCR}\) lower bound while all non-iterative methods do not. This observation validates the theoretical results in [3]. Figures 5, 6 and 7 also reveal why the problem of fitting concentric circles differs from the single circle fitting where algebraic fits and the MLE are optimal in the sense of reaching the KCR lower bound. The Hyper method and the Adjusted MLE, followed by the MLE, have the smallest biases among other method. This supports, based on the MSE criterion, why the MLE and the adjusted MLE are the best estimators among all other fits, and why Hyper fit outperforms all algebraic methods.
The behavior of the simple fit depends heavily on the length of the circular arcs. Its bias and MSE are close to the bias and the MSE of the Taubin method in the case of long circular arcs, but its bias blows out, and as such, its MSE does whenever the arc lengths reduce. For the \(\omega =60^\circ \) case, its NB is even close to 500, while the second largest bias does not exceed 53. Therefore, we omitted its bias curve from the figure.
The significance of the essential bias can be clearly seen in the case of long circular arcs, in which the following relations \(\mathrm{NB}(\hat{{\varvec{\theta }}}_\mathrm{A})> \mathrm{NB}(\hat{{\varvec{\theta }}}_\mathrm{T})>\mathrm{NB}(\hat{{\varvec{\theta }}}_\mathrm{H})\) hold, and as such, these relations also hold for their NMSEs. However, this significant difference between the Type-A and the Taubin method decreases whenever \(\omega \) is small. In Fig. 7b, the contribution of the nonessential biases becomes large, by which the Type-A and Taubin methods have nearly identical performance, but they still fall behind the Hyper method.
Finally, the numerical experiments show how the Renormalization method slightly outperforms the GRAF for long concentric arcs but it becomes unstable in the case of very short arcs (see Fig. 7a). In addition, its bias is the largest among the other fits (A, T, F, M, AM, H).
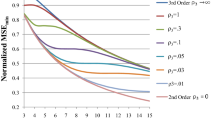
\(\mathrm{NMSE}(\hat{{\varvec{\theta }}})\) in (a) and the \(\mathrm{NB}(\hat{{\varvec{\theta }}})\) in (b) of the parameters of the fitted concentric circles at additive observation noise with standard deviation \(\sigma \). The settings are \(\tilde{{\varvec{\theta }}}=(0,0,1,2)^\mathrm{T}\), \(n_1=50\), \(n_2=100\), \( \omega =240^\circ \), and \(N=10^4\) independent trials. The tested fits are: the simple fit (S), the Taubin fit (T), the Type-A direct fit (A), the Type-B direct fit (B), the Hyper fit (H), the GRAF (F), the Renormalization (R) method, the MLE (M), and the adjusted MLE (AM). The horizontal dashed line represents the normalized KCR lower bound. a Normalized NMSE of \(\hat{{\varvec{\theta }}}\), \(\mathrm{NMSE}(\hat{{\varvec{\theta }}})\), in the case \(\omega =240^\circ \). b Normalized bias of \(\hat{{\varvec{\theta }}}\), \(\mathrm{NB}(\hat{{\varvec{\theta }}})\), in the case \(\omega =240^\circ \)
The \(\mathrm{NMSE}(\hat{{\varvec{\theta }}})\) in (a) and the \(\mathrm{NB}(\hat{{\varvec{\theta }}})\) in (b) of the parameters of the fitted concentric circles at additive observation noise with standard deviation \(\sigma \). The settings are \(\tilde{{\varvec{\theta }}}=(0,0,1,2)^\mathrm{T}\), \(n_1=50\), \(n_2=100\), \( \omega =120^\circ \) and \(N=10^4\) independent trials. The tested fits are: the simple fit (S), the Taubin fit (T), the Type-A direct fit (A), the Type-B direct fit (B), the Hyper fit (H), the GRAF (F), the Renormalization (R) method, the MLE (M), and the adjusted MLE (AM). The horizontal dashed line represents the normalized KCR lower bound. a The normalized NMSE of \(\hat{{\varvec{\theta }}}\), \(\mathrm{NMSE}(\hat{{\varvec{\theta }}})\), in the case \(\omega =120^\circ \). b The normalized bias of \(\hat{{\varvec{\theta }}}\), \(\mathrm{NB}(\hat{{\varvec{\theta }}})\), in the case \(\omega =120^\circ \)
The \(\mathrm{NMSE}(\hat{{\varvec{\theta }}})\) in (a) and the \(\mathrm{NB}(\hat{{\varvec{\theta }}})\) in (b) of the parameters of the fitted concentric circles at additive observation noise with standard deviation \(\sigma \). The settings are \(\tilde{{\varvec{\theta }}}=(0,0,1,2)^\mathrm{T}\), \(n_1=50\), \(n_2=100\), \( \omega =60^\circ \) and \(N=10^4\) independent trials. The tested fits are: the simple fit (S), the Taubin fit (T), the Type-A direct fit (A), the Type-B direct fit (B), the Hyper fit (H), the GRAF (F), the Renormalization (R) method, the MLE (M), and the adjusted MLE (AM). The horizontal dashed line represents the normalized KCR lower bound. The curves for the simple fit (S) were removed in this experiment. a The normalized NMSE of \(\hat{{\varvec{\theta }}}\), \(\mathrm{NMSE}(\hat{{\varvec{\theta }}})\), in the case \(\omega =60^\circ \). b The normalized bias of \(\hat{{\varvec{\theta }}}\), \(\mathrm{NB}(\hat{{\varvec{\theta }}})\), in the case \(\omega =60^\circ \)
7.2 Experiments on Real Data
We now turn our attention by corroborating our analytical studies and findings with a set of practical data points obtained from an image of a CD/DVD. The image in binary form is shown in Fig. 1, where Cannys edge detection method [5] is applied to extract the data points in the inner and outer circles. We have a total of \(n_1=50\) and \(n_2=100\) points from them respectively.
In the experiment, we directly apply various algorithms to the data, where we added uncorrelated Gaussian noise of standard deviation \(\sigma =0.05\) to the data points of the inner and outer circles. Only a segment of the data from 0 to 120 degrees is used, giving \(n_1=50\) and \(n_2=100\) points from the two concentric circles for estimation. We took a total of 100,000 ensemble runs. The averages of the estimation parameters are obtained for various fitting methods to examine the estimation bias, and they are listed in Table 7.
The corresponding fitted circles are shown in Fig. 8, where we have zoomed in to better observe the fitting performance. Both the Hyperfit (H) and the Adjusted MLE (AM) yield the best results as anticipated. Next best result is from the MLE (M), which tends to overestimate a little the parameters. The Renormalization method (R) under estimates the radii as indicated by our theoretical study. Furthermore, the Taubin (T) and Type-A (A), Type-B (B) fits overestimate the radii as the analytical investigation tells.
The experimental results from the real data confirm very well the theoretical studies and the improvements from the proposed H and AM methods. However, instead of underestimating the radii as the analytic results show, the GRAF (F), overestimates the radii. This problem might be more related to numerical issues and it requires further investigations.
The averages of estimators for \(N=10^5\) independent trials that were generated after adding \(\sigma =.05\) to the real data. The settings are \(n_1=50\) and \(n_2=100\) around a short concentric arcs with \(\omega \approx 120^\circ \). The tested fits are: the simple fit (S), the Taubin fit (T), the Type-A direct fit (A), the Type-B direct fit (B), the Hyper fit (H), the GRAF (F), the Renormalization (R) method, the MLE (M), and the adjusted MLE (AM)
8 Conclusions
In this paper, we applied the second-order error analysis to the problem of fitting concentric circles to a number of coordinate points. We derived the biases of the MLE, the algebraic fits, the GRAF, and the Renormalization method. We showed that the bias determines the performance of each method in its category (non-iterative and iterative). The smaller the bias, the smaller the MSE, and as such, the better the performance among each group. The most important part of the bias is the essential bias, and its order of magnitude \(\sigma ^4\) dominates the value of the second-order bias as long as the arcs are not too short, such as \(\omega <90^\circ \).
Accordingly, we rigorously showed that the essential bias of the center estimate is zero for each of the MLE, the GRAF, the Renormalization, the Taubin, and the Type-A direct fit. However, their essential biases for the radii persist and they, after normalized by the noise power, depend only on the values of \(\tilde{R}_1 \) and \(\tilde{R}_2\). Indeed, we showed that the ratio of the essential biases of \(\hat{R}_i\) obtained from the MLE to the Taubin fit and to the Type-A fit is 1:2:4. Also, the essential biases for the radii from the GRAF and the Renormalization method are equal, and they are identical to the negatives of those of the Taubin fit.
We also illustrated why the simple fit works well as the Taubin method in the case of long circular arcs but this excellent performance diminishes as the length of arcs becomes smaller. Furthermore, we gained understanding of how the performance of the two types of direct fits were related to each other, and how the relationship of their performance depends on the sign and the magnitude of \(n_1-n_2\).
Additionally, our analysis allowed us to develop a new non-iterative algebraic fit, called the Hyper-accurate method that has zero essential bias. We addressed its implementation and demonstrated its superiority over all existing algebraic fits. The Hyper-accurate method was the most accurate algebraic fit among those we examined, and hence, it is considered as the best initial guess to feed the LM-based MLE and the other iterative methods. Finally, we modified the MLE to reduce its bias. This modified version of the MLE, called the Adjusted MLE, showed significant improvement over the MLE in our numerical experiments.
We validated our theoretical results with a series of numerical experiments using synthetic data. The agreement between them was excellent. We also applied the methods to a practical data set taken from an image of a CD/DVD. The results show an excellent match of the analytic results in practical applications.
The investigation of various methods discussed in this paper is based on the mean squared error of the geometric parameters \((a,b,R_1,R_2)\) and their statistical properties. Accordingly, the numerical experiments are designed to maintain the consistency of the study. To have a full understanding of these methods, further work needs to be conducted using the geometric error [23–25] and confirm if the new estimators are indeed as good as they appear to be. The use of this measure is outside what we would like to cover in the current investigation. Depending on applications, the geometric distance measure could provide another dimension for evaluating algorithms. We plan to examine the performance of different algorithms in terms of the geometric distance measure and will report the results elsewhere when the study is complete.
References
Al-Sharadqah, A.: Further statistical analysis for circle fitting algorithms. Electron. J. Stat. 8(2), 2741–2778 (2014)
Al-Sharadqah, A., Chernov, N.: Error analysis for circle fitting algorithms. Electron. J. Stat. 3(1), 886–911 (2009)
Al-Sharadqah, A., Ho, K.C.: Solutions and evaluations for fitting of concentric circles. Signal Process. 120, 468–479 (2016)
Benko, P., Kós, G., Várady, T., Andor, L., Martin, R.: Constrained fitting in reverse engineering. Comput. Aided Geom. Des. 19(3), 173–205 (2002)
Canny, J.: A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 8, 679–698 (1986)
Chernov, N.: On the convergence of fitting algorithms in computer vision. J. Math. Imaging Vis. 27, 231–239 (2007)
Chernov, N., Lesort, C.: Statistical efficiency of curve fitting algorithms. Comput. Stat. Data Anal. 47, 713–728 (2004)
Chojnacki, W., Brooks, M.J., van den Hengel, A., Gawley, D.: On the fitting of surfaces to data with covariances. IEEE Trans. Pattern Anal. Mach. Intell. 22, 1294–1303 (2000)
Chojnacki, W., Brooks, M.J., van den Hengel, A.: Rationalising the renormalisation method of Kanatani. J. Math. Imaging Vis. 14, 21–38 (2001)
Dampegama, S.D.: Determination of original size of the abhayagiriya stupa. In: 21st Asian Conference on Remote Sensing (2000)
Isserlis, L.: On a formula for the product-moment coefficient of any order of a normal frequency distribution in any number of variables. Biometrika 12(1/2), 134–139 (1918)
Kanatani, K.: Renormalization for unbiased estimation. In: Proceedings 4th International Conference Computer Vision, Berlin, Germany, pp. 599–606 (1993)
Kanatani, K.: Statistical bias of conic fitting and renormalization. IEEE Trans. Pattern Anal. Mach. Intell. 16, 320–326 (1994)
Kanatani, K.: Statistical Optimization for Geometric Computation: Theory and Practice. Elsevier, Amsterdam (1996)
Kweon, I.S., Kim, J.S., Kim, H.-W.: A camera calibration method using concentric circles of vision applications. In: Asian Conference on Computer Vision, pp. 512–520 (2002)
Leedan, Y., Meer, P.: Heteroscedastic regression in computer vision: problems with bilinear constraint. Int. J. Comput. Vis. 37, 127–150 (2000)
Ma, Z., Ho, K.C.: Asymptotically efficient estimators for the fittings of coupled circles and ellipses. Dig. Signal Process. 25(2), 28–40 (2014)
Matei, B., Meer, P.: Reduction of bias in maximum likelihood ellipse fitting. In: 15th International Conference on Computer Vision and Pattern Recognition, vol. 3, Barcelona, Spain, pp. 802–806 (2000)
O’Leary, P., Harker, M., Zsombor Murray, P.: Direct and least square fitting of coupled geometric objects for metric vision. IIEE Proc. Vis. Image Signal Process. 152, 687–694 (2005)
Kanatani, K.: Statistical optimization for geometric fitting: theoretical accuracy bound and high order error analysis. Int. J. Comput. Vis. 80, 167–188 (2008)
Kanatani, K., Rangarajan, P.: Hyper least squares fitting of circles and ellipses. Comput. Stat. Data Anal. 55, 2197–2208 (2011)
Sampson, P.D.: Fitting conic sections to very scattered data: an iterative refinement of the Bookstein algorithm. Comput. Graph. Image Process. 18, 97–108 (1982)
Szpak, Z., Chojnacki, W., van den Hengel, A.: A comparison of ellipse fitting methods and implications for multiple-view geometry estimation. In: 2012 International Conference on Digital Image Computing Techniques and Applications (DICTA), pp. 1–8 (2012)
Szpak, Z., Chojnacki, W., van den Hengel, A.: Guaranteed ellipse fitting with the sampson distance. In: Fitzgibbon, A., Lazebnik, S., Perona, P., Sato, Y., Schmid, C. (eds.) Computer Vision ECCV 2012. Lecture Notes in Computer Science, vol. 7576, pp. 87–100. Springer, Berlin (2012)
Szpak, Z., Chojnacki, W., van den Hengel, A.: Guaranteed ellipse fitting with a confidence region and an uncertainty measure for centre, axes, and orientation. J. Math. Imaging Vis. 52(2), 173–199 (2015)
Yahya, A.E., Nordin, M.J.: A new technique for iris localization in iris recognition systems. J. Inf. Technol. 7, 924–929 (2008)
Acknowledgments
The authors would like to thank the reviewers and the editor for providing many suggestions that resulted in improving this paper.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Derivation of Eq. (32) First, we define
and
Now, for each \(i=1\), 2 and \(j=1,\ldots ,n_i\), expanding the distance \(d_{ij}\) to the second-order terms gives
This expression can be simplified further using the approximation
Keeping all terms of order \(\mathscr {O}_\mathrm{P}(\sigma ^2)\) and discarding the less significant terms in \(\sqrt{1+\zeta _{ij}}\), the above expression becomes
Since \(1-\tilde{u}_{ij}^2=\tilde{v}_{ij}^2\), we conclude
Proof of Lemma 1
The first three assertions will be proven if we show
Firstly, observe that for any \(j=1,\ldots ,n_i\)
which comes from the identity \(\Vert \tilde{\mathbf {t}}_{ij}\Vert _2^2=\tilde{u}_{ij}^2+\tilde{v}_{ij}^2=1\). Next, we compute \({\mathbb E}(\tau _{ij}^2)\). Since \(\mathrm{cov}({\Delta }_1\hat{{\varvec{\theta }}}_\mathrm{m})=\sigma ^2\tilde{\mathbf {R}}\), then, for any \(j=1,\ldots ,n_i\), one has
Finally, we compute \({\mathbb E}(\tau _{ij}\rho _{ij})\). Recall the definition of \({\Delta }_1\hat{{\varvec{\theta }}}_m=\tilde{\mathbf {K}}\mathbf {f}_1=\tilde{\mathbf {R}}\tilde{\mathbf {W}}^\mathrm{T}\mathbf {f}_1\), which can be rewritten as \(\tilde{\mathbf {R}}\mathbf {g}\) with
then for each \(t=1,\ldots ,n_i\), \({\mathbb E}(f_{1it}\rho _{ij})={\mathbb E}(f_{1it}(\check{\mathbf {n}}_{ij}^\mathrm{T}\tilde{\mathbf {t}}_{ij}))=0 \) for all \(j=1,\cdots ,n_i\). Thus, \({\mathbb E}(\tau _{ij}\rho _{ij})=0\).
Next, we compute the expectations of the outer products of \(\mathbf {a}_i\), \(\mathbf {b}_i\), and \(\mathbf {c}_i\) starting with \({\mathbb E}(\mathbf {a}_i\mathbf {a}_k^\mathrm{T})\). Since
Using the Isserlis’ Theorem [11] gives
But it is easy to show that \({\mathbb E}((\tilde{\mathbf {t}}_{ij}^\mathrm{T}\check{\mathbf {n}}_{ij})^2)=\sigma ^2\) and
Therefore,
Next, we compute \({\mathbb E}(b_{ij}b_{kl})=4{\mathbb E}\left( \tau _{ij}\rho _{ij}\tau _{kl} \rho _{kl}\right) \). The pair \((\tau _{ij},\rho _{kl})\) are uncorrelated for any choice of i and k. Besides,
Therefore,
Next we evaluate \({\mathbb E}(c_{ij}c_{kl})={\mathbb E}(\tau _{ij}^2\tau _{kl}^2)\). If \(\tilde{h}_{ijij}\) is expressed by \(\tilde{h}_{ij}\), then using the general formulas of the expected value of the product of two quadratic forms of random variables [11], we obtain
In the same analog, we find
because \(\tau _{ij}\) and \(\rho _{kl})\) are independent random variables. Finally, following the same reason, we observe that \({\mathbb E}(a_{ij}b_{kl})=-2\,{\mathbb E}(\rho _{ij}^2\tau _{kl} \rho _{kl})=0\) and also \( {\mathbb E}(b_{ij}c_{kl})=0\). From these results, we find the desired identities. This completes the proof of the lemma. \(\square \)
Derivation of Eqs. (41)–(43) The MSE of \({\Delta }_1\hat{{\varvec{\theta }}}_\mathrm{m}\) is equal to \(\sigma ^2\tilde{\mathbf {R}}\). We shall next evaluate \(\mathrm{MSE}({\Delta }_2\hat{{\varvec{\theta }}}_\mathrm{m})\). Let us define \(\check{\mathbf {a}}=(\check{\mathbf {a}}_1^\mathrm{T} , \, \check{\mathbf {a}}_2^\mathrm{T})^\mathrm{T}\) and other variables in the same manner. Then
where
Premultiplying and then postmultiplying \({\mathbb E}(\check{\mathbf {a}}\check{\mathbf {a}}^\mathrm{T})\) by \(\tilde{\mathbf {K}}\) and \(\tilde{\mathbf {K}}^\mathrm{T}\), respectively, lead to
Now we compute \({\mathbb E}\left( \check{\mathbf {a}}\check{\mathbf {c}}^\mathrm{T} \right) \). It is easy to show that
and as such, if it is premultiplied and then postmultiplied by \(\tilde{\mathbf {K}}\) and \(\tilde{\mathbf {K}}^\mathrm{T}\), respectively, we obtain
Finally, the less important but the most complicated expressions in the MSE of \({\Delta }_2 \hat{{\varvec{\theta }}}_\mathrm{m}\) come from \({\mathbb E}(\check{\mathbf {b}}\check{\mathbf {b}}^\mathrm{T})\) and \({\mathbb E}(\check{\mathbf {c}}\check{\mathbf {c}}^\mathrm{T})\). After lengthy but direct calculations, we have
where
and \(\check{\tilde{\mathbf {D}}}_{\tilde{\mathbf {h}}_1,\tilde{\mathbf {h}}_2}=\mathrm{diag}(\check{\tilde{\mathbf {h}}}_1, \check{\tilde{\mathbf {h}}}_2 )\). Premultiplying and postmultiplying this expression by \(\tilde{\mathbf {K}}\) and \(\tilde{\mathbf {K}}^\mathrm{T}\) give
Finally, combining all expressions together gives us the MSE of \({\Delta }_2\hat{{\varvec{\theta }}}_\mathrm{m}\).
Proof of Eq. (70)
Let \(\varvec{\varLambda }_{ij}=({\tilde{{\varvec{\phi }}}}^\mathrm{T}\tilde{\mathbf {V}}_{ij}\tilde{\mathbf {\mathscr {M}}}^-\Delta _1 ^1\mathbf {\mathscr {M}}{\tilde{{\varvec{\phi }}}})\Delta _1^1\mathbf {\mathscr {M}}\). Then
Here again \(\mathscr {S}(\bullet )= (\bullet + \bullet ^\mathrm{T})/2\) is the symmetrization operator. Recall that \(\gamma _{ij}={\hat{{\varvec{\phi }}}}^\mathrm{T}\mathbf {V}_{ij}{\hat{{\varvec{\phi }}}}\) and \({\Delta }_1\gamma _{ij}\) is given in Eq. (63). We shall evaluate Eq. (69) term by term. First, consider
By direct inspection, \({\mathbb E}\bigl (\Delta _1\, \mathbf {z}_{ij}^\mathrm{T}\tilde{\mathbf {\mathscr {M}}}^-\Delta _1\,\mathbf {z}_{ij}\bigr )=\sigma ^2\mathrm{tr}(\tilde{\mathbf {\mathscr {M}}}^-\tilde{\mathbf {V}}_{ij})\), hence if we using the definition of \(\tilde{\psi }_{ij}=\tilde{\mathbf {z}}_{ij}^\mathrm{T}\tilde{\mathbf {\mathscr {M}}}^{-}\tilde{\mathbf {z}}_{ij}\), then
We shall make use of an auxiliary formula below that follows from Eq. (67):
and hence \({\mathbb E}(\Delta _1\mathbf {z}_{ij}\Delta _1{\hat{{\varvec{\phi }}}}^\mathrm{T}) =-\sigma ^2\tilde{\zeta }_i^{-1}\tilde{\mathbf {V}}_{ij}{\tilde{{\varvec{\phi }}}}\tilde{\mathbf {z}}_i^\mathrm{T}\tilde{\mathbf {\mathscr {M}}}^-\). Next we compute
Using \({\Delta }_1^1\mathbf {\mathscr {M}}=\sum _{i=1}^2 \sum _{j=1}^{n_i}\tilde{\zeta }_i^{-1}{\Delta }_1\mathbf {M}_{ij}\), and then Eqs. (63) and (85) give
Now recall that \(\tilde{\mathbf {V}}_{ij}=\tilde{\mathbf {a}}_{ij}\tilde{\mathbf {a}}_{ij}^\mathrm{T}+\tilde{\mathbf {b}}_{ij}\tilde{\mathbf {b}}_{ij}^\mathrm{T}\); thus, the noisy version of \(\tilde{\mathbf {V}}_{ij}\) has the first-order error term expressed as
Thus, \({\tilde{{\varvec{\phi }}}}^\mathrm{T}{\Delta }_1\mathbf {V}_{ij}{\tilde{{\varvec{\phi }}}}=({\tilde{{\varvec{\phi }}}}^\mathrm{T}\tilde{\mathbf {T}}_{ij}{\tilde{{\varvec{\phi }}}})\delta _{ij} +({\tilde{{\varvec{\phi }}}}^\mathrm{T}\tilde{\mathbf {S}}_{ij}{\tilde{{\varvec{\phi }}}}){\epsilon }_{ij}\). Also \({\mathbb E}(\delta _{ij}{\Delta }_1\mathbf {M}_{ij})=2 \sigma ^2\mathscr {S}[\tilde{\mathbf {a}}_{ij}\tilde{\mathbf {z}}_{ij}^\mathrm{T}]\) and \({\mathbb E}({\epsilon }_{ij}{\Delta }_1\mathbf {M}_{ij})=2\sigma ^2\mathscr {S}[\tilde{\mathbf {b}}_{ij}\tilde{\mathbf {z}}_{ij}^\mathrm{T}]\), where \(\tilde{\mathbf {a}}_{ij}\) and \(\tilde{\mathbf {b}}_{ij}\) denote the first and second columns of \(\nabla \mathbf {z}_{ij}\). Therefore, \({\mathbb E}[({\tilde{{\varvec{\phi }}}}^\mathrm{T}\Delta _1\mathbf {V}_{ij}{\tilde{{\varvec{\phi }}}})\Delta _1\mathbf {M}_{ij}]\)
where \(\tilde{\varvec{\varGamma }}_{ij}\) is defined in Eq. (73). They imply that
Next, using \({\Delta }_2\mathbf {M}_{ij}=2\mathscr {S}[{\Delta }_2\mathbf {z}_{ij}\tilde{\mathbf {z}}_{ij}^\mathrm{T}]+{\Delta }_1\mathbf {z}_{ij}{\Delta }_1\mathbf {z}_{ij}^\mathrm{T}\) and \({\Delta }_2\mathbf {z}_{ij}=(\delta _{ij}^2+{\epsilon }_{ij}^2)\mathbf {e}_1'\) give
which simply becomes
Lastly, we evaluate
The first term comes from Eq. (85), and the second comes from Eq. (87). Thus,
This completes the integration of Eq. (69).
To prove Eq. (70), we multiply the identities in Eqs. (84), (88), (90), and (91) by \({\tilde{{\varvec{\phi }}}}\). First,
Using the following useful identities
We have \(\mathbf {I}_2{\tilde{{\varvec{\phi }}}}\)
and further,
Applying the definition of \(\tilde{\mathbf {\mathscr {M}}}\) and the identity \(\tilde{\mathbf {\mathscr {M}}}^-\tilde{\mathbf {\mathscr {M}}}\tilde{\mathbf {\mathscr {M}}}^-=\tilde{\mathbf {\mathscr {M}}}^-\) yields
Next
Lastly, we apply the above identities again to evaluate
Now, observing that \(\tilde{\mathbf {G}}_2^\mathrm{T} {\tilde{{\varvec{\phi }}}}={\mathbf {0}}\) and combining Eqs. (92), (93), and (94), (95) complete the derivation of Eq. (70). Note that some terms in Eq. (93) and Eq. (95) cancel each other. \(\square \)
Rights and permissions
About this article
Cite this article
Al-Sharadqah, A., Ho, K.C. Second-Order Performance Analysis and Unbiased Estimation for the Fitting of Concentric Circles. J Math Imaging Vis 57, 340–365 (2017). https://doi.org/10.1007/s10851-016-0681-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10851-016-0681-5