A fuzzy multi-criteria approach based on Clarke and Wright savings algorithm for vehicle routing problem in humanitarian aid distribution

Abstract

Natural disasters usually occur unexpectedly, causing loss of life and property. It is essential to quickly and effectively distribute aid materials to minimize the damage in the aftermath of a disaster. Aid organizations require decision-making mechanisms that provide hard data to make quick and accurate decisions during the distribution of aid materials. In this study, the delivery of aid materials to the victims of disasters is investigated as a vehicle routing problem. For this purpose, a new method is developed by integrating the interval type-2 fuzzy TOPSIS method with the Clarke and Wright savings algorithm. In this way, while determining the routes, different criteria specific to the problem could also be analyzed with the distance criterion. The proposed method is presented with a numerical example to show how it can be implemented in the humanitarian aid distribution problem. As a result of the numerical example, it is determined that the proposed method completed the delivery with 826 distance units in four rounds, and the classical Clarke and Wright savings algorithm completed the delivery at 820 distance units in four rounds. Although the proposed method provides a longer distance solution than the classical Clarke and Wright savings algorithm, it has the advantage of determining safer routes by taking into account the different risks that may arise during a disaster. Finally, well-known benchmark problems are solved using the proposed method.

Introduction

Natural disasters such as hurricanes, earthquakes, and floods have been causing significant losses worldwide. According to the records from the International Disaster Database, there were at least 396 natural disasters in 2019, killing 11,755 people, affecting 95 million people, and costing about 130 billion US$ (Froment & Below, 2020). These statistics emphasize the importance of aid distribution management to reduce the effects of natural disasters. It is a known fact that natural disasters cannot be prevented. However, their impact can be reduced if disaster preparedness activities are carried out effectively. It is crucial to manage humanitarian aid operations in disaster areas (DA) and promptly deliver aid materials. Therefore, efficient aid distribution management has an essential role in accessing humanitarian aid materials to the disaster victims on time.

The optimal planning of emergency transportation in the post-disaster humanitarian supply chain is different from traditional transportation problems (Wang et al., 2018). The distribution of aid materials to the victims of disasters is a vehicle routing problem (VRP). VRP should be flexible enough to accommodate different constraints other than the capacity and route length encountered in real-life applications (Cordeau et al., 2002). The traditional VRP aims to determine the best routes at a minimal cost. The classical Clarke and Wright (CW) savings algorithm consider distance or cost criteria when determining routes. However, in events that directly affect human life, such as natural disasters, decision-makers (DM) may need to consider different criteria other than distance or duration. The shortest route may not be the optimal solution. Different criteria, such as the traffic density, the physical condition of the road, and the suitability of combining orders in the same vehicle, may also need to be evaluated (Cengiz Toklu, 2017). Therefore, this motivates us to develop a new approach that can reach more need-oriented solutions.

The performance of aid distribution management may be affected by various criteria. Evaluating these criteria and finding the most effective solution becomes more difficult as the number of criteria increases. This study presents a modified CW savings algorithm based on interval type-2 fuzzy (IT2F) logic and Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS) method for the VRP in humanitarian aid distribution. The proposed method aims to evaluate the effect of different criteria when creating the savings matrix, which is one of the steps of the CW savings algorithm. For this reason, it is suggested to use importance coefficients while determining the savings matrix in the CW savings algorithm. The mentioned importance coefficients are determined by the IT2F TOPSIS method.

The distribution problem is one of the crucial issues in many studies. Distribution relates to the problem of providing goods from a depot to customers. The problem can be modeled using graph theory through the traveling salesman problem (TSP) and VRP. VRP is the extended version of TSP (Wahyuningsih et al., 2016). VRP, also knowns as the node routing problem (NRP), is one of the most studied issues in operational research. Because the allocation of goods is being affected by numerous factors, these factors are transformed into constraints or variables for the problem. As a result, different VRP variants are developed (Konstantakopoulos et al., 2020). The capacitated arc routing problem (ARP) is the problem of servicing a set of streets in a street network using a fleet of vehicles with a certain capacity initially located at a central depot (Wøhlk, 2008). According to Chu et al. (2005), the capacitated ARP includes obtaining a set of feasible vehicle tour that minimizes the total cost of traversed edges. A NRP and an ARP can be interconverted. The choice of an arc routing or node routing model must consider the distinct nature of the operations as well as the solution techniques. NRPs have been studied more intensely than ARPs (Assad & Golden, 1995). Despite these similarities between ARP and VRP, there has been a great effort to study NRPs. In this way, many solution methods have been developed on VRP. Because of this reason, some researchers have been motivated to transform ARPs into NRPs (Foulds et al., 2015). Besides, considering the capacity constraint of VRP and making both routing and assignment are among its advantages. Earthquake is one of the natural disasters where humanitarian aid is most needed. According to Anbuudayasankar et al. (2016), allocating food to areas that are affected by earthquakes is a complex distribution problem. It is necessary to plan optimal food supply patterns and inventory allocation for these areas. Similarly, it is also crucial to formulate the VRP as minimizing the amount of pain and suffering of the affected people instead of minimizing the travel distance. For these reasons, the VRP approach is preferred in this study. In addition, the proposed method does not only aim to minimize the distance as mentioned above. It also considers other criteria necessary to plan aid distribution.

This study aims to find an optimum solution that minimizes the travel distance and the number of routes, taking into account the different decision criteria encountered in real-world problems. It is not always possible to model and analyze real-world problems with deterministic mathematical methods. Because this kind of problem can sometimes have a very complex structure, incomplete or unidentified information, or may not reach a feasible solution under all constraints. Furthermore, it may be necessary to use linguistic expressions like few, many, more when defining problems. The fuzzy set theory was first introduced by Zadeh (1965) to solve these types of problems. The classical type-1 fuzzy (T1F) logic approach has been criticized for including one membership value for each precise parameter value. Afterward, Zadeh (1975) developed type-2 fuzzy (T2F) sets (Ucal Sari & Kahraman, 2015). IT2F sets (Karnik et al., 1999; Liang & Mendel, 2000; Mendel et al., 2006) are the particular case of T2F sets. According to Mendel et al. (2006), IT2F sets are used more often because general T2F sets involve computational complexity. For this reason, a multi-criteria decision-making (MCDM) technique integrated with IT2F sets is preferred in this study. Likewise, the TOPSIS method has an advantage that is the ability to identify the best alternative quickly (Sadeghzadeh & Salehi, 2011). Moreover, this method has a simple, rational, comprehensible concept and the computation involved is simple (Deng & Yeh, 2006; Roszkowska, 2011). In summary, the contributions of this paper include the following:

• A new method that enables the decisions taken in humanitarian aid operations to be quick and accurate is developed. Within this scope, the MCDM approach is proposed to determine the savings matrix in the CW savings algorithm. One of the strengths of the proposed method is that it can evaluate different criteria simultaneously. It derives its power from the MCDM technique added to the CW savings algorithm. Specifically, it is aimed to provide the flexibility required in humanitarian aid operations by prioritizing the determined criteria with the fuzzy MCDM technique.

• The proposed method extends the CW savings algorithm. Thus, this method can be used in different vehicle routing problems in manufacturing or supply chain management by determining subject-specific criteria.

The rest of this paper is organized as follows. Section 2 examines the literature on humanitarian aid distribution and CW savings algorithm separately. Section 3 focuses on the IT2F TOPSIS method and the CW savings algorithm. Moreover, in this section, the fundamental definitions and notations of the fuzzy set theory and IT2F sets are introduced briefly. Section 4 includes the proposed method, modified CW savings algorithm. Section 5 applies the proposed method to a vehicle routing problem in humanitarian aid distribution. Besides, well-known ten benchmark problems are solved using the proposed method and compared with the classical CW savings algorithm. Finally, the conclusions are discussed.

Literature review

In this section, the studies on humanitarian aid distribution and the CW savings algorithm are examined separately. Thus, the focused problem and the method, which is a part of the solution phase, are evaluated.

Humanitarian aid distribution

Natural disasters occur worldwide and have serious consequences that affect human life. In emergency events, the transportation of medical supplies is an important problem. The necessary aid materials at the emergency sites should be provided immediately (Li et al., 2017). There are studies in different disciplines on disaster management, emergency management, aid distribution management, and humanitarian supply chain to minimize disaster risk. Studies focusing on the performance evaluation of the humanitarian aid chain have increased in recent years (Anjomshoae et al., 2017; Beamon & Balcik, 2008; Kovács & Spens, 2007; Torabi et al., 2012).

Another issue that researchers (Celik et al., 2014; Pettit & Beresford, 2009; Zhou et al., 2011) focused on is crucial success factors in the humanitarian supply chain management. Likewise, studies involving optimization models have also been the focus of researchers. Sheu (2007) presented a hybrid fuzzy clustering optimization model for the critical relief demands. Yi and Kumar (2007) presented a model including ant colony optimization for logistics problems in disaster relief organizations. Likewise, Wang et al. (2018) formulated the emergency transportation problem with an integer linear programming model. Balcik and Beamon (2008) proposed a model that determines the locations of relief materials distribution centers and the number of relief materials at each distribution center in natural disasters. Vitoriano et al. (2011) developed a multi-criteria optimization model to allocate humanitarian aid. Huang et al. (2012) identified and formulated performance criteria in relief distribution based on efficacy and equity. H. Li et al. (2017) aimed to determine the most appropriate route to deliver medical supplies to the requested places as soon as possible in case of an emergency event using uncertain programming. Li et al. (2018) developed an optimization model under demand uncertainty in a relief operation. Loree and Aros-Vera (2018) proposed a model that determines the distribution locations for use in post-disaster relief activities. Song et al. (2018) developed an optimization model considering the lack of reliable prediction of customer demand in disasters. Sharifyazdi et al. (2018) developed a linear programming model that includes inventory cost, replenishment cost, and transportation cost. Liu et al. (2019) developed a model that determines the best temporary medical service locations and medical service allocation strategies for post-disaster situations. Maghfiroh and Hanaoka (2020) proposed a multi-modal aid distribution model. Ghorbani and Ramezanian (2020) dealt with the issue from a different perspective. They developed a stochastic model that offers an integrated approach to carrier selection and supplier selection problems in humanitarian logistics. Flexibility, adaptability, and agility are essential characteristics of disaster management. For disaster relief efforts, Day (2014) employed a complex adaptive supply network. Rasouli (2019) emphasized the importance of agility in disaster relief operations.

Finally, MCDM techniques used in disaster management are examined. Sheu (2010) proposed a model to manage emergency logistics processes using TOPSIS-based decision rules. Zhou et al. (2011) specified the critical success factors in emergency management with the fuzzy Decision Making Trail and Evaluating Laboratory (DEMATEL) method. Torabi et al. (2012) developed a model that includes fuzzy DEMATEL and fuzzy analytical network process (ANP) methods to measure humanitarian supply chain performance. Celik et al. (2014) evaluated critical success factors in humanitarian logistics using the trapezoidal T2F analytic hierarchy process (AHP) method. Kabra et al. (2015) determined the criteria for the coordination between aid organizations in humanitarian supply chain management and ranked these criteria with the fuzzy AHP method. In a similar study, Kabra and Ramesh (2015) used fuzzy AHP and fuzzy TOPSIS methods to determine the barriers to coordination in humanitarian supply chain management. Celik and Taskin Gumus (2016) proposed a model including T2F AHP and T2F PROMETHEE methods to measure emergency preparedness and response-ability performances. Yılmaz and Kabak (2020) proposed a model to identify distribution center locations for relief operations using AHP and TOPSIS methods under IT2F sets.

When the literature is examined, it is seen that studies including MCDM techniques focus on humanitarian supply chain management and its performance. This study differs from other studies in the limited literature by focusing on the aid distribution process, one of the main issues of humanitarian logistics.

Savings algorithm

Clarke and Wright (1964) developed a heuristic solution known as the CW savings method. This method is the first algorithm that became widely used (Rand, 2009), and it aims to combine the routes without exceeding the capacity while delivering goods to every customer to minimize the total transportation costs or distance. The details of the method are given in the methodology section.

Since 1964, several variations to the basic savings formula have been proposed. One of the first studies to extend the CW savings algorithm was conducted by Gaskell (1967) and Yellow (1970). Gaskell and Yellow proposed using generalized savings of form ${S}_{ij}={C}_{i0}+{C}_{0j}-\uplambda {\mathrm{C}}_{ij}$ to help assign more compact routes, where λ is a positive parameter (Cordeau et al., 2002). As the λ parameter increases, the distance between the customers becomes more important than the distance to the depot (Rand, 2009). Table 1 summarizes the methods based on the CW savings algorithm and the contribution of the proposed method to the literature.

Table 1 Modifications to the CW savings algorithm

As given in Table 1, Tillman and Cain (1972) examined the CW savings algorithm within the scope of more than one depot constraint. In this study, they proposed a formula as ${c}_{ik}^{mod}={min}_{m}\left\{{c}_{im}\right\}-\left({c}_{ik}-{min}_{m}\left\{{c}_{im}\right\}\right)$ where k is each depot and, i is each customer. Nelson et al. (1985) implemented six methods to the CW savings algorithm and contributed to the speed of the CW savings algorithm by using special data structures. Paessens (1988) proposed a new function as ${S}_{ij}={C}_{i0}+{C}_{0j}-\uplambda {\mathrm{C}}_{ij}+\mu \left|{C}_{0i}-{C}_{j0}\right|, 0<\uplambda \le 3$ and $0\le \mu \le 1$ to calculate savings. Altinkemer and Gavish (1991) proposed a new matching-based procedure for the parallel version of the CW savings algorithm. Altinel and Öncan (2005) proposed a function as ${S}_{ij}={C}_{i0}+{C}_{0j}-\uplambda {\mathrm{C}}_{ij}+\mu \left|{C}_{0i}-{C}_{j0}\right|+v\left({d}_{i}+{d}_{j}\right)/\overline{d }$ where ${d}_{i}$ is demand of customer i, $\overline{d }$ is average demand and $v$ is new parameter. With this function, they aimed to take customer demands into account and distances while calculating savings. Battarra et al. (2008) developed a genetic algorithm to determine the best parameters for the parametric version of the CW savings algorithm proposed by Altinel and Öncan (2005). Juan et al. (2011) enhanced the CW savings algorithm with the Monte Carlo simulation, cache, and splitting techniques. Pichpibul and Kawtummachai (2012a) proposed the two-phase probabilistic mechanism and the route post improvement. Caccetta et al. (2013) combined the CW savings algorithm with the domain reduction approach. The proposed method modifies the CW savings algorithm to analyze different criteria specific to the problem besides the distance criterion using IT2F TOPSIS method.

In addition to these, the studies that extend the CW savings algorithm by focusing on different constraints are briefly explained below. The extended version of VRP can be associated with constraints such as the vehicle capacity, route length, arrival/departure time at each node and service time, collection or delivery of goods (Goel & Maini, 2017). Some researchers (Atkinson, 1994, 1998; Balakrishnan, 1993; Bräysy, 2002; Homberger & Gehring, 1999; Solomon, 1987; Van Landeghem, 1988) studied VRP with time window based on the CW savings algorithm. VRP with time window takes into account the constraint of delivering to customers within a predetermined time windows.

When some elements such as demand and travel time in the VRP are random, the problem is called stochastic VRP (Gendreau et al., 1996). In this study, it is assumed that customer demands are predetermined. However, various studies investigated VRP within the context of stochastic demands by extending the CW savings algorithm (Berhan, 2016; Stewart & Golden, 1983; Tillman, 1969). Similarly, Lambert et al. (1993) studied the stochastic VRP in which travel times are random.

VRP evolves into the VRP with backhauls when the vehicle’s route contains deliveries and then collections (Rand, 2009). Some studies benefit from the CW savings algorithm within the scope of VRP with backhauls. Wassan (2007) generated an algorithm for the VRP with backhauls using two construction schemes developed by Osman and Wassan (2002) based on the savings algorithm.

There are also studies in the literature that extend the CW savings algorithm with metaheuristic approaches. Battarra et al. (2008) used genetic algorithm approach to determine the best sets of parameters. Studies that examine the classical heuristic and metaheuristic methods for the VRP in depth are also encountered in the literature. Laporte et al. (2000) examined classical and modern heuristics for the VRP and presented the comparative computational results. Likewise, Cordeau et al. (2002) compared classical and modern heuristics for the VRP. They also examined the CW savings algorithm in the category of classical heuristics and they stated that it is commonly used in practice despite some of its shortcomings and got high scores in simplicity and speed. Rand (2009) examined extensions of the classical CW method to analyze the developments.

When the literature is examined in recent years, the following studies have been encountered: Herdianto (2021) used machine learning analysis to determine the essential features of VRP. In another study, Mrad et al. (2021) proposed the genetic algorithm based on the CW savings algorithm to minimize the total transportation cost. Kunnapapdeelert and Thawnern (2021) used the CW savings algorithm to design the vehicle route for the distribution of the steel industry. Zheng et al. (2021) proposed a model to integrate metro for urban logistics delivery using the improved tabu search algorithm and the CW savings algorithm.

When the studies that included the MCDM and the CW savings algorithm are examined, the following studies are encountered. Balaji et al. (2019) used the AHP method to increase customer satisfaction in the VRP. Nowroozi et al. (2021) combined AHP and TOPSIS methods with the CW savings algorithm, arguing that the shortest route is not the best route in all situations.

In conclusion, several variations to the CW savings formula have been proposed to improve the computation speed since 1964. Moreover, many extensions of the basic VRP that allow for constraints such as route length and vehicle capacity have been investigated using adaptations of the CW savings algorithm (Rand, 2009). However, there is still a gap in the literature regarding the modified CW savings algorithm considering priority constraints specific to the problem. This study differs from other studies by including IT2F sets and modifying the formulation of the classical CW savings algorithm.

Methodology

Processing information linguistically and dealing with the incomplete and heterogeneous character of existing information are the main objectives of fuzzy sets (Pedrycz, 1993). In this section, IT2F sets, IT2F TOPSIS method, and CW savings algorithm are described briefly.

Fuzzy set theory and interval type-2 fuzzy sets

Some definitions of T2F sets and IT2F sets from Mendel et al. (2006) are reviewed in the following:

Definition 1

(Mendel et al., 2006): $\widetilde{{\tilde{A}}}$ is the T2F set that is characterized by a type-2 membership function ${\mu }_{\widetilde{{\tilde{A}}}}\left(x,u\right)$ where $x\in X$ and $u\in {J}_{x}\subseteq \left[\mathrm{0,1}\right]$, shown as follows:

$$ \begin{aligned} \widetilde{{\tilde{A}}} &= \left\{ {\left( {\left( {x,u} \right),\mu_{{\widetilde{{\tilde{A}}}}} \left( {x,u} \right)} \right){|} \forall x \in X,\forall u \in J_{x} }\right.\\ & \left. { \subseteq \left[ {0,1} \right], and 0 \le \mu_{{\widetilde{{\tilde{A}}}}} \left( {x,u} \right) \le 1} \right\}\end{aligned} $$

(1)

Also, $\widetilde{{\tilde{A}}}$ can be represented as;

$$ \widetilde{{\tilde{A}}} = \mathop \smallint \limits_{x \in X} \mathop \smallint \limits_{{u \in J_{x} }} \mu_{{\widetilde{{\tilde{A}}}}} \left( {x,u} \right)/\left( {x,u} \right) $$

(2)

where ${J}_{x}\subseteq \left[\mathrm{0,1}\right]$ and $\iint$ denotes union overall admissible $x$ and $u$.

Definition 2

(Mendel et al., 2006): $\widetilde{{\tilde{A}}}$ is called IT2F set, if all ${\mu }_{\widetilde{{\tilde{A}}}}\left(x,u\right)$=1. An IT2F set $\widetilde{{\tilde{A}}}$ can be represented as follows:

$$ \widetilde{{\tilde{A}}} = \mathop \smallint \limits_{x \in X} \mathop \smallint \limits_{{u \in J_{x} }} 1/\left( {x,u} \right), where J_{x} \subseteq \left[ {0,1} \right] $$

(3)

Definition 3

(Mendel et al., 2006): An IT2F set's upper and lower membership functions are T1F membership functions.

Figure 1 represents an r-polygonal IT2F set. Let ${\widetilde{{\tilde{A}}}}_{i}$=(${\tilde{A }}_{i}^{U}$,${\tilde{A }}_{i}^{L}$) are the upper and the lower membership functions of the IT2F set ${\tilde{A }}_{1}$, ${\tilde{A }}_{2}$, …, and ${\tilde{A }}_{n}$ respectively (Lee & Chen, 2008a).

$$ \begin{aligned} \widetilde{{\tilde{A}}}_{i} &= (\tilde{A}_{i}^{U} ,\tilde{A}_{i}^{L} )\\ & = \left( {\left( {a_{i1}^{U} ,{ }a_{i2}^{U} ,{ }...,{ }a_{ir}^{U} { };{ }H_{1} \left( {\tilde{A}_{i}^{U} } \right),.., H_{r - 2} \left( {\tilde{A}_{i}^{U} } \right)} \right),} \right. \\ &\quad \left. {\left( {a_{i1}^{L} ,{ }a_{i2}^{L} ,{ }...,{ }a_{ir}^{L} { };{ }H_{1} \left( {\tilde{A}_{i}^{L} } \right),.., H_{r - 2} \left( {\tilde{A}_{i}^{L} } \right)} \right)} \right) \end{aligned} $$

Fig. 1

The upper and lower r-polygonal membership functions ($\tilde{A}_{i}^{U} and \tilde{A}_{i}^{L} )$ of the IT2F set $\tilde{A}_{i}$ (Lee & Chen, 2008a)

Fig. 2

The upper and lower trapezoidal membership functions ($\tilde{A}_{i}^{U} , \tilde{A}_{i}^{L}$) of the IT2F set $\tilde{A}_{i}$ (S.-M. Chen & Lee, 2010)

where r Number of edges in the upper and the lower r-polygonal membership functions (${\tilde{A }}_{i}^{U}$ and ${\tilde{A }}_{i}^{L}$).

${H}_{J}\left({\tilde{A }}_{i}^{U}\right)$: Membership value of the element ${a}_{i(J+1)}^{U}$ in the upper r-polygonal membership function ${\tilde{A }}_{i}^{U}$, $1\le J\le r-2$

${H}_{J}\left({\tilde{A }}_{i}^{L}\right)$: Membership value of the element ${a}_{i(J+1)}^{L}$ in the lower r-polygonal membership function ${\tilde{A }}_{i}^{L}$,$1\le J\le r-2$

${H}_{1}\left({\tilde{A }}_{i}^{U}\right) \in \left[\mathrm{0,1}\right],.., {H}_{r-2}\left({\tilde{A }}_{i}^{U}\right)\in \left[\mathrm{0,1}\right]$, ${H}_{1}\left({\tilde{A }}_{i}^{L}\right) \in \left[\mathrm{0,1}\right],.., {H}_{r-2}\left({\tilde{A }}_{i}^{L}\right)\in \left[\mathrm{0,1}\right]$, r $\ge 3$ and $1\le i\le n$ (Lee & Chen, 2008b).

Lee and Chen (2008a) identified the notion of ranking values of IT2F sets. Furthermore, in another study, Lee and Chen (2008c) customized the notion of ranking values for trapezoidal IT2F sets in their numerical example. Figure 2 represents the upper and the lower trapezoidal membership functions of the IT2F set.

Fig. 3

Steps of the CW savings algorithm

The notion of the ranking value of the trapezoidal IT2F set is mentioned below (Lee & Chen, 2008c).

$$\mathrm{Rank}({\widetilde{{\tilde{A}}}}_{i})={ M}_{1}\left({\tilde{A }}_{i}^{U}\right)+{M}_{1}\left({\tilde{A }}_{i}^{L}\right)+{M}_{2}\left({\tilde{A }}_{i}^{U}\right)+{M}_{2}\left({\tilde{A }}_{i}^{L}\right)+{M}_{3}\left({\tilde{A }}_{i}^{U}\right)+{M}_{3}\left({\tilde{A }}_{i}^{L}\right) -\frac{1}{4}\left({s}_{1}\left({\tilde{A }}_{i}^{U}\right)+{s}_{1}\left({\tilde{A }}_{i}^{L}\right)+{s}_{2}\left({\tilde{A }}_{i}^{U}\right)+{s}_{2}\left({\tilde{A }}_{i}^{L}\right)+{s}_{3}\left({\tilde{A }}_{i}^{U}\right)+{s}_{3}\left({\tilde{A }}_{i}^{L}\right)+{s}_{4}\left({\tilde{A }}_{i}^{U}\right)+{s}_{4}\left({\tilde{A }}_{i}^{L}\right)\right)+{H}_{1}\left({\tilde{A }}_{i}^{U}\right)+{H}_{1}\left({\tilde{A }}_{i}^{L}\right)+{H}_{2}\left({\tilde{A }}_{i}^{U}\right)+{H}_{2}\left({\tilde{A }}_{i}^{L}\right)$$

(4)

where

$$ M_{p} \left( {\tilde{A}_{i}^{j} } \right) = \left( {a_{ip}^{j} + a_{{i\left( {p + 1} \right)}}^{j} } \right)/2,\quad 1 \le p \le 3, $$

$$ S_{q} \left( {\tilde{A}_{i}^{j} } \right) = \sqrt {\frac{1}{2}\mathop \sum \limits_{k = q}^{q + 1} \left( {a_{ik}^{j} - \frac{1}{2}\mathop \sum \limits_{k = q}^{q + 1} a_{ik}^{j} } \right)^{2} } , 1 \le q \le 3, $$

$$ S_{4} \left( {\tilde{A}_{i}^{j} } \right) = \sqrt {\frac{1}{4}\mathop \sum \limits_{k = 1}^{4} \left( {a_{ik}^{j} - \frac{1}{4}\mathop \sum \limits_{k = 1}^{4} a_{ik}^{j} } \right)^{2} } $$

$H_{p} \left( {\tilde{A}_{i}^{j} } \right)$ is the membership value of the element $a_{{i\left( {p + 1} \right)}}^{j}$ in the trapezoidal membership function $\tilde{A}_{i}^{j} ,1 \le p \le 2, j \in \left\{ {U,L} \right\}$ and $1 \le i \le n.$

In Eq. (4), the summation of $M_{1} \left( {\tilde{A}_{i}^{U} } \right),M_{1} \left( {\tilde{A}_{i}^{L} } \right),M_{2} \left( {\tilde{A}_{i}^{U} } \right),M_{2} \left( {\tilde{A}_{i}^{L} } \right),M_{3} \left( {\tilde{A}_{i}^{U} } \right),M_{3} \left( {\tilde{A}_{i}^{L} } \right)$, $H_{1} \left( {\tilde{A}_{i}^{U} } \right),H_{1} \left( {\tilde{A}_{i}^{L} } \right),H_{2} \left( {\tilde{A}_{i}^{U} } \right)$ and $H_{2} \left( {\tilde{A}_{i}^{L} } \right)$ is denoted the basic ranking score where deducted the average of$s_{1} \left( {\tilde{A}_{i}^{U} } \right),s_{1} \left( {\tilde{A}_{i}^{L} } \right),s_{2} \left( {\tilde{A}_{i}^{U} } \right),s_{2} \left( {\tilde{A}_{i}^{L} } \right),s_{3} \left( {\tilde{A}_{i}^{U} } \right)$, $s_{3} \left( {\tilde{A}_{i}^{L} } \right),s_{4} \left( {\tilde{A}_{i}^{U} } \right)$ and $s_{4} \left( {\tilde{A}_{i}^{L} } \right)$ from the basic ranking score to give the dispersive IT2F set a penalty, where $1 \le i \le n$ (S.-M. Chen & Lee, 2010).

Interval type-2 fuzzy TOPSIS

TOPSIS method (Hwang & Yoon, 1981) seeks the solution with the shortest Euclidean distance from the positive ideal solution (PIS) and the solution with the farthest Euclidean distance from the negative ideal solution (NIS) (Tzeng & Huang, 2011). In this study, the IT2F TOPSIS method is preferred to evaluate the decision criteria, because IT2F sets provide more flexibility in fuzzy group decision-making problems (Lee & Chen, 2008c). C.-T. Chen (2000) extended the TOPSIS method using T1F sets in triangular fuzzy numbers. Afterward, C.-T. (Chen et al., 2006) developed the TOPSIS method using linear trapezoidal membership functions. The steps of the IT2F TOPSIS method developed by S.-M. Chen and Lee (2010) and Lee and Chen (2008c) are described below:

Alternatives (X)	: X = $\left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}$
Attributes (F)	: F = $\left\{ {f_{1} ,f_{2} , \ldots ,f_{m} } \right\}$ F1(benefit attributes) and F2 (cost attributes), F1 $\cap$ F2 = Φ, and $F_{1} \cup F_{2} = F$
Decision-makers (DM)	: D = DM1, DM2,…, DMk

Step 1 The decision matrix of the $p$ th decision-maker $(Y_{p} )$ is created.

$$ Y_{p} = \left( {\tilde{f}_{ij}^{p} } \right)_{mxn} = \begin{array}{*{20}c} {} & {} \\ {} & {\left[ {\begin{array}{*{20}c} {\widetilde{{\tilde{f}}}_{11}^{p} } & {\widetilde{{\tilde{f}}}_{12}^{p} } & \ldots & {\widetilde{{\tilde{f}}}_{1n}^{p} } \\ {\widetilde{{\tilde{f}}}_{21}^{p} } & {\widetilde{{\tilde{f}}}_{22}^{p} } & \ldots & {\widetilde{{\tilde{f}}}_{2n}^{p} } \\ \vdots & \vdots & \vdots & \vdots \\ {\widetilde{{\tilde{f}}}_{m1}^{p} } & {\widetilde{{\tilde{f}}}_{m2}^{p} } & \ldots & {\tilde{f}_{mn}^{p} } \\ \end{array} } \right]} \\ \end{array} $$

(5)

$$ \overline{Y}\left( {\text{The average decision matrix}} \right) = (\widetilde{{\tilde{f}}}_{ij} )_{mxn} $$

(6)

where $\widetilde{{\tilde{f}}}_{ij} = \left( {\frac{{\widetilde{{\tilde{f}}}_{ij}^{1} \oplus \widetilde{{\tilde{f}}}_{ij}^{2} \oplus \ldots \oplus \widetilde{{\tilde{f}}}_{ij}^{k} }}{k}} \right)$, $\widetilde{{\tilde{f}}}_{ij}$ is an IT2F set, 1$\le i \le m$, 1$\le j \le n$, 1 $\le p \le k$

Step 2 The weighting matrix of the attributes of the $p$ th decision-maker (W_p) is realized.

$$ f_{1} f_{2} \cdots f_{m} $$

$$ {\text{W}}_{{\text{p}}} = \left( {\widetilde{{\tilde{w}}}_{i}^{p} } \right)_{1xm} = \left[ {\begin{array}{*{20}c} {\widetilde{{\tilde{w}}}_{1}^{p} } & {\widetilde{{\tilde{w}}}_{2}^{p} } & \ldots & {\widetilde{{\tilde{w}}}_{m}^{p} } \\ \end{array} } \right] $$

(7)

$$ \overline{W}\left( {\text{The average weighting matrix}} \right) = \left( {\widetilde{{\tilde{w}}}_{i} } \right)_{1xm} $$

(8)

where $\widetilde{{\tilde{w}}}_{i} = \left( {\frac{{\widetilde{{\tilde{w}}}_{i}^{1} \oplus \widetilde{{\tilde{w}}}_{i}^{2} \oplus \ldots \oplus \widetilde{{\tilde{w}}}_{i}^{k} }}{k}} \right)$, $\widetilde{{\tilde{w}}}_{i}$ is an IT2F set, 1 $\le i \le m$, 1 $\le p \le k$.

Step 3 Weighted decision-matrix ($\overline{Y}_{w}$) is created.

$$ \overline{Y}_{w} = (\widetilde{{\tilde{v}}}_{ij} )_{mxn} = \begin{array}{*{20}c} {} & {} \\ {} & {\left[ {\begin{array}{*{20}c} {\widetilde{{\tilde{v}}}_{11} } & {\widetilde{{\tilde{v}}}_{12} } & \ldots & {\widetilde{{\tilde{v}}}_{1n} } \\ {\widetilde{{\tilde{v}}}_{21} } & {\widetilde{{\tilde{v}}}_{22} } & \ldots & {\widetilde{{\tilde{v}}}_{2n} } \\ \vdots & \vdots & \vdots & \vdots \\ {\widetilde{{\tilde{v}}}_{m1} } & {\widetilde{{\tilde{v}}}_{m2} } & \ldots & {\widetilde{{\tilde{v}}}_{mm} } \\ \end{array} } \right]} \\ \end{array} $$

$$ \widetilde{{\tilde{V}}}_{ij} = \widetilde{{\tilde{w}}}_{i} \otimes \widetilde{{\tilde{f}}}_{ij} \,1 \le i \le m\,{\text{ and}}\, \, 1 \le j \le n. $$

(9)

Step 4 The ranking values of the IT2F set $\widetilde{{\tilde{v}}}_{ij}$ are calculated with Eq. (4)

$$ \overline{Y}_{w}^{*} = \left( {\text{Ranking weighted decision matrix}} \right) = \left( {Rank{ }\left( {\widetilde{{\tilde{v}}}_{ij} } \right)} \right)_{mxn} ,\,1 \le i \le m\,{\text{and}}\,1 \le j \le n $$

(10)

Step 5 $x^{ + } = \left( {v_{1}^{ + } ,v_{2}^{ + } , \ldots ,v_{m}^{ + } } \right),$ PIS and $x^{ - } = \left( {v_{1}^{ - } ,v_{2}^{ - } , \ldots ,v_{m}^{ - } } \right)$, NIS are calculated.

$$ v_{1}^{ + } = \left\{ {\begin{array}{*{20}c} {\mathop {\max }\limits_{1 \le j \le n} \left\{ {Rank\widetilde{{\tilde{v}}}_{ij} } \right\}, if f_{i} = \in F_{1} } \\ {\mathop {{\text{mix}}}\limits_{1 \le j \le n} \left\{ {Rank\widetilde{{\tilde{v}}}_{ij} } \right\}, if f_{i} = \in F_{2} } \\ \end{array} } \right. $$

(11)

$$ v_{1}^{ - } = \left\{ {\begin{array}{*{20}c} {\mathop {\min }\limits_{1 \le j \le n} \left\{ {Rank\widetilde{{\tilde{v}}}_{ij} } \right\}, if f_{i} = \in F_{1} } \\ {\mathop {\max }\limits_{1 \le j \le n} \left\{ {Rank\widetilde{{\tilde{v}}}_{ij} } \right\}, if f_{i} = \in F_{2} } \\ \end{array} } \right. $$

(12)

Step 6 $d^{ + } \left( {x_{j} } \right)$ and $d^{ - } \left( {x_{j} } \right)$ are calculated as;

$d^{ + } \left( {x_{j} } \right)$: The distance among each alternative ( $x_{j} )$ and the PIS $\left( {x^{ + } } \right)$

$d^{ - } \left( {x_{j} } \right)$: The distance among each alternative $\left( {x_{j} } \right)$ and the NIS $\left( {x^{ - } } \right)$

$$ d^{ + } \left( {x_{j} } \right) = \sqrt {\mathop \sum \limits_{i = 1}^{m} \left( {Rank\left( {\widetilde{{\tilde{v}}}_{ij} } \right) - v_{i}^{ + } } \right)^{2} } ,\quad {1} \le {\text{j}} \le {\text{n}} $$

(13)

$$ d^{ - } \left( {x_{j} } \right) = \sqrt {\mathop \sum \limits_{i = 1}^{m} \left( {Rank\left( {\widetilde{{\tilde{v}}}_{ij} } \right) - v_{i}^{ - } } \right)^{2} } ,\quad {1} \le {\text{j}} \le {\text{n}} $$

(14)

Step 7: The closeness coefficient for each alternative, $CC(x_{j}$) are calculated. Finally, alternatives are prioritized and evaluated according to the closeness coefficient.

$$ CC\left( {x_{j} } \right) = \frac{{d^{ - } \left( {x_{j} } \right)}}{{d^{ + } \left( {x_{j} } \right) + d^{ - } \left( {x_{j} } \right)}},\quad {1} \le {\text{j}} \le {\text{n}} $$

(15)

The Clarke and Wright savings algorithm

The CW savings algorithm is a widely applied heuristic algorithm for solving capacitated VRP. The steps of the algorithm are explained in Fig. 3. In the CW savings algorithm, only one depot is available in the problem. Goods must be delivered in a certain amount to given customers from the depot. A number of vehicles are available for the transportation of the goods. The vehicles have a limited capacity. All the routes in the problem–solution should start with the depot and end with the depot. Goods are taken from the depot and delivered to one or more customers. At the end of the route, the vehicle returns to the depot. This method aims to combine the routes without exceeding the capacity by visiting every customer to minimize the total transportation costs or distance specified driving from any customer to any other customer. Transportation costs between the same two points may vary depending on their directions (Lysgaard, 1997).

Fig. 4

The model of the savings concept. a: Two separate routes, b Joining the routes, c final route

Figure 4 is shown the savings concept. In Fig. 4a, customers i and j are visited on different routes. In Fig. 4b, the two customers are visited on the same route, and Fig. 4c is the final route. The algorithm calculates all the savings (S_ij) between customers i and j by using Eq. (16).

$$ {\text{S}}_{ij} = C_{i0} + C_{0j} - C_{ij} {\text{for}} i,j = 1, \ldots ,n {\text{and}} i \ne j $$

(16)

Fig. 5

Steps of the proposed method

where S_ij denotes all the savings between customers.

C_i0 denotes cost of traveling from the depot to customer i.

C_ij denotes cost of traveling from customer i to j.

The parallel version of the algorithm consistently implements the merge yielding the largest saving. In contrast, the sequential version keeps expanding the same route until this is no longer feasible (Cordeau et al., 2002). In the parallel version, when a link cannot be made into an existing route, a new route is created with that link (Rand, 2009). According to Cordeau et al. (2002), the parallel version is much more appropriate in practice. In the proposed method, the parallel version of the CW savings algorithm is adopted.

Proposed method

Many different heuristic and metaheuristic methods have been developed for the VRP. The most popular member of the classical heuristics class, the CW savings algorithm is the basis for many studies thanks to its advantages. These advantages can be listed as easiness of implementation (Vigo, 1996), speed, and simplicity (Rand, 2009) easiness to code (Rand, 2009; Volna & Kotyrba, 2016). Also, the savings method is included in most commercial software due to its advantages (Pichpibul & Kawtummachai, 2012b; Rand, 2009; Vigo, 1996). According to Altinel and Öncan (2005), classical heuristics conduct a limited investigation of the search area compared with metaheuristics. However, classical heuristics are simple, easy to implement and generate fairly good solutions very fast. For these reasons, the classical CW savings algorithm is used in the proposed method.

While the savings matrix is being created, distance or cost criterion is taken into account in the CW savings algorithm. However, in real-world problems, the distance or cost criteria may not be sufficient to decide. In this study, a new approach is proposed to solve the capacitated VRP based on the CW savings algorithm. The proposed method involves evaluating different criteria simultaneously while combining the routes. The evaluation criteria to be used while deciding to combine the routes are prioritized with the IT2F TOPSIS method, one of the MCDM techniques. The proposed method aims to find feasible solutions to minimize traveling distances and number of routes while reaching the optimal solution in light of the decision criteria by using Eq. (17).

$$ S_{ij}^{*} = (C_{i0} + C_{0j} - {\text{C}}_{ij} ) \times {\text{IC}}_{ij} $$

(17)

where ${\text{IC}}$ _ij: Importance Coefficient of the combined routes.

In the CW savings algorithm, the savings (S_ij) are sorted from largest to smallest, and nodes are combined in that order, considering the vehicle capacity constraint. If the savings are calculated using Eq. (16) as in the classical CW savings algorithm, only the distance criterion is taken into account, and the routes are combined. However, if Eq. (17) is used, other problem-specific criteria along with the distance criteria will also be influential in determining this order. For instance, assume that the savings to be obtained from the combination of two location pairs (S₁₃ and S₁₄) are calculated by Eq. (16) as follows, and the vehicle capacity is 30.

S₁₃ = 25 and S₁₄ = 18. According to the classical CW savings algorithm, locations 1 and 3, which have the highest savings value, are combined. However, assume that the importance coefficients for these location pairs are 0.08 and 0.12, respectively. So the new saving values according to the proposed model are calculated using Eq. (17) as follows:

S₁₃:$25 \times 0.08 = 2$ and S₁₄:$18 \times 0.12 = 2.16.$ In this case, locations 1 and 4 are first combined. Thus, the location pairs to be combined will change, thanks to their importance coefficients. With this change, different criteria are taken into account, as well as distance savings.

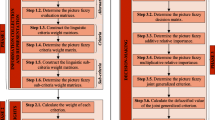
The steps of the proposed method are described in Fig. 5. The proposed method starts with the classical CW savings algorithm. In the first step of the proposed method, the CW savings matrix is created using the classical CW savings algorithm. Routes that can be combined under load constraint are determined. In the second step, problem-specific decision criteria are determined. Afterward, the importance coefficients of the decision criteria are determined by using the IT2F TOPSIS method. In the fourth step, a modified CW savings matrix is created. In this step, the importance coefficients are multiplied by the savings derived from the classical CW savings algorithm. In continuation of the proposed method, the classical CW savings algorithm steps are followed using the modified CW savings matrix.

Fig. 6

Combining DA₁ and DA₃ a: Two separate routes, b final route

The assumptions and limits of the proposed model are as follows. Node demands are not equal, but all demands are precise and pre-determined. There is a capacity restriction for vehicles. All vehicles have the same capacity. Although there is no restriction on the number of vehicles used, one of the objectives is to minimize the vehicle fleet. There is one depot. Routes start from the depot and end at the depot. The distances are symmetric (i to j and j to i is same distances). There is no legal restriction of the trip in hours.

Numerical example

In this section, a numerical example is presented to demonstrate how the proposed method can be implemented in real-world problems.

Problem definition

It is assumed that there are 3 DMs (DM₁, DM₂, and DM₃), and there is an aid distribution center (ADC) responsible for aid materials support to 7 different DAs. The distribution vehicles can carry less than or equal to 140 units. Disaster victims' demands and distances of DAs are given in Table 2.

Table 2 Demands and distances of DAs

Determination of the CW savings matrix

In this step, the CW savings matrix is generated, and routes that can be combined under load constraint are determined. First of all, the total distance is calculated without combining the loads as an initial solution. Assume that transportation is provided to each DA separately. Total Distance = 2 x (44 + 118 + 105 + 103 + 24 + 34 + 179) = 1214 Distance unit. The classical CW savings matrix is calculated by using Eq. (16) and shown in Table 3.

Table 3 Determined Savings by using classical CW savings algorithm

For instance, the saving value (124) is achieved by combining DA₁ and DA₃ demands. This value is calculated as follows:

Figure 6a shows the route that will occur if the demands of the routes are not combined. In this case, the distance value is calculated as follows:

$$ {\text{Distance}} = \left( {44 + 105} \right) \times 2 = 298 $$

Figure 6b shows the new route created by combining demands belonging to DAs. In this case, the new distance value is calculated as follows:

$$ {\text{Distance}} = \left( {44 + 25 + 105} \right) = 174 $$

The difference between the two cases gives the amount of savings and is calculated as follows:

$$ {\text{Saving}} = \left( {298 - 174} \right) = 124 $$

The saving can be calculated easier is by using Eq. (16) as follows:

$$ {\text{Saving}} = 105 + 44 - 25 = 124 $$

Thus, the new route was expressed as ADC-DA₁-DA₃-ADC. However, combining DA₁ and DA₂ demands is not possible because it exceeds the load constraint. The total demand for the two DAs is 189 units, which exceeds the 140-unit capacity. Similarly, the DAs that total demands that exceed the load limit are indicated with the "X" mark in Table 3. As a result, theoretically, a total of 14 route combining activities can be carried out. These routes and the savings they provide are given in Table 3.

Determination of decision criteria

DMs aim to save distance by visiting more than one DA on the same route by combining loads while providing access to the DAs. For this purpose, DMs considered six decision criteria along with distance criterion while evaluating the distance savings. These decision criteria are determined as traffic density, the physical condition of the road, suitability of aid material to be transported in the same vehicle, extra costs, disaster victim priority, and reliability and security of the routes. The decision criteria are briefly explained below.

Traffic density (C₁) In the classical CW savings algorithm, routes can be combined to save distance or cost. When the routes are combined, a new route from location i to location j is created (Fig. 3b). Traffic density on this new route should be an effective criterion in the decision to combine i and j locations.

The physical condition of the road (C₂) New routes may be physically damaged during a disaster, and they cannot be used safely (for instance, roads can be damaged due to the fault line in the earthquake, or the roads can be blocked due to the collapse of the bridges).

Suitability of aid material to be transported in the same vehicle (C₃) During route combination, aid materials will be transported in the same vehicle. Therefore, sometimes transporting materials in the same vehicle can create a safety problem. For instance, it is not appropriate to transport inflammable matter and caustic materials in the same vehicle.

Extra costs (C₄): While new routes save distance, new costs such as bridge tolls and toll roads may arise.

Disaster victim priority (C₅): If there is an aid material that needs to be delivered urgently, these routes will have to be given priority in the savings matrix. Thanks to this criterion, specific routes can be combined to give priority to urgent needs.

Reliability and security of the routes (C₆) Unlike "the physical condition of the road (C₂)" criterion, sometimes roads may be closed to traffic within the framework of the measures taken by the governments, or the new route created for savings may be located within the risky zone due to possible disaster hazards.

In the next section, the importance coefficients of the routes that can be combined are determined by considering these six criteria.

Determination of importance coefficients

Besides the distance criterion, six decision criteria that evaluate different situations in DAs are determined in the proposed method. Within the scope of these six decision criteria, importance coefficients are determined by using the IT2F TOPSIS method. The problem discussed is adapted to the IT2F TOPSIS method as follows:

• DMs: 3 decision-makers (DM₁, DM₂, and DM₃)

• Attributes: 6 different decision criteria (C₁, C₂, C₃, C₄, C₅, and C₆)

• Alternatives: 14 route combining activities (1–3, 1–5, 1–6, 2–3, 3–4, 3–5, 3–6, 3–7, 4–5, 4–6, 4–7, 5–6, 5–7, and 6–7)

DMs evaluate both decision criteria (attributes) and alternatives in terms of these criteria. The linguistic expressions used during the evaluation converts into fuzzy numbers by using Table 4.

Table 4 Linguistic expressions and their corresponding IT2F sets (S.-M. Chen & Lee, 2010)

The upper and the lower membership functions of the IT2F sets are shown in Fig. 7. Weights of the criteria evaluated with linguistic terms are shown in Table 5.

Fig. 7

The upper and the lower membership functions

Table 5 Weights of the criteria evaluated by the DMs (with linguistic terms)

DMs evaluated the alternatives with respect to the six evaluation criteria using the linguistic expressions shown in Table 4. Due to the space constraints, only the evaluations made within the scope of the C1 criterion are given in Table 6 as an example. The evaluations in Tables 5 and 6 are converted into fuzzy numbers using Table 4 and shown in Tables 7 and 8, respectively.

Table 6 Evaluating alternatives with respect to C₁(with linguistic terms)

Table 7 Weights of the criteria evaluated by the DMs (with type-2 fuzzy numbers)

Table 8 Evaluating alternatives with respect to C₁ (with type-2 fuzzy numbers)

The average of the evaluations given in Tables 7 and 8 are calculated using Eqs. (6) and (8). Then the steps of the IT2F TOPSIS method are applied by using Eqs. (9–14).

In Table 9, the distance $d^{ + } \left( {x_{j} } \right)$ between each alternative $\left( {x_{j} } \right)$ and the PIS and the distance $d^{ - } \left( {x_{j} } \right)$ between each alternative $\left( {x_{j} } \right)$ and the NIS are calculated using Eqs. (13–14). The relative degree of closeness of each alternative $CC\left( {x_{j} } \right)$ is calculated using Eq. (15) and shown in Table 9. Normalizing the sum of the relative degree of closeness values $CC\left( {x_{j} } \right)$ to 1, the importance coefficients are obtained. In Table 9, the sum of the relative degree of closeness $CC\left( {x_{j} } \right)$ column is 8.3782. Each location pair is normalized by dividing by the total value. For instance, location pairs 1–3 are normalized as 0.6046/8.3782 = 0.0722.

Table 9 Results of the IT2F TOPSIS method

Calculation of the modified CW savings algorithm

In this section, calculations of the classical CW savings algorithm are realized by using the modified CW savings matrix. Thus, the modified savings matrix is created with a new approach that considers the importance coefficients primarily. The classical savings matrix is created by considering only the distance criterion. The modified CW savings matrix is generated (Table 10) by multiplying the importance coefficients by savings derived from the classical CW savings algorithm given in Table 3.

Table 10 The modified CW savings matrix

Location pairs in the modified savings matrix are sorted in descending order. Then, the steps of the classical CW savings algorithm are applied by considering the modified savings matrix. Solutions of the classical CW savings algorithm and the modified CW savings algorithm are shown in Table 11.

Table 11 Results of the numerical example

When the classical and modified CW savings algorithms are compared, it is seen that the modified CW savings algorithm created a six-unit longer route plan. This is because the proposed modified CW savings algorithm does not only consider the distance criterion as in the classical CW savings algorithm. The proposed algorithm combines the routes, taking into account all six decision criteria.

Experimental results

This section presents the numerical experiment of the proposed method. The empirical performance of the proposed method is evaluated on a set of ten benchmark problem instances available in the literature. Augerat et al. (1995) suggested three datasets (A, B, and P). For the instances in dataset A, both customer locations and demands are randomly generated. In dataset B, the customer locations are clustered. Dataset P is a modified version of other instances. The proposed method is implemented as a Java application. Calculations of the instance P-n16-k8 (P: Set code, n: number of the node including a depot, k: number of vehicles) are detailed below. Note that there is no restriction on the number of vehicles used in the proposed model. Although the number of vehicles is determined in the instances, it is not considered in the solution. However, it is aimed to reach all nodes with the least number of the vehicle fleet. Location coordinates and demands for P-n16-k8 are given in Table 12. Load capacity of vehicles is 35 units.

Table 12 Location coordinates and demands for instance P-n16-k8

In the first step of the application, the location coordinates and demands of the customers (disaster victims) are entered into the system. Similarly, the capacity of the vehicles in the fleet is also entered. The distances between nodes and the distances between nodes and depot are calculated using Eq. (18).

$$ {\text{The Euclidean distance }}\left( {d_{i,j} } \right){ } = \sqrt {\left( {x_{i} - x_{j} } \right)^{2} + \left( {y_{i} - y_{j} } \right)^{2} } $$

(18)

where ($x_{i}$, $y_{i}$) and ($x_{j}$, $y_{j}$) are the geographical locations of point i and j.

Also, the classical CW savings matrix is calculated by using Eq. (16). The importance coefficients for each location pairs that can be combined without exceeding the capacity constraint are determined by using the IT2F TOPSIS method. If importance coefficients assigned as 1, the model becomes the classical CW savings algorithm. The importance coefficients determined for P-n16-k8 are shown in Table 13. Note that the location pairs in Table 13 are only locations that can be combined under the capacity constraint.

Table 13 The importance coefficients for instance P-n16-k8

After the importance coefficients are entered into the system, the modified savings matrix is created by using Eq. (17). The modified savings matrix of the P-n16-k8 instance is given in Table 14.

Table 14 Modified savings matrix of the P-n16-k8

For instance, the "X" mark is placed for the savings to be obtained by combining the locations numbered 3 and 2 (Table 14). Because the total demand amount of locations 3 and 2 exceeds the load capacity (19 + 30 = 49 > 35). However, when nodes 2 and 4 were examined, it was determined that they did not exceed the load capacity (19 + 16 = 35). The distances between depot (0) and node 2, depot (0) and node 4, nodes 2 and 4 are calculated by Eq. (18) as follows.

$$ {\text{The Euclidean distance }}\left( {{\text{d}}_{0,2} } \right){ } = \sqrt {\left( {30 - 37} \right)^{2} + \left( {40 - 52} \right)^{2} } = {13}.{892} $$

$$ {\text{The Euclidean distance }}\left( {{\text{d}}_{0,4} } \right){ } = \sqrt {\left( {30 - 52} \right)^{2} + \left( {40 - 64} \right)^{2} } = {32}.{557} $$

$$ {\text{The Euclidean distance }}\left( {{\text{d}}_{2,4} } \right){ } = \sqrt {\left( {37 - 52} \right)^{2} + \left( {52 - 64} \right)^{2} } = {19}.{2}0{9} $$

Therefore, S₂₄ is determined by using Eq. (16) as ${\text{S}}_{24} = C_{i0} + C_{0j} - C_{ij} = 13.892 + 32.557 - 19.209 = 27.24.$ The importance coefficient of combining nodes 2 and 4 is determined as 0.011 in Table 13. The following multiplication is performed as required by Eq. (17) and the modified saving value of nodes 2 and 4 ($S_{24}^{*}$) is calculated as $S_{24}^{*} = 27.24 \times 0.011 = 0.299$. These calculations are performed for all node pairs and Table 14 is created. Finally, the results of the classical and modified CW savings algorithm are given in Table 15.

Table 15 Results of the P-n16-k8

As shown in Table 15, the modified CW savings algorithm developed a five-unit longer route solution than the classical CW savings algorithm. The reason is that the proposed model focuses not only on realizing the shortest distance routes but also on the importance coefficients of the routes to be combined. Computational results between the modified CW and the classical CW for ten benchmark problem instances are given in Table 16.

Table 16 Computational results between the modified CW and the classical CW

In Table 16, ten different samples with nodes ranging from 16 to 38 are compared. Changing the importance coefficients also changes the priorities in the savings matrix. Therefore, the total route value obtained from the modified CW savings algorithm can be longer than from the classical CW savings algorithm. As shown in Table 16, for the A-n32-k5 sample, the 843-unit distance is obtained with the classical CW savings algorithm. In comparison, the 912-unit distance is obtained with the proposed method. Similarly, the proposed method produced slightly longer distance solutions than the classic CW savings algorithm for other samples. However, a shorter distance is obtained in the A-n34-k5 sample. This is an accidental situation, and the primary purpose is to create a safer route rather than a shorter solution. Of course, determining the shortest route is a fundamental goal. However, the shortest route will not always be the best solution according to the physical condition of the route. An increase in the length of the road means the use of a safer route. The proposed model also considers other criteria while determining the shortest path. There is no limitation on the number and type of criteria in the proposed model. Different evaluation criteria or alternatives can be added. Thus, this model can be adapted to a new problem. For instance, it can be applied to solve vehicle routing problems at all levels of supply chain management in the manufacturing sector. This is one of the advantages of the proposed model.

Discussion and conclusion

The geographical location, intensity, and timing of natural disasters are usually unpredictable. Therefore, effective disaster management is of great importance to minimize losses and damage during the delivery of post-disaster aid to the victims. Planning with a calm and rational approach becomes difficult during disasters. The complexity created by the crisis makes it difficult to make the correct decisions in a short time. Therefore, a method that will support aid organizations in delivering aid to disaster victims will be helpful. In this study, a new approach is proposed to solve the capacitated VRP based on modifying the CW savings algorithm. The proposed method involves evaluating the distance criteria and the different criteria caused by the current problem simultaneously. The proposed method is illustrated with a numerical example. The objective function of the proposed method is not focused only on the shortest distance. The aim of the proposed method is to determine the shortest distance under the specified decision criteria.

The classical CW savings algorithm is preferred in the proposed method due to its simple and fast solution development. The capability and limitations of the proposed method are limited by the capability of the underlying VRP solution algorithm. In future studies, this integration can also be realized with savings-based meta-heuristics, which guide classical heuristics to avoid local optimality. Improving the existing algorithm with meta-heuristic approaches that can evaluate different situations such as stochastic demands, asymmetric distances, and travel time constraints may contribute to an effective solution for the routing problem, which will be considered as a future study. Finally, different MCDM techniques can be implemented instead of the TOPSIS method in determining importance coefficients, and the effect of the techniques on route priorities can be examine.