A compact transformation of arc routing problems into node routing problems

Abstract

We describe a compact method to transform arc routing problem instances into node routing problem instances. Any node routing problem instance thus created must be solved by a branch-and-price process, such as the one described in this paper. The purpose is to make the number of nodes in the resulting transformed graphs greater by only one unit than the number $r$ of required arcs (arcs having demand) in the original graph, that is, $r+1$ nodes. This low increase in the number of nodes represents an improvement compared to the methods previously presented by Pearn, Assad and Golden ($3r+1$ nodes) and by Longo, Poggi de Aragão and Uchoa and also by Baldacci and Maniezzo ($2r+1$ nodes). Using an adapted version of an existing branch-cut-and-price algorithm for a capacitated node routing problem on the transformed graph results in an effective approach for a capacitated arc routing problem. Computational experiments using this approach produced useful lower bounds in reasonable computational time for many challenging numerical instances from the literature. Additionally, some such previously open instances were solved to optimality for the first time.

1 Introduction

Classical vehicle routing is concerned with the identification of a set of routes to be carried out by a fleet of vehicles in order to serve a given set of customers. The routes are valid circuits over an appropriate road network that start at a pre-defined depot, serve customers and return to the depot. Each route is carried out by a single vehicle such that all of the requirements of the customers it serves are fulfilled and the operational constraints on the vehicle are satisfied. The aim is to identify a set of such routes that satisfy all customers, with the lowest global transportation cost.

There are two main classes of vehicle routing problems, depending upon where in the road network the customers are located. In the Node Routing Problem, the customers are located at the connection points of the network—the network nodes. In the Arc Routing Problem, the customers are located on a full stretch of a road or street of the network—the network arcs.

The classical node routing problem was first introduced by Dantzig and Ramser (1959) for the delivery of fuel to gasoline stations. It involves a known quantity of a single commodity to be delivered by a single vehicle to each customer that is located at an individual node of the network. All the delivery routes begin and end at a depot that is located at a unique network node. The vehicles have known capacities to carry the commodity. Each arc of the network has a known transportation cost. These arc costs are summed to calculate the cost of each closed tour, a depot-to-depot connected sequence of nodes and arcs of the network. Each tour is performed by one vehicle and the aim is to identify a collection of closed tours of minimal total cost that satisfy all customer demands and the capacity constraint of each vehicle. The node routing problem is commonly applied to vehicle scheduling for activities such as: the collection or delivery of goods and the routing of salespeople or maintenance units.

The classical arc routing problem was first introduced by Golden and Wong (1981). It is similar to the node routing problem discussed earlier, with the main difference being that customer demand is now satisfied on the arcs of the network, rather than at its nodes. Once again, a fleet of vehicles each of limited capacity is based at a single depot node. There is a subset of the arcs of the network that have a demand in the form of a task (in common units) that must be completed by a single vehicle during one traversal of the arc. Such arcs are termed required. Each route is a closed walk, a depot-to-depot connected sequence of arcs. The arc routing problem involves identifying a set of routes of minimal total cost. Any required arc can be traversed more than once but serving takes place during exactly one traversal of the arc. Any other traversals of the arc do not involve serving of the arc but still incur the arc cost and are termed “deadheading”. The total demand of all required arcs on each route cannot exceed the capacity of the vehicle that traverses the route. The arc routing problem is commonly applied to vehicle scheduling activities such as: snow removal, street cleaning, municipal solid waste removal and the distribution of salt on roads in winter.

Despite these similarities, the arc routing problem and the node routing problem have been treated differently over the years. There has been a great effort to study node routing problems and this has contributed to a significant development of techniques for solving them. This situation has motivated the construction of arc-to-node graph transformations, to take advantage of the efficiency and robustness of existing node routing problem solution techniques in order to resolve specific arc routing problems. The goal of an arc-to-node graph transformation is to turn a graph that models an arc routing problem instance into a graph that models a node routing problem instance. Previously reported transformations are based on producing a node routing problem instance that is equivalent to the original arc routing problem instance. That is, any optimal solution to a transformed node routing problem instance corresponds to an optimal solution to the original arc routing problem instance.

The node routing problem instance resulting from the arc-to-node transformation of Pearn et al. (1987) contains $3r + 1$ nodes, where $r$ is the total number of required arcs in the original arc routing graph, while the transformations of Longo et al. (2004, 2006) and of Baldacci and Maniezzo (2004, 2006) result in a node routing instance with $2r + 1$ nodes. The basis of the Longo et al. and of the Baldacci and Maniezzo transformations is the elimination of one of every three nodes generated by the Pearn et al. transformation. Since this node was created by Pearn et al. with a specific, but redundant goal, both Longo et al. and also Baldacci and Maniezzo showed that it can be eliminated because the same objective can be achieved by other means. The present article proposes a transformation that eliminates two of every three nodes generated by the Pearn et al. transformation. In this case, the resulting node routing problem instance contains only $r + 1$ nodes. However, it must be said that any node routing problem instance thus constructed cannot be solved by any ordinary node routing algorithm. It is necessary to alter such algorithms to take into account the specific details of the node routing instances generated by the proposed transformation. One possibility is to adapt an existing node routing branch-and-price process, as explained in detail in Sect. 5. The transformations just introduced are described in the next section.

2 Arc routing to node routing graph transformations

The arc routing problem is here modeled as an undirected graph $G = (V, E)$, where $V = \left\{ 0, 1, \ldots , n \right\}$ is the set of nodes. The depot is represented by node 0, the customers by the other nodes in $V$ and $E$ is the set of edges. See Foulds (1991) for the necessary graph theory notation and terminology. Each undirected edge $\{i, j\} \in E$ has associated with it a real-valued, symmetric transportation cost $c(i, j)> 0$ that represents the cost of any vehicle traveling along $\{i,j\}$ in either direction. The set of edges in $E$ that represent actual customers, each with a positive demand $d(i, j)$ (the required edges) is denoted by $R\subseteq E$. Let $r=|R|$. Each required edge must be served by exactly one walk in $G$.

The node routing problem that is created by any of the transformations described later is modelled as an undirected graph $H=(N,A)$, where $N = \{0, 1, \ldots , m \}$ is the set of nodes and $A$ is the set of edges. The depot is represented by node 0 and each customer (a required edge in $R$) is associated with a unique subset of nodes in $N$. The customer demand $d(i,j)$ for each edge $\{i,j\}\in R$ is distributed among its associated subset of nodes in $N$ to create node demands in $H$. Each such demand must be served by exactly one tour in $H$. How the travel costs of the edges in $A$ are derived from the edge and path costs in $G$ are described in the following subsections. The objective of both the arc routing and the node routing problem is to identify a collection of feasible routes of minimal total cost.

2.1 The Pearn et al. (1987) transformation

In the arc-to-node transformation proposed by Pearn et al. (1987) each required edge $\{i, j\} \in E$ is represented by three new nodes in $N$: two lateral and one central ($s_{ij}, m_{ij}, s_{ji}$), over which $d(i, j)$ is distributed. The purpose of the central node $m_{ij}$ is to ensure that the shortest path between the two lateral nodes $s_{ij}$ and $s_{ji}$ is always the three nodes in the sequence $\langle s_{ij}, m_{ij}, s_{ji} \rangle$ or in the sequence $\langle s_{ji}, m_{ij}, s_{ij} \rangle$. The complete undirected graph $H = (N, A)$ for the node routing problem created by the transformation is defined as:

$$\begin{aligned} N = \left\{ 0\right\} \cup \left\{ s_{ij}, m_{ij}, s_{ji}\> |\>\{i,j\} \in R\right\} . \end{aligned}$$

(1)

The depot is represented by node $0$ and the customers (the required edges in $R$) by the other nodes in $N$.

The costs of the edges of $H$ are defined by Eqs. (2)–(4) below, where $dist(i, j)$ represents the cost of the shortest path between nodes $i$ and $j$ in the original graph $G$:

$$\begin{aligned} w(s_{ij},s_{k\ell })&= {\left\{ \begin{array}{ll} \frac{1}{4}(c(i,j)+c(k,\ell ))+ dist(i,k), &{} \text {if } \{i,j\} \ne \{k,\ell \}, \\ 0, &{} \text {if } \{i,j\} = \{k,\ell \}; \end{array}\right. } \end{aligned}$$

(2)

$$\begin{aligned} w(0,s_{ij})&= \begin{array}{l} \frac{1}{4}c(i,j) + dist(i,0); \end{array} \end{aligned}$$

(3)

$$\begin{aligned} w(m_{ij},v)&= {\left\{ \begin{array}{ll} \frac{1}{4}c(i,j), &{} \text {if } v = s_{ij} \text { or } v = s_{ji}, \\ \infty , &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(4)

Each demand $d(i,j) > 0$, of each edge $\{i,j\}\in E$ of the arc routing instance in $G$ must be distributed over the equivalent new nodes: $s_{ij}, m_{ij}$ and $s_{ji}$ in $H$, so that its sum is equal to the original demand. That is, it is required that:

$$\begin{aligned} f\left( s_{ij}\right) + f\left( s_{ji}\right) + f\left( m_{ij}\right) = d(i,j),\quad \forall \>\{i,j\}\in A. \end{aligned}$$

(5)

2.2 The Longo et al. and Baldacci and Maniezzo transformations

In the transformation described in Sect. 2.1, the only purpose of the central node $m_{ij}$, is to ensure that a route that passes through any lateral node also passes in sequence through the associated central node and then through the other associated lateral node. Both Longo et al. (2004, 2006) and Baldacci and Maniezzo (2004, 2006) proposed removing the central node, but still ensuring that the lateral nodes are traversed sequentially. Thus, the new node routing graph $H$ has only $2r + 1$ nodes.The node set is defined as:

$$\begin{aligned} N = \left\{ 0\right\} \cup \left\{ s_{ij}, s_{ji}\> |\>\{i,j\} \in R\right\} \!. \end{aligned}$$

(6)

The costs between a lateral node and the depot (node $0$) and between two lateral nodes are defined, respectively, by Eqs. (7) and (8) below. The expression $dist(i, j)$ again represents the cost of the shortest path between the nodes $i$ and $j$ in the original graph $G$:

$$\begin{aligned} w(0,s_{ij})&= dist(0,i); \end{aligned}$$

(7)

$$\begin{aligned} w(s_{ij},s_{k\ell })&= {\left\{ \begin{array}{ll} 0, &{} \text {if } \{i,j\} = \{k,\ell \} ,\\ c(i,j), &{} \text {if } \{i,j\} = \{\ell ,k\} ,\\ dist(i,k), &{} \text {if } \{i,j\} \ne \{k,\ell \} \text { and } \{i,j\} \ne \{\ell ,k\}. \end{array}\right. } \end{aligned}$$

(8)

The demand $d(i,j)$ of each edge $\{i,j\}\in R$ in $G$ is distributed between the equivalent new nodes $s_{ij}$ and $s_{ji}$ in $H$, so that the sum of the constituent parts equals $d(i, j)$:

$$\begin{aligned} f\left( s_{ij}\right) + f\left( s_{ji}\right) = d(i,j),\quad \forall \>\{i,j\}\in A. \end{aligned}$$

(9)

The proposed transformation that is the main subject of the present article is described in the next section.

2.3 The proposed transformation

For most practical instances arising in industry, representing each required edge of an arc routing problem graph by even only two nodes in the corresponding node routing problem graph creates a graph with an excessive number of nodes compared with the original arc routing graph. The proposed transformation described in this article represents each required edge by a single node, thus significantly reducing the number of nodes in the transformed node routing problem graph.

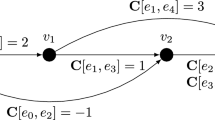
This proposed transformation is illustrated in Fig. 1. Each required edge of the arc routing graph $G$, is represented by a node in the node routing graph $H$. The proposed transformation generates a graph $H$, that has a number of nodes equal to the number of required edges in the arc routing graph $G$, plus one (the depot).

Fig. 1

Transforming an edge in $G$ to a node in $H$ and allocating the edge demand to the new node

The node set of the graph $H$ is defined as:

$$\begin{aligned} N = \left\{ 0\right\} \cup \left\{ m_{ij}\>|\>\{i,j\} \in R\text { and } i < j\right\} . \end{aligned}$$

(10)

$H$ is defined as the complete graph on $N$. Each node $m_{ij}\in N$ is defined only when $i < j$. The demand associated with each required edge of $R$ is assigned to the corresponding node in $N$ as follows:

$$\begin{aligned} f(m_ {ij}) = d (i, j),\quad \forall \>\{i,j\}\in R. \end{aligned}$$

(11)

3 Concepts and notation for problem equivalence

Consider a closed walk $W'$ say, being a route that is part of a feasible solution to an arc routing problem in a given graph $G$. (The definition of “a feasible solution” is provided in Sect. 3.2.) Let $R' \subseteq R$ denote the set of required edges that are served in $W'$, where $r' = |R'| \ge 1$. The walk $W'$ can be represented unambiguously by specifying: (i) the order in which the edges of $R'$ are visited, (ii) the direction in which each is traversed and (iii) the subwalks that connect them. We shall index the nodes incident with the required edges as they are served in $W'$ as $v_1, v_2,\ldots , v_{2r'}$; in the order that they are encountered during a traversal of $W'$. Thus, $R' = \{\{v_{2p - 1}, v_{2p}\}\>|\> p = 1, 2,\ldots ,r';\> v_{2p - 1}, v_{2p} \in V\}$ is the set of $r'$ required edges served by $W'$. During a traversal of $W'$, the edges in $R'$ are served in the order: $\{v_1, v_2\}, \{v_3, v_4\},\ldots ,\{v_{2r' - 1}, v_{2r'}\}$; and when served, each of these edges is traversed in the direction: $(v_{2p - 1}, v_{2p}), p = 1, 2,\ldots ,r'$. Furthermore, let $W(i, j)$ be the subwalk of $W'$ in $G$ from node $i$ to node $j$, where $i, j \in V$. Thus, $W'=\{W(0, v_1)\}\cup \{W(v_p, v_{p+1})\>|\> p = 1, 2,\ldots ,r'\}\cup \{W(v_{2r'}, 0)\}$.

In general, as depicted in Fig. 2a, $W'$ can be expressed unambiguously as:

$$\begin{aligned} W'&= \langle W(0, v_1), \{v_1, v_2\}, W(v_2, v_3),\ldots ,\nonumber \\&\quad \{v_{2p-1}, v_{2p}\}, W(v_{2p}, v_{2p+1}), \{v_{2p+1}, v_{2p+2}\},\ldots ,\nonumber \\&\quad \qquad W(v_{2r'-2}, v_{2r'-1}), \{v_{2r'-1}, v_{2r'}\}, W(v_{2r'}, 0)\rangle . \end{aligned}$$

(12)

A route in $H$ that serves the same set of customers as $W'$ can be expressed as:

$$\begin{aligned} T' = \langle 0, m_{u_1u_2}, m_{u_3u_4},\ldots ,m_{u_{2p-1}u_{2p}},m_{u_{2p+1}u_{2p+2}},\ldots ,m_{u_{2r'-1}u_{2r'}}, 0\rangle , \end{aligned}$$

(13)

where

$$\begin{aligned} \{u_{2p-1},u_{2p}\} = \{v_{2p-1},v_{2p}\},\quad p = 1, 2,\ldots ,2r'. \end{aligned}$$

(14)

Fig. 2

a A general route in $G$. b The degenerate cases where deadheading is absent in a route in $G$

3.1 Degeneracy in routes in $G$

Due to the structure of $G$ and the possibility of deadheading, there may a repetition of nodes or even of edges in $W'$. As observed earlier, even in these cases each required edge is served exactly once and any other traversals of it constitute deadheading with its traversal cost still incurred each time. We now cover the degenerate cases for (12) where deadheading does not occur in one or more of the subwalks of $W'$. Figure 2b depicts the special case where each subwalk $W'(i,j)$ degenerates to $W'(i,i)$ (which is also $W'(j,j)$) with distance zero:

• 1. If $v_1 = 0$ (the depot), then there is no deadheading immediately after leaving node $0$ and subwalk $W(0, v_1)$ degenerates to $W(0, 0)$ with distance zero and is removed from $W'$. Edge $\{v_1, v_2\}$ becomes the served edge $\{0, v_2\}$ and the initial part of $W'$ becomes $\langle 0, \{0, v_2\}, v_2,\ldots \rangle$.

• 2. If $v_{2p} = v_{2p+1}$ for any $p = 1, 2,\ldots ,r'-1$; then there is no deadheading between edges $\{v_{2p-1}, v_{2p}\}$ and $\{v_{2p+1}, v_{2p+2}\}$ and they are served in immediate succession. Subwalk $W(v_{2p}, v_{2p+1})$ degenerates to subwalk $W(v_{2p}, v_{2p})$ with distance zero and is removed from $W'$. The corresponding intermediate part of $W'$ becomes

  $$\begin{aligned} \langle \ldots ,v_{2p-1}, \{v_{2p-1}, v_{2p}\}, v_{2p}, \{v_{2p}, v_{2p+2}\}, v_{2p+2},\ldots \rangle . \end{aligned}$$

• 3. If $v_{2r'} = 0$, then there is no deadheading immediately before arriving at node $0$ and subwalk $W(2r', 0)$ degenerates to $W(0, 0)$ with distance zero and is removed from $W'$. Edge $\{v_{2r'-1}, v_{2r'}\}$ becomes the served edge $\{v_{2r'-1}, 0\}$ and the final part of $W'$ becomes $\langle \ldots ,v_{2r'-1}, \{0, v_{2r'-1}\}, 0\rangle$.

In each of these cases, the corresponding inter-node distance is zero and two successive nodes in (12) are the same actual node in $G$. However, without loss of generality and for the sake of simplicity, from now on we shall retain all the original vertices in (12), as shown in Fig. 2a, even if an absence of deadheading implies degeneracy. Case 3 above is illustrated in the numerical examples in Sect. 4.

3.2 Route feasibility in $G$

Consider an arc routing problem instance $\textit{AR}(G)$ say, for a given graph $G$. Suppose $S_{AR(G)}$ is a solution for ${\textit{AR}}(G)$. Let the set of closed walks, each containing $0$ (the depot node), that constitutes $S_{AR(G)}$ be denoted by $\{W_q\>|\>q = 1, 2,\ldots ,Q\}$, for some $Q$. Furthermore, for $q = 1, 2,\ldots ,Q$; let $R_q \subseteq R$ denote the set of required edges that are served in $W_q$. Then $S_{AR(G)}$ is a feasible solution for ${\textit{AR}}(G)$ if, and only if, (15)–(17) hold:

(15)

(16)

Equation (15) states that each walk in $S_{AR(G)}$ serves at least one required edge and (16) states that the set of required edges is partitioned and each required edge is served on exactly one walk. Additionally, the sum of demands associated with the subset $R_q$ of required edges may be limited to a given bound $C_q$ (for example, the capacity of the vehicle that serves $R_q$):

$$\begin{aligned}&\sum _{\{i, j\}\in R_q} d(i,j) \le C_q,\quad \forall \>q = 1, 2,\ldots ,Q. \end{aligned}$$

(17)

3.3 Dividing edge costs in $G$

In order to prepare for calculating edge costs in $H$, consider the four possible ways to serve required edges $\{i, j\}$ and then $\{k, \ell \}$ say, in $G$ in immediate succession with the shortest possible cost, as shown in Fig.  3a–d. The dashed circles and lines represent nodes and edges of $G$, respectively. The solid disks and undirected lines represent nodes and edges of $H$, respectively. The four ways are:

• (a) traverse edge $\{i, j\}$ in the direction $(i, j)$, follow a shortest path in $G$ connecting node $j$ to node $k$ and traverse edge $\{k, \ell \}$ in the direction $(k, \ell )$ (Fig. 3a); or

• (b) traverse edge $\{i, j\}$ in the direction $(i, j)$, follow a shortest path in $G$ connecting node $j$ to node $\ell$ and traverse edge $\{k, \ell \}$ in the direction $(\ell ,k)$ (Fig. 3b); or

• (c) traverse edge $\{i, j\}$ in the direction $(j, i)$, follow a shortest path in $G$ connecting node $i$ to node $k$ and traverse edge $\{k, \ell \}$ in the direction $(k, \ell )$ (Fig. 3c); or

• (d) traverse edge $\{i, j\}$ in the direction $(j, i)$, follow a shortest path in $G$ connecting node $i$ to node $\ell$ and traverse edge $\{k, \ell \}$ in the direction $(\ell ,k)$ (Fig. 3d).

The cost of (a) is $c(i, j) + dist(j, k) + c(k, \ell )$, where $dist(j, k)$ is the minimum cost of any subwalk between nodes $j$ and $k$ in $G$. The costs of (b), (c) and (d) are: $c(i, j) + dist(j, \ell ) + c(k, \ell ), c(i, j) + dist(i, k) + c(k, \ell )$ and $c(i, j) + dist(i, \ell ) + c(k, \ell )$, respectively. (Here, the function $c$ and hence the function $dist$ are assumed to be symmetric.) The equivalent subtours in graph $H$ serve node $m_{ij}$ and then serve node $m_{k\ell }$ in immediate succession. It is important to note that in $H$ (a node routing problem) a subtour that serves node $m_{ij}$ must be equivalent) to a subwalk in $G$ (an arc routing problem) that serves the required edge $\{i, j\}$. Thus, to ensure equivalence between the two problems, the cost $c(i, j)$ of a required edge $\{i, j\}$ in $R$ must be incurred by any route that serves node $m_{ij} \in N$. In other words, the cost $c(i, j)$ must be divided between the edge that arrives at node $m_{ij}$ and the edge that leaves node $m_{ij}$ in $H$. For example, if a tour reaches node $m_{ij}$ from node $m_{gh}$ say, and continues to node $m_{k\ell }$ say, then $c(i, j)$ must be divided between edges $\{m_{gh}, m_{ij}\}$ and $\{m_{ij}, m_{k\ell }\} \in A$. In this case, $c(i, j)$ will be incurred exactly when the route includes the edges $\{m_{gh}, m_{ij}\}$ and $\{m_{ij}, m_{k\ell }\}$. As will be seen later, without loss of generality, we adopt the convention that half of $c(i, j)$ is incurred when $\{m_{gh}, m_{ij}\}$ is traversed and the other half of $c(i, j)$ is incurred when $\{m_{ij}, m_{k\ell }\}$ is traversed.

Fig. 3

The four possible ways to traverse two required edges in $G$ in sequence

We wish to avoid the situation where a separate version of $H$ must be created with edge weights corresponding to each of the orientations illustrated in Fig. 3. In this case a node routing problem would have to be solved for each orientation and the optimal solution to the original arc routing problem could be deduced from the node routing problems in $H$ among those that are minimal. The major problem with this approach is that an exponential number of node routing problems has to be solved. In Sect. 5 we explain how a branch-cut-and-price algorithm achieves optimality for the transformed node routing problem by identifying the most favourable partition of $R$ (corresponding to routes) and simultaneously selects only the necessary combination of required edge directions, on an as-needed basis.

3.4 Edge costs in $H$

To prepare for the calculation of edge costs in $H$, consider two edges $\{i, j\}$ and $\{k, \ell \} \in R$ say, as shown in Fig. 3a–d. We now consider the direction of travel of a required edge $\{i, j\} \in R$ say, served in a route $W'$ of $G$ and the directions of travel of edges in the equivalent route in $H$ that are incident with the corresponding node $m_{ij} \in N$. In order to specify the direction of travel of such edges in $H$ we introduce pairs of binary variables $(a_{ij}, a_{k\ell })$, defined for all edges $\{m_{ij}, m_{k\ell }\} \in A$, only for $i< j$ and $k< \ell$, as:

• 1. $(a_{ij}, a_{k\ell }) = (0, 0)$, if $W'$ departs $\{i, j\}$ by node $i$ and arrives at $\{k, \ell \}$ at node $k$ (Fig. 3c),

• 2. $(a_{ij}, a_{k\ell }) = (0, 1)$, if $W'$ departs $\{i, j\}$ by node $i$ and arrives at $\{k, \ell \}$ at node $\ell$ (Fig. 3d),

• 3. $(a_{ij}, a_{k\ell }) = (1, 0)$, if $W'$ departs $\{i, j\}$ by node $j$ and arrives at $\{k, \ell \}$ at node $k$ (Fig. 3a), and

• 4. $(a_{ij}, a_{k\ell }) = (1, 1)$, if $W'$ departs $\{i, j\}$ by node $j$ and arrives at $\{k, \ell \}$ at node $\ell$ (Fig. 3b).

For the sake of consistency in 1–4 just defined, the following relation must hold:

$$\begin{aligned} \text {If }(a_{ij},a_{k\ell })=(0,0)\text { then }(a_{ij},a_{gh})=(0,\delta ),\>\forall \>\{g,h\}\in R\setminus \{\{i,j\},\{k,\ell \}\}, \end{aligned}$$

(18)

where $\delta \in \{0,1\}$.

Definitions 1–4 and relation (18) taken together ensure that the equivalent route in $H$ is consistent and are based on the facts that if $a_{ij}=0 (1)$ the travel direction of edge $\{i,j\}$ is $j$ to $i$ ($i$ to $j$), where $i<j$.

The notation $w(m^{a_{ij}}_{ij}, m^{a_{k\ell }}_{k\ell })$ denotes the cost associated with $\{m_{ij}, m_{k\ell }\}\in A$ when its node departure and arrival regime is defined as $(a_{ij}, a_{k\ell })$. With reference to Fig. 4a, $w(m^{a_{ij}}_{ij}, m^{a_{k\ell }}_{k\ell })$ can be calculated as the sum of:

• 1. $c(i, j)/2$, i.e., half of the cost of the edge $\{i, j\}$ (the departing edge),

• 2. the cost of the shortest path in $G$ from the departing node of $\{i, j\}$ (which is $(1- a_{ij}){\cdot }i + (a_{ij}){\cdot }j)$ to the arriving node of $\{k, \ell \}$ (which is $(1- a_{k\ell }){\cdot }k + (a_{k\ell }){\cdot }\ell )$ and

• 3. $c(k, \ell )/2$, i.e., half of the cost of the edge $\{k, \ell \}$ (the arriving edge).

The notation $w(0,m_{ij}^{a_{ij}})$ denotes the cost associated with $\{0,m_{ij}\}\in A$, when its arrival node is specified by $a_{ij}$. With reference to Fig. 4b, $w(0,m_{ij}^{a_{ij}})$ can be calculated as the sum of:

• 1. $c(i, j)/2$, i.e., half of the cost of the edge $\{i, j\}$ in $G$ and

• 2. the cost of the shortest path in $G$ from the arrival node of $\{i, j\}$, which is $(1- a_{ij}){\cdot }i + (a_{ij}){\cdot }j$.

The cost $w(m_{ij}^{a_{ij}},0)$ can be calculated analogously.

Fig. 4

a An edge connecting two customer nodes; b An edge connecting the depot to a customer node

With this convention, Eqs. (19)–(22) determine $w(m^{a_{ij}}_{ij}, m^{a_{k\ell }}_{k\ell })$ for all possible $(a_{ij}, a_{k\ell })$ pairs. Equations (23) and (24) determine $w(0, m^{a_{ij}}_{ij})$, the cost of traversing an edge in $H$ that connects node $0$ to any other node $m_{ij}\in N$. As the cost functions $c$ and $dist$ are symmetric, $w$ is also symmetric.

$$\begin{aligned} w(m^0_{ij}, m^0_{k\ell }) = w(m^0_{k\ell }, m^0_{ij})&= {c(i, j)}/{2} + dist(i, k) + {c(k, \ell )}/{2},\quad \forall \> m_{ij}, m_{k\ell } \in N;\end{aligned}$$

(19)

$$\begin{aligned} w(m^0_{ij}, m^1_{k\ell }) = w(m^1_{k\ell }, m^0_{ij})&= {c(i, j)}/{2} + dist(i, \ell ) + {c(k, \ell )}/{2},\quad \forall \> m_{ij}, m_{k\ell } \in N;\end{aligned}$$

(20)

$$\begin{aligned} w(m^1_{ij}, m^0_{k\ell }) = w(m^0_{k\ell }, m^1_{ij})&= {c(i, j)}/{2} + dist(j, k) + {c(k, \ell )}/{2},\quad \forall \> m_{ij}, m_{k\ell } \in N;\end{aligned}$$

(21)

$$\begin{aligned} w(m^1_{ij}, m^1_{k\ell }) = w(m^1_{k\ell }, m^1_{ij})&= {c(i, j)}/{2} + dist(j, \ell ) + {c(k, \ell )}/{2},\quad \forall \> m_{ij}, m_{k\ell } \in N;\end{aligned}$$

(22)

$$\begin{aligned} w(0,m^0_{ij}) = w(m^0_{ij},0)&= {c(i, j)}/{2} + dist(0, i),\quad \forall \> m_{ij} \in N;\end{aligned}$$

(23)

$$\begin{aligned} w(0,m^1_{ij}) = w(m^1_{ij},0)&= {c(i, j)}/{2} + dist(0, j),\quad \forall \> m_{ij} \in N. \end{aligned}$$

(24)

Equations (19)–(22) can be generalized as:

$$\begin{aligned} w(m^{a_{ij}}_{ij}, m^{a_{k\ell }}_{k\ell })&= w(m^{a_{k\ell }}_{k\ell }, m^{a_{ij}}_{ij}) = {c(i, j)}/{2} +\,dist((1-a_{ij}){\cdot }i\nonumber \\&\quad +\, (a_{ij}){\cdot }j, (1-a_{k\ell }){\cdot }k + (a_{k\ell }){\cdot }\ell ) \nonumber \\&\quad + \,{c(k, \ell )}/{2},\quad \forall \>m_{ij}, m_{k\ell } \in N. \end{aligned}$$

(25)

Equations (23) and (24) can be generalized as:

$$\begin{aligned} w(0,m^{a_{ij}}_{ij}) = w(m^{a_{ij}}_{ij},0) = {c(i, j)}/{2} + dist(0,(1-a_{ij}){\cdot }i + (a_{ij}){\cdot }j),\quad \forall \>m_{ij} \in N. \end{aligned}$$

(26)

We now complete the preparation for demonstrating that the proposed transformation produces equivalent problems by making some final remarks. The edge costs in $H$ are dependent upon the $(a_{ij},a_{k\ell })$ pairs where $\{i,j\}, \{k,\ell \} \in R$. If the binary values $a_{ij}$ are assembled in some fixed order into a binary vector $\varvec{a}$ say, it is evident that every binary vector $\varvec{a} \in \{0,1\}^r$ gives rise to a specification of the edge costs in $H$, that is, to a numerical instance of a node routing problem in $H$. The implication of this is as follows. Suppose there is an arc routing problem $(G,R)$ with given graph $G$ and required edge set $R$, that is turned into a node routing problem on graph $H$ by the proposed transformation. Since $H$ is the fixed, complete graph with node set $\{m_{ij}\>|\>\{i,j\}\in R\text { and } i<j\}\cup \{0\}$ there is exactly one node routing problem numerical instance for each binary vector $\varvec{a} \in \{0,1\}^r$. We now use these facts to demonstrate problem equivalence.

4 Problem equivalence

We now demonstrate the equivalence of the original arc routing problem and any of the node routing problems that arise from it via the proposed transformation.

Lemma 1

Suppose that the proposed transformation is used to turn a given arc routing problem instance based on a graph $G$, into a node routing problem instance based on a graph $H$. For any feasible solution $S_{AR(G)}$ say, to the arc routing problem instance in $G$, there exists a binary vector $\varvec{a} \in \{0,1\}^r$ such that there is a feasible solution to the corresponding node routing problem in $H$ with cost no greater than the cost of $S_{AR(G)}$.

(A numerical example illustrating Lemma 1 is provided immediately after the following proof).

Proof

Consider an arc routing problem instance ${\textit{AR}}(G)$ say, for a given graph $G$. Suppose that $S_{AR(G)}$ is any feasible solution to ${\textit{AR}}(G)$. Let the set of routes of $S_{AR(G)}$ be denoted by $\{W_q\>|\>q = 1, 2,\ldots ,Q\}$, for some $Q \ge 1$. Furthermore, for $q = 1, 2,\ldots ,Q$; let $R_q\subset R$ denote the set of required edges that are served in $W_q$. Following the discussion leading up to Eq. (12), if $|R_q|= r_q \ge 1$ say, each route $W_q \in S_{AR(G)}$ can be represented as:

$$\begin{aligned} W_q&= \langle W_q(0, v_1), \{v_1, v_2\}, W_q(v_2, v_3), \{v_3,v_4\},\ldots ,\nonumber \\&\quad W_q(v_{2r_q -2}, v_{2r_q -1}), \{v_{2r_q -1}, v_{2r_q}\}, W_q(v_{2r_q}, 0)\rangle . \end{aligned}$$

(27)

Let $z_{W_q}$ be the cost of $W_q$ and $z(W_q(i, j))$ be the cost of the subwalk $W_q(i, j)$. Then

$$\begin{aligned} z_{W_q}&= z(W_q(0, v_1)) + c(v_1, v_2) + z(W_q(v_2, v_3)) + c(v_3, v_4) +\cdots \nonumber \\&\quad +\, z(W_q(v_{2r_q-2}, v_{2r_q-1})) + c(v_{2r_q-1}, v_{2r_q}) + z(W_q(v_{2r_q}, 0)). \end{aligned}$$

(28)

We show how a feasible solution to a node routing problem instance in $H$ can be constructed from $S_{AR(G)}$. By using the proposed transformation, let $H$ be the graph constructed from $G$ and $NR(H)$ be the node routing problem instance constructed from ${\textit{AR}}(G)$. A feasible solution to $NR(H)$, denoted by $S_{NR(H)}$, can be constructed from $S_{AR(G)}$ as follows. Let $\{T_q\>|\>q = 1, 2,\ldots ,Q\}$ denote the set of routes in $H$ that constitutes $S_{NR(H)}$. There is a one-to-one correspondence between the routes in $S_{NR(H)}$ and the routes in $S_{AR(G)}$ because, for $q = 1, 2,\ldots ,Q$; $T_q$ is associated with $W_q$. Each route $T_q \in S_{NR(H)}$ is constructed as follows. The node set of $T_q$ is $\{0\}\cup \{m_{ij}\>|\>\{i, j\}\in R_q\}$. $T_q$ is defined by assembling its nodes in the same order as their corresponding required edges are encountered during a traversal of $W_q$. As each node $m_{ij}\in NR(H)$ is defined only for $i < j$, we have to introduce another index $u$, for the internal nodes: $v_1, v_2,\ldots , v_{2r_q}$ of $W_q$ as follows:

$$\begin{aligned} u_{2p-1} = v_{2p-1} \quad \text { and } \quad u_{2p} = v_{2p}, \quad \text { if } \quad v_{2p-1} < v_{2p} \end{aligned}$$

(29)

and

$$\begin{aligned} u_{2p-1} = v_{2p} \quad \text { and } \quad u_{2p} = v_{2p-1}, \quad \text { if }\quad v_{2p-1} > v_{2p},\quad \text { for }p = 1, 2,\ldots ,r_q. \end{aligned}$$

(30)

Then $T_q$ is defined as:

$$\begin{aligned} T_q = \langle 0, m_{u_1u_2}, m_{u_3u_4},\ldots ,m_{u_{2r_q-1}u_{2r_q}}, 0\rangle . \end{aligned}$$

(31)

With reference to (15)–(17), as $S_{AR(G)}$ is feasible for ${\textit{AR}}(G)$, by substituting $f(m_{ij})$ for $d(i, j)$ in (17), it is clear that $S_{NR(H)}$ is feasible for $NR(H)$. Letting $SP(i, j)$ denote any shortest path from node $i$ to node $j$ in $G, T_q$ can be interpreted in $G$ as:

$$\begin{aligned} T_q&= \langle SP(0, v_1), \{v_1, v_2\}, SP(v_2, v_3), \{v_3,v_4\},\ldots ,\nonumber \\&\quad SP(v_{2r_q-2}, v_{2r_q -1}), \{v_{2r_q -1}, v_{2r_q}\}, SP(v_{2r_q}, 0)\rangle . \end{aligned}$$

(32)

The cost $z_{T_q}$ say, of $T_q$ can be calculated as:

$$\begin{aligned} z_{T_q} = w(0, m^{a_{u_1u_2}}_{u_1u_2}) + w(m^{a_{u_1u_2}}_{u_1u_2}, m^{a_{u_3u_4}}_{u_3u_4}) +\cdots + w(m^{a_{u_{2r_q-1}u_{2r_q}}}_{u_{2r_q-1}u_{2r_q}}, 0). \end{aligned}$$

(33)

From (27) it can be seen that in $W_q$, for $p = 1, 2,\ldots ,r_q$, required edge $\{v_{2p-1}, v_{2p}\}$ is arrived at by node $v_{2p-1}$ and departed from by node $v_{2p}$. This implies that the relevant edge costs for $T_q$ are of the form: $w(0, m^{a_{u_1u_2}}_{u_1u_2})$, $w(m^{a_{u_{2p-1}u_{2p}}}_{u_{2p-1}u_{2p}}, m^{a_{u_{2p+1}u_{2p+2}}}_{u_{2p+1}u_{2p+2}})$ for $p = 1, 2,\ldots ,r_q - 1$; and $w(m^{a_{u_{2r_q-1}u_{2r_q}}}_{u_{2r_q-1}u_{2r_q}}, 0)$, where

$$\begin{aligned} w(0, m^{a_{u_1u_2}}_{u_1u_2})&= {\left\{ \begin{array}{ll} w(0, m^0_{u_1u_2}),\quad \text { if }v_1 < v_2,\\ w(0, m^1_{u_1u_2}),\quad \text { if }v_1 > v_2; \end{array}\right. } \end{aligned}$$

(34)

$$\begin{aligned} w(m^{a_{u_{2p-1}u_{2p}}}_{u_{2p-1}u_{2p}}, m^{a_{u_{2p+1}u_{2p+2}}}_{u_{2p+1}u_{2p+2}})&= {\left\{ \begin{array}{ll} w(m^1_{u_{2p-1}u_{2p}}, m^0_{u_{2p+1}u_{2p+2}}),\quad \text { if }v_{2p-1} < v_{2p}\,\text { and }\,v_{2p+1} < v_{2p+2},\\ w(m^1_{u_{2p-1}u_{2p}}, m^1_{u_{2p+1}u_{2p+2}}),\quad \text { if }v_{2p-1} < v_{2p}\, \text { and } \,v_{2p+1} > v_{2p+2},\\ w(m^0_{u_{2p-1}u_{2p}}, m^0_{u_{2p+1}u_{2p+2}}),\quad \text { if }v_{2p-1} > v_{2p} \,\text { and } \,v_{2p+1} < v_{2p+2},\\ w(m^0_{u_{2p-1}u_{2p}}, m^1_{u_{2p+1}u_{2p+2}}),\quad \text { if }v_{2p-1} > v_{2p} \,\text { and } \,v_{2p+1} > v_{2p+2},\\ \end{array}\right. } \nonumber \\ \end{aligned}$$

(35)

for $p = 1, 2,\ldots ,r_q-1$;

$$\begin{aligned} w(m^{a_{u_{2r_q-1}u_{2r_q}}}_{u_{2r_q-1}u_{2r_q}}, 0) = {\left\{ \begin{array}{ll} w(m^1_{u_{2r_q-1}u_{2r_q}}, 0),\quad \text { if }v_{2r_q-1} < v_{2r_q},\\ w(m^0_{u_{2r_q-1}u_{2r_q}}, 0),\quad \text { if }v_{2r_q-1} > v_{2r_q}. \end{array}\right. } \end{aligned}$$

(36)

With the use of (25), (26) and (34)–(36); and some rearrangement we have:

$$\begin{aligned} z_{T_q}&= dist(0, v_1) + c(v_1, v_2) + dist(v_2, v_3) + c(v_3, v_4) +\cdots \nonumber \\&\quad +\, dist(v_{2r_q-2}, v_{2r_q-1}) + c(v_{2r_q-1}, v_{2r_q}) + dist(v_{2r_q}, 0). \end{aligned}$$

(37)

By definition,

$$\begin{aligned} dist(0, v_1)&\le z(W(0, v_1)),\end{aligned}$$

(38)

$$\begin{aligned} dist(v_{2p-1}, v_{2p})&\le z(W(v_{2p}, v_{2p})),\quad p = 1, 2,\ldots ,r_q;\end{aligned}$$

(39)

$$\begin{aligned} dist(v_{2r_q}, 0)&\le z(W(v_{2r_q}, 0)). \end{aligned}$$

(40)

By using (38)–(40) to compare (28) and (37), we have:

$$\begin{aligned} z_{T_q} \le z_{W_q}. \end{aligned}$$

(41)

The above process can be repeated for all walks $W_q \in S_{AR(G)}$. Let $z_{S_{AR(G)}} (z_{S_{NR(H)}})$ be the cost of $S_{AR(G)} (S_{NR(H)})$. Then, by definition:

$$\begin{aligned} z_{S_{AR(G)}} = \sum ^Q_{q=1} z_{W_q} \end{aligned}$$

(42)

and

$$\begin{aligned} z_{S_{NR(H)}} = \sum ^Q_{q=1} z_{T_q}. \end{aligned}$$

(43)

By using (41) to compare (42) and (43), we have the following result, which completes the proof of Lemma 1:

$$\begin{aligned} z_{S_{NR(H)}} \le z_{S_{AR(G)}}. \end{aligned}$$

(44)

$\square$

Numerical illustration of Lemma 1

To illustrate Lemma 1, consider the arc routing problem instance shown in Fig. 5a as graph $G$, where $R = \{\{0, 3\},\{1, 2\}, \{4, 5\}\}$ (with the required edges shown in bold) and the numbers on the edges represent edge costs. The proposed transformation has been used to turn this problem into the node routing problem instance, shown in Fig. 5b as graph $H$, where nodes: $m_{12}, m_{45}$ and $m_{03}$ must be served. Graph $G$ is shown in Fig. 5b in dotted form. It is assumed that all three customers can be served on a single route. The following walk $W_1$, is a feasible solution to the arc routing problem for the graph $G$:

$$\begin{aligned} W_1&= \langle [W(0, 1)], \{1, 2\}, [W(2, 4)], \{4, 5\}, [W(5, 3)], \{0, 3\}, W(0, 0)\rangle \\&= \langle [0, \{0, 1\}, 1], \{1, 2\}, [2, \{2, 3\}, 3, \{3, 4\}, 4], \{4, 5\}, [5, \{3, 5\}, 3], \{0, 3\}, [0]\rangle . \end{aligned}$$

The order in which the nodes incident with the required edges are visited in $W_1$ is $\langle v_1, v_2, v_3, v_4, v_5, v_6\rangle = \langle 1, 2, 4, 5, 3, 0\rangle$. Note that subwalk $W(2, 4)$ is not a shortest path between nodes $2$ and $4$. $W_1$ has cost:

$$\begin{aligned} z_{S_{AR(G)}}= z_{W_1}&= [c(0, 1)]+c(1, 2)+[c(2, 3)+c(3, 4)]+c(4, 5)+[c(3, 5)] +c(0, 3)\\&= 2+2+2+2+2+2 +2\\&= 14. \end{aligned}$$

Fig. 5

a The original arc routing graph $G$. b The equivalent node routing graph $H$

Let $T_1$ be the corresponding feasible node routing tour for the graph $H$ in Fig. 5b. $T_1$ can be established by using Lemma 1. Observing the order in which the required edges are visited in $W_1$ leads to $T_1$ being constructed as:

$$\begin{aligned} T_1 = \langle 0, m_{12}, m_{45}, m_{03}, 0\rangle . \end{aligned}$$

The order of the revised node index is $\langle u_1, u_2, u_3, u_4, u_5, u_6 \rangle = \langle 1, 2, 4, 5, 0, 3\rangle$. $T_1$ has cost:

$$\begin{aligned} z_{S_{NR(H)}}&=z_{T_1} = w(0, m^0_{12}) + w(m^1_{12}, m^0_{45}) + w(m^1_{45}, m^1_{03}) + w(m^0_{03}, 0)\\&= dist(0, 1) + c(1, 2) + dist(2, 4) + c(4, 5) + dist(5, 3) + c(0, 3) + dist(0, 0)\\&= c(0, 1) + c(1, 2) + c(2, 4) + c(4, 5) + c(3, 5) + c(0, 3) + 0\\&= 2+2+2+2+2+2 = 12 \\&< z_{W_1} = z_{S_{AR(G)}}. \end{aligned}$$

$T_1$ can be interpreted in $G$ as an alternating sequence of shortest paths (SP) and required edges, as follows:

$$\begin{aligned}&\langle [SP(0, 1)], \{1, 2\}, [SP(2, 4)], \{4, 5\}, [SP(5, 3)], \{0, 3\}, [SP(0, 0)] \rangle \\&\qquad =\langle [0, \{0, 1\}, 1], \{1, 2\}, [2, \{2, 4\}, 4], \{4, 5\}, [5, \{3, 5\}, 3], \{0, 3\}, [0]\rangle . \end{aligned}$$

Note that the situation with no deadheading from node $3$ to node $0$ is an example of the degenerate Case 3 discussed in Sect. 3.1. Also, $T_1$ costs less than $W_1$ because $W_1$ does not minimize the cost of deadheading from node $2$ to node $4$. We now demonstrate that the cost of an optimal solution to a particular node routing problem instance in $H$ is equal to the cost of the optimal solution to the original arc routing problem instance in $G$.

Theorem 1

Suppose that the proposed transformation is used to turn a given arc routing problem instance ${\textit{AR}}(G)$ say, based on a graph $G$, into a node routing problem $NR(H)$ say, based on a graph $H$. Let $z^*_{AR(G)}$ be the cost of the optimal solution to ${\textit{AR}}(G)$. Further, for all $\varvec{a}\in \{0,1\}^r$, let $z^*_{\varvec{a}}$ be the optimal solution to the instance of $NR(H)$ with edge costs specified by $\varvec{a}$. Then

$$\begin{aligned} \min _{\varvec{a}\in \{0,1\}^r}z^*_{\varvec{a}}=z^*_{AR(G)}. \end{aligned}$$

(45)

(A numerical example illustrating Theorem 1 is provided immediately after the following proof).

Proof

We shall demonstrate how the optimal solution to a particular node routing problem instance in $H$ can be used to construct an optimal solution to the original arc routing problem instance ${\textit{AR}}(G)$ say, in $G$, with both solutions having the same cost. Consider a node routing problem $NR(H)$ say, for a graph $H$ that was created by the proposed transformation from an arc routing problem instance in a given graph $G$. As discussed in the last paragraph of Sect. 3.4 each vector $\varvec{a}\in \{0,1\}^r$ give rise to an instance $NR_{\varvec{a}}(H)$ say, of $NR(H)$. Now, $\forall \>\varvec{a}\in \{0,1\}^r$ let the optimal solution to $NR_{\varvec{a}}(H)$ and its cost be denoted by $S^*_{\varvec{a}}$ and $z^*_{\varvec{a}}$, respectively. Let the solution in $\{NR_{\varvec{a}}(H)\>|\>\varvec{a}\in \{0,1\}^r \}$ with least cost solution be denoted by $S^*_{NR(H)}$ and its cost by $z^*_{NR(H)}$. That is,

$$\begin{aligned} z^*_{NR(H)}=\min _{\varvec{a}\in \{0,1\}^r}z^*_{\varvec{a}}. \end{aligned}$$

(46)

Let the set of routes that constitutes $S^*_{NR(H)}$ be denoted by $\{T^*_q\>|\>q = 1, 2,\ldots ,Q\}$, for some $Q \ge 1$. Furthermore, for $q = 1, 2,\ldots ,Q$; let $N^*_q\subseteq N$ denote the nonempty set of internal nodes of $T^*_q$. Let $r^*_q=|N^*_q|$. In order to represent each tour $T^*_q \in S^*_{NR(H)}$ unambiguously, we must specify: $(i)$ the order in which its internal nodes (the set $N^*_q$) are visited, and $(ii)$ the traversal direction of each required edge that is represented by an internal node of $T^*_q$.

Let $N^*_q = \{m_{v_{2p - 1}v_{2p}}\>|\>p = 1, 2,\ldots ,r^*_q\}$ be the set of $r^*_q \ge 1$ nodes corresponding to the set of required edges $\{v_{2p - 1}, v_{2p}\}\in R$ for $p = 1, 2,\ldots ,r^*_q$; served in $T^*_q$. The subscripts of the elements of $N^*_q$ are indexed according to the order in which they are visited by a traversal of $T^*_q$ in the following sense. As $T^*_q$ is toured from node $0$, its nodes are encountered in the order: $m_{v_1v_2}, m_{v_3v_4},\ldots ,m_{v_{2r^*_q - 1}v_{2r^*_q}}$. Thus

$$\begin{aligned} T^*_q = \langle 0, m_{v_1v_2}, m_{v_3v_4},\ldots ,m_{v_{2r^*_q -1}v_{2r^*_q}}, 0\rangle . \end{aligned}$$

(47)

Let $z_{T^*_q}$ be the cost of $T^*_q$, where

$$\begin{aligned} z_{T^*_q} = w(0, m^{a_{v_1v_2}}_{v_1v_2}) + w(m^{a_{v_1v_2}}_{v_1v_2}, m^{a_{v_3v_4}}_{v_3v_4}) +\cdots + w(m^{a_{v_{2r^*_q-1}v_{2r^*_q}}}_{v_{2r^*_q-1}v_{2r^*_q}}, 0). \end{aligned}$$

(48)

With the use of (25) and (26); and some rearrangement we have:

$$\begin{aligned} z_{T^*_q}&= dist(0, (1 - a_{v_1v_2}){\cdot }v_1 + (a_{v_1v_2}){\cdot }v_2) + c(v_1, v_2) + \cdots + c(v_{2p-1}, v_{2p})\nonumber \\&\quad +\, dist((1 - a_{v_{2p-1}v_{2p}}){\cdot }v_{2p-1} + (a_{v_{2p-1}v_{2p}}){\cdot }v_{2p}, (1 - a_{v_{2p+1}v_{2p+2}}){\cdot }v_{2p+1}\nonumber \\&\quad +\,(a_{v_{2p+1}v_{2p+2}}){\cdot }v_{2p+2}) \nonumber \\&\quad +\, c(v_{2p+1}, v_{2p+2}) +\cdots + c(v_{2r^*_q-1}v_{2r^*_q}) + dist((1 - a_{v_{2r^*_q-1}v_{2r^*_q}}){\cdot }v_{2r^*_q-1} \nonumber \\&\quad +\,(a_{v_{2r^*_q-1}v_{2r^*_q}}){\cdot }v_{2r^*_q}, 0). \end{aligned}$$

(49)

Relationships (25) and (26) can be used to interpret $T^*_q$ as a route $W_q$ say, in $G$ as follows. Firstly, the arguments of the $dist()$ function in (49) correspond to the following shortest paths in $G$:

• 1. $SP(0, (1- a_{v_1v_2}){\cdot }v_1 + (a_{v_1v_2}){\cdot }v_2)$,

• 2. $SP((1 - a_{v_{2p-1}v_{2p}}){\cdot }v_{2p-1} \!+\! (a_{v_{2p-1}v_{2p}}){\cdot }v_{2p}, (1 - a_{v_{2p+1}v_{2p+2}}){\cdot }v_{2p+1} \!+\!(a_{v_{2p+1}v_{2p+2}}){\cdot }v_{2p+2})$, for $p = 1, 2,\ldots ,2r^*_q-1$;

• 3. $SP((1 - a_{v_{2r^*_q-1}v_{2r^*_q}}){\cdot }v_{2r^*_q-1} + (a_{v_{2r^*_q-1}v_{2r^*_q}}){\cdot }v_{2r^*_q}, 0)$,

  where $SP(i, j)$ is a shortest path in $G$ from node $i$ to node $j$. Secondly,

• 4. The required edges to be served in $W_q$ and the order in which they are served, are indicated by the subscripts in (47).

Assembling the information in 1– 4 above, allows the construction of $W_q$ as:

$$\begin{aligned} W_q&= \langle SP(0, (1 - a_{v_1v_2}){\cdot }v_1 + (a_{v_1v_2}){\cdot }v_2), \{v_1, v_2\},\ldots , \{v_{2p-1}, v_{2p}\},\nonumber \\&\quad SP((1 - a_{v_{2p-1}v_{2p}}){\cdot }v_{2p-1} + (a_{v_{2p-1}v_{2p}}){\cdot }v_{2p}, (1 - a_{v_{2p+1}v_{2p+2}}){\cdot }v_{2p+1}\nonumber \\&\qquad +\,(a_{v_{2p+1}v_{2p+2}}){\cdot }v_{2p+2}),\nonumber \\&\quad \{v_{2p+1}, v_{2p+2}\},\ldots ,\{v_{2r^*_q-1}, v_{2r^*_q}\}, SP((1 - a_{v_{2r^*_q-1}v_{2r^*_q}}){\cdot }v_{2r^*_q-1}\nonumber \\&\qquad +\,(a_{v_{2r^*_q-1}v_{2r^*_q}}){\cdot }v_{2r^*_q}, 0)\rangle . \end{aligned}$$

(50)

With reference to (15)–(17), as $T^*_q$ is feasible for $NR(H)$ it is clear that $W_q$ is feasible for ${\textit{AR}}(G)$. This means that walk $W_q$ can be considered as part of a feasible solution to ${\textit{AR}}(G)$. Indeed, the solution $S_{AR(G)}=\{W_q\>|\>q=1,2,\ldots ,Q\}$ is feasible for ${\textit{AR}}(G)$. Let $z_{W_q}$ be the cost of $W_q$. Then from (49) it is clear that

$$\begin{aligned} z_{W_q} = z_{T^*_q}. \end{aligned}$$

(51)

Let $z_{\textit{AR}(G)}$ be the cost of $S_{\textit{AR}(G)}$. Then, by definition:

$$\begin{aligned} z_{\textit{AR}(G)}&= \sum ^Q_{q=1} z_{W_q},\end{aligned}$$

(52)

$$\begin{aligned} z^*_{\textit{NR}(H)}&= \sum ^Q_{q=1} z_{T_q}. \end{aligned}$$

(53)

By using (51)–(53)

$$\begin{aligned} z^*_{\textit{NR}(H)} = z_{\textit{AR}(G)}. \end{aligned}$$

(54)

It remains to show only that $S_{\textit{AR}(G)}$ is optimal for ${\textit{AR}}(G)$. It is straightforward to prove this by contradiction as follows. Let us assume that $S_{\textit{AR}(G)}$ is suboptimal; that is, there exists a feasible solution for ${\textit{AR}}(G)$, $\overline{S}_{\textit{AR}(G)}$ say, with cost $\overline{z}_{\textit{AR}(G)}$ say, where

$$\begin{aligned} \overline{z}_{\textit{AR}(G)}\le {z}_{\textit{AR}(G)}. \end{aligned}$$

(55)

By Lemma 1, there exists a vector $\varvec{a}\in \{0,1\}^r$ such that there is a feasible solution to ${\textit{NR}}(H)$ with cost no greater than $\overline{z}_{AR(G)}$. But, (54) and (55) are contradictory, which completes the proof. $\square$

Numerical illustration of Theorem 1

To illustrate Theorem 1, consider once again the arc and node routing problems in Fig. 5a,b introduced earlier. Following the notation in (47), an optimal tour $T^*_2$ say, for $H$ in Fig. 5b is given in (56)–(58) and its cost $z_{T^*_2}$ is given in (59)–(62):

$$\begin{aligned} T^*_2&= \langle 0, m_{v_1v_2}, m_{v_3v_4},\ldots ,m_{v_{2r^*_q-1}v_{2r^*_q}}, 0\rangle \end{aligned}$$

(56)

$$\begin{aligned}&= \langle 0, m_{v_1v2}, m_{v_3v_4}, m_{v_5v_6}, 0\rangle \end{aligned}$$

(57)

$$\begin{aligned}&= \langle 0, m_{45}, m_{12}, m_{03}, 0\rangle .\end{aligned}$$

(58)

$$\begin{aligned} z_{T^*_2}&= w(0, m^0_{45}) + w(m^1_{45}, m^1_{12}) + w(m^0_{12}, m^1_{03}) + w(m^0_{03}, 0)\end{aligned}$$

(59)

$$\begin{aligned}&= c(0, 4) + c(4, 5) + c(2, 5) + c(1, 2) + c(1, 3) + c(0, 3) + 0\end{aligned}$$

(60)

$$\begin{aligned}&= 1 + 2 + 1 + 2 + 1 + 2\end{aligned}$$

(61)

$$\begin{aligned}&= 9. \end{aligned}$$

(62)

Once again, the distance $w(m^0_{03}, 0) = 0$, with no deadheading from node $3$ to node $0$, is an example of the degenerate Case 3, discussed in Sect. 3.1.

The corresponding optimal arc routing walk $W^*_2$ say, for the graph $G$ in Fig. 5a can be established by observing the subscripts and superscripts in (59). $W^*_2$ (with the required edges given in bold) is:

$$\begin{aligned} W^*_2&= \langle SP(0, 4), \pmb {\{4, 5\}}, SP(5, 2), \pmb {\{1, 2\}}, SP(1, 3), \pmb {\{0, 3\}}, SP(0, 0) \rangle \\&= \langle \{0, 4\}, \pmb {\{4, 5\}}, \{2, 5\}, \pmb {\{1, 2\}}, \{1, 3\}, \pmb {\{0, 3\}}\rangle . \end{aligned}$$

The walk $W^*_2$ has cost:

$$\begin{aligned} z_{\textit{AR}(G)}^*=z_{W^*_2}&= c(0, 4)+c(4, 5)+c(2, 5)+c(1, 2)+c(1, 3)+c(0, 3)\\&= 1+2+1+2+1+2 = 9\\&= z_{T^*_2}=\min _{a\in \{0,1\}^3}z_{\varvec{a}}^*. \end{aligned}$$

5 Applying the transformation to CARP

For the rest of this article we consider the special cases of the arc routing and node routing problems termed the Capacitated Arc Routing Problem (CARP) and the Capacitated Vehicle (node) Routing Problem (CVRP), respectively. Both problems involve the identification of a set of routes to be carried out by a fleet of identical vehicles (all with equal capacity $C$, say) in order to serve a given set of customers. The routes are feasible circuits over an appropriate road network that start at a pre-defined depot, serve customers and return to the depot. Each route is performed by a single vehicle such that the demand for a single commodity by each customer it serves is met and the vehicle capacity constraint is satisfied. Each arc of the network has a known transportation cost. These arc costs can be summed to calculate each route cost. The aim of both the CVRP and the CARP is to identify a set of routes that satisfy all customer demand with the lowest global transportation cost. In the CVRP the customers are located at the network nodes and in the CARP they are located along some of the network arcs.

We now show how the graph transformation described in Sect. 2.3 can be used to solve CARP instances. We follow the notation introduced in Sect. 2, including representing a CARP (CVRP) instance by graph $G (H)$. In particular we adapt the robust branch-cut-and-price (BCP) algorithm for the CVRP proposed by Fukasawa et al. (2006) to CARP by changing only the pricing sub-problem algorithm. This BCP uses the following formulation, which combines an exponential number of columns ($\lambda$ variables) with a classical formulation on edge variables (Laporte and Norbert 1983), to calculate valid lower bounds to CVRP instances:

$$\begin{aligned}&\text {Minimize } \sum _{j=1}^p\left( \sum _{e\in A}w_eq_j^e\right) \lambda _j,\end{aligned}$$

(63)

$$\begin{aligned}&\text {subject to} \nonumber \\&\qquad \qquad \qquad \sum _{j=1}^p\left( \sum _{e\in \delta (\{i\})} q_j^e\right) \lambda _j = 2, \quad \forall \>i \in N_+, \end{aligned}$$

(64)

$$\begin{aligned}&\qquad \qquad \qquad \sum _{j=1}^p\left( \sum _{e\in \delta (\{0\})} q_j^e\right) \lambda _j = 2K, \end{aligned}$$

(65)

$$\begin{aligned}&\qquad \qquad \qquad \sum _{j=1}^p\left( \sum _{e\in \delta (\{S\})} q_j^e\right) \lambda _j \ge 2k(S), \quad \forall \>S\subseteq N_+, \end{aligned}$$

(66)

$$\begin{aligned}&\qquad \qquad \qquad \qquad \sum _{j=1}^p q_j^e\lambda _j \le 1, \quad \forall \>e\in A\setminus \delta (\{0\}), \end{aligned}$$

(67)

$$\begin{aligned}&\qquad \qquad \qquad \qquad \lambda _j \ge 0, \quad \forall \> j\in \{1,\ldots ,p\}; \end{aligned}$$

(68)

where $K$ is the number of vehicles and $N_+ = \{1,\ldots , n\}$ denotes the set of customer nodes. Given a subset $S \subseteq N_+$, $d(S)$ is the sum of the demands of all nodes in $S, \delta (S)$ is the cut-set defined by $S$ and $k(S ) = \lceil d(S)/C\rceil$ is the minimum number of vehicles needed to serve the subset $S$ of customers. The number of times that edge $e$ appears in the $j$th column (variable $\lambda _j$) is denoted by $q_j^e$.

The pricing subproblem consists of finding columns of minimal reduced cost, that is, the minimal sum of reduced costs of the edges in the corresponding column. The reduced cost $\overline{w}_e$ of an edge $e\in A$ is given by:

$$\begin{aligned} \overline{w}_e = w_e - \gamma _e,\>\> e=\{i,j\} \in A, \end{aligned}$$

(69)

where $\gamma _e$ is the sum of the dual variables $\mu$, $\nu$, $\pi$, and $\rho$ associated with constraints (64), (65), (66) and (67), respectively:

$$\begin{aligned} \gamma _e = {\left\{ \begin{array}{ll} \mu _i + \mu _j + \sum \limits _{S\>|\>e\in \delta (S)}\pi _S + \rho _e, &{} e=\{i,j\} \in A \setminus \delta (\{0\});\\ \nu + \mu _j + \sum \limits _{S\>|\>e\in \delta (S)}\pi _S, &{} e=\{0,j\} \in \delta (\{0\}). \end{array}\right. } \end{aligned}$$

(70)

As observed by Christofides et al. (1981), the $\lambda$ variables could ideally be associated with elementary routes (without cycles). Unfortunately, this would require solving a pricing sub-problem that is NP-hard in the strong sense, which is the Elementary Shortest Path Problem with Resource Constraints with the only resource being the vehicle capacity $C$ (Dror 1994). When this pricing sub-problem is restricted to finding routes that are not necessarily elementary ($q$-routes) it corresponds to solving the Shortest Path Problem with Capacity Constraints, which, although still NP-hard, can be solved by an algorithm of pseudo-polynomial time complexity (Christofides et al. 1981). Therefore, from now on each variable $\lambda$ is associated with one of $p$ possible $q$-routes, that is, a walk that starts at the depot, traverses a sequence of customers with total demand at most $C$ and returns to the depot. (See Christofides et al. (1981) for a more detailed explanation of the concept of a $q$-route) As some customers may be visited more than once, the set of valid CVRP routes is strictly contained in the set of $q$-routes. Fukasawa et al. (2006) solved the pricing subproblem (69) by a dynamic programming (DP) algorithm. Now we show how their approach can be adapted to use the transformation described in Sect. 2.3.

Following the notation defined in Sect. 3.4, let $\tau (m_{k\ell }^{a_{k\ell }},c')$ denote the shortest $q$-route cost amongst all the $q$-routes, with arrival regime at node $m_{k\ell }$ defined by $a_{k\ell }$, and arriving at node $m_{k\ell }$ with $c'$ units of capacity still available. To extend this $q$-route to a node $m_{ij}$, adding the edge $e=\{m_{k\ell },m_{ij}\}$, it is necessary to calculate $\tau (m_{ij}^{a_{ij}},c)$, the cost to reach node $m_{ij}$, by node $m_{k\ell }$ with a vehicle capacity at least of $c=c'+f(m_{ij})$, which is the minimum necessary capacity to serve node $m_{ij}$ and all previous nodes on the $q$-route. For the calculation of $\tau (m_{ij}^{a_{ij}},c)$, one can use the following recurrence relation:

$$\begin{aligned} \tau (m_{ij}^{a_{ij}},c) = \mathop {\mathop {\min \limits _{a_{k\ell } \in \{0,1\}}}\limits _{c' = c - f(m_{ij})}}\limits _{m_{k\ell } \in N - \{m_{ij}\}}\left\{ \tau (m_{k\ell }^{a_{k\ell }}, c') + w(m_{k\ell }^{1-a_{k\ell }},m_{ij}^{a_{ij}}) - \gamma _{\{m_{k\ell },m_{ij}\}} \right\} , \end{aligned}$$

(71)

where $m_{ij} \in N, f(m_{ij})\le c\le C, a_{ij}\in \{0,1\}$. The cost for the return to the depot (node $0$) by any node $m_{gh}$ in $N$, with any remaining vehicle capacity, is as defined by (26) minus the sum $\gamma _{\{m_{gh},0\}}$ of dual variables. The variables $a_{ij},a_{k\ell } \in \left\{ 0,\>1\right\}$, as defined in Sect. 3.4, indicate the departure and arrival regimes to nodes $m_{ij}$ and $m_{k\ell }$, respectively. Since the node immediately preceding node $m_{ij}$ on the $q$-route is the node $m_{k\ell }$, the necessary capacity of the vehicle at the node $m_{k\ell }$ is given by $c' = c-f(m_{ij})$, where $c$ is the available capacity when arriving at the node $m_{ij}$ and $f(m_{ij})$ is the demand associated with this node.

Following Fukasawa et al. (2006), we propose a dynamic programming approach for (71) to solve the pricing subproblem. The basic data structure of the proposed DP algorithm is an $(r+1)\times C\times 2$ three-dimensional matrix $T$. Each entry $T[u, c , a_u]$ represents the least costly walk from the depot that reaches node $u$ of $N$, with arrival regime at node $u$ dictated by the value of $a_u$ in (25), with $c$ units of vehicle capacity still available. Each entry $T[u, c , a_u]$ contains two elements: the cost of the walk (for simplicity we will refer to it as $T[u,c,a_u]$) and a pointer to a $T$ entry representing the walk as far as the previous node. Initially, the empty path $\langle 0 \rangle$ (corresponding to entries $T[0, 0, 0]$ and $T[0, 0, 1]$) has cost zero. All other entries are initialized with labels representing empty walks with infinite cost. From entries $T[0, 0, 0]$ and $T[0, 0, 1]$ the matrix is filled, starting with lower values of $c$ (the remaining vehicle capacity). For each value $0<c\le C$, the algorithm goes through each node $v\in N$, dictated by the value of $a_v$ in (25), and for each neighbor $u\in N$ of $v$, evaluates the extension of the walk represented by $T[u, c'=c-f(v), a_u]$ to node $v$ dictated by the value of $a_v$. $T[v,c, a_v]$ is updated only if $T[u, c', a_u] + w(u^{1-a_u},v^{a_v}) - \gamma _{\{u,v\}} < T[v,c, a_v]$. Eventually, we shall have the most negative walk with accumulated demand at most $C$ that arrives at each node $v$. Extending the walk to the depot (whose demand is zero), we obtain the corresponding $q$-route. All $q$-routes with negative cost thus found (there will be at most $r$, one coming from each vertex) are added to the linear program (63)–(68). There are $2rC$ entries in the matrix $T$ to be evaluated and each one is processed in ${O}(r)$ time, so the total running time is ${O}(r^2C)$.

A similar approach was used by Longo et al. (2004, 2006), using the transformation described in Sect. 2.2 and the same BCP algorithm of Fukasawa et al. (2006). A key idea of the pricing algorithm of Longo et al. (2004, 2006) is to force each pair of successive nodes $s_{ij}$ and $s_{ji}$ in $N$, that arise from a required edge $\{i,j\}$ in $G$, to be traversed in sequence. Here the trick is to ensure that the value of the binary variable $a_{ij}$, which is associated with the node $m_{ij}$ in $N$ that arises from a required edge $\{i,j\}$ in $G$, is consistent with the traveling direction of $\{i,j\}$ in $G$. This point is crucial to ensure that any route that passes through a node in $N$, incurs exactly the cost of the equivalent edge in the original graph $G$.

Our implementation of the DP algorithm just described also prohibits 1 and 2-cycles in the $q$-route. That is, subpaths $i\rightarrow i$ and $i\rightarrow j \rightarrow i,\> i \ne 0$, are not allowed. Therefore, we restricted the $q$-routes to those without cycles or with cycles of size at least three since it improves the formulation and does not change the complexity of the pricing subproblem. Eliminating cycles of size three or greater is a hard task and we decided not to do it. An algorithm for eliminating cycles of any size is described by Irnich and Villeneuve (2006).

5.1 Algorithm correctness

The following theorem, that adopts the notation and terminology used in Sect. 3 establishes the correctness of the BCP algorithm just proposed.

Theorem 2

Suppose the proposed transformation is used to turn a given arc routing problem instance ${\textit{AR}}(G)$ say, on a graph $G$, into a node routing problem instance $NR(H)$ say, on a graph $H$. Then, when the proposed BCP algorithm is applied to $NR(H)$, it will identify the least-cost set of $q$-routes among all possible edge cost specifications for $NR(H)$ arising from all $\varvec{a}\in \{0,1\}^r$.

Proof

Consider a node routing problem instance $NR(H)$ say, for a graph $H$ that was produced by the proposed transformation from a given arc routing problem instance ${\textit{AR}}(G)$ say, on a given graph $G$ with $K$ identical vehicles that all have capacity $C$.

Each vector $\varvec{a}\in \{0,1\}^r$ gives rise to an instance $NR_{\varvec{a}}(H)$ say, of $NR(H)$. We now demonstrate, by induction on $r$, that the proposed DP algorithm to solve the pricing subproblem constructs in the matrix $T$ the least cost set of $q$-routes among all possible instances $NR_{\varvec{a}}(H)$.

The DP algorithm initially sets the costs of all $T$ entries as infinity, except entries $T[0,0,0]$ and $T[0,0,1]$ whose costs are set to zero. Although (23) and (24) allow the $q$-routes be constructed from only one of these two last entries, for the sake of simplicity we consider both possibilities.

We first show that the induction hypothesis is true for $r=1$. That is, we prove that the DP algorithm identifies the least-cost set of $q$-routes from all $\varvec{a}\in \{0,1\}$. Suppose that $r=1$, that is, there is only one node $v_1$ in $H$ to be served, which has demand $f(v_1)$ and arrival regime dictated by $a_{v_1}$. The DP algorithm extends the walk $\langle 0\rangle$, corresponding to entries $T[0,0,0]$ and $T[0,0,1]$, to $\langle 0,v_1\rangle$, corresponding to entries $T[v_1,C,0]$ and $T[v_1,C,1]$, that depict all possible vectors $\varvec{a}\in \{0,1\}^r$. Note that, for each value $0<c<f(v_1)$ and $a_{v_1}\in \{0,1\}$, it is not possible to update entries $T[v,c,a_{v_1}]$ because the vehicle capacity $c$ is not sufficient to serve the demand $f(v_1)$ at node $v_1$. For each value $f(v_1)< c\le C$, the walk cost at entries $T[v_1,c,a_{v_1}]$, $a_{v_1}\in \{0,1\}$, is updated to the same values at $T[v_1,f(v_1),a_{v_1}]$. So, the least cost walk from the depot to node $v_1$ can be found either at entry $T[v_1,C,0]$ or at $T[v_1,C,1]$ and thus, can be extended to the depot, producing the desired least-cost $q$-route. Thus, the hypothesis is true for $r=1$.

We next show that if the induction hypothesis is true for $r=k$, $k\in \mathbb {Z}$ and $k\ge 2$, it is true for $r=k+1$. Assume that the DP algorithm identifies the least-cost set of $q$-routes from all $\varvec{a}\in \{0,1\}^k$. That is, the DP algorithm constructs, for any subset of $k$ nodes $\{v_,\ldots ,v_k\}\subset N\backslash \{0\}$, walks of least cost from the depot to each one of the $k$ nodes over all possible vectors $\varvec{a}\in \{0,1\}^k$. We now use this hypothesis to extend to the set of $q$-routes from all $\varvec{a}\in \{0,1\}^{k+1}$.

Consider a $(k+1)$th node to be served, $v_{k+1}$ say. As $v_{k+1}\ne v_i,\>i=1,\ldots ,k$, then the walk cost at all entries $T[v_{k+1},c,a_{v_{k+1}}]$, for $0<c\le C$ and $a_v{_{k+1}}\in \{0,1\}$, are still fixed as infinity. Otherwise, node $v_{k+1}$ would be served by one of the walks that serve nodes $v_1,\ldots ,v_k$.

To update these entries, the DP algorithm first sets $a_{v_{k+1}}=0$ and, for each value $0<c \le C$, attempts to connect node $v_{k+1}$ to each node $v_i\in \{v_1,\ldots ,v_k\}$ using either $a_{v_i}=0$ or $a_{v_i}=1$. The same procedure is carried out for $a_{v_{k+1}}=1$. The entries $T[v_{k+1},c,a_{v_{k+1}}]$, for $c'+f(v_{k+1})\le c \le C$, are updated to $T[v_i,c',a_{v_i}] + w(v_i^{1-a_{v_i}},v_{k+1}^{a_{v_{k+1}}}) -\gamma _{\{v_i,v_{k+1}\}}$ only if $T[v_{k+1}, c,a_{v_{k+1}}] > T[v_i,c',a_{v_i}] + w(v_i^{1-a_{v_i}},v_{k+1}^{a_{v_{k+1}}}) -\gamma _{\{v_i,v_{k+1}\}}$, where $v_i\in \{v_1,\ldots ,v_k\}$ and $c'$ is the vehicle capacity sufficient to serve all the nodes in the route from the depot to $v_i$. Therefore, by the induction hypothesis for $r = k$, a least-cost $q$-route between the depot and node $v_{k+1}$ can be obtained by joining the walk in one of the entries $T[v_{k+1},C,0]$ and $T[v_{k+1},C,1]$ to the depot.

That is, two extensions $\varvec{a}^{\prime },\varvec{a}^{\prime \prime }\in \{0,1\}^{k+1}$ of each of the vectors $\varvec{a}\in \{0,1\}^k$ are considered by the DP algorithm, one with 0 as the last element and the other with 1 as the last element. Therefore, the DP algorithm identifies the least-cost set of $q$-routes from all $\varvec{a}\in \{0,1\}^{k+1}$. $\square$

5.2 Computational results

We report computational experience in applying the process just described to some classical numerical problems from the literature. We applied the CARP algorithm implementation to instances of the egl dataset of Li and Eglese (1996), available at http://www.uv.es/~belengue/carp.html. This dataset was constructed using an underlying CARP graph that is based on parts of the road network of the county of Lancashire in the United Kingdom. The original application involved the distribution of grit on certain roads in winter. The costs of all edges and demands of the required edges are proportional to their actual length. The algorithm was implemented in C++ using a Linux OS, gcc v. 4.6.1 compiler and IBM cplex v. 12.4. All the numerical tests were carried out on an Intel Core i3 personal computer with 3.0GHz clock speed and 8GB of RAM, using just one core.

The CARP algorithm implementation is an adaption of the CVRP algorithm described by Fukasawa et al. (2006) where the pricing sub-problem algorithm is changed, as described at the beginning of the present section. All the other modules of the algorithm (cut generation, branching rule and node selection) were unchanged and we used the default configuration that was originally defined for all of them. We used as initial upper bounds, unity plus the best upper bounds reported by Martinelli et al. (2011), Fu et al. (2010) and Santos et al. (2010).

Table 1 compares the lower bound (column ‘Our $LB$’) given by the root node solution to model (63)–(68) found by the proposed BCP algorithm with the lower bounds reported by Longo et al. (2006) (column ‘Prev. $LB_1$’), by Baldacci and Maniezzo (2006) (‘Prev. $LB_2$’) and by Martinelli et al. (2011) (‘Prev. $LB_3$’). These bounds were rounded up to the next integer. The other columns of the table provide: the name of each instance, its number of nodes $|V|$, its number of edges $|E|$, the number of required edges $r$, the minimum number $K$ of vehicles necessary to serve all demand, the best known upper bounds $UB$ (reported by Martinelli et al. (2011), Fu et al. (2010) and Santos et al. (2010)) and the total time in seconds to process the root node. The upper limits in bold face had already been proven to be the values of optimal solutions.

Table 1 Comparison of lower bounds for the egl instances

The lower bounds listed in column ‘Prev. $LB_1$’ were previously obtained with a branch-cut-and-price algorithm designed to solve the CVRP and adapted to solve the CARP. This algorithm makes use of a specialised version of the model (63)–(68) to take advantage of the fact that the instances arising from the CARP instances, using the transformation described in Sect. 2.2, have $r$ pairwise disconnected edges that must belong to every solution. Also, the formulation was improved by enforcing the restriction that the $q$-routes found by the pricing sub-problem must be free of 1, 2 and 3-cycles. ‘Prev. $LB_2$’ bounds were also obtained with the aid of the graph transformation described in Sect. 2.2, but with a branch-and-cut algorithm. The ‘Prev. $LB_3$’ bounds were obtained with a branch-cut-and-price algorithm designed specifically to solve the CARP that does not make use of any graph transformation.

For seven of the 24 test instances the approach proposed here found a lower bound greater than or equal to the one reported in column ‘Prev. $LB_1$’, for six instances compared with ‘Prev. $LB_2$’ and for two instances compared with ‘Prev. $LB_3$’. Regarding the 15 test instances reported either in column ‘Prev. $LB_1$’ or in ‘Prev. $LB_2$’ (e1-a to s1-c), our bounds are less sensitive to the number of vehicles and are better for most of the instances where $K \ge 10$. Overall, the proposed approach found an improved lower bound only once (result in bold face in column ‘Our $LB$’), compared to all previous known bounds. However, we believe that our bounds can be improved if the pricing algorithm restricts $q$-routes to those without cycles of size three or smaller.

Table 2 presents the instances solved to optimality by our approach within a time limit of 6 h (21,600 s) of processing. The first five columns of this table are the same as in the Table 1. The next columns show the optimal value of the instance, the number of nodes in the branch-and-bound tree, the CPU times spent in the pricing subproblem algorithm and in the cut generation procedures and the total CPU time. The optimal solutions to the first two instances in the table, e1-a and e1-b, were already known, as reported in Martinelli et al. (2011). The solutions (in bold face) corresponding to the upper bounds identified in Martinelli et al. (2011) for the remaining two (open) instances, e1-c and s1-c, have been proven to be optimal by the proposed BCP algorithm.

Table 2 Optimal solutions to the egl instances produced by the BCP algorithm

6 Conclusions

Two important examples of vehicle routing problems are the CVRP (Capacitated Vehicle Routing Problem) and the CARP (Capacitated Arc Routing Problem). As the best known computer codes reported in the open literature for solving the CVRP (Augerat et al. 1995; Blasum and Hochstättler 2000; Wenger 2003; Lysgaard et al. 2004; Ralphs et al. 2003; Fukasawa et al. 2006; Baldacci et al. 2008) resolved instances with up to only $150$ nodes, the practical application of the Pearn et al. (1987) transformation is somewhat limited.

With the transformations proposed by Longo et al. (2004, 2006) and by Baldacci and Maniezzo (2006) there is the possibility of using CVRP methods to solve more difficult instances of CARP in reasonable computational time. The decrease in the number of nodes provided by this transformation was sufficient to enable resolution of all CARP instances of three main classes of test instances (kshs—Kiuchi et al. (1995), gdb—Golden et al. (1983) and bccm—Benavent et al. (1992)). However, some important CARP numerical instances in the literature, such as some instances in the dataset egl (Li and Eglese 1996), have not yet been resolved satisfactorily.

The graph transformation proposed in Sect. 2.3 has made it possible to resolve some CARP numerical instances in the literature that were previously open. All theoretical aspects of the transformation developed suggest that it might be employed to provide further good results for other arc routing problem instances.