1 Introduction

The generation of action potentials, or spikes, by neurons consumes a significant amount of metabolic energy (Attwell and Laughlin 2001). Action potential generation and propagation can consume 20–50 % of a neuron’s energy budget (Sengupta et al. 2010; Laughlin 2001), imposing a considerable constraint on information transmission by neurons (Laughlin et al. 1998). Energy expenditure has been hypothesized to provide selective pressure on the evolution of neural codes (Niven and Laughlin 2008). It is reasonable to assume that neural codes have evolved which optimize a trade-off between encoding signals with high fidelity and minimizing metabolic energy expenditure.

Several previous efforts have been made to mathematically model the information capacity or rate of neural models subject to energy or spike-rate constraints (Berger and Levy 2010; Levy and Baxter 1996; Baddeley et al. 1997). Unlike these prior studies but similar to the formulation of Boerlin et al. (2013), our previous work (Jones et al. 2015) proposed that optimal neural encoding could be achieved for a given mean spike-rate by timing spikes such that the best possible reconstruction of the signal is produced. This can be achieved by tracking the reconstruction error internally and timing spikes to minimize the error. Spike-trains are reconstructed using a linear filtering operation, representing the possible filtering of the post-synaptic cell membrane (Hille et al. 2001). The reconstruction error is tracked internally using a mechanism similar to dynamic threshold models (Chacron et al. 2003; Brandman and Nelson 2002; Kobayashi et al. 2009). By deriving the optimal encoding parameters, our previous work showed an optimal, energy-constrained encoding strategy replicates experimental spike-times from peripheral and cortical neurons with considerable accuracy. Here we call this neural coder the optimal source-coding neuron.

How does the principle of optimal, energy constrained neural encoding relate to the current understanding of encoding by single neurons? Broadly, the two most common approaches to understanding encoding by individual neurons advocate either for rate coding or temporal coding (Eggermont 1998; Gautrais and Thorpe 1998; Van Rullen and Thorpe 2001). Rate codes assume that information is represented in the average spike-rate over some counting window. For example, a higher stimulus intensity would result in a higher average spike-rate. This is an idea dating back at least to Adrian (1926). Rate codes are robust to variability in spike-timing, which have led many to believe that rate-codes may serve as a fundamental coding strategy in neural systems (London et al. 2010). On the other hand, it has long been noted that rate-coding is not necessarily efficient at transmitting information. Temporal codes, which postulate that the precise timing of spikes carry information, have the potential to transmit more information in the same window of time (MacKay and McCulloch 1952). For example, the time-to-first-spike can be used to reliably distinguish between stimulus intensities with only a single spike (Gollisch and Meister 2008; Van Rullen and Thorpe 2001). In the auditory system of non-human primates, it has been shown that spike-trains with millisecond precision carry more information about the stimulus than spike-trains with coarser resolution (Kayser et al. 2010). In simulation, it can also be shown that the precise pattern of spiking carries more information than expected by a rate-code (Aldworth et al. 2011). There is still considerable debate on whether temporal codes or rate codes best describe the neural coding scheme.

Prior work has attempted to bridge the gap between these two, sometimes conflicting, approaches to understanding neural encoding. As the width of the temporal window decreases, the information entropy of a spike-train increases (Strong et al. 1998). Rate codes with decreasing averaging windows approach an instantaneous spike-rate code, which can be estimated as the inverse of the sequence of interspike intervals (Prescott and Sejnowski 2008). The instantaneous rate can also be interpreted as the probability of observing a spike at a particular time, and thus, can be estimated experimentally as a rescaling of the Peri-Stimulus Time Histogram (PSTH). Dayan and Abbott (2001) argue that observations of a slowly varying instantaneous rate is consistent with a rate-coding hypothesis and a more rapidly modulated instantaneous rate suggests temporal coding. Experimentally, it has been shown in the cricket auditory system that the instantaneous spike-rate over a small window provides a better estimate of responses to repetitive stimuli than the average spike-rate (Nabatiyan et al. 2003) and that the interspike intervals of short bursts of action potentials code modulation intensity in the electrosensory lobe of a weakly electric fish (Oswald et al. 2007).

This work seeks to reconcile some of these widely differing views. We connect the optimal source-coding neuron (Jones et al. 2015) with the views of rate and temporal coding. We derive, in the limit of high firing rates, an instantaneous-rate coder which minimizes reconstruction error subject to a constraint on energy expenditure. The instantaneous rate depends on the input signal, input signal derivative, and the reconstruction filter. The predictions of the instantaneous-rate coder are compared to data from two systems. The first is a peripheral sensory neuron of a weakly electric fish in vivo, and the second is the response of a neocortical neuron of a rat in vitro. The results indicate that estimates of the experimental spike-rate correspond closely to the predicted instantaneous rate, modeling spike-rate adaptation. Instantaneous rate coding also predicts the time-to-first-spike (a simple temporal code) and average spike-rate in the neocortical neuron. We conclude that the optimal source-coding neuron shows some key aspects of both rate and temporal coding.

2 An instantaneous-rate coder for minimum-error, energy-constrained neural coding

Here we consider the encoding (generation of spikes) and decoding (estimation of the input signal from spikes) of a non-negative, twice-differentiable input signal s(t). The coded spike train is composed as a sequence of spikes at times t i . For a given neuron, spike waveforms are essentially identical and are simply represented as a sum of impulses, \({\sum }_{i} \delta (t-t_{i})\) (Gabbiani 1996). The decoding process maps \({\sum }_{i} \delta (t-t_{i})\) to r(t), an estimate of the input signal s(t). In this work, the signal is recovered by filtering the spike-train with a fixed, linear reconstruction filter specified by the impulse response h(t),t≥0. This approach is consistent with the reconstruction of dynamic signals by spike-triggered average filters (Eggermont et al. 1983) or stimulus reconstruction filters (Bialek et al. 1991; Gabbiani 1996). A simple reconstruction filter is given by the impulse response \(h(t)=A \exp {(-t/ \tau )}, t \geq 0\). This filter form is based on the classic idea of a pre-synaptic and post-synaptic neuron, where the post-synaptic potential can by modeled by filtering the sum of impulses with a low-pass filter representing the post-synaptic membrane (Hille et al. 2001). The decaying exponential corresponds to a RC circuit model of the cell membrane, which is commonly used to model the passive dynamics of a cell membrane, for example in Hodgkin-Huxley models (Hodgkin and Huxley 1952). The reconstructed signal is then given by \(r(t)=h(t) \ast {\sum }_{i} \delta (t-t_{i})={\sum }_{i} h(t-t_{i})\).

Our previous work (Jones et al. 2015) hypothesized that a neuron encodes an input signal with minimal reconstruction error given a constraint on the available energy. In neurons, a major source of energy consumption over a period of time (T) is the number of spikes fired (Laughlin 2001; Sengupta et al. 2010). Energy expenditure in a neuron can be largely factored into generating post-synaptic potentials, maintaining baseline potentials, generating and propagating action potentials, and releasing and recycling vesicles. For a fixed input signal, energy expenditure can be divided into costs which do not depend on the number of action potentials, and those which are proportional to the number of action potentials. From the perspective of an encoding model, it is therefore possible to model energy expenditure per unit time as E = b + k R. Here E is the expended energy rate, b is the baseline cost, k is the cost per spike, and R is the spike rate. An optimal neural encoding strategy should therefore minimize reconstruction error such that an average spike-rate is maintained. In the proposed model, spikes are fired when the error reaches a threshold level γ. This leads to the following constrained optimization problem

$$\begin{array}{@{}rcl@{}} &&\min\limits_{A,\tau,\gamma} \frac{1}{T} {{\int}_{0}^{T}} (s(t)-r(t))^{2} dt \\ &&\text{subject to } R \leq (E-b)/k. \end{array} $$
(1)

In this problem, the parameter A is the value of the filter h(t) at time 0, the parameter τ is the time-constant of h(t), and γ is the variable threshold level. Previously, we derived an optimal strategy to solve this problem for the case of slowly varying signals which are approximately constant between spikes (Jones et al. 2015). In this case, an optimal strategy is to track the reconstruction error e(t) = s(t)−r(t) and to fire a spike when e(t i ) = γ(s(t),r(t)), where γ is a level-dependent firing threshold available in closed-form. This leads to a code which times spikes to minimize error. In the limit of large signals relative to the decoding filter parameter A, this rule reduces to γ = A/2. The complete treatment of this approach was given by Jones et al. (2015).

Here we propose an alternative method for generating spike times which are, in the limit of high spike-rates, equivalent to the neural source-coding model in Jones et al. (2015). Given the parameters A and τ we derive an instantaneous rate function. This instantaneous rate is then encoded as spikes with an integrate-and-fire model. For high rates, the optimal neural source coder and instantaneous rate coder have identical interspike-intervals. Since the intervals are identical for high firing rates, the instantaneous rate coder is an alternative approach to minimize reconstruction error subject to a constraint on the expended energy. Thus, in the limit of high spike-rates, the spike-timing code of Jones et al. (2015) and the instantaneous rate code are two different ways of describing the same code.

2.1 Instantaneous-Rate coding

For the case of a single-pole lowpass reconstruction filter given by \(h(t)=A\exp (-t/\tau ), t \geq 0\) and the asymptotic firing rule s(t)−r(t) = A/2, it is possible to derive an analytic expression for the instantaneous firing rate, defined as the inverse of the interspike interval, given the values of A and τ.

Assuming a high enough spike-rate, the decoded signal \(r(t)={\sum }_{i}{h(t-t_{i})}\) and input signal s(t) can be approximated, with small error, by their first-order Taylor series expansions at time t i

$$\begin{array}{@{}rcl@{}} r(t_{i}+t)=r(t_{i})+r^{\prime}(t_{i})t \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} s(t_{i}+t)=s(t_{i})+s^{\prime}(t_{i})t \end{array} $$
(3)

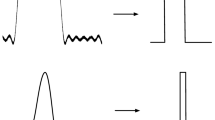
where \(r^{\prime }(t_{i})\) is the first right derivative. Taking t i to be the firing time of spike i, one can assume that r(t i+) = s(t i ) + A/2, if a spike was fired following the asymptotic spike-firing rule. An example of s(t) and r(t) are shown in Fig. 1. The linearization of r(t) is also shown. At time t i , the first right derivative of the reconstruction is

$$ r^{\prime}(t_{i})=-(s(t_{i})+A/2)/\tau. $$
(4)

Assuming that s(t i )>>A/2, this can be approximated as

$$ r^{\prime}(t_{i})\approx-s(t_{i})/\tau. $$
(5)
Fig. 1
figure 1

Illustration of the input signal s(t) and reconstructed waveform r(t). A spike is fired at time t i and the next spike is fired at time t i+1, following an interval of Δ t seconds. In this example, the input signal is assumed to be approximately linear between spike times. At time t i , a spike is emitted, causing a discontinuity in the reconstructed waveform r(t) of height A. The value of r(t i+) = s(t i ) + A/2, as the spike was fired when r(t i−) = s(t i )−A/2. For t>t i , the reconstructed waveform is given by \(r(t)=(s(t_{i})+A/2)\exp (-t/\tau )\). To derive the time between spikes in Eq. (7), first-order Taylor series approximations of r(t) and s(t) are used. The linear approximation of r(t) is shown as the dashed grey line. In this case, the predicted time between spikes using the linear approximation is given by the black circle. This leads to a slightly lower estimate of the time between spikes. As spike-rate increases, the estimate of the time between spikes using the linearizations approaches the true time between spikes

Full size image

Given these approximations, it is possible to calculate the time between the spikes.

$$\begin{array}{@{}rcl@{}} &&s(t_{i})+s^{\prime}(t_{i})(t_{i+1}-t_{i})-A/2\\ &&\quad= r(t_{i+})+r^{\prime}(t_{i})(t_{i+1}-t_{i})\\ &&\quad= s(t_{i})+A/2-(s(t_{i})/\tau)(t_{i+1}-t_{i}). \end{array} $$
(6)

Rearranging Eq. (6) to solve for the time between spikes gives

$$ (t_{i+1}-t_{i})={\frac{A}{(s^{\prime}(t_{i})+s(t_{i})/\tau)}}. $$
(7)

Inverting the expression for (t i+1−t i ) gives the instantaneous spike-rate, i(t)

$$ i(t)={\frac{s(t)/\tau+s^{\prime}(t)}{A}}{.} $$
(8)

The relationship of the instantaneous rate to the energy constraint in Eq. (1) is apparent if we consider a constant signal \(\bar {S}=s(t)\). Then the rate is constant and given by

$$ i(t)=\frac{\bar{S}}{A \tau}=R. $$
(9)

This expression agrees with the results from Jones et al. (2015) for the optimal neural source coder, where the rate generated by a constant stimulus was estimated from the average output level of the reconstruction filter. The instantaneous rate function i(t) given by Eq. (8) captures the spike-rate in the limit of high firing rates, when h(t) can be approximated linearly with low error. The rate function depends on the input signal, the derivative of the input signal, and the filter parameters A and τ.

The expression for the instantaneous rate suggests a new method to generate a spike-train which achieves the minimum (asymptotically in the limit of high spike-rates) of Eq. (1). First, generate the instantaneous rate function i(t) from s(t) using Eq. (8). Next, fire spikes proportionally to i(t) using a simple integrate and fire model. Given a spike at time t i , the next spike will be fired after an interval Δ t defined by

$$ {\int}_{t_{i}}^{(t_{i}+\Delta_{t})} i(t)dt = 1. $$
(10)

When a spike is fired, the output of the integrator is reset to 0. This model is compared to the optimal neural source coder proposed previously (Jones et al. 2015) in Fig. 2. The neural source-coder computes the error between the reconstruction r(t) and input signal s(t) to generate a spike-train which is the solution of Eq. (1) in the limit of high spike-rates. For high spike-rates, we show both coders produce spike sequences with identical interspike intervals.

Fig. 2
figure 2

Comparison of two neural encoding models. a shows the schematic of the optimal neural source coder proposed by Jones et al. (2015). The encoder is implemented using a dynamic threshold with a decoding filter impulse response of \(h(t)=A\exp {(-t/ \tau )}, t \geq 0\). The dynamic threshold encoder generates an internal error signal which is compared to a threshold firing rule. When the threshold is exceeded, a spike is fired. The decoder filters these spikes to generate the reconstructed signal. In the limit of high firing rates, this strategy achieves minimal error subject to a constraint on the spike rate. b shows an alternative interpretation of optimal, energy-constrained encoding which is also valid at high spike-rates. In this case, an instantaneous rate i(t) is computed from the signal s(t). Spikes are then fired proportionally to this function using an integrate and fire model. In the limit of high firing rates, the instantaneous rate approach generates a spike-train with interspike intervals identical to the encoder in A. Therefore, in the limit of high firing rates, this approach is an equivalent solution to Eq. (1)

Full size image

In the limit of high spike rates, the asymptotic expression for the interspike intervals of the optimal neural source coder shown in Fig. 2a is (Johnson et al. 2015)

$$ \Delta_{t} = {\frac{A}{(s^{\prime}(t_{i})+s(t_{i})/\tau)}}. $$
(11)

For the spike-firing rule defined in Eq. (10), the inter-spike interval, at high firing rates, can be approximated as

$$\begin{array}{@{}rcl@{}} {\int}_{t_{i}}^{(t_{i}+\Delta_{t})} i(t)dt \approx (t_{i}+\Delta_{t}-t_{i}) i(t_{i})= 1 \\ \Delta_{t} = \frac{1}{i(t_{i})} = {\frac{A}{(s^{\prime}(t_{i})+s(t_{i})/\tau)}}. \end{array} $$
(12)

The instantaneous rate is \({{\Delta }_{t}}^{-1}\). Since both methods produce spike-sequences with the same interspike intervals, in the limit of high spike rates, the instantaneous rate coder is also an asymptotically optimal solution to Eq. (1). This derivation holds for high firing rates because h(t) can be approximated as linear in this limit. The solution to the optimization problem can be viewed either as the optimal neural source coder, which computes reconstruction error internally, or an instantaneous rate coder defined by the signal, the signal derivative, and the filter parameters.

3 Methods

Responses of the proposed instantaneous rate coding model and a rate coding model were generated for three sets of data: 1) a simulated input with known functions for the signal and signal derivative, 2) responses of a P-type primary electrosensory afferent of a weakly electric fish, 3) responses to current injection from a rat somatosensory cortical neuron in an in vitro preparation (Gerstner and Naud 2009). This data was collected by Thomas Berger and Richard Naud in the laboratory of Henry Markram at the École Polytechnique Federale de Lausanne (EPFL), Switzerland and is publicly available from the International Neuroinformatics Coordinating Facility (INCF) 2009 Quantitative Spike-Time Prediction competition (www.incf.org). The data from the P-type electrosensory neuron and the somatosensory cortical neuron were previously used to validate the neural source coder (Jones et al. 2015). Here we will study the predictions of the instantaneous rate coder against these experimental data in order to better understand how minimum-error, energy-constrained encoding is related to rate and temporal coding.

Figure 3 shows the simulated function, which was modeled as two sigmoid functions with known slope parameters. The first sigmoid simulated a sudden positive change. By subtracting the second sigmoid from the first, a smaller negative step was simulated. The simulated function provided an example with known signal and signal derivative terms to test the instantaneous rate coding. Responses were simulated at a sampling rate of 5000 Hz for a duration of one second.

The responses of P-type afferents of a weakly electric fish were recorded in response to modulations in the fish’s Electric Organ Discharge (EOD) waveform. The experimental methods used to collect the data presented in this section are described in full in previous work (Nelson et al. 1997; Jones et al. 2015). Action potentials were recorded from pALLN afferents in a Brown Ghost Knife Fish (Apteronotus leptorhynchus) of unknown sex using glass micropipettes filled with 3M KCl solution. Spiking events were detected by a threshold, and the spike-times were stored for later analysis in the Matlab programming environment at a sampling rate of 16667Hz. The EOD waveforms were recorded using a silver wire electrode placed under the skin of the fish.

Fig. 3
figure 3

Encoding of a simulated waveform consisting of a sigmoid function centered at 500ms added to a second sigmoid function centered at 750ms, with a negative amplitude. This waveform had sudden changes but well-defined derivatives. The waveform was used as the input for the proposed instantaneous rate coder and a rate coder (integrate and fire model). a shows the reconstructed waveforms and resulting rate functions for A=0.002 and τ=50ms. The instantaneous rate code reconstruction tracks the input signal, providing minimum-error encoding. The rate code produces significant distortion. The theoretical instantaneous rate (Eq. (8), calculated using the sigmoid functions and their derivatives) and the rate of the instantaneous rate coder (estimated from the simulated spike-times, generated using the encoder specified by Eq. (10)) show nearly identical spike-rates, as expected. Both methods show spike-rate adaptation in response to the signal at the onset and offset of the waveform. The inset (a1) shows a small section of the simulation which emphasizes the spike-rate adaptation at the onset. The rate-code predicts a spike-rate which is proportional to the signal, resulting in worse reconstruction error. b shows the response of the instantaneous rate coder using the parameters A=0.008 and τ=10ms. Different parameter values change the instantaneous rate function predicted by Eq. (8). In this case, the term proportional to the signal s(t) is much larger than the term proportional to the signal derivative. This results in an optimal instantaneous rate function which is closer to the rate encoding approach. The inset (b1) shows the onset of the signal, where the instantaneous rate code is much closer to the rate code. Depending on the situation, the optimal instantaneous rate coder can show strong spike-rate adaptation or rate encoding

Full size image

Stimulation was provided by modulating the EOD with raised cosine waveforms of approximately 100ms duration delivered by carbon electrodes near the head and tail of the fish. An important detail to note is that the raw stimulus waveform recorded from the silver wire electrode does not necessarily correspond exactly to the transdermal potential at the electroreceptor. The stimulus strength depends on the distance and the orientation of the stimulus electrode relative to the electroreceptor (Nelson et al. 1997; Yager and Hopkins 1993). To compensate for this uncertainty, a scaling factor, a EOD, was introduced to correct the size of the stimulation. Any deviation from the baseline stimulus level was multiplied by this scaling factor.

The second set of experimental data was recorded in vitro from a regular spiking L5 pyramidal cell from rat somatosensory neocortex. This publicly available data (see above) consisted of 60 s of current injection stimulus and 13 voltage recordings of length 38 s digitized at 10kHz. The remaining 22 s of data were reserved for testing by the competition organizers and are not publicly available. The first 17.5 s of the current-clamp stimulus consisted of four step current inputs with a duration of 2 s and an inter-stimulus time of 2 s. This was followed by an injection of 2 s of white noise. The remaining 42.5 s consisted of six simulated spike trains generated by an inhomogeneous Poisson process. The intensities were chosen randomly to elicit firing rates between 5 and 10 Hz.

3.1 Parameter selection

To generate the instantaneous rate code, it is first necessary to determine the parameters A and τ, as well as the dataset specific parameters. In our previous work (Jones et al. 2015), the parameters of the optimal neural source coder shown in Fig. 2a were determined to maximize the spike-time coincidence factor between the model spike times and the experimental spike times. The coincidence factor (Kistler et al. 1997) compares two spike trains by counting the number of spikes which occur within a window of Δ seconds of a spike from the other spike train. The coincidence is then defined between an experimental spike train (data) and a predicted spike train (model) as

$$ \Gamma = \frac{N_{\text{coinc}}-E[N_{\text{coinc}}]}{N_{\text{data}}+N_{\text{model}}} \frac{2}{1-2 \nu \Delta} $$
(13)

where N coinc is the number of coincident spikes, E[N coinc] is the expected number of coincident spikes if the model was a homogenous Poisson process with the same spike rate as the model spike train, N data is the number of experimental spikes and N model is the number of spikes from the model. The second term normalizes the result, where ν is the spike rate of the model.

In this work, the optimal parameters derived by Jones et al. (2015) were also used to generate the instantaneous rate code. Briefly, spike-time coincidence was optimized by sweeping over τ and the stimulus-specific parameters. The neural source coder (Fig. 2a) with γ = A/2 was simulated for this parameter set. For each value of τ and the stimulus parameters, the following two steps were performed.

  1. 1.

    Select A so that the average spike-rate constraint is satisfied.

  2. 2.

    Use the optimal value of γ to generate an encoded spike-train using the optimal source coder. Compute the coincidence between the encoded spike-train and one experimental trial.

The parameter values which resulted in the highest coincidence were also used as the parameters for the proposed instantaneous rate coder.

For the experimental data from the P-type afferent of a weakly electric fish, the raw waveform was filtered with a second-order bandpass filter with a 3dB bandwidth of approximately 50Hz, centered at the EOD frequency. The values of A, τ, and a EOD were found for the stimulus levels (0dBV through -30dBV) in order to maximize the coincidence averaged over all stimulus levels. The value of a EOD was 5.30. The values of τ and A were 24.0ms and 2.92×10−4V. The same parameters were used for all 20 trials at all stimulus levels.

For the current-clamp injection data, the current waveform was first filtered with a first-order lowpass filter with unity gain and a time-constant of τ m . The parameter values were chosen to maximize average coincidence with the spike-times in response to the three positive DC steps included in the data. The optimal parameters were τ m = 26.3ms, τ=75ms, and A=487.4.

3.2 Instantaneous rate coding

For each set of data, the instantaneous-rate function was calculated using the reconstruction filter parameters, input function, and input function derivative following Eq. (8). For the simulated data, the input function was assumed to be the simulated waveform. For the weakly-electric-fish data, the input signal was taken to be the envelope of the EOD waveform after the band-pass filter. For the INCF data, the input signal was assumed to be the current-injection waveform after low-pass filtering. For the simulated data and the DC step stimuli in the current-clamp injection data, the signal derivative was computed analytically. For the modulations of the EOD waveform, the input signal derivative was found by filtering the input signal with an eleventh-order differentiating filter, implemented digitally with a frequency cut-off of π/2. These signals were used to calculate the theoretical instantaneous-rate function following Eq. (8). Using the instantaneous rate function, spikes were generated using Eq. (10). The integrator output was initialized to 0 for the weakly electric fish data. For rat cortical neuron data, the integrator output was initialized to 0.5. This is because the input signal value starts at 0. The error only needs to accumulate to a level of A/2 before the first spike should be fired.

A rate-coding strategy was also implemented using a simple integrate-and-fire model, which fires spikes proportional to the signal level. For each set of data, the input signal was rescaled by the mean firing rate from the experimental data, \(f_{\exp }\), divided by the mean input signal level, \(\bar {S}\). Given a spike at time t i , the next spike is fired after an interval Δ t such that

$$ {\int}_{t_{i}}^{t_{i}+\Delta_{t}} \frac{f_{\exp}}{\bar{S}} s(t) dt = 1. $$
(14)

When a spike is fired, the output of the integrator is set to 0. Spikes were reconstructed by filtering with the impulse response \(h(t)=A\exp (-t/\tau ), t\geq 0\), using the values of A and τ described above. To generate the spike-trains, the initial value of the integrator was set identically to the instantaneous rate coder.

The error between the reconstructed waveforms and stimuli was computed using the RMS value of the error divided by the RMS value of the stimulus, reported in dB as

$$ {10 \log_{10} \frac{\left( {{\int}_{0}^{T}} (s(t)-r(t))^{2} dt\right)^{1/2}}{\left.\left( {{\int}_{0}^{T}} s(t)^{2} dt\right)\right)^{1/2}}}{.} $$
(15)

This metric allows for better comparison across stimulus levels.

4 Results

The proposed instantaneous rate coder and a standard rate coder were applied to study the simulated data set, different modulation levels of the EOD waveform of a weakly electric fish, and current-clamp injection in the INCF data. The reconstructed waveforms and spike-times were compared to the experimental stimuli and spike-times.

First, the instantaneous rate coder was applied to a simulated waveform, consisting of two sigmoid functions, using the parameters A) A=0.002 and τ=50ms, B) A=0.008 and τ=10ms. Figure 3a and b show the reconstructed waveforms and spike-rates for these two sets of parameter values. The spike-rates were estimated using the inverse of the interspike interval. Panel A shows the case where A is smaller and τ is larger. These parameters emphasize the derivative term in Eq. (8). This leads to an increase in firing rates when the signal derivative is positive and a decrease in firing when the derivative is negative. The instantaneous-rate function predicts a constant rate whenever the signal is not changing (when the derivative is zero). This behavior is similar to spike-rate adaptation observed in many primary sensory neurons (Kiang et al. 1965). The rate coder, on the other hand, predicts a spike rate which is exactly proportional to the stimulus. Firing spikes proportionally to the signal leads to large errors in the reconstruction. Panel B shows the encoding for a larger value of A and a smaller value of τ. In this case, the term of Eq. (8) which is proportional to the signal dominates the rate. The instantaneous spike rate is close to the rate coder. The instantaneous rate coder predicts observed encoding behaviors, such as spike-rate adaptation and rate coding.

The proposed instantaneous rate coder and rate coder were applied to the weakly electric fish data to generate reconstructions of the signal envelope. Figure 4 shows reconstructed waveforms, Peri-Stimulus Time Histograms (PSTHs), and spike-time rasters for the instantaneous rate coder and rate coder. The instantaneous rate coder (red) closely follows the instantaneous-rate function for the −10dBV and −20dBV steps and matches the experimental PSTH (black, Fig. 4b). The rate coder (green) fires spikes proportionally to the signal envelope. This pattern of spiking does not follow the pattern seen in the experimental spikes. The reconstructed waveforms for the instantaneous rate code closely follow the signal envelopes for all three stimulus levels. The reconstructions of the rate code produce significant distortions in the signal envelope. The reconstruction lags the change in the input signal, resulting in higher error. Mean reconstruction errors (RMS) for the instantaneous rate code and rate code were: −12.8 dB and −4.0 dB (0dBV), −13.4 dB and −7.0 dB (−10dBV), −12.7 dB and −10.2 dB (−20dBV). These differences were all found to be significant using a Wilcoxon rank-sum test (20 trials, p<10−6).

Fig. 4
figure 4

Instantaneous rate coding and rate coding in response to AM modulation of the EOD waveform of a weakly electric fish. The predictions of the instantaneous rate code are shown in red, the predictions of the rate code in green, the experimental data is shown in black, and the instantaneous rate function Eq. (8) in blue. The fish was stimulated with three amplitudes of EOD waveform modulations (row (a), black traces) of duration 100ms. Row (a) shows the reconstructed waveform for the instantaneous rate code (red) and rate code (green). For the three stimulation levels, the reconstructed signal of the instantaneous rate code closely follows the signal envelope. The reconstruction of the rate code shows significant lag in reconstructing the signal, leading to higher error. Row (b) shows the Peri-Stimulus Time Histograms (PSTHs) for the experimental spikes, the instantaneous-rate-coded spikes and rate-coded spikes, calculated over 20 trials, along with the theoretical instantaneous-rate function from Eq. (8). Row (c) shows the spike-time rasters for the experimental, instantaneous rate coded, and rate coded spikes. For the −10dBV and −20dBV cases, the PSTH of the experimental spike-times, the PSTH of the instantaneous-rate-coded spikes, and instantaneous rate function coincide very closely. In the 0dBV case, it is clear that the experimental spikes are driven into saturation by firing once per EOD cycle. The instantaneous-rate function predicts a rate which is not realizable by the experimental neuron. In the case of −10dBV and −20dBV stimulation, however, the instantaneous-rate function is a very close match to the experimentally observed PSTH, suggesting that the instantaneous-rate coder closely models the spike-times recorded from the P-type afferent

Full size image

An interesting phenomenon can be observed in the responses to the 0dBV stimulus in Fig. 4b. Due to the rapid change in the input stimulus, the theoretically calculated instantaneous rate function predicts spike rates that exceed the maximum and minimum possible spike-rate for real neurons. In weakly electric fish, P-type afferents fire no faster than once per EOD cycle and can fire no slower than zero spikes per second. The instantaneous-rate function for the 0dBV stimulus predicts a spike rate that is too large at the onset of the stimulus. As the stimulus falls off, the theoretical function predicts a negative spike-rate. The instantaneous rate coder also predicts rates above the maximum allowable rate, but cannot fire with a negative spike-rate. Further constraints would be required to ensure the instantaneous rate function predicts spike-rates which are physically realizable.

It is important to note that over the entire window of 0.3 s shown, both rate coding models predict a stimulus-dependent change in the spike rate. Figure 5 shows the spike-rate for the rate coder, instantaneous rate coder, and experimental data. The rates are all quite close except at the 0dBV stimulus level, when the neuron is driven into saturation. In this case, the instantaneous rate coder predicts a rate which is too large. The increase in spike-rate with stimulus intensity is typically expected of a rate code. In this sense, the instantaneous rate code is consistent with observations of rate-coding in different sensory neurons, unless the neuron is driven into saturation. The instantaneous rate code, however, also follows the spike-rate at shorter time-scales and leads to lower reconstruction error, as seen in Fig. 4.

Fig. 5
figure 5

Shown here are the spike-rates for the experimental (black), instantaneous-rate encoded (red) and rate encoded spikes (green), averaged over a 0.3 second window. These are plotted as a function of five stimulus levels ranging from −30dBV to 0dBV. Error bars indicate the standard deviation over twenty trials. Both the instantaneous rate coder and the rate coder show a long-term average spike-rate close to the experimental data, except for the 0dBV case. As seen in Fig. 4, the instantaneous rate code does not show the saturation seen experimentally, leading to a higher spike-rate. The spike-rate varies with stimulus intensity. This suggests a possible rate-coding scheme, at least when the signal is not saturated. However, as seen in Fig. 4, the adaptation in the instantaneous spike-rate over shorter time windows leads to lower reconstruction error

Full size image

4.1 Response of a cortical neuron to current-clamp stimulation

The proposed instantaneous rate coder and rate coder were used to predict spike times in response to DC current-clamp injections. Figure 6 shows the response of the instantaneous rate coder, rate coder, and experimental neuron to three levels of DC stimulation. The reconstructed waveforms, spike-time rasters, and spike-rates are shown. The spike-rates are estimated using the inverse of the inter-spike interval. For the DC stimulation, the experimental data show an initial increase in spike-rate which returns to a constant level. This is also apparent in the instantaneous-rate function. The spikes are timed to code the sudden change in the signal level then maintain this new level. The instantaneous rate coder predicts this behavior at the two larger stimulus levels. The rate coder does not predict the initial increase in spike-rate. Because the initial spike-rate is not high, the change is not coded with low error by the rate coder, as seen in the reconstructed waveforms. The reconstruction errors for the instantaneous rate coder and rate coder were: −3.2dB and −2.4dB (Level 1), −5.8dB and −5.3dB (Level 2), −7.1dB and −6.7dB (Level 3). For this data, a single deterministic waveform was encoded with deterministic models, so a significance test was not appropriate. At the lowest signal level, the predicted instantaneous rate is somewhat higher than the experimental spike-rate. This is likely due to the derivation of the instantaneous rate using a linearization of the reconstructed waveform. At very low spike-rates, the exponential decay is not well modeled as a linear function.

Fig. 6
figure 6

Instantaneous-rate encoding and rate encoding of three amplitudes of DC step stimulation of a cortical neuron in vitro using a current-clamp configuration. a shows the input steps (top row, black trace), which are filtered with a first-order low-pass filter. The step is coarsely represented by the reconstructed signal of the instantaneous rate coder (red). The rate coder reconstruction (green) results in higher reconstruction error due to the lag in tracking the onset of the signal. The second row shows the spike-times from 13 experimental trials along with the instantaneous-rate-coded and rate-coded spike-trains. The third row shows the theoretical instantaneous-rate function from Eq. (8), the rate function of the experimental spikes (estimated using the inverse of the interspike interval), the rate-function of the instantaneous-rate-coded spikes and the rate-function of the rate-coded spikes. For the two larger stimuli, the experimental data, instantaneous-rate-coded spikes, and theoretical instantaneous rate function are in close agreement. All three show a sharp increase in spike rate, followed by a decay to a new baseline level. At the lowest stimulus level, the instantaneous rate function predicts a spike-rate which is higher than the experimental rate. This may be due to the linearizations and assumptions made in deriving Eq. (8), which do not hold for long interspike intervals. b shows that the instantaneous rate coder exhibits some characteristics of both a rate and a temporal code. The time-to-first-spike and the average rate (calculated over 2 s) both match the experimentally observed spikes. Although the rate-coded spikes match the experimental spike-rate, they do not show the same time-to-first-spike. Optimal encoding with an instantaneous rate coder can model some aspects of both temporal and rate codes

Full size image

Figure 6b shows two interesting properties of both the experimental data and the instantaneous rate coder. Averaged over the full two seconds of stimulation, the instantaneous rate coded, rate coded, and experimental spike trains all show a level-dependent change in firing rate, or rate-coding. Also interesting is the level-dependent change in the time-to-first-spike due to the interplay of the low-pass filtered input signal and the instantaneous rate function. The time-to-first-spike is determined by the increase in the signal derivative at the onset of the step. Larger steps have a steeper derivative and a faster first spike. The rate code predicts long first spike times. The times-to-first-spike are often interpreted as a simple temporal code (Gollisch and Meister 2008). The theory of minimum-error, energy constrained neural encoding is consistent with both experimental observations, suggesting that the instantaneous-rate function can help explain some aspects of both rate coding and temporal coding.

5 Discussion

The proposed instantaneous rate coder provides a method for firing spikes with ISIs determined by the instantaneous rate function in Eq. (8). This strategy is an alternative method, in the limit of high spike-firing rates, for generating spike trains with intervals which match our previously proposed optimal neural source coder (Jones et al. 2015, shown in Fig. 2a). Although the generated spike trains are asymptotically equal, these two methods give different insights about minimum-error, energy-constrained encoding. The optimal instantaneous rate is actually a function of the stimulus, stimulus derivative, and reconstruction filter parameters. Note that in the datasets considered here, such as the cortical neuron, the spike rate is often not high. Nevertheless, we find the instantaneous rate coder generates spike trains which show many features of the experimental data.

Comparing the modeled spike-times with the experimental data from a P-type afferent of a weakly electric fish (Fig. 4) and DC current injection (Fig. 6) of a rat cortical neuron, the instantaneous rate coder closely predicts the experimental spike-rates. The pattern of spiking observed experimentally is consistent with the proposed instantaneous rate function. For these stimuli, the instantaneous-rate coder makes much more accurate predictions than a rate coder which is proportional to the input stimulus. The rate-coding approach produces poor reconstructions as well.

For cases where the spike-rate is not saturated, Fig. 4b shows that the instantaneous rate function can be used as an estimator for the PSTH. Here, the PSTH is scaled by the bin size and the number of trials to produce units of spikes/s. After rescaling, the PSTH corresponds closely to the predicted instantaneous rate. This suggests an interpretation of experimental PSTHs from primary sensory neurons as a measure of the instantaneous rate. The high spike-rates observed in the primary neuron may be due to the requirement of encoding sensory signals in the periphery with high fidelity.

The concept that neural encoding performance must be optimized for a given energy constraint (a given spike-rate), is not necessarily a new one. Previous work has suggested that neurons attempt to maximize spike-train entropy for a given rate (Baddeley et al. 1997). Alternative approaches have maximized ratios of entropy or channel capacity to energy expenditure in simple neural models (Levy and Baxter 1996; Berger and Levy 2010). The neural source coder model is closely related to prior work on predictive coding in spiking networks (Boerlin et al. 2013). This study also proposed an optimization problem which balanced fidelity against spiking activity (as a surrogate for energy), where the goal was to encode the state variables of a dynamical system in the activity of a population of spiking neurons. This population was meant to simulate cortical networks. Assuming a fixed threshold, a neural model similar to the neural source coder was derived and studied in simulated populations of cortical neurons. Our previous work (Jones et al. 2015), derived a more general stimulus-dependent threshold for a single neuron and provided a detailed comparison to experimental data from sensory neurons. Our current analysis builds upon prior work by predicting a stimulus-specific instantaneous spike rate which, in the limit of high spike rates, produces a spike train which minimizes reconstruction error for a given energy constraint.

The predicted instantaneous-rate function is determined by two terms– one proportional to the signal level and one proportional to the signal derivative. For a constant or slowly varying signal, the instantaneous rate is proportional to the signal level. This is essentially rate coding. For more rapidly fluctuating signals, the signal derivative plays a role in determining the spike rate, typically leading to high spike rates for a brief period when the signal level changes. This spike-rate adaptation leads to spikes which are closely timed to changes in the signal. Instantaneous rates which are slowly varying favor a rate-encoding hypothesis, whereas rapidly varying instantaneous rates are thought to imply temporal codes (Dayan and Abbott 2001). The responses of the instantaneous rate coder to the DC step inputs (Fig. 6), match both the average spike-rate and time-to-first-spike. Due to the adaptation in the instantaneous spike-rate, the resulting code shows some properties of both rate and temporal coding. Previously, coding strategies have been developed which show aspects of both rate and temporal coding depending on the regime being tested (Panzeri and Schultz 2001). It has also been shown that neural models can be tuned on a continuum to act as coincidence detectors or integrators (Rudolph and Destexhe 2003). Populations of neural models can be tuned between synchronous firing (a kind of temporal code) and rate coding, depending on the model parameters (Masuda and Aihara 2003). Our result shows that an instantaneous rate code can operate in different regimes of a single underlying mechanism.

One important aspect of neural encoding which was not explicitly explored in our study was correlations between ISIs. Negative correlations between adjacent ISIs have been observed in a wide range of neurons (Farkhooi et al. 2009), and have been implicated as particularly important for encoding in P-type sensory afferents (Ratnam and Nelson 2000; Lüdtke and Nelson 2006). Previous studies of neural models which generate negative serial correlation coefficients have been shown to improve information transmission (Chacron et al. 2001) and detection of weak sensory signals (Goense and Ratnam 2003). More recent work has shown that a neural model with adaptation currents results in negatively correlated ISIs and uncorrelated adaptation current levels, leading to improved information transmission with low decoder complexity (Nesse et al. 2010). Our neural source coder is mathematically similar to some adaptive threshold models (Chacron et al. 2001; Brandman and Nelson 2002). As these adaptive threshold models produce negatively correlated ISIs, the neural source coder will likely result in similar ISI correlations. Our results show that the instantaneous rate coder generates the same ISI sequence as the neural source coder in the limit of high spike rates; therefore, the instantaneous rate coder should also produce negatively correlated ISIs. Further analysis will be required to understand the relationship between the instantaneous rate, negative ISI correlations, and optimal signal encoding.

Although the proposed instantaneous rate coder shows some aspects of both rate and temporal encoding, it is important to note that the temporal coding observed is due to the adaptation in spike-rate caused by the term proportional to the signal derivative. The instantaneous rate is sensitive to changes in the signal, which results in precise spike times when the signal level changes rapidly. In general, temporal coding is often poorly defined and refers to different observed phenomena which are not necessarily related to spike-rate adaptation. Many experimental observations of temporal encoding, such as encoding in spike-time correlations or phase-locking, are not addressed here. Further work will be needed to explore the proposed instantaneous rate coder (and the optimal neural source coder) in these contexts.

The instantaneous rate coder replicates many aspects of the experimental data, but the generation of an instantaneous rate function is not necessarily a biophysically plausible mechanism for implementing minimum-error, energy-constrained encoding. However, the instantaneous rate coder generates spike-intervals which are equivalent to the source coding neuron shown in Fig. 2a as developed in Jones et al. (2015). Previously, we have noted that adaptation currents such as the M-current, corresponding to the KCNQ/Kv7 family of channels (Brown and Adams 1980), could be a possible implementation for implementing the neural source coder (Jones et al. 2015), due to the fact that these channels regulate neural excitability and are coupled to metabolic processes (Delmas and Brown 2005). Benda and Herz (2003) showed that M-currents, AHP-type currents, and slow recovery from inactivation of fast sodium channels can introduce spike frequency adaptation in computational models. The value of the instantaneous rate coder is not as a possible biophysical mechanism, but rather as a tool for understanding neural encoding. Further work will be required to understand the biophysical mechanisms underlying the trade-off between encoding error and energy consumption.

6 Conclusions

We have shown that minimum-error, energy-constrained neural encoding by individual neurons can be achieved by a rate coder of an instantaneous-rate function which depends on the input signal, signal derivative, and the reconstruction filter parameters. In the limit of high spike-rates, this approach generates interspike intervals which are identical to the interspike intervals generated by an optimal source-coding neuron (Jones et al. 2015). Promisingly, the instantaneous-rate function closely models the spike-rates recorded experimentally from a P-type afferent of a weakly electric fish and reproduces the observed PSTHs. The instantaneous-rate coder also predicts the average spike-rate and time-to-first-spike of a cortical neuron’s response in vitro to DC step inputs. This result suggests that the instantaneous-rate coder can capture some aspects of both rate-coding and temporal coding at different levels of the sensory pathway. Certain experimental observations of rate and temporal coding may in fact arise from an underlying mechanism of optimal neural encoding subject to an energy constraint. Further work will be required to explore the encoding predicted by the instantaneous rate coder, for neural systems which exhibit other temporal coding effects.