1 Introduction

Since the last decades, the miniaturization of gadgets is in trend and big systems are converting into small chips and portable devices [1,2,3,4]. Going down from bigger to smaller dimensions with the same governing laws is called scaling. The scaling in a VLSI technology is well known, and technology for lower than 9 nm has been achieved. Like Moore’s law in VLSI, dimensions of the MEMS devices are also reducing year by year and moving toward NEMS. Miniaturization without proper laws leads to unwanted results and degrades device performance. Vertical isotropic scaling laws [3, 4] are proposed for the MEMS devices. However, MEMS devices are anisotropic means all the parameters are not scaled by the same factor. The device parameters like pull-in voltage, mechanical and electrical frequency, power consumption, speed, and lifetime are correlated with each other. These parameters are dependent upon basic parameters like length, width, and thickness [5, 6]. Any change in basic parameters will alter the functioning of the device. In MEMS, depending upon the working principle, scaling laws vary from device to device [7,8,9,10]. In the present paper, the generalized scaling laws are explored for RF MEMS devices for improvement in device performance. RF response of the MEMS devices is better than solid-state devices. However, electro-mechanical parameters, e.g., low switching speed, high operating voltage, stiction probabilities, are limiting factors for the MEMS devices. In addition to scaling, these limiting factors are also addressed.

2 RF MEMS Scaling

RF MEMS devices have advantages of low power consumption, high isolation, low insertion, and high linearity over the solid-state devices. RF MEMS switch is a basic building block for the majority of the RF devices, e.g., varactor, t-matrix, and phase shifter [11,12,13,14]. The scaling laws applicable to the RF MEMS switch are also applicable to other RF MEMS devices. In the present paper, generalized scaling for the RF MEMS switch is performed which is applicable for most of the RF MEMS components. The scaling laws are formed in such a way that existing limitations of the MEMS devices like low speed, high actuation voltage, low mechanical response, power handling, and self-actuation are minimized as described below:

2.1 Pull-in voltage

One of the major limitations of the RF MEMS devices is high pull-in voltage which needs to be scaled down. The pull-in voltage (Vp) of the RF MEMS switch is given by

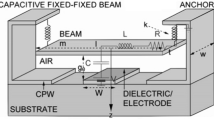
$$V_{p} = \sqrt {\frac{{8kg^{3} }}{{27\varepsilon_{o} wL_{el} }}}$$
(1)

where εo is the permittivity of free space. g, w, and Lel are a gap, width of structure/pull-in electrode, and length of electrode, respectively, as shown in Fig. 1. And k is a spring constant which is a function of structural geometry and force as listed in Table 1.

Fig. 1
figure 1

3D schematic of (a) cantilever- and (b) bridge-based MEMS devices

Full size image
Table 1 Spring constant for commonly used MEMS structures
Full size table

A generalized formula for spring constant is given by

$$k = C_{1} Ew\left( \frac{t}{L} \right)^{3}$$
(2)

where C1 is geometry/load dependent constant and E is Young’s modulus of the material. w and t are the width and thickness of the bridge/cantilever. The actuation electrode width (w) is taken equal to the cantilever width to reduce actuation voltage.

Combining equations (1) and (2)

$$V_{p} = \sqrt {C_{1} \frac{{8g^{3} E}}{{27\varepsilon_{o} L_{el} }}\left( \frac{t}{L} \right)^{3} }$$
(3)

With scaling, we can reduce its pull-in voltage.

From equations (2) and (3), scaling of ‘t and L’ by ‘β (< 1)’ would not change k and Vp. The scaling of ‘w’ would reduce k or stiffness which degrades its reliability. Hence, width (w) of the structure is kept constant and other parameters (t, L, and Lel) are scaled by β.

Scaling of ‘g’ is different from ‘t’ and ‘L’ as ‘g’ affects the RF isolation and involves fabrication complexities [15]. Hence, the scaling of ‘g’ is done with another factor α (< β). All the scaled parameters are listed in Table 2. With scaling, scaled spring constant (ks) and scaled actuation voltage (Vp,s) become

$$k_{s} = k$$
(4)
$$V_{p,s} = \sqrt {\frac{{\alpha^{3} }}{\upbeta }} V_{p}$$
(5)
Table 2 The scaling laws (β < α < 1) for the physical parameters of the switch
Full size table

Here, scaling is different in all three directions and optimized for RF MEMS switch applications.

Simulations are performed on CoventorWare software to verify the scaling laws.

The value of β and α is chosen ½ and 1/1.5, respectively, for the sake of simplicity. The original cantilever of parameters 400 × 50 × 3 µm3 is taken and scaling according to Table 2. 3D views of the original and scaled cantilevers are shown in Fig. 2. Here, scaling-1 means scaled by factor β and α, scaling-2 means scaled by factor β2 and α2, and so on. The scaling is called spring constant scaling as spring stiffness is not compromised and kept fixed as shown in Fig. 3.

Fig. 2
figure 2

3D view of (a) original, (b) scaled-1, (c) scaled-2 and d scaled-3 cantilevers

Full size image
Fig. 3
figure 3

Negligible change in the spring constant with the scaling

Full size image

The pull-in voltage of the switch decreases from 12.75 V to 5.25 V with scaling as shown in Fig. 4 which is a good achievement for the MEMS devices.

Fig. 4
figure 4

Pull-in voltage scaling for the switch

Full size image

2.2 Restoring force

The MEMS cantilever/bridge is moved down with the help of electrostatic force and moves upward with restoring force of the structure. If the restoring force is less, the cantilever will stick in its down position. Hence, restoring force should not degrade with scaling. The restoring force (Fres) for the mechanical structure is given by

$$F_{res} = - kx$$
(6)

where ‘x’ is the displacement of the MEMS structure. The maximum restoring force in downstate position is

$$F_{res,\max } = - kg$$
(7)

where ‘g’ is the gap between the electrode and cantilever/bridge which is equal to the maximum possible displacement of the structure. With scaling, from equation (4) and Table 2, scaled restoring force (Fres,s) would decrease by α.

$$F_{res,s} = \alpha F_{res}$$
(8)

However, stiction forces that are proportional to the contact area also decrease by a factor of β which is less than α. In other words, there is an overall improvement in the stiction probabilities of the switch.

2.3 Mechanical frequency

The mechanical resonance frequency (f) of the switch should be large for the quick response and is given by

$$f = \frac{1}{2\pi }\sqrt {\frac{k}{m}} = \frac{1}{2\pi }\sqrt {\frac{{C_{1} Ew}}{\rho Lwt}\left( \frac{t}{L} \right)^{3} } = \frac{1}{2\pi }\frac{t}{{L^{2} }}\sqrt {C_{1} \frac{E}{\rho }}$$
(9)

and scaled mechanical frequency (fs) is

$$f_{s} = f/\upbeta$$
(10)

The mechanical resonance frequency of the structure increases by a factor of 1/β which makes the device fast. The simulated result for the resonance frequency is shown in Fig. 5. The resonance frequency of the switch improves from 6.5 kHz to 52.9 kHz.

Fig. 5
figure 5

Improvement in the mechanical resonance frequency with the scaling

Full size image

2.4 Switching speed

The switching speed of the MEMS devices is slow as compared to solid-state devices. The scaling is done in such a way that it would help in improving the speed.

The switching speed for the switch is a function of damping. The switching time (tod) for overdamped system Q < 0.5, is given [12] by

$$t_{od} = \frac{{2bg^{3} }}{{3\varepsilon_{o} AV_{s}^{2} }} = \frac{{9V_{p}^{2} }}{{8\pi fQV_{s}^{2} }}$$
(11)

where b and Q damping constant and quality factor. Vp and Vs are pull-in and supplied voltage.

After scaling, the scaled switching time (tod,s) for the overdamped system is given by

$$t_{od,s} =\upbeta t_{od}$$
(12)

On the other hand, the switching time (tud) for an underdamped system (Q > 2) is given by,

$$t_{ud} = 3.67\frac{{V_{p} }}{{V_{s} \omega_{o} }}$$
(13)

After scaling, the scaled switching time (tud,s) of the switch improves by β.

$$t_{ud,s} =\upbeta t_{ud}$$
(14)

The simulated switching speed results are shown in Fig. 6. The switching speed improves from 52 µsec to 6.6 µsec with scaling.

Fig. 6
figure 6

Improvement in the switching speed with the scaling

Full size image

2.5 Power consumption

The power consumption (P) of the electronics component is given by

$$P = I^{2} R$$
(15)

where I and R are current and resistance.

In the case of an RF MEMS switch, the actuation voltage is applied through the dielectric material and there is no direct flow of current. Hence, the resistive power consumption is zero. However, the dielectric material between the MEMS structure and the actuation electrode leads to the formation of a capacitor. The energy (Eenergy) lost through the capacitor is given by

$$E_{energy} = \frac{{CV_{p}^{2} }}{2} = \frac{1}{2}\frac{{\varepsilon_{o} wL_{el} }}{g}V_{p}^{2}$$
(16)

where C is the capacitance between cantilever/bridge and actuation electrode.

After scaling, the scaled energy (Eenergy,s) consumption is given by

$$E_{energy,s} = \upalpha ^{2} E_{energy}$$
(17)

With scaling, energy consumption is also reduced by a factor of α2.

2.6 Stiction forces

In the MEMS devices, the cantilever/bridge moves down with the actuation voltage and contacts the bottom layer. Due to some forces called stiction forces like capillary, dielectric stiction, and van der Waals, etc., the structure may stick in its down position. These stiction forces are directly proportional to a contact area (wL) [15, 16]. With scaling, length decreases by β, and width remains constant as listed in Table 2. Hence, both the contact area and the stiction forces would decrease by β, and the reliability of the device gets improved. In the proposed design, the contact area decreases from 20 × 50 µm2 to 2.5 × 50 µm2 which reduces the stiction probabilities.

With scaling, from equation (17), capacitive coupling forces are reduced by α2. The dielectric stiction forces are directly proportional to capacitive coupling [17,18,19]. Hence, the dielectric stiction force is further decreased by α2.

2.7 Power handling limited by Self-actuation

The pull-in voltage required for actuation of the switch is given by [12]

$$V_{p} = \sqrt {\frac{{8kg^{3} }}{{27A\varepsilon_{o} }}}$$
(18)

where A is an area of overlap between the cantilever/bridge and electrode.

For no RF reflection, self-actuating RF power (Pself) of the switch [12] is given by

$$P_{self} = c_{2} \frac{{V_{p}^{2} }}{{Z_{o} }}$$
(19)

where c2 is constant whose value change from 1 to 0.25 depending upon the series /parallel configurations.

From equations (18) and (19), the power handling of the switch due to self-actuation is

$$P_{self} = c_{2} \frac{{8kg^{3} }}{{27\varepsilon_{o} AZ_{o} }}$$
(20)

After scaling, from equation (4) and Table 2, scaled self-actuating power (Pself,s) decreases by a factor of α3/β.

$$P_{self,s} = \upalpha ^{2} P_{self}$$
(21)

However, using broadside configuration or floating metal [7] or second electrode [8], the problem of self-actuation is controlled. All the switch parameters with scaling factor are listed in Table 3.

Table 3 The effect of the scaling laws on the switch characteristics (β < α < 1)
Full size table

2.8 Electromagnetic response

The electromagnetic response of the proposed ohmic switch is also simulated on high-frequency structural simulator (HFSS) to analyze scaling effects. Both insertion loss and Isolation are improved with scaling as shown in Fig. 7 and Fig. 8.

Fig. 7
figure 7

Change in insertion loss of the switch with scaling

Full size image
Fig. 8
figure 8

Change in isolation of the switch with scaling

Full size image

3 Conclusion

The generalized scaling laws for RF MEMS/NEMS switches are presented. The width of the switch structure is kept constant in the scaling. The length and thickness of the structure are scaled by the same factor (β). The gap between electrode and structure is scaled by a larger factor (α > β). By going from MEMS to NEMS, the important mechanical parameters like switching speed, mechanical frequency, and actuation voltage are improved with scaling. The electromagnetic response of the switch like insertion loss and isolation is also improving with scaling.