1 Introduction

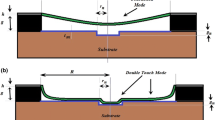
Capacitive pressure sensors have attracted significant attention for use in microelectromechanical systems (MEMS) [1, 2]. They represent a significant improvement over piezoresistive pressure sensors due to their low power consumption, near-linear output, large over-range pressure, robust structure, high sensitivity, and lower fabrication cost [3,4,5]. This wide array of advantages has attracted significant research attention to improve their functionality. One significant breakthrough was the discovery of a near-linear operating region that occurred when the two electrodes of the capacitive pressure sensor come into contact [6, 7]. This also provides large overload protection, as the substrate supports the diaphragm and prevents it from rupturing at high pressures. This class of capacitive sensors designed to operate in touch mode came to be known as touch-mode capacitive pressure sensors (TMCPS) [8,9,10]. The basic design of a capacitive pressure sensor is shown in Fig. 1.

Fig. 1
figure 1

Capacitive pressure sensor

Full size image

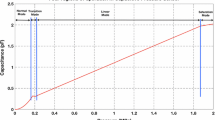
When an external pressure is applied on the diaphragm, a differential pressure greater than zero is generated between the external surface and internal cavity. This causes the diaphragm to bend inward into the cavity, in turn reducing the distance between the two electrodes. This causes a rise in capacitance, resulting in a direct relation between the pressure applied and capacitance generated [11, 12]. As long as the diaphragm and substrate are not in contact, the mode of operation is called the normal mode. On further increasing the pressure, the diaphragm touches the substrate, producing a highly nonlinear response in the capacitance, and thus the transition mode of operation is reached [13]. As the pressure is further increased, the capacitance generated is largely formed of a contribution from the parallel plate generated between the substrate and diaphragm separated by two insulation layers. This leads to a near-linear capacitance and pressure response, representing a desired mode of operation. The touch mode of operation gradually tapers off into a saturation mode as the diaphragm touching the substrate reaches a shearing limit and can no longer expand onto the substrate. These four modes of operation (normal, transition, touch, and saturation) are shown in the model graph in Fig. 2 and form the basis of the TMCPS [14].

Fig. 2
figure 2

Model graph of four modes of operation of a capacitive pressure sensor

Full size image

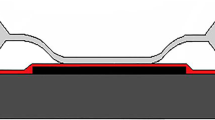
Notwithstanding, further improvements in the design have been incorporated by etching a second notch into the substrate and using two back-to-back sensors to improve the capacitance and sensitivity [15,16,17,18]. However, these designs come with an increase in complexity in terms of both analytical modeling and fabrication. Therefore, this work proposes a new TMCPS design where the substrate used is a convex dome rather than a flat circular plate. This design curbs the increase in complexity while yielding desirable results. The structure for such a design is depicted in Fig. 3. The theory for the proposed design is discussed in Sect. 2, while Sects. 3 and 4 present design specifications, brief fabrication techniques, and mathematical modeling. Such a model is essential for novel design proposals, as it provides initial understanding of the dimensions required and expected sensor results. Finally, an analytical model is constructed from the derived results using MATLAB, and the results are compared with our intuitive understanding of the model and with previous models [14] in Sect. 5.

2 Theory and principle

The proposed design is elucidated in Fig. 3. The substrate used is sliced out of a sphere, as depicted in Fig. 4. The substrate is therefore shaped as a convex dome. An intuitive analysis of the design proposed in Fig. 2 reveals that the substrate area increases, therefore causing a significant increase in the capacitance of the parallel plate formed during touch-mode operation. Also observe that the touch mode of operation is achieved sooner, since the depth of the gap at the center of the substrate is much lower. A more critical look at the substrate shape and its interaction with the diaphragm during touch-mode operation indicates that the diaphragm–substrate relationship must yield a slightly more linear response.

Fig. 3
figure 3

Basic structure of convex TMCPS

Full size image
Fig. 4
figure 4

Sphere from which substrate is sliced

Full size image

Such an increase in area could also be achieved with equal efficacy by using a concave well [10], but this is considered inferior to the convex dome structure for the following three reasons: Firstly, the gap depth would be greatly increased in case of a concave well, causing a delay in reaching touch-mode operation and hence reducing the operating range. Secondly, the diaphragm would have to stretch much more, causing it to reach the shearing limit much earlier compared with a flat substrate. This is the opposite case for the convex dome, since the diaphragm would be supported by the substrate much earlier, causing it to reach its shearing limit later. Thirdly, the shape of the concave well mimics the shape of the stretched substrate, therefore the area of first touch in the transition region will be much higher, increasing the transition range of operation and causing a slightly more nonlinear response in the touch mode. The overall operating range of the touch mode will therefore decrease.

3 Design specifications and fabrication

The depth of the gap at the center is taken equal to half the distance between the convex substrate base and the diaphragm. Therefore, the dome height is equal to the depth of the gap at the substrate center with a value of 1 \(\upmu \hbox {m}\). This dome height value can be varied to obtain different capacitance responses. However, since the ratio of the substrate base radius to the dome height is very high, this will not result in a significant change in operation.

The radius of the sphere from which the substrate is sliced is taken to be very large to allow the dome height to be small enough to fit inside the cavity, whose height has been limited to 2 \(\upmu \hbox {m}\) (gap depth + dome height). This was done to mimic the basic structural composition in [14] to allow fair comparison of performance metrics between the two structures. All other design considerations are exactly the same as those in the model developed in [14], for result comparison.

The fabrication of such a three-dimensional dome-shaped structure can be achieved by using surface machining, ion irradiation, grayscale lithography, multiple lithography, and deep reactive-ion etching (DRIE). Silicon–silicon dioxide structure micromachining is generally used for such designs [19]. In ion irradiation, a high-energy focused proton beam is followed by electrochemical anodization. This method is used to produce three-dimensional (3D) Si structures in a single etch step [20]. Grayscale patterning and DRIE require appropriate photoresist and Si profiles to develop 3D structures. The etch selectivity can be tailored to meet the specifications of the grayscale application to develop the 3D dome structure. This method allows etch selectivity and reduces surface roughness and nonuniformity [21].

Table 1 Design parameters
Full size table

4 Mathematical modeling and derivation

A change in pressure causes the area covered by the diaphragm on the substrate to increase, thereby increasing the capacitance. The derivation for the capacitance versus pressure relationship is divided into four parts. Part 1 derives the relationship between the area of the convex substrate and its base radius. This is done since the relationship between the pressure and area of the diaphragm (derived in part II) is given based on the radius of the substrate base. Part III gives the final relationship between the area of the diaphragm covering the substrate and the pressure applied, which allows the relationship between capacitance and pressure to be derived directly in part IV.

Part I. Surface area of convex dome substrate versus radius of substrate base

Consider the following nomenclature. The values for the same can be found in Table 1. Refer to Fig. 5 for a diagrammatic analogy, where h is the convex substrate height, a is the base radius of the substrate, \(r_\mathrm{c}\) is the radius of the parent sphere from which the convex substrate is sliced, A is the surface area of the convex substrate, and \(\theta \) is the conic angle of the substrate base.

Fig. 5
figure 5

Dimensional notation of convex TMCPS

Full size image

For the following derivation, refer to Figs. 4 and 5.

The surface area of the substrate is given by

$$\begin{aligned} A=2\pi r_\mathrm{c}h, \end{aligned}$$
(1)

where the substrate height is given by

$$\begin{aligned} h=r_\mathrm{c} (1-\cos \theta ). \end{aligned}$$
(2)

Therefore,

$$\begin{aligned} A= & {} 2\pi r_\mathrm {c} ^{2}(1-\cos \theta ), \end{aligned}$$
(3)
$$\begin{aligned} \sin \theta= & {} \frac{a}{r_\mathrm {c} }, \end{aligned}$$
(4)
$$\begin{aligned} A= & {} 2\pi r_\mathrm {c} ^{2}\left[ {1-\sqrt{1-\sin ^{2}\theta }} \right] . \end{aligned}$$
(5)

Substituting (4) into (5) yields

$$\begin{aligned} A=2\pi r_\mathrm {c} ^{2}\left[ {1-\sqrt{1-\left( {\frac{a}{r_\mathrm {c} }} \right) ^{2}}} \right] . \end{aligned}$$
(6)

Let \(a_\mathrm{b}\) be the base radius of the surface area covered by the diaphragm in touch mode. Then, the surface area of the cap formed by \(a_\mathrm{b}\) is given by

$$\begin{aligned} A=2\pi r_\mathrm {c} ^{2}\left[ {1-\sqrt{1-\left( {\frac{a_\mathrm {b} }{r_\mathrm {c} }} \right) ^{2}}} \right] . \end{aligned}$$
(7)

Here, \(r_\mathrm{c}\) is a constant, whereas \(a_\mathrm{b}\) is a variable, dependent on the pressure P.

Fig. 6
figure 6

Substrate–diaphragm interaction in normal mode

Full size image

Part II. Base radius of curved diaphragm versus applied pressure

The deflection of the diaphragm is given by Eq. (8) [13, 22]

$$\begin{aligned} w(r,\theta )=w_0 \left[ {1-\left( {\frac{r}{a}} \right) ^{2}} \right] ^{2}, \end{aligned}$$
(8)

where

$$\begin{aligned} w_0 =\frac{Pa^{4}}{64D}. \end{aligned}$$
(9)

Equation (8) is fundamental to the analysis of the diaphragm behavior, as it provides the relationship between the diaphragm deflection \(w(r,\theta )\), the applied pressure P, and the radius of the curved diaphragm r.

The curvature of the diaphragm for fixed value of pressure is depicted in Fig. 6 and discussed in Sect. 5.

The relationship between the base radius \(a_\mathrm{b}\) of the diaphragm cap that is formed in touch mode and the pressure applied P can be obtained by restricting the deflection to the sum of the gap depth \(g^{{\prime }}\) and cap height h, as shown in Fig. 5.

Let \(g=g'+h\), which is a constant for our design and is equal to 2 \(\upmu \)m.

Therefore, substituting g into Eq. (8) and accounting for \(a_\mathrm{b}\) gives

$$\begin{aligned} g=\frac{Pa^{4}}{64D}\left[ {1-\left( {\frac{a_\mathrm {b} }{a}} \right) ^{2}} \right] ^{2}. \end{aligned}$$
(10)

Rearranging the terms to find \(a_\mathrm{b}\) yields

$$\begin{aligned} a_\mathrm {b} =a\sqrt{1-\left[ {\frac{1}{a^{2}}\sqrt{\frac{64Dg}{P}}} \right] }. \end{aligned}$$
(11)

Part III. Area of diaphragm covering the substrate versus pressure

The area of the diaphragm covering the substrate is given by substituting Eq. (11) into Eq. (7), i.e.,

$$\begin{aligned} A=2\pi r_\mathrm {c}^2 \left[ {1-\sqrt{1-\frac{1}{r_\mathrm {c}^2 }\left( {a^{2}-\sqrt{\frac{64Dg}{P}}} \right) }} \right] . \end{aligned}$$
(12)

The graphical implications of Eqs. (11) and (12) are discussed in Sect. 5

Part IV. Capacitance versus pressure

The capacitance generated is contributed by two regions. The first is the capacitance due to the parallel-plate capacitor formed between the diaphragm and substrate that are in contact. Let this be called \(C_{\mathrm{contact}}\). The second is the capacitance generated by the region of substrate and diaphragm having a gap between them. Let this be called \(C_{\mathrm{noncontact}}\).

Therefore,

$$\begin{aligned} C=C_{\mathrm{contact}} +C_{\mathrm{noncontact}}. \end{aligned}$$
(13)

\(C_{\mathrm{contact}}\) is formed by a parallel-plate capacitor between the diaphragm and substrate. There are two insulation regions between the two plates. Therefore, the capacitance is given by

$$\begin{aligned} C_{\mathrm{contact}} =\frac{A\varepsilon _0 \varepsilon _\mathrm {r} }{2t}, \end{aligned}$$
(14)

where A is the area of the diaphragm touching the substrate and is given by Eq. (12), \(\varepsilon _{0}\) is the permittivity of free space, \(\varepsilon _\mathrm{r}\) is the dielectric constant of silicon dioxide (Table 1), and t is the thickness of each insulation layer (Table 1).

Substituting Eq. (12) into (14) gives the relationship of \(C_\mathrm{contact}\) with pressure, thus

$$\begin{aligned} C_\mathrm{contact} =\frac{2\pi r_\mathrm {c}^2 \varepsilon _0 \varepsilon _\mathrm {r} }{2t}\left[ {1-\sqrt{1-\frac{1}{r_\mathrm {c}^2 }}\left[ {a^{2}-\sqrt{\frac{64Dg}{P}}} \right] } \right] .\nonumber \\ \end{aligned}$$
(15)

The noncontact capacitance is derived by taking the deflection into account and subtracting the base touch radius from r and \(a_\mathrm{b}\). The small-deflection model is used for this analysis, where the total gap depth is less than half of the substrate thickness. In this case, bending effects at the diaphragm edges can be ignored.

$$\begin{aligned} w(r,\theta )=\frac{Pa^{4}}{64D}\left[ {1-\left[ {\frac{r-a_\mathrm {b} }{a-a_\mathrm {b} }} \right] ^{2}} \right] ^{2}, \end{aligned}$$
(16)

where

$$\begin{aligned} a-a_\mathrm {b} =a_\mathrm {v}. \end{aligned}$$
(17)

Refer to [13, 23] for the validation of Eq. (16).

Fig. 7
figure 7

Substrate–diaphragm interaction in touch mode

Full size image

The relationship between the capacitance and the deflection of the diaphragm is given by

$$\begin{aligned} C_\mathrm{nc} =\int _0^{2\pi } {\int _{a_\mathrm {b} }^a {\frac{\varepsilon _0 \varepsilon _\mathrm {r} r\hbox {d}r\hbox {d}\theta }{t+\varepsilon _\mathrm {r} [g-w(r,\theta )]}} }. \end{aligned}$$
(18)

Conversely,

$$\begin{aligned} C_\mathrm{nc}= & {} 2\pi \varepsilon _0 \varepsilon _\mathrm {r} \int _{a_\mathrm {b} }^a {\frac{r\hbox {d}r}{t+\varepsilon _\mathrm {r} [g-w(r,\theta )]}}\nonumber \\ C_\mathrm{nc}= & {} 2\pi \varepsilon _0 \varepsilon _\mathrm {r} \int _{a_\mathrm {b} }^a {\frac{r\hbox {d}r}{t+\varepsilon _\mathrm {r} \left[ {g-\frac{Pa^{4}}{64D}\left[ {1-\left[ {\frac{r-a_\mathrm {b} }{a_\mathrm {v} }} \right] ^{2}} \right] ^{2}} \right] }}, \end{aligned}$$
(19)
$$\begin{aligned} C_\mathrm{nc}= & {} \frac{2\pi \varepsilon _0 \varepsilon _\mathrm {r} }{t+\varepsilon _\mathrm {r} g}\int _{a_\mathrm {b} }^a {\frac{r\hbox {d}r}{1-\frac{w_0 \varepsilon _\mathrm {r} }{t+\varepsilon _\mathrm {r} g}\left[ {1-\left[ {\frac{r-a_\mathrm {b} }{a_\mathrm {v} }} \right] ^{2}} \right] ^{2}}}. \end{aligned}$$
(20)

Making the following substitutions for simplicity of representation:

$$\begin{aligned}&k=\frac{w_0 \varepsilon _\mathrm {r} }{t+\varepsilon _\mathrm {r} g}, \end{aligned}$$
(21)
$$\begin{aligned}&\psi =\frac{r-a_\mathrm {b} }{a_\mathrm {v} }, \end{aligned}$$
(22)
$$\begin{aligned}&\hbox {d}r=a_\mathrm {v} \hbox {d}\psi \nonumber \\&\varepsilon =\varepsilon _0 \varepsilon _\mathrm {r}, \end{aligned}$$
(23)

the capacitance is obtained as

$$\begin{aligned} C_\mathrm{nc} =\frac{2\pi \varepsilon }{t+\varepsilon _\mathrm {r} g}\int _0^1 {\frac{(a_\mathrm {v} \psi +a_\mathrm {b} )a_\mathrm {v} \hbox {d}\psi }{1-k\left[ {1-\psi ^{2}} \right] ^{2}}}. \end{aligned}$$
(24)

Let

$$\begin{aligned}&I_1 =\int _0^1 {\frac{\psi \hbox {d}\psi }{1-k\left[ {1-\psi ^{2}} \right] ^{2}}}, \end{aligned}$$
(25)
$$\begin{aligned}&I_2 =\int _0^1 {\frac{\hbox {d}\psi }{1-k\left[ {1-\psi ^{2}} \right] ^{2}}}, \end{aligned}$$
(26)
$$\begin{aligned}&C_\mathrm{nc} =\frac{2\pi \varepsilon }{t+\varepsilon _\mathrm {r} g}\left[ {a_\mathrm {v}^2 I_1 +a_\mathrm {v} a_\mathrm {b} I_2 } \right] . \end{aligned}$$
(27)

Solving for \(I_{1}\) and \(I_{2}\) yields

$$\begin{aligned} I_1= & {} \frac{1}{2}\frac{\arctan h\sqrt{k}}{\sqrt{k}}, \end{aligned}$$
(28)
$$\begin{aligned} I_2= & {} \frac{1}{2}\frac{\arctan \left( {\frac{\sqrt{k}}{\sqrt{\sqrt{k}-k}}} \right) }{2\sqrt{\sqrt{k}-k}}+\frac{1}{2}\frac{\arctan h\left( {\frac{\sqrt{k}}{\sqrt{\sqrt{k}+k}}} \right) }{2\sqrt{\sqrt{k}+k}}. \end{aligned}$$
(29)

Therefore, from Eqs. (27–29), the total capacitance versus pressure is found to be

$$\begin{aligned} C_{\mathrm{contact}}= & {} \frac{2\pi r_\mathrm {c}^2 \varepsilon _0 \varepsilon _\mathrm {r} }{2t}\left[ {1-\sqrt{1-\frac{1}{r_\mathrm {c}^2 }}\left[ {a^{2}-\sqrt{\frac{64Dg}{P}}} \right] } \right] \nonumber \\&+\frac{2\pi \varepsilon }{t+\varepsilon _\mathrm {r} g}\left[ {a_\mathrm {v}^2 I_1 +a_\mathrm {v} a_\mathrm {b} I_2 } \right] , \end{aligned}$$
(30)

where

$$\begin{aligned} I_1= & {} \frac{1}{2}\frac{\arctan h\sqrt{k}}{\sqrt{k}},\\ I_2= & {} \frac{1}{2}\frac{\arctan \left( {\frac{\sqrt{k}}{\sqrt{\sqrt{k}-k}}} \right) }{2\sqrt{\sqrt{k}-k}}+\frac{1}{2}\frac{\arctan h\left( {\frac{\sqrt{k}}{\sqrt{\sqrt{k}+k}}} \right) }{2\sqrt{\sqrt{k}+k}},\\ k= & {} \frac{Pa^{4}\varepsilon _\mathrm {r} }{64D(t+\varepsilon _\mathrm {r} g)},\\ a_\mathrm {b}= & {} a\sqrt{1-\left[ {\frac{1}{a^{2}}\sqrt{\frac{64Dg}{P}}} \right] },\\ a_\mathrm {v}= & {} a-a_\mathrm {b}. \end{aligned}$$

Therefore, Eq. (30) and the subsequent substitutions give the final relationship between the capacitance and pressure applied.

5 Results and discussion

The mathematical model derived above is now used to analyze various relationships to develop an analytical model and compare the same with the results generated in [14], and to see whether it fits the initial intuitive projections made in Sect. 2. Firstly, the variation in the diaphragm shape with respect to the substrate in normal mode is shown in Fig. 6. The diaphragm variation is obtained from Eq. (8). This shows the shearing strain increase at the edges where the diaphragm is clamped. As the applied pressure is increased, it descends into the cavity, eventually touching the substrate.

The touch-mode interaction between the diaphragm and substrate is depicted in Fig. 7. As can be seen, the diaphragm wraps over the convex substrate, forming a convex cap-like structure. The cap formed has a base radius that increases as the applied pressure is increased. This base radius variation with pressure is depicted in Fig. 8.

The variation in base radius of the cap (Fig. 8) formed when the diaphragm touches the substrate is revealing, since it accounts for the increase in the shear stress produced at the clamping of the diaphragm. This is evident in the graph, since the base radius of the diaphragm cap reaches a saturation point (170 \(\upmu \hbox {m}\)) before the base radius of the substrate (180 \(\upmu \hbox {m}\)). This saturation in base radius carries over to a saturation in the diaphragm cap covering the substrate. Therefore, the diaphragm cap can never fully cover the substrate, and the saturation thus produced is also reflected in the saturation of the capacitance versus pressure, as shown in Fig. 10. There is also a slight delay observed in the increase in the base radius at 0.23 MPa. This is evidence of the touch point. The touch point occurs only when the diaphragm descends far enough to touch the substrate, as shown in Fig. 9; until then, the base radius is zero. Therefore, the touch point pressure (TPP) is indicated in the graph obtained.

Fig. 8
figure 8

Variation in diaphragm cap base radius with pressure

Full size image
Fig. 9
figure 9

Touch point: transition between normal mode and touch mode

Full size image
Fig. 10
figure 10

Capacitance variation with pressure

Full size image

An amalgamation of the results found in the above three graphs is shown in Fig. 10. Here, observe the touch-mode operation capacitance developed with respect to pressure. The graph starts at 0.23 MPa, since it was observed that the touch mode starts there in the previous graph. A comparison with the results generated for a flat-substrate TMCPS from [14] is given. Also included is the variation in the capacitance developed for different substrate heights of 0.5, 1, and 1.5 microns. Note that the starting point of the touch-mode capacitance generated is incrementally higher for each case, since the parallel-plate depth becomes incrementally smaller. Also notice that the saturation region is reached earlier in the 1.5-micron case but later in the 0.5-micron case, since the substrate area is higher and lower, respectively. It is clearly observed that the increase in the area of contact between the diaphragm and substrate, which is the major contributor to the capacitance developed, results in the development of a much higher capacitance for given pressure. The linearity of the graph is also higher, as was expected due to the change in interaction between the convex substrate and diaphragm. The saturation region for the flat-substrate TMCPS occurs at the 1.2 MPa mark, whereas that for the convex substrate extends further, to nearly 1.8 MPa. Therefore, the range of near-linear operation is also wider, indicating a superior design. The touch mode of operation for the flat substrate begins at 0.3 MPa, as seen in [14], whereas for the convex substrate, the touch mode starts much earlier at 0.23 MPa. This was forecast above based on intuitive analysis and is now validated by Figs. 8 and 10. Therefore, all the forecasts made in our intuitive analysis are validated by the results obtained.

6 Conclusions

Section 1 briefly introduced the working of a capacitive pressure sensor in normal mode and touch mode. A proposal for a novel design upgrade was introduced. Section 2 delved into the intricate details of the design, and an intuitive projection of the predicted results was analyzed. Section 3 provided the design specifications needed for such a design to be compared with the existing flat-substrate model. Section 4 provided a comprehensive mathematical model for the proposed design. The mathematical model was executed step by step to provide better understanding of the implications of such a design in terms of sizing and to develop an analytical model. Section 5 discussed the analytical model in depth. It was found that the results of the analytical model concurred with the intuitive analysis performed before in Sect. 2. Also, the results show a considerable improvement over those in corresponding research of the flat-substrate TMCPS. The capacitance of the convex TMCPS is nearly 90 % higher than that of the flat-substrate TMCPS. Also an improvement of 0.07 MPa was observed in the starting point of touch-mode operation. The overall range of the touch mode increased from 0.9 MPa to 1.5 MPa. The linearity of the response was observed to be slightly higher. The overall results show a considerable improvement in performance for a small change in design. Therefore, a verdict may be drawn in favor of the convex TMCPS, as it serves as a novel improved design in the repertoire of capacitive pressure sensors.