Introduction

Computational prediction of pKa values is of considerable interest for a number of fields including pharmaceutical and material sciences [1,2,3]. Even though several methods have been developed to predict this value, the problem still remains a challenge [4,5,6]. Most prediction methods can be divided into two broad categories—empirical and ab initio ones.

The first set of methods use a cheminformatics based approach [7,8,9]. In this approach the compound is represented as a vector of molecular descriptors including constitutional, topological, electrostatic and quantum descriptors [10]. Machine learning models for specific functional groups are trained based on these descriptors [10]. Notably, these methods ignore the three dimensional conformation of the compound explicitly [11]. Although training the models might be expensive in terms of curating experimental pKa data for generating appropriate models, subsequent pKa prediction using trained models can be very fast and inexpensive.

Ab initio methods use a thermodynamic cycle combining with quantum mechanics (QM) calculations to compute the solvent-phase pKa [12,13,14,15,16,17,18,19,20] . It consists of the calculation of dissociation free energy in gas phase [21] along with solvation free energy of the acid and the conjugate base using dielectric continuum solvation models (DCSMs) [12, 22,23,24,25]. These methods have been very successful in calculating pKa. However, DCSMs cannot model the hydrogen bonding between solute and water, which can be important in the protonation or deprotonation process [26]. Their accuracy in describing the short-range electrostatics of polar solutes and ions is also limited [12]. Moreover, typically only one conformation is used for the estimation of free energy although an ensemble of conformations is required for a complete statistical mechanics treatment of the free energy [27]. Even if multiple low lying conformations are included in the calculation, the entropic variations associated with the deprotonation process still cannot be completely accounted for without explicitly considering the solvent dynamics and extensively exploring the potential energy landscape of the solute–solvent systems.

Calculation of solvation free energy during pKa estimation remains one of the bottlenecks in getting accurate values. An alternative way of calculating solvation free energy is to use molecular dynamics simulations with empirical force field [28,29,30]. Shirts et al. were able to do a very precise measurement of solvation free energy with 0.85 kcal/mol RMSE [31]. Gilson and co-workers used double decoupling method and achieved 1.3 kcal/mol RMSE. König et al. [29] used the annihilation approach and obtained accuracy on par with the quantum calculations. Mobley et al. have created the FreeSolv [30] database to catalog molecules with known experimental solvation free energy and assist in development of new methods from these resources.

Given the large number of diverse methods available for predicting pKa, the Statistical Assessment of the Modeling of Proteins and Ligands (SAMPL) [32] blind prediction challenge was organized to assess the methods on a common set of small drug-like molecules. Previous iterations of the SAMPL competitions have focussed on assessing methods for solvation free energy calculations [33], distribution coefficient and other challenges [34,35,36,37]. We note that in the SAMPL5 distribution coefficient competition, Pickard and coworkers have calculated pKa values with QM methods, and used computed pKa to further correct their prediction of distribution coefficients [34].

In this work we have presented a new method to computationally predict the pKa of small drug-like molecules in explicit solvent. This is a hybrid QM and MM approach that allows ab initio prediction of absolute pKa values and supports any chemistry. Since calculation of pKa requires relative solvation free energy between the acid (protonated species) and the conjugate base (deprotonated species), our method calculates this quantity directly rather than computing the absolute solvation free energies of both by employing two thermodynamic cycles.

This paper is organized as follows. In “Theory” section, we describe the theory behind the prediction of the microscopic and macroscopic pKa values. “Method” section covers the details of the description of the QM and MM methods that we used to carry out calculations. Next in “Result and discussion” section, we present our results that submitted to the SAMPL6 competition and analyze the accuracy of the results. Finally in “Conclusion” section, a brief conclusion is provided.

Theory

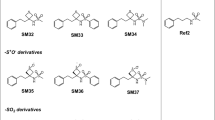
SAMPL6 pKa challenge involved blind computational prediction of pKa of 24 small drug-like molecules (Fig. 1). These molecules were similar to kinase inhibitors and were chosen for experimental tractability. All the molecules were polyprotic in nature i.e. there were multiple sites on each molecule where the molecule could lose a proton. For further details, please refer Isik et al. [38] where the organizers have described the rationale for choosing the molecules as well as the methods used for experimental pKa prediction.

Fig. 1
figure 1

Molecules in the SAMPL6 prediction challenge

Full size image

In order to compare the computational and experimental pKa predictions, it is important to understand the difference between the microscopic and macroscopic pKa of a molecule. The chemical environment around a functional group (in this case, the protonation state of other titrable moieties) affect the propensity of the group to lose its proton. This is referred to as the microscopic pKa, i.e. pKa for deprotonation at a site at a fixed protonation state of all other titrable sites in the molecule. This differs from the macroscopic pKa which is related to the dissociation constant of losing a proton from the molecule as a whole and can be experimentally measured. Converting microscopic pKas to macroscopic pKas or vice versa is complicated due to the large number of equilibrium processes involved [8, 39]. If, for a specific charge transition, the microscopic pKas are fairly well separated (ex. more than one pKa unit), the smallest pKa can be considered as the macroscopic pKa. However, if they are close, the macroscopic pKa is shifted as multiple microscopic transitions contribute to the macroscopic value. Several studies [40, 41] discuss this in greater detail. In our method, we calculate microscopic pKa value for each acid–base pair of microscopic states. We then assign one dominant microscopic pKa as the macroscopic pKa for each titration process, which can be directly compared with the experimental observables.

To calculate the microscopic pKa of a particular acid–base pair, let us consider the dissociation of acid HA

$$\begin{aligned} HA_{aq} \rightleftharpoons H^+_{aq} + A^-_{aq} \end{aligned}$$

Here the subscripts ‘’aq‘’ indicate that the species are solvated in water. The dissociation constant and pKa value for this dissociation are given by the following relations:

$$\begin{aligned} K_a= & {} \frac{ [H^+]_{aq}[A^-]_{aq} }{[HA]_{aq}}\\ pKa= & {} \frac{\varDelta G^*_{aq}}{RTln(10)} \end{aligned}$$

where

$$\begin{aligned} \varDelta G^*_{aq} = G^*(H^+_{aq}) + G^*(A^-_{aq} ) - G^*(HA_{aq}) \end{aligned}$$

Here, G refers to the absolute Gibbs free energy of the solvated species. The superscript * implies that the standard state of 1 mol/L and 298.15 K have been used. R and T are the gas constant and the absolute temperature respectively. Thus, to calculate pKa we need to calculate aqueous phase deprotation free energy \(\varDelta G_{aq}\).

Rather than calculating the absolute free energies in the aqueous phase directly, the aqueous phase calculations are coupled with gas phase calculation using the following thermodynamic cycle (Fig. 2a). The two vertical lines in the figure refer to the solvation of the species into aqueous phase. Thus, the \(\varDelta G_{aq}\) can be calculated as

$$\begin{aligned} \varDelta G^*_{aq}= & {} \varDelta G^*_{g} + \varDelta G^*_{solv}(H^+) + \varDelta G^*_{solv}(A^-) \\&- \varDelta G^*_{solv}(HA) \end{aligned}$$

The absolute free energy for proton \(H^+\) in the gas phase at standard temperature and pressure is calculated by Sackur–Tetrode equation and has been previously calculated as − 6.28 kcal/mol [42]. Solavtion free energy of proton (− 264.5 kcal/mol) has been taken from Tissandier et al. [43]. The gas phase calculations are done at standard gas conditions i.e. one atmosphere of pressure. Converting them to 1 mol/L further involves a standard state correction of − 1.89 kcal/mol.

Fig. 2
figure 2

Thermodynamic cycles used in the pKa calculations a chemical reaction of acid dissociation. This relates the free energy of dissociation in the aqueous phhase as with the gas phase free energy of dissociation and solvation free energies of the acid, base and proton. b Alchemical cycle for deprotonation. This cycle relates the solavtion free energy difference of the HA and A−\(^-\) with difference in free energy for deprotonation in the aqueous and gas phases

Full size image

The above equation involves the calculation of solvation free energies of the deprotonated \(\varDelta G^*_{solv}(A^-)\) and of the protonated species \(\varDelta G^*_{solv}(HA)\), respectively. Most ab initio pKa prediction methods compute them in implicit solvent using quantum chemistry and continuum solvent approaches. We note that, however, the only relevant quantity for pKa prediction is the difference of solvation free energies

$$\begin{aligned} \varDelta \varDelta G^*_{solv} = \varDelta G^*_{solv}(A^-) - \varDelta G^*_{solv}(HA) \end{aligned}$$

In the present work, we directly compute this solvation free energy difference in explicit solvent. The calculation is done at the force field level in order to be computationally tractable. Furthermore we consider a second thermodynamic cycle (Fig. 2b) that alchemically change HA into \(A^-\) in the gas and the aqueous phases. As we are interested in only the free energy difference between the two species HAand \(A^-\) and free energy is a state function so that its sum over a thermodynamic cycle equals zero, we can rewrite \(\varDelta \varDelta G^*_{solv}\) as

$$\begin{aligned} \varDelta \varDelta G^*_{solv}=\, & {} \varDelta G^*_{solv}(A^-) - \varDelta G^*_{solv}(HA) \\=\, & {} \varDelta G^*_{deprot,aq}(HA) - \varDelta G^*_{deprot,g}(HA) \end{aligned},$$

where \(\varDelta G^*_{deprot}(HA)\) can be calculated using free energy perturbation (FEP) methods such as the thermodynamics integration (TI) method. By introducing a number intermediate \(\lambda\) states that alchemically connecting two states 0 and 1, the free energy difference between the two end state is computed by TI as

$$\Delta G = \int\limits_{0}^{1} {\left\langle {\frac{{dU}}{{d\lambda }}} \right\rangle } _{\lambda } d\lambda$$

It’s worth pointing that for each acid–base pair only one relative free energy in the aqueous phase is computed, rather than two absolute solvation free energies. It has previously been shown by Jorgensen et al. [44] that this allows the cancellation of errors in MM calculations such as inaccuracy of force field parameters and inadequate conformational samplings. In their work they calculated the relative solvation free energy of methanol and ethane using alchemical transformation of methanol to ethane and vice versa and got results close to experimental relative solvation free energy value. The major advantage of using such a secondary thermodynamic cycle (Fig. 2b) is that the alchemical FEP only involves changing HA into \(A^-\) in the gas and the aqueous phase, instead of annihilating whole molecules in the aqueous phase. This greatly improves the efficiency, accuracy and the throughput of our calculations.

In summary, we calculate the \(\varDelta G^*_{aq}\) by the following equation

$$\begin{aligned} \varDelta G^*_{aq}=\, & {} \varDelta G^*_{g} + \varDelta G^*(H^+) + \varDelta G^*_{deprot,aq}(HA) \\&- \varDelta G^*_{deprot,g}(HA) \end{aligned},$$

where \(\varDelta G^*_{g}\) is calculated in the gas phase at the QM level, \(\varDelta G^*(H^+)\) is obtained from experimental value reported in literature, \(\varDelta G^*_{deprot,aq}(HA)\) is calculated using FEP in condensed phase at the MM level and \(\varDelta G^*_{deprot,g}(HA)\) in gas phase at the MM level.

Method

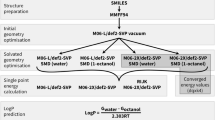
The work flow for the complete method is shown in Fig. 3. First the geometry of each microstate was optimized in gas phase. Then for each acid (protonated)–base (deprotonated) pair, \(\varDelta G\) for deprotonation in gas phase was calculated at the QM level. To carry out the MM simulations, force field parameters were generated for each of the microstates. Next, the gas phase and aqueous phase alchemical free energy difference between each acid–base pair were computed using FEP and MD simulations. All the QM calculations were performed with Gaussian16 [45] , while all the MD simulations were done with CHARMM [46, 47].

Fig. 3
figure 3

Workflow for the hybrid QM and MM pKa prediction approach

Full size image

Geometry optimization and gas phase QM calculation

SAMPL6 pKa challenge had 24 molecules, each with different number of microstates. SMILES [48] string of the microstates were converted to PDB files using OpenBabel [49]. Geometry optimization and gas phase deprotonation energy \(\varDelta G^*_{g}\) was calculated with the M06-2X density functional theory [50] and 6-31G* basis set for neutral–cationic microstate pairs and 6-31+G* for neutral–anionic microstate pairs. “Ultrafine grid” and “Tight” convergence criteria were used in all calculations.

We would like to point out that as the computed pKa are directly related to the calculated electronic energies, higher-level methods such as MP2 and larger basis sets such as cc-pVTZ would improve calculation results. These, however, have not been pursued in this study. We also did not test other functionals, which might potentially lead to better pKa prediction results.

Parameterization of microstates

In order to carry out molecular dynamics simulations, we first generated force field parameters for the microstates based on the fixed-charge molecular mechanics potential energy functions used in CHARMM [51]. The potential energy is given by a sum of bonded and non-bonded components:

$$\begin{aligned} U = U_{bonded} + U_{non\text{-}bonded} \end{aligned}$$

where,

$$\begin{aligned}&U_{bonded} = \Sigma _{bond} K_b(r_{ij} - r_0)^2 +\Sigma _{angle} K_{\theta }(\theta _{ij} - \theta _0)^2\\&+\Sigma _{dihedrals} K_{\chi } (1 + cos(n \chi - \delta )) +\Sigma _{improper} K_{imp} (\phi - \phi _{0})^2\\&U_{non-bonded} = \Sigma \frac{q_i q_j}{4\pi \epsilon _0 r_{ij}} + \epsilon _{ij}\left[ \left(\frac{R_{min}}{r_{ij}}\right)^{12} - 2\left(\frac{R_{min}}{r_{ij}}\right)^{6}\right] \end{aligned}$$

Here, \(K_b\) and \(r_0\) are bond force constant and equilibrium bond-length for each atom type pair. \(K_{\theta }\) and \(\theta _0\) are angle force constant and equilibrium angle for each angle type triplet. \(K_{imp}\) and \(\phi _0\) are improper angle force constant and equilibrium improper angle for each improper angle. \(K_{\chi }\), n, and \(\delta\) are the force constant, periodicity, and phase for each torsional degree of freedom. The non-bonded potential energy terms involve Coulombic interactions between partial charge \(q_i\) and \(q_j\), and the van der Waals (VdW) interactions modeled by the \(\epsilon _{ij}\) and \(R_{min}\) parameters.

We used Antechamber to generate GAFF parameters. Single point calculation was done on the optimized geometry mentioned above using Gaussian16 at MP2 level of theory with 6-31G* basis set. RESP charges were calculated using the protocol mentioned in Jakalian et al. [52]. Electrostatic potential was written in a data file using the option IOp(6/33=2) in Gaussian, and the RESP charges were fitted. Other parameters—bonded (bond, angle and torsion) and non-bonded (van der Waals) were assigned as per the General Amber Force Field (GAFF) [53] using the Antechamber [52] program in the AmberTools16 software. CHARMM formatted parameter and topology files were produced. These parameters were modified by in-house scripts to make the formats compatible with CHARMM molecular dynamics package. If the residues did not have an integer charge in the generated topology file (typically off by \(\pm 0.0-0.003\) ), an ad-hoc fix was done by adjusting the charge on a random non-hydrogen atom to round up the total charge of residue.

Free energy simulations

All molecular dynamics simulations were carried out with CHARMM [47] and parameter sets mentioned in the previous subsection. Thermodynamic Integration calculations were carried out using the PERT module of CHARMM. 12 \(\lambda\) windows were used (0.0. 0.075, 0.15, 0.25, 0.35, 0.45, 0.55, 0.65, 0.75, 0.85, 0.95, 1.00) for transforming the partial charges of the acid into those of the conjugate base, with the charge on the dissociating proton transforming to zero. Each \(\lambda\) window was equilibrated for 1 ps followed by 10 ps MD simulations for sampling.

MD simulations in the gas phase were carried out with Langevin dynamics at a temperature of 298 K and using a time step of 2 fs with a friction coefficient of 5 ps\(^{-1}\) on all the atoms. No cutoffs were used in calculation of nonbonded interactions for gas phase simulations. For aqueous phase simulations, we used 2022 water molecules to solvate the solute molecule, consituting a 38 Å cubic water box to start with. 50 ps NPT simulations were run at 298 K and 1 atm, after which NVT simulations at 298 K were carried out for TI calculations. A Nosé-Hoover thermostat [54] was used to maintain the microcanonical ensemble. Particle mesh ewald [55] was used to calculate the long range electrostatic interactions with a direct space cutoff of 10 Å. Charge was spread on a grid of 48 × 48 × 48 for reciprocal space calculation using 6th order B-spline interpolation method [56]. A cutoff of 12 Å was applied for van der Waals interactions, and the integration time step is 1 fs.

Result and discussion

The results discussed in this report are the ones that we submitted for the SAMPL6 competition [submission id: 0wfzo]. We submitted only the microscopic pKas for all acid–base pairs of all the 24 molecules. These results were compared to macroscopic pKas using two different approaches—closest and Hungarian. This analysis was done with the assumption that experimentally observed pKas with only one observed pKa or fairly-distant pKas (separated by more than 3 units) are equal to the microscopic pKa of the corresponding microscopic pKa. Only two molecules—SM14 and SM18—did not satisfy this criterion and hence they were excluded from this analysis. Detailed analysis of the results can be found at https://github.com/MobleyLab/SAMPL6/tree/master/physical_properties/pKa/analysis/analysis_of_typeI_predictions.

In the closest analysis approach, the experimentally observed pKa is matched with the microscopic pKa which minimizes the absolute error i.e. the one that is closest to the observed pKa (Table 1). We achieved a root mean squared error (RMSE) of 2.42 pKa units with respect to the experimental values. The mean absolute error (MAE) was 1.61 pKa units. The corresponding \(R^2\) for regression fit was 0.53 and the slope of line was 1.08.

Table 1 Statistics of the performance of the method using Hungarian and closest schemes
Full size table

In the hungarian approach [57], an optimum global match between experimentally observed pKa and predicted set of pKas is found by minimizing the linear sum of squared errors of the paired match (Table 1). We achieved a RMSE of 2.89 pKa units with respect to the experimental values. The MAE was 1.88 pKa units. The corresponding \(R^2\) for regression fit was 0.48 and the slope of line was 0.99.

Out of the 22 molecules whose results were compared to experimental results, 3 of the molecules (SM06, SM15 and SM22) had 2 macroscopic pKas in the 2–12 pKa range while the other molecules had just 1 pKa in this range. Among these 25 comparisons, only five predictions were more than 2 pKa units away from the experimental values (Table 2). The most erroneous one concerns SM15, of which the fist predicted pKa underestimated the experimental measurement by 8.86 pKa units, and the second pKa overestimated by 3.52 pKa units (Fig. 4).

Fig. 4
figure 4

Plot of the closest analysis scheme and experimental pKa values. Plot courtesy of the organizers https://github.com/MobleyLab/SAMPL6/blob/master/physical_properties/pKa/analysis/analysis_of_typeI_predictions/analysis_outputs_closest/pKaCorrelationPlots/0wfzo.pdf

Full size image
Table 2 Comparison of experimental and calculated values using the closest scheme
Full size table

In general, our results compare less favorably to some of the more-established methods of pKa prediction, as used by other submissions in the SAMPL6 challenge. By carefully examining our calculations after the submission, a few mistakes were spotted, which are further analyzed and discussed here.

One major error is that the standard state correction was missed in our submission. The QM level gas phase calculation are done at standard state of gas while the aqueous phase species are at 1M concentration. This standard state correction needs to be applied while calculation of the overall free energy difference. This contribution is equal to − 1.89 kcal/mol, i.e. 1.4 pKa units.

Another source of error comes from the inconsistency with GAFF protocol. Standard AMBER and GAFF force fields scale the electrostatic interaction between third-neighbors (1–4 interactions) by 0.833, while CHARMM force fields on the other hand do not scale the electrostatic 1–4 interactions. In the CHARMM program, an option e14fac (electrostatic 1–4 interaction scaling factor) should be set to 0.833 to use GAFF force fields, however its default value of 1.0 was used in our simulations by mistake. Furthermore, the CHARMM modified TIP3P parameter were used for water molecules which place a small \(\epsilon\) value on the water hydrogen atom. These deviations to the standard GAFF practice render the force field parameters used in this work less optimal.

Other methods to generate more CHARMM-like force field parameters for the microstates have been attempted. The Paramchem server [58], which generates CGENFF force field parameters, was found to report error messages when parametrizing several charged species. The force field ToolKit (ffTK) [59], which is a plugin in VMD that generates CHARMM parameters, was found to be difficult in automatically generating parameters for all the microstates. Since we needed a method that could parameterize all the microstates in a high throughput fashion, we instead opted for using for Antechamber from AmberTools package.

From the absolute error analysis (Supplementary Fig. 2) we can assume that SM15 parameters are not optimal as the errors for both pKa are very high for this molecule. Force field parameterization for small molecules is indeed difficult due to the very large chemical space of these molecules as compared to the amino acids [60]. The latter have seen several decades of work for a very limited number of species. The general strategy of optimization of parameters of molecules involves the use experimental hydration free energy data [61]. Optimization with this parameter would also be helpful as we indeed need to predict the solvation free energy difference. However, many of microstates of these molecules are charged species and getting high accuracy experimental hydration free energy data would be difficult. Even Self-Consistent Reaction Field based implcit solvent model calculations have one order of magnitude higher error as compared to neutral species [23, 62]. One way to study the SM15 errors would be to generate parameters with a different force field and compare their relative performance. While Antechamber generates GAFF-based parameters, ffTK can be used to used to generate CHARMM-based parameters.

Our simulation runs also suffered from inadequate sampling of the phase space in the aqueous phase simulation. For the calculation of hydration free energy in SAMPL4 competition with similar system sizes, Gilson and co-workers [28] had simulated each λ point for 5 ns. König et al. [29] for the same set of molecules had used a 0.5–1 ns simulation for each λ state in aqueous phase. In principle much less sampling time would be required in our FEP calculations as relative free energies instead of absolute solvation free energies were being computed. However, the MD simulation time used in this study was still too short (10 ps per λ state), not allowing full water reorganization upon solute deprotonation. The number of simulations that we were performing was much larger (~ 650 in SAMPL6 vs. 24 in SAMPL4) and hence we performed only 0.12 ns simulations for each acid–base pair. Achieving proper sampling is an area of active research in the molecular dynamics field. Indeed, one of the competitions in the SAMPL6 challenge focused on benchmarking this quantity especially in a blind setup. The results from that study would be able to set community-wide guidelines for benchmarking. A heuristic that we should have used to reduce the number of microstate pairs should have been to exclude all microstates that had charges more than 1 or less than − 1 i.e. consider only neutral and singly-charged microstates. Some of the other submissions, have used this strategy to limit the number of microstate pairs that needs to be considered without loss in accuracy.

The FEP scheme we used for alchemical transformation included only the transformation of charges on all atoms from the protonated acid to the its deprotonated conjugate base. This was similar in principle to the strategy used by Lee et al. in their enveloping distribution sampling (EDS) based constant-pH simulations [63], where each state differed from the reference state in only the charges on the residue of deprotonation. The changes in the parameters for VdW interactions as well as the internal degrees of freedom during the solute deprotonation process will also contribute to free energy difference, which is not captured in our FEP calculations. We note that it’s feasible to include these effects by interpolating all force field parameters, although the bonded interactions might need to be carefully handled [64].

Another possible source of error comes from the value of \(\varDelta G^*(H^+)\). Solvation free energy of proton is a contentious value and a range of values from − 259 to − 264 kcal/mol are available in the literature. This can lead to large errors in the absolute prediction of pKa as just an difference of 1.36 kcal/mol is equivalent to 1 pKa unit. One way to handle this error is to use isodesmic reactions with another acid with known experimental pKa and couple two thermodynamic cycles together such that the solvation free energy of proton cancels out. The second acid chosen should also be similar to the original acid that we are interested in. Essentially, the pKa shift is calculated with respect to a simpler model compound with known experiemental pKa values, as being done in most constant pH simulation methods [63, 65, 66]. Our approach instead aims at prediciting the absolute pKa, and a fixed value of − 264.5 kcal/mol is used for \(\varDelta G^*(H^+)\) as derived from cluster-ion solvation data by Tissandier et al. [43]. An alternative way to handle this issue, as well as other systematic errors in absolute pKa calculations, is to perform a linear free energy regression against molecules with known experimental pKa, i.e., to consider \(\varDelta G^*(H^+)\) as a variable whose value is fitted to best reproduce a set of known pKa values. The empirical correction has been shown to improve the results although the slope of the regression still remains a debatable issue [12]. We have also used the assumption that only one microscopic pKa contributes to the macroscopic pKa if the former are fairly well separated. However, this is an approximation as for a given charge transition, multiple protonated–deprotonated pairs of microstates contribute to the macroscopic pKa [41].

In our approach the \(\varDelta G^*_{g}\) is computed using QM calculations at the M06-2X level using 6-31G* basis set (6-31+G* for microstate pairs involving anionic species). Higher level of ab initio methods, larger basis set, and including counterpoise correction should improve our results. Although our method allows the sampling of the phase space during the calculation of the solvation free energy difference, only one conformation (the energy minimized one) is considered for the calculation of \(\varDelta G^*_{g}\) by QM in the gas phase. This is again an approximation as previous work by Bochevarov et al. [11] have shown that multiple low lying conformations do contribute to the deprotonation free energy. There can be a couple of different strategies to handle this phenomenon. Multiple low lying conformations can be sampled and the deprotonation energy of each important conformation can be calculated separately and combined together in a Boltzmann weighted sum. Another solution for this problem is to use reweighting as used by Tao et al. [67]. Free energy of constraining the geometry to the ones used the calculation of gas-phase QM step, can be calculated separately and will have to be added for the protonated microstate and subtracted for the deprotonated microstate.

One of the key physics behind the free energy of deprotonation and hence pKa is the water reorganization when the solute is protonated or deprotonated, which involves water response to the sudden changes of charge distributions. In this case, polarizable force fields should in principle provide higher accuracy in our approach as fixed charge force-fields are limited in their ability to account for the change in charges during the course of the simulation. A theoretically-promising method to handle this effect is to use polarizable force fields such as AMOEBA [68, 69], Drude [70] or a recently formulated multipole and induced dipole (MPID) model [71]. Any of these polarizable models should improve the pKa prediction results of our method, given high quality polarizable force field parameters for general drug-like molecules are available.

Conclusion

This work reports our submission for the SAMPL6 pKa prediction challenge, where we have attempted to calculate pKa of small drug-like molecules in explicit solvent using a hybrid QM and MM approach. While including multiple solvation shells is difficult in pure ab initio (QM) methods, modeling the dissociation of a proton is difficult at the MM level using conventional force fields. The novel contribution of this work is devising a method to allow the calculation of \(\varDelta\)G in explicit solvent while limiting the cost of the calculations. This is important for a high throughput prediction where a large number of microstates need to be considered.

However, traditional limitations in molecular dynamics simulation approaches limits its competitiveness as compared to a machine learning approach or a full-quantum level implicit solvent approach. At the same time we committed a few avoidable mistakes in carrying out the simulations. Due to these results from the present version of our method did not do very well in the SAMPL6 pKa challenge. More work needs to be done to optimize and automate the protocols.

We are currently working on improving the method. We need to improve force field parameters for the small molecules, ensure proper sampling of the intermediate lambda points during free energy calculations and utilize a higher level of theory for the gas phase QM calculations. Our new version of the method is an open source tool where we can use test the method easily for each of these factors. It will allow the method to be used for not just pKa calculation of small molecules but for larger proteins of interest as well. The open source tool, currently in development, is available at https://github.com/samarjeet/hpka.