Poisson–Nernst–Planck model of multiple ion transport across an ion-selective membrane under conditions close to chlor-alkali electrolysis

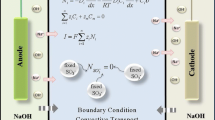
Abstract

The assumption of electrochemical equilibrium at membrane–electrolyte interfaces is frequently accepted in a mathematical simulation of multiple ion transport (MIT) across a single-layer perfluorinated sulfonated cation-selective membrane (CM). This assumption is obviously inaccurate at high electric current loads typical of industrial applications, e.g. brine electrolysis. An assessment of this problem is one of the main objectives of this contribution. For this purpose, a one-dimensional stationary Poisson–Nernst–Planck (PNP) model was employed to describe MIT across a CM. The model input parameters used correspond closely to industrial chlor-alkali electrolysis. The model results are compared with those of an equivalent model published earlier that considered the classical Nernst–Planck equation and Donnan equilibrium at the CM–electrolyte interfaces (denoted as the DNP model). Both the DNP and the PNP models provide identical results at low current loads. However, a comparison at high current loads close to ‘industrial scale’ was impossible due to convergence problems of the DNP model. The ion transport numbers and membrane permselectivity were estimated by means of the PNP model. This model predicts conditions at the membrane interfaces close to thermodynamic equilibrium even in a current density range up to 10,000 A m⁻². Additionally, the PNP model takes into account the kinetics of water autoprotolysis. It was shown that a high flux of OH⁻ ions across a CM effectively alkalizes the catholyte diffusion layer, ensuring a precipitation of alkaline earth cations outside the CM and thus minimizing internal CM blockage.

Graphical abstract

1 Introduction

Ion-selective membranes (ISMs) belong to the group of materials known as polymer electrolytes. They are utilized in many state-of-the-art electrochemical technologies as an ion-selective barrier or as a solid–polymer electrolyte. The reason is that ISMs allow the operation of conventional processes in a thin-gap cell set-up at higher selectivity and efficiency. A broad range of ISM types is frequently utilized in technical practice where perfluorinated sulfonated membranes (e.g. Nafion^®) exhibit extraordinary chemical stability and mechanical strength [1]. Important aspects and applications of polymer electrolytes, in particular ISMs, have recently been reviewed in [2, 3]. Currently, the development of ISMs is proceeding in three main fields of applied electrochemistry: (a) electromembrane separations (electrodialysis [4–7], electrodeionization [8]), (b) membrane electrolysis (brine electrolysis [9]) and (c) electromembrane processes for conversion of energy (fuel cells [6, 10], water electrolysis [11, 12], redox-flow batteries [13] and reverse electrodialysis [14]). The importance of these technologies is dramatically increasing in parallel with rising demands for conventional processes to be replaced by highly efficient, pollution-free ones. The need for a more fundamental understanding of ISM behaviour is a logical consequence of this trend. A theoretical study of this system can be effectively performed by means of mathematical modelling. Compared to an experimental investigation, mathematical modelling represents a more powerful approach with respect to a description of local phenomena and the ability to perform broad multi-parametric studies.

A macrohomogeneous modelling approach is frequently employed for the study of mass and charge transport in systems comprising ISM. This approach represents a reasonable compromise with respect to accuracy and the demands on computational hardware performance, compared, for example, to models based on a detailed description of membrane microstructure. The application of a macrohomogeneous approach in this field was verified, for instance, by Verbrugge et al. [15], comprehensively discussed in a review by Buck [16] and successfully employed by several authors [17–22].

The published models of ion transport in ISM significantly differ according to the complexity of the model physics. For example, a one-dimensional (1D) mathematical model of a multiple ion transport (MIT) in the chlor-alkali electrolysis process was developed by van der Stegen et al. [17] and Hogendoorn et al. [18]. They employed the Maxwell–Stefan theory to describe the transport phenomena. The composition at the membrane interface was calculated by a modified Pitzer equilibrium model, by which the activities of ions were predicted using the Pitzer method [23]. The theoretical background of these models was based on fundamental principles of interionic interactions and, as such, promises high accuracy and prediction ability in a broad range of operating conditions. However, these models [17, 18] yielded some quantitatively and qualitatively unrealistic results. Nevertheless, important qualitative conclusions were also obtained. For example, strong alkalization (pH > 12) of the anodic diffusion layer (ADL) at the membrane surface in a wide range of initial anolyte pH from 1 to 6 and a negligible effect of the ionic strength of the anolyte on the membrane performance were predicted.

A simplified MIT mathematical model also aimed at chlor-alkali electrolysis process was employed by Fila and Bouzek [19, 20]. The modelling system was 1D comprising one cation-selective membrane (CM, Nafion^® 117) and two external diffusion layers, anodic (ADL) and cathodic (CDL), adjacent to the membrane surface. MIT was approximated by the Nernst–Planck equation together with the assumption of electroneutrality in the entire model system. The convective motion of the electrolyte induced by electroosmosis inside the CM [19] and also, in the next step, in the diffusion layers [20] was taken into account. The interface between the CM and the diffusion layers was approximated by Donnan equilibrium. In further discussion in this paper, this model is denoted as the Donnan equilibrium Nernst–Planck model (DNP).

Strong concentration gradients of ions resulting from mass transport limitation in the diffusion layers were observed in former work [19]. The consideration of the convective mass transport mechanism also in the diffusion layers [20] resulted in flattening of the concentration profiles inside the membrane at higher current loads. However, the convection in the diffusion layers had an adverse impact on the membrane permselectivity. Despite initial ambitions of these two studies to demonstrate characteristics of MIT across a CM in the industrial chlor-alkali process, the calculations were completed only for current loads less than 2500 A m⁻². This is below the typical operational range of 2000–5000 A m⁻² [17]. One of the suggested reasons was the problem of numerical stability of the DNP model primarily due to the enormous gradients (stiff behaviour) of the integrated variables and discontinuity of the concentrations and potential at the CM–electrolyte interfaces.

Moreover, it appeared that the Donnan equilibrium assumption adopted in the DNP model is inaccurate or far from reality in the case of the high current loads applied in industrial chlor-alkali processes. The reason is that the Donnan theory assumes instant thermodynamic equilibrium at the membrane interface [24, Chap. 4]. For example, Cwirko et al. [25] have stated that (a) Donnan equilibrium can underestimate more than 10 times the real partitioning of counter-ions in ISMs and (b) the discrepancy of the theoretical description and reality increases with decreasing ionic strength of the external electrolytes.

The validity of Donnan equilibrium at current load conditions has not yet been thoroughly studied. The work of Manzanares et al. [21] who used a one-dimensional dynamic model to describe the transport of a symmetric binary electrolyte and space charge distribution in an ADL–CM–CDL system is an exception. The migration–diffusion species transport was described by the Nernst–Planck equation, while, contrary to the DNP model, the electric field was approximated by Poisson’s equation. Models accounting for both Nernst–Planck and Poisson’s equations are frequently denoted as Poisson–Nernst–Planck (PNP) models. The application of Poisson’s equation allowed a description of the electric potential distribution at the membrane–electrolyte interface on the basis of fundamental principles of electrostatic interactions between charged species. In contrast to Donnan theory, therefore, it enabled both the dynamics of establishing of interfacial equilibrium and the impact of charge flow at current load conditions on this equilibrium to be addressed. In their study, the authors demonstrated a discrepancy of up to 50 % between the DNP and PNP models.

A general PNP model considering transport of up to 6 ionic components in both monopolar and bipolar ISMs and adjacent diffusion layers was proposed by Volgin and Davydov [22]. Compared to the Manzanares’s study [21], they implemented a water splitting/recombination reaction (WSR) enabling an evaluation of local pH development. The results obtained agreed with current theoretical knowledge on the behaviour of these two types of ISM.

The present contribution forms part of a systematic study performed by our research group and dedicated to the mathematical modelling of MIT across CM. It commenced with the two papers of this series discussed above [19, 20]. This work is motivated by the need to extend the theoretical description of the mass transport behaviour of ISM, especially under high current load conditions, which previously published DNP models have failed to deliver. Our study aims to provide realistic data on membrane selectivity towards the desired ion production at high current loads. This information is highly interesting with respect to the optimization and intensification of membrane technologies. For this purpose, the PNP model has been adopted. Furthermore, in this case the most widespread industrial application of ISMs, i.e. chlor-alkali electrolysis, has been selected as the studied system. Additionally, the previous model [20] has been extended to include the WSR as the next step of the model development. The inclusion of the WSR enables the pH distribution in the CM and diffusion layers to be predicted. This information is of particular interest for the prediction of local conditions inside/outside the membrane and identification of regions of potential precipitation of the alkaline earth metals.

2 Mathematical model description

The 1D macrohomogeneous PNP model approach was utilized to describe stationary MIT across CM for the same system and input parameters as in the previous papers [19, 20]. For the purpose of this paper, the DNP model presented in the first paper in the series [19] is denoted as DNP1 which presented in the second paper [20] as DNP2. The model geometry is shown in Fig. 1. An acidic NaCl solution (pH 2, 5 mol dm⁻³) and a highly concentrated solution of NaOH (13 mol dm⁻³) represent the anolyte and the catholyte, respectively. The model considers the transport of OH⁻, H⁺, Na⁺ and Cl⁻ across the CM. Moreover, Ca²⁺ is taken into account as the main impurity in the process solution. The concentrations of the individual ions in the anolyte and catholyte are summarized in Table 1 and discussed in Sect. 2.3. Supplementary to the previous models [19, 20], the concentration of H⁺ and OH⁻ ions is coupled with the WSR expressed by Reaction (1).

Fig. 1

Schematic sketch of the 1-dimensional computational model geometry oriented along the x-coordinate; CM cation-selective membrane, ADL anodic diffusion layer, CDL cathodic diffusion layer, widths of the layers [19, 20]: w _CM = x ₂ − x ₁ = 0.120 mm, w _ADL = x ₁ − x ₀ = 0.474 mm, w _CDL = x ₃ − x ₂ = 0.146 mm, x ₀ located in origin

Table 1 Input parameters

$${\text{H}}_{2} {\text{O }}\begin{array}{*{20}c} {k_{f} } \\ \rightleftharpoons \\ {k_{b} } \\ \end{array} {\text{H}}^{ + } + {\text{OH}}^{ - }.$$

(1)

2.1 Model equations

The material balance of ion i is represented by Eq. (2), where $J_{i}$ denotes the molar flux density oriented along the x-coordinate.

$$0 = \frac{{{\text{d}}J_{\text{i}} }}{{{\text{d}}x}} - S_{\text{i}}$$

(2)

$J_{\text{i}}$ is predicted by the Nernst–Planck equation in the form of Eq. (3):

$$J_{\text{i}} = - D_{\text{i}}^{\text{p}} \left( {\frac{{{\text{d}}c_{\text{i}} }}{{{\text{d}}x}} + z_{\text{i}} c_{\text{i}} \frac{{{\text{d}}\phi }}{{{\text{d}}x}}\frac{F}{RT}} \right) + v_{\text{p}} c_{\text{i}}.$$

(3)

$D_{\text{i}}^{\text{p}}$ denotes the effective diffusion coefficient of the i-th ion in the phase p ≈ ADL, CM, CDL. Furthermore, $c_{\text{i}}$ represents the molar concentration, $z_{\text{i}}$ the charge number and $F$, $R$ and $T$ are Faraday’s constant, universal gas constant and absolute temperature, respectively. $\phi$ denotes the electric potential. Finally, $v_{\text{p}}$ is the effective solution flow velocity in phase ${\text{p}}$. A description of the solution flow across CM will be given in more detail later.

The source term, $S_{\text{i}}$, in Eq. (2) is zero for i ≈ Na⁺, Cl⁻ and Ca²⁺ because these ions do not participate in any chemical reaction. The source terms of H⁺ and OH⁻ are non-zero due to the WSR. $S_{{{\text{H}}^{ + } }}$ and $S_{{{\text{OH}}^{ - } }}$ are given by Eqs. (4) and (5), where $k_{f}$ and $k_{b}$ denote the rate constants of the forward and backward reactions, respectively. $K_{w}$ is the water autoprotolysis constant of Reaction (1).

$$S_{{{\text{H}}^{ + } }} = S_{{{\text{OH}}^{ - } }} = k_{f} c_{{{\text{H}}_{ 2} {\text{O}}}} - k_{b} c_{{{\text{OH}}^{ - } }} c_{{{\text{H}}^{ + } }} = k_{b} (K_{w} - c_{{{\text{H}}^{ + } }} c_{{{\text{OH}}^{ - } }} )$$

(4)

$$K_{w} = c_{{{\text{OH}}^{ - } }} c_{{{\text{H}}^{ + } }} = \frac{{k_{f} }}{{k_{b} }}c_{{{\text{H}}_{ 2} {\text{O}}}}$$

(5)

The approach adopted to describe the WSR is used in many studies mainly because of its simplicity [8, 22–30]. However, in the system including ISM and under an applied electric field the exact description of the WSR process can be more complex. The main features of this reaction were summarized, for example, in the work of Jialin et al. [31]. Firstly, according to the second Wien’s effect, the dissociation of water molecules is accelerated by a strong electric field, while the rate of the recombination reaction is not [32–34]. Consequently, the value of autoprotolysis constant, $K_{w}$, shifts towards the dissociation. For example, about 5 × 10⁷ times faster water splitting was observed in a bipolar membrane at the interface between the anion- and cation-selective layers compared to free water [35]. It is precisely this interface that is characterized by enormous electric field intensity. Neglecting the second Wien’s effect may thus lead to underestimation of the water splitting mainly at the membrane–electrolyte interface and characterized by higher electric field gradients as well. This problem has recently been studied by Danielsson et al. [30] who proposed a Butler–Volmer type kinetic description of the WSR, applied it in a 1D model of a bipolar membrane and obtained satisfactory agreement with experimental observations.

Furthermore, it was observed that water splitting is more intensive at the surface of an AM compared to a CM. In the former case, the quaternary ammonium groups degrade over time to tertiary amines [30]. These amines can then act as a weak base catalysing water molecule splitting [36]. The role of the functional groups within the WSR has not yet been adequately explained. It is, therefore, clear that the problem of the kinetics of the WSR has not yet been fully resolved. Since the primary aim of this study is not to fully describe the phenomenon of the kinetics of water splitting in the presence of polymer electrolyte, a simplified conventional approach, represented by Eqs. (4) and (5), is employed.

The electric charge flux, $j$, defined by Eq. (6), obeys conservation principles expressed by Eq. (7).

$$j = F\mathop \sum \limits_{i = 1}^{N} z_{i} J_{i}$$

(6)

$$0 = \frac{{{\text{d}}j}}{{{\text{d}}x}}$$

(7)

The electric field induced in the system consists of two contributions: (a) electric field imposed from the external DC source and (b) electric field caused by electric charge of the fixed functional groups in CM, $q_{\text{fix}}$, introduced by Eq. (8), where $c_{\text{fix}}$ and $z_{\text{fix}}$ are the molar concentration and charge number, respectively.

$$q_{\text{fix}} = c_{\text{fix}} z_{\text{fix}} F$$

(8)

The electric field can be approximated by Poisson’s equation in the form of Eq. (9), where q is the charge density of the solution given by Eq. (10) and $\varepsilon_{0} \varepsilon_{r}$ stands for the permittivity of the environment.

$$\frac{{{\text{d}}^{2} \phi }}{{{\text{d}}x^{2} }} = - \frac{{q + q_{fix} }}{{\varepsilon_{0} \varepsilon_{r} }}$$

(9)

$$q = \mathop \sum \limits_{i = 1}^{N} z_{i} c_{i}$$

(10)

The exclusion of co-ions from the internal membrane phase due to electrostatic repulsion is included in Eq. (9). Any other chemical and steric interactions affecting the membrane selectivity are, to a certain degree, encompassed in the effective diffusion coefficient of the ions, $D_{i}^{p}$.

Regarding the convective motion of the electrolyte in the system, this is induced by electroosmotic phenomena in the membrane [24]. The macroscopic convective velocity in the membrane, $v_{CM}$, is estimated by means of Schlögl’s equation [Eq. (11)] [16, 19, 20, 24, 37–39].

$$v_{\text{CM}} = \frac{{k_{\text{CM}} }}{{\eta_{\text{CM}} }}\left( {q_{\text{fix}} \frac{{{\text{d}}\phi }}{{{\text{d}}x}} - \frac{{{\text{d}}p}}{{{\text{d}}x}}} \right)$$

(11)

$k_{\text{CM}}$ and $\eta_{\text{CM}}$ are the hydraulic permeability of the membrane and the effective dynamic viscosity of the membrane pore fluid, respectively. The driving force of the electroosmotic flow is the electric force acting upon the charged solution present in the membrane pores. The energy dissipation of the flow results in the non-zero gradient of the hydrostatic pressure, $p$, inside the membrane. The solution inside the membrane is incompressible, thus mass conservation takes the form of Eq. (12):

$$0 = \frac{{{\text{d}}v_{\text{CM}} }}{{{\text{d}}x}}.$$

(12)

To fulfil conservation of the mass at the membrane–electrolyte interface, the convective motion in the diffusion layers in the direction normal to the membrane is taken into account as well. This issue is discussed in [20]. In this contribution, the convective velocity in the diffusion layers is simply equal to the electroosmotic velocity in the membrane. This is expressed by Eq. (13):

$$v = v_{\text{CM}} = v_{\text{ADL}} = v_{\text{CDL}}.$$

(13)

An alternative approach to Schlögl’s equation [Eq. (11)] for a description of electroosmotic flow is, for example, a Helmholtz–Smoluchowski approximation [40]. However, Schlögl’s equation is theoretically more straightforward. Due to this fact and for the sake of coherence with the previous papers in this series [19, 20], Schlögl’s equation is also used in this study.

In the case of a high difference in ionic strength across the membrane, the electroosmotic velocity defined by Eq. (11) can be affected by osmosis of the solvent. This phenomenon was not included in the model.

2.2 Boundary conditions

The model geometry consists of 2 external ($x_{0}$,$x_{3}$) and 2 internal ($x_{1}$,$x_{2}$) boundaries, see Fig. 1. The applied boundary conditions are summarized in Table 2. The internal boundaries are characterized by continuity of the dependent variables and fluxes. Because the mass balance given by Eq. (12) is only calculated in the CM phase, constant pressures at reference zero level are used as the boundary conditions at $x_{1}$ and $x_{2}$.

Table 2 Boundary conditions

The model assumes perfect stirring of the anolyte and catholyte bulk. This implies a constant solution composition at the outer boundaries $x_{0}$ and $x_{3}$ of ADL and CDL, respectively. On both sides, the electroneutrality condition and autoprotolysis equilibrium between H⁺ and OH⁻ is considered. The boundary $x_{0}$ is then determined by a fixed concentration of Na⁺ $\left( {c_{{Na^{ + } }}^{{x_{0} }} } \right)$, Ca²⁺ $\left( {c_{{Ca^{2 + } }}^{{x_{0} }} } \right)$ and pH value (${\text{pH}}^{{x_{0} }}$). On the other hand, for boundary $x_{3}$ a fixed concentration of OH⁻ $(c_{{OH^{ - } }}^{{x_{3} }} )$ and zero content of Cl⁻ and Ca²⁺ are taken into account. At $x_{3},$ a zero reference value of electric potential was chosen, while the value of electric potential at $x_{0}$ is equal to total applied voltage, U.

2.3 Input parameters

The input parameters were adopted from the previous work [19] in order to enable a direct comparison and are summarized in Table 1. Extra input data associated with the modification of DNP2 to the PNP model proposed in this paper are discussed in this section.

Firstly, $k_{b}$ known for free water unaffected by external electric field, adopted from [41], was used in the present study. The second Wien’s effect and catalytic influence of functional groups in the membrane on the rate constant, $k_{b}$, were neglected, see discussion in Sect. 2.1.

The relative permittivity of the environment may change with temperature and solution composition. This effect is neglected and the value of relative permittivity of pure water at ambient temperature was used instead. The situation is more complicated in the ISM and its interfaces. The reason is that the dielectric constant notably depends on the electric field intensity, mainly due to alignment of the dipole of water molecules and consequent change in the hydration of ions [25, 42–44]. For example, by means of Booth’s equation [45] Cwirko et al. [42] have calculated the electric field distribution and permittivity in a single straight cylindrical pore of an ISM. An electric field stronger than 5 × 10⁷ V m⁻¹ in the radial direction and dielectric constants below 6 near the pore wall were predicted. The problem of estimating the effective dielectric constant in the membrane is complex primarily due to the difficult and still not fully clear interactions of the electrolyte and the membrane with the electric field. This phenomenon was, therefore, excluded at this stage and the permittivity of pure water was also considered for the ISM phase.

2.4 Model summary

The proposed PNP model consists of 7 dependent variables: molar concentrations of individual ions, c _i , hydraulic pressure, p, and electric potential, ϕ. The set of model equations is formed by 6 material balances [Eq. (2)] and one elliptic Poisson’s equation [Eq. (9)]. The set of the model partial differential equations (PDEs) was solved by the finite element method implemented in the COMSOL Multiphysics™ environment.

3 Results and discussion

The calculations of the proposed PNP are performed even for current density values slightly above the typical range for chlor-alkali electrolysis of up to 10,000 A m⁻². By studying the membrane function outside the typical operating range, it is possible to rationalize the phenomena taking place under normal operating conditions. Such information is interesting not only from the point of view of a deeper understanding of the processes taking place, but it also contributes towards optimizing and intensifying the industrial process. The results of PNP are confronted with the calculation of DNP2 [20].

3.1 Distribution of local electric potential and molar concentrations

The distribution of the electric potential in the studied system calculated by the proposed PNP model is shown in Fig. 2. According to expectations, the most pronounced potential drop, i.e. main electric energy loss, is identified in the membrane. For current density >200 A m⁻², the potential gradients are solely negative, but below this level positive. This is due to the liquid junction potential across the membrane dominating at current density <200 A m⁻². For current density >3000 A m⁻², the potential profiles are almost ideally linear in all model domains solely indicating the ohmic behaviour.

Fig. 2

Electric potential distribution in the membrane and adjacent diffusion layers in dependence on current density; initial anolyte and catholyte composition—Table 1; fields at the bottom of the figure: black membrane region, grey cathodic diffusion layer, white anodic diffusion layer; electric current flows in the positive direction of coordinate x

In the membrane interfacial regions (x ₁, x ₂), the electric potential varies due to Donnan exclusion. The electric potential across these interfaces changes continuously, see Fig. 3, where figure sets (A) and (B) correspond to CM–ADL and CM–CDL, respectively. The related change in the potential has a value of units to tens of millivolts across the relatively narrow region of approximately 20 nm. This region is referred to as the Donnan exclusion region (DER) in this paper. In accordance with the theory, the electric potential decreases in the direction from external solutions into the membrane. The agreement of the prediction of the electric potential step at the membrane interface by means of Poisson’s equation and Donnan theory is discussed in Sect. 3.5 in greater detail.

Fig. 3

Distribution of electric potential and molar concentration of OH⁻ across the membrane interfaces for selected current densities; figure sets A and B—electric potential distribution at the CM–ADL and CM–CDL, respectively; figure sets C and D—distribution of concentration of OH⁻ at the CM–ADL and CM–CDL, respectively; figure sets 1, 2 and 3 correspond to applied current density of 481, 3004 and 9930 A m⁻², respectively; points p—borders of DER, where subscripts m and s denote the membrane and external solution phase, respectively, and subscripts a and c correspond to anodic and cathodic side; initial composition of external solutions—Table 1; grey field membrane region

The calculated concentration fields of the major ions (Na⁺, Cl⁻ and OH⁻) are presented in Figs. 4, 5 and 6, and those of the minor ions (H⁺ and Ca²⁺) in Figs. 7 and 8, respectively. The concentration fields calculated by PNP model, except for H⁺, agree with the results of DNP2 model [20] for current density <1500 A m⁻². One of the common characteristics of these concentration fields is the continuous decrease in the concentration of all ions in the membrane with increasing current density above a current load of 1500 A m⁻². This occurs rapidly in the range of 1500–5000 A m⁻², but only moderately at current densities >5000 A m⁻². Moreover, the concentration gradients decrease almost to zero in the bulk of each domain, but significantly increase in the vicinity of the membrane interfaces, x _1, and x ₂, and at the boundary x ₃. This behaviour indicates that the mass transport is dominated by the convective solution flow in the system in a high current density range. The solution convection is induced by electroosmosis in the membrane. By definition, see Eqs. (11), (12) and (13), the electroosmotic velocity increases proportionally to the electric potential gradient in the membrane, as will be discussed in Sect. 3.2. The enhanced concentration gradients observed near the membrane interfaces and the CDL boundary x ₃ indicate enhanced diffusion fluxes compensating the convective fluxes oriented in the opposite direction.

Fig. 4

Concentration profiles of Na⁺ in CM, ADL and CDL in dependence on current density; U = −0.018 to 1.511 V; initial anolyte and catholyte composition—Table 1; fields at the bottom of the figure: black CM region, grey CDL region, white ADL region; electric current flows in the direction of coordinate x

Fig. 5

Concentration profiles of the Cl⁻ in CM, ADL and CDL in dependence on current density; U = −0.018 to 1.511 V; initial anolyte and catholyte composition—Table 1; fields at the bottom of the figure: black CM region, grey CDL region, white ADL region; electric current flows in the direction of coordinate x

Fig. 6

Concentration profiles of the OH⁻ in CM, ADL and CDL in dependence on current density; U = −0.018 to 1.511 V; initial anolyte and catholyte composition—Table 1; fields at the bottom of the figure: black CM region, grey CDL region, white ADL region; electric current flows in the direction of coordinate x

Fig. 7

Concentration profiles of the H⁺ in CM, ADL and CDL in dependence on current density; U = −0.018 to 1.511 V; initial anolyte and catholyte composition—Table 1; fields at the bottom of the figure: black CM region, grey CDL region, white ADL region; electric current flows in the direction of coordinate x

Fig. 8

Concentration profiles of the Ca²⁺ in CM, ADL and CDL in dependence on current density; U = −0.018 V to 1.511 V; initial anolyte and catholyte composition—Table 1; fields at the bottom of the figure: black CM region, grey CDL region, white ADL region; electric current flows in the direction of coordinate x

The steepest concentration gradients are, however, located in the DER caused by Donnan exclusion of co-ions and inclusion of counter-ions. The concentration distribution calculated by the PNP model is in accordance with the orientation of the electric field across the membrane interfaces. For example, the concentration of OH⁻, as the main co-ion, decreases in the direction from the diffusion layer to the membrane phase, see Fig. 3 in figure sets (C) and (D) for the CM–ADL and CM–CDL interfaces, respectively.

Another interesting feature is observed in the OH⁻ concentration field presented in Fig. 6. As the current density increases, the average concentration of OH⁻ in the membrane decreases significantly below its concentration in the CDL, but it does not drop below its concentration in the ADL. It is due to the electroosmotic flux from the ADL to the CDL being partly compensated by intensive migration and diffusion flux of OH⁻ in the opposite direction.

Figure 9 shows the distribution of local pH in the system. This enables an assessment of the potential risk of membrane blockage by insoluble compounds of the alkaline earth metals. The ions of alkaline earth metals are impurities contained in the brine. It is crucial to minimize this risk from the point of view of long-term reliability and high selectivity of the membrane. The presented model predicts that, despite the decreasing content of OH⁻ with increasing current density, see Fig. 6, the pH remains at a sufficiently high value >13 almost throughout the entire system. This is in agreement with the observations of van der Stegen et al. [17] and Hogendoorn et al. [18]. A rapid drop in pH to 2 can be observed in the ADL at a sufficiently far distance from the membrane. Moreover, the position of the alkaline pH front does not notably change with increasing current density. Moderate pH changes, caused primarily by Donnan exclusion, occur in the interfacial region of the membrane. The main reason for the high pH in the system is the significantly higher concentration of OH⁻ in the catholyte than the H⁺ content in the anolyte, and consequently significantly higher OH^- flux across the membrane. Under these conditions, the precipitation of alkaline earth metals would already take place in the ADL sufficiently far from the membrane surface. For this reason, a minimal risk of membrane blockage and deactivation is predicted. However, in the industrial chlor-alkali process the situation will be different from that demonstrated in this paper. That is because of the dual-layer CM used in practice compared to the single-layer CM (Nafion^® 117) considered in this work. The carboxylic layer gives the dual-layer membrane higher selectivity for cations and significantly suppresses OH^- flux. This phenomenon thus requires further study.

Fig. 9

Distribution of local pH in CM, ADL and CDL in dependence on current density; U = −0.018 to 1.511 V; initial anolyte and catholyte composition—Table 1; fields at the bottom of the figure: black CM region, grey CDL region, white ADL region; electric current flows in the direction of coordinate x

With respect to H⁺ and Ca²⁺, a very low content of these ions is present and thus they do not affect the calculated transport rate of the major ions. Figure 7 shows the concentration field of H⁺, which is significantly lower compared to that calculated by DNP2 model. It is due the WSR (ignored in the DNP2 model [20]) causing H⁺ recombination with OH^- present in the system in a high concentration. The H⁺ concentration rapidly increases only in near vicinity of the boundary x ₀ due to the acidic anolyte solution.

With regard to Ca²⁺, it should first be noted that its precipitation was not included in the model at this stage. The development of Ca²⁺ concentration with increasing current density up to 1500 A m⁻² agrees with that observed in [20]. The development of the shape of the concentration dependence on the coordinate indicates the increasing influence of the migration and electroosmotic mass transfer. A positive consequence of this mass transport regime is that the concentration of Ca²⁺ in the membrane is reduced significantly below its level in the anolyte due to the intensification of the mass transport by applying a stronger electric field.

3.2 Molar fluxes of ions and of electric charge

The molar fluxes of ions dominating in the system (Na⁺, Cl⁻ and OH⁻) and of minor ions (H⁺, Ca²⁺) in dependence on the current density calculated by PNP are plotted in Fig. 10. The results of DNP2 are displayed in the same figure for comparison. Except for the case of H⁺ flux, both models provide identical results at current density lower than 1500 A m⁻², for which DNP2 results are available. For a deeper analysis of the observed trends in this current density range, we refer to the discussion provided in [20]. At the current density below approximately 500 A m⁻², the MIT is dominated by diffusion mechanism. With a further increase in current load, the migration and convection mass transport mechanisms become more significant, whereas diffusion is inherently independent of this parameter.

Fig. 10

Dependence of molar fluxes of a major ions (Na⁺, OH⁻ and Cl⁻) and b minor ions (H⁺ and Ca²⁺) in dependence on current density; solid line results of PNP, solid line with open circles results of DNP2 adopted from [20]; initial anolyte and catholyte composition—Table 1

Next, Fig. 10 shows that, in the current density range from 3000 to 5000 A m⁻², the dependence of all fluxes on the current density is practically linear. This trend was verified for current density of up to 10,000 A m⁻² by simulations of the PNP model (intentionally omitted in Fig. 10). The linear dependencies support the conclusion formulated in the previous section that migration and convection represent the dominating mass transport mechanism in a high current density range. Furthermore, it is interesting to note that OH⁻ flux is not fully hindered by the gradually increasing convective velocity. With respect to the flux of H⁺, the PNP model provides results evidently closer to reality because of the consideration of the WSR. Due to the WSR and the high concentration of OH^-, the H⁺ flux remains on a negligible level.

The dependencies of electroosmotic flow velocity on current load calculated by both the PNP and DNP2 models are in congruence in the available current density range, see Fig. 11. In a current density range up to 2500 A m⁻², the flow velocity shows a non-linear trend because in this range the system is affected by the changes in the composition of the solution in the membrane phase. Once the solution composition in the membrane becomes less dependent on the current load at current density >2500 A m⁻², the dependence of velocity on current load becomes linear.

Fig. 11

Dependence of convective velocity in dependence on current density; solid line results of PNP, solid line with open circles results of DNP2 adopted from [20]; initial anolyte and catholyte composition—Table 1

The dependence of applied voltage on the model system on the current load is shown for both DNP2 and PNP models in Fig. 12a. This figure shows a non-linear region for current load <2500 A m⁻² and linear region above this level due to similar reasons as velocity dependence on the current load. The voltage changes are connected with the local variation in the concentration of ions, i.e. of ionic conductivity. The dependence of the mean conductivity of the individual system layers, ADL, CM and CDL, on the current load is presented in Fig. 12b. The conductivity values were calculated by means of Eq. (14), where ${\text{p}} \approx \;{\text{ADL}}$, CM or CDL and $w_{\text{p}}$ denotes the width of p-th layers. $U_{\text{p}}$ represents the ohmic drop in the p-th layer.

Fig. 12

a Dependence of the electric potential drop (voltage) throughout the studied system on current density; solid line results of PNP model, solid line with open circles results of DNP2 adopted from [20]. b Dependence of the conductivity of ADL, CM and CDL for various current densities calculated by PNP model: σ _CM = 0.97 S m⁻¹ at 10,000 A m⁻²; initial anolyte and catholyte composition—Table 1

$$\sigma_{p} = \frac{{j w_{\text{p}} }}{{U_{\text{p}} }}$$

(14)

As expected, the membrane is the least conductive region in the entire model system, while the most conductive is the anolyte. The conductivity of the CDL and CM continuously decreases with current density, rapidly at a low current density range and moderately at a high one, and levels off at around 10,000 A m⁻². This behaviour is associated with the continuous decrease in the concentration of ions in these regions, as discussed above, and the increasing influence of migration and convective transport mechanisms with increasing current load. The calculated conductivity of the CM is around 43 S m⁻¹ at 200 A m⁻², i.e. comparable to currentless conditions where the membrane is equilibrated with external solutions, and it approaches a minimum value of 0.97 S m⁻¹ at 10,000 A m⁻². The calculated values are similar to those determined experimentally [46, 47]. By contrast, the dependence of conductivity of the ADL on current load exhibits a minimum at around 4000 A m⁻². This behaviour is produced by two counteracting effects. The rapid decrease in conductivity is caused by the fast drop in Na⁺ and Cl⁻ concentration with increasing current density which levels off due to the increasing importance of convection, see Figs. 4 and 5. However, the concentration of OH^- in the ADL moderately increases with increasing current load in the entire current load range studied, see Fig. 6. It is probably more important than the former effect approximately at current loads >4000 A m⁻².

3.3 Transport numbers of ions and membrane permselectivity

The selectivity of the membrane for i-th ion can be quantified by transport number according to Eq. (15) or by means of permselectivity defined by Eq. (16).

$$t_{\text{i}} = \frac{{z_{\text{i}} FJ_{\text{i}} }}{j}$$

(15)

$$P_{\text{i}} = \frac{{|J_{\text{i}} |}}{{\mathop \sum \nolimits_{j = 1}^{N} |J_{j} |}}$$

(16)

The dependences of the transport number and the permselectivity for Na⁺, Cl⁻ and OH⁻ on the current density are presented in Fig. 13. The displayed values are calculated for the anolyte solution pH 1 and 4 (pH at boundary x ₀ was set to 1 or 4, respectively). Aspects associated with anolyte pH variation are discussed in Sect. 3.4. In accordance with the dependence of the molar fluxes on the current density shown in Fig. 10a, the transport number and permselectivity of Na⁺ rapidly increase in the current load range of 0–3000 A m⁻². By contrast, the transport characteristics of OH^- and Cl^- rapidly decrease in this current density range. The negative values of $t_{{{\text{Cl}}^{ - } }}$ are due to Cl⁻ carrying a negative charge in the positive direction of the x-coordinate, i.e. from the ADL to the CDL. At current density >5000 A m⁻², the transport number and membrane permselectivity of all three ions level off. Under conditions of high current density, almost the entire electric charge is transported by Na⁺. The electric charge transported via movement of OH^- is compensated by Cl^- transferred in the opposite direction.

Fig. 13

Calculated value of a transport numbers and b permselectivity of major ions (Na⁺, OH⁻ and Cl⁻) in dependence on current density and anolyte pH; solid line ${\text{pH}}^{{x_{0} }} = 1$, open circles ${\text{pH}}^{{x_{0} }} = 4$; U = −0.018 to 1.511 V; initial anolyte composition recalculated according to ${\text{pH}}^{{x_{0} }}$, initial catholyte composition see Table 1, negative values of $t_{{{\text{Cl}}^{ - } }}$ indicate flux of Cl⁻ in the direction of electric current flux

3.4 Effect of the anolyte pH

In the present work, the effect of initial anolyte pH on the transport of mass and charge, membrane efficiency and selectivity is analysed. This is practically important with regard to pH distribution in the membrane and diffusion layers associated with a membrane blockage by the precipitates of alkaline earth metals. For this purpose, the value of anolyte pH (${\text{pH}}^{{x_{0} }}$) was changed from 1 to 4. The results are shown in Fig. 13. It is evident that the effect of this parameter on the MIT is minimal in the range studied. This is due to the dominant effect of the catholyte composition characterized by a several orders of magnitude higher concentration of OH⁻.

The calculated pH profiles in the model domain are plotted in Fig. 14 for constant voltage U = 0.70 V. A shift of the pH front in the ADL towards the membrane surface with decreasing anolyte pH, i.e. extending the acidified region of the ADL, was observed. This is evidently caused by increased H⁺ flux from the anolyte to the membrane as the anolyte pH decreases. A change of anolyte pH from 1.5 to 1 already causes a moderate decrease in pH at the membrane surface. However, the pH inside the membrane and the CDL remains unaffected in the entire anolyte pH range studied.

Fig. 14

Local pH distribution in the system for various anolyte pH: a ${\text{pH}}^{{x_{0} }} = 1$, b ${\text{pH}}^{{x_{0} }} = 1.5$, c ${\text{pH}}^{{x_{0} }} = 2$ and d ${\text{pH}}^{{x_{0} }} = 4$; parameters: j = 5135 A m⁻² and U = 0.70 V, initial anolyte composition recalculated according to ${\text{pH}}^{{x_{0} }}$, initial catholyte composition see Table 1; grey field membrane region

3.5 Examination of the validity of Donnan equilibrium

The objective of this section is to examine the validity of the Donnan equilibrium approximation at the membrane interfaces at high current densities. According to this theory, the electric potential difference, ${{\Delta }}\phi_{{{\text{Don}} }}^{\phi }$, and the difference in the chemical potentials of the i-th ion, ${{\Delta }}\phi_{{{\text{Don}} }}^{{c_{i} }}$, across DER should be equal. Therefore, the validity of the Donnan approximation can be verified by a comparison of ${{\Delta }}\phi_{{{\text{Don}} }}^{\phi }$ and ${{\Delta }}\phi_{{{\text{Don}} }}^{{c_{\text{i}} }}$ calculated by the presented PNP model from the local distribution of the ion concentration and electric potential across the DER shown in Fig. 3.

The only problem was to determine the exact borders of the DER to evaluate electric and chemical potential differences associated solely with the Donnan exclusion. Especially from figures (A3), (B3), (C1), (C2), (C3) and (D3) in Fig. 3, it is apparent that the local distributions in the DER are notably affected by the mass and charge transport processes occurring on both sides of the membrane interface. To overcome this problem, we considered an identical position of the DER borders for the entire range of the current density studied located at a distance of 10 nm to both sides of the membrane interface, see black points p in Fig. 3. ${{\Delta }}\phi_{{{\text{Don}} }}^{\phi }$ is then calculated by means of Eqs. (17) and (18), and ${{\Delta }}\phi_{{{\text{Don}} }}^{{c_{i} }}$ according to Eqs. (19) and (20), both for the CM–ADL and CM–CDL interface, respectively.

$$\left. {{{\Delta }}\phi_{{{\text{Don}} }}^{\phi } } \right|_{{{\text{CM}} - {\text{ADL}}}} = \phi \left( {p_{ma} } \right) - \phi (p_{sa} )$$

(17)

$$\left. {{{\Delta }}\phi_{\text{Don }}^{\phi } } \right|_{{{\text{CM}} - {\text{CDL}}}} = \phi \left( {p_{mc} } \right) - \phi (p_{sc} )$$

(18)

$$\left. {{{\Delta }}\phi_{{{\text{Don}} }}^{{c_{i} }} } \right|_{{{\text{CM}} - {\text{ADL}}}} = \frac{\text{RT}}{{z_{i} F}}\ln \left( {\frac{{c_{i} (p_{sa} )}}{{c_{i} (p_{ma} )}}} \right)$$

(19)

$$\left. {{{\Delta }}\phi_{{{\text{Don}} }}^{{c_{\text{i}} }} } \right|_{{{\text{CM}} - {\text{CDL}}}} = \frac{\text{RT}}{{z_{i} F}}\ln \left( {\frac{{c_{i} (p_{sc} )}}{{c_{i} (p_{mc} )}}} \right)$$

(20)

The resulting values are plotted in Fig. 15. The values of ${{\Delta }}\phi_{\text{Don }}^{\phi }$ and ${{\Delta }}\phi_{{{\text{Don}} }}^{{c_{\text{i}} }}$ are negative according to the function of the CM. Moreover, these values are rather low (units of millivolts) and lower at CM−CDL than at CM−ADL. This is due to the high ionic strength of the external solutions, which is even higher in the CDL than in the ADL. Additionally, ${{\Delta }}\phi_{\text{Don }}^{\phi }$ and ${{\Delta }}\phi_{{{\text{Don}} }}^{{c_{\text{i}} }}$ increase with increasing current density. The Donnan exclusion effect thus becomes more pronounced at high current density. This can be rationalized by the decreasing concentration of ions in the external solutions adjacent to the membrane interfaces, as discussed in Sect. 3.1.

Fig. 15

Dependence of electric potential difference, ${{\Delta }}\phi_{{{\text{Don}} }}^{\phi }$, and chemical potential difference of OH⁻ and Na⁺ ions across the phase interface, ${{\Delta }}\phi_{{{\text{Don}} }}^{{c_{{{\text{Na}}^{ + } }} }}$ and ${{\Delta }}\phi_{{{\text{Don}} }}^{{c_{{{\text{OH}}^{ - } }} }}$, in dependence on current density at both CM–ADL and CM–CDL; U = −0.018 to 1.511 V; initial anolyte and catholyte composition—Table 1

The relative discrepancy between ${{\Delta }}\phi_{{{\text{Don}} }}^{{c_{\text{i}} }}$, ${{\Delta }}\phi_{{{\text{Don}} }}^{{c_{{{\text{Na}}^{ + } }} }}$ and ${{\Delta }}\phi_{{{\text{Don}} }}^{{c_{{{\text{OH}}^{ - } }} }}$ is minor and is similar on both sides of the membrane, but it gradually increases with increasing current load. The observed discrepancy can be explained by increasing gradients of OH⁻ concentration and the electric potential formed in the CM in the vicinity of the DER with rising current load, see figures (A3), (B3), (C1 to C3) and (D3) in Fig. 3. Higher absolute values of ${{\Delta }}\phi_{\text{Don }}^{\phi }$ over ${{\Delta }}\phi_{{{\text{Don}} }}^{{c_{{{\text{OH}}^{ - } }} }}$ and ${{\Delta }}\phi_{{{\text{Don}} }}^{{c_{{{\text{Na}}^{ + } }} }}$ at the CM–ADL interface suggest more pronounced space charge separation across the DER.

In summary, the PNP model predicts that the CM–CDL and CM–ADL interfaces remain almost completely in equilibrium state in the entire range of current densities that are of practical importance for the chlor-alkali electrolysis. Qualitatively similar observations have also been made by Manzanares et al. [21], who observed that significant shift from equilibrium was only observed when the current density exceeded 10,000 A m⁻². Actually, such a conclusion could be expected intuitively for two reasons. Firstly, both the definition of Donnan potential and Poisson’s equation are based on the identical physical definition of electric potential as a useful work associated with a transfer of a unit charge from a reference point. Secondly, both the DNP and PNP models assume ideal solution behaviour, which represents the main model limitation with respect to an accurate description of reality. The solution of this problem will be the subject of future work.

4 Conclusions

A one-dimensional stationary PNP model was successfully applied to describe the multi-ion transport across a cation-selective membrane (CM) under conditions simulating the chlor-alkali electrolysis process operated on a single-layer perfluorinated sulfonated membrane. The presented model represents an extension of the previously published version of the model considering Donnan equilibrium at the membrane interface [20]. At low current loads, both models provided similar results. Therefore, the PNP model was employed for an analysis of multiple ion transfer at industrially relevant current loads (between 2000 and 5000 A m⁻²) and extremely high current loads up to 10,000 A m⁻².

The analysis of the membrane behaviour at extreme current loads, for example, mimics a scenario when a controlling system fails, resulting in local or global membrane overloading. Marked mass transport limitation behaviour was predicted with a dominant role of convection and migration transport mechanism at current load >3000 A m⁻². Moreover, the extended PNP model considered the water splitting/recombination reaction. A corresponding analysis of the pH distribution revealed strong alkalization of the solution in the anodic diffusion layer. It is, therefore, concluded that the risk of internal membrane blockage due to precipitation of alkaline earth metals is minor in the case of the system under study. Last, but not least, an analysis of the membrane interface by means of the PNP model predicted only minor shift from Donnan equilibrium in the entire current load range studied. The observed discrepancy arises due to the high electric potential and concentration gradients formed in the vicinity of the membrane interface associated with intensive mass and charge transfer at higher current loads.