1 Introduction

As already stated previously [1], ion-selective membranes represent a vital part of important, well established and also emerging electrochemical technologies [2, 3]. Another important field of their applications is electroanalytical devices, such as ion-selective electrodes. Even though they are widely used in practice and their potential for extending into novel applications is extremely high, the principle of their function and mass-transfer behaviour under current load is not yet completely understood. A broad spectrum of membrane materials is known and used in practice. Perfluorinated sulphonated materials represent one special class. This is due both to their extremely high chemical and mechanical stability as well as to their excellent electrochemical properties. Therefore, numerous studies of the membranes based on this type of material have been undertaken, e.g., [4–12], aiming to understand their internal structure and thus to explain their transport properties.

Mathematical modelling represents a complementary approach to the experimental studies. In the last two decades mathematical models have often been used to verify various mechanisms of mass transfer across membranes or to identify membrane transport parameters. A comprehensive review of the early beginnings in this field was published by Buck [13]. In the early stages the emphasis was mainly put on separation processes, like dialysis [14, 15] or more often electrodialysis [16, 17]. During the last decade attention has turned mainly to the field of proton exchange membranes (PEM) fuel cells. The number of papers published on this phenomenon is rising exponentially. Weber and Newman compiled a review of the published approaches to the mathematical modelling of PEM fuel cells [18]. Advances in this field with the focus on the simulation of the polymer electrolyte were summarised by Kreuer et al. [19]. Interest in this field is still rising and the proposed models are characterised by steadily increasing complexity [20–26]. One study [27] claiming to provide a simple and reliable model of the water transport across a Nafion membrane represents an exception. Recently, attention has mainly been paid to the transport of water molecules across the membrane in connection with the transport of protons. Increasing attention is also being paid to the membrane water electrolysis process [28, 29].

The majority of the published models deal with membranes based on perfluorinated sulphonated materials used on a large scale in chlor-alkali electrolysis. This technology is most widely used amongst the ion-selective membranes applied on an industrial scale. When compared with the two competitive technologies (mercury and diaphragm electrolysis) the major advantages of this process are the lower energy consumption, high purity of caustic produced and less strong environmental impact [30]. Therefore, in the near future the chlor-alkali industry will be based predominantly on this technology [31, 32]. This is one reason for the intensive research to solve the critical aspects of this process, such as deterioration of membrane properties caused by alkali earth metal cations chemisorbed on its ion exchange sites [33]. The source of these cations is brine impurities. The most important contributions in this field have been summarised by Pillay [34]. Although chlor-alkali electrolysis is widely used in practice, only a few studies that attempt to explain the behaviour of the membrane in this particular process have been published, e.g., [1, 35, 36]. Nafion 117 was selected as an example for the present study of this problem even it differs into certain extent from the bilayer membrane materials used typically in the chlor-alkaline industry. This was because of the availability of the input parameters values, possibility to compare directly the results with the previous model and thus to assess impact of the external mass transfer on the membrane performance.

Mathematical modelling is an efficient tool for optimising both the chemical and the electrochemical processes. This is also valid for membrane brine electrolysis. The models of the charge transfer across the ion-selective membrane published so far can be divided into three main groups:

  • the macrohomogeneous approach [1, 14, 15, 17, 20, 27, 34, 37–39, 40], including irreversible thermodynamics [24–26, 41–43, ].

  • physical models based on models of the perfluorinated sulphonated membrane structure. Whereas in the early stages the parallel cylindrical pores were considered [44–46], in the latest studies the percolation model has been introduced [22].

  • the microscopic approach, including mainly molecular dynamics [47–49] and statistical mechanics [50–54].

As has been shown, the mass transfer across the Nernst diffusion layers adjacent to the membrane under current load conditions results in a significant change in the ion concentration profiles in the vicinity of the membrane [17, 55]. This finding was also confirmed by Leah et al. [56] for brine electrolysis. The first attempt to quantify this phenomenon was provided in our previous study [1]. Besides the membrane, the macrohomogeneous model proposed also considers ion transfer across the two Nernst diffusion layers. The serious deficiency of this model is that, in agreement with the general theory of the film model of mass transfer to the phase interface, the convection term of the Nernst–Planck equation used was neglected. This was done in order to simplify the resulting set of model equations and to ensure the convergence of the numerical method used. At the same time electroosmotic flow was considered inside the membrane. The aim of this paper is to solve this problem and to propose a model that accounts for the continuity of the solvent flux on the solution-membrane interfaces. Here one important point should be stressed: in the present case, introducing the convective flux in the Nernst diffusion layer is not in disagreement with the general film theory of mass transfer to the phase interface. This is because the convective flux induced by the flow hydrodynamics in the bulk of the channel is not considered inside the film. Only the flux compensating electroosmotic flux across the membrane is taken into consideration. A comparison with the previous results will allow an assessment of the significance of the convective term in the model equations. The results will provide more exact insight into the processes taking place in an industrial membrane electrochemical reactor for a chlor-alkali process.

2 Mathematical model

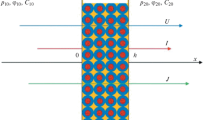
In agreement with the previous work [1] a one dimensional macrohomogeneous model was employed. This has proven to be a suitable approach to solving the industrially relevant problems. The graphical schema of the model system is shown together with definition of dimensional variables in Fig. 1.

Fig. 1
figure 1

Schematic sketch of the system. Symbol l indicates electrolyte boundary layers, s the membrane layer

Full size image

2.1 Material balance

The general material balance of the individual system components may be written as follows.

$$ \frac{\partial \hbox{c}_{\rm i} }{\partial \tau}=\Upphi_{\rm i}-\hbox{div}{\rm {\bf N}}_{\rm i} $$
(1)

The molar flux density can then be defined by means of the following expression.

$$ {\rm {\bf N}}_{\rm i} =-\hbox{c}_{\rm i} \left( \frac{\hbox{D}_{\rm i} }{\hbox{RT}} \right)\nabla \tilde {\mu }_{\rm i} +\hbox{c}_{\rm i} {\rm {\bf v}} $$
(2)

The electrochemical potential of the particles carrying an electrical charge (ions) can be expressed using the Guggenheim equation,

$$ \tilde {\mu }_{\rm i} =\mu_{\rm i} +\hbox{z}_{\rm i} \hbox{F}\varphi $$
(3)

where the chemical potential of each component μ i is defined by (Eq. 4).

$$ \mu_{\rm i} =\mu_{\rm i}^0 +\hbox{RT}\ln \hbox{a}_{\rm i} $$
(4)

The activity of the ions can be defined as

$$ \hbox{a}_{\rm i} =\frac{\gamma_{\rm i} \hbox{c}_{\rm i} }{\hbox{c}_{\rm i}^0 } $$
(5)

Introducing (Eq. 5) into (Eq. 4) and after rearrangement we obtain an expression for the chemical potential in a new form, including molar concentrations.

$$ \mu_{\rm i} =\mu_{\rm i}^0 +\hbox{RT}\ln \gamma_{\rm i} +\hbox{RT}\ln \frac{\hbox{c}_{\rm i}}{\hbox{c}_{\rm i}^0 } $$
(6)

By introducing (Eq. 3) and (Eq. 6) into (Eq. 2), the relationship for the molar flux density of ion i can be expressed for the isotherm system and constant diffusivities (i.e., independent of the solution composition) as

$$ {\rm {\bf N}}_{\rm i} =-\hbox{D}_{\rm i} \left( {\frac{\hbox{d}\ln \gamma_{\rm i}}{\hbox{d}\ln \hbox{c}_{\rm i}}+1} \right)\nabla \hbox{c}_{\rm i} -\hbox{c}_{\rm i} \left( {\frac{\hbox{D}_{\rm i} }{\hbox{RT}}} \right)\hbox{z}_{\rm i} \hbox{F}\nabla \varphi +\hbox{c}_{\rm i} {\rm {\bf v}} $$
(7)

Generally, the dependence of the activity coefficients of the individual ions in an electrolyte solution of complex composition is not known. A possible solution to this problem is to apply a suitable prediction method. Probably the most widespread solution for the highly concentrated solution has been presented by Pitzer [57]. Several problems arise when this approach is applied to solve the activity coefficient problem in the mathematical model of the polymer electrolyte membrane. The first consists in the definition of the empirical coefficients for the Pitzer correlation equations. This problem was partly solved by van der Stegen et al. [58], who published values of coefficients valid for NaCl and NaOH electrolytes in a hydrated Nafion membrane. To derive the required constants the authors assumed the fixed sulpho groups to be evenly distributed in the solution inside the membrane pores. The concentration of the fixed groups in the membrane has to be multiplied by a constant representing the shielding term dependent on the membrane equivalent weight. The second, more important problem represents the convergence of the model equations, especially on the electrolyte-membrane interface. Because of the latter problem the validity of the simplifying assumption for the diluted electrolytes \(\left( {\frac{\text{d}\ln {\gamma}_i}{\text{d}\ln c_i }+1} \right)\approx 1\) is also being considered in the present case. (Eq. 7) can thus be simplified to the following form.

$$ {\rm {\bf N}}_{\rm i} =-\hbox{D}_{\rm i} \nabla \hbox{c}_{\rm i}-\hbox{c}_{\rm i} \left( {\frac{\hbox{D}_{\rm i} }{\hbox{RT}}} \right)\hbox{z}_{\rm i} \hbox{F}\nabla \varphi +\hbox{c}_{\rm i} {\rm {\bf v}} $$
(8)

For the steady state without chemical reactions (Eq. 1) takes the following form.

$$ \hbox{div}{\rm {\bf N}}_{\rm i} =0 $$
(9)

By inserting (Eq. 8) into (Eq. 9), it turns into (Eq. 10).

$$ 0=\hbox{div}(-\hbox{D}_{\rm i} \nabla \hbox{c}_{\rm i} -\hbox{c}_{\rm i} \left( {\frac{\hbox{D}_{\rm i} }{\hbox{RT}}} \right)\hbox{z}_{\rm i} \hbox{F}\nabla \varphi +\hbox{c}_{\rm i} {\rm {\bf v}}) $$
(10)

The current density in the electrolyte solution can be expressed as a sum of the charge carried by the individual ions as given by (Eq. 11).

$$ \hbox{j}=\hbox{F}\sum_{\rm i}^{\hbox{N}_{\rm ions} } {\hbox{z}_{\rm i} {\rm {\bf N}}_{\rm i} } $$
(11)

2.2 Membrane phase

The material balance in the membrane phase is expressed by (Eq. 10). In the present case the Schlögl [37] equation was used to express the convective flux induced by the Galvani potential and pressure gradient imposed on the membrane.

$$ {\rm {\bf v}}=\frac{\eta_{\rm M} }{\hbox{k}_{\rm M} }\left( {\hbox{z}_{\rm M} \hbox{c}_{\rm M} \hbox{F}\nabla \varphi^{\left( \hbox{M} \right)}-\nabla p^{\left( \hbox{M} \right)}} \right) $$
(12)

By introducing this expression into (Eq. 8), the final expression for the molar flux density inside the membrane is obtained.

$$ {\rm {\bf N}}_{\rm {\bf i}} =-\hbox{D}_{\rm i}^{\rm (M)} \nabla \hbox{c}_{\rm i}^{\rm (M)}-\hbox{c}_{\rm i}^{\rm (M)} \left( {\frac{\hbox{D}_{\rm i}^{\rm (M)} }{\hbox{RT}}} \right)\hbox{z}_{\rm i} \hbox{F}\nabla \varphi^{\rm (M)} +\hbox{c}_{\rm i}^{\rm (M)} \frac{\eta_{\rm M} }{\hbox{k}_{\rm M} }\left( {\hbox{z}_{\rm M} \hbox{c}_{\rm M} \hbox{F}\nabla \varphi^{\rm (M)} -\nabla \hbox{p}^{\rm (M)} } \right) $$
(13)

The Schlögl equation (12) can also be used to describe the pressure and pressure gradient inside the membrane in dependence on the coordinate.

The last important condition to be satisfied is the electroneutrality. In the bulk of the ion-selective membrane it takes the form of (Eq. 14).

$$ \sum_{\rm i}^{{\rm N}_{\rm ions} } {\hbox{z}_{\rm i} \hbox{c}_{\rm i} } +\hbox{z}_{\rm M} \hbox{c}_{\rm M} =0 $$
(14)

The final set of equations describing the concentration, pressure and potential profile as well as molar flux densities inside the membrane is given by (Eqs. 9, 11–13). The concentration profile of the last ion including is then described by (Eq. 14).

2.3 Nernst diffusion layer

The molar flux density of ions in the Nernst diffusion layer is again described by (Eq. 8). (Eq. 9) is valid as well. In the free electrolyte solution the electroneutrality condition is expressed by (Eq. 15).

$$ \sum_{\rm i}^{{\rm N}_{\rm ions} } {\hbox{z}_{\rm i} \hbox{c}_{\rm i}^{{\rm (l_k )}} } =0 $$
(15)

The convective flux velocity v remains undefined. From (Eq. 9) it follows that

$$ \sum_{\rm i}^{{\rm N}_{\rm tot} } {\hbox{N}_{\rm i} =\hbox{const.}} $$
(16)

The definition of the diffusion flux gives rise to the expression given in (Eq. 17).

$$ \sum_{\rm i}^{{\rm N}_{\rm tot} } {\hbox{D}_{\rm i}^{{\rm (l_k )}} \nabla \hbox{c}_{\rm i}^{{\rm (l_k )}} =0} $$
(17)

By inserting (Eqs. 8 and 17) into (Eq. 16), N tot expression for the total molar flux density in the diffusion layer is obtained.

$$ \sum_{\rm i}^{{\rm N}_{\rm tot} } {\hbox{N}_{\rm i} } =-\frac{\hbox{F}}{\hbox{RT}}\nabla \varphi^{({\rm l}_{\rm k})} \sum_{\rm i}^{{\rm N}_{\rm tot} } {\hbox{c}_{\rm i}^{{\rm (l_k )}} \hbox{D}_{\rm i}^{{\rm (l_k )}} \hbox{z}_{\rm i} } +\hbox{vc}_{\rm tot}^{({\rm l}_{\rm k})} $$
(18)

Using (Eq. 18); the linear flow velocity can be iteratively obtained on the basis of sufficiently accurate initial assessment values of the individual component fluxes.

2.4 Boundary conditions

The following boundary conditions were used in the calculation. For the meaning of the individual symbols, see the list of symbols and Fig. 1.

$$ \left. {{\rm {\bf c}}^{({\rm l}_1)} } \right|_{{\rm x}_{{\rm l}_1 } =0} ={\rm {\bf c}}^{(1)} $$
(19)
$$ \left. {{\rm {\bf c}}^{({\rm l}_2 )} } \right|_{{\rm x}_{{\rm l}_2 } =\delta _{{\rm l}_2 } } ={\rm {\bf c}}^{(2)} $$
(20)
$$ \left. {\varphi^{({\rm l}_1 )} } \right|_{{\rm x}_{{\rm l}_1 }\,=\,0}\,=\,0 $$
(21)
$$ \left. {\hbox{p}^{({\rm l}_1 )} } \right|_{{\rm x}_{{\rm l}_1 }\,=\,0}\,=\,\hbox{p}^{\left( 1 \right)} $$
(22)
$$ \left. {\hbox{p}^{({\rm l}_2 )} } \right|_{{\rm x}_{{\rm l}_2 }\,=\,\delta _{{\rm l}_2 } }\,=\,\hbox{p}^{\left( 2 \right)} $$
(23)

On the solution-membrane interface the conditions take the following form:

$$ \Updelta \varphi _{\rm Don}^{({\rm l}_1 ,{\rm s})} \left. {=\,\varphi^{\left( {{\rm l}_1 } \right)} } \right|_{{\rm x}_{{\rm l}_1 }\,=\,\delta _{{\rm l}_1 } } -\left. {\varphi^{\left( {\rm s} \right)} } \right|_{{\rm x}_{\rm s}\,=\,0}\,=\,\frac{\hbox{RT}}{\hbox{F}}\ln \left[ {\frac{\left. {\hbox{c}_{\rm i}^{\left( {{\rm l}_1 } \right)} } \right|_{{\rm x}_{{\rm l}_1 }\,=\,\delta _{{\rm l}_1 } } }{\left. {\hbox{c}_{\rm i}^{\left( {\rm s} \right)} } \right|_{{\rm x}_{\rm s}\,=\,0} }} \right]^{\frac{1}{\hbox{z}_{\rm i} }} $$
(24)
$$ \sum_{\rm i}^{{\rm N}_{\rm ions} } {\hbox{z}_{\rm i} \left. {\hbox{c}_{\rm i}^{{\rm (s)}} } \right|_{{\rm x}_{\rm s} =0} } +\hbox{z}_{\rm M} \hbox{c}_{\rm M} =0 $$
(25)
$$ \left. {{\rm {\bf N}}_{\rm i} } \right|_{{\rm x}_{{\rm l}_1 } =\delta _{{\rm l}_1 } } =\left. {{\rm {\bf N}}_{\rm i} } \right|_{{\rm x}_{\rm s} =0} $$
(26)

On the membrane-solution interface the conditions are expressed as follows:

$$ \Updelta \varphi _{\rm Don}^{({\rm l}_2 ,{\rm s})} \left. {=\varphi^{\left( {{\rm l}_2 } \right)} } \right|_{{\rm x}_{{\rm l}_2 } =0} -\left. {\varphi^{\left( {\rm s} \right)} } \right|_{{\rm x}_{\rm s} =\delta_{\rm s} } =\frac{\hbox{RT}}{\hbox{F}}\ln \left[ {\frac{\left. {\hbox{c}_{\rm i}^{\left( {\rm s} \right)} } \right|_{{\rm x}_{\rm s} =\delta_{\rm s}}}{\left. {\hbox{c}}_{\rm i}^{\left( {{\rm l}_2 } \right)} \right|_{{\rm x}_{{\rm l}_2 } =0}}} \right]^{\frac{1}{\hbox{z}_{\rm i} }} $$
(27)
$$ \sum_{\rm i}^{{\rm N}_{\rm ions} } {\hbox{z}_{\rm i} \left. {\hbox{c}_{\rm i}^{({\rm l}_2 )} } \right|_{{\rm x}_{{\rm l}_2 } =0}} =0 $$
(28)
$$ \left. {{\rm {\bf N}}_{\rm i}} \right|_{{\rm x}_{{\rm l}_2 } =0} =\left. {{\rm {\bf N}}_{\rm i}} \right|_{{\rm x}_{\rm s} =\delta _{\rm s}} $$
(29)

The average thickness of the Nernst diffusion layer was calculated using an expression proposed by Roušar et al. [59] which is valid for a laminar flow.

$$ \hbox{Sh}=1.85\left( {\frac{\hbox{d}_{\rm e} }{\hbox{L}}\cdot \hbox{Re}\cdot \hbox{Sc}} \right)^{1/3} $$
(30)

2.5 Electrolyte density calculation

The local electrolyte composition changes significantly with the position in the system under study. This results in considerable changes in solution density. In contrast to the previous work [1], the present version of the model accounts for this fact. The local electrolyte solution density is calculated from the molar volume of the liquid mixture using (Eq. 31).

$$ \rho_{\rm m}^{{\rm (l)}} =\frac{1}{\hbox{V}_{\rm m}^{{\rm (l)}} }\overline{\hbox{M}}=\frac{1}{\hbox{V}_{\rm m}^{{\rm (l)}} }\sum_{\rm i} {\hbox{x}_{\rm i} \hbox{M}_{\rm i} } $$
(31)

The Clarke model [60] is used to calculate the molar volume of the electrolyte solution. The model is based on Amagat’s law (Eq. 32) and the relationship between the partial molar volume of individual electrolytes and their mole fractions in the solvent (Eq. 33)

$$ \hbox{V}_{\rm m}^{{\rm (l)}} =\sum_{\rm i}{\hbox{x}_{\rm i} } \hbox{V}_{\rm i} $$
(32)
$$ \hbox{V}_{\rm ca} =\hbox{V}_{\rm ca}^\infty +\hbox{A}_{\rm ca} \frac{\sqrt{\hbox{x}_{\rm ca} }}{1+\sqrt{\hbox{x}_{\rm ca} }} $$
(33)

All quantities are expressed in terms of apparent components.

The technique of constructing a set of arbitrary mole fractions of all possible apparent components from a mixture described in terms of compositions of true components (ions, solvent) proposed in [60, 61] is used. All possible apparent components ca formed by cations c and anions a are considered. In our particular case the NaCl, NaOH, CaCl2, Ca(OH)2 and HCl are considered for the liquid film. An additional component is the solvent, i.e., water. For the membrane phase additional “electrolytes” H-RSO3, Na-RSO3, Ca-(RSO3)2 are introduced into the model. Amongst all the possible solutions, one arbitrary solution of the amounts of apparent electrolytes is used, where the concentration of apparent electrolytes is defined as follows:

$$ \hbox{c}_{\rm ca}^{\rm a} =\frac{\hbox{c}_{\rm c}^{\rm t} \hbox{c}_{\rm a}^{\rm t} }{\sum\limits_{\rm c} {\hbox{z}_{\rm c} \hbox{c}_{\rm c}^{\rm t} } } $$
(34)

From this value the apparent molar fraction of the individual electrolytes can be calculated.

$$ \hbox{x}_{\rm i}^{\rm a} =\frac{\hbox{c}_{\rm i}^{\rm a} }{\sum\limits_{\rm i} {\hbox{c}_{\rm i}^{\rm a} }} $$
(35)

All molar fractions of apparent electrolytes used in the calculation have a nonzero value. Their values are arbitrary. For a given composition of the ionic solution Clarke’s model always yields identical volume, independent of the molar fractions of the individual apparent electrolytes. This results in some constraints valid between parameters of Clarke’s model.

Due to the extremely low Ca2+ concentration, the effect of its apparent components was neglected. In the present calculation these components were replaced by water.

In the membrane containing fixed sulpho groups the issue of molar volumes of fictive apparent electrolytes had to be solved. In the present case the molar volume of HCl was used for H-RSO3 and water for Ca-(RSO3)2. Finally the Na-RSO3 was split into two parts. For the first part the molar volume of NaOH was used. For the second the molar volume of NaCl was considered. The ratio between these two parts was defined on the basis of the local apparent concentrations of NaCl and NaOH in the membrane phase. The concentration added to the apparent concentration of NaCl and NaOH, calculated using (Eq. 34), is defined by (Eq. 36),

$$ \hbox{c}_{\rm k}^{{\rm a,add}} =\frac{\hbox{c}_{\rm k}^{\rm a} }{\hbox{c}_{\rm NaCl}^{\rm a} +\hbox{c}_{\rm NaOH}^{\rm a} }\hbox{c}_{{\rm Na-RSO}_3}^{\rm a} $$
(36)

where k is for NaOH or NaCl. By this means a new apparent composition, taking into account only the apparent electrolytes NaCl, NaOH, HCl and water, was obtained.

The Clarke parameters of all electrolytes were calculated by nonlinear regression from the sets of experimental densities of binary water-electrolyte mixtures [62] and the ternary NaCl–NaOH–water mixture [63]. The values of the parameters are summarized in Table 1.

Table 1 Parameters of the Clarke equation for NaCl, NaOH and HCl (Eq. 33)
Full size table

The molar volume of water was calculated using CRC Handbook data [62]. A cubic equation in the form of (Eq. 37) was used. It is valid in a temperature temperature range 20–90 °C.

$$ \hbox{V}_{\hbox{H}_2 \hbox{O}} = \hbox{AT}^3+\hbox{BT}^2+\hbox{CT}+\hbox{D} $$
(37)

where

$$ \begin{array}{l} \hbox{A} = 1.097\times 10^{-14}\hbox{m}^{3}\hbox{mol}^{-1}\deg \hbox{C}^{-3} \\ \hbox{B} = 5.999\times 10^{-11}\hbox{m}^{3}\hbox{mol}^{-1}\deg \hbox{C}^{-2} \\ \hbox{C} = 1.735\times 10^{-9}\hbox{m}^{3}\hbox{mol}^{-1}\deg \hbox{C}^{-1}\\ \hbox{D} =1.800\times 10^{-5}\hbox{m}^{3}\hbox{mol}^{-1} \end{array}$$

2.6 Method of solving the model equation

The above set of differential and algebraic equations (DAEs) was solved by a shooting method. In the individual sections, the set of equations was integrated using the multistep implicit method based on the BDF Gears formula which is suitable for difficult problems (library procedure DDASPK [64]). During integration of DAEs using DDASPK a numerical difficulty was encountered when the inconsistent initial values of independent variables were used. An initialisation procedure was developed to handle this issue.

The distribution of the concentrations on the electrolyte-membrane interface was evaluated using the ZREAL [65] library procedure designed to calculate the roots of real function. The set of non-linear equations, resulting from the principle of the shooting method, was solved using the Newton–Raphson method.

2.7 Input parameters

A Nafion 117 membrane was chosen for this study. The reasons are given in the previous paper [1]. The values of the input parameters used previously, including the hydrodynamic analysis in the anode and cathode compartments [1], were also applied in the present case. This enables a direct comparison with the previous version of the model.

Identically to the previous case, the pH of the 5 M brine solution on the anode side was set equal to 2 and it was assumed to contain 0.2 mM CaCl2. The catholyte was formed by 13 M NaOH solution.

3 Results and discussion

The results of the model for the ions with the three highest concentrations, i.e., Na+, OH−and Cl−, are shown in Figs. 2–5. The results obtained during the previous study [1] are shown in the same figures for comparison. The concentration profiles calculated correspond in general to the previous results. The main difference consists clearly in averaging of the concentration fields calculated. Concentration maxima decreased considerably or disappeared completely. This phenomenon is most significant for the sodium ion. Since hydroxyl ions compensate the charge of the sodium ions in the catholyte solution, where the most significant maxima in the concentration were observed, the behaviour is identical. In the case of the chloride anion the concentration averaging results mainly in the disappearance of the significant concentration minima in the membrane phase.

Fig. 2
figure 2

Concentration profiles of the Na+ ion at various current densities; anolyte: 5000 mol  NaCl  m−3, 0.2 mol CaCl2 m−3, pH = 2; catholyte: 13000 mol NaOH m−3. The grey field at the bottom indicates the membrane region. The current flows in the direction of coordinate x. The inset shows identical dependence calculated by the previous version of the model [1]

Full size image
Fig. 3
figure 3

Concentration profiles of the OH− ion at various current densities; anolyte: 5000 mol NaCl m−3, 0.2 mol CaCl2 m−3, pH = 2; catholyte: 13000 mol NaOH m−3. The grey field at the bottom indicates the membrane region. The current flows in the direction of coordinate x. The inset shows identical dependence calculated by the previous version of the model [1]

Full size image
Fig. 4
figure 4

Concentration profiles of the Cl− ion at various current densities; anolyte: 5000 mol NaCl m−3, 0.2 mol CaCl2 m−3, pH = 2; catholyte: 13000 mol NaOH m−3. The grey field at the bottom indicates the membrane region. The current flows in the direction of coordinate x. The inset shows identical dependence calculated by the previous version of the model [1]

Full size image

The reason for this phenomenon is the convective flux in the diffusion layer in the direction normal to the membrane surface. As shown in the previous study, it becomes significant with increasing current density. Under such conditions the convective mechanism contributes significantly to the overall charge and mass transfer across the simulated domain. This is indicated by the reduced values of the concentration gradients which represent a driving force of the diffusion mass transfer mechanism being the predominant one in the case of the neglected convection term in the domain of the Nernst diffusion layers. This has very important consequences in terms of the calculated membrane selectivity.

In the case of the chloride ion the phenomenon connected with the convective mass transfer results in the less significant decrease in the concentration of the chloride on the membrane anode side with increasing current load. Also the concentration increase in the chloride ion at the membrane surface on the catholyte side is substantially less significant. These values represent a boundary condition for the integration of Eq. 9. This results in a significant increase of the chloride concentration gradient inside the membrane. This behaviour is different from that of the two ions discussed previously. As a consequence, decreasing selectivity of the mass transfer across the membrane with respect to the sodium could be assumed.

Another interesting issue is the concentration profiles of the chloride ions inside the membrane, especially at a higher current density. The reason for this development is that the role of the chloride as a species compensating the charge of the sodium ion in the anolyte region is taken over by the hydroxyl ion at a certain position. In this respect this starts to play a decisive role in the membrane region close to the cathode compartment.

This theory is proven by the dependence of the ionic fluxes on the current load, shown in Fig. 5. With respect to the convective flux in the diffusion layer, it can be clearly seen that the flux of the sodium ion is enhanced, while at the same time the hydroxyl ion transfer is reduced. This confirms the above theory of the role of convective mass transfer in the external diffusion layers. This results in a significant reduction in membrane current load under which the diffusional flux of the hydroxyl ion clearly prevailing under current-less conditions is exceeded by the sodium ion flux. Whereas, in the original model, disregarding the convectional mass transfer mechanism has reached such an equilibrium in fluxes at a current density of 1550 A m−2, in the present case an identical situation was obtained at just 820 A m−2. As a direct consequence the membrane selectivity for the sodium ion transport improves. It increases at a current density of 1500 A m−2 from 52%, obtained using the model disregarding the convective flux in the diffusion layer, to 76% obtained in the present case.

Fig. 5
figure 5

Molar flux densities of Na+, OH− and Cl− ions at various current densities; anolyte: 5000 mol  NaCl m−3, 0.2 mol CaCl2 m−3, pH = 2; catholyte: 13000 mol NaOH m−3. Flow in the direction of coordinate x (Figs. 2–4) is considered to be positive. The full lines show results of the present version, the dashed lines of the previous [1] version of the model

Full size image

The remaining ions, i.e., proton and calcium, are treated in Figs. 6–8. It can be seen that the effect of the convectional mass transport mechanism is identical to that of the sodium ion. This is due to the fact that both these cations are originally present in the anolyte solution. Therefore they are subject of phenomena identical to the sodium ion and the discussion of that case also applies. The concentration profiles of both ions show identical characteristics in the two model versions. The main difference consists in the reduction of the concentration maxima at high current loads. This is documented by Figs. 6 and 7. Figure 8 confirms that in this case, too, the flux of the two ions increases in the present model results, when compared to the previous one. The consequences of this behaviour for membrane performance are two-fold: whereas the reduced concentration of the calcium ion in the membrane interior is clearly positive, the reduced proton concentration results in an increase in the pH value inside the membrane and thus reduce its resistance to blockage by the calcium ions. Moreover, the increased proton flux across the membrane results in the reduced efficiency of the process. In the present case it has reached a value of 1.15 × 10−4 mol H+ m−2 s−1 at a current density of 1500 A m−2. This value represents 0.97% of that of the sodium ion. Nevertheless, under industrial conditions this is already a significant value.

Fig. 6
figure 6

Concentration profiles of the H+ ion at various current densities; anolyte: 5000 mol NaCl m−3, 0.2 mol CaCl2 m−3, pH = 2; catholyte: 13000 mol NaOH m−3. The grey field at the bottom indicates the membrane region. The current flows in the direction of coordinate x. The inset shows identical dependence calculated by the previous version of the model [1]

Full size image
Fig. 7
figure 7

Concentration profiles of the Ca2+ ion at various current densities; anolyte: 5000 mol NaCl m−3, 0.2 mol CaCl2 m−3, pH = 2; catholyte: 13000 mol NaOH m−3. The grey field at the bottom indicates the membrane region. The current flows in the direction of coordinate x. The inset shows identical dependence calculated by the previous version of the model [1]

Full size image
Fig. 8
figure 8

Molar flux densities of H+ and Ca2+ ions at various current densities; anolyte: 5000 mol NaCl m−3, 0.2 mol CaCl2 m−3, pH = 2; catholyte: 13000 mol NaOH m−3. Flow in the direction of coordinate x (Figs. 6 and 7) is considered to be positive. The full lines show results of the present and the dashed of the previous [1] version of the model

Full size image

The role of the electroosmotic convective flux in the overall mass transport across the membrane under current load was discussed in detail in the previous paper [1]. As seen in Fig. 9, a similar effect was also observed for the present version of the model. It is difficult to compare the absolute values calculated by these two models because the present model considers the variation in solution density. Thus, the electrolyte flow rate depends on the position. The flow rate in the middle of the membrane was, therefore, chosen for purposes of comparison. At a current load of 1500 A m−2 it has a value of 8.9 × 10−7 m s−1. This is an increase of almost 40% compared to 6.4 × 10−7 m s−1 calculated using the previous model. This clearly shows that allowing the convective flux inside the Nernst diffusion films results in an increase in the formal hydraulic permeability of the overall domain involved in the model. This is in accordance with the explanation of the results of the model given so far. Besides the acceleration of the mass transfer by taking into account the convective mechanism in the Nernst diffusion film, further enhancement is achieved by the general increase in the solution flow rate.

Fig. 9
figure 9

The rate of pore fluid flow at various current densities; anolyte: 5000 mol NaCl m−3, 0.2 mol CaCl2 m−3, pH = 2; catholyte: 13000 mol NaOH m−3. The flow in the direction of coordinate x is considered to be positive. The grey field at the bottom indicates the membrane region

Full size image

Related changes in the solution density are shown in Fig. 10. As discussed already in Sect. 2, the electrolyte density is connected with the concentration of dissolved salts. The density changes mainly across the membrane domain. Therefore here the density gradient is most significant. The changes are more pronounced at higher current loads. This is connected with the increasing depletion mainly of the anolyte solution near the membrane surface.

Fig. 10
figure 10

Electrolyte solution density at various current densities; anolyte: 5000 mol NaCl m−3, 0.2 mol CaCl2 m−3, pH = 2; catholyte: 13000 mol NaOH m−3. The flow in the direction of coordinate x is considered to be positive. The grey field at the bottom indicates the membrane region

Full size image

The last mass transfer mechanism in the electrolyte solution is migration. The Galvani potential field across the domain under study is shown in Fig. 11. No difference can be observed between the results of the previous and the present model because the basic characteristics of the system are retained and the ohmic resistance of the system remains approximately constant.

Fig. 11
figure 11

Galvani potential profiles at various current densities; anolyte: 5000 mol NaCl m−3, 0.2 mol CaCl2 m−3, pH = 2; catholyte: 13000 mol NaOH m−3. The grey field at the bottom indicates the membrane region. The current flows in the direction of coordinate x

Full size image

The issue of the reliability of the diffusivity values of the individual ions was treated in the previous paper [1]. No significant difference can be expected in this particular case. Therefore, it is not treated in this paper. On the other hand, the value of the ratio k M /η M (inverse value of the hydraulic resistance of the membrane) is an important parameter, whose influence on the characteristics of the system can be expected to depend strongly on the hydrodynamics in the Nernst diffusion layer. Therefore this was also the subject of closer study in this paper. The related dependence of the fluxes of the sodium, hydroxyl and chloride ions across the membrane, together with the dependence of the efficiency of the transport of the sodium ions from the anolyte to the catholyte on the current load and the inverse value of the membrane hydraulic resistance are shown in Fig. 12a–d.

Fig. 12
figure 12

Molar flux densities of (a) Na+ and (b) OH− and (c) Cl− and (d) efficiency of the Na+ transport across the membrane at various current densities and k/η M ratio; anolyte: 5000 mol NaCl m−3, 0.2 mol CaCl2 m−3, pH = 2; catholyte: 13000 mol NaOH m−3. Flow in the direction of coordinate x is considered to be positive

Full size image

As can be seen in Fig. 12a, the increase in k M /η M causes a significant increase in the sodium ion flux intensity across the membrane. The dependence on current density and on ratio value shows almost linear dependence. Both anions studied, i.e., hydroxide and chloride shown in Fig. 12b and c respectively, exhibit significantly different behaviour. In the case of the hydroxyl ion the absolute value of the flux density is enhanced by the increasing current load for the low values of the k M /η M ratio. With the increasing ratio value the situation changes and the absolute value of the flux of these ions starts to decrease with the increasing current load. For the chloride ion the situation is just the reverse. Thus, the efficiency of the sodium ion transfer across the membrane shown in Fig. 12d increases significantly with the hydraulic permeability of the membrane. Whereas at a current density of 1160 A m−2 and for k M /η M  = 1.0 × 10−18 m3 s kg−1 it reaches a value of 26%, for k M /η M  = 1.52 × 10−17 m3 s kg−1, at the same current load it increases to 92%.

The explanation for this behaviour is the development of the linear flow rate of the solution in the centre of the membrane shown in Fig. 13. This parameter shows a significant increase in electrolyte linear flow rate with reduced hydraulic resistance of the membrane. The shape of the dependency closely resembles the flux of the sodium and especially of the chloride ions. In the range of this parameter studied it changes by approximately one order of magnitude. It has, namely, a value of 5.1 × 10−8 m s−1 at a current density of 1100 A m−2 and k M /η M  = 1.0 × 10−18 m3 s kg−1. At the same current density and k M /η M  = 1.52 × 10−17 m3 s kg−1 it rises to 9.22 × 10−7 m s−1. Under identical conditions the chloride mass transfer rate increases from 1.31 × 10−4 mol m−2 s−1 to 2.12 × 10−3 mol m−2 s−1. It is apparent that the increase in the linear flow rate is closely related to the molar flux of the chloride ions. This is connected with the migration which counteracts the transport of this ion from the anolyte solution to the catholyte. To a certain degree it compensates the diffusional flux between these two solutions caused by the concentration gradient. Convective flux thus represents the only mechanism enhancing chloride diffusional transport in this direction. On the other hand, hydroxyl ions are transported in the direction from the catholyte to the anolyte by both the diffusion and the migration mechanisms. The convective term becomes increasingly important with increasing hydraulic permeability of the membrane which allows this flux to be minimised and thus enhances the membrane selectivity for the sodium ion. It is, however, important to bear in mind the danger of contaminating the catholyte solution by the unacceptably high level of chlorides when using a membrane with enhanced hydraulic permeability.

Fig. 13
figure 13

Pore fluid flow rate at various current densities and k/η M ratio; anolyte: 5000 mol NaCl m−3, 0.2 mol CaCl2 m−3, pH = 2; catholyte: 13000 mol NaOH m−3. The flow in the direction of coordinate x is considered to be positive

Full size image

4 Conclusions

The phenomenological mathematical model developed significantly extends the previously published version [1]. It stresses the importance of the mass transfer processes in the Nernst diffusion layers for the overall behaviour of the membrane. In this particular case the attention has focused on the role of the convective term of the Nenrnst–Planck equation. Convective mass transfer significantly reduces the concentration maxima resulting from the formation of the concentration gradient necessary to induce mass transfer intensity corresponding to the current load applied. This is connected with the increased hydraulic permeability of the system. The convective mass transfer at the interface produces enhanced mass transport. The role of the convective flux was further stressed by results of the parametric study on this factor. It has been shown that, under current load, enhancement of the hydraulic permeability of the membrane results in a significant increase in its selectivity for the sodium ion. However, at the same time it also causes enhancement of chloride penetration to the catholyte solution, thus reducing the degree of purity of the alkali metal hydroxide solution produced.