1 Introduction

Quantum teleportation is one of the essential parts of quantum information development. By combining quantum and classical channels, quantum teleportation allows the faithful transfer of an arbitrary quantum state from one party to another at a distance [1]. Later, many variations were introduced as an extension of the protocol.

One of the variations is the bidirectional teleportation, in which the transmission occurs from a sender to a receiver and vice versa. It was first proposed by Zha et al. [2], who used a maximally entangled five-qubit channel, with one of the qubits belonging to a controller, followed by Shukla et al. [3], who evaluated it in a more general view. Yang et al. [4] proposed an asymmetric bidirectional protocol that simultaneously transmits one and two qubits in two directions. Li et al. [5] propose a similar scheme that can transmit a two-qubit state in both directions; they used a maximally nine-qubit entangled state as the quantum channel. Recently, Cao et al. [6] proposed a bidirectional quantum transmission with different levels of control that can transmit two-qubit states with different levels of importance represented by different numbers of controllers’ cooperation. Many different variations of the bidirectional protocol were reported in [7,8,9,10,11,12,13,14,15]. For example, Ahmadkhaniha et al. [16] proposed an alternative teleportation method, namely an enable-based bidirectional quantum teleportation protocol that makes use of distributed quantum gates. They demonstrated that using their proposed method, the entangled state required for the quantum channel can be reduced to a more efficient number. Some studies also consider the effect of noises on the protocol’s performance [17,18,19,20,21,22,23]. The use of a joint state as a quantum channel resource has similarities to the quantum broadcast protocol. Mafi et al. [24] evaluated two controlled quantum broadcast protocols, using 6-qubit and 6n-qubit (generalized scheme) cluster states as the quantum channel. They demonstrated that arbitrary states can be communicated across a quantum channel, and receivers can reconstruct the input information with the authorization of the controller parties. The protocols may be useful in future communication applications.

All of the bidirectional studies mentioned use a maximally entangled state as the channel. However, in a real situation, the channel used in the teleportation may not have maximal entanglement due to some imperfection of the source [25,26,27]. The work in [27,28,29,30,31,32,33,34,35] evaluated teleportation protocols via a non-maximally entangled channel state. All the studies show that the non-maximal entanglement leads to a probabilistic teleportation, i.e., it has unit fidelity but less than one probability. Hence, it may lead to a conclusion that a non-maximally entangled five-qubit channel state will always produce a probabilistic bidirectional controlled teleportation.

In this work, we will show that there exists a particular non-maximally entangled five-qubit channel state that can still produce a deterministic teleportation. That is, by making the non-maximally entangled part only happen between the controller and other parties but keeping the maximal entanglement between every sender-measurement parties pair. We will show that by using the particular state and a measurement bases combination, the perfect teleportation performance will always be achievable. Furthermore, we evaluate the proposed protocol’s performance under phase-damping noise and compare it with a well-known maximally entangled channel protocol [3] and discuss the result.

The bidirectional studies via a non-maximally entangled channel were recently evaluated by Jiang et al. [26]. They showed that the protocol could not reach a unit fidelity value. To solve the problem, they performed an appropriate unitary transformation on the non-maximally entangled state with the help of an auxiliary qubit, which could improve a probabilistic teleportation to a deterministic teleportation. Our work is different. We do not use any additional transformation or auxiliary qubit. We use the standard protocol procedures: joint state measurements by the senders and a single qubit measurement by the controller. We will show that the teleportation can still have perfect fidelity and probability even though the channel is non-maximally entangled.

This article is composed of five sections. The first section discusses the introduction, followed by the evaluation of the bidirectional quantum controlled teleportation via a particular entangled five-qubit channel state, which became the basis of the proposed non-maximally entangled protocol. The third section is the evaluation of the proposed bidirectional teleportation via a non-maximally entangled five-qubit channel state. The fourth section discusses the effect of the phase-damping noise on the protocol’s fidelity value. We end with a comparison with other similar studies and conclusion.

2 Bidirectional Quantum Controlled Teleportation via a Particular Entangled Five-Qubit Channel State

In this section, we evaluate a bidirectional quantum controller teleportation via a particular entangled five-qubit channel state, which will become the basis of the proposed non-maximally protocol in the next section. We have evaluated a lot of bidirectional quantum teleportation protocol and arrived at a unique channel state which can produce a deterministic teleportation, i.e., has unit probability and fidelity, as described below.

2.1 Protocol Description

In the teleportation process, it is assume that there are three parties: Alice as the first sender (second receiver), Bob as the first receiver (second sender), and Charlie as a controller. Before the teleportation process, the parties pre-shared a particular entangled five-qubit channel state as

$$\begin{aligned} | \Phi \rangle _{A_1B_1B_2A_2C}= & {} {N \left\{ \left( a_1| 00 \rangle +a_2| 01 \rangle -a_2^*| 10 \rangle +a_1^*| 11 \rangle \right) _{A_1B_1} \right. } \nonumber \\ {}{} & {} { \otimes \left( b_1| 00 \rangle +b_2| 01 \rangle -b_2^*| 10 \rangle +b_1^*| 11 \rangle \right) _{B_2A_2} \otimes | 0 \rangle _C }\nonumber \\ {}{} & {} { +n \left( a_2| 00 \rangle +a_1| 01 \rangle +a_1^*| 10 \rangle -a_2^*| 11 \rangle \right) _{A_1B_1}} \nonumber \\ {}{} & {} { \left. \otimes \left( b_2| 00 \rangle +b_1| 01 \rangle +b_1^*| 10 \rangle -b_2^*| 11 \rangle \right) _{A_2B_2} \otimes | 1 \rangle _C \right\} ,} \end{aligned}$$
(1)

with \(N=\left( 2\sqrt{(1+|n|^2)(|a_1|^2+|a_2|^2)(|b_1|^2+|b_2|^2)}\right) ^{-1}\). Indexes \(A_1\) and \(A_2\) represent the corresponding qubits belonging to Alice, \(B_1\) and \(B_2\) to Bob, and C to Charlie. The parameters \(a_1\), \(a_2\), \(b_1\), \(b_2\), and n are complex numbers. If we choose the n such that satisfy \(0<|n|<\infty \), the state will be in a completely entangled state [27, 36], which is the requirement for the bidirectional transmission with a controller [1, 2]. The channel state can be build by operations as follows.

2.2 Channel Preparation

Firstly, five single qubit states are prepared. The states are

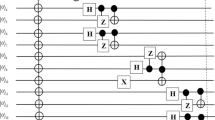
$$\begin{aligned} {| \psi _1 \rangle _{A_1} | \psi _2 \rangle _{B_1} | \psi _3 \rangle _{B_2} | \psi _4 \rangle _{A_2} | \psi _5 \rangle _{C}}= & {} {| 0 \rangle _{A_1} \otimes e^{i\theta _a}(r_a | 0 \rangle + \sqrt{1-r_a^2} e^{i\phi _a} | 1 \rangle )_{B_1} } \nonumber \\{} & {} {\otimes | 0 \rangle _{B_2} \otimes e^{i\theta _b}(r_b | 0 \rangle + \sqrt{1-r_b^2} e^{i\phi _b} | 1 \rangle )_{A_2}} \nonumber \\{} & {} {\otimes (r_n | 0 \rangle + \sqrt{1-r_n^2} e^{i\phi _n} | 1 \rangle )_C,} \end{aligned}$$
(2)

with \(r_a\), \(r_b\), \(r_n\) are real parameters, \(\theta _a\), \(\theta _b\) are global phases, and \(\phi _a\), \(\phi _b\), \(\phi _n\) are relative phases. A Hadamard gate is applied to qubit \(A_1\) (as well as qubit \(B_2\)), followed by applications of a controlled global-phase-shift gate about \(-2\theta _a\) (\(-2\theta _b\)) [37], controlled relative-phase-shift gate about \(-2\phi _a\) (\(-2\phi _b\)), controlled Pauli-Z gate, and controlled Pauli-X gate on qubit \(B_1\) (\(A_2\)) with qubit \(A_1\) (\(B_2\)) as the control qubit for all of the gates applied. The circuit diagram is shown in Fig. 1. By rewritting the parameters as

$$\begin{aligned} \frac{r_a e^{i\theta _a}}{\sqrt{2}}= & {} \frac{a_1}{N_a}; ~~\frac{\sqrt{1-r_a^2}e^{i\theta _a}e^{i\phi _a}}{\sqrt{2}}=\frac{a_2}{N_a}; \nonumber \\ \frac{r_b e^{i\theta _b}}{\sqrt{2}}= & {} \frac{b_1}{N_b}; ~~~\frac{\sqrt{1-r_b^2}e^{i\theta _b} e^{i\phi _b}}{\sqrt{2}}=\frac{b_2}{N_b}; \\ {r_n}= & {} \frac{1}{N_n};~~~\sqrt{1-r_n^2}e^{i\phi _n}=\frac{n}{N_n}\nonumber \end{aligned}$$
(3)

with \(N_a = \sqrt{|a_1|^2+|a_2|^2}\), \(N_b = \sqrt{|b_1|^2+|b_2|^2}\), and \(N_n = \sqrt{1+|n|^2}\), the resulting five-qubit state can be expressed as

$$\begin{aligned} { | \psi '_{12} \rangle _{A_1B_1}| \psi '_{34} \rangle _{B_2A_2} | \psi _5 \rangle _C}= & {} { \frac{1}{\sqrt{|a_1|^2+|a_2|^2}}(a_1| 00 \rangle +a_2| 01 \rangle -a_2^*| 10 \rangle +a_1^*| 11 \rangle )_{A_1B_1}} \nonumber \\{} & {} { \otimes \frac{1}{\sqrt{|b_1|^2+|b_2|^2}} \left( b_1| 00 \rangle +b_2| 01 \rangle -b_2^*| 10 \rangle +b_1^*| 11 \rangle \right) _{A_2B_2}} \nonumber \\{} & {} { \otimes \frac{1}{\sqrt{1+|n|^2}}(| 0 \rangle +n| 1 \rangle )_C} \end{aligned}$$
(4)

After that, two controlled Pauli-X gates are applied on qubit \(A_2\) and \(B_2\) (one gate for each qubit) with qubit C as the control qubit, resulting the channel state in (1). We will discuss the entanglement of the state after the step-by-step teleportation process description below.

Fig. 1
figure 1

The proposed teleportation circuit diagram described in Section 2. JSM, CBM, \(U_A\), \(U_B\), and CC, refers to joint-state measurement, computational bases measurement, Alice’s unitary operation, Bob’s unitary operation, and classical channel, respectively. The states \(| \psi _2 \rangle _{B_1}\), \(| \psi _4 \rangle _{A_2}\), and \(| \psi _5 \rangle _{C}\) are described in (2). The gates H, \(Ph(-2\theta _i)\), \(P(-2\phi _i)\), Z, and X, are Hadamard gate, controlled global-phase-shift gate about \(-2\theta _i\), controlled relative-phase-shift gate about \(-2\phi _i\), controlled Pauli-Z gate, and controlled Pauli-X gate, respectively

Full size image

2.3 Step 1: The Teleportation is Started by Charlie

In the teleportation process, Alice and Bob have an arbitrary initial state as

$$\begin{aligned} | \alpha \rangle _a= & {} x_0| 0 \rangle +x_1| 1 \rangle , \end{aligned}$$
(5)
$$\begin{aligned} | \beta \rangle _b= & {} y_0| 0 \rangle +y_1| 1 \rangle , \end{aligned}$$
(6)

respectively, with \(x_k\) and \(y_l\) (for \(\{k,l\} \in \{0,1\}\)) are complex numbers satisfying normalization conditions: \(\sum _{m=0}^{1} \left|z_m \right|^2 =1\) for \(\{z\} \in \{x,y\}\). Alice wants to teleport her state to Bob, and vice versa, with Charlie’s cooperation.

The teleportation is started by Charlie, by measuring qubit C on a computational basis. Indeed, a controller measures first before the senders is not a common procedure [2,3,4,5,6,7,8,9,10,11,12,13,14,15, 25]. However, at the end of this section, we will show that the role of the controller, i.e., he can decide wheter the teleportation will succeed or not, can still be done just as well as the common one. We will also explain that the change becomes an advantage when considering a noisy environment in Section 4. The teleportation circuit diagram is shown in Fig. 1.

After Charlie’s measurement, the channel state will collapse into two possible states. If the measurement result is \(| 0 \rangle \), which happens with \(\frac{1}{1+|n|^2}\) probability, the remaining channel qubit state can be expressed as

$$\begin{aligned} | \Phi '_1 \rangle _{A_1B_1B_2A_2}= & {} N'\left( a_1| 00 \rangle +a_2| 01 \rangle -a_2^*| 10 \rangle +a_1^*| 11 \rangle \right) \nonumber \\ {}{} & {} \otimes \left( b_1| 00 \rangle +b_2| 01 \rangle -b_2^*| 10 \rangle +b_1^*| 11 \rangle \right) , \end{aligned}$$
(7)

with \(N'=\left( 2\sqrt{(|a_1|^2+|a_2|^2)(|b_1|^2+|b_2|^2)}\right) ^{-1}\). If the result is \(| 1 \rangle \), which happens with \(\frac{|n|^2}{1+|n|^2}\) probability, the remaining qubit state is

$$\begin{aligned} | \Phi '_2 \rangle _{A_1B_1B_2A_2}= & {} N' \left( a_2| 00 \rangle +a_1| 01 \rangle +a_1^*| 10 \rangle -a_2^*| 11 \rangle \right) \nonumber \\ {}{} & {} \otimes \left( b_2| 00 \rangle +b_1| 01 \rangle +b_1^*| 10 \rangle -b_2^*| 11 \rangle \right) . \end{aligned}$$
(8)

Equations (7) and (8) are orthogonal, whatever the choice of the coefficients is. Charlie does not announce his measurement result but keeps it secret. Hence, Alice and Bob do not know in which state the channel state collapses.

2.3.1 Step 2: Alice and Bob’s Measurements

Suppose we take the \(| 0 \rangle \) Charlie’s measurement result case. Alice and Bob mix their initial states with the qubit state as \(| \Psi _{mix} \rangle _{abA_1B_1B_2A_2C}=| \alpha \rangle _a\otimes | \beta \rangle _b\otimes | \Phi '_1 \rangle _{A_1B_1B_2A_2C}\) and perform a joint-state measurement independently in \(\left\{ | \Pi _1^\pm ((a_1,a_2)) \rangle , | \Pi _2^\pm (a_1,a_2) \rangle \right\} \) and \(\left\{ | \Pi _1^\pm (b_1,b_2) \rangle , | \Pi _2^\pm (b_1,b_2) \rangle \right\} \) basis, respectively, with

$$\begin{aligned} | \Pi _1^\pm (k_1,k_2) \rangle= & {} \left( 2|k_1|^2+2|k_2|^2\right) ^{-\frac{1}{2}}\left( k_1| 00 \rangle -k_2^*| 01 \rangle \pm k_2| 10 \rangle \pm k_1^*| 11 \rangle \right) , \end{aligned}$$
(9)
$$\begin{aligned} | \Pi _2^\pm (k_1,k_2) \rangle= & {} \left( 2|k_1|^2+2|k_2|^2\right) ^{-\frac{1}{2}}\left( -k_2| 00 \rangle -k_1^*| 01 \rangle \pm k_1| 10 \rangle \mp k_2^*| 11 \rangle \right) , \end{aligned}$$
(10)

\(k_1=a_1\) and \(k_2=a_2\) for Alice, and \(k_1=b_1\) and \(k_2=b_2\) for Bob. The (9) and (10) form a complete orthogonal measurement basis set. The channel (1) form and the measurement basis (9)-(10) correlation become the novelty of the this work’s protocol.

Table 1 List of Alice, Bob, and Charlie’s measurement results, Alice and Bob’s qubit state, and Alice and Bob’s unitary operator for the proposed generalized protocol
Full size table

2.4 Step 3: Alice and Bob’s Unitary Operations

Suppose Alice and Bob’s measurement result are \(| \Pi _1^-(a_1,a_2) \rangle \) and \(| \Pi _1^-(b_1,b_2) \rangle \), respectively, the remaining qubits collapse to

$$\begin{aligned} | \Phi '' \rangle _{B_1A_2}= & {} \left( x_0| 0 \rangle -x_1| 1 \rangle \right) \otimes \left( y_0| 0 \rangle -y_1| 1 \rangle \right) . \end{aligned}$$
(11)

Alice informs Bob about her measurement result and vice versa, followed by Charlie broadcasting his result to them. Using the information received, in this case, both Alice and Bob perform \(\sigma _z\) operator on their qubits to reconstruct the corresponding initial states. The other possible measurement result is shown in Table 1. The table shows that the receivers’ unitary operators are correlated with the controllers’ measurement result. Hence, even though Charlie measures his qubit in the very beginning, the receivers can not rebuild their initial state without Charlie’s cooperation. The table also shows that whatever the measurement result is, the receivers can always unitarily transform their state to the original state, which means the teleportation has a unit probability and fidelity [38], resulting in deterministic teleportation.

2.5 Discussion

The channel state (1) form and measurement bases (9)-(10) correlation are already sufficient to make the teleportation is faithful for any choise of the coefficients. Hence, the channel state can be in an arbitrary entangled state, i.e., can be maximally or non-maximally entangled. For the entanglement analysis, we can rewrite the channel state using (9) and (10) as

$$\begin{aligned} | \Phi \rangle _{A_1B_1B_2A_2C}= & {} \frac{1}{\sqrt{1+|n|^2}} \left\{ | \Pi _1^+(a_1,a_2) \rangle _{A_1B_1} | \Pi _1^+(b_1,b_2) \rangle _{A_2B_2} | 0 \rangle _C \right. \nonumber \\ {}{} & {} \left. + n | \Pi _2^-(a_1,a_2) \rangle _{A_1B_1} | \Pi _2^-(b_1,b_2) \rangle _{A_2B_2} | 1 \rangle _C \right\} . \end{aligned}$$
(12)

The \(| \Pi _1^+(a_1,a_2) \rangle \), \(| \Pi _1^+(b_1,b_2) \rangle \), \(| \Pi _2^-(a_1,a_2) \rangle \), and \(| \Pi _2^-(b_1,b_2) \rangle \) states can always be decomposed using Schmidt Decomposition. It can be shown that the states always have maximal entanglement for any choise of the \(a_1\), \(a_2\), \(b_1\), and \(b_2\) coefficient [27]. The concurence and entanglement entropy of the states also show that the state always has its maximum value for any choice of \(a_1\), \(a_2\), \(b_1\), and \(b_2\) coefficients. Hence, the entanglement between Alice and Bob’s qubits are always maximal.

But what about the entanglement of the whole five-qubit channel state? Considering that for multipartite entanglement, it is generally very difficult to find an unambiguous definition of entanglement measures, then, we approach it analogously as a bipartite state. That is, by supposing qubit \(A_1B_1A_2B_2\) as a unified single party. We can write the channel state as

$$\begin{aligned} {\frac{1}{\sqrt{1+|n|^2}} \left\{ | \text {unified}_1 \rangle | 0 \rangle _C + n | \text {unified}_2 \rangle | 1 \rangle _C \right\} ,} \end{aligned}$$
(13)

with \(| \text {unified}_1 \rangle \!=\!| \Pi _1^+(a_1,a_2) \rangle _{A_1B_1}~ | \Pi _1^+(b_1,b_2) \rangle _{A_2B_2}\) and \(| \text {unified}_2 \rangle \!=\!| \Pi _2^-(a_1,a_2) \rangle _{A_1B_1}\) \(| \Pi _2^-(b_1,b_2) \rangle _{A_2B_2}\). It is clear that \(| \text {unified}_1 \rangle \) and \(| \text {unified}_2 \rangle \) states are orthogonal. Hence, the entanglement between the unified party and qubit C will depend on the coefficient n, i.e., it will has a maximal entanglement for \(|n|=1\), separable for \(|n|=0\) or \(|n|=\infty \), and a non-maximal entanglement for the other values.

Uniquely, the proposed protocol description (Section 2.1) show that the the n parameter vanishes after the controller measures the channel state, see (7)-(8). Hence, the protocol will always resulting a deterministic teleportation regardless of its entanglement, which becomes the protocol’s advantage.

This work wants to highlight that a deterministic bidirectional quantum-controlled teleportation does not always require a maximally entangled five-qubit channel state. It has been showed that there exists a particular non-maximally entangled state that still can be used to do the job; that is, the particular state is distributed to each party such that the non-maximal entanglement part happens between the controller and other parties only. Moreover, our particular channel state can be usefull in optimizing teleportation performance under the influence of noises that will be discussed in Section 4 later.

Suppose we choose \(a_1=1\), \(a_2=0\), \(b_1=1\), \(b_2=0\), and \(n=1\), the channel will be in a maximally entangled state:

$$\begin{aligned} {\frac{1}{\sqrt{2}} \left\{ | \Phi ^+ \rangle _{A_1B_1}| \Phi ^+ \rangle _{A_2B_2}| 0 \rangle _C + | \Psi ^+ \rangle _{A_1B_1}| \Psi ^+ \rangle _{A_2B_2}| 1 \rangle _C \right\} }, \end{aligned}$$
(14)

with \(| \Phi ^+ \rangle = \frac{1}{\sqrt{2}} (| 00 \rangle +| 11 \rangle )\) and \(| \Psi ^+ \rangle = \frac{1}{\sqrt{2}} (| 01 \rangle +| 10 \rangle )\) are Bell states [1], which becomes one of the well-known bidirectional channels described in [3]. However, we interested in the non-maximally case, which will be evaluated in the next section.

3 Bidirectional Quantum Controlled Teleportation via a Non-Maximally Entangled Five-Qubit Channel State

In this section, based on the result of the previous section, we propose a bidirectional quantum controller teleportation via a non-maximally entangled five-qubit channel state. The protocol details are still the same, except for the channel. We choose \(a_1=1\), \(a_2=\sqrt{7}\), \(b_1=1\), \(b_2=0\), and \(n=\sqrt{51}\) for this section protocol’s channel state, and the state can be expressed as

$$\begin{aligned} | \psi \rangle _{A_1B_1B_2A_2C}= & {} \frac{1}{40\sqrt{2}}(7| 00000 \rangle +7| 00110 \rangle +7\sqrt{7}| 01000 \rangle +7\sqrt{7}| 01110 \rangle \nonumber \\ {}{} & {} -7\sqrt{7}| 10000 \rangle -7\sqrt{7}| 10110 \rangle +7| 11000 \rangle +7| 11110 \rangle \nonumber \\ {}{} & {} +\sqrt{51}| 01011 \rangle +\sqrt{51}| 01101 \rangle +\sqrt{357}| 00011 \rangle +\sqrt{357}| 00101 \rangle \nonumber \\ {}{} & {} -\sqrt{357}| 11011 \rangle -\sqrt{357}| 11101 \rangle +\sqrt{51}| 10011 \rangle +\sqrt{51}| 10101 \rangle ),\nonumber \\ \end{aligned}$$
(15)

which has a non-maximally entanglement, see Section 2.2. There is no specific reason for our choice of these coefficients; we simply choose it. One can choose other coefficients and will get a similar result due to the guarantee of the previous section evaluation.

3.1 Step 1: Charlie’s Measurement

In the teleportation process, Charlie measures qubit C in computational basis. Suppose Charlie’s measurement result is \(| 0 \rangle \), which happens with 0.49 probability, the remaining channel qubit state collapse to

$$\begin{aligned} | \phi _1 \rangle _{A_1B_1B_2A_2}= & {} \frac{1}{4}\left( | 00 \rangle +\sqrt{7}| 01 \rangle -\sqrt{7}| 10 \rangle +| 11 \rangle \right) \otimes \frac{1}{\sqrt{2}}\left( | 00 \rangle +| 11 \rangle \right) . \end{aligned}$$
(16)

3.2 Step 2: Alice and Bob’s Measurements

Alice and Bob mix their initial states with the qubit state as \(| \Psi _{mix} \rangle _{abA_1B_1B_2A_2C}=| \alpha \rangle _a\otimes | \beta \rangle _b\otimes | \phi _1 \rangle _{A_1B_1B_2A_2C}\) and perform a joint-state measurement. Using channel state (1) and measurement bases (9)-(10) correlation, Alice measures qubit \(aA_1\) in a particular orthogonal basis set as

$$\begin{aligned} | \pi _1^\pm \rangle&\equiv | \Pi _1^\pm (1,\sqrt{7}) \rangle =&\frac{1}{4}| 00 \rangle -\frac{\sqrt{7}}{4}| 01 \rangle \pm \frac{\sqrt{7}}{4}| 10 \rangle \pm \frac{1}{4}| 11 \rangle , \end{aligned}$$
(17)
$$\begin{aligned} | \pi _2^\pm \rangle&\equiv | \Pi _2^\pm (1,\sqrt{7}) \rangle =&-\frac{\sqrt{7}}{4}| 00 \rangle -\frac{1}{4}| 01 \rangle \pm \frac{1}{4}| 10 \rangle \mp \frac{\sqrt{7}}{4}| 11 \rangle , \end{aligned}$$
(18)

while Bob measures qubit \(bB_2\) in Bell basis [1], i.e., \(| \Phi ^\pm \rangle \equiv | \Pi _1^\pm (1,0) \rangle = \frac{1}{\sqrt{2}} (| 00 \rangle \pm | 11 \rangle )\) and \(| \Psi ^\pm \rangle \equiv | \Pi _2^\mp (1,0) \rangle = \frac{1}{\sqrt{2}} (| 01 \rangle \pm | 10 \rangle )\). Suppose Alice and Bob’s measurement results are \(| \pi _1^- \rangle \) and \(| \Phi ^+ \rangle \), respectively, the remaining qubit state collapses to

$$\begin{aligned} | \Psi '' \rangle _{B_1A_2}= & {} \left( x_0| 0 \rangle -x_1| 1 \rangle \right) \otimes \left( y_0| 0 \rangle +y_1| 1 \rangle \right) . \end{aligned}$$
(19)

3.3 Step 3: Alice and Bob’s Unitary Operations

Alice informs Bob about her measurement result and vice versa, followed by Charlie broadcasting his result to them. Using the information received, in this case, Bob and Alice perform \(\sigma _z\) and I operators to rebuild their corresponding initial state, respectively. The other measurement results can be evaluated similarly and is shown in Table 2. The table shows that whatever the measurement result is, the receivers can always unitarily transform their state to the original state, which means the teleportation has a unit probability and fidelity. The main novelty of the proposed protocol is that even though the five-qubit channel (15) is non-maximally entangled (see Section 2.2), the teleportation is successful with certainty.

Table 2 List of Alice, Bob, and Charlie’s measurement results, Alice and Bob’s qubit state, and Alice and Bob’s unitary operator for the proposed non-maximally entangled channel protocol
Full size table

4 Effect of the Phase-Damping Noise on the Teleportation’s Fidelity

Considering that noise is an unavoidable phenomenon, it is interesting to see how the the proposed non-maximally protocol in Section 3 performs in the presence of the noise. Phase-damping noise is one of the most common noises [39, 40]. We will use the noise for this section’s evaluation, while the other noise types can be done similarly.

Phase-damping noise is a type of noise that loses the relative phase between the eigenstates of a system. In other words, it decays the off-diagonal elements of the system’s density matrix [40]. For a single qubit state, the noise can be represented by a Kraus Operator [19, 41] as

$$\begin{aligned} {\rho '_{\text {output}} \left( \rho _{\text {input}}\right) = \sum _{i=0}^{2} E_{i} \rho _{\text {input}} E_{i}^\dagger ,} \end{aligned}$$
(20)

with elements

$$\begin{aligned} E_0 = \sqrt{1-\eta _P} I,~ E_1 = \sqrt{\eta _P} | 0 \rangle \langle 0 |,~ E_2 = \sqrt{\eta _P} | 1 \rangle \langle 1 |. \end{aligned}$$
(21)

The \(\eta _P\) parameter is the decoherence rate parameter value, with \(0\le \eta _P \le 1\), representing the probability of the noise decaying the off-diagonal elements of the state’s density matrix.

In this section, we assume that Charlie (the controller) prepares the channel state. The protocols described in Sections 2 and 3 allow Charlie to measure his own qubit immediately and then distribute the remaining qubits to the other parties. The arrangement makes the noise only affect the senders’ (and receivers’) qubit and not the controller’s (because it does not have a chance to travel in space and time), which is the advantage we mentioned in Section 2. It also makes the evaluation simpler, i.e., we do not need to deal with a large number of qubits because the teleportation from Alice to Bob and Bob to Alice can be treated independently. We can write the channel’s density operator as a composition from \(A_1\) to \(B_1\) and \(B_2\) to \(A_2\) operator as \(\rho _{A_1B_1B_2A_2}=\rho _{A_1B_1} \otimes \rho _{B_2A_2}\). It is also assumed that each qubit experience the phase damping noise independently, but all of them experience the same decoherence rate parameter value for simplicity. Hence, the channel density operator affected by the noise can be expressed as \(\xi _{A_1B_1B_2A_2}=\xi (\rho _{A_1 B_1}) \otimes \xi (\rho _{B_2A_2})\) with

$$\begin{aligned} \xi \left( \rho _{SR}\right) = \sum _{m_S=0}^{2} \sum _{m_R=0}^{2} E_{m_S} E_{m_R} \rho _{SR} E_{m_S}^\dagger E_{m_R}^\dagger , \end{aligned}$$
(22)

for \(\{S\}\in \{A_1,B_2\}\) and \(\{R\}\in \{A_2, B_1\}\). The indexes \(m_S\) and \(m_R\) represent which qubit the Kraus operator is acting at.

The noise evaluation will be evaluated for two cases: the proposed non-maximally entangled five-qubit channel state case (from Section 3), followed by the well-known maximally entangled five-qubit case (see (14) and [3]), and compared the result.

4.1 The Proposed Non-Maximally Entangled Case

We use the protocol described in Section 3 to represent the non-maximally entangled case. Charlie, as a controller, prepares the channel state and measures his own qubit right after. Suppose we take the \(| 0 \rangle \) Charlie’s measurement result case (that happens with probability \(P_{| 0 \rangle }=0.49\)) for the demonstration, while the \(| 1 \rangle \) case can be done similarly. After some calculations, the channel density operator can be written as

$$\begin{aligned} \xi _{A_1B_1B_2A_2}= & {} \frac{1}{16} \left\{ (1-\eta _P)^2\right. (| 00 \rangle +\sqrt{7}| 01 \rangle -\sqrt{7}| 10 \rangle +| 11 \rangle ) \nonumber \\ {}{} & {} \otimes (\langle 00 |+\sqrt{7}\langle 01 |-\sqrt{7}\langle 10 |+\langle 11 |) \nonumber \\ {}{} & {} +\eta _P(1-\eta _P)| 0 \rangle (| 0 \rangle +\sqrt{7}| 1 \rangle ) \otimes \langle 0 |(\langle 0 |+\sqrt{7}\langle 1 |) \nonumber \\ {}{} & {} +\eta _P(1-\eta _P) | 1 \rangle (-\sqrt{7}| 0 \rangle +| 1 \rangle ) \otimes \langle 1 |(-\sqrt{7}\langle 0 |+\langle 1 |) \nonumber \\ {}{} & {} +\eta _P(1-\eta _P)(| 0 \rangle -\sqrt{7}| 1 \rangle )| 0 \rangle \otimes (\langle 0 |-\sqrt{7}\langle 1 |)\langle 0 | \nonumber \\ {}{} & {} +\eta _P(1-\eta _P)(\sqrt{7}| 0 \rangle +| 1 \rangle )| 1 \rangle \otimes (\sqrt{7}\langle 0 |+\langle 1 |)\langle 1 | \nonumber \\ {}{} & {} +\eta _P^2 | 00 \rangle \langle 00 | +7\eta _P^2 | 01 \rangle \langle 01 | \left. +7 \eta _P^2 | 10 \rangle \langle 10 | +\eta _P^2 | 11 \rangle \langle 11 | \right\} \nonumber \\ {}{} & {} \otimes \frac{1}{2} \left\{ (1-\eta _P)^2\right. (| 00 \rangle +| 11 \rangle ) \otimes (\langle 00 |+\langle 11 |) \nonumber \\ {}{} & {} \left. +\eta _P(2-\eta _P) \left( | 00 \rangle \langle 00 | + | 11 \rangle \langle 11 | \right) \right\} . \end{aligned}$$
(23)

It shows that the \(A_1B_1\) density operator (\(\rho _{A_1 B_1}\)) affected by the noise is more complicated than the \(B_2A_2\) one (\(\rho _{B_2A_2}\)). For simplicity, we do the evaluation separately.

In the \(A_1\) to \(B_1\) teleportation process, Alice mixes her initial state with the channel state. The density operator of the system is \(\rho _{aA_1B_1}=\rho _a \otimes \xi _{A_1B_1}\) with \(\rho _a=| \alpha \rangle _a \langle \alpha |_a\) from (5). Alice performs a joint state projection measurement on qubit \(aA_1\) in (17)-(18) basis. Suppose her measurement result is \(| \pi _1^- \rangle \), as described in Section 3, Bob performs a \(\sigma _z\) operator on his qubit. After tracing out qubit a and \(A_1\), the output density operator (qubit \(B_1\)) is

$$\begin{aligned} \rho _{B_1,| 0 \rangle ,| \pi _1^- \rangle }= & {} (1-\eta _P)^2 (x_0| 0 \rangle +x_1| 1 \rangle ) \otimes (x_0^*\langle 0 |+x_1^*\langle 1 |) \nonumber \\ {}{} & {} +\frac{1}{2^6}\eta _P(1-\eta _P)|x_0-\sqrt{7}x_1|^2(| 0 \rangle -\sqrt{7}| 1 \rangle ) \otimes (\langle 0 |-\sqrt{7}\langle 1 |) \nonumber \\ {}{} & {} +\frac{1}{2^6}\eta _P(1-\eta _P) |\sqrt{7}x_0+x_1|^2(\sqrt{7}| 0 \rangle +| 1 \rangle )\otimes (\sqrt{7}\langle 0 |+\langle 1 |) \nonumber \\ {}{} & {} +\frac{1}{2^2}\eta _P(1-\eta _P)|x_0|^2| 0 \rangle \langle 0 | +\frac{1}{2^2}\eta _P(1-\eta _P)|x_1|^2| 1 \rangle \langle 1 | \nonumber \\ {}{} & {} +\frac{1}{2^6}\eta _P^2|x_0-x_1\sqrt{7}|^2| 0 \rangle \langle 0 | +\frac{7}{2^6}\eta _P^2 |\sqrt{7}x_0+x_1|^2|| 0 \rangle \langle 0 | \nonumber \\ {}{} & {} +\frac{7}{2^6}\eta _P^2|x_0-x_1\sqrt{7}|^2| 1 \rangle \langle 1 | +\frac{1}{2^6}\eta _P^2 |\sqrt{7}x_0+x_1|^2 | 1 \rangle \langle 1 |. \end{aligned}$$
(24)

This results happens with probability

$$\begin{aligned} P_{| \pi _1^- \rangle }= & {} \frac{1}{2^2}(1-\eta _P) +\frac{1}{2^5}\eta _P|x_0-\sqrt{7}x_1|^2 +\frac{1}{2^5}\eta _P |\sqrt{7}x_0+x_1|^2. \end{aligned}$$
(25)

If we re-parameterize (5) to \(| \alpha \rangle _a=\exp {i\theta }\left( r| 0 \rangle +\sqrt{1-r^2}\exp {i\gamma }| 1 \rangle \right) \), i.e, \(x_0=r\exp {i\theta }\) and \(x_1=\sqrt{1-r^2}\exp {i(\gamma +\theta )}\), with r is a real number, \(\theta \) and \(\gamma \) are global and relative phase parameter, respectively, the \(P_{| \pi _1^- \rangle }\) value can be calculated easily and is equal to \(\frac{1}{4}\).

The fidelity of the output density operator is \(F_{| 0 \rangle ,| \pi _1^- \rangle }= | \langle \alpha | \rho _{B_1,| 0 \rangle ,| \pi _1^- \rangle } | \alpha \rangle |^2\), or can be written as

$$\begin{aligned} F_{| 0 \rangle ,| \pi _1^- \rangle }= & {} (1-\eta _P)^2 +\frac{1}{2^6}\eta _P(1-\eta _P)(|x_0-\sqrt{7}x_1|^4 + |\sqrt{7}x_0+x_1|^4) \nonumber \\ {}{} & {} +\eta _P(1-\eta _P)(|x_0|^4+|x_1|^4) +\frac{1}{2^6}\eta _P^2|x_0-\sqrt{7}x_1|^2(|x_0|^2+7|x_1|^2) \nonumber \\ {}{} & {} +\frac{1}{2^6}\eta _P^2 |\sqrt{7}x_0+x_1|^2(7|x_0|^2+|x_1|^2). \end{aligned}$$
(26)

It is the fidelity formula if Charlie’s measurement result is \(| 0 \rangle \) and Alice’s result is \(| \pi _1^- \rangle \), which happens with probability \(P_{| 0 \rangle }\times P_{| \pi _1^- \rangle }=0.49\times \frac{1}{4}\). It shows that the fidelity depends on the decoherence rate parameter and the initial state’s coefficients. The other possible measurement results can be evaluated similarly.

We define the \(A_1\) to \(B_1\) average fidelity value as \( F_{A_1\rightarrow B_1} = \sum _{m}\sum _{n} P_{| m \rangle }P_{| n \rangle } F_{| m \rangle ,| n \rangle } \), with \(P_{| m \rangle }\) (\(P_{| n \rangle }\)) is Charlie’s (Alice’s) probability value to get a \(| m \rangle \) (\(| n \rangle \)) result, with \(\{m\} \in \{0,1\}\) and \(\{n\} \in \{\pi _1^+,\pi _1^-,\pi _2^+,\pi _2^-\}\), which produces

$$\begin{aligned} F_{A_1\rightarrow B_1}= & {} 0.49\left\{ \frac{1}{2} \left( (1-\eta _P)^2 +\frac{1}{2^6}\eta _P(1-\eta _P)(|x_0-\sqrt{7}x_1|^4 + |\sqrt{7}x_0+x_1|^4) \right. \right. \nonumber \\ {}{} & {} +\eta _P(1-\eta _P)(|x_0|^4+|x_1|^4) +\frac{1}{2^6}\eta _P^2|x_0-\sqrt{7}x_1|^2(|x_0|^2+7|x_1|^2) \nonumber \\ {}{} & {} \left. +\frac{1}{2^6}\eta _P^2 |\sqrt{7}x_0+x_1|^2(7|x_0|^2+|x_1|^2) \right) \nonumber \\ {}{} & {} + \frac{1}{2} \left( (1-\eta _P)^2 +\frac{1}{2^6}\eta _P(1-\eta _P)|x_0+\sqrt{7}x_1|^2|x_0-\sqrt{7}x_1|^2 \right. \nonumber \\ {}{} & {} +\frac{1}{2^6}\eta _P(1-\eta _P) |\sqrt{7}x_0-x_1|^2|\sqrt{7}x_0+x_1|^2 \nonumber \\ {}{} & {} +\eta _P(1-\eta _P)(|x_0|^4+|x_1|^4) +\frac{1}{2^6}\eta _P^2|x_0+\sqrt{7}x_1|^2(|x_0|^2+7|x_1|^2) \nonumber \\ {}{} & {} \left. \left. +\frac{1}{2^6}\eta _P^2 |\sqrt{7}x_0-x_1|^2(7|x_0|^2+|x_1|^2) \right) \right\} \nonumber \\ {}{} & {} + 0.51\left\{ \frac{1}{2} \left( (1-\eta _P)^2 +\frac{1}{2^6}\eta _P(1-\eta _P)(|\sqrt{7}x_0-x_1|^4+|x_0+\sqrt{7}x_1|^4) \right. \right. \nonumber \\ {}{} & {} +\eta _P(1-\eta _P)(|x_0|^4+|x_1|^4) +\frac{1}{2^6}\eta _P^2|\sqrt{7}x_0-x_1|^2 (7|x_0|^2+|x_1|^2) \nonumber \\ {}{} & {} \left. +\frac{1}{2^6}\eta _P^2 |x_0+\sqrt{7}x_1|^2 (|x_0|^2+7|x_1|^2) \right) \nonumber \\ {}{} & {} + \frac{1}{2} \left( (1-\eta _P)^2 +\frac{1}{2^6}\eta _P(1-\eta _P)|\sqrt{7}x_0+x_1|^2|\sqrt{7}x_0-x_1|^2 \right. \nonumber \\ {}{} & {} +\frac{1}{2^6}\eta _P(1-\eta _P) |x_0-\sqrt{7}x_1|^2|x_0+\sqrt{7}x_1|^2 \nonumber \\ {}{} & {} +\eta _P(1-\eta _P)(|x_0|^4+|x_1|^4) +\frac{1}{2^6}\eta _P^2|\sqrt{7}x_0+x_1|^2(7|x_0|^2+|x_1|^2) \nonumber \\ {}{} & {} \left. \left. +\frac{1}{2^6}\eta _P^2 |x_0-\sqrt{7}x_1|^2(|x_0|^2+7|x_1|^2) \right) \right\} . \end{aligned}$$
(27)

The \(B_2\) to \(A_2\) teleportation process can be evaluated similarly. Suppose Bob’s measurement result is \(| \Phi ^- \rangle =\frac{1}{\sqrt{2}}(| 00 \rangle -| 11 \rangle )\), the output density operator is

$$\begin{aligned} \rho _{A_2,| 0 \rangle ,| \Phi ^- \rangle }= & {} (1-\eta _P)^2 (y_0| 0 \rangle +y_1| 1 \rangle ) \otimes (y_0^*\langle 0 |+y_1^*\langle 1 |) \nonumber \\ {}{} & {} +\eta _P(2-\eta _P)(|y_0|^2| 0 \rangle \langle 0 | + |y_1|^2| 1 \rangle \langle 1 |). \end{aligned}$$
(28)

It happens with probability \(P_{\Phi ^-}=\frac{1}{4}\). The \(B_2\) to \(A_2\) average fidelity value is \( F_{B_2\rightarrow A_2} = \sum _{q}\sum _{r} P_{| q \rangle }P_{| r \rangle } F_{| q \rangle ,| r \rangle } \), with \(\{q\} \in \{0,1\}\) and \(\{r\} \in \{\Psi ^+, \Psi ^-, \Phi ^+, \Phi ^- \}\). After some calculations, one can find that the \(B_2\) to \(A_2\) teleportation fidelity can be expressed as

$$\begin{aligned} F_{B_2\rightarrow A_2}= & {} (1-\eta _P)^2 +\eta _P(2-\eta _P)(|y_0|^4 + |y_1|^4) . \end{aligned}$$
(29)

It shows that the fidelity depends on the decoherence rate and the initial state’s amplitude parameter.

Fig. 2
figure 2

The proposed non-maximal channel protocol’s fidelity plot for various \(x_0\) and \(\eta _P\) value (30). We take the coefficients of (5) and (6) as real numbers and \(x_0=y_0\), while for \(x_0=y_1\) also produces a similar graph. The black curve indicates the contour line of some fidelity values

Full size image

The whole teleportation process average fidelity is

$$\begin{aligned} F_{tot} = F_{A_1\rightarrow B_1} \times F_{B_2\rightarrow A_2}. \end{aligned}$$
(30)

We illustrate the result by plotting it with respect to the decoherence rate parameter and some initial states’ coefficients. We take the coefficients as real numbers for simplicity, while the complex ones can be done similarly and will get a similar result. The resulting plot is shown in Fig. 2 for \(x_0=y_0\), while for \(x_0=y_1\) also produces a similar graph. We use \(x_0^2\) and \(y_0^2\) as the x-axis to generate the symmetrical shape of the graphs. We also add contour lines to represent the face of some fidelity values. The graph shows that the greater the decoherence rate parameter, the lower the fidelity, which is a typical result. However, we find an interesting result in its comparison with the well-known maximally entangled channel in (14), as described below.

Fig. 3
figure 3

The teleportation fidelity plot of the well-known maximal protocol (32) for various \(x_0\) and \(\eta _P\) value. We take the coefficients of (5) and (6) as real numbers and \(y_0=x_0\); while for \(y_0=x_1\) also produces a similar graph. The black curve indicates the contour line of some fidelity values

Full size image

4.2 The Well-Known Maximally Entangled Case

In the noiseless case, our proposed non-maximally entangled channel protocol (henceforth we refer to as proposed protocol) described in Section 3 performs just as well as the well-known maximally entangled channel protocol [3], i.e., both of them can have a unit probability and fidelity. However, we are also interested in the comparison under the presence of the noise as follows. We simply change the channel state in our protocol into the well-known maximally one as

$$\begin{aligned} {| \Phi \rangle _{A_1B_1B_2A_2C}}= & {} {\frac{1}{\sqrt{2}} \left\{ | \Phi ^+ \rangle _{A_1B_1}| \Phi ^+ \rangle _{A_2B_2}| 0 \rangle _C + | \Psi ^+ \rangle _{A_1B_1}| \Psi ^+ \rangle _{A_2B_2}| 1 \rangle _C \right\} }, \end{aligned}$$
(31)

which is one of the channel classes described in [3], see Section 2.2. The protocol steps are similar to the previous section, as well as the noise evaluation. Alice and Bob use the Bell States as their measurement basis. After some calculations, one can find that the average fidelity under the phase-damping noise is

$$\begin{aligned} \tilde{F}_{tot}= & {} \left( (1-\eta _P)^2 +\eta _P(2-\eta _P)(|x_0|^4 + |x_1|^4)\right) \nonumber \\ {}{} & {} \times \left( (1-\eta _P)^2 +\eta _P(2-\eta _P)(|y_0|^4 + |y_1|^4)\right) . \end{aligned}$$
(32)

The equation shows that the fidelity only depends on the decoherence rate and the initial state’s amplitude parameter only.

We evaluate the fidelity by plotting it with respect to the decoherence rate parameter and the initial states’s parameter, as shown in Fig. 3 for \(x_0=y_0\) and \(x_0=y_1\). We take the coefficients of (5) and (6) as real numbers as previously. The plot shows that there exist some particular states that make the fidelity always equal to one for any decoherence rate parameter value, i.e., for \(x_0^2\in \{0,1\}\) and \(y_0^2\in \{0,1\}\) (which also can be seen in (32) directly), indicating that the well-known one performs better under the noise than the proposed one for the particular states.

Fig. 4
figure 4

The fidelities difference, i.e., \(\Delta F = F_{tot} - \tilde{F}_{tot}\), with \(F_{tot}\) from Fig. 2 and \(\tilde{F}_{tot}\) from Fig. 3. The black contour indicates zero \(\Delta F\) values, i.e., both fidelities have the same value

Full size image
Fig. 5
figure 5

The fidelities comparison for \(F_1=F_{tot}\) of the proposed protocol from (30), and \(F_2=\tilde{F}_{tot}\) of the well-known protocol from (32) for \(| \alpha \rangle _a=| \beta \rangle _b=\frac{1}{\sqrt{2}} \left( | 0 \rangle +| 1 \rangle \right) \)

Full size image

4.3 Discussion

The previous subsection’s result showed that the maximal protocol performs better under the noise for for \(x_0^2\in \{0,1\}\) and \(y_0^2\in \{0,1\}\) rather than the proposed one. But, how are the other states? We evaluate it by defining a fidelity difference, i.e., \(\Delta F = F_{tot} - \tilde{F}_{tot}\), and plot it in Fig. 4. We also add black contour lines to present zero \(\Delta F\) values, which divide the plot into three zones. The centre zone (left and right zones) has (have) positive (negative) \(\Delta F\) values, indicating that the proposed protocol performs better (worse) than the well-known one. It is interesting to note that the center zone is much larger than the left and right zones, which means the proposed protocol outperforms the well-known one for most of the initial states’ parameter values. We also plot the fidelities comparison for some initial states in Figs. 5 and 6, which further supports the statement.

Fig. 6
figure 6

The fidelities comparison for \(F_1=F_{tot}\) of the proposed protocol from (30), and \(F_2=\tilde{F}_{tot}\) of the well-known protocol from (32) for \(| \alpha \rangle _a=| \beta \rangle _b=\frac{1}{2} \left( | 0 \rangle +\sqrt{3}| 1 \rangle \right) \); while for \(| \alpha \rangle _a=| \beta \rangle _b=\frac{1}{2} \left( \sqrt{3}| 0 \rangle +| 1 \rangle \right) \) also produces a similar graph

Full size image
Table 3 Comparison between the proposed bidirectional quantum teleportation protocol with other similar studies
Full size table

Hence, we conclude that even the proposed and well-known protocol performs equally well in the ideal case, i.e., both of them have a unit probability and fidelity in the noiseless case, our choise on the channel coefficient in Section 3 outperforms the well-known maximally entangled channel one under the presence of the phase-damping noise, which adds to the proposed protocol’s advantages.

5 Comparison and Conclusion

In this section, we compare our proposed protocol’s efficiency to other similar studies. We use an efficiency formula as [42]

$$\begin{aligned} \eta =\frac{q_t}{q_c+b_c}, \end{aligned}$$
(33)

with \(q_t, q_c\), and \(b_c\) as the numbers of teleported qubits, numbers of channel qubits required, and numbers of classical bits required, respectively. The protocols’ efficiency are presented in Table 3, showing that our protocol efficiency is not among the highest. However, if we only compare the symmetric 1-1 protocols [2, 6, 23, 26], our protocol’s efficiency is one of the highest. We also highlight that the main novelty of the proposed one is that even if it uses a non-maximally entangled five-qubit channel state, it can produce a unit probability and fidelity teleportation, which widens the future bidirectional teleportation applicability, i.e., it does not require a maximally entangled five-qubit channel state to make a perfect teleportation anymore. The work in [26] produces a similar result. However, it needs additional transformation and an auxiliary qubit. Our proposed protocol does not; it only uses the standard protocol procedures: joint state measurements by the senders and a single qubit measurement by the controller, which has become its advantage.

We also compare the proposed protocol’s evaluation under the presence of phase-damping noise with other similar studies [5, 17,18,19, 21]. We showed that our evaluation also produces a similar result, i.e., the fidelity affected by the noise depends on the decoherence rate and the initial states’ parameters only. However, our noise approach is different from the studies, i.e., we run indexes of the Kraus Operators in (22) while the other studies do not. The trace of the resulting output density operators of the previous studies may have a non-unit value, which can be seen if we set the decoherence rate parameter to be equal to one. The non-unit trace value causes density operator interpretation difficulties. In comparison, our approach keeps (23)’s trace value always equal to one for any decoherence rate parameter, which does not experience the difficulties.

The work in [43] evaluated one-way quantum teleportation in a noisy environment, showing that a particular state performs better under a particular noise, leading a better teleportation performance. Our results also show a similar behavior. We showed that under phase-damping noise, the choice of the state in (15) as the proposed non-maximal protocol’s channel state outperformed the well-known maximally entangled channel one in (31). We show it by calculating its teleportation fidelity and comparing it with the well-known one. We highlighted that its fidelity is higher for most of the initial state, indicating that our protocol performs better under the noise rather than the well-known one.

In summary, we proposed a deterministic bidirectional quantum controlled teleportation via a non-maximally entangled five-qubit channel state. We showed that there exists a particular non-maximally entangled five-qubit channel state and measurement bases combination that can make a faithful teleportation, i.e., has a unit fidelity and probability. The main novelty of the proposed protocol is that the channel and measurement bases combination guarantees the performance of the protocol even if the five-qubit channel is non-maximally entangled, i.e., the teleportation will always have a unit fidelity and probability. We also evaluated the proposed protocol in the presence of phase-damping noise and compared it with the well-known maximally entangled channel protocol. We showed that the fidelity of the proposed non-maximal protocol is higher than the well-known maximal one for most of the initial state parameters, showing that the proposed protocol’s channel state that we choose outperforms the well-known one, which adds to the proposed protocol’s advantages.