1 Introduction

Quantum entanglement is one of the most striking features of quantum mechanics, and entangled states of matter find nowadays many applications in quantum information processing [1,2,3,4,5,6,7,8,9]. For example, quantum teleportation is physically implementable with the help of entanglement. Further applications of entanglement are found in the process of, super-dense coding [10], quantum key distribution [11], quantum telecloning [12] which are technologically implementable with the help of entanglement between quantum systems. G.Vidal in [13] showed that, entanglement also plays important role in quantum transitional phase occurring in interacting lattice systems.

Even though entanglement is known to be very useful, it has been shown that it is very fragile and is easily destroyed when the quantum system interacts with its environment, since a quantum system is almost impossible to be completely isolated from its environment so, it needs to be protected [14, 15], from unwanted effects such as decoherence [16, 17], and dissipation [17, 18]. This is a fundamental problem when trying to characterize the dynamical properties of entanglement. Thus, maximally entangled states are known as an important resources of several quantum error correction algorithm and communication processes [9, 19,20,21].

Within the past few decades, one of the major tasks in engineering of quantum computation has been the search of a suitable many-qubit system whose entanglement is robust enough for it to be used in quantum computing tasks; some of the suitable proposed so far have included superconducting Josephson junctions, semi-conductor nanostructure [22], optical gates lattice and quantum dots [23], spin systems. The latest has been proven to be among the favorite spin chains to implement quantum computers especially the Heisenberg spin\(-\frac {1}{2}\) chain due to their properties, their coherence and their relaxation time [24]. Therefore, several models using Heisenberg spin\(-\frac {1}{2}\) chain have been deeply investigated recently. For examples, the isotropic XX model which means that the coupling strength is the same in the direction of x and y and does not exist in the z direction. We also denote the XY model where the coupling strength is different along the x and y axis and nonexistent along the z direction [25]. This model presents an advantage from the first one that it can be exactly solved by mapping to a spinless fermionic models. Apart from the two models above one can also have the XXX, XXZ, and XYZ models [26,27,28]. These models show that the coupling strength exists in all the directions but the XXX is isotropic and the XXZ is isotropic only in x and y directions. We particularly pay great attention to the latest model in this work, since couplings are different for all the directions and it denotes the most general case. This last model has greatly attracted the attention of physicists these past few decades since it provides the best description of the reality of spin-spin coupling systems [29, 30]. In general, the XYZ model was assimilated to the massive Thirring model [31]. Apart from the Heisenberg interactions, another important kind of interaction which arises in spin systems comes from the coupling of the electron to the angular momentum of the positive ion cores. This interaction was first introduced by Dzyaloshinskii and analyzed later by Moriya to better explain the spin systems magnetic properties [32, 33]. Recently, this type of interaction has been deeply investigated for the effects it may have on a spin based qubit system entanglement dynamics. In this idea, Gou F. Zhang studied thermal entanglement of two qubits XYZ spin chain, considering the DM effects and he found that entanglement can be considerably affected by this interaction [34]. Decoherence effects in two-qubits XYZ anisotropic model have also been studied by C.Tao et al. [35] considering the model under anisotropic magnetic field effects. The concurrence time history was considered, they found that sudden death of entanglement (ESD) collapses and sudden birth of entanglement (ESB) appears as well as revivals of entanglement due to decoherence effects, consequently, concurrence of entanglement changes in an important way under anisotropic magnetic field action on the system. Entanglement sudden death here introduces the process of finite-time disentanglement in an initially entangled quantum system. Particular attention was paid to entanglement dynamics of systems interacting with non-Markovian reservoirs [36,37,38,39]. In addition, squeezed reservoir also leads to steady-state [36] and revival of entanglement [40, 41]. ESD and ESB have recently been deeply discussed in the case of two atoms interacting with a non-Markovian bath, based on Dicke model [42]. Furthermore, Yang et al. [43] studied the dynamics of quantum correlations in two-qubits XYZ model. They came out with remarkable conclusion that, the ESD time interval strongly depends on the initial state and it is highly affected by an inhomogeneous magnetic field. Further investigations have been made by Meng Qin et al. [44] who found that, with the z-component of DM interaction (Dz), the dynamics of the system presents a kind of symmetry function about the Heisenberg coupling J and entanglement highly depends on the initial state. Moreover, in [45] it is pointed out that the DM interaction can create or strengthen entanglement. Zhang also showed [46] that, it can force ferromagnetic spin chain to be a better quantum channel for quantum communication processes.

It turns out that, a good deal of research work has been investigated in this field. However, the dynamics of entanglement of a two qubits XYZ spin chain model under both the time dependent DM interaction and the time dependent inhomogeneous magnetic field effects through a noisy environment has not yet been studied.

So, our main interest in this work is to study the evolution in time of entanglement in two qubits XYZ spin chain considering the above conditions. We are interested in this study because through it we expect to gain a better understanding of the phenomenon of entanglement by changing simultaneously the strength of the external magnetic field and that of the DM coupling to observe the corresponding system response. It is also expected that in the above conditions, adding to the time varying spin-spin anisotropic coupling, the system can be better protected from its environment and thus, entanglement can be preserved from unwanted effects. The time dependency character of the DM coupling, and that of the spin-spin interaction are due to the fact that, the system constantly interacts with its environment and also from the nature of the crystals. Furthermore, the DM interaction can be turned by an external electric field hence, if a time dependent electric field is used then, it becomes also time dependent. It has been shown that the magnetic field has several effects on qubits [47]. These effects have been studied, both for uniform and for anisotropic magnetic field and has been shown that some of them tend to enhance the strength of the coupling between qubits, thus preserving entanglement, while some other like transversal magnetic fields tend to destroy effective coupling between qubits thus, creating decoherence [48]. Moreover, using an on/off magnetic field with correct frequency, the effects of decoherence can be countered [49]. However, the DM interactions are recognized very useful both for weak ferromagnetism and antiferromagnetism spin arrangements in low symmetry, these interactions also play crucial role for entanglement as well. This proves their effectiveness in a system but these interactions are naturally present in the system and might be influenced by many parameters like the temperature of the medium, the nature of the material. So, it is considerably important to consider them as been varying in time when studying the dynamics of these types of systems.

The main objective we would like to achieve in this work is the following: we would like to show that the time dependency character of the spin-spin coupling J(t), the spin-spin anisotropic coupling Δ(t), the DM interaction D(t) and the inhomogeneous magnetic field including its anisotropy B(t) and b(t) can strongly improve entanglement in a quantum system by turning the field frequency ω. To achieve this, we structured the paper as follows: after providing the historical background in Section 1, we develop in Section 2 the dynamics of entanglement of two qubits XYZ Heisenberg spin chain assuming the system in a noisy environment and approaching the study by the Lindblad master equation method. Section 3 is devoted to numerical results and discussion and finally, we end this work with concluding remarks in Section 4.

2 Entanglement Evolution of Two-qubits XYZ Spin Chain

Beyond the interest given to quantum entanglement static behavior of many body systems, its dynamical behavior has attracted significant attention too. Under the effects of different system’s parameters both internal and external, one may have entanglement transfer, decay, creation or entanglement vanishing in the quantum system. In most of the cases, it was found that systems suddenly changed from their initial state to another inducing sudden change of entanglement as well. Moreover, the system might be in some kind of interaction with its environment creating the loss of entanglement in the system. However, it was shown that entanglement might be a key ingredient for physical implementation of quantum computers [50] and it can be measured through several methods including the concurrence, the Von-Neumann entropy, quantum discord, negativity [51,52,53,54,55,56]. This is the reason why in this section, the dynamics of entanglement is studied considering the system’s parameters as time varying within a noisy environment and considering the weak system-bath interaction known as the Born-Markov approximation [57]. The dynamics is approached by the Lindblad master equation assuming the concurrence as the main measurement feature of entanglement.

2.1 Model Description and Derivation of the System’s Dynamics

Let us define a two-qubit spin system under the effects of both the DM interaction and the inhomogeneous magnetic field by the following Hamiltonian [27, 58, 59]:

$$ \begin{array}{@{}rcl@{}} H=J_{x}{S}_{x}^{1}{S}_{x}^{2}+J_{y}{S}_{y}^{1}{S}_{y}^{2}+J_{z}{S}_{z}^{1}{S}_{z}^{2}+(B-b){S}_{z}^{1}+(B+b){S}_{z}^{2}+\overrightarrow{D}\cdot(\overrightarrow{S}^{1}\wedge\overrightarrow{S}^{2}), \end{array} $$
(1)

where in this Hamiltonian the indexes 1 and 2 stand for qubit 1 and 2 respectively, Ji (for i = x,y,z) stand for the spin-spin interactions in the system. As defined in the previous section, if Jx = Jy≠ 0 and Jz = 0, one has an XX Heisenberg model. While the case Jx = Jy≠Jz≠ 0 denotes that of XXZ Heisenberg model. But our main interest in this work is the case where we have Jx≠Jy≠Jz≠ 0 representing the XYZ Heisenberg spin chain. \(\overrightarrow {D}\) stands for the DM coupling vector between qubits. This kind of interaction arises in spin systems from the coupling of the electron to the angular momentum of the positive ion cores. It also introduces in the system the effects of anisotropic antisymmetric spin-orbit interactions which is most often neglected in several works but, which may have a particular effect on dynamical properties of quantum systems. By definition of the spin vector, one has:

$$ \begin{array}{@{}rcl@{}} \overrightarrow{S}=\frac{\hbar}{2}\overrightarrow{\sigma}, \end{array} $$
(2)

where \(\overrightarrow {\sigma }\) defines the Pauli matrix. Assuming the Planck constant as \( \hbar =1\) and considering (2) the Hamiltonian (1) becomes:

$$ H=\frac{1}{4}(J_{x}{\sigma}_{x}^{1}{\sigma}_{x}^{2}+J_{y}{\sigma}_{y}^{1}{\sigma}_{y}^{2})+\frac{J_{z}}{4}{\sigma}_{z}^{1}{\sigma}_{z}^{2}+\frac{1}{2}((B-b){\sigma}_{z}^{1}+(B+b){\sigma}_{z}^{2})+\frac{1}{4}\overrightarrow{D}\cdot(\overrightarrow{\sigma}^{1}\wedge\overrightarrow{\sigma}^{2}). $$
(3)

For reasons of simplicity, let us assume that the DM interaction is unidirectional and is oriented only along the (oz) axis, this implies we have \(\overrightarrow {D}=D_{z}\overrightarrow {k}\), which allows us to write:

$$ \begin{array}{@{}rcl@{}} \overrightarrow{D}\cdot(\overrightarrow{S}^{1}\wedge\overrightarrow{S}^{2})=\frac{D_{z}}{4} \left( {\sigma}_{x}^{1}{\sigma}_{y}^{2}-{\sigma}_{y}^{1}{\sigma}_{x}^{2}\right). \end{array} $$

For further simplification let us introduce the raising and lowering operators defined by:

$$ \begin{array}{@{}rcl@{}} \sigma_{\pm}=\sigma_{x}\pm i\sigma_{y}, \end{array} $$

from where the Pauli matrices are derived as follows, \(\sigma _{x}=\frac {1}{2}(\sigma _{+} +\sigma _{-})\) and \(\sigma _{y}=\frac {1}{2i}(\sigma _{+} -\sigma _{-})\). Considering these transformations, it follows that:

$$ \begin{array}{@{}rcl@{}} \begin{cases} \frac{1}{4}(J_{x}{\sigma}_{x}^{1}{\sigma}_{x}^{2}+J_{y}{\sigma}_{y}^{1}{\sigma}_{y}^{2})=\left( \frac{J_{x}+J_{y}}{4}\right)({\sigma}_{-}^{1}{\sigma}_{+}^{2}+{\sigma}_{+}^{1}{\sigma}_{-}^{2})+\left( \frac{J_{x}-J_{y}}{4}\right)\left( {\sigma}_{+}^{1}{\sigma}_{+}^{2}+{\sigma}_{-}^{1}{\sigma}_{-}^{2}\right),\\ D_{z} \left( {\sigma}_{x}^{1}{\sigma}_{y}^{2}-{\sigma}_{y}^{1}{\sigma}_{x}^{2}\right)=\frac{iD_{z}}{2}\left( {\sigma}_{+}^{1}{\sigma}_{-}^{2}-{\sigma}_{-}^{1}{\sigma}_{+}^{2}\right). \end{cases} \end{array} $$
(4)

Finally, the simplified Hamiltonian is thus given by:

$$ \begin{array}{@{}rcl@{}} H(t)=&{\varDelta}(t)\left( {\sigma}_{-}^{1}{\sigma}_{-}^{2}+{\sigma}_{+}^{1}{\sigma}_{+}^{2}\right)+J(t)\left( {\sigma}_{+}^{1}{\sigma}_{-}^{2}+{\sigma}_{-}^{1}{\sigma}_{+}^{2}\right)+\frac{iD(t)}{2}\left( {\sigma}_{+}^{1}{\sigma}_{-}^{2}-{\sigma}_{-}^{1}{\sigma}_{+}^{2}\right)&\\&+\frac{J_{z}(t)}{4}{\sigma}_{z}^{1}{\sigma}_{z}^{2}+\frac{B(t)}{2}({\sigma}_{z}^{1}+{\sigma}_{z}^{2})+\frac{b(t)}{2}({\sigma}_{z}^{2}-{\sigma}_{z}^{1}),& \end{array} $$
(5)

with \(J(t)=\frac {J_{x}+J_{y}}{4}\) defining the spin-spin coupling, \({\varDelta }(t)=\frac {J_{x}-J_{y}}{4}\) introducing the anisotropy of the spin-spin coupling in the xy-plane, and \(D(t)=\frac {D_{z}}{4}\). This form of Hamiltonian has already been introduced by C. Tao et al. [60], but they did not take into consideration the effect of the DM coupling, while M. Qin and Zhong-Zhou [44] studied a similar model considering only the z-component of the DM interactions and in the absence of the anisotropic magnetic field. In addition, our model looks very similar in the form with that of A. Mohammed and T. El-Shahat [58], however, our system’s parameters are time dependent, making significant difference, and which is the most important contribution in this work. Here, we mean, the anisotropic coupling constant, the DM coupling, the Heisenberg spin-spin coupling and finally the inhomogeneous magnetic field are considered to be time varying and are defined as follows:

$$ \begin{array}{@{}rcl@{}} \begin{cases} {\varDelta}(t) ={\varDelta}_{0}+{\varDelta}_{1}\cos(\omega t),\\ D(t) =D_{0}+D_{1}\cos(\omega t),\\ J(t) =J_{0}+J_{1}\cos(\omega t),\\ B(t) =B_{0}+B_{1}\cos(\omega t),\\ b(t) =b_{0}+b_{1}\cos(\omega t). \end{cases} \end{array} $$
(6)

The reasons for taking these parameters time dependent are the following: the spin-spin coupling J(t), the anisotropy Δ(t), are time dependent since these quantities depend not only on the nature of the material but also can strongly be affected by other parameters such as the temperature of the medium which may vary in time. So, their time dependency character is very important and describes the best the reality of these types of interactions. However, the magnetic field including its anisotropy are considered to be varying in time and are taken in the above forms, since the periodic structure of external or internal fields can cause the spin alignment along one direction [61]. It might also happen that this filed structure makes the concurrence oscillates and then, reaches some maximum which could not be possible with constant fields see Fig. 2. For the reasons of simplicity, let Δ(t) = Δ, J(t) = J, D(t) = D, B(t) = B, b(t) = b. In order to write the Hamiltonian in the matrix form let us consider the definition of Pauli matrices defined previously. Considering (5), one obtain:

$$ \begin{array}{@{}rcl@{}} H=\begin{bmatrix} B+\frac{J_{z}}{4} & 0& 0 & {\varDelta} \\ 0 & -b-\frac{J_{z}}{4} & J-\frac{iD}{2} & 0 \\ 0 & J+\frac{iD}{2} & b+\frac{J_{z}}{4} & 0 \\ {\varDelta} & 0 & 0 & -B+\frac{J_{z}}{4} \end{bmatrix}. \end{array} $$
(7)

Equation (7) depicts the Hamiltonian of our system as function of the system’s parameters in the matrix form. It is seen that this Hamiltonian satisfies the hermicity property since H‡ = H and presents an X-form matrix, the DM interaction introduces a complex part in the off-diagonal element of this matrix. Based on this observation, we expect decohenrence to be seriously impacted by this interaction. The eigenvalues of this matrix are all real and are determined in the Bell states [62] |00〉, |01〉, |10〉, |11〉 as follows: \([-\frac {J_{z}}{4 }+\frac {1}{2} \sqrt {4 b^{2}+4 J^{2}+D^{2}}]\), \([-\frac {J_{z}}{4 }-\frac {1}{2} \sqrt {4 b^{2}+4 J^{2}+D^{2}}]\), \([\frac {J_{z}}{4 }+\sqrt {({\varDelta }^{2}+B^{2})}]\), \([\frac {J_{z}}{4 }-\sqrt {({\varDelta }^{2}+B^{2})}]\), which are all real.

Let us consider the density matrix of the system as defined in Section 2, and define the initial state to be maximally entangled in the general form as follows:

$$ \begin{array}{@{}rcl@{}} \rho(0)=\frac{1}{4}\left( I_{4}-\sum\limits_{i=1}^{3}K_{i}{\sigma}_{y}^{i}{\otimes{\sigma}_{y}^{i}}\right)=\begin{bmatrix} 1+K_{3} & 0 & 0 & K_{1}-K_{2} \\ 0 & 1-K_{3} & K_{1}+K_{2} & 0 \\ 0 & K_{1}+K_{2} & 1-K_{3} & 0 \\ K_{1}-K_{2} & 0 & 0 & 1+K_{3} \end{bmatrix}, \end{array} $$
(8)

where Ki are the coefficients defined such that 0 < |Ki| < 1 ∀ i = {1,2,3}.

This is an X-matrix form, so called from its physical representation as the alphabetical letter X. Such a matrix is very useful because of its invariant symmetry that helps explaining some analytical results. It is important to mention that, this symmetry also allows the computations involving such state easily tractable since it preserves its structure during the evolution [58, 63,64,65], these include and no limited to unitary operations on their evolution, evaluation of entanglement. Therefore, considering ρ(t) as the density state at time t of a system with an X-initial density state, it remains an X-matrix form at any time. With this assumption, the dynamics of our system at zero temperature is provided using the weak system-environment interaction and the Born-Markov approximation [60] as follows:

$$ \begin{array}{@{}rcl@{}} \frac{d\rho(t)}{d t}=-i[H,\rho]+\sum\limits_{k=1}^{N}{\varGamma}_{k}[{\sigma}_{-}^{k}\rho{\sigma}_{+}^{k}-\frac{1}{2}\{{\sigma}_{-}^{k}{\sigma}_{+}^{k},\rho\}], \end{array} $$
(9)

where in this equation, we have set the Planck’s constant \(\hbar =1\), the term under summation describes all possible transitions that the system may undergo due to environmental effects, and \({\sigma }_{-}^{k}\) are the Lindblad jump operators defined so that \({\sigma }_{-}^{k}=[0]\) in the absence of the environment. Γk gives the decay rate of the system due to its interaction with the environment which might differ from one to another qubit since N denotes the number of qubits and k a particular qubit. In this case, k takes two values which are 1 and 2 representing the qubits. Equation (9) gives the dynamics of our system in the compact form. However, a complete understanding and the study of the system’s properties requires to rewrite (9) describing the dynamics of the system in the simplest form as possible. This might be possible if the dynamics is traduced in the matrix form. Considering therefore, the form of the initial density state as described by (8), after a given period of time, the density matrix ρ(t) remain an X matrix form, since X-form density matrices have a particularity that, their evolution in time does not affect their form. With this assumption, we expect the density state of our system at any time to be written as:

$$ \begin{array}{@{}rcl@{}} \rho(t)=\begin{bmatrix} \rho^{11}(t) & 0 & 0& \rho^{14}(t) \\ 0 & \rho^{22}(t) & \rho^{32}(t) & 0 \\ 0 & \rho^{23}(t) & \rho^{33}(t)& 0 \\ \rho^{41}(t) & 0 & 0 & \rho^{44}(t) \end{bmatrix}. \end{array} $$
(10)

Considering (10) and our Hamiltonian in the matrix form given by (7), we can derive the dynamics of our system in an explicit form as follows:

$$ \begin{array}{@{}rcl@{}} \begin{cases} \frac{d}{d t}\rho^{11}=-2{\varGamma}\rho^{11}-i{\varDelta}(\rho^{41}-\rho^{14}),\\ \frac{d}{d t}\rho^{22}={\varGamma}(\rho^{11}-\rho^{22})-iJ(\rho^{32}-\rho^{23})+D(\rho^{32}+\rho^{23}),\\ \frac{d}{d t}\rho^{33}={\varGamma}(\rho^{11}-\rho^{33})+iJ(\rho^{32}-\rho^{23})-D(\rho^{32}+\rho^{23}),\\ \frac{d}{d t}\rho^{44}={\varGamma}(\rho^{22}+\rho^{33})-i{\varDelta}(\rho^{14}-\rho^{41}),\\ \frac{d}{d t}\rho^{23}=-({\varGamma}+2ib)\rho^{23} -(D-iJ)(\rho^{22}-\rho^{33}),\\ \frac{d}{d t}\rho^{32}=-({\varGamma}-2ib) \rho^{32} +(D+iJ)(\rho^{33}-\rho^{22}),\\ \frac{d}{d t}\rho^{14}=-({\varGamma}+2iB) \rho^{14} -i{\varDelta}(\rho^{44}-\rho^{11}),\\ \frac{d}{d t}\rho^{41}=-({\varGamma}-2iB) \rho^{41} -i{\varDelta}(\rho^{11}-\rho^{44}). \end{cases} \end{array} $$
(11)

Thus, the time evolution of our system can be obtained from (11) which is a system of 8 coupled first order differential equations defined in the complex-plane, with all parameters in the equation well known. Having this equation, we will therefore, study the phenomenon of entanglement of our system through concurrence in the next section.

2.2 Analytical Study of Two-qubit Entanglement for Time-dependent System Parameters

Entanglement is a property of strongly correlated quantum systems, which plays a crucial role in the process of quantum information. It can be defined for pure and mixed state. A mixed quantum state means that the system state cannot be represented as a mixture of disentangled pure states. Let us consider two particles A and B, the total quantum system may take the form |a〉⊗|b〉, where |a〉 and |b〉 are respectively the local Hilbert spaces Ha and Hb elements. The state given in this form is not entangled, but they are separable. Thus, given a quantum state in the form :

$$ \begin{array}{@{}rcl@{}} \vert{\varPsi}\rangle=\frac{1}{N}(\vert a_{1}\rangle\otimes\vert b_{1}\rangle+\vert a_{2}\rangle\otimes\vert b_{2}\rangle), \end{array} $$
(12)

where N assures the normalization, since |Ψ〉≠|a〉⊗|b〉 then, the state |Ψ〉 is known to be entangled. We have as example of entangled state \(\vert {\varPsi }\rangle =\frac {1}{\sqrt {2}}(\vert 00\rangle +\vert 11\rangle )\) or \(\vert {\varPsi }\rangle =\frac {1}{\sqrt {2}}(\vert 01\rangle +\vert 10\rangle )\). For both pure and mixed state, there are good measures of entanglement.

For pure states, one may have a single widely accepted measure of entanglement, whereas for mixed state we have as measures of concurrence to multipartite systems entanglement of formation, the concurrence of entanglement to bipartite systems [17, 56, 66].

For bipartite systems, the notion of concurrence is the most relevant measure of entanglement, it was first introduced by Wooters [56, 67] and quantifies the degree of entanglement between two central qubits systems. The concurrence varies between 0 and 1. When it is 0, systems are said to be disentangled or separated. However, when it is 1, both systems are said to be maximally or completely entangled, meaning that, they are in some strange and extremely strong correlation [68]. The concurrence of entanglement can be evaluated using the following relation [17, 56, 69]:

$$ \begin{array}{@{}rcl@{}} C(t)=max(0,\sqrt{\lambda_{1}(t)}-\sqrt{\lambda_{2}(t)}-\sqrt{\lambda_{3}(t)}-\sqrt{\lambda_{4}}(t)), \end{array} $$
(13)

where λi(t) i = 1,⋯ ,4 denote the eigenvalues of the following matrix:

$$ \begin{array}{@{}rcl@{}} T=\rho(\sigma_{y}\otimes\sigma_{y})\rho^{*}(\sigma_{y}\otimes\sigma_{y}), \end{array} $$
(14)

with ρ∗ the complex conjugate of the density state matrix ρ obtained from (11), σy the y-component of the Pauli operator which is the well known true reversal operator for spin\(-\frac {1}{2}\) in quantum mechanics. But, despite a huge investigation made to carry out the entanglement measure in bipartite systems, it remains a big challenge since the measurement may destroys the actual state of the system. Thus, its manipulation requires an extraordinary techniques, however this phenomenon remains very interesting from its potential applications. In order to evaluate the concurrence, let’s reconsider (11), which is physically defined in the complex-plane, but can be easily transformed into a system of first order differential equation in R8 where the numerical solution is easily implementable. For this purpose, let us recall first some properties of the density matrix. It is recognized that the density matrix of quantum open systems should is always Hermitian [70]. Considering this property it follows that:

$$ \begin{array}{@{}rcl@{}} \begin{cases} \rho^{23}=(\rho^{32})^{*},\\ \rho^{14}=(\rho^{41})^{*}, \end{cases} \end{array} $$
(15)

implying that, these components are complex conjugate each other. For the Hermicity property of the density matrix to be satisfied, we need additional conditions which are the following:

$$ \begin{array}{@{}rcl@{}} \begin{cases} (\rho^{11})^{*}=\rho^{11},\\ (\rho^{22})^{*}=\rho^{22},\\ (\rho^{33})^{*}=\rho^{33},\\ (\rho^{44})^{*}=\rho^{44}, \end{cases} \end{array} $$
(16)

implying that ρ11,ρ22,ρ33,ρ44 must be real. In order to fully simplify (11), let:

$$ \begin{array}{@{}rcl@{}} \begin{cases} \rho^{11}=X_{1},\\ \rho^{22}=X_{2},\\ \rho^{33}=X_{3},\\ \rho^{44}=X_{4},\\ \rho^{23}=X_{5}+iX_{6},\\ \rho^{32}=X_{5}-iX_{6},\\ \rho^{14}=X_{7}+iX_{8},\\ \rho^{41}=X_{7}-iX_{8}, \end{cases}\Rightarrow\begin{cases} \rho^{11}=X_{1},\\ \rho^{22}=X_{2},\\ \rho^{33}=X_{3},\\ \rho^{44}=X_{4},\\ (\rho^{23}+\rho^{32})=2X_{5},\\ (\rho^{23}-\rho^{32})=2iX_{6},\\ \rho^{14}+\rho^{41})=2X_{7},\\ (\rho^{14}-\rho^{41})=2iX_{8}. \end{cases} \end{array} $$
(17)

Considering these transformations, (11) becomes:

$$ \begin{array}{@{}rcl@{}} \begin{cases} \frac{d}{d t}X_{1}=-2{\varGamma} X_{1}-2{\varDelta}(t) X_{8},\\ \frac{d}{d t}X_{2}={\varGamma}(X_{1}-X_{2})-2J(t)X_{6}+2D(t)X_{5},\\ \frac{d}{d t}X_{3}={\varGamma}(X_{1}-X_{3})+2J(t) X_{6}-2D(t)X_{5},\\ \frac{d}{d t}X_{4}={\varGamma}(X_{2}+X_{3})+2{\varDelta}(t) X_{8},\\ \frac{d}{d t}X_{5}=-{\varGamma} X_{5}+2b(t)X_{6} -D(t)(X_{2}-X_{3}),\\ \frac{d}{d t}X_{6}=-{\varGamma} X_{6}-2b(t)X_{5}-J(t)(X_{3}-X_{2}),\\ \frac{d}{d t}X_{7}=-{\varGamma} X_{7}+2B(t)X_{8},\\ \frac{d}{d t}X_{8}=-{\varGamma} X_{8}-2B(t)X_{7} -{\varDelta}(t)(X_{4}-X_{1}). \end{cases} \end{array} $$
(18)

Equation (18) is a system of 8 first order differential equations. We recall that our main goal is to measure the degree of entanglement via concurrence, which is given for a bipartite system using (13) as follows:

$$ \begin{array}{@{}rcl@{}} C(t)&= 2max\left\{0,\sqrt{\rho^{14}\rho^{14}}-\sqrt{\rho^{22}\rho^{33}},\sqrt{\rho^{23}\rho^{32}}-\sqrt{\rho^{11}\rho^{44}}\right\}&\\ &= 2max\left\{0,\sqrt{{X}_{5}^{2}+{X}_{6}^{2}}-\sqrt{X_{1}X_{4}},\sqrt{{X}_{7}^{2}+{X}_{8}^{2}}-\sqrt{X_{2}X_{3}}\right\}.& \end{array} $$
(19)

The time dependency character of Δ(t), B(t), b(t) and J(t) in (18) makes the computation of its analytical solution so difficult, however numerical solutions are easily implementable. Having said that, our main task in the following subsections is to study the evolution in time of the concurrence characterizing the degree of entanglement in our system numerically.

3 Numerical Simulations and Discussion

In the present section, numerical simulation of entanglement dynamics considering two different maximally entangled initial states is presented. For this reason, we reconsider (18) describing the full simplified dynamics of our system. As defined in the previous section, concurrence is assumed to be the most suitable method to quantify entanglement of pure and mixed bipartite quantum systems [71]. It is highly influenced by the system and environmental parameters. However, in this work our purpose is to study its variation with respect to the DM interaction rate D, the anisotropic magnetic field, the Heisenberg spin-spin anisotropic coupling Δ, which are all assumed time dependent and the decoherence rate Γ due to permanent interaction of the system with the bath. In all our simulations the time is scaled by the decoherence rate Γ, which by definition has the inverse dimension of time.

3.1 Dynamical Behavior of the Concurrence for Two-qubits XYZ-Heisenberg Spin Chain: Effects of the Field Frequency

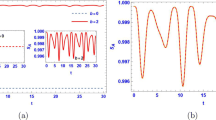
Regarding (6) defining the parameters of the system, let’s recall that, ω = kπ (k = 0,1,2⋯) displays the time independent system’s parameters and ω≠kπ (k = 0,1,2⋯), the time dependent ones. It is therefore observed from simulations that, for \(\omega =\frac {2\pi }{{\varGamma }}=\frac {2\pi }{0.5}\) with Γ defining the decoherence rate, the response time of the system is equal to the decoherence rate (the curve in green color Fig. 1), when the response time of the system and the decoherence rate coincide, the system behaves like all the system’s parameters were constant, however, when \(\omega =\frac {2\pi }{{\varGamma }}\leq 2\) as shown on the graph by the curve in red, especially between 0 and π, the concurrence is quietly preserved mining that, for the physical implementation a time dependent field with a frequency quietly selected might be used to protect the system from unwanted effects due to the environment (environment with high decoherence rate). For further interpretation of the time varying fields, Fig. 2 depicts the evolution in time of the concurrence for constant and time varying values of the system’s parameters both on the same graph and for two maximally entangled initial states. One observes that, both dynamics present a similar behavior for short time. However, as the time grows, we realize that, for the first state we have an interval of time where the system is disentangled (loss of entanglement in the system), but it happens that, when the time keep increasing, both dynamics tend to the same threshold value and the time dependence character becomes more and more significant so that at some point it takes the control of the system inducing the oscillating behavior of entanglement. So, the constant part might be interpreted as, the average of the real concurrence. This better characterizes the behavior of the concurrence in the physical sense. This result confirms the fact that, the time varying system’s parameters is of great importance and might be very useful to protect entanglement in the physical implementation of two qubits XYZ-Heisenberg spin system.

Fig. 1
figure 1

Dynamical behavior of the concurrence as main measure of entanglement of two qubits XYZ-Heisenberg model, for different frequencies of the field and for two different maximally entangled initial states (K1 = K2 = 1, K3 = − 1 Fig. 1a) and (K1 = K2 = − 1, K3 = 1 Fig. 1b), with Γ = 0.5,B0 = 0.2,b0 = 0.4,Δ0 = 0.2,J0 = 1,D0 = 0.5, B1 = 0.02,b1 = 0.04,Δ1 = 0.08,J1 = 0.1,D1 = 0.05

Full size image
Fig. 2
figure 2

Dynamical behavior of the concurrence as main measurement quantity of entanglement of two qubits XYZ Heisenberg spins chain, for different maximally entangled initial states (K1 = K2 = 1, K3 = − 1 Fig. 2a) and (K1 = K2 = − 1, K3 = 1 Fig. 2b). The dash line corresponds to constant parameters (i.e. B1 = b1 = Δ1 = J1 = D1 = 0, and Γ = 0.5,B0 = 0.2,b0 = 0.4,Δ0 = 0.2,J0 = 1,D0 = 0.5), while the solid line corresponds to time dependent parameters (i.e. Γ = 0.5,B0 = 0.2,b0 = 0.4,Δ0 = 0.2,J0 = 1,D0 = 0.5 and B1 = 0.02,b1 = 0.04,Δ1 = 0.08,J1 = 0.1,D1 = 0.05)

Full size image

3.2 Effects of the Anisotropic Time-varying Magnetic Field and the Anisotropic Heisenberg Spin-spin Coupling on Entanglement

Here, we study the effects of the magnetic field including its anisotropic behavior on the dynamical behavior of entanglement. That is, its behavior with respect to time is simulated for different values of B and b respectively,which are shown on Figs. 3 and 4. Taking Γ = 0.5, J0 = 1, Δ0 = 0.2, D0 = 0.5, J1 = 0.1, Δ1 = 0.05 and D1 = 0.05 it happens that the anisotropic behavior of the magnetic field considerably affects the dynamics of the concurrence in the sense that, the concurrence is improved as b(t) increase. That means, when realizing the experiment, one should make sure that, the anisotropic effects of the magnetic field acting on both qubits is raised to allow the enhancement of entanglement. Moreover, observing carefully these curves, we realize that, for relatively short period of time the phenomenon of ESD appears and the time interval of this disentanglement in the system reduces considerably with the increasing in the anisotropic magnetic field. Furthermore, the concurrence presents an oscillating behavior due to the fact that, the magnetic field is time-dependent inducing the nearest concurrence to reach its maximum value. This is in agreement with the results found by Chen Tao et al. [60] and confirms the fact that, the time varying b-field can enhance the coupling strength between two qubits.

Fig. 3
figure 3

Time evolution of the Concurrence for different time dependent magnetic field. Considering different maximally entangled initial states (K1 = K2 = 1, K3 = − 1 Fig. 3a) and (K1 = K2 = − 1, K3 = 1 Fig. 3b), Γ = 0.5

Full size image
Fig. 4
figure 4

Dynamical behavior of the concurrence for different anisotropic magnetic fields assuming to be varying as the time increases for different maximally entangled initial states (K1 = K2 = 1, K3 = − 1 Fig. 4a) and (K1 = K2 = − 1, K3 = 1 Fig. 4b), Γ = 0.5

Full size image

Figure 5 shows the concurrence dynamics for different values of the spin-spin coupling Δ. Observing carefully this picture, it is clear that, increasing the anisotropic spin-spin coupling (Δ) in a system of two qubits Heisenberg spin chain increase the degree of correlation in the system then, inducing an increase of the degree of entanglement, this is shown by the dash curve. However, it is observed that the phenomenon of ESD appears in the system traducing a loss of correlation in the system with an interval of time depending on the initial state chosen. However, the revival of entanglement and the phenomenon of ESB appears in the system with the increasing of this anisotropy. These results confirm our prediction in Chapter 1 for which the XYZ Heisenberg model was the most suitable candidate in the realization of quantum computing since it is observed that, more Jx differs from Jy, more the concurrence of entanglement becomes important.

Fig. 5
figure 5

Dynamical behavior of the concurrence for different spin-spin anisotropic coupling Δ assumed to be varying as the time increases for different maximally entangled initial states (K1 = K2 = 1, K3 = − 1 Fig. 5a) and (K1 = K2 = − 1, K3 = 1 Fig. 5b), Γ = 0.5

Full size image

3.3 Decoherence and Time-varying Dzyaloshinskii-Morya Coupling Effects on the Dynamical Properties of Entanglement

Figure 6 presents the variation in time of the concurrence as function of the Dzyaloshinskii-Moriya (DM) interaction. We first recall that, we assumed this interaction to be oriented along the z-direction. It is observed that, entanglement reaches its maximum as the DM coupling increases and this for both initial states. In addition, the DM coupling enhances the quantum fluctuations frequency, thus increasing entanglement in a two qubits XYZ spin model. The concurrence also oscillatory behavior when the DM interaction effects become more and more important. This may be associated to the competing effects existing between the anti-symmetric DM interaction behavior and the symmetric behavior of the Heisenberg interactions simultaneously present in the system. It is also due to the fact that, in contrast to the Heisenberg interactions tending to render neighbor spins parallel, the DM interactions will turn them perpendicular one to another. Furthermore, the ESD that appears in the system can be avoided by increasing the DM interactions strengh. Finally, it is observed from the graph that, increasing the DM interactions effects in the system, the time interval of the phenomenon of ESD considerably reduces. Similar results were found by Zad [72].

Fig. 6
figure 6

Dynamical behavior of the concurrence for different DM interaction D assumed to be varying as the time increases for different maximally entangled initial states (K1 = K2 = 1, K3 = − 1 Fig. 6a) and (K1 = K2 = − 1, K3 = 1 Fig. 6b), Γ = 0.5

Full size image

As regards to decoherence effects, Fig. 7 depicts the evolution in time of the concurrence as main measurement quantity of entanglement for two maximally entangled initial states. It is seen from this picture that, the environmental decays rate (decoherence) affects seriously entanglement of the system. From the graph, it is clear that, in the absence of this effect, the concurrence is maximum (almost constant and equal to 1) as Γ increases, the phenomenon of ESD appears and this independently from the maximally entangled initial state considered. The main problem is that, the interaction of the system with is surrounding may randomize the relative phases of the possible states of the system, thus the system loses all quantum interference effects and may end up behaving classically, this is the so called quantum decoherence. This is in agreement with the literature and with our prediction in the introductory paragraph for which decoherence is the major problem in quantum information processing tasks.

Fig. 7
figure 7

Decoherence effects on the dynamics of entanglement for two different maximally entangled initial states (K1 = K2 = 1, K3 = − 1 Fig. 7a) and (K1 = K2 = − 1, K3 = 1 Fig. 7b). The dash line corresponds to constant parameters (i.e. B1 = b1 = Δ1 = J1 = D1 = 0, and B0 = 0.2,b0 = 0.4,Δ0 = 0.2,J0 = 1,D0 = 0.5), while the solid line corresponds to time dependent parameters (i.e. B0 = 0.2,b0 = 0.4,Δ0 = 0.2,J0 = 1,D0 = 0.5 and B1 = 0.02,b1 = 0.04,Δ1 = 0.08,J1 = 0.1,D1 = 0.05)

Full size image

4 Concluding Remarks

In the present paper, we study the dynamics of entanglement of two qubits XYZ Heisenberg model under simultaneously an anisotropic magnetic field and a DM interaction effects both varying with time. For this purpose, we have considered not only the magnetic field and the DM interactions to be time dependent but also the Heisenberg spin-spin coupling and defined respectively by \(B_{0}+B_{1}\cos \limits (\omega t)\), \(b_{0}+b_{1}\cos \limits (\omega t)\), \(J_{0}+J_{1}\cos \limits (\omega t)\), \({\varDelta }_{0}+{\varDelta }_{1}\cos \limits (\omega t)\), \(D_{0}+D_{1}\cos \limits (\omega t)\). This, because our system is considered as being permanently in interaction with its environment, which includes the nature of the material (inhomogeneous material) and the temperature of the medium. We have also considered our system to be surrounded by a noisy environment (non-Markovian environment or dissipative environment) [37, 38, 73]. Due to this non-Markovian nature, we have therefore, studied the dynamics of the system considering the weak coupling system-bath and using the Born-Markov approximation so that the equation of motion is approached by the Lindblad master equation. We discovered, based on simulations of the concurrence that, the correlation that exists between quantum systems (entanglement) is quietly improved due to the time dependency nature of the system’s parameters (B, b, J, Δ and D). It followed that, as the time grows, the concurrence admits an oscillating behavior traducing the fact that, its nearest neighbors may reach some maximum values, which are impossible with constant parameters.

In addition, we have found that, decoherence seriously affects the dynamics of entanglement in the system in the sense that, it induces the appearance of disentanglement (ESD). However, the anisotropic magnetic nature of the field was observed to improve the concurrence and then, induces in a non negligible way the appearance of the phenomenon of ESB in the system as well as revivals of entanglement, The time interval of the phenomenon of ESD is considerably reduced with an increasing in that anisotropic nature of the magnetic field. Moreover, the spin-spin anisotropic interaction was found in this work to be very important in quantum entanglement since we observed that, increasing this anisotropy enhances the degree of entanglement which is the proof that an XYZ Heisenberg model is among other the most suitable candidate for quantum information processing tasks, which is a similar conclusion with refs. [53, 58, 74]. Furthermore, we have discovered after simulations that, the dynamics of the concurrence present different behavior when considering two different maximally entangled initial states. This allows us to conclude that, entanglement in a bipartite system strongly depend on the initial state chosen. Although the DM coupling is neglected in many works, it was found in this paper to have a serious impact on the entanglement, since we discovered that it can strengthen the strength of correlations between quantum systems so that good turning of this coupling may provide good protection of entanglement from unwanted effects (decoherence, dissipassion) of the environment.