1 Introduction

Quantum teleportation requires the transfer of quantum state and quantum entanglement with the best quality. This can be performed in different methods, such as spin chains [1], ion traps, [2], optical lattices, [3] and quantum dots [4]. Recently, research has shown that spin chains as quantum wires can transfer quantum states and entanglement over short distance scales [1, 5,6,7,8,9].

Although the experiments showed that the perfect state transfer cannot be obtained within spin-1/2 chains with nearest-neighbor couplings, some studies have indicated that using coupled spin chains can produce pretty good state transfer in short-distance quantum channels [10].

Markovian and non-Markovian behavior of the entanglement dynamics affects the teleportation properties. Markovian behavior is the decoherence of system induced by the memoryless environment. Non-Markovian behavior is defined as the decoherence induced by the non Markovian environment [11]. The nature of a quantum non-Markovian behavior is the flow of lost information from the environment back to the open system, which leads to the oscillations of correlation [12].

Some research found that the memory effect of the non- Markovian environment can be useful for maintaining the quantum fidelity and entanglement [13,14,15,16,17]. Various research has studied the effect of three- spin interaction on the dynamics of quantum entanglement [18,19,20]. The research has found that three-spin interaction can generate the dynamical phase transition from the Markovian to the non-Markovian regime [21]. The one-dimensional spin-1/2 model with three- spin interaction precisely characterizes the dynamics of two bosons trapped in an optical lattice with a triangular configuration [22, 23]. DM interaction is important for the weak ferromagnetism of antiferromagnetic crystals (α − Fe2O3, MnCO3, and CrF3), as well as the spin arrangement in anti-ferromagnetic systems with low symmetry [24]. The Dzyaloshinski-Moriya interaction has been found to enhance the revival of fidelity in the non- Markovian environment [24] and improves the efficiency of the quantum channel for teleporting quantum states [25, 26]. The Ref. [24] examined the two qubits Heisenberg chain in a non-Markovian environment to teleport the quantum bipartite state. The results showed that the average fidelity decays to a critical value of 2/3 as the concurrence of the channel tends to zero. Increasing the strength of DM improved the average fidelity of entanglement and fidelity.

In the present paper, we investigate the dynamical behavior of the quantum entanglement and fidelity in the 1D spin-1/2 XX model with added DM Interaction and three-spin interaction. The initial quantum state is prepared in such a way that the entanglement is only between two nearest-neighbor (NN) spins. The main purpose of the paper is to investigate the effect of the XX- Heisenberg interaction, DM interaction, and three- spin interaction on the quality of the fidelity and entanglement between the nearest neighbor pair spins. The main questions of the paper are: Is the fidelity a desired measurement to indicate the quantum correlation of the system? And can non- Markovian behavior of the system be helpful for a better compatibility of the fidelity and entanglement?

2 Model

The model used in this work describes two entangled spins, as the system, coupled to a spin chain, as the environment or quantum channel. The total Hamiltonian of the system and environment is:

$$ \mathrm{H}=\mathrm{J}\sum \left({\mathrm{S}}_{\mathrm{n}}^{\mathrm{x}}{\mathrm{S}}_{\mathrm{n}+1}^{\mathrm{x}}+{\mathrm{S}}_{\mathrm{n}}^{\mathrm{y}}{\mathrm{S}}_{\mathrm{n}+1}^{\mathrm{y}}\right)-{\mathrm{J}}^{\prime}\sum \left({\mathrm{S}}_{\mathrm{n}}^{\mathrm{x}}{\mathrm{S}}_{\mathrm{n}+2}^{\mathrm{x}}+{\mathrm{S}}_{\mathrm{n}}^{\mathrm{y}}{\mathrm{S}}_{\mathrm{n}+2}^{\mathrm{y}}\right){\mathrm{S}}_{\mathrm{n}+1}^{\mathrm{z}}+\overrightarrow{\mathrm{D}}\cdotp \sum \left(\overrightarrow{{\mathrm{S}}_{\mathrm{n}}}\times \overrightarrow{{\mathrm{S}}_{\mathrm{n}+1}}\right) $$
(1)

Where Sn presents the spin-1/2 operator on the n- th site. J denotes the exchange coupling between the nearest neighbor spins. J′ presents the exchange strength between the next-nearest neighbor spins. D indicates the Dzyaloshinskii–Moriya interaction between the nearest neighbor spins. We consider uniform DM vector as \( \overrightarrow{D}=D\hat{z} \). We assume periodic boundary conditions. Considering the nearest neighbor pair spins located at sites m and m + 1 as an open quantum system, the rest of the chain plays the role of the environment. Therefore, the Hamiltonian can be rewritten as:

$$ \mathrm{H}={H}_S+{H}_E+{H}_{SE} $$
(2)

Where

$$ {H}_E=\mathrm{J}{\sum}_{n=m+1}^N\left({\mathrm{S}}_{\mathrm{n}}^{\mathrm{x}}{\mathrm{S}}_{\mathrm{n}+1}^{\mathrm{x}}+{\mathrm{S}}_{\mathrm{n}}^{\mathrm{y}}{\mathrm{S}}_{\mathrm{n}+1}^{\mathrm{y}}\right)+\overrightarrow{\mathrm{D}}\cdotp {\sum}_{n=m+1}^N\left(\overrightarrow{{\mathrm{S}}_{\mathrm{n}}}\times \overrightarrow{{\mathrm{S}}_{\mathrm{n}+1}}\right)-J^{\prime }{\sum}_{n\ne m-2,m-1,m,m+1}^N\left({\mathrm{S}}_{\mathrm{n}}^{\mathrm{x}}{\mathrm{S}}_{\mathrm{n}+2}^{\mathrm{x}}+{\mathrm{S}}_{\mathrm{n}}^{\mathrm{y}}{\mathrm{S}}_{\mathrm{n}+2}^{\mathrm{y}}\right){S}_{n+1}^z $$
(3-a)
$$ {H}_S=\mathrm{J}\left({\mathrm{S}}_{\mathrm{m}}^{\mathrm{x}}{\mathrm{S}}_{\mathrm{m}+1}^{\mathrm{x}}+{\mathrm{S}}_{\mathrm{m}}^{\mathrm{y}}{\mathrm{S}}_{\mathrm{m}+1}^{\mathrm{y}}\right)+\overrightarrow{\mathrm{D}}\cdotp \left(\overrightarrow{{\mathrm{S}}_{\mathrm{m}}}\times \overrightarrow{{\mathrm{S}}_{\mathrm{m}+1}}\right) $$
(3-b)
$$ {H}_{SE}=\mathrm{J}\left({\mathrm{S}}_{\mathrm{m}-1}^{\mathrm{x}}{\mathrm{S}}_{\mathrm{m}}^{\mathrm{x}}+{\mathrm{S}}_{\mathrm{m}-1}^{\mathrm{y}}{\mathrm{S}}_{\mathrm{m}}^{\mathrm{y}}+{\mathrm{S}}_{\mathrm{m}+1}^{\mathrm{x}}{\mathrm{S}}_{\mathrm{m}+2}^{\mathrm{x}}+{\mathrm{S}}_{\mathrm{m}+1}^{\mathrm{y}}{\mathrm{S}}_{\mathrm{m}+2}^{\mathrm{y}}\right)+\overrightarrow{\mathrm{D}}\cdotp \left(\overrightarrow{{\mathrm{S}}_{\mathrm{m}-1}}\times \overrightarrow{{\mathrm{S}}_{\mathrm{m}}}+\overrightarrow{{\mathrm{S}}_{\mathrm{m}+1}}\times \overrightarrow{{\mathrm{S}}_{\mathrm{m}+2}}\right)-J^{\prime }{\sum}_{n=m-2}^{m+1}\left({S}_n^x{S}_{n+2}^x+{S}_n^y{S}_{n+2}^y\right){S}_{n+1}^z $$
(3-c)

In order to diagonalize the spin chain model, the fermionization technique is applied on the Hamiltonian. Using Jordan-Wigner transformation, spins are mapped onto a 1D model of non-interacting spinless fermions with creation and annihilation operator:

$$ {\displaystyle \begin{array}{c}{S}_n^z={a}_n^{\dagger }{a}_n-\frac{1}{2}\\ {}{S}_n^{+}={a}_n^{\dagger}\exp \left( i\pi \sum \limits_{l<n}{a}_l^{\dagger }{a}_l\right)\\ {}{S}_n^{+}={a}_n\exp \left(- i\pi \sum \limits_{l<n}{a}_l^{\dagger }{a}_l\right)\end{array}} $$
(4)

And therefore:

$$ \mathrm{H}=\left(\mathrm{J}+\mathrm{iD}\right){\sum}_{\mathrm{n}}\left({\mathrm{a}}_{\mathrm{n}}^{\dagger }{\mathrm{a}}_{\mathrm{n}+1}+{\mathrm{a}}_{\mathrm{n}+1}^{\dagger }{\mathrm{a}}_{\mathrm{n}}\right)-\frac{{\mathrm{J}}^{\prime }}{2}{\sum}_{\mathrm{n}}\left({\mathrm{a}}_{\mathrm{n}}^{\dagger }{\mathrm{a}}_{\mathrm{n}+2}+{\mathrm{a}}_{\mathrm{n}+2}^{\dagger }{\mathrm{a}}_{\mathrm{n}}\right) $$
(5)

The fermion representation of this Hamiltonian is not yet diagonal. So, the energy spectrum of the Hamiltonian can’t be obtained easily. By performing a Fourier transformation into the momentum space as \( {\mathrm{a}}_{\mathrm{n}}=\frac{1}{\sqrt{\mathrm{N}}}{\sum}_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{e}}^{-\mathrm{ikn}}{\mathrm{a}}_{\mathrm{k}} \),the Hamiltonian is diagonalized:

$$ \mathrm{H}={\sum}_{\mathrm{k}}\upvarepsilon \left(\mathrm{k}\right){\mathrm{a}}_{\mathrm{k}}^{\dagger }{\mathrm{a}}_{\mathrm{k}} $$
(6)

where ε(k) is the dispersion relation:

$$ \upvarepsilon \left(\mathrm{k}\right)=\mathrm{JCos}\left(\mathrm{k}\right)+\mathrm{D}\ \mathrm{Sin}\left(\mathrm{k}\right)-\frac{\mathrm{J}^{\prime }}{2}\mathrm{Cos}\left(2\mathrm{k}\right)\kern0.5em $$
(7)

In the following, we determine the dynamics of the open quantum system. For this purpose, we focus on the pairwise entanglement between the nearest neighbor pair spins located at sites m and m + 1 in the system. The rest of the chain plays as an environment (Fig. 1). The initial state of the system is maximally entangled:

Fig. 1
figure 1

Scheme of the system and environment of the model

Full size image
$$ {\uppsi}_S(0)=\frac{1}{\sqrt{2}}\left(|\uparrow \downarrow >+|\downarrow \uparrow >\right) $$
(8)

and the initial state of the environment is disentangled:

$$ {\uppsi}_E(0)=\mid \downarrow \downarrow \downarrow \dots \downarrow \downarrow > $$
(9)

Therefore, the initial state of the spin chain can be written as:

$$ \uppsi (0)=\frac{1}{\sqrt{2}}\left({\mathrm{a}}_{\mathrm{m}}^{\dagger}\mid 0>+{\mathrm{a}}_{\mathrm{m}+1}^{\dagger}\mid 0>\right) $$
(10)

Where ∣0> denotes the vacuum state. Using the evolution operator, U(t) = exp(−iHt), we obtain the state of the system at time t (ℏ = 1):

$$ \uppsi \left(\mathrm{t}\right)=\frac{1}{\sqrt{2\mathrm{N}}}{\sum}_{\mathrm{k}}\left({\mathrm{e}}^{\mathrm{i}\left(\mathrm{k}\mathrm{m}-\upvarepsilon \left(\mathrm{k}\right)\mathrm{t}\right)}\left(1+{\mathrm{e}}^{\mathrm{i}\mathrm{k}}\right){\mathrm{a}}_{\mathrm{k}}^{\dagger}\mid 0>\right) $$
(11)

In order to measure the entanglement of a two-qubit system, concurrence [27] is extensively used in many contexts. The concurrence is defined as:

$$ {\mathrm{C}}_{\mathrm{ij}}=\max \left\{0.{\uplambda}_1-{\uplambda}_2-{\uplambda}_3-{\uplambda}_4\right\} $$
(12)

Where λi′s are the eigenvalues in descending order of the matrix \( \sqrt{\sqrt{\uprho}\overset{\sim }{\uprho}\sqrt{\uprho}} \). Here

$$ \overset{\sim }{\uprho}={\uprho}_{\mathrm{s}}\left({\upsigma}^{\mathrm{y}}\otimes {\upsigma}^{\mathrm{y}}\right){\uprho}_{\mathrm{s}}^{\ast}\left({\upsigma}^{\mathrm{y}}\otimes {\upsigma}^{\mathrm{y}}\right) $$
(13)

Here, ρ∗is the conjugate of ρ and σy is the Pauli operator. For maximally entangled states, C yields 1 while for separable states C = 0.

In addition to the entanglement, we also determine the fidelity between states Ψ(0) and Ψ(t) of the open quantum system. Fidelity is defined as the probability that the state of the system at time t, is that which we would obtain ideally (in this paper, this would just be the initial state):

$$ F=\left\langle \varPsi (0)|\varPsi (t)\right\rangle =\left\langle \varPsi (0)|U(t)\Big\Vert \varPsi (0)\right\rangle $$
(14)

since it shows how close the state at time t and the initial state are. The fidelity is very close to 1, if Ψ(t) and Ψ(0) are identical.

3 Results and Discussion

In the following, we study the concurrence and fidelity between nearest neighbor spins for different values of J, D and J′. Then, we investigate the dynamic behavior of the concurrence and fidelity. We consider the case of a system initially prepared in a maximally entangled singlet-like state on sites m and m ′  = m + 1 (Fig. 1). The main question is that under what conditions, there is more consistency between fidelity and entanglement. This depends on the interaction parameters of the system. Firstly, we study the dynamic behavior of the one-dimensional spin-1/2 XX model with XX Heisenberg interaction.

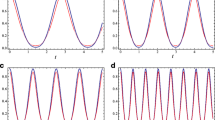
Figure 2 shows the dynamic behavior of fidelity and concurrence in the 1/2-spin chain with XX Heisenberg interaction. The dynamics of fidelity and concurrence are plotted for different exchange coefficients. In this system, fidelity and concurrence decrease asymptotically with time. As seen in the figure, if the spins of the system are weakly coupled, they can better maintain the quantum correlation of the system. As expected, fidelity and concurrence are closely related together. The results demonstrate the fidelity and the concurrence show a similar behavior. In fact, in weak Heisenberg interaction (Fig. 2-a), the quantum correlation of the system disappears when the fidelity reaches below 0.4. In strong Heisenberg interaction, the death of the quantum correlation happens when fidelity reaches below 0.2. Therefore, one can conclude that increasing the exchange interaction parameter improves the consistency between fidelity and entanglement of the system.

Fig. 2
figure 2

Time dependence of fidelity and entanglement in the XX Heisenberg spin chain for a) J = 0.1, b) J = 1.1

Full size image

Figure 3 depicts the system with the Heisenberg model plus DM interaction. It seems that DM interaction doesn’t play any effective role in the dynamics of entanglement and fidelity. It is also observed that in this model, the concurrence of the system tends to zero as the fidelity decays below 0.2. Some research has reported that the DM interactions play an important role in the weak inter-qubit coupling limit [28]. We have repeated the calculations for a weak Heisenberg interaction with J = 0.1. As plotted in Fig. 3-b. In the presence of the weak XX Heisenberg interaction, DM interaction improves the dynamics of quantum entanglement and fidelity.

Fig. 3
figure 3

Time dependence of fidelity and entanglement in the spin chain with XX Heisenberg and DM interaction: (a) J = 1, (b) J = 0.1

Full size image

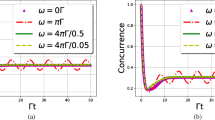
In the next step, we investigate an interesting phenomenon in which a non-Markovian behavior happens for the fidelity as well as entanglement. Adding three spin interaction (TSI) to the XX Heisenberg spin chain leads to phase transition from Markovian to non-Markovian regime in the system.

The results indicate that the non-Markovian behavior can improve the fidelity and entanglement of the system. As shown in Fig. 4, for J′ < J, dynamics of fidelity and concurrence present a Markovian behavior. For J′ > J, where three spin interaction dominates the XX Heisenberg interaction, the non-Markovian dynamics appears. In the Markovian regime, due to connecting the system to its environment, there is a steady flow of the quantum correlation into the environment which leads to an asymptotic drop of the system correlation. To the contrary, in non- Markovian regime, the quantum correlation drops sharply and disappears in the finite time and then regains. This behavior which is repeated periodically in time, is known as the revival of the quantum correlation.

Fig. 4
figure 4

Time dependence of fidelity and entanglement in the (a) Markovian and (b), (c) non-Markovian regime

Full size image

As Fig. 4 illustrates, the revival phenomenon of quantum entanglement is detected in systems with non- Markovian behavior. The noticeable fact is that in the non- Markovian regime, fidelity follows the same dynamic pattern as entanglement. The results show that the dynamics of the fidelity as well as entanglement strongly depend on the non-Markovian nature of the environment. We observe that for high TSI parameter, the revival of the entanglement and fidelity is high, too.

The most striking fact is that although fidelity exhibits a better stability by passing the time, both the entanglement and fidelity tend to zero and vanish at the same time. This behavior has not been reported in other research, so far.

Despite findings of some research which demonstrated when fidelity reaches below 2/3, the death of entanglement occurs in system, in the model of the present study, the entanglement of the system tends to zero as the fidelity decays below 0.4 for weak spin interaction and 0.2 for strong spin interaction.

4 Conclusion

The dynamical behavior of the quantum entanglement and fidelity in the 1D spin-1/2 XX model with added DM interaction and three-spin interaction was studied under Markovian and non- Markovian conditions. The initial quantum state was prepared in such a way that the entanglement is only between two nearest-neighbor (NN) spins. The effect of the XX- Heisenberg interaction, DM interaction, and three- spin interaction on the dynamics of the fidelity and entanglement between the nearest neighbor pair spins was investigated. A comparison of fidelity with concurrence was performed in all three models. The results showed that the fidelity can be used as a desired measurement to indicate the quantum correlation of the spin chain.

The analysis of the system revealed that factors enhancing the entanglement of the system would also improve the fidelity. The decrease of fidelity reduces the quality of the transmission of the system’s state and therefore leads to the decoherence in the quantum system. The decoherence will significantly reduce the entanglement of the system.

An important result was that in the non- Markovian regime, fidelity followed the same dynamic pattern as entanglement. The results showed that the dynamics of the fidelity as well as entanglement strongly depended on the non-Markovian nature of the environment. We observed that for high TSI parameter, the revival of the entanglement and fidelity is high, too.

An interesting feature of the non- Markovian regime was that although fidelity exhibited a better stability by passing the time, both the entanglement and fidelity tended to zero and vanished at the same time.

In several studies, it has been found that if fidelity reaches a critical value, the entanglement (concurrence) of the system disappears. It has been shown that there is a linear relation between fidelity and concurrence. In the present study, although in non-zero points of concurrence diagram, there is an almost linear relation between F and C, in zero points of concurrence, the fidelity also simultaneously tends to zero. This behavior has not been reported by other research, so far.

It is also observed that in the model investigated in the present study, the entanglement of the system tends to zero as the fidelity decays below 0.4 for weak spin interaction and 0.2 for strong spin interaction. However, we don’t generalize this conclusion and at this time, we limit this finding to our model.

In summary, the investigation of the entanglement dynamics implied that by suitable choice of environment and system parameters, the entanglement sudden death and decoherence can be avoided by keeping fidelity greater than a certain value.