1 Introduction

Opto-mechanical system is an important candidate for the investigation of quantum mechanical features at mesoscopic and even macroscopic scales. In a typical opto-mechanical system (i.e. a simple optical cavity with a movable end mirror), the radiation pressure of cavity field drives the unfixed mirror to vibrate at its eigen frequency while the mechanical vibration of unfixed mirror modulates, in turn, the mode frequency of cavity field [1]. Some coherent optical systems [2–6] are expected to generate opto-mechanical coupling efficiently by combining with micro-mechanical devices, which may enable the development of quantum information technologies and the observation of macroscopic quantum behaviors [7]. Recently, there are many interesting phenomena envisioned or demonstrated in various opto-mechanical systems, such as the ground state cooling of micromechanical oscillators [8–11], normal mode splitting of cavity [12, 13], and quantum entanglement generation [14–17]. The typical opto-mechanical system also can be coupled to other physical entities, for example, two Josephson-junction phase qubits [18], an LC circuit [19], a single trapped atom [20], and a cold atomic lattice [21].

Because of the convenience in experimental realization and flexibility in optical manipulation, atom-assisted opto-mechanical systems are the most favorite hybrid opto-mechanical systems. So the atomic medium plays an important role in the interaction of cavity electrodynamics. Genes et al. [10] showed cooling the ground state of micromechanical oscillators by resonant coupling of the mirror vibrations to a two-level atomic bath. Zhou et al. [17] proposed a scheme for three-level cascade atoms to entangle two opto-mechanical oscillators as well as two-mode fields. In Ref. [20] Hammerer et al. have shown that it is possible to achieve strong cavity-mediated coupling between a single microscopic atom and a macroscopic mechanical oscillator. Furthermore, Genes [22] studied tripartite entanglement among the atom, mirror, and cavity field. In Ref. [23], Ian found that two-level atoms effectively enhance the radiation pressure of the cavity field upon the oscillating mirror. In addition, it is possible to further realize a few nonlinear phenomena in virtue of the mutual influence between atom-light and opto-mechanical interactions when atomic internal states are involved. For example, there is a bistable behavior for the steady-state position of two-level cold atoms trapped in a typical opto-mechanical cavity, and the cavity’s standing-wave mode pattern could be modified by the collective atomic back-action [24]. When the trapped cold atoms were driven into the three-level Λ configuration of electromagnetically induced transparency (EIT) [25], both mirror displacement and atomic susceptibility might have multiple steady-state solutions [26, 27].

As known from three-level atomic systems [28, 29], the action of one strong coupling field gives rise to an EIT window in the absorption profile of the probe field. In contrast to the three-level atomic systems, however, a second EIT window can occur and can be modified in a four-level atomic system due to the additional coupling field. Such a double EIT system has been the subject of a few theoretical and experimental studies since it may enhance nonlinear optical processes in comparison with single EIT system [30]. Therefore, we extend here the work shown in Refs. [26, 27] to the more complex case where the cold atoms trapped in a typical opto-mechanical cavity were driven into the four-level tripod configuration, by examining the steady-state behaviors of movable mirror, cavity field, and trapped atoms with realistic experimental parameters. As a result, we find five and three steady-state solutions for relevant variables near two-photon resonance, among which only one steady-state solution is present in the alternative frequency region of ω 0 − ω 41 < −2.3 MHz. In fact, the second and third steady-state solutions emerge only when the movable mirror severely deviates from its equilibrium position in the steady state, indicating an enhanced feedback mechanism originating from the coupling between atom-light and opto-mechanical interactions due to trapping a four-level atomic system in a typical opto-mechanical cavity. Such an enhanced nonlinear feedback mechanism then allows us to observe the difference in the double-EIT phenomenon between the atom-assisted opto-mechanical system and usual atom-field system [31].

2 Model and Equations

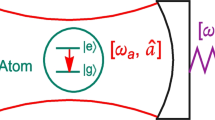
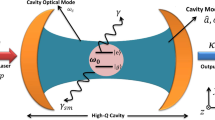
In this system, we consider a single-mode optical cavity with one fixed, partially transmitting mirror and one movable, perfectly reflecting mirrors showed in Fig. 1. The cavity mode of frequency ω L is excited by a driving field of frequency ω d via entering the cavity region from the left fixed mirror. N identical cold atoms confined in the cavity are driven into the four-level tripod configuration by a quantum cavity field ω L , a classical pump field ω p , and a classical coupling field ω c . Levels |1〉, |2〉, |3〉, and |4〉 may correspond, respectively, to states |52 S 1/2, F = 2, m F = −2〉, |52 S 1/2, F = 2, m F = −1〉, |52 S 1/2, F = 2, m F = 0〉, and |52 P 1/2, F = 2, m F = −1〉 on the D1 line of87Rb atoms. For the convenience of a potential experiment, we assume that the pump field ω p and coupling field ω c propagate in a direction perpendicular to the cavity axis. On the other hand, the movable mirror is described as a quantum harmonic oscillator with frequency ω m and mass m. Then we have the total Hamiltonian for the hybrid system

$$ H=H_{L}+H_{m}+H_{a}+H_{m-L}+H_{a-L}, $$
(1)

where the five terms of the total Hamiltonian describe, respectively, the free optical cavity, the free oscillating mirror, the free atomic sample, the mirror-cavity interaction, and the atom-light interaction as given below

$$\begin{array}{@{}rcl@{}} H_{L}& =&\hbar \omega_{0}a^{\dag} a, \\ H_{m}& =&\frac{p^{2}}{2m}+\frac{1}{2}m{\omega_{m}^{2}}x^{2}, \\ H_{a}& =&\sum\limits_{i=1}^{N}\hbar \left( \omega_{41}\sigma_{44}^{\left( i\right)} +\omega_{31}\sigma_{33}^{\left( i\right)} +\omega_{21}\sigma_{22}^{\left( i\right)} \right) , \\ H_{m-L}& =&-\hbar \frac{\omega_{0}}{l_{L}}xa^{\dag} a, \\ H_{a-L}& =&\sum\limits_{i=1}^{N}\hbar \left( {\Omega}_{c}e^{-i\omega_{c}t}\sigma_{43}^{\left( i\right)} +{\Omega}_{p}e^{-i\omega_{p}t}\sigma_{42}^{\left( i\right)} +ga\sigma_{41}^{\left( i\right)} +H.c.\right). \end{array} $$
(2)

where a(a †) is the annihilation (creation) operator of the single-mode cavity field; p (x) is the momentum (displacement) operator of the oscillating mirror; ω 0 (l L ) is the effective cavity frequency (length) for 〈x〉 = 〈p〉 = 0; \(\sigma _{\alpha \beta }^{\left (i\right )} =\left \vert \alpha \rangle _{ii}\langle \beta \right \vert \) (α, β = 1, 2, 3, 4) is the projection (α = β) or transition (α≠β) operator of the ith cold atom; ω α1(α = 2,3,4) is the transition frequency between level |α〉 and level |1〉; Ω p (Ω c ) is the Rabi frequency of the pump (coupling) field; \(g=\mu \sqrt {\omega _{0}/2\hbar V\epsilon _{0}}\) is the coupling constant of the cavity field with μ being the dipole moment, V the cavity volume, and 𝜖 0 the vacuum permittivity.

Fig. 1
figure 1

Schematic diagram of a typical opto-mechanical cavity containing N identical cold87Rb atoms with a movable end mirror. An external field \(\protect \omega _{d}\) is applied to drive the mirror’s mechanical oscillation via radiation pressure after exciting the cavity field \(\protect \omega _{L}\). The confined cold87Rb atoms are driven into a four-level tripod configuration on the D1 line by the quantum cavity field \(\protect \omega _{L} \), a classical pump field \(\protect \omega _{p}\), and a classical coupling field \(\protect \omega _{c}\). The pump field and the coupling field are assumed to travel in a direction perpendicular to the cavity axis. Note also that the cavity frequency \(\protect \omega _{L}\) depends on the mirror displacement \(\left \langle x\right \rangle \) and is usually expressed as \( \protect \omega _{L}=\protect \omega _{0}(1-\left \langle x\right \rangle /l_{L}) \) with l L being the cavity length for \(\left \langle x\right \rangle =0\)

Full size image

The dynamics of the system is determined by the following quantum Langevin equations:

$$\begin{array}{@{}rcl@{}} \partial_{t}p& =&-m{\omega_{m}^{2}}x+\hbar \left( \omega_{0}/l_{L}\right) a^{\dag} a-\gamma_{m}p-\sqrt{\gamma_{m}}\epsilon_{in}\left( t\right) , \\ \partial_{t}a& =&-\left( \gamma_{L}/2\right) a-i\omega_{0}a\left( 1-x/l_{L}\right) -ig\sum\limits_{i=1}^{N}\sigma_{14}^{\left( i\right)} + \sqrt{\gamma_{L}}a_{d}\left( t\right) , \\ \partial_{t}\sum\limits_{i=1}^{N}\sigma_{14}^{\left( i\right)} & =&-i{\Omega}_{c}e^{-i\omega_{c}t}\sum\limits_{i=1}^{N}\sigma_{13}^{\left( i\right)} -i{\Omega}_{p}e^{-i\omega_{p}t}\sum\limits_{i=1}^{N}\sigma_{12}^{\left( i\right)} +\sqrt{N}f_{14}\left( t\right) \\ && -\, iga\sum\limits_{i=1}^{N}\left( \sigma_{11}^{\left( i\right)} -\sigma_{44}^{\left( i\right)} \right) -\left( i\omega_{41}+\gamma_{14}\right) \sum\limits_{i=1}^{N}\sigma_{14}^{\left( i\right)} , \\ \partial_{t}\sum\limits_{i=1}^{N}\sigma_{13}^{\left( i\right)} & =&-\left( i\omega_{31}+\gamma_{13}\right) \sum\limits_{i=1}^{N}\sigma_{13}^{\left( i\right)} -i{\Omega}_{c}e^{i\omega_{c}t}\sum\limits_{i=1}^{N}\sigma_{14}^{\left( i\right)} \\ && +\, \sqrt{N}f_{13}\left( t\right) +iga\sum\limits_{i=1}^{N}\sigma_{43}^{\left( i\right)} , \\ \partial_{t}\sum\limits_{i=1}^{N}\sigma_{12}^{\left( i\right)} & =&-\left( i\omega_{21}+\gamma_{12}\right) \sum\limits_{i=1}^{N}\sigma_{12}^{\left( i\right)} -i{\Omega}_{p}e^{i\omega_{p}t}\sum\limits_{i=1}^{N}\sigma_{14}^{\left( i\right)} \\ && +\, \sqrt{N}f_{12}\left( t\right) +iga\sum\limits_{i=1}^{N}\sigma_{42}^{\left( i\right)} , \end{array} $$
(3)

where γ m is the mirror damping rate, γ L is the cavity decay rate, and γ i j are the coherence dephasing rate. And 𝜖 i n (t) and f i j (t) (i, j = 1, 2, 3, 4) are the quantum fluctuation terms for the oscillating mirror and the dressed atoms, respectively. a d (t) is the external driving term for the cavity field. In (3), We have set ω d = ω 0 for the driving field and ∂ t x = p/m for the oscillating mirror.

In this paper, our interest is only the steady-state solutions of the hybrid system. So we simplify the (3) by defining the collective projection and transition operators as follows

$$\begin{array}{@{}rcl@{}} \sigma_{44}& =&\sum\limits_{i=1}^{N}\sigma_{44}^{\left( i\right)} , \sigma_{14}=\frac{1}{\sqrt{N}}\sum\limits_{i=1}^{N}\sigma_{14}^{\left( i\right)} , \\ \sigma_{24}& =&\sum\limits_{i=1}^{N}\sigma_{24}^{\left( i\right)} , \sigma_{34}=\sum\limits_{i=1}^{N}\sigma_{34}^{\left( i\right)} , \sigma_{11}=\frac{1}{N}\sum\limits_{i=1}^{N}\sigma_{11}^{\left( i\right)} , \\ \sigma_{13}& =&\frac{1}{\sqrt{N}}\sum\limits_{i=1}^{N}\sigma_{13}^{\left( i\right)} , \sigma_{12}=\frac{1}{\sqrt{N}}\sum\limits_{i=1}^{N} \sigma_{12}^{\left( i\right)}. \end{array} $$
(4)

Then we can rewrite the (3) into a more compact form by considering the weak cavity field assumption

$$\begin{array}{@{}rcl@{}} \partial_{t}p& =&-m{\omega_{m}^{2}}x+\hbar \left( \omega_{0}/l_{L}\right) a^{\dag} a-\gamma_{m}p-\sqrt{\gamma_{m}}\epsilon_{in}\left( t\right) , \\ \partial_{t}a& =&-\left( \gamma_{L}/2\right) a-i\omega_{0}a\left( 1-x/l_{L}\right) -ig\sqrt{N}\sigma_{14}+\sqrt{\gamma_{L}}a_{d}\left( t\right) , \\ \partial_{t}\sigma_{14}& =&-\left( i\omega_{41}+\gamma_{14}\right) \sigma_{14}-i{\Omega}_{c}e^{-i\omega_{c}t}\sigma_{13}-i{\Omega}_{p}e^{-i\omega_{p}t}\sigma_{12}-ig\sqrt{N}a\sigma_{11}+f_{14}\left( t\right) , \\ \partial_{t}\sigma_{13}& =&-i{\Omega}_{c}e^{i\omega_{c}t}\sigma_{14}-\left( i\omega_{31}+\gamma_{13}\right) \sigma_{13}+f_{13}\left( t\right) , \\ \partial_{t}\sigma_{12}& =&-i{\Omega}_{p}e^{i\omega_{p}t}\sigma_{14}-\left( i\omega_{21}+\gamma_{12}\right) \sigma_{12}+f_{12}\left( t\right) . \end{array} $$
(5)

The moveable mirror may deviate from its equilibrium position, so the cavity frequency ω L = ω 0 −〈x〉ω 0/l L and 〈x〉 ≠ 0. After that, we define \( b/a=b_{d}\left (t\right ) /a_{d}\left (t\right ) =e^{i\omega _{L}t}, \rho _{14}/\sigma _{14}=\rho _{11}/\sigma _{11}=g_{14}/f_{14}=e^{i\omega _{L}t}, \rho _{13}/\sigma _{13}=g_{13}/f_{13}=e^{-it\left ({\Delta }_{L}-{\Delta }_{c}-\omega _{31}\right )} \), and \(\rho _{12}/\sigma _{12}=g_{12}/f_{12}=e^{-it\left ({\Delta }_{L}-{\Delta }_{p}-\omega _{21}\right )} \) to remove the fast-varying factors from (5). The dynamic equations of mean values are as follows

$$\begin{array}{@{}rcl@{}} \partial_{t}\left\langle p\right\rangle & =&-m{\omega_{m}^{2}}\left\langle x\right\rangle +\hbar \left( \omega_{0}/l_{L}\right) \left\langle b^{\dag} \right\rangle \left\langle b\right\rangle -\gamma_{m}\left\langle p\right\rangle , \\ \partial_{t}\left\langle b\right\rangle & =&-\left( \gamma_{L}/2\right) \left\langle b\right\rangle -ig\sqrt{N}\left\langle \rho_{14}\right\rangle + \sqrt{\gamma_{L}}\beta_{d}, \\ \partial_{t}\left\langle \rho_{14}\right\rangle & =&-\left[ i{\Delta}_{L}+\gamma_{14}\right] \left\langle \rho_{14}\right\rangle -i{\Omega}_{c}\left\langle \rho_{13}\right\rangle -i{\Omega}_{p}\left\langle \rho_{12}\right\rangle -ig\sqrt{N}\left\langle b\right\rangle , \\ \partial_{t}\left\langle \rho_{13}\right\rangle & =&-\left[ i\left( {\Delta}_{L}-{\Delta}_{c}\right) +\gamma_{13}\right] \left\langle \rho_{13}\right\rangle -i{\Omega}_{c}\left\langle \rho_{14}\right\rangle , \\ \partial_{t}\left\langle \rho_{12}\right\rangle & =&-\left[ i\left( {\Delta}_{L}-{\Delta}_{p}\right) +\gamma_{12}\right] \left\langle \rho_{12}\right\rangle -i{\Omega}_{p}\left\langle \rho_{14}\right\rangle , \end{array} $$
(6)

here we set 〈𝜖 i n 〉 = 0, 〈b d 〉 = β d , 〈g i j 〉 = 0, and 〈b † b〉 = 〈b †〉〈b〉, so Δ L = ω 41 − ω L , Δ p = ω 42 − ω p , and Δ c = ω 43 − ω c are frequency detunings of the cavity field, the pump field, and the coupling field, respectively. Replacing 〈b † b〉 with 〈b †〉〈b〉 indicates that the quantum fluctuation correlation 〈(δ b †)(δ b)〉 near the steady state is very small compared to the corresponding mean-value product 〈b †〉〈b〉 in the steady state [26, 27].

By setting all time derivatives to be zero in (6), we can obtain all involved mean values in the steady state. Here we specially have

$$\begin{array}{@{}rcl@{}} \left\langle x\right\rangle & =&\frac{({\Delta}_{L}-{\Delta}_{0})l_{L}}{\omega_{0}}=\frac{\hbar \omega_{0}}{m{\omega_{m}^{2}}l_{L}}\left\langle b^{\dag} \right\rangle \left\langle b\right\rangle , \\ \left\langle b\right\rangle & =&\frac{2\beta_{d}}{\sqrt{\gamma_{L}}}-\frac{ 2ig\sqrt{N}}{\gamma_{L}}\left\langle \rho_{14}\right\rangle , \\ \left\langle \rho_{14}\right\rangle & =&\frac{-ig\sqrt{N\gamma_{L}}\beta _{d}{\Omega}_{1}{\Omega}_{2}}{{\Omega}_{1}{\Omega}_{2}G+\gamma_{L}\left( {\Omega} _{2}{{\Omega}_{c}^{2}}+{\Omega}_{1}{{\Omega}_{p}^{2}}\right) /2}, \end{array} $$
(7)

where Ω1 = γ 13 + i(Δ L −Δ c ) ,Ω2 = γ 12 + i(Δ L −Δ p ) , G = g 2 N + γ L (γ 14 + iΔ L ) /2, Δ0 = ω 41−ω 0, and \(\beta _{d}=\sqrt {2\wp _{d}/\hbar \omega _{0}}\) with ℘ d being the driving field power. Without the loss of generality, we have taken Ω p ,Ω c , g, and β d as real parameters. Obviously, 〈x〉, 〈b〉, and 〈ρ 14〉 are coupled mutually because of the opto-mechanical and atom-light interactions sharing one and the same cavity field of variable frequency ω L . Then the expected nonlinear feedback mechanism occurs in our atom-assisted opto-mechanical system, and 〈x〉, 〈b〉, and 〈ρ 14〉 may have multiple steady solutions as shown in refs. [26, 27]. Because the macroscopic polarization P = N μ〈ρ 14〉 /V = 𝜖 0 χ 14 E L , we get the atomic susceptibility

$$ \chi_{14}=-\frac{2\sqrt{N}g}{\omega_{0}}\frac{\left\langle \rho_{14}\right\rangle} {\left\langle b\right\rangle} , $$
(8)

describing the absorption and dispersion properties of cavity field. In our system, χ 14 is not simply proportional to 〈ρ 14〉 as for atoms in the free space because 〈b〉 is not independent of 〈ρ 14〉.

3 Results and Discussion

For the experimental feasibility of our system, we set the following realistic parameters: l L = 1.0 mm, γ L = 104 kHz, ω 0 = 377.37 THz (λ 0 = 794.98 nm); m = 0.4 ng, ω m = 1.3 MHz; Δ c = −Δ p = 5.0 MHz, Ω p =Ω c = 11.5 MHz, γ 14 = 5.75 MHz, γ 12 = γ 13 = 1000 Hz, g = 10 kHz, N = 108. Then we plot 〈x〉, β = |〈b〉|, and Δ L in Fig. 2 as a function of Δ0 for β d = 108 Hz1/2 (℘ d = 1.25 mW). From the curves of the Fig. 2, we can see that 〈x〉, β, and Δ L have five different steady-state solutions in the region of Δ0 ∈ [−28.0 MHz, − 8.2 MHz] as labelled by \(\left \langle x\right \rangle _{s}^{i}, {\beta _{s}^{i}}\), and \({\Delta }_{Ls}^{i}\) (i = 1, 2, 3, 4, 5), have three different steady-state solutions in the region of Δ0 ∈ (−8.2 MHz, 2.3 MHz] as labelled by \(\left \langle x\right \rangle _{s}^{i}, {\beta _{s}^{i}}\), and \({\Delta }_{Ls}^{i}\) (i = 1, 2, 3), and only have one steady-state solution in the region of Δ0 ∈ (2.3 MHz, 28.0 MHz] as labelled by \(\left \langle x\right \rangle _{s}^{1}, {\beta _{s}^{1}}\), and \({\Delta }_{Ls}^{1}\).

Fig. 2
figure 2

Multiple steady-state solutions of \(\left \langle x\right \rangle , \protect \beta \), and Δ L against Δ0 with \(\protect \beta _{d}=10^{8}\) Hz1/2. Other relevant parameters can be found at the beginning of Section 3. Superscripts (i = 1, 2, 3, 4, 5) are used in plots to distinguish the five steady-state solutions of \(\left \langle x\right \rangle , \protect \beta \), and Δ L

Full size image

Now we will explain why the number of steady-state solutions of relevant variables are different in the three regions of Δ0 ∈ [−28.0 MHz, − 8.2 MHz], Δ0 ∈ (−8.2 MHz, 2.3 MHz ], and Δ0 ∈ (2.3 MHz, 28.0 MHz ]. Because 〈x〉 is positive due to the unidirectionality of radiation pressure and the two-photon resonance (i. e. Δ L = Δ0 + 〈x〉ω 0/l L = Δ p as well as Δ L = Δ0 + 〈x〉ω 0/l L = Δ c )is a crucial condition for attaining the efficient interaction of atom-light. So in the region of Δ0 ∈ [−28.0 MHz, − 8.2 MHz], an efficient opto-mechanical interaction characterized by a large 〈x〉 is always consistent with an efficient atom-light interaction because of Δ L ≈ Δ p as well as Δ L ≈ Δ c . Therefore we can observe five steady-state solutions due to the effective feedback between opto-mechanical and atom-light interactions. In the region of Δ0 ∈ (−8.2 MHz, 2.3 MHz ], an efficient opto-mechanical interaction is not completely consistent with an efficient atom-light interaction because a two-photon resonant condition Δ L ≈ Δ p is gradually destroyed with the increasing of Δ0. So we can observe three steady-state solutions. Finally, in the region of Δ0 ∈ (2.3 MHz, 28.0 MHz ], there exists an apparent contradiction between an efficient opto-mechanical interaction and an efficient atom-light interaction. The main reason should be that we have a sufficiently large 〈x〉 for Δ0 > 2.3 MHz so that the two-photon resonant conditions Δ L ≈ Δ p and Δ L ≈ Δ c are severely destroyed. So we can observe only one steady-state solution when there is no an effective feedback among opto-mechanical and atom-light interactions.

Figure 3 shows Im(ρ 14),Im(χ 14), and Re(χ 14) as a function of Δ0 for the same parameters as in Fig. 2. We find that the curves for \(\operatorname {Im}(\rho _{14}^{5}), \operatorname {Im} (\chi _{14}^{5})\), and \(\operatorname {Re}(\chi _{14}^{5})\) in the region of \({\Delta }_{0}\in \left [ -28.0\text { MHz,} -8.2\text { MHz}\right ] , \operatorname {Im} (\rho _{14}^{3}), \operatorname {Im}(\chi _{14}^{3})\), and \(\operatorname {Re}(\chi _{14}^{3})\) in the region of Δ0 ∈ (−8.2 MHz, 2.3 MHz ], and \(\operatorname {Im}(\rho _{14}^{1}), \operatorname {Im}(\chi _{14}^{1})\), and \(\operatorname {Re} (\chi _{14}^{1})\) in the region of Δ0 ∈ (2.3 MHz, 28.0 MHz ] are similar to those in the usual double-EIT phenomenon [31]. Furthermore, a typical double EIT absorption spectrum is seen by connecting curve \(\operatorname {Im}(\chi _{14}^{5})\) in the region of Δ0 ∈ [−28.0 MHz, − 8.2 MHz], curve \(\operatorname {Im}(\chi _{14}^{3})\) in the region of Δ0 ∈ (−8.2 MHz, 2.3 MHz ], to curve \( \operatorname {Im}(\chi _{14}^{1})\) in the region of Δ0 ∈ (2.3 MHz, 28.0 MHz ]. The reason is that an inefficient opto-mechanical interaction has no feedback on an atom-light interaction. However, the curves for \(\operatorname { Im}(\rho _{14}^{1,2,3,4}), \operatorname {Im}(\chi _{14}^{1,2,3,4})\), and \(\operatorname {Re} (\chi _{14}^{1,2,3,4})\) in the region of Δ0 ∈ [−28.0 MHz, − 8.2 MHz] and \(\operatorname {Im}(\rho _{14}^{1,2}), \operatorname {Im}(\chi _{14}^{1,2})\), and \(\operatorname {Re}(\chi _{14}^{1,2})\) in the region of Δ0 ∈ (−8.2 MHz, 2.3 MHz ] like the “tails” are quite different from those in the usual double-EIT phenomenon [31]. The reason is that an efficient opto-mechanical interaction has an effective feedback on an atom-light interaction.

Fig. 3
figure 3

Multiple steady-state solutions of \(\operatorname {Im}(\protect \rho _{14}), \operatorname {Im}(\protect \chi _{14})\), and \(\operatorname {Re}(\protect \chi _{14})\) against Δ0 obtained with the same parameters and distinguished by the same superscripts as in Fig. 2

Full size image

In contrast to the hybrid opto-mechanical systems [26, 27], a main feature of the present work is that, by trapping a four-level atomic ensemble instead of a three-level atomic ensemble, the feedback mechanism originating from the coupling between atom-light and opto-mechanical interactions can be significantly enhanced. The characteristic signature is the emergence of the second and third steady-state solutions in our atom-assisted opto-mechanical system.

4 Conclusions

We have studied the steady-state behaviors of movable mirror, cavity field, and trapped atoms driven into the four-level tripod configuration in a hybrid opto-mechanical system. We obtain the numerical results with setting realistic experimental parameters. It show that this atom-assisted opto-mechanical system has five steady-state solutions for relevant variables in the region where the cavity frequency ω 0 is much larger than the atomic resonance ω 41, three steady-state solutions in the region where the resonant condition ω 0 ≈ ω 41 is approximately satisfied, and only one steady-state solution in the region where ω 0 is much smaller than ω 41 mainly due to the unidirectionality of radiation pressure and mirror displacement. In addition, we find that the steady-state solutions for \(\operatorname {Im}(\rho _{14}^{1,2,3,4}), \operatorname {Im}(\chi _{14}^{1,2,3,4})\), and \(\operatorname {Re}(\chi _{14}^{1,2,3,4})\) will display the difference from those in the usual double-EIT phenomenon in the corresponding parameter regions. All these interesting behaviors should be attributed to an enhanced feedback mechanism which originates from the coupling among atom-light and opto-mechanical interactions by trapping a four-level atomic system in a typical opto-mechanical cavity. The results obtained could be used to improve the measurement precision of the extremely tiny mirror displacement based on the EIT effect, when the ensemble of N identical cold atoms is placed inside an optical microcavity with a movable end mirror and the cavity field acts as the probe light.