1 Introduction

A practical strategy for establishing a connection between mechanical phonons and electromagnetic photons involves utilizing cavity optomechanical systems. One effective method to create such a system is by constructing a Fabry-Perot cavity, where one of the mirrors is movable [1,2,3]. The mobility of this mirror leads to oscillations influenced by the radiation pressure exerted by photons, which has been measured and confirmed phenomenon from experiments long ago [4,5,6]. Substantial progress, encompassing both experimental and theoretical advancements, has been made to explore the diverse possibilities of these systems [7,8,9,10]. This concept has been applied across a wide range of sizes and setups, including macroscopic mirrors [11], nano- and micro-mechanical cantilevers [12, 13], micro-toroids [14], membranes [15]. Optomechanical systems have a wide range of applications, encompassing coherent optical wavelength conversion [16], the precise modulation of properties like the speed and phase of the transmitted probe field [17, 18], and the generation and manipulation of mechanical Schrödinger cat states [19, 20]. Moreover, these systems play a crucial role in cooling applications, facilitating the reduction of mechanical resonator temperatures toward the quantum ground state [21, 22], as well as the cooling of floating nanoparticles [23].

Numerous studies have delved into the examination of the interaction between the optomechanical cavity and atoms within it. Many articles adopt the weak limit, where both the cavity-mirror coupling and atom-photon coupling are significantly weaker than the angular frequency of the movable mirror. Within this limit, a coarse-grained method is often applied, simplifying the problem to an effective Hamiltonian that allows for analytical solutions. Research following this approach explores various aspects, such as investigating the temporal evolution of entanglement in a system featuring a two-level atom inside an optomechanical cavity, leading to the generation of Greenberger-Horne-Zeilinger-like states [24] and other effects [25,26,27]. Another exploration involves a three-level atom interacting with a two-mode quantized field, analyzing multiple observables [28]. The negativity of a two-level trapped ion is also scrutinized for different subsystems under varying parameters [29]. Additionally, the dynamical evolution of several nonclassical effects is investigated, with the cavity initially prepared in the optical coherent state [30]. Recent studies, addressing various effects, can be found in [31,32,33]. Conversely, stronger limits are typically explored through methods such as solving the Heisenberg-Langevin equations of motion and applying mathematical tools from atomic physics. These investigations often concentrate on analyzing steady-state solutions after incorporating multiple effects, as demonstrated by studies in [34,35,36].

In this article, our focus centers on investigating the hybrid optomechanical cavity system with a two-level atom inside it, in the limit where both the cavity-mirror coupling and atom-photon coupling are approximately equal to the angular frequency of the movable mirror (strong coupling limit). Our interest lies in exploring the dynamics of various statistical and nonclassical effects within this particular limit. This limit is considered to be richer compared to the weak limit, as the impact of each constituent of the system becomes more pronounced, as we will elucidate. Moreover, we introduce the influence of multi-photon processes for the sake of generality. While numerous articles have explored this limit primarily in the context of steady-state and equilibrium, our emphasis here is on studying the temporal evolution of selected measurements. Building upon previous analyses that concentrated on the weak limit, as outlined in the preceding paragraph, our aspiration is to employ analogous analyses within this stronger limit. Specifically, our attention is mostly directed towards the dynamics of the movable mirror, initially considered to be in a vacuum at the beginning of the interaction. Concurrently, we consider two cases for the cavity mode: a Fock state (FS) and a coherent state (CS). Furthermore, this study aims to compare the obtained results with two sub-models: the Cavity Optomechanical System (COS) and the Jaynes-Cummings Model (JCM), as explored in related studies such as [37,38,39,40].

The structure of this article unfolds as follows: In Section 2, we delve into the analysis of the system, discuss the numerical solution, and explore the impact of various limits. Section 3 is dedicated to exploring statistical properties, specifically focusing on the position of the movable mirror and the atomic inversion. In Section 4, we scrutinize nonclassical properties, delving into the linear entropy, Q Mandel parameter, and squeezing of the mechanical mode. Finally, Section 5 presents concluding remarks.

2 The Physical System

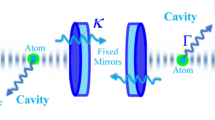
The considered system involves an optomechanical cavity with a two-level atom, illustrated in Fig. 1. The two-level atom interacts with a single-mode quantized light field, while one of the mirrors is movable and quantized to a single phonon mode. The excited state of the atom is denoted as \(|e\rangle \), and its ground state is denoted as \(|g\rangle \). The complete Hamiltonian of the system can be expressed as [24, 26, 39]

$$\begin{aligned} \hat{H}/\hbar \!=\! \omega _a \hat{a}^\dagger \hat{a} +\omega _b \hat{b}^\dagger \hat{b} +\omega _e |e\rangle \langle e| + \omega _g |g \rangle \langle g| -G \hat{a}^\dagger \hat{a} (\hat{b} +\hat{b}^\dagger ) +\Omega (\hat{a}^k |e\rangle \langle g| +\hat{a}^{\dagger k} |g\rangle \langle e|). \end{aligned}$$
(1)

where \(\omega _a\) (\(\omega _b\)) is the angular frequency of the light (movable mirror) mode, G is the cavity-mirror coupling coefficient, \(\Omega \) is the atom-photon coupling strength, and \(\hat{a}\) (\(\hat{b}\)) is the annihilation operator of the cavity (mechanical) mode. \(\hbar \omega _e\) and \(\hbar \omega _g\) denote the energies of the excited and ground states, respectively. The parameter k corresponds to the multi-photon processes.

Fig. 1
figure 1

Schematic representation of the system, illustrating the fixed and movable mirrors along with the enclosed atom within the cavity. The right mirror, connected to a spring, is movable and signifies the mechanical mode with angular frequency \(\omega _b\). Simultaneously, the cavity mode, characterized by angular frequency \(\omega _a\), interacts with the atom of the two-level states \(|e\rangle \) and \(|g\rangle \)

Full size image

We examine a high-finesse optical cavity system at near-zero temperature conditions. Given these circumstances, it is reasonable to exclude various dissipation mechanisms. Incorporating dissipation processes would require working with the density matrix and solving the Lindblad master equation, involving additional procedures. However, addressing these kind of interactions is beyond the scope of the current study.

The Hamiltonian can be decomposed into two parts

$$\begin{aligned} \hat{H}= \hat{H}_0 + \hat{H}_I, \end{aligned}$$
(2)

with

$$\begin{aligned} \hat{H}_0/\hbar = \omega _a \hat{a}^\dagger \hat{a} +\omega _b \hat{b}^\dagger \hat{b} +\omega _e |e\rangle \langle e|+\omega _g |g \rangle \langle g|, \qquad \hat{H}_I/\hbar = -G \hat{a}^\dagger \hat{a} (\hat{b} +\hat{b}^\dagger ) +\Omega (\hat{a}^k |e\rangle \langle g| +\hat{a}^{\dagger k} |g\rangle \langle e|). \end{aligned}$$
(3)

Calculating the interaction Hamiltonian yield

$$\begin{aligned} \hat{\mathcal {H}}/\hbar = e^{i \hat{H}_0 t /\hbar } \frac{\hat{H}_I}{\hbar } e^{-i \hat{H}_0 t/\hbar }= -G \hat{a}^\dagger \hat{a} ( \hat{b} e^{-i \omega _b t} +\hat{b}^\dagger e^{i \omega _b t}) + \Omega (\hat{a}^k e^{i \Delta _c t} |e\rangle \langle g| +\hat{a}^{\dagger k} e^{-i \Delta _c t} |g\rangle \langle e|), \end{aligned}$$
(4)

with \(\Delta _c = \omega _e-\omega _g -k \omega _a\). Now, we assume that the formula of the wave function is provided as

$$\begin{aligned} |\psi (t)\rangle = \sum _{n=0}^\infty \sum _{m=0}^\infty \biggl [ A_{n,m} |n, m, g\rangle +B_{n,m} |n, m, e\rangle \biggr ]. \end{aligned}$$
(5)

Here, \(A_{n,m}\) and \(B_{n,m}\) represent the amplitude probabilities of the ground and excited states, respectively. Applying the Schrödinger equation

$$\begin{aligned} \frac{\partial }{\partial t} |\psi (t) \rangle = -i \frac{\hat{\mathcal {H}}}{\hbar } |\psi (t) \rangle , \end{aligned}$$
(6)

yields the following two coupled differential equations

$$\begin{aligned} \dot{A}_{n,m} \!=\! -i \left[ \! - G e^{-i \omega _b t} \, n \sqrt{m\!+\!1} A_{n,m\!+\!1} \!-\! G e^{i \omega _b t} \, n \sqrt{m} A_{n,m-1} \!+\!\Omega e^{-i \Delta _c t}\sqrt{\frac{n!}{(n\!-\!k)!}} B_{n-k,m}\! \right] , \end{aligned}$$
(7)

and

$$\begin{aligned} \dot{B}_{n,m} \!=\!-i \left[ - G e^{-i \omega _b t} \, n \sqrt{m\!+\!1} B_{n,m+1} \!-\! G e^{i \omega _b t} \, n \sqrt{m} B_{n,m-1} \!+\!\Omega e^{i \Delta _c t}\sqrt{\frac{(n\!+\!k)!}{n !}} A_{n+k,m} \right] . \end{aligned}$$
(8)

These coupled differential equations, unfortunately, do not form a closed loop. Therefore, we need to solve them simultaneously through numerical methods. For our numerical approach, we utilize the Wolfram Mathematica software, employing the NDSolve command to obtain the results. In the simulation, the cutoff values for both n and m are chosen to be sufficiently large, and their determination depends on the selected values.

In our investigation, we assume the mechanical mode to be initially in the vacuum state throughout the study. The atom is initialized in a qubit state represented as

$$\begin{aligned} |\psi (0)\rangle _{atom} = \cos (\theta ) |g \rangle + \sin (\theta ) |e\rangle . \end{aligned}$$
(9)

Here, \(\theta \) denotes a phase that determines the specific superposition. The exact value of \(\theta \) will be specified later in the study. As for the cavity mode, we explore two options: Fock states (FS) \(|N \rangle \) and the coherent state (CS) \(|\alpha \rangle \). The value of N will be provided in the text, while \(\alpha \) is consistently set to \(\sqrt{2}\), corresponding to an average of two photons. The detuning \(\Delta _c \) is set to be zero. Therefore, the full initial state of the system is

$$\begin{aligned} |\psi (0) \rangle = \sum _{n=0}^\infty C_n \biggl [ \cos (\theta ) |g \rangle |0\rangle _m |n \rangle _c+ \sin (\theta ) |e\rangle |0\rangle _m |n \rangle _c \biggr ], \end{aligned}$$
(10)

where \(C_n\) represents the initial photonic amplitudes. Specifically, with CS, it is given by \(C_n = e^{-\frac{1}{2} |\alpha |^2} \frac{\alpha ^n}{n!} \), and with FS, it is given as \(C_n =\delta _{n,N}\), where \(\delta \) is the Kronecker delta. So at \( t = 0\) the initial condition of the amplitudes reads \(A_{n,0} (0) = C_n \cos (\theta )\), \(A_{n, m \ne 0} (0) = 0\), \(B_{n,0}(0) = C_n \sin (\theta )\) and \(B_{n, m \ne 0} (0) = 0\).

Fig. 2
figure 2

The average number of photons is indicated on the right (orange), and the average number of phonons is represented on the left (red). The cavity mode is set to FS with \(N = 0\), \(\theta = \pi /2\), and \(k = 1\). Subfigures (a) and (b) correspond to the weak limit with \(\Omega = G = 0.04 \omega _b\). Subfigures (c) and (d) depict the strong coupling limit with \(\Omega = G = 0.4 \omega _b\). Lastly, subfigures (e) and (f) are within the very strong regime with \(\Omega = G = 4 \omega _b\)

Full size image

Now, in the scenario where \(G = 0\), the system transforms into the Jaynes-Cummings Model (JCM), which is exactly solvable, and its general solution has been thoroughly discussed [37, 40]. Notably, the amplitudes exhibit oscillations with the Rabi angular frequency, represented by

$$\begin{aligned} V_n = \Omega \sqrt{4 (1+n) +\left( \frac{\Delta }{\Omega }\right) ^2}, \end{aligned}$$
(11)

where \(\Delta \) here is atom-field detuning. On the other hand, when \(\Omega = 0\), the system reduces to the Cavity Optomechanical System (COS), also exactly solvable as outlined in [38, 39]. Notably, in this configuration, the system demonstrates oscillations with an angular frequency of \(\omega _b\) for nearly all observables. The exploration of these two subsystems promises to provide valuable insights into our current problem.

2.1 The Parameters

In this section, we delve into the influence of the cavity-mirror coupling (G) and the atom-photon coupling (\(\Omega \)). We maintain the assumption that both parameters are equal, \(\Omega = G\) throughout the study, a commonly employed practice [25, 26, 28, 30]. To assess the impact of these parameters, we set \(k = 1\), \(\theta = \pi /2\). Additionally, we consider the cavity to be initially in a vacuum state, \(N = 0\), and the Hilbert space spans (250, 1) for the mechanical and cavity modes, respectively. It is essential to note that the Hilbert space for the cavity is restricted to \(|0\rangle \) and \(|1\rangle \) since, in this case, the atom can only produce one photon. In Fig. 2, we present plots illustrating the average number of photons and phonons for three distinct values of \(G = \Omega \), namely \(G/\omega _b = (4, 0.4, 0.04)\).

In the absence of an atom (COS model), the average number of photons remains constant, and the average number of phonons oscillates between vacuum and a maximum value, with an angular frequency of \(\omega _b\) detailed in [38]. When an atom is introduced, it alters the average number of photons in the optomechanical cavity, consequently influencing the behavior of the movable mirror. In the weak limit, \(\Omega = G \ll \omega _b\), as our value \(G/\omega _b = 0.04\), the growth of \(\langle \hat{n} \rangle \) is gradual compared to \(\omega _b\) since \(V_0\) from (11) is \(0.08 \omega _b\) in this case. As a result, in this scenario, \(\langle \hat{m} \rangle \) closely follows the behavior of the mean number of photons. However, it contributes a minimal number of phonons, as evident in Fig. 2 (a and b). Moreover, the photonic average is nearly identical to the prediction by JCM.

In the regime where \(\Omega = G\) closely approaches \(\omega _b/2\) (as exemplified by our selected value \(G/\omega _b = 0.4\)), the resulting Rabi angular frequency becomes comparable to \(\omega _b\), specifically yielding \(V_0 = 0.8 \omega _b\) for our value. At this limit, the COS and JCM subsystems exhibit nearly the same frequency, leading to mutual influence and causing \(\langle \hat{m} \rangle \) to display chaotic behavior with numerous rapid oscillations. The photonic oscillations undergo modification, deviating from the predictions of JCM. Although the general structure of \(\langle \hat{n} \rangle \) nearly maintains its characteristic sinusoidal oscillations, it modifies the amplitude of the oscillations, ranging from 0 to approximately 0.95, and it is aperiodic as can be seen in Fig. 2 (c and d).

In the very strong regime where \(\Omega = G \gg \omega _b/2\), exemplified by \(G/\omega _b = 4\), the Rabi angular frequency significantly surpasses \(\omega _b\), reaching \(V_0 = 8 \omega _b\) in our case. In this setting, the behavior of the movable mirror becomes more regular than in the previous case. Due to the fast changes in the average number of photons, the mirror ceases to discern small fluctuation details and begins to perceive the time-averaged behavior. This results in less chaotic behavior in the average number of phonons, characterized by fewer rapid oscillations. Notably, the photonic average no longer tends to zero, and its width experiences a substantial contraction. However, the introduced number of phonons is now enhanced as evident in Fig. 2 (e and f).

From this discussion, we observe that the general behavior of the system is primarily determined by \(V_n\) and \(\omega _b\) when \(G = \Omega \). Therefore, we choose the intermediate limit where the oscillations of the mechanical mode can exhibit more chaotic behavior. Specifically, we set \(\Omega = G = 0.5 \omega _b\), corresponding to \(V_0 = \omega _b\). Other values will be considered in the nonclassical properties section. In the following, we will investigate six cases as outlined in Table 1.

Table 1 The table displays the cases that will be investigated in this study along with their corresponding values
Full size table

3 Statistical Properties

3.1 The Position of The Movable Mirror

The dynamics of the position of the movable mirror can be determined by evaluating the expectation value of the operator

$$\begin{aligned} \hat{X} =\frac{\hat{b} +\hat{b}^\dagger }{2}. \end{aligned}$$
(12)

The average of the annihilation and creation operators of the mechanical mode, obtained from (5), is given by

$$\begin{aligned} \langle \hat{b} \rangle = \sum _{n=0}^\infty \sum _{m=0}^\infty \sqrt{m+1} \biggl [ A^*_{n,m} A_{n,m+1} +B^*_{n,m} B_{n,m+1} \biggr ], \end{aligned}$$
(13)

and \(\langle \hat{b}^\dagger \rangle = \langle \hat{b} \rangle ^*\). The average value of \(\hat{X}\), denoted as \(X_M = \langle \hat{X} \rangle \), is then computed for the six cases specified in Table 1 and illustrated in Fig. 3.

In the absence of the atom (COS model), the behavior of \(X_M\) is sinusoidal with an angular frequency of \(\omega _b\), directly proportional to the average number of photons [38]. This characteristic remains unchanged regardless of the input cavity state as long as \(\langle \hat{n} \rangle \) is held constant. However, in our present study, where \(\langle \hat{n} \rangle \) is fixed at 2 for cases (c, d, e, and f), distinct patterns emerge. Broadly, rapid oscillations in all cases are nearly equivalent to \(\omega _b\), accompanied by additional, slower oscillations evident in all cases. Interestingly, \(X_M\) demonstrates a discernible signature for different input cavity states, even when some atomic parameters are altered, as observed in cases (a and b), (c and d), and (e and f), where they share the same input state but differ in values of k or \(\theta \). There is also evident sensitivity to these parameters (\(\theta \) and k), as seen in the same cases, resulting in varying amplitudes due to alterations in one of these atomic parameters.

Fig. 3
figure 3

The position of the movable mirror \(X_M\), plotted against \(\omega _b t\) for the six cases outlined in Table 1. The abbreviation of each case is provided under its respective subfigure

Full size image

3.2 The Atomic Inversion

The population inversion of the atomic system, represented by the difference in population between the excited and ground states, provides insights into the dynamic nature of the atom. In our system, it can be calculated by

$$\begin{aligned} W = \sum _{n=0}^\infty \sum _{m=0}^\infty \biggl [ |B_{n,m}|^2 -|A_{n,m}|^2 \biggr ]. \end{aligned}$$
(14)

In Fig. 4, we present the W for the six selected cases outlined in Table 1. In the JCM, the CS interacting with a two-level atom typically exhibits a collapse and revival pattern [37]. However, this distinctive behavior is not observed in our results, particularly in cases (e) and (f), where W shows a more chaotic pattern. Conversely, when the system interacts with a Fock state (FS), it generates larger amplitude oscillations. In the absence of a movable mirror (JCM scenario), the interaction of the atom with an FS results in sinusoidal vibrations. However, in our case with a movable mirror, we observe that the atom also exhibits chaotic behavior. The amplitude, overall, appears to be influenced more by the initial state introduced into the system than by other parameters.

Fig. 4
figure 4

The atomic population inversion W versus \(\omega _b t\) for the six cases described in Table 1. The abbreviation of each case is provided under its respective subfigure

Full size image

4 Nonclassical Properties

4.1 Linear Entropy

Entanglement stands out as a crucial resource in quantum information and quantum computation [41]. The assessment of entanglement dynamics between the atom and the subsystem, encompassing the cavity mode and the mechanical mode, can be quantified using linear entropy. A higher (lower) entropy signifies a greater (smaller) degree of entanglement. This quantity is formally defined as

$$\begin{aligned} S_A= 1- \text {Tr} \hat{\rho }_A^2, \end{aligned}$$
(15)

where \(\hat{\rho }_A\) is atomic reduced density matrix, and it can be obtained as

$$\begin{aligned} \hat{\rho }_A = \text {Tr}_{Field + Mirror} \hat{\rho } = \begin{pmatrix} \rho _{gg} &{} \rho _{ge} \\ \rho _{eg} &{} \rho _{ee} \end{pmatrix}, \end{aligned}$$
(16)

with

$$\begin{aligned} \rho _{gg}= & {} \sum _{n=0}^\infty \sum _{m=0}^\infty |A_{n,m}|^2, \qquad \qquad \qquad \qquad \rho _{ee} = \sum _{n=0}^\infty \sum _{m=0}^\infty |B_{n,m}|^2 \end{aligned}$$
(17)
$$\begin{aligned} \rho _{ge}= & {} \sum _{n=0}^\infty \sum _{m=0}^\infty A_{n,m} B^*_{n,m}, \qquad \qquad \qquad \qquad \rho _{eg} = \sum _{n=0}^\infty \sum _{m=0}^\infty A^*_{n,m} B_{n,m}. \end{aligned}$$
(18)

And consequently the linear entropy becomes

$$\begin{aligned} S_A = 1- \rho _{gg}^2 -\rho _{ee}^2 - 2 \rho _{eg} \rho _{ge}. \end{aligned}$$
(19)
Fig. 5
figure 5

The linear entropy \(S_A\) versus \(\omega _b t\) for the six cases described in Table 1. The abbreviation of each case is provided under its respective subfigure

Full size image

In Fig. 5, the linear entropy for the six previously mentioned cases is presented. Generally, the system exhibits values ranging from 0 to 0.5 for all cases, characterized by numerous fluctuations. All cases start from zero, and after a delay time, they attain their maximum values. The delay time is much shorter with Fock states (FS) in cases (a, b, c, and d), on the order of \(\omega _b t \approx 1\), while with CS of cases (e and f), it takes much longer, approximately \(\omega _b t \approx 5\). This delay is possibly due to the fact that CS introduces multiple atomic frequencies \(V_n\), as described in (11).

Interestingly, starting from an atomic superposition state, as observed in cases (d and f), provides entanglement within a narrower band compared to starting from the excited state. For instance, in case (e), the width of the data after reaching its peak is approximately \(0.15-0.2\), whereas in the case of the superposition (f), it narrows down to \(0.1-0.14\). The most frequent case to reach the highest values is case (c), involving FS with \(N = 2\). This frequent occurrence is suppressed when \(\theta = \pi /4\) in case (d). The effect of multi-photon processing parameter k does not seem to inhibit this frequent occurrence of reaching the highest peaks, as shown in cases (a and b).

4.2 Q Mandel Parameter

Determining whether the quantum distribution is Poissonian or sub(super)-Poissonian provides crucial insights into the nonclassicality status of the state under consideration. One of the most effective measures for this task is the Q Mandel parameter, defined as [42].

$$\begin{aligned} Q_M = \frac{ \langle \hat{m}^2 \rangle -\langle \hat{m} \rangle ^2}{\langle \hat{m} \rangle } -1, \end{aligned}$$
(20)

where \(\hat{m}\) is the number operator of the mechanical mode, and the two averages are given as

$$\begin{aligned} \langle \hat{m} \rangle = \sum _{n=0}^\infty \sum _{m=0}^\infty m \biggl [ |A_{n,m}|^2 +|B_{n,m}|^2 \biggr ], \end{aligned}$$
(21)

and

$$\begin{aligned} \langle \hat{m}^2 \rangle = \sum _{n=0}^\infty \sum _{m=0}^\infty m^2 \biggl [ |A_{n,m}|^2 +|B_{n,m}|^2 \biggr ]. \end{aligned}$$
(22)

If the parameter \(Q_M\) is greater (less) than zero, the state is super (sub)-Poissonian. A state is considered nonclassical if it demonstrates \(Q_M < 0\).

Fig. 6
figure 6

The Q Mandel parameter \(Q_M\) of the mechanical mode plotted against \(\omega _b t\) for the six cases outlined in Table 1. The abbreviation of each case is provided under its respective subfigure

Full size image

The Q Mandel parameter for the mechanical mode is illustrated for the six cases detailed in Table 1. In the COS model, \(Q_M\) cannot be negative for any input photonic state within our protocol when the mechanical mode is initially set in vacuum, as in our case [38]. However, notably, in this model, it can exhibit negative values, as evident in cases (a, b, and c) of Fig. 6, where \(Q_M\) dips below zero in various regions. Case (a), in particular, consistently displays strong negative values, indicating the induction of nonclassicality by the atom in the system. Conversely, when the inserted state is a coherent state (cases e and f), there is no evidence of sub-Poissonian behavior; instead, it exhibits robust super-Poissonian characteristics with relatively oscillatory behavior in a repetitive manner. In scenarios involving two photons (cases c and d), the oscillations are more pronounced, less regular, and generally smaller in magnitude compared to the coherent states. Notably, case (c) even demonstrates intervals where the parameter becomes negative (Fig. 6).

Case (a) exhibits nonclassicality because, in this instance, \(V_n = \omega _b\) and \(\Omega = G = 0.5\), resulting in strong interaction in this regime for both models. If we allow the value of \(\Omega \) to be changed while maintaining \(\Omega = G\) and \(V_n = \omega _b\), other states may exhibit sub-Poissonian distribution. To explore this, we insert different Fock states, and from (11), we find

$$\begin{aligned} G = \Omega = \frac{V_n}{2\sqrt{1+n}} =\frac{\omega _b}{2\sqrt{1+n}}. \end{aligned}$$
(23)

We now introduce four additional cases detailed in Table 2.

Table 2 The table presents the cases to be investigated for the mechanical Q Mandel parameter, along with their corresponding values
Full size table

In Fig. 7, the cases outlined in Table 2 are presented, and it is evident that all cases induce sub-Poissonian statistics with distinctive patterns and amplitudes. An interesting observation is that as the number of photons increases, the number of negative regions and their duration decrease. Additionally, the average of the data consistently deviates from zero, becoming larger than zero, as the value of N for FS increases. The negativity of \(Q_M\) in these cases emphasizes the effectiveness of the proposed method for detecting nonclassicality by examining the frequencies of the sub-models (COS model and JCM).

Fig. 7
figure 7

The Q Mandel parameter \(Q_M\) for the mechanical mode is plotted against \(\omega _b t\) for the four cases outlined in Table 2. The abbreviation of each case corresponds to the notation in Table 2

Full size image

4.3 Squeezing

One crucial nonclassical characteristic is squeezing, where a state is said to be squeezed when the fluctuations in one of its quadratures (either position or momentum) are smaller than the minimum value prescribed by the uncertainty principle. A way to quantify this phenomenon is through the linear squeezing parameter for the mechanical mode, which is defined as [43, 44]

$$\begin{aligned} S_M = e^{-2 i \phi } \langle \hat{b}^2 \rangle + e^{2 i \phi } \langle \hat{b}^{\dagger 2} \rangle + 2 \langle \hat{b}^\dagger \hat{b} \rangle - \left( e^{- i \phi } \langle \hat{b} \rangle + e^{ i \phi } \langle \hat{b}^\dagger \rangle \right) ^2, \end{aligned}$$
(24)

where \( \langle \hat{b}^\dagger \hat{b} \rangle \) is \(\langle \hat{m} \rangle \) and can be calculated from (21). The value of \(\langle \hat{b} \rangle \) can be determined from (13), while \(\langle \hat{b}^2 \rangle \) is given by

$$\begin{aligned} \langle \hat{b}^2 \rangle = \sum _{n=0}^\infty \sum _{m=0}^\infty \sqrt{m+2} \sqrt{m+1}\biggl [ A^*_{n,m} A_{n,m+2} + B^*_{n, m} B_{n,m+2}\biggr ], \end{aligned}$$
(25)

with \(\langle \hat{b}^{\dagger 2} \rangle = \langle \hat{b}^2 \rangle \). If \(S_M\) is less than zero, it indicates that the state exhibits squeezing.

In Fig. 8, the linear squeezing parameter for the mechanical mode, \(S_M\), is plotted for the six cases with \(\phi = 0\). In the absence of an atom (COS model), this particular protocol, as discussed in [38], cannot induce mechanical squeezing. However, the presence of an atom in this model does induce squeezing, as evident in the case of FS with two photons in subfigure c, where a region between \(\omega _b t \approx 40 - 60\) becomes negative, indicating squeezing. On the other hand, interactions with the vacuum or with CS do not seem to induce squeezing, as seen in cases (a, b, e, and f). However, with CS, there is some evidence of the collapse and revival phenomenon between the periods \(50-80\) in both cases (e and f). Small negative values can also be observed with the interaction with the vacuum, as in case (a).

Fig. 8
figure 8

The linear squeeing parameter \(S_M\) of the mechanical mode versus \(\omega _b t\) for the six cases outlined in Table 1. The abbreviation of each case is provided under its respective subfigure

Full size image

As we extended our search for nonclassicality with the Q Mandel parameter by varying the value of \(G =\Omega \), we apply the same technique here. Case (c) exhibits strong squeezing, and we wish to explore the possibility of obtaining additional cases by fixing the frequencies of the two sub-models. The mechanical mode has a main frequency equal to \(\omega _b\), while the main frequency of the cavity mode for the two-photon case can be obtained from (11), yielding \(V_2 = 1.732 \omega _b\). Allowing G and \(\Omega \) to vary while keeping them equal and the two frequencies invariant yields

$$\begin{aligned} G = \Omega = \frac{V_n}{2\sqrt{1+n}} = \frac{1.732\omega _b}{2\sqrt{1+n}}. \end{aligned}$$
(26)

This may lead us to discover other Fock states capable of producing squeezing. Four new cases are detailed in Table 3.

Table 3 The table presents the cases to be investigated for the linear squeezing, along with their corresponding values
Full size table
Fig. 9
figure 9

The linear squeezing parameter \(S_M\) versus \(\omega _b t\) for the four cases outlined in Table 3. The abbreviation of each case corresponds to the notation in Table 3

Full size image

In Fig. 9, the cases mentioned in Table 3 are plotted, and it is apparent that all cases induce squeezing with similar behavior. The first squeezed region occurs between \(\omega _b t \approx 5\) and 20 and exhibits two dips. Subsequently, a second region occurs at different positions depending on the value of N for FS. Generally, the starting point of the second squeezed period increases with an increase in N, along with an extended duration of this squeezing. Additionally, we observe a general similarity in all behaviors, as if there is an overarching mechanism driving the system. The case with the deepest squeezing is (d) with \(N = 6\), and the lowest point is approximately at \((123, -0.494)\). This illustrates the effectiveness of the searching method, considering the frequencies of the two sub-models, in identifying squeezing.

5 Conclusion

In this study, we explored a regime where the coupling strengths between the cavity-mirror and atom-photon interactions are approximately equal to the angular frequency of the mechanical mode. Employing numerical solutions, we investigated the system dynamics with two distinct input photonic states: coherent state and Fock state. Our analysis incorporated the multi-photon processes parameter and a generic two-level qubit atom. The examination of the movable mirror’s position revealed a consistently similar behavior for the same input state, even when certain atomic parameters were varied. We further delved into the atomic inversion, discovering that the amplitudes were heavily dependent on the initial cavity state. A comprehensive analysis of the linear entropy highlighted the entanglement patterns within each state. Additionally, we scrutinized the Q Mandel parameter, unveiling the largest sub-Poissonian distribution when interacting with a vacuum state. The study of squeezing phenomena demonstrated intriguing results, particularly with two photons leading to the identification of two distinct squeezed periods in the system.

The proposed search method proved effective in identifying nonclassical features within the system. The protocol of the method unfolds as follows: Initially, we scrutinize the two sub-models (COS model and JCM) and compare their respective frequencies. Subsequently, we focus on a specific nonclassical feature, such as squeezing, identifying a case where the system exhibits this characteristic. Following this, we broaden our search for other nonclassical possibilities by adjusting both G and \(\Omega \) while preserving the exact values of the two frequencies of the sub-models. This approach enhances the likelihood of discovering additional nonclassical features. The effectiveness of this method was demonstrated with the Q Mandel parameter and squeezing, particularly when applied to Fock states. Consequently, this approach holds potential for optimization and exploration studies aimed at uncovering emergent behaviors or identifying various nonclassical phenomena.

Ultimately, this study opens avenues for further exploration in several directions. Future extensions may involve incorporating the effects of decoherence and pumping mechanisms, providing insights into the search method’s performance under such circumstances. Investigating the impact of unbalanced couplings, namely \(\Omega \) and G, and exploring their emergent behavior presents another intriguing avenue. Examining the influence of alternative input mechanical states beyond vacuum or cavity states could offer valuable insights. Additionally, introducing post-measurements to the system may reveal potential shifts in behavior, enhancing the comprehensiveness of the system.